Altered Grey Wolf Optimization and Taguchi Method with FEA for Six-Phase Copper Squirrel Cage Rotor Induction Motor Design
Abstract
:1. Introduction
2. Initial Specification and Configuration of SCSCRIM
3. High-Performance Design of SCSCRIM with Multi-Objective Optimization Method
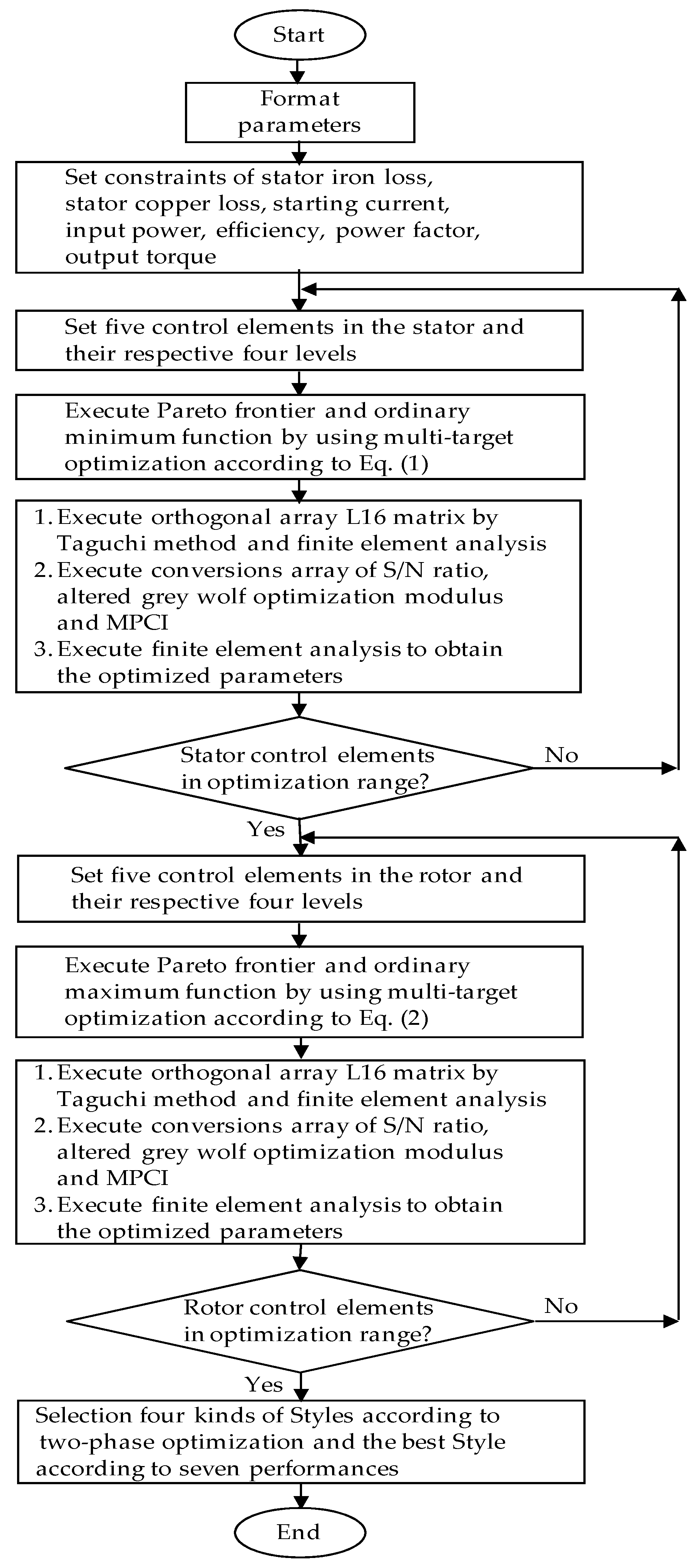
4. Programs of High-Performance Design
4.1. The First-Phase Program
4.2. The Second-Phase Program
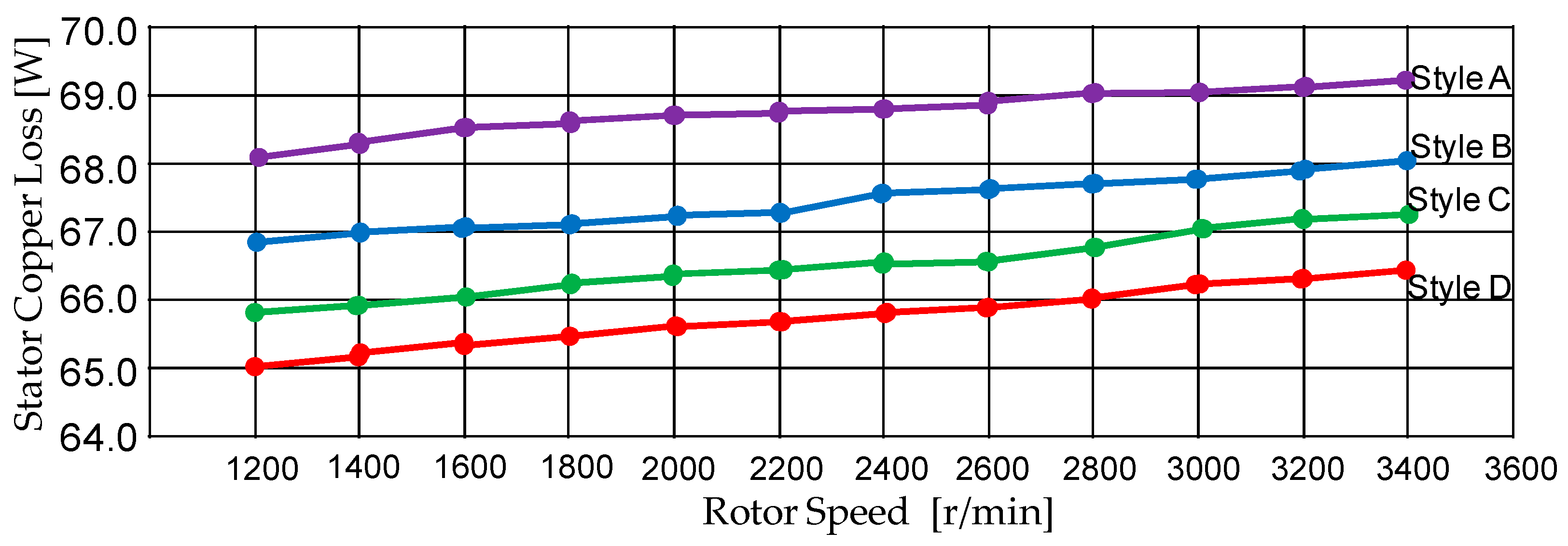
5. Performance Tests
6. Results and Discussion
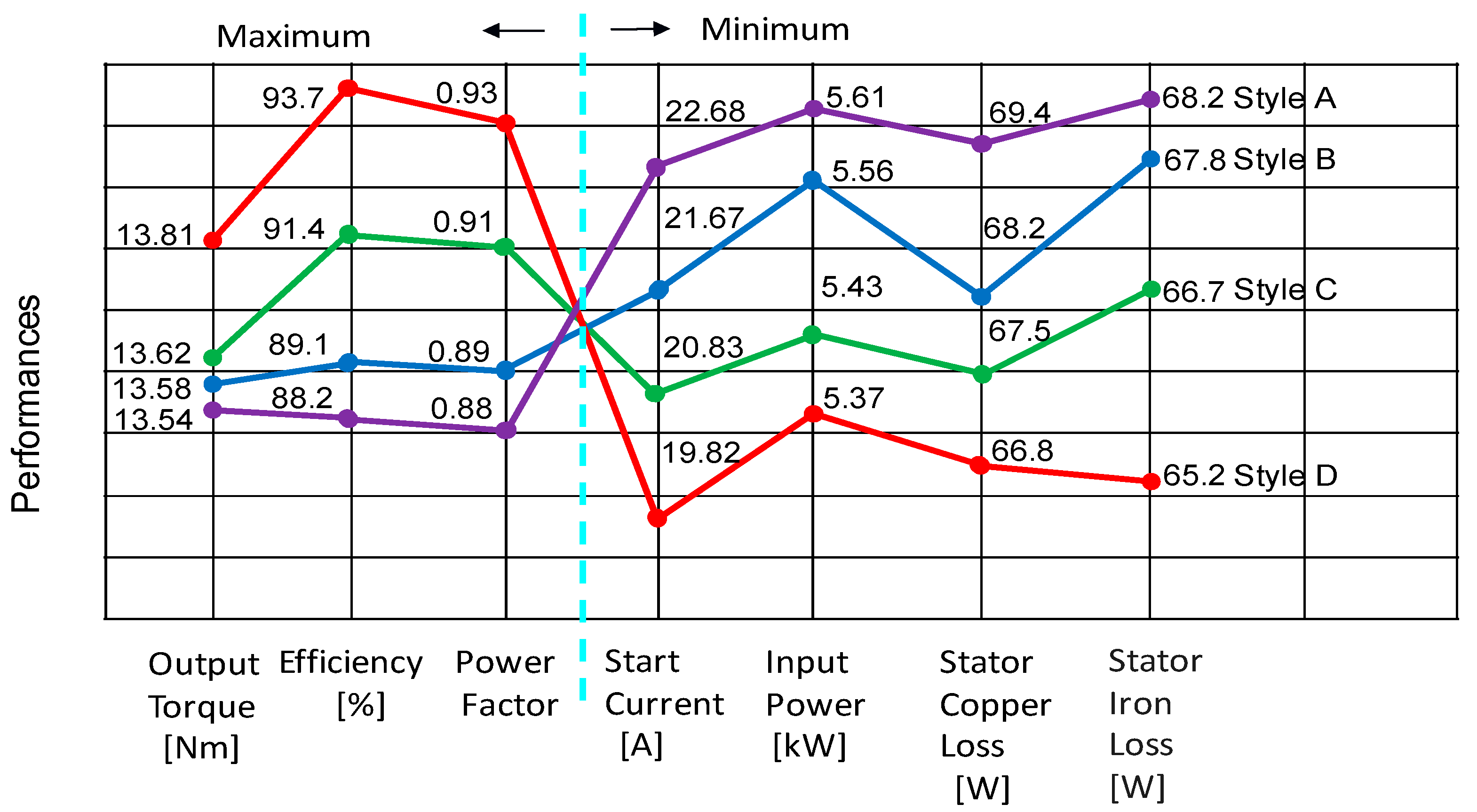
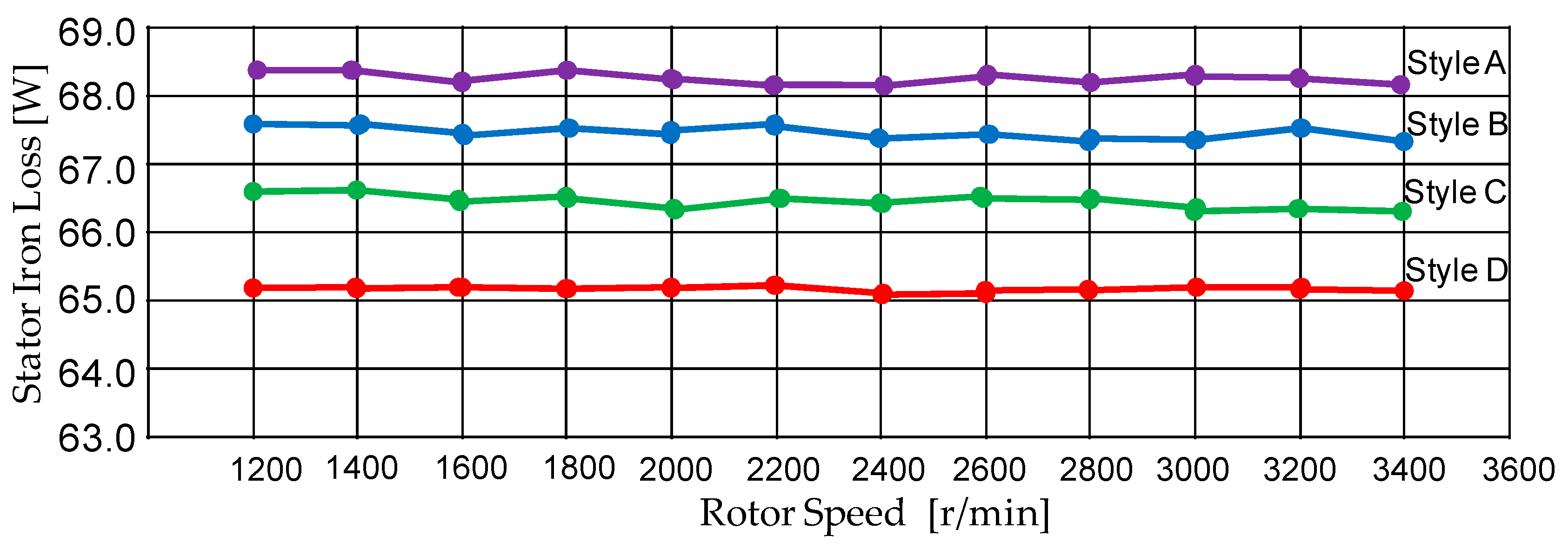
- The stator iron loss is cut down to 65.2 W in Style D.
- The stator copper loss is cut down to 66.8 W in Style D.
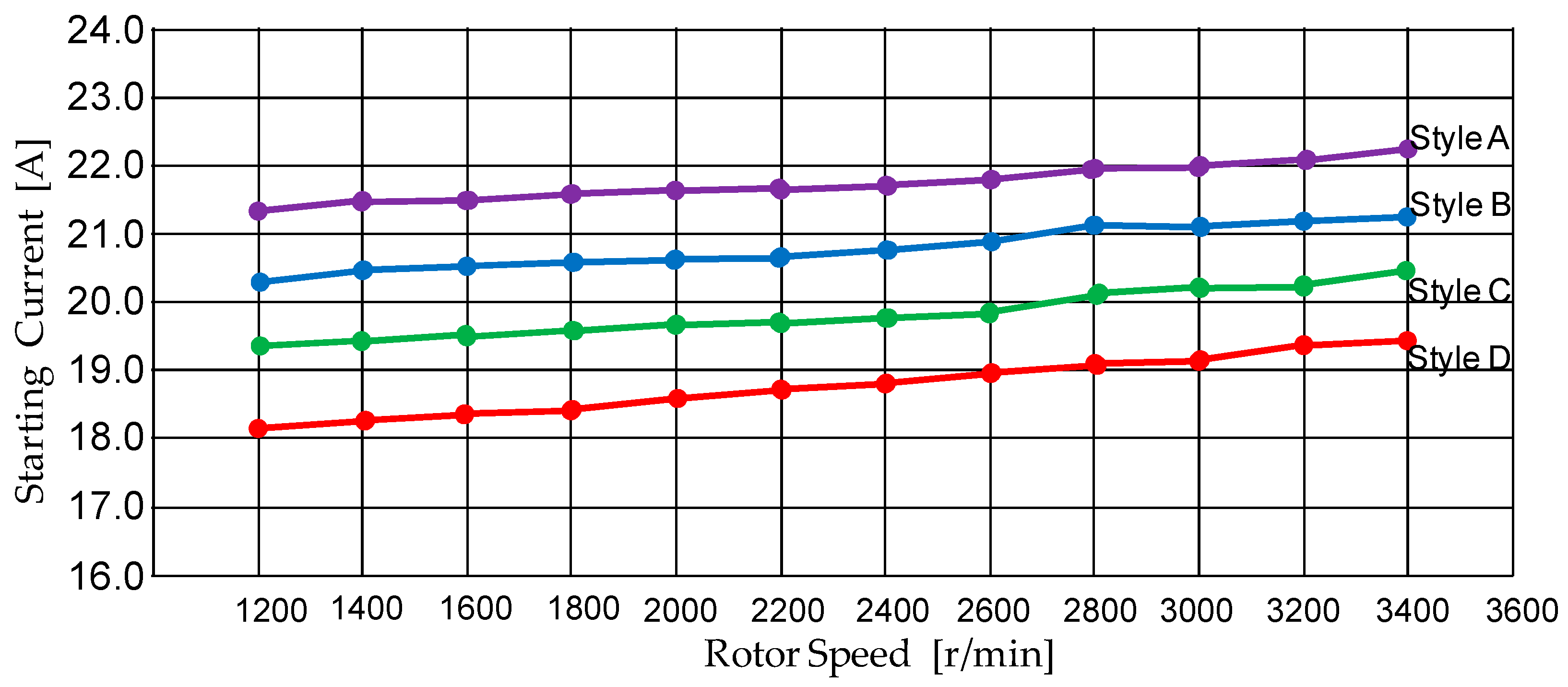
- The starting current is cut down to 19.82 A in Style D.
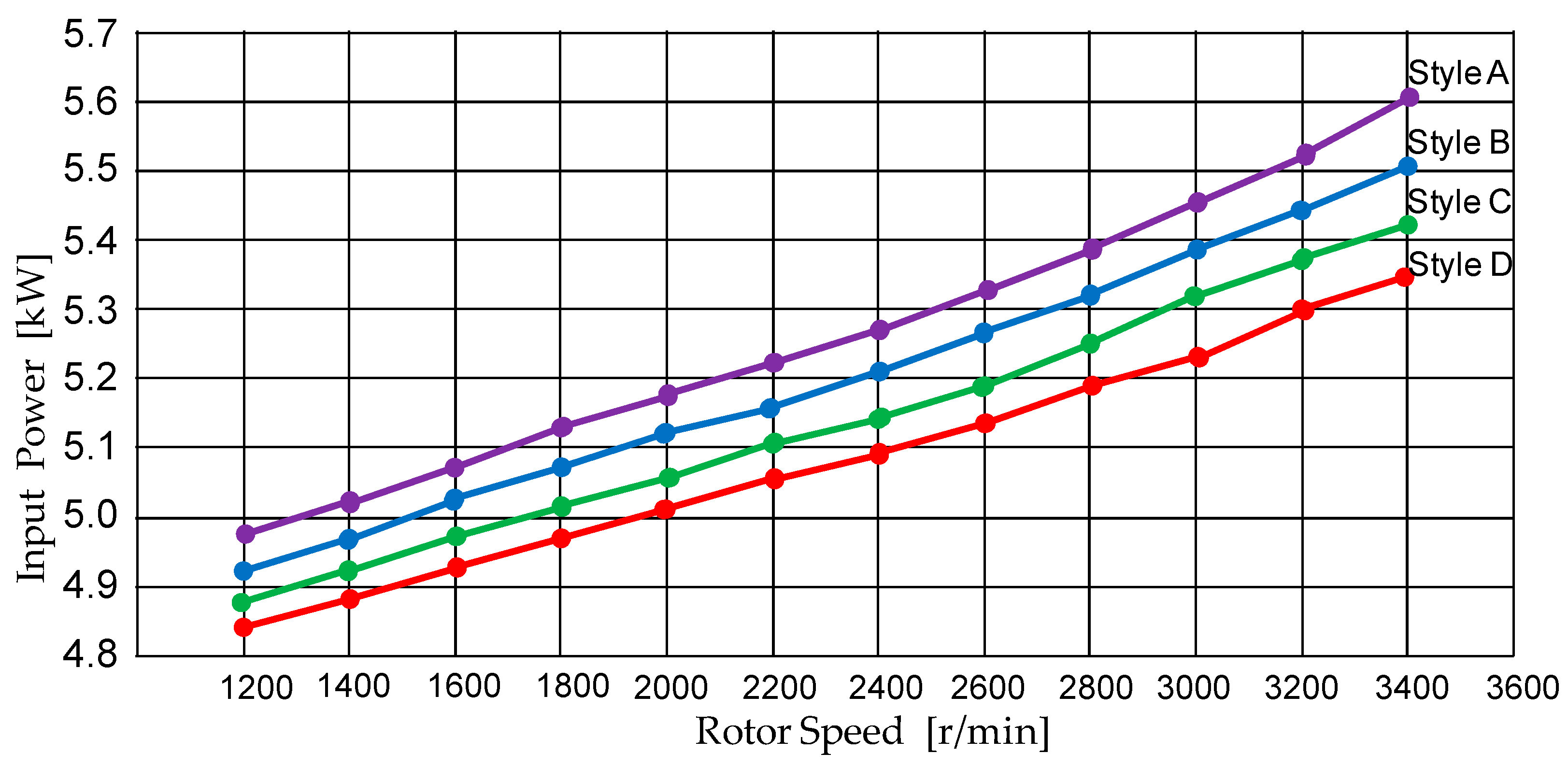
- The input power is cut down to 5.37 kW in Style D.
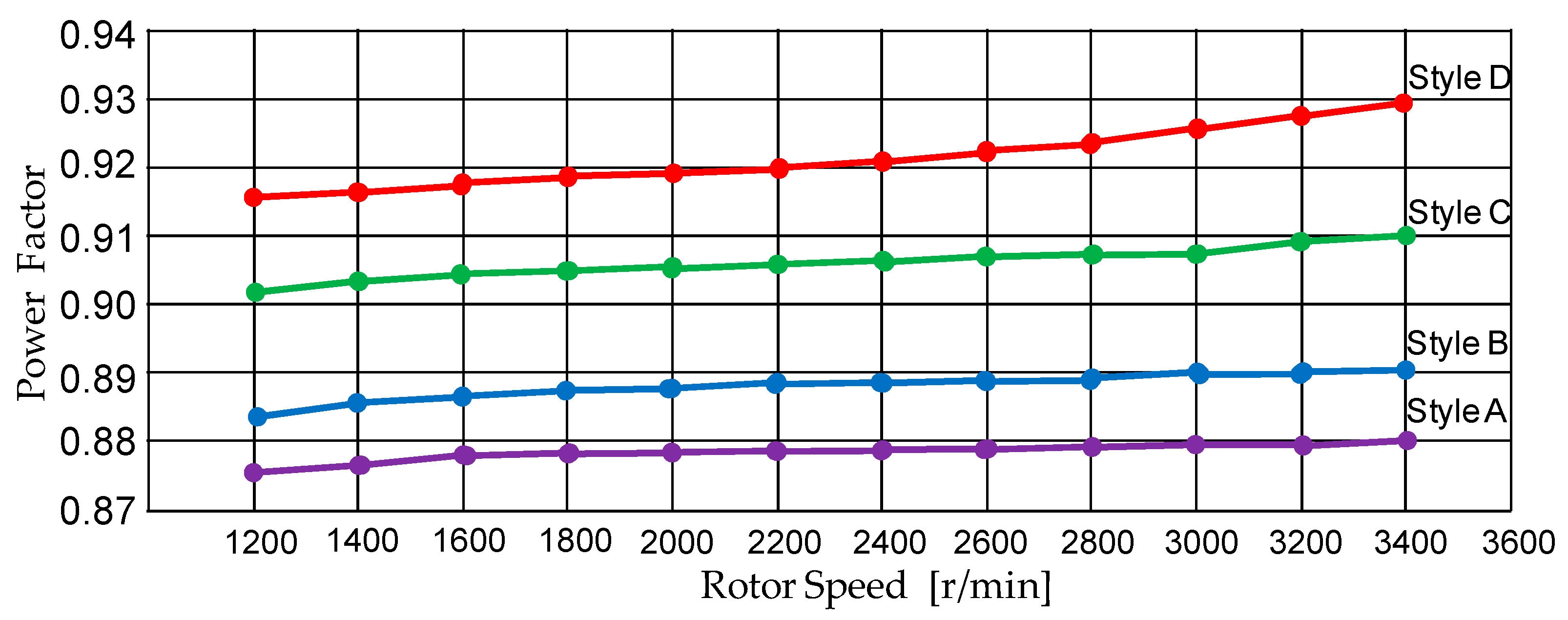
- The power factor is increased to 0.93 in Style D.
- The efficiency is increased to 93.7% in Style D.
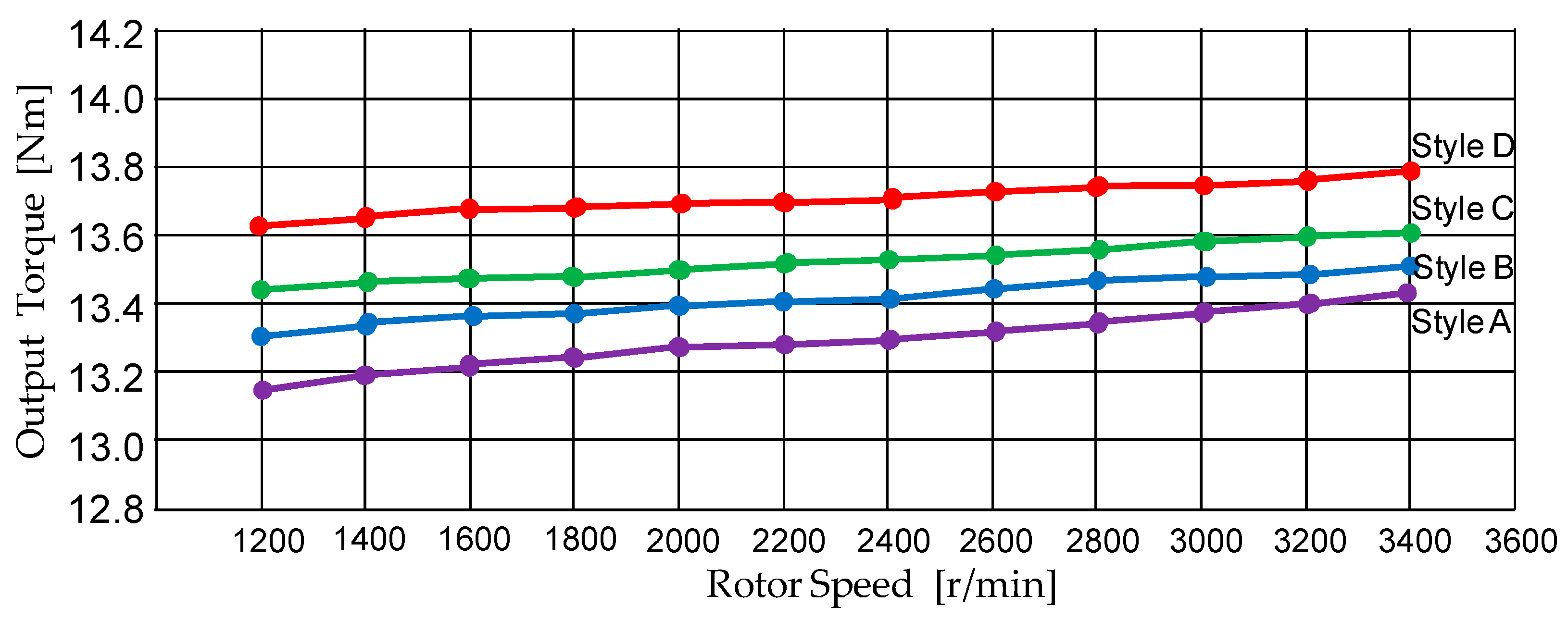
- The output torque is increased to 13.81 Nm in Style D.
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nanoty, A.; Chudasama, A.R. Design and control of multiphase induction motor. In Proceedings of the IEEE International Electric Machines and Drives Conference, Niagara Falls, ON, Canada, 15–18 May 2011; pp. 354–358. [Google Scholar]
- Lin, C.H.; Hwang, C.C. Multiobjective optimization design for a six-phase copper rotor induction motor mounted with a scroll compressor. IEEE Trans. Magn. 2016, 52, 9401604. [Google Scholar] [CrossRef]
- Lin, C.H.; Hwang, C.C. Multi-objective optimization design using amended particle swarm optimization and Taguchi method for a six-phase copper rotor induction motor. Eng. Optim. 2017, 49, 693–708. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, J.; Wang, X.; Wang, Q.; Liu, X.; Luo, Y. A design method for cage induction motors with non-skewed rotor bars. IEEE Trans. Magn. 2014, 50, 769–772. [Google Scholar]
- Cunkas, M.; Akkaya, R. Design optimization of induction motor by genetic algorithm and comparison with existing motor. Math. Comput. Appl. 2006, 11, 193–203. [Google Scholar]
- Sun, Y.; Tang, J.; Shi, K. Design of a bearingless outer rotor induction motor. Energies 2017, 10, 705. [Google Scholar]
- Parasiliti, F.; Villani, M. Design of high efficiency induction motors with die-casting copper rotors. In Energy Efficiency in Motor Driven Systems; Springer: Berlin/Heidelberg, Germany, 2003; pp. 144–151. ISBN 3-540-00666-4. [Google Scholar]
- Daut, I.; Anayet, K.; Fauzi, A. Development of copper rotor of AC induction motor. Aust. J. Basic Appl. Sci. 2010, 4, 5941–5946. [Google Scholar]
- Kane, M. Design of copper rotor induction motor for mild-hybrid electric vehicle. In Proceedings of the IEEE International Transportation Electrification Conference, Chennai, India, 27–29 August 2015; pp. 1–6. [Google Scholar]
- Zhang, Q.; Liu, H.; Zhang, Z.; Song, T. A cast copper rotor induction motor for small commercial EV traction: Electromagnetic design, analysis, and template tests. CES Trans. Electr. Mach. Syst. 2018, 2, 417–424. [Google Scholar] [CrossRef]
- Mittelstedt, M.; Hansen, C.; Mertiny, P. Design and multi-objective optimization of fiber-reinforced polymer composite flywheel rotors. Appl. Sci. 2018, 8, 1256. [Google Scholar] [CrossRef] [Green Version]
- Anwar, N.; Deng, H. A hybrid metaheuristic for multi-objective scientific workflow scheduling in a cloud environment. Appl. Sci. 2018, 8, 538. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Wang, X.; Chen, J. Wind power forecasting using multi-objective evolutionary algorithms for wavelet neural network-optimized prediction intervals. Appl. Sci. 2018, 8, 185. [Google Scholar] [CrossRef] [Green Version]
- Mathur, V.K. How well do we know Pareto optimality. J. Econ. Educ. 1991, 22, 172–178. [Google Scholar] [CrossRef]
- Kanbur, R. Pareto’s revenge. J. Soc. Econ. Dev. 2005, 7, 1–11. [Google Scholar]
- Barr, N. The Relevance of Efficiency to Different Theories of Society, Economics of the Welfare State, 5th ed.; Oxford University Press: Oxford, UK, 2012; pp. 46–51. ISBN 978-0-19-929781-8. [Google Scholar]
- Yamazaki, K.; Suzuki, A.; Ohto, M.; Takakura, T.; Nakagawa, S. Equivalent circuit modeling of induction motors considering stray load loss and harmonic torques using finite element method. IEEE TRANS. MAGN. 2011, 47, 986–989. [Google Scholar] [CrossRef]
- Ahn, J.; Lee, D.; Park, G.J.; Kim, Y.J.; Kim, J.; Jung, S.Y. Numerical design compatibility of induction motor with respect to voltage and current sources. IEEE TRANS. MAGN. 2014, 50, 773–776. [Google Scholar] [CrossRef]
- Emary, E.; Yamany, W.; Hassanien, A.E.; Snasel, V. Multi-objective gray-wolf optimization for attribute reduction. Procedia Comput. Sci. 2015, 65, 623–632. [Google Scholar] [CrossRef] [Green Version]
- Mosavi, M.; Khishe, M.; Ghamgosar, A. Classification of sonar data set using neural network trained by gray wolf optimization. Neural Netw. World 2016, 26, 393–415. [Google Scholar] [CrossRef] [Green Version]
- Parsian, A.; Ramezani, M.; Ghadimi, N. A hybrid neural network-gray wolf optimization algorithm for melanoma detection. Biomed. Res. 2017, 28, 3408–3411. [Google Scholar]
- Sanchez, D.; Melin, P.; Castillo, O. A grey wolf optimizer for modular granular neural networks for human recognition. Comput. Intell. Neurosci. 2017, 8, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Khandelwal, A.; Bhargava, A.; Sharma, A.; Sharma, H. Modified grey wolf optimization algorithm for transmission network expansion planning problem. Arab. J. Sci. Eng. 2018, 43, 2899–2908. [Google Scholar] [CrossRef]
- Hwang, C.C.; Chang, C.M.; Liu, C.T. A fuzzy-based Taguchi method for multiobjective design of PM motors. IEEE TRANS. MAGN. 2013, 49, 2153–2156. [Google Scholar] [CrossRef]
- Lin, C.H.; Hwang, C.C. High performances design of a six-phase synchronous reluctance motor using multi-objective optimization with altered bee colony optimization and Taguchi method. Energies 2018, 11, 2716. [Google Scholar] [CrossRef] [Green Version]
- Kahhal, P.; Brooghani, S.Y.A.; Azodi, H.D. Multi-objective optimization of sheet metal forming die using FEA coupled with RSM. J. Mech. Sci. Technol. 2013, 27, 3835–3842. [Google Scholar] [CrossRef]
- Moghaddami, M.; Anzalchi, A.; Moghsdasi, A.; Sarwat, A. Pareto optimization of circular power pads for contactless electric vehicle battery charger. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Portland, OR, USA, 2–6 October 2016; pp. 1–6. [Google Scholar]
- Faiz, J.; Sharifian, M.B.B. Optimal design of three phase induction motors and their comparison with a typical industrial motor. Comput. Electr. Eng. 2001, 27, 133–144. [Google Scholar] [CrossRef]
- Faiz, J.; Sharifian, M.B.B.; Keyhani, A.; Proca, A. Performance comparison of optimally designed induction motors with aluminum and copper squirrel-cages. Electr. Mach. Power Syst. 2000, 28, 1195–1207. [Google Scholar]
- Fei, R.; Fuchs, E.F.; Huang, H. Comparison of two optimization techniques as applied to three-phase induction motor design. IEEE Trans. Energy Convers. 1989, 4, 651–660. [Google Scholar] [CrossRef]
- Lin, C.H. Backstepping control and revamped recurrent fuzzy neural network with mended ant colony optimization applied in SCRIM drive system. J. Intell. Fuzzy Syst. 2019, 36, 3447–3459. [Google Scholar] [CrossRef]




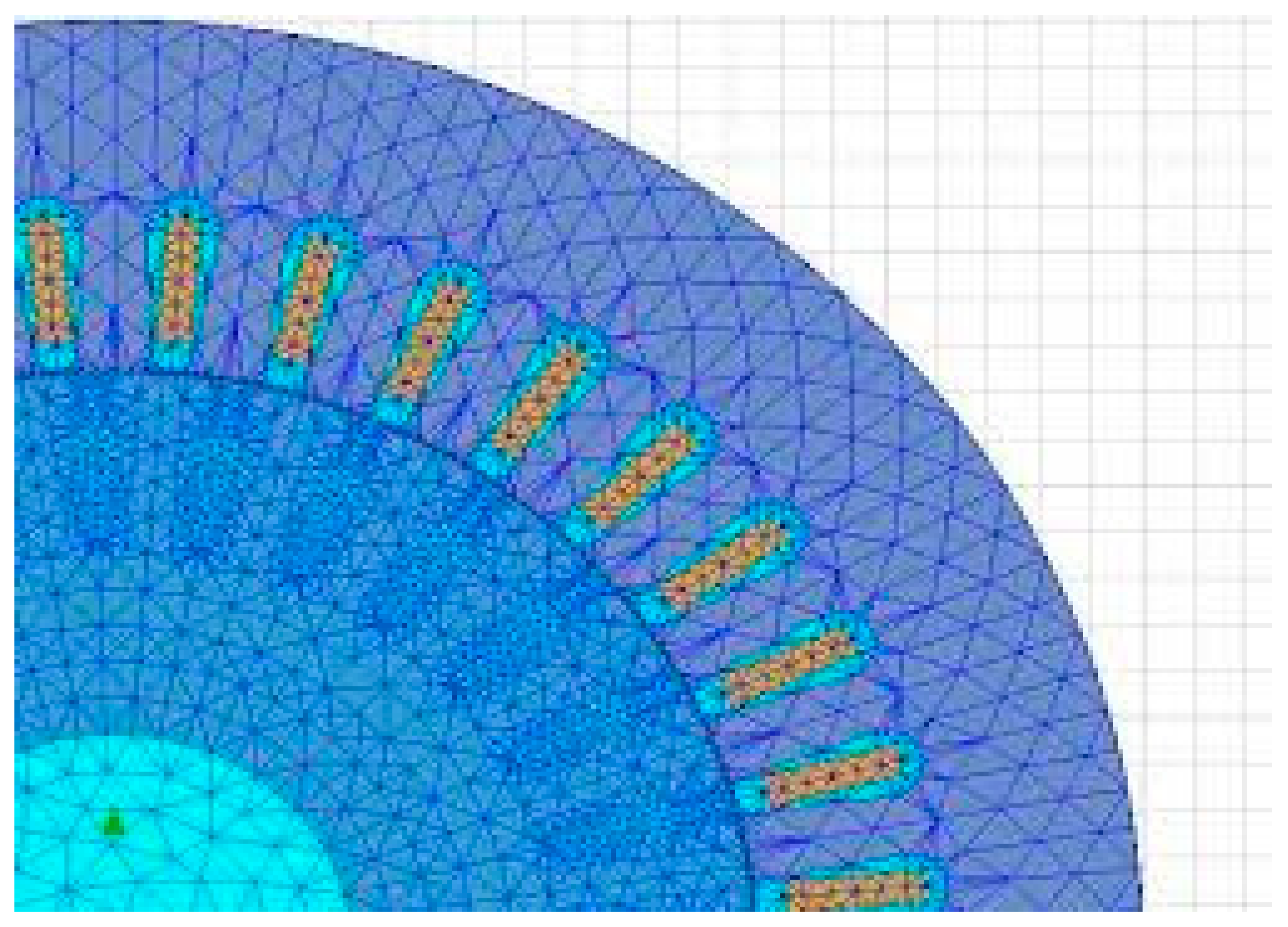
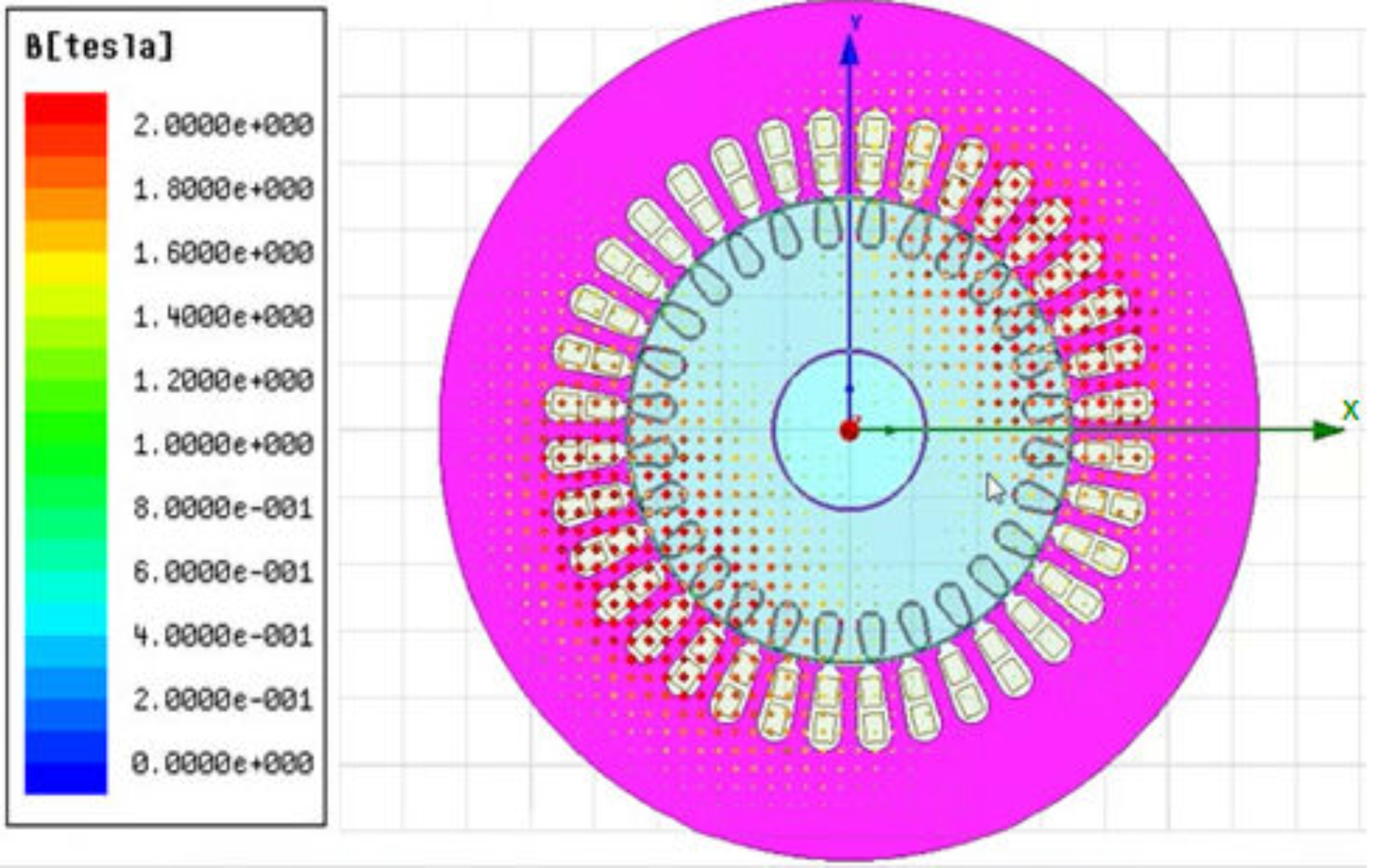
| Parameter | Value |
|---|---|
| Stator outer diameter [mm] | 128.5 |
| Stator inner diameter [mm] | 65.5 |
| Rotor outer diameter [mm] | 65.0 |
| Rotor inner diameter [mm] | 28.0 |
| Air gap length [mm] | 0.5 |
| Stack length [mm] | 76 |
| Number of poles | 2 |
| Stator slot number | 36 |
| Rotor slot number | 32 |
| Rated output power [kW] | 5 |
| Rated speed [r/min] | 3476 |
| Rated current [A] | 10.6 |
| Iron material | ASTM 532 |
| No. | Control Elements | Stator Iron Loss | Stator Copper Loss | Starting Current | Input Power | ||||
|---|---|---|---|---|---|---|---|---|---|
| E | D | C | B | A | [W] | [W] | [A] | [kW] | |
| 1 | 1 | 1 | 1 | 1 | 1 | 68.8 | 70.9 | 23.45 | 5.94 |
| 2 | 2 | 2 | 2 | 2 | 1 | 69.1 | 70.6 | 24.94 | 5.86 |
| 3 | 3 | 3 | 3 | 3 | 1 | 67.8 | 68.2 | 21.67 | 5.56 |
| 4 | 4 | 4 | 4 | 4 | 1 | 68.6 | 69.1 | 23.52 | 5.79 |
| 5 | 4 | 3 | 2 | 1 | 2 | 70.2 | 71.1 | 22.86 | 5.72 |
| 6 | 3 | 4 | 1 | 2 | 2 | 69.5 | 67.1 | 23.56 | 5.75 |
| 7 | 2 | 1 | 4 | 3 | 2 | 69.6 | 69.8 | 22.93 | 5.87 |
| 8 | 1 | 2 | 3 | 4 | 2 | 65.2 | 66.8 | 19.82 | 5.37 |
| 9 | 2 | 4 | 3 | 1 | 3 | 69.9 | 70.1 | 23.01 | 5.86 |
| 10 | 1 | 3 | 4 | 2 | 3 | 66.7 | 67.5 | 20.83 | 5.43 |
| 11 | 4 | 1 | 1 | 3 | 3 | 68.9 | 70.2 | 23.82 | 5.92 |
| 12 | 3 | 2 | 2 | 4 | 3 | 70.1 | 69.9 | 23.13 | 5.87 |
| 13 | 3 | 2 | 4 | 1 | 4 | 70.4 | 67.4 | 23.13 | 5.76 |
| 14 | 4 | 1 | 3 | 2 | 4 | 69.1 | 69.7 | 23.36 | 5.86 |
| 15 | 1 | 4 | 2 | 3 | 4 | 68.2 | 69.4 | 22.68 | 5.61 |
| 16 | 2 | 3 | 1 | 4 | 4 | 69.4 | 69.9 | 26.51 | 5.86 |
| No. | S/N Ratio | Altered Grey Wolf Optimization Modulus | MPCI | FEA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Stator Iron Loss | Stator Copper Loss | Starting Current | Input Power | Stator Iron Loss | Stator Copper Loss | Starting Current | Input Power | |||
| 1 | 1.4 | 1.6 | 1.4 | 2.8 | 0.97 | 0.36 | 0.68 | 0.81 | 0.68 | 441.04 |
| 2 | 1.1 | 1.9 | 1.1 | 2.9 | 0.81 | 0.26 | 0.69 | 0.82 | 0.65 | 418.15 |
| 3 | 0.8 | 1.4 | 0.9 | 2.4 | 0.56 | 0.26 | 0.65 | 0.68 | 0.60 | 364.57 |
| 4 | 1.6 | 1.5 | 1.6 | 2.7 | 0.63 | 0.38 | 0.67 | 0.90 | 0.64 | 404.76 |
| 5 | 1.3 | 1.8 | 1.7 | 2.6 | 0.73 | 0.26 | 0.69 | 0.74 | 0.63 | 393.94 |
| 6 | 1.1 | 1.6 | 1.1 | 2.7 | 0.68 | 0.31 | 0.73 | 0.86 | 0.61 | 383.12 |
| 7 | 0.9 | 1.6 | 0.9 | 2.7 | 0.69 | 0.28 | 0.66 | 0.76 | 0.62 | 397.45 |
| 8 | 0.6 | 1.1 | 0.7 | 2.2 | 0.48 | 0.24 | 0.58 | 0.61 | 0.56 | 328.61 |
| 9 | 0.8 | 1.4 | 1.8 | 2.9 | 0.57 | 0.28 | 0.69 | 0.81 | 0.64 | 409.64 |
| 10 | 0.7 | 1.2 | 0.7 | 2.3 | 0.50 | 0.25 | 0.61 | 0.62 | 0.58 | 344.24 |
| 11 | 1.1 | 1.5 | 1.1 | 2.5 | 0.60 | 0.34 | 0.85 | 0.71 | 0.68 | 439.57 |
| 12 | 1.0 | 1.7 | 1.0 | 2.6 | 0.81 | 0.29 | 0.79 | 0.68 | 0.62 | 397.51 |
| 13 | 0.9 | 1.8 | 0.9 | 2.8 | 0.51 | 0.28 | 0.68 | 0.74 | 0.61 | 383.82 |
| 14 | 1.1 | 1.6 | 1.1 | 2.7 | 0.70 | 0.27 | 0.74 | 0.86 | 0.66 | 422.38 |
| 15 | 0.7 | 1.4 | 0.8 | 2.5 | 0.55 | 0.26 | 0.64 | 0.68 | 0.61 | 374.06 |
| 16 | 1.1 | 1.8 | 1.1 | 2.9 | 0.69 | 0.33 | 0.85 | 0.76 | 0.65 | 418.24 |
| No. | Control Elements | Output Torque | Efficiency | Power Factor | ||||
|---|---|---|---|---|---|---|---|---|
| e | d | c | b | a | [Nm] | [%] | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 12.85 | 87.7 | 0.86 |
| 2 | 2 | 2 | 2 | 2 | 1 | 13.15 | 87.4 | 0.84 |
| 3 | 3 | 3 | 3 | 3 | 1 | 13.58 | 89.0 | 0.89 |
| 4 | 4 | 4 | 4 | 4 | 1 | 13.03 | 87.9 | 0.85 |
| 5 | 4 | 3 | 2 | 1 | 2 | 13.20 | 88.0 | 0.81 |
| 6 | 3 | 4 | 1 | 2 | 2 | 13.00 | 87.4 | 0.84 |
| 7 | 2 | 1 | 4 | 3 | 2 | 13.31 | 87.1 | 0.86 |
| 8 | 1 | 2 | 3 | 4 | 2 | 13.61 | 91.4 | 0.91 |
| 9 | 2 | 4 | 3 | 1 | 3 | 13.44 | 87.4 | 0.81 |
| 10 | 1 | 3 | 4 | 2 | 3 | 13.81 | 93.7 | 0.93 |
| 11 | 4 | 1 | 1 | 3 | 3 | 13.12 | 87.6 | 0.87 |
| 12 | 3 | 2 | 2 | 4 | 3 | 12.70 | 86.9 | 0.83 |
| 13 | 3 | 2 | 4 | 1 | 4 | 12.40 | 88.1 | 0.87 |
| 14 | 4 | 1 | 3 | 2 | 4 | 13.12 | 87.3 | 0.85 |
| 15 | 1 | 4 | 2 | 3 | 4 | 13.54 | 88.2 | 0.88 |
| 16 | 2 | 3 | 1 | 4 | 4 | 13.36 | 86.5 | 0.82 |
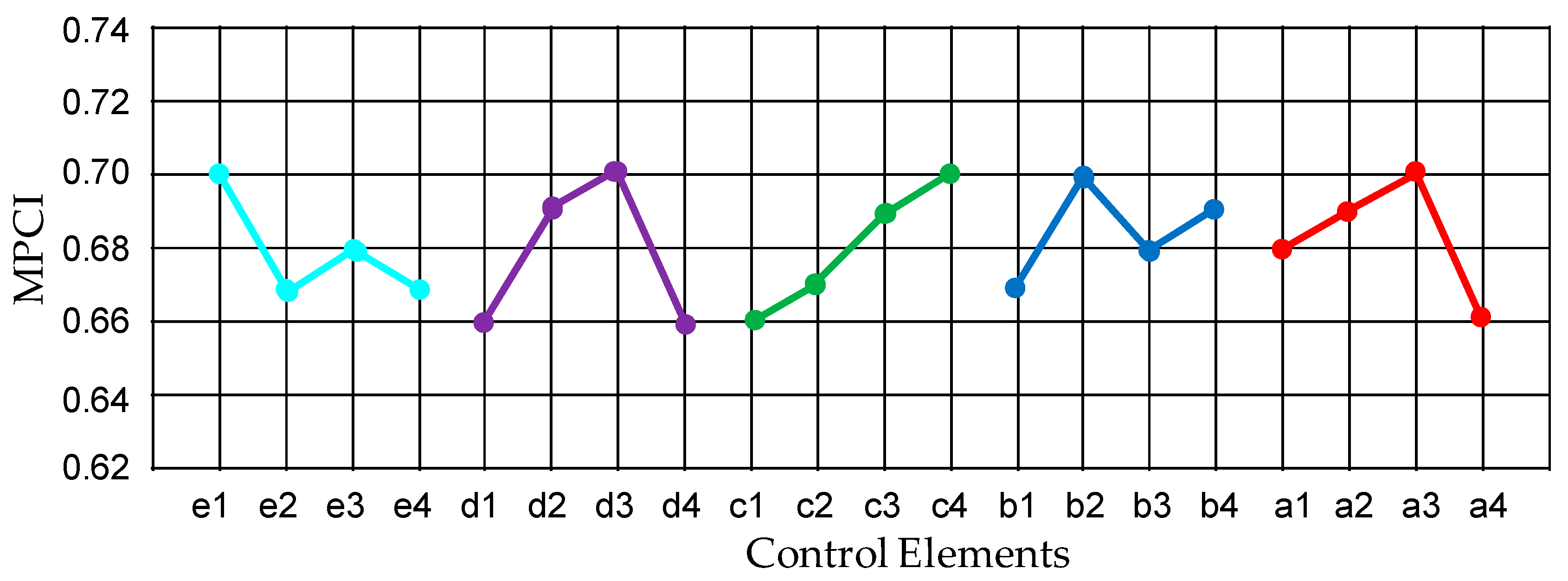
| No. | S/N Ratio | Altered Grey Wolf Optimization Modulus | MPCI | FEA | ||||
|---|---|---|---|---|---|---|---|---|
| Efficiency | Power Factor | Output Torque | Efficiency | Power Factor | Output Torque | |||
| 1 | −2.40 | −1.86 | −2.89 | 0.77 | 0.67 | 0.71 | 0.66 | 6.55 |
| 2 | −2.17 | −1.99 | −2.93 | 0.81 | 0.66 | 0.73 | 0.67 | 6.64 |
| 3 | −1.85 | −1.48 | −2.59 | 0.83 | 0.68 | 0.76 | 0.68 | 6.88 |
| 4 | −1.92 | −1.89 | −2.98 | 0.73 | 0.60 | 0.66 | 0.64 | 6.37 |
| 5 | −2.20 | −1.84 | −2.80 | 0.73 | 0.66 | 0.64 | 0.67 | 6.68 |
| 6 | −2.10 | −1.76 | −2.72 | 0.68 | 0.62 | 0.70 | 0.62 | 6.14 |
| 7 | −1.96 | −1.85 | −2.75 | 0.79 | 0.64 | 0.68 | 0.58 | 5.74 |
| 8 | −1.84 | −1.38 | −2.51 | 0.86 | 0.74 | 0.78 | 0.69 | 7.14 |
| 9 | −1.93 | −1.59 | −2.90 | 0.71 | 0.63 | 0.64 | 0.64 | 6.36 |
| 10 | −1.82 | −1.30 | −2.48 | 0.88 | 0.76 | 0.79 | 0.70 | 7.42 |
| 11 | −2.01 | −1.50 | −2.88 | 0.70 | 0.64 | 0.67 | 0.56 | 5.56 |
| 12 | −2.00 | −1.63 | −2.92 | 0.76 | 0.61 | 0.66 | 0.60 | 5.89 |
| 13 | −1.92 | −1.59 | −2.67 | 0.76 | 0.68 | 0.68 | 0.62 | 6.14 |
| 14 | −2.16 | −1.63 | −2.77 | 0.70 | 0.67 | 0.73 | 0.61 | 6.04 |
| 15 | −1.87 | −1.42 | −2.54 | 0.84 | 0.70 | 0.76 | 0.67 | 6.72 |
| 16 | −1.89 | −1.56 | −2.83 | 0.79 | 0.68 | 0.76 | 0.63 | 6.20 |
| Configurations | Style A | Style B | Style C | Style D |
|---|---|---|---|---|
| Stator iron loss [W] | 68.2 | 67.8 | 66.7 | 65.2 |
| Stator copper loss [W] | 69.4 | 68.2 | 67.5 | 66.8 |
| Starting current [A] | 22.68 | 21.67 | 20.83 | 19.82 |
| Input power [kW] | 5.61 | 5.56 | 5.43 | 5.37 |
| Efficiency [%] | 88.2 | 89.1 | 91.4 | 93.7 |
| Power factor [-] | 0.88 | 0.89 | 0.91 | 0.93 |
| Output torque [Nm] | 13.54 | 13.58 | 13.62 | 13.81 |
| Configurations | Particle Swarm Optimization [3] | Bee Colony Optimization [25] | Ant Colony Optimization [31] | Proposed Altered Grey Wolf Optimization |
|---|---|---|---|---|
| Stator iron loss [W] | 65.6 | 65.8 | 65.7 | 65.2 |
| Stator copper loss [W] | 67.1 | 67.5 | 67.8 | 66.8 |
| Starting current [A] | 19.95 | 20.17 | 20.23 | 19.82 |
| Input power [kW] | 5.43 | 5.47 | 5.49 | 5.37 |
| Efficiency [%] | 93.2 | 93.0 | 92.8 | 93.7 |
| Power factor [-] | 0.92 | 0.91 | 0.91 | 0.93 |
| Output torque [Nm] | 13.74 | 13.65 | 13.56 | 13.81 |
| Computing time [s] | 16.52 | 17.35 | 17.86 | 15.58 |
| Time spent searching for optimized value [s] | 18.68 | 19.46 | 19.81 | 17.36 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-H. Altered Grey Wolf Optimization and Taguchi Method with FEA for Six-Phase Copper Squirrel Cage Rotor Induction Motor Design. Energies 2020, 13, 2282. https://doi.org/10.3390/en13092282
Lin C-H. Altered Grey Wolf Optimization and Taguchi Method with FEA for Six-Phase Copper Squirrel Cage Rotor Induction Motor Design. Energies. 2020; 13(9):2282. https://doi.org/10.3390/en13092282
Chicago/Turabian StyleLin, Chih-Hong. 2020. "Altered Grey Wolf Optimization and Taguchi Method with FEA for Six-Phase Copper Squirrel Cage Rotor Induction Motor Design" Energies 13, no. 9: 2282. https://doi.org/10.3390/en13092282
APA StyleLin, C.-H. (2020). Altered Grey Wolf Optimization and Taguchi Method with FEA for Six-Phase Copper Squirrel Cage Rotor Induction Motor Design. Energies, 13(9), 2282. https://doi.org/10.3390/en13092282





