Numerical Study of Heat Transfer Intensification in a Circular Tube Using a Thin, Radiation-Absorbing Insert. Part 1: Thermo-Hydraulic Characteristics
Abstract
:1. Introduction
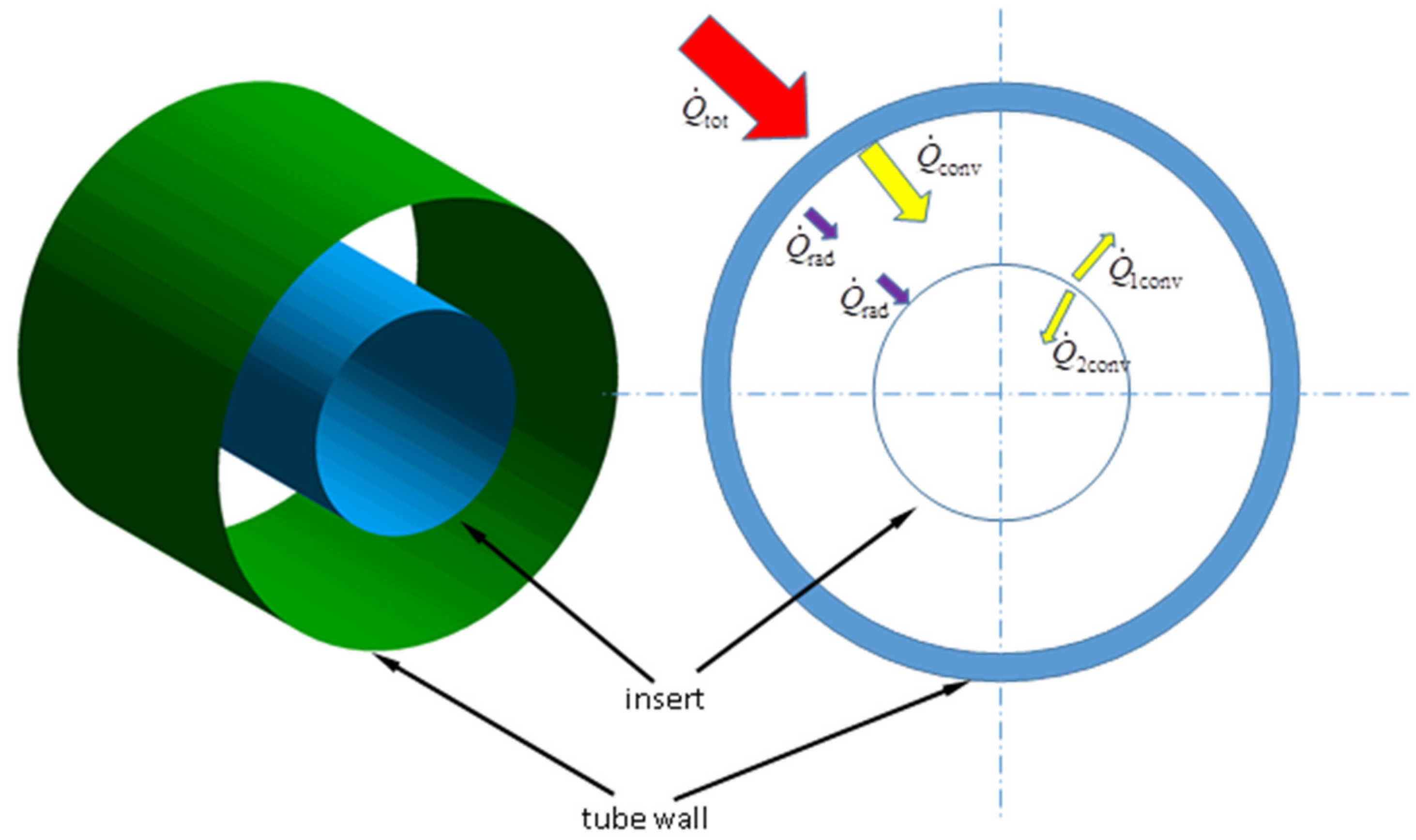
2. Geometry of Insert and Principle of Operation
3. Numerical Model
4. Grid, Turbulence Model and Radiation Model
4.1. Governing Equations
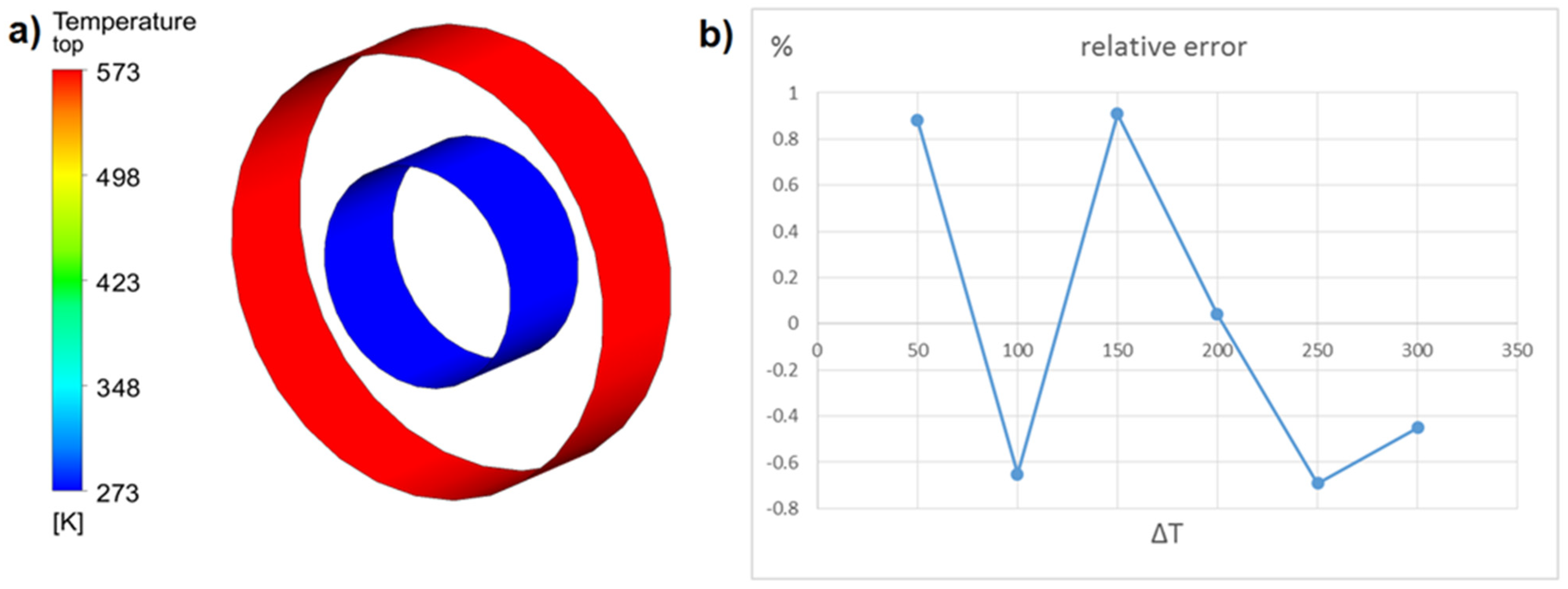
4.2. Grid Independence
4.3. Turbulence Model
4.4. Radiation Model
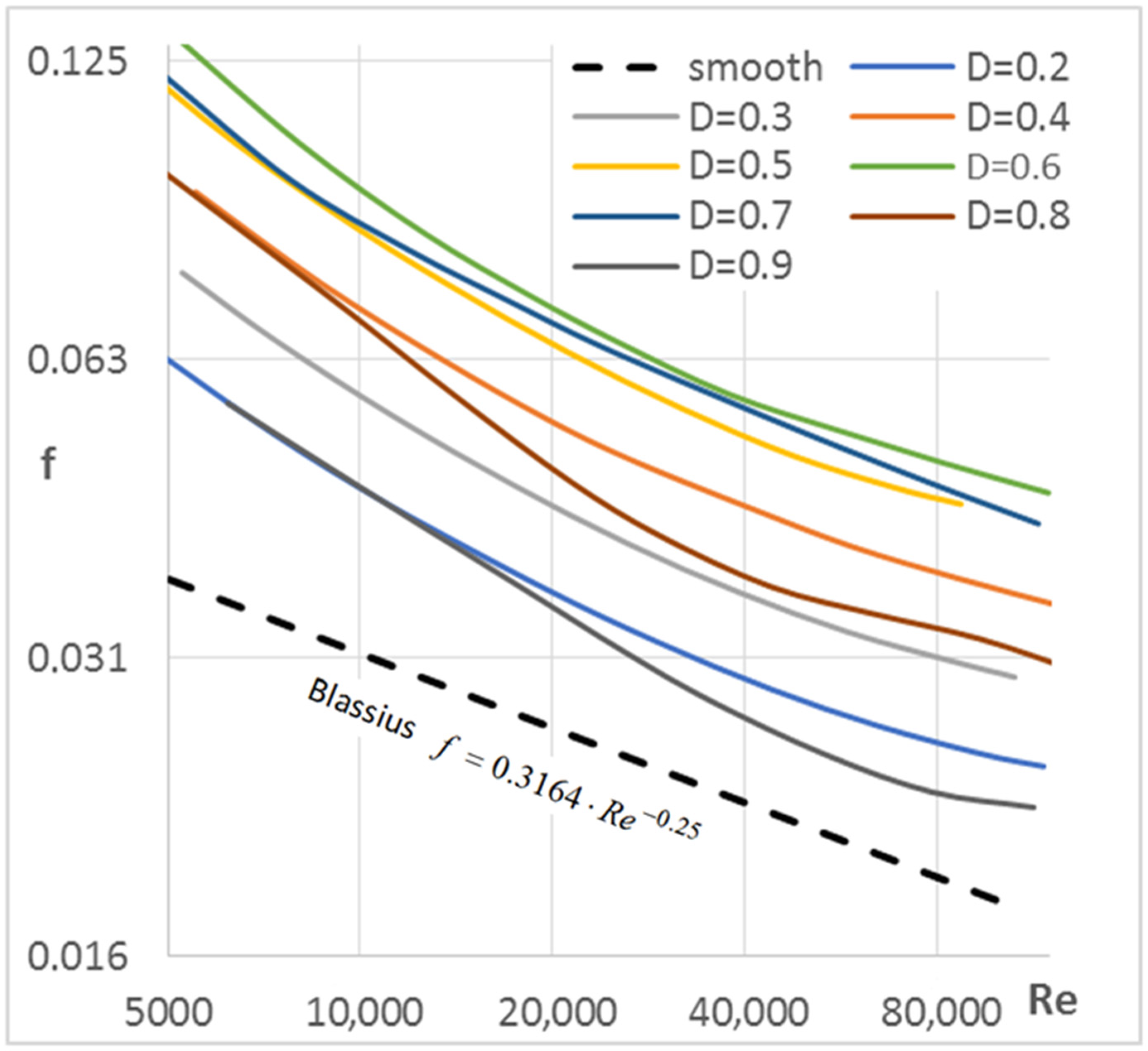
5. Hydraulic Characteristics—Friction Factor
5.1. Data Processing
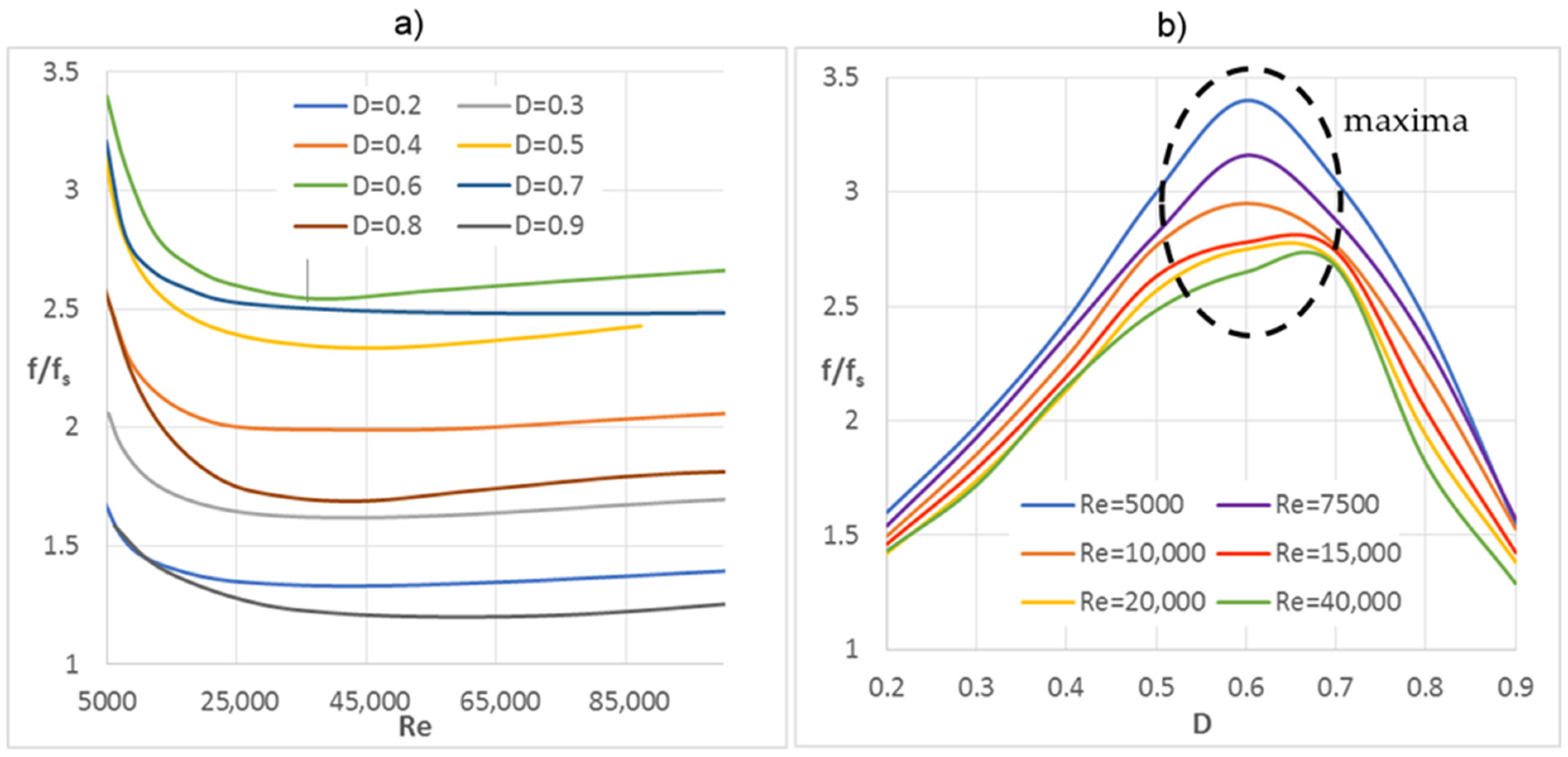
5.2. Results and Discussion—Friction Factor
6. Thermal Characteristics—Nusselt Number
6.1. Data Processing
6.2. Results and Discussion
7. Summary and Conclusions
- (1)
- The highest increase in friction resistance (the friction factor ratio f/fs) was observed for inserts with diameters D = 0.5–0.7, while the lowest values were recorded for inserts with the smallest diameter D = 0.2 and the largest diameter D = 0.9;
- (2)
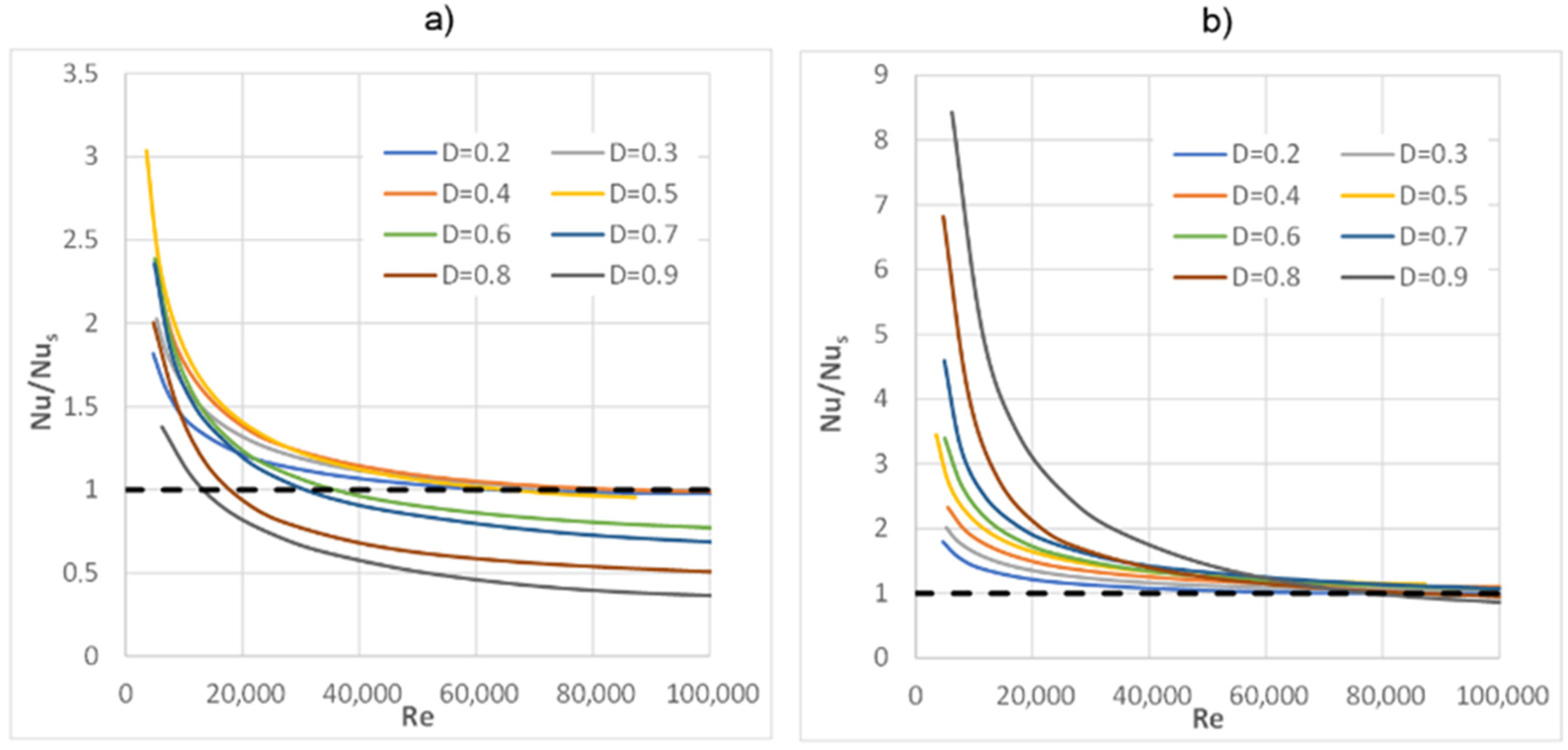
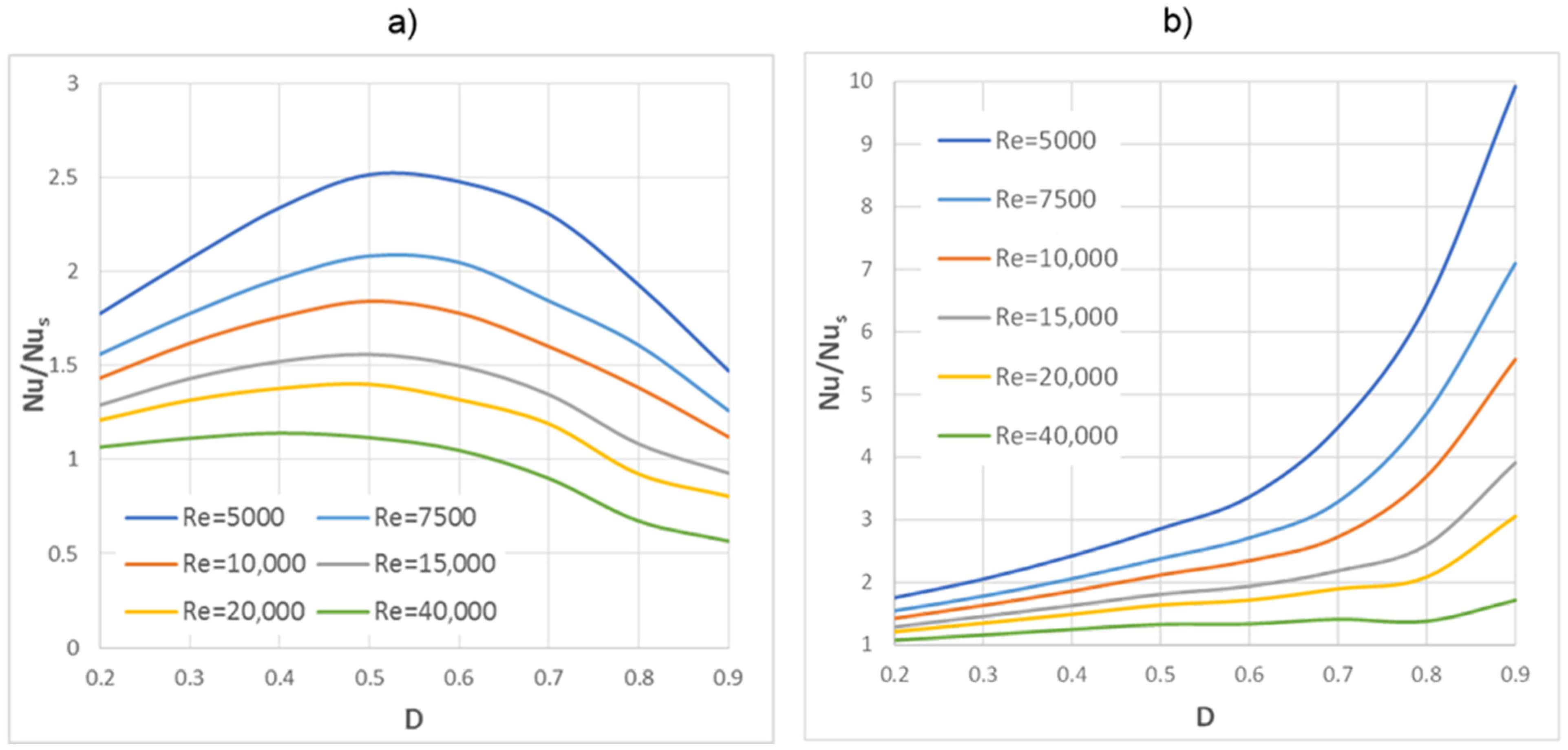
- The Nu number, which is the intensity of heat transfer, can be calculated in two ways that give different results. As mentioned earlier, there are two methods to determine the temperature Tb in formula (6). At the moment, the author suggests the “classical” way, (a), i.e., calculating the temperature Tb as an average over the entire volume channel. This method gives smaller, or one may say, “safer”, values of the Nu number than method (b). The Nu values obtained using method b) are quite large, up to about nine times larger than for a smooth pipe (for D = 0.9 and small Re numbers), but at relatively small velocities and pressure drops. Comparing the obtained results to the results of other insert geometries described in the available literature, it can be concluded that these are very high Nu numbers. Therefore, these values should be approached with caution, and the issue should still be thoroughly investigated and analysed;
- (3)
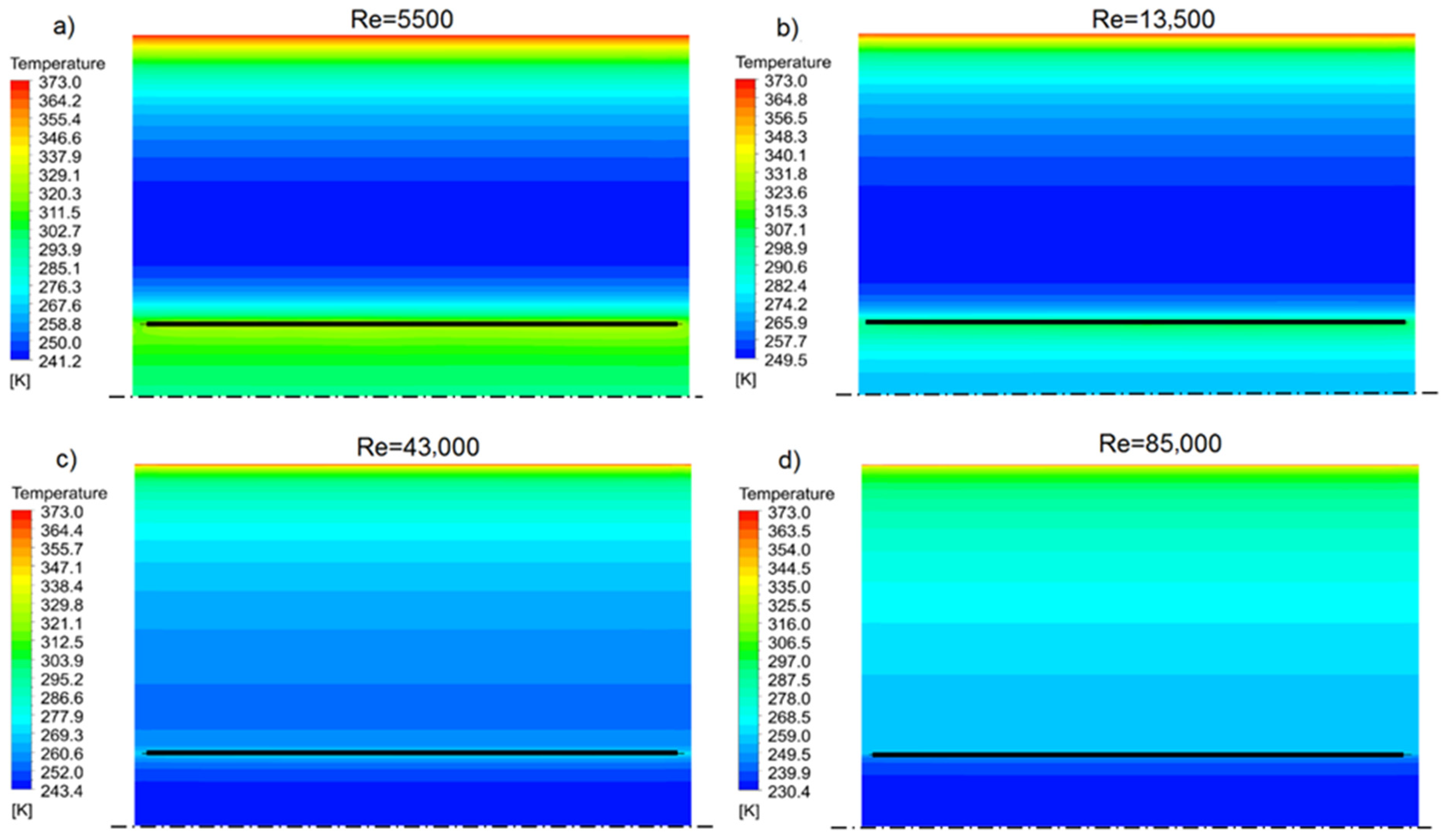
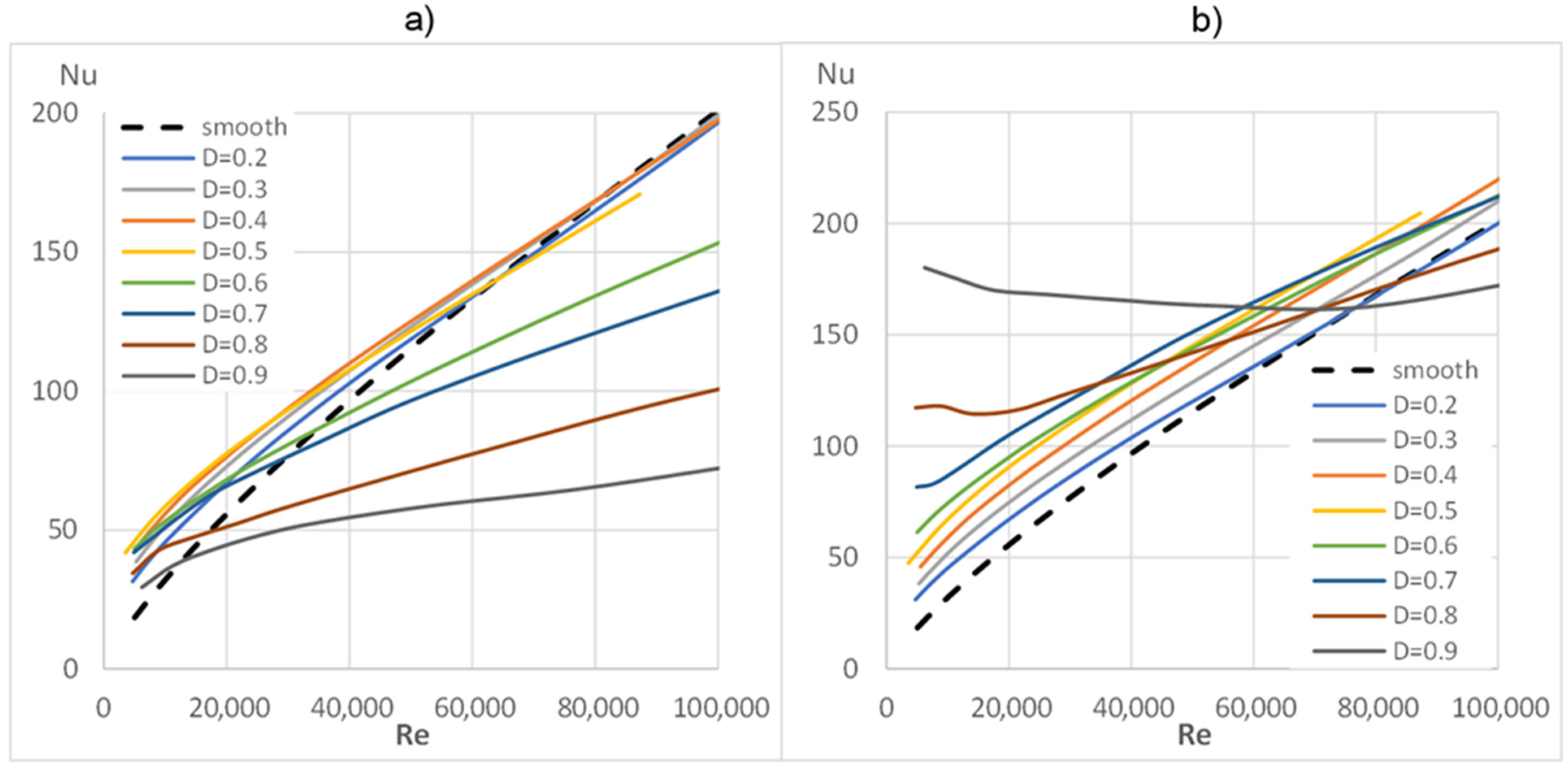
- The influence of radiation on heat transfer is shown in Figure 11 and Figure 12. Compared to a smooth pipe, the highest Nu numbers are noted for their small Re numbers. As the Re number increases, the difference between the Nu number of the tested inserts and that of a smooth pipe decreases quite quickly, and with large Re numbers, the Nu numbers of the values are comparable to those of a smooth pipe. This is a correct phenomenon because as the Re number and the gas flow velocity increase, the convective heat flux also increases, and the fraction of radiative heat flux decreases in the total heat flux, which is transferred from the wall to the fluid;
- (4)
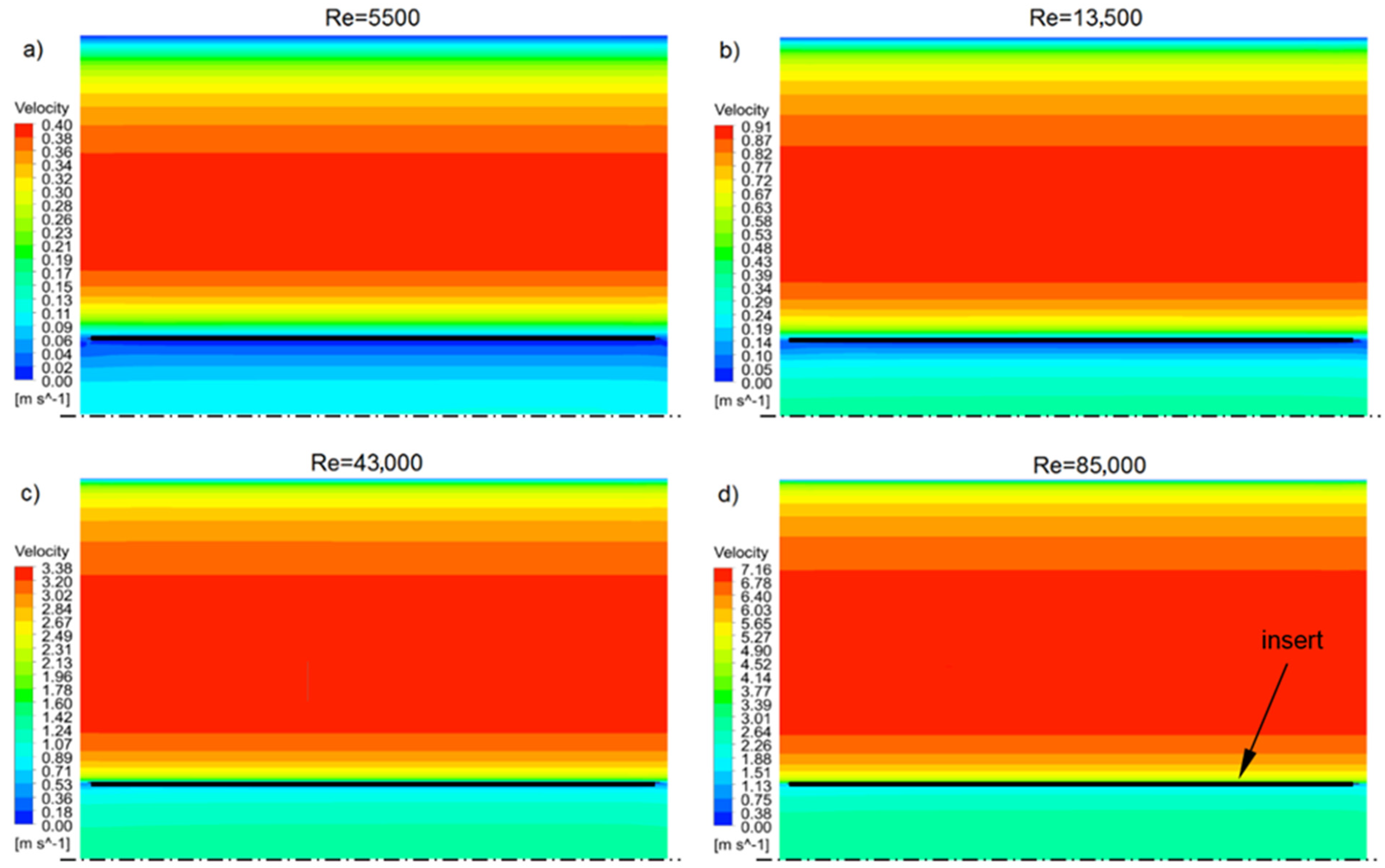
- For the largest diameters D = 0.9, 0.8, 0.7, 0.6 (Figure 11a), a decrease in Nu numbers below the reference level, which is a smooth pipe, was observed. As previously mentioned, the tested insert does not turbulise the flow and therefore does not increase the convective heat flux. On the other hand, at larger insert diameters, the mainstream of fluid flows inside the insert, and the outer (annular) space becomes thinner, which causes a significant reduction in gas velocity in this region. As a result, the annular part, instead of participating in the heat transport to the gas, due to its low velocities, actually becomes an insulating layer inside the pipe. As it can be seen from the research, this phenomenon causes a deterioration of the overall heat transfer, even when compared to a smooth pipe.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | heat transfer area (m2) |
| di | insert diameter (m) |
| dp | pipe diameter (m) |
| D | diameter ratio, (di/dp) |
| dp/dx | pressure gradient (Pa/m) |
| f | friction factor |
| k | thermal conductivity (W/mK) |
| L | domain length (m) |
| Nu | Nusselt number |
| total heat flux (W/m2) | |
| radiative heat flux (W/m2) | |
| convective heat flux (W/m2) | |
| Pr | Prandtl number |
| Re | Reynolds number |
| Tb | bulk temperature (K) |
| Tw | wall temperature (K) |
| u | average velocity (m/s) |
| ν | kinematic viscosity (m2/s) |
| ∆T | temperature difference (K) |
| δ | relative error (%) |
| ε | emissivity |
| ε12 | interchange factor |
| ρ | density (kg/m3) |
| indexes: | |
| s | smooth tube |
| 1 | for smaller heat transfer area |
| 2 | for bigger heat transfer area |
References
- Ozceyhan, V.; Gunes, S.; Buyukalaca, O.; Altuntop, N. Heat transfer enhancement in a tube using circular cross sectional rings separated from wall. Appl. Energy 2008, 85, 988–1001. [Google Scholar] [CrossRef]
- Min, C.; Qi, C.; Wang, E.; Tian, L.; Qin, Y. Numerical investigation of turbulent flow and heat transfer in a channel with novel longitudinal vortex generators. Int. J. Heat Mass Transf. 2012, 55, 7268–7277. [Google Scholar] [CrossRef]
- Lotfi, B.; Sundén, B.; Wang, Q. An investigation of the thermo-hydraulic performance of the smooth wavy fin-and-elliptical tube heat exchangers utilizing new type vortex generators. Appl. Energy 2016, 162, 1282–1302. [Google Scholar] [CrossRef]
- Jasiński, P. Numerical Study of Friction Factor and Heat Transfer Characteristics for Single-Phase Turbulent Flow in Tubes with Helical Micro-Fins. Arch. Mech. Eng. 2012, 59, 469–485. [Google Scholar] [CrossRef] [Green Version]
- Yeom, T.; Simon, T.; Zhang, T.; Zhang, M.; North, M.; Cui, T. Enhanced heat transfer of heat sink channels with micro pin fin roughened walls. Int. J. Heat Mass Transf. 2016, 92, 617–627. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Yang, C.; Zhang, J.; Zong, H.; Xu, B.; Qian, J.-Y. Internal Flow Analysis of a Heat Transfer Enhanced Tube with a Segmented Twisted Tape Insert. Energies 2020, 13, 207. [Google Scholar] [CrossRef] [Green Version]
- Wijayanta, A.T.; Mirmanto, P.; Kristiawan, B.; Aziz, M. Internal Flow in an Enhanced Tube Having Square-cut Twisted Tape Insert. Energies 2019, 12, 306. [Google Scholar] [CrossRef] [Green Version]
- Bellos, E.; Tzivanidis, C. Enhancing the Performance of Evacuated and Non-Evacuated Parabolic Trough Collectors Using Twisted Tape Inserts, Perforated Plate Inserts and Internally Finned Absorber. Energies 2018, 11, 1129. [Google Scholar] [CrossRef] [Green Version]
- Mwesigye, A.; Bello-Ochende, T.; Meyer, J.P. Heat transfer and thermodynamic performance of a parabolic trough receiver with centrally placed perforated plate inserts. Appl. Energy 2014, 136, 989–1003. [Google Scholar] [CrossRef] [Green Version]
- Cerón, J.F.; Pérez-García, J.; Solano, J.P.; García, A.; Herrero-Martín, R. A coupled numerical model for tube-on-sheet flat-plate solar liquid collectors. Analysis and validation of the heat transfer mechanisms. Appl. Energy 2015, 140, 275–287. [Google Scholar] [CrossRef]
- Luo, L.; Wen, F.; Wang, L.; Sundén, B.; Wang, S. Thermal enhancement by using grooves and ribs combined with delta-winglet vortex generator in a solar receiver heat exchanger. Appl. Energy 2016, 183, 1317–1332. [Google Scholar] [CrossRef]
- Eiamsa-Ard, S.; Promvonge, P. Thermal characterization of turbulent tube flows over diamond-shaped elements in tandem. Int. J. Therm. Sci. 2010, 49, 1051–1062. [Google Scholar] [CrossRef]
- Kongkaitpaiboon, V.; Nanan, K.; Eiamsa-Ard, S. Experimental investigation of convective heat transfer and pressure loss in a round tube fitted with circular-ring turbulators. Int. Commun. Heat Mass Transf. 2010, 37, 568–574. [Google Scholar] [CrossRef]
- Aydin, D. Heat transfer and exergy loss in cut out conical turbulators. Energy Convers. Manag. 2004, 45, 785–796. [Google Scholar]
- Jasiński, P.B. Numerical study of thermal-hydraulic characteristics in a circular tube with ball turbulators. Part 1: PIV experiment and pressure drop. Int. J. Heat Mass Transf. 2014, 74, 48–59. [Google Scholar] [CrossRef]
- Jasiński, P.B. Numerical study of thermal-hydraulic characteristics in a circular tube with ball turbulators. Part 2: Heat transfer. Int. J. Heat Mass Transf. 2014, 74, 473–483. [Google Scholar] [CrossRef]
- Jasiński, P. Numerical study of thermo-hydraulic characteristics in a circular tube with ball turbulators. Part 3: Thermal performance analysis. Int. J. Heat Mass Transf. 2017, 107, 1138–1147. [Google Scholar] [CrossRef]
- Bas, H.; Ozceyhan, V. Heat transfer enhancement in a tube with twisted tape inserts placed separately from the tube wall. Exp. Therm. Fluid Sci. 2012, 41, 51–58. [Google Scholar] [CrossRef]
- Jasiński, P. Numerical optimization of flow-heat ducts with helical micro-fins, using Entropy Generation Minimization (EGM) method. In Proceedings of the WSEAS International Conferences (HTE’11), Florence, Italy, 23–25 August 2011; pp. 47–54. [Google Scholar]
- Fodemski, T.; Górecki, G.; Jasiński, P. Corrugated channels heat transfer efficiency Analysis based on velocity fields resulting from computer simulation and PIV Measurements. In Proceedings of the 8th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, HEFAT 2011, Pointe Aux Piments, Mauritius, 11–13 July 2011. [Google Scholar]
- Li, X.-W.; Meng, J.-A.; Guo, Z.-Y. Turbulent flow and heat transfer in discrete double inclined ribs tube. Int. J. Heat Mass Transf. 2009, 52, 962–970. [Google Scholar] [CrossRef]
- ANSYS-CFX Manual v. 18.1. Available online: http://www.ansys.com (accessed on 25 July 2021).
- Gutkowski, A.N.; Łęcki, M.; Jasiński, P.; Jędrowiak, B. Flame behavior during propagation in small isothermal tubes characterized by different degrees of the end opening. Combust. Sci. Technol. 2018, 191, 711–725. [Google Scholar] [CrossRef]
- Karwa, R. Heat and Mass Transfer; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Fakheri, A. Intermediate Heat Transfer; Taylor & Francis: Abingdon, UK, 2014. [Google Scholar]
- Arjmandi, H.; Amiri, P.; Pour, M.S. Geometric optimization of a double pipe heat exchanger with combined vortex generator and twisted tape: A CFD and response surface methodology (RSM) study. Therm. Sci. Eng. Prog. 2020, 18, 100514. [Google Scholar] [CrossRef]
- Wijayanta, A.T.; Yaningsih, I.; Aziz, M.; Miyazaki, T.; Koyama, S. Double-sided delta-wing tape inserts to enhance convective heat transfer and fluid flow characteristics of a double-pipe heat exchanger. Appl. Therm. Eng. 2018, 145, 27–37. [Google Scholar] [CrossRef]
- Zheng, N.; Liu, P.; Wang, X.; Shan, F.; Liu, Z.; Liu, W. Numerical simulation and optimization of heat transfer enhancement in a heat exchanger tube fitted with vortex rod inserts. Appl. Therm. Eng. 2017, 123, 471–484. [Google Scholar] [CrossRef]
- Huanga, S.; Chena, H.; Zhang, X. Experimental evaluation of thermal performance in a circular tube with Y-branch insert. Int. Commun. Heat Mass Transf. 2019, 106, 15–21. [Google Scholar] [CrossRef]
- Bhuiyaa, M.; Ahamed, J. Heat transfer enhancement and development of correlation for turbulent flow through a tube with triple helical tape inserts. Int. Commun. Heat Mass Transf. 2012, 39, 94–101. [Google Scholar] [CrossRef]
- Hasanpour, A.; Farhadi, M.; Sedighi, K. A review study on twisted tape inserts on turbulent flow heat exchangers: The overall enhancement ratio criteria. Int. Commun. Heat Mass Transf. 2014, 55, 53–62. [Google Scholar] [CrossRef]
- Jasiński, P.; Kowalczyk, M.; Romaniak, A.; Warwas, B.; Obidowski, D.; Gutkowski, A. Investigation of Thermal-Flow Characteristics of Pipes with Helical Micro-Fins of Variable Height. Energies 2021, 14, 2048. [Google Scholar] [CrossRef]
- Ho, C.; Liu, Y.-C.; Yang, T.-F.; Ghalambaz, M.; Yan, W.-M. Convective heat transfer of nano-encapsulated phase change material suspension in a divergent minichannel heatsink. Int. J. Heat Mass Transf. 2021, 165, 120717. [Google Scholar] [CrossRef]
- Ho, C.; Liu, Y.-C.; Ghalambaz, M.; Yan, W.-M. Forced convection heat transfer of Nano-Encapsulated Phase Change Material (NEPCM) suspension in a mini-channel heatsink. Int. J. Heat Mass Transf. 2020, 155, 119858. [Google Scholar] [CrossRef]
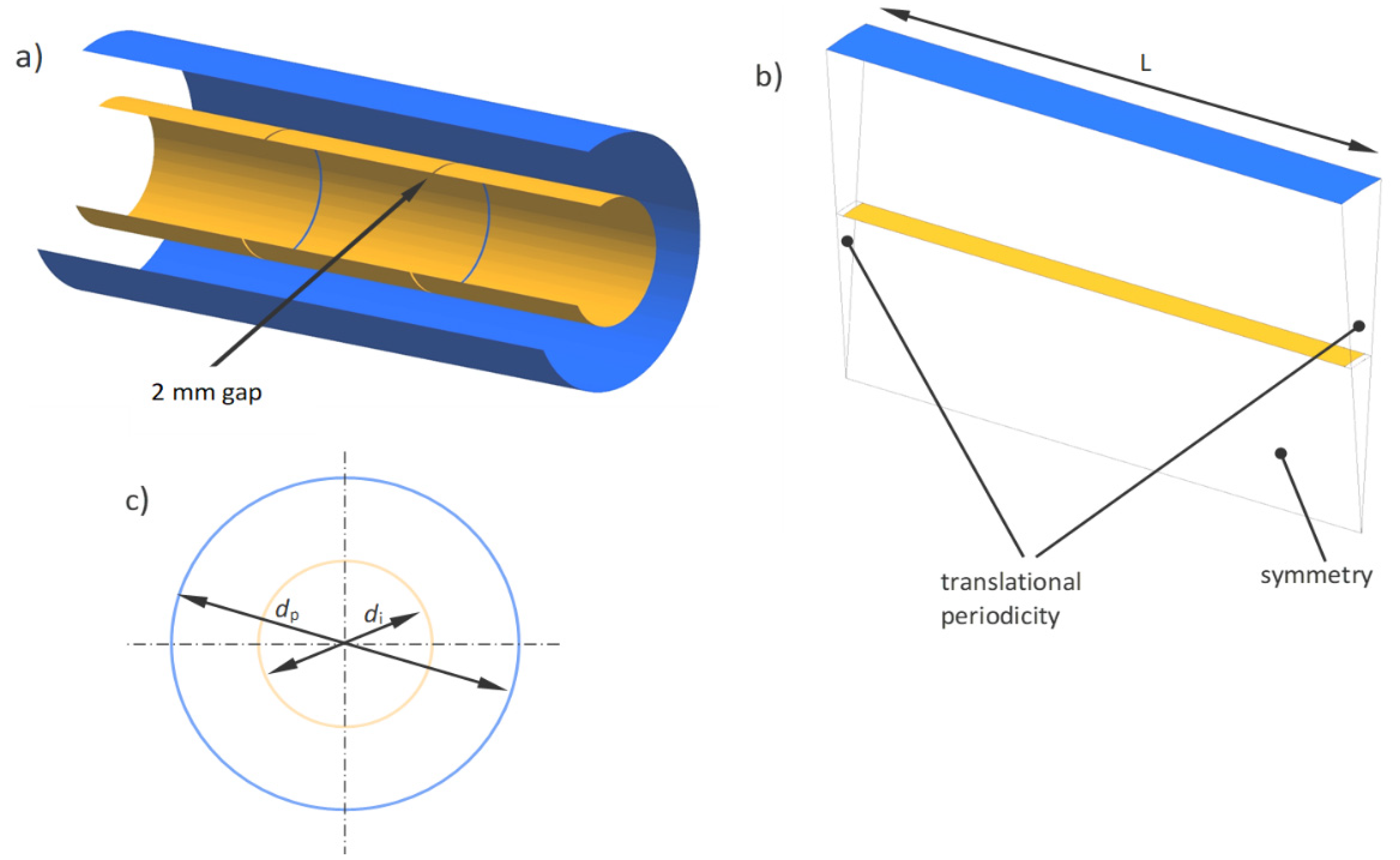

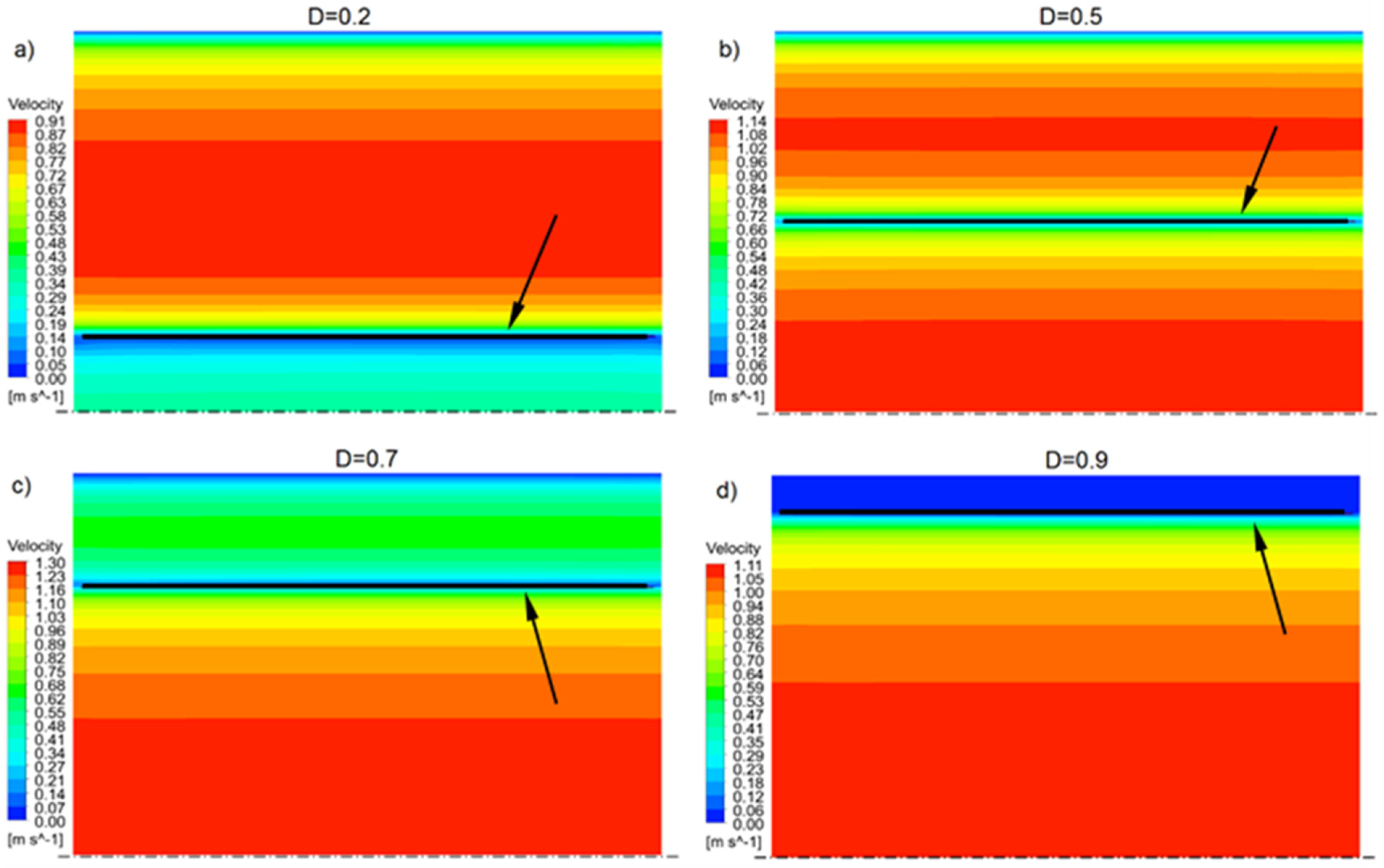
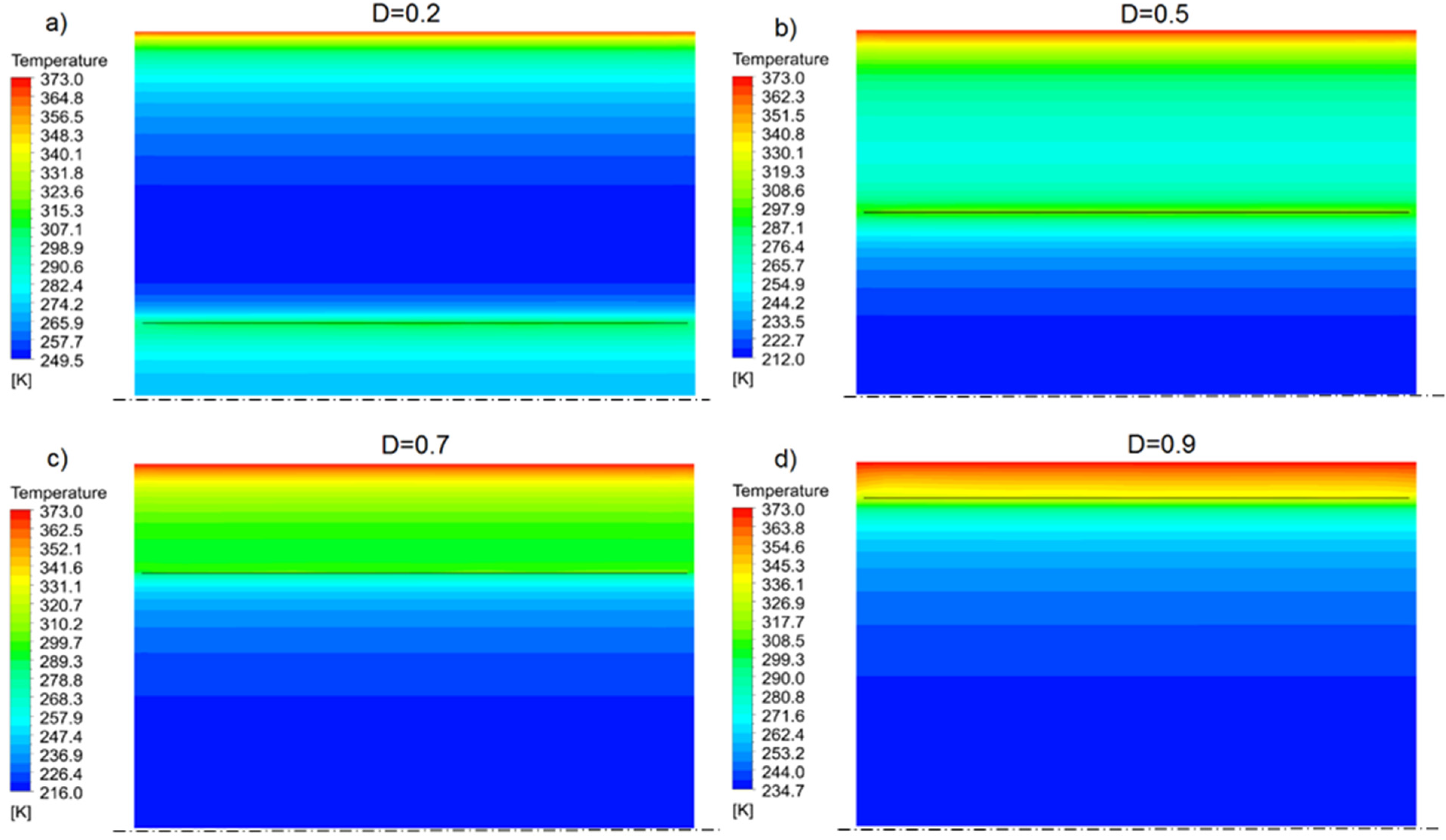
| di [mm] | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
|---|---|---|---|---|---|---|---|---|
| D [—] | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| No. of Elements | f | Dev. % | Nu | Dev. % |
|---|---|---|---|---|
| 6140 | 0.0461 | - | 73.23 | - |
| 11,960 | 0.0508 | 9.38 | 78.05 | 6.18 |
| 18,230 | 0.0543 | 6.32 | 80.13 | 2.60 |
| 25,440 | 0.0551 | 1.45 | 80.62 | 0.61 |
| 49,820 | 0.0556 | 0.9 | 80.80 | 0.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jasiński, P.B. Numerical Study of Heat Transfer Intensification in a Circular Tube Using a Thin, Radiation-Absorbing Insert. Part 1: Thermo-Hydraulic Characteristics. Energies 2021, 14, 4596. https://doi.org/10.3390/en14154596
Jasiński PB. Numerical Study of Heat Transfer Intensification in a Circular Tube Using a Thin, Radiation-Absorbing Insert. Part 1: Thermo-Hydraulic Characteristics. Energies. 2021; 14(15):4596. https://doi.org/10.3390/en14154596
Chicago/Turabian StyleJasiński, Piotr Bogusław. 2021. "Numerical Study of Heat Transfer Intensification in a Circular Tube Using a Thin, Radiation-Absorbing Insert. Part 1: Thermo-Hydraulic Characteristics" Energies 14, no. 15: 4596. https://doi.org/10.3390/en14154596
APA StyleJasiński, P. B. (2021). Numerical Study of Heat Transfer Intensification in a Circular Tube Using a Thin, Radiation-Absorbing Insert. Part 1: Thermo-Hydraulic Characteristics. Energies, 14(15), 4596. https://doi.org/10.3390/en14154596





