Method for Designing Robust and Energy Efficient Railway Schedules
Abstract
:1. Introduction
2. Literature Review
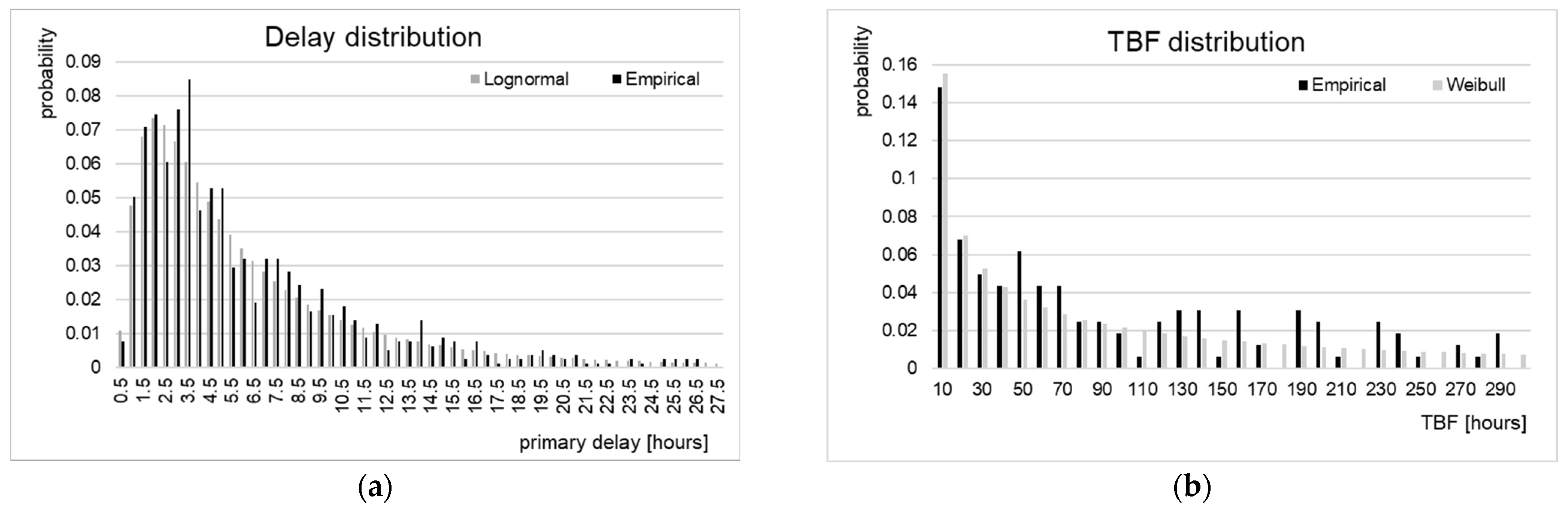
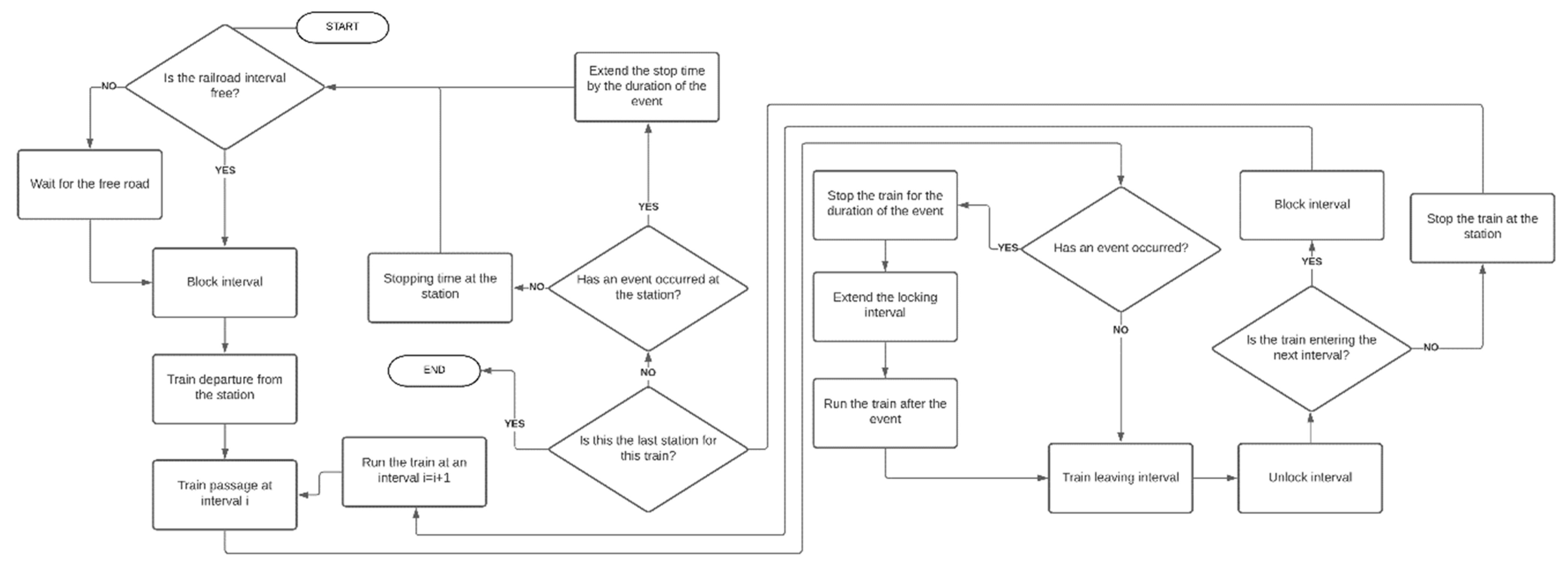
3. Time Margins Development Method
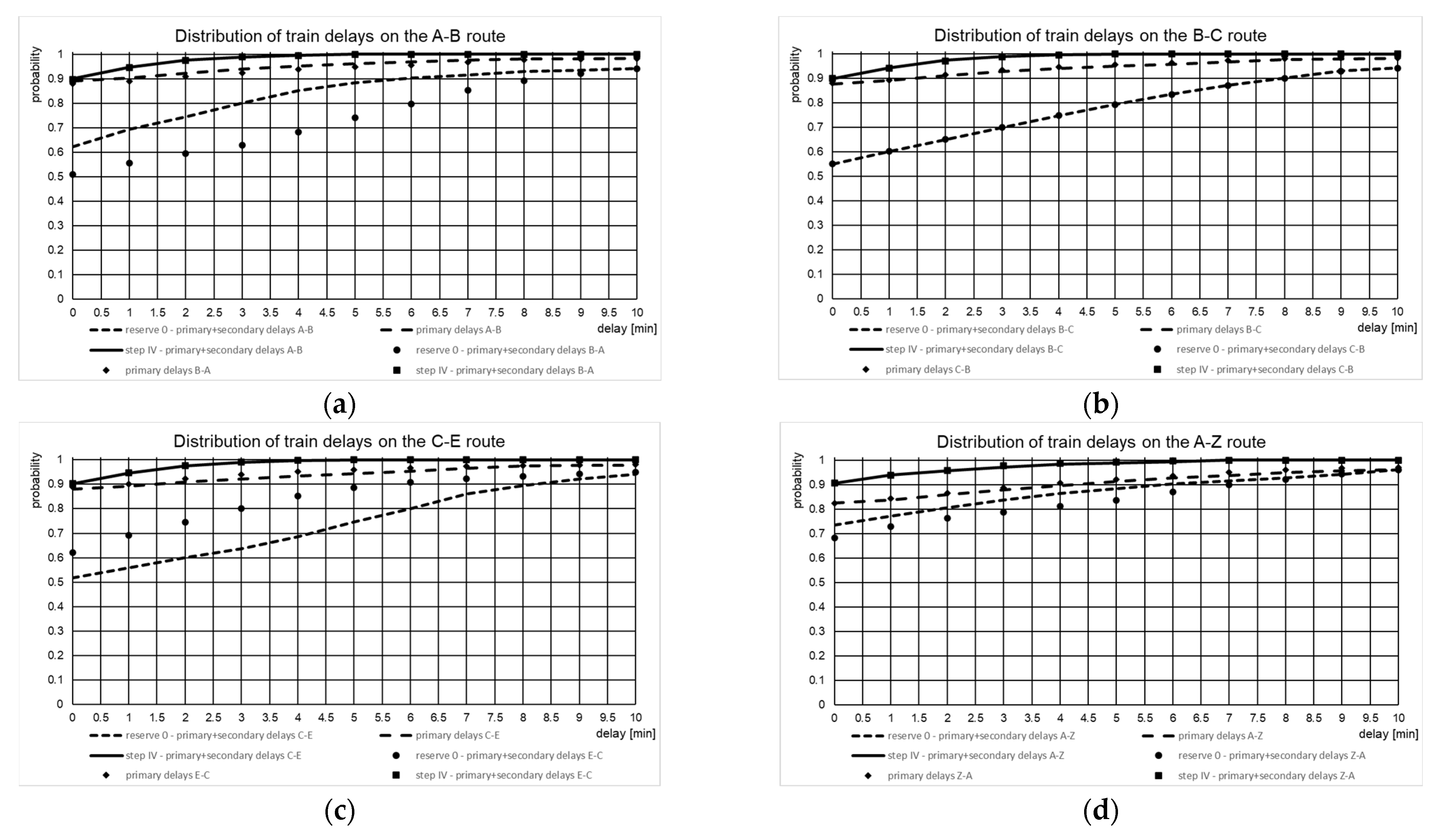
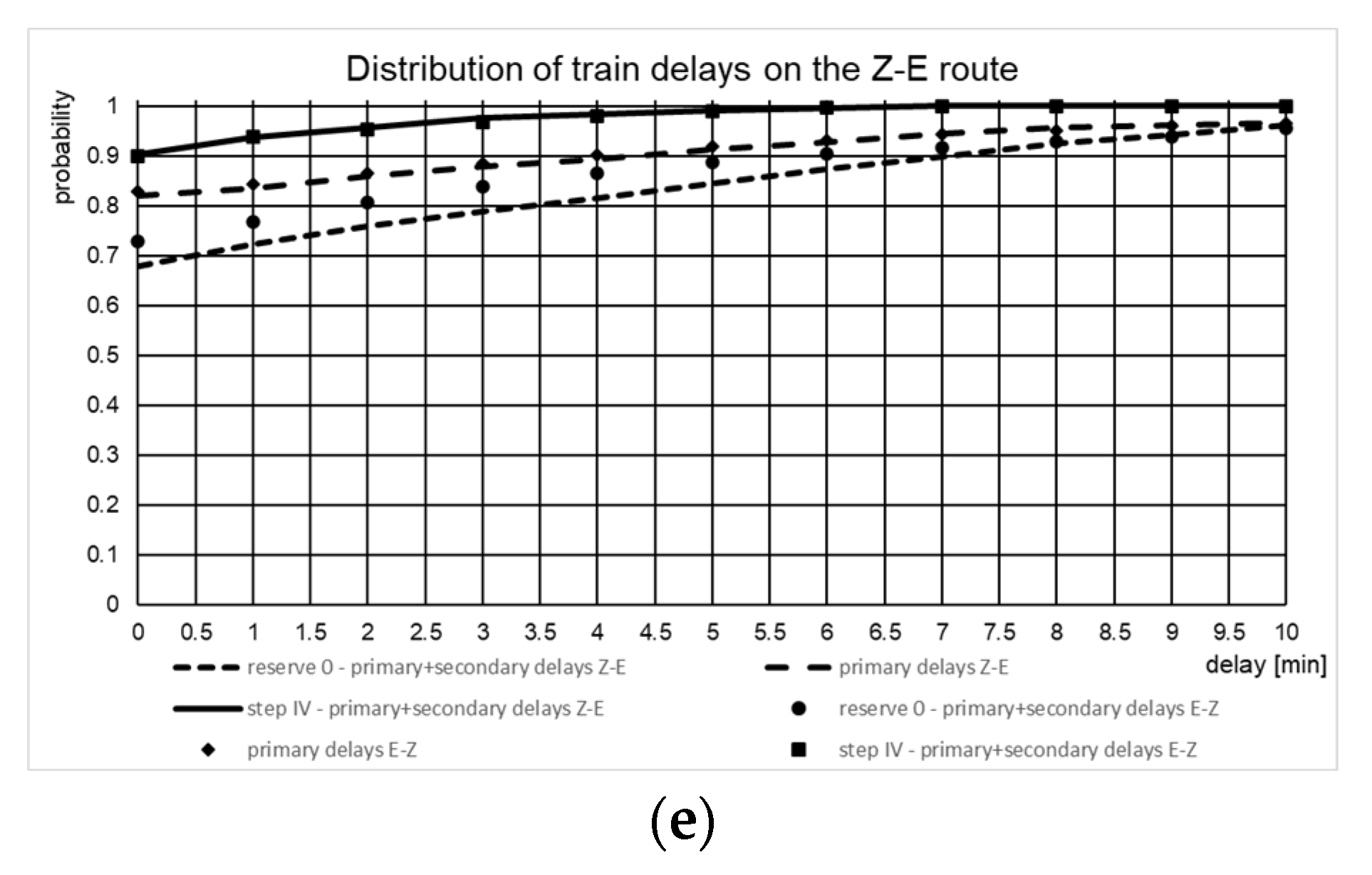
4. Case Description
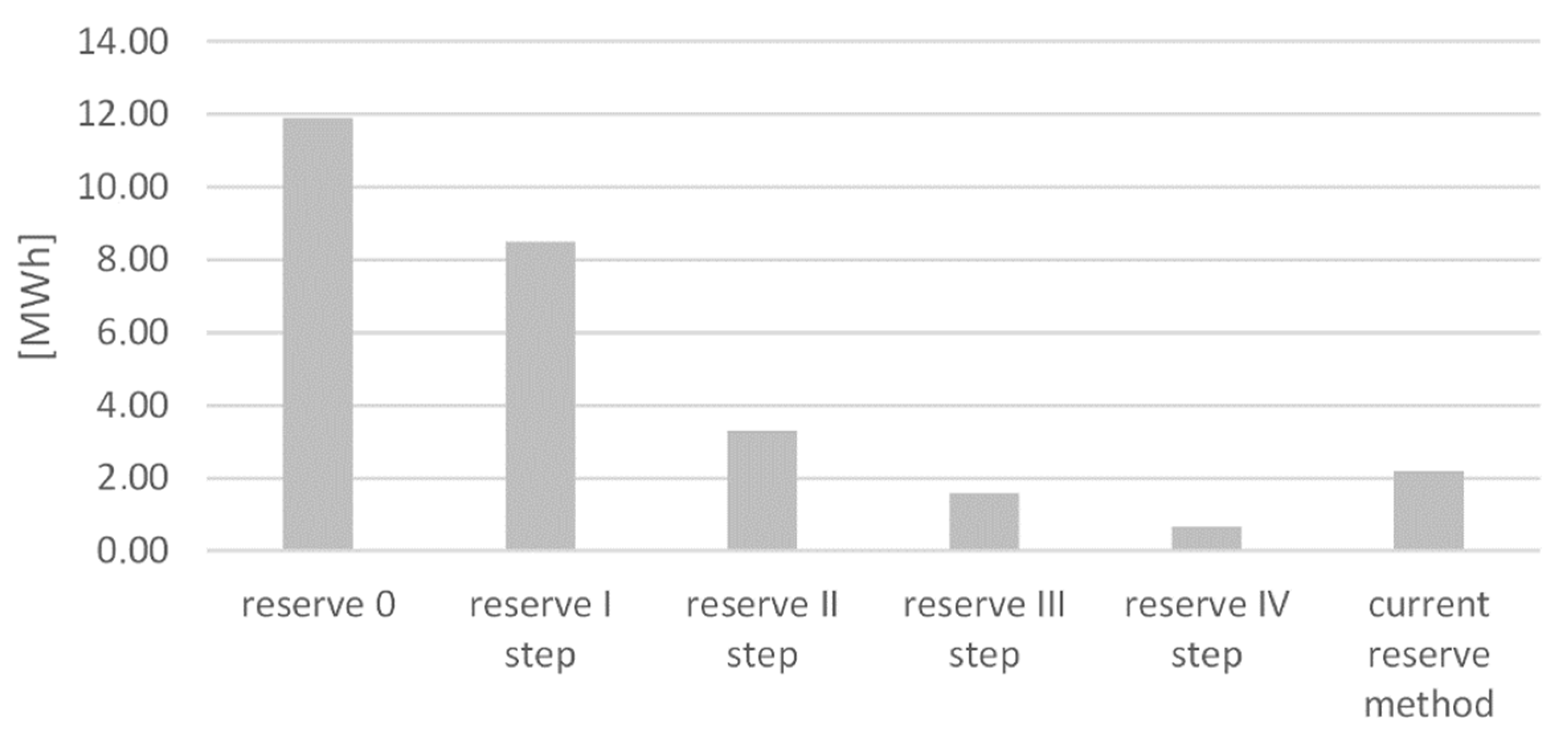
5. Discussion of Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, P.; Goverde, R.M. Multi-train trajectory optimization for energy-efficient timetabling. Eur. J. Oper. Res. 2019, 272, 621–635. [Google Scholar] [CrossRef]
- Tian, Z.; Zhao, N.; Hillmansen, S.; Su, S.; Wen, C. Traction Power Substation Load Analysis with Various Train Operating Styles and Substation Fault Modes. Energies 2020, 13, 2788. [Google Scholar] [CrossRef]
- Pröhl, L.; Aschemann, H.; Palacin, R. The Influence of Operating Strategies regarding an Energy Optimized Driving Style for Electrically Driven Railway Vehicles. Energies 2021, 14, 583. [Google Scholar] [CrossRef]
- Cunillera, A.; Fernández-Rodríguez, A.; Cucala, A.P.; Fernández-Cardador, A.; Falvo, M.C. Assessment of the Worthwhileness of Efficient Driving in Railway Systems with High-Receptivity Power Supplies. Energies 2020, 13, 1836. [Google Scholar] [CrossRef]
- Zhao, N.; Roberts, C.; Hillmansen, S.; Tian, Z.; Weston, P.; Chen, L. An integrated metro operation optimization to minimize energy consumption. Transp. Res. Part C 2017, 75, 168–182. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Chen, A.; Ning, B.; Tang, T. A stochastic model for the integrated optimization on metro timetable and speed profile with uncertain train mass. Transp. Res. Part B 2016, 91, 424–445. [Google Scholar] [CrossRef]
- González-Gil, A.; Palacin, R.; Batty, P.; Powell, J.P. A systems approach to reduce urban rail energy consumption. Energy Convers. Manag. 2014, 80, 509–524. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Yang, L.; Tang, T.; Gao, Z.; Cao, F.; Li, K. Train speed profile optimization with on-board energy storage devices: A dynamic programming based approach. Comput. Ind. Eng. 2018, 126, 149–164. [Google Scholar] [CrossRef]
- Gerben, M.; Scheepmaker, R.; Goverde, M.P. The interplay between energy-efficient train control and scheduled running time supplements. J. Rail Transp. Plan. Manag. 2015, 5, 225–239. [Google Scholar] [CrossRef]
- Kwaśnikowski, J. Elementy Teorii Ruchu i Racjonalizacja Prowadzenia Pociągu; Naukowe Instytutu Technologii Eksploatacji—PIB: Radom, Poland, 2013. [Google Scholar]
- Wang, P.; Goverde, M.P. Two-Train Trajectory Optimization with a Green-Wave Policy. Transp. Res. Rec. Transp. Res. Board 2016, 2546, 112–120. [Google Scholar] [CrossRef]
- Yang, X.; Ning, B.; Li, X.; Tang, T. A two-objective timetable optimization model in subway systems. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1913–1921. [Google Scholar] [CrossRef]
- Yang, L.X.; Li, K.P.; Gao, Z.Y.; Li, X. Optimizing trains movement on a railway network. Omega 2012, 40, 619–633. [Google Scholar] [CrossRef]
- Gu, Q.; Tang, T.; Cao, F.; Song, Y.D. Energy-efficient train operation in urban rail transit using real-time traffic information. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1216–1233. [Google Scholar] [CrossRef]
- ShangGuan, W.; Yan, X.H.; Cai, B.G.; Wang, J. Multiobjective optimization for train speed trajectory in CTCS high-speed railway with hybrid evolutionary algorithm. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2215–2225. [Google Scholar] [CrossRef]
- Ke, B.R.; Lin, C.L.; Yang, C.C. Optimization of train energy-efficient operation for mass rapid transit systems. IET Intell. Transp. Syst. 2012, 6, 58–66. [Google Scholar] [CrossRef]
- Lu, S.; Hillmansen, S.; Ho, T.K.; Roberts, C. Single-train trajectory optimization. IEEE Trans. Intell. Transp. Syst. 2013, 14, 743–750. [Google Scholar] [CrossRef]
- Azad, N.; Hassini, E.; Verma, M. Disruption risk management in railroad networks: An optimization-based methodology and a case study. Transp. Res. Part B 2016, 85, 70–88. [Google Scholar] [CrossRef]
- Wen, C.; Li, Z.; Lessan, J.; Fu, L.; Huang, P.; Jiang, C. Statistical investigation on train primary delay based on real records: Evidence from Wuhan–Guangzhou HSR. Int. J. Rail Transp. 2017, 5, 170–189. [Google Scholar] [CrossRef]
- Roßler, D.; Reisch, J.; Hauck, F.; Kliewer, N. Discerning Primary and Secondary Delays in Railway Networks using Explainable A.I. In Transportation Research Procedia; Elsevier: Amsterdam, The Netherslands, 2021; pp. 171–178. [Google Scholar] [CrossRef]
- Goverde, M.P. A delay propagation algorithm for large-scale railway traffic networks. Transp. Res. Part C Emerg. Technol. 2010, 18, 269–287. [Google Scholar] [CrossRef]
- Büker, T.; Seybold, B. Stochastic modelling of delay propagation in large networks. J. Rail Transp. Plan. Manag. 2012, 2, 34–50. [Google Scholar] [CrossRef]
- Şahin, İ. Markov chain model for delay distribution in train schedules: Assessing the effectiveness of time allowances. J. Rail Transp. Plan. Manag. 2017, 7, 101–113. [Google Scholar] [CrossRef]
- Vromans, M.J.C.M.; Dekker, R.; Kroon, L.G. Reliability and heterogeneity of railway services. Eur J. Oper. Res. 2006, 172, 647–665. [Google Scholar] [CrossRef]
- Andersson, E.V.; Peterson, A.; Törnquist, J. Quantifying railway timetable robustness in critical points. J. Rail Transp. Plan. Manag. 2014, 3, 95–110. [Google Scholar] [CrossRef] [Green Version]
- Salido, M.; Barber, F.; Ingolotti, L. Robustness in railway transportation scheduling. In Proceedings of the 2008 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 2880–2885. [Google Scholar]
- Salido, M.A.; Barber, F.; Ingolotti, L. Robustness for a single railway line: Analytical and simulation methods. Expert Syst. Appl. 2012, 39, 13305–13327. [Google Scholar] [CrossRef] [Green Version]
- Cerreto, F. Micro-simulation based analysis of railway lines robustness. In Proceedings of the 6th International Conference on Railway Operations Modelling and Analysis, Tokyo, Japan, 23–26 March 2015. [Google Scholar]
- Corman, F.; D’Ariano, A.; Hansen, I.A. Evaluating disturbance robustness of railway schedules. J. Intell. Transp. Syst. 2014, 18, 106–120. [Google Scholar] [CrossRef]
- Cacchiani, V.; Toth, P. Robust Train Timetabling. In Handbook of Optimization in the Railway Industry; International Series in Operations Research and Management Science 268; Springer: New York, NY, USA, 2018; pp. 93–115. [Google Scholar] [CrossRef]
- Schipper, D.; Gerrits, L. Differences and similarities in European railway disruption management practices. J. Rail Transp. Plan. Manag. 2018, 8, 42–55. [Google Scholar] [CrossRef]
- Takeuchi, Y.; Tomii, N. Robustness indices for train rescheduling. In Proceedings of the CDROM Proceedings of the 1st International Seminar on Railway Operations Modelling and Analysis, Delft, The Nethrlands, 7–9 June 2005. [Google Scholar]
- Goverde, R.M.P. Railway timetable stability analysis using max-plus system theory. Transp. Res. Part B Methodol. 2007, 41, 179–201. [Google Scholar] [CrossRef]
- Bešinović, N.; Goverde, R.M.P.; Quaglietta, E.; Roberti, R. An integrated micro-macro approach to robust railway timetabling. Transp. Res. Part B Methodol. 2016, 87, 14–32. [Google Scholar] [CrossRef] [Green Version]
- Andersson, E.V. Assessment of Robustness in Railway Traffic Timetables; Linköping University Electronic Press: Linköping, Sweden, 2014; p. 99. [Google Scholar]
- Shafia, M.A.; Pourseyed Aghaee, M.; Sadjadi, S.J.; Jamili, A. Robust train timetabling problem: Mathematical model and branch and bound algorithm. IEEE Trans. Intell. Transp. Syst. 2012, 13, 307–317. [Google Scholar] [CrossRef]
- Vansteenwegen, P.; Van Oudheusden, D. Developing railway timetables which guarantee a better service. Eur. J. Oper. Res. 2006, 173, 337–350. [Google Scholar] [CrossRef]
- Kroon, L.G.; Dekker, R.; Vromans, M.J.C.M. Cyclic railway timetabling: A stochastic optimization approach. In Algorithmic Methods in Railway Optimization; Geraets, F., Kroon, L.G., Schobel, A., Wagner, D., Zaroliagis, C., Eds.; Lecture Notes in Computer Science 4359; Erasmus Research Institute of Management: Rotterdam, The Netherlands, 2007; Volume 4359, pp. 41–66. [Google Scholar] [CrossRef]
- Andersson, E.V.; Peterson, A.; Törnquist Krasemann, J. Reduced railway traffic delays using a MILP approach to increase Robustness in Critical Points. J. Rail Transp. Plan. Manag. 2015, 5, 110–127. [Google Scholar] [CrossRef]
- Lee, Y.; Lu, L.S.; Wu, M.L.; Lin, D.Y. Balance of efficiency and robustness in passenger railway timetables. Transp. Res. Part B Methodol. 2017, 97, 142–156. [Google Scholar] [CrossRef]
- Meng, L.; Muneeb Abid, M.; Jiang, X.; Khattak, A.; Babar Khan, M. Increasing Robustness by Reallocating the Margins in the Timetable. J. Adv. Transp. 2019, 2019, 1382394. [Google Scholar] [CrossRef] [Green Version]
- Khoshniyat, F.; Peterson, A. Robustness Improvements in a Train Timetable with Travel Time Dependent Minimum Headways sures. In Proceedings of the 6th International Conference on Railway Operations Modelling and Analysis, Tokyo, Japan, 23–26 March 2015; pp. 1–17. [Google Scholar]
- Huang, P.; Wen, C.; Peng, Q.; Lessan, J.; Fu, L.; Jiang, C. A data-driven time supplements allocation model for train operations on high-speed railways. Int. J. Rail Transp. 2019, 7, 140–157. [Google Scholar] [CrossRef]
- Yang, X.; Hou, Y.; Li, L. Buffer time allocation according to train delay expectation at stations. Int. J. Rail Transp. 2020, 8, 249–263. [Google Scholar] [CrossRef]
- Burggraeve, S.; Vansteenwegen, P. Optimization of supplements and buffer times in passenger robust timetabling. J. Rail Transp. Plan. Manag. 2017, 7, 171–186. [Google Scholar] [CrossRef]
- Yuan, J.; Hansen, I.A. Optimizing capacity utilization of stations by estimating knock-on train delays. J. Transp. Res. Part B Methodol. 2007, 41, 202–217. [Google Scholar] [CrossRef]
- Yuan, J.; Hansen, I.A. Closed form expressions of optimal buffer times between scheduled trains at railway bottlenecks. In Proceedings of the 11th International IEEE Conference on Intelligent Transportation Systems, Beijing, China, 12–15 October 2008; pp. 675–680. [Google Scholar]
- Jovanović, P.; Kecman, P.; Bojović, N.; Mandić, D. Optimal allocation of buffer times to increase train schedule robustness. Eur. J. Oper. Res. 2017, 256, 44–54. [Google Scholar] [CrossRef]
- Nyström, B.; Söderholm, P. Improved railway punctuality by effective maintenance—A case study. In Advances in Safety and Reliability; Tylor & Francis Group: London, UK, 2005. [Google Scholar]
- Haładyn, S. The Problem of Train Scheduling in the Context of the Load on the Power Supply Infrastructure. A Case Study. Energies 2021, 14, 4781. [Google Scholar] [CrossRef]

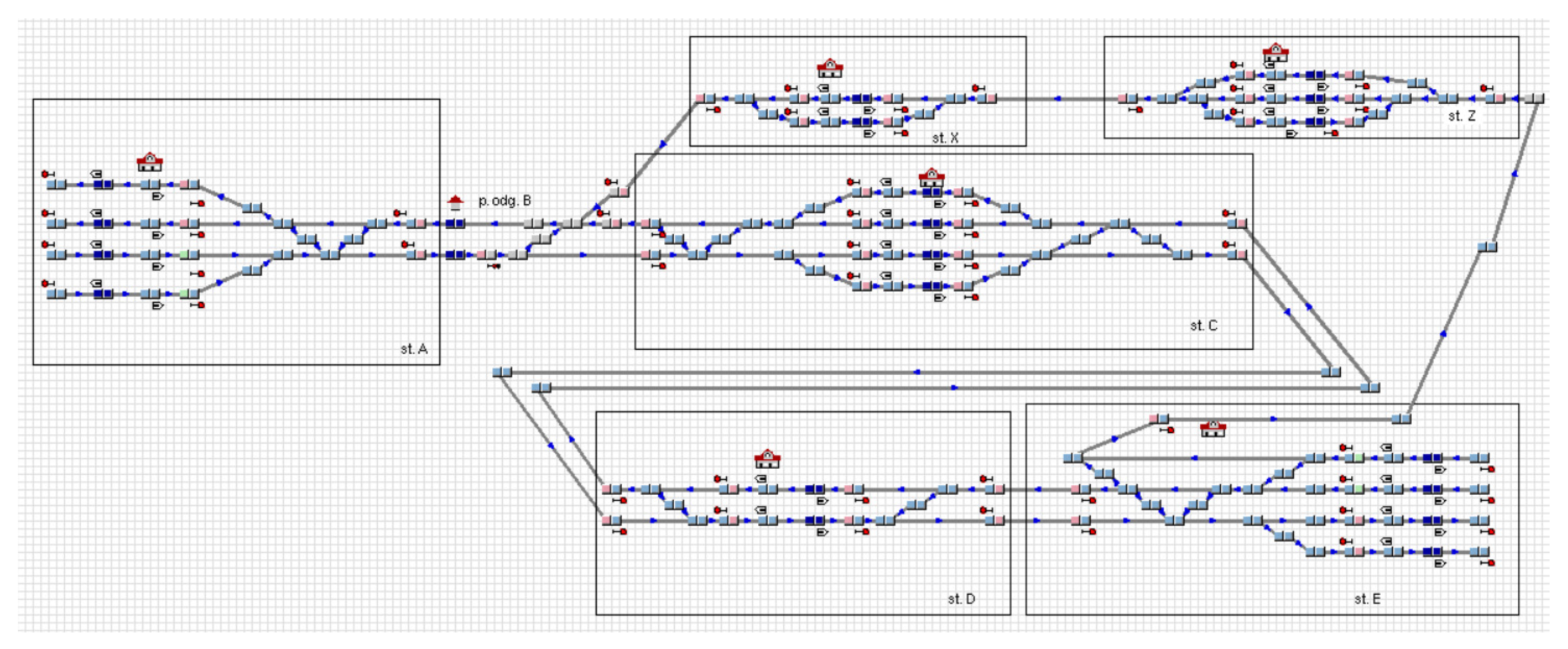
| Station | Number of Platforms | Number of Tracks |
|---|---|---|
| A | 5 | 4 |
| C | 4 | 4 |
| D | 2 | 2 |
| E | 5 | 4 |
| X | 1 | 2 |
| Z | 2 | 2 |
| Train Type | Target velocity | Distance to Reach the Target Velocity from Standstill during Acceleration | Time to Get the Target velocity from Standstill during Acceleration | Resistance force Under target Velocity | Energy Consumption for One Acceleration from Standstill to the Target Velocity | Energy Consumption for Movement with Constant Velocity (Target Velocity) | Increased Energy Consumption per One Acceleration from Standstill to the Target Velocity |
|---|---|---|---|---|---|---|---|
| (km/h) | (km) | (min) | (kN) | (kWh) | (kWh) | (kWh) | |
| Electric multiple unit 45We | 120 | 1.17 | 0.93 | 14.80 | 37.38 | 4.81 | 32.57 |
| EU07 locomotive with 6 passenger coaches | 2.72 | 2.03 | 30.50 | 89.68 | 23.04 | 66.64 |
| Section | Current Reserve (min) | Delay for 95% (min) | Reserve 0 (min) | Delay for 95% (min) | Reserve I Step (min) | Delay for 95% (min) | Reserve II Step (min) | Delay for 95% (min) | Reserve III Step (min) | Delay for 95% (min) | Reserve IV Step (min) | Delay for 95% (min) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A–B | 2.5 | 3 | 0 | 12 | 0.5 | 7 | 1.5 | 5 | 2.5 | 3 | 3 | 1.5 |
| B–C | 3 | 4 | 0 | 11 | 1.5 | 7 | 2.5 | 5 | 3 | 4 | 4 | 1.5 |
| C–E | 5 | 3 | 0 | 11 | 1.5 | 6 | 3.5 | 4 | 4.5 | 4 | 5.5 | 1.5 |
| A–Z | 5 | 2.5 | 0 | 9.5 | 2 | 6 | 2.5 | 5 | 4.5 | 3 | 5.5 | 2 |
| Z–E | 3.5 | 3 | 0 | 9.5 | 2 | 5 | 3.5 | 5 | 4 | 4 | 4.5 | 2 |
| Reserve | Express Train | Regio Train | ||
|---|---|---|---|---|
| No. of Unscheduled Stops | Energy Loss (MWh) | No. of Unscheduled Stops | Energy Loss (MWh) | |
| current reserve method | 21 | 1.40 | 24 | 0.79 |
| reserve 0 | 117 | 7.80 | 126 | 4.10 |
| reserve I step | 82 | 5.46 | 93 | 3.03 |
| reserve II step | 31 | 2.07 | 38 | 1.24 |
| reserve III step | 15 | 1.00 | 18 | 0.59 |
| reserve IV step | 6 | 0.40 | 8 | 0.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Restel, F.; Wolniewicz, Ł.; Mikulčić, M. Method for Designing Robust and Energy Efficient Railway Schedules. Energies 2021, 14, 8248. https://doi.org/10.3390/en14248248
Restel F, Wolniewicz Ł, Mikulčić M. Method for Designing Robust and Energy Efficient Railway Schedules. Energies. 2021; 14(24):8248. https://doi.org/10.3390/en14248248
Chicago/Turabian StyleRestel, Franciszek, Łukasz Wolniewicz, and Matea Mikulčić. 2021. "Method for Designing Robust and Energy Efficient Railway Schedules" Energies 14, no. 24: 8248. https://doi.org/10.3390/en14248248
APA StyleRestel, F., Wolniewicz, Ł., & Mikulčić, M. (2021). Method for Designing Robust and Energy Efficient Railway Schedules. Energies, 14(24), 8248. https://doi.org/10.3390/en14248248






