Physical Dimensions as a Design Objective in Heat Transfer Equipment: The Case of Plate and Fin Heat Exchangers †
Abstract
:1. Introduction
2. Surface Engineering
- Steady-state operation
- Continuous fin geometrical variables
- Single-phase heat transfer process
- Constant fluid properties
- Adiabatic operation
- Negligible longitudinal conduction effects
- Uniform heat transfer coefficient
- Uniform flow distribution
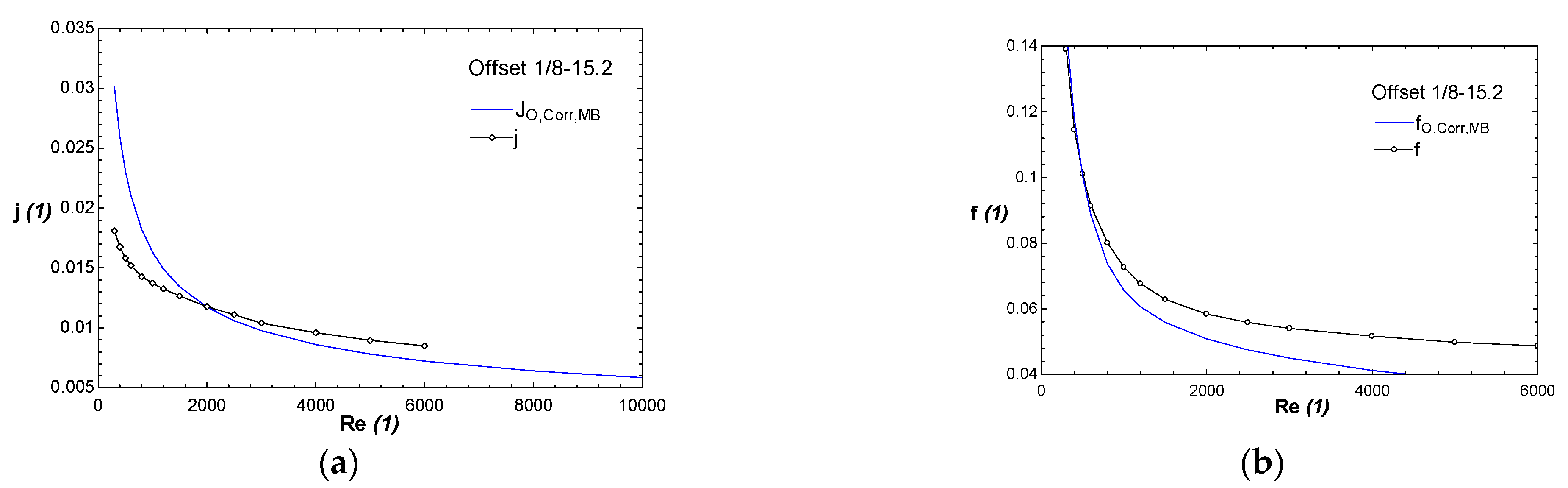
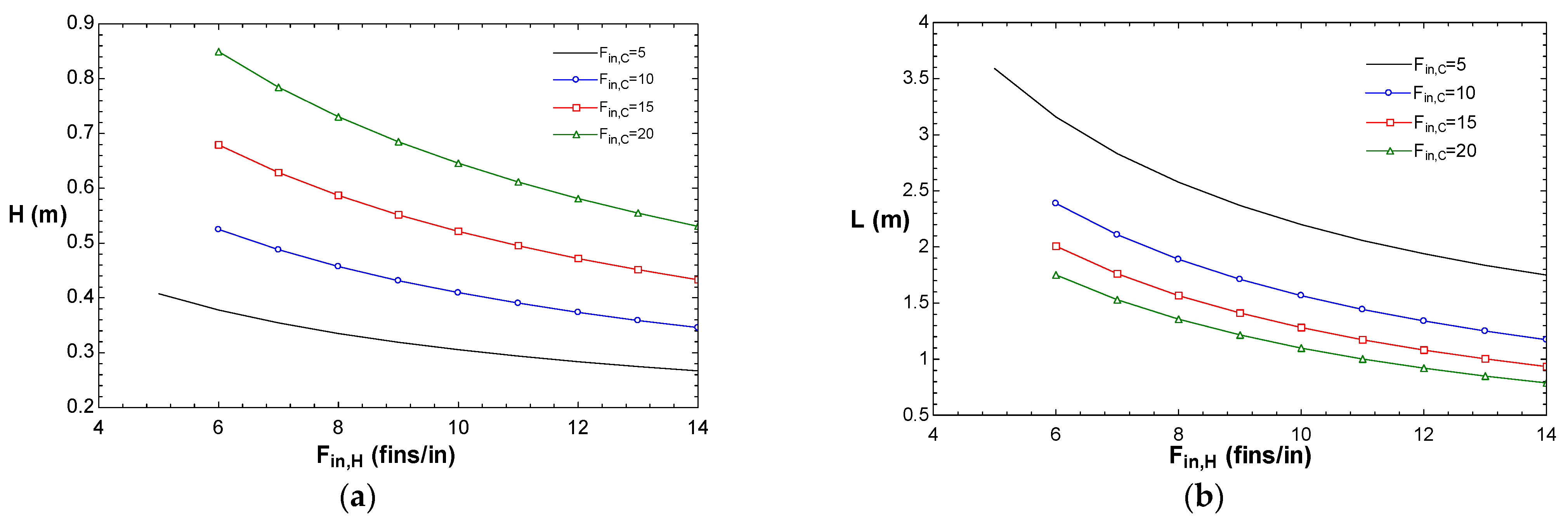
3. Choice of Generalised Correlations
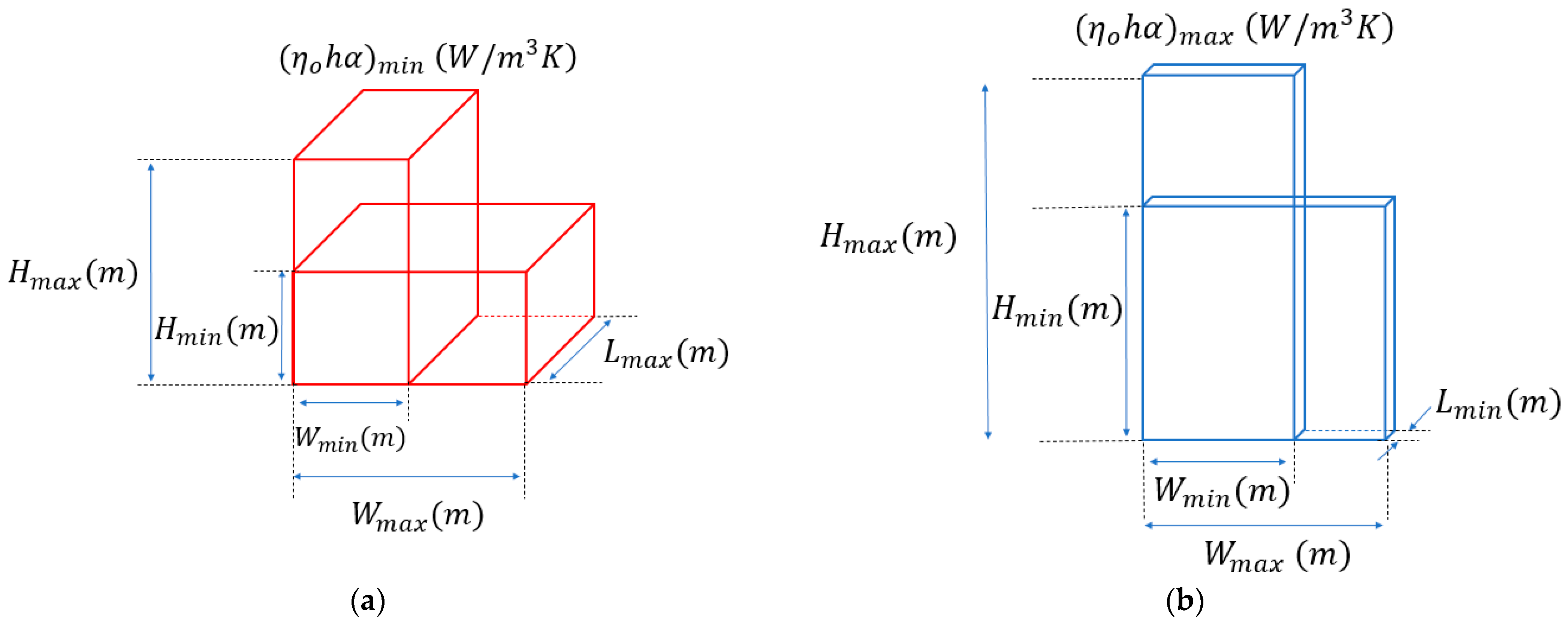
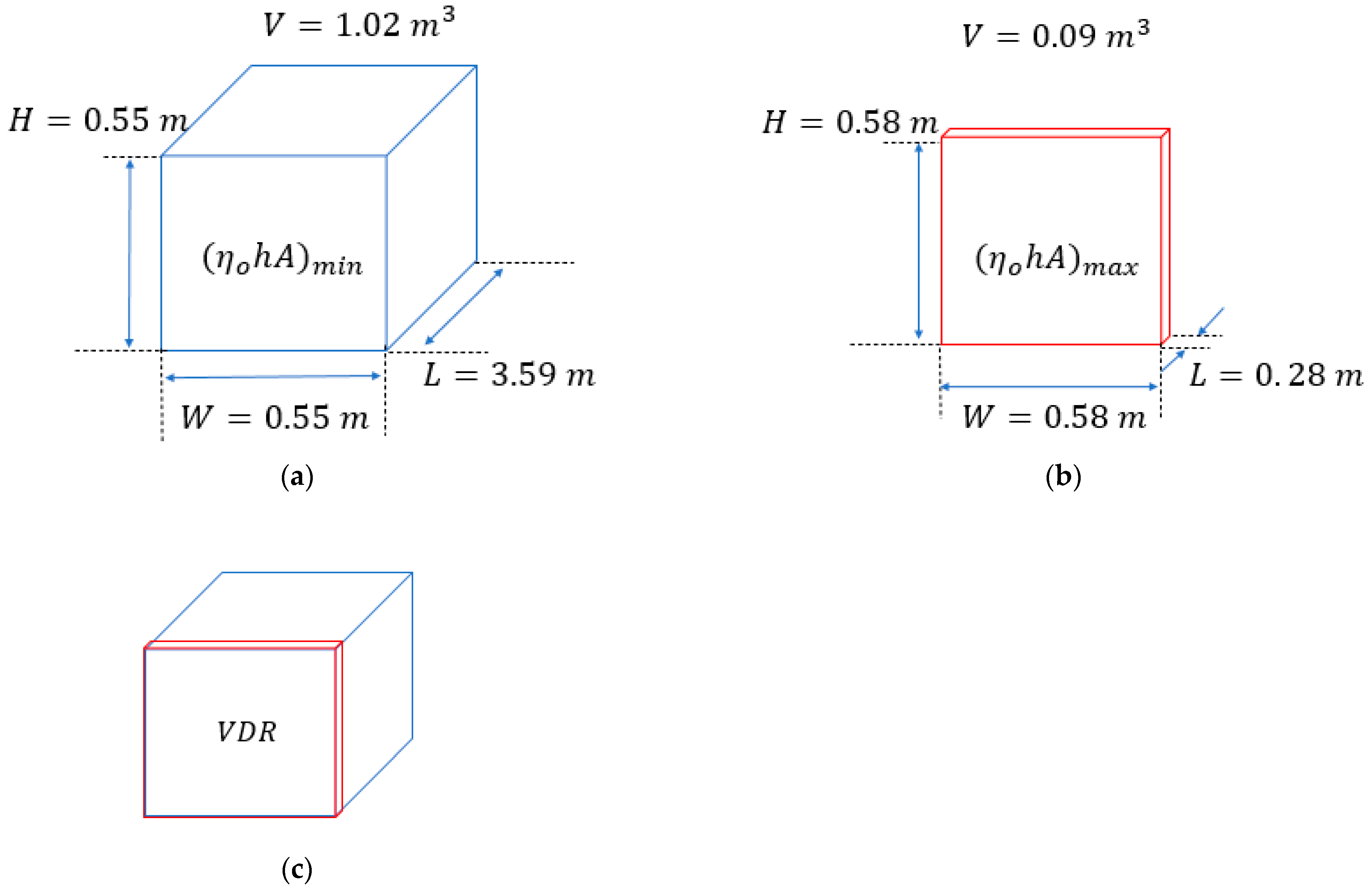
4. Volume Design Region
5. Case Study
6. Discussion
7. Conclusions
- The approach introduced in this work extended the typical scope of any design methodology. In the case of plate and fin exchangers, it was extended to cover the concept of the volume design region. In the case study discussed, it was demonstrated that for the same pressure drop, a 227.4 m2 shell and tube heat exchanger could be replaced by a plate and fin exchanger within a volume range from 1.96 m3 to 0.035 m3. The choice of the volume would depend on the exchanger dimensions required. For example, if the width and height were fixed at 0.75 m, the height would be 0.85 m giving a volume of 0.39 m3. This design was achieved with triangular surfaces with fin densities of 10.7 and 20 on the hot and cold sides.
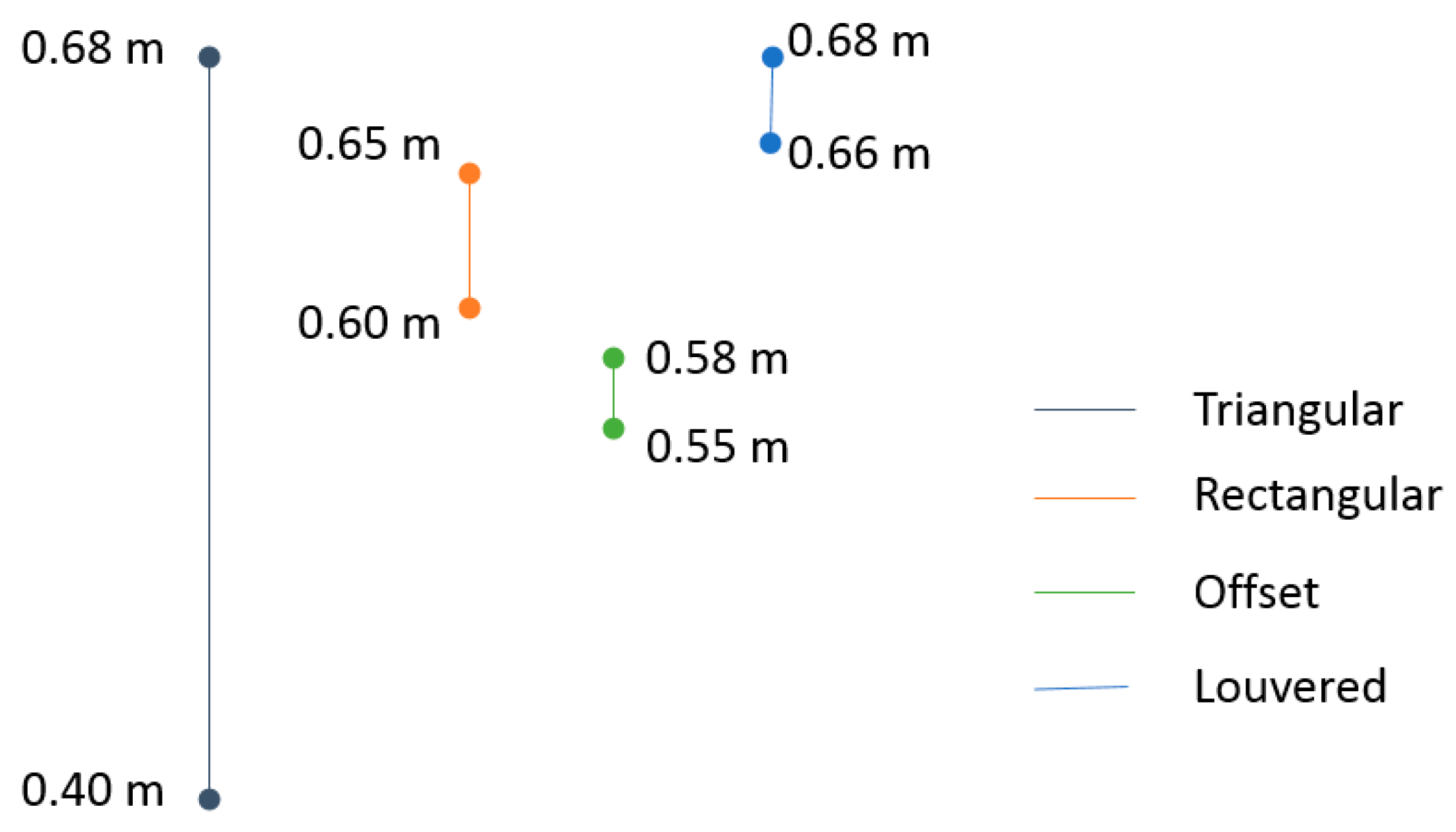
- Volume design regions were surface-type dependent. The volume design region using other surfaces such as louvered, offset strip, and rectangular fins were: 1.68 m3–0.045 m3; 1.02 m3–0.09 m3; and 3.37 m3–0.012 m3.
- Within the limits established by the volume design region, any surface frontal area and flow length could be designed. If offset strip-fins were chosen, the case study could be designed with a volume design region defined by height: 0.58 m; width: 0.58 m; and length: 3.59 m.
- The approach was limited by the Reynolds number range of validity of the generalised expressions for the heat transfer and friction factors. This called for the development of new generalised heat transfer and friction factor correlations.
- Fin density was the main geometrical parameter for the design specification of the secondary surface since all the other geometrical parameters could be derived from it.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Total surface area (m2) | |
| Surface area for side 1 or 2 (m2) | |
| Half the length of the base of the triangular fin (m) | |
| Ac | Free flow area (m2) |
| Surface area per fin (m2) | |
| Half the length of the base of the louvred fin (m) | |
| Base of offset fin (m) | |
| Total area of the secondary surface (m2) | |
| AR | Aspect ratio (1) |
| Base of the rectangular fin (m) | |
| Height of the louvered fin (m) | |
| Height of the triangular fin (m) | |
| Height of the offset fin (m) | |
| Height of the rectangular fin (m) | |
| Heat capacity (J/kg K) | |
| CP | Heat capacity-flow rate (W/K) |
| Deviation between experimental and correlation values of the Colburn factor (%) | |
| Average deviation between experimental and correlation values of the Colburn factor (%) | |
| Deviation between experimental and correlation values of the friction factor (%) | |
| Average deviation between experimental and correlation values of the friction factor (%) | |
| Hydraulic diameter (m) | |
| F | Correction factor of the mean temperature difference (1) |
| Flow depth in louvred surfaces (m) | |
| Fin density (fins per inch) | |
| Fin pitch (m) | |
| Fin thickness (m) | |
| Friction factor (1) | |
| Friction factor obtained from correlations (1) | |
| Friction factor obtained experimentally (1) | |
| Ratio of the secondary surface area to total surface area (1) | |
| H | Exchanger height (m) |
| Total exchanger height (m) | |
| Heat transfer coefficient (W/m2 K) | |
| Colburn factor (1) | |
| Colburn factor obtained from correlations (1) | |
| Colburn factor obtained experimentally (1) | |
| L | Exchanger length (m) |
| Louvered angle (°) | |
| Louvered pitch (m) | |
| Length of the uninterrupted flow in offset fin (m) | |
| m | Mass flow rate (kg/s) |
| n | Number of experimental elements (1) |
| Number of passages per stream (1) | |
| Number of total passages (1) | |
| Pr | Prandtl number (1) |
| Plate thickness (m) | |
| Wetted perimeter (m) | |
| Q | Heat load (W) |
| Reynolds number (1) | |
| Rf | Thermal resistance due to fouling (m2 K/W) |
| Wall thermal resistance (m2 K/W) | |
| Stanton number (1) | |
| T | Temperature (K) |
| Temperature of the cold stream (K) | |
| Temperature of the hot stream (K) | |
| Overall heat transfer coefficient, W/m2 K | |
| Total exchanger volume (m3) | |
| Volume of one side of the exchanger (m3) | |
| W | Exchanger width (m) |
| Subscripts | |
| 1 | Side 1 |
| 2 | Side 2 |
| C | Cold side |
| H | Hot side |
| t | Triangular fin |
| R | Rectangular fin |
| O | Offset fin |
| Louvered fin | |
| Greek letters | |
| Total heat transfer area of side i of the exchanger to total exchanger volume (m2/m3) | |
| Area density (m2/m3) | |
| Pressure drop (Pa) | |
| Logarithmic mean temperature difference (K) | |
| Plate spacing (m) | |
| Fin efficiency (1) | |
| Overall fin temperature effectiveness (1) | |
| Half the value of the characteristic angle for triangular surfaces (°) | |
| Half the value of the characteristic angle for louvred surfaces (°) | |
| Thermal conductivity (W/m K) | |
| Thermal conductivity of the fin material (W/m K) | |
| Viscosity (kg/m s) | |
| Fluid density (kg/m3) | |
| Geometrical parameter in offset surfaces (1) | |
| Geometrical parameter in offset surfaces (1) | |
| Geometrical parameter in offset surfaces (1) | |
References
- Arie, M.A.; Shooshtari, A.H.; Ohadi, M.M. Experimental characterization of an additively manufactured heat exchanger for dry cooling of power plants. Appl. Therm. Eng. 2018, 129, 187–198. [Google Scholar] [CrossRef]
- Hathaway, B.J.; Garde, K.; Mantell, S.C.; Davidson, J.H. Design and characterization of an additive manufactured hydraulic oil cooler. Int. J. Heat Mass Transfer. 2018, 117, 188–200. [Google Scholar] [CrossRef]
- Buyruk, E.; Karabulut, K. Research of Heat Transfer Augmentation in Plate Fin Heat Exchangers Having Different Fin Types. J. Eng. Thermophys. 2020, 29, 316–330. [Google Scholar] [CrossRef]
- García, J.L.; Picón, M. The Sizing of Plate-Fin Exchangers to Fixed Dimensions Within a Volume Design Region. Chem. Eng. Trans. 2020, 81, 559–564. [Google Scholar]
- Jiang, Q.; Zhuanga, M.; Zhang, Q.; Zhua, Z.; Geng, M.; Sheng, L.; Zhu, P. Experimental study on the thermal hydraulic performance of plate-fin heat exchangers for cryogenic applications. Cryogenics 2018, 91, 58–67. [Google Scholar] [CrossRef]
- Yang, H.; Li, Y.; Yang, Y.; Zhu, Y.; Wen, J. Effect of surface efficiency on the thermal design of plate-fin heat exchangers with passages stack arrangement. Int. J. Heat Mass Transf. 2019, 143, 118494. [Google Scholar] [CrossRef]
- Aasi, H.; Mishra, M. Experimental investigation and ANN modelling on thermo-hydraulic efficacy of cross-flow three-fluid plate-fin heat exchanger. Int. J. Therm. Sci. 2021, 164, 106870. [Google Scholar] [CrossRef]
- Kays, W.M.; London, A.L. Compact Heat Exchangers; Mac Graw Hill: New York, NY, USA, 1984. [Google Scholar]
- Rui, S.; Mengmeng, C.; Jianjun, L. A correlation for heat transfer and flow friction characteristics of the offset strip fin heat exchanger. Int. J. Heat Mass Transf. 2017, 115, 695–705. [Google Scholar]
- Gong, J.; Onishi, J.; He, A.; Hasegawa, Y.; Shikazono, N. Heat transfer enhancement and pressure loss in a plate-fin heat exchanger with V-shaped oblique wavy surface. Int. J. Heat Mass Transf. 2020, 161, 120263. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Si, B.; Zheng, J. Heat transfer performances of cryogenic fluids in offset strip fin-channels considering the effect of fin efficiency. Int. J. Heat Mass Transf. 2017, 114, 1114–1125. [Google Scholar] [CrossRef]
- Hu, H.; Li, J. Experimental investigation on heat transfer characteristics of two-phase flow boiling in offset strip fin channels of plate-fin heat exchangers. Appl. Therm Eng. 2021, 185, 116404. [Google Scholar] [CrossRef]
- Wang, G.; Dbouk, T.; Wang, D.; Pei, Y.; Peng, X.; Yuan, H.; Xiang, S. Experimental and numerical investigation on hydraulic and thermal performance in the tube-side of helically coiled-twisted trilobal tube heat exchanger. Int. J. Therm. Sci. 2020, 153, 106328. [Google Scholar] [CrossRef]
- Bianco, N.; Iasiello, M.; Mauro, G.M.; Pagano, L. Multi-objective optimization of finned metal foam heat sinks: Tradeoff between heat transfer and pressure drop. Appl. Therm. Eng. 2021, 182, 116058. [Google Scholar] [CrossRef]
- Han, Y.; Wang, X.S.; Zhang, H.N.; Chen, Q.Z.; Zhang, Z. Multi-objective optimization of helically coiled tube heat exchanger based on entropy generation theory. Int. J. Therm. Sci. 2020, 147, 106150. [Google Scholar] [CrossRef]
- Kunpeng, G.; Shang, N.; Smith, R. Optimization of fin selection and thermal design of counter-current plate-fin heat exchangers. Appl Therm. Eng. 2015, 78, 491–499. [Google Scholar]
- Khan, T.A.; Li, W. Optimal design of plate-fin heat exchanger by combining multi-objective algorithms. Int. J. Heat Mass Transf. 2017, 108, 1560–1572. [Google Scholar] [CrossRef] [Green Version]
- Ramezanpour, R.; Ghazi, M.; Sotoodeh, A.F.; Nikian, M. Plate-fin heat exchanger network modeling, design and optimization—A novel and comprehensive algorithm. J. Eng. Des. Tech. 2021, in press. [Google Scholar]
- do Nascimento, C.; Mariani, V.; Coelho, L. Integrative numerical modeling and thermodynamic optimal design of counter-flow plate-fin heat exchanger applying neural networks. Int. J. Heat Mass Transf. 2020, 159, 120097. [Google Scholar] [CrossRef]
- Yu, C.; Xue, X.; Shi, K.; Shao, M. A three-dimensional numerical and multi-objective optimal design of wavy plate-fins heat exchangers. Processes 2021, 9, 9. [Google Scholar] [CrossRef]
- Li, K.; Wen, J.; Liu, Y.; Wang, S.; Tu, J. Application of entransy theory on structure optimization of serrated fin in plate-fin heat exchanger. Appl. Therm. Eng. 2020, 173, 114809. [Google Scholar] [CrossRef]
- Tariqa, A.; Altafa, K.; Ahmada, S.; Hussainc, G.; Ratlamwalad, T. Comparative numerical and experimental analysis of thermal and hydraulic performance of improved plate fin heat sinks. Appl. Therm. Eng. 2021, 182, 115949. [Google Scholar] [CrossRef]
- Tao, C.; Jie, W.; Wei, P. Flow and heat transfer analyses of a plate-fin heat exchanger in an HTGR. Ann. Nucl. Energy 2017, 108, 316–328. [Google Scholar]
- Picón, M.; Carreon, C.E.; Polley, G.T. The Engineering of Compact Exchangers to Required Dimensions. In Proceedings of the 1st Annual Gas Processing Symposium, Doha, Qatar, 10–12 January 2009; Elsevier B.V.: Amsterdam, The Netherlands, 2018; pp. 88–95. [Google Scholar]
- García, J.L.; Picón, M. Design of plate-fin surfaces for multi-fluid heat exchanger applications. Energy 2019, 181, 294–306. [Google Scholar] [CrossRef]
- Chennu, R. Numerical analysis of compact plate-fin heat exchangers for aerospace applications. Int. J. Numer. Method H 2018, 24, 395–412. [Google Scholar] [CrossRef]
- Picón, M.; Polley, G.T.; Torres, E.; Gallegos, A. Surface selection and design of plate fin heat exchangers. Appl. Therm. Eng. 1999, 19, 917–931. [Google Scholar] [CrossRef]
- Diani, A.; Mancin, S.; Rossetto, L. Experimental and numerical analyses of different extended surfaces. JPCS 2012, 395, 012045. [Google Scholar] [CrossRef]
- Erbay, L.B.; Doğan, B.; Öztürk, M. Comprehensive Study of Heat Exchangers with Louvered Fins. In Heat Exchangers Advances Features and Applications; Mushed, S., Matos, M., Eds.; InTechOpen: Rijeka, Croatia, 2017. [Google Scholar]
- Costa, A.L.; Queiroz, E.M. Design optimization of Shell and tube heat exchangers. Appl. Therm. Eng. 2008, 28, 1798–1805. [Google Scholar] [CrossRef]
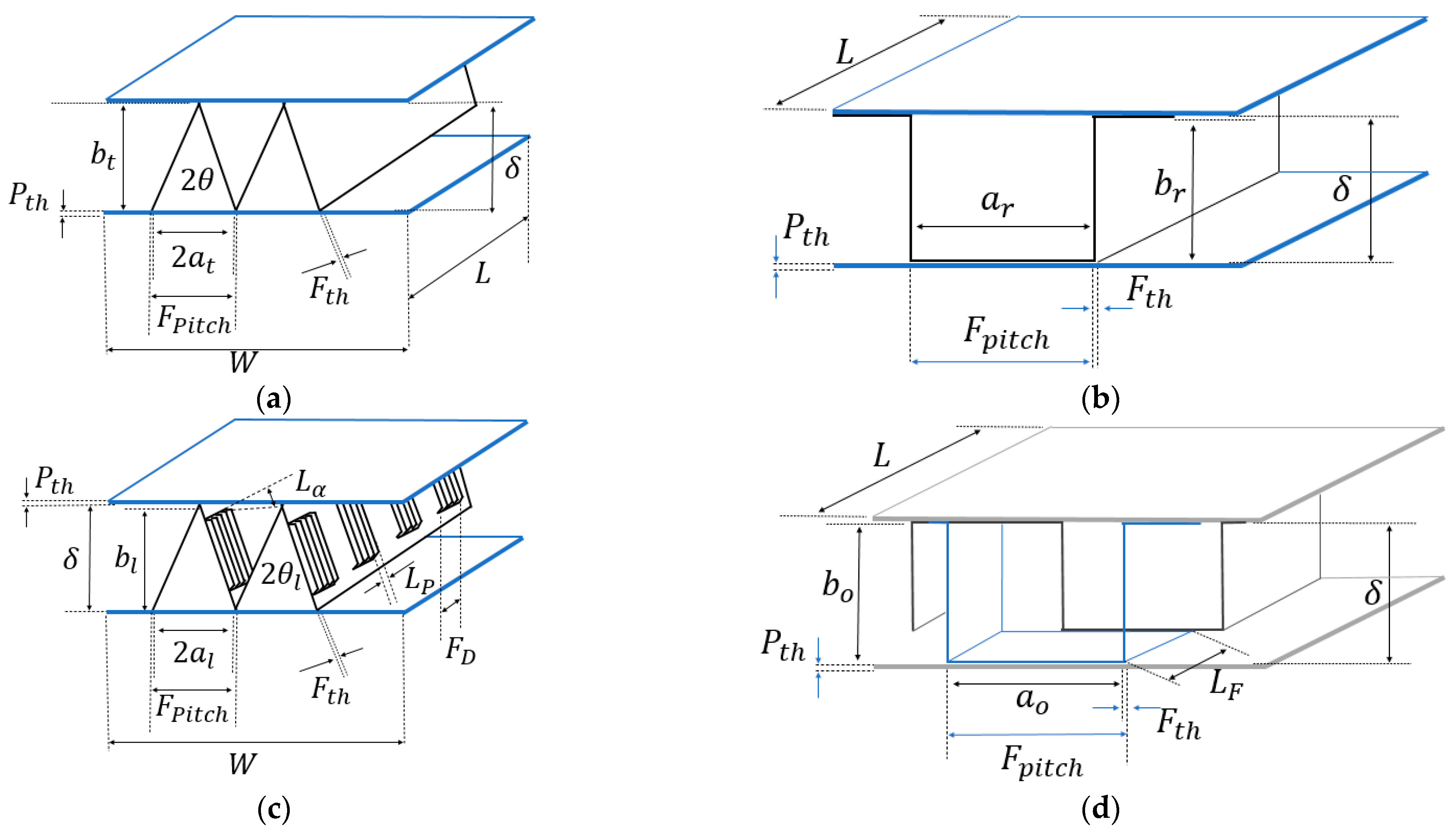
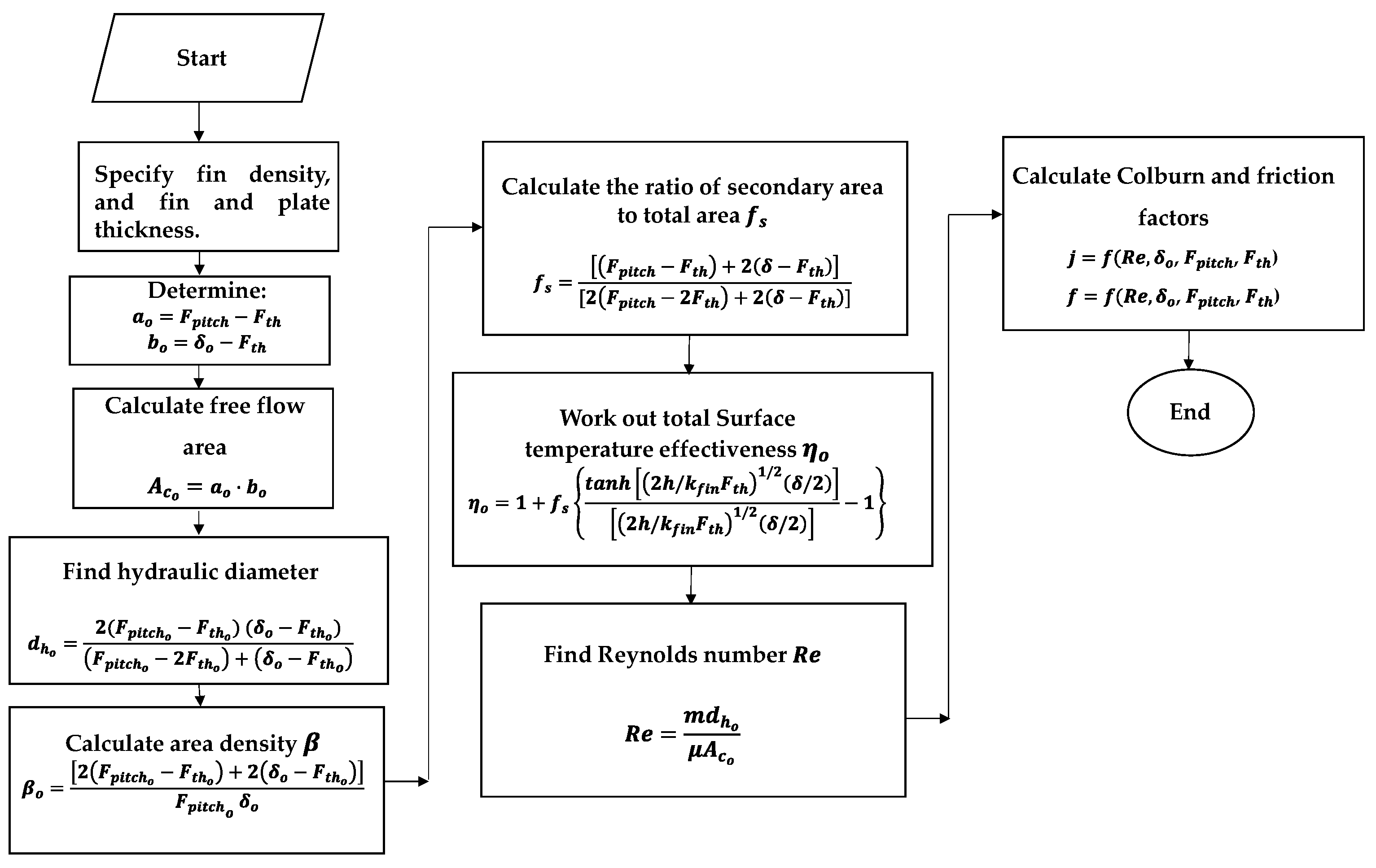
| Surface Type | ||||
|---|---|---|---|---|
| Triangular | (7) | (8) | ||
| Rectangular | (9) | (10) | ||
| Offset | (11) | (12) | ||
| Louvered | (13) | (14) |
| Surface Type | ||||
|---|---|---|---|---|
| Triangular | (15) | (16) | ||
| Rectangular | (17) | (18) | ||
| Offset | (19) | (20) | ||
| Louvered | (21) | (22) |
| Expression | Range of Validity | Std Dev | Notes | |
|---|---|---|---|---|
| Rectangular surfaces | ||||
| (34) | ±5.3% | [28] | ||
| (35) | ±3.4% | [28] | ||
| (36) | ||||
| Triangular surfaces | ||||
| (37) | ±12% | [28] | ||
| (38) | ±12% | [28] | ||
| (39) | ±11% | [28] | ||
| (40) | ±11% | [28] | ||
| Offset strip-fin surfaces | ||||
| (41) | [9] | |||
| (42), | ||||
| (43) | ||||
| (44) | ||||
| (45) | [9] | |||
| (46) | ||||
| (47) | [9] | |||
| (48) | ||||
| (49) | (50) | |||
| Louvered surfaces | ||||
| (51) | [29] | |||
| (52) | ||||
| (53) | [29] | |||
| (1) | (1) | (1) | (1) | (1) | (1) | (1) | (%) | (%) |
|---|---|---|---|---|---|---|---|---|
| 300 | 0.0181 | 0.139 | 0.03017 | 0.01938 | 0.1456 | −67% | −7% | −5% |
| 400 | 0.01675 | 0.1145 | 0.02595 | 0.01777 | 0.1178 | −55% | −6% | −3% |
| 500 | 0.0158 | 0.101 | 0.02312 | 0.01677 | 0.1003 | −46% | −6% | 1% |
| 600 | 0.0152 | 0.0913 | 0.02106 | 0.01607 | 0.0883 | −39% | −6% | 3% |
| 800 | 0.01427 | 0.08 | 0.01821 | 0.01512 | 0.07358 | −28% | −6% | 8% |
| 1000 | 0.01373 | 0.0726 | 0.01631 | 0.01447 | 0.06546 | −19% | −5% | 10% |
| 1200 | 0.01327 | 0.0676 | 0.01492 | 0.01397 | 0.06051 | −12% | −5% | 10% |
| 1500 | 0.01267 | 0.0628 | 0.01341 | 0.01337 | 0.05577 | −6% | −6% | 11% |
| 2000 | 0.01177 | 0.0584 | 0.01173 | 0.01259 | 0.0508 | 0% | −7% | 13% |
| 2500 | 0.0111 | 0.0558 | 0.0106 | 0.01195 | 0.04744 | 5% | −8% | 15% |
| 3000 | 0.0104 | 0.054 | 0.009769 | 0.0114 | 0.04489 | 6% | −10% | 17% |
| 4000 | 0.00959 | 0.0516 | 0.00861 | 0.01047 | 0.04117 | 10% | −9% | 20% |
| 5000 | 0.00896 | 0.0498 | 0.007821 | 0.00969 | 0.03851 | 13% | −8% | 23% |
| 6000 | 0.0085 | 0.0487 | 0.007236 | 0.009017 | 0.03646 | 15% | −6% | 25% |
| Standard Deviation (%) | |||
|---|---|---|---|
| Surface | j Equation (43) | j Equation (49) | f Equation (47) |
| 1/8-15.2 | 27% | 1% | 9% |
| 1/8-19.82 (D) | 2% | 2% | 7% |
| 1/8-13.95 | 5% | 13% | 5% |
| 1/8-15.61 | 20% | 5% | 13% |
| 1/8-19.86 | 18% | 4% | 2% |
| 1/8-16.12 (T) | 18% | 11% | 14% |
| 1/8-20.06 (D) | 16% | 4% | 4% |
| 1/8-16.00 (D) | 16% | 4% | 4% |
| 1/8-16.12 (D) | 17% | 9% | 5% |
| 1/8-24.12 | 14% | 2% | 14% |
| 1/9-25.01 | 14% | 3% | 4% |
| 1/9-22.68 | 26% | 26% | 3% |
| 1/10-27.03 | 17% | 2% | 2% |
| 1/10-19.35 | 16% | 3% | 8% |
| 1/10-19.74 | 16% | 6% | 10% |
| Avg std dev | 16% | 6% | 7% |
| Flow Stream Parameters | Cold Stream | Hot Stream |
|---|---|---|
| Mass flow rate (kg/s) | 101.40 | 30 |
| Pressure drop (Pa) | 10,000 | 25,000 |
| Inlet temperature (K) | 303.15 | 363.15 |
| Outlet temperature (K) | 313.15 | 313.15 |
| Density (kg/m3) | 995.0 | 750 |
| Heat capacity (J/kg K) | 4200 | 2840 |
| Thermal conductivity (W/m K) | 0.59 | 0.19 |
| Viscosity (kg/m s) | 0.00034 | 0.0008 |
| Heat capacity mass flow rate CP (W/K) | 425,880 | 85,200 |
| Thermal conductivity material of construction (W/m K) | 16.30 | |
| Heat load (W) | 4,260,000 | |
| Plate spacing (m) | 0.0065 | |
| Fin thickness (m) | 0.0003 | |
| Plate thickness (m) | 0.002 | |
| Dimension | Triangular | Rectangular | Offset Strip-Fin | Louvered | ||||
|---|---|---|---|---|---|---|---|---|
| Fin (Fins/In) | Fin (Fins/In) | Fin (Fins/In) | Fin (Fins/In) | |||||
| Fin = 4 | Fin = 28.2 | Fin = 1 | Fin = 28.2 | Fin = 5 | Fin = 28.2 | Fin = 1 | Fin = 28.2 | |
| Volume (m3) | 1.96 | 0.035 | 3.37 | 0.012 | 1.02 | 0.09 | 1.68 | 0.045 |
| Width (m) | 0.405 | 0.68 | 0.60 | 0.65 | 0.55 | 0.58 | 0.68 | 0.66 |
| Height (m) | 0.405 | 0.68 | 0.60 | 0.65 | 0.55 | 0.58 | 0.68 | 0.66 |
| Length (m) | 14.73 | 0.09 | 10.17 | 0.03 | 3.59 | 0.28 | 4.25 | 0.28 |
| Free flow area (m2) | 0.058 0.058 | 0.061 0.061 | 0.16 0.16 | 0.13 0.13 | 0.13 0.13 | 0.10 0.10 | 0.19 0.19 | 0.12 0.12 |
| Reynolds number (1) | 2520 20,040 | 198 1580 | 5164 41,070 | 340.7 2710 | 4435 35,270 | 852.40 6780 | 1714 13,630 | 184.6 1470 |
| Surface area (m2) | 778.3 778.3 | 62.63 62.63 | 283.2 283.2 | 131.7 131.7 | 234.2 234.2 | 96.35 96.35 | 340.50 340.50 | 89 89 |
| Pressure drop (Pa) | 7791 10,000 | 8637 10,000 | 1161 10,000 | 1161 10,000 | 2160 10,000 | 2215 10,000 | 817.70 10,000 | 277.40 10,000 |
| Dimension | Triangular | Rectangular | Offset Strip-Fin | Louvered | ||||
|---|---|---|---|---|---|---|---|---|
| Fin (Fins/In) | Fin (Fins/In) | Fin (Fins/In) | Fin (Fins/in) | |||||
| Hot Side | Cold Side | Hot Side | Cold Side | Hot Side | Cold Side | Hot Side | Cold Side | |
| Fin = 10.7 | Fin = 20 | Fin = 8.4 | Fin = 20 | Fin = 7.6 | Fin = 20 | Fin = 17.6 | Fin = 20 | |
| Volume (m3) | 0.39 | 0.63 | 0.74 | 0.09 | ||||
| Width (m) | 0.75 | 0.75 | 0.75 | 0.75 | ||||
| Height (m) | 0.75 | 0.75 | 0.75 | 0.75 | ||||
| Length (m) | 0.85 | 1.20 | 1.42 | 0.18 | ||||
| Free flow area (m2) | 0.16 | 0.12 | 0.23 | 0.20 | 0.23 | 0.19 | 0.19 | 0.18 |
| Reynolds number (1) | 381.70 | 1788 | 1706 | 5679 | 1706 | 5679 | 226.4 | 1599 |
| Surface area (m2) | 301 | 512.60 | 220.70 | 484.50 | 241.1 | 576.6 | 113.7 | 128 |
| Pressure drop (Pa) | 1257 | 10,000 | 332.60 | 10,000 | 488.2 | 10,000 | 88.54 | 10,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Castillo, J.; Picón-Núñez, M. Physical Dimensions as a Design Objective in Heat Transfer Equipment: The Case of Plate and Fin Heat Exchangers . Energies 2021, 14, 2318. https://doi.org/10.3390/en14082318
García-Castillo J, Picón-Núñez M. Physical Dimensions as a Design Objective in Heat Transfer Equipment: The Case of Plate and Fin Heat Exchangers . Energies. 2021; 14(8):2318. https://doi.org/10.3390/en14082318
Chicago/Turabian StyleGarcía-Castillo, Jorge, and Martín Picón-Núñez. 2021. "Physical Dimensions as a Design Objective in Heat Transfer Equipment: The Case of Plate and Fin Heat Exchangers " Energies 14, no. 8: 2318. https://doi.org/10.3390/en14082318
APA StyleGarcía-Castillo, J., & Picón-Núñez, M. (2021). Physical Dimensions as a Design Objective in Heat Transfer Equipment: The Case of Plate and Fin Heat Exchangers . Energies, 14(8), 2318. https://doi.org/10.3390/en14082318






