Research on the Power Capture and Wake Characteristics of a Wind Turbine Based on a Modified Actuator Line Model
Abstract
1. Introduction
2. Materials and Method
2.1. Governing Equations
2.2. Modified Actuator Line Model
2.3. Simulation Setup
2.3.1. Reference Wind Turbine
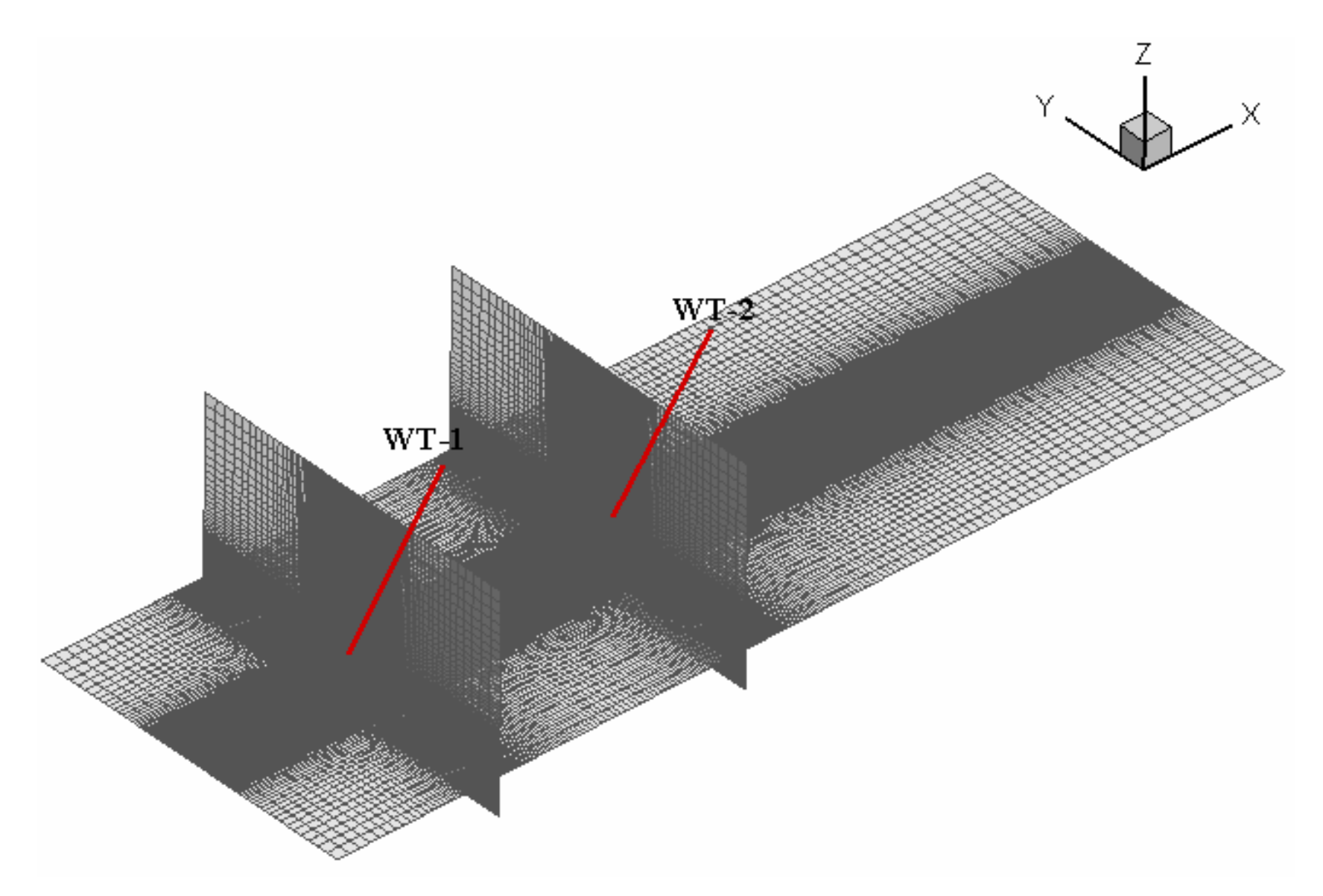
2.3.2. Computational Domain and Grid Setup
2.3.3. Boundary Conditions and Model Settings
3. Results and Discussion
3.1. Verification of the Modified Actuator Line Model
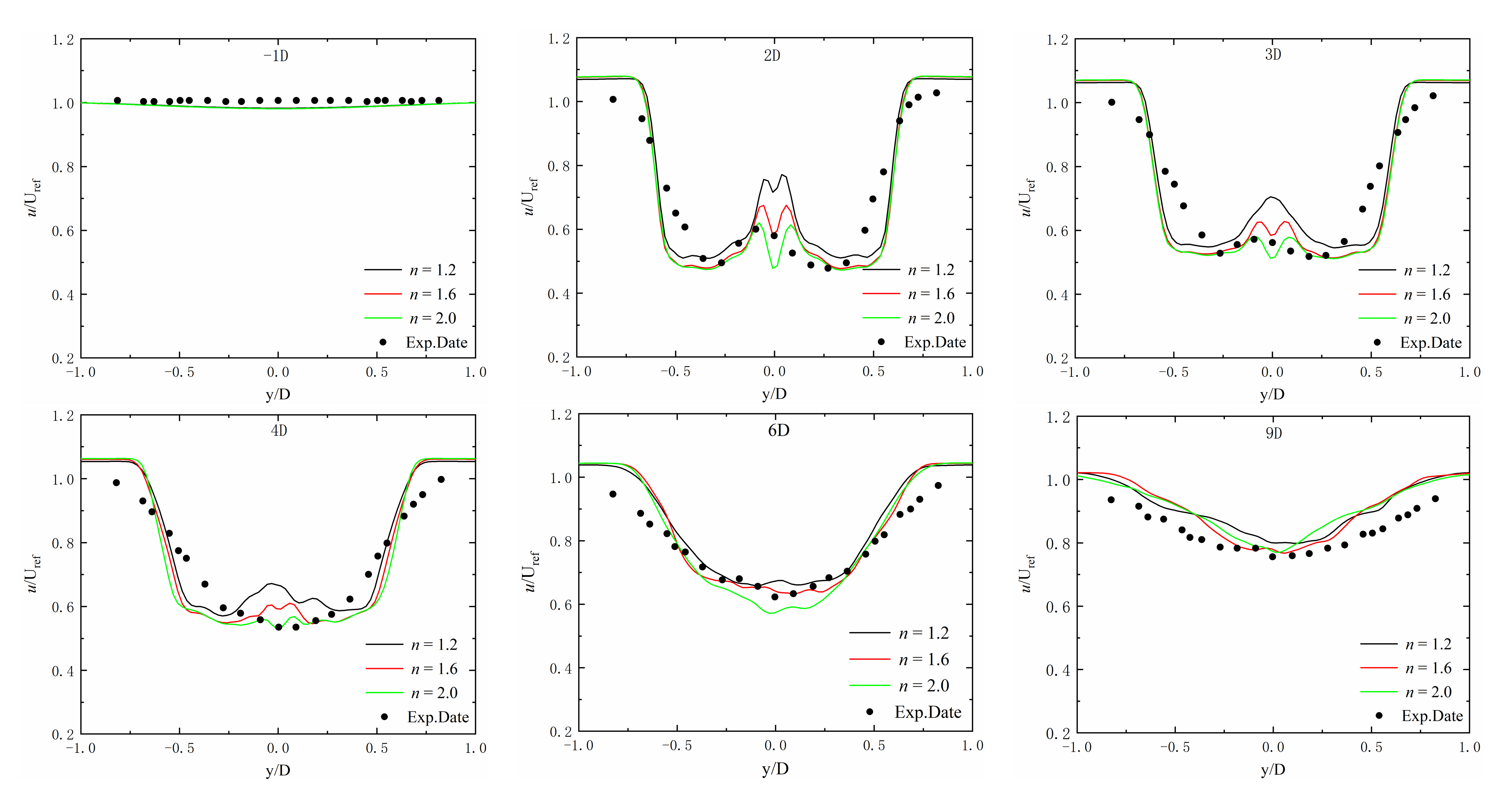
3.1.1. Analysis of Smoothing Parameters
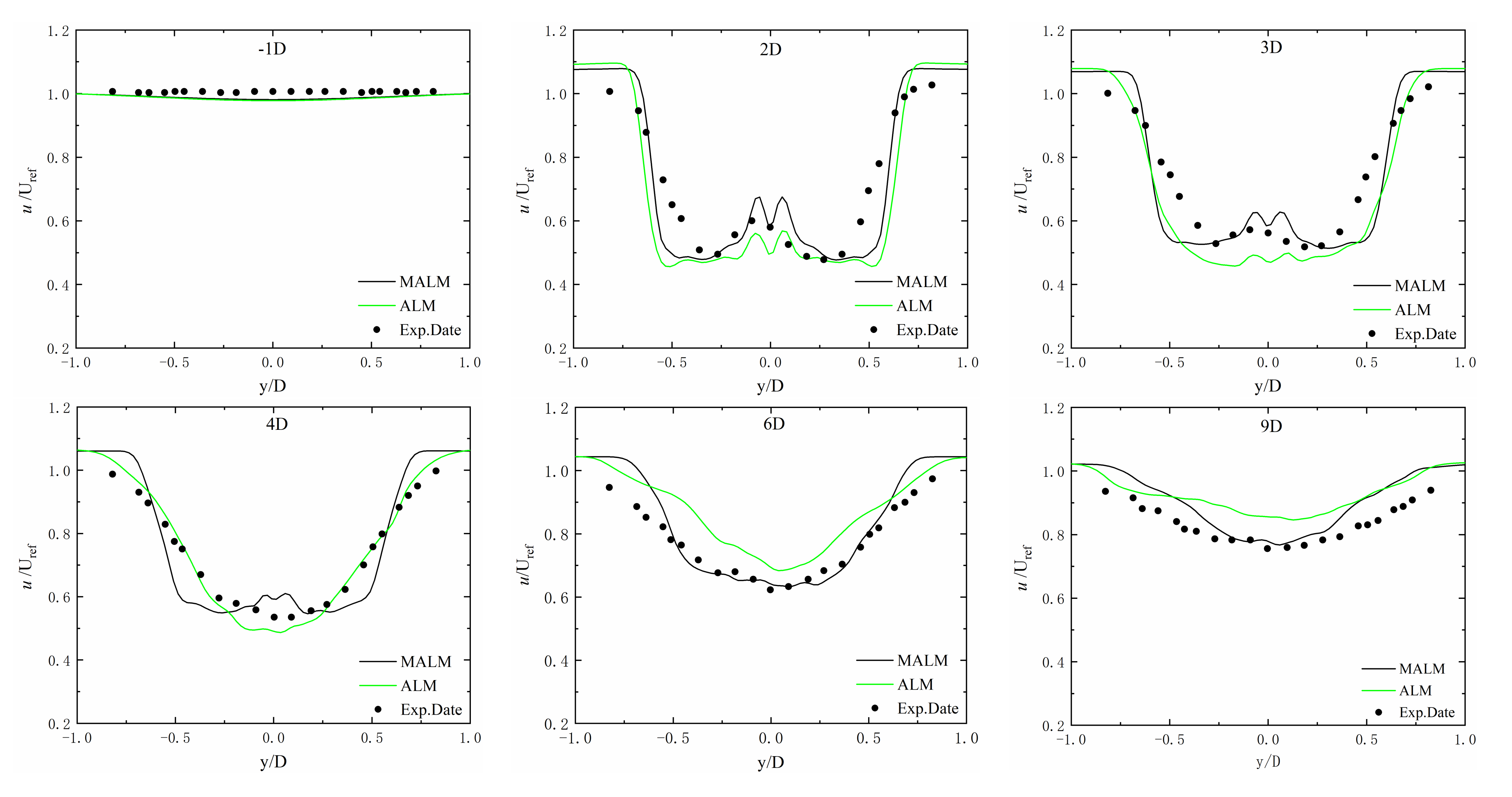
3.1.2. Model Validation
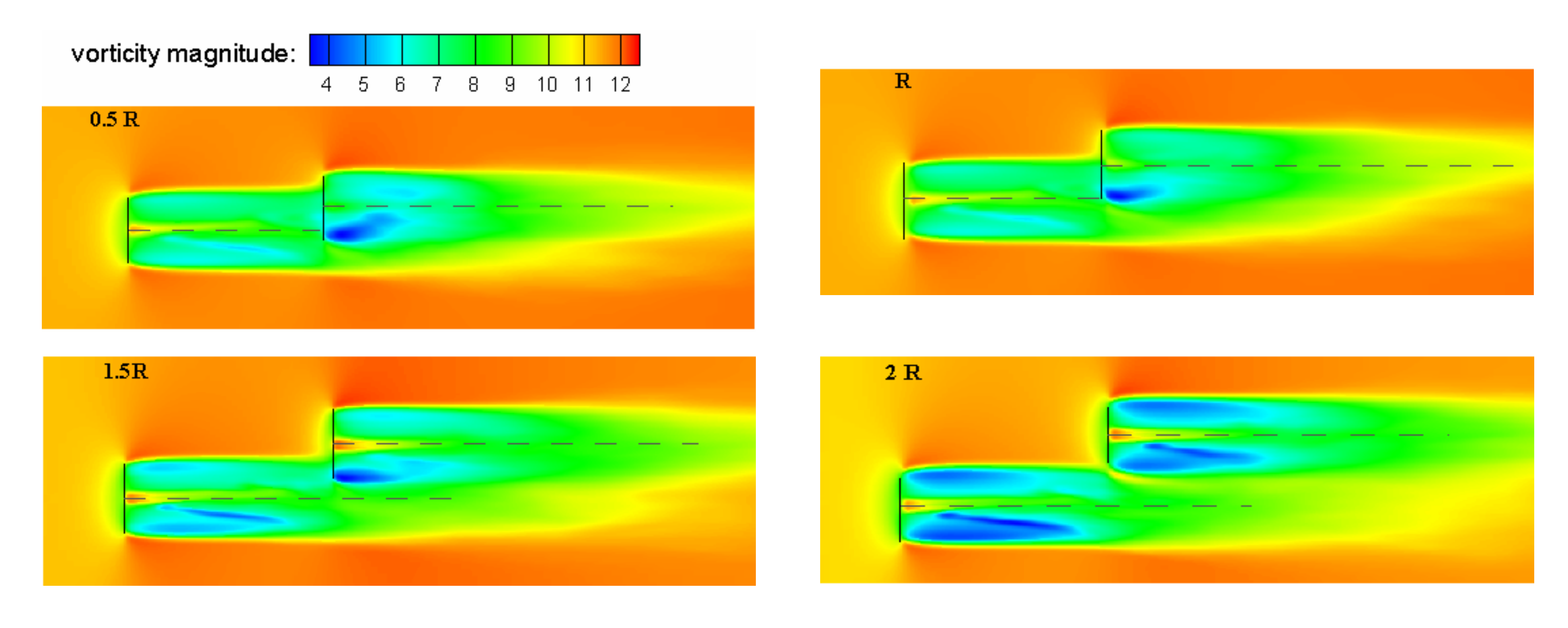
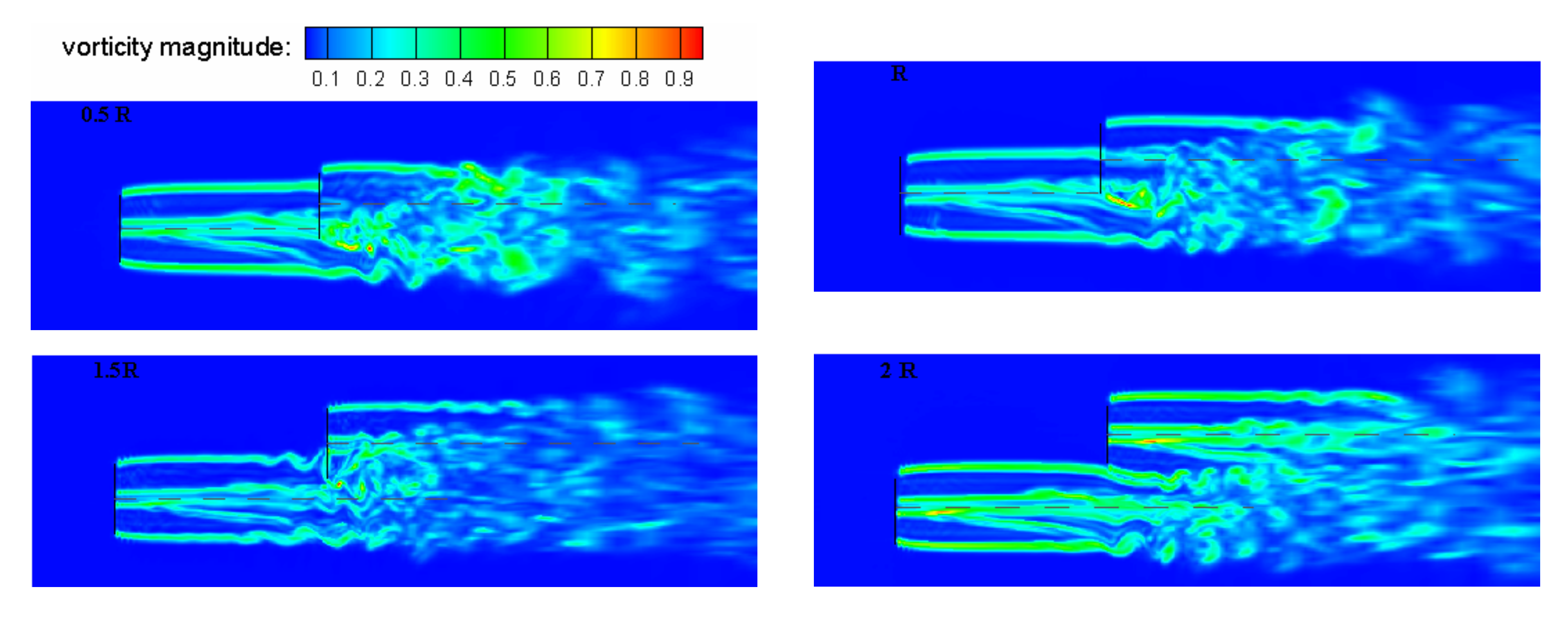
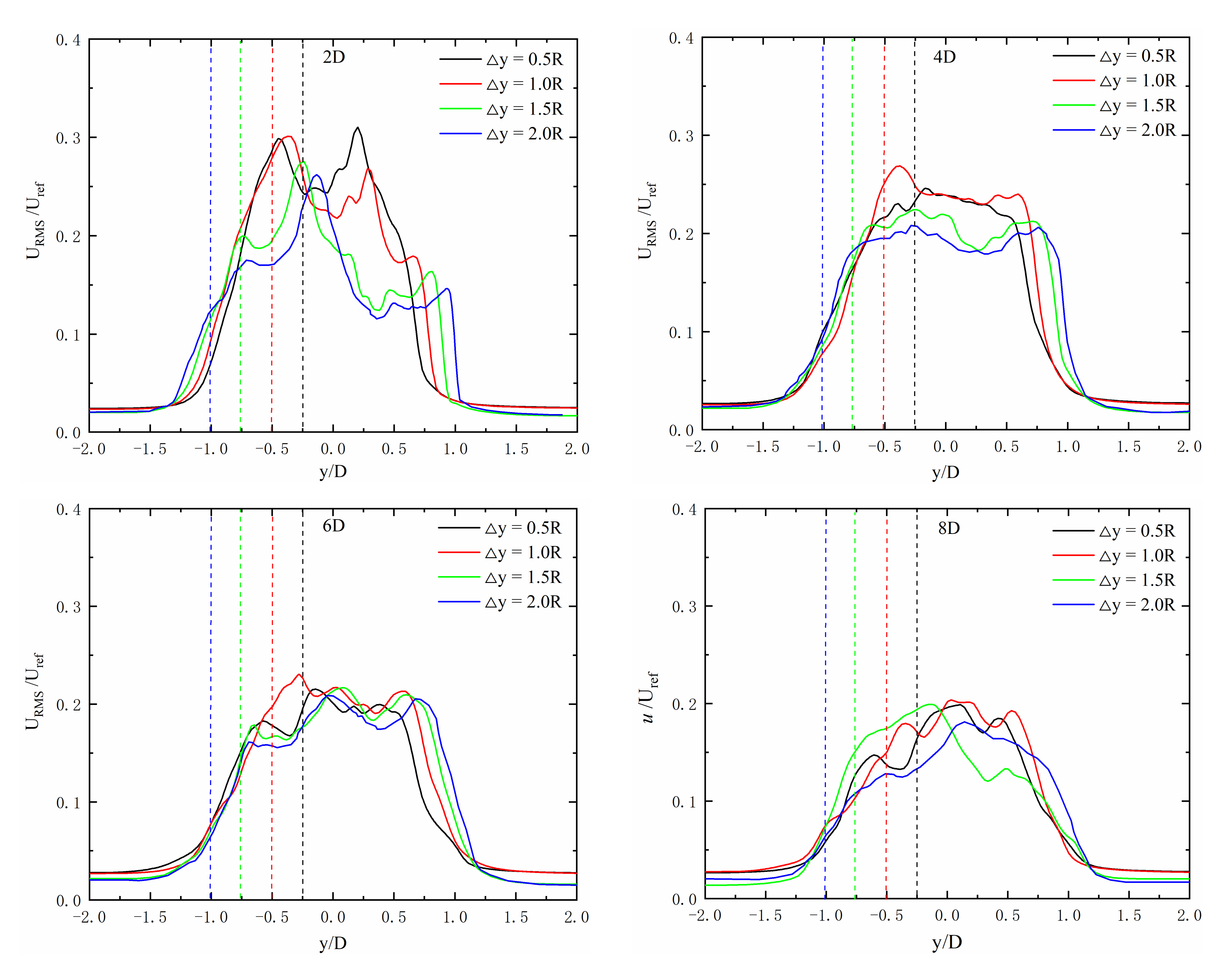
3.2. Analysis of Staggered Spacing Conditions
3.2.1. Wind Turbine Output
3.2.2. Analysis of Coupling Fields
4. Conclusions
- (1)
- The MALM is verified by the G1 experimental turbine with a uniform wind speed of 5.0 m/s. The thrust coefficient, power coefficient, and wake velocity of the wind turbine were all consistent with the experimental values. Under the condition of the smoothing parameter ε = 1.6DX, the simulated values of the thrust and power of MALM are more accurate, and the wake distribution is also close to the experimental values.
- (2)
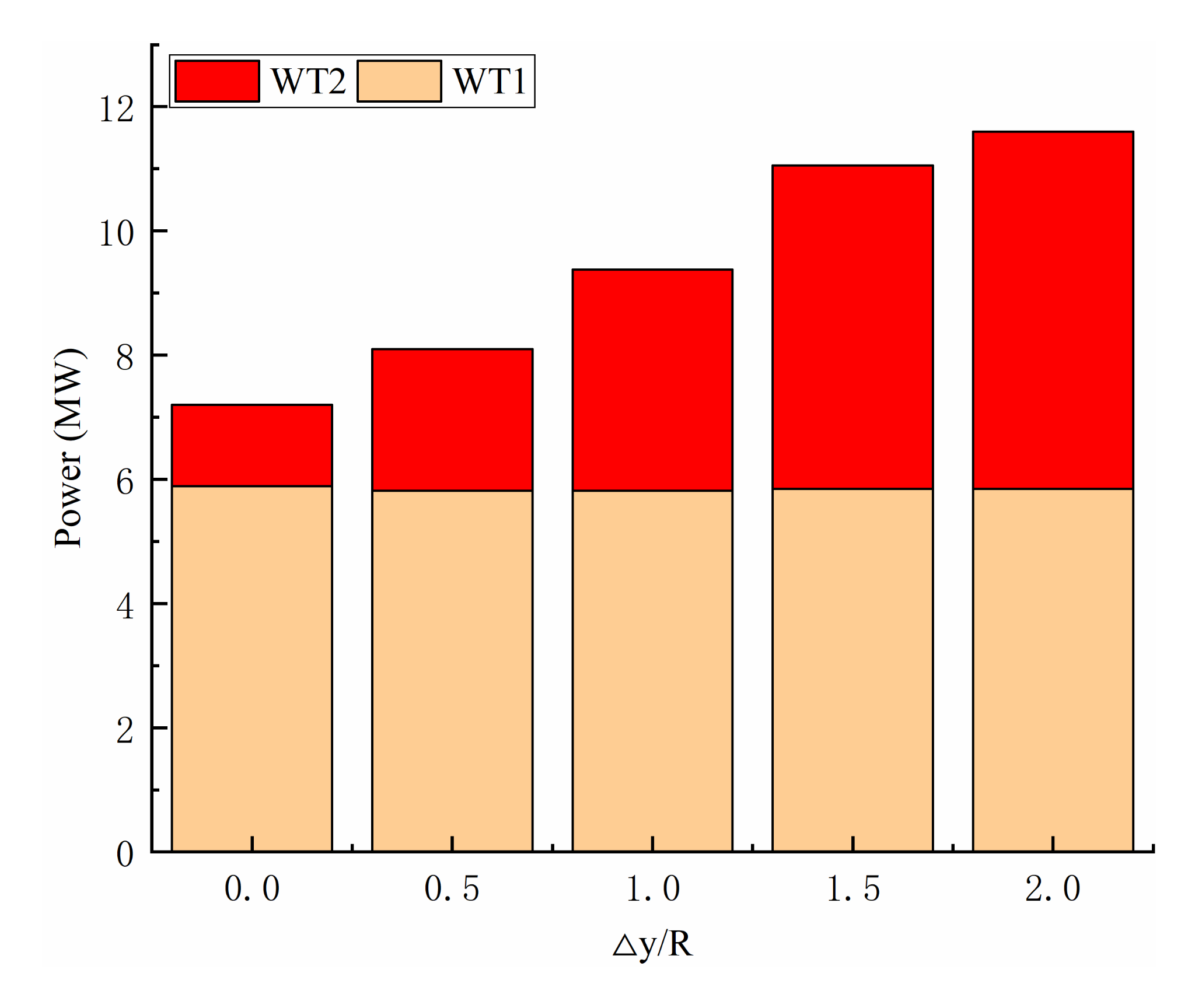
- In the case of Δy = R, and 1.5R, the output power and thrust of WT-2 decreased significantly when one of three blades was passing near the center vortex of WT-1. This phenomenon was observed three times per rotor revolution at the azimuth angles of 60+, 180+, and 270+. In the case of Δy = 0.5R, the power of WT-2 decreased by 33.3%, and the thrust decreased by 11.2% compared with the average results of when only one blade passed near the wake center of WT-1. In comparison with Δy = 0.5R, the maximum loss of power and thrust was reduced by half, to Δy = 1.5R. Furthermore, the peaks are significantly wider than Δy = 0.5R, resulting in longer periods of an unstable fatigue load on the blade, and unstable output power. Contrastingly, Δy = 2R and 0.5R only cause small dips in power.
- (3)
- As the staggered spacing Δy increased, the output power of WT-1 stabilized at 5.9 MW, and the total output power was enhanced. When the staggered spacing between the two wind turbines continued to increase, the part of the WT-2 plane located in the wake of WT-1 decreased, and the wake was asymmetrically distributed along the centerline. The significant difference in air velocity and turbulence intensity causes an uneven force on the wind turbine blades, and the mutual interference between the two wind turbines gradually weakens. Following this, the output power then slows down and stabilizes.
- (4)
- With an increase in staggered spacing Δy, the axial extent of the wake width increases, the wake becomes more complex, and the velocity of WT-2 is added to the wake center, making the difference of velocity in the near-wake larger. It is observed that the wake of WT-2 recovery slows down with the increase of Δy. Along with the main wind, the output power of WT-2 will fluctuate greatly, and the wake will become complex with 0.5R < Δy < 1.5R, which is not conducive to a safe and stable operation of downstream wind turbines.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALM | Actuator line model |
| MALM | Modified actuator line model |
| BEM | Blade element theory |
| LES | Large eddy simulation |
| WT-1 | Upstream wind turbine |
| WT-2 | Downstream wind turbine |
| Δy | Staggered spacing of two wind turbines in the y-axis direction |
| NREL | National Renewable Energy Laboratory |
| CFD | Computational Fluid Dynamics |
| N-S | Navier–Stokes |
| UDF | User-Defined Function |
| PANS | Partially-Averaged Navier–Stokes |
| GCI | The grid convergence index |
Nomenclature
| x, y, z | Coordinates |
| xwt, ywt, zwt | Three-dimensional coordinates of the hub center of the wind turbine |
| ρ | Air density, kg/m3 |
| Three-dimensional velocity vector | |
| p | Pressure acting on the fluid micro-element, Pa |
| fi | Volume force, KN |
| μ | Dynamic viscosity, N·s/m2 |
| ui | Averaged velocity in the i-th direction, m/s |
| Φ | Rotation angle of the blade i in the current time step, deg |
| Υ | Starting phase angle of the blade, deg |
| B | Number of blades |
| δ | Rotation angle of the blade in the current time step, deg |
| ω | Rotational angular velocity of the turbine rotor, rad/s |
| t | Time of rotation, s |
| xi | Coordinate of the blade element point, m |
| xi_cell | Grid cell centroid coordinate, m |
| DXi | Grid cell size, m |
| ui | Velocity at the blade element point, m/s |
| ucell | Grid centroid velocity closest to the blade element point, m/s |
| Velocity gradient of the flow field | |
| dS | Distance from the blade element point to the nearest grid centroid |
| c | Chord length of the airfoil, m |
| Cl | Lift coefficient |
| Cd | Drag coefficient |
| φ | Inflow angle, deg |
| β | Twist angle, deg |
| dr | Blade element span |
| d | Distance between M and blade element, m |
| ε | Smoothing parameter |
| R | Radius of the blade, m |
| D | Diameter of the turbine rotor, m |
| Rhub | Radius at the root of the rotor of the turbine, m |
| αmax | Angle of attack according to the maximum lift coefficient |
| α0 | Angle of attack according to the zero-lift coefficient |
| n | Empirical value, 1.0 |
| dfx,tow | Airflow axial resistance of a tower element |
| U | Wind speed, m/s |
| Fnac | Nacelle resistance |
| utow | Incoming wind speed at the center of the tower element, m/s |
| dtow | Circular cross-sectional diameter of the center of the tower element, m |
| dh | Element height of the tower, m |
| CD,tow | Resistance coefficient of the tower, 1.0 |
| Anac | Cross-sectional area of the nacelle, m2 |
| CD,nac | Resistance coefficient of the nacelle, 1.0 |
| z | Height above the ground, m |
| κ | Von Karman constant, 0.4187 |
| u* | Friction velocity, m/s |
| z0 | Surface roughness, m |
| n | Multiple |
| DX | the grid size, m |
| φ | the simulated variable value of the simulation study for the k-th grid |
| fε | the volume force after smoothing |
| f | the volume force on the blade element |
| B | the number of blades |
| fij | the volume force on a leaf element point |
| δ | the relative error |
| r | the grid growth rate |
| e | the convergence order |
| Uref | the reference wind speed, m/s |
| URMS | the root mean square of wind speed |
References
- Kim, H.-G.; Kim, J.-Y. Analysis of wind turbine aging through operation data calibrated by LiDAR measurement. Energies 2021, 14, 2319. [Google Scholar] [CrossRef]
- Howland, M.F.; Dabiri, J.O. Influence of wake model superposition and secondary steering on model-based wake steering control with SCADA data assimilation. Energies 2021, 14, 52. [Google Scholar] [CrossRef]
- Martinez-Tossas, L.A.; Churchfield, M.J.; Leonardi, S. Large eddy simulations of the flow past wind turbines: Actuator line and disk modeling. Wind Energy 2015, 18, 1047–1060. [Google Scholar] [CrossRef]
- Kim, T.; Oh, S.; Yee, K. Improved actuator surface method for wind turbine application. Renew. Energy 2015, 76, 16–26. [Google Scholar] [CrossRef]
- Ivanell, S.; Sørensen, J.N.; Mikkelsen, R.; Henningson, D. Analysis of numerically generated wake structures. Wind Energy 2009, 12, 63–80. [Google Scholar] [CrossRef]
- Ivanell, S.; Mikkelsen, R.; Sørensen, J.N.; Henningson, D. Stability analysis of the tip vortices of a wind turbine. Wind Energy 2010, 13, 705–715. [Google Scholar] [CrossRef]
- Shen, W.Z.; Zhu, W.J.; Sorensen, J.N. Actuator line/Navier-Stokes computations for the MEXICO rotor: Comparison with detailed measurements. Wind Energy 2012, 15, 811–825. [Google Scholar] [CrossRef]
- Fredriksson, S.T.; Broström, G.; Bergqvist, B.; Lennblad, J.; Nilsson, H. Modelling Deep Green tidal power plant using large eddy simulations and the actuator line method. Renew. Energy 2021, 179, 1140–1155. [Google Scholar] [CrossRef]
- Qian, Y.; Wang, T.; Yuan, Y.; Zhang, Y. Comparative study on wind turbine wakes using a modified partially-averaged navier-stokes method and large eddy simulation. Energy 2020, 206, 118147. [Google Scholar] [CrossRef]
- Baratchi, F.; Jeans, T.L.; Gerber, A.G. A modified implementation of actuator line method for simulating ducted tidal turbines. Ocean Eng. 2019, 193, 106586. [Google Scholar] [CrossRef]
- Réthoré, P.; van der Laan, P.; Troldborg, N.; Zahle, F.; Sørensen, N.N. Verification and validation of an actuator disc model. Wind Energy 2014, 17, 919–937. [Google Scholar] [CrossRef]
- Martínez-Tossas, L.A.; Meneveau, C.; National Renewable Energy Lab (NREL). Filtered lifting line theory and application to the actuator line model. J. Fluid Mech. 2019, 863, 269–292. [Google Scholar] [CrossRef]
- Tabib, M.; Rasheed, A.; Kvamsdal, T. Investigation of the impact of wakes and stratification on the performance of an onshore wind farm. Energy Procedia 2015, 80, 302–311. [Google Scholar] [CrossRef][Green Version]
- Xie, S.; Archer, C.L.; Ghaisas, N.; Meneveau, C. Benefits of collocating vertical-axis and horizontal-axis wind turbines in large wind farms. Wind Energy 2017, 20, 45–62. [Google Scholar] [CrossRef]
- Zhang, M.; Arendshorst, M.G.; Stevens, R.J.A.M. Large eddy simulations of the effect of vertical staggering in large wind farms. Wind Energy 2019, 22, 189–204. [Google Scholar] [CrossRef]
- Meyers, J.; Meneveau, C. Optimal turbine spacing in fully developed wind farm boundary layers. Wind Energy 2012, 15, 305–317. [Google Scholar] [CrossRef]
- Albatal, S.A.; Mohamed, M.H. Optimization of H-Rotor Darrieus turbines’ mutual interaction in staggered arrangements. Renew. Energy 2018, 125, 87–99. [Google Scholar] [CrossRef]
- Parada, L.; Herrera, C.; Flores, P.; Parada, V. Assessing the energy benefit of using a wind turbine micro-siting model. Renew. Energy 2018, 118, 591–601. [Google Scholar] [CrossRef]
- Hezaveh, S.H.; Bou-Zeid, E.; Dabiri, J.; Kinzel, M.; Cortina, G.; Martinelli, L. Increasing the power production of vertical-axis wind-turbine farms using synergistic clustering. Bound. Layer Meteorol. 2018, 169, 275–296. [Google Scholar] [CrossRef]
- Nilsson, K.; Shen, W.Z.; Sørensen, J.N.; Breton, S.-P.; Ivanell, S. Validation of the actuator line method using near wake measurements of the MEXICO rotor. Wind Energy 2015, 18, 499–514. [Google Scholar] [CrossRef]
- Gao, Z.; Li, Y.; Wang, T.; Ke, S.; Li, D. Recent improvements of actuator line-large-eddy simulation method for wind turbine wakes. Appl. Math. Mech. 2021, 42, 511–526. [Google Scholar] [CrossRef]
- Troldborg, N.; Sorensen, J.N.; Mikkelsen, R. Actuator line simulation of wake of wind turbine operating in turbulent inflow. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2007. [Google Scholar] [CrossRef]
- Martinez-Tossas, L.A.; Churchfield, M.J.; Yilmaz, A.E.; Sarlak, H.; Johnson, P.L.; Sorensen, J.N.; Meyers, J.; Meneveau, C. Comparison of four large-eddy simulation research codes and effects of model coefficient and inflow turbulence in actuator-line-based wind turbine modeling. J. Renew. Sustain. Energy 2018, 10, 33301. [Google Scholar] [CrossRef]
- Campagnolo, F.; Petrovi, V.; Schreiber, J.; Nanos, E.M.; Croce, A.; Bottasso, C.L. Wind tunnel testing of a closed-loop wake deflection controller for wind farm power maximization. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2016; Volume 753. [Google Scholar] [CrossRef]
- Campobasso, M.S.; Baba-Ahmadi, M.H. Analysis of unsteady flows past horizontal axis wind turbine airfoils based on harmonic balance compressible Navier-Stokes equations with low-speed preconditioning. J. Turbomach. 2012, 134, 61020. [Google Scholar] [CrossRef]
- Felten, F.; Fautrelle, Y.; Du Terrail, Y.; Metais, O. Numerical modeling of electromagnetically-riven turbulent flows using LES methods. Appl. Math. Model. 2004, 28, 15–27. [Google Scholar] [CrossRef]
- Shen, W.Z.; Mikkelsen, R.; Sørensen, J.N.; Bak, C. Tip loss corrections for wind turbine computations. Wind Energy 2005, 8, 457–475. [Google Scholar] [CrossRef]
- Corrigan, J.J.; Schilling, J.J. Empirical model for stall delay due to rotation. In Proceedings of the American Helicopter Society Aeromechanics Specialists Conference, San Francisco, CA, USA, 19–21 January 1994. [Google Scholar]
- Shives, M.; Crawford, C. Mesh and load distribution requirements for actuator line CFD simulations: Mesh and load distribution requirements for actuator line simulations. Wind Energy 2012, 16, 1183–1196. [Google Scholar] [CrossRef]
- Santoni, C.; Carrasquillo, K.; Arenas-Navarro, I.; Leonardi, S. Effect of tower and nacelle on the flow past a wind turbine. Wind Energy 2017, 20, 1927–1939. [Google Scholar] [CrossRef]
- Richards, R. Appropriate boundary conditions for computational wind engineering models using the k-ϵ turbulence model. J. Wind Eng. Ind. Aerodyn. 1993, 46, 145–153. [Google Scholar] [CrossRef]
- Takizawa, K.; Henicke, B.; Tezduyar, T.E.; Hsu, M.; Bazilevs, Y. Stabilized space–time computation of wind-turbine rotor aerodynamics. Comput. Mech. 2011, 48, 333–344. [Google Scholar] [CrossRef]
- Draper, M.; Guggeri, A.; Mendina, M.; Usera, G.; Campagnolo, F. A large eddy simulation-actuator line model framework to simulate a scaled wind energy facility and its application. J. Wind Eng. Ind. Aerodyn. 2018, 182, 146–159. [Google Scholar] [CrossRef]
- Nejad, A.R.; Guo, Y.; Gao, Z.; Moan, T.; National Renewable Energy Lab (NREL). Development of a 5 MW reference gearbox for offshore wind turbines: 5 MW reference gearbox. Wind Energy 2015, 19, 1089–1106. [Google Scholar] [CrossRef]
- Yu, Z.; Zheng, X.; Ma, Q. Study on actuator line modeling of two NREL 5-MW wind turbine wakes. Appl. Sci. 2018, 8, 434. [Google Scholar] [CrossRef]
- Sosnowski, M. Evaluation of heat transfer performance of a multi-disc sorption bed dedicated for adsorption cooling technology. Energies 2019, 12, 4660. [Google Scholar] [CrossRef]
- Roache, P. Perspective—A method for uniform reporting of grid refinement studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Y.; Shen, Y.; Wang, Y.; Xu, Y.; Zhang, X. CFD studies of wake characteristics and power capture of wind turbines with trailing edge flaps. IEEE Access 2020, 8, 7349–7361. [Google Scholar] [CrossRef]
- Martínez-Tossas, L.A.; Churchfield, M.J.; Meneveau, C. Optimal smoothing length scale for actuator line models of wind turbine blades based on gaussian body force distribution. Wind Energy 2017, 20, 1083–1096. [Google Scholar] [CrossRef]
- Jha, P.K.; Churchfield, M.J.; Moriarty, P.J.; Schmitz, S. Guidelines for volume force distributions within actuator line modeling of wind turbines on large-eddy simulation-type grids. J. Sol. Energy Eng. 2014, 136, 31003. [Google Scholar] [CrossRef]






| Diameter | Blade Radius | Hub Diameter | Tower Height | Rated Velocity | Airfoil |
|---|---|---|---|---|---|
| 1.1 m | 0.55 m | 0.03 m | 0.8 m | 850 rpm | RG14 |
| Diameter | Blade Radius | Rated Speed | Tower Height | Rated Velocity | Rated Power |
|---|---|---|---|---|---|
| 126 m | 61.5 m | 11.4 m/s | 90 m | 12.1 rpm | 5.3 MW |
| Parameter | Coarse | Medium | Fine |
|---|---|---|---|
| φ/KN | 726 | 743 | 751 |
| N/106 | 1.82 | 2.91 | 4.23 |
| δ | - | 0.02 | 0.01 |
| r | - | 1.17 | 1.13 |
| e | - | 6.17 | - |
| GCI/% | - | 1.22 | 0.89 |
| Parameter | n = 1.2 | n = 1.6 | n = 2.0 | |||
|---|---|---|---|---|---|---|
| Ct | Cp | Ct | Cp | Ct | Cp | |
| Experimental value | 0.788 | 0.453 | 0.788 | 0.453 | 0.788 | 0.453 |
| Simulated results | 0.749 | 0.407 | 0.791 | 0.457 | 0.801 | 0.470 |
| Difference (%) | −4.90 | −10.25 | 0.38 | 0.88 | 1.63 | 3.71 |
| Model | MALM | ALM | ||
|---|---|---|---|---|
| Parameter | Ct | Cp | Ct | Cp |
| Experimental value | 0.788 | 0.453 | 0.788 | 0.453 |
| Simulated results | 0.791 | 0.457 | 0.961 | 0.472 |
| Difference (%) | 0.38 | 0.88 | 21.95 | 4.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, F.; Duan, H.; Xu, C.; Han, X.; Shangguan, Y.; Li, T.; Fen, Z. Research on the Power Capture and Wake Characteristics of a Wind Turbine Based on a Modified Actuator Line Model. Energies 2022, 15, 282. https://doi.org/10.3390/en15010282
Xue F, Duan H, Xu C, Han X, Shangguan Y, Li T, Fen Z. Research on the Power Capture and Wake Characteristics of a Wind Turbine Based on a Modified Actuator Line Model. Energies. 2022; 15(1):282. https://doi.org/10.3390/en15010282
Chicago/Turabian StyleXue, Feifei, Heping Duan, Chang Xu, Xingxing Han, Yanqing Shangguan, Tongtong Li, and Zhefei Fen. 2022. "Research on the Power Capture and Wake Characteristics of a Wind Turbine Based on a Modified Actuator Line Model" Energies 15, no. 1: 282. https://doi.org/10.3390/en15010282
APA StyleXue, F., Duan, H., Xu, C., Han, X., Shangguan, Y., Li, T., & Fen, Z. (2022). Research on the Power Capture and Wake Characteristics of a Wind Turbine Based on a Modified Actuator Line Model. Energies, 15(1), 282. https://doi.org/10.3390/en15010282






