Modeling and Experimental Investigation of the Anode Inlet Relative Humidity Effect on a PEM Fuel Cell
Abstract
:1. Introduction
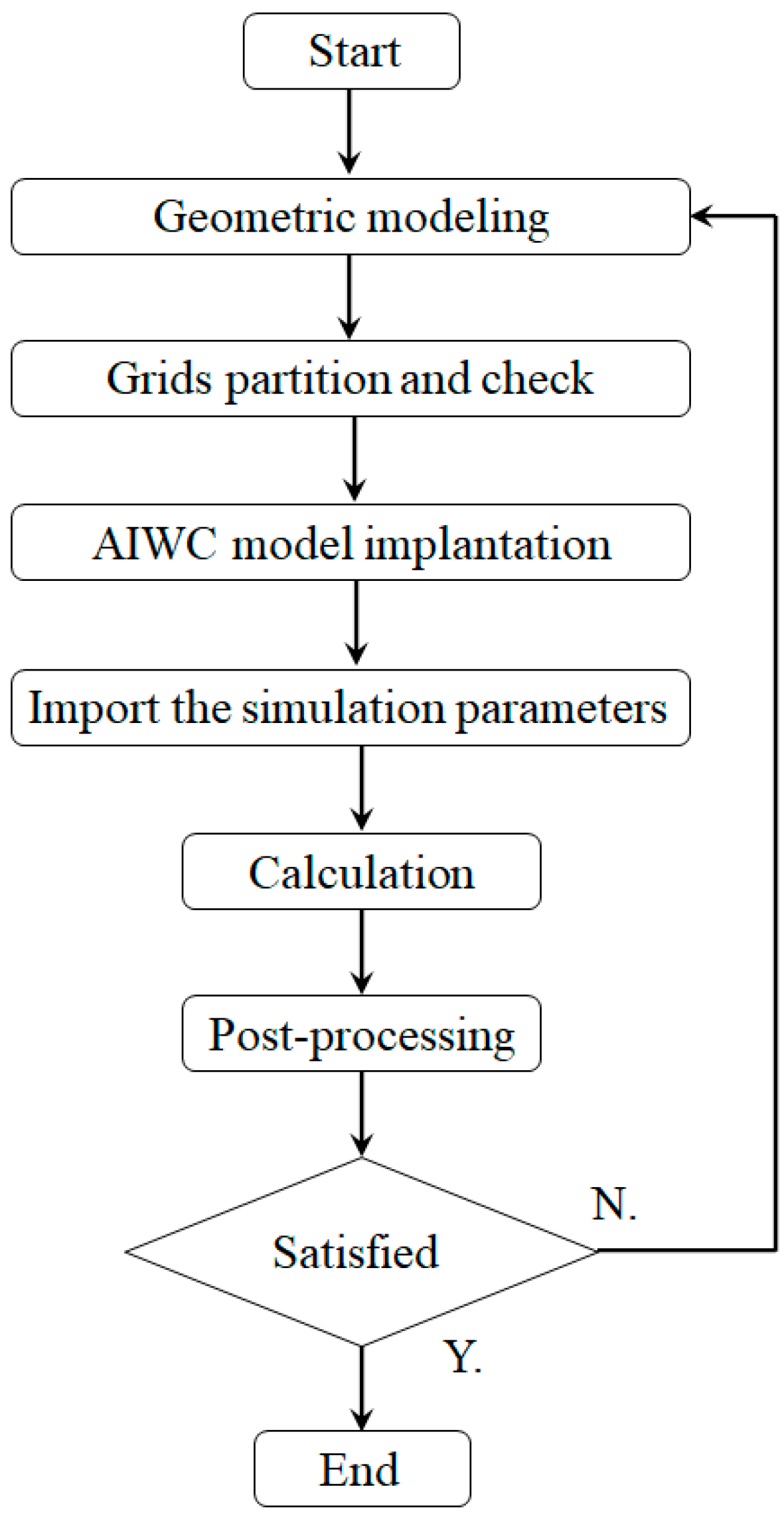
2. Model Establishment
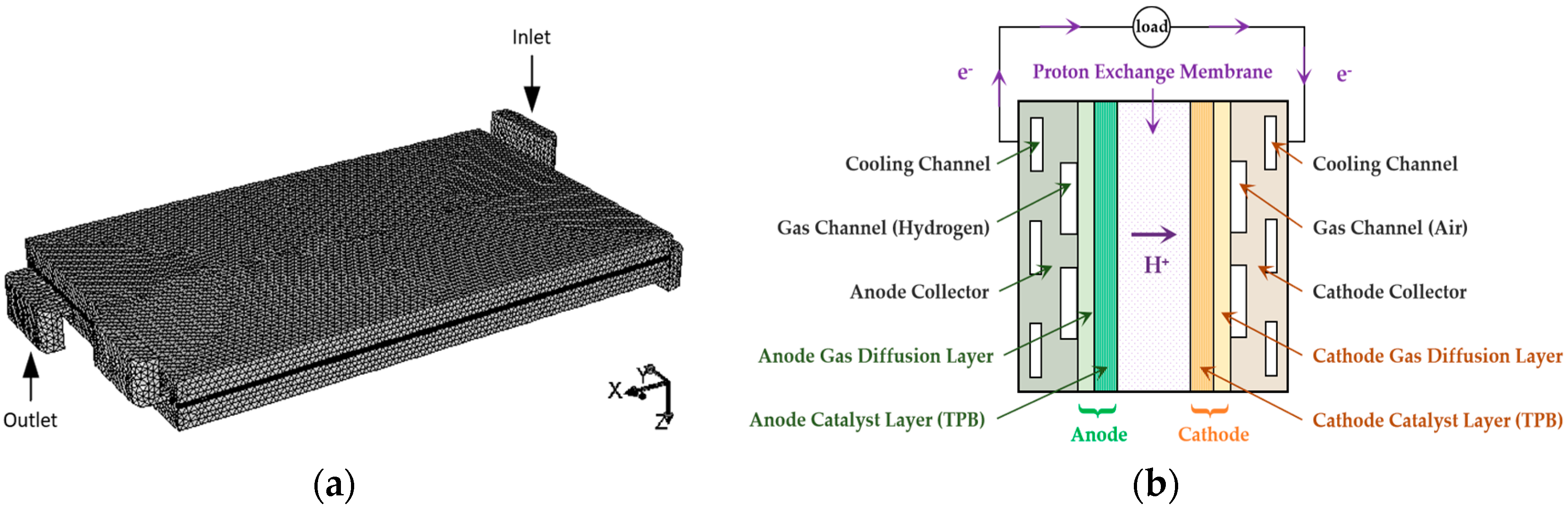
2.1. Model Computational Domain
2.2. Governing Equations
- (1)
- The simulation model for a PEMFC is a non-isothermal steady state model.
- (2)
- The flow in parallel flow channel is laminar flow due to the low Reynolds number.
- (3)
- The reactant gas in the fuel cell is regarded as an incompressible ideal gas, which follows the ideal gas law.
- (4)
- The proton exchange membrane, catalytic layer, micro-porous layer, and gas diffusion layer are a homogeneous porous structure.
2.3. Anode Inlet Water Content (AIWC) Model Development
2.4. Model Parameters and Boundary Conditions
3. Experiment
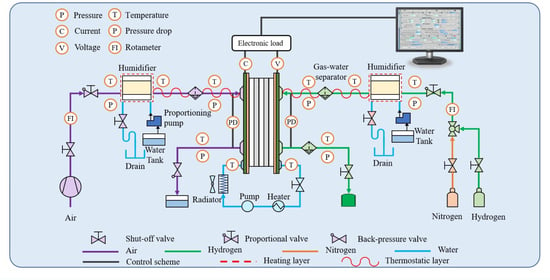
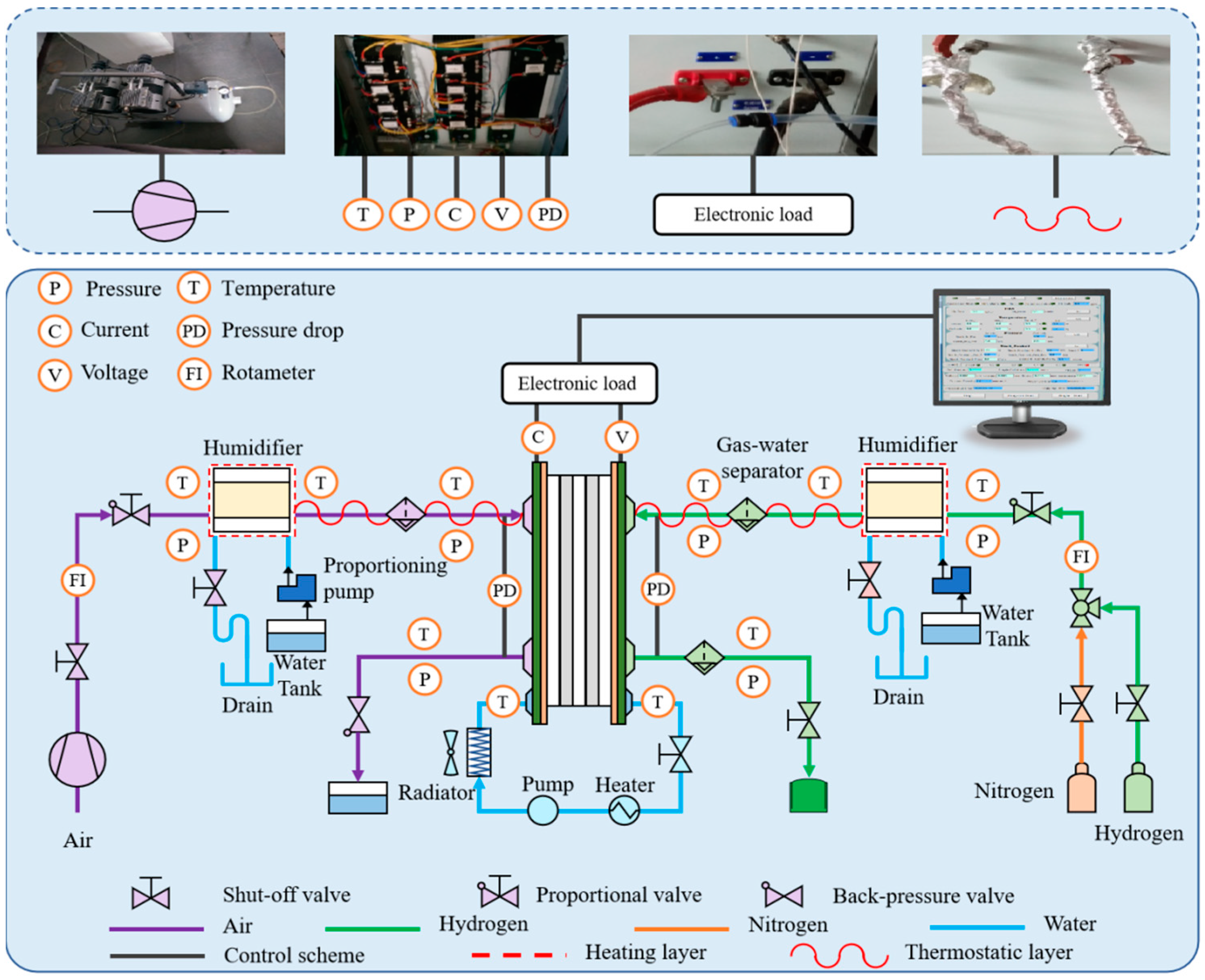
3.1. Apparatus and Schematic
3.2. Experimental Conditions
4. Results and Discussion
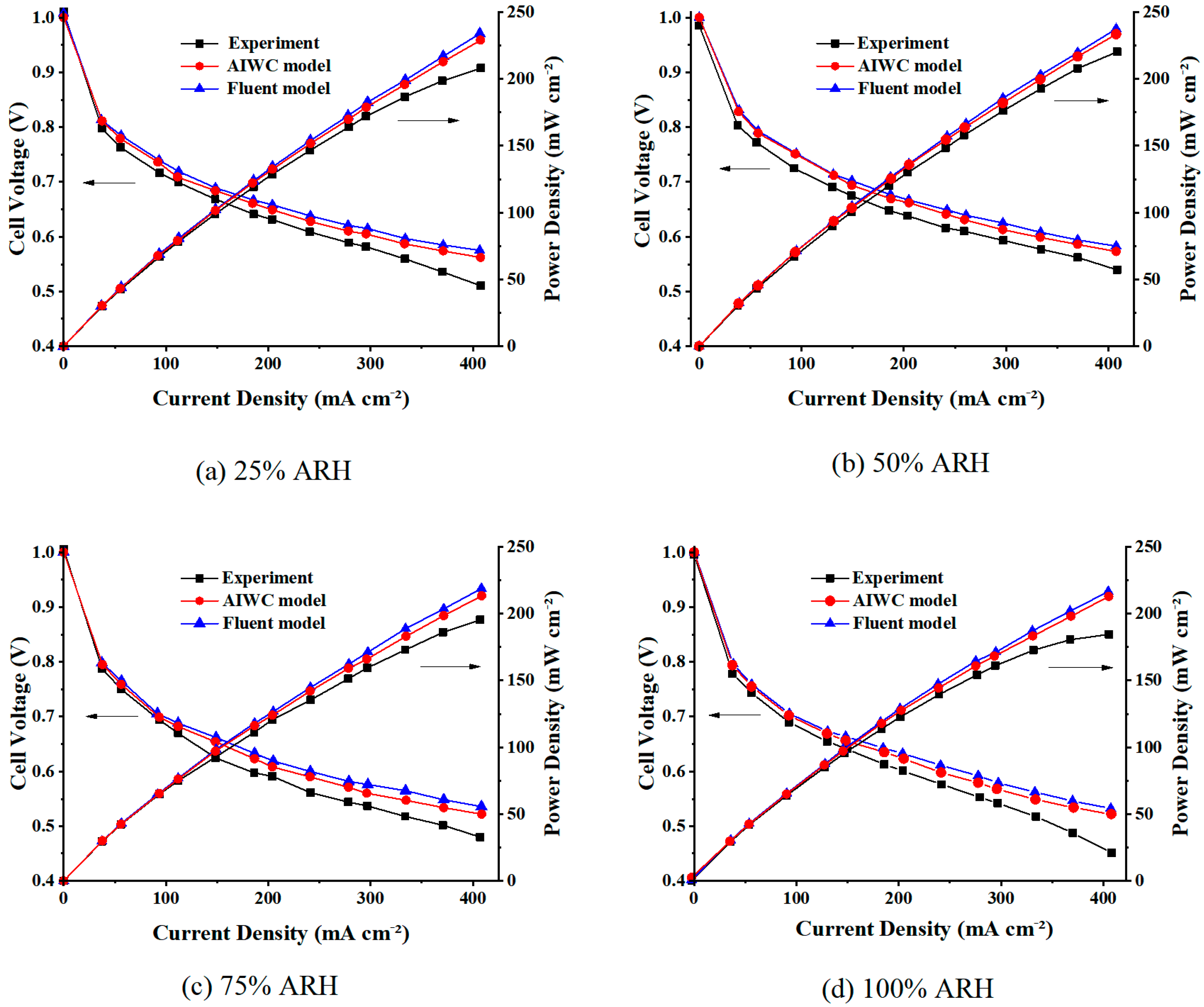
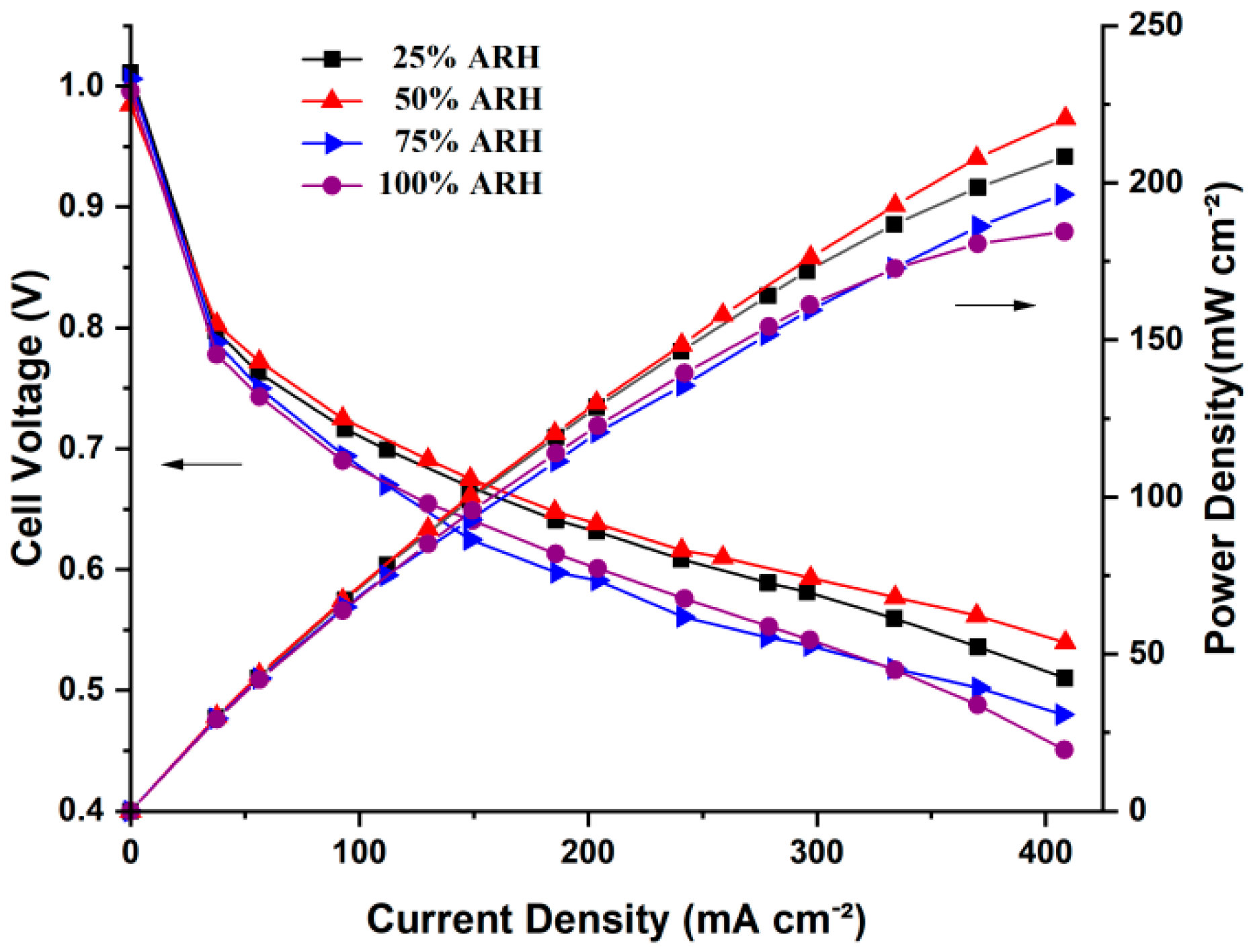
4.1. Polarization Curves
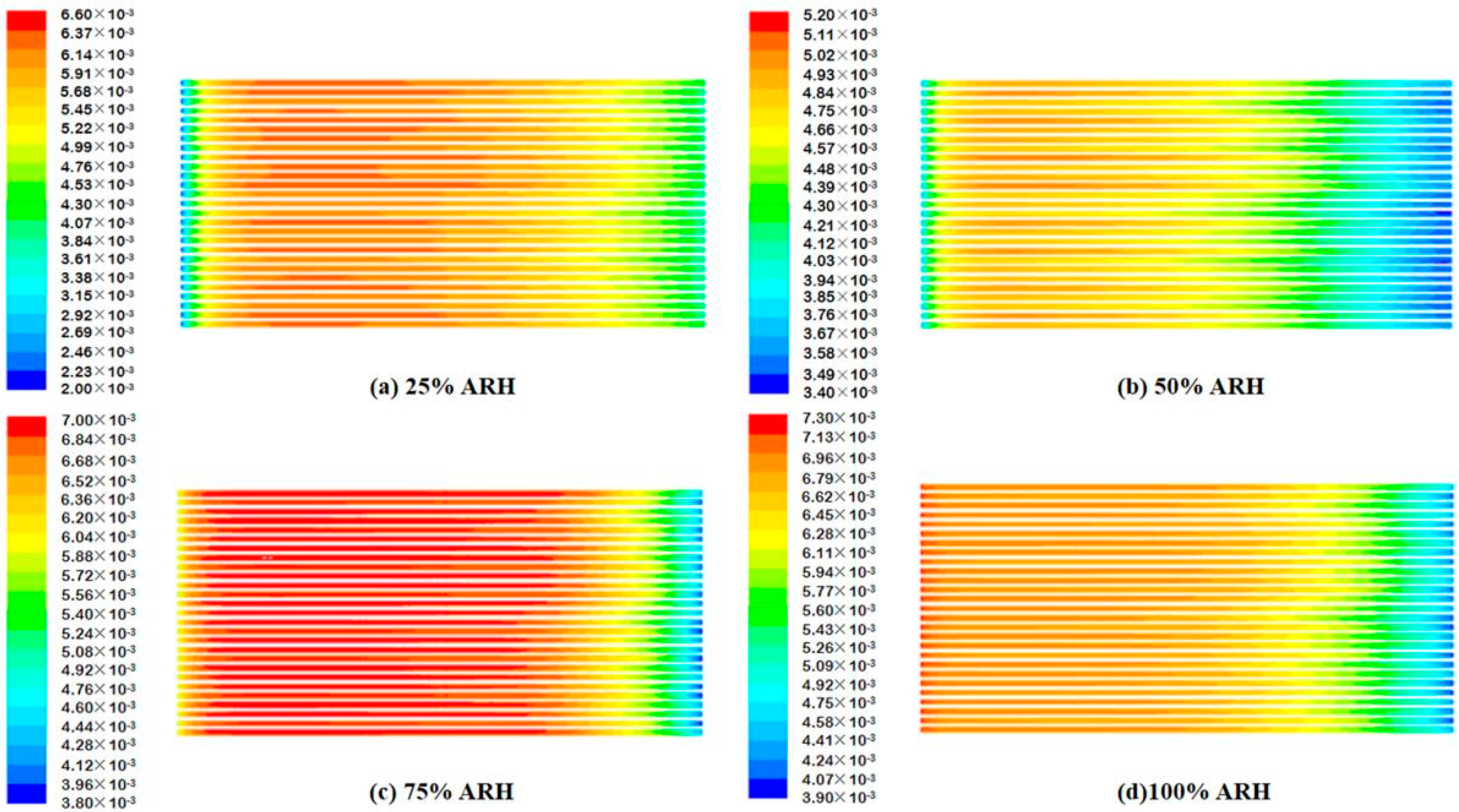
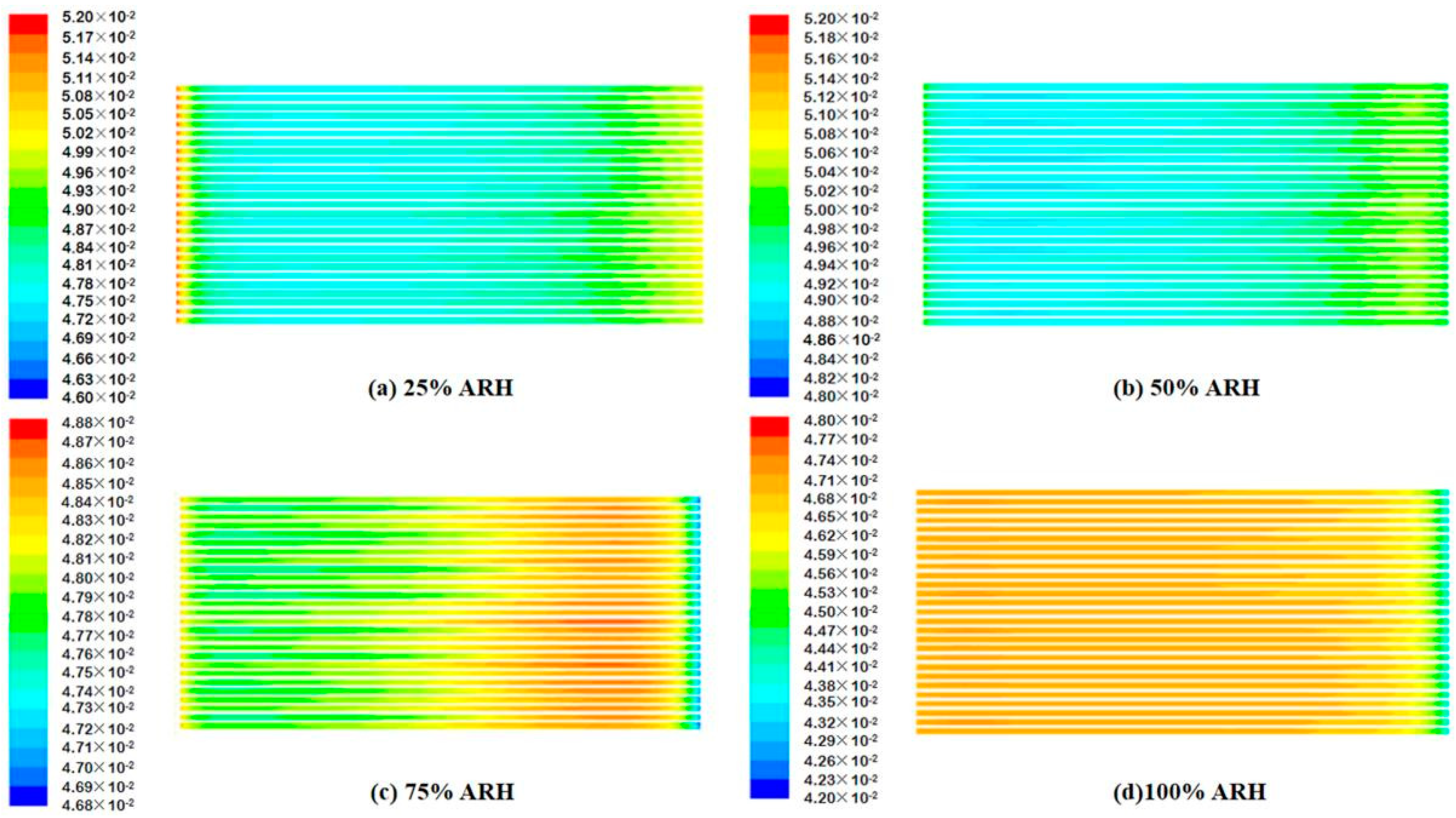
4.2. Contours of Fuel Cell Species Distribution
5. Conclusions
- The AIWC model is more applicable to study the anode inlet relative humidity on the PEMFC performance than the Fluent model. The relative error of the voltage results derived from the AIWC model has been reduced to 3.2% (the original is 4.6% in the Fluent model), especially at 240 mA cm−2 for 50% ARH. At 50% ARH, 100% CRH, and 60 °C, the water content and hydrogen distribution are more uniform all over the anode channels, and the maximum power density is achieved.
- At low relative humidity (25% ARH and 50% ARH), an increase in hydrogen humidity can improve the performance of the PEM fuel cell at low current density. The water content and hydrogen distribution is more uniform all over the anode channels at 50% ARH. At high relative humidity (100% ARH), the excess water produced by condensation does not play a positive role in the fuel cell performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khalil, Y.F. Science-based framework for ensuring safe use of hydrogen as an energy carrier and an emission-free transportation fuel. Process Saf. Environ. Prot. 2018, 117, 326–340. [Google Scholar] [CrossRef]
- Chen, D.; Pei, P.; Li, Y.; Ren, P.; Meng, Y.; Song, X.; Wu, Z. Proton exchange membrane fuel cell stack consistency: Evaluation methods, influencing factors, membrane electrode assembly parameters and improvement measures. Energy Convers. Manag. 2022, 261, 115651. [Google Scholar] [CrossRef]
- Pei, P.; Chen, D.; Wu, Z.; Ren, P. Nonlinear methods for evaluating and online predicting the lifetime of fuel cells. Appl. Energy 2019, 254, 113730. [Google Scholar] [CrossRef]
- Ren, P.; Pei, P.; Chen, D.; Li, Y.; Wang, H.; Fu, X.; Zhang, L.; Wang, M.; Song, X. Micro-current excitation for efficient diagnosis of membrane electrode assemblies in fuel cell stacks: Error analysis and method optimization. Energy Convers. Manag. 2022, 258, 115489. [Google Scholar] [CrossRef]
- Ren, P.; Pei, P.; Li, Y.; Wu, Z.; Chen, D.; Huang, S. Degradation mechanisms of proton exchange membrane fuel cell under typical automotive operating conditions. Prog. Energy Combust. Sci. 2020, 80, 100859. [Google Scholar] [CrossRef]
- Liu, Q.; Lan, F.; Chen, J.; Zeng, C.; Wang, J. A review of proton exchange membrane fuel cell water management: Membrane electrode assembly. J. Power Sources 2022, 517, 230723. [Google Scholar] [CrossRef]
- Ren, P.; Pei, P.; Li, Y.; Wu, Z.; Chen, D.; Huang, S.; Jia, X. Diagnosis of water failures in proton exchange membrane fuel cell with zero-phase ohmic resistance and fixed-low-frequency impedance. Appl. Energy 2019, 239, 785–792. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Water transport in polymer electrolyte membrane fuel cells. Prog. Energy Combust. Sci. 2011, 37, 221–291. [Google Scholar] [CrossRef]
- Li, Y.; Pei, P.; Wu, Z.; Ren, P.; Jia, X.; Chen, D.; Huang, S. Approaches to avoid flooding in association with pressure drop in proton exchange membrane fuel cells. Appl. Energy 2018, 224, 42–51. [Google Scholar] [CrossRef]
- Sun, C.; Negro, E.; Nale, A.; Vezzù, K.; Zawodzinski, T.A.; Meda, L.; Gambaro, C.; Noto, V.D. An efficient barrier toward vanadium crossover in redox flow batteries: The bilayer [Nafion/(WO3)x] hybrid inorganic-organic membrane. Electrochim. Acta 2021, 378, 138133. [Google Scholar] [CrossRef]
- Dutta, K.; Das, S.; Kundu, P.P. Partially sulfonated polyaniline induced high ion-exchange capacity and selectivity of Nafion membrane for application in direct methanol fuel cells. J. Membr. Sci. 2015, 473, 94–101. [Google Scholar] [CrossRef]
- Peng, Z.; Badets, V.; Huguet, P.; Morin, A.; Schott, P.; Tran, T.B.H.; Porozhnyy, M.; Nikonenko, V.; Deabate, S. Operando μ-Raman study of the actual water content of perfluorosulfonic acid membranes in the fuel cell. J. Power Sources 2017, 356, 200–211. [Google Scholar] [CrossRef]
- Martinez, N.; Peng, Z.; Morin, A.; Porcar, L.; Gebel, G.; Lyonnard, S. Real time monitoring of water distribution in an operando fuel cell during transient states. J. Power Sources 2017, 365, 230–234. [Google Scholar] [CrossRef]
- Pineda-Delgado, J.L.; Chávez-Ramirez, A.U.; Gutierrez, B.C.K.; Rivas, S.; Marisela, C.-R.; de Jesús Hernández-Cortes, R.; Menchaca-Rivera, J.A.; Pérez-Robles, J.F. Effect of relative humidity and temperature on the performance of an electrochemical hydrogen compressor. Appl. Energy 2022, 311, 118617. [Google Scholar] [CrossRef]
- Akhtar, N.; Kerkhof, P. Effect of channel and rib width on transport phenomena within the cathode of a proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2011, 36, 5536–5549. [Google Scholar] [CrossRef]
- Owejan, J.P.; Owejan, J.E.; Gu, W.; Trabold, T.A.; Tighe, T.W.; Mathias, M.F. Water transport mechanisms in PEMFC gas diffusion layers. J. Electrochem. Soc. 2010, 157, B1456. [Google Scholar] [CrossRef]
- Jo, A.; Gwak, G.; Moazzam, M.; Lee, J.; Ju, H. Analysis of water film formation and low-humidity operation characteristics of a polymer electrolyte fuel cell (PEFC). Int. J. Hydrogen Energy 2017, 42, 3731–3747. [Google Scholar] [CrossRef]
- Nandjou, F.; Poirot-Crouvezier, J.P.; Chandesris, M.; Blachot, J.F.; Bonnaud, C.; Bultel, Y. Impact of heat and water management on proton exchange membrane fuel cells degradation in automotive application. J. Power Sources 2016, 326, 182–192. [Google Scholar] [CrossRef]
- Askaripour, H. Effect of operating conditions on the performance of a PEM fuel cell. Int. J. Heat Mass Transf. 2019, 144, 118705. [Google Scholar] [CrossRef]
- Zhu, M.; Xie, X.; Wu, K.; Jiao, K. Experimental investigation of the effect of membrane water content on PEM fuel cell cold start. Energy Procedia 2019, 158, 1724–1729. [Google Scholar] [CrossRef]
- Ren, P.; Pei, P.; Chen, D.; Li, Y.; Wu, Z.; Zhang, L.; Li, Z.; Wang, M.; Wang, H.; Wang, B.; et al. Novel analytic method of membrane electrode assembly parameters for fuel cell consistency evaluation by micro-current excitation. Appl. Energy 2022, 306, 118068. [Google Scholar] [CrossRef]
- Song, D.; Wang, Q.; Liu, Z.; Huang, C. Transient analysis for the cathode gas diffusion layer of PEM fuel cells. J. Power Sources 2006, 159, 928–942. [Google Scholar] [CrossRef]
- He, W.; Yi, J.S.; Van Nguyen, T. Two-phase flow model of the cathode of PEM fuel cells using interdigitated flow fields. AIChE J. 2000, 46, 2053–2064. [Google Scholar] [CrossRef]
- Wang, Z.H.; Wang, C.Y.; Chen, K.S. Two-phase flow and transport in the air cathode of proton exchange membrane fuel cells. J. Power Sources 2001, 94, 40–50. [Google Scholar] [CrossRef] [Green Version]
- Sahraoui, M.; Bichioui, Y.; Halouani, K. Three–dimensional modeling of water transport in PEMFC. Int. J. Hydrogen Energy 2013, 38, 8524–8531. [Google Scholar] [CrossRef]
- Hao, L.; Moriyama, K.; Gu, W.; Wang, C. Three dimensional computations and experimental comparisons for a large-scale proton exchange membrane fuel cell. J. Electrochem. Soc. 2016, 163, F744. [Google Scholar] [CrossRef]
- Falcão, D.S.; Gomes, P.J.; Oliveira, V.B.; Pinho, C.; Pinto, A. 1D and 3D numerical simulations in PEM fuel cells. Int. J. Hydrogen Energy 2011, 36, 12486–12498. [Google Scholar] [CrossRef]
- Pasaogullari, U.; Wang, C.Y. Two-phase modeling and flooding prediction of polymer electrolyte fuel cells. J. Electrochem. Soc. 2005, 152, A380. [Google Scholar] [CrossRef]
- Arama, F.Z.; Mammar, K.; Laribi, S.; Necaibia, A.; Ghaitaoui, T. Implementation of sensor based on neural networks technique to predict the PEM fuel cell hydration state. J. Energy Storage 2020, 27, 101051. [Google Scholar] [CrossRef]
- Pei, P.; Ouyang, M.; Feng, W.; Lu, L.; Huang, H.; Zhang, J. Hydrogen pressure drop characteristics in a fuel cell stack. Int. J. Hydrogen Energy 2006, 31, 371–377. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Pei, P.; Liu, X.; Wang, L.; Wan, Y. Variation characteristic analysis of water content at the flow channel of proton exchange membrane fuel cell. Energies 2022, 15, 3280. [Google Scholar] [CrossRef]
- Arvay, A.; Ahmed, A.; Peng, X.H.; Kannan, A.M. Convergence criteria establishment for 3D simulation of proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2012, 37, 2482–2489. [Google Scholar] [CrossRef]
- Carton, J.G.; Olabi, A.G. Three-dimensional proton exchange membrane fuel cell model: Comparison of double channel and open pore cellular foam flow plates. Energy 2017, 136, 185–195. [Google Scholar] [CrossRef] [Green Version]
- Cheddie, D.; Munroe, M. Mathematical model of a PEMFC using a PBI membrane. Energy Convers. Manag. 2006, 47, 1490–1504. [Google Scholar] [CrossRef]
- Liu, Y.; Tu, Z.; Chan, S.H. Performance enhancement in a H2/O2 PEMFC with dual-ejector recirculation. Int. J. Hydrogen Energy 2022, 47, 12698–12710. [Google Scholar] [CrossRef]
- Dickinson, E.J.F.; Hinds, G. The Butler-Volmer equation for polymer electrolyte membrane fuel cell (PEMFC) electrode kinetics: A critical discussion. J. Electrochem. Soc. 2019, 166, F221. [Google Scholar] [CrossRef]
- ANSYS, Inc. ANSYS FLUENT 15.0 Fuel Cells Module Manual. November 2013. Available online: https://documents.pub/document/fluent-udf-manual-fluent-udfansys-fluent-udf-manual-ansys-inc-release-150.html?page=1 (accessed on 9 March 2022).
- Cheng, Z.; Luo, L.; Huang, B.; Jian, O. Effect of humidification on distribution and uniformity of reactants and water content in PEMFC. Int. J. Hydrogen Energy 2021, 46, 26560–26574. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, G.; Guo, L.J.; Dehua, S.; Liu, H. Effects of humidification temperatures on local current characteristics in a PEM fuel cell. J. Power Sources 2007, 168, 400–407. [Google Scholar] [CrossRef]
- Choi, K.H. Water transport in polymer membranes for PEMFC. J. Power Sources 2000, 86, 197–201. [Google Scholar] [CrossRef]
- Kim, Y.B. Study on the effect of humidity and stoichiometry on the water saturation of PEM fuel cells. Int. J. Energy Res. 2012, 36, 509–522. [Google Scholar] [CrossRef]
- Caglayan, D.G.; Sezgin, B.; Devrim, Y.; Eroglu, I. Three–dimensional modeling of a high temperature polymer electrolyte membrane fuel cell at different operation temperatures. Int. J. Hydrogen Energy 2016, 41, 10060–10070. [Google Scholar] [CrossRef]
| Structure | Value | Units |
|---|---|---|
| Active area | ||
| Channel width | ||
| Channel depth | ||
| Channel number | 27.00 | -- |
| Thickness of proton exchange membrane | ||
| Thickness of gas diffusion layer | ||
| Thickness of catalytic layer |
| PEMFC 3D Model | Number | Type |
|---|---|---|
| Anode Collector | 806,291 | Hybrid |
| Anode Channel | 195,641 | Hybrid |
| Anode Gas Diffusion Layer | 260,749 | Hex |
| Anode Catalyst Layer | 260,749 | Hex |
| Proton Exchange Membrane | 260,749 | Hex |
| Cathode Catalyst Layer | 260,749 | Hex |
| Cathode Gas Diffusion Layer | 260,749 | Hex |
| Cathode Channel | 195,641 | Hybrid |
| Cathode Collector | 806,291 | Hybrid |
| Parameter | Value | Units |
|---|---|---|
| Reference diffusivity of hydrogen () | 9.15 × 10−5 | m2 s−1 |
| Reference diffusivity of oxygen () | 2.2 × 10−5 | m2 s−1 |
| Reference diffusivity of water () | 2.56 × 10−5 | m2 s−1 |
| Thermal conductivity of the membrane () | 0.4 | W (m K)−1 |
| Thermal conductivity of the GDL () | 1.2 | W (m K)−1 |
| Thermal conductivity of the CL () | 1.5 | W (m K)−1 |
| Thermal conductivity of the current collector () | 20 | W (m K)−1 |
| Electrical conductivity of the GDL () | 2500 | S m−1 |
| Electrical conductivity of the CL () | 2500 | S m−1 |
| Electrical conductivity of the current collector () | 20,000 | S m−1 |
| Hydrogen reference exchange current density () | 4000 | A m−2 |
| Oxygen reference exchange current density () | 5.75 | A m−2 |
| Hydrogen reference concentration () | 1.00 | Kmol m−3 |
| Oxygen reference concentration () | 1.00 | Kmol m−3 |
| Concentration dependence at anode () | 0.5 | -- |
| Concentration dependence at cathode () | 1 | -- |
| Anode transfer coefficient for the anode electrode () | 0.5 | -- |
| Cathode transfer coefficient for the anode electrode () | 0.5 | -- |
| Anode transfer coefficient for the cathode electrode () | 0.5 | -- |
| Cathode transfer coefficient for the cathode electrode () | 0.5 | -- |
| Equivalent weight of membrane () | 1100 | Kg kmol−1 |
| Density of the membrane () | 1980 | kg m−3 |
| Porosity of the GDL () | 0.5 | -- |
| Porosity of the CL () | 0.28 | -- |
| Permeability of the GDL () | 1.18 × 10−12 | m2 |
| Permeability of the CL () | 2.3 × 10−13 | m2 |
| Molecular weight of H2 () | 2 × 10−3 | Kg mol−1 |
| Molecular weight of O2 () | 32 × 10−3 | Kg mol−1 |
| Molecular weight of H2O () | 18 × 10−3 | Kg mol−1 |
| Faraday constant (F) | 9.65 × 107 | C kmol−1 |
| Universal gas constant (R) | 8.3134 | J mol−1 K−1 |
| Open circuit voltage () | 0.95 | V |
| Operating temperature (T) | 60 | °C |
| Operating pressure (P) | 0.1 | MPa |
| Anode inlet gas flow rate () | 2 | L min−1 |
| Cathode inlet gas flow rate () | 5 | L min−1 |
| Anode relative humidity (ARH) | 25, 50, 75, 100 | % |
| Cathode relative humidity (CRH) | 100 | % |
| Parameter | Fuel Cell |
|---|---|
| Area of membrane (cm2) | 275 |
| Flow field | Parallel |
| Membrane | NafionTM 212 |
| GDL | Toray 200 µm |
| Cat. loading | 0.1/0.3 mg cm−2 |
| Material of bipolar plate | Metal |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Liu, Y.; Bi, G.; Liu, X.; Wang, L.; Wan, Y.; Sun, H. Modeling and Experimental Investigation of the Anode Inlet Relative Humidity Effect on a PEM Fuel Cell. Energies 2022, 15, 4532. https://doi.org/10.3390/en15134532
Zhang L, Liu Y, Bi G, Liu X, Wang L, Wan Y, Sun H. Modeling and Experimental Investigation of the Anode Inlet Relative Humidity Effect on a PEM Fuel Cell. Energies. 2022; 15(13):4532. https://doi.org/10.3390/en15134532
Chicago/Turabian StyleZhang, Lu, Yongfeng Liu, Guijun Bi, Xintong Liu, Long Wang, Yuan Wan, and Hua Sun. 2022. "Modeling and Experimental Investigation of the Anode Inlet Relative Humidity Effect on a PEM Fuel Cell" Energies 15, no. 13: 4532. https://doi.org/10.3390/en15134532
APA StyleZhang, L., Liu, Y., Bi, G., Liu, X., Wang, L., Wan, Y., & Sun, H. (2022). Modeling and Experimental Investigation of the Anode Inlet Relative Humidity Effect on a PEM Fuel Cell. Energies, 15(13), 4532. https://doi.org/10.3390/en15134532