Short-Term Load Forecasting with a Novel Wavelet-Based Ensemble Method
Abstract
:1. Introduction
- (1).
- Mitigation of inconsistency
- (2).
- Reduction in overtraining
- (3).
- Improvement of predictive performance
- (4).
- (5).
- Resolving the bias issues of fixed wavelet parameters
- (6).
- Using individual reference indicators associated with imperfect wavelet parameters to improve predictive accuracy.
2. Methodology
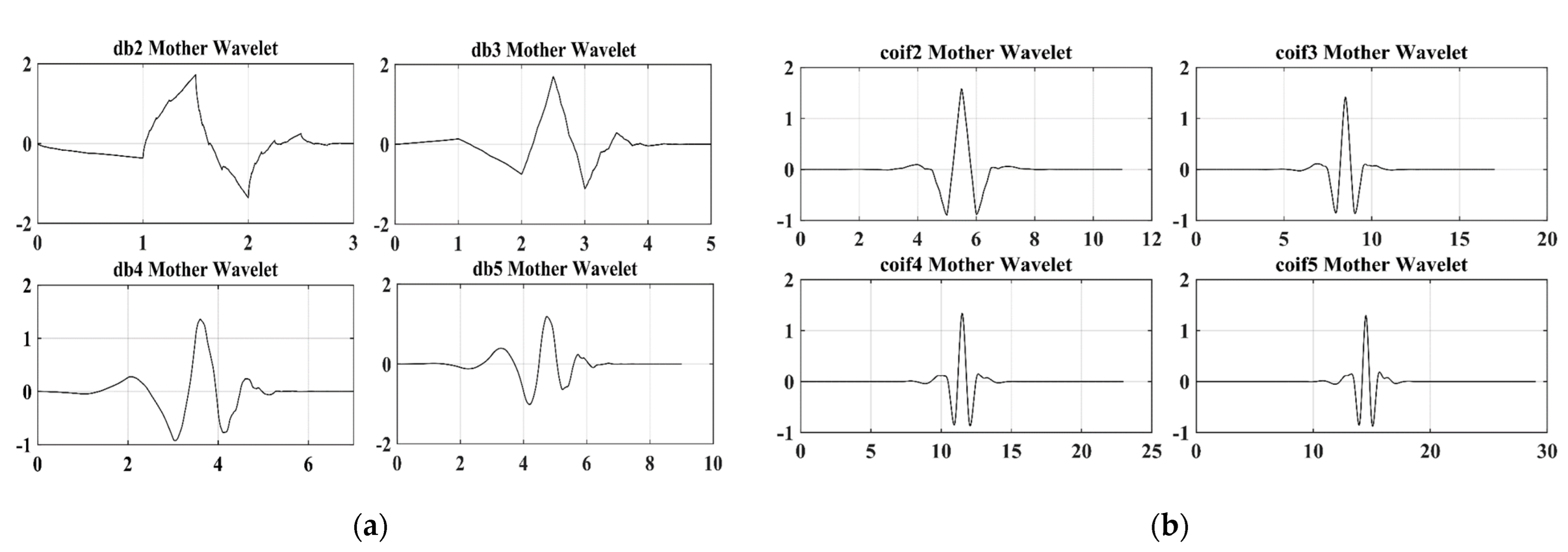
2.1. Wavelet Transform
- (i)
- Scale parameter (
- (ii)
- Mother function (
- (iii)
- Shifting parameter ()
- (iv)
- Scaling function (
2.2. Wavelet-Based Ensemble Approach
- Normally, it would take an excessively long amount of time to test a variety of wavelet specifications.
- The load series may not always be accurately represented by the fixed specification [29].
- Third, a given set of wavelet coefficients cannot always provide the best predicting outcomes in all perspectives.
3. Description of the Input Data
3.1. About the Input Data
3.2. Statistical Summary Analysis of Input Data
4. Results and Discussion
- (1).
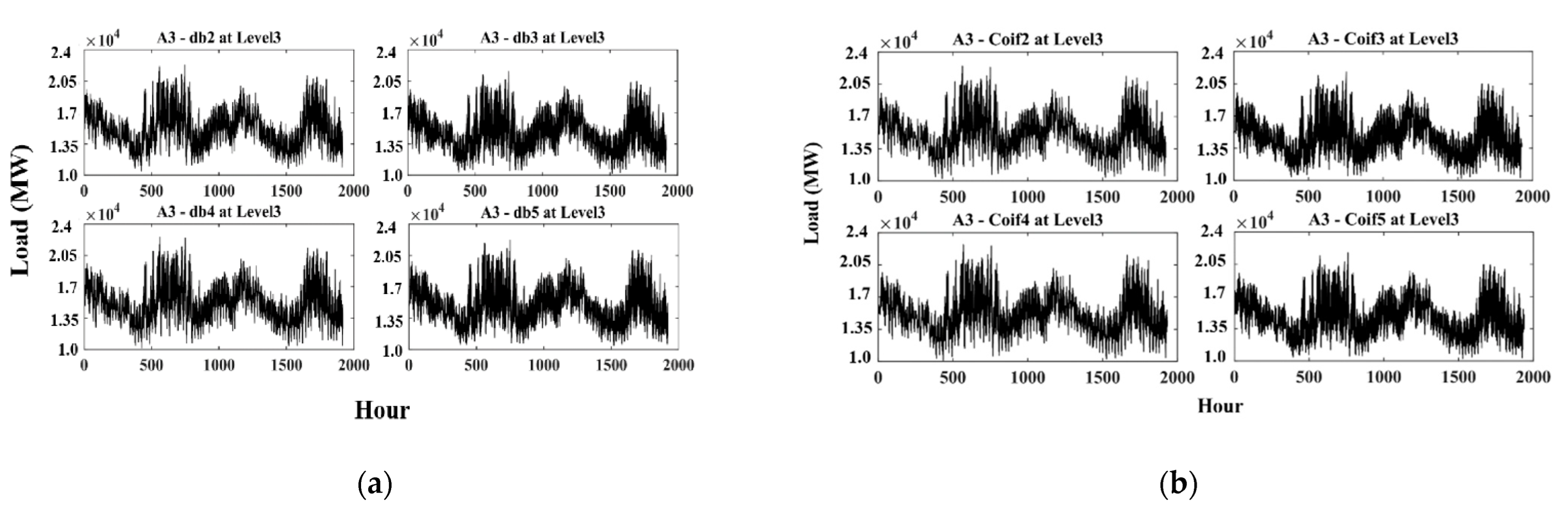
- Model-1 (M1): db wavelets were used in three blocks. The arrangement of this model is shown in Figure 2a.
- (2).
- Model-2 (M2): In this case, the model M1 blocks were replaced with coif wavelets.
- (3).
- Model-3 (M3): The proposed model was tested in 4 optimum ways from all the possible combinations with db and coif, resulting in the appropriate model (M3).
- (4).
- Model-4 (M4): Based on Model M3, we developed an ensemble wavelet-based model, as shown in Figure 2b.
4.1. Case Studies Analysis
- The errors in the results when estimating all-season loads using the model M1 are as follows: First, the summer season weekday (1.1576%) had the lowest error. Second, there was an error of 1.1353% and 1.4758% during the winter weekends and seasons, respectively.
- When estimating all-season loads with the help of model M2, the spring season had error values of 1.2445% and 1.3641%, respectively. However, in winter, the error value was 1.2163%.
- The model M3 had an error value of 1.1153% and 1.2379%, respectively, during the summer season weekdays, and 1.3532% during the months of fall.
- Based on the productivity results of the suggested model (M4), the spring weekday had an error of 0.1521%, and the weekend had an error of 0.2482%.
4.2. Validation of the Proposed Model with Various Datasets
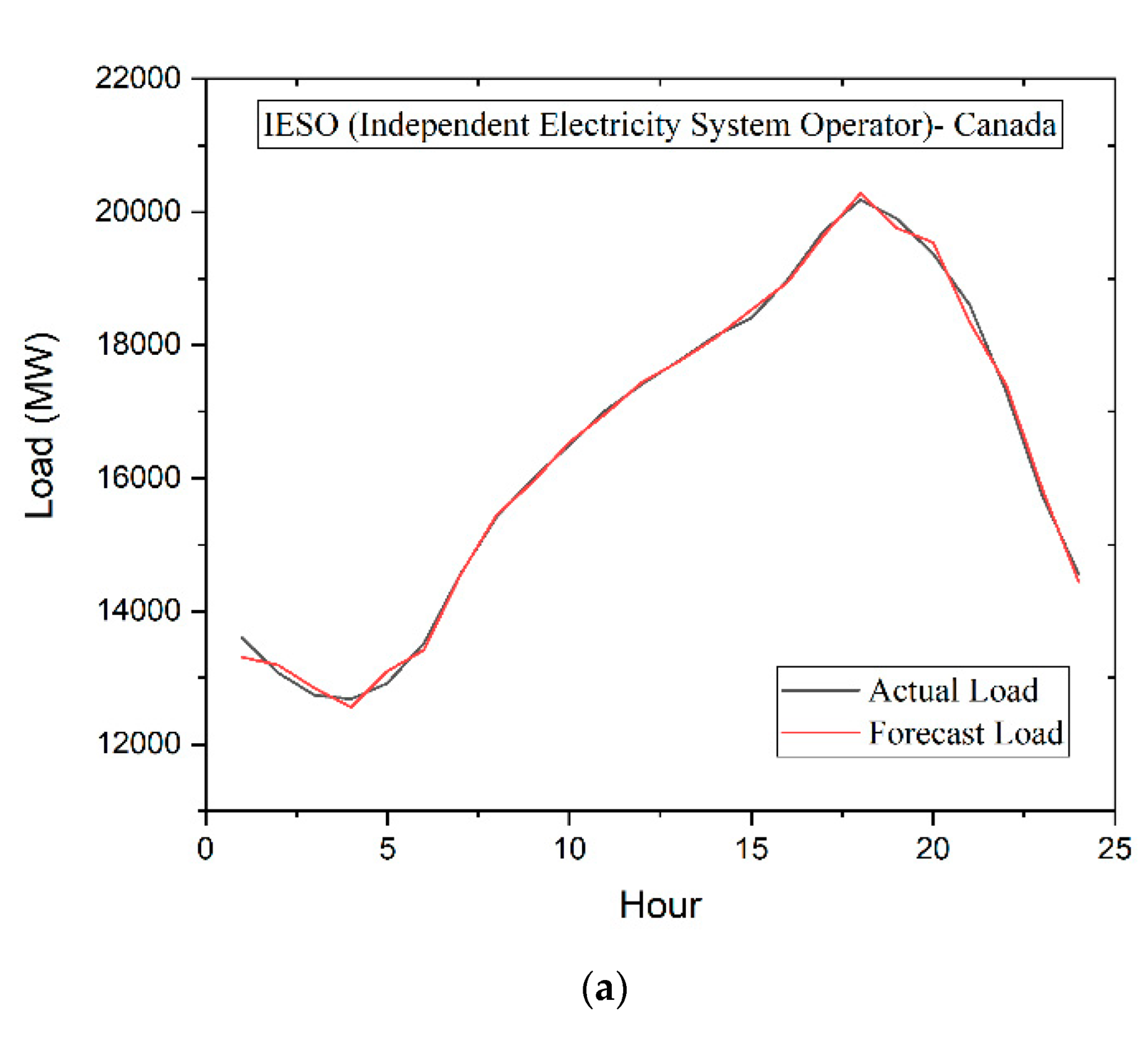
4.2.1. IESO-Canada
4.2.2. ENTSO-E
4.2.3. ISO-NE
Test Case 1
Test Case 2
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Young, P.C. Book Review: Comparative Models for Electrical Load Forecasting. IEE Proc. D Control Theory Appl. 1986, 133, 143. [Google Scholar] [CrossRef]
- Raza, M.Q.; Khosravi, A. A Review on Artificial Intelligence Based Load Demand Forecasting Techniques for Smart Grid and Buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Cheepati, K.R.; Nageswara Prasad, T. Performance Comparison of Short Term Load Forecasting Techniques. Int. J. Grid Distrib. Comput. 2016, 9, 287–302. [Google Scholar] [CrossRef]
- Kondaiah, V.Y.; Saravanan, B.; Sanjeevikumar, P.; Khan, B. Review on Short-term Load Forecasting Models for Micro-grid Application. J. Eng. 2022, 2022, 665–689. [Google Scholar] [CrossRef]
- Paparoditis, E.; Sapatinas, T. Short-Term Load Forecasting: The Similar Shape Functional Time-Series Predictor. IEEE Trans. Power Syst. 2013, 28, 3818–3825. [Google Scholar] [CrossRef] [Green Version]
- Dodamani, S.N.; Shetty, V.J.; Magadum, R.B. Short Term Load Forecast Based on Time Series Analysis: A Case Study. In Proceedings of the IEEE International Conference on Technological Advancements in Power and Energy, TAP Energy, Kollam, India, 24–26 June 2015. [Google Scholar]
- Haq, M.R.; Ni, Z. A New Hybrid Model for Short-Term Electricity Load Forecasting. IEEE Access 2019, 7, 125413–125423. [Google Scholar] [CrossRef]
- Dhaval, B.; Deshpande, A. Short-Term Load Forecasting with Using Multiple Linear Regression. Int. J. Electr. Comput. Eng. 2020, 10, 3911–3917. [Google Scholar] [CrossRef]
- Li, C.; Chiang, T.W. Complex Neurofuzzy ARIMA Forecasting—A New Approach Using Complex Fuzzy Sets. IEEE Trans. Fuzzy Syst. 2013, 21, 567–584. [Google Scholar] [CrossRef]
- Lopez, J.C.; Rider, M.J.; Wu, Q. Parsimonious Short-Term Load Forecasting for Optimal Operation Planning of Electrical Distribution Systems. IEEE Trans. Power Syst. 2019, 34, 1427–1437. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.; Huang, M. Traffic Flow Forecast through Time Series Analysis Based on Deep Learning. IEEE Access 2020, 8, 82562–82570. [Google Scholar] [CrossRef]
- Rocha, L.G.; Goias, E.D.; Alcala, S.G.S.; Garces Negrete, L.P. Short-Term Electric Load Forecasting Using Neural Networks: A Comparative Study. In Proceedings of the 2020 IEEE PES Transmission and Distribution Conference and Exhibition—Latin America, Montevideo, Uruguay, 28 September–2 October 2020. [Google Scholar]
- Dagdougui, H.; Bagheri, F.; Le, H.; Dessaint, L. Neural Network Model for Short-Term and Very-Short-Term Load Forecasting in District Buildings. Energy Build. 2019, 203, 109408. [Google Scholar] [CrossRef]
- Drgoňa, J.; Arroyo, J.; Cupeiro Figueroa, I.; Blum, D.; Arendt, K.; Kim, D.; Ollé, E.P.; Oravec, J.; Wetter, M.; Vrabie, D.L.; et al. All You Need to Know about Model Predictive Control for Buildings. Annu. Rev. Control 2020, 50, 190–232. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S. Load Forecasting Using Interval Type-2 Fuzzy Logic Systems: Optimal Type Reduction. IEEE Trans. Ind. Inform. 2014, 10, 1055–1063. [Google Scholar] [CrossRef]
- Wu, J.; Cui, Z.; Chen, Y.; Kong, D.; Wang, Y.G. A New Hybrid Model to Predict the Electrical Load in Five States of Australia. Energy 2019, 166, 598–609. [Google Scholar] [CrossRef]
- Cecati, C.; Kolbusz, J.; Rózycki, P.; Siano, P.; Wilamowski, B.M. A Novel RBF Training Algorithm for Short-Term Electric Load Forecasting and Comparative Studies. IEEE Trans. Ind. Electron. 2015, 62, 6519–6529. [Google Scholar] [CrossRef]
- Kalakova, A.; Kumar Nunna, H.S.V.S.; Jamwal, P.K.; Doolla, S. A Novel Genetic Algorithm Based Dynamic Economic Dispatch with Short-Term Load Forecasting. IEEE Trans. Ind. Appl. 2021, 57, 2972–2982. [Google Scholar] [CrossRef]
- Liao, Z.; Pan, H.; Fan, X.; Zhang, Y.; Kuang, L. Multiple Wavelet Convolutional Neural Network for Short-Term Load Forecasting. IEEE Internet Things J. 2021, 8, 9730–9739. [Google Scholar] [CrossRef]
- Liu, Y.; Dutta, S.; Kong, A.W.K.; Yeo, C.K. An Image Inpainting Approach to Short-Term Load Forecasting. IEEE Trans. Power Syst. 2022, in press. [Google Scholar] [CrossRef]
- Li, S.; Goel, L.; Wang, P. An Ensemble Approach for Short-Term Load Forecasting by Extreme Learning Machine. Appl. Energy 2016, 170, 22–29. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Liang, X.; Huang, B. Event-Triggered-Based Distributed Cooperative Energy Management for Multienergy Systems. IEEE Trans. Ind. Inform. 2019, 15, 2008–2022. [Google Scholar] [CrossRef]
- Liu, Z.; Li, W.; Sun, W. A Novel Method of Short-Term Load Forecasting Based on Multiwavelet Transform and Multiple Neural Networks. Neural Comput. Appl. 2013, 22, 271–277. [Google Scholar] [CrossRef]
- Tayab, U.B.; Zia, A.; Yang, F.; Lu, J.; Kashif, M. Short-Term Load Forecasting for Microgrid Energy Management System Using Hybrid HHO-FNN Model with Best-Basis Stationary Wavelet Packet Transform. Energy 2020, 203, 117857. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Zakeri, S.; Shoaran, M.; Mohammadi-Ivatloo, B.; Mohammadi, F. Short-Term Load Forecasting of Microgrid via Hybrid Support Vector Regression and Long Short-Term Memory Algorithms. Sustainability 2020, 12, 7076. [Google Scholar] [CrossRef]
- Aly, H.H.H. A Proposed Intelligent Short-Term Load Forecasting Hybrid Models of ANN, WNN and KF Based on Clustering Techniques for Smart Grid. Electr. Power Syst. Res. 2020, 182, 106191. [Google Scholar] [CrossRef]
- Li, H.; Phung, D. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2014, 3, 1157–1182. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets. Math. Comput. 1993, 61, 941–942. [Google Scholar] [CrossRef]
- Anbazhagan, S.; Vaidehi, K. Short-Term Load Forecasting Using Wavelet De-Noising Signal Processing Techniques. In Data Engineering and Communication Technology; Advances in Intelligent Systems and Computing; Springer: Singapore, 2020. [Google Scholar]
- Bento, P.M.R.; Pombo, J.A.N.; Calado, M.R.A.; Mariano, S.J.P.S. Optimization of Neural Network with Wavelet Transform and Improved Data Selection Using Bat Algorithm for Short-Term Load Forecasting. Neurocomputing 2019, 358, 53–71. [Google Scholar] [CrossRef]
- El-Hendawi, M.; Wang, Z. An Ensemble Method of Full Wavelet Packet Transform and Neural Network for Short Term Electrical Load Forecasting. Electr. Power Syst. Res. 2020, 182, 106265. [Google Scholar] [CrossRef]
- Li, S.; Wang, P.; Goel, L. A Novel Wavelet-Based Ensemble Method for Short-Term Load Forecasting with Hybrid Neural Networks and Feature Selection. IEEE Trans. Power Syst. 2016, 31, 1788–1798. [Google Scholar] [CrossRef]
- Bessec, M.; Fouquau, J. Short-Run Electricity Load Forecasting with Combinations of Stationary Wavelet Transforms. Eur. J. Oper. Res. 2018, 264, 149–164. [Google Scholar] [CrossRef]
- Chen, Y.; Luh, P.B.; Guan, C.; Zhao, Y.; Michel, L.D.; Coolbeth, M.A.; Friedland, P.B.; Rourke, S.J. Short-Term Load Forecasting: Similar Day-Based Wavelet Neural Networks. IEEE Trans. Power Syst. 2010, 25, 322–330. [Google Scholar] [CrossRef]
- Ofori-Ntow, E., Jr.; Ziggah, Y.Y.; Relvas, S. Hybrid Ensemble Intelligent Model Based on Wavelet Transform, Swarm Intelligence and Artificial Neural Network for Electricity Demand Forecasting. Sustain. Cities Soc. 2021, 66, 102679. [Google Scholar] [CrossRef]
- Zhang, G.; Guo, J. A Novel Method for Hourly Electricity Demand Forecasting. IEEE Trans. Power Syst. 2020, 35, 1351–1363. [Google Scholar] [CrossRef]
- Suryanarayana, G.; Lago, J.; Geysen, D.; Aleksiejuk, P.; Johansson, C. Thermal Load Forecasting in District Heating Networks Using Deep Learning and Advanced Feature Selection Methods. Energy 2018, 157, 141–149. [Google Scholar] [CrossRef]
- Dai, Y.; Zhao, P. A Hybrid Load Forecasting Model Based on Support Vector Machine with Intelligent Methods for Feature Selection and Parameter Optimization. Appl. Energy 2020, 279, 115332. [Google Scholar] [CrossRef]
- Rafati, A.; Joorabian, M.; Mashhour, E. An Efficient Hour-Ahead Electrical Load Forecasting Method Based on Innovative Features. Energy 2020, 201, 117511. [Google Scholar] [CrossRef]
- Valente, J.M.; Maldonado, S. SVR-FFS: A Novel Forward Feature Selection Approach for High-Frequency Time Series Forecasting Using Support Vector Regression. Expert Syst. Appl. 2020, 160, 113729. [Google Scholar] [CrossRef]
- Lahouar, A.; Ben Hadj Slama, J. Day-Ahead Load Forecast Using Random Forest and Expert Input Selection. Energy Convers. Manag. 2015, 103, 1040–1051. [Google Scholar] [CrossRef]
- Pramono, S.H.; Rohmatillah, M.; Maulana, E.; Hasanah, R.N.; Hario, F. Deep Learning-Based Short-Term Load Forecasting for Supporting Demand Response Program in Hybrid Energy System. Energies 2019, 12, 3359. [Google Scholar] [CrossRef] [Green Version]
- Tian, C.; Ma, J.; Zhang, C.; Zhan, P. A Deep Neural Network Model for Short-Term Load Forecast Based on Long Short-Term Memory Network and Convolutional Neural Network. Energies 2018, 11, 3493. [Google Scholar] [CrossRef] [Green Version]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Chen, K.; Chen, K.; Wang, Q.; He, Z.; Hu, J.; He, J. Short-Term Load Forecasting with Deep Residual Networks. IEEE Trans. Smart Grid 2019, 10, 3943–3952. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Wang, P.; Goel, L. Short-Term Load Forecasting by Wavelet Transform and Evolutionary Extreme Learning Machine. Electr. Power Syst. Res. 2015, 122, 96–103. [Google Scholar] [CrossRef]
- Yu, H.; Reiner, P.D.; Xie, T.; Bartczak, T.; Wilamowski, B.M. An Incremental Design of Radial Basis Function Networks. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1793–1803. [Google Scholar] [CrossRef] [PubMed]



| Input Data | Season | Output (To Forecast Month) | Training Set | Testing Set (Last Two Months from Input Data) |
|---|---|---|---|---|
| IESO Dataset 1 January 2017 To 30 September 2019 | Winter | January 2019 | January 17 to October 18 | November 18 to December 18 |
| Spring | April 2019 | April 17 to January 19 | February 19 to March 19 | |
| Summer | July 2019 | July 17 to April 19 | May 19 to June 19 | |
| Fall | October 2019 | October 17 to July 19 | August 19 to September 19 |
| Statistical Summary Analysis | ||||||
|---|---|---|---|---|---|---|
| Season | Training Set | |||||
| Mean (MW) | Minimum (MW) | Maximum (MW) | Range (MW) | Sum (MW) | Count (Hour) | |
| Winter | 15,689.10342 | 10,541 | 23,240 | 12,699 | 137,436,546 | 8760 |
| Spring | 15,769.39189 | 10,541 | 23,240 | 12,699 | 138,139,873 | 8760 |
| Summer | 15,610.72996 | 10,328 | 23,240 | 12,912 | 147,989,720 | 9480 |
| Fall | 15,465.89030 | 10,328 | 21,791 | 11,463 | 135,481,199 | 8760 |
| Testing Set | ||||||
| Winter | 15,881.27 | 11,765 | 20,152 | 8387 | 23,250,178 | 1464 |
| Spring | 16,207.93 | 12,210 | 20,500 | 8290 | 22,950,422 | 1416 |
| Summer | 14,060.91 | 10,328 | 20,248 | 9920 | 20,585,179 | 1464 |
| Fall | 15,125.40 | 10,477 | 21,354 | 10,877 | 22,143,585 | 1464 |
| Model | Day | Winter Season | Spring Season | Summer Season | Fall Season | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAPE (%) | MAE (MW) | RMSE (MW) | MAPE (%) | MAE (MW) | RMSE (MW) | MAPE (%) | MAE (MW) | RMSE (MW) | MAPE (%) | MAE (MW) | RMSE (MW) | ||
| M1 | Weekday | 1.3405 | 247 | 353 | 1.6586 | 200 | 286 | 1.1576 | 669 | 914 | 1.6022 | 486 | 660 |
| Weekend | 1.1353 | 292 | 418 | 1.9111 | 174 | 248 | 1.4561 | 532 | 727 | 1.2843 | 603 | 823 | |
| M2 | Weekday | 1.6952 | 171 | 237 | 1.2445 | 267 | 323 | 1.5313 | 506 | 625 | 1.9801 | 343 | 483 |
| Weekend | 1.5211 | 190 | 264 | 1.3641 | 243 | 294 | 1.9007 | 407 | 503 | 1.6412 | 413 | 583 | |
| M3 | Weekday | 1.4767 | 156 | 218 | 1.6586 | 139 | 182 | 1.3869 | 488 | 540 | 1.1153 | 482 | 672 |
| Weekend | 1.5561 | 132 | 183 | 1.7245 | 134 | 176 | 1.8321 | 370 | 408 | 1.2379 | 435 | 605 | |
| M4 | Weekday | 0.1871 | 111 | 129 | 0.1521 | 113 | 122 | 0.3432 | 342 | 380 | 0.4274 | 424 | 551 |
| Weekend | 0.4274 | 91 | 109 | 0.5183 | 93 | 102 | 0.2482 | 321 | 353 | 0.2503 | 404 | 521 | |
| Model | Winter Season | Spring Season | Summer Season | Fall Season | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAPE (%) | MAE (MW) | RMSE (MW) | MAPE (%) | MAE (MW) | RMSE (MW) | MAPE (%) | MAE (MW) | RMSE (MW) | MAPE (%) | MAE (MW) | RMSE (MW) | |
| M1 | 1.4758 | 94 | 321 | 1.5697 | 88 | 301 | 1.6137 | 86 | 294 | 1.7375 | 80 | 608 |
| M2 | 1.2163 | 70 | 331 | 1.3086 | 65 | 246 | 1.9320 | 56 | 208 | 1.6211 | 51 | 590 |
| M3 | 1.5328 | 72 | 210 | 1.3831 | 79 | 219 | 1.7150 | 107 | 187 | 1.3532 | 80 | 553 |
| M4 | 0.6145 | 55 | 130 | 0.6704 | 62 | 169 | 0.5914 | 51 | 139 | 0.6777 | 60 | 427 |
| MAPE (%) of the Proposed Method with IESO-Dataset | ||
|---|---|---|
| Month | WT based NN [28] | Proposed Model |
| January | 1.504 | 1.354 |
| February | 1.618 | 1.266 |
| March | 1.888 | 1.339 |
| April | 1.763 | 1.634 |
| May | 1.406 | 1.354 |
| June | 1.961 | 1.799 |
| July | 1.638 | 1.323 |
| August | 1.627 | 1.512 |
| September | 1.508 | 1.236 |
| October | 1.434 | 1.273 |
| November | 1.757 | 1.554 |
| December | 2.024 | 1.692 |
| Day(s) | ||
| Weekday | 1.03 | 0.96 |
| Weekend | 1.33 | 1.01 |
| Model | MAPE (%) | MAE (MW) | RMSE (MW) |
|---|---|---|---|
| CNN-LSTM [44] | 2.45 | 171.71 | 240.57 |
| RNN-LSTM [45] | 2.22 | 155.83 | 222.44 |
| Waavenet [43] | 2.24 | 157.28 | 217.98 |
| CNN-LSTM [43] | 2.02 | 142.23 | 203.23 |
| Proposed | 1.97 | 127.18 | 188.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kondaiah, V.Y.; Saravanan, B. Short-Term Load Forecasting with a Novel Wavelet-Based Ensemble Method. Energies 2022, 15, 5299. https://doi.org/10.3390/en15145299
Kondaiah VY, Saravanan B. Short-Term Load Forecasting with a Novel Wavelet-Based Ensemble Method. Energies. 2022; 15(14):5299. https://doi.org/10.3390/en15145299
Chicago/Turabian StyleKondaiah, V. Y., and B. Saravanan. 2022. "Short-Term Load Forecasting with a Novel Wavelet-Based Ensemble Method" Energies 15, no. 14: 5299. https://doi.org/10.3390/en15145299
APA StyleKondaiah, V. Y., & Saravanan, B. (2022). Short-Term Load Forecasting with a Novel Wavelet-Based Ensemble Method. Energies, 15(14), 5299. https://doi.org/10.3390/en15145299





