A Review on Popular Control Applications in Wind Energy Conversion System Based on Permanent Magnet Generator PMSG
Abstract
:1. Introduction
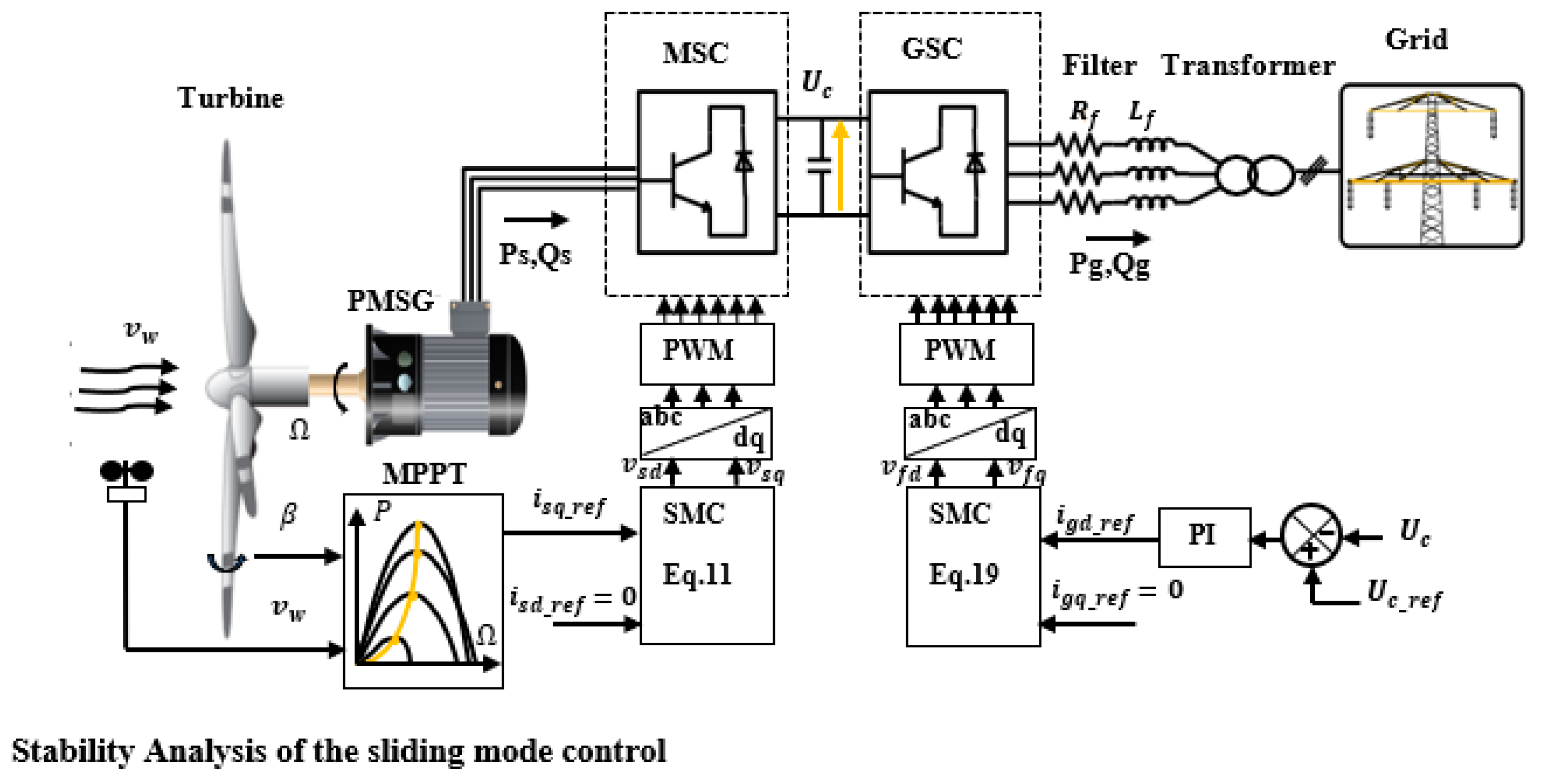
2. Sliding Mode Control
2.1. Review of the Sliding Mode Control
2.2. Application of Sliding Mode Control on the PMSG Wind Power System
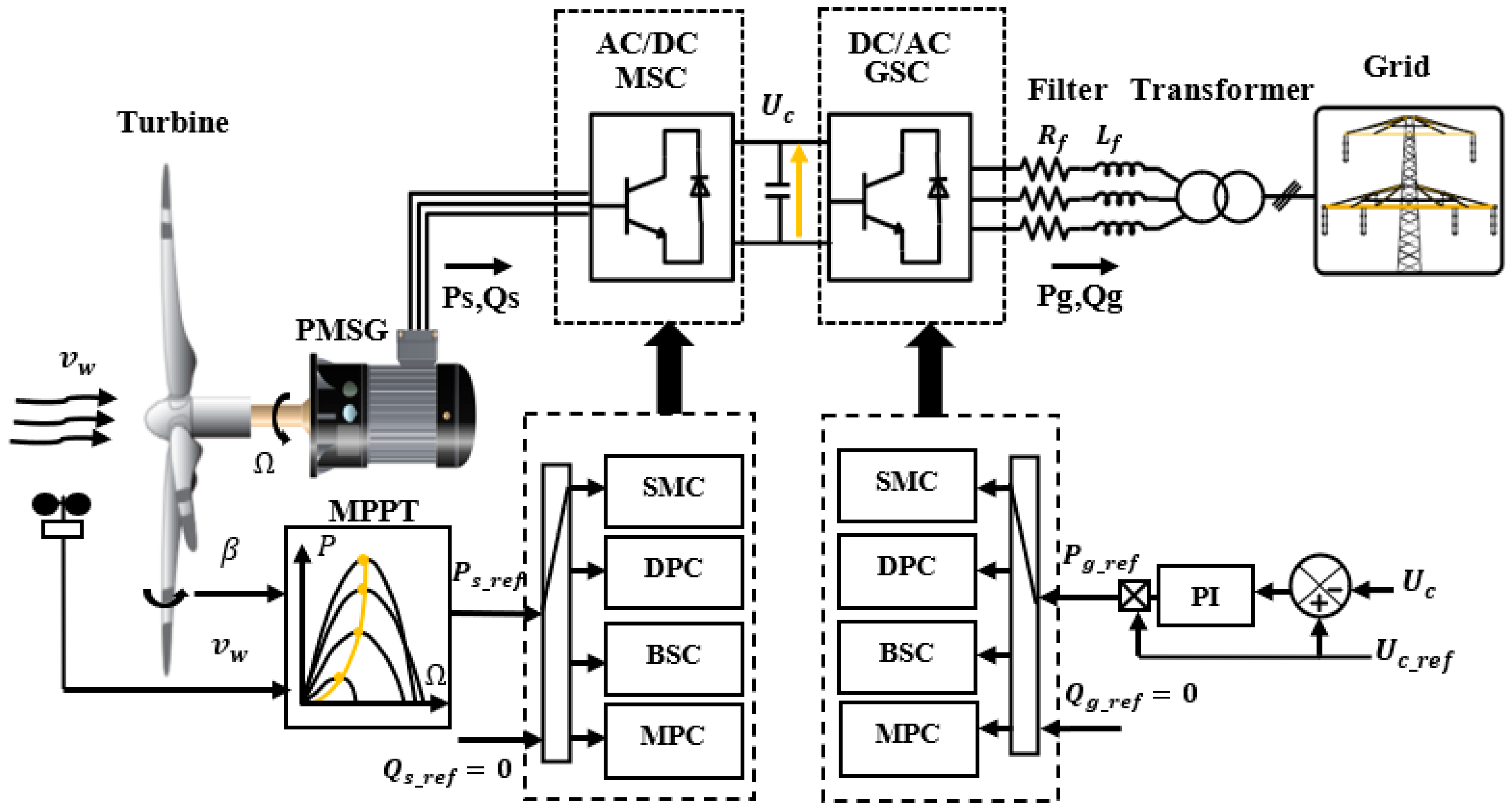
2.2.1. Machine-Side Control
2.2.2. Grid-Side Control
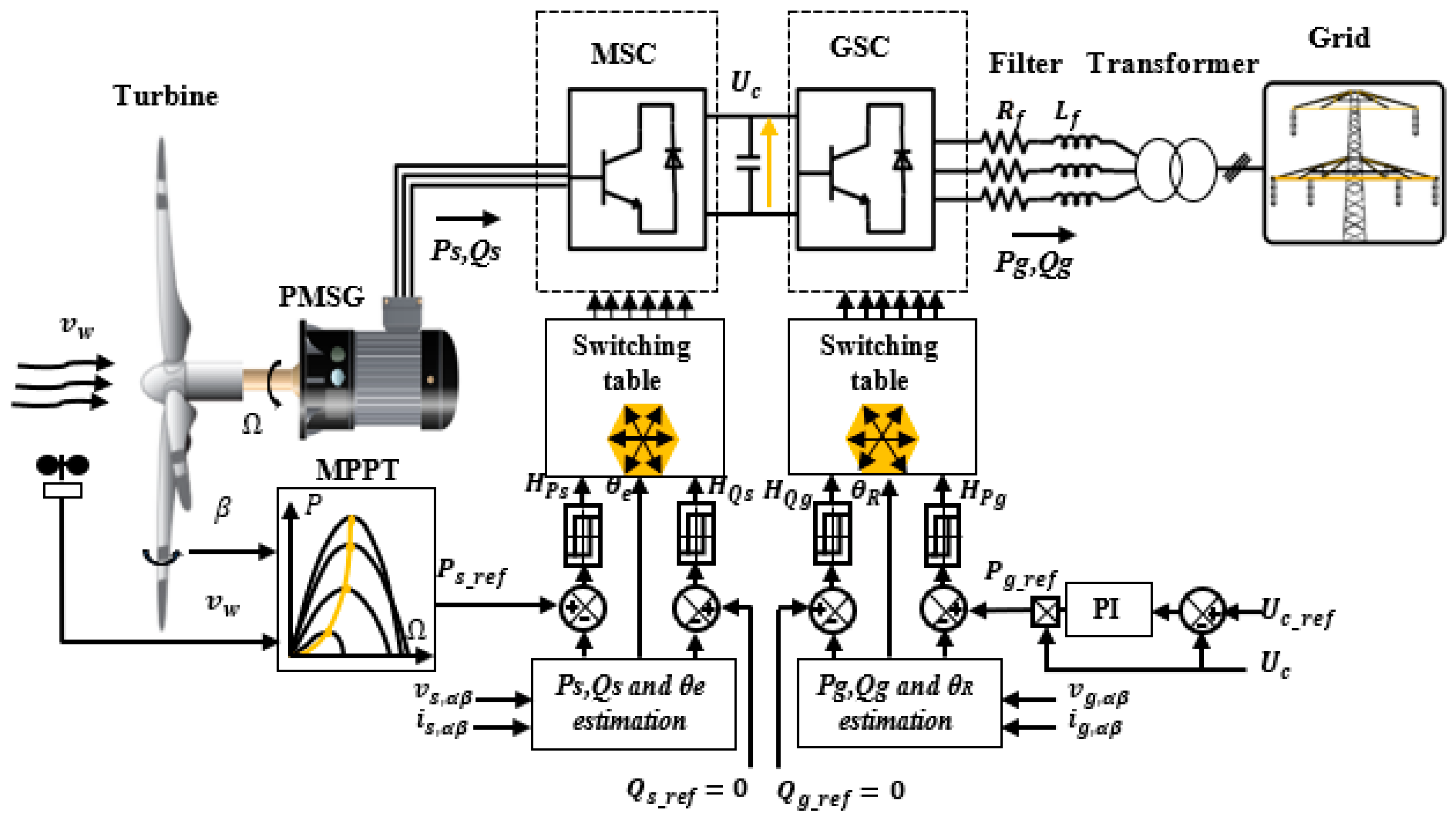
3. Direct Power Control
3.1. Review of Direct Power Control
3.2. Application of Direct Power Control on the PMSG Wind Power System
Grid Side Converter
- a.
- Switching table-based direct power control
- b.
- Dynamics performance:
- ▪
- An increase in reactive power is obtained by applying the voltage vectors , .
- ▪
- A decrease in reactive power is obtained by applying the voltage vectors , .
- ▪
- An increase in active power is obtained by applying the voltage vectors .
- ▪
- A decrease in reactive power is obtained by applying the voltage vectors .
4. Backstepping Control
4.1. Review of Backstepping Control
4.2. Application of Backstepping Control on the PMSG Wind Power System
4.2.1. Machine Side Control
4.2.2. Grid-Side Converter Control
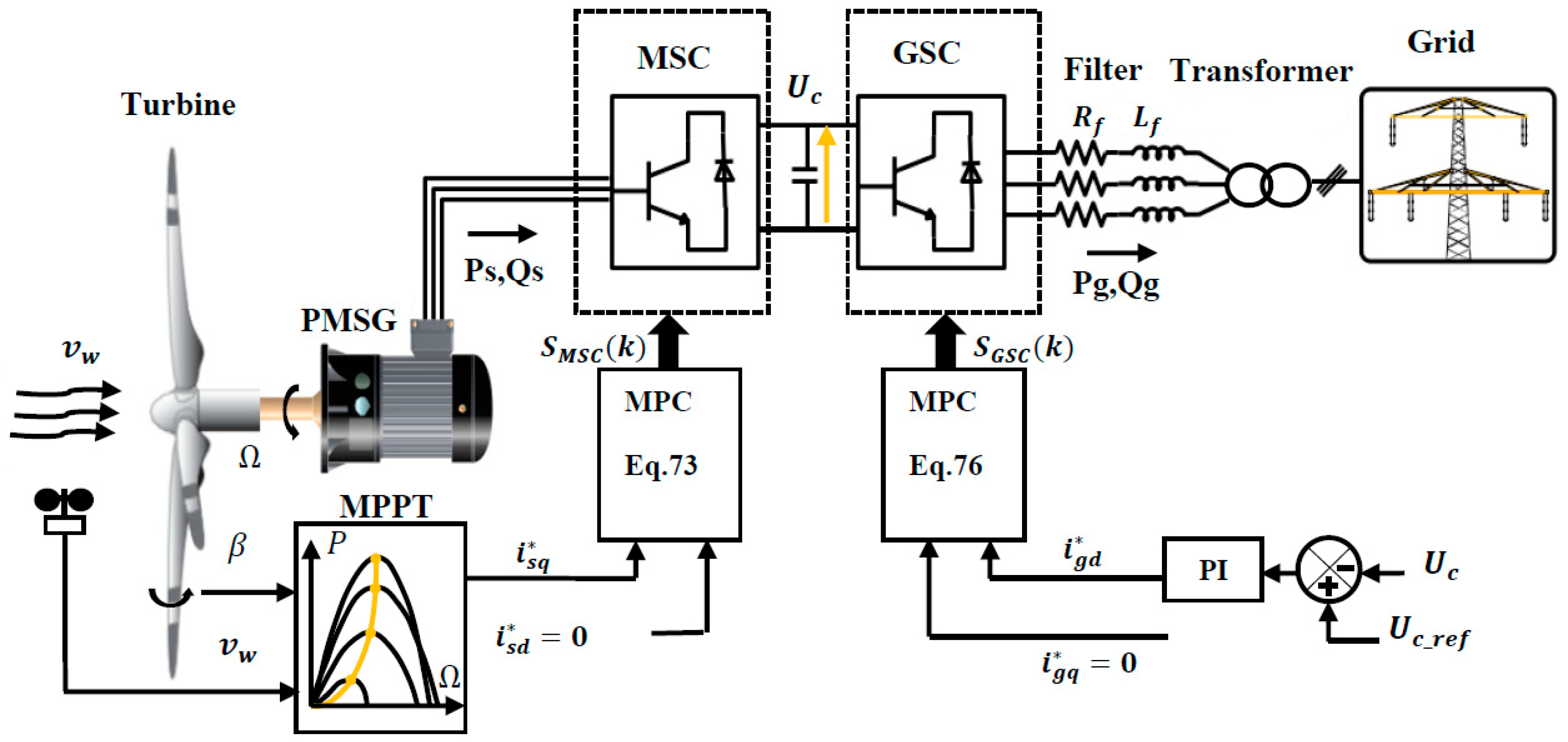
5. Model Predictive Control
5.1. Review of Model Predictive Control
5.2. Application of Model Predictive Control on the PMSG Wind Power System
- Reference calculation: In this step, the reference control value (x ∈ voltage, current, power, torque, flux, etc.) is calculated depending on the application’s nature.
- Prediction: this subsystem predicts the future values of the control variables based on the DT model, the system parameters and the converter switching state combinations S(K).
- Extrapolation: the future value of the reference control variable is estimated in this step based on the current and past sample values .
- Cost Function Minimization: this function is used to minimize the error between the predicted and extrapolated references g = .
5.2.1. Machine-Side Control
5.2.2. Grid-Side Control Scheme
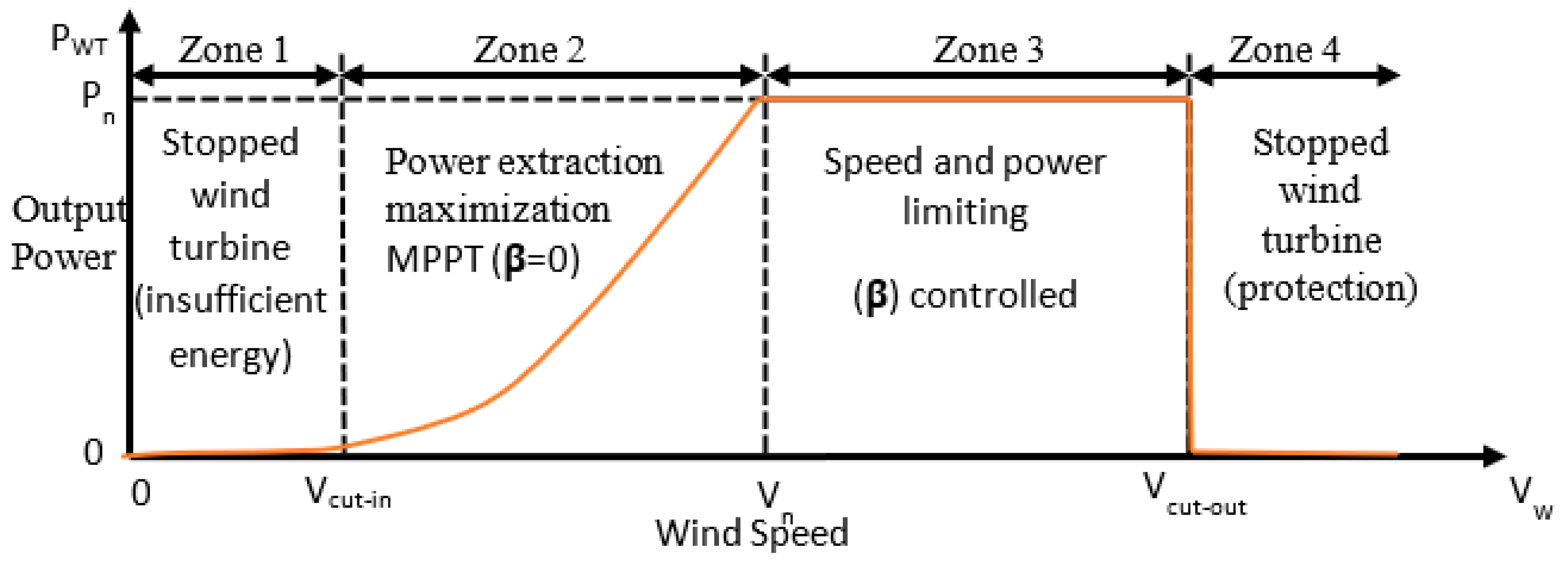
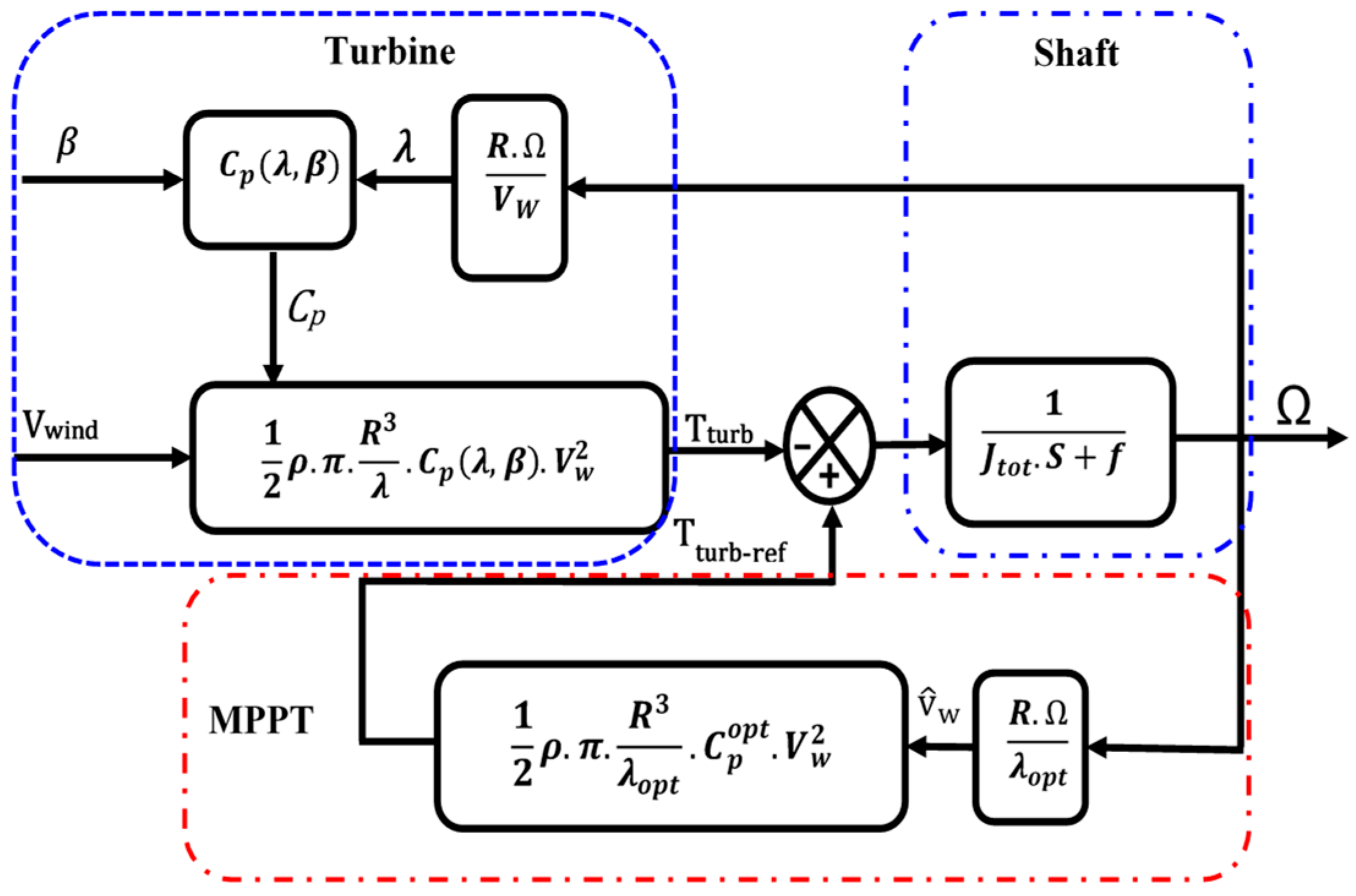
6. MPPT Control
7. Results and Discussion
- The WECS parameters are mentioned in the Appendix A.
- The wind speed varies between 3.5 m/s and 8.5 m/s for 10 s.
- Grid frequency f = 50 Hz.
- To commute IGBT devices of two-level converters, pulse width modulation (PWM) was used in both SMC and BSC.
- A phase-locked loop (PLL) was used to synchronize the GSC to the grid in all control schemes except the DPC control scheme.
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Pturb | Ψ(d,q) | d-q axis flux |
| vw/Pwind | ∅f | Generator flux |
| Ω | Pg | Active grid power |
| Ωt | Qg | Reactive grid power |
| Tem | UC | DC-link voltage |
| Tem_ref | Vg(d,q) | d-q axis grid voltage |
| Tturb | Vf(d,q) | d-q axis filter voltage |
| Cp(λ, β) | ig(d,q) | d-q axis grid current |
| λ | if(d,q) | d-q axis filter current |
| β | ωg | Grid pulsation |
| ρ | Rf | Filter resistance |
| p | Lf | Filter inductance |
| S | WT | Wind turbine |
| R | WECS | Wind energy conversion system |
| Ωe | MPPT | Maximum power point tracking |
| Ps | MPC | Model predictive control |
| Qs | SMC | Sliding mode control |
| Rs | DPC | Direct power control |
| Ls(d,q) | BSC | Backstepping control |
| Vs(d,q) | Tr | Response time |
| is(d,q) | THD | Total harmonic distortion |
| fc | PMSG | Permanent magnet synchronous generator |
| IGBT | PWM | Pulse width modulation |
Appendix A
| PMSG Parameters | Symbol | Values | Turbine Parameters | Symbol | Values |
|---|---|---|---|---|---|
| Power generator | Pn | 1.5 MW | Radius of the turbine blade | R | 55 m |
| Pole number | P | 75 | |||
| Stator resistance | Rs | 6.25 × 10−3 Ω | Turbine+ generator moment | Jtot | 10,000 N.m |
| d axis inductance | Lsd | 4.229 × 10−3 H | Specific density of air | ρ | 1.22 kg/m3 |
| q axis inductance | Lsq | 4.229 × 10−3 H | Tip-speed ratio | λopt | 8 |
| Generator flux | ∅f | 11.1464 Wb | Optimal power coefficient | Cp_max | 0.426 |
| Coefficient of friction | fc | 0.0142 N.m.s/rad |
- Wind turbine modelling:
- Permanent Magnet Synchronous Generator Model:
- Stator Electric equations:
- Stator Magnetic equations:
- Mechanical equations:
- Grid Model:
References
- IEA. Key World Energy Statistics 2020; IEA: Paris, France, 2020; Available online: https://www.iea.org/reports/key-world-energy-statistics-2020 (accessed on 15 May 2022).
- Allouhi, A.; Kousksou, T.; Jamil, A.; Bruel, P.; Mourad, Y.; Zeraouli, Y. Solar driven cooling systems: An updated review. Renew. Sustain. Energy Rev. 2015, 44, 159–181. [Google Scholar] [CrossRef]
- REN21. Renewables 2015 Global Status Report (Paris: REN21 Secretariat); REN21: Paris, France, 2015; ISBN 978-3-9815934-6-4. [Google Scholar]
- Kalogirou, S.A. Chapter 3—Solar Energy Collectors. In Solar Energy Engineering, 2nd ed.; Academic Press: Boston, MA, USA, 2014; pp. 125–220. [Google Scholar]
- Cheng, M.; Zhu, Y. The state of the art of wind energy conversion systems and technologies: A review. Energy Convers. Manag. 2014, 88, 332–347. [Google Scholar] [CrossRef]
- Boulouiha, H.M.; Allali, A.; Denai, M. Grid integration of wind energy systems: Control design, stability, and power quality issues. In Clean Energy for Sustainable Development; Elsevier: Amsterdam, The Netherlands, 2017; pp. 239–335. [Google Scholar]
- Khare, V.; Nema, S.; Baredar, P. Solar–wind hybrid renewable energy system: A review. Renew. Sustain. Energy Rev. 2016, 58, 23–33. [Google Scholar] [CrossRef]
- Bundi, J.M.; Ban, X.; Wekesa, D.W.; Ding, S. Pitch control of small H-type Darrieus vertical axis wind turbines using advanced gain scheduling techniques. Renew. Energy 2020, 161, 756–765. [Google Scholar] [CrossRef]
- Zhao, Y.; Wei, C.; Zhang, Z.; Qiao, W. A review on position/speed sensorless control for permanent magnet synchronous machine-based wind energy conversion systems. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 203–216. [Google Scholar] [CrossRef]
- Mourabit, Y.E.; Derouich, A.; Allouhi, A.; Ghzizal, A.E.; Ouanjli, N.E.; Zamzoumyes, O. Sustainable production of wind energy in the main Morocco’s sites using permanent magnet synchronous generators. Int. Trans. Electr. Energy Syst. 2020, 30, e12390. [Google Scholar] [CrossRef]
- Bossoufi, B.; Karim, M.; Lagrioui, A. Contribution à la Commande de la Machine Synchrone à Aimant Permanent, Utilisation des Solutions Numériques FPGA; Presses Académiques Francophones (PAF): Sarrebruck, Germany, 2015; p. 184. [Google Scholar]
- Bossoufi, B. Contrôle des Machines Electriques et Convertisseurs de Puissance; Editions Universitaires Européennes: Sarrebruck, Germany, 2020. [Google Scholar]
- Bekiroglu, E.; Yazar, M.D. MPPT Control of Grid Connected DFIG at Variable Wind Speed. Energies 2022, 15, 3146. [Google Scholar] [CrossRef]
- Pande, J.; Nasikkar, P.; Kotecha, K.; Varadarajan, V. A Review of Maximum Power Point Tracking Algorithms for Wind Energy Conversion Systems. J. Mar. Sci. Eng. 2021, 9, 1187. [Google Scholar] [CrossRef]
- Dahbi, A.; Nait-Said, N.; Nait-Said, M.-S. A novel combined MPPT-pitch angle control for wide range variable speed wind turbine based on neural network. Int. J. Hydrogen Energy 2016, 41, 9427–9442. [Google Scholar] [CrossRef]
- Taoussi, M.; Karim, M.; Hammoumi, D.; el Bekkali, C.; Bossoufi, B.; el Ouanjli, N. Comparative study between Backstepping adaptive and Field-oriented control of the DFIG applied to wind turbines. In Proceedings of the 3rd IEEE International Conference on Advanced Technologies for Signal and Image Processing, Fez, Morocco, 22–24 May 2017. [Google Scholar]
- Bouderbala, M.; Bossoufi, B.; Lagrioui, A.; Taoussi, M.; Aroussi, H.A.; Ihedrane, Y. Direct and indirect vector control of a doubly fed induction generator based in a wind energy conversion system. Int. J. Electr. Comput. Eng. (IJECE) 2019, 9, 1531–1540. [Google Scholar] [CrossRef]
- Saady, I.; Karim, M.; Bossoufi, B.; Motahhir, S.; Adouairi, M.S.; Majout, B.; Lamnadi, M.; Masud, M.; Al-Amri, J.F. Optimisation for a photovoltaic pumping system using indirect Field Oriented Control of Induction Motor. Electronics 2021, 10, 3076. [Google Scholar] [CrossRef]
- Tiwari, R.; Kumar, K.; Babu, N.R.; Prabhu, K.R. Coordinated MPPT and DPC Strategies for PMSG based Grid Connected Wind Energy Conversion System. Energy Procedia 2018, 145, 339–344. [Google Scholar] [CrossRef]
- Majout, B.; Bossoufi, B.; Karim, M.; Ouanjli, N.; Saady, I.; Laggoun, Z.; Mahfoud, M.; Yessef, M. Model Reference Adaptive System Based DPC-SVM Control for Permanent Magnet Synchronous Generator. In Digital Technologies and Applications; ICDTA 2022: Lecture Notes in Networks and Systems; Motahhir, S., Bossoufi, B., Eds.; Springer: Cham, Switzerland, 2022; Volume 454, pp. 535–544. [Google Scholar]
- Mahfoud, M.E.L.; Bossoufi, B.; Ouanjli, N.E.L.; Mahfoud, S.; Taoussi, M. Improved Direct Torque Control of Doubly Fed Induction Motor Using Space Vector Modulation. Int. J. Intell. Eng. Syst. 2021, 14, 177–188. [Google Scholar] [CrossRef]
- Zaihidee, F.M.; Mekhilef, S.; Mubin, M. Robust Speed Control of PMSM Using Sliding Mode Control (SMC)—A Review. Energies 2019, 12, 1669. [Google Scholar] [CrossRef]
- Bossoufi, B.; Karim, M.; Lagrioui, A.; Taoussi, M.; Derouich, A. Observer backstepping control of DFIG-Generators for wind turbines variable-speed: FPGA-based implementation. Renew Energy 2015, 81, 903–917. [Google Scholar] [CrossRef]
- Yang, Z.-J.; Nagai, T.; Kanae, S.; Wada, K. Dynamic surface control approach to adaptive robust control of nonlinear systems in semi-strict feedback form. Int. J. Syst. Sci. 2007, 38, 709–724. [Google Scholar] [CrossRef]
- Ouanjli, N.E.L.; TaoussI, M.; Derouich, A.; Chebabhi, A.; Ghzizal, A.E.L.; Bossoufi, B. High Performance Direct Torque Control of Doubly Fed Induction Motor using Fuzzy Logic. Gazi Univ. J. Sci. Syst. 2018, 31, 532–542. [Google Scholar]
- el Karaoui, I.; Maaroufi, M.; Bossoufi, B. Fuzzy sliding mode power control for wind power generation systems connected to the grid. IJPEDS Int. J. Power Electron. Drive Syst. 2022, 13, 606–619. [Google Scholar]
- Mekrini, Z.; Bri, S.; Bouchnaif, J.; Bossoufi, B. Experimental results of vector control for an asynchronous machine. TELKOMNIKA (Telecommun. Comput. Electron. Control) 2020, 18, 3285–3292. [Google Scholar] [CrossRef]
- Taoussi, M.; Bossoufi, B.; Bouderbala, M.; Motahhir, S.; Alkhammash, E.H.; Masud, M.; ZineLabidine, N.; Karim, M. Implementation and Validation of Hybrid Control for Wind Turbine Using FPGA Controller Board. Electronics 2021, 10, 3154. [Google Scholar] [CrossRef]
- El Ouanjli, N.; Derouich, A.; El Ghzizal, A.; Bouchnaif, J.; Taoussi, M.; Bossoufi, B. Real-time Implementation in dSPACE of DTC-Backstepping for Doubly Fed Induction Motor. Eur. Phys. J. Plus 2019, 135, 2–9. [Google Scholar] [CrossRef]
- Bouderbala, M.; Bossoufi, B.; Deblecker, O.; Alami Aroussi, H.; Taoussi, M.; Lagrioui, A.; Motahhir, S.; Masud, M.; Alraddady, F.A. Experimental Validation of Predictive Current Control for DFIG: FPGA Implementation. Electronics 2021, 10, 2670. [Google Scholar] [CrossRef]
- Orlando, N.A.; Liserre, M.; Mastromauro, R.A.; Dell’Aquila, A. A Survey of Control Issues in PMSG-Based Small Wind-Turbine Systems. IEEE Trans. Ind. Inform. 2013, 9, 1211–1221. [Google Scholar] [CrossRef]
- Majout, B.; Bossoufi, B.; Bouderbala, M.; Masud, M.; Al-Amri, J.F.; Taoussi, M.; El Mahfoud, M.; Motahhir, S.; Karim, M. Improvement of PMSG-Based Wind Energy Conversion System Using Developed Sliding Mode Control. Energies 2022, 15, 1625. [Google Scholar] [CrossRef]
- Zribi, M.; Alrifai, M.; Rayan, M. Sliding Mode Control of a Variable—Speed Wind Energy Conversion System Using a Squirrel Cage Induction Generator. Energies 2017, 10, 604. [Google Scholar] [CrossRef]
- Osman, A.M.; Alsokhiry, F. Sliding Mode Control for Grid Integration of Wind Power System Based on Direct Drive PMSG. IEEE Access 2022, 10, 26567–26579. [Google Scholar] [CrossRef]
- Jena, N.K.; Pradhan, H.; Choudhury, A.; Mohanty, K.B.; Sanyal, S.K. A novel SMC based vector control strategy used for decoupled control of PMSG based variable speed wind turbine system. In Proceedings of the 2017 International Conference on Circuit, Power and Computing Technologies (ICCPCT), Kollam, India, 20–21 April 2017; pp. 1–6. [Google Scholar]
- Errami, Y.; Ouassaid, M.; Cherkaoui, M.; Maaroufi, M. SlidingMode Control Scheme of Variable Speed Wind Energy Conversion System Based on the PMSG for Utility Network Connection. In Advances and Applications in Sliding Mode Control Systems, Studies in Computational Intelligence, 1st ed.; Azar, A.T., Zhu, Q., Eds.; Springer: Cham, Switzerland, 2015; pp. 167–200. [Google Scholar]
- Majout, B.; Abrahmi, D.; Ihedrane, Y.; El Bakkali, C.; Mohammed, K.; Bossoufi, B. Improvement of sliding mode power control applied to wind system based on doubly-fed induction generator. Int. J. Power Electron. Drive Syst. 2021, 12, 441–452. [Google Scholar] [CrossRef]
- Valenciaga, F.; Puleston, P. High-Order Sliding Control for a Wind Energy Conversion System Based on a Permanent Magnet Synchronous Generator. IEEE Trans. Energy Convers. 2008, 23, 860–867. [Google Scholar] [CrossRef]
- Matraji, I.; Al-Durra, A.; Errouissi, R. Design and experimental validation of enhanced adaptive second-order SMC for PMSG-based wind energy conversion system. Int. J. Electr. Power Energy Syst. 2018, 103, 21–30. [Google Scholar] [CrossRef]
- Benbouzid, M.; Beltran, B.; Amirat, Y.; Yao, G.; Han, J.; Mangel, H. Second-order sliding mode control for DFIG-based wind turbines fault ride-through capability enhancement. ISA Trans. 2014, 53, 827–833. [Google Scholar] [CrossRef]
- Shen, X.; Liu, J.; Alcaide, A.M.; Yin, Y.; Leon, J.I.; Vazquez, S.; Wu, L.; Franquelo, L.G. Adaptive Second-Order Sliding Mode Control for Grid-Connected NPC Converters with Enhanced Disturbance Rejection. IEEE Trans. Power Electron. 2022, 37, 206–220. [Google Scholar] [CrossRef]
- Benelghali, S.; El Hachemi Benbouzid, M.; Charpentier, J.F.; AhmedAli, T.; Munteanu, I. Experimental validation of a marine current turbine simulator: Application to a permanent magnet synchronous generator-based system second-order sliding mode control. IEEE Trans. Ind. Electron. 2011, 58, 118–126. [Google Scholar] [CrossRef] [Green Version]
- Phan, D.; Huang, S. Super-Twisting Sliding Mode Control Design for Cascaded Control System of PMSG Wind Turbine. J. Power Electron. 2015, 15, 1358–1366. [Google Scholar] [CrossRef]
- Zholtayev, D.; Rubagotti, M.; Do, T.D. Adaptive super-twisting sliding mode control for maximum power point tracking of PMSG-based wind energy conversion systems. Renew Energy 2022, 183, 877–889. [Google Scholar] [CrossRef]
- Yaichi, I.; Semmah, A.; Wira, P.; Djeriri, Y. Super-twisting Sliding Mode Control of a Doubly-fed Induction Generator Based on the SVM Strategy. Period. Polytech. Electr. Eng. Comput. Sci. 2019, 63, 178–190. [Google Scholar] [CrossRef]
- Swikir, A.; Utkin, V. Chattering analysis of conventional and super twisting sliding mode control algorithm. Proc. IEEE Int. Work. Var. Struct. Syst. 2016, 2016, 98–102. [Google Scholar]
- Shtessel, Y.; Taleb, M.; Plestan, F. A novel adaptive-gain super twisting sliding mode controller: Methodology and application. Automatica 2012, 48, 759–769. [Google Scholar] [CrossRef]
- Li, S.; Zhou, M.; Yu, X. Design and Implementation of Terminal Sliding Mode Control Method for PMSM Speed Regulation System. IEEE Trans. Ind. Inform. 2013, 9, 1879–1891. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Jin, M.; Lee, J.; Chang, P.H.; Choi, C. Practical Nonsingular Terminal Sliding-Mode Control of Robot Manipulators for High-Accuracy Tracking Control. IEEE Trans. Ind. Electron. 2009, 56, 3593–3601. [Google Scholar]
- Shi, R.; Zhang, X. Adaptive Fractional-order Non-singular Fast Terminal Sliding Mode Control Based on Fixed Time Observer. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 7006–7016. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, K.; Yan, F.; Chen, B. Adaptive super-twisting nonsingular fast terminal sliding mode control for cable-driven manipulators using time-delay estimation. Adv. Eng. Softw. J. 2019, 128, 113–124. [Google Scholar] [CrossRef]
- Solis, C.U.; Clempner, J.B.; Poznyak, A.S. Fast terminal sliding mode control with an integral filter applied to a van der pol oscillator. IEEE Trans. Ind. Electron. 2017, 64, 5622–5628. [Google Scholar] [CrossRef]
- Madani, T.; Daachi, B.; Djouani, K. Modular controller design based fast terminal sliding mode for articulated exoskeleton systems. IEEE Trans. Control. Syst. Technol. 2016, 25, 1133–1140. [Google Scholar] [CrossRef]
- Sun, G.; Wu, L.; Kuang, Z.; Ma, Z.; Liu, J. Practical tracking control of linear motor via fractional-order sliding mode. Automatica 2018, 94, 221–235. [Google Scholar] [CrossRef]
- Saravanakumar, R.; Jena, D. Validation of an integral sliding mode control for optimal control of a three blade variable speed variable pitch wind turbine. Int. J. Electr. Power Energy Syst. 2015, 69, 421–429. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, F.; Zhao, C.; Wang, Z. A PI-Type Sliding Mode Controller Design for PMSG-Based Wind Turbine. Complexity 2019, 2019, 2538206. [Google Scholar] [CrossRef]
- Maaruf, M.; El Ferik, S.; Mahmoud, M.S. Integral Sliding Mode Control with Power Exponential Reaching Law for DFIG. In Proceedings of the 17th International Multi-Conference on Systems, Signals & Devices (SSD), Monastir, Tunisia, 20–23 July 2020; pp. 1122–1127. [Google Scholar]
- Lin, S.-C.; Chen, Y.-Y. Design of self-learning fuzzy sliding mode controllers based on genetic algorithms. Fuzzy Sets Syst. 1997, 86, 139–153. [Google Scholar] [CrossRef]
- Kharabian, B.; Mirinejad, H. Hybrid Sliding Mode/H-Infinity Control Approach for Uncertain Flexible Manipulators. IEEE Access 2020, 8, 170452–170460. [Google Scholar] [CrossRef]
- Lian, J.; Zhao, J. Robust H-infinity integral sliding mode control for a class of uncertain switched nonlinear systems. J. Control Theory Appl. 2010, 8, 521–526. [Google Scholar] [CrossRef]
- Lin, F.-J.; Chang, C.-K.; Huang, P.-K. FPGA-Based Adaptive Backstepping Sliding-Mode Control for Linear Induction Motor Drive. IEEE Trans. Power Electron. 2007, 22, 1222–1231. [Google Scholar] [CrossRef]
- Rajendran, S.; Jena, D. Backstepping sliding mode control of a variable speed wind turbine for power optimization. J. Mod. Power Syst. Clean Energy 2015, 3, 402–410. [Google Scholar] [CrossRef]
- Shang, L.; Hu, J. Sliding-Mode-Based Direct Power Control of Grid-Connected Wind-Turbine-Driven Doubly Fed Induction Generators Under Unbalanced Grid Voltage Conditions. IEEE Trans. Energy Convers. 2012, 27, 362–373. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Boudjema, Z.; Bizon, N.; Thounthong, P.; Takorabet, N. Direct Power Control Based on Modified Sliding Mode Controller for a Variable-Speed Multi-Rotor Wind Turbine System Using PWM Strategy. Energies 2022, 15, 3689. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Ahmed, A.A.; Abdelsalam, H.A. Fuzzy-based Adaptive Sliding Mode Control for a Direct-Driven PMSG Wind Energy System. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019; pp. 81–88. [Google Scholar] [CrossRef]
- Yin, X.-X.; Lin, Y.-G.; Li, W.; Gu, Y.-J.; Liu, H.-W.; Lei, P.-F. A novel fuzzy integral sliding mode current control strategy for maximizing wind power extraction and eliminating voltage harmonics. Energy 2015, 85, 677–686. [Google Scholar] [CrossRef]
- Saghafinia, A.; Wooi Ping, H.; Nasir Uddin, M. Fuzzy sliding mode control based on boundary layer theory for chattering-free and robust induction motor drive. Int. J. Adv. Manuf. Technol. 2014, 71, 57–68. [Google Scholar] [CrossRef]
- Hong, C.-M.; Huang, C.-H.; Cheng, F.-S. Sliding mode control for variable-speed wind turbine generation systems using artificial neural network. Energy Procedia 2014, 61, 1626–1629. [Google Scholar] [CrossRef]
- Babaie, M.; Al-Haddad, K. ANN Based Model-Free Sliding Mode Control for Grid-Connected Compact Multilevel Converters: An Experimental Validation. In Proceedings of the 2021 IEEE 30th International Symposium on Industrial Electronics (ISIE), Kyoto, Japan, 20–23 June 2021; pp. 1–6. [Google Scholar]
- Baek, S.; Baek, J.; Han, S. An Adaptive sliding mode control with effective switching gain tuning near the sliding surface. IEEE Access 2019, 7, 15563–15572. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.T.; Nguyen, V.Q.; Le, K.M.; Tran, H.N.; Jeon, J.W. An Adaptive Sliding-Mode Controller with a Modified Reduced-Order Proportional Integral Observer for Speed Regulation of a Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Electron. 2022, 69, 7181–7191. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Zhang, Y.; Chen, J.; Sang, Y.; Jiang, L. Passivity-based sliding-mode control design for optimal power extraction of a PMSG based variable speed wind turbine. Renew. Energy 2018, 119, 577–589. [Google Scholar] [CrossRef]
- Wei, C.; Qiao, W.; Zhao, Y. Sliding-mode observer-based sensorless direct power control of DFIGs for wind power applications. In Proceedings of the IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Yang, B.; Yu, T.; Shu, H.; Dong, J.; Jiang, L. Robust sliding-mode control of wind energy conversion systems for optimal power extraction via nonlinear perturbation observers. Appl. Energy 2018, 210, 711–723. [Google Scholar] [CrossRef]
- Kim, H.; Son, J.; Lee, J. A high-speed sliding-mode observer for the sensorless speed control of a PMSM. IEEE Trans. Ind. Elect. 2011, 58, 4069–4077. [Google Scholar]
- Mi, Y.; Fu, Y.; Li, D.; Wang, C.; Loh, P.C.; Wang, P. The sliding mode load frequency control for hybrid power system based on disturbance observer. Int. J. Electr. Power Energy Syst. 2016, 74, 446–452. [Google Scholar] [CrossRef]
- Wang, M.; Wang, H.; Shi, Y.; Shen, M.; Song, J. A modified sliding-mode controller-based mode predictive control strategy for three-phase rectifier. Int. J. Circuit Theory Appl. 2020, 48, 1564. [Google Scholar] [CrossRef]
- Jeeranantasin, N.; Nungam, S. Sliding Mode Control of Three-Phase AC/DC Converters using Exponential Rate Reaching Law. J. Syst. Eng. Electron. 2022, 33, 210–221. [Google Scholar] [CrossRef]
- Mozayan, S.M.; Saad, M.; Vahedi, H.; Fortin-Blanchette, H.; Soltani, M. Sliding Mode Control of PMSG Wind Turbine Based on Enhanced Exponential Reaching Law. IEEE Trans. Ind. Electron. 2016, 63, 6148–6159. [Google Scholar] [CrossRef]
- Fallaha, C.J.; Saad, M.; Kanaan, H.Y.; Al-Haddad, K. Sliding mode robot control with exponential reaching law. IEEE Trans. Ind. Electron. 2011, 58, 600–610. [Google Scholar] [CrossRef]
- El Makrini, I.; Guerrero, C.R.; Lefeber, D.; Vanderborght, B. The Variable Boundary Layer Sliding Mode Control: A Safe and Performant Control for Compliant Joint Manipulators. IEEE Robot. Autom. Lett. 2016, 2, 187–192. [Google Scholar] [CrossRef]
- Ohnishi, T. Three phase PWM converter/inverter by means of instantaneous active and reactive power control. In Proceedings of the IECON ’91: 1991 International Conference on Industrial Electronics, Control and Instrumentation, Kobe, Japan, 26 October–1 November 1991; Volume 91, pp. 819–824. [Google Scholar]
- Noguchi, T.; Tomiki, H.; Kondo, S.; Takahashi, I. Direct power control of PWM converter without power-source voltage sensors. IEEE Trans. Ind. Appl. 1998, 34, 473–479. [Google Scholar] [CrossRef]
- Nadour, M.; Essadki, A.; Nasser, T. Comparative analysis between PI & backstepping control strategies of DFIG driven by wind turbine. Int. J. Renew. Energy Resour. 2017, 7, 1307–1316. [Google Scholar]
- Razali, A.; Rahman, A.; George, G.; Rahim, N. Analysis and design of new switching look-up table for virtual flux direct power control of grid connected three phase PWM AC-DC converter. IEEE Trans. Ind. Appl. 2014, 51, 1189–1200. [Google Scholar] [CrossRef]
- Zhi, D.; Xu, L.; Williams, B.W. Improved Direct Power Control of Grid-Connected DC/AC Converters. IEEE Trans. Power Electron. 2009, 24, 1280–1292. [Google Scholar] [CrossRef]
- Malinowski, M.; Kazmierkowski, M.P.; Hansen, S.; Blaabjerg, F.; Marques, G.D. Virtualflux-based direct power control of three-phase PWM rectifiers. IEEE Trans. Ind. Appl. 2001, 37, 1019–1027. [Google Scholar] [CrossRef]
- Chaoui, A.; Krim, F.; Gaubert, J.-P.; Rambault, L. DPC controlled three-phase active filter for power quality improvement. Int. J. Electr. Power Energy Syst. 2008, 30, 476–485. [Google Scholar] [CrossRef]
- Cirrincione, M.; Pucci, M.; Vitale, G. Direct power control of three-phase VSIs for the minimization of common-mode emissions in distributed generation systems. Electr. Power Syst. Res. 2011, 81, 830–839. [Google Scholar] [CrossRef]
- Chaoui, A.; Gaubert, J.-P.; Krim, F. Power quality improvement using DPC controlled three-phase shunt active filter. Electr. Power Syst. Res. 2010, 80, 657–666. [Google Scholar] [CrossRef]
- Zhang, Y.; Qu, C. Table-based direct power control for three-phase AC/DC converters under unbalanced grid voltages. IEEE Trans. Power Electron. 2015, 30, 7090–7099. [Google Scholar] [CrossRef]
- Bouafia, A.; Gaubert, J.-P.; Krim, F. Analysis and design of new switching table for direct power control of three-phase PWM rectifier. In Proceedings of the 13th International Power Electronics and Motion Control Conference, Poznan, Poland, 1–3 September 2008; pp. 703–709. [Google Scholar]
- Aissaoui, H.E.; Ougli, A.E.; Tidhaf, B. Neural Networks and Fuzzy Logic Based Maximum Power Point Tracking Control for Wind Energy Conversion System. Adv. Sci. Technol. Eng. Syst. J. 2021, 6, 586–592. [Google Scholar] [CrossRef]
- Kwak, S.; Park, J.-C. Model-Predictive Direct Power Control with Vector Preselection Technique for Highly Efficient Active Rectifiers. IEEE Trans. Ind. Inform. 2015, 11, 44–52. [Google Scholar] [CrossRef]
- Kwak, S.; Moon, U.-C.; Park, J.-C. Predictive-Control-Based Direct Power Control with an Adaptive Parameter Identification Technique for Improved AFE Performance. IEEE Trans. Power Electron. 2014, 29, 6178–6187. [Google Scholar] [CrossRef]
- Antoniewicz, P.; Kazmierkowski, M.P. Virtual-Flux-Based Predictive Direct Power Control of AC/DC Converters with Online Inductance Estimation. IEEE Trans. Ind. Electron. 2008, 55, 4381–4390. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, W.; Li, Z.; Zhang, Y. Model predictive direct power control of a PWM rectifier with duty cycle optimization. IEEE Trans. Power Electron. 2013, 28, 5343–5351. [Google Scholar] [CrossRef]
- Song, Z.; Tian, Y.; Chen, W.; Zou, Z.; Chen, Z. Predictive Duty Cycle Control of Three-Phase Active-Front-End Rectifiers. IEEE Trans. Power Electron. 2015, 31, 698–710. [Google Scholar] [CrossRef]
- Hu, J. Improved Dead-Beat Predictive DPC Strategy of Grid-Connected DC–AC Converters with Switching Loss Minimization and Delay Compensations. IEEE Trans. Ind. Inform. 2012, 9, 728–738. [Google Scholar] [CrossRef]
- Choi, D.; Lee, K.; Member, S. Dynamic performance improvement of AC/DC converter using model predictive direct power control with finite control set. IEEE Trans. Ind. Electron. 2015, 62, 757–767. [Google Scholar] [CrossRef]
- Aurtenechea, S.; Rodríguez, M.; Oyarbide, E.; Torrealday, J.R. Predictive control strategy for DC/AC converters based on direct power control. IEEE Trans. Ind. Electron. 2007, 54, 1261–1271. [Google Scholar]
- Hu, J.; Zhu, Z.Q. Improved voltage-vector sequences on dead-beat predictive direct power control of reversible three-phase grid-connected voltage-source converters. IEEE Trans. Power Electron. 2013, 28, 254–267. [Google Scholar] [CrossRef]
- Song, Z.; Chen, W.; Xia, C. Predictive direct power control for three-phase gridconnected converters without sector information and voltage vector selection. IEEE Trans. Power Electron. 2014, 29, 5518–5531. [Google Scholar] [CrossRef]
- Vazquez, S.; Marquez, A.; Aguilera, R.; Quevedo, D.; Leon, J.I.; Franquelo, L.G. Power control for grid-connected power converters. IEEE Trans. Ind. Electron. 2015, 62, 2010–2020. [Google Scholar] [CrossRef]
- Zhang, Y.; Qu, C. Model predictive direct power control of PWM rectifiers under unbalanced network conditions. IEEE Trans. Ind. Electron. 2015, 62, 4011–4022. [Google Scholar] [CrossRef]
- Cho, Y.; Beum, L.K. Virtual-flux-based direct power control of three-phase PWM rectifiers with fast dynamic response. IEEE Trans. Ind. Appl. 2016, 31, 3348–3359. [Google Scholar] [CrossRef]
- Zhang, Y.; Qu, C. Direct power control of a pulse width modulation rectifier using space vector modulation under unbalanced grid voltages. IEEE Trans. Power Electron. 2015, 30, 5892–5901. [Google Scholar] [CrossRef]
- Fischer, J.R.; Gonz, S.A.; Carugati, I.; Herr, M.A.; Judewicz, M.G.; Carrica, D.O. Robust predictive control of grid-tied converters based on direct power control. IEEE Trans. Power Electron. 2014, 29, 5634–5643. [Google Scholar] [CrossRef]
- Bouafia, A.; Gaubert, J.-P.; Krim, F. Predictive direct power control of three-phase pulsewidth modulation (PWM) rectifier using space vector modulation (SVM). IEEE Trans. Power Electron. 2010, 25, 228–236. [Google Scholar] [CrossRef]
- Restrepo, J.A.; Aller, J.M.; Viola, J.C.; Bueno, A.; Habetler, T.G. Optimum space vector computation technique for direct power control. IEEE Trans. Power Electron. 2009, 24, 1637–1645. [Google Scholar] [CrossRef]
- Tao, Y.K.; Wang, L.; Wu, Q.H.; Tang, W.H. Virtual-flux-based predictive direct power control of three-phase AC/DC converters. In Proceedings of the IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Hong Kong, China, 7–10 December 2014; pp. 1–6. [Google Scholar]
- Hu, J.; Shang, L.; He, Y.; Zhu, Z.Q. Direct active and reactive power regulation of grid connected DC/AC converters using sliding mode control approach. IEEE Trans. Power Electron. 2011, 26, 210–222. [Google Scholar] [CrossRef]
- Bouafia, A.; Krim, F.; Gaubert, J.-P. Fuzzy-logic-based switching state selection for direct power control of three-phase PWM rectifier. IEEE Trans. Ind. Electron. 2009, 56, 1984–1992. [Google Scholar] [CrossRef]
- Bouafia, A.; Krim, F.; Gaubert, J.-P. Design and implementation of high performance direct power control of three-phase PWM rectifier, via fuzzy and PI controller for output voltage regulation. Energy Convers. Manag. 2009, 50, 6–13. [Google Scholar] [CrossRef]
- Portillo, R.; Vazquez, S.; Leon, J.I.; Prats, M.M.; Franquelo, L.G. Model based adaptive direct power control for three-level NPC converters. IEEE Trans. Ind. Inform. 2013, 9, 1148–1157. [Google Scholar] [CrossRef]
- Vazquez, S.; Sanchez, J.A.; Carrasco, J.M.; Leon, J.I.; Galvan, E. A model-based direct power control for three-phase power converters. IEEE Trans. Ind. Electron. 2008, 55, 1647–1657. [Google Scholar] [CrossRef]
- Malinowski, M.; Jasin, M.; Kazmierkowski, M.P. Simple direct power control of three phase PWM rectifier using space-vector modulation (DPC-SCM). IEEE Trans. Ind. Electron. 2004, 51, 447–454. [Google Scholar] [CrossRef]
- Escobar, G.; Stankovic, A.M.; Carrasco, J.M.; Galvan, E.; Ortega, R. Analysis and design of direct power control (DPC) for a three phase synchronous rectifier via output regulation subspaces. IEEE Trans. Power Electron. 2003, 18, 823–830. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Zhang, Y.; Xie, W.; Piao, Z.; Hu, C. Performance improvement of direct power control of PWM rectifier with simple calculation. IEEE Trans. Power Electron. 2013, 28, 3428–3437. [Google Scholar] [CrossRef]
- Suul, J.A.; Luna, A.; Rodríguez, P.; Undeland, T. Virtual-flux-based voltage-sensor-less power control for unbalanced grid conditions. IEEE Trans. Power Electron. 2012, 27, 4071–4087. [Google Scholar] [CrossRef]
- Malinowski, M.; Marques, G. New direct power control of three-phase PWM boost rectifiers under distorted and imbalanced line voltage conditions. In Proceedings of the International Symposium on Industrial Electronics, Rio de Janeiro, Brazil, 9–11 June 2003; pp. 438–443. [Google Scholar]
- Nian, H.; Shen, Y.; Yang, H.; Quan, Y. Flexible grid connection technique of voltage source inverter under unbalanced grid conditions based on direct power control. IEEE Trans. Ind. Appl. 2015, 51, 4041–4050. [Google Scholar] [CrossRef]
- Eloy-Garcia, J.; Arnaltes, S.; Rodriguez-Amenedo, J.L. Extended direct power control of a three-level neutral point clamped voltage source inverter with unbalanced voltages. In Proceedings of the IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 3396–3400. [Google Scholar]
- Komatsu, Y.; Kawaba, T. A control method of active power filter in unsymmetrical voltage system. In Proceedings of the International Conference on Power Electronics and Drive Systems, Singapore, 26–29 May 1997; pp. 839–843. [Google Scholar]
- Malinowski, M. Sensorless Control Strategies for Three-Phase PWM Rectifiers. Ph.D. Thesis, Politechnika Warszawska, Warszawa, Poland, 2001. [Google Scholar]
- Norniella, J.G.; Cano, J.M.; Orcajo, G.A.; Rojas, C.H.; Pedrayes, J.F.; Cabanas, M.F.; Melero, M.G. Improving the dynamics of virtual-flux-based control of three-phase active rectifiers. IEEE Trans. Ind. Electron. 2014, 61, 177–187. [Google Scholar] [CrossRef]
- Shan, D.-l.; Song, S.-z.; Ma, J.-w.; Wang, X.-b. Direct power control of PWM rectifiers based on virtual flux. In Proceedings of the International Conference on Computer Application and System Modeling, Taiyuan, China, 22–24 October 2010; pp. 613–616. [Google Scholar]
- Bouafia, A.; Gaubert, J.P.; Chaoui, A. Direct power control scheme based on disturbance rejection principle for three-phase PWM AC/DC converter under different input voltage conditions. J. Electr. Syst. 2012, 4, 367–383. [Google Scholar]
- Hu, J.; Zhu, Z.Q. Investigation on switching patterns of direct power control strategies for grid-connected DC-AC converters based on power variation rates. IEEE Trans. Power Electron. 2011, 26, 3582–3598. [Google Scholar] [CrossRef]
- Chen, B.S.; Joos, G. Direct power control of active filters with averaged switching frequency regulation. IEEE Trans. Power Electron. 2008, 23, 2729–2737. [Google Scholar] [CrossRef]
- Gong, B.; Wang, K.; Zhang, J.; You, J.; Luo, Y.; Zhang, W. Advanced switching table for direct power control of a three-phase PWM rectifier. In Proceedings of the IEEE Conference and Expo Transportation Electrification Asia-Pacific, Beijing, China, 31 August–3 September 2014; pp. 1–5. [Google Scholar]
- Baktash, A.; Vahedi, A.; Masoum, M.A.S. Improved switching table for direct power control of three-phase PWM rectifier. In Proceedings of the 2007 Australasian Universities Power Engineering Conference, Perth, Australia, 9–12 December 2007; Volume 2, pp. 592–596. [Google Scholar]
- Zhang, Y.; Peng, Y.; Qu, C. Comparative study of model predictive control and direct power control for PWM rectifiers with active power ripple minimization. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 3823–3830. [Google Scholar]
- Li, P.; Xiong, L.; Wu, F.; Ma, M.; Wang, J. Sliding mode controller based on feedback linearization for damping of sub-synchronous control interaction in DFIG-based wind power plants. Int. J. Electr. Power Energy Syst. 2019, 107, 239–250. [Google Scholar] [CrossRef]
- Drhorhi, I.; El Fadili, A.; Berrahal, C.; Lajouad, R.; El Magri, A.; Giri, F.; Azar, A.T.; Vaidyanathan, S. Chapter 11—Adaptive backstepping controller for DFIG-based wind energy conversion system. In Advances in Nonlinear Dynamics and Chaos (ANDC), Backstepping Control of Nonlinear Dynamical Systems; Vaidyanathan, S., Azar, A.T., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 235–260. ISBN 9780128175828. [Google Scholar]
- Ghamrasni, M.E.L.; Mahmoudi, H.; Bossoufi, B. Modelling and simulation of a wind system using variable wind regimes with Backstepping control of DFIG. IOP Conf. Ser. Earth Environ. Sci. 2018, 161, 012026. [Google Scholar] [CrossRef]
- Shen, X.; Xie, T.; Wang, T. A Fuzzy Adaptative Backstepping Control Strategy for Marine Current Turbine under Disturbances and Uncertainties. Energies 2020, 13, 6550. [Google Scholar] [CrossRef]
- Roy, T.K.; Mahmud, M.A.; Islam, S.N.; Oo, A.M.T. Nonlinear Adaptive Backstepping Controller Design for Permanent Magnet Synchronous Generator (PMSG)-Based Wind Farms to Enhance Fault Ride Through Capabilities. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Mahersi, E.; Khedher, A. Backstepping flux observer for nonlinear control of the direct-drive permanent magnet synchronous generator wind turbines. Wind Eng. 2016, 40, 540–554. [Google Scholar] [CrossRef]
- Liu, Y.-H. Adaptive dynamic surface asymptotic tracking for a class of uncertain nonlinear systems. Int. J. Robust Nonlinear Control 2017, 28, 1233–1245. [Google Scholar] [CrossRef]
- Min, W.; Liu, Q. An improved adaptive fuzzy backstepping control for nonlinear mechanical systems with mismatched uncertainties. Automatika 2019, 60, 1–10. [Google Scholar] [CrossRef]
- Shuai, S.; Baoyong, Z.; Xiaona, S.; Zhengqiang, Z. Adaptive neuro-fuzzy Backstepping dynamic surface control for uncertain fractional-order nonlinear systems. Neurocomputing 2019, 360, 172–184. [Google Scholar]
- Xue, G.; Lin, F.; Li, S.; Liu, H. Adaptive fuzzy finite-time backstepping control of fractional-order nonlinear systems with actuator faults via command-filtering and sliding mode technique. Inf. Sci. 2022, 600, 189–208. [Google Scholar] [CrossRef]
- Wang, F.; Guo, Y.; Wang, K.; Zhang, Z.; Hua, C.; Zong, Q. Disturbance observer based robust backstepping control design of flexible air-breathing hypersonic vehicle. IET Control Theory Appl. 2019, 13, 572–583. [Google Scholar] [CrossRef]
- Hui, J.; Ling, J.; Gu, K.; Yuan, J. Adaptive backstepping controller with extended state observer for load following of nuclear power plant. Prog. Nucl. Energy 2021, 137, 103745. [Google Scholar] [CrossRef]
- Kim, Y.; Park, T.; Lee, J.M. Integration of model predictive control and backstepping approach and its stability analysis. IFAC-PapersOnLine 2018, 51, 405–410. [Google Scholar] [CrossRef]
- Nizami, T.K.; Chakravarty, A. Neural Network Integrated Adaptive Backstepping Control of DC-DC Boost Converter. IFAC-PapersOnLine 2020, 53, 549–554. [Google Scholar] [CrossRef]
- El-Sousy, F.F.M.; El-Naggar, M.F.; Amin, M.; Abu-Siada, A.; Abuhasel, K.A. Robust Adaptive Neural-Network Backstepping Control Design for High-Speed Permanent-Magnet Synchronous Motor Drives: Theory and Experiments. IEEE Access 2019, 7, 99327–99348. [Google Scholar] [CrossRef]
- Bossoufi, B.; Karim, M.; Taoussi, M.; Aroussi, H.A.; Bouderbala, M.; Deblecker, O.; Motahhir, S.; Nayyar, A.; Alzain, M.A. Rooted Tree Optimization for the Backstepping Power Control of a Doubly Fed Induction Generator Wind Turbine: dSPACE Implementation. IEEE Access 2021, 9, 26512–26522. [Google Scholar] [CrossRef]
- Makhad, M.; Zazi, M.; Loulijat, A.; Simon, A.O. Robust Integral Backstepping control for Optimal Power Extraction of a PMSG-based Variable Speed Wind Turbines. In Proceedings of the 1st International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), Meknes, Morocco, 16–19 April 2020; pp. 1–6. [Google Scholar]
- Armghan, H.; Yang, M.; Wang, M.; Ali, N.; Armghan, A. Nonlinear integral backstepping based control of a DC microgrid with renewable generation and energy storage systems. Int. J. Electr. Power Energy Syst. 2019, 117, 105613. [Google Scholar] [CrossRef]
- Loucif, M.; Mechernene, A.; Bossoufi, B. Integral Backstepping Power Control of DFIG Based Nonlinear Modeling Using Voltage Oriented Control. In Proceedings of the Springer-ICDTA’2021 the International Conference on Digital Technologies and Applications, Fez, Morocco, 29–30 January 2021. [Google Scholar]
- Prasad, N.V.D.V.E.; Sahani, M.; Dash, P.K. A new adaptive integral back stepping fractional order sliding mode control approach for PV and wind with battery system based DC microgrid. Sustain. Energy Technol. Assess. 2022, 52, 102261. [Google Scholar] [CrossRef]
- Belkhier, Y.; Achour, A. An intelligent passivity-based backstepping approach for optimal control for grid-connecting permanent magnet synchronous generator-based tidal conversion system. Int. J. Energy Res. 2021, 45, 5433–5448. [Google Scholar] [CrossRef]
- Zu, H.; Zhang, G.-B.; Fei, S.-M. Enhanced model reference adaptive backstepping control of permanent magnet synchronous generator equipped wind energy conversion system with stator parameters varying. In Proceedings of the 2011 Chinese Control and Decision Conference (CCDC), Mianyang, China, 23–25 May 2011; pp. 133–138. [Google Scholar]
- Bossoufi, B.; Karim, M.; Taoussi, M.; Aroussi, H.A.; Bouderbala, M.; Motahhir, S.; Camara, M.B. DSPACE-based implementation for observer backstepping power control of DFIG wind turbine. IET Electr. Power Appl. 2020, 14, 2395–2403. [Google Scholar] [CrossRef]
- Bossoufi, B.; Karim, M.; Lagrioui, A. MATLAB & Simulink simulation with FPGA Based Implementation adaptative and not adaptative backstepping nonlinear control of a permanent magnet synchronous machine drive. WSEAS Trans. Syst. Control 2014, 9, 86–100. [Google Scholar]
- Rajendran, S.; Jena, D. Backstepping Sliding Mode Control for variable speed wind turbine. In Proceedings of the 2014 Annual IEEE India Conference (INDICON), Pune, India, 11–13 December 2014; pp. 1–6. [Google Scholar]
- Mourabit, Y.E.L.; Derouich, A.; Ghzizal, A.E.L.; Bouchnaif, J.; Ouanjli, N.E.L.; Zamzoum, O.; Mezioui, K.; Bossoufi, B. Implementation and validation of Backstepping control for PMSG wind turbine using dSPACE controller board. Energy Rep. J. 2019, 5, 807–821. [Google Scholar]
- Polinder, H.; Ferreira, J.; Jensen, B.; Abrahamsen, A.; Atallah, K.; McMahon, R. Trends in wind turbine generator systems. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 174–185. [Google Scholar] [CrossRef]
- Bossoufi, B.; Lagrioui, A. High Performance Predictive Control for Permanent Magnet Synchronous Machine Drive: FPGA-Based Im-plementation. In Proceedings of the Springer-ICDTA’2021 the International Conference on Digital Technologies and Applications, Fez, Morocco, 29–30 January 2021. [Google Scholar]
- Yaramasu, V.; Wu, B.; Sen, P.C.; Kouro, S.; Narimani, M. High-power wind energy conversion systems: State-of-the-art and emerging technologies. Proc. IEEE 2015, 103, 740–788. [Google Scholar] [CrossRef]
- Polinder, H.; van der Pijl, F.; de Vilder, G.-J.; Tavner, P. Comparison of direct-drive and geared generator concepts for wind turbines. IEEE Trans. Energy Convers. 2006, 21, 725–733. [Google Scholar] [CrossRef]
- Li, H.; Chen, Z.; Polinder, H. Optimization of Multibrid Permanent-Magnet Wind Generator Systems. IEEE Trans. Energy Convers. 2009, 24, 82–92. [Google Scholar] [CrossRef]
- Liserre, M.; Cardenas, R.; Molinas, M.; Rodríguez, J. Overview of multi-MW wind turbines and wind parks. IEEE Trans. Ind. Electron. 2011, 58, 1081–1095. [Google Scholar] [CrossRef]
- Yang, X.; Patterson, D.; Hudgins, J. Permanent magnet generator design and control for large wind turbines. In Proceedings of the IEEE Symposium on Power Electronics and Machines in Wind Applications (PEMWA), Denver, CO, USA, 16–18 July 2012; pp. 1–5. [Google Scholar]
- Zhong, L.; Rahman, M.; Hu, W.; Lim, K. Analysis of direct torque control in permanent magnet synchronous motor drives. IEEE Trans. Power Electron. 1997, 12, 528–536. [Google Scholar] [CrossRef]
- Geyer, T. A Comparison of Control and Modulation Schemes for Medium-Voltage Drives: Emerging Predictive Control Concepts Versus PWM-Based Schemes. IEEE Trans. Ind. Appl. 2011, 47, 1380–1389. [Google Scholar] [CrossRef]
- Rodriguez, J.; Kennel, R.M.; Espinoza, J.R.; Trincado, M.; Silva, C.A.; Rojas, C.A. High-Performance Control Strategies for Electrical Drives: An Experimental Assessment. IEEE Trans. Ind. Electron. 2012, 59, 812–820. [Google Scholar] [CrossRef]
- Chivite-Zabalza, J.; Girones, C.; Carcar, A.; Larrazabal, I.; Olea, E.; Zabaleta, M. Comparison of power conversion topologies for a multi-megawatt off-shore wind turbine, based on commercial power electronic building blocks. In Proceedings of the IEEE Industrial Electronics Conference (IECON), Vienna, Austria, 10–13 November 2013; pp. 5242–5247. [Google Scholar]
- Yazdani, A.; Iravani, R. A Neutral-Point Clamped Converter System for Direct-Drive Variable-Speed Wind Power Unit. IEEE Trans. Energy Convers. 2006, 21, 596–607. [Google Scholar] [CrossRef]
- Faulstich, A.; Stinke, J.; Wittwer, F. Medium voltage converter for permanent magnet wind power generators up to 5 MW. In Proceedings of the European Conference on Power Electronics and Applications (EPE), Dresden, Germany, 11–14 September 2005; p. 9. [Google Scholar]
- Alepuz, S.; Calle, A.; Busquets-Monge, S.; Kouro, S.; Wu, B. Use of Stored Energy in PMSG Rotor Inertia for Low-Voltage Ride-Through in Back-to-Back NPC Converter-Based Wind Power Systems. IEEE Trans. Ind. Electron. 2013, 60, 1787–1796. [Google Scholar] [CrossRef]
- Rodriguez, J.; Bernet, S.; Steimer, P.K.; Lizama, I.E. A Survey on Neutral-Point-Clamped Inverters. IEEE Trans. Ind. Electron. 2010, 57, 2219–2230. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B.; Rodriguez, J.; Perez, M.A.; Leon, J.I. Recent Advances and Industrial Applications of Multilevel Converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Ma, K. Future on power electronics for wind turbine systems. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 139–152. [Google Scholar] [CrossRef]
- Preindl, M.; Bolognani, S. Model predictive direct torque control with finite control set for PMSM drive systems, Part 1: Maximum torque per ampere operation. IEEE Trans. Ind. Inform. 2013, 9, 1912–1921. [Google Scholar] [CrossRef]
- Nguen, H.T.; Al Sumaiti, A.S.; Al Hosani, K.; El Moursi, M.S. Multifunctional Control of Wind Turbine Based Nano-Grid Connected to Distroted Utility-Grid. IEEE Trans. Power Syst. 2021, 37, 576–589. [Google Scholar] [CrossRef]
- Bouderbala, M.; Bossoufi, B.; Aroussi, H.A.; Taoussi, M.; Lagrioui, A. Novel deadbeat predictive control strategy for DFIG’s back to back power converter. IJPEDS Int. J. Power Electron. Drive Syst. 2022, 13, 2731–2741. [Google Scholar] [CrossRef]
- Bouderbala, M.; Bossoufi, B.; Lagrioui, A.; Taoussi, M.; Aroussi, H.A.; Livinti, P. DEADBEAT Control Applied to Wind Power System. In Proceedings of the 5th International Conference on Renewable Energies for Developing Countries—REDEC, Marrakech, Morocco, 25–26 June 2020. [Google Scholar]
- Balamurugan, A.; Baskaran, P. Load Usage Self Regulating Control of Dynamic Response of the Grid Tied Wind Power Generator under Unbalanced Non-Linear Load. J. Green Eng. 2020, 10, 13688–13697. [Google Scholar]
- Shehata, E.G.; Thomas, J. Simple Model Predictive Control of High Power Direct-Driven PMSG Wind Energy Systems. In Proceedings of the 2021 22nd IEEE International Conference on Industrial Technology (ICIT), Valencia, Spain, 10–12 March 2021; Volume 1, pp. 482–487. [Google Scholar]
- Prince, M.K.K.; Arif, M.T.; Gargoom, A.; Oo, A.M.T.; Haque, E. Modeling, Parameter Measurement, and Control of PMSG-based Grid-connected Wind Energy Conversion System. J. Mod. Power Syst. Clean Energy 2021, 9, 1054–1065. [Google Scholar] [CrossRef]
- Cortes-Vega, D.; Ornelas-Tellez, F.; Anzurez-Marin, J.; Cordova-Aguilar, C. Optimal tracking control for a Permanent Magnet Synchronous Generator. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; pp. 691–696. [Google Scholar]
- Yip, S.Y.; Che, H.S.; Tan, C.P.; Chong, W.T. A lookup table model predictive direct torque control of permanent-magnet synchronous generator based on Vienna rectifier. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 1208–1222. [Google Scholar] [CrossRef]
- El Alami, H.; Bossoufi, B.; Motahhir, S.; Alkhammash, E.H.; Masud, M.; Karim, M.; Taoussi, M.; Bouderbala, M.; Lamnadi, M.; El Mahfoud, M. FPGA in the Loop Implementation for Observer Sliding Mode Control of DFIG-Generators for Wind Turbines. Electronics 2021, 11, 116. [Google Scholar] [CrossRef]
- Mohammed, E.M.; Badre, B.; Najib, E.O.; Abdelilah, H.; Houda, E.A.; Btissam, M.; Said, M. Predictive Torque and Direct Torque Controls for Doubly Fed Induction Motor: A Comparative Study. In Proceedings of the International Conference on Digital Technologies and Applications, Fez, Morocco, 28–30 January 2021; Springer: Cham, Switzerland, 2021; pp. 825–835. [Google Scholar]
- Bossoufi, B.; Lagrioui, A. Speed Control for PMSM Drive System Using Predictive Control. J. Autom. Syst. Eng. JSAE 2017, 11, 208–221. [Google Scholar]
- Yaramasu, V.; Wu, B.; Chen, J. Model-Predictive Control of Grid-Tied Four-Level Diode-Clamped Inverters for High-Power Wind Energy Conversion Systems. IEEE Trans. Power Electron. 2013, 29, 2861–2873. [Google Scholar] [CrossRef]
- Laggoun, Z.E.Z.; Khalile, N.; Benalla, H. A Comparative study between DPC-SVM and PDPC-SVM. In Proceedings of the International Conference on Advanced Electrical Engineering (ICAEE), Algiers, Algeria, 19–21 November 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Rivera, M.; Yaramasu, V.; Rodriguez, J.; Wu, B. Model Predictive Current Control of Two-Level Four-Leg Inverters—Part II: Experimental Implementation and Validation. IEEE Trans. Power Electron. 2013, 28, 3469–3478. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B.; Rivera, M.; Rodriguez, J. Enhanced model predictive voltage control of four-leg inverters with switching frequency reduction for standalone power systems. In Proceedings of the IEEE 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 4–6 September 2012; pp. 1–5. [Google Scholar]
- Laggoun, Z.E.Z.; Benalla, H.; Nebti, K. A Power Quality Enhanced for the Wind Turbine with Sensorless Direct Power Control under Different Input Voltage Conditions. Electr. Eng. Electromech. 2021, 16, 64–71. [Google Scholar] [CrossRef]
- Chai, S.; Wang, L.; Rogers, E. Model predictive control of a permanent magnet synchronous motor with experimental validation. Control. Eng. Pract. 2013, 21, 1584–1593. [Google Scholar] [CrossRef]
- Zhang, G.; Gao, L.; Yang, H.; Mei, L. A novel method of model predictive control on permanent magnet synchronous machine with Laguerre functions. Alex. Eng. J. 2021, 60, 5485–5494. [Google Scholar] [CrossRef]
- Barros, J.D.; Silva, J.F.A.; Jesus, É.G. Fast-predictive optimal control of NPC multilevel converters. IEEE Trans. Ind. Electron. 2012, 60, 619–627. [Google Scholar] [CrossRef]
- Bolognani, S.; Bolognani, S.; Peretti, L.; Zigliotto, M. Design and implementation of model predictive control for electrical motor drives. IEEE Trans. Ind. Electron. 2008, 56, 1925–1936. [Google Scholar] [CrossRef]
- Schwenzer, M.; Ay, M.; Bergs, T.; Abel, D. Review on model predictive control: An engineering perspective. Int. J. Adv. Manuf. Technol. 2021, 117, 1327–1349. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model Predictive Control: A Review of Its Applications in Power Electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Lagrioui, A.; Mahmoudi, H.; Bossoufi, B. Discrete linear predictive control of permanent magnet synchronous motor (pmsm). J. Theor. Appl. Inf. Technol. 2011, 31, 21–28. [Google Scholar]
- Bossoufi, B.; Karim, M.; Ionita, S.; Lagrioui, A. Nonlinear non adaptive backstepping with sliding-mode torque control approach for pmsm motor. J. Electr. Syst. 2012, 8, 236–248. [Google Scholar]
- Bossoufi, B.; Karim, M.; Lagrioui, A.; Taoussi, M.; EL Hafyani, M.L. Backstepping control of DFIG Generators for Wide-Range Variable-Speed Wind Turbines. Int. J. Autom. Control 2014, 8, 122–140. [Google Scholar] [CrossRef]
- Bossoufi, B.; Karim, M.; Lagrioui, A.; Taoussi, M.; Derouich, A. Adaptive Backstepping Control of DFIG Generators for Wide-Range Variable-speed Wind Turbines system. J. Electr. Syst. 2014, 10, 317–330. [Google Scholar]
- Barara, M.; Bennassar, A.; Abbou, A.; Akherraz, M.; Bossoufi, B. Advanced Control of Wind Electric Pumping System for Isolat-ed Areas Application. Int. J. Power Electron. Drive Syst. 2014, 4, 66–77. [Google Scholar]
- Xiao, F.; Zhang, Z.; Yin, X. Fault Current Characteristics of the DFIG under Asymmetrical Fault Conditions. Energies 2015, 8, 10971–10992. [Google Scholar] [CrossRef]
- Song, Z.; Xia, C.; Liu, T. Predictive current control of three-phase grid-connected converters with constant switching frequency for wind energy systems. IEEE Trans. Ind. Electron. 2013, 60, 2451–2464. [Google Scholar] [CrossRef]
- Rivera, M.; Wilson, A.; Rojas, C.A.; Rodríguez, J.; Espinoza, J.R.; Wheeler, P.W.; Empringham, L. A comparative assessment of model predictive current control and space vector modulation ina direct matrix converter. IEEE Trans. Ind. Electron. 2013, 60, 578–588. [Google Scholar] [CrossRef]
- Sun, X.; Wu, M.; Lei, G.; Guo, Y.; Zhu, J. An Improved Model Predictive Current Control for PMSM Drives Based on Current Track Circle. IEEE Trans. Ind. Electron. 2021, 68, 3782–3793. [Google Scholar] [CrossRef]














| Techniques | Researchers | |
|---|---|---|
| Sliding Mode Control | Hight order | Valenciaga F et al. [38] |
| Second order | Matraji I et al. [39]; Benbouzid M et al. [40]; Xiaoning S et al. [41]; Benelghali S et al. [42] | |
| Super twisting | Phan D et al. [43]; Zholtayev D et al. [44]; Yaichi I et al. [45]; | |
| Terminal | Shihua L et al. [48]; | |
| Integral | Saravanakumar R et al. [56]; Jun Liu et al. [57]; Muhammad M et al. [58]; | |
| H∞ technique | Kharabian B et al. [60]; Lian J et al. [61]; | |
| Backstepping-SMC | Faa-Jeng L et al. [62]; Rajendran S et al. [63]; | |
| Direct power control | Shang L et al. [64]; Benbouhenni H et al. [65]; | |
| Fuzzy logic | Diab A. A. Z et al. [66]; Yin, X.-X et al. [67]; El Karaoui I et al. [68]; Saghafinia A et al. [69]; | |
| Artificial neural network | Hong C-M et al. [70]; Mohammad B et al. [71]; | |
| Adaptive model | Baek S et al. [72]; Ton Hoang Nguyen et al. [73]; | |
| Observer | Kim H et al. [77]; Mi Y et al. [78,79,80]; | |
| Reaching law | Mozayan S. M et al. [81]; Fallaha, C.J. et al. [82]; El Makrini I et al. [83] |
| Techniques | Researchers | |
|---|---|---|
| Virtual flux | Proportional-Integral PI | Malinowski M et al. [121] |
| Vector Duty Cycle Control Predictive | Antoniewicz P et al. [100] | |
| SVM Predictive | Tao YK et al. [115]; Cho Y et al. [110] | |
| Table | Baktash A et al. [87]; Razali A et al. [88]; Zhi D et al. [89]; Malinowski M et al. [90] | |
| Voltage | Model Predictive | Kwak S et al. [97,99]; Cortes P et al. [98] |
| Vector Duty Cycle Control Predictive | Zhang Y et al. [111]; Fischer JR et al. [112]; Bouafia A et al. [113]; Restrepo JA et al. [114] | |
| SVM Predictive | Hu J et al. [103,106]; Choi D et al. [104]; Aurtenechea S et al. [105]; Song Z et al. [107]; Vazquez S et al. [108]; Zhang Y et al. [109] | |
| Model Adaptive | Portillo R et al. [119]; Vazquez S et al. [120] | |
| Vector Duty Cycle Control Table-based | Zhang Y et al. [123] | |
| Output Regulation Subspaces Table-based | Escobar G et al. [122] | |
| Sliding Mode | Hu J et al. [116] | |
| Fuzzy Logic | Bouafia A et al. [117,118] | |
| 1, 0, 0 | |||
| 1, 1, 0 | |||
| 0, 1, 0 | |||
| 0, 1, 1 | |||
| 0, 0, 1 | |||
| 1, 0, 1 | |||
| 0, 0, 0 | |||
| 1, 1, 1 |
| θR | θR1 [−30°,30°] | θR2 [30°,90°] | θR3 [90°,150°] | θR4 [150°,210°] | θR5 [210°,270°] | θR6 [270°,360°] | |
|---|---|---|---|---|---|---|---|
| Active Power: | Reactive Power: | ||||||
| 1 | 0 | ||||||
| 1 | |||||||
| 0 | 0 | ||||||
| 1 | |||||||
| _ _ | _ | ++ | + | + | _ | + | _ | |
| + | _ | _ | + | ++ | ++ | + | + |
| Reference Paper | Table-Based DPC | Active Power Variation | Voltage Sensors | Current THD | Active Power Ripple | Response Time | Switching Loss | |
|---|---|---|---|---|---|---|---|---|
| [94] | RV-DPC | Little | Zero | Include | Low | Minimal | Slow | Small |
| [90] | VF-DPC | Medium | Zero | Exclude | High | Maximal | Slow | Small |
| [88] | Little | Very little | Include | Low | Minimal | Slow | Small | |
| [130] | Little | Zero | Exclude | Low | Minimal | Slow | Small | |
| [131] | Medium | Zero | Exclude | High | Maximal | Slow | Small | |
| [96] | V-DPC | Medium | Zero | Exclude | High | Maximal | Slow | Small |
| [95] | Little | Big | Exclude | Medium | Medium | Medium | Medium | |
| [132] | Very little | Big | Exclude | Medium | Medium | Fast | Large | |
| [133] | Little | Medium | Include | Low | Minimal | Slow | Small | |
| [134] | Very little | Very little | Include | Medium | Medium | Medium | Medium | |
| [135] | Big | Very little | Include | Medium | Medium | Fast | Large | |
| [136] | Little | Very little | Include | Low | Minimal | Slow | Small | |
| [137] | Little | Zero | Include | Low | Minimal | Slow | Small | |
| [138] | Little | Big | Include | Medium | Medium | Medium | Medium | |
| [139] | Little | Big | Include | Medium | Medium | Medium | Medium | |
| Techniques | Researchers | |
|---|---|---|
| Backstepping | Filter | Liu Y-H [145]; Nizami et al. [152] |
| Artificial intelligence | Shen X et al. [142]; Min W [146]; Song S [147]; Belkhier Y [159] | |
| Integral BSC | Makhad M et al. [155]; Loucif, M et al. [157]; Eluri N.V.D.V. Prasad et al. [158] | |
| Disturbance observer | Wang F et al. [149]; | |
| Extended state observer | Jiuwu et al. [150] | |
| MPC-BSC | Yeonsoo K et al. [151] | |
| SMC-BSC | Rajendran, S et al. [160] |
| Techniques | Researchers | |
|---|---|---|
| With Modulator | Deadbeat predictive control (DBPC) | Nguyen, H et al. [183]; Bouderbala, M et al. [184] |
| Continuous control-set (MPC-CCS-MP) | Balamurugan, A et al. [185,186] | |
| Other predictive control (GPC, DCC) | Shehata, E et al. [187] | |
| Without Modulator | Hysteresis based (MPC) | Prince, M et al. [188] |
| Trajectory tracking (MPC) | Cortes-Vega, D et al. [189] | |
| Direct model predictive control | Yip, S. Y. et al. [190] | |
| Other (P-DPC, M2PC, S-MPC) | Shehata, E. G. et al. [191] |
| Simulations Results | Literatures | |||||
|---|---|---|---|---|---|---|
| Controller | Tr (s) | ξ % | TDH % | Ease of Implementation | Remarkable Properties | Disadvantages |
| SMC | 0.025 | 0.25 | 3.12 | Simple | Strong performance in the face of uncertainties and disturbances. The system stability is guaranteed by using lyapunov function. | Requires the mathematical model of the system. Chattering problem. |
| DPC | 0.048 | 0.32 | 2.77 | Very Simple | Easier implementation and low complexity. PWM modulation blocks and internal regulating loops are not included. | Variable switching frequency. Large active and reactive power ripple bands. |
| BSC | 0.030 | 0.17 | 1.91 | Complicated | Uncertainties can be handled. Stability is ensured at every design step using the Lyapunov function. | Requires the mathematical model of the system. Complex design. Explosion of terms. |
| MPC | 0.05 | 1.15 | 1.25 | Simple | Easier implementation. Excellent performance under varying wind conditions. High flexibility. | Requires the mathematical model of the system. Excessive computational load. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Majout, B.; El Alami, H.; Salime, H.; Zine Laabidine, N.; El Mourabit, Y.; Motahhir, S.; Bouderbala, M.; Karim, M.; Bossoufi, B. A Review on Popular Control Applications in Wind Energy Conversion System Based on Permanent Magnet Generator PMSG. Energies 2022, 15, 6238. https://doi.org/10.3390/en15176238
Majout B, El Alami H, Salime H, Zine Laabidine N, El Mourabit Y, Motahhir S, Bouderbala M, Karim M, Bossoufi B. A Review on Popular Control Applications in Wind Energy Conversion System Based on Permanent Magnet Generator PMSG. Energies. 2022; 15(17):6238. https://doi.org/10.3390/en15176238
Chicago/Turabian StyleMajout, Btissam, Houda El Alami, Hassna Salime, Nada Zine Laabidine, Youness El Mourabit, Saad Motahhir, Manale Bouderbala, Mohammed Karim, and Badre Bossoufi. 2022. "A Review on Popular Control Applications in Wind Energy Conversion System Based on Permanent Magnet Generator PMSG" Energies 15, no. 17: 6238. https://doi.org/10.3390/en15176238
APA StyleMajout, B., El Alami, H., Salime, H., Zine Laabidine, N., El Mourabit, Y., Motahhir, S., Bouderbala, M., Karim, M., & Bossoufi, B. (2022). A Review on Popular Control Applications in Wind Energy Conversion System Based on Permanent Magnet Generator PMSG. Energies, 15(17), 6238. https://doi.org/10.3390/en15176238










