Dual Extended Kalman Filter for State of Charge Estimation of Lithium–Sulfur Batteries
Abstract
1. Introduction
2. Methodology
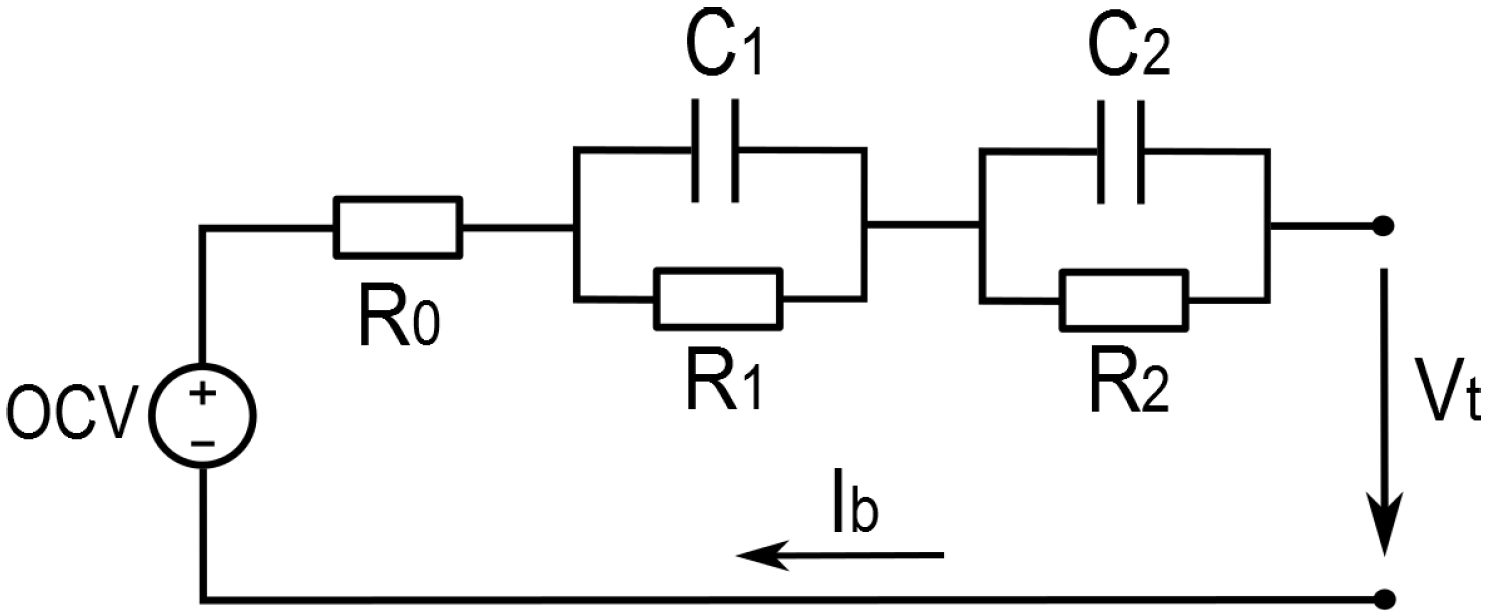
2.1. Cell Model Description
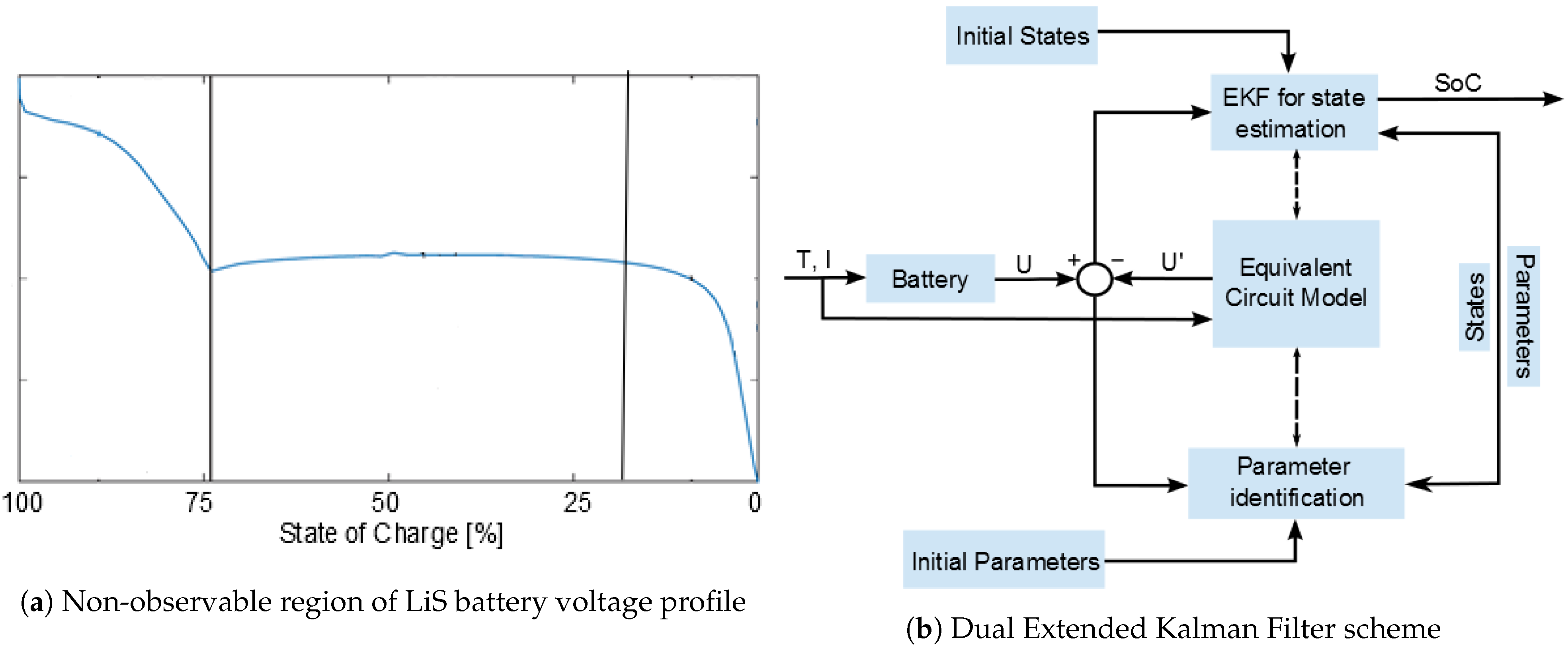
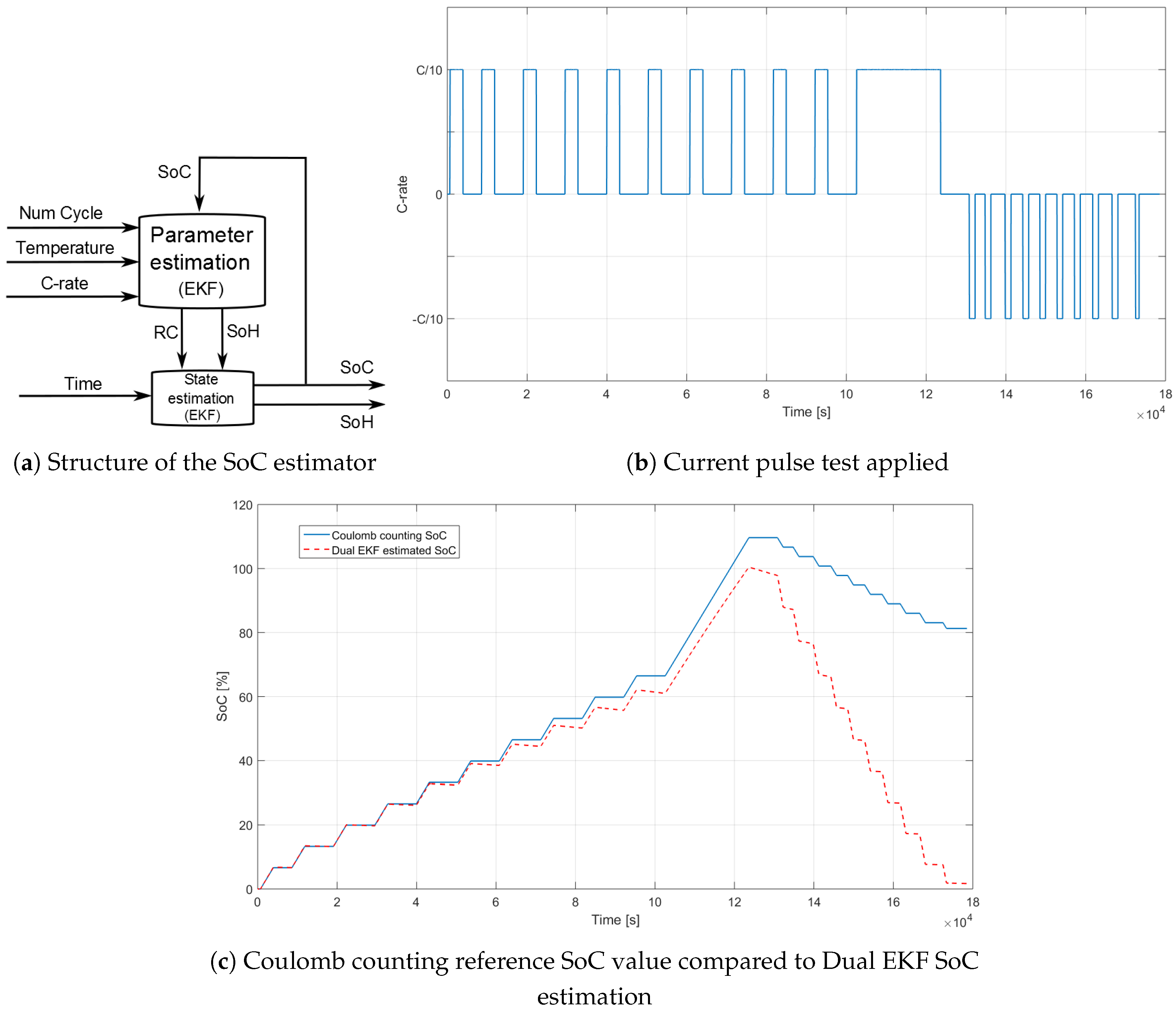
2.2. LiS Cell State Estimation
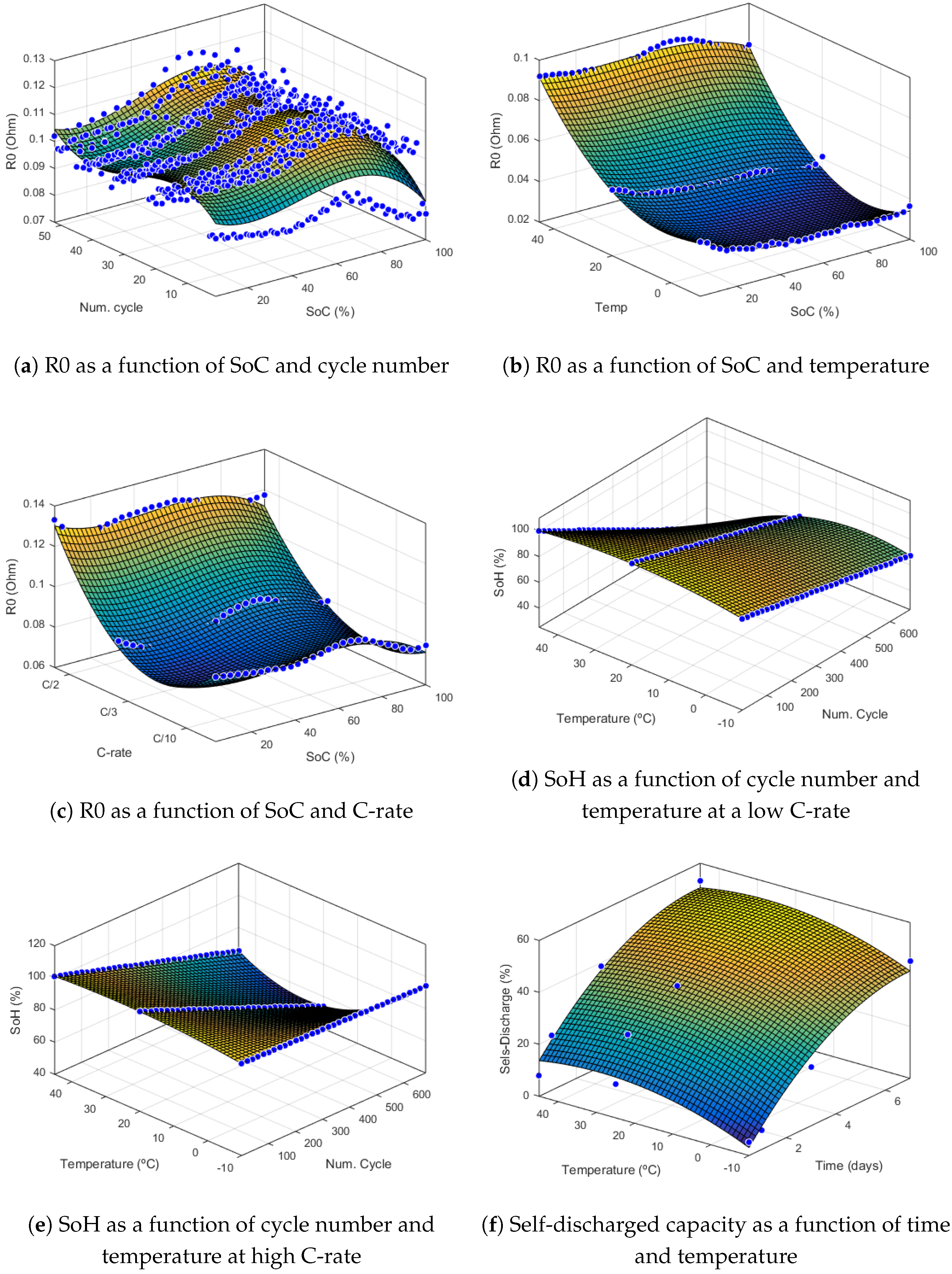
3. Experimental Results
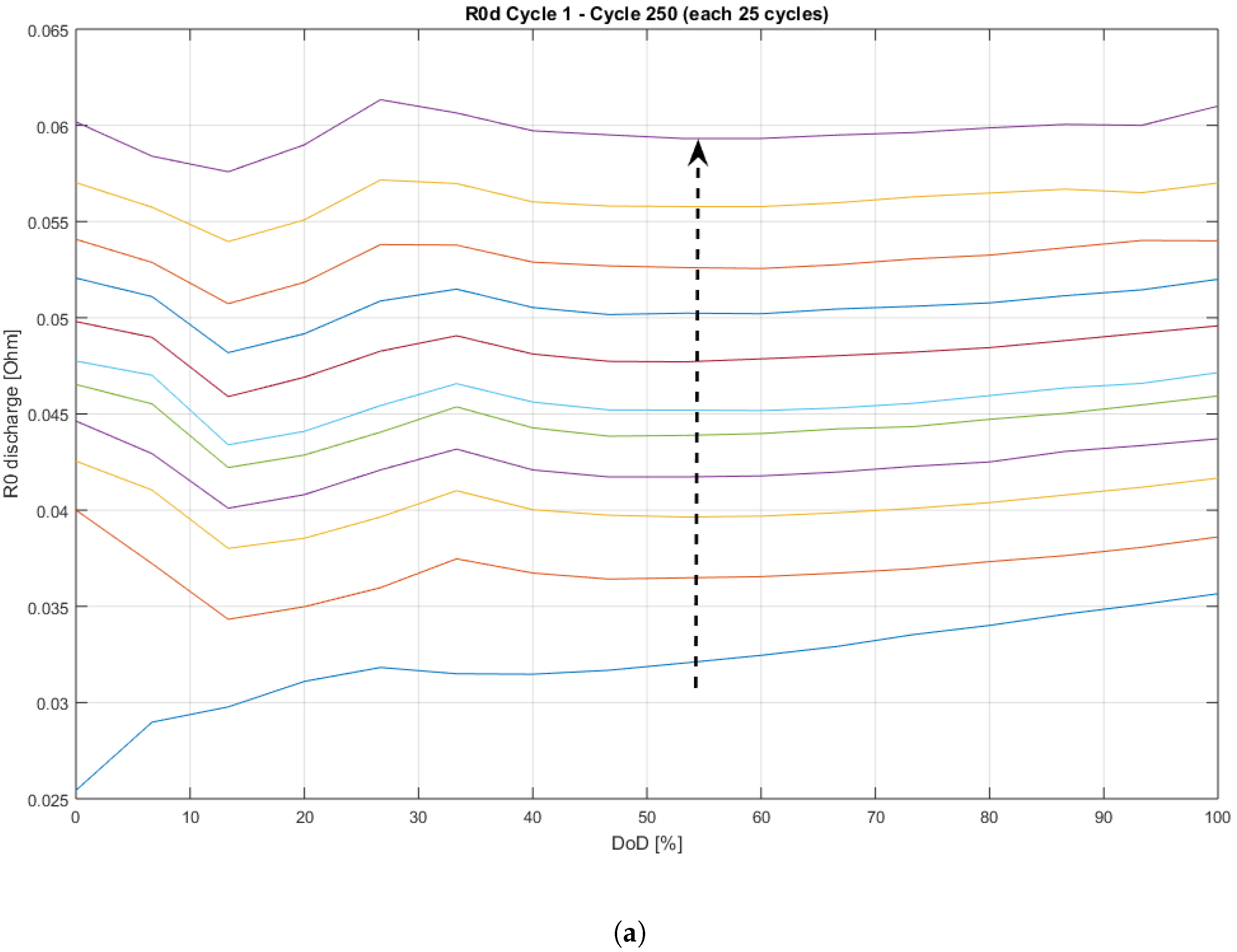
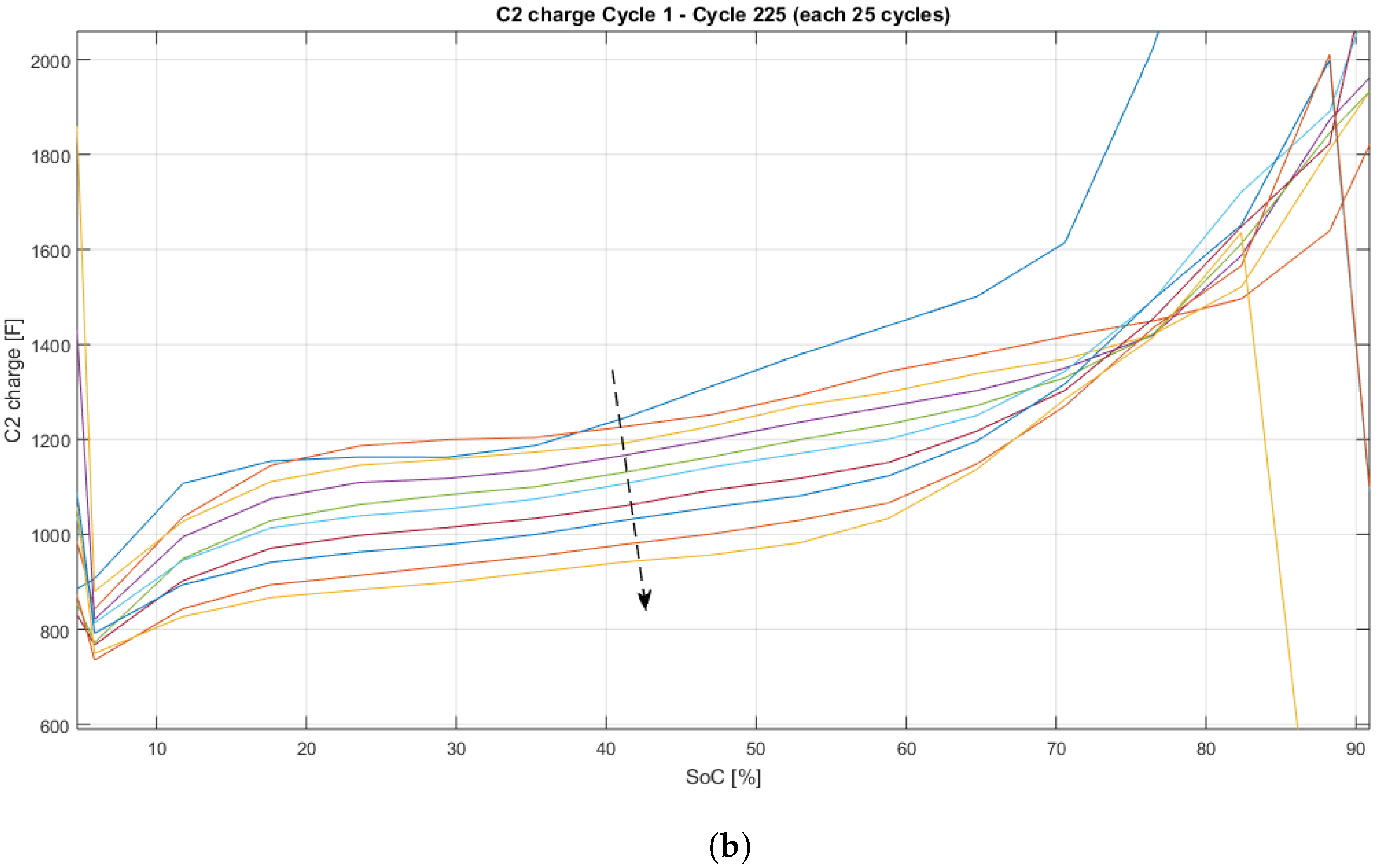
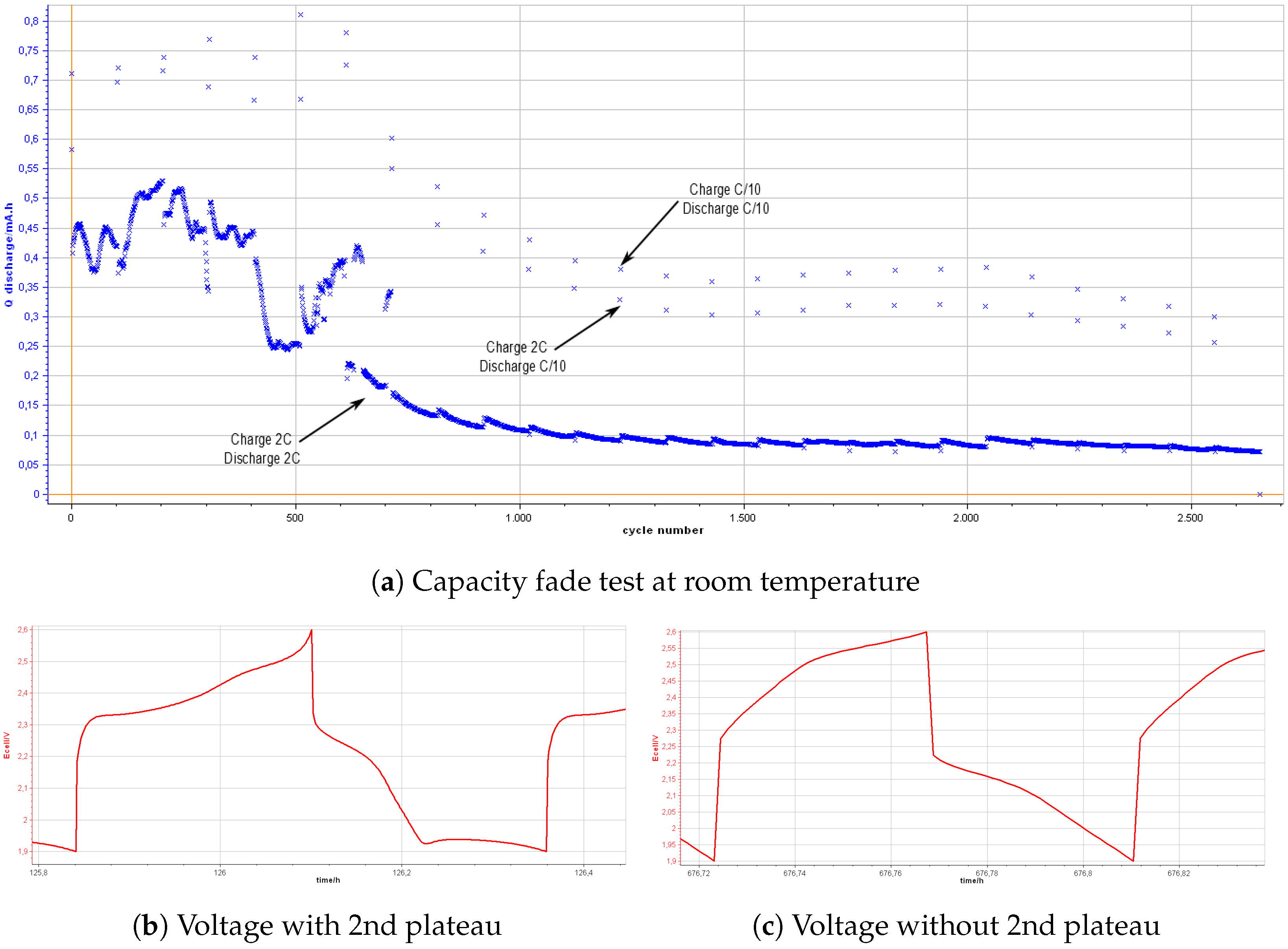
Capacity Fade and Self-Discharge
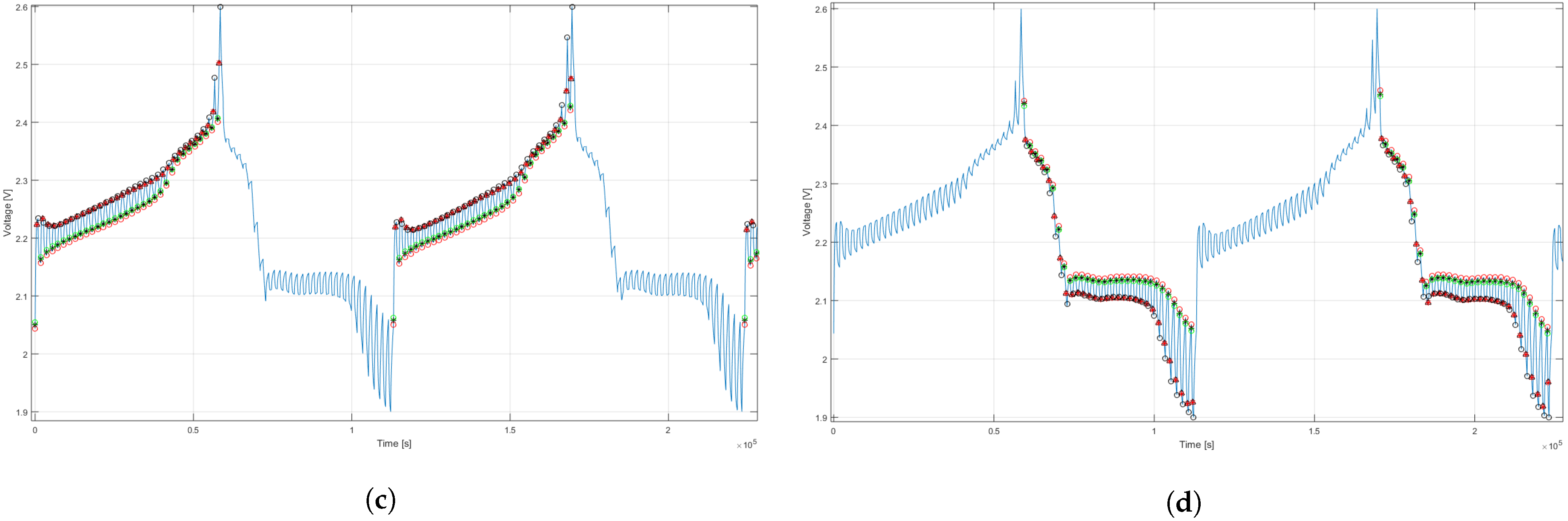
4. Resulting SoC Estimation
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BMS | Battery Management System |
| EV | Electric Vehicle |
| ECM | Equivalent Circuit Model |
| SoC | State of Charge |
| SoH | State of Health |
| SoX | State of X |
| RUL | Remaining Useful Life |
| DoD | Depth of Discharge |
| GITT | Galvanostatic Intermittent Titration Technique |
| EKF | Extended Kalman Filter |
| CPE | Constant Phase Element |
| LiS | Lithium Sulfur |
| SD | Self Discharge |
| CPE | Constant Phase Element |
| RMSE | Root Mean Square Error |
| RT | Room Temperature |
| OCV | Open Circuit Voltage |
References
- Benveniste, G.; Rallo, H.; Canals, L.; Merino, A.; Amante, B. Comparison of the state of lithium-sulphur and lithium-ion batteries applied to electromobility. J. Environ. Manag. 2018, 226, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.J.; Huang, J.Q.; Cheng, X.B.; Zhang, Q. Review on High-Loading and High-Energy Lithium–Sulfur Batteries. Adv. Energy Mater. 2017, 7, 1700260. [Google Scholar] [CrossRef]
- Kotak, Y.; Marchante Fernández, C.; Canals Casals, L.; Kotak, B.S.; Koch, D.; Geisbauer, C.; Trilla, L.; Gómez-Núñez, A.; Schweiger, H.-G. End of Electric Vehicle Batteries: Reuse vs. Recycle. Energies 2021, 14, 2217. [Google Scholar] [CrossRef]
- Zhang, C.; Biendicho, J.; Zhang, T.; Du, R.; Li, J.; Yang, X.; Arbiol, J.; Zhou, Y.; Morante, J.; Cabot, A. Combined High Catalytic Activity and Efficient Polar Tubular Nanostructure in Urchin-Like Metallic NiCo2Se4 for High-Performance Lithium-Sulfur Batteries. Adv. Funct. Mater. 2019, 29, 1903842. [Google Scholar] [CrossRef]
- Varzi, A.; Thanner, K.; Scipioni, R.; Di Lecce, D.; Hassoun, J.; Dörfler, S.; Altheus, H.; Kaskel, S.; Prehal, C.; Freunberger, S. Current status and future perspectives of lithium metal batteries. J. Power Sources 2020, 480, 228803. [Google Scholar] [CrossRef]
- Zhu, K.; Wang, C.; Chi, Z.; Ke, F.; Yang, Y.; Wang, A.; Wang, W.; Miao, L. How Far Away Are Lithium-Sulfur Batteries from Commercialization? Front. Energy Res. 2019, 7, 123. [Google Scholar] [CrossRef]
- Alise Project. Project Website. 2020. Available online: gvi.eu/project-highlight/alise-project/ (accessed on 1 September 2020).
- Narayanaswamy, S. Design, Modeling and Implementation of Distributed Architectures for Modular Battery Packs. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2019. [Google Scholar]
- Woody, M.; Arbabzadeh, M.; Lewis, G.M.; Keoleian, G.A.; Stefanopoulou, A. Strategies to limit degradation and maximize Li-ion battery service lifetime—Critical review and guidance for stakeholders. J. Energy Storage 2020, 28, 101231. [Google Scholar] [CrossRef]
- Balagopal, B.; Huang, C.S.; Chow, M. Effect of calendar aging on li-ion battery degradation and SoH. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 7647–7652. [Google Scholar]
- Liu, K.; Ashwin, T.R.; Hu, X.; Lucu, M.; Widanage, W.D. An evaluation study of different modelling techniques for calendar ageing prediction of lithium-ion batteries. Renew. Sustain. Energy Rev. 2020, 131, 110017. [Google Scholar] [CrossRef]
- Wolff, D.; Canals Casals, L.; Benveniste, G.; Corchero, C.; Trilla, L. The Effects of Lithium Sulfur Battery Ageing on Second-Life Possibilities and Environmental Life Cycle Assessment Studies. Energies 2019, 12, 2440. [Google Scholar] [CrossRef]
- Casals, L.C.; González, A.M.S.; García, B.A.; Llorca, J. PHEV Battery Aging Study Using Voltage Recovery and Internal Resistance from Onboard Data. IEEE Trans. Veh. Technol. 2016, 65, 4209–4216. [Google Scholar] [CrossRef]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S. Electric vehicle battery parameter identification and SOC observability analysis: NiMH and Li-S case studies. In Proceedings of the 8th IET International Conference on Power Electronics, Machines and Drives (PEMD), Glasgow, UK, 19–21 April 2016; pp. 1–6. [Google Scholar]
- Fotouhi, A.; Auger, D.J.; O’Neill, L.; Cleaver, T.; Walus, S. Lithium-Sulfur Battery Technology Readiness and Applications—A Review. Energies 2017, 10, 1937. [Google Scholar] [CrossRef]
- Propp, K.; Auger, D.J.; Fotouhi, A.; Longo, S.; Knap, V. Auger and Abbas Fotouhi and Stefano Longo and Vaclav Knap. Kalman-variant estimators for state of charge in lithium-sulfur batteries. J. Power Sources 2017, 343, 254–267. [Google Scholar] [CrossRef]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S. Lithium–Sulfur Battery State-of-Charge Observability Analysis and Estimation. IEEE Trans. Power Electron. 2018, 33, 5847–5859. [Google Scholar] [CrossRef]
- Dörfler, S.; Walus, S.; Locke, J.; Fotouhi, A.; Auger, D.J.; Shateri, N.; Abendroth, T.; Härtel, P.; Althues, H.; Kaskel, S. Recent Progress and Emerging Application Areas for Lithium–Sulfur Battery Technology. Energy Technol. 2021, 9, 2000694. [Google Scholar] [CrossRef] [PubMed]
- Knap, V.; Stroe, D.; Teodorescu, R.; Swierczynski, M.; Stanciu, T. Electrical circuit models for performance modeling of Lithium-Sulfur batteries. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 1375–1381. [Google Scholar]
- da Silva, C.T.; Dias, B.M.d.A.; Araújo, R.E.; Pellini, E.L.; Laganá, A.A.M. Battery Model Identification Approach for Electric Forklift Application. Energies 2021, 4, 6221. [Google Scholar] [CrossRef]
- Plett, G.L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1: Introduction and state estimation. J. Power Sources 2006, 161, 1356–1368. [Google Scholar] [CrossRef]
- Rahimi-Eichi, H.; Baronti, F.; MChow, M. Online Adaptive Parameter Identification and State-of-Charge Coestimation for Lithium-Polymer Battery Cells. IEEE Trans. Ind. Electron. 2014, 61, 2053–2061. [Google Scholar] [CrossRef]
- Fridholm, B.; Nilsson, M.; Wik, T. Robustness Comparison of Battery State of Charge Observers for Automotive Applications. IFAC Proc. 2014, 47, 2138–2146. [Google Scholar] [CrossRef]
- Azis, N.A.; Joelianto, E.; Widyotriatmo, A. State of Charge (SoC) and State of Health (SoH) Estimation of Lithium-Ion Battery Using Dual Extended Kalman Filter Based on Polynomial Battery Model. In Proceedings of the 6th International Conference on Instrumentation, Control, and Automation (ICA), Bandung, Indonesia, 31 July–2 August 2019; pp. 88–93. [Google Scholar]
- Lee, S.J.; Kim, J.H.; Lee, J.M.; Cho, B.H. The State and Parameter Estimation of an Li-Ion Battery Using a New OCV-SOC Concept. In Proceedings of the IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 2799–2803. [Google Scholar]
- Yang, N.; Zhang, X.; Li, G. State of charge estimation for pulse discharge of a LiFePO4 battery by a revised Ah counting. Electrochim. Acta 2015, 151, 63–71. [Google Scholar] [CrossRef]
- Aylor, J.H.; Thieme, A.; Johnson, B.W. A battery state-of-charge indicator for electric wheelchairs. IEEE Trans. Ind. Electron. 1992, 39, 398–409. [Google Scholar] [CrossRef]
- Knap, V.; Stroe, D.; Teodorescu, R.; Swierczynski, M.; Stanciu, T. Comparison of parametrization techniques for an electrical circuit model of Lithium-Sulfur batteries. In Proceedings of the IEEE 13th International Conference on Industrial Informatics (INDIN), Cambridge, UK, 22–24 July 2015; pp. 1278–1283. [Google Scholar]
- Conder, J.; Bouchet, R.; Trabesinger, S.; Marino, C.; Gubler, L.; Villevieille, C. Direct observation of lithium polysulfides in lithium-sulfur batteries using operando X-ray diffraction. Nat. Energy 2017, 2, 17069. [Google Scholar] [CrossRef]


| Cell No | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| C-rate | C/10 | C/10 | C/10 | C/2 | C/2 | C/2 | 2C | 2C | 2C |
| Temperature | −10 °C | RT | 45°C | −10 °C | RT | 45°C | −10 °C | RT | 45 °C |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trilla, L.; Canals Casals, L.; Jacas, J.; Paradell, P. Dual Extended Kalman Filter for State of Charge Estimation of Lithium–Sulfur Batteries. Energies 2022, 15, 6989. https://doi.org/10.3390/en15196989
Trilla L, Canals Casals L, Jacas J, Paradell P. Dual Extended Kalman Filter for State of Charge Estimation of Lithium–Sulfur Batteries. Energies. 2022; 15(19):6989. https://doi.org/10.3390/en15196989
Chicago/Turabian StyleTrilla, Lluís, Lluc Canals Casals, Jordi Jacas, and Pol Paradell. 2022. "Dual Extended Kalman Filter for State of Charge Estimation of Lithium–Sulfur Batteries" Energies 15, no. 19: 6989. https://doi.org/10.3390/en15196989
APA StyleTrilla, L., Canals Casals, L., Jacas, J., & Paradell, P. (2022). Dual Extended Kalman Filter for State of Charge Estimation of Lithium–Sulfur Batteries. Energies, 15(19), 6989. https://doi.org/10.3390/en15196989








