A Particle-Scale Model of Surface Tension for Two-Phase Flow: Model Description and Validation
Abstract
:1. Introduction
2. Mathematical Formulations
2.1. Governing Equations for SPH
2.2. Particle-Scale Surface Tension Force
3. Validations and Results
3.1. Validation Case 1 for the Kernel: Dam-Break
3.2. Validation Case 2 for the Surface Tension: A Square Drop with a Free Surface
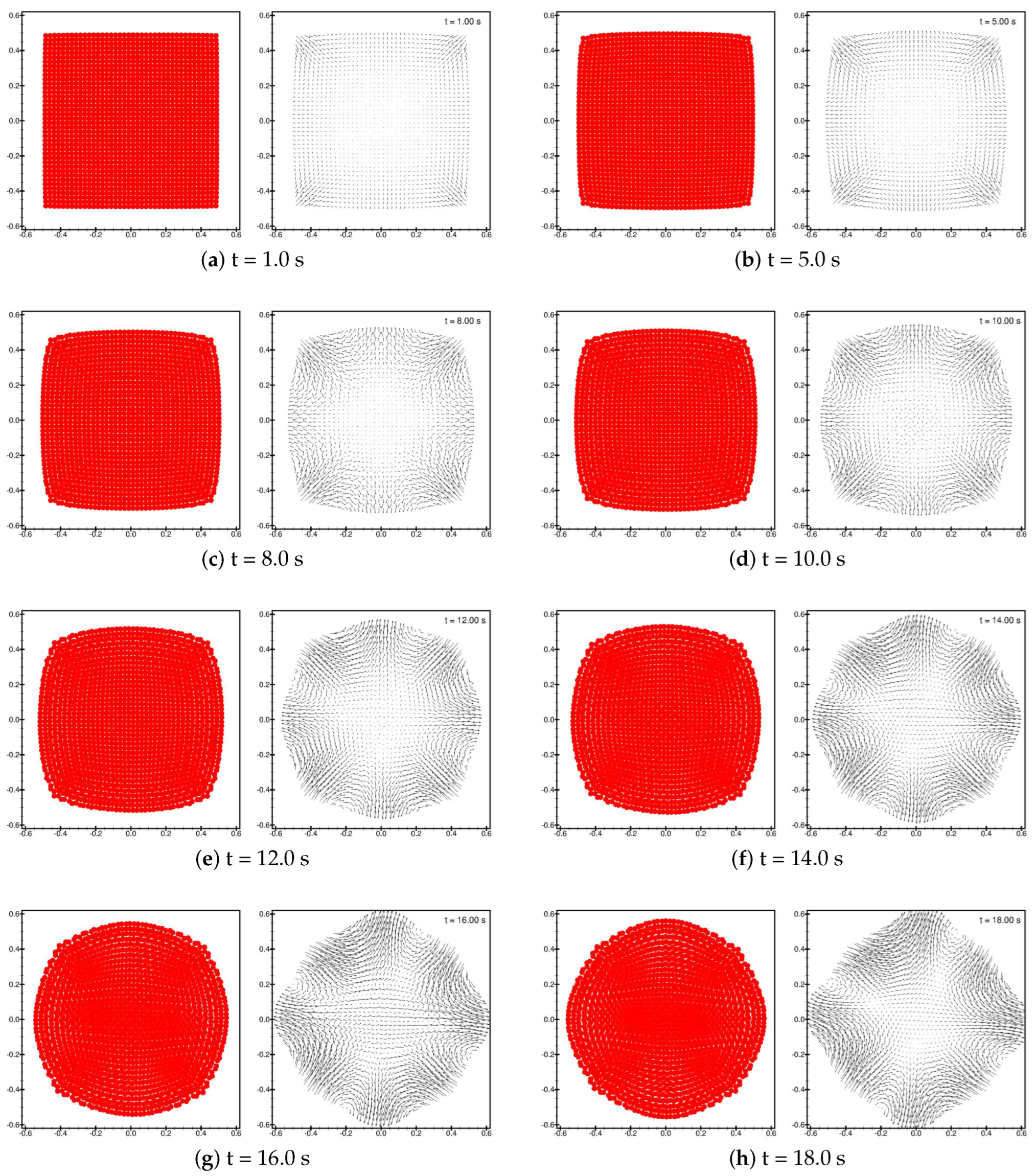
3.3. Validation Case 3 for the Surface Tension: A Square Bubble with an Inter-Phase Surface
4. Numerical Results
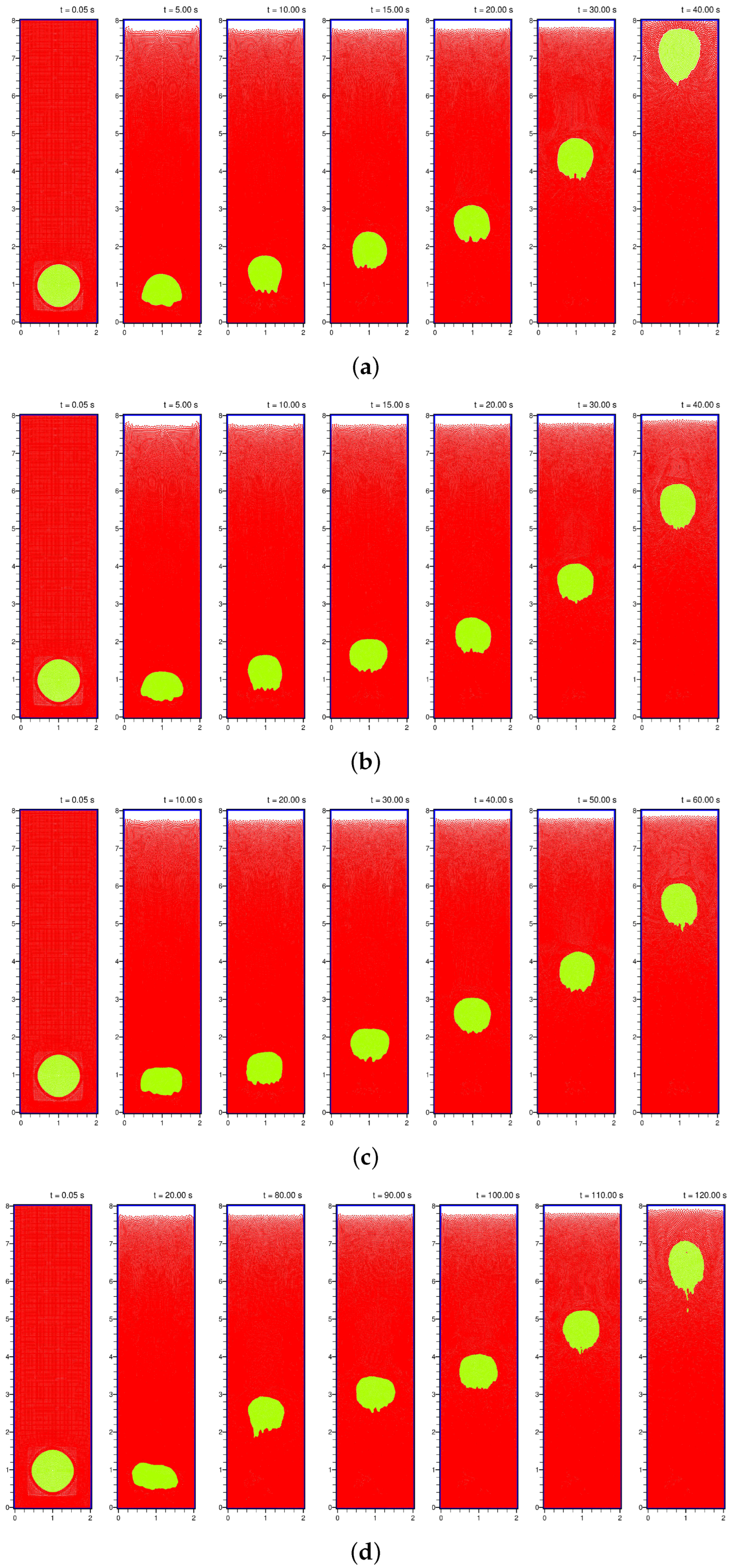
4.1. Case A: A Single Rising Bubble
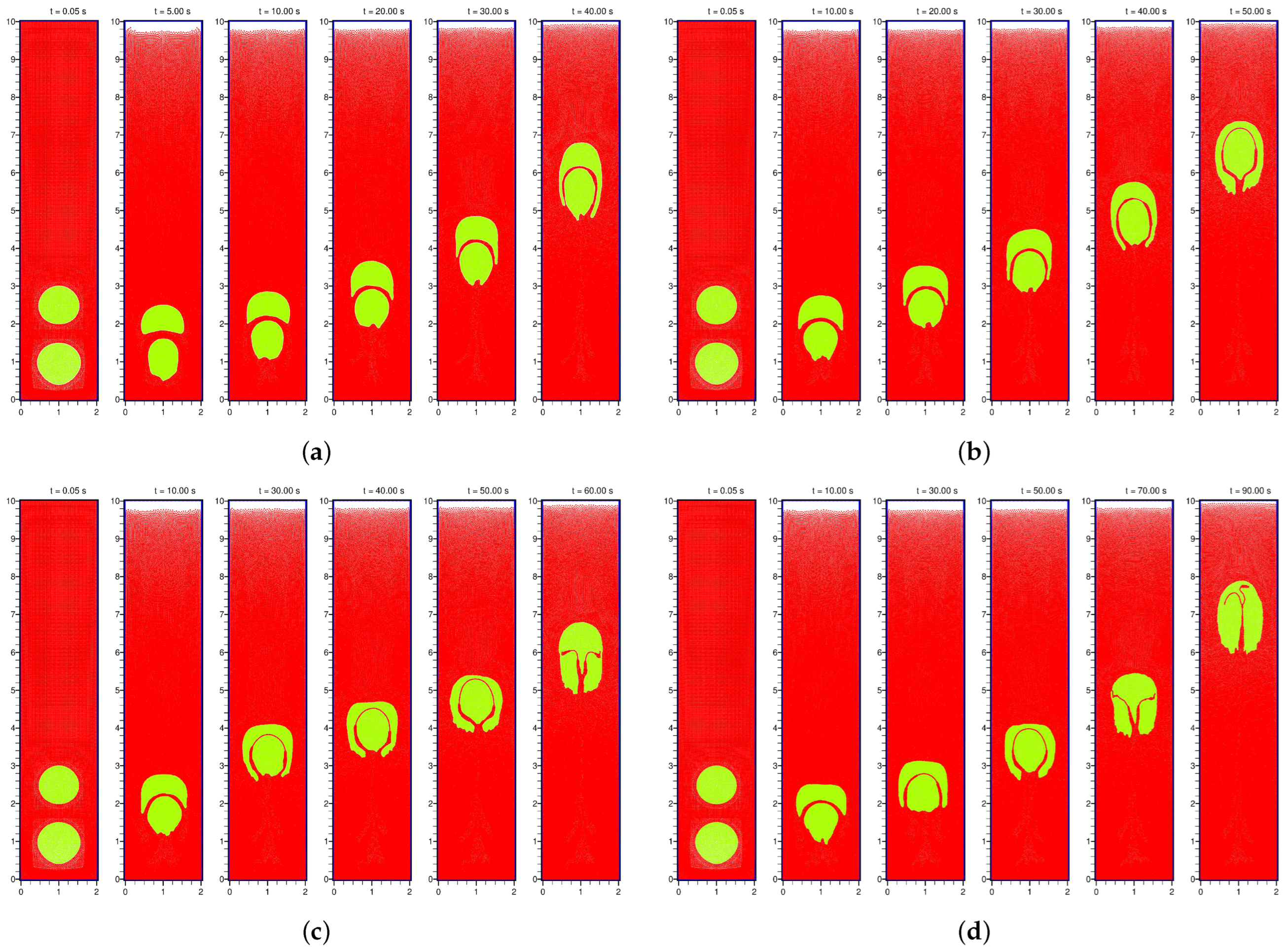
4.1.1. Snapshots of a Rising Bubble
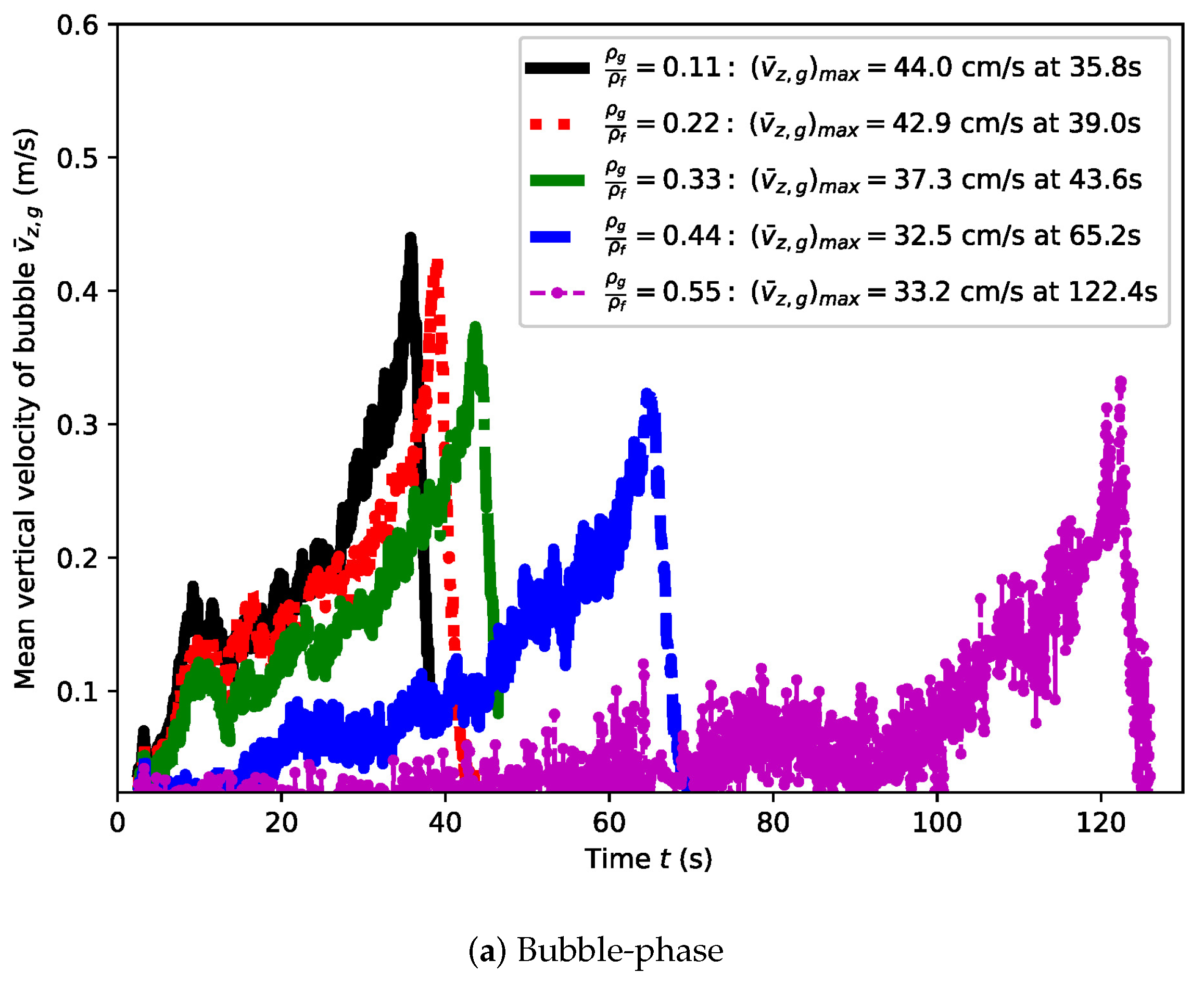
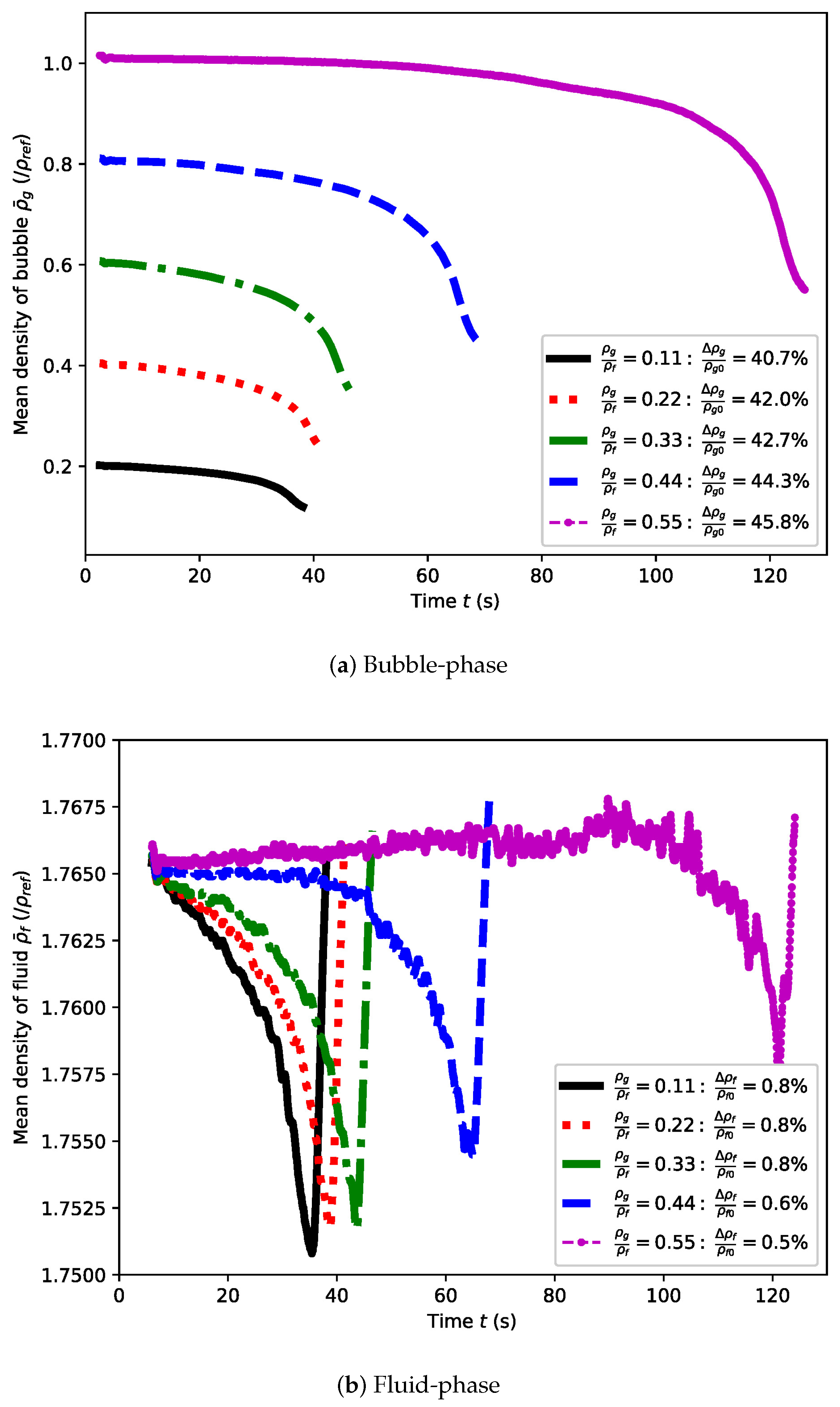
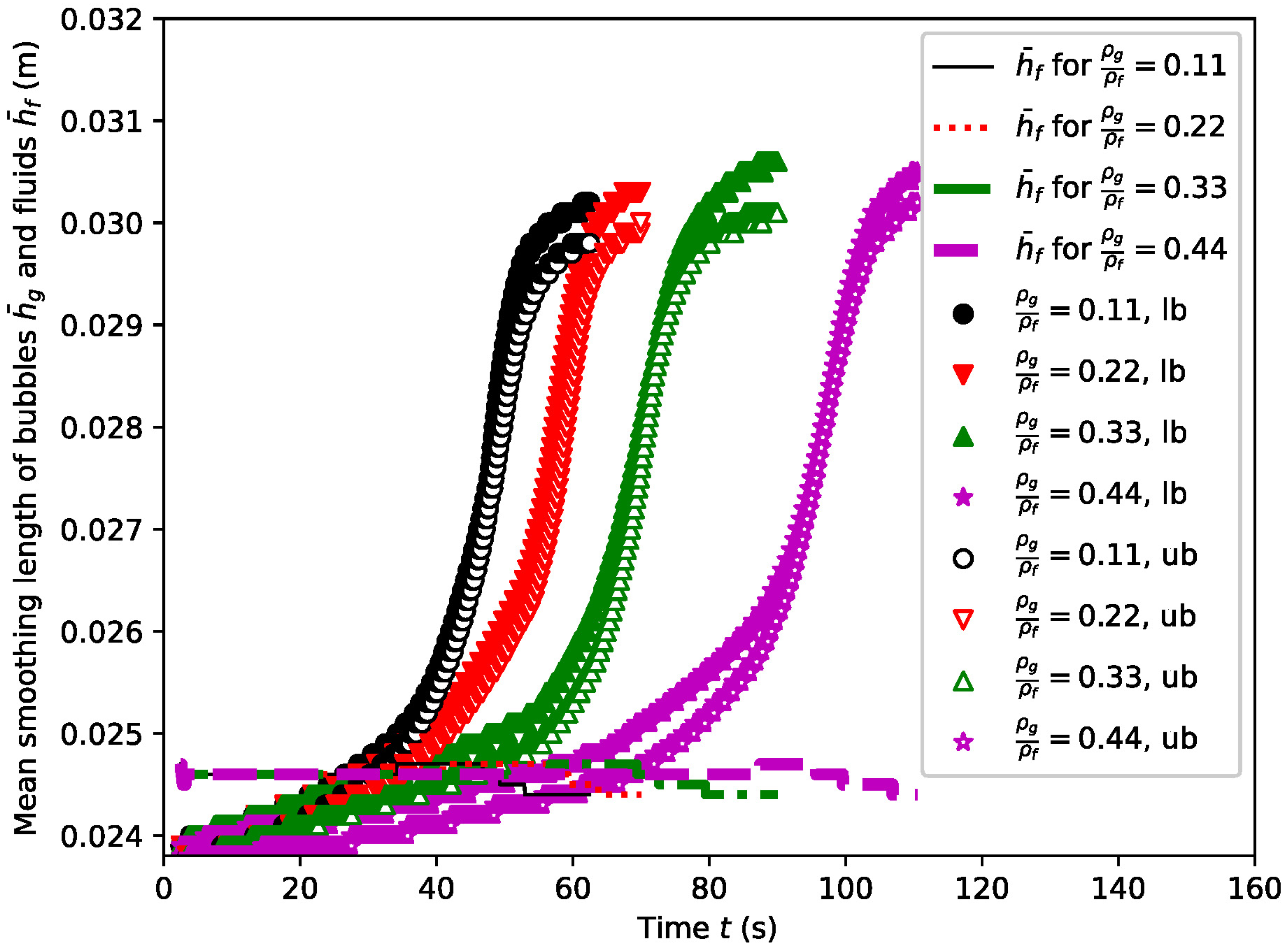
4.1.2. Rising Velocities and Densities
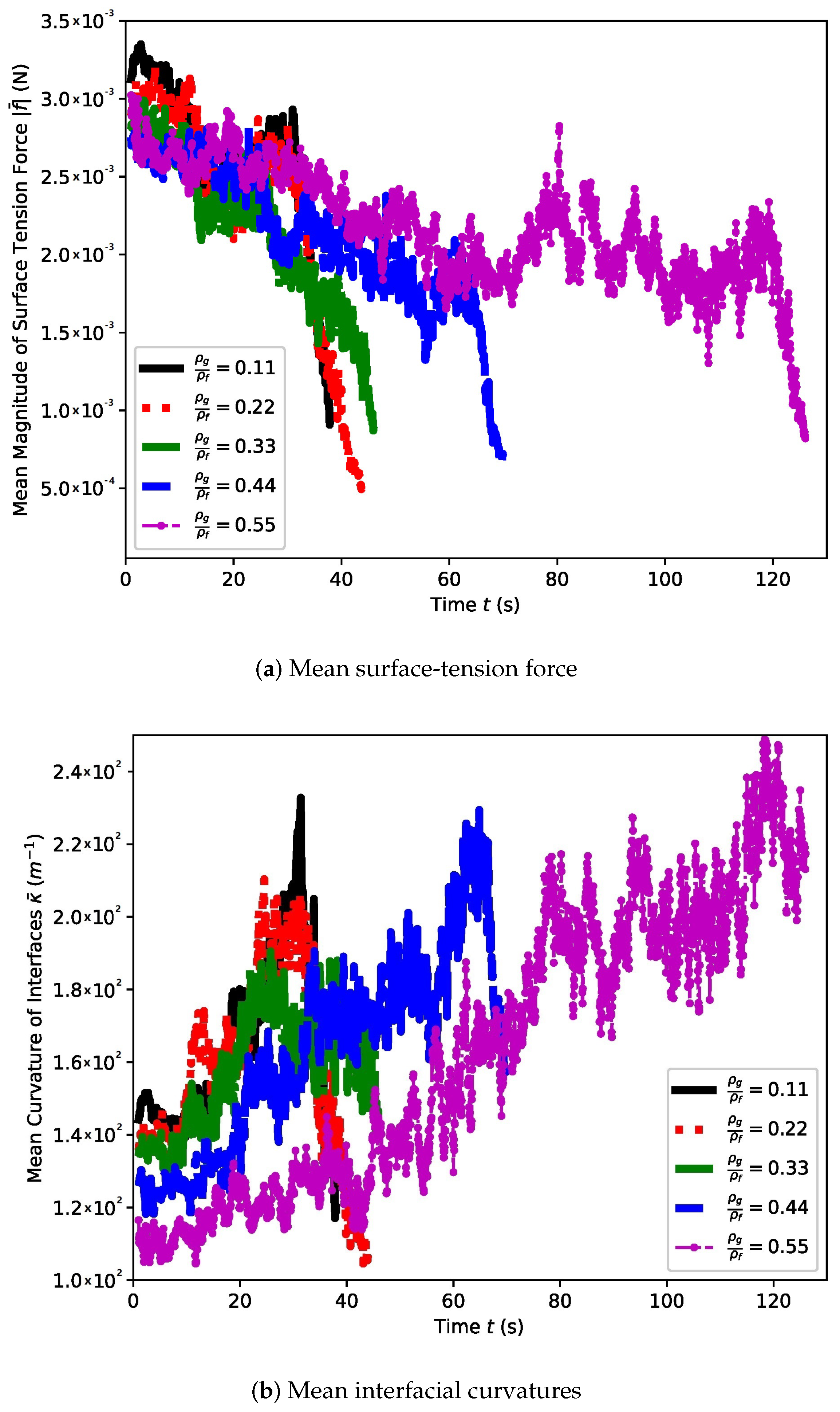
4.1.3. Mean Surface Tension Force, Curvature, and Its Power
4.2. Case B: A Pair of Rising Bubbles
5. Further Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CSF | Continuous Surface Force model |
| CSS | Continuum Stress Surface method |
| DPD | Dissipative Particle Dynamics |
| LS | Level Set method |
| MPS | Moving Particle Semi-implicit method |
| SPH | Smoothed Hydrodynamics Particle |
| STF | Surface Tension Force |
| VOF | Volume Of Fluid method |
References
- Mittal, H.; Ray, R.K.; Gadêlha, H.; Patil, D.V. A coupled immersed interface and level set method for simulation of interfacial flows steered by surface tension. Exp. Computat. Multiphase Flow 2021, 3, 21–37. [Google Scholar] [CrossRef]
- Liu, J.M.; Wang, Y.Q.; Gao, Y.S.; Liu, C. Galilean invariance of Omega vortex identification method. J. Hydrodyn. 2019, 31, 249–255. [Google Scholar] [CrossRef]
- Lin, M.; Zhong, M.; Li, Y.; Yuan, M.; Yang, Y. Numerical analysis on molten droplet hydrodynamic deformation and surface waves under high pressure pulse. Ann. Nucl. Energy 2015, 77, 133–141. [Google Scholar] [CrossRef]
- Osher, S.; Fedkiw, R.P. Level Set Methods: An Overview and Some Recent Results. J. Comput. Phys. 2001, 169, 463–502. [Google Scholar] [CrossRef]
- Tryggvason, G.; Bunner, B.; Esmaeeli, A.; Juric, D.; Jan, Y.J. A Front-Tracking Method for the Computations of Multiphase Flow. J. Comput. Phys. 2001, 169, 708–759. [Google Scholar] [CrossRef]
- Liu, C.; Xu, H.; Cai, X.; Gao, Y. Chapter 6—Liutex and third generation of vortex identification methods. In Liutex and Its Applications in Turbulence Research; Liu, C., Xu, H., Cai, X., Gao, Y., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 119–149. [Google Scholar]
- Krimi, A.; Rezoug, M.; Khelladi, S.; Nogueira, X.; Deligant, M.; Ramírez, L. Smoothed Particle Hydrodynamics: A consistent model for interfacial multiphase fluid flow simulations. J. Comput. Phys. 2018, 358, 53–87. [Google Scholar] [CrossRef]
- Zhu, Y.; Qiu, Z.; Xiong, J.; Yang, Y. Verification and validation of MPS potential force interface tension model for stratification simulation. Ann. Nucl. Energy 2020, 148, 107753. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.J.; Koelman, J. Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics. EPL (Europhys. Lett.) 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Abdolahzadeh, M.; Tayebi, A.; Omidvar, P. Thermal effects on two-phase flow in 2D mixers using SPH. Int. Commun. Heat Mass Transf. 2021, 120, 105055. [Google Scholar] [CrossRef]
- Wang, Z.B.; Rong, C.; Hong, W.; Liao, Q.; Zhu, X.; Li, S.Z. An overview of smoothed particle hydrodynamics for simulating multiphase flow. Appl. Math. Model. 2016, 40, 9625–9655. [Google Scholar] [CrossRef]
- Vergnaud, A.; Oger, G.; Touzé, D.L.; DeLeffe, M.; Chiron, L. C-CSF: Accurate, robust and efficient surface tension and contact angle models for single-phase flows using SPH. Comput. Methods Appl. Mech. Eng. 2022, 389, 114292. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Lafaurie, B.; Nardone, C.; Scardovelli, R.; Zaleski, S.; Zanetti, G. Modelling merging and fragmentation in multiphase flows with SURFER. J. Comput. Phys. 1994, 113, 134–147. [Google Scholar] [CrossRef]
- Amt, A.; Ap, B. Pairwise Force Smoothed Particle Hydrodynamics model for multiphase flow: Surface tension and contact line dynamics. J. Comput. Phys. 2016, 305, 1119–1146. [Google Scholar]
- Scardovelli, R. Direct Numerical Simulation of Free-Surface and Interfacial Flow. Annu. Rev. Fluid Mech. 2003, 31, 567–603. [Google Scholar] [CrossRef]
- Nugent, S.; Posch, H.A. Liquid drops and surface tension with smoothed particle applied mechanics. Phys. Rev. E 2000, 62, 4968–4975. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Zhang, H.; Zheng, L.L. Simulation of droplet spreading, splashing and solidification using smoothed particle hydrodynamics method. Int. J. Heat Mass Transf. 2008, 51, 3410–3419. [Google Scholar] [CrossRef]
- Crespo, A.; Gomez-Gesteira, M.; Dalrymple, R.A. Modeling Dam Break Behavior over a Wet Bed by a SPH Technique. J. Waterw. Port Coast. Ocean Eng. 2008, 134, 313–320. [Google Scholar] [CrossRef]
- Farzin, A.S.; Fatehi, B.R.; Hassanzadeh, C.Y. Position explicit and iterative implicit consistent incompressible SPH methods for free surface flow. Comput. Fluids 2019, 179, 52–66. [Google Scholar] [CrossRef]
- Ye, Y.; Xu, T.; Zhu, D.Z. Numerical analysis of dam-break waves propagating over dry and wet beds by the mesh-free method. Ocean Eng. 2020, 217, 107969. [Google Scholar] [CrossRef]
- Jánosi, I.; Jan, D.; Szabó, K.; Tél, T. Turbulent drag reduction in dam-break flows. Exp. Fluids 2004, 37, 219–229. [Google Scholar] [CrossRef] [Green Version]







| Parameters | Values |
|---|---|
| Width (m) | 1.0 |
| Number of particles | 1600 |
| in Equation (8) (-) | 2 |
| Reference pressure in EOS (Pa) | 1.0 |
| Background pressure in EOS (Pa) | 1.0 |
| Reference density in EOS (kg/m) | 1.0 |
| Viscosity of fluids (Pa·s) | 0.001 |
| coefficient of surface tension force (N/m) (Pa·s) | 10 |
| Time step (s) | 5.0 × |
| Time in simulation (s) | 150.0 |
| Parameters | Phase ‘l’ | Phase ‘g’ |
|---|---|---|
| Width × height () (m) | 2.0 × 2.0 | 1.0 × 1.0 |
| Number of particles | 4879 | 1521 |
| in EOS (-) | 7 | 7 |
| Reference pressure in EOS (kg/m) | 1.0 | 1.0 |
| Background pressure in EOS (kg/m) | 1.0 | 1.5 |
| Reference density in EOS (kg/m) | 1.0 | 0.1 |
| Viscosity of fluids (Pa·s) | 1.0 × 10 | 1.0 × 10 |
| coefficient of surface tension force (N/m) (Pa·s) | 72 | 72 |
| Time step (s) | 5.0 × 10 | 5.0 × 10 |
| Time in simulation (s) | 5.0 | 5.0 |
| Parameters | Phase ‘l’ | Phase ‘g’ |
|---|---|---|
| Width of Bed () (m) | 2 | - |
| Height of Bed () (m) | 8 in CA & 10.0 in CB | - |
| Height of bubbles () (m) | - | 1.0 and 2.5 |
| Initial Diameter (m) | - | 1 |
| Number of particles | 24,273 in CA & 29346 in CB | 1083 in CA & 2166 in CB |
| in EOS (-) | 7 | 7 |
| Reference pressure in EOS (kg/m) | 1.0 | 1.0 |
| Background pressure in EOS (kg/m) | 3.92 | 3.92 |
| Reference density in EOS (kg/m) | 1.0 | - |
| Density ratios () | - | 0.11, 0.22, 0.33, 0.44, 0.55 |
| Viscosity of fluids (Pa·s) | 2.0 × 10 | 2.0 × 10 |
| Coefficient of surface tension (N/m) (Pa·s) | 0.72 | 0.72 |
| Time step (s) | 5.0 × | 5.0 × |
| Time in simulation (s) | 5.0 | 38∼125.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Cao, C.; Gui, N.; Huang, X.; Yang, X.; Tu, J.; Jiang, S.; Zhao, Q. A Particle-Scale Model of Surface Tension for Two-Phase Flow: Model Description and Validation. Energies 2022, 15, 7132. https://doi.org/10.3390/en15197132
Zhang X, Cao C, Gui N, Huang X, Yang X, Tu J, Jiang S, Zhao Q. A Particle-Scale Model of Surface Tension for Two-Phase Flow: Model Description and Validation. Energies. 2022; 15(19):7132. https://doi.org/10.3390/en15197132
Chicago/Turabian StyleZhang, Xiaoxi, Can Cao, Nan Gui, Xiaoli Huang, Xingtuan Yang, Jiyuan Tu, Shengyao Jiang, and Qian Zhao. 2022. "A Particle-Scale Model of Surface Tension for Two-Phase Flow: Model Description and Validation" Energies 15, no. 19: 7132. https://doi.org/10.3390/en15197132
APA StyleZhang, X., Cao, C., Gui, N., Huang, X., Yang, X., Tu, J., Jiang, S., & Zhao, Q. (2022). A Particle-Scale Model of Surface Tension for Two-Phase Flow: Model Description and Validation. Energies, 15(19), 7132. https://doi.org/10.3390/en15197132







