Perspective of Thermal Analysis and Management for Permanent Magnet Machines, with Particular Reference to Hotspot Temperatures
Abstract
:1. Introduction
2. PM Machines and Heat Transfer Mechanisms
3. Machine Loss Estimation
3.1. Stator and Rotor Iron Losses
3.2. Copper Loss
3.3. PM Eddy Current Loss
3.4. Mechancial Loss
4. Cooling Techniques
4.1. Passive Cooling
4.2. Forced Air Cooling
4.3. Forced Liquid Cooling
4.3.1. Indirect Forced Liquid Cooling
4.3.2. Direct Forced Liquid Cooling
4.4. Hybrid Cooling
- 2012 Tesla Roadster IM: inner forced air + finned housing + outer fan [22].
- 2013 Tesla S60 IM: frame liquid + shaft cooling [24].
- 2014 Porsche Panamera E-hybrid 416: frame liquid + forced air cooling [24].
- GE IPMSM: frame liquid + end-winding spray + rotor cooling [177].
- Zytek PMSM: frame liquid + forced fan cooling [178].
5. Thermal Analysis Methods
5.1. Numerical Techniques
5.2. Conventional High-Order Lumped-Parameter Thermal Model
5.3. Hybrid Thermal Model and Analytical Thermal Modelling
- The PM temperature distributions and hotspots are strongly affected by the uneven distributions of PM eddy current loss and the boundary conditions.
- The PM end-surface temperature is lower than the PM hotspot due to enhanced convection heat transfer.
- The assumption of uniform PM eddy current loss distribution could cause severe misestimation of PM hotspots.
- For the SPM, the PM loss can be dissipated to airgap via convection. Thus, the SPM hotspots are concentrated on the outer surfaces when the retaining rotor sleeve is not considered.
- For IPM, the PM loss can only be dissipated to the rotor core via conduction. Consequently, the IPM hotspots occur in the upper part inside the PMs due to conduction heat transfer between the PM and the upper rotor core.
- For SPM retained by a rotor sleeve, different sleeve materials have a significant impact on rotor thermal behaviors. Due to the low thermal conductivity of carbon fibre, the hotspot rotor temperature occurs on the adjacent interface between the PM and carbon fibre sleeve. In contrast, the metallic sleeve is beneficial for heat dissipation from the permanent magnet to the airgap. However, the additional eddy current loss induced on the metallic sleeve cannot be ignored.
5.4. Evalaution and Assessment
5.5. Determination of Uncertain Thermal Parameters
- Material physical properties, including thermal conductivities, specific heat capacities, and mass density.
- Contact thermal resistances of adjacent components caused by imperfect assembling, such as between the frame and the stator core, between the stator lamination and the winding, and between the shaft and the rotor core.
- CHT coefficients within the machine under different cooling conditions.
6. Online Temperature Estimation
6.1. Electrical Parameter Based Methods
6.2. Thermal Model Based Methods
- Ability of predicting transient thermal behaviours.
- Computation time and computing power of the processor.
- Ability to track hotspots (desirable).
6.2.1. White-Box Based Thermal Model
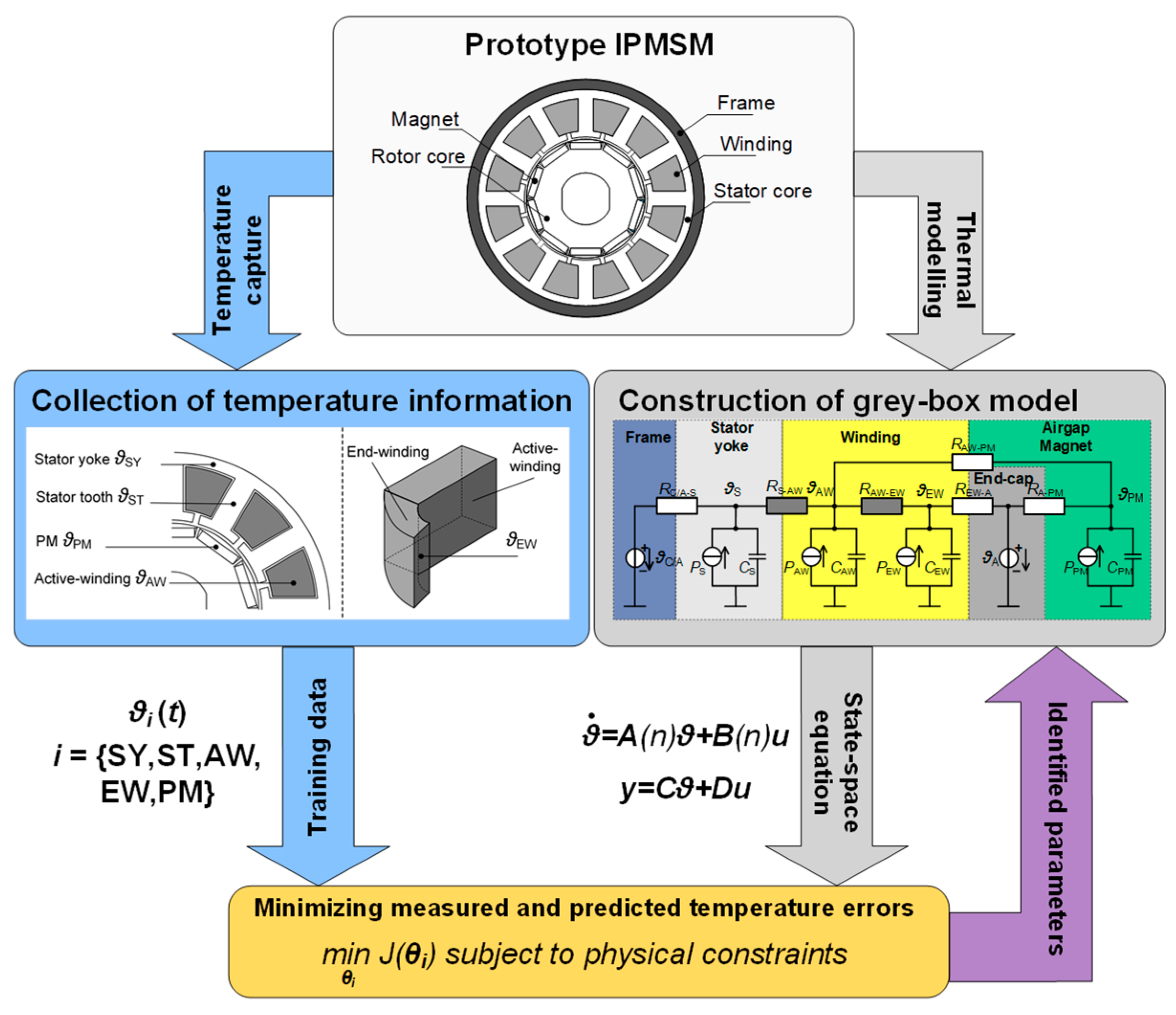
6.2.2. Grey-Box Based Thermal Model
6.3. Evaluation and Assessment
7. Conclusions and Future Research Trends
- 1.
- Development of an accurate elementary thermal network.
- 2.
- Accurate identification of thermal parameters and properties.
- 3.
- Hotspot detection methods for different types of electrical machines.
- 4.
- Investigation and application of advanced cooling techniques in different applications of PM machines.
- 5.
- Systematic thermal analysis, modelling, and management of the integrated system of PM machine and inverter.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Acronyms
| ATM | Analytical thermal model |
| BLAC | Brushless alternating current |
| BLDC | Brushless direct current |
| CFD | Computational fluid dynamics |
| CHT | Convection heat transfer |
| ETFEM | Electromagnetic-thermal coupled FEM |
| FEM/A | Finite element method/analysis |
| HF | High frequency |
| IM | Induction machines |
| IPM | Interior permanent magnet |
| LPTM | Lumped-parameter thermal model |
| PM | Permanent magnet |
| PMSM | Permanent magnet synchronous machine |
| PWM | Pulse-width modulation |
| SPM | Surface-mounted permanent magnet |
| SDTM | Sub-domain thermal model |
| SynRM | Synchronous reluctance machine |
| TEFC | Totally enclosed fan-cooled |
Appendix A
| Ref. | Machine | Methodology | Cooling Method | Remark | ||
|---|---|---|---|---|---|---|
| FEA | CFD | LPTM | ||||
| 1990s | ||||||
| [34,35,36,37,38,39] | IM | ✓ | TEFC | Detailed instruction of LPTM for IMs. | ||
| [40,41,42,43] | IM | ✓ | TEFC | 2-D/3-D FEMs obtained by solving transient/steady-state governing equations. | ||
| [44,45,195] | IM | ✓ | TEFC | Estimation of fluid fields within the end-cap. | ||
| [131] | IM | ✓ | Forced air | Mechanical loss estimation and thermal modelling based on LPTM. | ||
| 2000s | ||||||
| [8] | IM, SynRM | ✓ | Fan | Thermal comparison of IM and SynRM. | ||
| [13] | IM | ✓ | ✓ | ✓ | - | Review of thermal analysis methods for electrical machine. |
| [14] | Electrical machine | ✓ | ✓ | Water/liquid | Review of empirical rules of CHT coefficients. | |
| [15] | IM | ✓ | ✓ | TEFC | Review of CHT coefficients with the end-cap. | |
| [16] | PM machine | ✓ | ✓ | Fan, natural | Comparison of accuracy of CFD and Motor-CAD. | |
| [17] | IM | ✓ | ✓ | ✓ | - | Review of thermal modelling of winding and CHT coefficients. |
| [38] | SPM | ✓ | Liquid | Applying LPTM from IM to PM machine for traction application. | ||
| [46] | IPM machine | ✓ | Water | Applying LPTM [34] into IPM machine. | ||
| [49] | Axial flux PM machine | ✓ | ✓ | Natural | Electromagnetic, thermal, and fluid-dynamic analysis for axial flux PM machine. | |
| [51] | SPM machine, IM | ✓ | ✓ | Water | Instruction of electromagnetic-thermal analysis of Motor-CAD. | |
| [52] | BLDC, SRM | ✓ | ✓ | Oil | Electromagnetic and thermal analysis for BLDC and SRM for aerospace application. | |
| [53] | IM | ✓ | ✓ | TEFC | Combined CFD and LPTM for fast calculation. | |
| [141] | IM | Experimental | Finned with fan | Evaluation of heat transfer capability of a finned frame for different velocities of the cooling fan. | ||
| [153] | IM | ✓ | ✓ | TEFC | Comparison of estimation accuracy of temperatures predicted by CFD and LPTM. | |
| [196] | IM | ✓ | Fan | Investigation of shapes of axial fan for open-type IM. | ||
| [211,212] | Electrical machines | ✓ | - | Improved 1-D “I-type” elementary thermal network to restrain temperature overestimation. | ||
| 2010s to present | ||||||
| [22] | PM machines | Various cooling methods | Review of cooling methods for traction machines. | |||
| [30] | PM machines | ✓ | Natural | Review of empirical rules of CHT coefficients within PM machines. | ||
| [47] | SPM machine | ✓ | Natural | Real-time implementation based on a conventional high-order LPTM. | ||
| [48] | SPM machine | ✓ | Water | Applying LPTM [34] to a SPM machine considering driving cycle. | ||
| [55,56,57] | PM machines | ✓ | ✓ | Oil-, fan | Combined partial CFD and LPTM to ease computational burden. | |
| [58] | PMaSynRM | ✓ | ✓ | Water cooling | Combined LPTM and partial FEM to estimate overall and slot temperatures. | |
| [59] | High-speed PM machines | ✓ | Natural, forced | 2-D analytical PM thermal model to compensate for axial heat transfer in LPTM. | ||
| [60,61,63] | SPMSM, IPMSM | ✓ | ✓ | Natural | Analytical thermal modelling of SPM and IPM machine based on a hybrid thermal model. | |
| [62] | High-speed PM machines | ✓ | ✓ | Forced air | Analytical thermal multi-modelling of PM and rotor sleeve. | |
| [58,65] | IPM | ✓ | ✓ | Water | Multilayer thermal modelling for winding based on FEA or analytical model. | |
| [66] | IPMSM | ✓ | ✓ | Natural | Hybrid thermal model predicting temperature distributions of active- and end-windings. | |
| [81] | PM machine | ✓ | Natural | Thermal parameter tuning for stator part. | ||
| [85] | SPMSM | ✓ | ✓ | Natural | Online tracking of hotspots of windings and PM based on the sub-domain thermal model | |
| [86,87] | PM machines | Machine learning | - | Neural network based black thermal modelling. | ||
| [136,192] | High-speed PM machine | ✓ | ✓ | Fan | Loss and thermal analysis for high-speed PM machines | |
| [143] | IM | ✓ | TEFC | 2-D analytical optimization of cooling fin for IMs | ||
| [154,191] | IPM machines | ✓ | ✓ | Water | Electromagnetic thermal analysis for traction IPMSMs | |
| [162] | PM machines | ✓ | Water | Developing a 3-D LPTM developed for hollow conductors with direct cooling | ||
| [164,165,166] | PM machine | ✓ | Oil-based shaft cooling | Determination of convection coefficient of oil-based hollow shaft via CFD | ||
| [185] | IPM machine | ✓ | Water | Developing a full CFD model for IPM machine considering different rotor blade shapes | ||
| [186] | PMaSynRM | ✓ | ✓ | Natural | Comprehensive analysis of PMaSynRM for traction application accounting for drive system | |
| [187] | PMaSynRM | ✓ | ✓ | Oil | Developing LPTMs for triple 9-phase PMaSynRM under various fault conditions | |
| [188] | Axial flux PM machines | ✓ | Fan | Investigation of different fan blade designs for rotor cooling of axial flux PM machines by CFD | ||
| [190] | Axial flux PM machine | ✓ | Water | Grooving water-cooling jackets in the housing | ||
| [196] | PM machine | ✓ | Natural | Determination of convection coefficients within the end-cap | ||
| [199] | Disc-type PM machine | ✓ | Forced air | Determination of convection coefficient by CFD | ||
| [204] | IPM machine | ✓ | ✓ | Natural | A local discretized slot LPTM modelled to investigate the AC copper loss effect | |
| [206] | PM machine | ✓ | Water | A local discretized slot LPTM modelled to investigate the back-iron extension effect | ||
| [207] | Flux-switching PM machine | ✓ | ✓ | Water | FEM and LPTM modelling for flux-switching PM machines | |
| [208] | SPM machine | ✓ | ✓ | ✓ | Natural | Optimization of SPM machine accounting for electromagnetic, vibratory, and thermal behaviour |
| [210] | Flux-switching PM machine | ✓ | ✓ | Natural | Thermal–electromagnetic analysis for flux-switching PM machine considering driving cycle | |
| [202,203] | Basic element | ✓ | ✓ | - | Analytical derivations of 3-D “T-type” thermal networks for cubic and cylindrical elements. | |
References
- Waide, P.; Brunner, C. Energy-Efficiency Policy Opportunities for Electric Motor-Driven Systems; International Energy Agency: Paris, France, 2011; Available online: https://www.iea.org/reports/energy-efficiency-policy-opportunities-for-electric-motor-driven-systems (accessed on 1 May 2011).
- Rahman, M.A. History of interior permanent magnet motors [History]. IEEE Ind. Appl. Mag. 2013, 19, 10–15. [Google Scholar] [CrossRef]
- Cao, W.; Mecrow, B.C.; Atkinson, G.J.; Bennett, J.W.; Atkinson, D.J. Overview of electric motor technologies used for more electric aircraft (MEA). IEEE Trans. Ind. Electron. 2012, 59, 3523–3531. [Google Scholar]
- Chi, S.; Zhang, Z.; Xu, L. Sliding-mode sensorless control of direct-drive PM synchronous motors for washing machine applications. IEEE Trans. Ind. Appl. 2009, 45, 582–590. [Google Scholar] [CrossRef]
- He, T.; Zhu, Z.Q.; Eastham, F.; Wang, Y.; Bin, H.; Wu, D.; Gong, L.; Chen, J.T. Permanent magnet machines for high-speed applications. World Electr. Veh. J. 2022, 13, 18. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D. Electrical machines and drives for electric, hybrid, and fuel cell vehicles. Proc. of IEEE 2007, 95, 746–765. [Google Scholar] [CrossRef]
- Polinder, H.; Ferreira, J.A.; Jensen, B.B.; Abrahamsen, A.B.; Atallah, K.; McMahon, R.A. Trends in wind turbine generator systems. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 174–185. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Pastorelli, M.; Staton, D.; Vagati, A. Thermal analysis of induction and synchronous reluctance motors. IEEE Trans. Ind. Appl. 2006, 42, 675–680. [Google Scholar] [CrossRef] [Green Version]
- National Electrical Manufacturers Association. Motors and Generators. Available online: https://www.nema.org/Standards/view/Motors-and-Generators (accessed on 1 December 2021).
- Gao, Z.; Cecati, C.; Ding, S. A survey of fault diagnosis and fault-tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Cecati, C.; Ding, S. A survey of fault diagnosis and fault-tolerant techniques—Part II: Fault diagnosis with knowledge-based and hybrid/active approaches. IEEE Trans. Ind. Electron. 2015, 62, 3768–3774. [Google Scholar]
- Liu, S.; Kuhl, G. Temperature coefficients of rare earth permanent magnets. IEEE Trans. Magn. 1999, 35, 3271–3273. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Staton, D.; Shanel, M.; Mueller, M.; Mejuto, C. Evolution and modern approaches for thermal analysis of electrical machines. IEEE Trans. Ind. Electron. 2009, 56, 871–882. [Google Scholar] [CrossRef] [Green Version]
- Boglietti, A.; Cavagnino, A.; Staton, D. Determination of critical parameters in electrical machine thermal models. IEEE Trans. Ind. Appl. 2008, 44, 1150–1159. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A. Analysis of the endwinding cooling effects in TEFC induction motors. IEEE Trans. Ind. Appl. 2007, 43, 1214–1222. [Google Scholar] [CrossRef] [Green Version]
- Staton, D.; Pickering, S.J.; Lampard, D. Recent advancement in the thermal design of electric motors. In Proceedings of the SMMA Fall Technical Conference, Durham, NC, USA, 3–5 October 2001; pp. 1–11. [Google Scholar]
- Staton, D.; Boglietti, A.; Cavagnino, A. Solving the more difficult aspects of electric motor thermal analysis in small and medium size industrial induction motors. IEEE Trans. Energy Convers. 2005, 20, 620–628. [Google Scholar] [CrossRef] [Green Version]
- Staton, D.; Cavagnino, A. Convection heat transfer and flow calculations suitable for electric machines thermal models. IEEE Trans. Ind. Electron. 2008, 55, 3509–3516. [Google Scholar] [CrossRef] [Green Version]
- Taras, P.; Nilifard, R.; Zhu, Z.Q.; Azar, Z. Cooling techniques in direct-drive generators for wind power application. Energies 2022, 15, 5986. [Google Scholar] [CrossRef]
- Dong, C.; Qian, Y.; Zhang, Y.; Zhuge, W. A review of thermal designs for improving power density in electrical machines. IEEE Trans. Transp. Electr. 2020, 6, 1386–1400. [Google Scholar] [CrossRef]
- Deisenroth, D.C.; Ohadi, M. Thermal management of high-power density electric motors for electrification of aviation and beyond. Energies 2019, 12, 3594. [Google Scholar] [CrossRef] [Green Version]
- Gai, Y.; Kimiabeigi, M.; Chuan Chong, Y.; Widmer, J.; Deng, X.; Popescu, M.; Goss, J.; Staton, D.; Steven, A. Cooling of automotive traction motors: Schemes, examples, and computation methods. IEEE Trans. Ind. Electron. 2019, 66, 1681–1692. [Google Scholar] [CrossRef] [Green Version]
- Gronwald, P.; Kern, T. Traction motor cooling systems: A literature review and comparative study. IEEE Trans. Transp. Electr. 2021, 7, 2892–2913. [Google Scholar] [CrossRef]
- Popescu, M.; Staton, D.; Boglietti, A.; Cavagnino, A.; Hawkins, D.; Goss, J. Modern heat extraction systems for power traction machines—A review. IEEE Trans. Ind. Appl. 2016, 52, 2167–2175. [Google Scholar] [CrossRef]
- Wallscheid, O. Thermal monitoring of electric motors: State-of-the-art review and future challenges. IEEE Open J. Ind. Appl. 2021, 2, 204–223. [Google Scholar] [CrossRef]
- Zhu, T.; Zhang, Y.; Li, Q.; Wang, Y.; Geng, W. Overview of hybrid cooling system for high power density motor. J. Electr. Eng. 2022, 23, 1–16. [Google Scholar]
- Wang, Q.; Wu, Y.; Niu, S.; Zhao, X. Advances in thermal management technologies of electrical machines. Energies 2022, 15, 3249. [Google Scholar] [CrossRef]
- Ghahfarokhi, P.; Podgornovs, A.; Kallaste, A.; Cardoso, A.; Belahcen, A.; Vaimann, T.; Tiismus, H.; Asad, B. Opportunities and challenges of utilizing additive manufacturing approaches in thermal management of electrical machines. IEEE Access 2021, 9, 36368–36381. [Google Scholar] [CrossRef]
- Kulan, M.; Sahin, S.; Baker, N. An overview of modern thermo-conductive materials for heat extraction in electrical machines. IEEE Access 2020, 8, 212114–212129. [Google Scholar] [CrossRef]
- Liang, D.; Zhu, Z.Q.; Feng, J.; Guo, S.; Li, Y.; Wu, J.; Zhao, A. Influence of critical parameters in lumped-parameter thermal models for electrical machines. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems, Harbin, China, 11–14 August 2019; pp. 1–6. [Google Scholar]
- Bradford, M. The application of heat pipes to cooling rotating electrical machines. In Proceedings of the 1989 4th IEEE International Electric Machines & Drives Conference, London, UK, 13–15 September 1989; pp. 145–149. [Google Scholar]
- Wrobel, R.; McGlen, R.J. Opportunities and challenges of employing heat-pipes in thermal management of electrical machines. In Proceedings of the 2020 International Conference on Electrical Machines, Gothenburg, Sweden, 23–26 August 2020; pp. 961–967. [Google Scholar]
- Zhu, Z.Q.; Liang, D.; Liu, K. Online parameter estimation for permanent magnet synchronous machines: An overview. IEEE Access 2021, 9, 59059–59084. [Google Scholar] [CrossRef]
- Mellor, P.H.; Roberts, D.; Turner, D. Lumped parameter thermal model for electrical machines of TEFC design. IEE Proc. B Electr. Power Appl. 1991, 138, 205–218. [Google Scholar] [CrossRef]
- Liu, Z.; Howe, D.; Mellor, P.H.; Jenkins, M. Thermal analysis of permanent magnet machines. In Proceedings of the Sixth International Conference on Electrical Machines and Drives, Oxford, UK, 8–10 September 1993; pp. 359–364. [Google Scholar]
- Gerlando, A.D.; Vistoli, I. Improved thermal modelling of induction motors for design purposes. In Proceedings of the Sixth International Conference on Electrical Machines and Drives, Oxford, UK, 8–10 September 1993; pp. 381–386. [Google Scholar]
- Kylander, G. Thermal Modelling of Small Cage Induction Motors. Ph.D. Thesis, Department of Electric Power Engineering, Chalmers University of Technology, Gothenburg, Sweden, April 1995. [Google Scholar]
- Lindström, J. Thermal Model of a Permanent-Magnet Motor for a Hybrid Electric Vehicle; Department of Electric Power Engineering, Chalmers University of Technology: Göteborg, Sweden, April 1999. [Google Scholar]
- Boglietti, A.; Cavagnino, A.; Lazzari, M.; Pastorelli, M. A simplified thermal model for variable-speed self-cooled industrial induction motor. IEEE Trans. Ind. Appl. 2003, 39, 945–952. [Google Scholar] [CrossRef]
- Siyambalapitiya, D.J.T.; McLaren, P.G.; Tavner, P.J. Transient thermal characteristics of induction machine rotor cage. IEEE Trans. Energy Convers. 1988, 3, 849–854. [Google Scholar] [CrossRef]
- Sarkar, D.; Mukherjee, P.K.; Sen, S.K. Temperature rise of an induction motor during plugging. IEEE Trans. Energy Convers. 1992, 7, 116–124. [Google Scholar] [CrossRef]
- Chan, C.C.; Yan, L.; Chen, P.; Wang, Z.; Chau, K. Analysis of electromagnetic and thermal fields for induction motors during starting. IEEE Trans. Energy Convers. 1994, 9, 53–60. [Google Scholar] [CrossRef]
- Rajagopal, M.S.; Seetharamu, K.N.; Ashwathnarayana, P.A. Transient thermal analysis of induction motors. IEEE Trans. Energy Convers. 1998, 13, 62–69. [Google Scholar] [CrossRef]
- Mugglestone, J.; Lampard, D.; Pickering, S. Effects of end winding porosity upon the flow field and ventilation losses in the end region of TEFC induction machines. IEE Proc. Electr. Power Appl. 1998, 145, 423–428. [Google Scholar] [CrossRef]
- Mugglestone, J.; Pickering, S.J.; Lampard, D. Effect of geometric changes on the flow and heat transfer in the end region of a TEFC induction motor. In Proceedings of the 9th International Conference on Electrical Machines and Drives, Canterbury, UK, 1–3 September 1999; pp. 40–44. [Google Scholar]
- EL-Refaie, A.M.; Harris, N.C.; Jahns, T.M.; Rahman, K.M. Thermal analysis of multibarrier interior PM synchronous machine using lumped parameter model. IEEE Trans. Energy Convers. 2004, 19, 303–309. [Google Scholar] [CrossRef] [Green Version]
- Demetriades, G.; Parra, H.D.L.; Andersson, E.; Olsson, H. A real-time thermal model of a permanent-magnet synchronous motor. IEEE Trans. Power Electron. 2010, 25, 463–474. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, C.; Wang, Z.; Dong, Y.; Nino, C.E.; Tariq, A.R.; Strangas, E.G. Thermal analysis of permanent magnet motor for the electric vehicle application considering driving duty cycle. IEEE Trans. Magn. 2010, 46, 2493–2496. [Google Scholar] [CrossRef]
- Marignetti, F.; Colli, V.; Coia, Y. Design of axial flux PM synchronous machines through 3-D coupled electromagnetic thermal and fluid-dynamical finite-element analysis. IEEE Trans. Ind. Electron. 2018, 55, 3591–3601. [Google Scholar] [CrossRef]
- Dorrrell, D.G.; Staton, D.A.; Hahout, J.; Hawkins, D.; McGilp, M.I. Linked electromagnetic and thermal modelling of a permanent magnet motor. In Proceedings of the 3rd IET International Conference on Power Electronics, Machines and Drives (PEMD), Dublin, Ireland, 4–6 April 2006; pp. 536–540. [Google Scholar]
- Dorrell, D.G. Combined thermal and electromagnetic analysis of permanent-magnet and induction machines to aid calculation. IEEE Trans. Ind. Electron. 2008, 55, 3566–3574. [Google Scholar] [CrossRef]
- Powell, D.J. Modelling of High Power Density Electrical Machines for Aerospace. Ph.D. Thesis, Department of Electronic and Electrical Engineering, The University of Sheffield, Sheffield, UK, 2003. [Google Scholar]
- Trigeol, J.F.; Bertin, Y.; Lagonotte, P. Thermal modeling of an induction machine through the association of two numerical approaches. IEEE Trans. Energy Convers. 2006, 21, 314–323. [Google Scholar] [CrossRef]
- Motor-CAD. (v14). Motor Design Ltd. Available online: https://www.motor-design.com (accessed on 1 January 2021).
- Nategh, S.; Huang, Z.; Krings, A.; Wallmark, O.; Leksell, M. Thermal modeling of directly cooled electric machines using lumped parameter and limited CFD analysis. IEEE Trans. Energy Convers. 2013, 28, 979–990. [Google Scholar] [CrossRef]
- Nategh, S.; Zhang, H.; Wallmark, O.; Boglietti, A.; Nassen, T.; Bazant, M. Transient thermal modeling and analysis of railway traction motors. IEEE Trans. Ind. Electron. 2019, 66, 79–89. [Google Scholar] [CrossRef]
- SanAndres, U.; Almandoz, G.; Poza, J.; Ugalde, G. Design of cooling systems using computational fluid dynamics and analytical thermal models. IEEE Trans. Ind. Electron. 2014, 61, 4383–4391. [Google Scholar] [CrossRef]
- Nategh, S.; Wallmark, O.; Leksell, M.; Zhao, S. Thermal analysis of a PMaSRM using partial FEA and lumped parameter modeling. IEEE Trans. Energy Convers. 2012, 27, 477–488. [Google Scholar] [CrossRef]
- Grobler, A.J.; Holm, S.R.; Schoor, G.V. A two-dimensional analytic thermal model for a high-speed PMSM magnet. IEEE Trans. Ind. Electron. 2015, 62, 6756–6764. [Google Scholar] [CrossRef]
- Liang, D.; Zhu, Z.Q.; Feng, J.; Guo, S.; Li, Y.; Zhao, A.; Hou, J. Estimation of 3-D magnet temperature distribution based on lumped-parameter and analytical hybrid thermal model for SPMSM. IEEE Trans. Energy Convers. 2022, 37, 515–525. [Google Scholar] [CrossRef]
- Liang, D.; Zhu, Z.Q.; Feng, J.; Guo, S.; Li, Y.; Zhao, A.; Hou, J. Simplified 3-D hybrid analytical modeling of magnet temperature distribution for surface mounted PMSM with segmented magnets. IEEE Trans. Ind. Appl. 2022, 58, 4474–4487. [Google Scholar] [CrossRef]
- Liang, D.; Zhu, Z.Q.; He, T.R. Analytical rotor thermal modelling accounting for retaining sleeve in high-speed PM machines. In Proceedings of the IEEE International Conference on Electrical Machine (ICEM), Valencia, Spain, 5–8 September 2022. [Google Scholar]
- Liang, D.; Zhu, Z.Q.; Shao, B.; Feng, J.; Guo, S.; Li, Y.; Zhao, A. Estimation of two- and three-dimensional spatial magnet temperature distributions for interior PMSMs based on hybrid thermal model. IEEE Trans. Energy Convers. 2022, 37, 2175–2189. [Google Scholar]
- Dotz, B.; Ippisch, M.; Gerling, D. Analytical calculation of winding overtemperatures and estimation of feasible current densities for electrical machines. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 1081–1087. [Google Scholar]
- Fan, X.; Li, D.; Qu, R.; Wang, C. A dynamic multilayer winding thermal model for electrical machines with concentrated windings. IEEE Trans. Ind. Electron. 2019, 66, 6189–6199. [Google Scholar] [CrossRef]
- Liang, D.; Zhu, Z.Q.; Zhang, Y.; Feng, J.; Guo, S.; Li, Y.; Wu, J.; Zhao, A. A hybrid lumped-parameter and two-dimensional analytical thermal model for electrical machines. IEEE Trans. Ind. Appl. 2021, 57, 246–258. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, Q.; Chen, J.; Zhu, Z.Q.; Zhang, J. Online multiparameter estimation of nonsalient-pole pm synchronous machines with temperature variation tracking. IEEE Trans. Ind. Electron. 2011, 58, 1776–1788. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Zhu, Z.Q.; Stone, D.A. Parameter estimation for condition monitoring of PMSM stator winding and rotor permanent magnets. IEEE Trans. Ind. Electron. 2013, 60, 5902–5913. [Google Scholar] [CrossRef] [Green Version]
- Wilson, S.; Stewart, P.; Taylor, B. Methods of resistance estimation in permanent magnet synchronous motors for real-time thermal management. IEEE Trans. Energy Convers. 2010, 25, 698–707. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Zhu, Z.Q. Position-offset-based parameter estimation using the Adaline NN for condition monitoring of permanent-magnet synchronous machines. IEEE Trans. Ind. Electron. 2015, 62, 2372–2383. [Google Scholar] [CrossRef]
- Liu, K.; Zhu, Z.Q. Quantum genetic algorithm-based parameter estimation of PMSM under variable speed control accounting for system identifiability and VSI nonlinearity. IEEE Trans. Ind. Electron. 2015, 62, 2363–2371. [Google Scholar] [CrossRef]
- Reigosa, D.; Briz, F.; Garcia, P.; Guerrero, J.; Degner, M. Magnet temperature estimation in surface PM machines using high-frequency signal injection. IEEE Trans. Ind. Appl. 2010, 46, 1468–1475. [Google Scholar] [CrossRef]
- Reigosa, D.; Briz, F.; Degner, M.W.; García, P.; Guerrero, J.M. Magnet temperature estimation in surface PM machines during six-step operation. IEEE Trans. Ind. Appl. 2012, 48, 2353–2361. [Google Scholar] [CrossRef]
- Reigosa, D.; Fernandez, D.; Tanimoto, T.; Kato, T.; Briz, F. Permanent-magnet temperature distribution estimation in permanent-magnet synchronous machines using back electromotive force harmonics. IEEE Trans. Ind. Appl. 2016, 52, 3093–3103. [Google Scholar] [CrossRef] [Green Version]
- Reigosa, D.; Fernandez, D.; Martínez, M.; Guerrero, J.M.; Diez, A.B.; Briz, F. Magnet temperature estimation in permanent magnet synchronous machines using the high frequency inductance. IEEE Trans. Ind. Appl. 2019, 55, 2750–2757. [Google Scholar] [CrossRef]
- Feng, G.; Lai, C.; Tjong, J.; Kar, N.C. Noninvasive Kalman filter based permanent magnet temperature estimation for permanent magnet synchronous machines. IEEE Trans. Power Electron. 2018, 33, 10673–10682. [Google Scholar] [CrossRef]
- Wallscheid, O.; Specht, A.; Böcker, J. Observing the permanent-magnet temperature of synchronous motors based on electrical fundamental wave model quantities. IEEE Trans. Ind. Electron. 2017, 64, 3921–3929. [Google Scholar] [CrossRef]
- Kral, C.; Haumer, A.; Lee, S.B. A practical thermal model for the estimation of permanent magnet and stator winding temperatures. IEEE Trans. Power Electron. 2014, 29, 455–464. [Google Scholar] [CrossRef]
- Huber, T.; Böcker, J.; Peters, W. A low-order thermal model for monitoring critical temperatures in permanent magnet synchronous motors. In Proceedings of the 7th IET International Conference on Power Electronics, Machines and Drives (PEMD 2014), Manchester, UK, 8–10 April 2014; pp. 1–6. [Google Scholar]
- Xiao, S.; Griffo, A. Online thermal parameter identification for permanent magnet synchronous machines. IET Electr. Power Appl. 2020, 14, 2340–2347. [Google Scholar] [CrossRef]
- Sciascera, C.; Giangrande, P.; Papini, L.; Gerada, C.; Galea, M. Analytical thermal model for fast stator winding temperature prediction. IEEE Trans. Ind. Electron. 2017, 64, 6116–6126. [Google Scholar] [CrossRef]
- Wallscheid, O.; Böcker, J. Global identification of a low-order lumped-parameter thermal network for permanent magnet synchronous motors. IEEE Trans. Energy Convers. 2016, 31, 354–365. [Google Scholar] [CrossRef]
- Wang, E.; Grabherr, P.; Wieske, P.; Doppelbauer, M. A low-order lumped parameter thermal network of electrically excited synchronous motor for critical temperature estimation. In Proceedings of the 2022 XIII International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022. [Google Scholar]
- Feng, J.; Liang, D.; Zhu, Z.Q.; Guo, S.; Li, Y.; Zhao, A.; Hou, J. Improved low-order thermal models for critical temperature estimation of PMSM. IEEE Trans. Energy Convers. 2022, 37, 413–423. [Google Scholar] [CrossRef]
- Liang, D.; Zhu, Z.Q.; Shao, B.; Feng, J.; Guo, S.; Li, Y.; Zhao, A. Tracking of winding and magnet hotspots in SPMSMs based on synergized lumped-parameter and sub-domain thermal models. IEEE Trans. Energy Convers. 2022, 37, 2147–2161. [Google Scholar] [CrossRef]
- Kirchgässner, W.; Wallscheid, O.; Böcker, J. Data-driven permanent magnet temperature estimation in synchronous motors with supervised machine learning: A benchmark. IEEE Trans. Energy Convers. 2021, 36, 2059–2067. [Google Scholar] [CrossRef]
- Kirchgässner, W.; Wallscheid, O.; Böcker, J. Estimating electric motor temperatures with deep residual machine learning. IEEE Trans. Power Electron. 2021, 36, 7480–7488. [Google Scholar] [CrossRef]
- Rogers, G.; Mayhew, Y. Engineering Thermodynamics: Work and Heat Transfer; Longman Scientific & Technical: Harlow, UK, 1992. [Google Scholar]
- Bergman, T. Fundamentals of Heat and Mass Transfer; J. Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Anonymous. VII. Scala graduum caloris. Philos. Trans. R. Soc. Lond. 1701, 22, 824–829. [Google Scholar]
- Holman, J.P. Heat Transfer; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Steinmetz, C. On the law of hysteresis. Trans. Am. Inst. Electr. Eng. 1892, 9, 1–64. [Google Scholar] [CrossRef]
- Bertotti, G. A general statistical approach to the problem of eddy current losses. J. Magn. Magn. Mater. 1984, 41, 253–260. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Lazzari, M.; Pastorelli, M. Predicting iron losses in soft magnetic materials with arbitrary voltage supply: An engineering approach. IEEE Trans. Magn. 2003, 39, 981–989. [Google Scholar] [CrossRef]
- Ionel, D.; Popescu, M.; McGilp, M.; Miller, T.; Dellinger, S.; Heideman, R. Computation of core losses in electrical machines using improved models for laminated steel. IEEE Trans. Ind. Appl. 2007, 43, 1554–1564. [Google Scholar] [CrossRef] [Green Version]
- Bertotti, G. General properties of power losses in soft ferromagnetic materials. IEEE Trans. Magn. 1988, 24, 621–630. [Google Scholar] [CrossRef]
- Atallah, K.; Zhu, Z.Q.; Howe, D. An improved method for predicting iron losses in brushless permanent magnet DC drives. IEEE Trans. Magn. 1992, 28, 2997–2999. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Xue, S.; Chu, W.; Feng, J.; Guo, S.; Chen, Z.; Peng, J. Evaluation of iron loss models in electrical machines. IEEE Trans. Ind. Appl. 2019, 55, 1461–1472. [Google Scholar] [CrossRef]
- Xue, S.; Chu, W.; Zhu, Z.Q.; Peng, J.; Guo, S.; Feng, J. Iron loss calculation considering temperature influence in non-oriented steel laminations. Proc. IET Sci. Meas. Technol. 2016, 10, 846–854. [Google Scholar] [CrossRef]
- Xue, S. Investigation of Iron Losses in Permanent Magnet Machines Accounting for Temperature Effect. Ph.D. Thesis, Department of Electronic and Electrical Engineering, The University of Sheffield, Sheffield, UK, 2017. [Google Scholar]
- Chen, J.; Wang, D.; Cheng, S.; Wang, Y.; Zhu, Y.; Liu, Q. Modeling of temperature effects on magnetic property of nonoriented silicon steel lamination. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Bourchas, K.; Stening, A.; Soulard, J.; Broddefalk, A.; Lindenmo, M.; Dahlén, M.; Gyllensten, F. Influence of cutting and welding on magnetic properties of electrical steels. In Proceedings of the 2016 XXIIth International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 1815–1821. [Google Scholar]
- Wu, F.; Zhou, L.; Soulard, J.; Silvester, B.; Davis, C. Quantitative characterisation and modelling of the effect of cut edge damage on the magnetic properties in NGO electrical steel. J. Magn. Magn. Mater. 2022, 551, 169185. [Google Scholar] [CrossRef]
- Takahashi, N.; Miyagi, D. Effect of stress on iron loss of motor core. In Proceedings of the 2011 IEEE International Electric Machines & Drives Conference (IEMDC), Niagara Falls, ON, Canada, 15–18 May 2011. [Google Scholar]
- Iwasaki, S.; Deodhar, R.P.; Liu, Y.; Pride, A.; Zhu, Z.Q.; Bremner, J.J. Influence of PWM on the proximity loss in permanent-magnet brushless AC machines. IEEE Trans. Ind. Appl. 2009, 45, 1359–1367. [Google Scholar] [CrossRef] [Green Version]
- Murgatroyd, P.N. Calculation of proximity losses in multistranded conductor bunches. Proc. Inst. Electr. Eng. A Sci. Meas. Technol. 1989, 136, 115–120. [Google Scholar] [CrossRef]
- Thomas, A.S.; Zhu, Z.Q.; Jewell, G.W. Proximity loss study in high speed flux-switching permanent magnet machine. IEEE Trans. Magn. 2009, 45, 4748–4751. [Google Scholar] [CrossRef]
- Wu, L.J.; Zhu, Z.Q. Simplified analytical model and investigation of open-circuit AC winding loss of permanent-magnet machines. IEEE Trans. Ind. Electron. 2014, 61, 4990–4999. [Google Scholar] [CrossRef]
- Wrobel, R.; Salt, D.; Griffo, A.; Simpson, N.; Mellor, P.H. Derivation and scaling of AC copper loss in thermal modeling of electrical machines. IEEE Trans. Ind. Electron. 2014, 61, 4412–4420. [Google Scholar] [CrossRef]
- Mellor, P.H.; Wrobel, R.; McNeill, N. Investigation of proximity losses in a high speed brushless permanent magnet motor. In Proceedings of the 41st IAS Annual Meeting, Tampa, FL, USA, 8–12 October 2006; pp. 1514–1518. [Google Scholar]
- Popescu, M.; Goss, J.; Staton, D.A.; Hawkins, D.; Chong, Y.C.; Boglietti, A. Electrical vehicles—Practical solutions for power traction motor systems. IEEE Trans. Ind. Appl. 2018, 54, 2751–2762. [Google Scholar] [CrossRef] [Green Version]
- Dimier, T.; Cossale, M.; Wellerdieck, T. Comparison of stator winding technologies for high-speed motors in electric propulsion systems. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 23–26 August 2020; pp. 2406–2412. [Google Scholar]
- Nagarkatti, A.K.; Mohammed, O.A.; Demerdash, N.A. Special losses in rotors of electronically commutated brushless DC motors induced by non-uniformly rotating armature MMFs. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 4502–4507. [Google Scholar] [CrossRef]
- Atallah, K.; Howe, D.; Mellor, P.H.; Stone, D.A. Rotor loss in permanent-magnet brushless AC machines. IEEE Trans. Ind. Appl. 2000, 36, 1612–1618. [Google Scholar]
- Hor, P.J.; Zhu, Z.Q.; Howe, D. Eddy current loss in a moving-coil tubular permanent magnet motor. IEEE Trans. Magn. 1999, 35, 3601–3603. [Google Scholar] [CrossRef]
- Wu, L.J.; Zhu, Z.Q.; Staton, D.; Popescu, M.; Hawkins, D. Analytical modeling and analysis of open-circuit magnet loss in surface-mounted permanent-magnet machines. IEEE Trans. Magn. 2012, 48, 1234–1247. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Ng, K.; Schofield, N.; Howe, D. Analytical prediction of rotor eddy current loss in brushless machines equipped with surface-mounted permanent magnets. II. Accounting for eddy current reaction field. In Proceedings of the 5th International Conference on Electrical Machines and Systems, Shenyang, China, 18–20 August 2001; pp. 810–813. [Google Scholar]
- Zhu, Z.Q.; Ng, K.; Schofield, N.; Howe, D. Improved analytical modelling of rotor eddy current loss in brushless machines equipped with surface-mounted permanent magnets. IEE Proc. Electr. Power Appl. 2004, 151, 641–650. [Google Scholar] [CrossRef]
- Yamazaki, K.; Watari, S. Loss analysis of permanent-magnet motor considering carrier harmonics of PWM inverter using combination of 2-D and 3-D finite-element method. IEEE Trans. Magn. 2005, 41, 1980–1983. [Google Scholar] [CrossRef]
- Cheng, M.; Zhu, S. Calculation of PM eddy current loss in IPM machine under PWM VSI supply with combined 2-D FE and analytical Method. IEEE Trans. Magn. 2017, 53, 1–12. [Google Scholar] [CrossRef]
- Ou, J.; Liu, Y.; Liang, D.; Doppelbauer, M. Investigation of PM eddy current losses in surface-mounted PM motors caused by PWM. IEEE Trans. Power Electron. 2019, 34, 11253–11263. [Google Scholar] [CrossRef]
- Ishak, D.; Zhu, Z.Q.; Howe, D. Eddy-current loss in the rotor magnets of permanent-magnet brushless machines having a fractional number of slots per pole. IEEE Trans. Magn. 2005, 41, 2462–2469. [Google Scholar] [CrossRef] [Green Version]
- Toda, H.; Xia, Z.; Wang, J.; Atallah, K.; Howe, D. Rotor eddy-current loss in permanent magnet brushless machines. IEEE Trans. Magn. 2004, 40, 2104–2106. [Google Scholar] [CrossRef]
- Sergeant, P.; Bossche, A.V.D. Segmentation of magnets to reduce losses in permanent-magnet synchronous machines. IEEE Trans. Magn. 2008, 44, 4409–4412. [Google Scholar] [CrossRef]
- Huang, W.; Bettayeb, A.; Kaczmarek, R.; Vannier, J.C. Optimisation of magnet segmentation for reduction of eddy-current losses in permanent magnet synchronous machine. IEEE Trans. Energy Convers. 2010, 25, 381–387. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Ma, J.; Liu, C.; Lei, G.; Guo, Y.; Zhu, J. Reduction of magnet eddy current loss in PMSM by using partial magnet segment method. IEEE Trans. Magn. 2019, 55, 1–5. [Google Scholar] [CrossRef]
- Shen, J.; Hao, H.; Jin, M.; Yuan, C. Reduction of rotor eddy current loss in high speed pm brushless machines by grooving retaining sleeve. IEEE Trans. Magn. 2013, 49, 3973–3976. [Google Scholar] [CrossRef]
- Choi, G.; Jahns, T.M. Reduction of eddy-current losses in fractional slot concentrated-winding synchronous PM machines. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Ma, J.; Zhu, Z.Q. Magnet eddy current loss reduction in permanent magnet machines. IEEE Trans. Ind. Appl. 2019, 55, 1309–1320. [Google Scholar] [CrossRef]
- Chaithongsuk, S.; Takorabet, N.; Kreuawan, S. Reduction of eddy-current losses in fractional-slot concentrated-winding synchronous PM motors. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Saari, J. Thermal Analysis of High-Speed Induction Machines. Ph.D. Thesis, Department of Electrical and Communications Engineering, Helsinki University of Technology, Espoo, Finland, 1998. [Google Scholar]
- Wendt, F. Turbulente Strömungen zwischen zwei rotierenden konaxialen Zylindern. Ingenieur-Archiv 1993, 4, 577–595. [Google Scholar] [CrossRef]
- Bilgen., E.; Boulos, R. Functional dependence of torque coefficient of coaxial cylinders on gap width and Reynolds numbers. J. Fluids Eng. 1973, 95, 122–126. [Google Scholar] [CrossRef]
- Reynolds, A.J. Turbulent Flows in Engineering; John Wiley & Sons Ltd.: New York, NY, USA, 1974. [Google Scholar]
- Polkowski, J. Turbulent flow between coaxial cylinders with the inner cylinder rotating. J. Eng. Gas Turbines Power 1984, 106, 128–135. [Google Scholar] [CrossRef]
- Huang, Z.; Fang, J.; Liu, X.; Han, B. Loss calculation and thermal analysis of rotors supported by active magnetic bearings for high-speed permanent-magnet electrical machines. IEEE Trans. Ind. Electron. 2016, 63, 2027–2035. [Google Scholar] [CrossRef]
- SKF. Skf.com. Available online: https://www.skf.com/sg (accessed on 1 October 2018).
- Ćalasan, M.; Ostojić, M.; Petrović, D. The retardation method for bearings loss determination. In Proceedings of the International Symposium on Power Electronics Power Electronics, Sorrento, Italy, 20–22 June 2012; pp. 25–29. [Google Scholar]
- Gilson, A.; Sindjui, R.; Chareyron, B.; Milosavljevic, M. No-load loss separation of high-speed electric motors for electrically-assisted turbochargers. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 23–26 August 2020; pp. 2439–2444. [Google Scholar]
- Staton, D.; Chong, E.; Pickering, S.; Boglietti, A. Cooling of Rotating Electrical Machines; The Institute of Engineering and Technology: Saint-Laurent, MO, Canada, 2022. [Google Scholar]
- Valenzuela, M.A.; Tapia, J.A. Heat transfer and thermal design of finned frames for TEFC variable-speed motors. IEEE Trans. Ind. Electron. 2008, 55, 3500–3508. [Google Scholar] [CrossRef]
- Staton, D.; So, E. Determination of optimal thermal parameters for brushless permanent magnet motor design. In Proceedings of the Thirty-Third IAS Annual Meeting, St. Louis, MO, USA, 12–15 October 1998; pp. 41–49. [Google Scholar]
- Ulbrich, S.; Kopte, J.; Proske, J. Cooling fin optimization on a TEFC electrical machine housing using a 2-D conjugate heat transfer model. IEEE Trans. Ind. Electron. 2018, 66, 1711–1718. [Google Scholar] [CrossRef]
- Galea, M.; Gerada, C.; Raminosoa, T.; Wheeler, P. A thermal improvement technique for the phase windings of electrical machines. IEEE Trans. Ind. Appl. 2012, 48, 79–87. [Google Scholar] [CrossRef]
- Zhang, F.; Gerada, D.; Xu, Z.; Zhang, X.; Tighe, C.; Zhang, H.; Gerada, C. Back-iron extension thermal benefits for electrical machines with concentrated windings. IEEE Trans. Ind. Electron. 2020, 67, 1711–1718. [Google Scholar] [CrossRef]
- Nategh, S.; Boglietti, A.; Barber, D.; Liu, Y.; Brammer, R. Thermal and management aspects of traction motors potting: A deep experimental evaluation. IEEE Trans. Energy Convers. 2020, 35, 1026–1034. [Google Scholar] [CrossRef]
- Polikarpova, M.; Ponomarev, P.; Lindh, P.; Petrov, I.; Jara, W.; Naumanen, V.; Tapia, J.A.; Pyrhönen, J. Hybrid cooling method of axial-flux permanent-magnet machines for vehicle applications. IEEE Trans. Ind. Electron. 2015, 62, 1711–1718. [Google Scholar] [CrossRef]
- Song, F.; Ewing, D.; Ching, C.Y. Heat transfer in the evaporator section of moderate-speed rotating heat pipes. Int. J. Heat Mass Transf. 2008, 51, 1542–1550. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, S.; Chen, G.; Tang, Y.; Liang, F. Experimental and numerical investigation on a novel heat pipe based cooling strategy for permanent magnet synchronous motors. Appl. Therm. Eng. 2020, 170, 114970. [Google Scholar] [CrossRef]
- Mueller, M.A.; Burchell, J.; Chong, Y.C.; Keysan, O.; McDonald, A.; Galbraith, M.; Echenique Subiabre, E. Improving the thermal performance of rotary and linear air-cored permanent magnet machines for direct drive wind and wave energy applications. IEEE Trans. Energy Convers. 2019, 34, 773–781. [Google Scholar] [CrossRef]
- Roffi, M.; Ferreira, F.; De Almeida, A.T. Comparison of different cooling fan designs for electric motors. In Proceedings of the 2017 IEEE International Electric Machines & Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017. [Google Scholar]
- Yung, C. Cool facts about cooling electric motors. In Proceedings of the Industry Applications Society 60th Annual Petroleum and Chemical Industry Conference, Chicago, IL, USA, 23–25 September 2013. [Google Scholar]
- Kral, C.; Haumer, A.; Haigis, M.; Lang, H.; Kapeller, H. Comparison of a CFD analysis and a thermal equivalent circuit model of a TEFC induction machine with measurements. IEEE Trans. Energy Convers. 2009, 24, 809–818. [Google Scholar] [CrossRef]
- Zhang, B.; Qu, R.; Wang, J.; Xu, W.; Fan, X.; Chen, Y. Thermal model of totally enclosed water-cooled permanent-magnet synchronous machines for electric vehicle application. IEEE Trans. Ind. Appl. 2015, 51, 3020–3029. [Google Scholar] [CrossRef]
- Chen, Q.; Wu, D.; Li, G.; Cao, W.; Qian, Z.; Wang, Q. Development of a fast thermal model for calculating the temperature of the interior PMSM. Energies 2021, 14, 7455. [Google Scholar] [CrossRef]
- Chen, Q.; Liang, D.; Gao, L.; Wang, Q.; Liu, Y. Hierarchical thermal network analysis of axial-flux permanent-magnet synchronous machine for electric motorcycle. IET Electr. Power Appl. 2018, 12, 859–866. [Google Scholar] [CrossRef]
- Zheng, P.; Liu, R.; Thelin, P.; Nordlund, E.; Sadarangani, C. Research on the cooling system of a 4QT prototype machine used for HEV. IEEE Trans. Energy Convers. 2008, 23, 61–67. [Google Scholar] [CrossRef]
- Sikora, M.; Vlach, R.; Navr’atil, B. The unusual water cooling applied on small asynchronous motor. J. Eng. Mech. 2011, 18, 143–153. [Google Scholar]
- Lu, Q.; Zhang, X.; Chen, Y.; Huang, X.; Ye, Y.; Zhu, Z.Q. Modeling and investigation of thermal characteristics of a water-cooled permanent-magnet linear motor. IEEE Trans. Ind. Appl. 2015, 51, 2086–2096. [Google Scholar] [CrossRef]
- Zhang, B.; Seidler, T.; Dierken, R.; Doppelbauer, M. Development of a yokeless and segmented armature axial flux machine. IEEE Trans. Ind. Electron. 2016, 63, 2062–2071. [Google Scholar] [CrossRef]
- Semidey, S.A.; Mayor, J.R. Experimentation of an electric machine technology demonstrator incorporating direct winding heat exchangers. IEEE Trans. Ind. Electron. 2014, 61, 5771–5778. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J.; Griffo, A.; Spagnolo, A. Thermal modeling of hollow conductors for direct cooling of electrical machines. IEEE Trans. Ind. Electron. 2020, 67, 895–905. [Google Scholar] [CrossRef]
- Madonna, V.; Walker, A.; Giangrande, P.; Serra, F.; Gerada, C.; Galea, M. Improved thermal management and analysis for stator end-windings of electrical machines. IEEE Trans. Ind. Electron. 2019, 66, 5057–5069. [Google Scholar] [CrossRef]
- Gai, Y.; Kimiabeigi, M.; Chong, Y.; Widmer, J.; Goss, J.; Andres, U.; Steven, A.; Staton, D. On the measurement and modeling of the heat transfer coefficient of a hollow-shaft rotary cooling system for a traction motor. IEEE Trans. Ind. Appl. 2018, 54, 5978–5987. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Fan, X.; Li, D.; Qu, R. Comparison of two hollow-shaft liquid cooling methods for high speed permanent magnet synchronous machines. In Proceedings of the 2020 IEEE Energy Conversion Congress & Expo, Detroit, MI, USA, 11–15 October 2020; pp. 3511–3517. [Google Scholar]
- Gai, Y.; Widmer, J.; Steven, A.; Chong, Y.; Kimiabeigi, M.; Goss, J.; Popescu, M. Numerical and experimental calculation of CHTC in an oil-based shaft cooling system for a high-speed high-power PMSM. IEEE Trans. Ind. Electron. 2020, 67, 4371–4380. [Google Scholar] [CrossRef]
- Shen, Y.; Jin, C. Water cooling system analysis of permanent magnet traction motor of mining electric-drive dump truck. SAE Tech. Pap. Ser. 2014, 1, 662. [Google Scholar]
- Ponomarev, P.; Polikarpova, M.; Pyrhönen, J. Thermal modeling of directly-oil-cooled permanent magnet synchronous machine. In Proceedings of the 2012 XXth IEEE International Conference on Electrical Machine (ICEM), Marseille, France, 2–5 September 2012; pp. 1882–1887. [Google Scholar]
- Xu, Z.; Rocca, A.; Arumugam, P.; Pickering, S.; Gerada, C.; Bozhko, S.; Gerada, D.; Zhang, H. A semi-flooded cooling for a high speed machine: Concept, design and practice of an oil sleeve. In Proceedings of the 43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 8557–8562. [Google Scholar]
- Camilleri, R.; Beard, P.; Howey, D.; McCulloch, M. Prediction and measurement of the heat transfer coefficient in a direct oil-cooled electrical machine with segmented stator. IEEE Trans. Ind. Electron. 2018, 65, 94–102. [Google Scholar] [CrossRef]
- Li, Z.; Lin, R.; Longyao, T. Heat transfer characteristics of spray evaporative cooling system for large electrical machines. In Proceedings of the 18th International Conference on Electrical Machines and Systems (ICEMS), Pattaya, Thailand, 25–28 October 2015; pp. 1740–1743. [Google Scholar]
- Chong, Y.; Goss, J.; Popescu, M.; Staton, D.; Liu, C.; Gerada, D.; Xu, Z.; Gerada, C. Experimental characterisation of radial oil spray cooling on a stator with hairpin windings. In Proceedings of the 10th IET International Conference on Power Electronics, Machines and Drives (PEMD), Online, 15–17 December 2020; pp. 879–884. [Google Scholar]
- Liu, C.; Xu, Z.; Gerada, D.; Li, J.; Gerada, C.; Chong, Y.; Popescu, M.; Goss, J.; Staton, D.; Zhang, H. Experimental investigation on oil spray cooling with hairpin windings. IEEE Trans. Ind. Electron. 2020, 67, 7343–7353. [Google Scholar] [CrossRef]
- Ghahfarokhi, P.; Podgornovs, A.; Kallaste, A.; Vaimann, T.; Belahcen, A.; Cardoso, A. Oil spray cooling with hairpin windings in high-performance electric vehicle motors. In Proceedings of the 2021 28th International Workshop on Electric Drives: Improving Reliability of Electric Drives (IWED), Moscow, Russia, 27–29 January 2021; pp. 1–5. [Google Scholar]
- Liu, C.; Gerada, D.; Xu, Z.; Chong, Y.; Michon, M.; Goss, J.; Li, J.; Gerada, C.; Zhang, H. Estimation of oil spray cooling heat transfer coefficients on hairpin windings with reduced-parameter models. IEEE Trans. Transp. Electr. 2021, 7, 793–803. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, S.; Pauli, F.; Charrin, C.; Hameyer, K. Material compatibility of cooling oil and winding insulation system of electrical machines. In Proceedings of the 2022 XXVth IEEE International Conference on Electrical Machine (ICEM), Valencia, Spain, 5–8 September 2022. [Google Scholar]
- El-Refaie, A.M.; Alexander, J.P.; Galioto, S.; Reddy, P.B.; Huh, K.; Bock, P. Advanced high-power-density interior permanent magnet motor for traction applications. IEEE Trans. Ind. Appl. 2014, 50, 3235–3248. [Google Scholar] [CrossRef]
- Zytek. Available online: http://www.zytekautomotive.co.uk (accessed on 1 April 2014).
- Sizov, G.Y.; Lonel, D.M.; Demerdash, N.A.O. Modeling and parametric design of permanent-magnet AC machines using computationally efficient-finite element analysis. IEEE Trans. Ind. Electron. 2012, 59, 2403–2413. [Google Scholar] [CrossRef]
- Duan, Y.; Ionel, D.M. A review of recent developments in electrical machine design optimization methods with a permanent magnet synchronous motor benchmark study. IEEE Trans. Ind. Appl. 2013, 49, 1268–1275. [Google Scholar] [CrossRef]
- Liang, D. Critical Temperature Estimation for Permanent Magnet Synchronous Machines. Ph.D. Thesis, Department of Electronic and Electrical Engineering, The University of Sheffield, Sheffield, UK, 2022. [Google Scholar]
- Armor, A.F. Transient, three-dimensional, finite-element analysis of heat flow in turbine-generator rotors. IEEE Trans. Power Appar. Syst. 1980, PAS-99, 934–946. [Google Scholar] [CrossRef]
- JSOL. JMAG-Designer (v19). Available online: https://www.jmag-international.com/products/jmag-designer/index_v190/ (accessed on 16 January 2020).
- Ansys, Inc. ANSYS (2022 R2). Available online: https://www.ansys.com/ (accessed on 1 May 2021).
- Jungreuthmayer, C.; Baeuml, T.; Winter, O.; Ganchev, M.; Kapeller, H.; Haumer, A.; Kral, C. A detailed heat and fluid flow analysis of an internal permanent magnet synchronous machine by means of computational fluid dynamics. IEEE Trans. Ind. Electron. 2012, 59, 4568–4578. [Google Scholar] [CrossRef]
- Hao, L.; Namuduri, C.; Gopalakrishnan, S.; Mavuru, C.; Atluri, P.; Nehl, T.W. PM-assisted synchronous reluctance machine drive system for micro-hybrid application. IEEE Trans. Ind. Appl. 2019, 55, 4790–4799. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, J.; Wang, B. Transient 3-D lumped parameter and 3-D FE thermal models of a PMASynRM under fault conditions with asymmetric temperature distribution. IEEE Trans. Ind. Electron. 2012, 68, 4623–4633. [Google Scholar] [CrossRef]
- Fawzal, A.; Cirstea, R.; Gyftakis, K.; Woolmer, T.; Dickison, M.; Blundell, M. Fan performance analysis for rotor cooling of axial flux permanent magnet machines. IEEE Trans. Ind. Appl. 2017, 53, 3295–3304. [Google Scholar] [CrossRef]
- Nasiri-Zarandi, R.; Ghaheri, A.; Abbaszadeh, K. Thermal modeling and analysis of a novel transverse flux HAPM generator for small-scale wind turbine application. IEEE Trans. Energy Convers. 2020, 35, 445–453. [Google Scholar] [CrossRef]
- Le, W.; Lin, M.; Lin, K.; Jia, L.; Wang, S. A Rotor cooling enhanced method for axial flux permanent magnet synchronous machine with housing-cooling. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar] [CrossRef]
- Fan, X.; Zhang, B.; Qu, R.; Li, D.; Li, J.; Huo, Y. Comparative thermal analysis of IPMSMs with integral-slot distributed-winding (ISDW) and fractional-slot concentrated-winding (FSCW) for electric vehicle application. IEEE Trans. Ind. Appl. 2019, 55, 3577–3588. [Google Scholar] [CrossRef]
- Du, G.; Huang, N.; He, H.; Lei, G.; Zhu, J. Parameter design for a high-speed permanent magnet machine under multiphysics constraints. IEEE Trans. Energy Convers. 2020, 35, 2025–2035. [Google Scholar] [CrossRef]
- Ou, J.; Liu, Y.; Doppelbauer, M. Comparison study of a surface-mounted PM rotor and an interior PM rotor made from amorphous metal of high-speed motors. IEEE Trans. Ind. Electron. 2021, 68, 9148–9159. [Google Scholar] [CrossRef]
- He, T.; Zhu, Z.Q.; Xu, F.; Bin, H.; Wu, D.; Gong, L.; Chen, J.T. Comparative study of 6-slot/2-pole high-speed permanent magnet motors with different winding configurations. IEEE Trans. Ind. Appl. 2021, 57, 5864–5875. [Google Scholar] [CrossRef]
- Christopher, M. End Winding Cooling Modelling in Electric Machines. Ph.D. Thesis, The University of Nottingham, Nottingham, UK, 2006. [Google Scholar]
- Nakahama, T.; Biswas, D.; Kawano, K.; Ishibashi, F. Improved cooling performance of large motors using fans. IEEE Trans. Energy Convers. 2006, 21, 324–331. [Google Scholar] [CrossRef]
- Nachouane, A.B.; Abdelli, A.; Friedrich, G.; Vivier, S. Numerical study of convective heat transfer in the end regions of a totally enclosed permanent magnet synchronous machine. IEEE Trans. Ind. Appl. 2017, 53, 3538–3547. [Google Scholar] [CrossRef]
- Acquaviva, A.; Wallmark, O.; Grunditz, E.A.; Lundmark, S.T.; Thiringer, T. Computationally efficient modeling of electrical machines with cooling jacket. IEEE Trans. Transp. Electr. 2019, 5, 618–629. [Google Scholar] [CrossRef]
- Howey, D.A.; Holmes, A.S.; Pullen, K.R. Measurement and CFD prediction of heat transfer in air-cooled disc-type electrical machines. IEEE Trans. Ind. Appl. 2011, 47, 1716–1723. [Google Scholar] [CrossRef] [Green Version]
- Chong, Y.C.; Staton, D.; Gai, Y.; Adam, H.; Popescu, M. Review of advanced cooling systems of modern electric machines for Emobility application. In Proceedings of the IEEE Workshop on Electrical Machine Design, Control and Diagnostics, Modena, Italy, 8–9 April 2021; pp. 149–154. [Google Scholar]
- Dong, J.; Huang, Y.; Jin, L.; Guo, B.; Lin, H.; Dong, J.; Cheng, M.; Yang, H. Electromagnetic and thermal analysis of open-circuit air cooled high-speed permanent magnet machines with gramme ring windings. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Wrobel, R.; Mellor, P.H. A general cuboidal element for three-dimensional thermal modelling. IEEE Trans. Magn. 2010, 46, 3197–3200. [Google Scholar] [CrossRef]
- Simpson, N.; Wrobel, R.; Mellor, P.H. A general arc-segment element for three-dimensional thermal modeling. IEEE Trans. Magn. 2014, 50, 265–268. [Google Scholar] [CrossRef]
- Dong, T.; Zhang, X.; Zhou, F.; Zhao, B. Correction of winding peak temperature detection in high-frequency automotive electric machines. IEEE Trans. Ind. Electron. 2020, 67, 5615–5625. [Google Scholar] [CrossRef]
- Corey, C.; Wink, W. 3D thermal network modeling for axial-flux permanent magnet machines with experimental validation. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition, Vancouver, BC, Canada, 10–14 October 2021; pp. 4059–4066. [Google Scholar]
- Zhang, F.; Gerada, D.; Xu, Z.; Zhang, X.; Tighe, C.; Zhang, H.; Liang, Y.; Gerada, C. Electrical machine slot thermal condition effects on back iron extension thermal benefits. IEEE Trans. Transp. Electr. 2021, 7, 2927–2938. [Google Scholar] [CrossRef]
- Cai, X.; Cheng, M.; Zhu, S.; Zhang, J. Thermal modeling of flux-switching permanent-magnet machines considering anisotropic conductivity and thermal contact resistance. IEEE Trans. Ind. Electron. 2016, 63, 3355–3365. [Google Scholar] [CrossRef]
- González, A. Development of a Multidisciplinary and Optimized Design Mythology for Surface Permanent Magnets Synchronous Machines. Ph.D. Thesis, Universidad de Santiago de Compostela, Santiago de Compostela, Galicia, Spain, 2014. [Google Scholar]
- Lee, B.; Kim, K.; Jung, J.; Hong, J.; Kim, Y. Temperature estimation of IPMSM using thermal equivalent circuit. IEEE Trans. Magn. 2012, 48, 2949–2952. [Google Scholar] [CrossRef]
- Li, G.; Ojeda, J.; Hoang, E.; Gabsi, M.; Lecrivain, M. Thermal–electromagnetic analysis for driving cycles of embedded flux-switching permanent-magnet motors. IEEE Trans. Veh. Technol. 2012, 61, 140–151. [Google Scholar] [CrossRef] [Green Version]
- Gerling, D.; Dajaku, G. Novel lumped parameter thermal model for electrical systems. In Proceedings of the 11th European Conference on Power Electronics and Applications, Dresden, Germany, 11–14 September 2005; pp. 1–10. [Google Scholar]
- Gerling, D.; Dajaku, G. Thermal calculation of systems with distributed heat generation. In Proceedings of the 10th Intersociety Conference on Phenomena in Electronics Systems, San Diego, CA, USA, 30 May–2 June 2006; pp. 645–652. [Google Scholar]
- Qi, J.; Zhu, Z.Q.; Yan, L.; Jewell, G.; Gan, C.; Ren, Y.; Brockway, S.; Hilton, C. Suppression of torque ripple for consequent pole PM machine by asymmetric pole shaping method. IEEE Trans. Ind. Appl. 2022, 58, 3545–3557. [Google Scholar] [CrossRef]
- Soderberg, C.R. Steady flow of heat in large turbine-generators. Trans. Am. Inst. Electr. Eng. 1931, 50, 782–798. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the effective magnetic permeability of multiphase materials. J. Appl. Phys. 1962, 33, 3125–3131. [Google Scholar] [CrossRef]
- Simpson, N.; Wrobel, R.; Mellor, P.H. Estimation of equivalent thermal parameters of impregnated electrical windings. IEEE Trans. Ind. Appl. 2013, 49, 2505–2515. [Google Scholar] [CrossRef]
- Farag, S.; Bartheld, R.; Habetler, T. An integrated on-line motor protection system. IEEE Trans. Ind. Appl. 1996, 2, 21–26. [Google Scholar] [CrossRef]
- Hou, Z.; Guo, G. Wireless rotor temperature measurement system based on MSP430 and nRF401. In Proceedings of the International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008; pp. 858–861. [Google Scholar]
- Mejuto, C.; Mueller, M.; Shanel, M.; Mebarki, A.; Reekie, M.; Staton, D. Improved synchronous machine thermal modelling. In Proceedings of the 2008 18th IEEE International Conference on Electrical Machine (ICEM), Vilamoura, Portugal, 6–9 September 2008; pp. 1–6. [Google Scholar]
- Ganchev, M.; Umschaden, H.; Kapeller, H. Rotor temperature distribution measuring system. In Proceedings of the IEEE 37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011; pp. 2006–2011. [Google Scholar]
- Ganchev, M.; Kral, C.; Wolbank, T.M. Compensation of speed dependence in sensorless rotor temperature estimation for permanent-magnet synchronous motor. IEEE Trans. Ind. Appl. 2013, 49, 2487–2495. [Google Scholar] [CrossRef]
- Ichikawa, S.; Tomita, M.; Doki, S.; Okuma, S. Sensorless control of permanent-magnet synchronous motors using online parameter identification based on system identification theory. IEEE Trans. Ind. Electron. 2006, 53, 363–372. [Google Scholar] [CrossRef]
- Inoue, Y.; Yamada, K.; Morimoto, S.; Sanada, M.S. Effectiveness of voltage error compensation and parameter identification for model-based sensorless control of IPMSM. IEEE Trans. Ind. Appl. 2009, 45, 213–221. [Google Scholar] [CrossRef]
- Choi, J.-W.; Sul, S.-K. Inverter output voltage synthesis using novel dead time compensation. IEEE Trans. Power Electron. 1996, 11, 221–227. [Google Scholar] [CrossRef]
- Kim, H.-W.; Youn, M.-J.; Cho, K.-Y.; Kim, H.-S. Nonlinearity estimation and compensation of PWM VSI for PMSM under resistance and flux linkage uncertainty. IEEE Trans. Contr. Syst. Technol. 2006, 14, 589–601. [Google Scholar]









































| Property | Ferrite | AlNiCo* | SmCo* | NdFeB |
|---|---|---|---|---|
| [T] | 0.2~0.46 | 1.1~1.3 | 0.8~1.2 | 1.1~1.5 |
| [kA/m] | 210~360 | 50~150 | 1300~2400 | 880~2300 |
| [kJ/m3] | 6.5~42 | 35~80 | 140~260 | 250~400 |
| [°C] | 180~300 | 450~525 | 250 | 130~230 |
| [%/°C] | −0.2 | −0.03 | −0.06~−0.02 | −0.15~−0.1 |
| [%/°C] | 0.2~0.5 | 0.2 | −0.4~−0.2 | −0.6~−0.4 |
| ρ [Ω⋅cm]×10−6 | 104 | 50−80 | 50–90 | 110–170 |
| Ref. | Cooling Methods | Thermal Analysis | Online Temperature Estimation | Remarks | ||||
|---|---|---|---|---|---|---|---|---|
| Passive | Active | Hybrid | Convection | Conduction | Electrical Parameters | Thermal Models | ||
| [19] | ✓ | ✓ | ✓ | -- | -- | -- | -- | Specific to direct-drive PM generator. |
| [20] | ✓ | ✓ | -- | -- | -- | -- | -- | Analyses of reliability and cost issues. |
| [21] | ✓ | ✓ | -- | -- | -- | -- | -- | Review of both electrical machine and power electronics device thermal management. |
| [22,23,24] | ✓ | ✓ | ✓ | ✓ | -- | -- | -- | Specific to traction applications and summary of CHT* coefficient equations. |
| [25] | -- | -- | -- | -- | -- | ✓ | ✓ | Review of electrical parameters, low order and neural network models. |
| [26] | ✓ | ✓ | ✓ | -- | -- | -- | -- | Focusing on hybrid cooling systems on the basis of forced air and liquid cooling. |
| [27] | ✓ | ✓ | -- | -- | -- | -- | -- | Summary of relationships between different cooling systems and machine power. |
| [28] | ✓ | ✓ | -- | -- | -- | -- | -- | Focusing on additive manufacturing approaches. |
| [29] | ✓ | -- | -- | -- | -- | -- | -- | Review of thermo-conductive materials used for winding insulation system. |
| [30] | ✓ | -- | -- | ✓ | ✓ | -- | -- | Review of uncertain thermal parameters and CHT coefficient equations. |
| [31,32] | ✓ | -- | -- | -- | -- | -- | -- | Applications of heat pipes in electrical machine cooling system. |
| [33] | -- | -- | -- | -- | -- | ✓ | -- | Online temperature monitoring based on electrical-parameter estimation. |
| This paper | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Comprehensive review of thermal analysis and management with focus on hotspot temperature. |
| Features | Passive | Forced Air | Forced Liquid | ||||
|---|---|---|---|---|---|---|---|
| Indirect | Direct | ||||||
| Frame or Stator Core | Winding | Shaft | Immersed | Spray oil | |||
| Winding hotspot reduction |    |    |    |    |    |    |    |
| PM hotspot reduction |    |    |    |    |    |    |    |
| Overall effectiveness |    |    |    |    |    |    |    |
| Low complexity |    |    |    |    |    |    |    |
| Low cost |    |    |    |    |    |    |    |
| Maintenance |    |    |    |    |    |    |    |
| Corrosion/leakage risks |    |    |    |    |    |    |    |
 : Poor.
: Poor.  : Medium.
: Medium.  : Excellent.
: Excellent.| “T-type” LPTM | Hybrid Thermal Model | Thermal FEA | |
|---|---|---|---|
| Active-winding | |||
| Average temperature [°C] | 122.9 | 115.0 | 114.6 |
| Hotspot temperature [°C] | Not predictable | 127.6 | 127.8 |
| End-winding | |||
| Average temperature [°C] | 123.2 | 128.2 | 128.4 |
| Hotspot temperature [°C] | Not predictable | 139.7 | 139.3 |
| “T-type” LPTM | Hybrid Thermal Model | Thermal FEA | |
|---|---|---|---|
| Surface-mounted PM [60] | |||
| Average temperature [°C] | 164.7 | 162.8 | 162.9 |
| Hotspot temperature [°C] | Not predictable | 167.7 | 168.0 |
| Interior PM [63] | |||
| Average temperature [°C] | 165.5 | 164.7 | 165.1 |
| Hotspot temperature [°C] | Not predictable | 167.9 | 168.0 |
| Component | Ref. | Modelling Plane | Coordinates | Boundary Condition | Analytical Solution |
|---|---|---|---|---|---|
| Active-winding | [66,85] | r-θ plane | Polar | Dirichlet () | Exponential × cosine (sine) |
| End-winding | [66,85] | x-y plane | Cylindrical | Dirichlet () | Hyperbolic × cosine (sine) |
| Cartesian | Dirichlet () | Bessel function × cosine (sine) | |||
| SPM | [60,61] | r-θ plane | Polar | Robin () Neumann (θ = θ1/2, PM) Dirichlet () | Polynomial + logarithm |
| r-z plane | Cartesian | Dirichlet () | Hyperbolic × cosine (sine) | ||
| SPM with sleeve | [62] | r-θ plane | Polar | Continuities of temperature and heat flux | Polynomial + logarithm |
| IPM | [63] | x-z plane | Cartesian | Dirichlet () Neumann (x = w1/2, PM) | Polynomial |
| y-z plane | Cartesian | Dirichlet () | Hyperbolic × cosine (sine) |
| Feature | Numerical Techniques | LPTM | Hybrid Thermal Model |
|---|---|---|---|
| Accuracy | High | Relatively low | High |
| Complex structure | Capable | Medium | Incapable |
| Computational burden | High | Low | Low |
| Modelling complexity | High | Low | Low |
| Estimation of hotspot | Capable | Incapable | Capable |
| Generality | High | High | Medium |
| Ref. | Approximation Formulae |
|---|---|
| [34] | |
| [37] | |
| [17] | |
| [14] | |
| [215] | |
| [216] |
| Feature | ATM | SDTMs |
|---|---|---|
| Governing equation | Conduction heat transfer equation | |
| Boundary condition | Transient/steady-state condition (Table 7) | |
| Loss model | Distributed loss generation | |
| Form of solution | Fourier series with exponential function | Linear equation system |
| Dependency of accuracy | Accumulated eigenvalues | Mesh grid |
| Features | Electrical Parameter Based | Thermal Model Based | ||
|---|---|---|---|---|
| Requirement of thermal sensors |  | Unnecessary |  | At least one sensor |
| Difficulty of setup or implementation |  | Easily integrated |  | Knowledge of thermal properties |
| Applicability of different PM machines |  | Salient-/nonsalient-pole |  | Required individual modelling |
| Feasibility in entire speed-torque range |  | Rotor speed dependent |  | Feasible in the entire range |
| Capability of multiple temperature estimation |  | Only coil and PM |  | All components |
| Robustness against measurement errors, parameter variations |  | Sensitive |  | Robust |
| Disturbance of drive system |  | Disturbances (injected signal) |  | No disturbance |
| Capability of hotspot tracking |  | Only average temperatures of coil and PM |  | Conventional white-box LPTM |
 | Low-order grey-box (possible) | |||
 | Synergized white-box | |||
 : Poor.
: Poor.  Medium.
Medium. : Excellent.
: Excellent.Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.-Q.; Liang, D. Perspective of Thermal Analysis and Management for Permanent Magnet Machines, with Particular Reference to Hotspot Temperatures. Energies 2022, 15, 8189. https://doi.org/10.3390/en15218189
Zhu Z-Q, Liang D. Perspective of Thermal Analysis and Management for Permanent Magnet Machines, with Particular Reference to Hotspot Temperatures. Energies. 2022; 15(21):8189. https://doi.org/10.3390/en15218189
Chicago/Turabian StyleZhu, Zi-Qiang, and Dawei Liang. 2022. "Perspective of Thermal Analysis and Management for Permanent Magnet Machines, with Particular Reference to Hotspot Temperatures" Energies 15, no. 21: 8189. https://doi.org/10.3390/en15218189
APA StyleZhu, Z.-Q., & Liang, D. (2022). Perspective of Thermal Analysis and Management for Permanent Magnet Machines, with Particular Reference to Hotspot Temperatures. Energies, 15(21), 8189. https://doi.org/10.3390/en15218189









