Thermal Cloaking in Nanoscale Porous Silicon Structure by Molecular Dynamics
Abstract
:1. Introduction
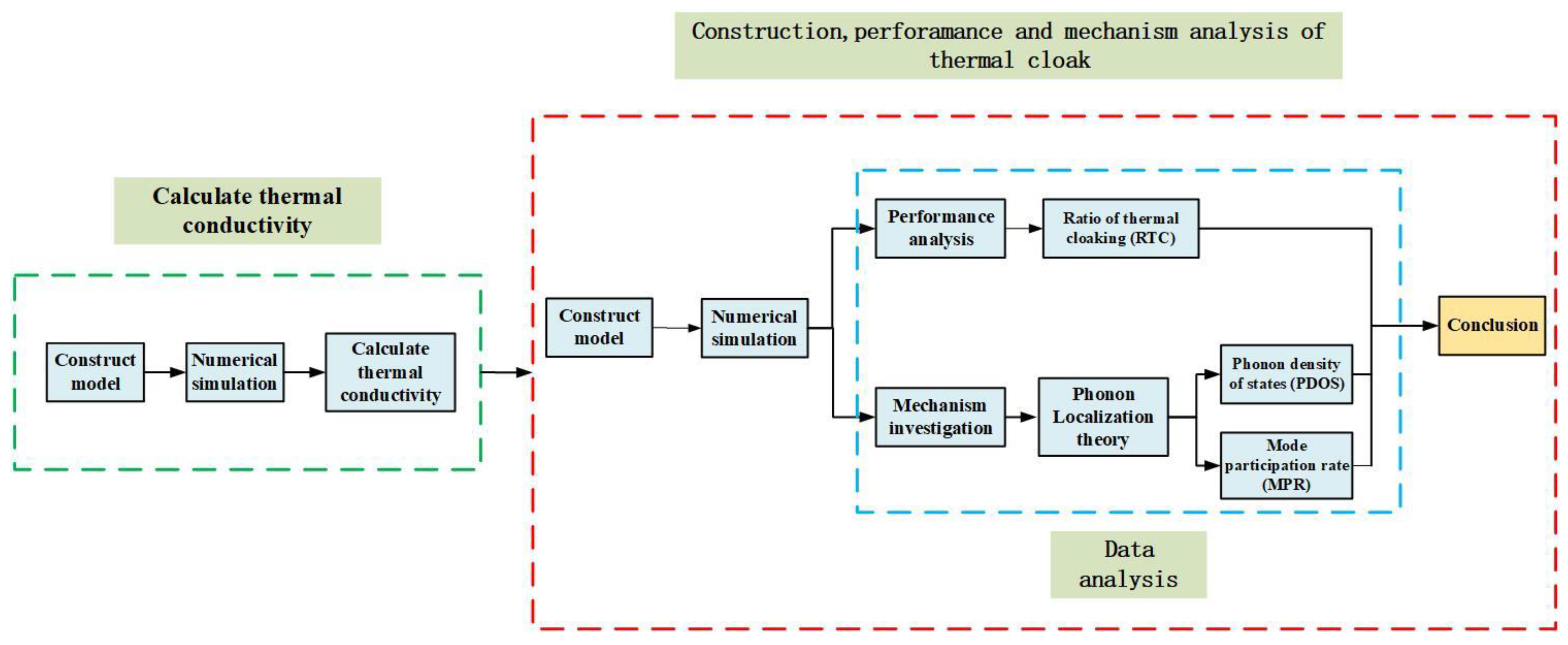
2. Model and Methodology
2.1. Construction of Computational Models
2.2. Methodology
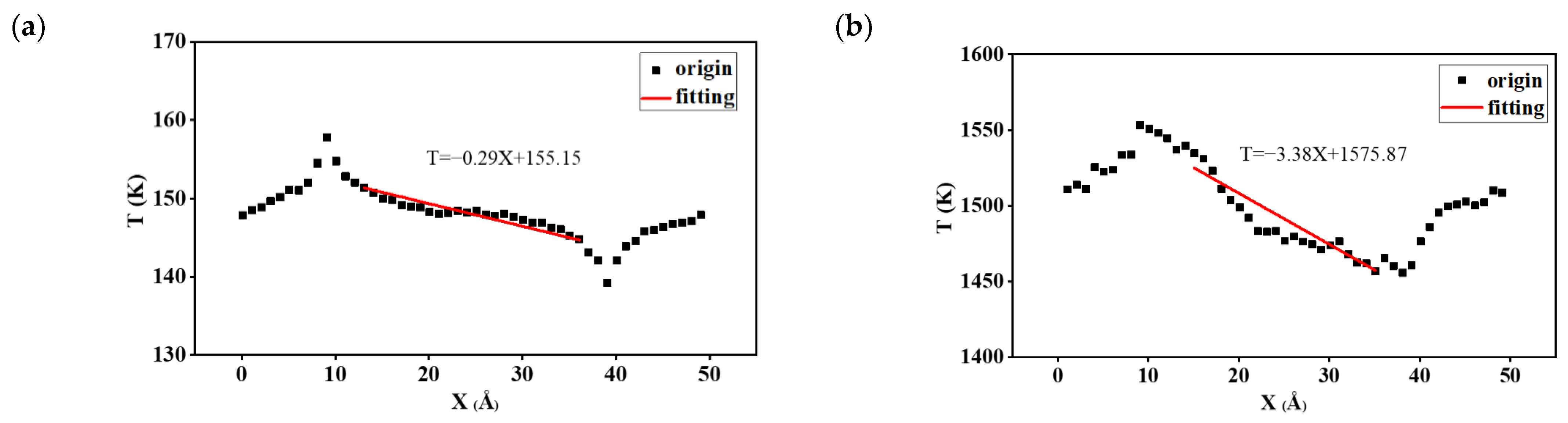
2.2.1. Thermal Conductivity Calculation
2.2.2. Heat Flux and Temperature Calculation
2.2.3. Phonon Localization Theory
2.3. Simulation Process
3. Results and Discussion
3.1. The Thermal Conductivity
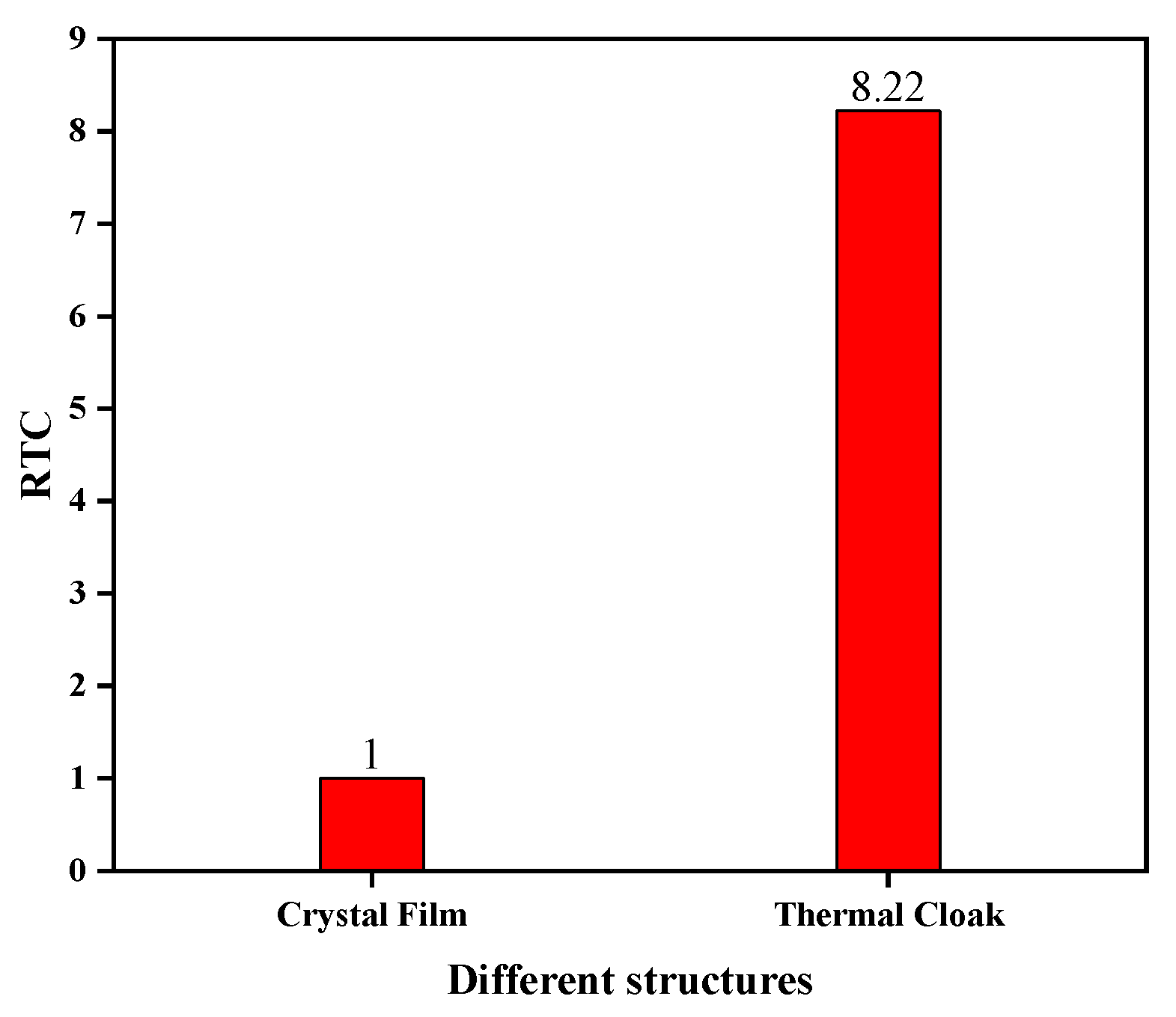
3.2. The Calculation of Thermal Cloak Performance
3.3. Analysis of Cloaking Mechanism of Nanocloak
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fan, C.Z.; Gao, Y.; Huang, J.P. Shaped graded materials with an apparent negative thermal conductivity. Appl. Phys. Lett. 2008, 92, 251907. [Google Scholar] [CrossRef]
- Han, T.C.; Zhao, J.J.; Yuan, T.; Lei, D.Y.; Li, B.W.; Qiu, C.W. Theoretical realization of an ultra-efficient thermal-energy harvesting cell made of natural materials. Energy Environ. Sci. 2013, 6, 3537–3541. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.Z.; Huang, L.J.; Chen, F.; Xu, W.K. Heat flux and temperature field cloaks for arbitrarily shaped objects. J. Phys. D Appl. Phys. 2013, 46, 305102. [Google Scholar] [CrossRef]
- Han, T.C.; Bai, X.; Gao, D.L.; Thong, J.T.L.; Li, B.W.; Qiu, C.W. Experimental Demonstration of a Bilayer Thermal Cloak. Phys. Rev. Lett. 2014, 112, 054302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, D.M.; Xu, H.G.; Zhang, Y.M.; Zhang, B.L. Active thermal cloak. Appl. Phys. Lett. 2015, 107, 121901. [Google Scholar] [CrossRef]
- Han, T.C.; Bai, X.; Liu, D.; Gao, D.L.; Li, B.W.; Thong, J.T.L.; Qiu, C.W. Manipulating Steady Heat Conduction by Sensu-shaped Thermal Metamaterials. Sci. Rep. 2015, 5, 10242. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, T.Z.; Bai, X.; Gao, D.L.; Wu, L.Z.; Li, B.W.; Thong, J.T.L.; Qiu, C.W. Invisible Sensors: Simultaneous Sensing and Camouflaging in Multiphysical Fields. Adv. Mater. 2015, 27, 7752–7758. [Google Scholar] [CrossRef] [Green Version]
- Li, T.H.; Zhu, D.L.; Mao, F.C.; Huang, M.; Yang, J.J.; Li, S.B. Design of diamond-shaped transient thermal cloaks with homogeneous isotropic materials. Front. Phys. 2016, 11, 110503. [Google Scholar] [CrossRef]
- Shen, X.Y.; Li, Y.; Jiang, C.R.; Ni, Y.S.; Huang, J.P. Thermal cloak-concentrator. Appl. Phys. Lett. 2016, 109, 031907. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.L.; Huang, S.Y.; Wang, M.; Hu, R.; Luo, X.B. While rotating while cloaking. Phys. Lett. A 2019, 383, 759–763. [Google Scholar] [CrossRef]
- Zhu, Z.; Ren, X.C.; Sha, W.; Xiao, M.; Hu, R.; Luo, X.B. Inverse design of rotating metadevice for adaptive thermal cloaking. Int. J. Heat Mass Transf. 2021, 176, 121417. [Google Scholar] [CrossRef]
- Hu, R.; Wei, X.L.; Hu, J.Y.; Luo, X.B. Local heating realization by reverse thermal cloak. Sci. Rep. 2014, 4, 3600. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Lei, D.Y. Experimental Realization of Extreme Heat Flux Concentration with Easy-to-Make Thermal Metamaterials. Sci. Rep. 2015, 5, 11552. [Google Scholar] [CrossRef]
- Guenneau, S.; Amra, C. Anisotropic conductivity rotates heat fluxes in transient regimes. Opt. Express 2013, 21, 6578–6583. [Google Scholar] [CrossRef]
- Han, T.C.; Bai, X.; Thong, J.T.L.; Li, B.W.; Qiu, C.W. Full Control and Manipulation of Heat Signatures: Cloaking, Camouflage and Thermal Metamaterials. Adv. Mater. 2014, 26, 1731–1734. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.Z.; Su, Y.S.; Xu, W.K.; Yang, X.D. Transient thermal camouflage and heat signature control. Appl. Phys. Lett. 2016, 109, 121905. [Google Scholar] [CrossRef]
- Wang, J.; Bi, Y.Q.; Hou, Q.W. Three-dimensional illusion thermal device for location camouflage. Sci. Rep. 2017, 7, 7541. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Bai, X.; Yang, T.Z.; Luo, H.L.; Qiu, C.W. Structured thermal surface for radiative camouflage. Nat. Commun. 2018, 9, 273. [Google Scholar] [CrossRef] [Green Version]
- Qu, Y.R.; Li, Q.; Cai, L.; Pan, M.Y.; Ghosh, P.; Du, K.K.; Qiu, M. Thermal camouflage based on the phase-changing material GST. Light Sci. Appl. 2018, 7, 26. [Google Scholar] [CrossRef] [PubMed]
- Hu, R.; Xi, W.; Liu, Y.D.; Tang, K.C.; Song, J.L.; Luo, X.B.; Wu, J.Q.; Qiu, C.W. Thermal camouflaging metamaterials. Mater. Today 2020, 45, 120–141. [Google Scholar] [CrossRef]
- Liu, Y.D.; Song, J.L.; Zhao, W.X.; Ren, X.C.; Cheng, Q.; Luo, X.B.; Fang, N.X.; Hu, R. Dynamic thermal camouflage via a liquid-crystal-based radiative metasurface. Nanophotonics 2020, 9, 855–863. [Google Scholar] [CrossRef] [Green Version]
- Zhu, N.Q.; Shen, X.Y.; Huang, J.P. Converting the patterns of local heat flux via thermal illusion device. AIP Adv. 2015, 5, 053401. [Google Scholar] [CrossRef]
- Alwakil, A.; Zerrad, M.; Bellieud, M.; Amra, C. Inverse heat mimicking of given objects. Sci. Rep. 2017, 7, 43288. [Google Scholar] [CrossRef]
- Hu, R.; Zhou, S.L.; Li, Y.; Lei, D.Y.; Luo, X.B.; Qiu, C.W. Illusion Thermotics. Adv. Mater. 2018, 30, 1707237. [Google Scholar] [CrossRef]
- Zhou, S.L.; Hu, R.; Luo, X.B. Thermal illusion with twinborn-like heat signatures. Int. J. Heat Mass Transf. 2018, 127, 607–613. [Google Scholar] [CrossRef]
- Hu, R.; Huang, S.Y.; Wang, M.; Luo, X.B.; Shiomi, J.; Qiu, C.W. Encrypted Thermal Printing with Regionalization Transformation. Adv. Mater. 2019, 31, 1807849. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.Q.; Zhang, H.C.; Zhang, X.; Jin, Y. Investigating the thermodynamic performances of TO-based metamaterial tunable cells with an entropy generation approach. Entropy 2017, 19, 538. [Google Scholar] [CrossRef] [Green Version]
- Xu, G.Q.; Zhang, H.C.; Zou, Q.; Jin, Y. Predicting and analyzing interaction of the thermal cloaking performance through response surface method. Int. J. Heat Mass Transf. 2017, 109, 746–754. [Google Scholar] [CrossRef]
- Li, Y.Y.; Zhang, H.C.; Sun, M.Y.; Zhang, Z.H.; Zhang, H.M. Environmental Response of 2D Thermal Cloak under Dynamic External Temperature Field. Entropy 2020, 22, 461. [Google Scholar] [CrossRef] [Green Version]
- Xu, G.Q.; Zhou, X.; Zhang, H.C.; Tan, H.P. Creating illusion of discrete source array by simultaneously allocating thermal and DC fields with homogeneous media. Energy Convers. Manag. 2019, 187, 546–553. [Google Scholar] [CrossRef]
- Li, Y.Y.; Zhang, H.C.; Chen, Y.J.; Zhang, D.; Huang, Z.L.; Wang, H.M. Realization and analysis of an Intelligent flux transfer regulator by allocating thermal and DC electric fields. Int. J. Heat Mass Transf. 2021, 179, 121677. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Xu, Y.; Zhang, S.C.; Duan, W.H. Model for topological phononics and phonon diode. Phys. Rev. B 2017, 96, 064106. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Cottrill, A.L.; Kunai, Y.; Toland, A.R.; Liu, P.W.; Wang, W.J.; Strano, M.S. Microscale solid-state thermal diodes enabling ambient temperature thermal circuits for energy applications. Phys. Chem. Chem. Phys. 2017, 19, 13172–13181. [Google Scholar] [CrossRef]
- Zhang, L.F.; Ren, J.; Wang, J.S.; Li, B.W. Topological Nature of the Phonon Hall Effect. Phys. Rev. Lett. 2010, 105, 225901. [Google Scholar] [CrossRef] [Green Version]
- Qin, T.; Zhou, J.H.; Shi, J.R. Berry curvature and the phonon Hall effect. Phys. Rev. B 2012, 86, 104305. [Google Scholar] [CrossRef] [Green Version]
- Li, N.B.; Ren, J.; Wang, L.; Zhang, G.; Haenggi, P.; Li, B.W. Colloquium: Phononics: Manipulating heat flow with electronic analogs and beyond. Rev. Mod. Phys. 2012, 84, 1045–1066. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.W.; Okawa, D.; Majumdar, A.; Zettl, A. Solid-state thermal rectifier. Science 2006, 314, 1121–1124. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.N.; Ruan, X.L.; Chen, Y.P. Molecular Dynamics Study of Thermal Rectification in Graphene Nanoribbons. Int. J. Thermophys. 2012, 33, 986–991. [Google Scholar] [CrossRef]
- Tian, H.; Xie, D.; Yang, Y.; Ren, T.L.; Zhang, G.; Wang, Y.F.; Zhou, C.J.; Peng, P.G.; Wang, L.G.; Liu, L.T. A Novel Solid-State Thermal Rectifier Based on Reduced Graphene Oxide. Sci. Rep. 2012, 2, 523. [Google Scholar] [CrossRef]
- Wang, Y.; Vallabhaneni, A.; Hu, J.N.; Qiu, B.; Chen, Y.P.; Ruan, X.L. Phonon Lateral Confinement Enables Thermal Rectification in Asymmetric Single-Material Nanostructures. Nano Lett. 2014, 14, 592–596. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ye, Z.Q.; Cao, B.Y. Nanoscale thermal cloaking in graphene via chemical functionalization. Phys. Chem. Chem. Phys. 2016, 18, 32952–32961. [Google Scholar] [CrossRef]
- Liu, Y.D.; Cheng, Y.H.; Hu, R.; Luo, X.B. Nanoscale thermal cloaking by in-situ annealing silicon membrane. Phys. Lett. A 2019, 383, 2296–2301. [Google Scholar] [CrossRef]
- Choe, H.S.; Prabhakar, R.; Wehmeyer, G.; Allen, F.; Lee, W.; Jin, L.; Li, Y.; Yang, P.D.; Qiu, C.W.; Dames, C.; et al. Ion Write Microthermotics: Programing Thermal Metamaterials at the Microscale. Nano Lett. 2019, 19, 3830–3837. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhang, H.C.; Li, Y.Y.; Zhang, D.; Wang, H.M. Numerical analysis on nanoscale thermal cloak in three-dimensional silicon film with circular cavities. Numer. Heat Transf. Part A Appl. 2022, 81, 1–14. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.C.; Sun, W.B.; Wang, Q. Mechanism analysis of double-layer nanoscale thermal cloak by silicon film. Colloids Surf. A Physicochem. Eng. Asp. 2022, 634, 128022. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Wang, H.; Xu, C.; Wang, Q. Performance prediction of nanoscale thermal cloak by molecular dynamics. Appl. Phys. A 2021, 127, 790. [Google Scholar] [CrossRef]
- Xiao, Y.; Chen, Q.Y.; Hao, Q. Inverse thermal design of nanoporous thin films for thermal cloaking. Mater. Today Phys. 2021, 21, 100477. [Google Scholar] [CrossRef]
- Chen, G.; Dresselhaus, M.S.; Dresselhaus, G.; Fleutial, J.P.; Caillat, T. Recent developments in thermoelectric materials. Int. Mater. Rev. 2003, 48, 45–66. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.H.; Feller, S.E.; Brooks, B.R.; Pastor, R.W. Computer simulation of liquid/liquid interfaces. I. Theory and application to octane/water. J. Chem. Phys. 1995, 103, 10252–10266. [Google Scholar] [CrossRef]
- Tersoff, J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B 1989, 39, 5566–5568. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.K.; Vu-Bac, N.; Rabczuk, T. A stochastic multiscale method for the prediction of the thermal conductivity of Polymer nanocomposites through hybrid machine learning algorithms. Compos. Struct. 2021, 273, 114269. [Google Scholar] [CrossRef]
- Rabizadeh, E.; Bagherzadeh, A.S.; Anitescu, C.; Alajlan, N.; Rabczuk, T. Pointwise dual weighted residual based goal-oriented a posteriori error estimation and adaptive mesh refinement in 2D/3D thermo-mechanical multifield problems. Comput. Methods Appl. Mech. Eng. 2020, 359, 112666. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Duong, T.X.; Lahmer, T.; Zhang, X.; Sauer, R.A.; Park, H.S.; Rabczuk, T. A NURBS-based inverse analysis for reconstruction of nonlinear deformations of thin shell structures. Comput. Methods Appl. Mech. Eng. 2018, 331, 427–455. [Google Scholar] [CrossRef] [Green Version]
- Rabczuk, T.; Ren, H.L.; Zhuang, X.Y. A Nonlocal Operator Method for Partial Differential Equations with Application to Electromagnetic Waveguide Problem. Comput. Mater. Contin. 2019, 59, 31–55. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.K.; Hu, J.W.; Wu, X.J.; Jia, P.; Peng, Z.H.; Chen, K.Q. Tunable Thermal Rectification in Graphene/Hexagonal Boron Nitride Hybrid Structures. J. Phys. D 2018, 51, 396–400. [Google Scholar] [CrossRef]
- Loh, G.C.; Teo, E.H.T.; Tay, B.K. Phonon localization around vacancies in graphene nanoribbons. Diam. Relat. Mater. 2012, 23, 88–92. [Google Scholar] [CrossRef]
- Jiang, P.F.; Hu, S.Q.; Ouyang, Y.L.; Ren, W.J.; Ren, C.Q.; Zhang, Z.W.; Chen, J. Remarkable thermal rectification in pristine and symmetric monolayer graphene enabled by asymmetric thermal contact. J. Appl. Phys. 2020, 127, 235101. [Google Scholar] [CrossRef]
- Lu, S.; Ouyang, Y.L.; Yu, C.Q.; Jiang, P.F.; He, J.; Chen, J. Tunable phononic thermal transport in two-dimensional C6CaC6 via guest atom intercalation. J. Appl. Phys. 2021, 129, 225106. [Google Scholar] [CrossRef]
- Liang, T.; Zhou, M.; Zhang, P.; Yuan, P.; Yang, D.G. Multilayer in-plane graphene/hexagonal boron nitride heterostructures: Insights into the interfacial thermal transport properties. Int. J. Heat Mass Transf. 2020, 151, 119395. [Google Scholar] [CrossRef]
- Wu, X.; Han, Q. Thermal transport in pristine and defective two-dimensional polyaniline (C3N). Int. J. Heat Mass Transf. 2021, 173, 121235. [Google Scholar] [CrossRef]
- Zhou, M.; Liang, T.; Wu, B.Y.; Liu, J.J.; Zhang, P. Phonon transport in antisite-substituted hexagonal boron nitride nanosheets: A molecular dynamics study. J. Appl. Phys. 2020, 128, 234304. [Google Scholar] [CrossRef]
- Loh, G.C.; Teo, E.H.T.; Tay, B.K. Phononic and structural response to strain in wurtzite-gallium nitride nanowires. J. Appl. Phys. 2012, 111, 103506. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Li, H.P.; Zhang, R.Q. Anomalous effect of hydrogenation on phonon thermal conductivity in thin silicon nanowires. Eur. Lett. 2014, 105, 56003. [Google Scholar] [CrossRef]
- Ma, D.K.; Ding, H.R.; Meng, H.; Feng, L.; Wu, Y.; Shiomi, J.; Yang, N. Nano-cross-junction effect on phonon transport in silicon nanowire cages. Phys. Rev. B 2016, 94, 165434. [Google Scholar] [CrossRef] [Green Version]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhang, H.; Li, Y.; Wang, Q.; Sun, W. Thermal Cloaking in Nanoscale Porous Silicon Structure by Molecular Dynamics. Energies 2022, 15, 1827. https://doi.org/10.3390/en15051827
Zhang J, Zhang H, Li Y, Wang Q, Sun W. Thermal Cloaking in Nanoscale Porous Silicon Structure by Molecular Dynamics. Energies. 2022; 15(5):1827. https://doi.org/10.3390/en15051827
Chicago/Turabian StyleZhang, Jian, Haochun Zhang, Yiyi Li, Qi Wang, and Wenbo Sun. 2022. "Thermal Cloaking in Nanoscale Porous Silicon Structure by Molecular Dynamics" Energies 15, no. 5: 1827. https://doi.org/10.3390/en15051827
APA StyleZhang, J., Zhang, H., Li, Y., Wang, Q., & Sun, W. (2022). Thermal Cloaking in Nanoscale Porous Silicon Structure by Molecular Dynamics. Energies, 15(5), 1827. https://doi.org/10.3390/en15051827






