Investigating the Capability of PD-Type Recognition Based on UHF Signals Recorded with Different Antennas Using Supervised Machine Learning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup for Partial Discharge Measurements
2.2. Selection of Features and Classification Method Applied
3. Results and Discussion
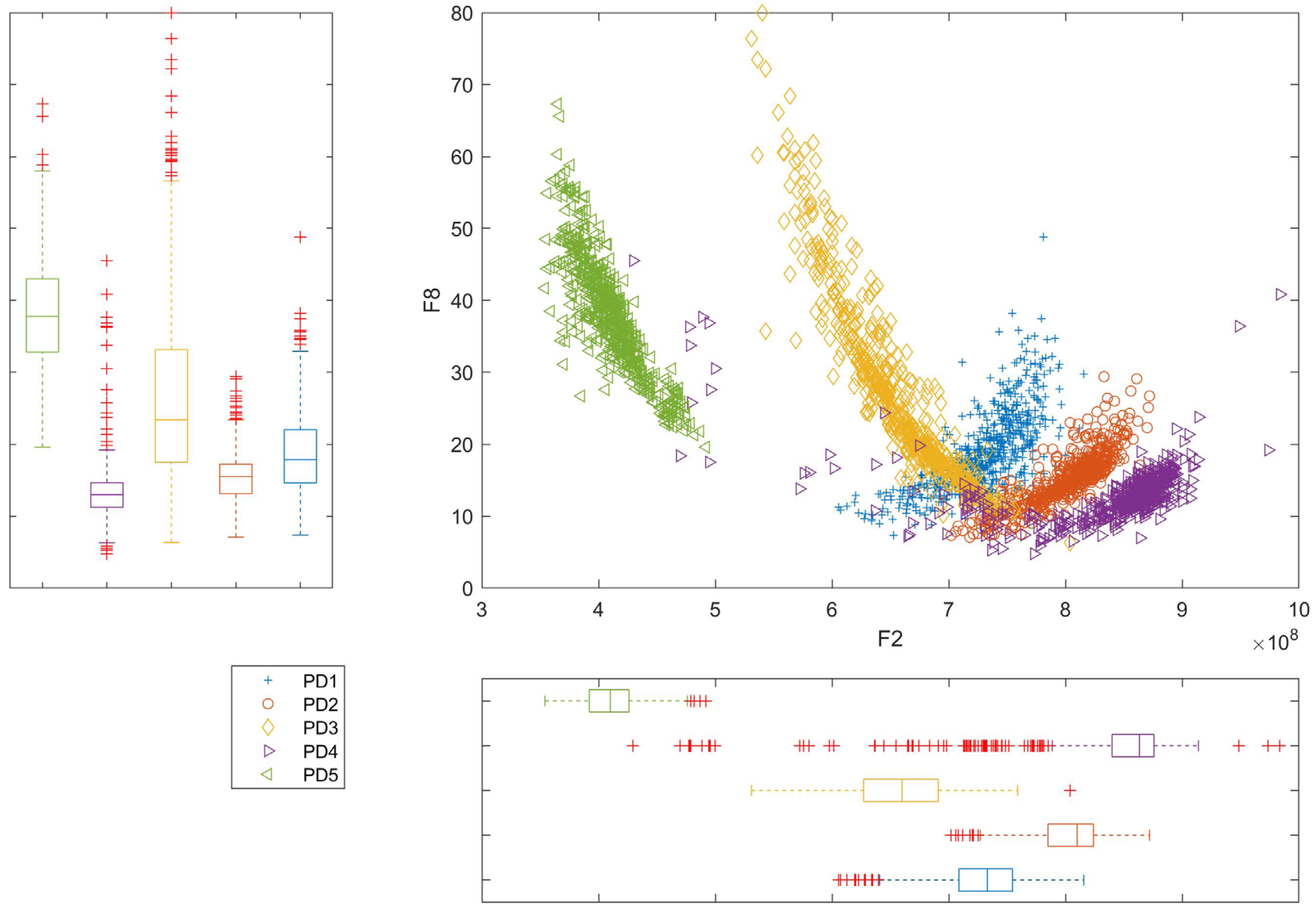
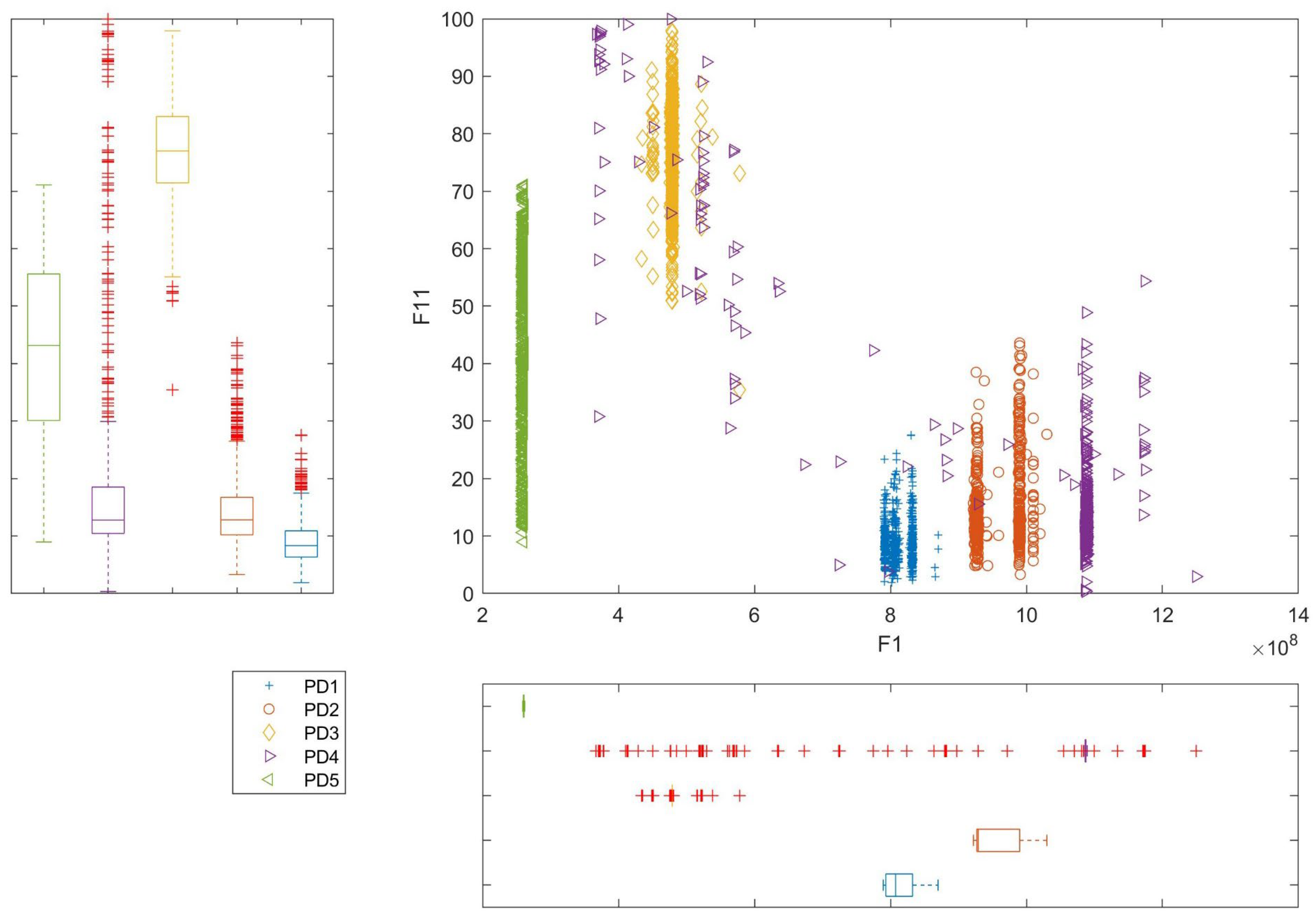
3.1. Single Feature Analysis
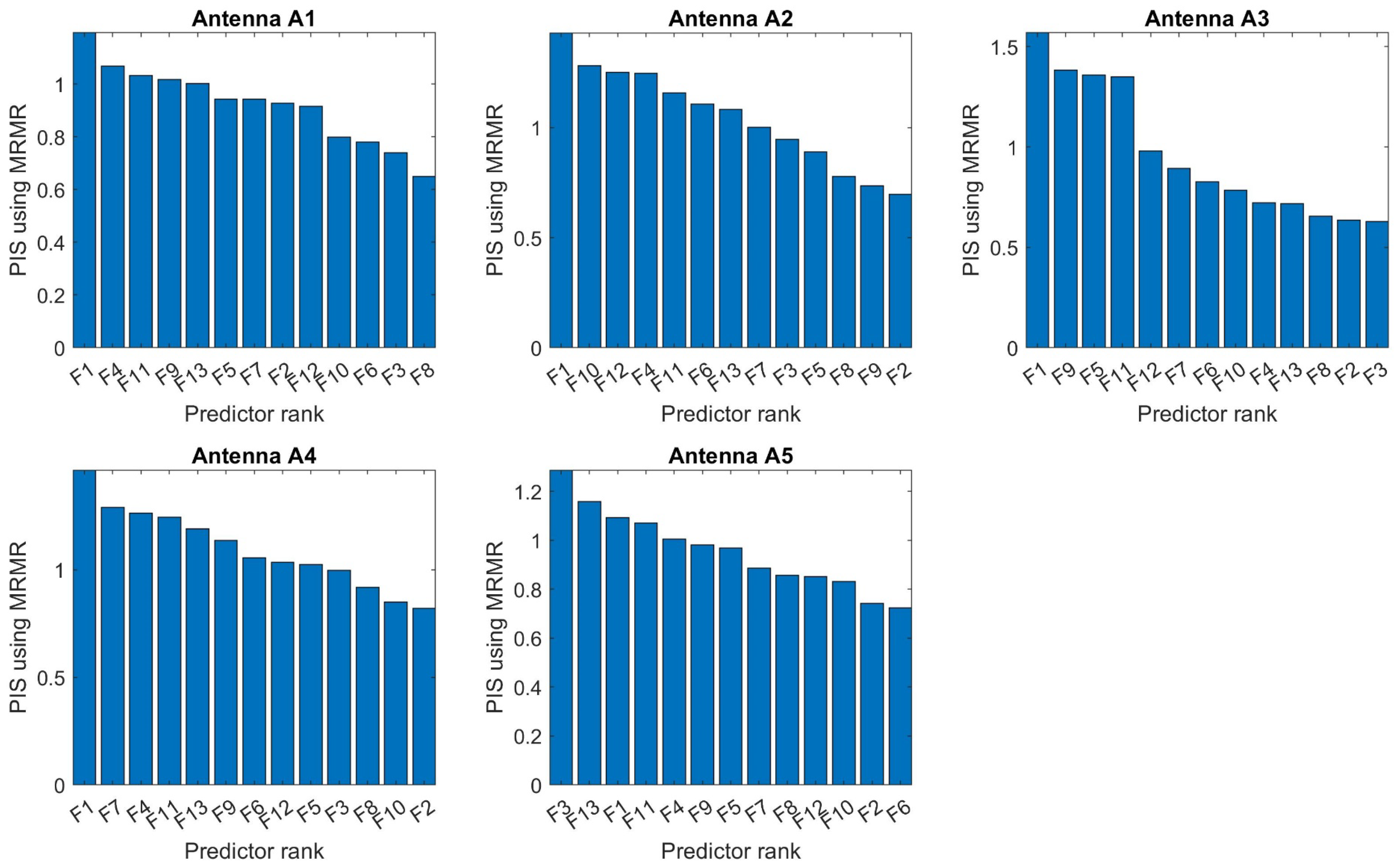
3.2. Feature Analysis According to MRMR
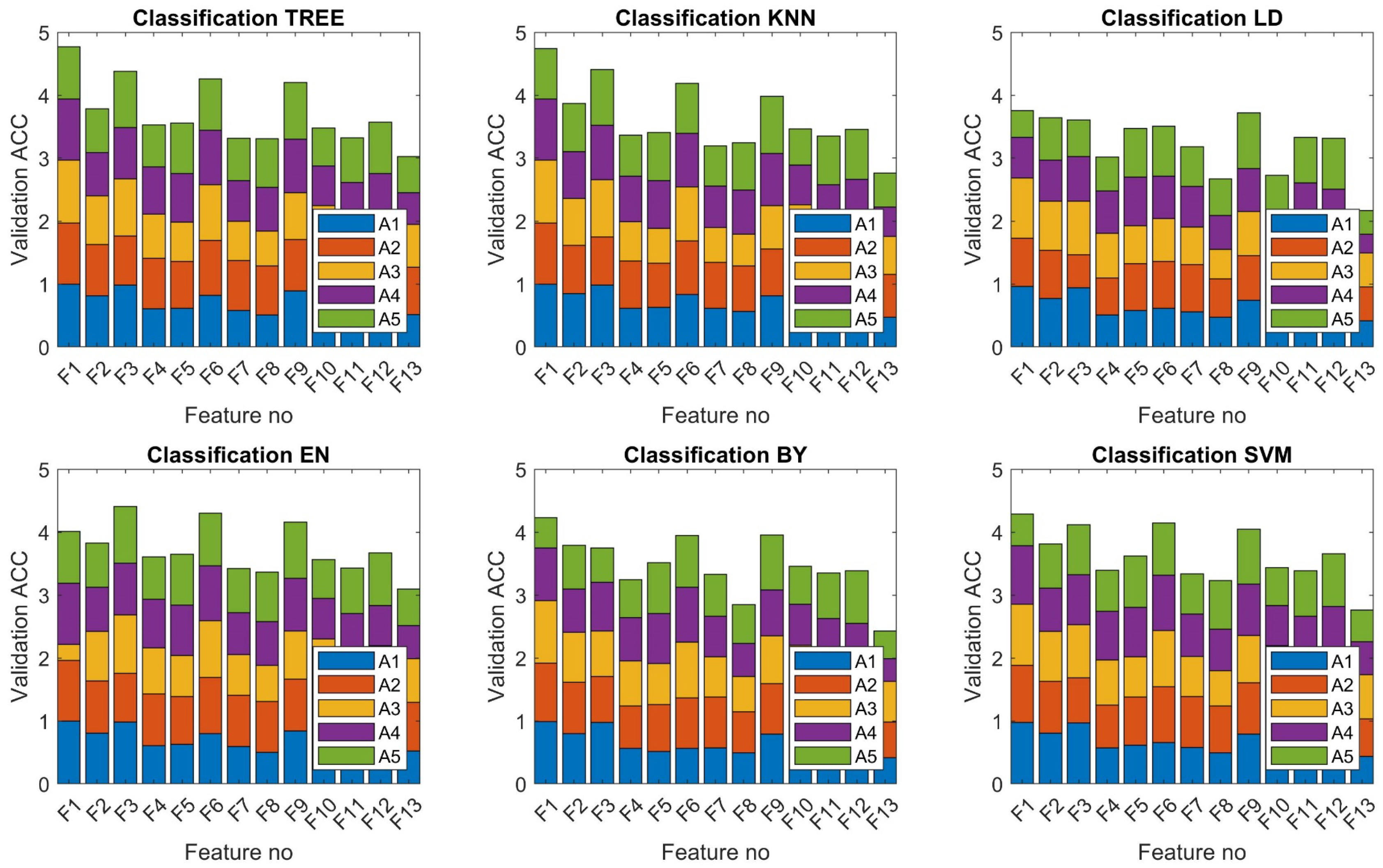
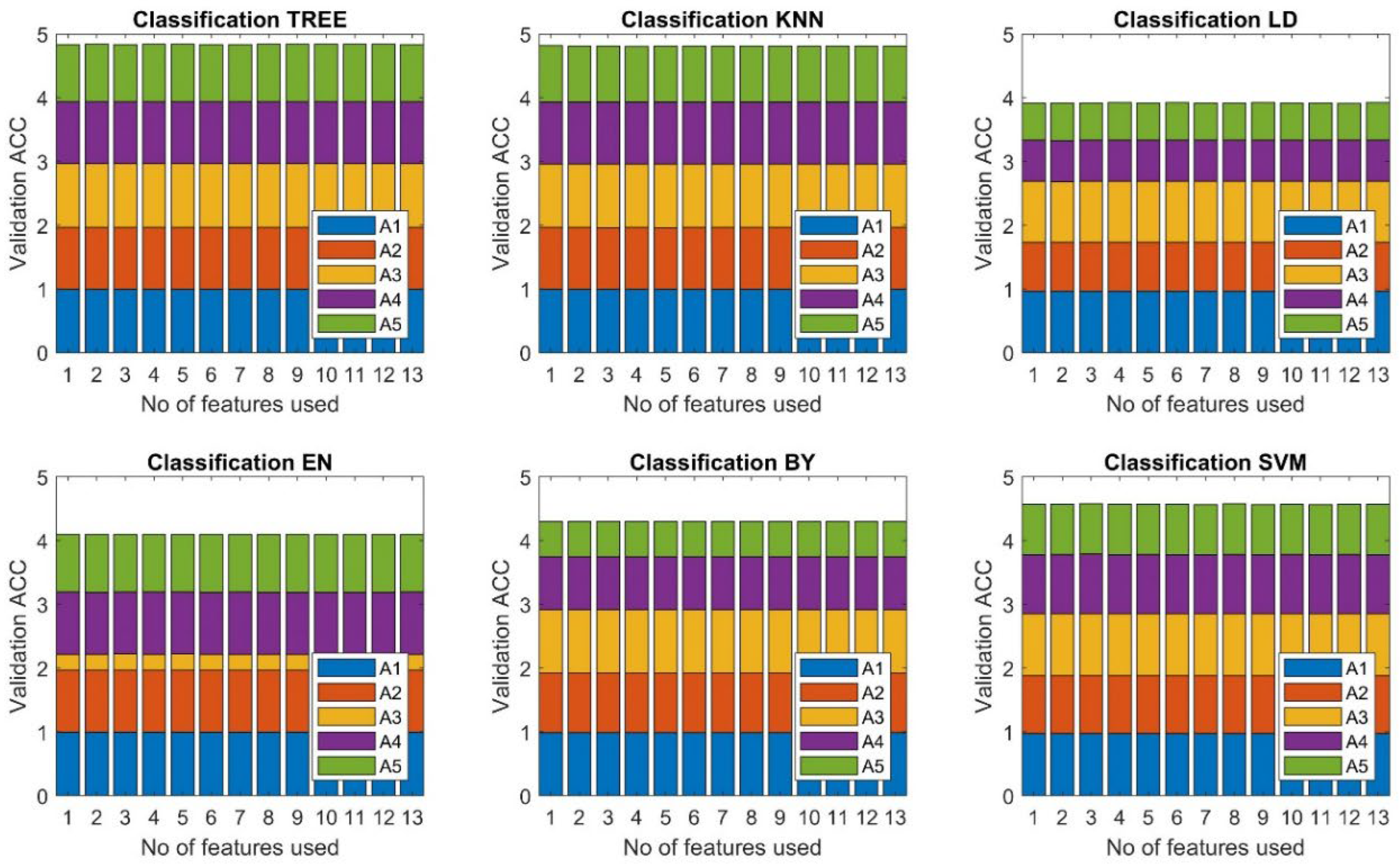
3.3. Evaluation of Classification Performance
4. Conclusions
- Relatively high scores of efficiency measures were calculated for the feature representing peak frequency (F1). When applied as a predictor using the TREE and KNN algorithm, it allowed for classifications with accuracy exceeding 94%.
- Application of features F3, F6, and F9 resulted in accuracies exceeding 80%.
- Application of the MRMR method enabled reduction of the number of features from 13 to 1 while maintaining very high effectiveness. Best scores were achieved for two features.
- The highest efficiency (100%) was obtained for the broadband log-periodic antenna intended for research purposes. Comparably high efficiency of defect recognition was obtained for antennas installed in the dielectric window of the transformer tank. For these types of antennas, the efficiency was 99.3% for the UHF disk antenna, 97.5% for the Hilbert curve fractal antenna, and 97.2% for the meandered planar inverted-F antenna, respectively. Slightly lower efficiency (89.7%) was obtained for the monopole antenna installed in the oil drain valve.
- The high values of both ACC and MCC and Kappa coefficients indicate that the data set was well-balanced.
- Accuracies above 99.7% were obtained for the PD1 recorded with A1 and A3, and for PD2 recorded with A1, A2, and A3.
- Classification of PD5 was performed with 100% accuracy regardless of the type of antenna.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, M.; Cao, H.; Cao, J.; Nguyen, H.L.; Gomes, J.B.; Krishnaswamy, S.P. An Overview of state-of-the-art partial discharge analysis techniques for condition monitoring. IEEE Electr. Insul. Mag. 2015, 31, 22–35. [Google Scholar] [CrossRef]
- Tenbohlen, S.; Jagers, J.; Vahidi, F.; Bastos, G.; Desai, B.; Diggin, B.; Fuhr, J.; Gebauer, J.; Krüger, M.; Lapworth, J.; et al. Transformer Reliability Survey; Technical Brochure 642; CIGRE: Paris, France, 2015. [Google Scholar]
- International Electrotechnical Commission (IEC). IEC TS 62478:2016, High Voltage Test Techniques—Measurement of Partial Discharges by Electromagnetic and Acoustic Methods; International Electrotechnical Commission (IEC): Geneva, Switzerland, 2016. [Google Scholar]
- IEEE Guide for the Detection. Location and Interpretation of Sources of Acoustic Emissions from Electrical Discharges in Power Transformers and Power Reactors; IEEE Std C57.127-2018 (Revision of IEEE Std C57.127-2007); IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Bakar, N.; Abu-Siada, A.; Islam, S. A review of dissolved gas analysis measurement and interpretation techniques. IEEE Electr. Insul. Mag. 2014, 30, 39–49. [Google Scholar] [CrossRef]
- Cruz, J.d.N.; Serres, A.J.R.; de Oliveira, A.C.; Xavier, G.V.R.; de Albuquerque, C.C.R.; da Costa, E.G.; Freire, R.C.S. Bio-inspired printed monopole antenna applied to partial discharge detection. Sensors 2019, 19, 628. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mor, A.R.; Heredia, L.C.; Muñoz, F.A. A magnetic loop antenna for partial discharge measurements on GIS. Int. J. Electr. Power Energy Syst. 2020, 115, 105514. [Google Scholar]
- Szymczak, C. PIFA antenna for partial discharge detection in power transformers. Metrol. Meas. Syst. 2021, 28, 343–355. [Google Scholar] [CrossRef]
- Sikorski, W. Active Dielectric Window: A new concept of combined acoustic emission and electromagnetic partial discharge detector for power transformers. Energies 2019, 12, 115. [Google Scholar] [CrossRef] [Green Version]
- Si, W.; Fu, C.; Yuan, P. An integrated sensor with AE and UHF methods for partial discharges detection in transformers based on oil valve. IEEE Sens. Lett. 2019, 3, 1–3. [Google Scholar] [CrossRef]
- Siegel, M.; Coenen, S.; Beltle, M.; Tenbohlen, S.; Weber, M.; Fehlmann, P.; Hoek, S.M.; Kempf, U.; Schwarz, R.; Linn, T.; et al. Calibration proposal for UHF partial discharge measurements at power transformers. Energies 2019, 12, 3058. [Google Scholar] [CrossRef] [Green Version]
- Xue, N.; Yang, J.; Shen, D.; Xu, P.; Yang, K.; Zhuo, Z.; Zhang, J. The location of partial discharge sources inside power transformers based on TDOA database with UHF sensors. IEEE Access 2019, 7, 146732–146744. [Google Scholar] [CrossRef]
- Polak, F.; Sikorski, W.; Siodla, K. Location of partial discharges sources using sensor arrays. In Proceedings of the 2014 ICHVE International Conference on High Voltage Engineering and Application, Poznan, Poland, 8–11 September 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Zhou, N.; Luo, L.; Sheng, G.; Jiang, X. Direction of arrival estimation method for multiple UHF partial discharge sources based on virtual array extension. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 1526–1534. [Google Scholar] [CrossRef]
- Li, Z.; Luo, L.; Sheng, G.; Liu, Y.; Jiang, X. UHF partial discharge localisation method in substation based on dimension-reduced RSSI fingerprint. IET Gener. Transm. Distrib. 2018, 12, 398–405. [Google Scholar] [CrossRef]
- Zheng, Q.; Luo, L.; Song, H.; Sheng, G.; Jiang, X. A RSSI-AOA-based UHF partial discharge localization method using MUSIC algorithm. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Karami, H.; Azadifar, M.; Mostajabi, A.; Rubinstein, M.; Karami, H.; Gharehpetian, G.B.; Rachidi, F. Partial discharge localization using time reversal: Application to power transformers. Sensors 2020, 20, 1419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karami, H.; Askari, F.; Rachidi, F.; Rubinstein, M.; Sikorski, W. An inverse-filter-based method to locate partial discharge sources in power transformers. Energies 2022, 15, 1988. [Google Scholar] [CrossRef]
- Sikorski, W.; Walczak, K.; Gil, W.; Szymczak, C. On-line partial discharge monitoring system for power transformers based on the simultaneous detection of high frequency, ultra-high frequency, and acoustic emission signals. Energies 2020, 13, 3271. [Google Scholar] [CrossRef]
- Raymond, W.J.K.; Illias, H.A.; Mokhlis, H. Partial discharge classifications: Review of recent progress. Measurement 2015, 68, 164–181. [Google Scholar] [CrossRef] [Green Version]
- Sinaga, H.H.; Phung, B.T.; Blackburn, T.R. Recognition of single and multiple partial discharge sources in transformers based on ultra-high frequency signals. IET Gener. Transm. Distrib. 2014, 8, 160–169. [Google Scholar] [CrossRef]
- Jineeth, J.; Mallepally, R.; Sindhu, T.K. Classification of partial discharge sources in XLPE cables by artificial neural networks and support vector machine. In Proceedings of the 2018 IEEE Electrical Insulation Conference (EIC), San Antonio, TX, USA, 17–20 June 2018; pp. 407–411. [Google Scholar]
- Tuyet-Doan, V.-N.; Do, T.-D.; Tran-Thi, N.-D.; Youn, Y.-W.; Kim, Y.-H. One-shot learning for partial discharge diagnosis using ultra-high-frequency sensor in gas-insulated switchgear. Sensors 2020, 20, 5562. [Google Scholar] [CrossRef]
- Janani, H.; Shahabi, S.; Kordi, B. Separation and classification of concurrent partial discharge signals using statistical-based feature analysis. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 1933–1941. [Google Scholar] [CrossRef]
- Zhou, L.; Yang, F.; Zhang, Y.; Hou, S. Feature extraction and classification of partial discharge signal in GIS based on Hilbert transform. In Proceedings of the 2021 International Conference on Information Control, Electrical Engineering and Rail Transit (ICEERT), Lanzhou, China, 30 October–1 November 2021; pp. 208–213. [Google Scholar]
- Tang, J.; Wang, D.; Fan, L.; Zhuo, R.; Zhang, X. Feature parameters extraction of GIS partial discharge signal with multifractal detrended fluctuation analysis. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 3037–3045. [Google Scholar] [CrossRef]
- Yang, L.; Judd, M.D. Recognising multiple partial discharge sources in power transformers by wavelet analysis of UHF signals. IEE Proc.-Sci. Meas. Technol. 2003, 150, 119–127. [Google Scholar] [CrossRef]
- Xie, Y.; Tang, J.; Zhou, Q. Feature extraction and recognition of UHF partial discharge signals in GIS based on dual-tree complex wavelet transform. Eur. Trans. Electr. Power 2010, 20, 639–649. [Google Scholar] [CrossRef]
- Dey, D.; Chatterjee, B.; Chakravorti, S.; Munshi, S. Rough-granular approach for impulse fault classification of transformers using cross-wavelet transform. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1297–1304. [Google Scholar] [CrossRef]
- Nguyen, M.-T.; Nguyen, V.-H.; Yun, S.-J.; Kim, Y.-H. Recurrent neural network for partial discharge diagnosis in gas-insulated switchgear. Energies 2018, 11, 1202. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Wang, X.; Li, X.; Yang, A.; Rong, M. Partial discharge recognition with a multi-resolution convolutional neural network. Sensors 2018, 18, 3512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zeng, F.; Lei, Z.; Yang, X.; Tang, J.; Yao, Q.; Miao, Y. Evaluating DC partial discharge with SF6 decomposition characteristics. IEEE Trans. Power Deliv. 2019, 34, 1383–1392. [Google Scholar] [CrossRef]
- Gao, J.; Zhu, Y.; Jia, Y. Pattern recognition of unknown partial discharge based on improved SVDD. IET Sci. Meas. Technol. 2018, 12, 907–916. [Google Scholar] [CrossRef]
- Han, L.; Yan, J.; Fan, S.; Xu, M.; Liu, Z.; Geng, Y.; Guan, C. Feature extraction of UHF PD signals based on diode envelope detection and linear discriminant analysis. In Proceedings of the 2019 5th International Conference on Electric Power Equipment-Switching Technology (ICEPE-ST), Kitakyushu, Japan, 13–16 October 2019; pp. 598–602. [Google Scholar]
- Li, J.; Jiang, T.; Harrison, R.F.; Grzybowski, S. Recognition of ultra high frequency partial discharge signals using multi-scale features. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1412–1420. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, S.; Shu, N. GIS partial discharge pattern recognition based on the chaos theory. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 783–790. [Google Scholar] [CrossRef]
- Chan, J.C.; Saha, T.K.; Ekanayake, C. Pattern recognition techniques and their applications for automatic classification of artificial partial discharge sources. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 468–478. [Google Scholar]
- Gao, W.; Ding, D.; Liu, W. Research on the typical partial discharge using the UHF detection method for GIS. IEEE Trans. Power Deliv. 2011, 26, 2621–2629. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Wang, X.; Rong, M.; Liu, D. Chromatic processing for feature extraction of PD-induced UHF signals in GIS. Glob. Energy Interconnect. 2020, 3, 494–503. [Google Scholar] [CrossRef]
- Harbaji, M.M.O.; Zahed, A.H.; Habboub, S.A.; Almajidi, M.A.; Assaf, M.J.; El-Hag, A.H.; Qaddoumi, N.N. Design of Hilbert fractal antenna for partial discharge classification in oil-paper insulated system. IEEE Sens. J. 2017, 17, 1037–1045. [Google Scholar] [CrossRef]
- Wu, Y.; Ding, D.; Wang, Y.; Zhou, C.; Lu, H.; Zhang, X. Defect recognition and condition assessment of epoxy insulators in gas insulated switchgear based on multi-information fusion. Measurement 2022, 190, 110701. [Google Scholar] [CrossRef]
- Darwish, A.; El-Hag, A.H.; Refaat, S.S.; Abu-Rub, H.; Toliyat, H.A. Impact of dimensionality reduction techniques on the classification of ceramic insulators defects. In Proceedings of the 2021 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Vancouver, BC, Canada, 12–15 December 2021; pp. 243–246. [Google Scholar]
- Wong, S.Y.; Ye, X.; Guo, F.; Goh, H.H. Computational intelligence for preventive maintenance of power transformers. Appl. Soft Comput. 2022, 114, 108129. [Google Scholar] [CrossRef]
- Xavier, G.V.R.; Silva, H.S.; Da Costa, E.G.; Serres, A.J.R.; Carvalho, N.B.; Oliveira, A.S.R. Detection, classification and location of sources of partial discharges using the radiometric method: Trends, challenges and open issues. IEEE Access 2021, 9, 110787–110810. [Google Scholar] [CrossRef]
- Lopez-Roldan, J.; Tang, T.; Gaskin, M. Design and testing of UHF sensors for partial discharge detection in transformers. 2008 International Conference on Condition Monitoring and Diagnosis, Beijing, China, 21–24 April 2008; pp. 1052–1055. [Google Scholar] [CrossRef]
- Beura, C.P.; Beltle, M.; Tenbohlen, S. Study of the influence of winding and sensor design on ultra-high frequency partial discharge signals in power transformers. Sensors 2020, 20, 5113. [Google Scholar] [CrossRef]
- Chai, H.; Phung, B.T.; Mitchell, S. Application of UHF Sensors in power system equipment for partial discharge detection: A review. Sensors 2019, 19, 1029. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhang, X.; Xiao, S. Antipodal vivaldi antenna to detect UHF signals that leaked out of the joint of a transformer. Int. J. Antennas Propag. 2017, 2017, 9627649. [Google Scholar] [CrossRef] [Green Version]
- Xavier, G.V.R.; Serres, A.J.R.; da Costa, E.G.; de Oliveira, A.C.; Nobrega, L.A.M.M.; de Souza, V.C. Design and application of a metamaterial superstrate on a bio-inspired antenna for partial discharge detection through dielectric windows. Sensors 2019, 19, 4255. [Google Scholar] [CrossRef] [Green Version]
- Xavier, G.V.R.; De Oliveira, A.C.; Silva, A.D.; Nobrega, L.A.; Da Costa, E.G.; Serres, A.J. Application of time difference of arrival methods in the localization of partial discharge sources detected using bio-inspired UHF sensors. IEEE Sens. J. 2020, 21, 1947–1956. [Google Scholar] [CrossRef]
- Khosronejad, M.; Gentili, G.G. Design of an archimedean spiral UHF antenna for pulse monitoring application. In Proceedings of the Loughborough Antennas and Propagation Conference (LAPC), Loughborough, UK, 2–3 November 2015; pp. 1–4. [Google Scholar]
- Wu, Q.; Liu, G.; Xia, Z.; Lu, L. The study of archimedean spiral antenna for partial discharge measurement. In Proceedings of the IVth International Conference on Intelligent Control and Information Processing (ICICIP), Beijing, China, 9–11 June 2013; pp. 694–698. [Google Scholar]
- Li, M.; Guo, C.; Peng, Z. Design of meander antenna for UHF partial discharge detection of transformers. Sens. Transducers 2014, 171, 232–238. [Google Scholar]
- Li, T.; Rong, M.; Zheng, C.; Wang, X. Development simulation and experiment study on UHF Partial Discharge Sensor in GIS. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1421–1430. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, G.; Dong, J.; Wang, J. Study on miniaturized UHF antennas for partial discharge detection in high-voltage electrical equipment. Sensors 2015, 15, 29434–29451. [Google Scholar] [CrossRef]
- Li, J.; Jiang, T.; Wang, C.; Cheng, C. Optimization of UHF Hilbert antenna for partial discharge detection of transformers. IEEE Trans. Antennas Propag. 2012, 60, 2536–2540. [Google Scholar]
- Wang, F.; Bin, F.; Sun, Q.; Fan, J.; Liang, F.; Xiao, X. A novel UHF Minkowski fractal antenna for partial discharge detection. Microw. Opt. Technol. Lett. 2017, 59, 1812–1819. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Du, L.; Cao, M.; Qian, G. An intelligent sensor for the ultra-high-frequency partial discharge online monitoring of power transformers. Energies 2016, 9, 383. [Google Scholar] [CrossRef] [Green Version]
- PD Monitoring Solution for Transformers. Available online: https://www.qualitrolcorp.com/wp-content/uploads/2019/08/Qualitrol_QPDM_Partial_Discharge_Monitor_for_Transformers.pdf (accessed on 18 February 2022).
- Sikorski, W.; Szymczak, C.; Siodła, K.; Polak, F. Hilbert curve fractal antenna for detection and on-line monitoring of partial discharges in power transformers. Eksploat. I Niezawodn. 2018, 20, 343–351. [Google Scholar] [CrossRef]
- Schwarzbeck.de. Available online: http://schwarzbeck.de/Datenblatt/k9118a.pdf (accessed on 18 February 2022).
- International Electrotechnical Commission. IEC 60270: High-Voltage Test Techniques—Partial Discharge Measurements; International Electrotechnical Commission: Geneva, Switzerland, 2015. [Google Scholar]
- Wang, D.; Du, L.; Yao, C.; Yan, J. UHF PD measurement system with scanning and comparing method. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 199–206. [Google Scholar] [CrossRef]
- Yu, X.; Jianjun, W.; Weihao, L.; Yijun, J.; Ting, X.; Jinbo, Z. Online monitoring device for partial discharge in high-voltage switchgear based on capacitance coupling method. In Proceedings of the 2019 IEEE 3rd International Conference on Green Energy and Applications (ICGEA), Taiyuan, China, 16–18 March 2019; pp. 56–60. [Google Scholar]
- Karim, E.; Memon, T.D.; Hussain, I. FPGA based on-line fault diagnostic of induction motors using electrical signature analysis. Int. J. Inf. Technol. 2019, 11, 165–169. [Google Scholar] [CrossRef]
- Kozioł, M.; Nagi, Ł.; Kunicki, M.; Urbaniec, I. Analysis of radiation in the UHF and optical range emitted by surface partial discharges. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Arivamudhan, M.; Santhi, S. FPGA Realization of FFT and DWT algorithms for the detection of transformer winding deformation. In Proceedings of the 2018 Second International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 14–15 June 2018; pp. 210–214. [Google Scholar]
- Sowmya, K.B.; Mathew, J.A. Discrete wavelet transform based on coextensive distributive computation on FPGA. Mater. Today Proc. 2018, 5, 10860–10866. [Google Scholar] [CrossRef]
- Wang, X.; Yuan, H. Wavelet decomposition transform system based on FPGA. In Proceedings of the 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 2698–2703. [Google Scholar] [CrossRef]
- Sause, M.G.; Horn, S. Simulation of acoustic emission in planar carbon fiber reinforced plastic specimens. J. Nondestruct. Eval. 2010, 29, 123–142. [Google Scholar] [CrossRef]
- Ardila-Rey, J.A.; Albarracín, R.; Álvarez, F.; Barrueto, A. A Validation of the spectral power clustering technique (SPCT) by using a Rogowski coil in partial discharge measurements. Sensors 2015, 15, 25898–25918. [Google Scholar] [CrossRef] [Green Version]
- Chiang, S.; Vankov, E.R.; Yeh, H.J.; Guindani, M.; Vannucci, M.; Haneef, Z.; Stern, J.M. Temporal and spectral characteristics of dynamic functional connectivity between resting-state networks reveal information beyond static connectivity. PLoS ONE 2018, 13, e0190220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vahidi, B.; Ghaffarzadeh, N.; Hosseinian, S.H. A wavelet-based method to discriminate internal faults from inrush currents using correlation coefficient. Int. J. Electr. Power Energy Syst. 2010, 32, 788–793. [Google Scholar] [CrossRef]
- Long, J.; Wang, X.; Zhou, W.; Zhang, J.; Dai, D.; Zhu, G. A comprehensive review of signal processing and machine learning technologies for UHF PD detection and diagnosis (I): Preprocessing and Localization Approaches. IEEE Access 2021, 9, 69876–69904. [Google Scholar] [CrossRef]
- Lu, S.; Chai, H.; Sahoo, A.; Phung, B.T. Condition monitoring based on partial discharge diagnostics using machine learning methods: A comprehensive state-of-the-art review. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 1861–1888. [Google Scholar] [CrossRef]
- Ding, C.; Peng, H. Minimum redundancy feature selection from microarray gene expression data. J. Bioinform. Comput. Biol. 2005, 3, 185–205. [Google Scholar] [CrossRef]
- Yang, W.; Wang, K.; Zuo, W. Neighborhood component feature selection for high-dimensional data. J. Comput. 2012, 7, 162–168. [Google Scholar] [CrossRef]
- Hao, L.; Lewin, P.L.; Hunter, J.A.; Swaffield, D.J.; Contin, A.; Walton, C.; Michel, M. Discrimination of multiple PD sources using wavelet decomposition and principal component analysis. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 1702–1711. [Google Scholar] [CrossRef]
- Duan, R.; Wang, F. Fault Diagnosis of on-load tap-changer in converter transformer based on time-frequency vibration analysis. IEEE Trans. Ind. Electron. 2016, 63, 3815–3823. [Google Scholar] [CrossRef]
- Wang, Y.B.; Chang, D.G.; Qin, S.R.; Fan, Y.H.; Mu, H.B.; Zhang, G.J. Separating multi-source partial discharge signals using linear prediction analysis and isolation forest algorithm. IEEE Trans. Instrum. Meas. 2020, 69, 2734–2742. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McHugh, M.L. Interrater reliability: The kappa statistic. Biochem. Med. 2012, 22, 276. [Google Scholar] [CrossRef]
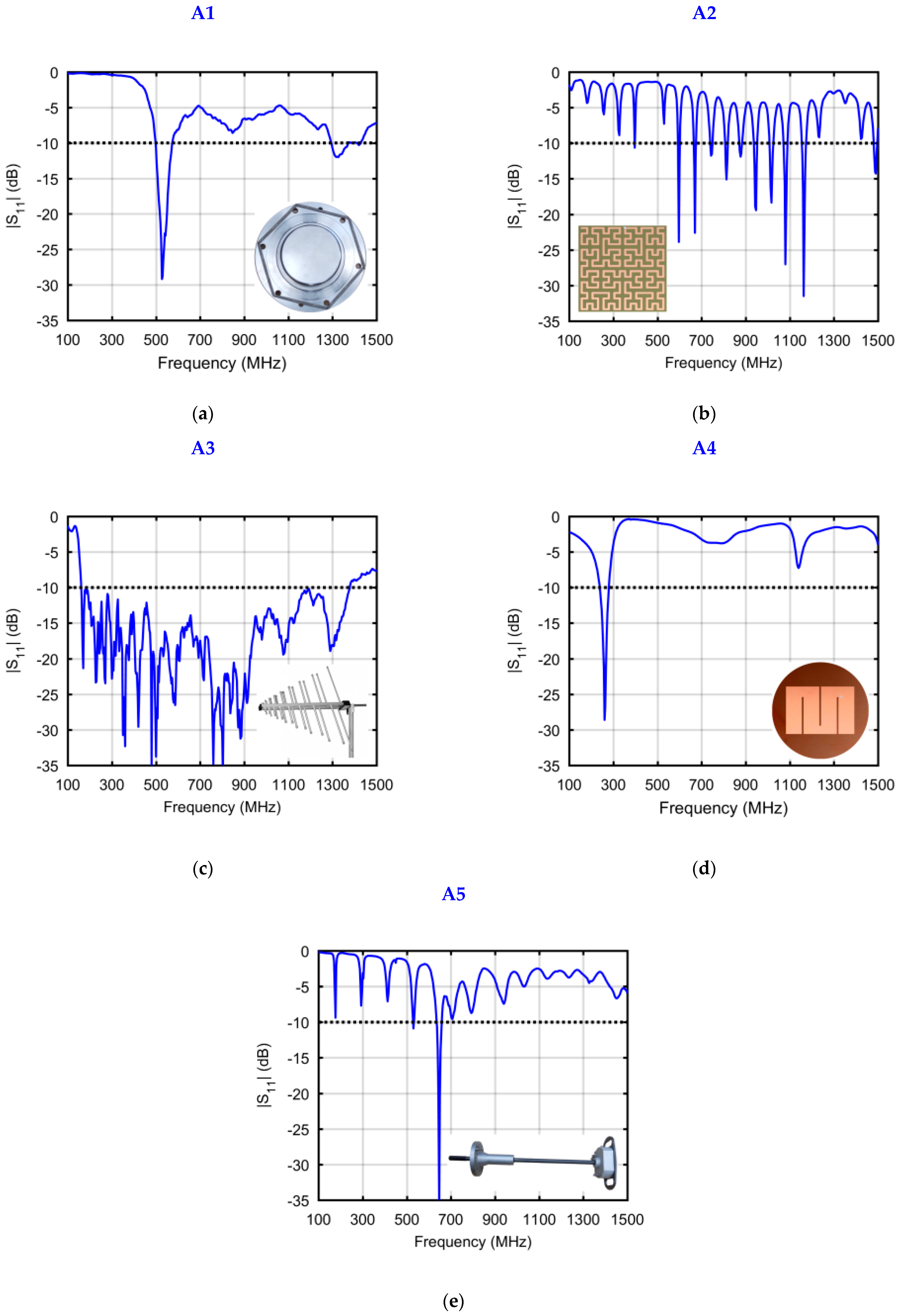




| Label | Sensor Type | Measured Bandwidth (MHz) | Largest Dimension of the Antenna Aperture L [mm] | Sensor Mounting Method | Ref. |
|---|---|---|---|---|---|
| A1 | Disk sensor type IC43 | 497–573; 1293–1427 | 150 | Dielectric window | [59] |
| A2 | Hilbert curve fractal antenna | 397; 593–603; 664–676; 740–750 807–820; 870–884; 937–953; 1007–1027; 1070–1093; 1157–1173; 1477–1497 | 110 | Dielectric window | [60] |
| A3 | Log-periodic antenna type VULP 9118 A | 160–1377 1 | 980 | N/A | [61] |
| A4 | Meandered planar inverted-F antenna | 237–280 | 100 | Dielectric window | [19] |
| A5 | UHF drain valve sensor | 527–533; 633–660 | 38 | Oil drain valve | [59] |
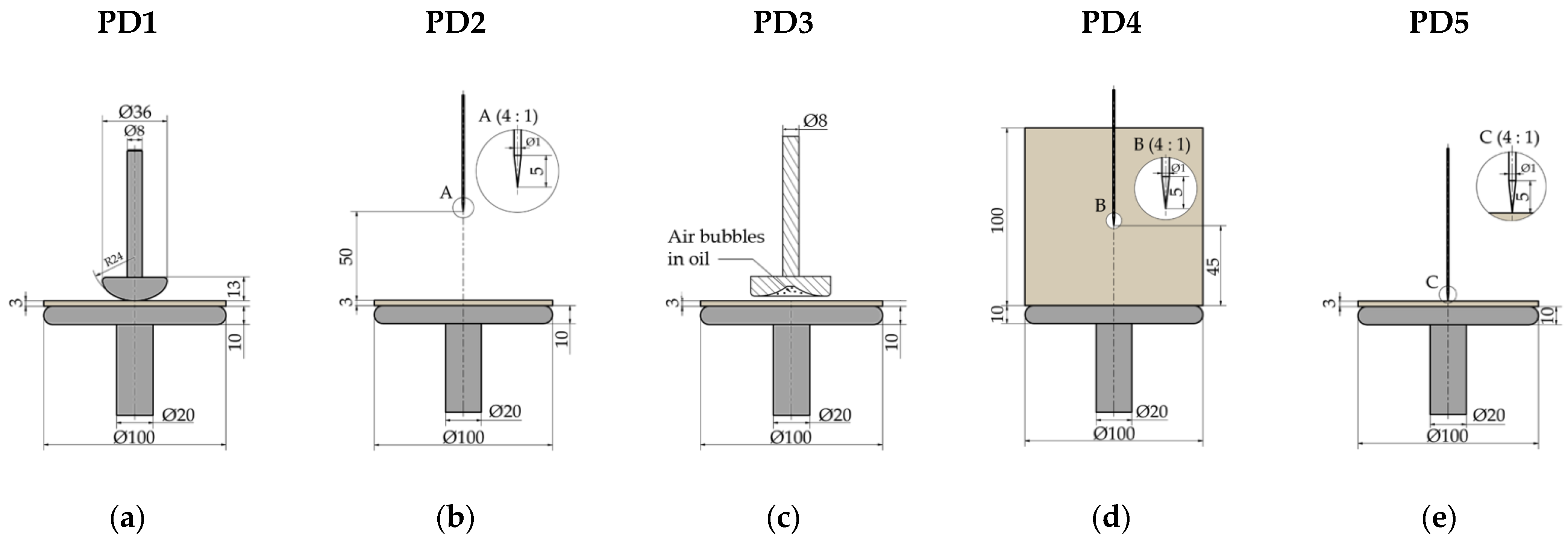
| Label | PD Type | PD Inception Voltage Ui (kV) | Test Voltage Range Ut (kV) | Max. Value of PD Apparent Charge qmax (pC) | Mean Value of PD Apparent Charge qmean (pC) | Median Value of PD Apparent Charge qmed (pC) |
|---|---|---|---|---|---|---|
| PD1 | PD in oil gap | 14.3 | 14.3–27.0 | 16,286 | 4273 | 3004 |
| PD2 | PD in oil | 24.1 | 24.1–30.2 | 2151 | 421 | 310 |
| PD3 | PD in air bubbles | 10.7 | 10.7–20.8 | 834 | 306 | 102 |
| PD4 | Surface discharges | 21.6 | 21.6–28.2 | 657 | 208 | 157 |
| PD5 | Creeping discharges | 11.9 | 11.9–24.0 | 12,971 | 1777 | 1305 |
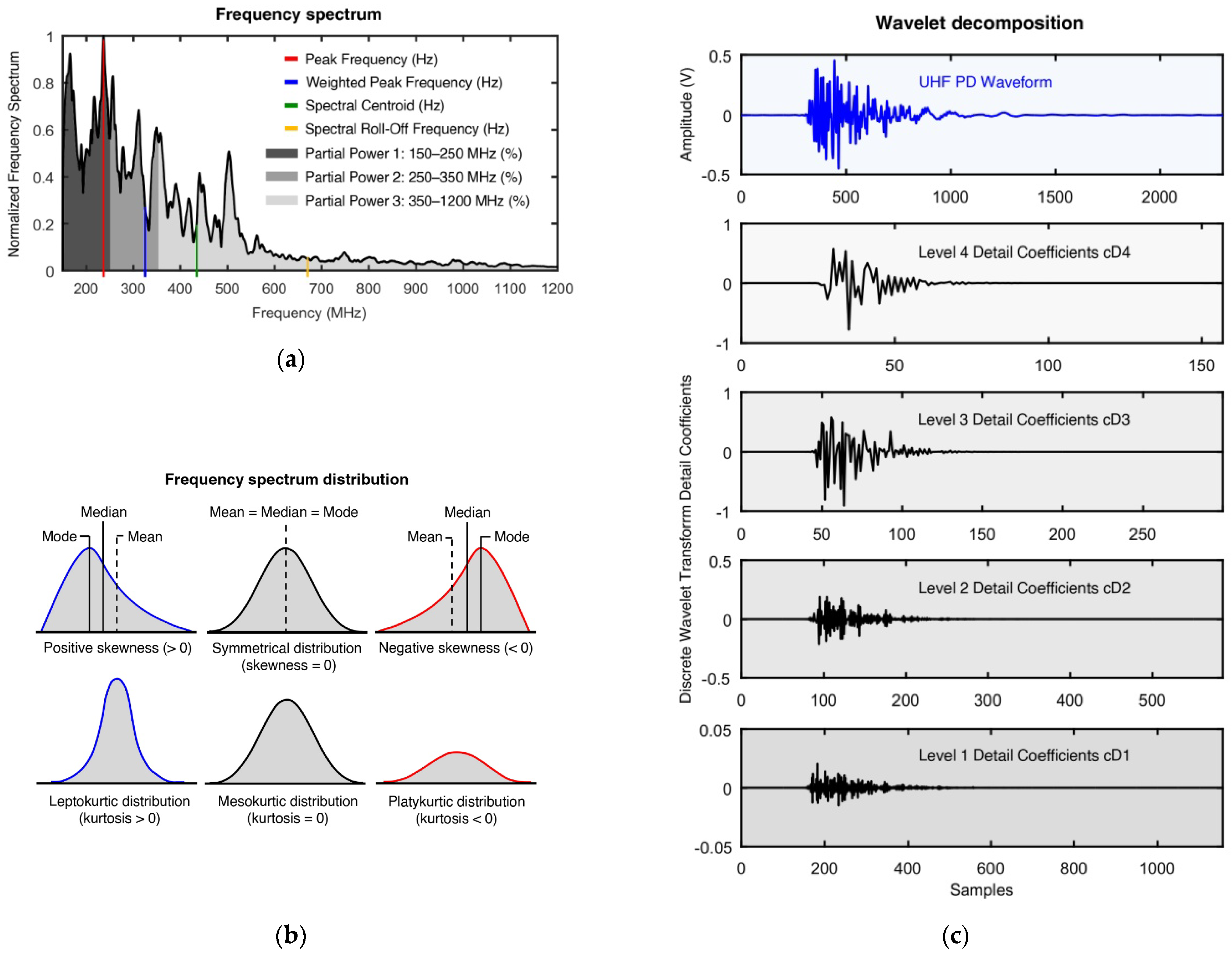
| Label | Feature | Description | Unit | Ref. |
|---|---|---|---|---|
| F1 | Peak Frequency | Frequency corresponding to the highest magnitude in the spectrum | Hz | [70] |
| F2 | Spectral Centroid | Spectral centroid indicates where the center of mass of the frequency spectrum is located | Hz | [70] |
| F3 | Weighted Peak Frequency | Geometric mean of the peak frequency and the spectral centroid | Hz | [70] |
| F4 | Partial Power 1 | This parameter specifies the percentage of the signal energy in the given frequency range (Partial Power 1: 150–250 MHz; Partial Power 2: 250–350 MHz; Partial Power 3: 350–1200 MHz) | % | [71] |
| F5 | Partial Power 2 | |||
| F6 | Partial Power 3 | |||
| F7 | Spectral Skewness | Skewness of the frequency spectrum; this feature measures the symmetry of the spectrum around its arithmetic mean | – | [72] |
| F8 | Spectral Kurtosis | Kurtosis of the frequency spectrum; this feature measures the intensity of the outlier values of the frequency spectrum distribution in relation to the intensity of the outlier values of the normal distribution curve | – | [72] |
| F9 | Spectral Roll-Off Frequency | Frequency below which 85% of the accumulated magnitude of the spectrum is concentrated | Hz | [72] |
| F10 | Energy of Detail Coefficients cD1 | This parameter specifies the percentage of the details coefficients energy of the discrete wavelet transform (DWT) at the first, second, third, and fourth decomposition level, respectively | % | [73] |
| F11 | Energy of Detail Coefficients cD2 | |||
| F12 | Energy of Detail Coefficients cD3 | |||
| F13 | Energy of Detail Coefficients cD4 |
| Averaged Accuracy Calculated for All Five Antennas | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 |
| TREE | 95.4 | 75.6 | 87.6 | 70.5 | 71.1 | 85.2 | 66.4 | 66.1 | 84.1 | 69.5 | 66.5 | 71.4 | 60.5 |
| KNN | 94.8 | 77.4 | 88.1 | 67.4 | 68.2 | 83.8 | 63.9 | 64.8 | 79.6 | 69.3 | 67.0 | 69.1 | 55.3 |
| LD | 75.1 | 72.9 | 72.2 | 60.4 | 69.5 | 70.2 | 63.7 | 53.4 | 74.3 | 54.5 | 66.6 | 66.3 | 43.3 |
| EN | 80.3 | 76.5 | 88.2 | 72.2 | 73.0 | 86.0 | 68.5 | 67.4 | 83.2 | 71.2 | 68.6 | 73.4 | 61.9 |
| BY | 84.6 | 75.8 | 75.0 | 64.9 | 70.3 | 79.0 | 66.6 | 57.0 | 79.0 | 69.1 | 67.0 | 67.7 | 48.6 |
| SVM | 85.8 | 76.3 | 82.3 | 67.9 | 72.4 | 82.9 | 66.8 | 64.6 | 80.9 | 68.7 | 67.8 | 73.1 | 55.3 |
| Average | 85.99 | 75.74 | 82.25 | 67.19 | 70.75 | 81.17 | 65.98 | 62.22 | 80.19 | 67.06 | 67.25 | 70.18 | 54.14 |
| Average Accuracies for All Features Applied Singularly | |||||
|---|---|---|---|---|---|
| TREE | KNN | LD | EN | BY | SVM |
| 74.62% | 72.98% | 64.79% | 74.63% | 69.59 | 72.67 |
| Alg. | Averages Accuracies [%] Dependent from the No of Features Applied for Classification | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| TREE | 96.7 | 96.8 | 96.7 | 96.8 | 96.8 | 96.7 | 96.7 | 96.8 | 96.8 | 96.8 | 96.8 | 96.7 | 96.7 |
| KNN | 96.3 | 96.2 | 96.3 | 96.2 | 96.3 | 96.3 | 96.3 | 96.3 | 96.3 | 96.3 | 96.3 | 96.3 | 96.3 |
| LD | 78.4 | 78.3 | 78.4 | 78.5 | 78.4 | 78.5 | 78.4 | 78.4 | 78.6 | 78.4 | 78.4 | 78.3 | 78.4 |
| EN | 81.9 | 81.8 | 81.9 | 81.9 | 81.9 | 81.8 | 81.8 | 81.9 | 81.9 | 81.9 | 81.9 | 81.9 | 81.9 |
| BY | 86.0 | 86.0 | 86.0 | 86.0 | 85.9 | 86.0 | 86.0 | 86.0 | 86.0 | 86.0 | 86.0 | 86.0 | 86.0 |
| SVM | 91.3 | 91.4 | 91.5 | 91.4 | 91.4 | 91.3 | 91.2 | 91.5 | 91.2 | 91.4 | 91.3 | 91.4 | 91.3 |
| Averaged Accuracies for the Considered Algorithms | |||||
|---|---|---|---|---|---|
| TREE | KNN | LD | EN | BY | SVM |
| 96.75% | 96.28% | 78.40% | 81.87% | 85.99% | 91.35% |
| Antenna | ACC | F1-Score | MCC | Kappa |
|---|---|---|---|---|
| A1 | 0.993 | 0.993 | 0.991 | 0.977 |
| A2 | 0.975 | 0.974 | 0.968 | 0.922 |
| A3 | 1.000 | 1.000 | 1.000 | 1.000 |
| A4 | 0.972 | 0.973 | 0.966 | 0.912 |
| A5 | 0.897 | 0.897 | 0.873 | 0.679 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wotzka, D.; Sikorski, W.; Szymczak, C. Investigating the Capability of PD-Type Recognition Based on UHF Signals Recorded with Different Antennas Using Supervised Machine Learning. Energies 2022, 15, 3167. https://doi.org/10.3390/en15093167
Wotzka D, Sikorski W, Szymczak C. Investigating the Capability of PD-Type Recognition Based on UHF Signals Recorded with Different Antennas Using Supervised Machine Learning. Energies. 2022; 15(9):3167. https://doi.org/10.3390/en15093167
Chicago/Turabian StyleWotzka, Daria, Wojciech Sikorski, and Cyprian Szymczak. 2022. "Investigating the Capability of PD-Type Recognition Based on UHF Signals Recorded with Different Antennas Using Supervised Machine Learning" Energies 15, no. 9: 3167. https://doi.org/10.3390/en15093167
APA StyleWotzka, D., Sikorski, W., & Szymczak, C. (2022). Investigating the Capability of PD-Type Recognition Based on UHF Signals Recorded with Different Antennas Using Supervised Machine Learning. Energies, 15(9), 3167. https://doi.org/10.3390/en15093167








