Investigation of the Electrochemical and Thermal Characteristics of NCM811-21700 Cylindrical Lithium-Ion Battery: A Numerical Study and Model Validation
Abstract
:1. Introduction
2. Numerical Methods
2.1. Model Description
| Electrochemical Model | Governing Equations | |
|---|---|---|
| Lithium conservation in the solid phase: | (1) | |
| Lithium conservation in the electrolyte phase: | (2) | |
| Charge conservation in solid phase: | (3) | |
| Charge conservation in the electrolyte phase: | (4) | |
| The Butler–Volmer equation: | The current flux at the active material pore-wall surface due to lithium intercalation reaction as a function of over-potential η: | |
| (5) | ||
| where η is defined by: | ||
| (6) | ||
| and i0 is the exchange current density defined by: | ||
| (7) | ||
| Effective properties: | (8) | |
| (9) | ||
| (10) | ||
| (11) | ||
| (12) | ||
| (13) | ||
| (14) | ||
| Thermal model | Governing equations | |
| The energy conservation equation | (15) | |
| (16) | ||
| (17) | ||
| (18) | ||
| (19) | ||
| (20) | ||
2.2. Model Parameters
2.3. Mesh, Boundary Conditions, and Initial Conditions
3. Results and Discussion
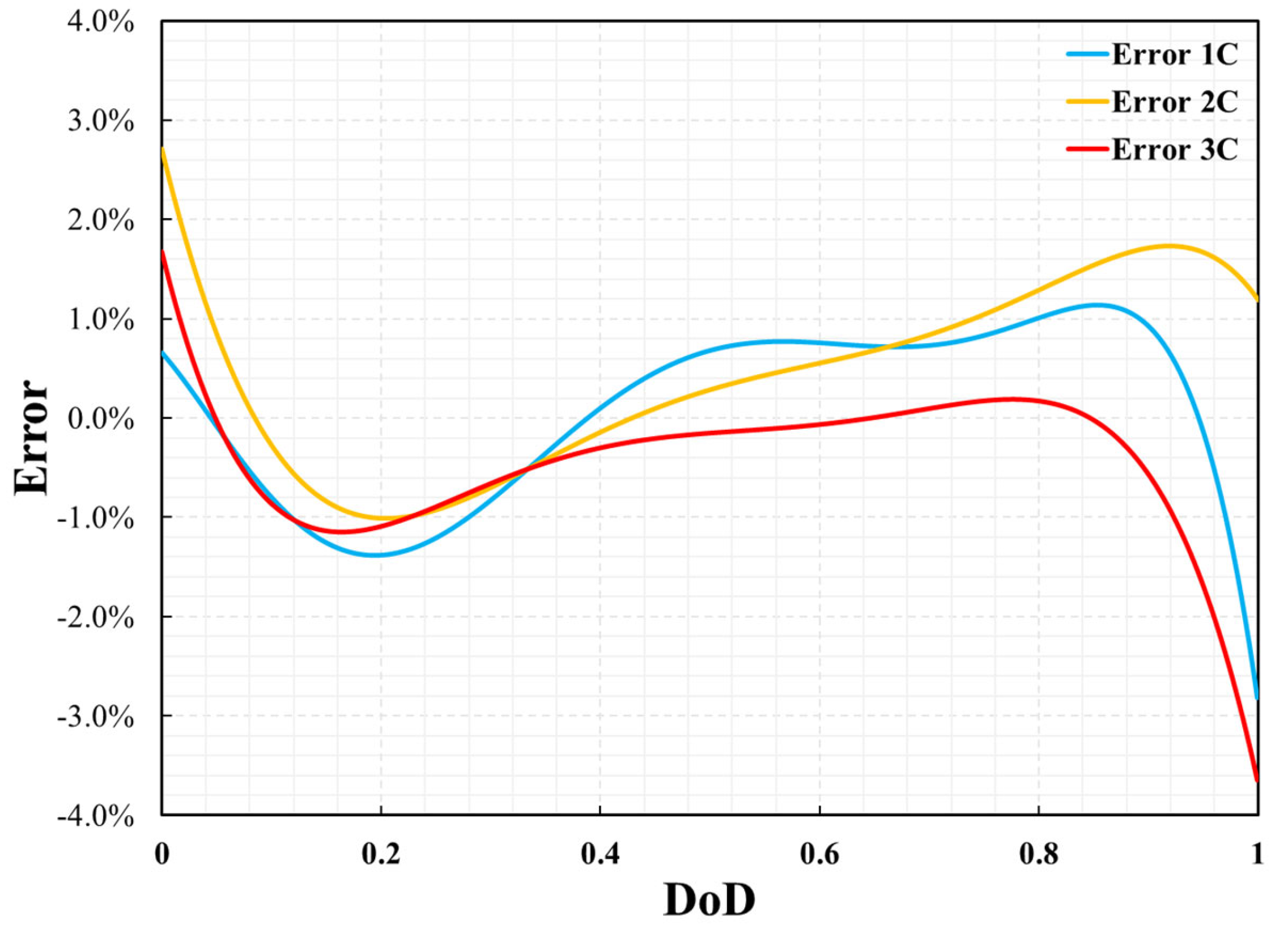
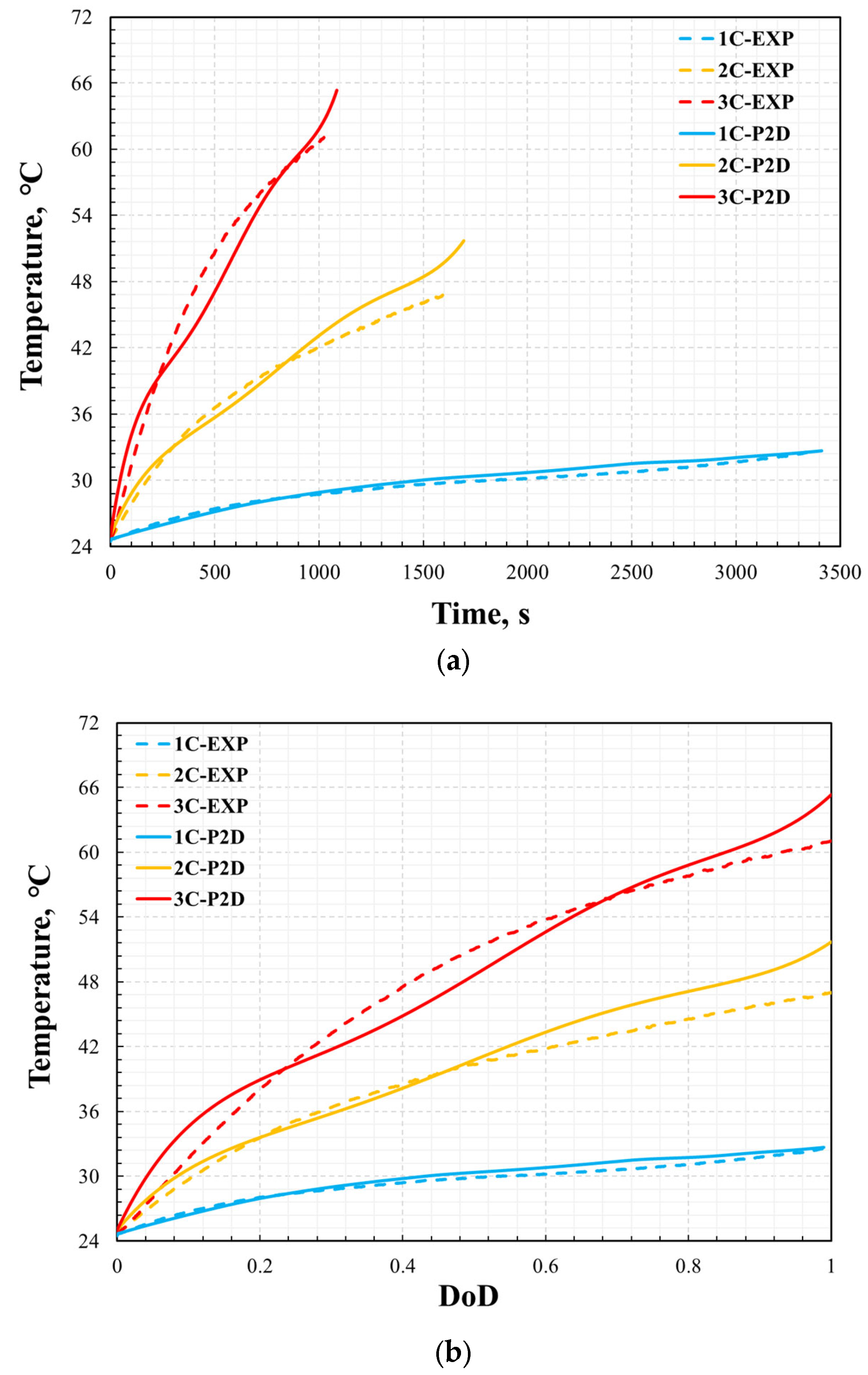
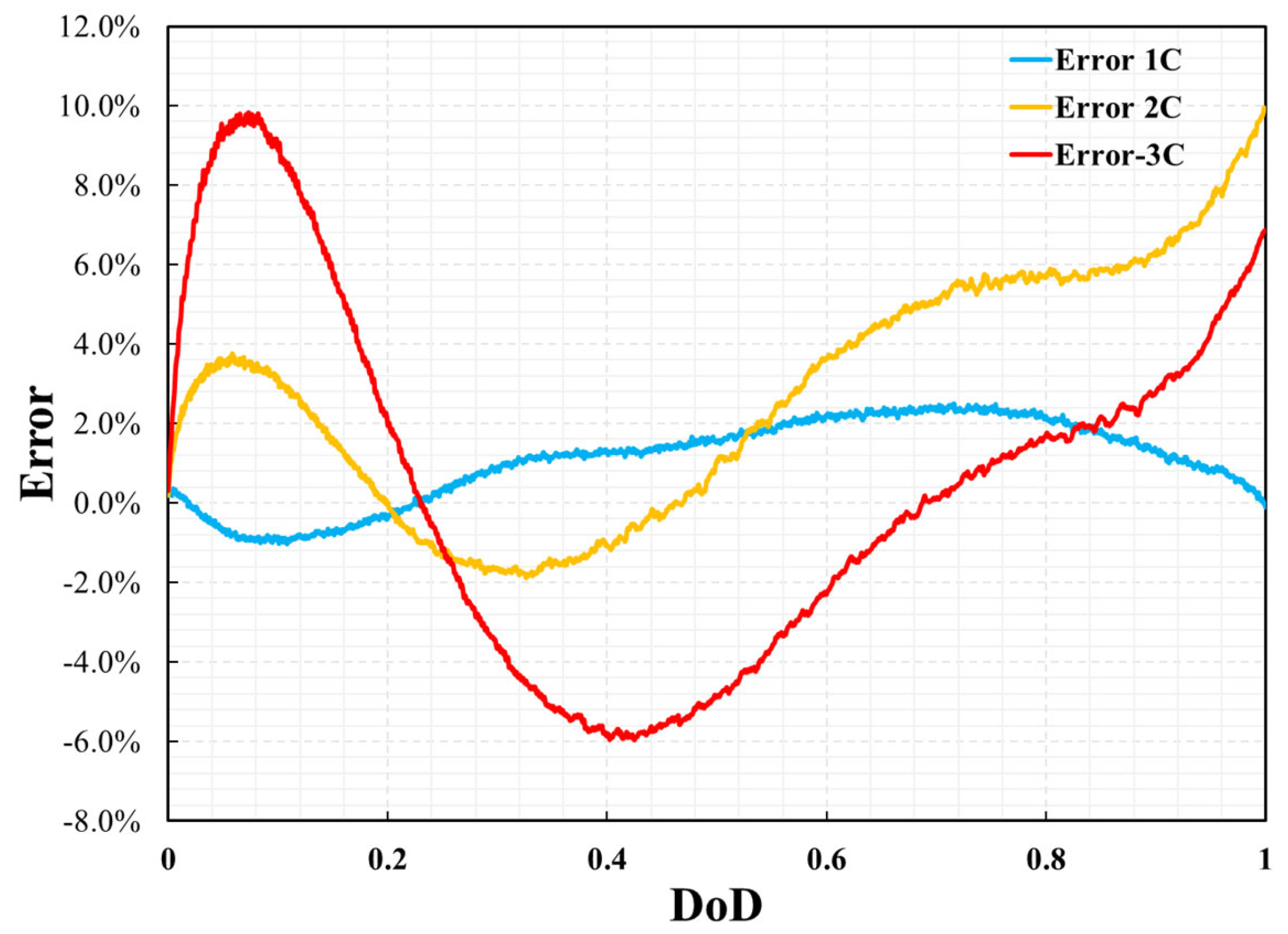
3.1. Model Validation
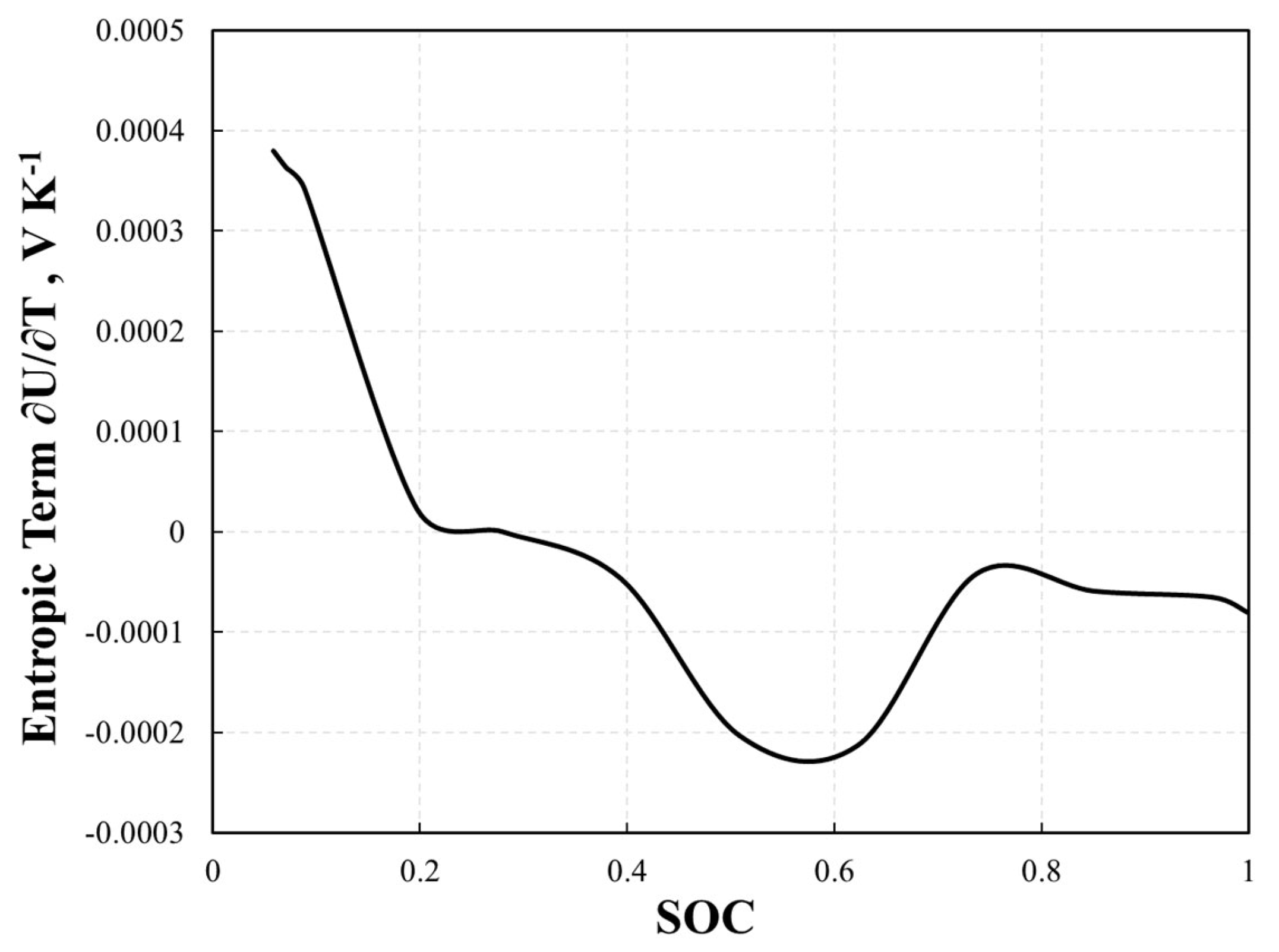
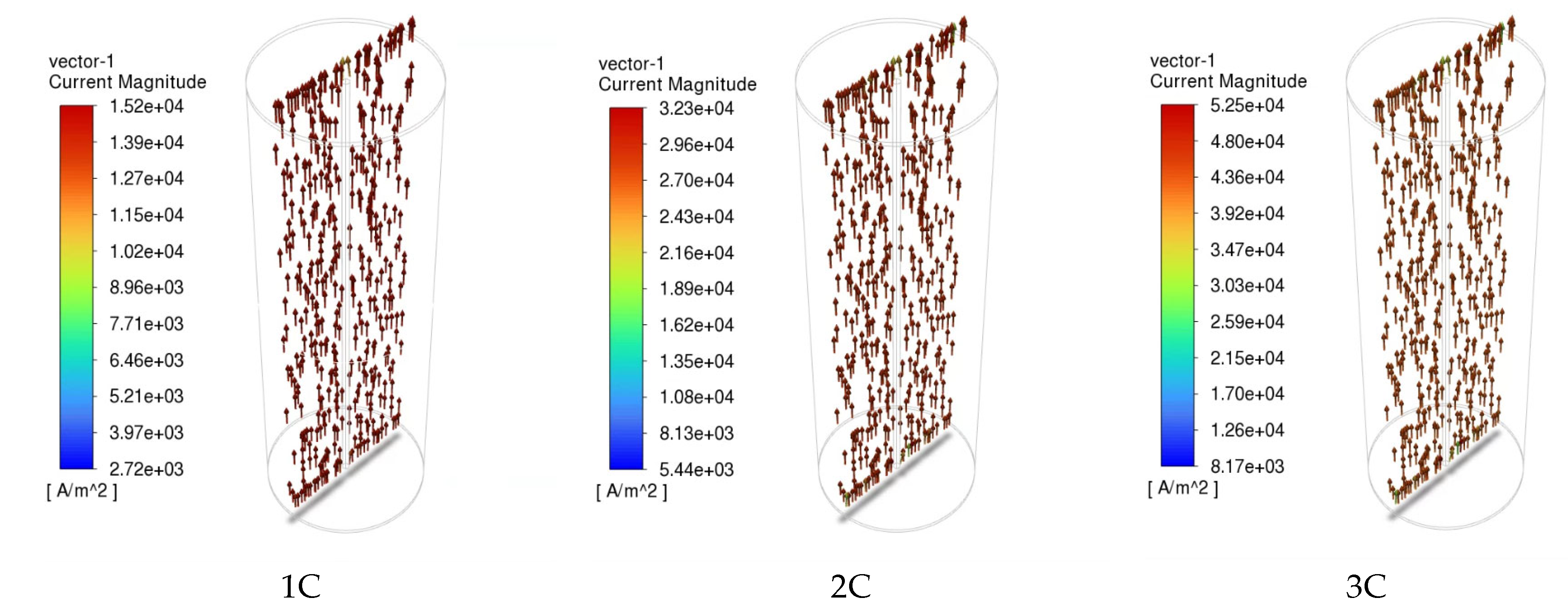
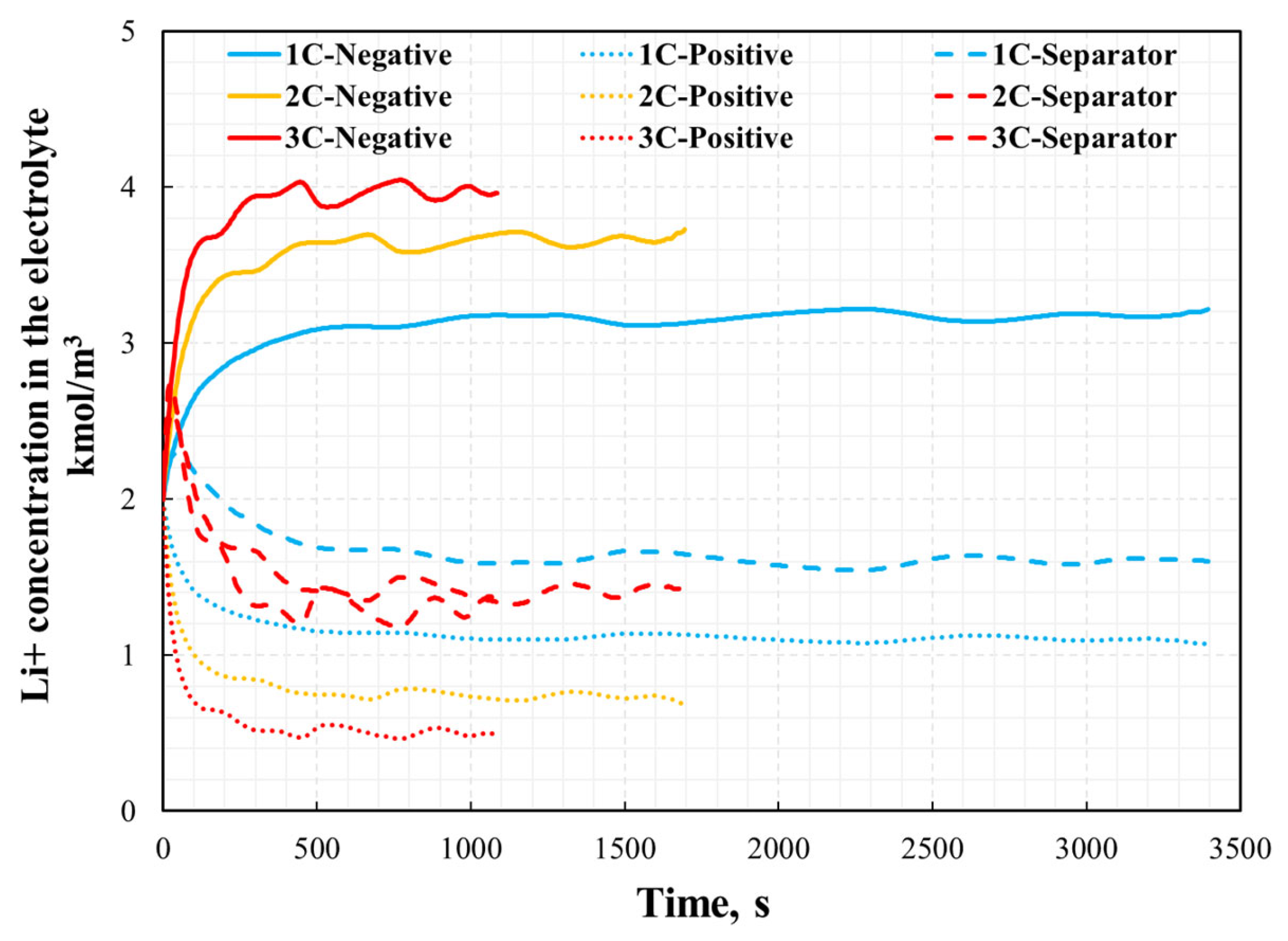
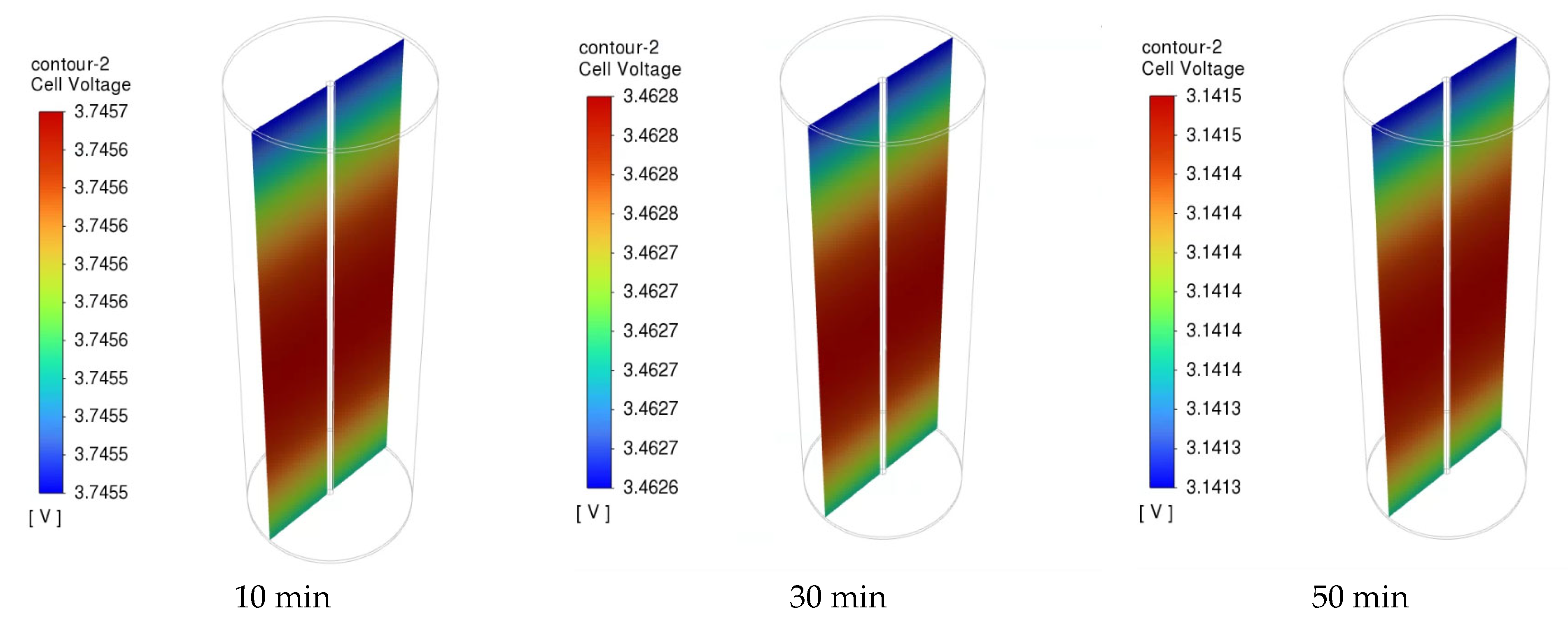
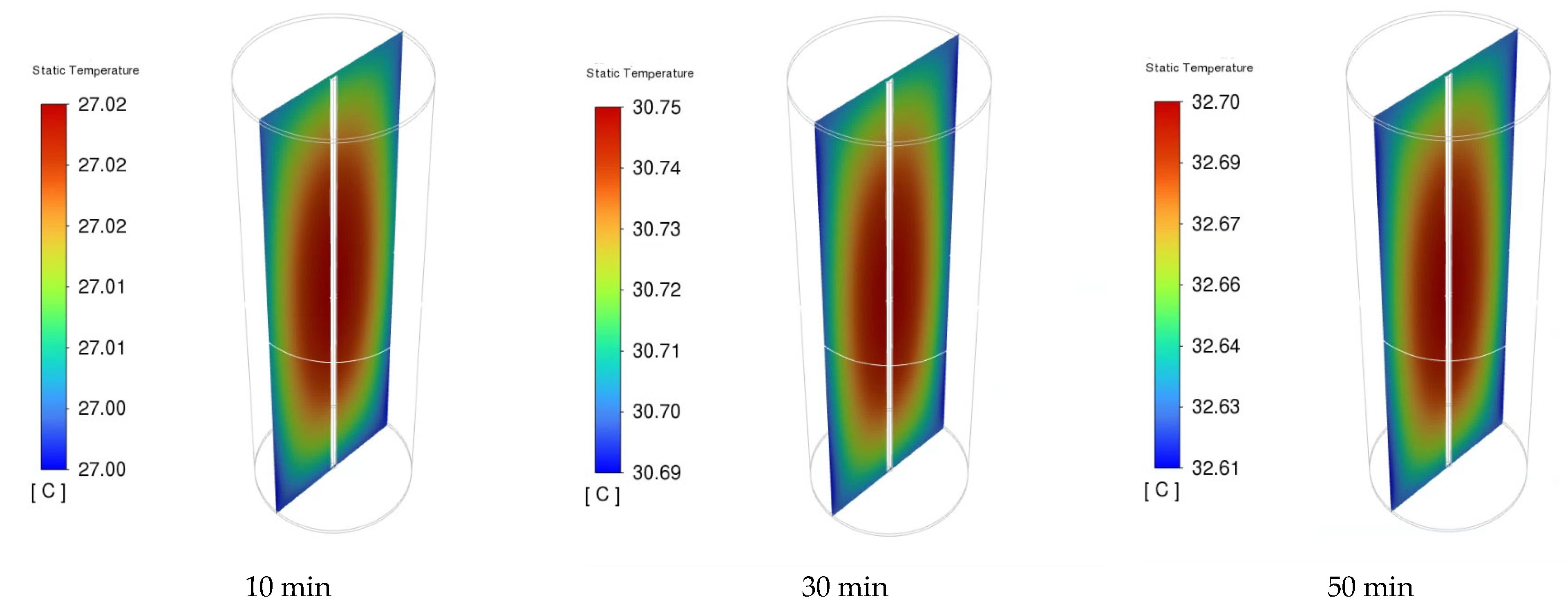
3.2. Electrochemical and Thermal Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| as | Solid/electrolyte interfacial area per unit volume, m2/m3 | |
| ce | Concentration of lithium in the electrolyte, mol/m3 | |
| cs | Concentration of lithium in the active material particles, mol/m3 | |
| Cp | Specific heat capacity, J/kgK | |
| De | Diffusion coefficient of electrolyte, m2/s | |
| Ds | Diffusion coefficient of lithium in the active material, m2/s | |
| Ed | Diffusion activation energy, kJ/mol | |
| Er | Reaction activation energy, kJ/mol | |
| F | Faraday’s constant, C/mol | |
| f± | Average molar activity coefficient | |
| i0 | Exchange current density, A/m2 | |
| jint | Pore-wall current flux due to lithium intercalation reaction, A/m2 | |
| jside | Pore-wall current flux due to side reactions, A/m2 | |
| km | Reaction rate constant, m2.5/mol0.5s | |
| l | Thickness, µm | |
| Q | Cell capacity, Ah | |
| q | Volumetric heat generation, W/m3 | |
| r | Particle radius, µm | |
| R | Gas constant, J/mol2K | |
| t+ | Transference number lithium ion | |
| T | Temperature, K | |
| U | Open circuit voltage of the cell, V | |
| Un | Open circuit potential of the negative electrode, V | |
| Up | Open circuit potential of the positive electrode, V | |
| V | Cell voltage, V | |
| v | Cell volume, m3 | |
| Greek letters | ||
| αa | Charge transfer coefficient at anode | |
| αc | Charge transfer coefficient at cathode | |
| β | Bruggeman exponent | |
| εe | Electrolyte volume fraction | |
| εs | Active material volume fraction | |
| λ | Thermal conductivity, W/m2K | |
| ρ | Density, kg/m3 | |
| σe | Ionic conductivity of electrolyte, S/m | |
| σs | Electronic conductivity in solid phase material, S/m | |
| ϕe | Electrolyte phase potential, V | |
| ϕs | Solid phase potential, V | |
| η | Local surface over potential, V | |
| Subscripts and superscripts | ||
| 0 | Initial value | |
| n | Negative electrode | |
| p | Positive electrode | |
| e | Electrolyte phase | |
| s | Solid phase | |
| max | Maximum | |
| min | Minimum | |
| eff | Effective value | |
| amb | Ambient | |
References
- Jaguemont, J.; Mierlo, J.V. A comprehensive review of future thermal management systems for battery-electrified vehicles. J. Energy Storage 2000, 31, 101551. [Google Scholar] [CrossRef]
- Alptekin, E. Emission, injection and combustion characteristics of biodiesel and oxygenated fuel blends in a common rail diesel engine. Energy 2017, 119, 44–52. [Google Scholar] [CrossRef]
- Tete, P.R.; Gupta, M.M.; Joshi, S.S. Developments in battery thermal management systems for electric vehicles: A technical review. J. Energy Storage 2021, 35, 102255. [Google Scholar] [CrossRef]
- Thakur, A.K.; Prabakaran, R.; Elkadeem, M.R.; Sharshir, S.W.; Arıcı, M.; Wang, C.; Zhao, W.; Hwang, J.Y.; Saidur, R. A state of art review and future viewpoint on advance cooling techniques for Lithium–ion battery system of electric vehicles. J. Energy Storage 2020, 32, 101771. [Google Scholar] [CrossRef]
- Chen, Z.; Qin, Y.; Dong, Z.; Zheng, J.; Liu, Y. Numerical study on the heat generation and thermal control of lithium-ion battery. Appl. Therm. Eng. 2023, 211, 119852. [Google Scholar] [CrossRef]
- Zhang, C.; Li, K.; Mcloone, S.; Yang, Z. Battery Modelling Methods for Electric Vehicles–A Review. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014. [Google Scholar]
- Zadeh, P.G.; Gholamalizadeh, E.; Wang, Y.; Chung, J.D. Electrochemical modeling of a thermal management system for cylindrical lithium-ion battery pack considering battery capacity fade. Case Stud. Therm. Eng. 2022, 32, 101878. [Google Scholar] [CrossRef]
- Li, Y.; Qi, F.; Guo, H.; Guo, Z.; Li, M.; Wu, W. Characteristic investigation of an electrochemical-thermal coupled model for a LiFePO4/Graphene hybrid cathode lithium-ion battery. Case Stud. Therm. Eng. 2019, 13, 100387. [Google Scholar]
- Liu, Z.; Wang, H.; Yang, C.; Zhao, J. Simulation study of lithium-ion battery thermal management system based on a variable flow velocity method with liquid metal. Appl. Therm. Eng. 2020, 179, 115578. [Google Scholar] [CrossRef]
- Chiew, J.; Chinb, C.S.; Toh, W.D.; Gao, Z.; Jia, J.; Zhang, C.Z. A pseudo three-dimensional electrochemical-thermal model of a cylindrical LiFePO4/graphite battery. Appl. Therm. Eng. 2019, 147, 450–463. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, S.; Li, L.; Liu, F.; Jiang, L.; Jia, M.; Ai, Y.; Yao, C.; Gu, H. Simulation and parameter identification based on electrochemical-thermal coupling model of power lithium ion-battery. J. Alloys Compd. 2020, 844, 156003. [Google Scholar]
- Waldmann, T.; Scurtu, R.G.; Richter, K.; Wohlfahrt-Mehrens, M. 18650 vs. 21700 Li-ion cells–A direct comparison of electrochemical, thermal, and geometrical properties. J. Power Sources 2020, 472, 228614. [Google Scholar] [CrossRef]
- Kumar, R.; Chavan, S. Thermal Investigation of Cylindrical Lithium-ion Batteries for Different Loading using Experimental and Numerical Techniques. J. Electrochem. Soc. 2022, 169, 120504. [Google Scholar] [CrossRef]
- Yang, T.F.; Lin, P.Y.; Teng, L.T.; Rashidi, S.; Yan, W.M. Numerical and experimental study on thermal management of NCM-21700 Li-ion battery. J. Power Sources 2022, 548, 232068. [Google Scholar] [CrossRef]
- Moosavi, A.; Ljung, A.L.; Lundström, T.S. Design considerations to prevent thermal hazards in cylindrical lithium-ion batteries: An analytical study. J. Energy Storage 2021, 38, 102525. [Google Scholar] [CrossRef]
- Lin, C.; Wen, H.; Liu, L.; Liu, S.; Ma, T.; Fan, B.; Wang, F. Heat generation quantification of high-specific-energy 21700 battery cell using average and variable specific heat capacities. Appl. Therm. Eng. 2021, 184, 116215. [Google Scholar] [CrossRef]
- Zhang, C.; Amietszajew, T.; Li, S.; Marinescu; Offer, G.; Wang, C.; Guo, Y.; Bhagat, R. Real-time estimation of negative electrode potential and state of charge of lithium-ion battery based on a half-cell-level equivalent circuit model. J. Energy Storage 2022, 51, 104362. [Google Scholar] [CrossRef]
- Rahmani, E.; Fattahi, A.; Panahi, E.; Mahmoudi, Y. Thermal management improvement for a pack of cylindrical batteries using nanofluids and topological modifications. J. Power Sources 2023, 564, 232876. [Google Scholar] [CrossRef]
- Kang, T.; Park, S.; Lee, P.Y.; Cho, I.H.; Yoo, K.; Kim, J. Thermal Analysis of a Parallel-Configured Battery Pack (1S18P) Using 21700 Cells for a Battery-Powered Train. Electronics 2020, 9, 447. [Google Scholar] [CrossRef]
- Sahin, R.C.; Gocmen, S.; Cetkin, E. Thermal management system for air-cooled battery packs with flow-disturbing structures. J. Power Sources 2022, 551, 232214. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y.; Hu, F.; Shi, W.; Hu, X.; Li, H.; Chen, S.; Lin, H.; Jiang, C. Heat generation measurement and thermal management with phase change material based on heat flux for high specific energy power battery. Appl. Therm. Eng. 2021, 194, 117053. [Google Scholar] [CrossRef]
- Sheng, L.; Zhang, H.; Su, L.; Zhang, Z.; Zhang, H.; Li, K.; Fang, Y.; Ye, W. Effect analysis on thermal profile management of a cylindrical lithium-ion battery utilizing a cellular liquid cooling jacket. Energy 2021, 220, 119725. [Google Scholar] [CrossRef]
- Zhang, X.; Li, P.; Huang, B.; Zhang, H. Numerical investigation on the thermal behavior of cylindrical lithium-ion batteries based on the electrochemical-thermal coupling model. Int. J. Heat Mass Transf. 2022, 199, 123449. [Google Scholar] [CrossRef]
- Li, H.; Saini, A.; Liu, C.; Yang, J.; Wang, Y.; Yang, T.; Pan, C.; Chen, L.; Jiang, H. Electrochemical and thermal characteristics of prismatic lithium-ion battery based on a three-dimensional electrochemical-thermal coupled model. J. Energy Storage 2021, 42, 102976. [Google Scholar] [CrossRef]
- Li, H.; Liu, C.; Saini, A.; Wang, Y.; Jiang, H.; Yang, T.; Chen, L.; Pan, C.; Shen, H. Coupling multi-physics simulation and response surface methodology for the thermal optimization of ternary prismatic lithium-ion battery. J. Power Sources 2019, 438, 226974. [Google Scholar] [CrossRef]
- Ansys Fluent Theory Guide; Ansys, Inc.: Canonsburg, PA, USA, 2021.
- Astaneh, M.; Andric, J.; Löfdahl, L.; Stopp, P. Multiphysics simulation optimization framework for lithium-ion battery pack design for electric vehicle applications. Energy 2022, 239, 122092. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140–146, 1526–1533. [Google Scholar] [CrossRef]
- Crawford, A.J.; Choi, D.; Balducci, P.J.; Subramanian, V.R.; Viswanathan, V.V. Lithium-ion battery physics and statistics-based state of health model. J. Power Sources 2021, 501, 230032. [Google Scholar] [CrossRef]
- Chen, C.H.; Planella, F.B.; O’Regan, K.; Gastol, D.; Widanage, W.D.; Kendrick, E. Development of Experimental Techniques for Parameterization of Multi-scale Lithium-ion Battery Models. J. Electrochem. Soc. 2020, 167, 080534. [Google Scholar] [CrossRef]
- O’Regan, K.; Planella, F.B.; Widanage, W.D.; Kendrick, E. Thermal-electrochemical parameters of a high energy lithium-ion cylindrical battery. Electrochim. Acta 2022, 425, 140700. [Google Scholar] [CrossRef]
- Nie, P.; Zhang, S.W.; Ran, A.; Yang, C.; Chen, S.; Li, Z.; Zhang, X.; Deng, W.; Liu, T.; Kang, F.; et al. Full-cycle electrochemical-thermal coupling analysis for commercial lithium-ion batteries. Appl. Therm. Eng. 2021, 184, 116258. [Google Scholar] [CrossRef]
- Catenaro, E.; Rizzo, D.M.; Onori, S. Experimental analysis and analytical modeling of Enhanced-Ragone plot. Appl. Eng. 2021, 291, 116473. [Google Scholar] [CrossRef]
- Chen, Z.; Danilov, D.L.; Eichel, R.A.; Notten, P.H.L. Li+ concentration waves in a liquid electrolyte of Li-ion batteries with porous graphite-based electrodes. Energy Storage Mater. 2022, 48, 475–486. [Google Scholar] [CrossRef]
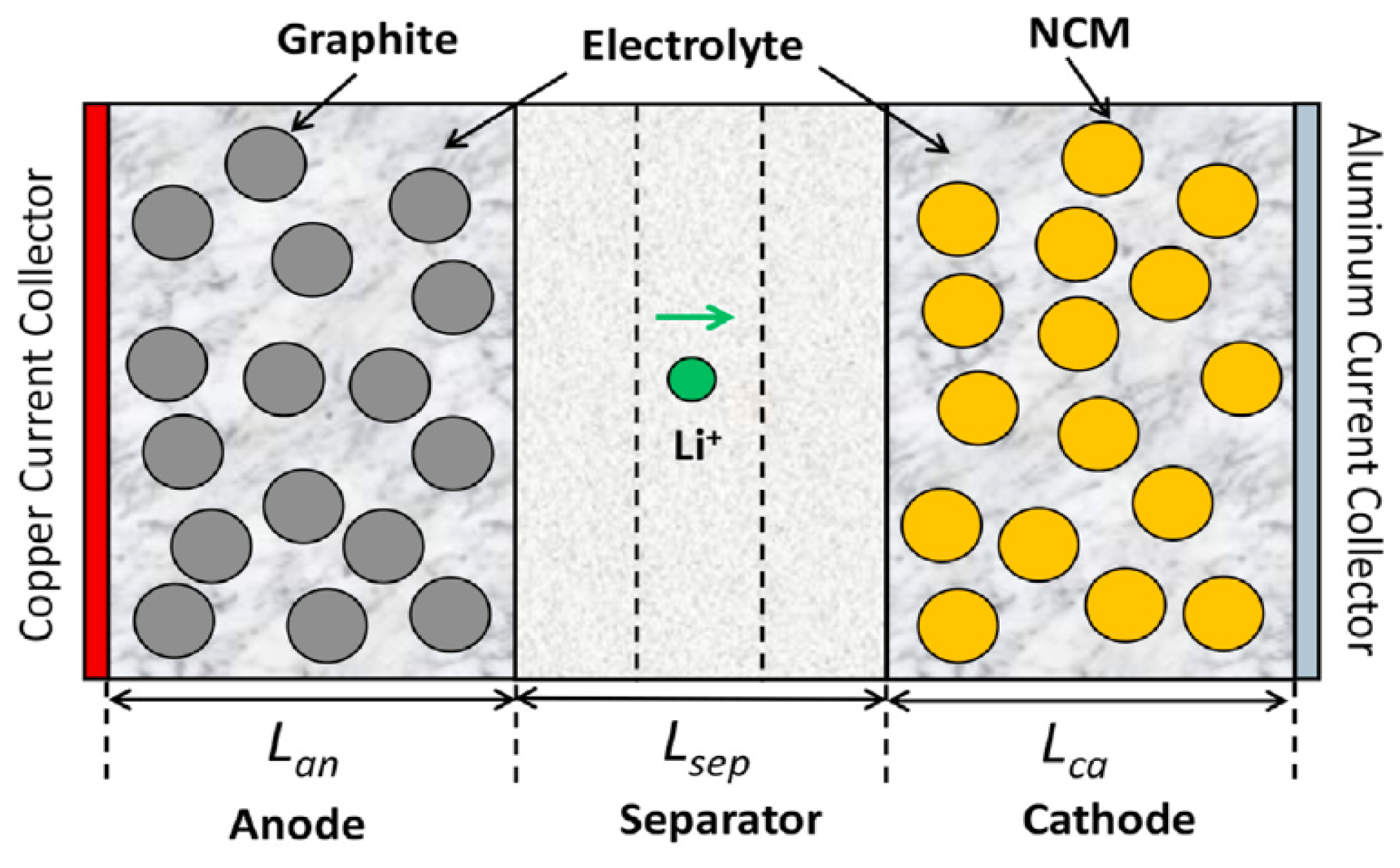



| Parameters | Positive Electrode | Separator | Negative Electrode | Unit |
|---|---|---|---|---|
| Electrode thickness, l | 75.6 | 12 | 85.2 | µm |
| Current collector thickness, lc | 16 | - | 12 | µm |
| Particle radius, R | 5.22 | - | 5.86 | µm |
| Maximum solid Li+ concentration for electrode, cs,max | 63,104 | - | 33,133 | mol/m3 |
| Initial solid Li+ concentration for electrode, cs,0 | 17,038 | - | 29,866 | mol/m3 |
| Initial electrolyte concentration, ce,0 | 2000 | 20,000 | 2000 | mol/m3 |
| Electrolyte volume fraction, εe | 33.5 | 47 | 25 | % |
| Active material volume fraction, εs | 66.5 | - | 75 | % |
| Bruggeman exponent, β | 1.5 | 1.5 | 1.5 | - |
| Reference diffusivity for electrode, Ds | 1.48 × 10−15 | - | 1.74 × 10−15 | m2/s |
| Stoi. at 0% SOC for electrode, Stoi0 | 0.9084 | - | 0.0279 | - |
| Stoi. at 100% SOC for electrode, Stoi100 | 0.2661 | - | 0.9014 | - |
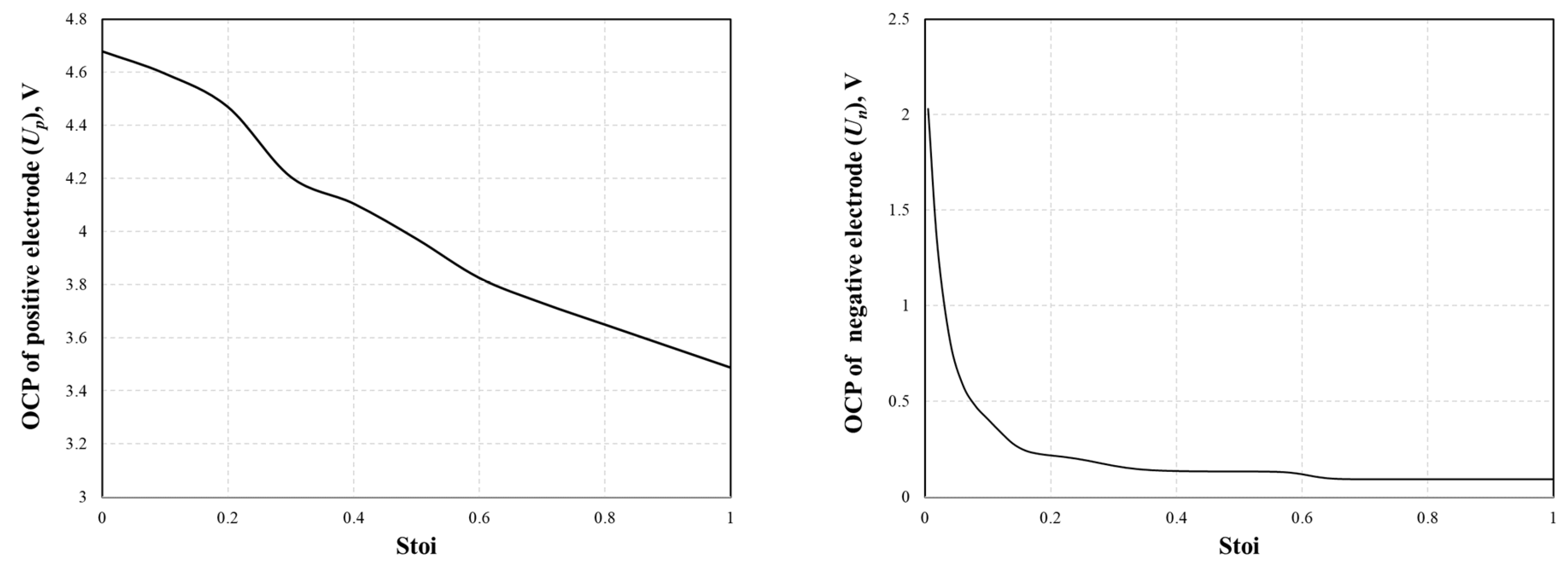
| Open circuit potential (OCP), Up,Un | Equation (25) and Figure 2 | Equation (26) and Figure 2 | ||
| Conductivity for electrode, σ | 0.18 | - | 215 | S/m |
| Reference rate constant for electrode, k | 3.42 × 10−6 | - | 6.48 × 10−7 | m2.5 s/mol1.5 |
| Density, ρ | 1200 | 525 | 2860 | kg/m3 |
| Thermal conductivity, λ | 0.807 | 0.3344 | 3.793 | W/m2K |
| Specific heat capacity, Cp | 990 | 1128 | 960 | J/kgK |
| Electrolyte diffusivity for electrode, De | Equation (27) and Figure 3 | m2/s | ||
| Conductivity for electrolyte, σe | Equation (28) and Figure 3 | S/m | ||
| t+ factor for electrode, t+ | 0.2594 | - | ||
| Nominal capacity of cell, C | 5 | Ah | ||
| Minimum stop voltage, Vmin | 2.5 | V | ||
| Maximum stop voltage, Vmax | 4.2 | V | ||
| Reference temperature, Tref | 25 | °C | ||
| Universal gas constant, R | 8.314 | kJ/kg mol K | ||
| Faraday’s constant, F | 96,485 | Columb/mol | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Chavan, S.; Kim, S.-C. Investigation of the Electrochemical and Thermal Characteristics of NCM811-21700 Cylindrical Lithium-Ion Battery: A Numerical Study and Model Validation. Energies 2023, 16, 6407. https://doi.org/10.3390/en16176407
Liu J, Chavan S, Kim S-C. Investigation of the Electrochemical and Thermal Characteristics of NCM811-21700 Cylindrical Lithium-Ion Battery: A Numerical Study and Model Validation. Energies. 2023; 16(17):6407. https://doi.org/10.3390/en16176407
Chicago/Turabian StyleLiu, Jie, Santosh Chavan, and Sung-Chul Kim. 2023. "Investigation of the Electrochemical and Thermal Characteristics of NCM811-21700 Cylindrical Lithium-Ion Battery: A Numerical Study and Model Validation" Energies 16, no. 17: 6407. https://doi.org/10.3390/en16176407
APA StyleLiu, J., Chavan, S., & Kim, S.-C. (2023). Investigation of the Electrochemical and Thermal Characteristics of NCM811-21700 Cylindrical Lithium-Ion Battery: A Numerical Study and Model Validation. Energies, 16(17), 6407. https://doi.org/10.3390/en16176407






