Localization of HV Insulation Defects Using a System of Associated Capacitive Sensors
Abstract
:1. Introduction
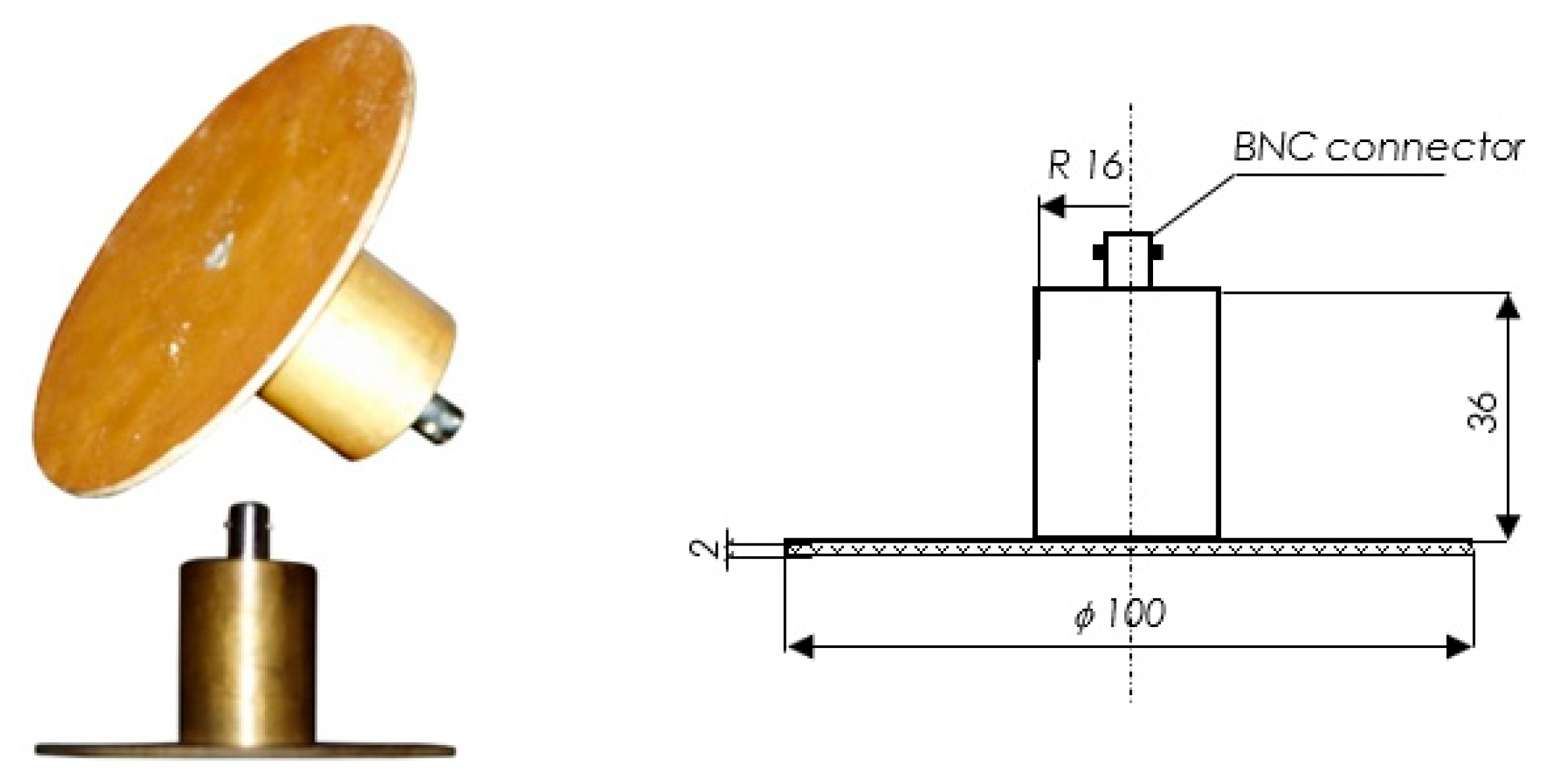
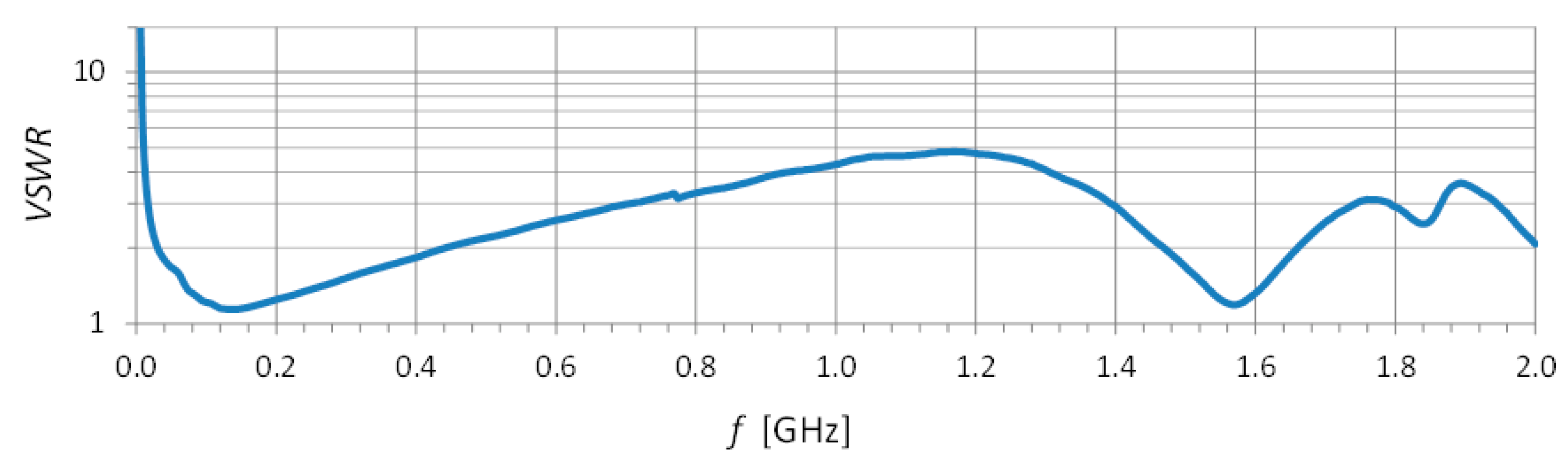
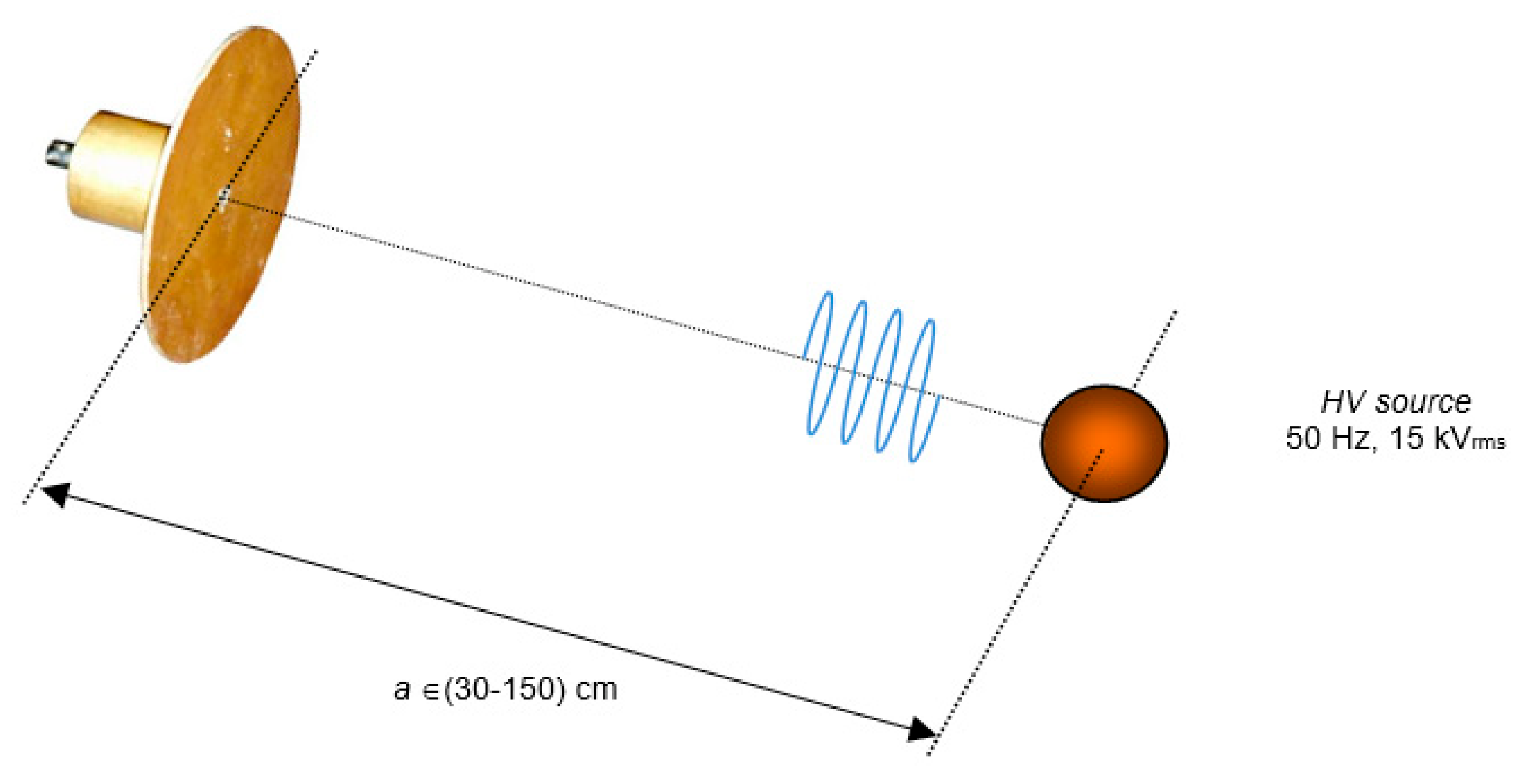
2. Materials and Methods
- Γ—voltage reflection coefficient;
- Pi—input power;
- Pr—power reflected from the input.
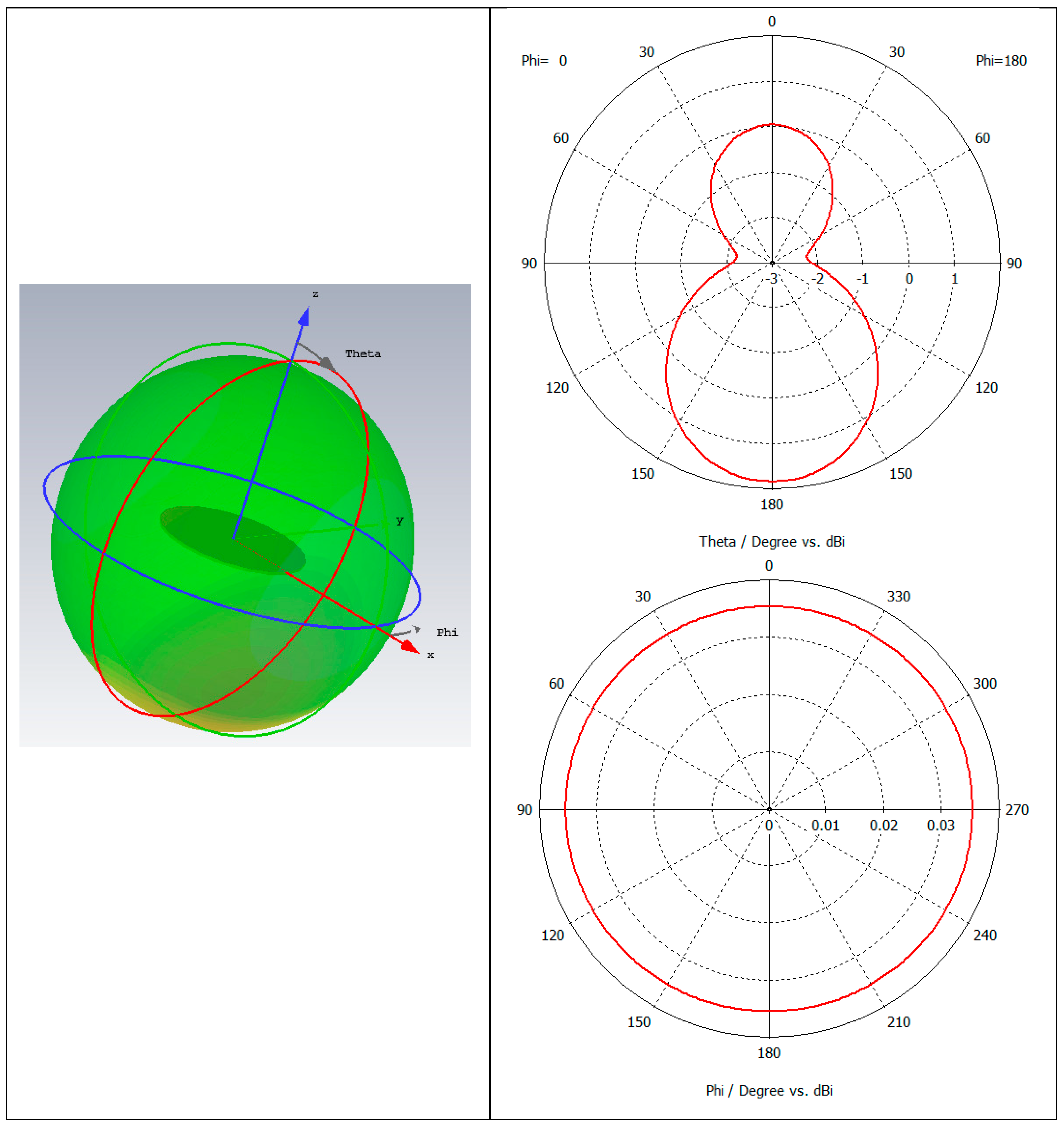
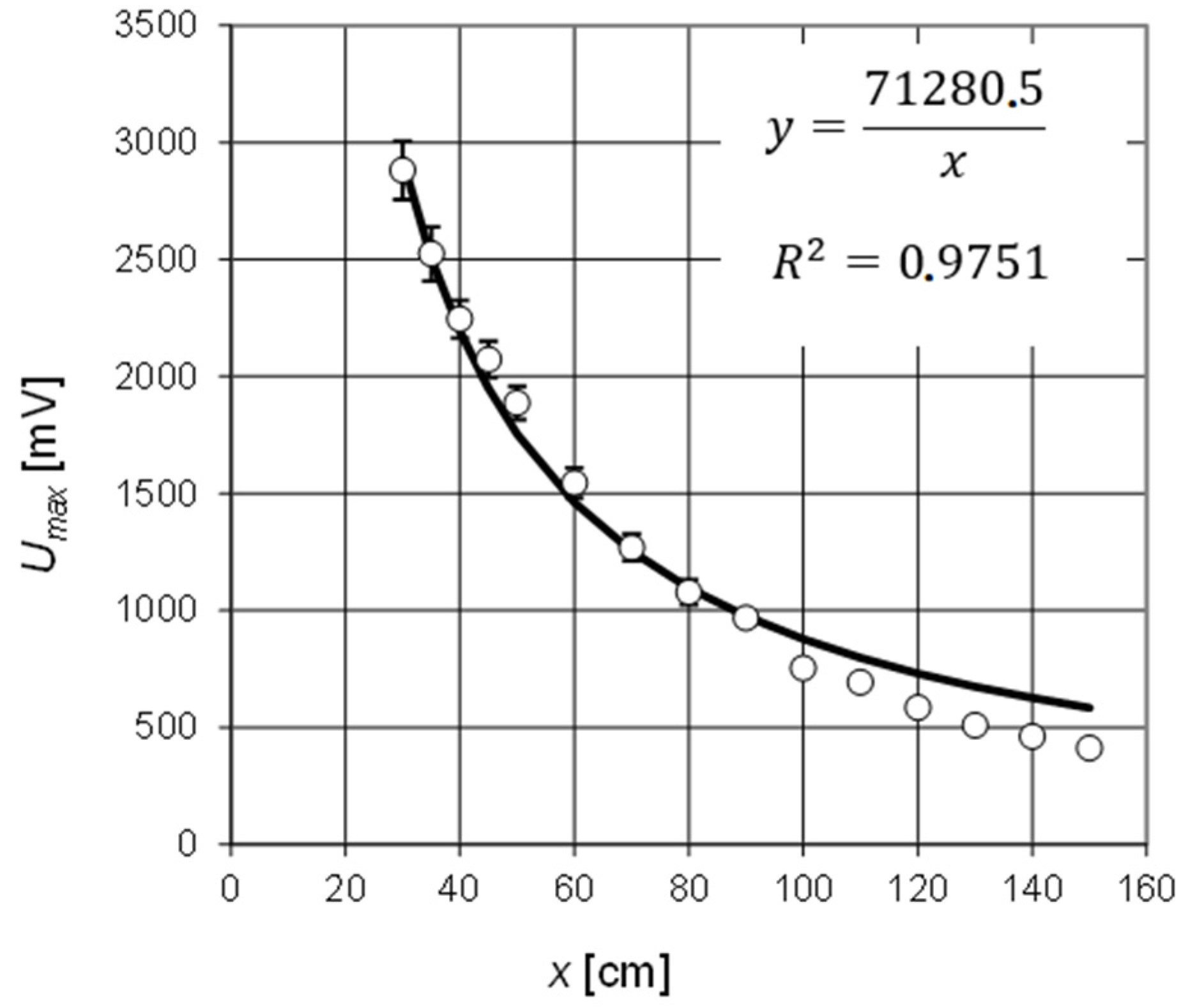
- Um—the maximum radiation density of a given antenna;
- Uave—average radiation density.
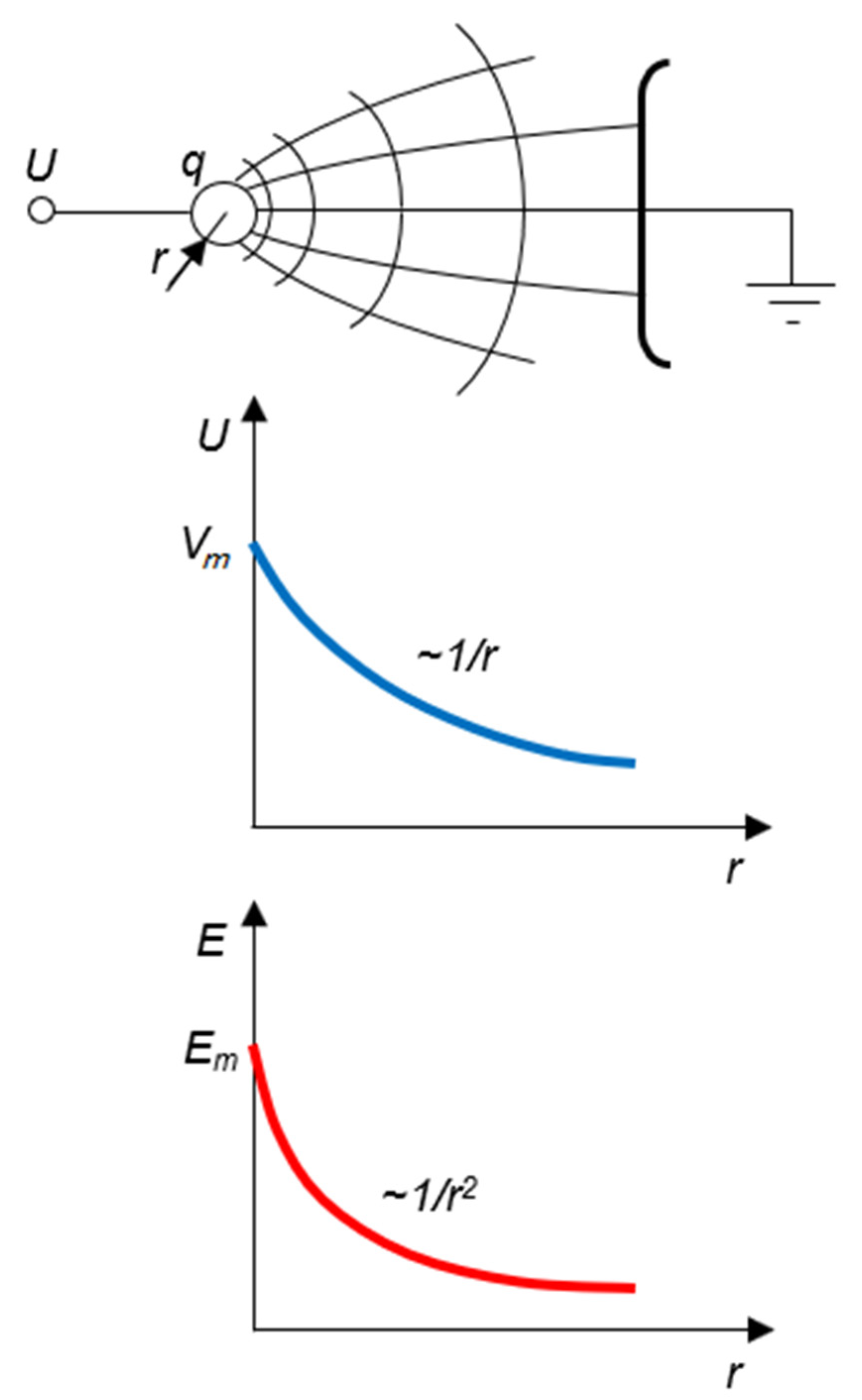
- q—the total electric charge of the ball;
- A—a function parameter.
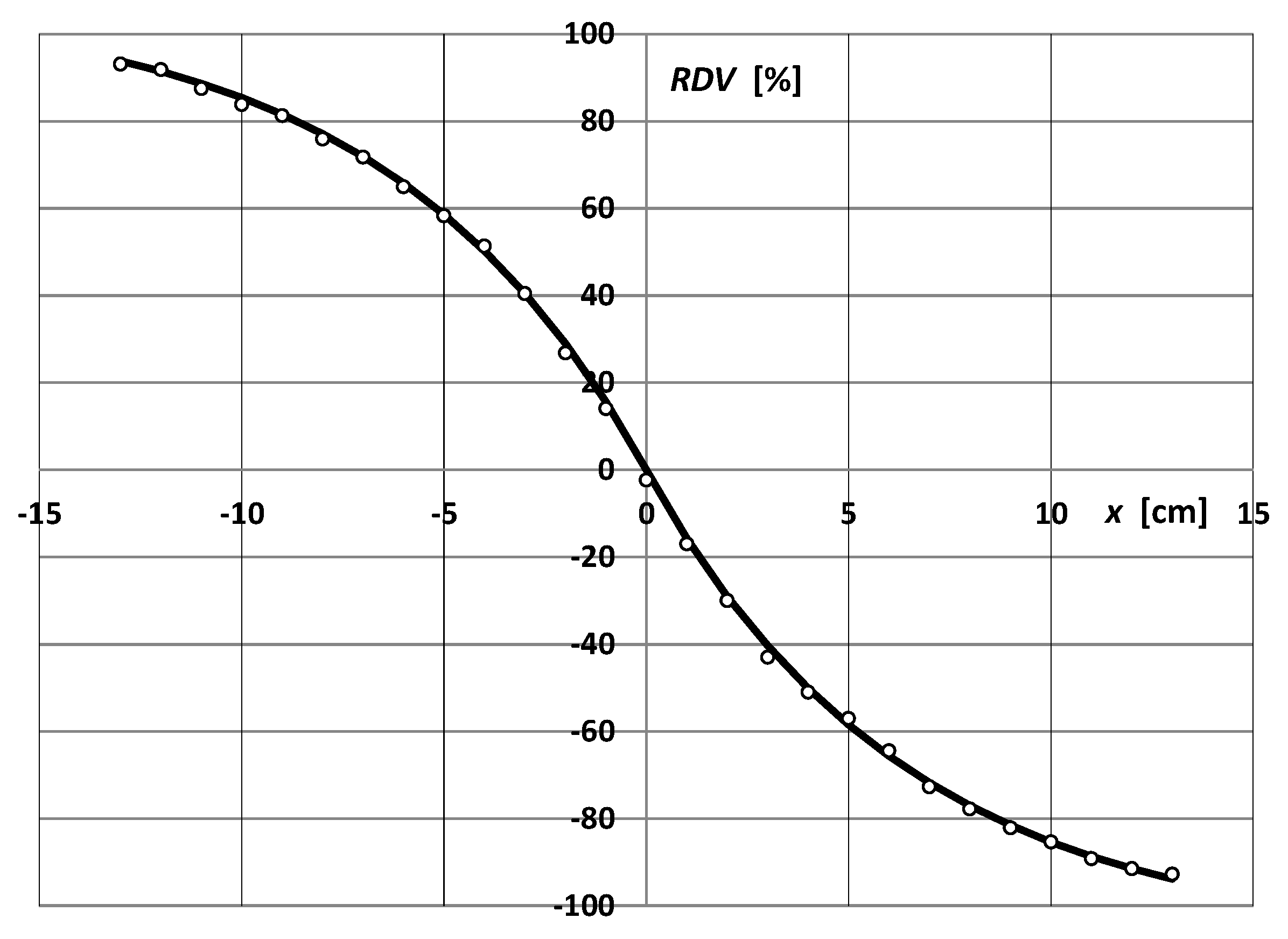
3. The Idea of the Localization Method Using a Pair of Capacitive Probes
- RDV—the relative difference in the values of the signals recorded by the two probes;
- x—the position of the PD source in the axis;
- t, A—the constants.
- x, y—the position of PD source after correction;
- xp, yp—the coordinates determined on the basis of the Formula (7);
- k—the correction factor.
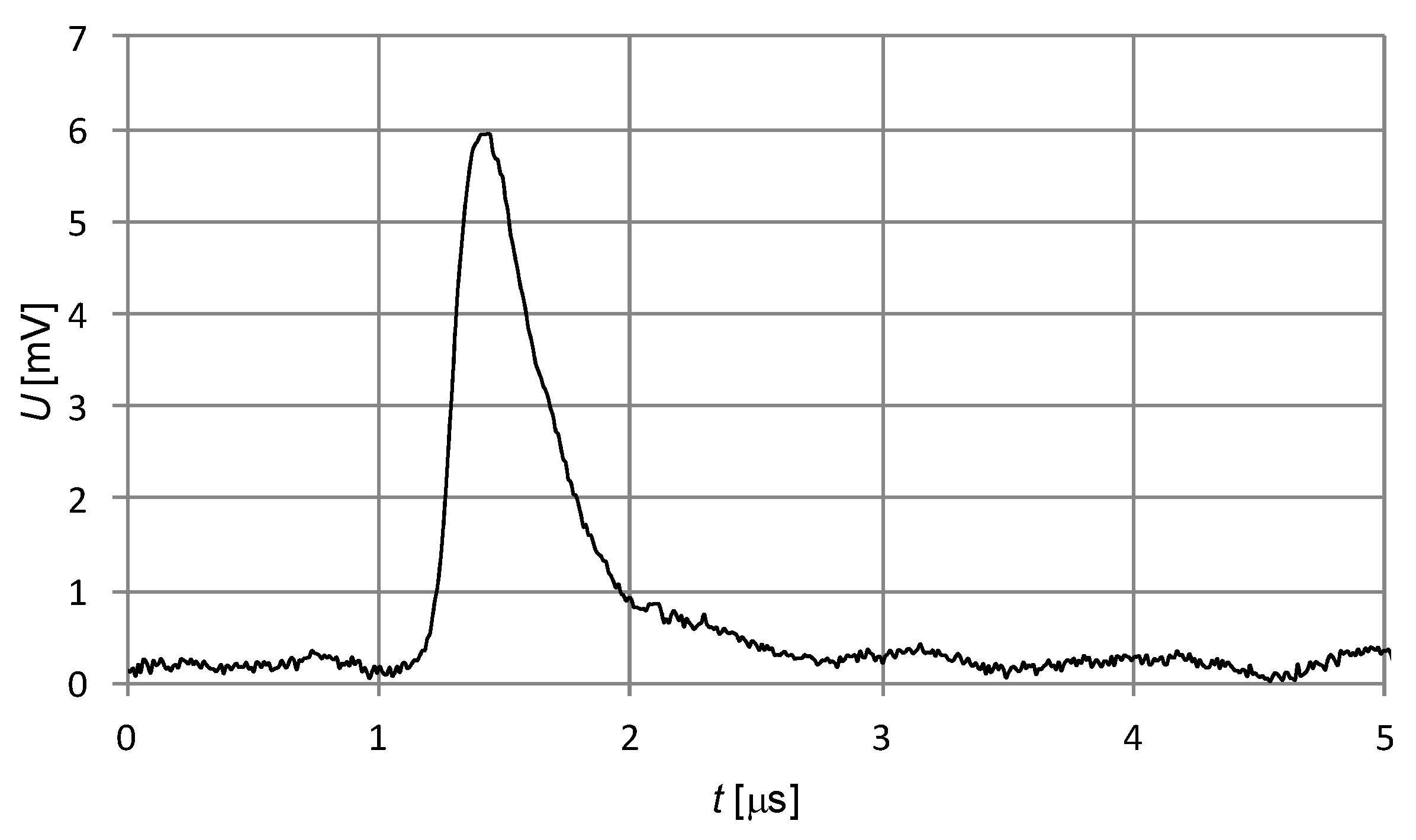
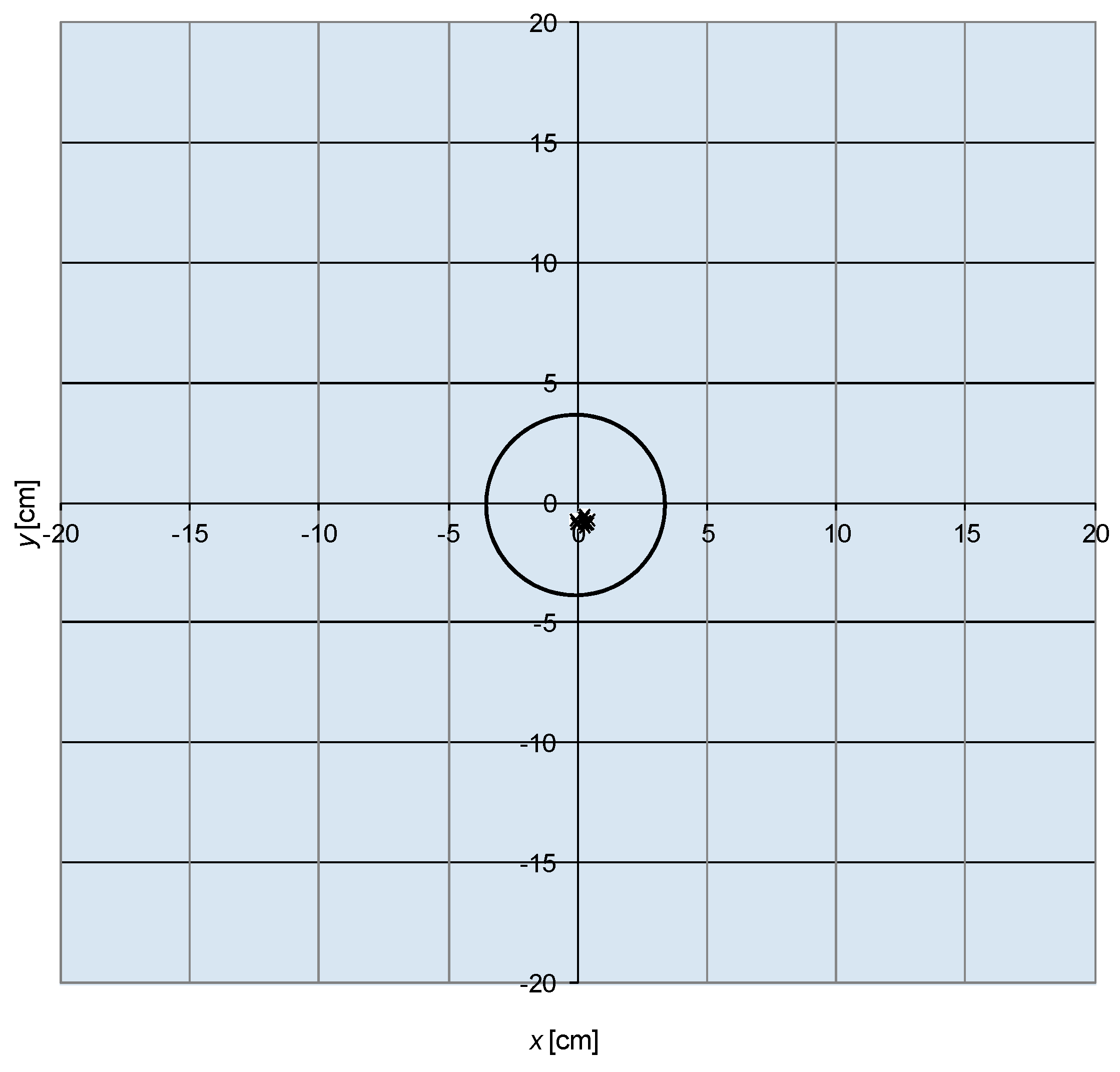
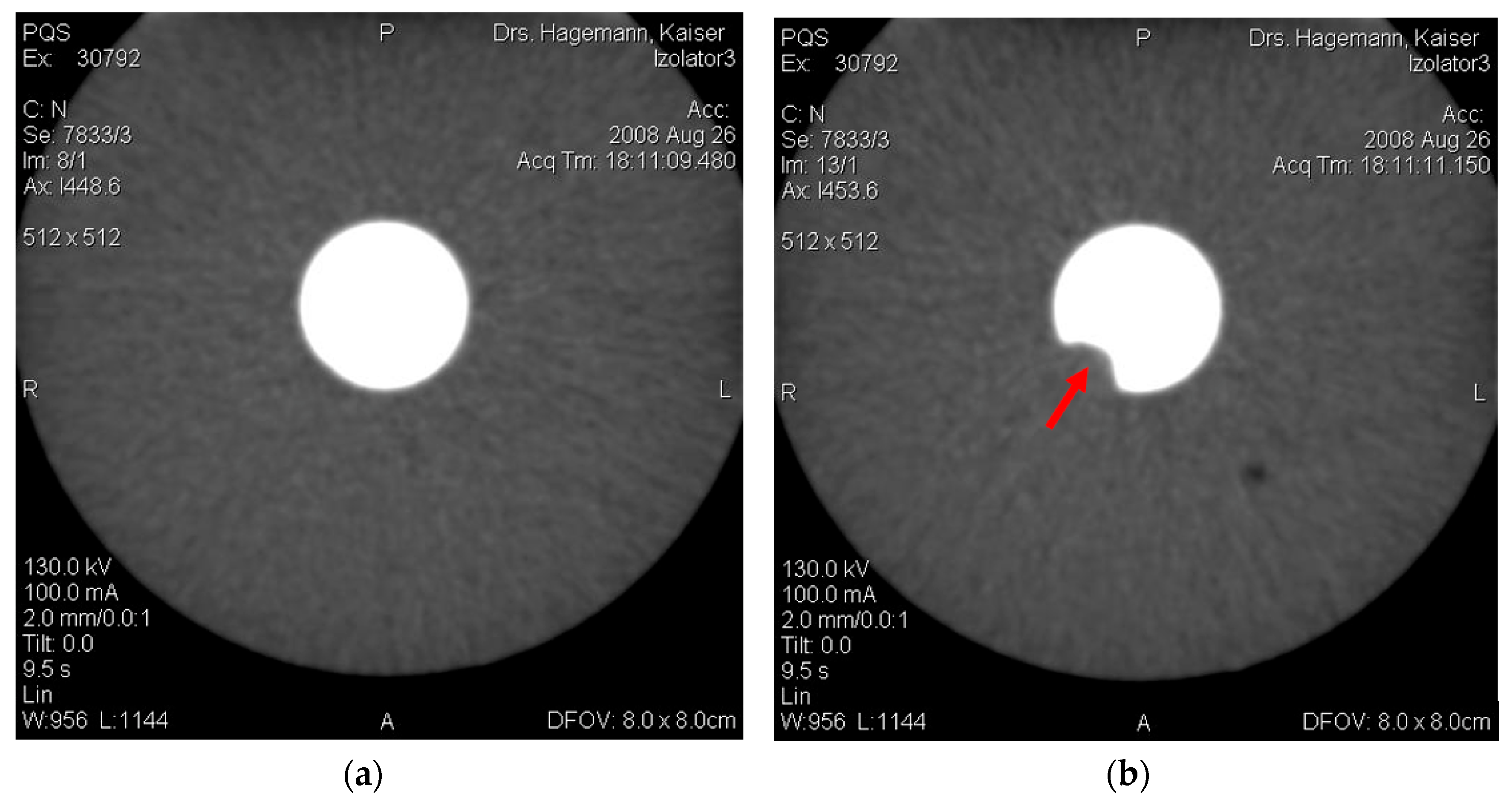
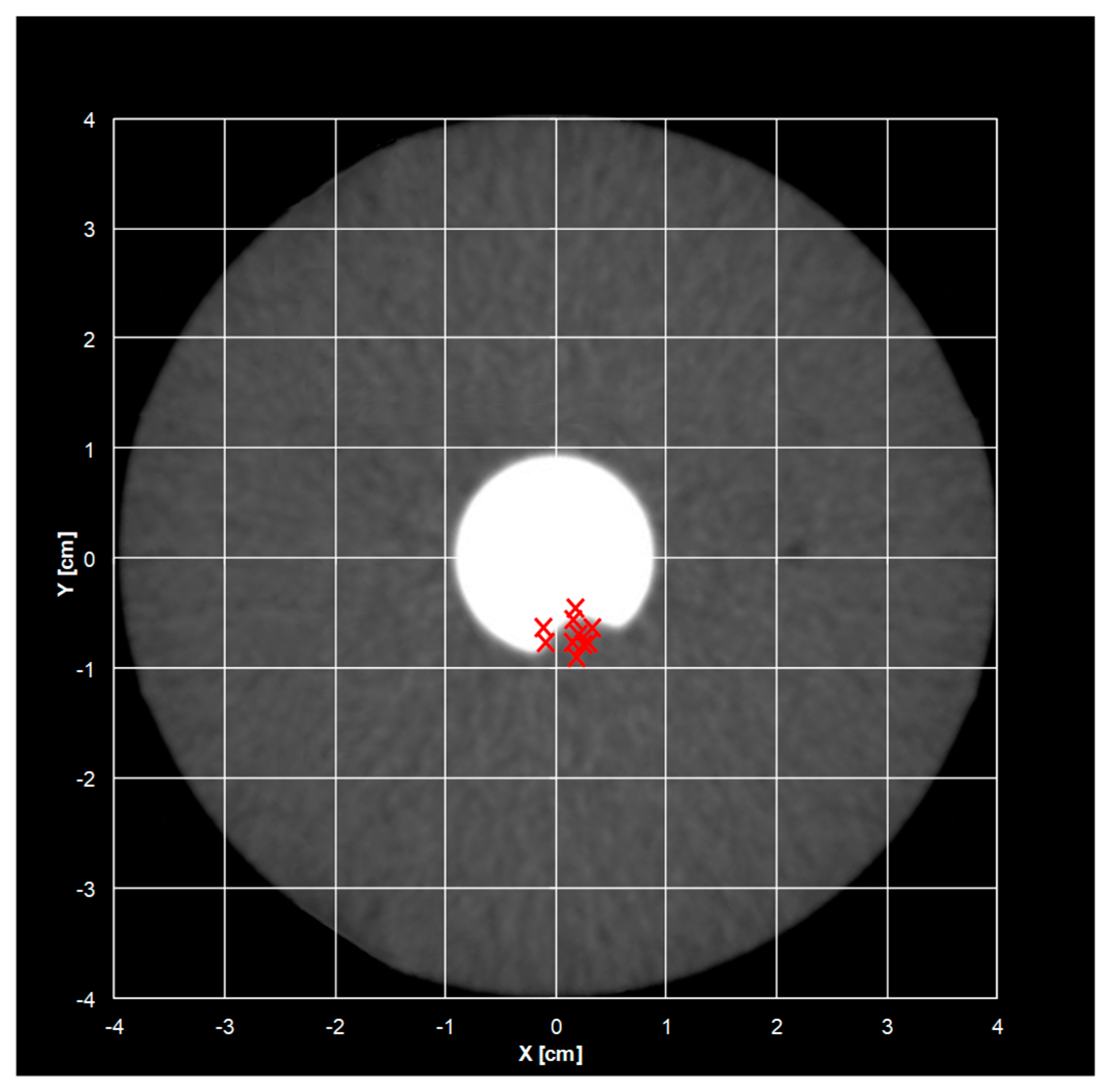
4. Results and Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nadolny, Z. Electric Field Distribution and Dielectric Losses in XLPE Insulation and Semiconductor Screens of High-Voltage Cables. Energies 2022, 15, 4692. [Google Scholar] [CrossRef]
- Sikorski, W.; Walczak, K.; Szymczak, C.; Gil, W. On-Line Partial Discharge Monitoring System for Power Transformers Based on the Simultaneous Detection of High Frequency, Ultra-High Frequency, and Acoustic Emission Signals. Energies 2020, 13, 3271. [Google Scholar] [CrossRef]
- Luo, Y.; Li, Z.; Wang, H. A Review of Online Partial Discharge Measurement of Large Generators. Energies 2017, 10, 1694. [Google Scholar] [CrossRef] [Green Version]
- Wotzka, D.; Sikorski, W.; Szymczak, C. Investigating the Capability of PD-Type Recognition Based on UHF Signals Recorded with Different Antennas Using Supervised Machine Learning. Energies 2022, 15, 3167. [Google Scholar] [CrossRef]
- Florkowski, M. Classification of Partial Discharge Images Using Deep Convolutional Neural Networks. Energies 2020, 13, 5496. [Google Scholar] [CrossRef]
- Kumar, H.; Shafiq, M.; Hussain, G.A.; Kumpulainen, L.; Kauhaniemi, K. Classification of PD Faults Using Features Extraction and K-Means Clustering Techniques. In Proceedings of the 2020 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), The Hague, The Netherlands, 26–28 October 2020; pp. 919–923. [Google Scholar]
- Cai, J.; Zhou, L.; Zhang, Y.; Wang, D.; Liao, W.; Zhang, C. Convenient Online Approach to Multisource Partial Discharge Localization in Transformer. IEEE Trans. Ind. Electron. 2022, 69, 9440–9450. [Google Scholar] [CrossRef]
- Sikorski, W. Development of Acoustic Emission Sensor Optimized for Partial Discharge Monitoring in Power Transformers. Sensors 2019, 19, 1865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ilkhechi, H.D.; Samimi, M.H. Applications of the Acoustic Method in Partial Discharge Measurement: A Review. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 42–51. [Google Scholar] [CrossRef]
- Besharatifard, H.; Hasanzadeh, S.; Heydarian-Forushani, E.; Alhelou, H.H.; Siano, P. Detection and Analysis of Partial Discharges in Oil-Immersed Power Transformers Using Low-Cost Acoustic Sensors. Appl. Sci. 2022, 12, 3010. [Google Scholar] [CrossRef]
- Chai, H.; Phung, B.T.; Mitchell, S. Application of UHF Sensors in Power System Equipment for Partial Discharge Detection: A Review. Sensors 2019, 19, 1029. [Google Scholar] [CrossRef] [Green Version]
- Karami, H.; Askari, F.; Rachidi, F.; Rubinstein, M.; Sikorski, W. An Inverse-Filter-Based Method to Locate Partial Discharge Sources in Power Transformers. Energies 2022, 15, 1988. [Google Scholar] [CrossRef]
- Lee, H.M.; Lee, G.S.; Kwon, G.-Y.; Bang, S.S.; Shin, Y.-J. Industrial Applications of Cable Diagnostics and Monitoring Cables via Time–Frequency Domain Reflectometry. IEEE Sens. J. 2021, 21, 1082–1091. [Google Scholar] [CrossRef]
- Ariannik, M.; Azirani, M.A.; Werle, P.; Azirani, A.A. UHF Measurement in Power Transformers: An Algorithm to Optimize Accuracy of Arrival Time Detection and PD Localization. IEEE Trans. Power Deliv. 2019, 34, 1530–1539. [Google Scholar] [CrossRef]
- Sikorski, W. Active Dielectric Window: A New Concept of Combined Acoustic Emission and Electromagnetic Partial Discharge Detector for Power Transformers. Energies 2019, 12, 115. [Google Scholar] [CrossRef] [Green Version]
- Si, W.; Fu, C.; Yuan, P. An Integrated Sensor With AE and UHF Methods for Partial Discharges Detection in Transformers Based on Oil Valve. IEEE Sens. Lett. 2019, 3, 1–3. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple Emitter Location and Signal Parameter—Estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Agoris, P.; Meijer, S.; Smit, J.J. Sensitivity Check of an Internal VHF/UHF Sensor for Trans-former Partial Discharge Measurements. In Proceedings of the POWERTECH’07, Lausanne, Switzerland, 1–5 July 2007; pp. 2065–2069. [Google Scholar]
- Cleary, G.P.; Judd, M.D. UHF and Current Pulse Measurements of Partial Discharge Activity in Mineral Oil. IEE Sci. Meas. Technol. 2006, 153, 47–54. [Google Scholar] [CrossRef]
- Coenen, S.; Tenbohlen, S.; Markalous, S.M.; Strehl, T. Attenuation of UHF Signals Regarding the Sensitivity Verification for UHF PD Measurements on Power Transformers. In Proceedings of the International Conference on Condition Monitoring and Diagnosis, Beijing, China, 21–24 April 2008. [Google Scholar]
- Judd, M.D. Transient Calibration of Electric Field Sensors. IEE Sci. Meas. Technol. 1999, 146, 113–116. [Google Scholar] [CrossRef] [Green Version]
- Li, J.H.; Si, W.R.; Yuan, P.; Li, Y.M.; Li, Y.M. Propagation Characteristic Study of Partial Discharge UHF Signal outside Transformer. In Proceedings of the International Conference on Condition Monitoring and Diagnosis, Beijing, China, 21–24 April 2008; pp. 1078–1080. [Google Scholar]
- Lopez-Roldan, J.; Tang, T.; Gaskin, M. Design and Testing of UHF Sensors for Partial Discharge Detection in Transformers. In Proceedings of the International Conference on Condition Monitoring and Diagnosis, Beijing, China, 21–24 April 2008; pp. 1052–1055. [Google Scholar]
- Ono, M.; Matsuyama, Y.; Otaka, N.; Yamagiwa, T.; Kato, T. Experience of GIS Condition Diagnosis Using Partial Discharge Monitoring by UHF Method. In Proceedings of the International Conference on Condition Monitoring and Diagnosis, Beijing, China, 21–24 April 2008; pp. 1108–1110. [Google Scholar]
- Wu, Q.; Liu, G.; Xia, Z.; Lu, L. The study of Archimedean spiral antenna for partial discharge measurement. In Proceedings of the Fourth International Conference on Intelligent Control and Information Processing (ICICIP), Beijing, China, 9–11 June 2013; pp. 694–698. [Google Scholar]
- Sikorski, W.; Szymczak, C.; Siodla, K.; Polak, F. Hilbert curve fractal antenna for detection and on-line monitoring of partial discharges in power transformers. Eksploat. I Niezawodn. 2018, 20, 343–351. [Google Scholar] [CrossRef]
- Hai-Feng, Y.; Yong, Q.; Yue, D.; Ge-Hao, S.; Xiu-Chen, J. Development of Multi-Band Ultra-High-Frequency Sensor for Partial Discharge Monitoring Based on the Meandering Technique. IET Sci. Meas. Technol. 2014, 8, 327–335. [Google Scholar] [CrossRef]
- Sarkar, B.; Mishra, D.K.; Koley, C.; Roy, N.K. Microstrip patch antenna based UHF sensor for detection of Partial Discharge in High Voltage electrical equipments. In Proceedings of the India Conference (INDICON), Pune, India, 11–13 December 2014; pp. 1–6. [Google Scholar]
- Suryandi, A.A.; Khayam, U. New Designed Bowtie Antenna with Middle Sliced Modification as UHF Sensor for Partial Discharge Measurement. In Proceedings of the International Conference on Smart Green Technology in Electrical and Information Systems (ICSGTEIS), Kuta, Indonesia, 5–7 November 2014; pp. 98–101. [Google Scholar]
- Slone, R. Practical Antenna Handbook; McGraw-Hill Education: New York, NY, USA, 2011. [Google Scholar]
- Walczak, K.; Sikorski, W. Non-Contact High Voltage Measurement in the Online Partial Discharge Monitoring System. Energies 2021, 14, 5777. [Google Scholar] [CrossRef]
- Nadolny, Z. Determination of Dielectric Losses in a Power Transformer. Energies 2022, 15, 993. [Google Scholar] [CrossRef]
- Nefyodov, E.I.; Smolsky, S.M. Electromagnetic Fields and Waves. Microwaves and mmWave Engineering with Generalized Macroscopic Electrodynamics; Springer: New York, NY, USA, 2019. [Google Scholar]
- Walczak, K.; Waszkiewicz, A. Detection of defects in the solid insulation of power devices using X-rays. Przegląd Elektrotechniczny 2010, 86, 279–282. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walczak, K. Localization of HV Insulation Defects Using a System of Associated Capacitive Sensors. Energies 2023, 16, 2297. https://doi.org/10.3390/en16052297
Walczak K. Localization of HV Insulation Defects Using a System of Associated Capacitive Sensors. Energies. 2023; 16(5):2297. https://doi.org/10.3390/en16052297
Chicago/Turabian StyleWalczak, Krzysztof. 2023. "Localization of HV Insulation Defects Using a System of Associated Capacitive Sensors" Energies 16, no. 5: 2297. https://doi.org/10.3390/en16052297
APA StyleWalczak, K. (2023). Localization of HV Insulation Defects Using a System of Associated Capacitive Sensors. Energies, 16(5), 2297. https://doi.org/10.3390/en16052297




