Energy Management Strategies of Grid-Connected Microgrids under Different Reliability Conditions
Abstract
1. Introduction
2. Literature on Energy Management of Microgrids
- An intelligent EMS is developed for optimal use of grid-connected microgrids consisting of grid, P.V. and battery storage systems that could ensure reliable operation of the system at low cost using fuzzy logic.
- A procedure has been proposed for the evaluation of expected energy, not supply, evaluation of a microgrid that could guarantee reliable and continuous system operations.
- A systematic procedure has been proposed for the construction of the system cycle.
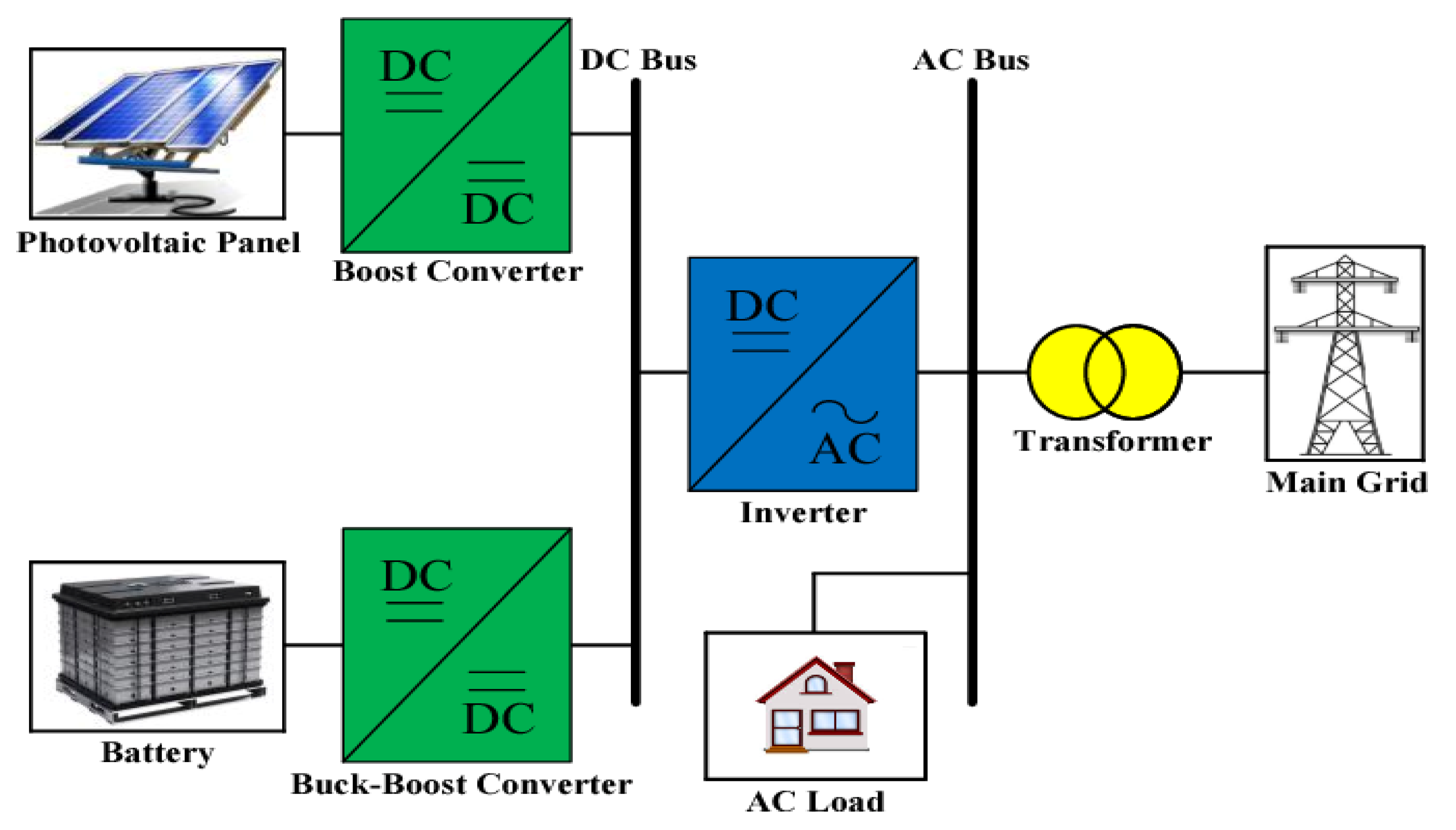
3. System Configuration and Operations
4. Mathematical Models of the Microgrid System Configuration
4.1. P.V. System Model
4.2. Energy Storage System Modelling
4.3. Grid Cost Model
5. Simulations and Fuzzy Logic Design
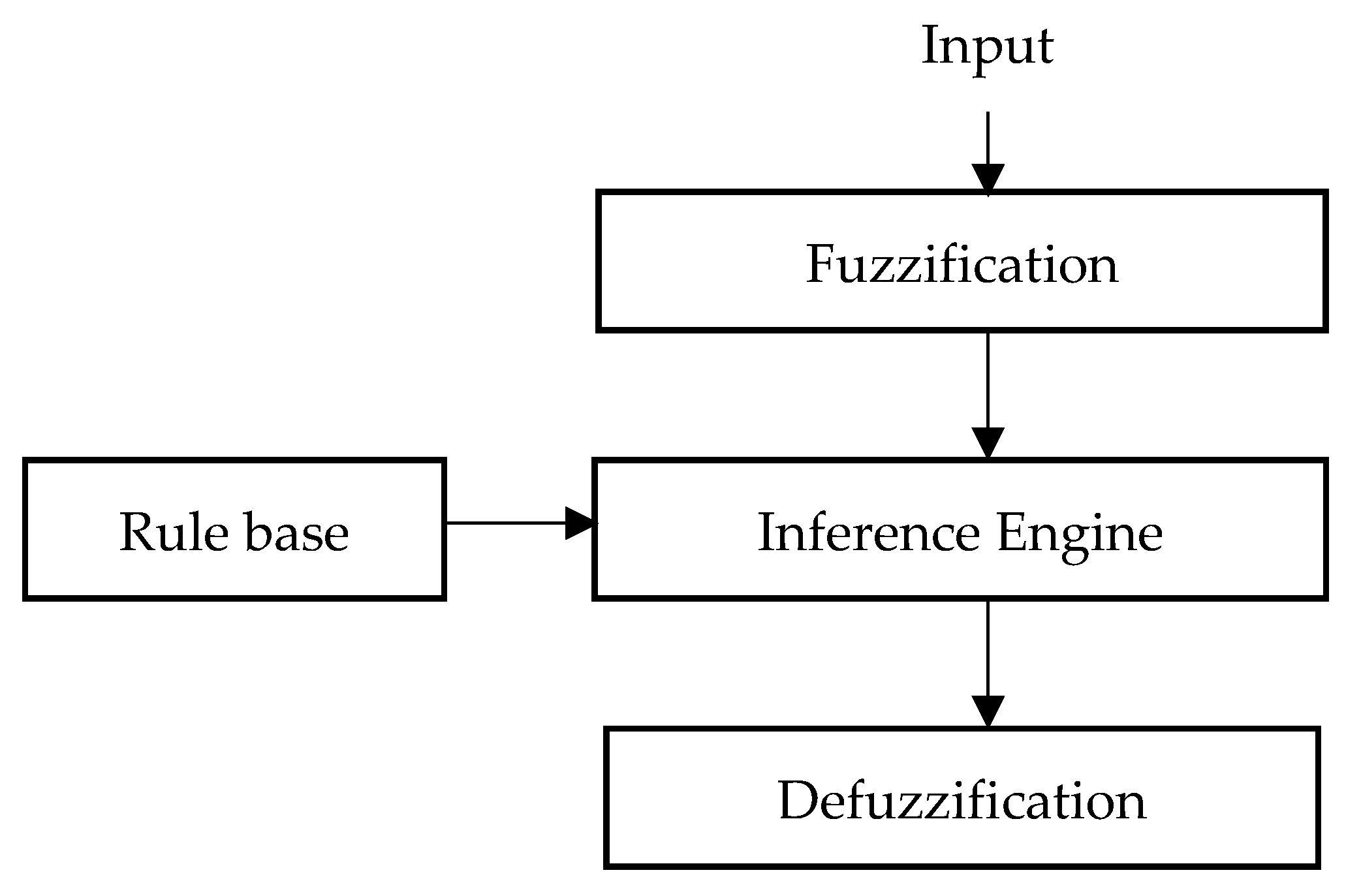
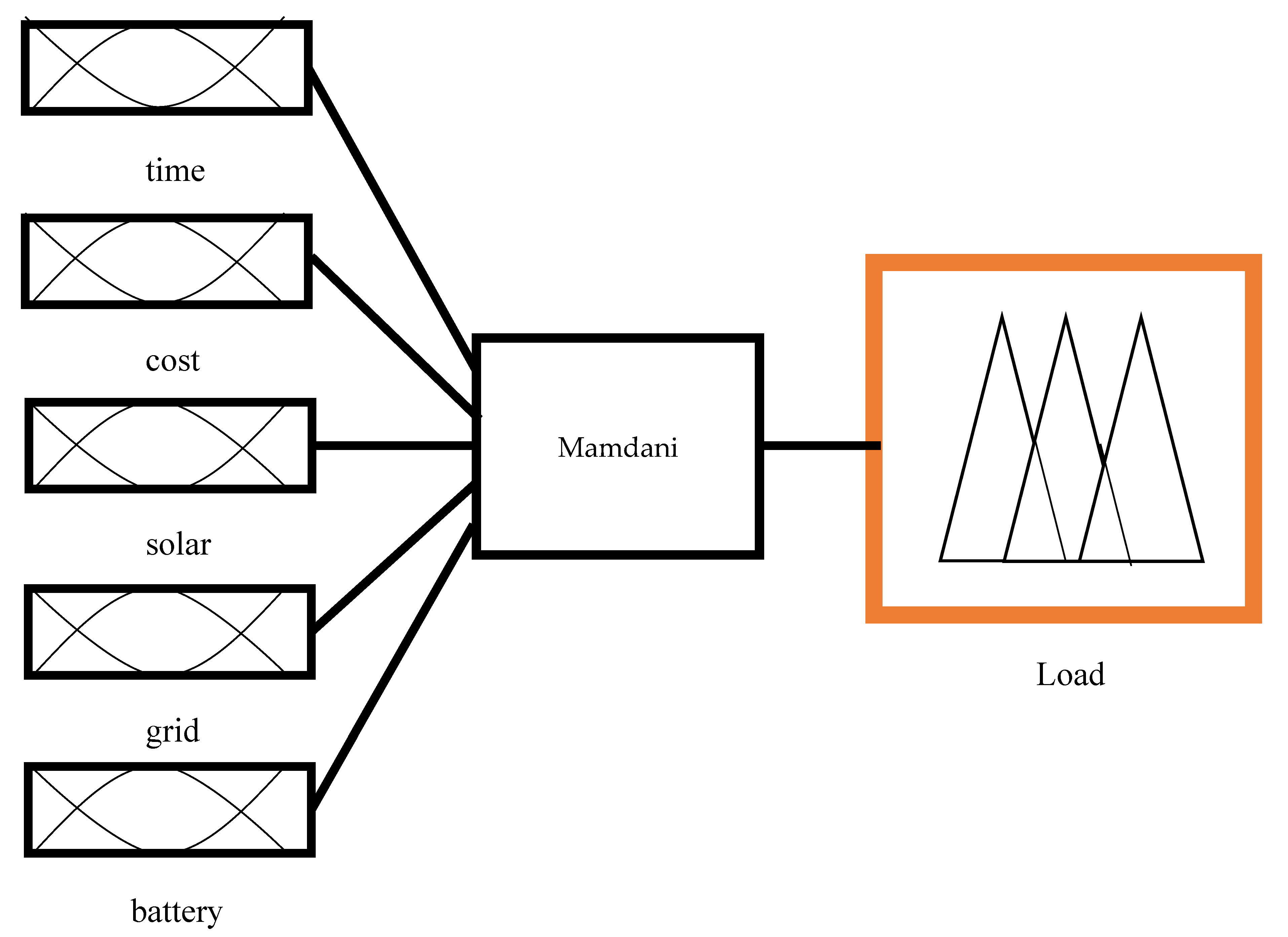
5.1. Fuzzy Logic Controller Design
| S/N | Time | Range |
|---|---|---|
| 1 | Day | 1–12 |
| 2 | Night | 12–24 |
| Cost | Range | |
|---|---|---|
| 1 | Off-peak | 0–43.3 |
| 2 | Peak | 43–58.5 |
| S/N | Solar PV | Range |
|---|---|---|
| 1 | Low | 0–9 |
| 2 | High | 10–20 |
| S/N | Grid | Range |
|---|---|---|
| 1 | No | 0–0.1 |
| 2 | Yes | 1–6 |
- I.
- Load demand must be fulfilled at any particular time of the day.
- II.
- Energy sources must be managed based on cost.
- III.
- State of charge should not go below a given threshold to avoid overcharge and discharging.
- IV.
- Grid energy as the primary source of energy.
- V.
- Manage the fluctuation of solar PV.
| Time | Cost | Battery | Grid | P.V. | Fuzzy Output |
|---|---|---|---|---|---|
| Day | off-peak | Basic | YES | Low | Connect to grid |
| High | Connect to grid | ||||
| No | Low | Connect to P.V./Battery | |||
| High | Connect to P.V./Battery | ||||
| Heavy | YES | Low | Connect to grid | ||
| High | Connect to grid | ||||
| No | Low | Connect to P.V./Battery | |||
| High | Connect to P.V./Battery | ||||
| peak | Basic | YES | Low | Connect to grid | |
| High | Connect to P.V./Battery | ||||
| No | Low | Connect to P.V./Battery | |||
| High | Connect to P.V./Battery | ||||
| Heavy | YES | Low | Connect to grid | ||
| High | Connect to P.V./Battery | ||||
| No | Low | Connect to P.V./Battery | |||
| High | Connect to P.V./Battery | ||||
| Night | off-peak | Basic | YES | Low | Connect to grid |
| High | Connect to grid | ||||
| No | Low | Connect to P.V./Battery | |||
| High | Connect to P.V./Battery | ||||
| Heavy | YES | Low | Connect to grid | ||
| High | Connect to P.V./Battery | ||||
| No | Low | Connect to P.V./Battery | |||
| High | Connect to P.V./Battery | ||||
| Peak | Basic | YES | Low | Connect to grid | |
| High | Connect to grid | ||||
| No | Low | Connect to P.V./Battery | |||
| High | Connect to P.V./Battery | ||||
| Heavy | YES | Low | Connect to grid | ||
| High | Connect to P.V./Battery | ||||
| No | Low | Connect to P.V./Battery | |||
| High | Connect to P.V./Battery |
5.2. Case I
5.3. Case II
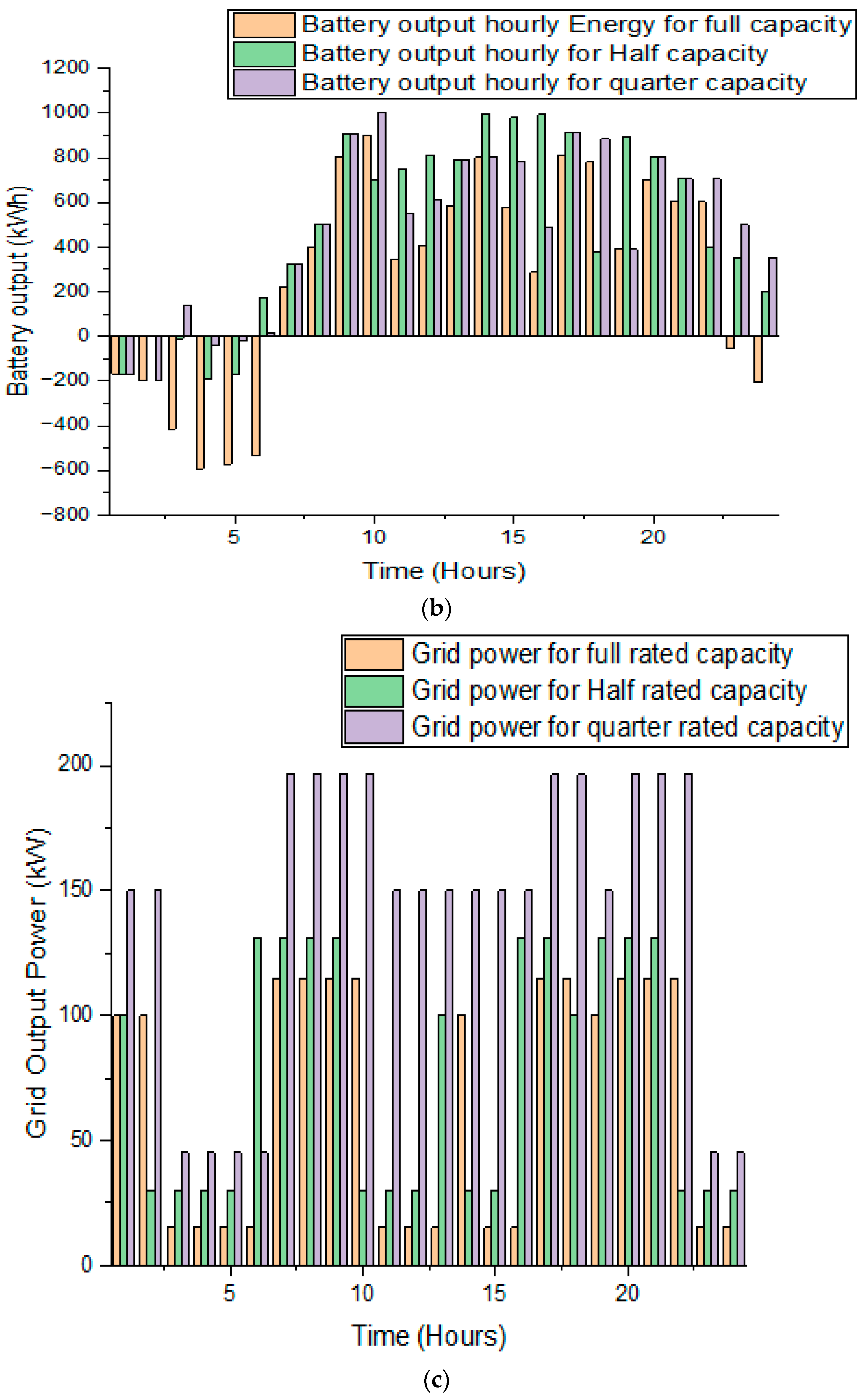
6. Output Power Management
- System reliability improvement by capacity of renewable energy system;
- System reliability improvement by the use of storage units;
- System reliability improvement by increasing output power of the grid.
7. Proposed Reliability Improvement Options for the Microgrid
7.1. System Reliability Improvement by Capacity of P.V. System Energy System
- where = rated power of P.V. system, and the factor that this alternative capacity increment is defined as A.
- New energy output can be is obtained using:number of states
- Annual grid energy annual energy is defined:
- Fuel saving is defined as:
- New annual system cost can be defined as follows:where = capital cost of P.V. system.
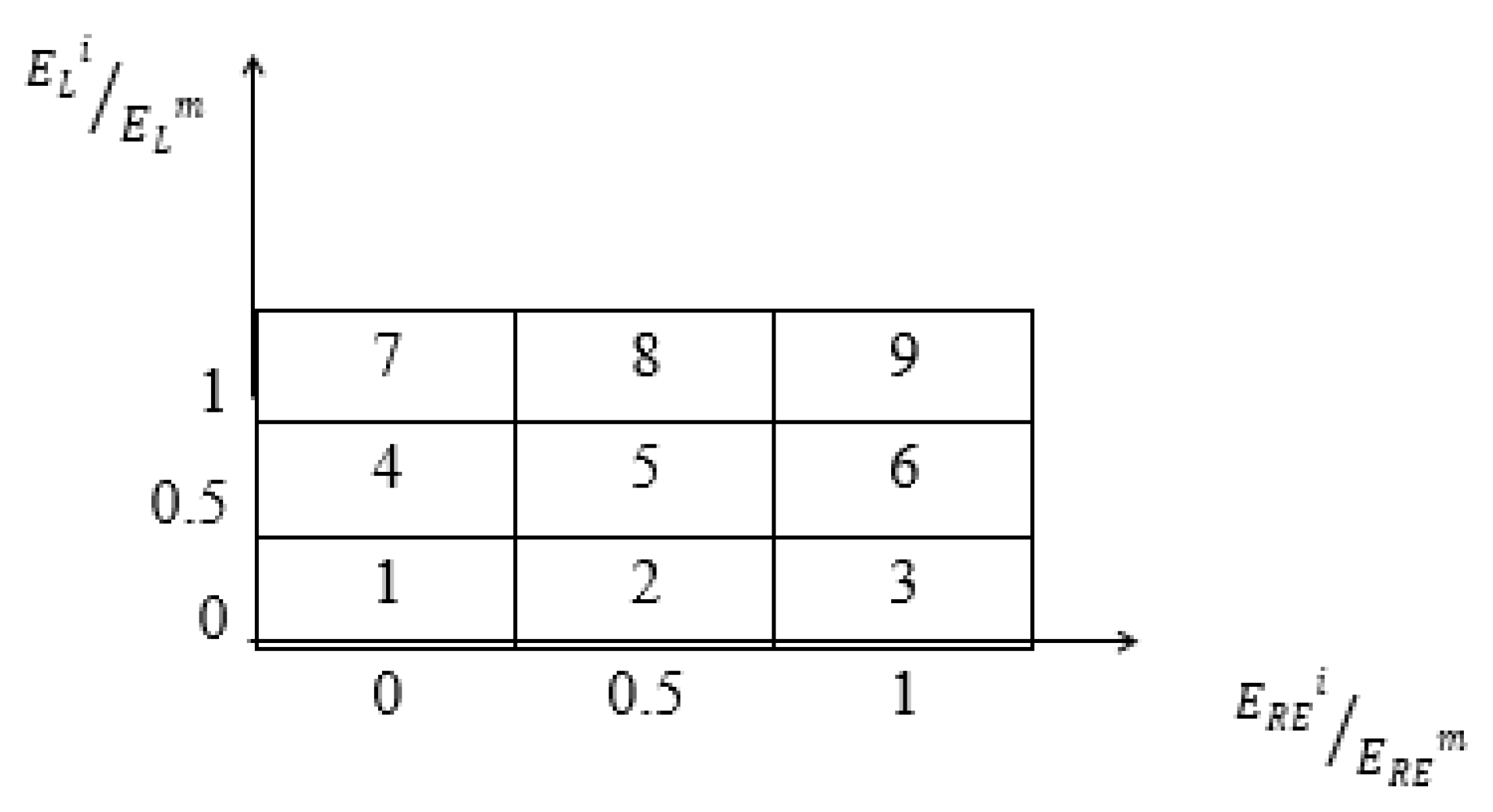
- In each case, the EEENS is obtained with a view of making it equal to zero (EENS = 0).
7.2. Battery Storage Option
- ❖
- Duration in each state:
7.3. System Reliability Improvement by Increasing the Output Power from the Grid
- When the P.V. power is equal or greater than the system demand:
- When the P.V. output power is less than the demand:
- When the power is provided by the solar energy sources only.
- When the load is fully supply by the external grid.
- The battery storage is added into the microgrid.
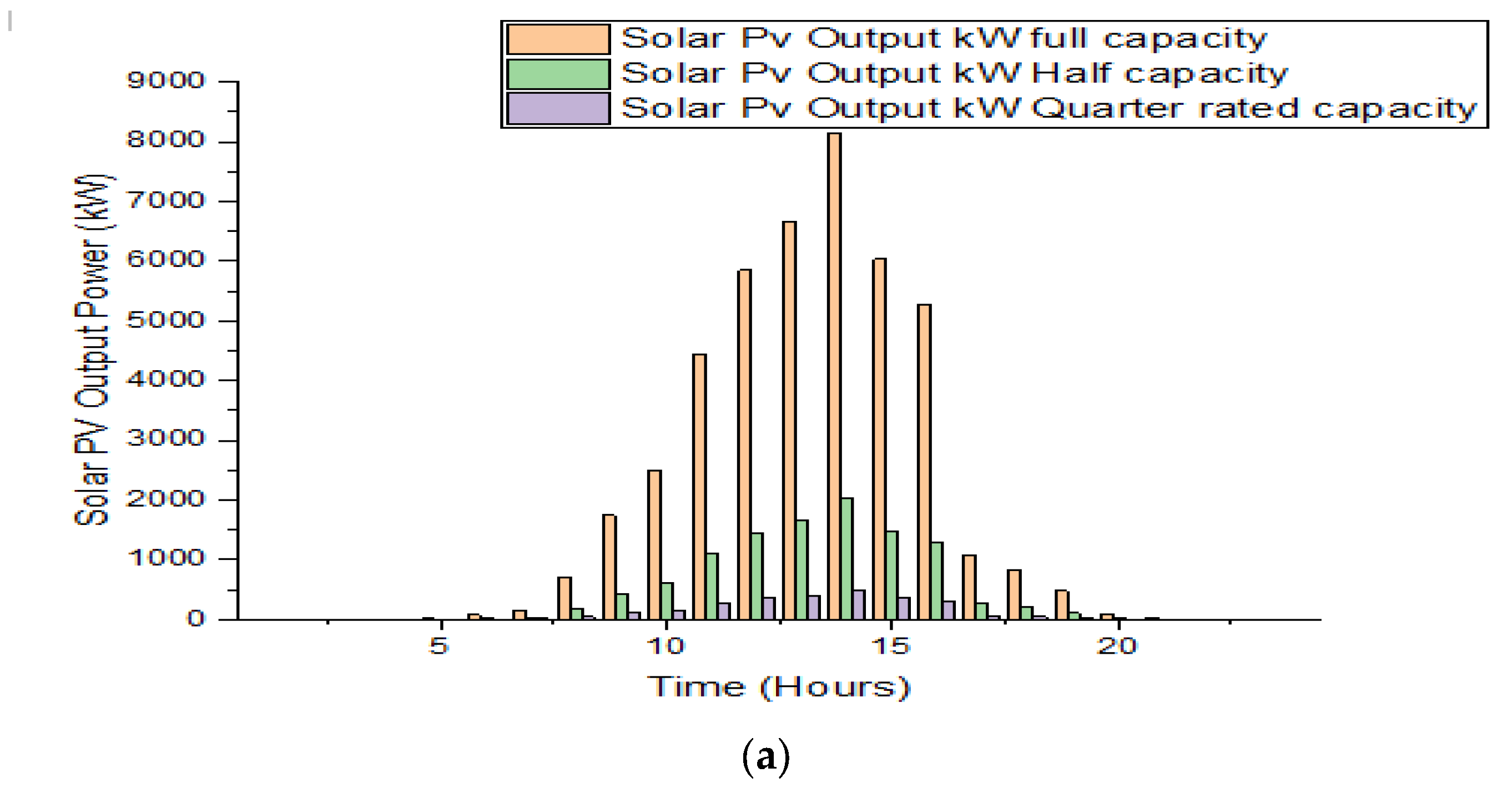
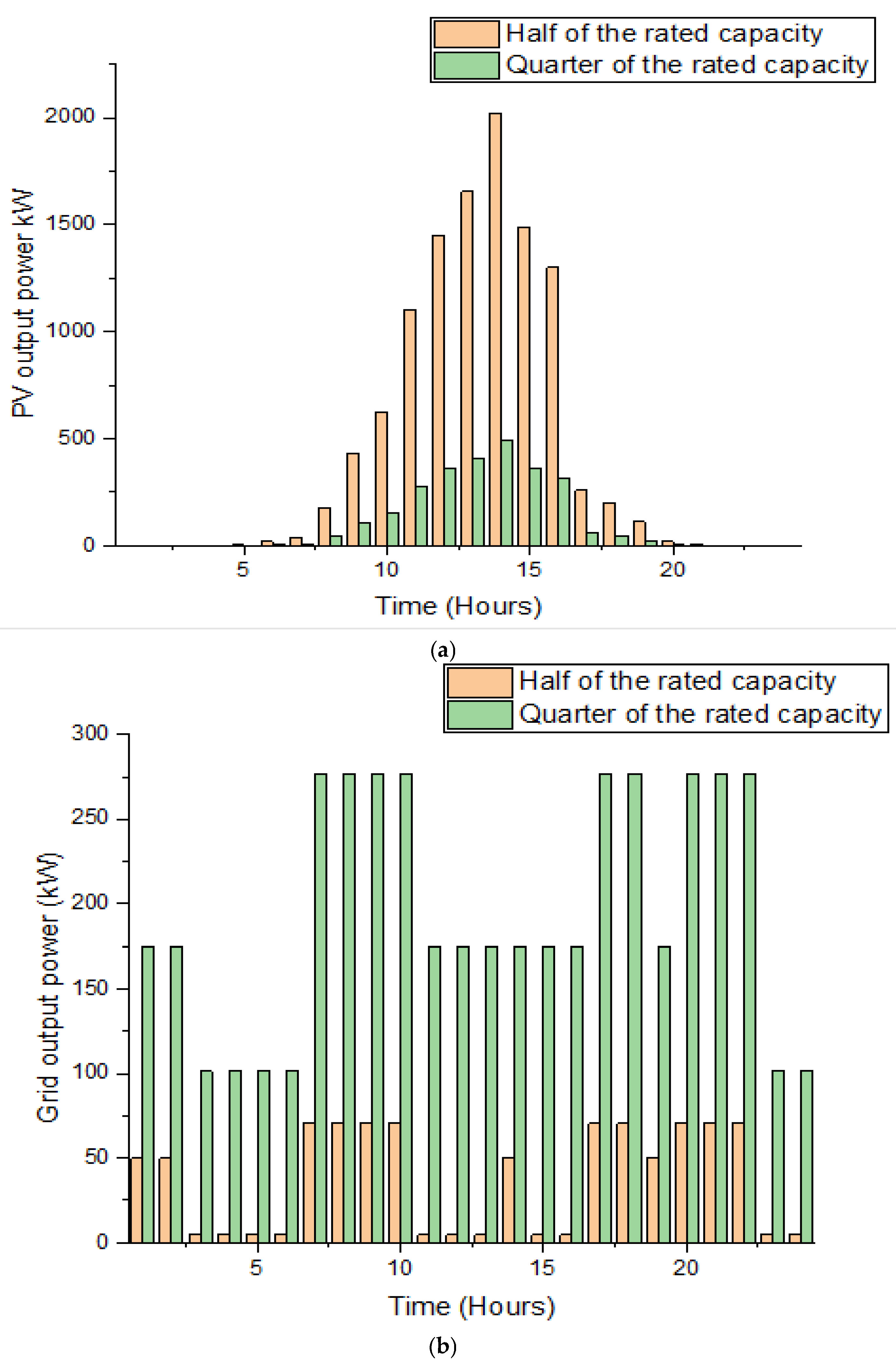
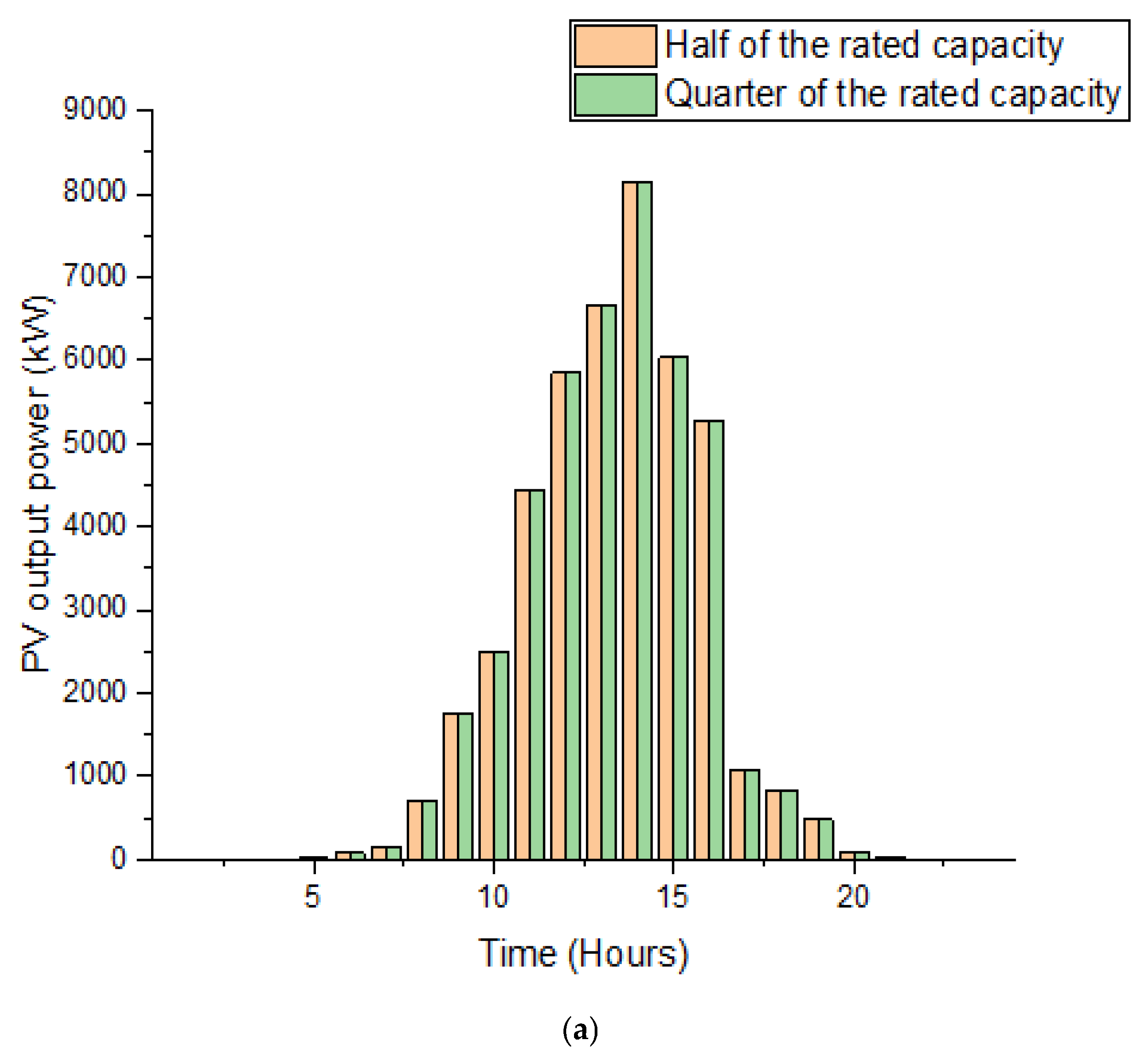
7.4. PV System Variation
7.5. Battery Storage Characteristics
7.6. Grid Variations
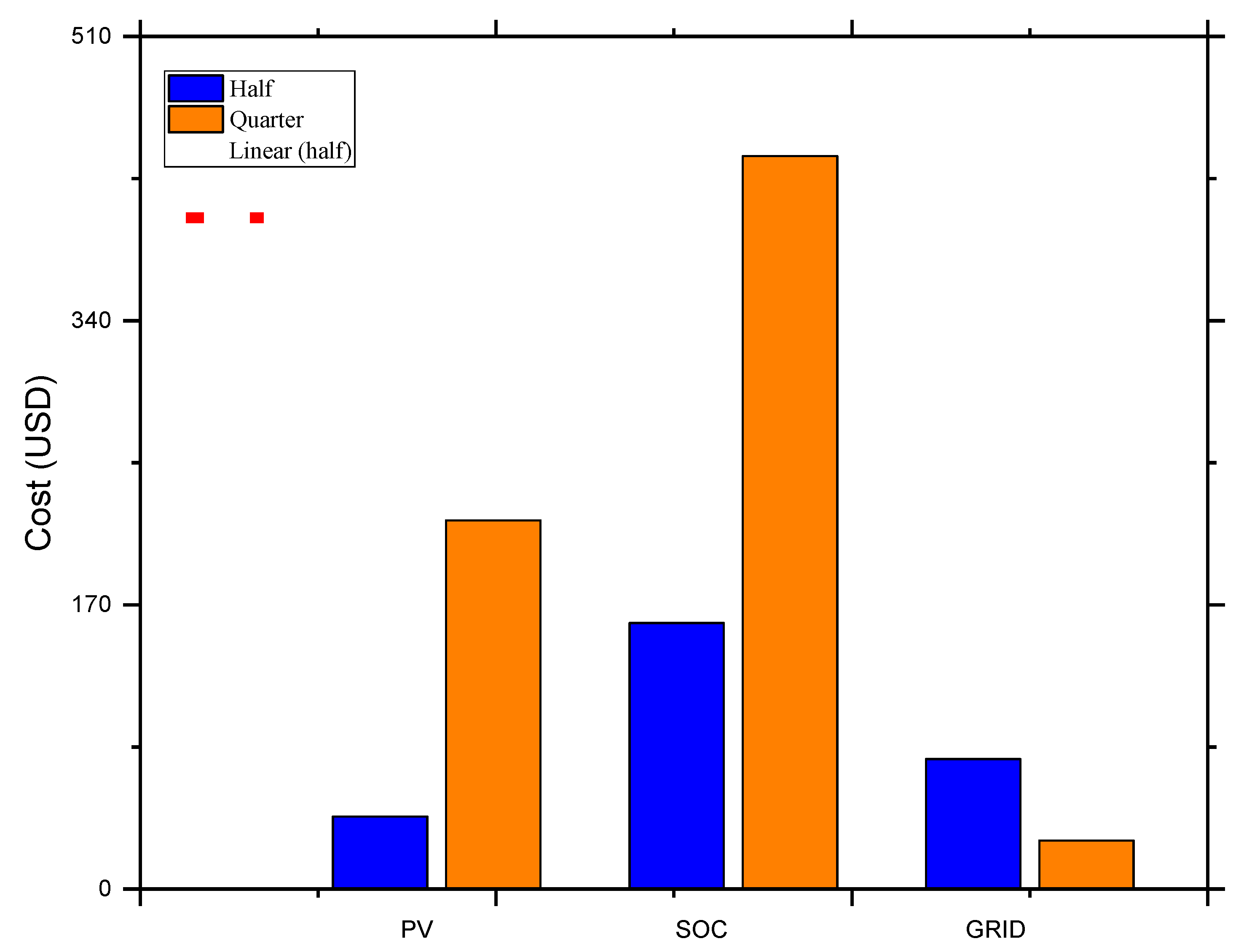
8. Economic Analyses of the Model
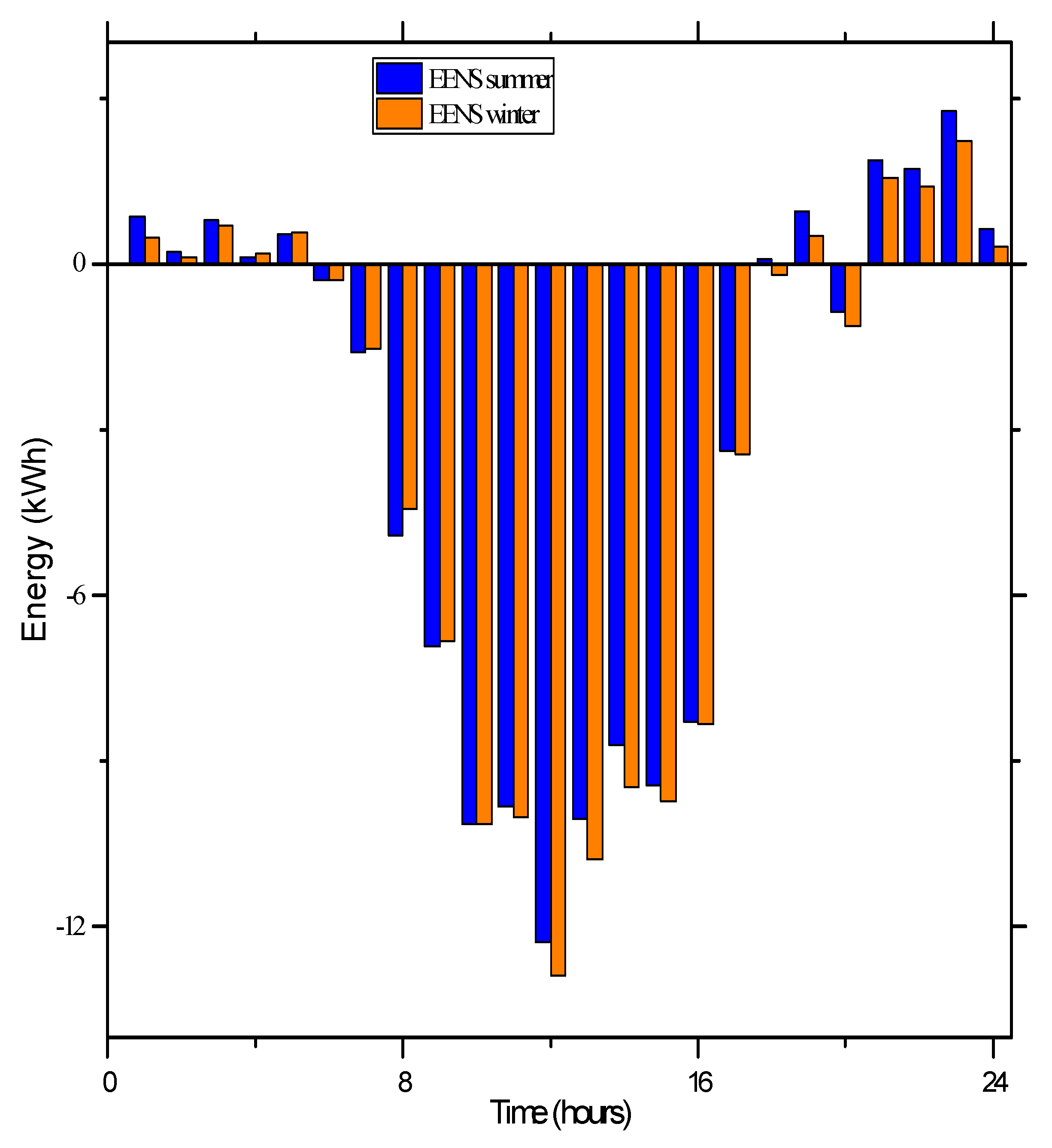
9. Development of System Cycle
10. Results Discussion
11. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Parhizi, S.; Lotfi, H.; Khodaei, A.; Bahramirad, S. State of the Art in Research on Microgrids: A Review. IEEE Access 2015, 3, 890–925. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Loh, P.C.; Lee, T.L.; Chandorkar, M. Advanced Control Architectures for Intelligent Microgrids—Part II: Power Quality, Energy Storage, and AC/DC Microgrids. IEEE Trans. Ind. Electron. 2013, 60, 1263–1270. [Google Scholar] [CrossRef]
- Xia, Y.; Wei, W.; Yu, M.; Wang, X.; Peng, Y. Power Management for a Hybrid AC/DC Microgrid with Multiple Subgrids. IEEE Trans. Power Electron. 2018, 33, 3520–3533. [Google Scholar] [CrossRef]
- Radwan, A.A.A.; Mohamed, Y.A.R.I. Networked Control and Power Management of AC/DC Hybrid Microgrids. IEEE Syst. J. 2017, 11, 1662–1673. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Sinha, A.K.; Kishore, N.K. Control Techniques in AC, DC, and Hybrid A.C.–D.C. Microgrid: A Review. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 738–759. [Google Scholar]
- Meng, J.; Wang, Y.; Wang, C.; Wang, H. Design and Implementation of Hardware-in-the-loop Simulation System for Testing Control and Operation of DC Microgrid with Multiple Distributed Generation Units. IET Gener. Transm. Distrib. 2016, 11, 3065–3072. [Google Scholar] [CrossRef]
- Li, Z.; Shahidehpour, M.; Aminifar, F.; Alabdulwahab, A.; Al-Turki, Y. Networked Microgrids for Enhancing the Power System Resilience. Proc. IEEE 2017, 105, 1289–1310. [Google Scholar] [CrossRef]
- Jap, L.; Moreira, C.L.; Madureira, A.G. Defining Control Strategies for MicroGrids Islanded Operation. IEEE Trans. Power Syst. 2006, 21, 916–924. [Google Scholar]
- Che, L.; Shahidehpour, M.; Alabdulwahab, A.; Al-Turki, Y. Hierarchical Coordination of a Community Microgrid with AC and DC Microgrids. IEEE Trans. Smart Grid 2015, 6, 3042–3051. [Google Scholar] [CrossRef]
- Waqar, A.; Tanveer, M.S.; Ahmad, J.; Aamir, M.; Yaqoob, M.; Anwar, F. Multi-Objective Analysis of a CHP Plant Integrated Microgrid in Pakistan. Energies 2017, 10, 1625. [Google Scholar] [CrossRef]
- Rehman, S.U.; Rehman, S.; Shoaib, M.; Siddiqui, I.A. Feasibility Study of a Grid-tied Photovoltaic System for Household in Pakistan: Considering an Unreliable Dlectric grid. Environ. Prog. Sustain. Energy 2019. [Google Scholar] [CrossRef]
- Gao, H.-C.; Choi, J.-H.; Yun, S.-Y.; Lee, H.-J.; Ahn, S.-J. Optimal scheduling and real-time control schemes of battery energy storage system for microgrids considering contract demand and forecast uncertainty. Energies 2018, 11, 1371. [Google Scholar] [CrossRef]
- Nasir, M.; Khan, H.A.; Khan, I.; Hassan, N.U.; Zaffar, N.A.; Mehmood, A.; Sauter, T.; Muyeen, S.M. Grid load reduction through optimized PV power utilization in intermittent grids using a low-cost hardware platform. Energies 2019, 12, 1764. [Google Scholar] [CrossRef]
- Vejdan, S.; Grijalva, S. Analysis of multiple revenue streams for privately-owned energy storage systems. In Proceedings of the IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 22–23 February 2018; pp. 1–5. [Google Scholar]
- Zhang, S.G.X. Smart energy campus: A smart grid test bed for advanced modeling, simulation, and decision-making. In Proceedings of the Carnegie Mellon Conference on the Electricity Industry, Pittsburgh, PA, USA, 30 March 2015; pp. 1–5. [Google Scholar]
- Zheng, Y.; Zhao, J.; Song, Y.; Luo, F.; Meng, K.; Qiu, J.; Hill, D.J. Optimal operation of battery energy storage system considering distribution system uncertainty. IEEE Trans. Sustain. Energy 2018, 9, 1051–1060. [Google Scholar] [CrossRef]
- Perkovi, L.; Mikul, H.; Dui, N. Multi-objective optimization of a simplied factory model acting as a prosumer on the electricity market. J. Clean. Prod. 2017, 167, 1438–1449. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Hannan, M.A.; Mohamed, A.; Amiruldin, U.A.U.; Abidin, I.Z.; Uddin, M.N. An optimal scheduling controller for virtual power plant and microgrid integration using binary backtracking search algorithm. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 4 October 2017; pp. 1–8. [Google Scholar]
- Teo, T.T.; Logenthiran, T.; Woo, W.L.; Abidi, K. Near-optimal dayahead scheduling of energy storage system in grid-connected microgrid. In Proceedings of the IEEE Innovative Smart Grid Technologies Conference Asia (ISGT Asia), Singapore, 22–25 May 2018; pp. 1257–1261. [Google Scholar]
- Vahedipour-Dahraie, M.; Rashidizadeh-Kermani, H.; Anvari-Moghaddam, A.; Guerrero, J.M. Stochastic frequencysecurity constrained scheduling of a microgrid considering price-driven demand response. In Proceedings of the International Symposium on Power Electronics Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 716–721. [Google Scholar]
- Sattarpour, T.; Nazarpour, D.; Golshannavaz, S. A multi-objective HEM strategy for smart home energy scheduling: A collaborative approach to support microgrid operation. Sustain. Cities Soc. 2018, 37, 26–33. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, F.; Wang, G.; Meng, K. Coordinated optimal scheduling of multi-energy microgrid considering uncertainties. In Proceedings of the IEEE International Conference on Energy Internet (ICEI), Beijing, China, 21–25 May 2018; pp. 315–320. [Google Scholar]
- Li, Y.; Yang, Z.; Li, G.; Mu, Y.; Zhao, D.; Chen, C.; Shen, B. Optimal scheduling of isolated microgrid with an electric vehicle battery swapping station in multi-stakeholder scenarios: A bi-level programming approach via real-time pricing. Appl. Energy 2018, 232, 54–68. [Google Scholar] [CrossRef]
- Chen, Y.; Trifkovic, M. Optimal scheduling of a microgrid in a volatile electricity market environment: Portfolio optimization approach. Appl. Energy 2018, 226, 703–712. [Google Scholar] [CrossRef]
- Hwang, T.; Yoo, Y.; Kang, S.; Lee, I. Design of a prosumer EMS for energy trading. IOP Conf. Earth Environ. Sci. 2018, 136, 012006. [Google Scholar] [CrossRef]
- Raj, P.; Kowli, A. Honoring grid commitments: Prosumer scheduling under uncertainty. In Proceedings of the IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Bangalore, India, 8–10 November 2017; pp. 1–6. [Google Scholar]
- Gautier, A. The Prosumers and the Grid. Prosumers Grid 2018, 53, 100–126. [Google Scholar]
- Hao, S.; Coe, S. Scheduling of site battery energy storage for demand response capacity. In Proceedings of the Annual IEEE GreenTech Conference, New Orleans, LA, USA, 15–17 April 2015; pp. 169–175. [Google Scholar]
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.S. Modeling of lithium-ion battery degradation for cell life assessment. IEEE Trans. Smart Grid 2018, 9, 1131–1140. [Google Scholar] [CrossRef]
- Mutarraf, M.; Terriche, Y.; Niazi, K.A.K.; Khan, F.; Vasquez, J.; Guerrero, J. Control of hybrid diesel/PV/battery/ultra-capacitor systems for future shipboard microgrids. Energies 2019, 12, 3460. [Google Scholar] [CrossRef]
- Vahedipour-Dahraie, M.; Rashidizadeh-Kermani, H.; Anvari-Moghaddam, A.; Guerrero, J.M. Stochastic risk-constrained scheduling of renewable-powered autonomous microgrids with demand response actions: Reliability and economic implications. IEEE Trans. Ind. Appl. 2020, 56, 1882–1895. [Google Scholar] [CrossRef]
- Abhinav, R.; Pindoriya, N.M. Grid integration of wind turbine and battery energy storage system: Review and key challenges. In Proceedings of the IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar]
- Mohiti, M.; Monsef, H.; Anvari-Moghaddam, A.; Lesani, H. Twostage robust optimization for resilient operation of microgrids considering hierarchical frequency control structure. IEEE Trans. Ind. Electron. 2019, 67, 9439–9449. [Google Scholar] [CrossRef]
- Muqeet, H.A.; Sajjad, I.A.; Ahmad, A.; Iqbal, M.M.; Ali, S.; Guerrero, J.M. Optimal operation of energy storage system for a prosumer microgrid considering economical and environmental effects. In Proceedings of the International Symposium on Recent Advances in Electrical Engineering (RAEE), Islamabad, Pakistan, 28–29 August 2019; Volume 4, pp. 1–6. [Google Scholar]
- Kyriakopoulos, G.L.; Arabatz, G. Electrical energy storage systems in electricity generation: Energy policies, innovative technologies, and regulatory regimes. Renew. Sustain. Energy Rev. 2016, 56, 1044–1067. [Google Scholar] [CrossRef]
- Abdeltawab, H.H.; Mohamed, Y.A.-R.-I. Mobile energy storage scheduling and operation in active distribution systems. IEEE Trans. Ind. Electron. 2017, 64, 6828–6840. [Google Scholar] [CrossRef]
- Parhizi, S.; Khodaei, A.; Shahidehpour, M. Market-based versus price based microgrid optimal scheduling. IEEE Trans. Smart Grid 2018, 9, 615–623. [Google Scholar] [CrossRef]
- Saxena, N.; Hussain, I.; Singh, B.; Vyas, A.L. Implementation of a grid-integrated PV-battery system for residential and electrical vehicle applications. IEEE Trans. Ind. Electron. 2018, 65, 6592–6601. [Google Scholar] [CrossRef]
- Meshcheryakov, V.A.; Denisov, I.V. Operation algorithm of adaptive network-based fuzzy control system for a jib crane. Autom. Remote Control 2013, 74, 1393–1398. [Google Scholar] [CrossRef]
- Obasi, J.; Kihato, P.; Ngoo, L.; Muriithi, C. Fuzzy Logic Energy Management for a Renewable Hybrid Energy System. J. Multidiscip. Eng. Sci. Technol. 2016, 3, 3949. [Google Scholar]
- Uddin, N.; Islam, M.S. Optimal Fuzzy Logic Based Smart Energy Management System For Real Time Application Integrating RES, Grid and Battery. In Proceedings of the 2018 4th International Conference on Electrical Engineering and Information Communication Technology (iCEEiCT), Dhaka, Bangladesh, 13–15 September 2018. [Google Scholar]







| Battery Parameter | P.V. Parameter |
|---|---|
| Nominal voltage = 24 v Rated capacity = 50 Ah Initial state of charge = 45% Battery response time = 1 s Cut off voltage = 18 v Fully charged voltage = 27.9 v Nominal discharge current = 21.7 A Internal resistance = 0.0048 ohms | Shunt resistance = 415.5 ohms Series resistance = 0.221 ohms Total number of cells in series = 54 Total number of cells in parallel = 1 Short circuit current = 8.21 A Open circuit voltage = 32.9 v Current at maximum power = 7.58 A Voltage at maximum power = 26.4 v Rated power = 200 w Nominal tempt = 298 k Electron charge = 1.6 × 10−19 C Boltzmann’s constant = 1.38 × 10−23 Band gap energy of the semiconductor = 1.1 eV The ideality factor of the diode = 1.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshehri, M.A.H.; Guo, Y.; Lei, G. Energy Management Strategies of Grid-Connected Microgrids under Different Reliability Conditions. Energies 2023, 16, 3951. https://doi.org/10.3390/en16093951
Alshehri MAH, Guo Y, Lei G. Energy Management Strategies of Grid-Connected Microgrids under Different Reliability Conditions. Energies. 2023; 16(9):3951. https://doi.org/10.3390/en16093951
Chicago/Turabian StyleAlshehri, Mohammed Abdullah H., Youguang Guo, and Gang Lei. 2023. "Energy Management Strategies of Grid-Connected Microgrids under Different Reliability Conditions" Energies 16, no. 9: 3951. https://doi.org/10.3390/en16093951
APA StyleAlshehri, M. A. H., Guo, Y., & Lei, G. (2023). Energy Management Strategies of Grid-Connected Microgrids under Different Reliability Conditions. Energies, 16(9), 3951. https://doi.org/10.3390/en16093951










