A Comprehensive Review of Behind-the-Meter Distributed Energy Resources Load Forecasting: Models, Challenges, and Emerging Technologies
Abstract
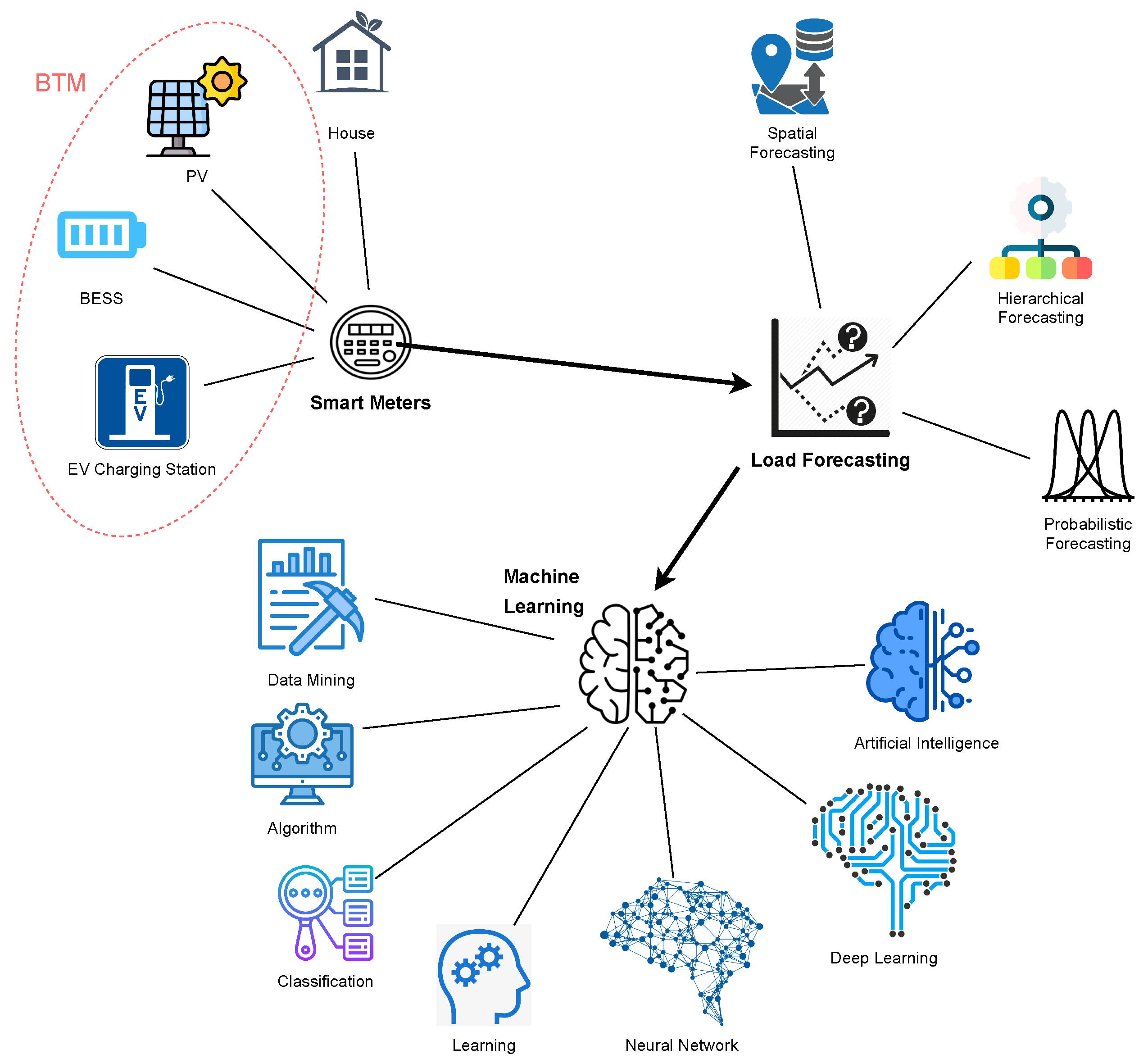
:1. Introduction
1.1. Background
1.2. Problem Statement
1.3. Contributions
- A comprehensive survey on how the load forecasting process of BTM DERs in residential locations regarding different combinations of PVs, BESSs, and EV charging infrastructures has been provided with state-of-the-art technologies in recent years.
- This review encompasses a wide range of models employed in load forecasting processes, showcasing a broad spectrum, from conventional approaches to state-of-the-art ML algorithms. This study delves into the applicability of each model, providing a thorough understanding of their capabilities and limitations. Furthermore, a systematic methodology for model selection and optimization has been introduced, considering the computational effort, and offering a structured approach to identifying the most suitable forecasting techniques for specific use cases.
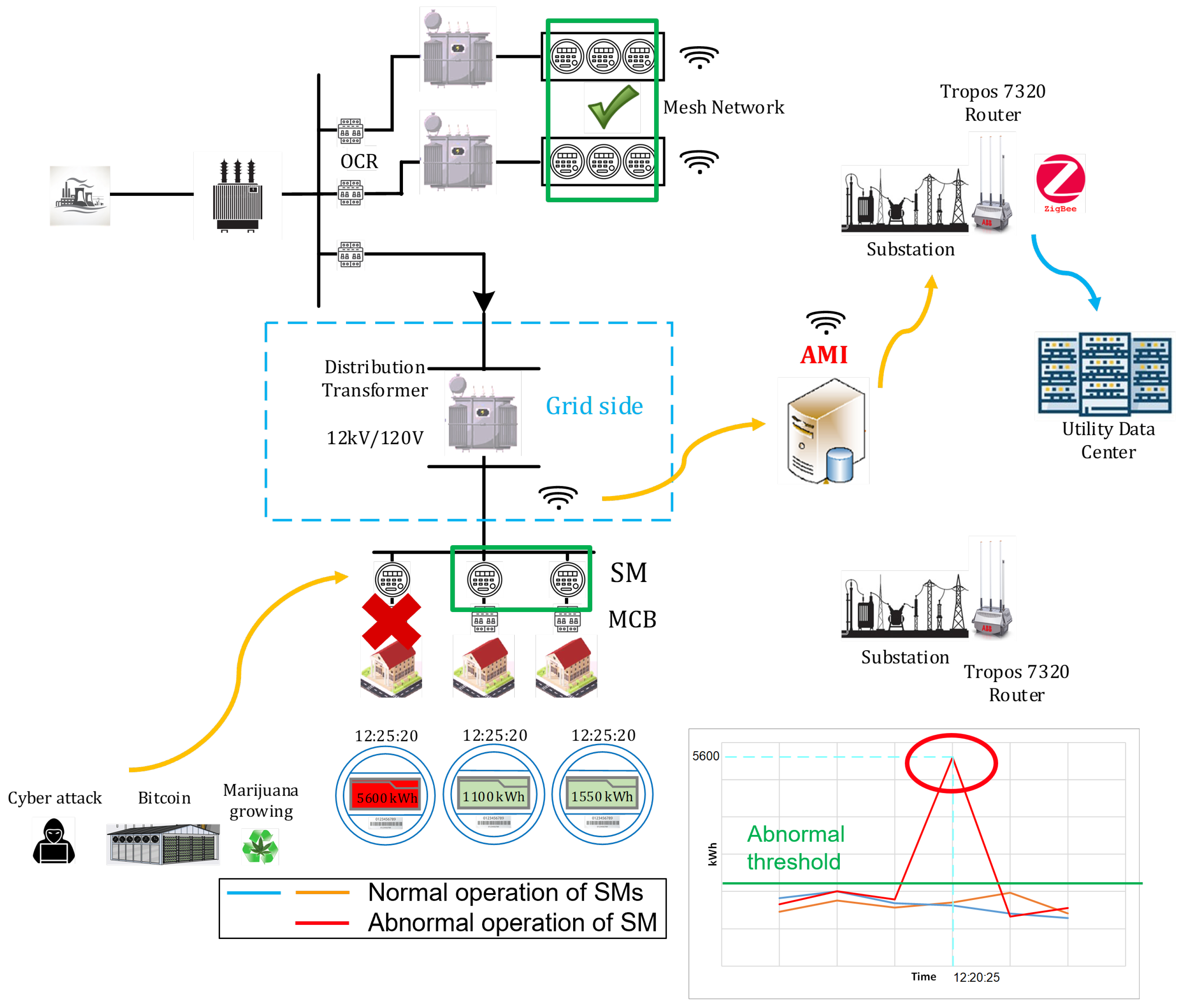
- Some case studies considering abnormal activities (e.g., Bitcoin mining) in residential households with BTM DERs are considered for the first time as potential proposed scenarios that make the anomaly process challenging. These attacks/anomalies can also occur in digital substations through communication messages [15] that are in a loop with residential/commercial locations. A proposed conceptual framework for anomaly detection has been introduced to elucidate the pivotal nature of this process. An LLM-based anomaly detection can be considered as a new methodology to handle this process with less effort and with acceptable accuracy in terms of performance evaluation metrics. Moreover, an extensive analysis of the potential challenges associated with BTM DERs and load forecasting algorithms has been initially conducted, providing valuable insights for future research and development.
1.4. Paper Structure
2. Related Work on Load Forecasting
| Ref. | Application | Contributions | Constrains/Challenges |
|---|---|---|---|
| Li et al. [18] | - A fusion of multiple features extracted from current signals across time and frequency domains. | - Implementation of a two-stream convolution network to acquire spatial representation. - A load identification model designed to distinguish between low power and multi-state appliances. | - The inherent variability of electrical signals presents challenges in the precise identification of loads. |
| Hong et al. [33] | - A short-term forecasting process of electricity usage for residential users. | - A framework for short-term residential load forecasting. - A proposed approach utilizing deep neural networks (DNN) and iterative ResBlocks to capture the correlations among various electricity consumption behaviors. | - The dynamic and stochastic nature of consumption behavior, driven by variability in daily activities, presents significant challenges for load forecasting. |
| Wang et al. [21] | - Delineating socio-demographic details regarding the consumers. | - A flexible automatic feature extraction method based on DL techniques is utilized to learn features from various datasets. - A comparison of cutting-edge and advanced ML techniques, encompassing PCA, sparse coding, and sparse auto-encoder. | - The privacy implications of SM data can be influenced by both the granularity and duration of the data. - Enhanced identification accuracy by integrating CNN with additional feature extraction methods. |
| Khodayar et al. [22] | - A forecasting framework for analyzing BTM load patterns and PV generation. | - A unique spatio-temporal graph auto-encoder (ST-GAE) was developed to extract intricate spatial and temporal features from the net load dataset. - Used a DL model to extract robust spatio-temporal features for various applications in power systems. | - Voltage limit breaches, voltage profile fluctuations, reverse power flow, and malfunctioning protection devices are common issues encountered in distribution networks. - Due to the complex interplay of spatial and temporal variability, and to the uncertainties inherent in solar generation, meticulous analysis of comparable regional data is essential for reliable prediction. |
| Du et al. [19] | - Extraction of features. - An identification of loads. | - The proposed FSM representation offers a powerful analytical framework, enabling the extraction of RMS current and time values associated with individual states. The technique also allows for identification of critical states and the detection of patterns that recur within the dataset. | - Repeating patterns may not be identical and the duration between their occurrences varies. - Fails to offer overall duration of operation in different modes over a specific period. - These methods solely rely on power consumption data. |
| Akarslan et al. [20] | - Selecting features and a classifier. | - A new approach is introduced, which integrates a feature selection method (ReliefF) with classifiers for load identification. - A comparison is made between the performances of two classifiers, Elman and RBF. | - ML techniques exhibit high computational complexity, which is aggravated by the increasing number of inputs. - The uniqueness of the features utilized may vary depending on the dataset employed. |
| Oprea et al. [23] | - Examine SM data to identify reading inaccuracies, abnormal activity, malfunctions, cyber threats, and tampering with meters. | - Changes within time-series data streams are identified through the combined application of a spectral residual CNN (SR-CNN) and a model designed for anomaly detection. - A two-class boosted decision tree and Fisher linear discriminant analysis are employed on pre-processed datasets. | - The algorithm may erroneously classify consumers as suspicious and is also unable to determine those consumers who engage in electricity theft when the real-time data from SMs are unlabeled. |
3. An Illustration of Behind-the-Meter Operations in Distribution Networks
4. Load Forecasting Models
4.1. Introduction
| Algorithm 1 A Load Forecasting Process for Residential Households Considering BTM DERs. |
|
4.2. Historical Development of Load Forecasting Models
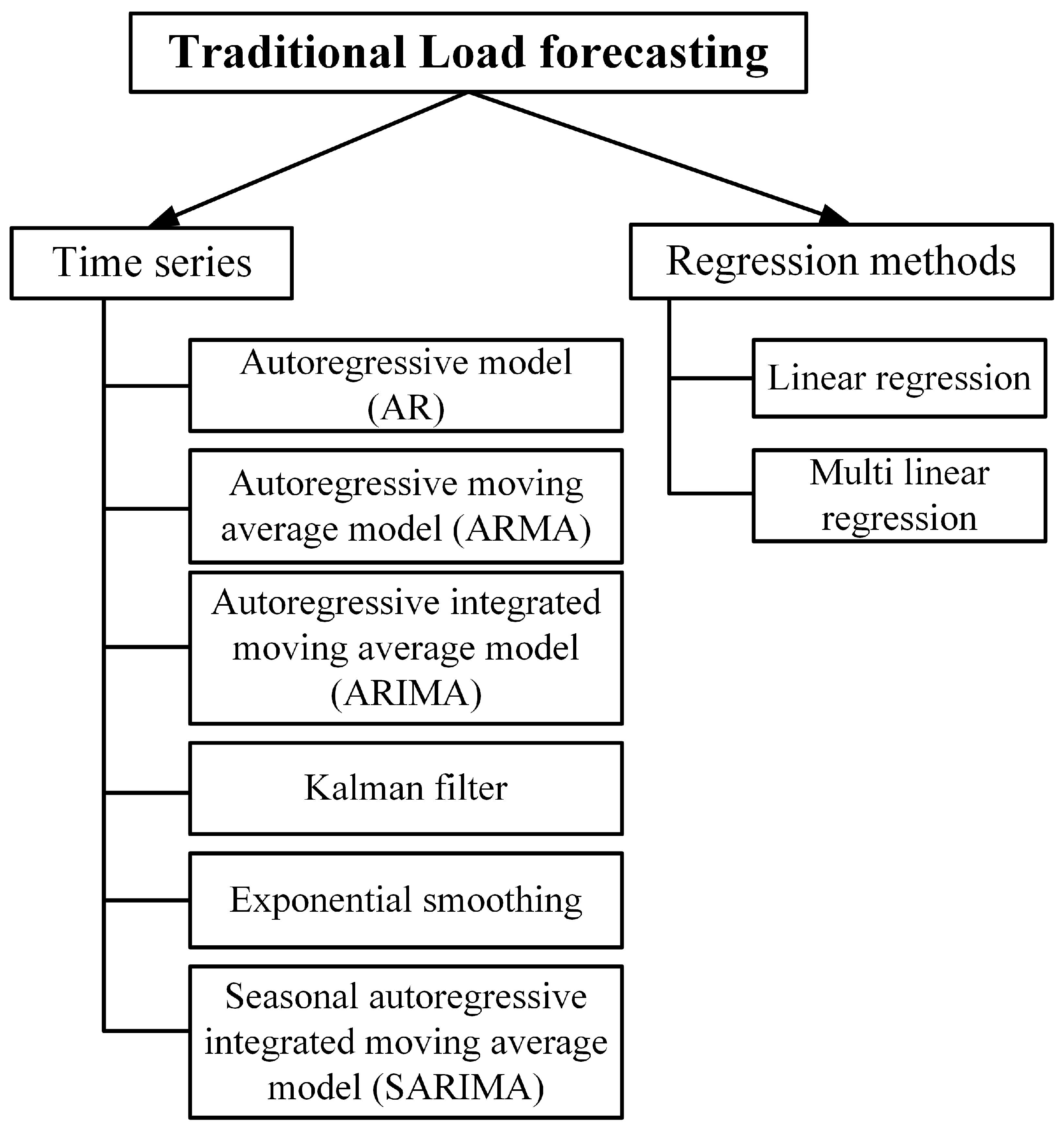
4.3. Traditional Load Forecasting Models
| Ref. | Traditional Forecasting Models | Statistical Formulae | Parameters |
|---|---|---|---|
| [53] | Auto-regressive | = random noise are auto-regressive coefficients that are unknown = time-series output | |
| [53] | Model based on moving average | Duality of auto-regressive model | |
| [54,55] | ARMA model | p = auto-regressive order q = moving average (MA) order = return series of original time series x | |
| [56] | ARIMA model | P = order of seasonal auto-regressive Q = order of seasonal MA term p = the order of a non-seasonal difference q is the order of non-seasonal MA term | |
| [57] | (S)ARIMAX and (S)ARMAX | i = exogenous factor and are adequate coefficient polynomials | |
| [58,61] | Kalman filtering algorithm | are zero mean small white noise signals with covariance matrices and = system state vector = state observation vector H = state observation matrix = gain matrix | |
| [59,63] | Gray system theory | where () | = original sequence a = development co-efficient u = Gray constant |
| [60] | Exponential smoothening | = smooth value at time t = actual observation value at time t = smooth value at time = smoothing constant, ranging from 0 to 1 |
4.4. Machine Learning in Load Forecasting Models
4.4.1. Supervised ML Model
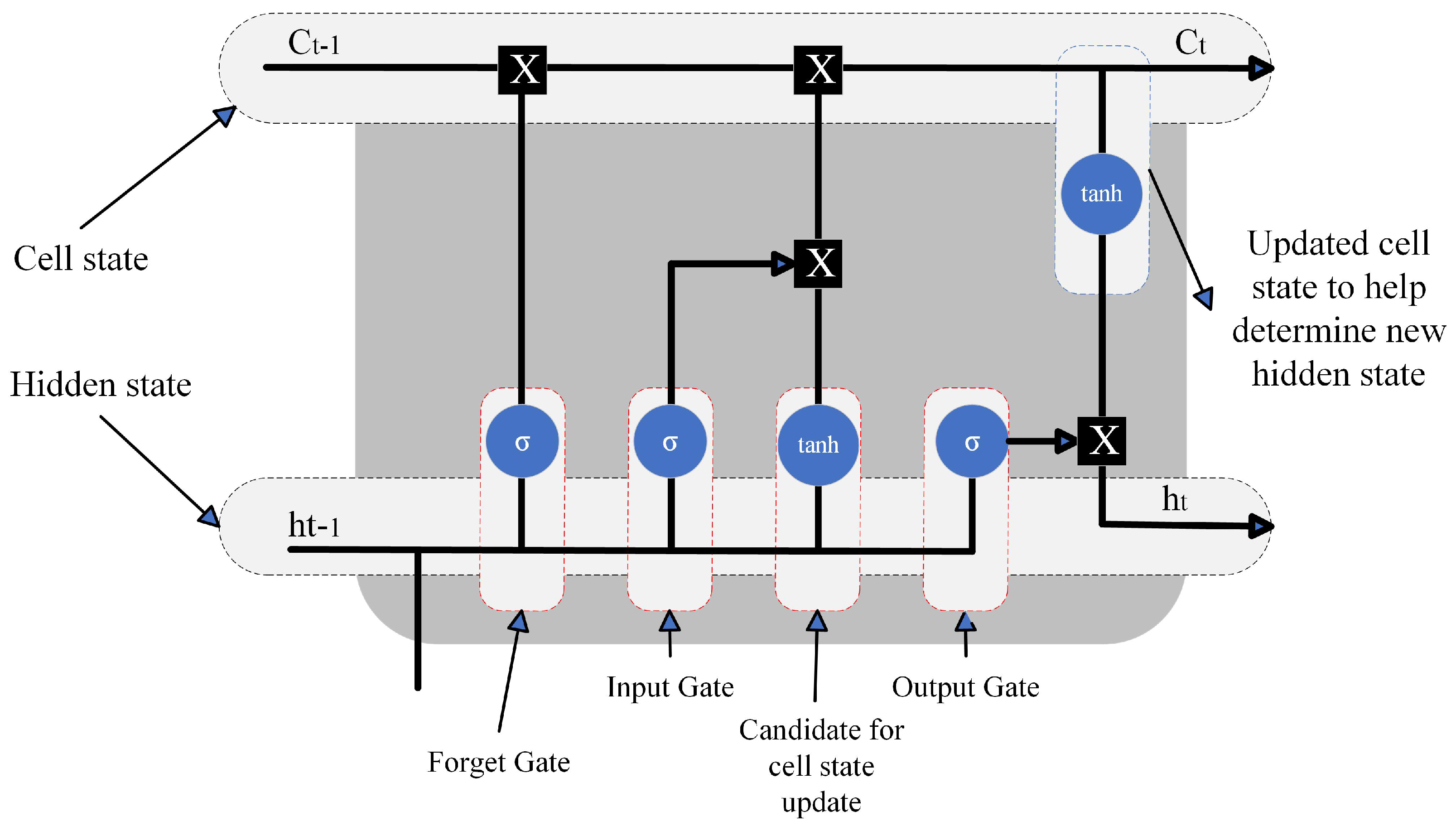
4.4.2. Artificial Neural Networks
4.4.3. Evaluation Metrics
4.5. Model Selection and Optimization
4.6. Computational Burden of Load Forecasting Process
5. Abnormal Activities in Residential Households with BTM Systems: A Case Study
6. Challenges and Emerging Models
- The variability and uncertainty in BTM PV generation provide a range of issues (e.g., voltage limits violations, voltage profile fluctuation, reverse power flow, and protection device failure) in distribution networks [40,79]. Also, energy consumption is influenced by non-technical loss detection, environment, building features, and users’ behavior [80].
- An NILM process makes it challenging to achieve high-accuracy load identification using a single waveform characteristic (i.e., low load detection accuracy). Choosing the perfect combination of features is challenging [18].
- The unpredictability associated with residential activities and energy consumption exhibits dynamic variability, even within the context of a single user’s specific application [33].
- Implementing functional encryption at the SM level introduces significant complexity, both in terms of cryptographic operations and the management of decryption keys by the system operator in cases where there are some anomalies in the SMs. Also, the system operator can have constraints in a comprehensive analysis for an effective load forecasting process [83,84].
- Spatial resolution of the recorded datasets, data gaps, and measurement errors in the datasets could be challenges in the process [85].
- Uniqueness of the characteristics utilized may differ depending on the data collection [20].
- Data time resolution and using average consumption of residential customers are questionable. Some SM data quality issues (e.g., duplicating, missing, outliers, or anomalous data samples) are the factors for less accuracy in the load forecasting performance [24].
- Repeating patterns of current waveform may not be similar, and the time intervals between their occurrences may not be identical [19].
- Adaptability of DL algorithms is challenging because of no accessibility to a huge number of datasets [85].
- Most clustering methods suffer from the dimensionality presented by time-series SM data because of the divergence in a high-dimensional domain. Also, there are certain algorithmic restrictions (e.g., sensitivity) to outliers by hierarchical clustering models [24].
- A fault management system can be effective in a low-voltage grid because the smart transformer is not able to provide the full short-circuit current to the fault point, due to the limited capacity of semiconductor devices. A lower efficiency regarding the conventional transformers can be debatable [86].
- Utilities use the customer daily peak demand to approximate flexibility for peak-shaving programs, which can cause errors because it cannot be coincided with the peak [24].
- AI-Driven Models: The application of AI in the forecasting of BTM DERs is set to expand. These models are capable of capturing nonlinear and complex patterns of energy usage and generation, factoring in variables such as weather conditions, user behavior, and electricity prices.
- LLM-Based Load Forecasting: LLMs are leveraging huge amounts of textual and numerical data to predict energy demand. Unlike traditional ML models that require extensive feature engineering and pre-processing, LLMs can directly analyze and interpret the data, making them highly efficient for processing large datasets from SMs.
- Hybrid Models: Combining AI-driven approaches with LLM capabilities, hybrid models offer a comprehensive solution that benefits from the predictive power of AI and the contextual understanding of LLMs. These models can dynamically adapt to changing energy patterns and integrate different data sources for improved forecast accuracy. Some advantages of LLMs in this process can be mentioned as follows:
- -
- Adaptability: They can quickly adapt to new data and patterns, making them ideal for the continuously changing area of residential energy systems.
- -
- Time Efficiency: LLM-based models lessen the need for manual feature selection and pre-processing, accelerating the forecasting process.
- -
- Efficiency in Large Datasets: LLMs can handle huge amounts of data more efficiently than traditional ML models, making them particularly appropriate for analyzing extensive SM datasets.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wen, M.; Yu, Z.; Li, W.; Luo, S.; Zhong, Y.; Changqing, C. Short-term load forecasting based on feature mining and deep learning of big data of user electricity consumption. AIP Adv. 2023, 13, 125315. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, T.; Peng, X.; Zhang, X. A novel long-term power forecasting based smart grid hybrid energy storage system optimal sizing method considering uncertainties. Inf. Sci. 2022, 610, 326–344. [Google Scholar] [CrossRef]
- Pan, K.; Chen, Z.; Lai, C.S.; Xie, C.; Wang, D.; Li, X.; Zhao, Z.; Tong, N.; Lai, L.L. An unsupervised data-driven approach for behind-the-meter photovoltaic power generation disaggregation. Appl. Energy 2022, 309, 118450. [Google Scholar] [CrossRef]
- Lin, J.; Ma, J.; Zhu, J. A privacy-preserving federated learning method for probabilistic community-level behind-the-meter solar generation disaggregation. IEEE Trans. Smart Grid 2021, 13, 268–279. [Google Scholar] [CrossRef]
- Zaboli, A.; Tuyet-Doan, V.N.; Kim, Y.H.; Hong, J.; Su, W. An LSTM-SAE-based Behind-the-Meter Load Forecasting Method. IEEE Access 2023, 11, 49378–49392. [Google Scholar] [CrossRef]
- Zaboli, A.; Hong, J.; Tuyet-Doan, V.N.; Kim, Y.H. A Machine Learning-based Short-term Load Forecasting Method for Behind-the-meter DERs. In Proceedings of the 2023 IEEE Power & Energy Society General Meeting (PESGM), Orlando, FL, USA, 16–20 July 2023; pp. 1–5. [Google Scholar]
- Rafi, S.H.; Nahid-Al-Masood; Deeba, S.R.; Hossain, E. A short-term load forecasting method using integrated CNN and LSTM network. IEEE Access 2021, 9, 32436–32448. [Google Scholar] [CrossRef]
- Saeedi, R.; Sadanandan, S.K.; Srivastava, A.K.; Davies, K.L.; Gebremedhin, A.H. An adaptive machine learning framework for behind-the-meter load/PV disaggregation. IEEE Trans. Ind. Inform. 2021, 17, 7060–7069. [Google Scholar] [CrossRef]
- Ahmad, N.; Ghadi, Y.; Adnan, M.; Ali, M. Load forecasting techniques for power system: Research challenges and survey. IEEE Access 2022, 10, 71054–71090. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, Z.; Li, X. Enhancing Short-Term Power Load Forecasting for Industrial and Commercial Buildings: A Hybrid Approach Using TimeGAN, CNN, and LSTM. IEEE Open J. Ind. Electron. Soc. 2023, 4, 451–462. [Google Scholar] [CrossRef]
- Geng, G.; He, Y.; Zhang, J.; Qin, T.; Yang, B. Short-Term Power Load Forecasting Based on PSO-Optimized VMD-TCN-Attention Mechanism. Energies 2023, 16, 4616. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, J.; Li, X.; Zhang, Y. Long-Term Power Load Forecasting Using LSTM-Informer with Ensemble Learning. Electronics 2023, 12, 2175. [Google Scholar] [CrossRef]
- Wang, X.; Yao, Z.; Papaefthymiou, M. A real-time electrical load forecasting and unsupervised anomaly detection framework. Appl. Energy 2023, 330, 120279. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H.; Bhandari, B.; Cheng, L. AI-Empowered Methods for Smart Energy Consumption: A Review of Load Forecasting, Anomaly Detection and Demand Response. Int. J. Precis. Eng.-Manuf.-Green Technol. 2023, 11, 963–993. [Google Scholar] [CrossRef]
- Zaboli, A.; Choi, S.L.; Song, T.J.; Hong, J. ChatGPT and other Large Language Models for Cybersecurity of Smart Grid Applications. arXiv 2023, arXiv:2311.05462. [Google Scholar]
- Ghayoor, F.; Zaboli, A.; Ghannadpour, S.F. A Coordinated Power Grid optimization Considering Reliability and Chance-Constrained Approaches. In Proceedings of the 2023 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, Kansas, 27–28 April 2023; pp. 1–6. [Google Scholar]
- Deivamani, K.; Norouzi, F.; Shekhar, A.; Bauer, P. A Comparison of Various Deep Learning Methods for Household Load Forecasting. In Proceedings of the 2023 IEEE PES Innovative Smart Grid Technologies Europe (ISGT EUROPE), Grenoble, France, 23–26 October 2023; pp. 1–5. [Google Scholar]
- Li, K.; Yin, B.; Du, Z.; Sun, Y. A nonintrusive load identification model based on time-frequency features fusion. IEEE Access 2020, 9, 1376–1387. [Google Scholar] [CrossRef]
- Du, L.; Yang, Y.; He, D.; Harley, R.G.; Habetler, T.G. Feature extraction for load identification using long-term operating waveforms. IEEE Trans. Smart Grid 2014, 6, 819–826. [Google Scholar] [CrossRef]
- Akarslan, E.; Doğan, R. A novel approach based on a feature selection procedure for residential load identification. Sustain. Energy Grids Netw. 2021, 27, 100488. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Gan, D.; Yang, J.; Kirschen, D.S.; Kang, C. Deep learning-based socio-demographic information identification from smart meter data. IEEE Trans. Smart Grid 2018, 10, 2593–2602. [Google Scholar] [CrossRef]
- Khodayar, M.; Liu, G.; Wang, J.; Kaynak, O.; Khodayar, M.E. Spatiotemporal behind-the-meter load and PV power forecasting via deep graph dictionary learning. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4713–4727. [Google Scholar] [CrossRef]
- Oprea, S.V.; Bâra, A.; Puican, F.C.; Radu, I.C. Anomaly detection with machine learning algorithms and big data in electricity consumption. Sustainability 2021, 13, 10963. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, Z. Mining smart meter data to enhance distribution grid observability for behind-the-meter load control: Significantly improving system situational awareness and providing valuable insights. IEEE Electrif. Mag. 2021, 9, 92–103. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Mohammadi-Ivatloo, B.; Abapour, M.; Anvari-Moghaddam, A.; Roy, S.S. Heating and cooling loads forecasting for residential buildings based on hybrid machine learning applications: A comprehensive review and comparative analysis. IEEE Access 2021, 10, 2196–2215. [Google Scholar] [CrossRef]
- Shakeel, A.; Chong, D.; Wang, J. District heating load forecasting with a hybrid model based on LightGBM and FB-prophet. J. Clean. Prod. 2023, 409, 137130. [Google Scholar] [CrossRef]
- Xia, L.; Ren, Y.; Wang, Y. Forecasting China’s total renewable energy capacity using a novel dynamic fractional order discrete grey model. Expert Syst. Appl. 2024, 239, 122019. [Google Scholar] [CrossRef]
- Real, A.C.; Luz, G.P.; Sousa, J.; Brito, M.; Vieira, S. Optimization of a photovoltaic-battery system using deep reinforcement learning and load forecasting. Energy AI 2024, 16, 100347. [Google Scholar] [CrossRef]
- Luo, Z.; Peng, J.; Tan, Y.; Yin, R.; Zou, B.; Hu, M.; Yan, J. A novel forecast-based operation strategy for residential PV-battery-flexible loads systems considering the flexibility of battery and loads. Energy Convers. Manag. 2023, 278, 116705. [Google Scholar] [CrossRef]
- Welikala, S.; Dinesh, C.; Ekanayake, M.P.B.; Godaliyadda, R.I.; Ekanayake, J. Incorporating appliance usage patterns for non-intrusive load monitoring and load forecasting. IEEE Trans. Smart Grid 2017, 10, 448–461. [Google Scholar] [CrossRef]
- Shi, Y.; Zhao, X.; Zhang, F.; Kong, Y. Non-intrusive load monitoring based on swin-transformer with adaptive scaling recurrence plot. Energies 2022, 15, 7800. [Google Scholar] [CrossRef]
- Irani Azad, M.; Rajabi, R.; Estebsari, A. Nonintrusive Load Monitoring (NILM) Using a Deep Learning Model with a Transformer-Based Attention Mechanism and Temporal Pooling. Electronics 2024, 13, 407. [Google Scholar] [CrossRef]
- Hong, Y.; Zhou, Y.; Li, Q.; Xu, W.; Zheng, X. A deep learning method for short-term residential load forecasting in smart grid. IEEE Access 2020, 8, 55785–55797. [Google Scholar] [CrossRef]
- He, L.; Zhang, J. Energy trading in local electricity markets with behind-the-meter solar and energy storage. IEEE Trans. Energy Mark. Policy Regul. 2023, 1, 107–117. [Google Scholar] [CrossRef]
- Lindberg, K.; Seljom, P.; Madsen, H.; Fischer, D.; Korpås, M. Long-term electricity load forecasting: Current and future trends. Util. Policy 2019, 58, 102–119. [Google Scholar] [CrossRef]
- Das, P.; Mathur, J.; Bhakar, R.; Kanudia, A. Implications of short-term renewable energy resource intermittency in long-term power system planning. Energy Strategy Rev. 2018, 22, 1–15. [Google Scholar] [CrossRef]
- Forero-Quintero, J.F.; Villafafila-Robles, R.; Barja-Martinez, S.; Codina-Escolar, M.; Montesinos-Miracle, D. A flexibility management system for behind-the-meter flexibility with distributed energy resources: A sensitivity analysis. Sustain. Energy Technol. Assess. 2023, 60, 103404. [Google Scholar] [CrossRef]
- Madadi, M.; Beddingfield, R.; Ohodnicki, P.; Bhattacharya, S. Utilizing Smart Inverter Virtual-Sensor Nodes for Enhanced Behind-the-Meter Visibility in High PV Penetration Distribution Feeders. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 610–616. [Google Scholar]
- Smart Energy International. US Smart Meter Penetration to Reach 93% by 2027—Berg Insight. 2023. Available online: https://www.smart-energy.com/regional-news/north-america/us-smart-meter-penetration-to-reach-93-by-2027-berg-insight/ (accessed on 20 March 2024).
- Wang, Y.; Zhang, N.; Chen, Q.; Kirschen, D.S.; Li, P.; Xia, Q. Data-driven probabilistic net load forecasting with high penetration of behind-the-meter PV. IEEE Trans. Power Syst. 2017, 33, 3255–3264. [Google Scholar] [CrossRef]
- Stratman, A.; Hong, T.; Yi, M.; Zhao, D. Net load forecasting with disaggregated behind-the-meter PV generation. IEEE Trans. Ind. Appl. 2023, 59, 5341–5351. [Google Scholar] [CrossRef]
- Tziolis, G.; Livera, A.; Michail, A.; Makrides, G.; Georghiou, G.E. Direct Against Indirect Short-Term Net Load Forecasting Using Machine Learning Principles for Renewable Microgrids. In Proceedings of the 2023 IEEE International Smart Cities Conference (ISC2), Bucharest, Romania, 24–27 September 2023; pp. 1–5. [Google Scholar]
- Grabner, M.; Wang, Y.; Wen, Q.; Blažič, B.; Štruc, V. A Global Modeling Framework for Load Forecasting in Distribution Networks. IEEE Trans. Smart Grid 2023, 14, 4927–4941. [Google Scholar] [CrossRef]
- Montero-Manso, P.; Hyndman, R.J. Principles and algorithms for forecasting groups of time series: Locality and globality. Int. J. Forecast. 2021, 37, 1632–1653. [Google Scholar] [CrossRef]
- Ghayoor, F.; Ghannadpour, S.F.; Zaboli, A. Power network-planning optimization considering average power not supplied reliability index: Modified by chance-constrained programming. Comput. Ind. Eng. 2022, 164, 107900. [Google Scholar] [CrossRef]
- Abumohsen, M.; Owda, A.Y.; Owda, M. Electrical load forecasting using LSTM, GRU, and RNN algorithms. Energies 2023, 16, 2283. [Google Scholar] [CrossRef]
- Habbak, H.; Mahmoud, M.; Metwally, K.; Fouda, M.M.; Ibrahem, M.I. Load forecasting techniques and their applications in smart grids. Energies 2023, 16, 1480. [Google Scholar] [CrossRef]
- Ahmad, A.; Javaid, N.; Mateen, A.; Awais, M.; Khan, Z.A. Short-Term Load Forecasting in Smart Grids: An Intelligent Modular Approach. Energies 2019, 12, 164. [Google Scholar] [CrossRef]
- Som, T. Time Load Forecasting: A Smarter Expertise Through Modern Methods. In Prediction Techniques for Renewable Energy Generation and Load Demand Forecasting; Tomar, A., Gaur, P., Jin, X., Eds.; Springer Nature: Singapore, 2023; pp. 153–176. [Google Scholar] [CrossRef]
- Erdener, B.C.; Feng, C.; Doubleday, K.; Florita, A.; Hodge, B.M. A review of behind-the-meter solar forecasting. Renew. Sustain. Energy Rev. 2022, 160, 112224. [Google Scholar] [CrossRef]
- Takiyar, S. Grid reliability enhancement by peak load forecasting with a PSO hybridized ANN model. In Proceedings of the 2015 4th International Conference on Reliability, Infocom Technologies and Optimization (ICRITO) (Trends and Future Directions), Noida, India, 2–4 September 2015; pp. 1–6. [Google Scholar]
- Selakov, A.; Ilić, S.; Vukmirović, S.; Kulić, F.; Erdeljan, A.; Gorecan, Z.; Gorečan, Z. A comparative analysis of SVM and ANN based hybrid model for short term load forecasting. In Proceedings of the PES T&D 2012, Orlando, FL, USA, 7–10 May 2012; pp. 1–5. [Google Scholar]
- Jacob, M.; Neves, C.; Vukadinović Greetham, D. Short Term Load Forecasting. In Forecasting and Assessing Risk of Individual Electricity Peaks; Springer International Publishing: Cham, Switzerland, 2020; pp. 15–37. [Google Scholar] [CrossRef]
- Sharma, D.; Lie, T.T.; Nair, N.K.C.; Vallès, B. Wind speed forecasting using ANN, ARMA and AIC hybrid to ensure power grid reliability. In Proceedings of the 2015 IEEE Innovative Smart Grid Technologies-Asia (ISGT ASIA), Bangkok, Thailand, 3–6 November 2015; pp. 1–5. [Google Scholar]
- Colak, I.; Yesilbudak, M.; Genc, N.; Bayindir, R. Multi-period prediction of solar radiation using ARMA and ARIMA models. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015; pp. 1045–1049. [Google Scholar]
- Karthika, S.; Margaret, V.; Balaraman, K. Hybrid short term load forecasting using ARIMA-SVM. In Proceedings of the 2017 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 21–22 April 2017; pp. 1–7. [Google Scholar]
- Al Amin, M.A.; Hoque, M.A. Comparison of ARIMA and SVM for short-term load forecasting. In Proceedings of the 2019 9th Annual Information Technology, Electromechanical Engineering and Microelectronics Conference (IEMECON), Jaipur, India, 13–15 March 2019; pp. 1–6. [Google Scholar]
- Zhang, X. Dynamic Forecasting of Power System Load Based on Kalman Filter. In Proceedings of the 2022 2nd International Conference on Electrical Engineering and Mechatronics Technology (ICEEMT), Virtual, 1–3 July 2022; pp. 337–342. [Google Scholar]
- Li, X.; Hu, L.; Zhai, L. Power load forecasting based on Improved Grey Model of particle swarm optimization. In Proceedings of the 2021 4th International Conference on Advanced Electronic Materials, Computers and Software Engineering (AEMCSE), Changsha, China, 26–28 March 2021; pp. 237–240. [Google Scholar]
- Ji, P.; Xiong, D.; Wang, P.; Chen, J. A study on exponential smoothing model for load forecasting. In Proceedings of the 2012 Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 March 2012; pp. 1–4. [Google Scholar]
- ElMenshawy, M.S.; Massoud, A.M. Short-Term Load Forecasting in Active Distribution Networks using Forgetting Factor Adaptive Extended Kalman Filter. IEEE Access 2023, 11, 103916–103924. [Google Scholar] [CrossRef]
- Cecati, C.; Kolbusz, J.; Różycki, P.; Siano, P.; Wilamowski, B.M. A novel RBF training algorithm for short-term electric load forecasting and comparative studies. IEEE Trans. Ind. Electron. 2015, 62, 6519–6529. [Google Scholar] [CrossRef]
- Jin, M.; Zhou, X.; Zhang, Z.M.; Tentzeris, M.M. Short-term power load forecasting using grey correlation contest modeling. Expert Syst. Appl. 2012, 39, 773–779. [Google Scholar] [CrossRef]
- Farhoumandi, M.; Bahrami, A.; Shahidehpour, M.; Jones, J.; Madvesh, C.; Kakumanu, K.; Ludlow, T.; Alarian, H.; Mishra, A.; Abdul-Rahman, K.H. Short-term Forecasting of Non-Conforming Net Load Using a Fusion Model with Machine Learning and Deep Learning Methods. In Proceedings of the 2023 9th International Conference on Control, Decision and Information Technologies (CoDIT), Rome, Italy, 3–6 July 2023; pp. 2414–2419. [Google Scholar]
- Dai, Y.; Zhao, P. A hybrid load forecasting model based on support vector machine with intelligent methods for feature selection and parameter optimization. Appl. Energy 2020, 279, 115332. [Google Scholar] [CrossRef]
- Ye, N.; Liu, Y.; Wang, Y. Short-term power load forecasting based on SVM. In Proceedings of the World Automation Congress 2012, Puerto Vallarta, Mexico, 24–28 June 2012; pp. 47–51. [Google Scholar]
- Khan, R.A.; Dewangan, C.; Srivastava, S.; Chakrabarti, S. Short term load forecasting using SVM models. In Proceedings of the 2018 IEEE 8th Power India International Conference (PIICON), Kurukshetra, India, 10–12 December 2018; pp. 1–5. [Google Scholar]
- Huy, T.H.B.; Vo, D.N.; Nguyen, K.P.; Huynh, V.Q.; Huynh, M.Q.; Truong, K.H. Short-Term Load Forecasting in Power System Using CNN-LSTM Neural Network. In Proceedings of the 2023 Asia Meeting on Environment and Electrical Engineering (EEE-AM), Hanoi, Vietnam, 13–15 November 2023; pp. 1–6. [Google Scholar]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Hossain, M.S.; Mahmood, H. Short-term load forecasting using an LSTM neural network. In Proceedings of the 2020 IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 27–28 February 2020; pp. 1–6. [Google Scholar]
- Mansoor, M.; Grimaccia, F.; Leva, S.; Mussetta, M. Comparison of echo state network and feed-forward neural networks in electrical load forecasting for demand response programs. Math. Comput. Simul. 2021, 184, 282–293. [Google Scholar] [CrossRef]
- Zheng, J.; Xu, C.; Zhang, Z.; Li, X. Electric load forecasting in smart grids using long-short-term-memory based recurrent neural network. In Proceedings of the 2017 51st Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2017; pp. 1–6. [Google Scholar]
- Rodrigues, F.; Cardeira, C.; Calado, J.M.; Melicio, R. Short-Term Load Forecasting of Electricity Demand for the Residential Sector Based on Modelling Techniques: A Systematic Review. Energies 2023, 16, 4098. [Google Scholar] [CrossRef]
- Bacanin, N.; Stoean, C.; Zivkovic, M.; Rakic, M.; Strulak-Wójcikiewicz, R.; Stoean, R. On the benefits of using metaheuristics in the hyperparameter tuning of deep learning models for energy load forecasting. Energies 2023, 16, 1434. [Google Scholar] [CrossRef]
- Shabbir, N.; Vassiljeva, K.; Nourollahi Hokmabad, H.; Husev, O.; Petlenkov, E.; Belikov, J. Comparative Analysis of Machine Learning Techniques for Non-Intrusive Load Monitoring. Electronics 2024, 13, 1420. [Google Scholar] [CrossRef]
- Wood, M.; Ogliari, E.; Nespoli, A.; Simpkins, T.; Leva, S. Day Ahead Electric Load Forecast: A Comprehensive LSTM-EMD Methodology and Several Diverse Case Studies. Forecasting 2023, 5, 297–314. [Google Scholar] [CrossRef]
- U.S. Energy Information Administration Press Release. Available online: https://www.eia.gov/pressroom/releases/press550.php (accessed on 15 March 2024).
- DeRoche, M. Cryptocurrency Miners Need to Report Their Energy Use. Available online: https://earthjustice.org/experts/mandy-deroche/cryptocurrency-miners-need-to-report-their-energy-use (accessed on 15 March 2024).
- Cha, J.W.; Joo, S.K. Probabilistic Short-Term Load Forecasting Incorporating Behind-the-Meter (BTM) Photovoltaic (PV) Generation and Battery Energy Storage Systems (BESSs). Energies 2021, 14, 7067. [Google Scholar] [CrossRef]
- Hasan, A.J.; Rahman, M.S.; Islam, M.S.; Yusuf, J. Data driven energy theft localization in a distribution network. In Proceedings of the 2023 International Conference on Information and Communication Technology for Sustainable Development (ICICT4SD), Dhaka, Bangladesh, 21–23 September 2023; pp. 388–392. [Google Scholar]
- Fekri, M.N.; Patel, H.; Grolinger, K.; Sharma, V. Deep learning for load forecasting with smart meter data: Online Adaptive Recurrent Neural Network. Appl. Energy 2021, 282, 116177. [Google Scholar] [CrossRef]
- Andriopoulos, N.; Magklaras, A.; Birbas, A.; Papalexopoulos, A.; Valouxis, C.; Daskalaki, S.; Birbas, M.; Housos, E.; Papaioannou, G.P. Short term electric load forecasting based on data transformation and statistical machine learning. Appl. Sci. 2020, 11, 158. [Google Scholar] [CrossRef]
- Ibrahem, M.I.; Nabil, M.; Fouda, M.M.; Mahmoud, M.M.; Alasmary, W.; Alsolami, F. Efficient privacy-preserving electricity theft detection with dynamic billing and load monitoring for AMI networks. IEEE Internet Things J. 2020, 8, 1243–1258. [Google Scholar] [CrossRef]
- Abdalzaher, M.S.; Fouda, M.M.; Ibrahem, M.I. Data privacy preservation and security in smart metering systems. Energies 2022, 15, 7419. [Google Scholar] [CrossRef]
- Proedrou, E. A comprehensive review of residential electricity load profile models. IEEE Access 2021, 9, 12114–12133. [Google Scholar] [CrossRef]
- De Carne, G.; Bruno, S.; Liserre, M.; La Scala, M. Distributed online load sensitivity identification by smart transformer and industrial metering. IEEE Trans. Ind. Appl. 2019, 55, 7328–7337. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaboli, A.; Kasimalla, S.R.; Park, K.; Hong, Y.; Hong, J. A Comprehensive Review of Behind-the-Meter Distributed Energy Resources Load Forecasting: Models, Challenges, and Emerging Technologies. Energies 2024, 17, 2534. https://doi.org/10.3390/en17112534
Zaboli A, Kasimalla SR, Park K, Hong Y, Hong J. A Comprehensive Review of Behind-the-Meter Distributed Energy Resources Load Forecasting: Models, Challenges, and Emerging Technologies. Energies. 2024; 17(11):2534. https://doi.org/10.3390/en17112534
Chicago/Turabian StyleZaboli, Aydin, Swetha Rani Kasimalla, Kuchan Park, Younggi Hong, and Junho Hong. 2024. "A Comprehensive Review of Behind-the-Meter Distributed Energy Resources Load Forecasting: Models, Challenges, and Emerging Technologies" Energies 17, no. 11: 2534. https://doi.org/10.3390/en17112534
APA StyleZaboli, A., Kasimalla, S. R., Park, K., Hong, Y., & Hong, J. (2024). A Comprehensive Review of Behind-the-Meter Distributed Energy Resources Load Forecasting: Models, Challenges, and Emerging Technologies. Energies, 17(11), 2534. https://doi.org/10.3390/en17112534








