Novel Hierarchical Energy Management System for Enhanced Black Start Capabilities at Distribution and Transmission Networks
Abstract
1. Introduction
- Conceptualising a hierarchical energy management system highlighting black start capability and load prioritisation across transmission and distribution networks.
- Formulating a unique optimisation problem coordinating with the hierarchical energy management system to enhance system inertia, load shedding, and renewable integration.
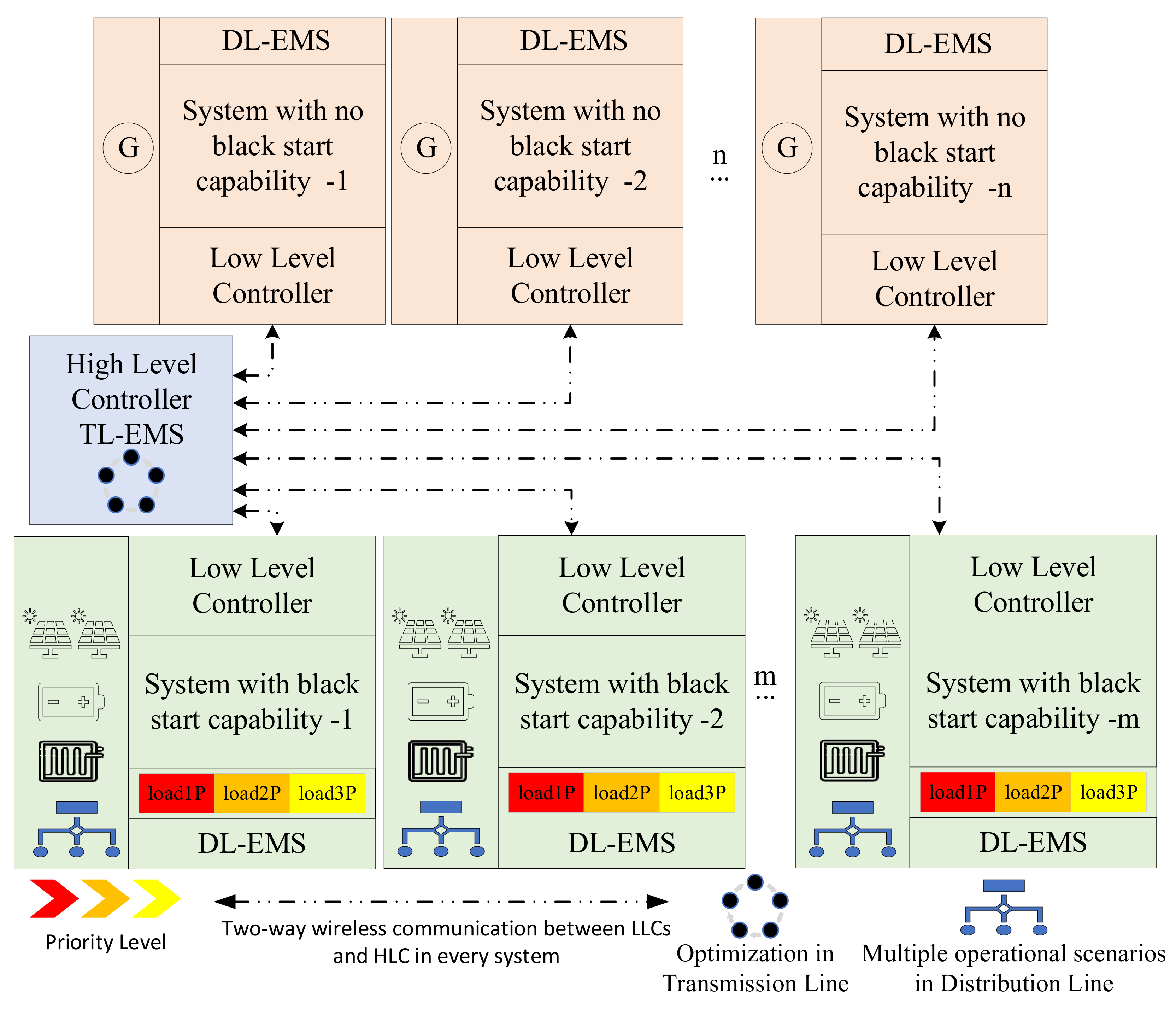
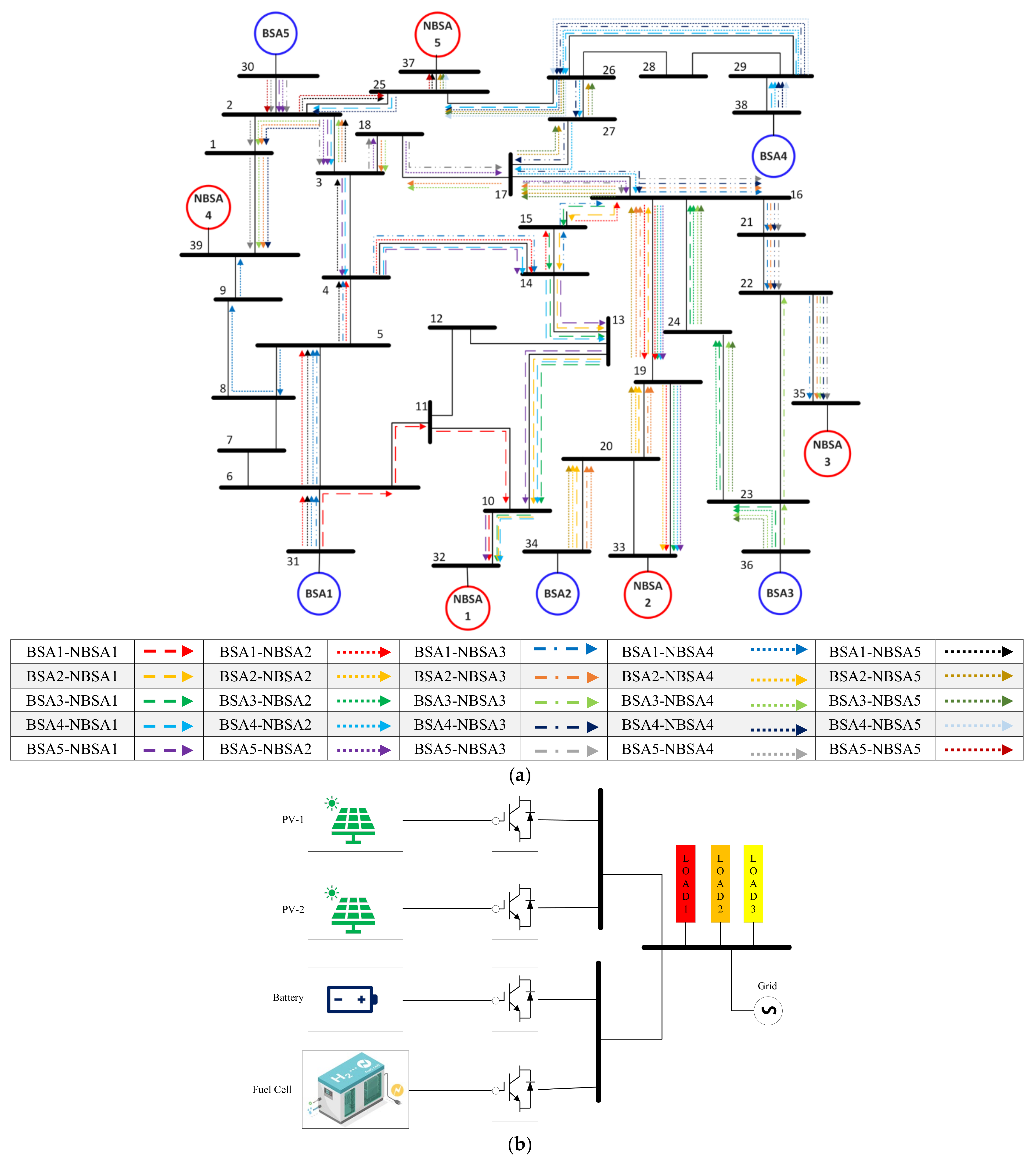
2. Proposed Hierarchical Energy Management System
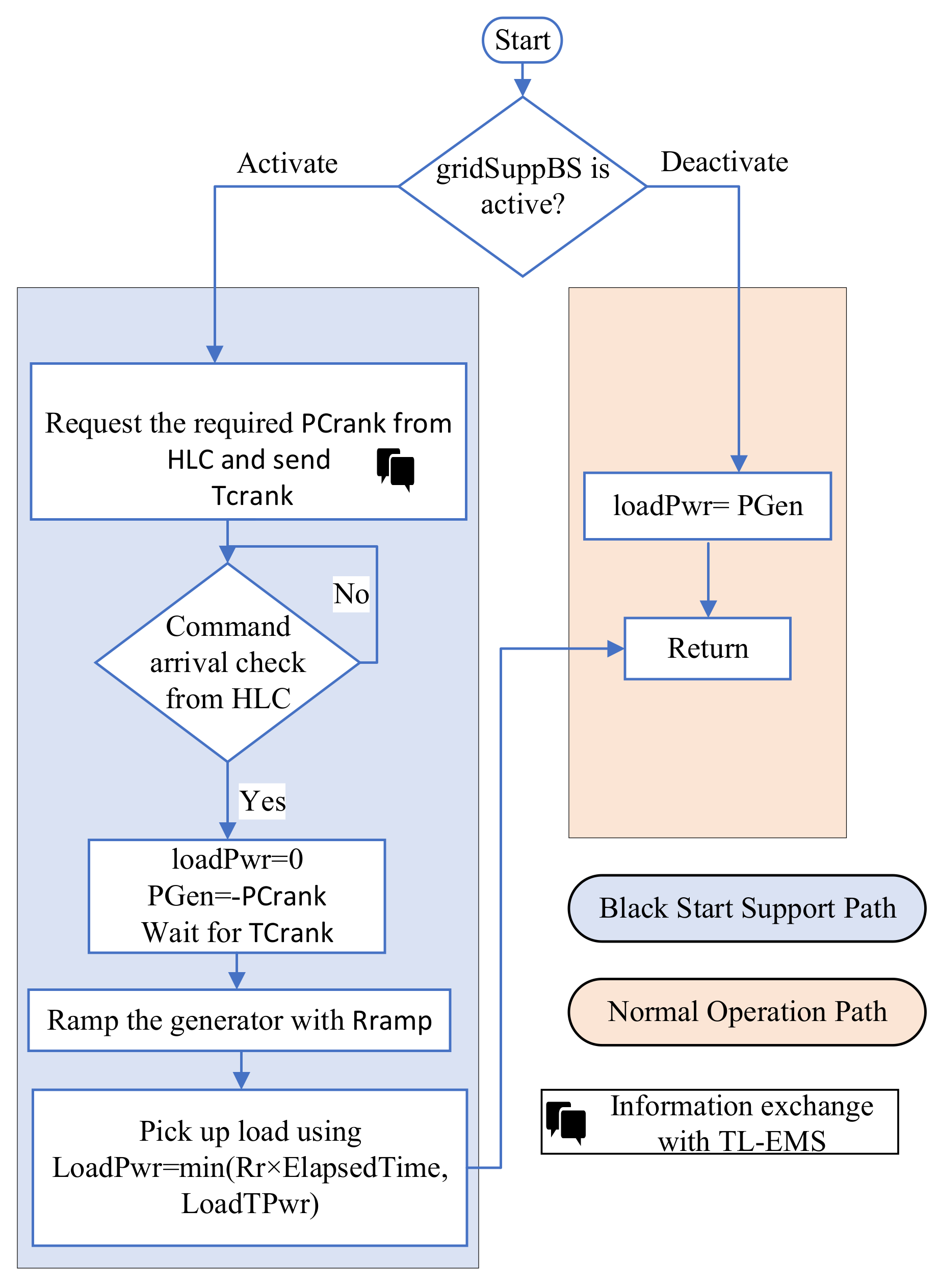
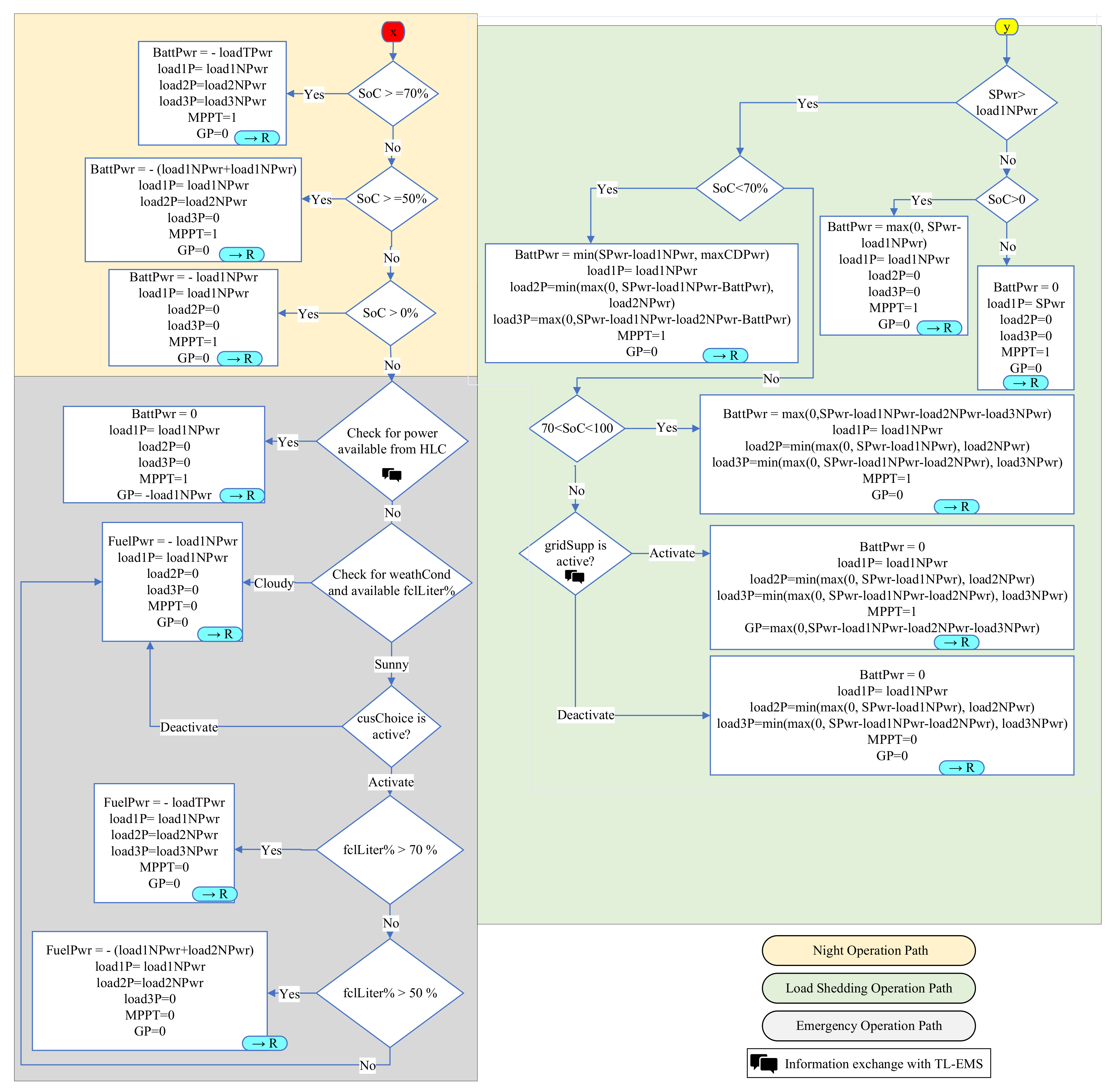
2.1. Operational Framework of DL-EMS in Non-Black Start-Capable Areas (NBSAs)
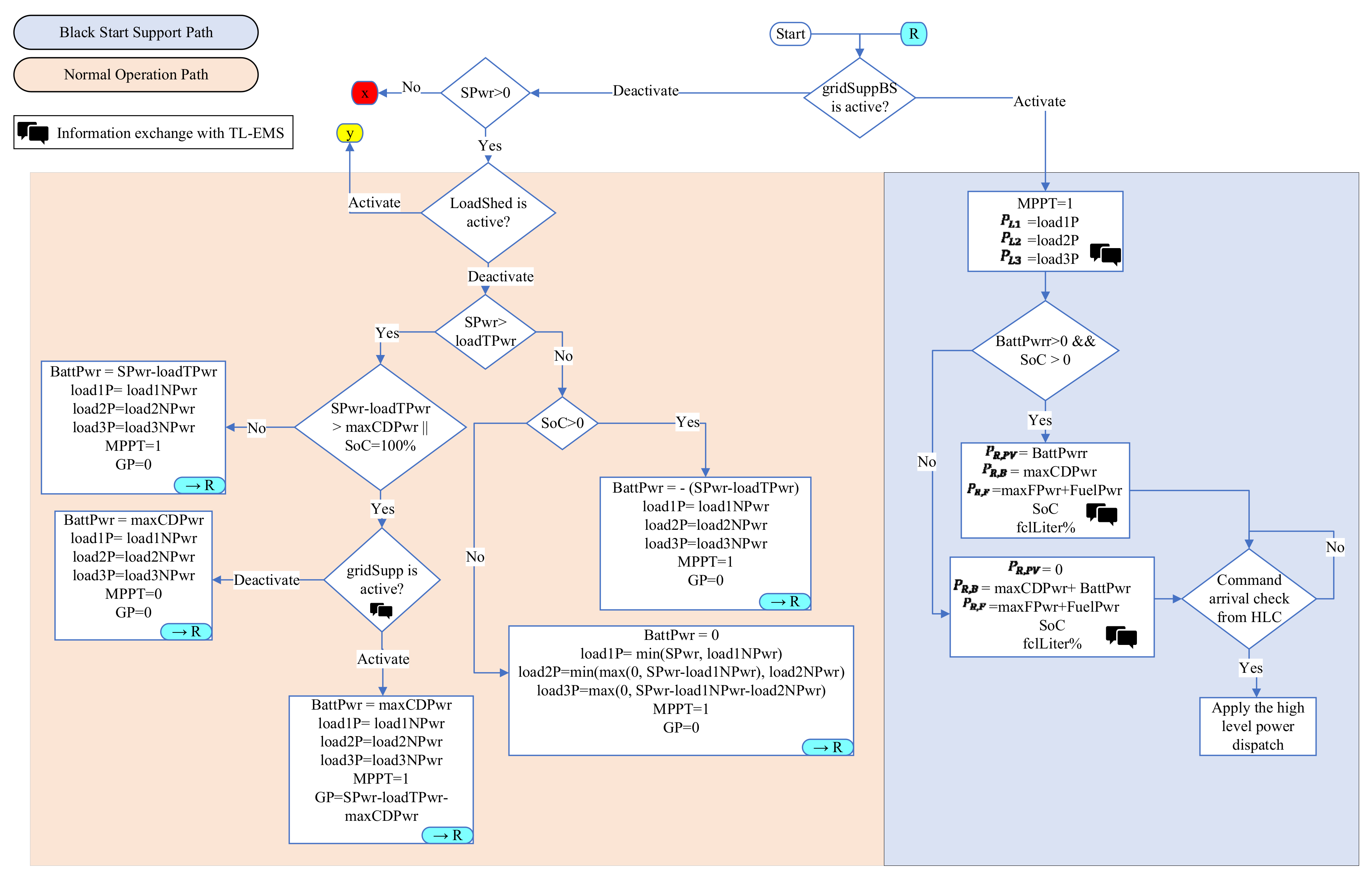
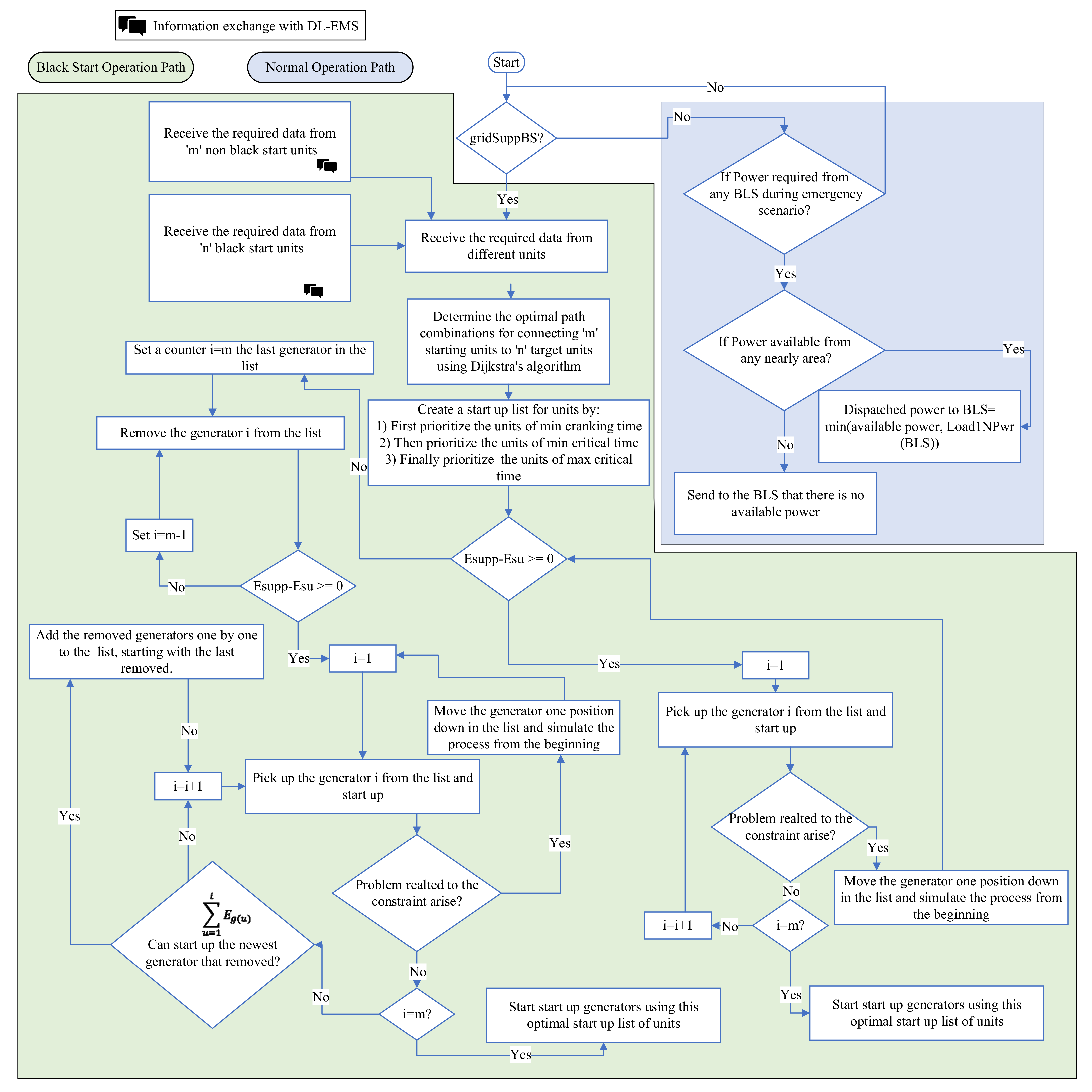
2.2. Operational Framework of DL-EMS in Black Start-Capable Areas (BSAs)
2.2.1. Normal Operation Path
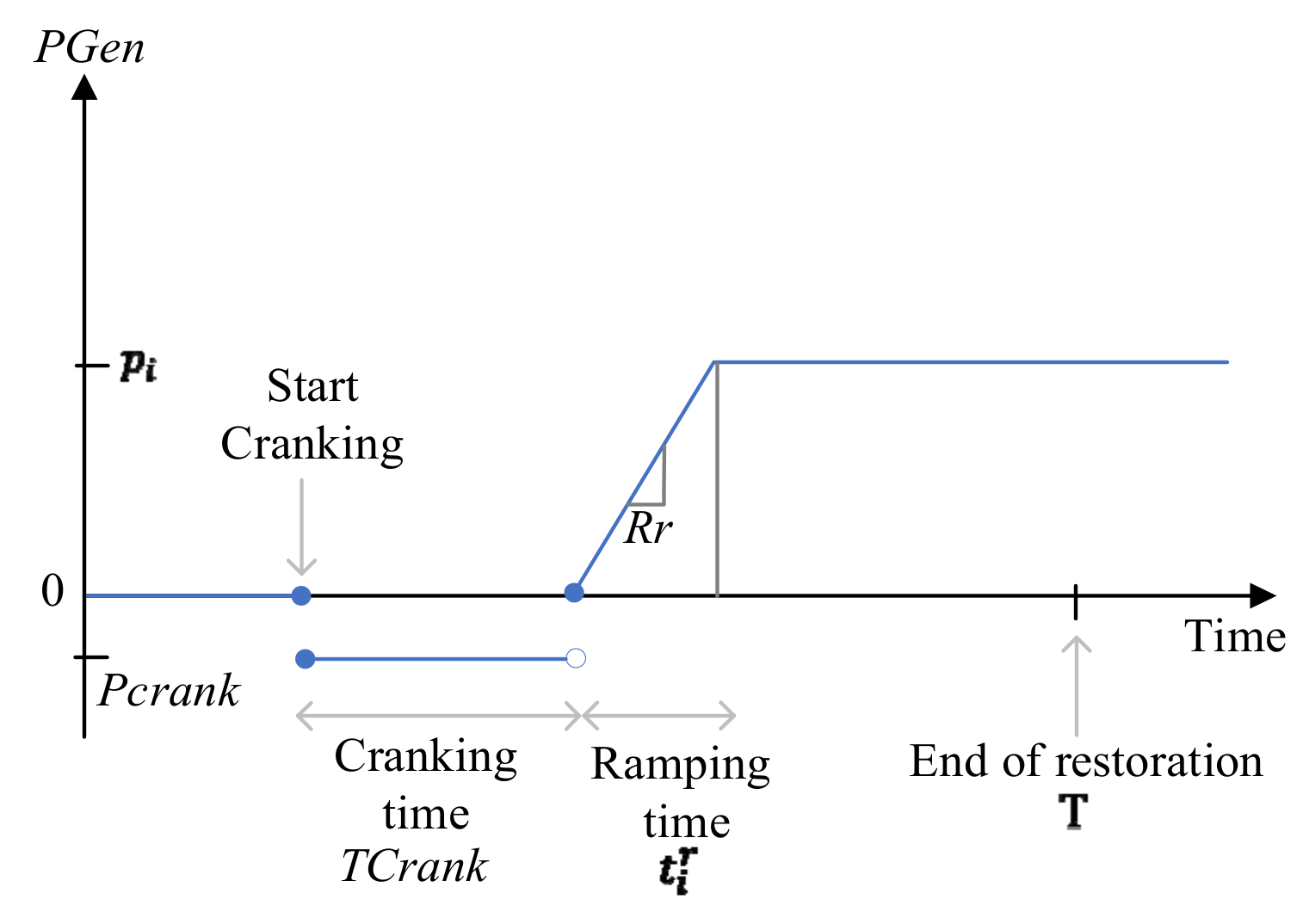
2.2.2. Black Start Operation Path
2.2.3. Load Shedding Path
2.2.4. Night Operation Path
2.2.5. Emergency Operation Path
2.3. Operational Framework of TL-EMS for High-Level Controller (HLC)
3. Objective Function of the Optimisation Problem
Constraints of the Optimisation Problem
- Distribution factor constraint:
- 2.
- Power balance constraint:
- 3.
- Voltage and power transmission constraints:
- 4.
- Operational characteristics and capacities:
- 5.
- Operational Timing Constraints for Generator Startup
4. Results and Discussion
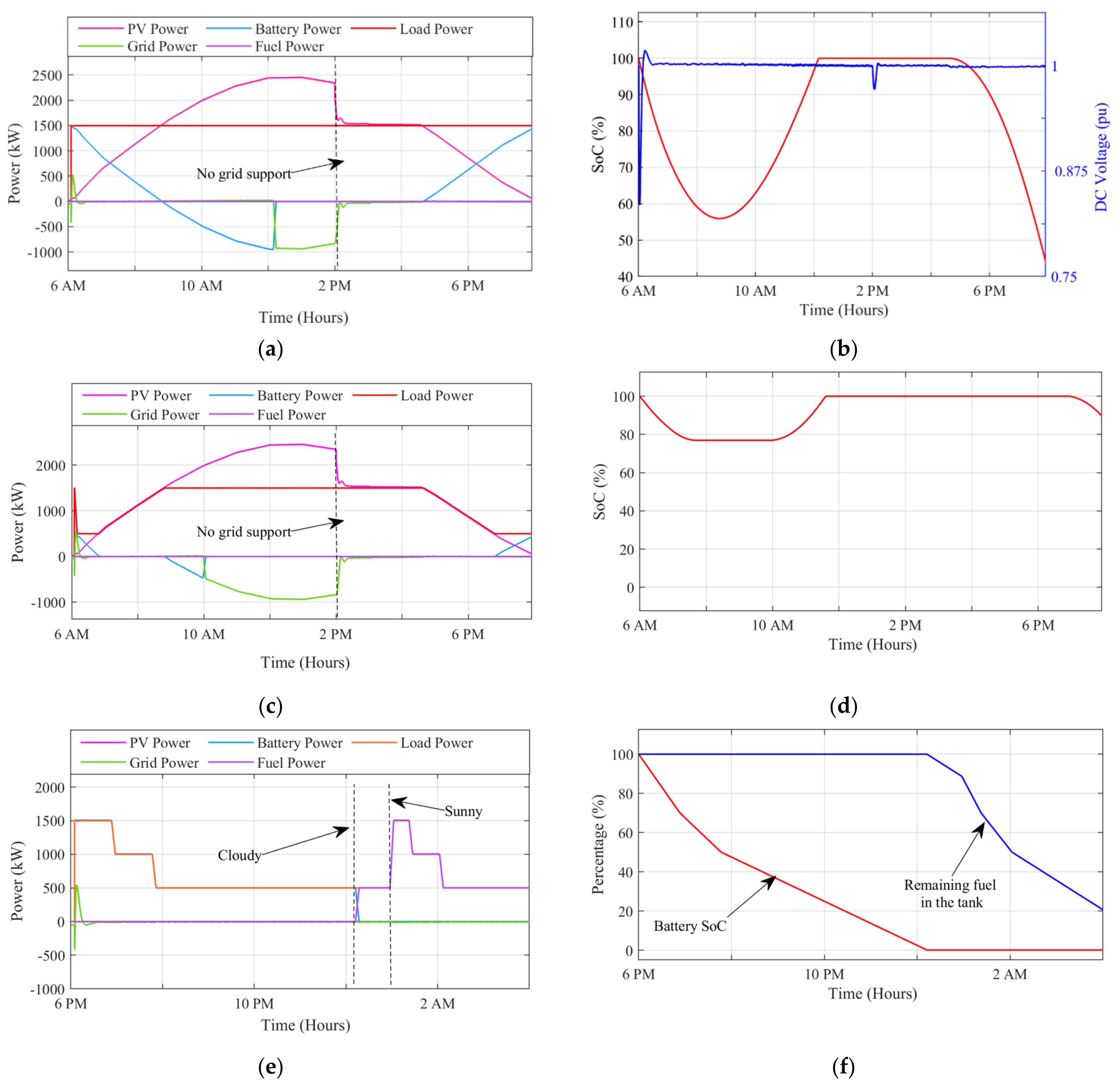
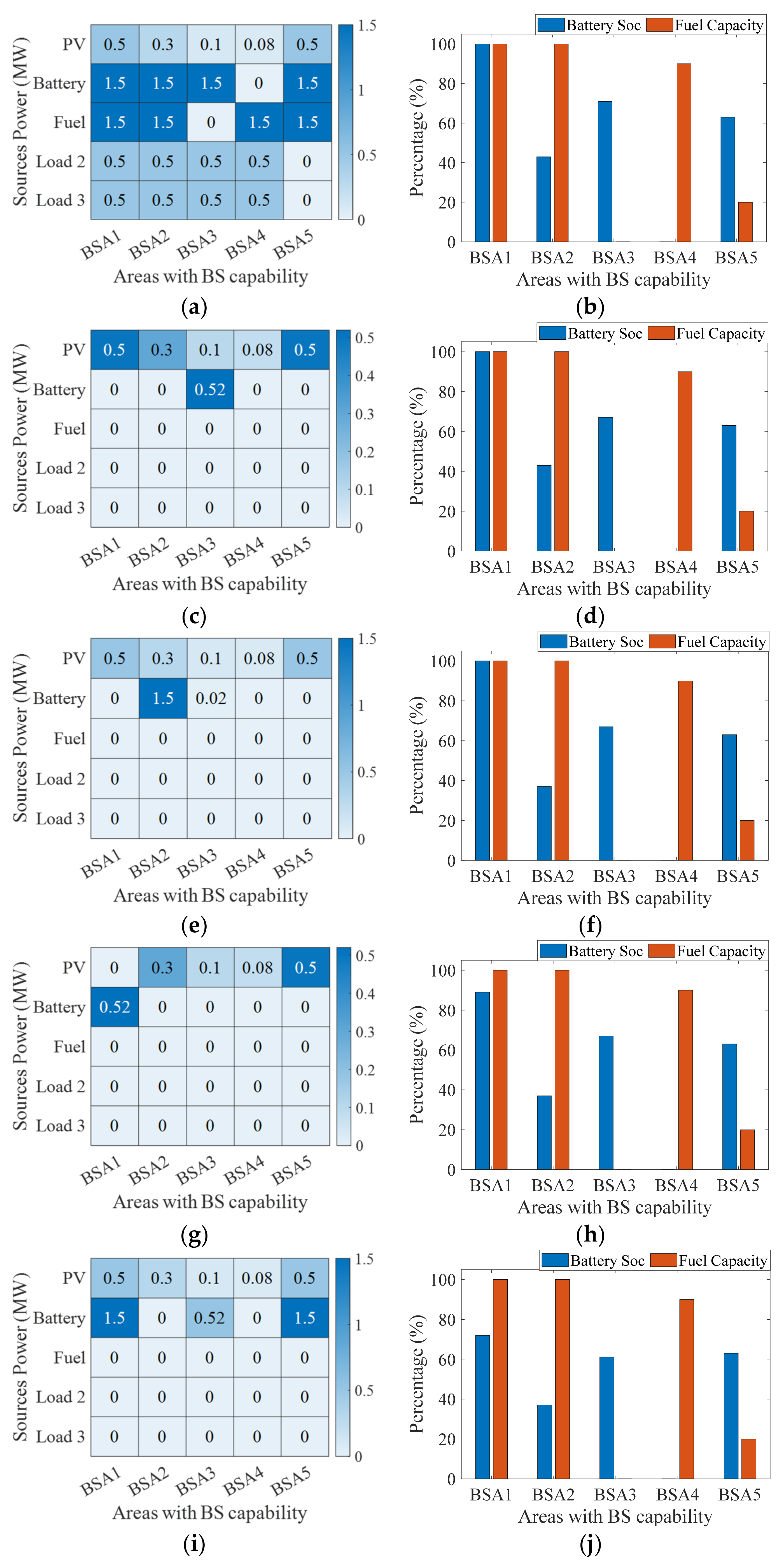
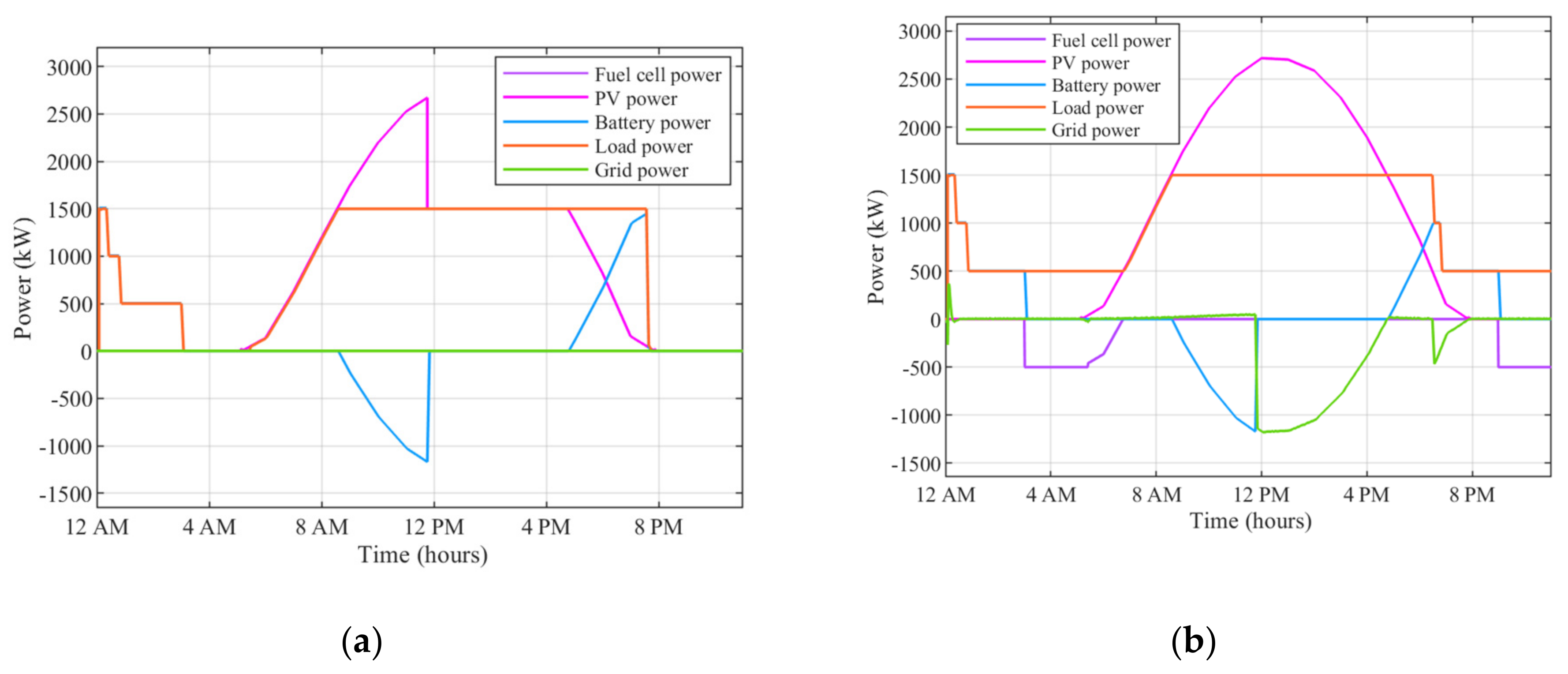
4.1. DL-EMS in a BSA
4.2. TL-EMS under the HLC
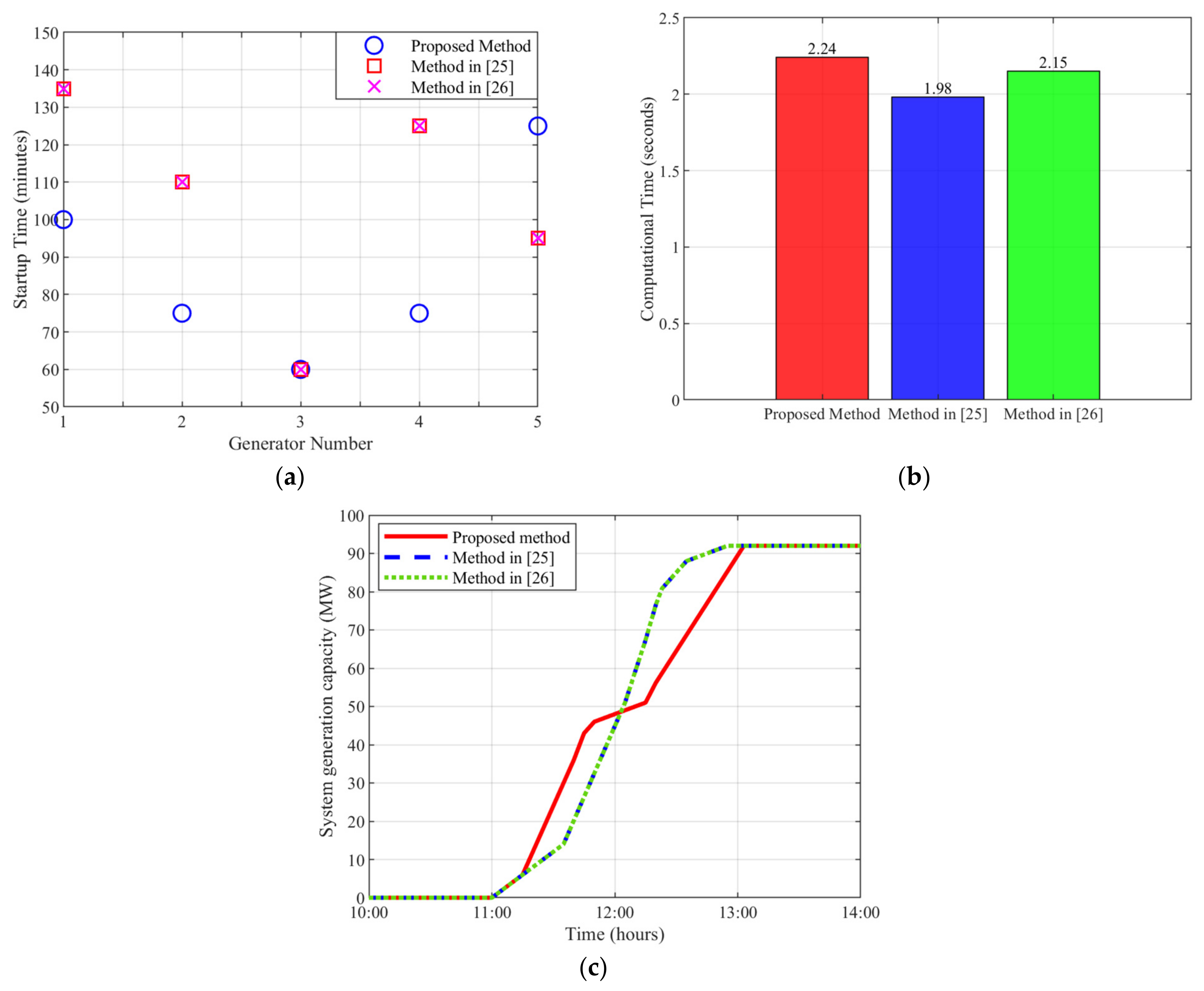
4.3. Comparative Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sundarajoo, S.; Soomro, D.M. Under voltage load shedding and penetration of renewable energy sources in distribution systems: A review. Int. J. Model. Simul. 2023, 43, 1002–1020. [Google Scholar] [CrossRef]
- Khalid, M. Smart grids and renewable energy systems: Perspectives and grid integration challenges. Energy Strategy Rev. 2024, 51, 101299. [Google Scholar] [CrossRef]
- Alhasnawi, B.N.; Jasim, B.H. A Novel Hierarchical Energy Management System Based on Optimization for Multi-Microgrid. Int. J. Electr. Eng. Inform. 2020, 12. [Google Scholar] [CrossRef]
- Umetani, S.; Fukushima, Y.; Morita, H. A linear programming based heuristic algorithm for charge and discharge scheduling of electric vehicles in a building energy management system. Omega 2017, 67, 115–122. [Google Scholar] [CrossRef]
- Tomin, N.; Shakirov, V.; Kozlov, A.; Sidorov, D.; Kurbatsky, V.; Rehtanz, C.; Lora, E.E. Design and optimal energy management of community microgrids with flexible renewable energy sources. Renew. Energy 2022, 183, 903–921. [Google Scholar] [CrossRef]
- Lissa, P.; Deane, C.; Schukat, M.; Seri, F.; Keane, M.; Barrett, E. Deep reinforcement learning for home energy management system control. Energy AI 2021, 3, 100043. [Google Scholar] [CrossRef]
- Musbah, H.; Ali, G.; Aly, H.H.; Little, T.A. Energy management using multi-criteria decision making and machine learning classification algorithms for intelligent system. Electr. Power Syst. Res. 2022, 203, 107645. [Google Scholar] [CrossRef]
- Musbah, H.; Aly, H.H.; Little, T.A. Energy management of hybrid energy system sources based on machine learning classification algorithms. Electr. Power Syst. Res. 2021, 199, 107436. [Google Scholar] [CrossRef]
- Mosa, M.A.; Ali, A. Energy management system of low voltage dc microgrid using mixed-integer nonlinear programing and a global optimization technique. Electr. Power Syst. Res. 2021, 192, 106971. [Google Scholar] [CrossRef]
- Fu, Z.; Li, Z.; Si, P.; Tao, F. A hierarchical energy management strategy for fuel cell/battery/supercapacitor hybrid electric vehicles. Int. J. Hydrogen Energy 2019, 44, 22146–22159. [Google Scholar] [CrossRef]
- Hu, W.; Wang, P.; Gooi, H.B. Toward optimal energy management of microgrids via robust two-stage optimization. IEEE Trans. Smart Grid 2016, 9, 1161–1174. [Google Scholar] [CrossRef]
- Cagnano, A.; Bugliari, A.C.; De Tuglie, E. A cooperative control for the reserve management of isolated microgrids. Appl. Energy 2018, 218, 256–265. [Google Scholar] [CrossRef]
- Mohiti, M.; Monsef, H.; Anvari-Moghaddam, A.; Lesani, H. Two-stage robust optimization for resilient operation of microgrids considering hierarchical frequency control structure. IEEE Trans. Ind. Electron. 2019, 67, 9439–9449. [Google Scholar] [CrossRef]
- Di Piazza, M.; La Tona, G.; Luna, M.; Di Piazza, A. A two-stage Energy Management System for smart buildings reducing the impact of demand uncertainty. Energy Build. 2017, 139, 1–9. [Google Scholar] [CrossRef]
- Li, J.; You, H.; Qi, J.; Kong, M.; Zhang, S.; Zhang, H. Stratified optimization strategy used for restoration with photovoltaic-battery energy storage systems as black-start resources. IEEE Access 2019, 7, 127339–127352. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, P.; Zeng, Z.; Peng, J.; Zhao, Z. Black start strategy for PV-ESS multi-microgrids with three-phase/single-phase architecture. Energies 2016, 9, 372. [Google Scholar] [CrossRef]
- Fu, Q.; Nasiri, A.; Bhavaraju, V.; Solanki, A.; Abdallah, T.; David, C.Y. Transition management of microgrids with high penetration of renewable energy. IEEE Trans. Smart Grid 2013, 5, 539–549. [Google Scholar] [CrossRef]
- Bazmohammadi, N.; Tahsiri, A.; Anvari-Moghaddam, A.; Guerrero, J.M. Stochastic predictive control of multi-microgrid systems. IEEE Trans. Ind. Appl. 2019, 55, 5311–5319. [Google Scholar] [CrossRef]
- Dao, V.; Ishii, H.; Takenobu, Y.; Yoshizawa, S.; Hayashi, Y. Intensive quadratic programming approach for home energy management systems with power utility requirements. Int. J. Electr. Power Energy Syst. 2020, 115, 105473. [Google Scholar] [CrossRef]
- Bazmohammadi, N.; Tahsiri, A.; Anvari-Moghaddam, A.; Guerrero, J.M. A hierarchical energy management strategy for interconnected microgrids considering uncertainty. Int. J. Electr. Power Energy Syst. 2019, 109, 597–608. [Google Scholar] [CrossRef]
- Tabar, V.S.; Jirdehi, M.A.; Hemmati, R. Energy management in microgrid based on the multi objective stochastic programming incorporating portable renewable energy resource as demand response option. Energy 2017, 118, 827–839. [Google Scholar] [CrossRef]
- Varasteh, F.; Nazar, M.S.; Heidari, A.; Shafie-khah, M.; Catalão, J.P. Distributed energy resource and network expansion planning of a CCHP based active microgrid considering demand response programs. Energy 2019, 172, 79–105. [Google Scholar] [CrossRef]
- Movahednia, M.; Karimi, H.; Jadid, S. Optimal hierarchical energy management scheme for networked microgrids considering uncertainties, demand response, and adjustable power. IET Gener. Transm. Distrib. 2020, 14, 4352–4362. [Google Scholar] [CrossRef]
- Sun, W.; Liu, C.-C.; Zhang, L. Optimal generator start-up strategy for bulk power system restoration. IEEE Trans. Power Syst. 2010, 26, 1357–1366. [Google Scholar] [CrossRef]
- El-Zonkoly, A.M. Renewable energy sources for complete optimal power system black-start restoration. IET Gener. Transm. Distrib. 2015, 9, 531–539. [Google Scholar] [CrossRef]
- Su, J.; Chen, C.; Bie, Z. Optimal Generator Start-Up Sequence Strategy Considering Renewable Energy Participation. In Annual Conference of China Electrotechnical Society; Springer: Berlin/Heidelberg, Germany, 2022; pp. 934–945. [Google Scholar]
- Alassi, A.; Ellabban, O. Design of an intelligent energy management system for standalone PV/battery DC microgrids. In Proceedings of the 2019 2nd International Conference on Smart Grid and Renewable Energy (SGRE), Doha, Qatar, 19–21 November 2019. [Google Scholar]
| Refs. | Black Start Support | Level Implementation | Maximising Renewable Energy | Complexity | Timeframe |
|---|---|---|---|---|---|
| [3,4] | No | Distribution network | Yes | Linear programming | Day ahead |
| [5,6] | No | Distribution network | Yes | Reinforcement learning | Day ahead |
| [7,8] | No | Distribution network | Yes | Machine learning | Day ahead |
| [9,10] | No | Distribution network | No | Nonlinear programming | Day ahead |
| [11,14] | No | Distribution network | Yes | Two-stage nonlinear optimisation | Day ahead |
| [12] | No | Distribution network | Yes | Nonlinear optimisation problem | Real time |
| [13] | No | Distribution network | Yes | Mixed-integer linear programming | Day ahead |
| [15] | Yes | Distribution network | Yes | Model predictive control | Day ahead |
| [16] | Yes | Distribution network | Yes | Algorithmic approach | Day ahead |
| [17] | Yes | Distribution network | Yes | No optimisation included | Real time |
| [18,19] | No | Distribution network | No | Quadratic programming | Real time |
| [20,21] | No | Distribution network | No | Stochastic programming | Real time |
| [22] | No | Distribution network | Yes | Bi-level iterative optimisation | Real time |
| [23] | No | Transmission network | Yes | Dynamic programming | Real time |
| Gen. | (h) | (h) | (h) | (MW/h) | (MW) | (MW) |
|---|---|---|---|---|---|---|
| G1 | 0:20 | N/A | 0:40 | 12 | 1.5 | 8 |
| G2 | 0:10 | 0:50 | N/A | 24 | 1 | 12 |
| G3 | 0:20 | N/A | N/A | 24 | 2 | 20 |
| G4 | 0:10 | 0:20 | N/A | 24 | 1 | 12 |
| G5 | 0:30 | N/A | N/A | 50 | 5 | 40 |
| Generic Restoration Action | Time (mins) |
|---|---|
| Energise busbar from BSU/busbar/line | 5 |
| Synchronise between busbar/line | 10 |
| Pick up load | 5 |
| Time (H) | Action | Target | Comment |
|---|---|---|---|
| 10:00 | Optimisation | Define the best sequence to start the generators | |
| 10:05 | Energise | Buses 36, 23, 22, 25 Branches BSA3–36, 36–22, 23–22, 22–25 | |
| 10:05 | Energise | Buses 34, 20, 19, 16, 21, 24, 33; Branches BSA2–34, 34–20, 20–19, 19–16, 16–21, 16–24, 20–33, 19–33 | |
| 10:05 | Energise | Buses 38, 29, 26, 27, 17, 28 Branches BSA4–38, 38–29, 29–26, 26–27, 27–17, 29–28, 28–26 | |
| 10:05 | Energise | Buses 30, 2, 3, 18, 1, 25, 37, 39 Branches BSA5–30, 20–2, 2–3, 3–18, 2–1, 2–25, 25–37, 1–39 | |
| 10:05 | Energise | Buses 31, 6, 5, 4, 14, 15, 7, 8,9, 11, 12, 10 Branches BSA1–31, 31–6, 6–5, 5–4, 4–14, 14–15, 6–7, 7–8, 8–5,8–9, 6–11,11–12, 11–10 | Tries to energise buses 13 and 32 and branches 12–13 and 10–32 but fails due to high reactive power that may cause instability |
| 10:10 | Synchronise | Between BSA3 and BSA2; Bus 21 with Bus 22 Between BSA1, BSA4 and BSA5, Bus 18 and Bus 17, Bus 4 and Bus 3 | |
| 10:20 | Energise | Bus 13, 32 Branch 12–13, 14–13, 10–13, 10–32, 21–22 9–39, 4–3, 25–26, 24–23 | |
| 10:25 | Synchronise | Between BSA3/BSA2 and BSA4/BSA5/BSA1 | |
| 10:35 | Energise | Branches 18–17, 17–16, 15–16 | |
| 10:40 | Crank | G3 | |
| 10:60 | Parallel | G3 | Successful |
| 11:05 | Crank | G4, G2 | |
| 11:15 | Parallel | G4, G2 | Successful |
| 11:20 | Crank | G1 | |
| 11:40 | Parallel | G1 | Successful |
| 11:45 | Crank | G5 | |
| 12:05 | Parallel | G5 | Successful |
| 12:10 | End of black start |
| Feature/Method | Proposed Method | Method in [25] | Method in [26] | Method in [27] |
|---|---|---|---|---|
| Levels addressed | Both distribution and transmission | Transmission only | Transmission only | Distribution only |
| Scenarios addressed | Normal and contingency scenarios at both levels | Black start only | Black start only | Normal scenarios only |
| Optimisation at transmission level | maximise synthetic inertia, minimise load shedding, and maximise use of renewable energies | Optimise system generation capability curve only | Optimise system generation capability curve only | N/A |
| Emergency scenarios at distribution level | Yes | N/A | N/A | No |
| Grid connectivity at distribution level | Yes | N/A | N/A | No |
| Interoperability of generation sources | Yes | Yes | Yes | No |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colak, A.; Abouyehia, M.; Ahmed, K. Novel Hierarchical Energy Management System for Enhanced Black Start Capabilities at Distribution and Transmission Networks. Energies 2024, 17, 2605. https://doi.org/10.3390/en17112605
Colak A, Abouyehia M, Ahmed K. Novel Hierarchical Energy Management System for Enhanced Black Start Capabilities at Distribution and Transmission Networks. Energies. 2024; 17(11):2605. https://doi.org/10.3390/en17112605
Chicago/Turabian StyleColak, Ayse, Mohamed Abouyehia, and Khaled Ahmed. 2024. "Novel Hierarchical Energy Management System for Enhanced Black Start Capabilities at Distribution and Transmission Networks" Energies 17, no. 11: 2605. https://doi.org/10.3390/en17112605
APA StyleColak, A., Abouyehia, M., & Ahmed, K. (2024). Novel Hierarchical Energy Management System for Enhanced Black Start Capabilities at Distribution and Transmission Networks. Energies, 17(11), 2605. https://doi.org/10.3390/en17112605







