Control and Stability of Grid-Forming Inverters: A Comprehensive Review
Abstract
:1. Introduction
2. Grid-Following and Grid-Forming Inverters
2.1. Grid-Following Inverters
2.2. Grid-Forming Inverters
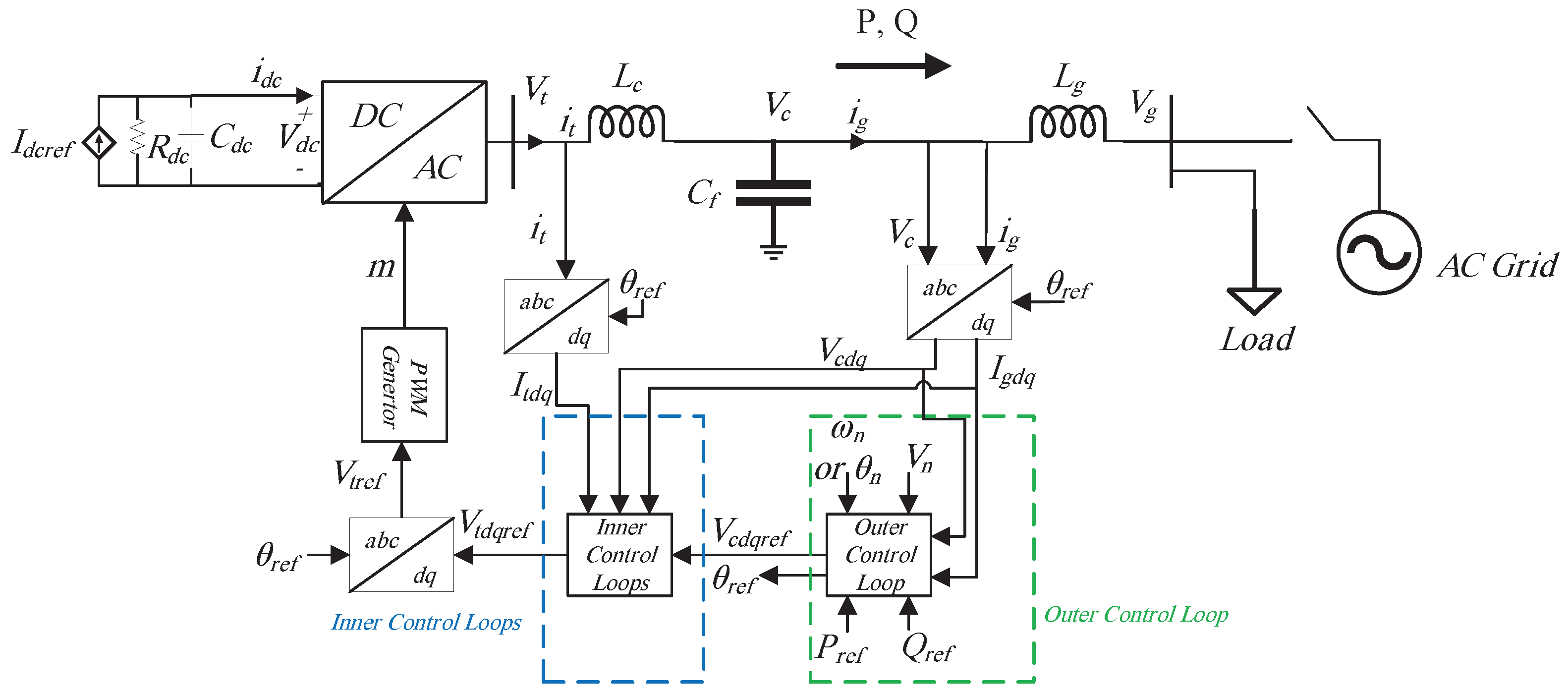
3. Control of GFMIs
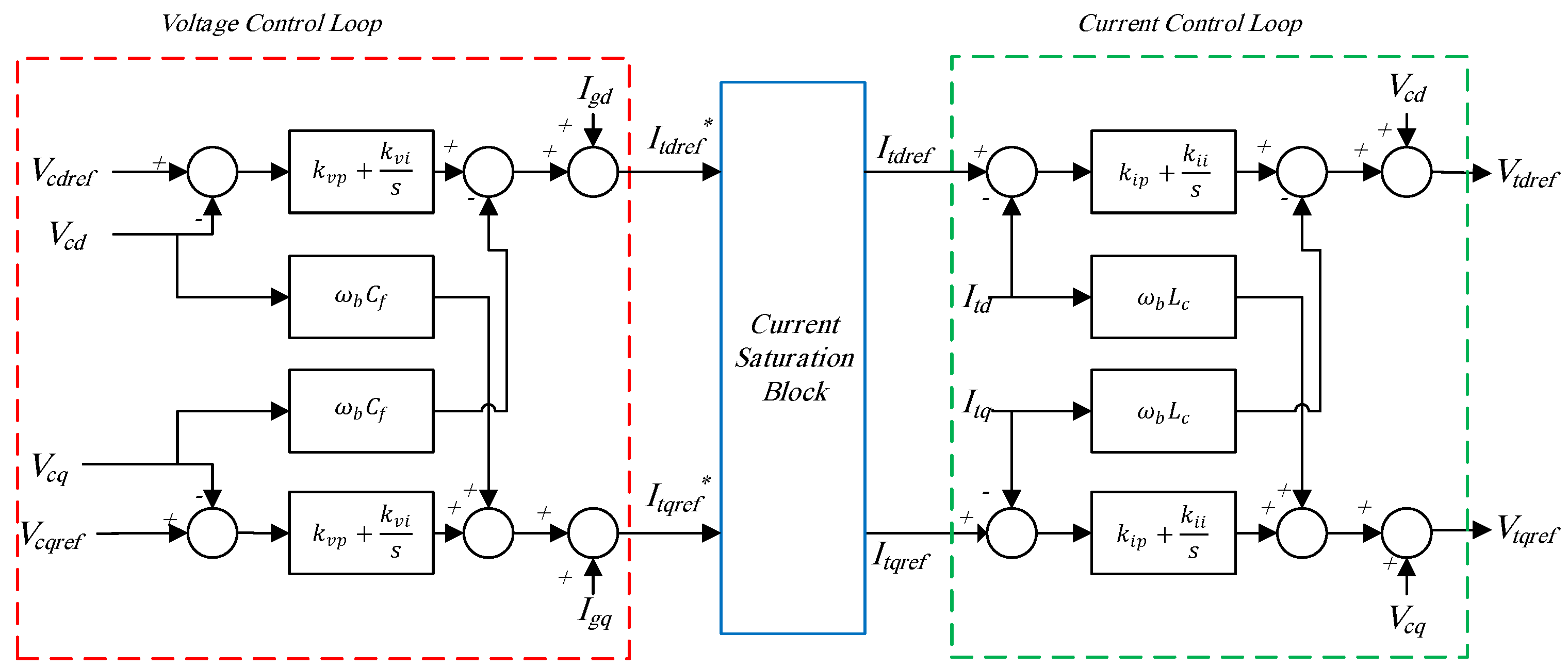
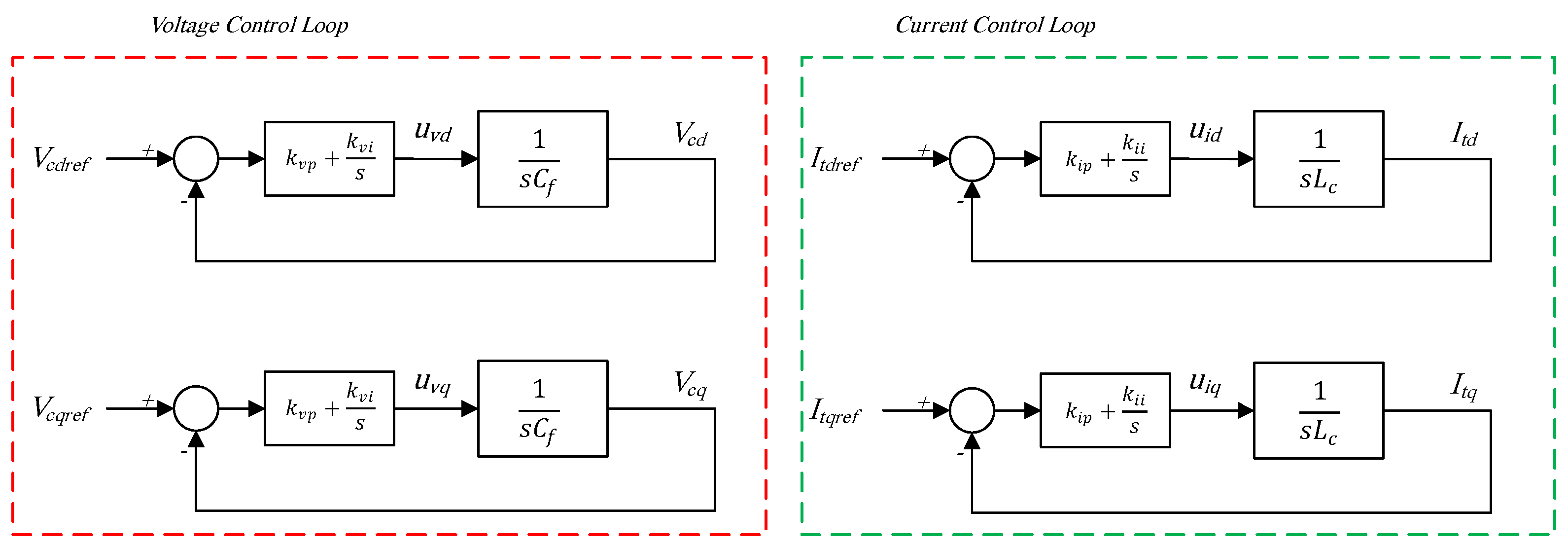
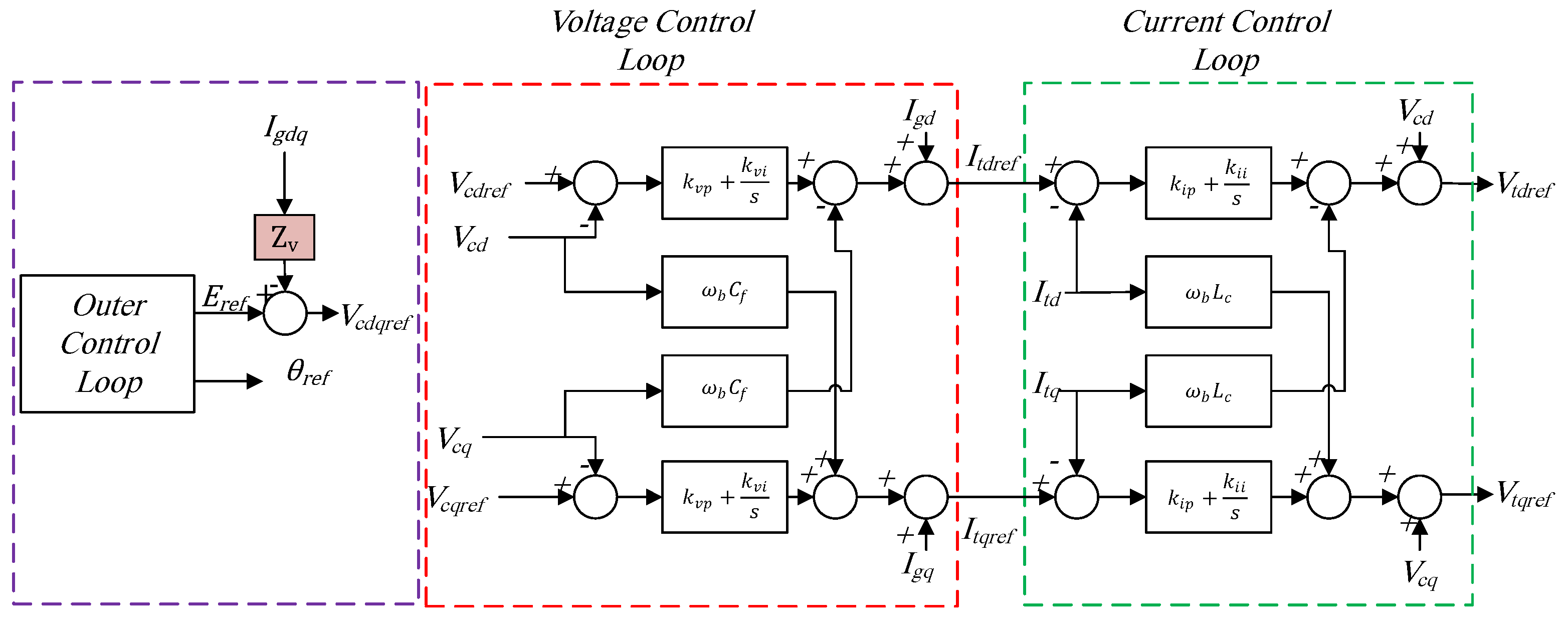
3.1. Inner Control Loops of GFMIs
3.1.1. Voltage-Mode Control
3.1.2. Current-Mode Control
3.1.3. Virtual Impedance Method
3.2. Outer Control Loop of GFMIs
3.2.1. Frequency-Droop Control
3.2.2. Angle-Droop Control
3.2.3. Power Synchronization Control (PSC)
3.2.4. Synchronverter
3.2.5. Virtual Synchronous Machine (VSM)
3.2.6. Matching Control
3.2.7. Virtual Oscillator Control (VOC)
3.2.8. Summary
4. Stability of GFMIs
4.1. Small-Signal Stability
4.1.1. Eigenvalue Analysis
4.1.2. Impedance-Based Analysis
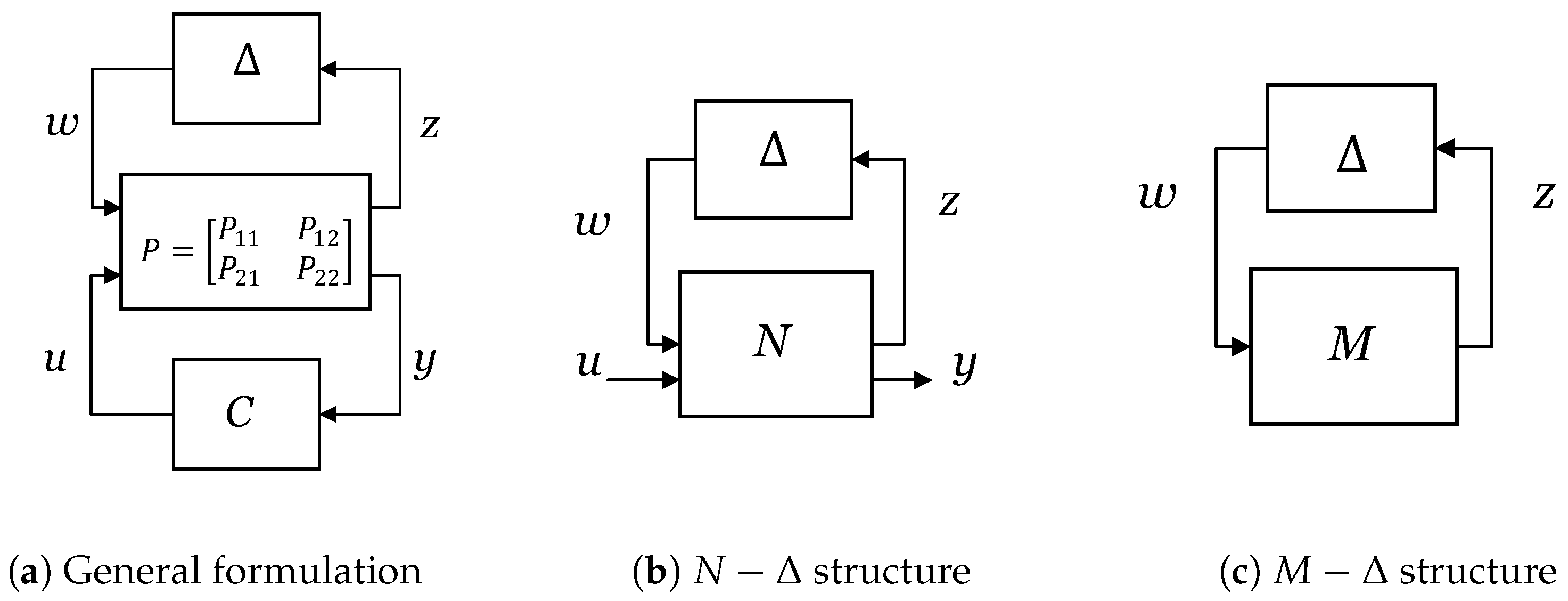
4.1.3. Robust Stability Analysis
4.1.4. Small-Signal Stability of GFMIs
Droop Control Scheme
PSC Scheme
Synchronverter
VSM Control Scheme
Matching Control Scheme
dVOC Scheme
4.1.5. Summary
4.2. Transient Stability
4.2.1. Methods for Transient Stability Analysis
Equal Area Criterion
Lyapunov’s Direct Method
Numerical or Graphical Methods
- curves: curves are used to depict how changes in response to a change in the output active power of generating units [79].
- and curves: curves are used to provide a better understanding of how changes when changes [117]. curves are used to depict how changes with respect to the voltage changes. These curves are usually used when an analytical solution of is difficult to obtain, or the solution does not provide enough insight to the behavior of the system [117]. Based on the dynamics of the system, these curves can be derived either analytically or numerically. Using these curves, the role of different variables and parameters in changes in can be easily shown [117].
4.2.2. Transient Stability of GFMIs
Droop Control Scheme
PSC Scheme
VSM Control Scheme
4.2.3. Summary
5. Future Research
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| RES | Renewable energy source |
| HVDC | High-voltage direct current |
| SG | Synchronous generator |
| GFLI | Grid-following inverter |
| GFMI | Grid-forming inverter |
| AC | Alternating current |
| PLL | Phase-locked loop |
| BESS | Battery energy storage system |
| GESS | Grid energy storage system |
| PSC | Power synchronization control |
| VSM | Virtual synchronous machine |
| VOC | Virtual oscillator control |
| dVOC | Dispatchable virtual oscillator control |
| PCC | Point of common coupling |
| dq0 | Direct-quadrature-zero |
| SRF-PLL | Synchronous reference frame phase-locked loop |
| PI | Proportional-integral |
| PWM | Pulse-width modulation |
| LPF | Low-pass filter |
| DC | Direct current |
| DZO | Dead-zone oscillator |
| SSR | Subsynchronous resonance |
| DFIG | Doubly-fed induction generators |
| ODE | Ordinary differential equation |
| EAC | Equal area criterion |
| EP | Equilibrium point |
| SEP | Stable equilibrium point |
| UEP | Unstable equilibrium point |
| PR | Proportional-resonant |
References
- Rathnayake, D.B.; Akrami, M.; Phurailatpam, C.; Me, S.P.; Hadavi, S.; Jayasinghe, G.; Zabihi, S.; Bahrani, B. Grid Forming Inverter Modeling, Control, and Applications. IEEE Access 2021, 9, 114781–114807. [Google Scholar] [CrossRef]
- Abdel-Rahim, O.; Chub, A.; Vinnikov, D.; Blinov, A. DC Integration of Residential Photovoltaic Systems: A Survey. IEEE Access 2022, 10, 66974–66991. [Google Scholar] [CrossRef]
- Kroposki, B.; Johnson, B.; Zhang, Y.; Gevorgian, V.; Denholm, P.; Hodge, B.M.; Hannegan, B. Achieving a 100 with Extremely High Levels of Variable Renewable Energy. IEEE Power Energy Mag. 2017, 15, 61–73. [Google Scholar] [CrossRef]
- Arghir, C.; Jouini, T.; Dörfler, F. Grid-forming control for power converters based on matching of synchronous machines. Automatica 2018, 95, 273–282. [Google Scholar] [CrossRef]
- Donnini, G.; Carlini, E.; Giannuzzi, G.; Zaottini, R.; Pisani, C.; Chiodo, E.; Lauria, D.; Mottola, F. On the Estimation of Power System Inertia accounting for Renewable Generation Penetration. In Proceedings of the 2020 AEIT International Annual Conference (AEIT), Catania, Italy, 23–25 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Nouti, D.; Ponci, F.; Monti, A. Heterogeneous Inertia Estimation for Power Systems with High Penetration of Converter-Interfaced Generation. Energies 2021, 14, 5047. [Google Scholar] [CrossRef]
- Milano, F.; Dörfler, F.; Hug, G.; Hill, D.J.; Verbič, G. Foundations and Challenges of Low-Inertia Systems (Invited Paper). In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–25. [Google Scholar] [CrossRef]
- Yin, C.; Xie, X.; Xu, S.; Zou, C. Review of oscillations in VSC-HVDC systems caused by control interactions. J. Eng. 2019, 2019, 1204–1207. [Google Scholar] [CrossRef]
- Li, Y.; Gu, Y.; Green, T.C. Revisiting Grid-Forming and Grid-Following Inverters: A Duality Theory. IEEE Trans. Power Syst. 2022, 37, 4541–4554. [Google Scholar] [CrossRef]
- Sajadi, A.; Rañola, J.A.; Kenyon, R.W.; Hodge, B.M.; Mather, B. Dynamics and Stability of Power Systems With High Shares of Grid-Following Inverter-Based Resources: A Tutorial. IEEE Access 2023, 11, 29591–29613. [Google Scholar] [CrossRef]
- Yuefeng, Y.; Jie, Y.; Zhiyuan, H.; Haitian, W. Research on control and protection system for Shanghai Nanhui MMC VSC-HVDC demonstration project. In Proceedings of the 10th IET International Conference on AC and DC Power Transmission (ACDC 2012), Birmingham, UK, 4–5 December 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Guo, X.; Deng, M.; Wang, K. Characteristics and performance of Xiamen VSC-HVDC transmission demonstration project. In Proceedings of the 2016 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Chengdu, China, 19–22 September 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Bodin, A. HVDC Light®—A preferable power transmission system for renewable energies. In Proceedings of the 2011 3rd International Youth Conference on Energetics (IYCE), Leiria, Portugal, 7–9 July 2011; pp. 1–4. [Google Scholar]
- Saad, H.; Fillion, Y.; Deschanvres, S.; Vernay, Y.; Dennetière, S. On Resonances and Harmonics in HVDC-MMC Station Connected to AC Grid. IEEE Trans. Power Deliv. 2017, 32, 1565–1573. [Google Scholar] [CrossRef]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of D-Q Small-Signal Impedance of Grid-Tied Inverters. IEEE Trans. Power Electron. 2016, 31, 675–687. [Google Scholar] [CrossRef]
- Dong, D.; Wen, B.; Boroyevich, D.; Mattavelli, P.; Xue, Y. Analysis of Phase-Locked Loop Low-Frequency Stability in Three-Phase Grid-Connected Power Converters Considering Impedance Interactions. IEEE Trans. Ind. Electron. 2015, 62, 310–321. [Google Scholar] [CrossRef]
- Ding, L.; Du, Y.; Lu, X.; Dong, S.; Hoke, A.; Tan, J. Small-Signal Stability Support From Dynamically Configurable Grid-Forming/Following Inverters for Distribution Systems. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Huang, L.; Wu, C.; Zhou, D.; Blaabjerg, F. Impact of Virtual Admittance on Small-Signal Stability of Grid-Forming Inverters. In Proceedings of the 2021 6th IEEE Workshop on the Electronic Grid (eGRID), New Orleans, LA, USA, 8–10 November 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Ding, L.; Lu, X.; Tan, J. Comparative Small-Signal Stability Analysis of Grid-Forming and Grid-Following Inverters in Low-Inertia Power Systems. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Musca, R.; Vasile, A.; Zizzo, G. Grid-forming converters. A critical review of pilot projects and demonstrators. Renew. Sustain. Energy Rev. 2022, 165, 112551. [Google Scholar] [CrossRef]
- Koller, M.; González Vayá, M.; Chacko, A.; Borsche, T.; Ulbig, A. Primary control reserves provision with battery energy storage systems in the largest European ancillary services cooperation. In Set of Papers, CIGRE Session 46: 21–26 August 2016, Paris, France; ETH: Zurich, Switzerland, 2016; p. 361. [Google Scholar]
- Mcgregor-Lowndes, M.; Hannah, F. ACPNS Legal Case Notes Series: 2023-87; Matthews v Ausnet Electricity Services Pty Ltd. & Ors; Rowe v Ausnet Electricity Services Pty Ltd. & Ors (Final Ruling): Melbourne, Australia, 2023; Available online: https://eprints.qut.edu.au/241169/ (accessed on 24 June 2024).
- Manty, A.; Marz, M.; Copp, K.; Sankar, S.; Rector, J.; Fairly, P.; Irwin, G.D. ATC’s Mackinac Back-to-Back HVDC Project: Planning and Operation Considerations for Michigan’s Eastern Upper and Northern Lower Peninsulas; CIGRE USNC-2013 Grid of the Future Symposium, ISO New England Inc.: Holyoke, MA, USA, 2013. [Google Scholar]
- Marz, M.; Dickmander, D.; Johansson, F.; Irwin, G.; Sankar, S.; Copp, K.; Danielsson, J.; Holmberg, P.; B&v, E.; Manty, A.; et al. Mackinac HVDC Converter Automatic Runback Utilizing Locally Measured Quantities. In Proceedings of the CIGRE Conference, Toronto, ON, Canada, 22–24 September 2014. [Google Scholar]
- Reserve-Year, H.P. Hornsdale Power Reserve-Year 1 Technical and Market Impact Case Study. Available online: https://www.aurecongroup.com/-/media/files/downloads-library/thought-leadership/aurecon-hornsdale-power-reserve-impact-study-2018.pdf (accessed on 20 April 2024).
- Gleeson, P. Hornsdale Power Reserve Year 2 Report–Technical and Market Impact Case Study; Aurecon: Sydney, Australia, 2020. [Google Scholar]
- Tuckey, A.; Round, S. Practical application of a complete virtual synchronous generator control method for microgrid and grid-edge applications. In Proceedings of the 2018 IEEE 19th Workshop on Control and Modeling for Power Electronics (COMPEL), Padua, Italy, 25–28 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Schömann, O.; Sadri, H.; Krüger, W.; Bülo, T.; Hardt, C.; Hesse, R.; Falk, A.; Stankat, P.R. Experiences with Large Grid-Forming Inverters on Various Island and Microgrid Projects. In Proceedings of the Hybrid Power Systems Workshop, Crete, Greece, 22–23 May 2019. [Google Scholar]
- Anttila, S.; Döhler, J.S.; Oliveira, J.G.; Boström, C. Grid Forming Inverters: A Review of the State of the Art of Key Elements for Microgrid Operation. Energies 2022, 15, 5517. [Google Scholar] [CrossRef]
- Ebinyu, E.; Abdel-Rahim, O.; Mansour, D.E.A.; Shoyama, M.; Abdelkader, S.M. Grid-Forming Control: Advancements towards 100% Inverter-Based Grids—A Review. Energies 2023, 16, 7579. [Google Scholar] [CrossRef]
- Aragon, D.; Unamuno, E.; Ceballos, S.; Barrena, J. Comparative small-signal evaluation of advanced grid-forming control techniques. Electr. Power Syst. Res. 2022, 211, 108154. [Google Scholar] [CrossRef]
- Chandorkar, M.; Divan, D.; Adapa, R. Control of parallel connected inverters in standalone AC supply systems. IEEE Trans. Ind. Appl. 1993, 29, 136–143. [Google Scholar] [CrossRef]
- Majumder, R.; Chaudhuri, B.; Ghosh, A.; Majumder, R.; Ledwich, G.; Zare, F. Improvement of stability and load sharing in an autonomous microgrid using supplementary droop control loop. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010; p. 1. [Google Scholar] [CrossRef]
- Yazdani, S.; Ferdowsi, M.; Shamsi, P. Power Synchronization PID Control Method for Grid-Connected Voltage-Source Converters. In Proceedings of the 2020 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 13–14 July 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Guan, M.; Pan, W.; Zhang, J.; Hao, Q.; Cheng, J.; Zheng, X. Synchronous Generator Emulation Control Strategy for Voltage Source Converter (VSC) Stations. IEEE Trans. Power Syst. 2015, 30, 3093–3101. [Google Scholar] [CrossRef]
- Rokrok, E.; Qoria, T.; Bruyere, A.; Francois, B.; Guillaud, X. Classification and dynamic assessment of droop-based grid-forming control schemes: Application in HVDC systems. Electr. Power Syst. Res. 2020, 189, 106765. [Google Scholar] [CrossRef]
- Cvetkovic, I.; Boroyevich, D.; Burgos, R.; Li, C.; Mattavelli, P. Modeling and control of grid-connected voltage-source converters emulating isotropic and anisotropic synchronous machines. In Proceedings of the 2015 IEEE 16th Workshop on Control and Modeling for Power Electronics (COMPEL), Vancouver, BC, Canada, 12–15 July 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Curi, S.; Groß, D.; Dörfler, F. Control of low-inertia power grids: A model reduction approach. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, Australia, 12–15 December 2017; pp. 5708–5713. [Google Scholar] [CrossRef]
- Arghir, C.; Dörfler, F. The Electronic Realization of Synchronous Machines: Model Matching, Angle Tracking, and Energy Shaping Techniques. IEEE Trans. Power Electron. 2020, 35, 4398–4410. [Google Scholar] [CrossRef]
- Leyba, E.R.M.; Opila, D.F.; Keith Kintzley, C. Three Phase Dead-Zone Oscillator Control Under Unbalanced Load Conditions. In Proceedings of the 2019 IEEE Electric Ship Technologies Symposium (ESTS), Washington, DC, USA, 14–16 August 2019; pp. 134–140. [Google Scholar] [CrossRef]
- Tôrres, L.A.B.; Hespanha, J.P.; Moehlis, J. Power supply synchronization without communication. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, W.; Cantarellas, A.M.; Rocabert, J.; Luna, A.; Rodriguez, P. Synchronous Power Controller With Flexible Droop Characteristics for Renewable Power Generation Systems. IEEE Trans. Sustain. Energy 2016, 7, 1572–1582. [Google Scholar] [CrossRef]
- Meng, X.; Liu, J.; Liu, Z. A Generalized Droop Control for Grid-Supporting Inverter Based on Comparison Between Traditional Droop Control and Virtual Synchronous Generator Control. IEEE Trans. Power Electron. 2019, 34, 5416–5438. [Google Scholar] [CrossRef]
- Awal, M.; Husain, I. Unified virtual oscillator control for grid-forming and grid-following converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 4573–4586. [Google Scholar] [CrossRef]
- Kammer, C.; Karimi, A. Decentralized and Distributed Transient Control for Microgrids. IEEE Trans. Control. Syst. Technol. 2019, 27, 311–322. [Google Scholar] [CrossRef]
- Madani, S.S.; Kammer, C.; Karimi, A. Data-Driven Distributed Combined Primary and Secondary Control in Microgrids. IEEE Trans. Control. Syst. Technol. 2021, 29, 1340–1347. [Google Scholar] [CrossRef]
- Jiang, Y.; Bernstein, A.; Vorobev, P.; Mallada, E. Grid-Forming Frequency Shaping Control for Low-Inertia Power Systems. IEEE Control. Syst. Lett. 2021, 5, 1988–1993. [Google Scholar] [CrossRef]
- Du, W.; Tuffner, F.K.; Schneider, K.P.; Lasseter, R.H.; Xie, J.; Chen, Z.; Bhattarai, B. Modeling of Grid-Forming and Grid-Following Inverters for Dynamic Simulation of Large-Scale Distribution Systems. IEEE Trans. Power Deliv. 2021, 36, 2035–2045. [Google Scholar] [CrossRef]
- Golestan, S.; Monfared, M.; Freijedo, F.D.; Guerrero, J.M. Performance Improvement of a Prefiltered Synchronous-Reference-Frame PLL by Using a PID-Type Loop Filter. IEEE Trans. Ind. Electron. 2014, 61, 3469–3479. [Google Scholar] [CrossRef]
- Karimi-Ghartema, M. IEEE Press Series on Microelectronic Systems. In Enhanced Phase-Locked Loop Structures for Power and Energy Applications; IEEE: Piscataway, NJ, USA, 2014; p. 204. [Google Scholar] [CrossRef]
- Castilla, M.; Vicuna, L.; Miret, J. Control of Power Converters in AC Microgrids; Springer: Berlin/Heidelberg, Germany, 2019; pp. 139–170. [Google Scholar] [CrossRef]
- Li, S.; Fu, X.; Ramezani, M.; Sun, Y.; Won, H. A novel direct-current vector control technique for single-phase inverter with L, LC and LCL filters. Electr. Power Syst. Res. 2015, 125, 235–244. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. Controlled-Frequency VSC System. In Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010; pp. 245–269. [Google Scholar] [CrossRef]
- Qoria, T.; Gruson, F.; Colas, F.; Kestelyn, X.; Guillaud, X. Current limiting algorithms and transient stability analysis of grid-forming VSCs. Electr. Power Syst. Res. 2020, 189, 106726. [Google Scholar] [CrossRef]
- Fan, B.; Liu, T.; Zhao, F.; Wu, H.; Wang, X. A Review of Current-Limiting Control of Grid-Forming Inverters Under Symmetrical Disturbances. IEEE Open J. Power Electron. 2022, 3, 955–969. [Google Scholar] [CrossRef]
- Qoria, T.; Gruson, F.; Colas, F.; Guillaud, X.; Debry, M.S.; Prevost, T. Tuning of Cascaded Controllers for Robust Grid-Forming Voltage Source Converter. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–7. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A.; Fosso, O.B. Automatic Tuning of Cascaded Controllers for Power Converters Using Eigenvalue Parametric Sensitivities. IEEE Trans. Ind. Appl. 2015, 51, 1743–1753. [Google Scholar] [CrossRef]
- Du, W.; Chen, Z.; Schneider, K.P.; Lasseter, R.H.; Pushpak Nandanoori, S.; Tuffner, F.K.; Kundu, S. A Comparative Study of Two Widely Used Grid-Forming Droop Controls on Microgrid Small-Signal Stability. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 963–975. [Google Scholar] [CrossRef]
- Salha, F.; Colas, F.; Guillaud, X. Virtual resistance principle for the overcurrent protection of PWM voltage source inverter. In Proceedings of the 2010 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenburg, Sweden, 11–13 October 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Chen, Z. Autonomous Control of Inverter-Interfaced Distributed Generation Units for Harmonic Current Filtering and Resonance Damping in an Islanded Microgrid. IEEE Trans. Ind. Appl. 2014, 50, 452–461. [Google Scholar] [CrossRef]
- Cheng, P.T.; Chen, C.A.; Lee, T.L.; Kuo, S.Y. A Cooperative Imbalance Compensation Method for Distributed-Generation Interface Converters. IEEE Trans. Ind. Appl. 2009, 45, 805–815. [Google Scholar] [CrossRef]
- Rowe, C.N.; Summers, T.J.; Betz, R.E.; Moore, T.G.; Townsend, C.D. Implementing the virtual output impedance concept in a three phase system utilising cascaded PI controllers in the dq rotating reference frame for microgrid inverter control. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.W.; Blaabjerg, F.; Loh, P.C. Virtual-Impedance-Based Control for Voltage-Source and Current-Source Converters. IEEE Trans. Power Electron. 2015, 30, 7019–7037. [Google Scholar] [CrossRef]
- Kong, L.; Xue, Y.; Qiao, L.; Wang, F.F. Angle Droop Design for Grid-Forming Inverters Considering Impacts of Virtual Impedance Control. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 1006–1013. [Google Scholar] [CrossRef]
- Paquette, A.D.; Divan, D.M. Virtual impedance current limiting for inverters in microgrids with synchronous generators. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 1039–1046. [Google Scholar] [CrossRef]
- Rodriguez, P.; Candela, I.; Luna, A. Control of PV generation systems using the synchronous power controller. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 993–998. [Google Scholar] [CrossRef]
- Glover, J.D. Sarma. Power Systems Analysis and Design; PWS Publishing Co.: Pacific Grove, CA, USA, 1987. [Google Scholar]
- Tielens, P.; Van Hertem, D. The relevance of inertia in power systems. Renew. Sustain. Energy Rev. 2016, 55, 999–1009. [Google Scholar] [CrossRef]
- Raza, M.; Prieto-Araujo, E.; Gomis-Bellmunt, O. Small-Signal Stability Analysis of Offshore AC Network Having Multiple VSC-HVDC Systems. IEEE Trans. Power Deliv. 2018, 33, 830–839. [Google Scholar] [CrossRef]
- Pan, D.; Wang, X.; Liu, F.; Shi, R. Transient Stability of Voltage-Source Converters With Grid-Forming Control: A Design-Oriented Study. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1019–1033. [Google Scholar] [CrossRef]
- Shabshab, S.C. Dead Zone Oscillator Control for Communication-Free Synchronization of Paralleled, Three-Phase, Current-Controlled Inverters; US Naval Academy: Philadelphia, PA, USA, 2016. [Google Scholar]
- Johnson, B.B.; Dhople, S.V.; Hamadeh, A.O.; Krein, P.T. Synchronization of Parallel Single-Phase Inverters With Virtual Oscillator Control. IEEE Trans. Power Electron. 2014, 29, 6124–6138. [Google Scholar] [CrossRef]
- Dhople, S.V.; Johnson, B.B.; Hamadeh, A.O. Virtual Oscillator Control for voltage source inverters. In Proceedings of the 2013 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 2–4 October 2013; pp. 1359–1363. [Google Scholar] [CrossRef]
- Johnson, B.B.; Dhople, S.V.; Hamadeh, A.O.; Krein, P.T. Synchronization of Nonlinear Oscillators in an LTI Electrical Power Network. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 834–844. [Google Scholar] [CrossRef]
- Seo, G.S.; Colombino, M.; Subotic, I.; Johnson, B.; Groß, D.; Dörfler, F. Dispatchable Virtual Oscillator Control for Decentralized Inverter-dominated Power Systems: Analysis and Experiments. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 561–566. [Google Scholar] [CrossRef]
- Azizi Aghdam, S.; Agamy, M. Virtual oscillator-based methods for grid-forming inverter control: A review. IET Renew. Power Gener. 2022, 16, 835–855. [Google Scholar] [CrossRef]
- Tayyebi, A.; Groß, D.; Anta, A.; Kupzog, F.; Dörfler, F. Frequency Stability of Synchronous Machines and Grid-Forming Power Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1004–1018. [Google Scholar] [CrossRef]
- Kundur, P.; Balu, N.; Lauby, M. Power System Stability and Control; EPRI Power System Engineering Series; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C.; et al. Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C.; Ajjarapu, V.; Canizares, C.; Erlich, I.; Hill, D.; Hiskens, I.; Kamwa, I.; Pal, B.; et al. Definition and Classification of Power System Stability—Revisited & Extended. IEEE Trans. Power Syst. 2021, 36, 3271–3281. [Google Scholar] [CrossRef]
- Terms, Definitions and Symbols for Subsynchronous Oscillations IEEE Subsynchronous Resonance Working Group of the System Dynamic Performance Subcommittee Power System Engineering Committee. IEEE Power Eng. Rev. 1985, PER-5, 37. [CrossRef]
- Cai, W.; Ying, G.; Li, W.; Wang, Z. The Analysis of a Generator Shaft Crack Cause by Torsional Vibration due to SSR. J. Phys. Conf. Ser. 2021, 2101, 012022. [Google Scholar] [CrossRef]
- Reader’s guide to subsynchronous resonance. IEEE Trans. Power Syst. 1992, 7, 150–157. [CrossRef]
- Pourbeik, P.; Ramey, D.G.; Abi-Samra, N.; Brooks, D.; Gaikwad, A. Vulnerability of Large Steam Turbine Generators to Torsional Interactions During Electrical Grid Disturbances. IEEE Trans. Power Syst. 2007, 22, 1250–1258. [Google Scholar] [CrossRef]
- Shair, J.; Xie, X.; Wang, L.; Liu, W.; He, J.; Liu, H. Overview of emerging subsynchronous oscillations in practical wind power systems. Renew. Sustain. Energy Rev. 2019, 99, 159–168. [Google Scholar] [CrossRef]
- Milanovic, J.V.; Adrees, A. Identifying Generators at Risk of SSR in Meshed Compensated AC/DC Power Networks. IEEE Trans. Power Syst. 2013, 28, 4438–4447. [Google Scholar] [CrossRef]
- Adrees, A.; Milanović, J.V. Methodology for Evaluation of Risk of Subsynchronous Resonance in Meshed Compensated Networks. IEEE Trans. Power Syst. 2014, 29, 815–823. [Google Scholar] [CrossRef]
- Pourbeik, P.; Koessler, R.; Dickmander, D.; Wong, W. Integration of large wind farms into utility grids (part 2—Performance issues). In Proceedings of the 2003 IEEE Power Engineering Society General Meeting (IEEE Cat. No.03CH37491), Toronto, ON, Canada, 13–17 July 2003; Volume 3, pp. 1520–1525. [Google Scholar] [CrossRef]
- Leon, A.E.; Solsona, J.A. Sub-Synchronous Interaction Damping Control for DFIG Wind Turbines. IEEE Trans. Power Syst. 2015, 30, 419–428. [Google Scholar] [CrossRef]
- Adams, J.; Carter, C.; Huang, S.H. ERCOT experience with Sub-synchronous Control Interaction and proposed remediation. In Proceedings of the PES T&D 2012, Orlando, FL, USA, 7–10 May 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Cheng, Y.; Huang, S.H.; Rose, J.; Pappu, V.A.; Conto, J. ERCOT subsynchronous resonance topology and frequency scan tool development. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Narendra, K.; Fedirchuk, D.; Midence, R.; Zhang, N.; Mulawarman, A.; Mysore, P.; Sood, V. New microprocessor based relay to monitor and protect power systems against sub-harmonics. In Proceedings of the 2011 IEEE Electrical Power and Energy Conference, Winnipeg, MB, Canada, 3–5 October 2011; pp. 438–443. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F. Harmonic Stability in Power Electronic-Based Power Systems: Concept, Modeling, and Analysis. IEEE Trans. Smart Grid 2019, 10, 2858–2870. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Wu, W. Modeling and Analysis of Harmonic Stability in an AC Power-Electronics-Based Power System. IEEE Trans. Power Electron. 2014, 29, 6421–6432. [Google Scholar] [CrossRef]
- Ebrahimzadeh, E.; Blaabjerg, F.; Wang, X.; Bak, C.L. Harmonic Stability and Resonance Analysis in Large PMSG-Based Wind Power Plants. IEEE Trans. Sustain. Energy 2018, 9, 12–23. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Liserre, M.; Chen, Z.; He, J.; Li, Y. An Active Damper for Stabilizing Power-Electronics-Based AC Systems. IEEE Trans. Power Electron. 2014, 29, 3318–3329. [Google Scholar] [CrossRef]
- Yoon, C.; Bai, H.; Beres, R.N.; Wang, X.; Bak, C.L.; Blaabjerg, F. Harmonic Stability Assessment for Multiparalleled, Grid-Connected Inverters. IEEE Trans. Sustain. Energy 2016, 7, 1388–1397. [Google Scholar] [CrossRef]
- Ebrahimzadeh, E.; Blaabjerg, F.; Wang, X.; Bak, C.L. Modeling and identification of harmonic instability problems in wind farms. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Fan, L. Modeling Type-4 Wind in Weak Grids. IEEE Trans. Sustain. Energy 2019, 10, 853–864. [Google Scholar] [CrossRef]
- Li, Y.; Fan, L.; Miao, Z. Stability Control for Wind in Weak Grids. IEEE Trans. Sustain. Energy 2019, 10, 2094–2103. [Google Scholar] [CrossRef]
- Zhou, J.Z.; Ding, H.; Fan, S.; Zhang, Y.; Gole, A.M. Impact of Short-Circuit Ratio and Phase-Locked-Loop Parameters on the Small-Signal Behavior of a VSC-HVDC Converter. IEEE Trans. Power Deliv. 2014, 29, 2287–2296. [Google Scholar] [CrossRef]
- Papangelis, L.; Debry, M.S.; Prevost, T.; Panciatici, P.; Van Cutsem, T. Stability of a Voltage Source Converter Subject to Decrease of Short-Circuit Capacity: A Case Study. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Liu, H.; Xie, X.; Zhang, C.; Li, Y.; Liu, H.; Hu, Y. Quantitative SSR Analysis of Series-Compensated DFIG-Based Wind Farms Using Aggregated RLC Circuit Model. IEEE Trans. Power Syst. 2017, 32, 474–483. [Google Scholar] [CrossRef]
- Zhao, F.; Wang, X.; Zhou, Z.; Harnefors, L.; Svensson, J.R.; Kocewiak, L.; Gryning, M.P.S. A General Integration Method for Small-Signal Stability Analysis of Grid-Forming Converter Connecting to Power System. In Proceedings of the 2020 IEEE 21st Workshop on Control and Modeling for Power Electronics (COMPEL), Aalborg, Denmark, 9–12 November 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Qi, Y.; Deng, H.; Wang, J.; Tang, Y. Passivity-Based Synchronization Stability Analysis for Power-Electronic-Interfaced Distributed Generations. IEEE Trans. Sustain. Energy 2021, 12, 1141–1150. [Google Scholar] [CrossRef]
- Rosso, R.; Cassoli, J.; Buticchi, G.; Engelken, S.; Liserre, M. Robust Stability Analysis of LCL Filter Based Synchronverter Under Different Grid Conditions. IEEE Trans. Power Electron. 2019, 34, 5842–5853. [Google Scholar] [CrossRef]
- Sumsurooah, S.; Odavic, M.; Bozhko, S. μ Approach to Robust Stability Domains in the Space of Parametric Uncertainties for a Power System With Ideal CPL. IEEE Trans. Power Electron. 2018, 33, 833–844. [Google Scholar] [CrossRef]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Bryant, J.S.; McGrath, B.; Meegahapola, L.; Sokolowski, P. Small-Signal Modeling and Stability Analysis of a Droop-Controlled Grid-Forming Inverter. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 17–21 July 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Singh, A.; Debusschere, V.; Hadjsaid, N.; Legrand, X.; Bouzigon, B. Slow-interaction Converter-driven Stability in the Distribution Grid: Small-Signal Stability Analysis with Grid-Following and Grid-Forming Inverters. IEEE Trans. Power Syst. 2023, 39, 4521–4536. [Google Scholar] [CrossRef]
- Yazdani, S.; Ferdowsi, M.; Davari, M.; Shamsi, P. Advanced Current-Limiting and Power-Sharing Control in a PV-Based Grid-Forming Inverter Under Unbalanced Grid Conditions. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1084–1096. [Google Scholar] [CrossRef]
- Henriquez-Auba, R.; Lara, J.D.; Roberts, C.; Callaway, D.S. Grid Forming Inverter Small Signal Stability: Examining Role of Line and Voltage Dynamics. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 4063–4068. [Google Scholar] [CrossRef]
- Luo, C.; Ma, X.; Liu, T.; Wang, X. Controller-Saturation-Based Transient Stability Enhancement for Grid-Forming Inverters. IEEE Trans. Power Electron. 2023, 38, 2646–2657. [Google Scholar] [CrossRef]
- Khalil, H. Nonlinear Control; Always Learning; Pearson: London, UK, 2014. [Google Scholar]
- Shuai, Z.; Shen, C.; Liu, X.; Li, Z.; Shen, Z.J. Transient Angle Stability of Virtual Synchronous Generators Using Lyapunov’s Direct Method. IEEE Trans. Smart Grid 2019, 10, 4648–4661. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Design-Oriented Transient Stability Analysis of Grid-Connected Converters With Power Synchronization Control. IEEE Trans. Ind. Electron. 2019, 66, 6473–6482. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. A Mode-Adaptive Power-Angle Control Method for Transient Stability Enhancement of Virtual Synchronous Generators. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1034–1049. [Google Scholar] [CrossRef]
- Fu, X.; Sun, J.; Huang, M.; Tian, Z.; Yan, H.; Iu, H.H.C.; Hu, P.; Zha, X. Large-Signal Stability of Grid-Forming and Grid-Following Controls in Voltage Source Converter: A Comparative Study. IEEE Trans. Power Electron. 2021, 36, 7832–7840. [Google Scholar] [CrossRef]
- Jin, Z.; Wang, X. A DQ-Frame Asymmetrical Virtual Impedance Control for Enhancing Transient Stability of Grid-Forming Inverters. IEEE Trans. Power Electron. 2022, 37, 4535–4544. [Google Scholar] [CrossRef]
- Hadjileonidas, A.; Li, Y.; Green, T.C. Comparative Analysis of Transient Stability of Grid-Forming and Grid-Following Inverters. In Proceedings of the 2022 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Guangzhou, China, 4–7 November 2022; pp. 296–301. [Google Scholar] [CrossRef]
- Hou, X.; Han, H.; Zhong, C.; Yuan, W.; Yi, M.; Chen, Y. Improvement of transient stability in inverter-based AC microgrid via adaptive virtual inertia. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Ávila Martínez, R.E.; Renedo, J.; Rouco, L.; Garcia-Cerrada, A.; Sigrist, L.; Qoria, T.; Guillaud, X. Fast Voltage Boosters to Improve Transient Stability of Power Systems With 100. IEEE Trans. Energy Convers. 2022, 37, 2777–2789. [Google Scholar] [CrossRef]
- Yu, H.; Awal, M.A.; Tu, H.; Husain, I.; Lukic, S. Comparative Transient Stability Assessment of Droop and Dispatchable Virtual Oscillator Controlled Grid-Connected Inverters. IEEE Trans. Power Electron. 2021, 36, 2119–2130. [Google Scholar] [CrossRef]

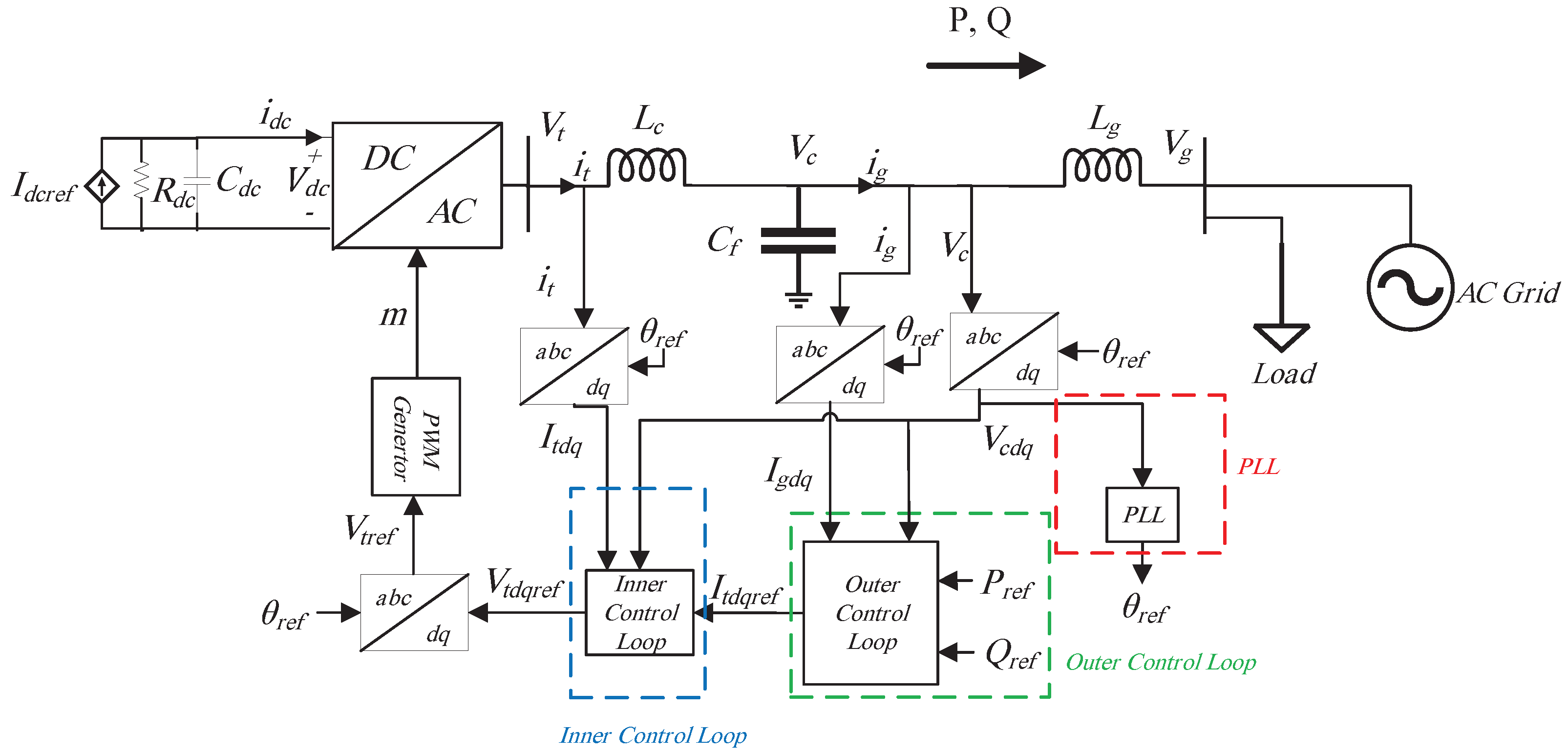
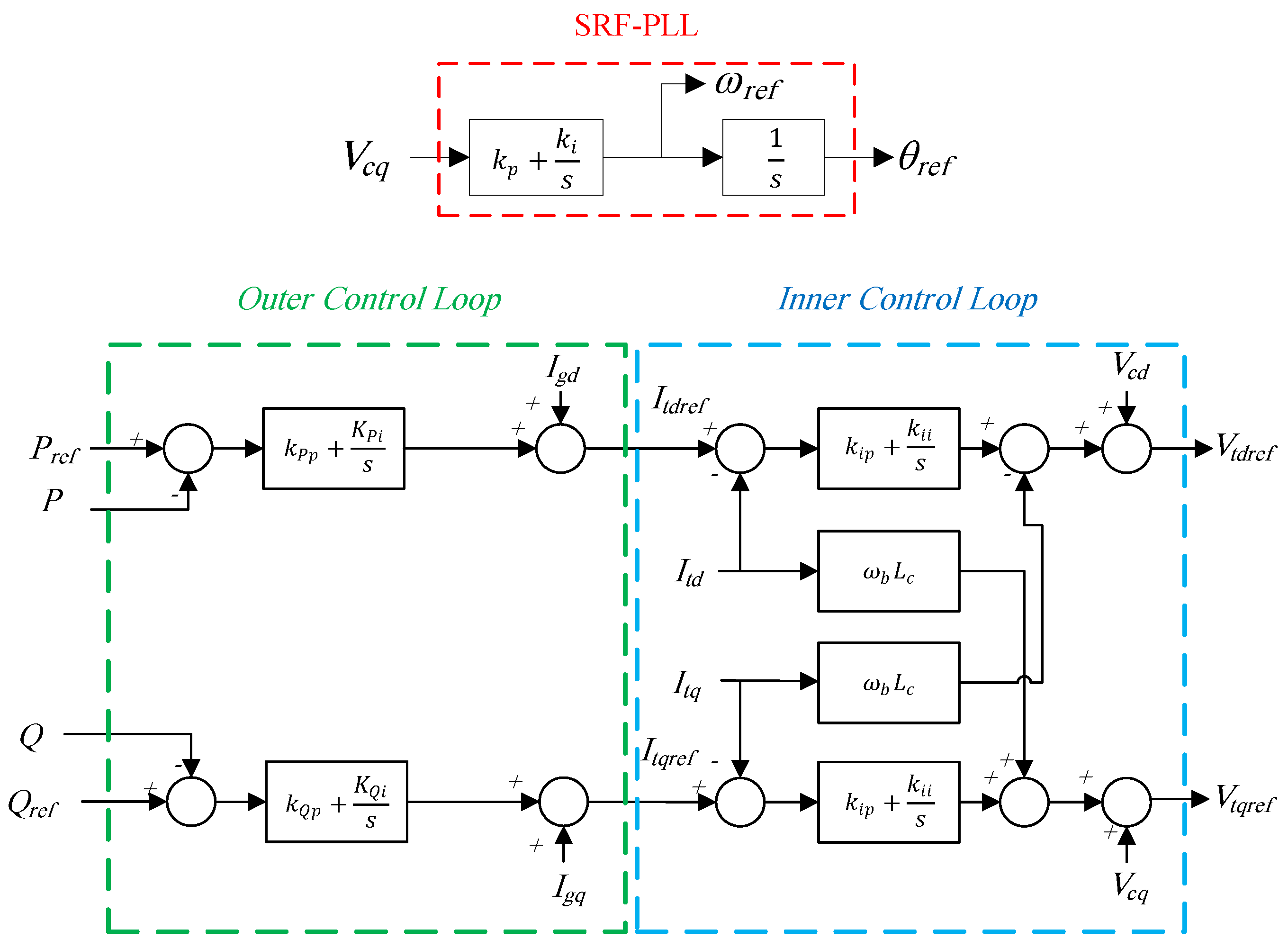
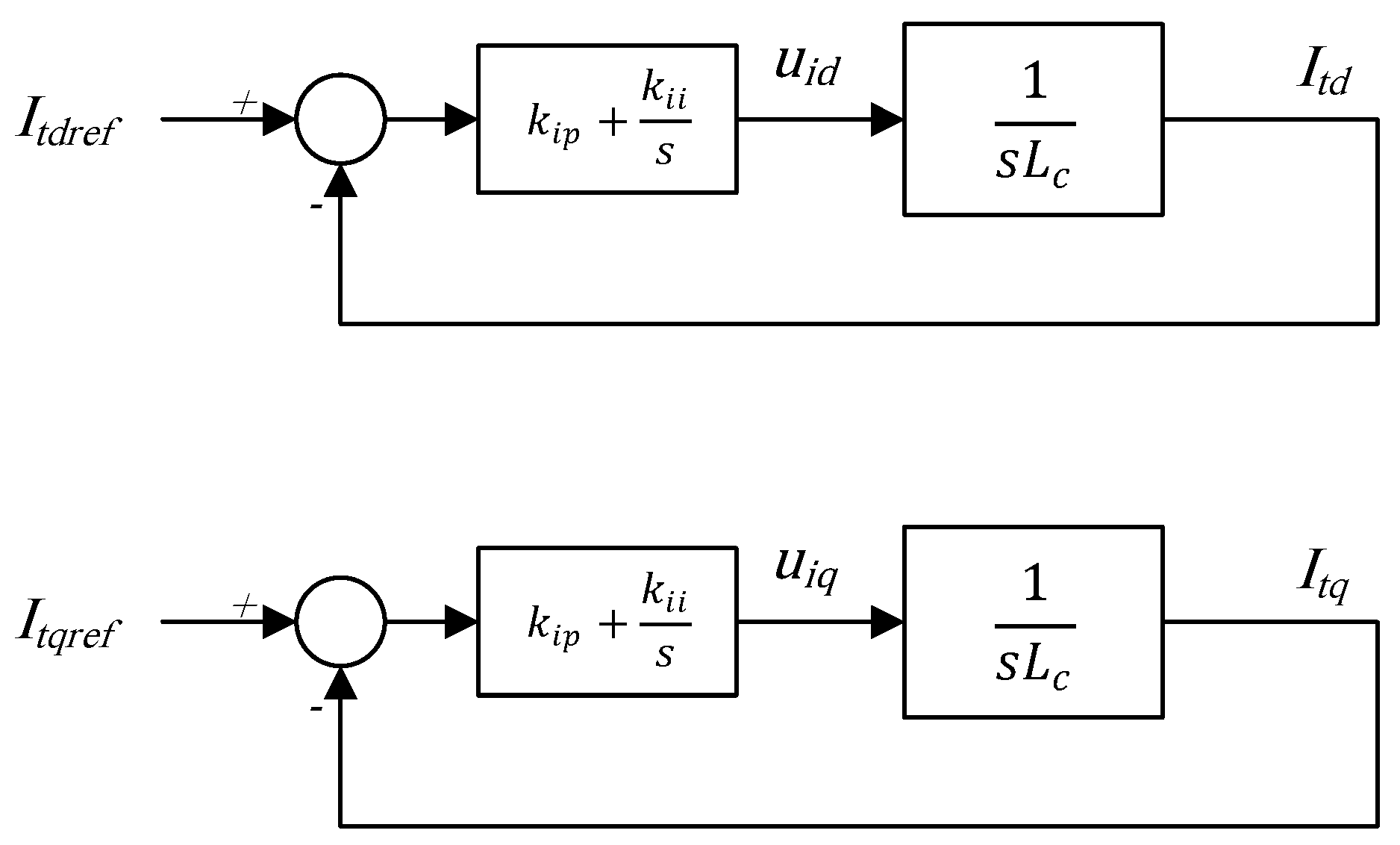
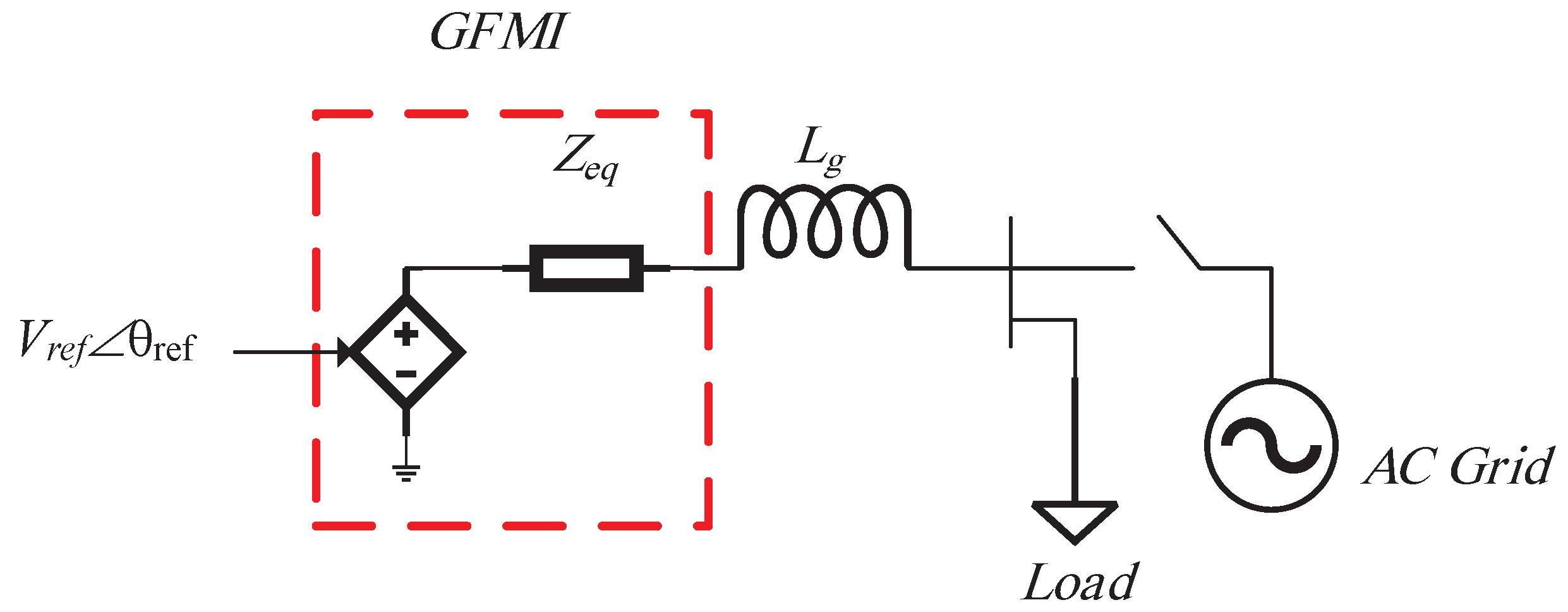

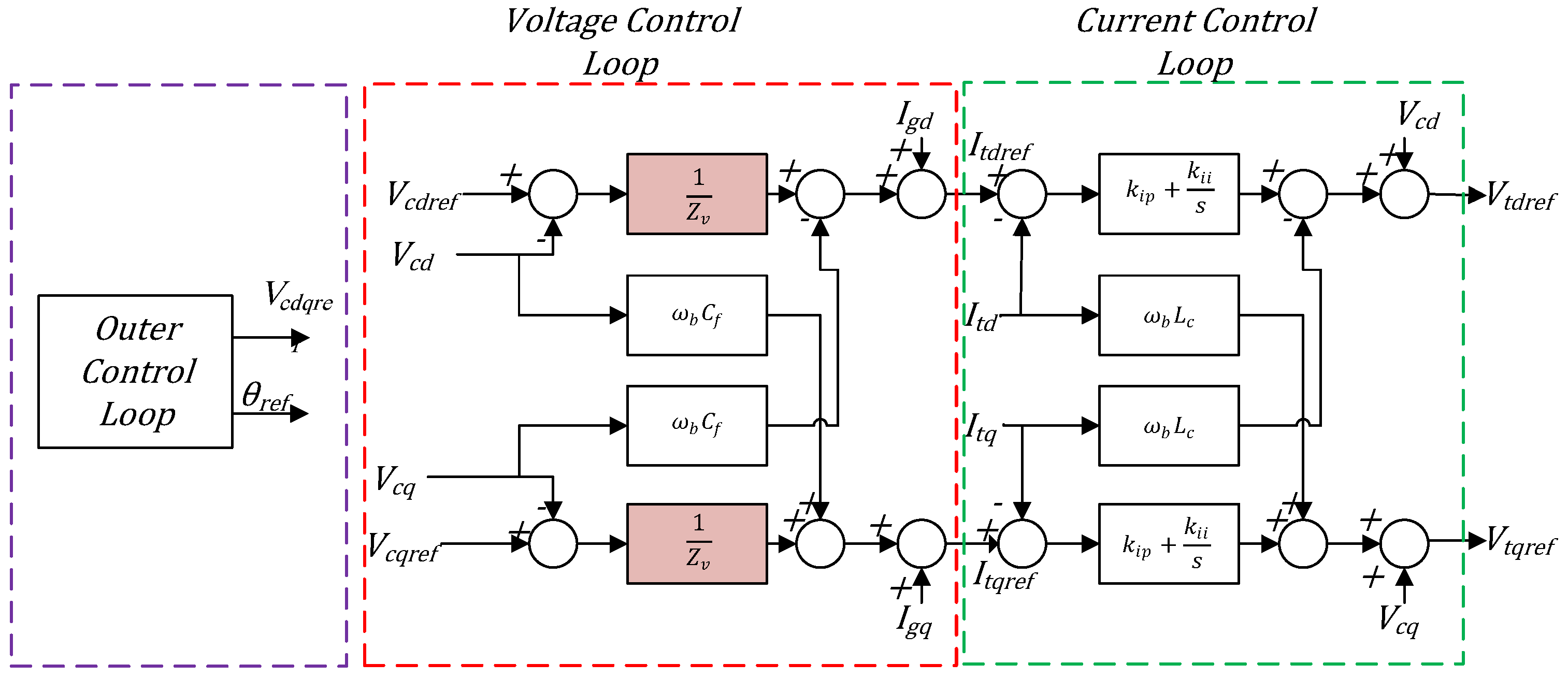
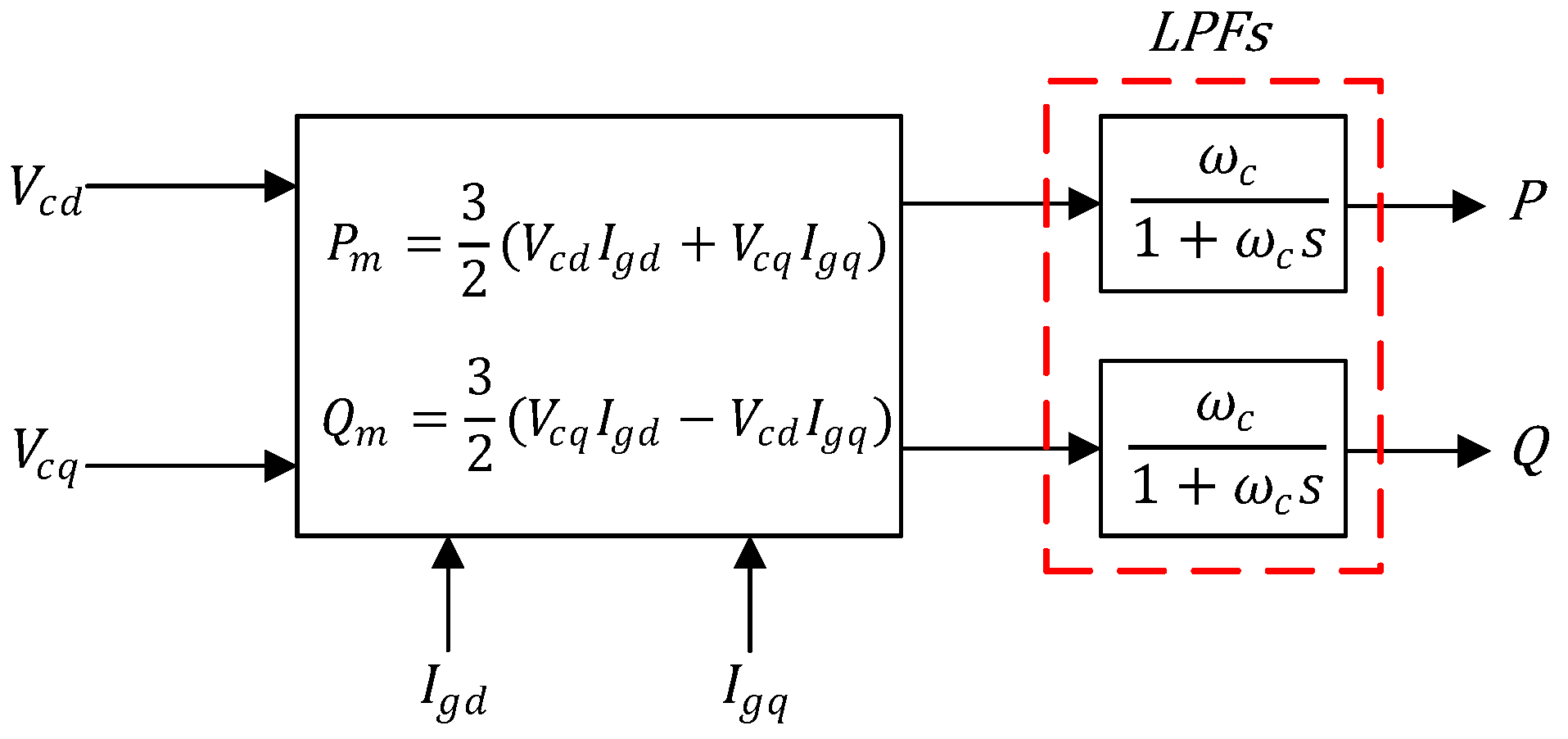

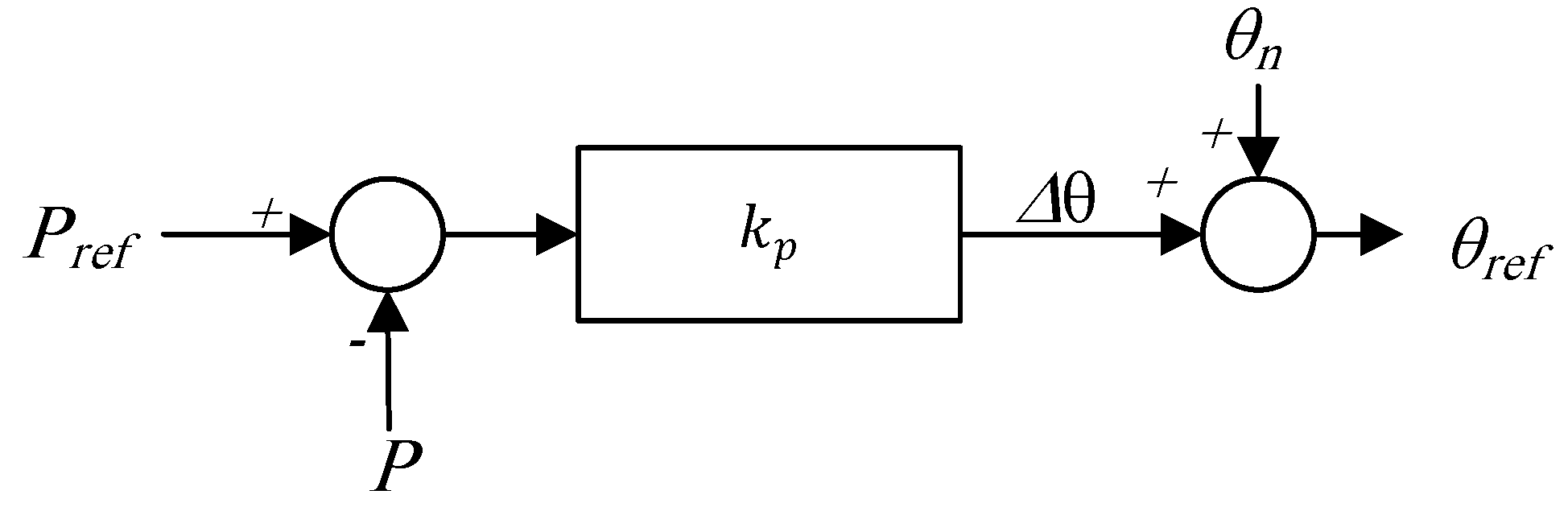
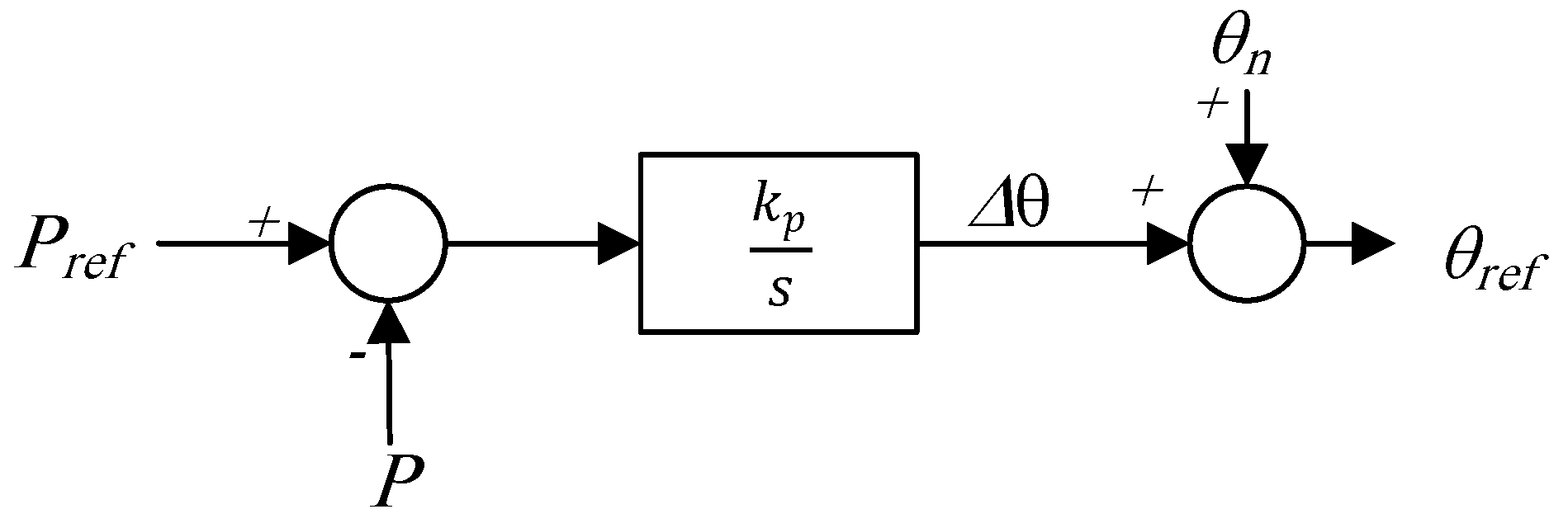

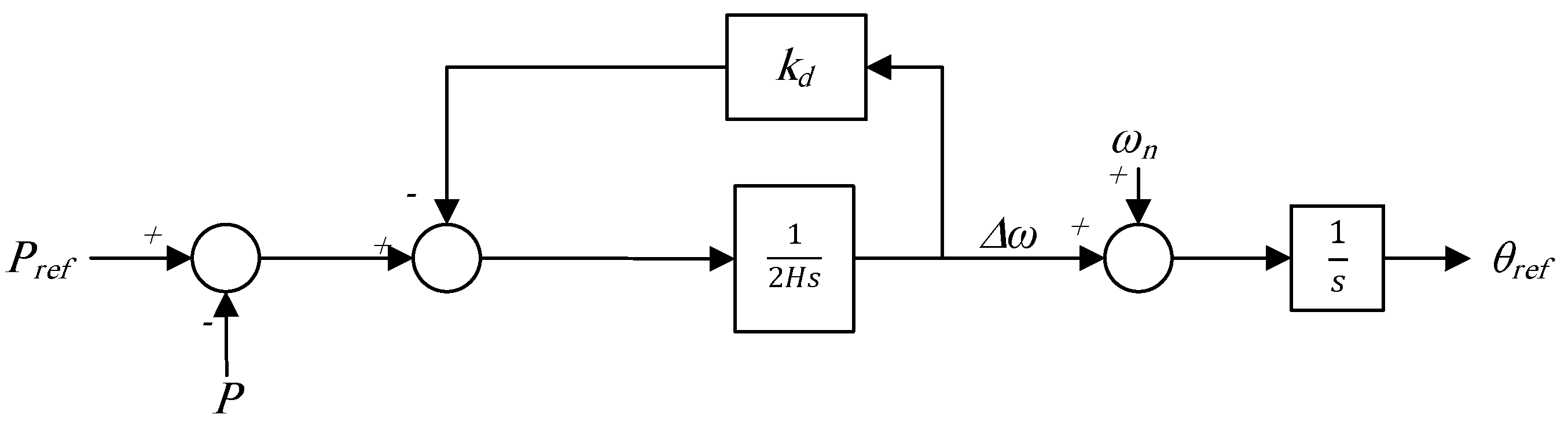
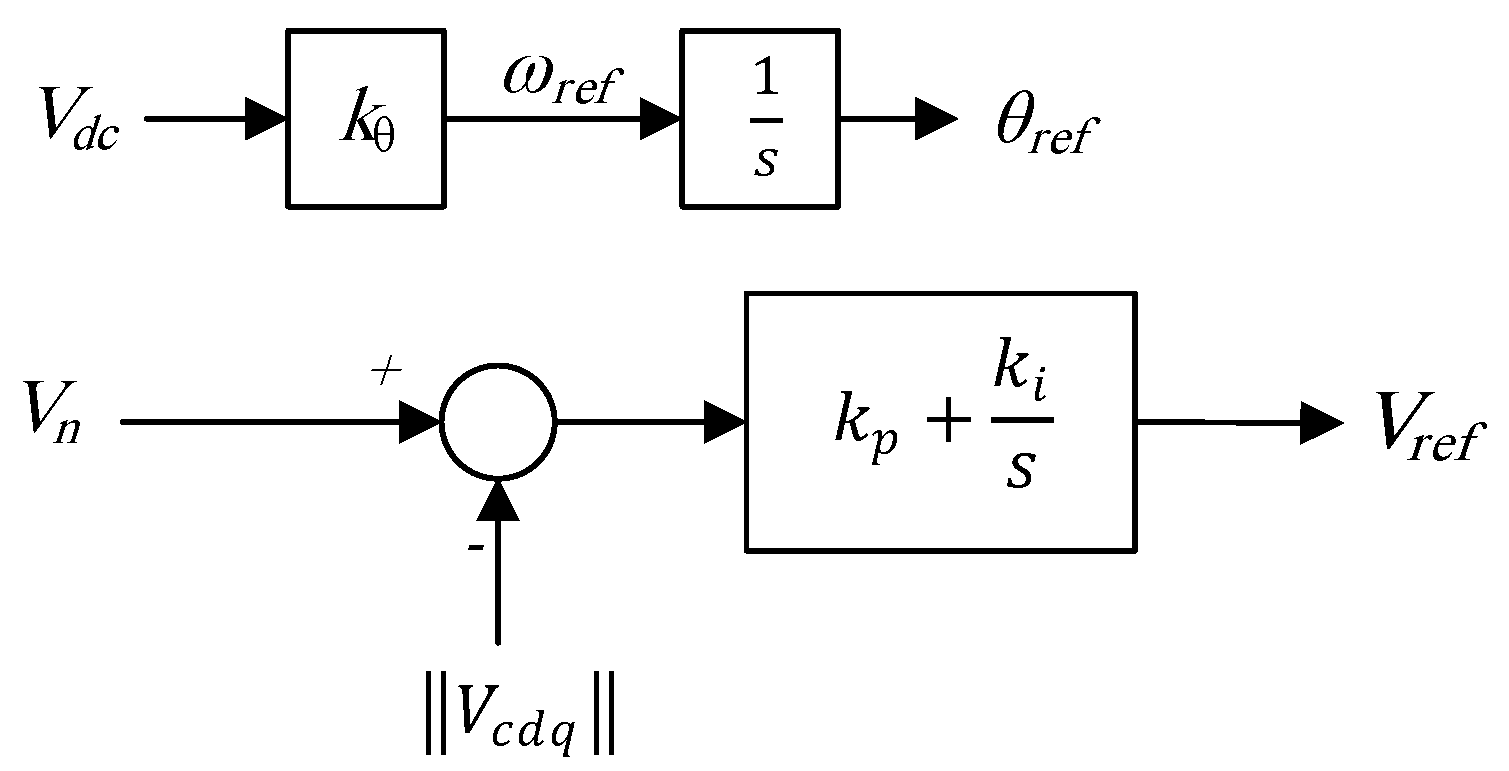

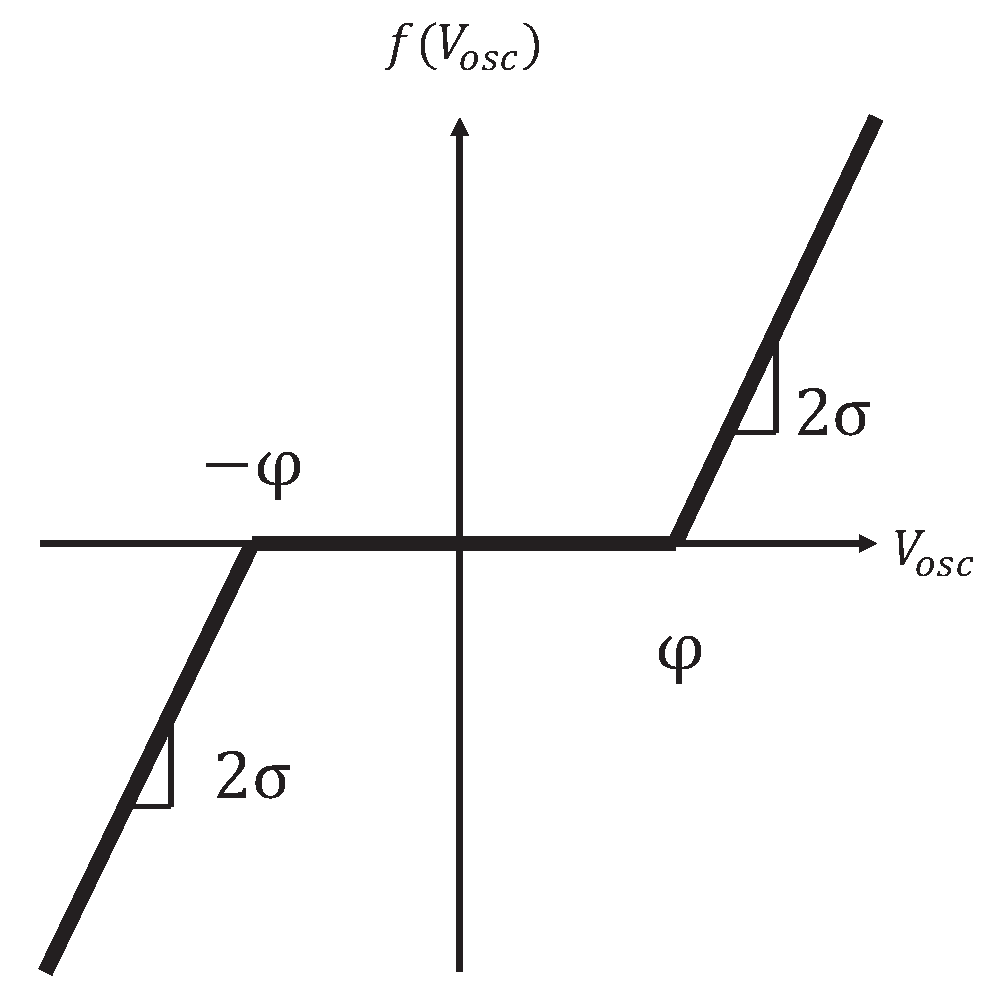
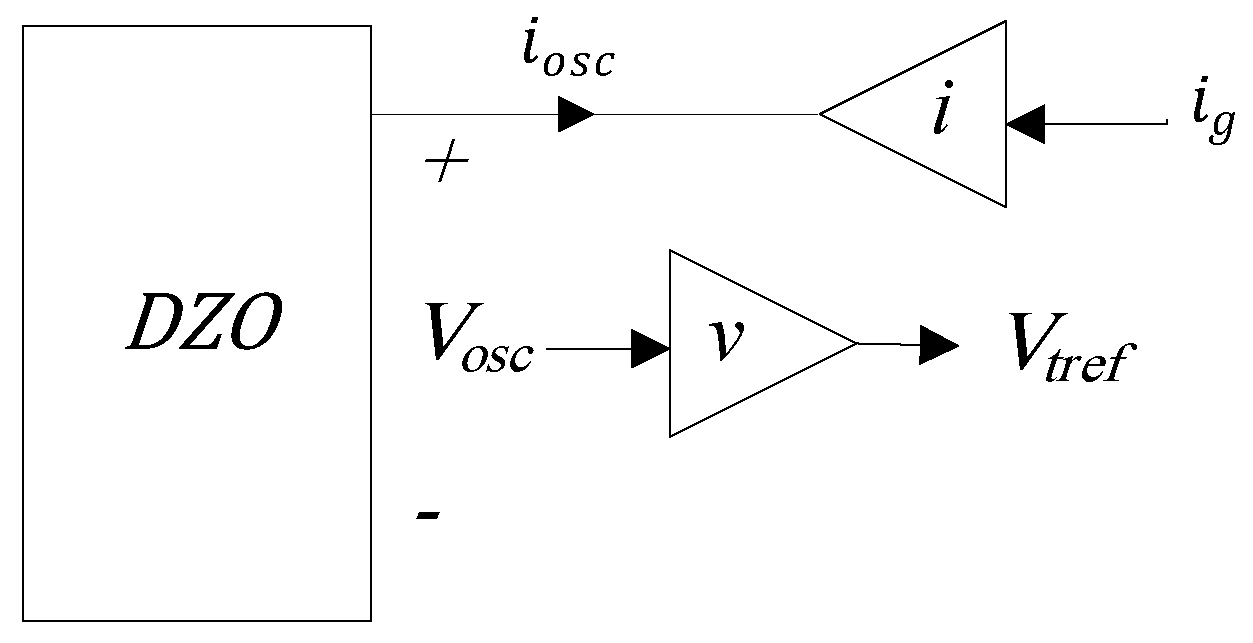
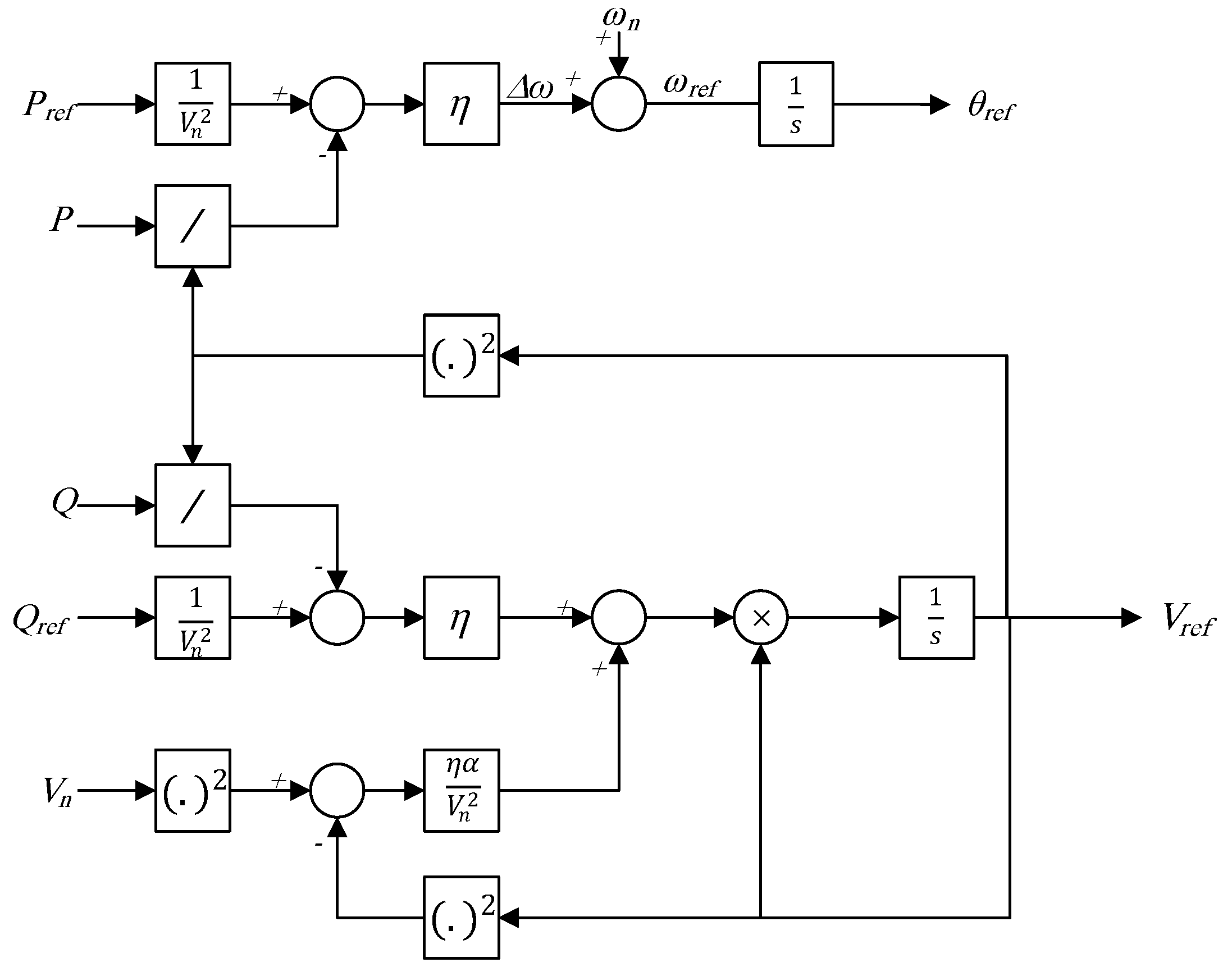
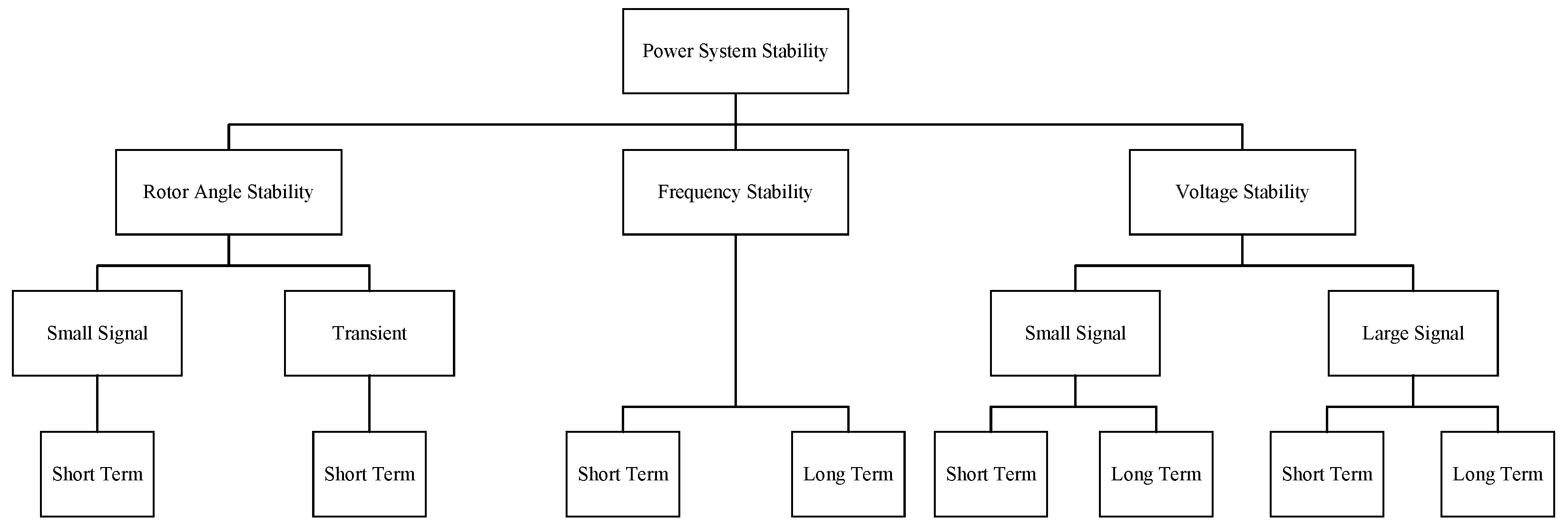
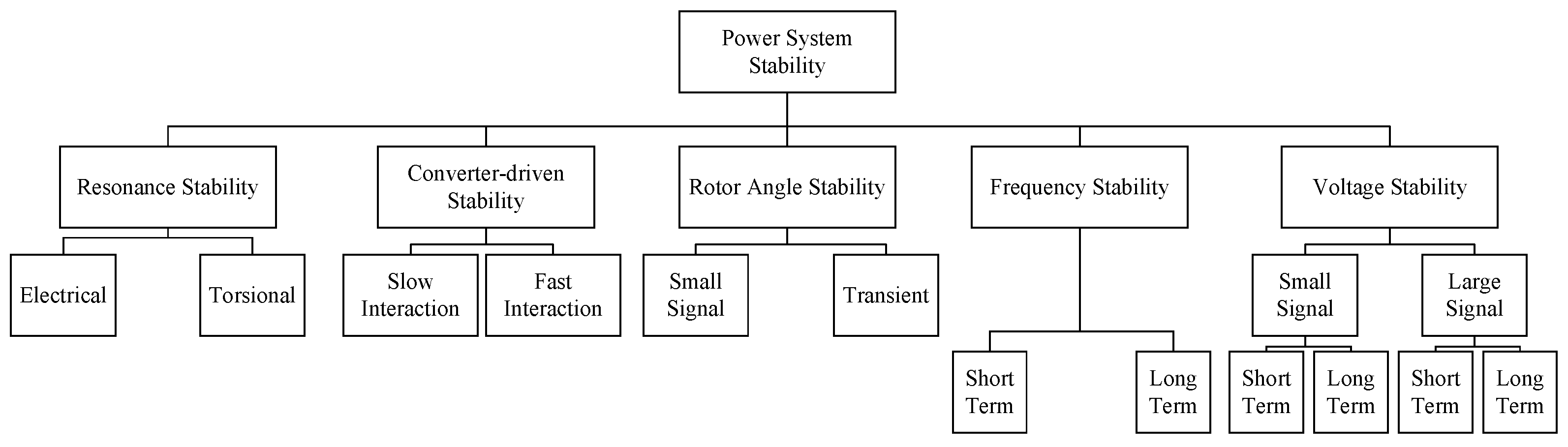

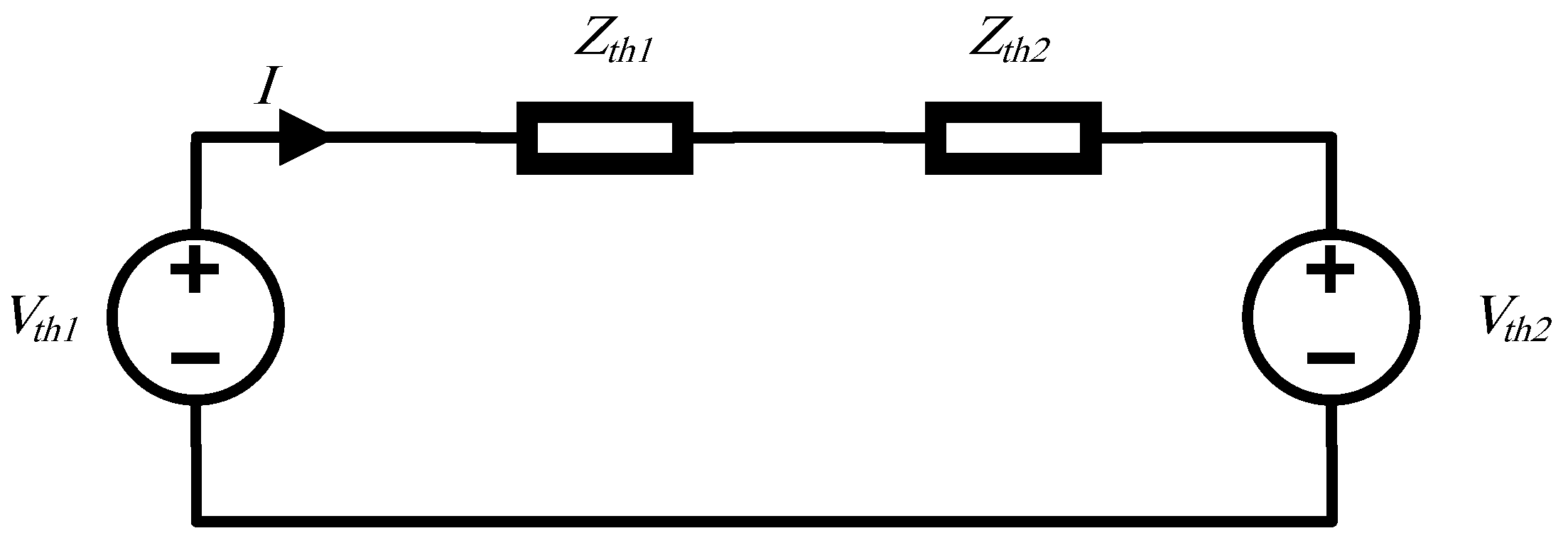
| Criterion | GFLIs | GFMIs |
|---|---|---|
| Simplified Equivalent Model | Controllable current source | Controllable voltage source |
| Stable Operation Requirement | Connection to strong grids | Connection to weak grids or in standalone operation mode |
| Synchronization Method | PLL | Outer control loop |
| Black Start Capability | No | Yes |
| Current Limiting Capability | Yes | Possible with specific control methods |
| Impact on the Grid Strength | Decreasing | Increasing |
| Control Scheme | Tunable Virtual Inertia | Current Limiting Capability | Dispatchability |
|---|---|---|---|
| Frequency-droop | No | Yes | Yes |
| Angle-droop | No | Yes | Yes |
| PSC | No | Yes | Yes |
| Synchronverter | Yes | No | Yes |
| VSM | Yes | Yes | Yes |
| Matching Control | Yes | Yes | Yes |
| VOC | No | No | No |
| dVOC | No | Yes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirmohammad, M.; Azad, S.P. Control and Stability of Grid-Forming Inverters: A Comprehensive Review. Energies 2024, 17, 3186. https://doi.org/10.3390/en17133186
Mirmohammad M, Azad SP. Control and Stability of Grid-Forming Inverters: A Comprehensive Review. Energies. 2024; 17(13):3186. https://doi.org/10.3390/en17133186
Chicago/Turabian StyleMirmohammad, Marzie, and Sahar Pirooz Azad. 2024. "Control and Stability of Grid-Forming Inverters: A Comprehensive Review" Energies 17, no. 13: 3186. https://doi.org/10.3390/en17133186





