Evaluation of Prediction Model for Compressor Performance Using Artificial Neural Network Models and Reduced-Order Models
Abstract
:1. Introduction
2. Modeling
2.1. Response Surface Methodology (RSM)
2.2. Data Batch
3. Validation Methods
3.1. Experimental Results
3.2. Extended ROM
4. Results and Discussion
5. Conclusions
- (1)
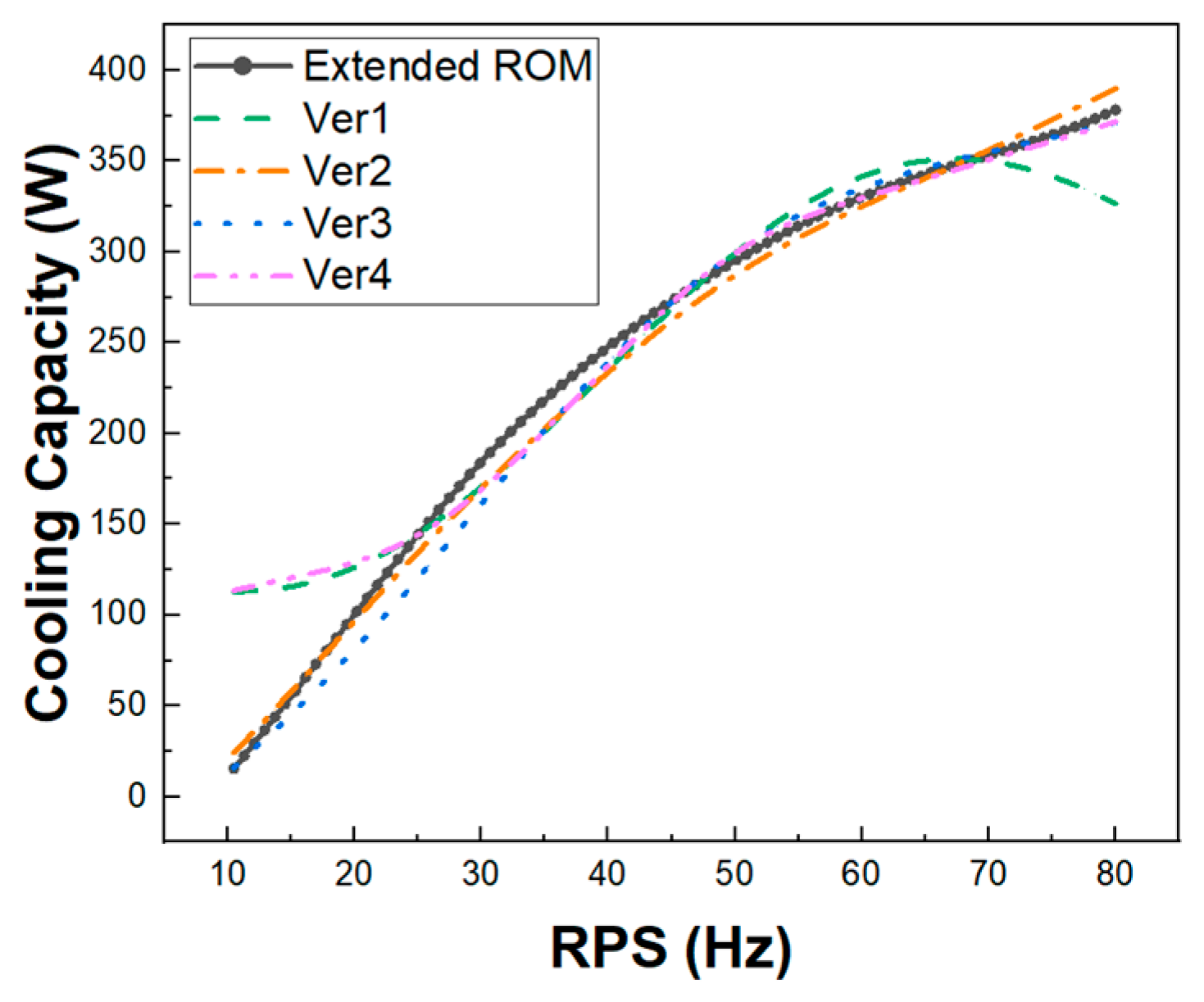
- The response surface of the ROM is formed through central composite design (CCD). The data number equation of CCD was used as the standard for the minimum number of input data required to generate the ROM. Since there were four factors and five levels, the minimum number of input data was twenty-five. The ROM was generated according to four versions of data arrangement, with the range of each factor changed.
- (2)
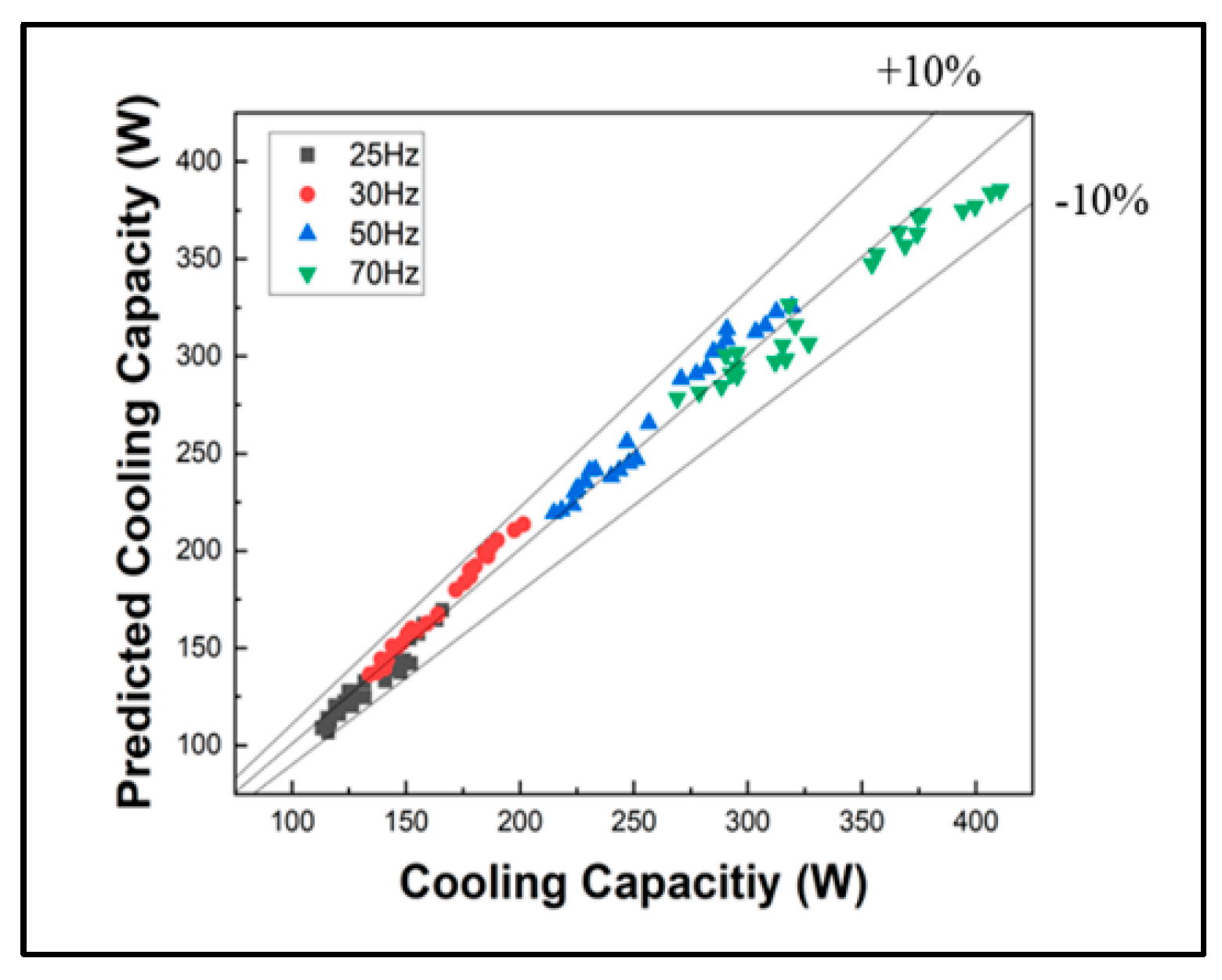
- Experimental results and an extended ROM were used to verify the accuracy of the four versions of the ROM. The extended ROM was generated using response surface methodology (RSM) and the artificial neural network (ANN) method. The extended ROM was generated using a total of 191 input data, and its accuracy was verified through experimental results.
- (3)
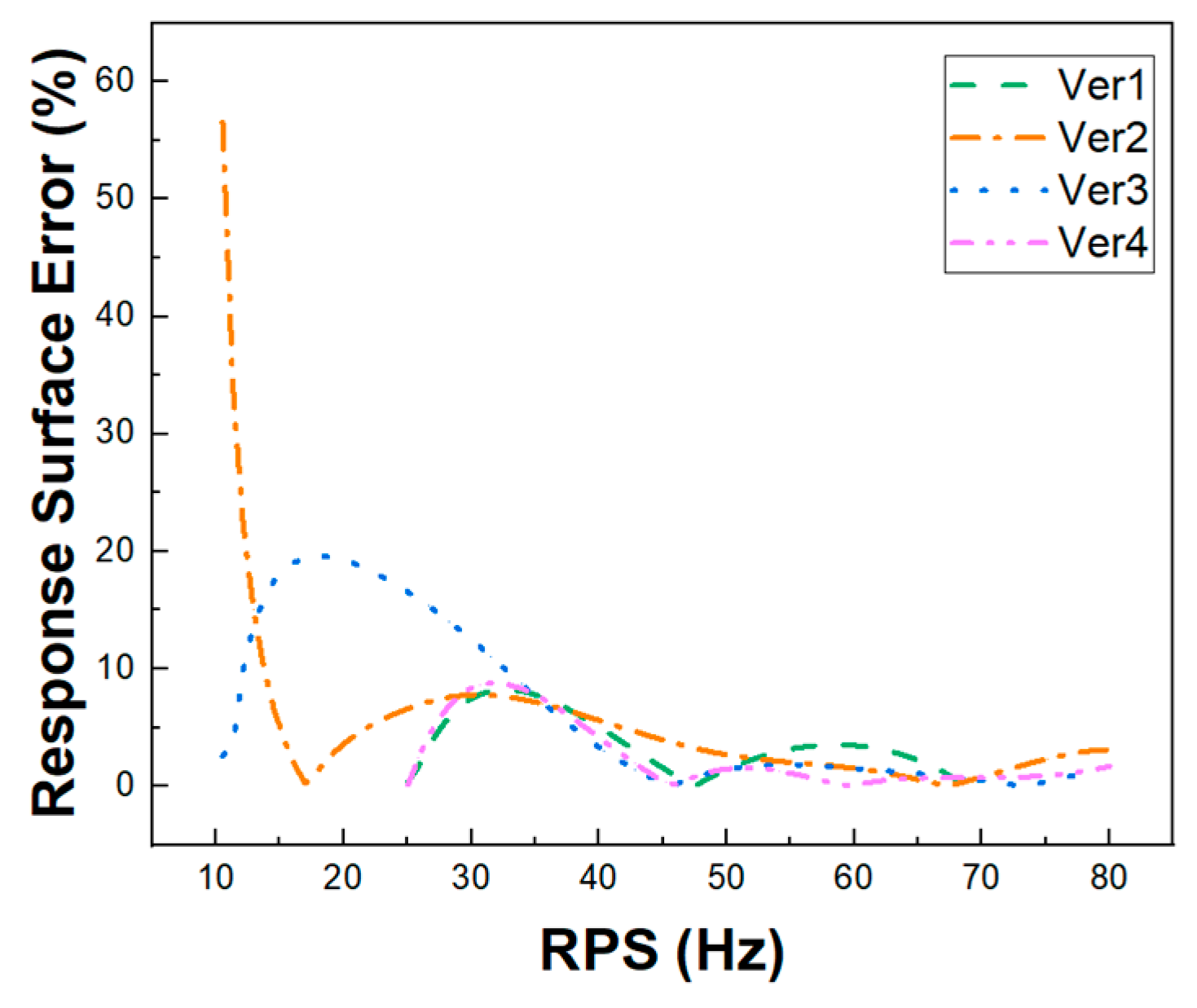
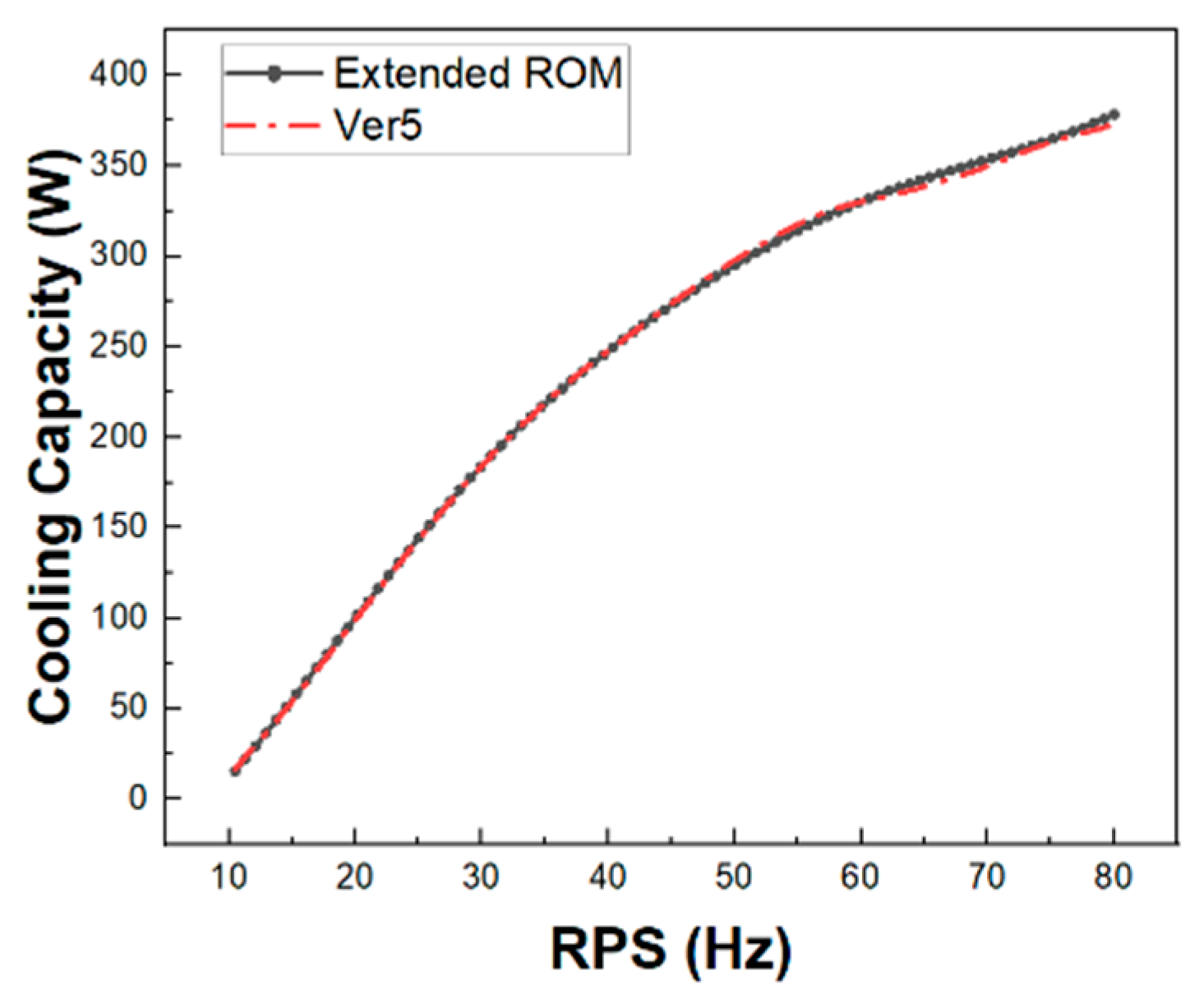
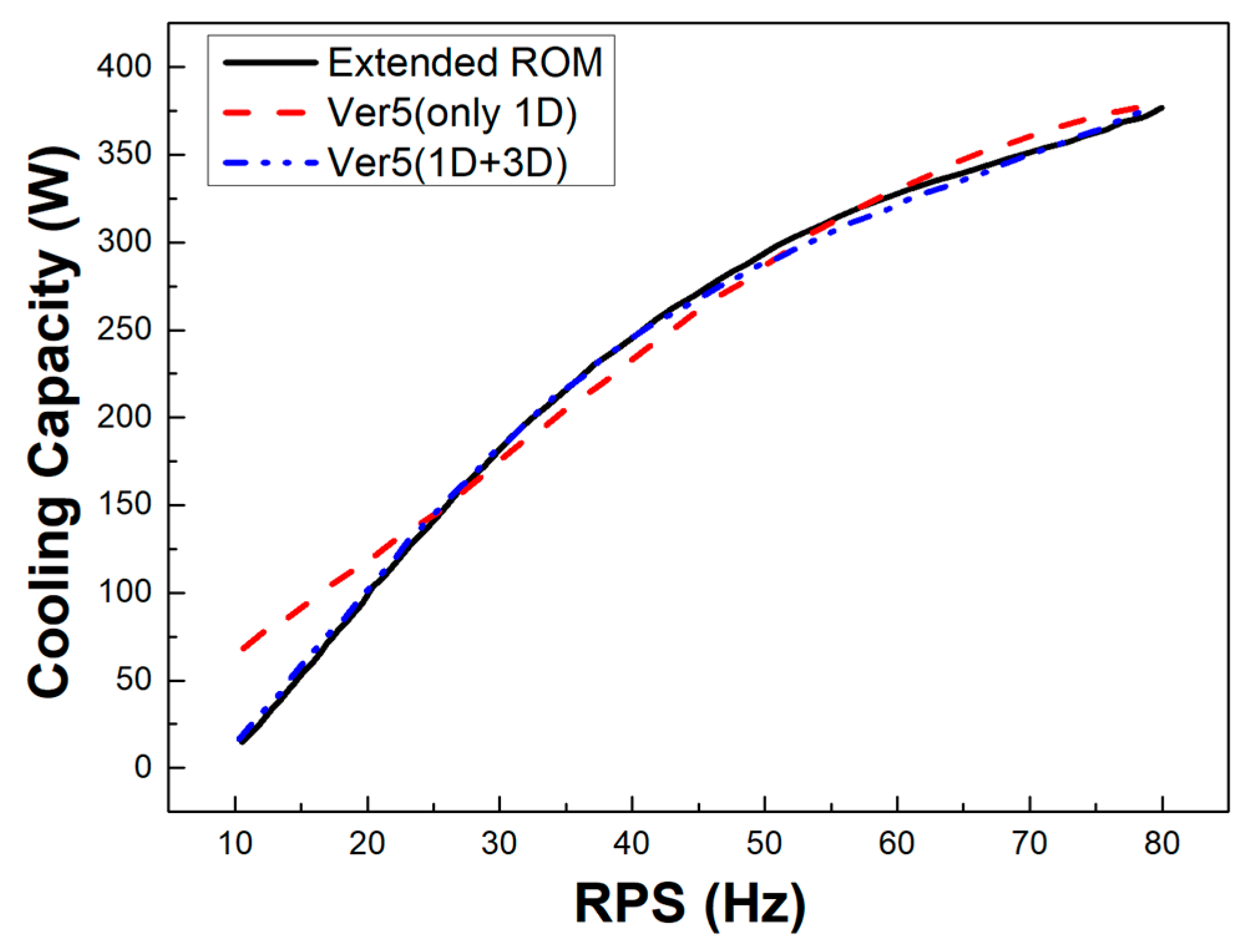
- The four versions of the ROM had limitations in the extrapolation and curvature. To compensate for this problem, the data arrangement of Ver5, which was a combination of input data from Ver3 and Ver4, was used to generate the ROM. The ROM accuracy of Ver5 has been verified through experimental results. The ROM accuracy of Ver5 was 100, the average error rate was 3.8%, and the maximum error rate was 9.8%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Costagliola, M. The theory of spring-loaded valves for reciprocating compressors. Appl. Mech. 1950, 17, 415–420. [Google Scholar] [CrossRef]
- Touber, S. A Contribution to the Improvement of Compressor Valve Design. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1976. [Google Scholar]
- Ferreira, T.S. Analysis of the Influence of Valve Geometric Parameters on the Effective Flow and Force Areas. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 4–7 August 1986; pp. 558–646. [Google Scholar]
- Lang, W.; Almbauer, R.; Burgstaller, A.; Nagy, D. Coupling of 0-, 1- and 3-d tool for the simulation of the suction line of a hermetic reciprocating compressor. Int. Comp. Eng 2008, 1272, 1–8. [Google Scholar]
- Hu, J.; Yang, L.; Shao, L.L.; Zhang, C.L. Generic network modeling of reciprocating compressor. Int. J. Refrig. 2014, 45, 107–119. [Google Scholar] [CrossRef]
- Lohn, S.K.; Diniz, M.C.; Deschamps, C.J. A thermal model for analysis of hermetic reciprocating compressors under the on-off cycling operating condition. Int. IOP Conf. Ser. Mater. Sci. Eng. 2015, 90, 012068. [Google Scholar] [CrossRef]
- Damle, R.; Rigola, J.; Pérez-Segarra, C.D.; Castro, J.; Oliva, A. Object-oriented simulation of reciprocating compressors: Numerical verification and experimental comparison. Int. J. Refrig. 2011, 34, 1989–1998. [Google Scholar] [CrossRef]
- El Bouzidi, S.; Hassan, M.; Ziada, S. Experimental characterization of the self-excited vibrations of spring-loaded valves. J. Fluids Struct. 2018, 76, 558–572. [Google Scholar] [CrossRef]
- Keramat, A.; Fathi-Moghadam, M.; Zanganeh, R.; Rahmanshahi, M.; Tijsseling, A.S.; Jabbari, E. Experimental investigation of transients-induced fluid–structure interaction in a pipeline with multiple-axial supports. J. Fluids Struct. 2020, 93, 102848. [Google Scholar] [CrossRef]
- Hwang, I.S.; Park, S.J.; Oh, W.; Lee, Y.L. Linear compressor discharge valve behavior using a rigid body valve model and a FSI valve model. Int. J. Refrig. 2017, 82, 509–519. [Google Scholar] [CrossRef]
- Park, S.J.; Hwang, I.S.; Oh, W.S.; Lee, Y.L. A study on cycle performance variation of a linear compressor considering valve behavior. J. Mech. Sci. Technol. 2017, 31, 4481–4488. [Google Scholar] [CrossRef]
- Zhao, B.; Jia, X.; Sun, S.; Wen, J.; Peng, X. FSI model of valve motion and pressure pulsation for investigating thermodynamic process and internal flow inside a reciprocating compressor. Appl. Therm. Eng. 2018, 131, 998–1007. [Google Scholar] [CrossRef]
- Liu, Z.; Cao, X.; Wang, T.; Jia, W.; Duan, Z. Comparative evaluation of the refrigeration compressor performance under different valve parameters in a trans-critical CO2 cycle. Int. J. Refrig. 2019, 101, 34–46. [Google Scholar] [CrossRef]
- Tao, W.; Guo, Y.; He, Z.; Peng, X. Investigation on the delayed closure of the suction valve in the refrigerator compressor by FSI modeling. Int. J. Refrig. 2018, 91, 111–121. [Google Scholar] [CrossRef]
- Bacak, A.; Pınarbaşı, A.; Dalkılıç, A.S. A 3-D FSI simulation for the performance prediction and valve dynamic analysis of a hermetic reciprocating compressor. Int. J. Refrig. 2023, 150, 135–148. [Google Scholar] [CrossRef]
- Lucia, D.J.; Beran, P.S.; Silva, W.A. Reduced-order modeling: New approaches for computational physic. Prog. Aerosp. Sci. 2004, 40, 51–117. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Younis, M.I.; Abdel-Rahman, E.M. Reduced-order models for MEMS applications. Nonlinear Dyn. 2005, 41, 211–236. [Google Scholar] [CrossRef]
- Lang, Y.-D.; Malacina, A.; Biegler, L.T.; Munteanu, S.; Madsen, J.I.; Zitney, S.E. Reduced order model based on principal component analysis for process simulation and optimization. Energy Fuels 2009, 23, 1695–1706. [Google Scholar] [CrossRef]
- Stabile, G.; Rozza, G. Finite volume POD-Galerkin stabilized reduced order methods for the parametrized incompressible Navier-Stokes equations. Comput. Fluids 2018, 173, 273–284. [Google Scholar] [CrossRef]
- Mathews, P.G. Design of Experiments with MINITAB; Quality Press: Milwaukee, WI, USA, 2004. [Google Scholar]
- Vatanparast, M.; Sarkar, A.; Sahaf, S.A. Optimization of asphalt mixture design using response surface method for stone matrix warm mix asphalt incorporating crumb rubber modified binder. Constr. Build. Mater. 2023, 369, 130401. [Google Scholar] [CrossRef]
- Suparmaniam, U.; Lam, M.K.; Rawindran, H.; Lim, J.W.; Pa’ee, K.F.; Yong, K.T.L.; Tan, I.S.; Chin, B.L.F.; Show, P.L.; Lee, K.T. Optimizing extraction of antioxidative bio stimulant from waste onion peels for microalgae cultivation via response surface model. Energy Convers. Manag. 2023, 286, 117023. [Google Scholar] [CrossRef]
- Rastogi, P.M.; Kumar, N.; Sharma, A. Use of response surface methodology approach for development of sustainable Jojoba biodiesel blend with CuO nanoparticles for four stroke diesel engine. Fuel 2023, 339, 127367. [Google Scholar] [CrossRef]
- Waday, Y.A.; Aklilu, E.G.; Bultum, M.S.; Ancha, V.R. Optimization of soluble phosphate and IAA production using response surface methodology and ANN approach. Heliyon 2022, 8, e12224. [Google Scholar] [CrossRef] [PubMed]
- JIS B8606; Testing of Refrigerant Compressors. Japanese Standards Association: Tokyo, Japan, 2021.
- JIS B8600; Standard Condition of Rating Temperature for Refrigerant Compressors. Japanese Standards Association: Tokyo, Japan, 2021.
- Jeong, H.; Oh, B.; Kim, D.; Lee, K.; Kim, H.; Kim, J.; Choi, G. Development of reduced order model for performance prediction of reciprocating compressor. In 13th International Conference on Compressors and Their Systems; Springer Nature Switzerland: Cham, Switzerland, 2023; pp. 395–407. [Google Scholar]
- Park, Y.; Choi, M.; Kim, K.; Li, X.; Jung, C.; Na, S.; Choi, G. Prediction of operating characteristics for industrial gas turbine combustor using an optimized artificial neural network. Energy 2020, 213, 118769. [Google Scholar] [CrossRef]
- Sun, Q.Q.; Zhang, H.C.; Sun, Z.J.; Xia, Y. Ridge regression and artificial neural network to predict the thermodynamic properties of alkali metal Rankine cycles for space nuclear power. Energy Convers. Manag. 2022, 273, 116385. [Google Scholar] [CrossRef]
- Kim, H.S. Design Techniques for Heat Sink Thermal Analysis Using a Reduced Order Model (ROM). Korean Inst. Power Electron. 2020, 25, 44–49. [Google Scholar]
- Jin, X.; Zhang, C.; Wang, C. Response surface optimization of machine tool column based on ANSYS workbench. Acad. J. Manuf. Eng. 2020, 18, 162–170. [Google Scholar]
- Song, B.C.; Bang, I.K.; Han, D.S.; Han, G.J.; Lee, K.H. Structural design of a container crane part-jaw using metamodels. J. Korean Soc. Manuf. Process Eng. 2008, 7, 17–24. [Google Scholar]
- Veza, I.; Spraggon, M.; Fattah, I.R.; Idris, M. Response surface methodology (RSM) for optimizing engine performance and emissions fueled with biofuel: Review of RSM for sustainability energy transition. Results Eng. 2023, 18, 101213. [Google Scholar] [CrossRef]
- Im, R.-H.; Yoo, J.-Y.; Lee, K.-W. Method for reducing torque pulsation in reciprocating compressor. In Proceedings of the Korean Electrical Society Conference, Busan, Republic of Korea, 19 July 2010; pp. 21–23. [Google Scholar]
- Kim, J.-h.; Yang, J.-h.; Ha, J.-i. Design of an extended state observer to improve compressor low-speed operation characteristics. In Proceedings of the Power Electronics Society Conference, Miami, FL, USA, 24–26 September 2023; pp. 252–254. [Google Scholar]




| Ts [°C] | RPS [Hz] | Te [°C] | Tc [°C] | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ver | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| −α | 25 | 10 | 10 | 10 | 25 | 10 | 10 | 25 | −25 | −27 | −27 | −27 | 35 | 32 | 32 | 32 |
| −1 | 25 | 25 | 10 | 10 | 25 | 25 | 10 | 25 | −25 | −25 | −27 | −27 | 35 | 35 | 32 | 32 |
| 0 | 35 | 32 | 25 | 25 | 50 | 50 | 50 | 50 | −22 | −22 | −22 | −22 | 45 | 45 | 45 | 45 |
| +1 | 43 | 35 | 43 | 43 | 70 | 70 | 80 | 80 | −20 | −20 | −17 | −17 | 55 | 55 | 58 | 58 |
| +α | 43 | 43 | 43 | 43 | 70 | 80 | 80 | 80 | −20 | −17 | −17 | −17 | 55 | 58 | 58 | 58 |
| No. | Ts | RPS | Te | Tc | No. | Ts | RPS | Te | Tc |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 14 | 1 | −1 | 1 | 1 |
| 2 | +α | 0 | 0 | 0 | 15 | −1 | 1 | 1 | 1 |
| 3 | 0 | +α | 0 | 0 | 16 | 1 | 1 | −1 | −1 |
| 4 | 0 | 0 | +α | 0 | 17 | 1 | −1 | 1 | −1 |
| 5 | 0 | 0 | 0 | +α | 18 | −1 | 1 | 1 | −1 |
| 6 | −α | 0 | 0 | 0 | 19 | 1 | −1 | −1 | 1 |
| 7 | 0 | −α | 0 | 0 | 20 | −1 | 1 | −1 | 1 |
| 8 | 0 | 0 | −α | 0 | 21 | −1 | −1 | 1 | 1 |
| 9 | 0 | 0 | 0 | −α | 22 | 1 | −1 | −1 | −1 |
| 10 | −1 | −1 | −1 | −1 | 23 | −1 | 1 | −1 | −1 |
| 11 | 1 | 1 | 1 | 1 | 24 | −1 | −1 | 1 | −1 |
| 12 | 1 | 1 | 1 | −1 | 25 | −1 | −1 | −1 | 1 |
| 13 | 1 | 1 | −1 | 1 |
| Number of Input Data | 191 | |||
|---|---|---|---|---|
| Response Surface Type | Genetic Aggregation | Non-Parametric Regression | Kriging | Standard Response Surface |
| ROM accuracy [%] | 100 | 97 | 93 | 96 |
| Average error rate [%] | 4.3 | 4.6 | 5.1 | 4.4 |
| Max. error rate [%] | 9.8 | 13.0 | 12.5 | 11.1 |
| Standard deviation of error rate | 2.4 | 2.8 | 3.3 | 2.8 |
| 25 | ||||
|---|---|---|---|---|
| Design Point | Ver1 | Ver2 | Ver3 | Ver4 |
| ROM Accuracy [%] | 99 | 97 | 78 | 98 |
| Average Error Rate [%] | 4.2 | 3.0 | 7.2 | 3.3 |
| Max. Error Rate [%] | 10.7 | 12. | 21.9 | 10.7 |
| Standard deviation of error rate | 2.6 | 2.5 | 5.1 | 2.4 |
| Number of input data | 34 |
| Design points | Ver5 |
| ROM accuracy | 100/100 |
| Average error rate [%] | 3.8 |
| Max. error rate [%] | 9.8 |
| Standard deviation of error rate | 2.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, H.; Ko, K.; Kim, J.; Kim, J.; Eom, S.; Na, S.; Choi, G. Evaluation of Prediction Model for Compressor Performance Using Artificial Neural Network Models and Reduced-Order Models. Energies 2024, 17, 3686. https://doi.org/10.3390/en17153686
Jeong H, Ko K, Kim J, Kim J, Eom S, Na S, Choi G. Evaluation of Prediction Model for Compressor Performance Using Artificial Neural Network Models and Reduced-Order Models. Energies. 2024; 17(15):3686. https://doi.org/10.3390/en17153686
Chicago/Turabian StyleJeong, Hosik, Kanghyuk Ko, Junsung Kim, Jongsoo Kim, Seongyong Eom, Sangkyung Na, and Gyungmin Choi. 2024. "Evaluation of Prediction Model for Compressor Performance Using Artificial Neural Network Models and Reduced-Order Models" Energies 17, no. 15: 3686. https://doi.org/10.3390/en17153686
APA StyleJeong, H., Ko, K., Kim, J., Kim, J., Eom, S., Na, S., & Choi, G. (2024). Evaluation of Prediction Model for Compressor Performance Using Artificial Neural Network Models and Reduced-Order Models. Energies, 17(15), 3686. https://doi.org/10.3390/en17153686





