Load Prediction of Regional Heat Exchange Station Based on Fuzzy Clustering Based on Fourier Distance and Convolutional Neural Network–Bidirectional Long Short-Term Memory Network
Abstract
1. Introduction
2. Research Subject
2.1. Heating System
2.2. Influencing Factors’ Analysis of Heat Load
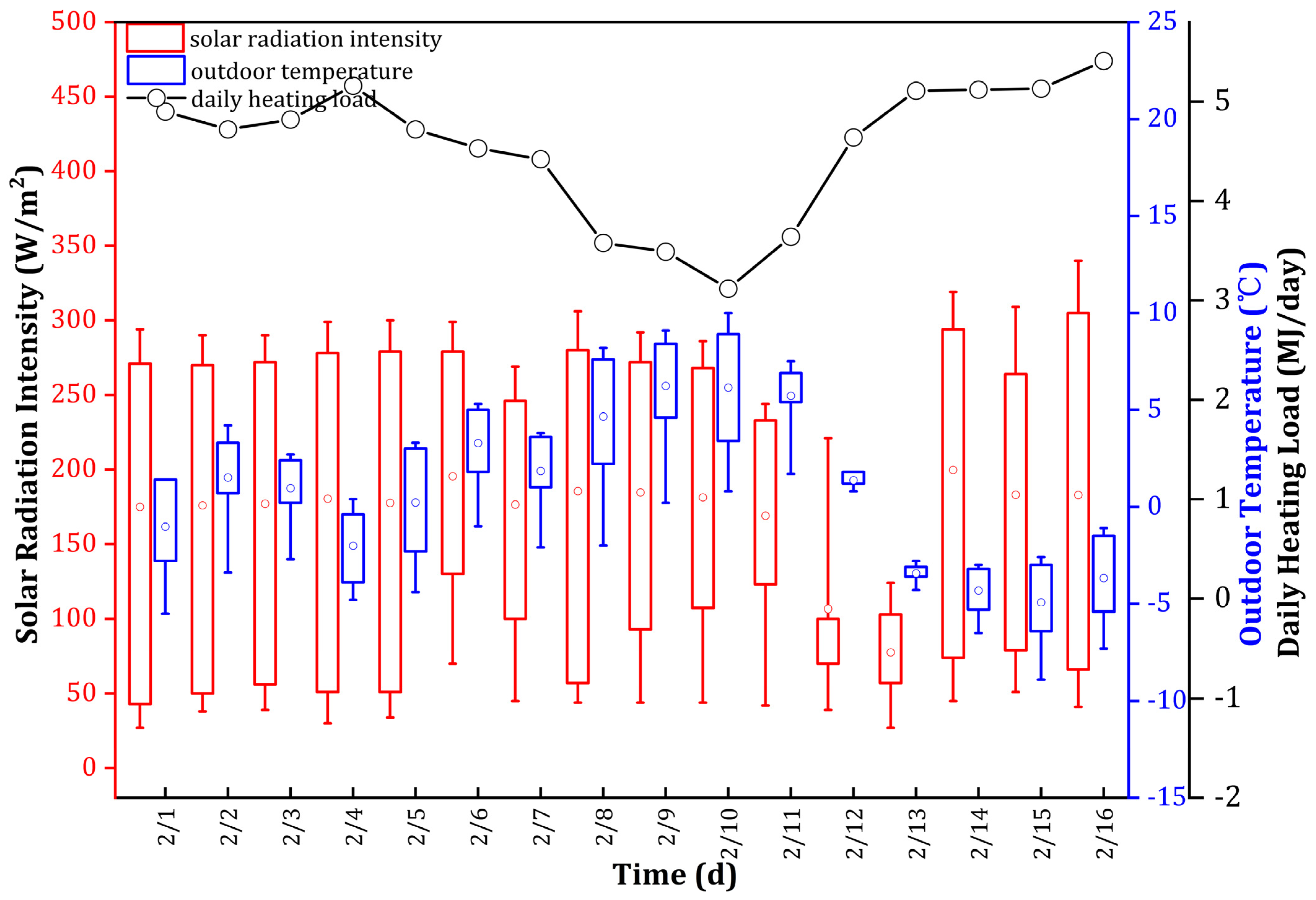
2.2.1. Variation in Heat Load with Meteorological Parameters
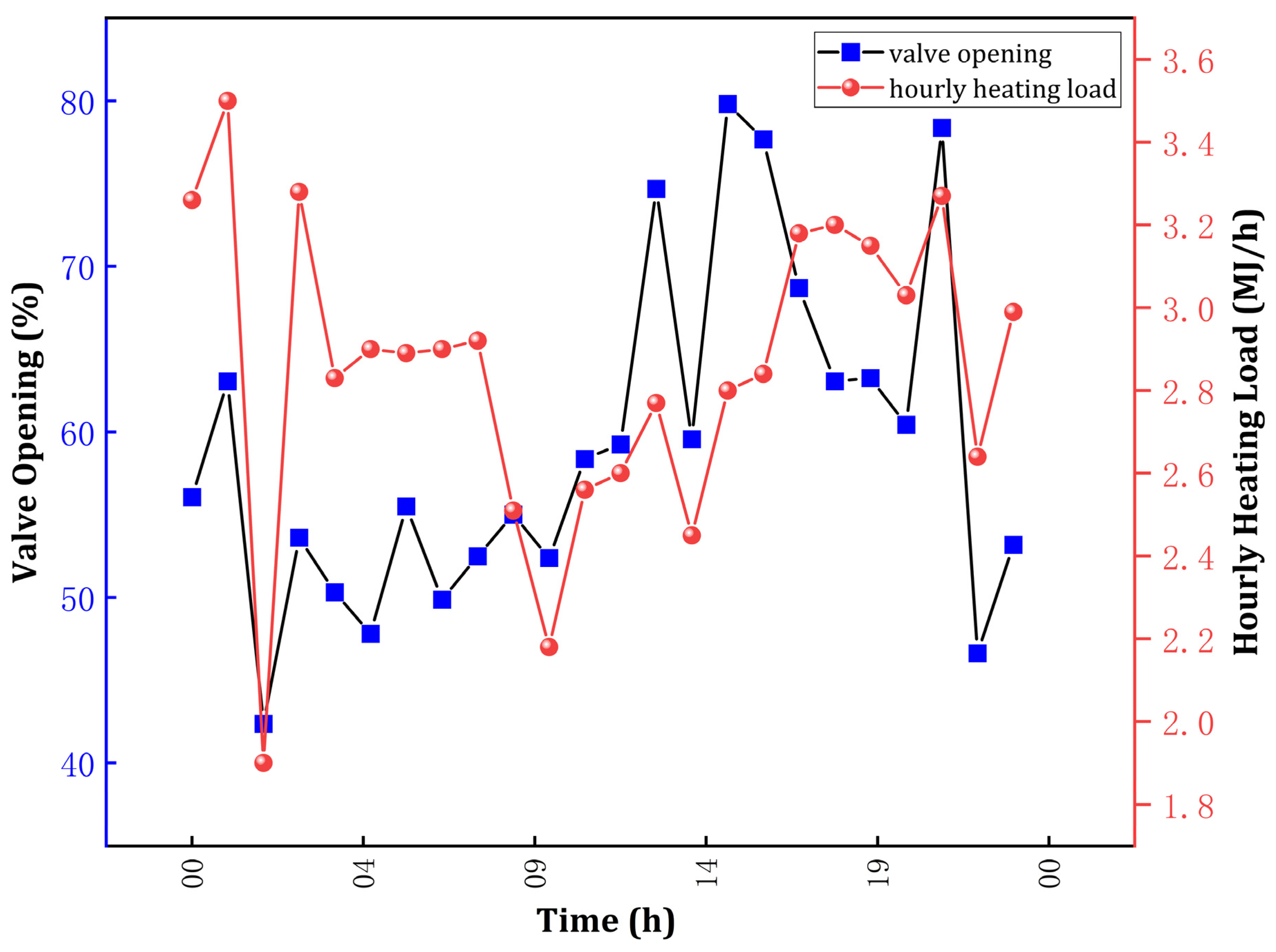
2.2.2. Variation in Heating Load with Dynamic Control Settings
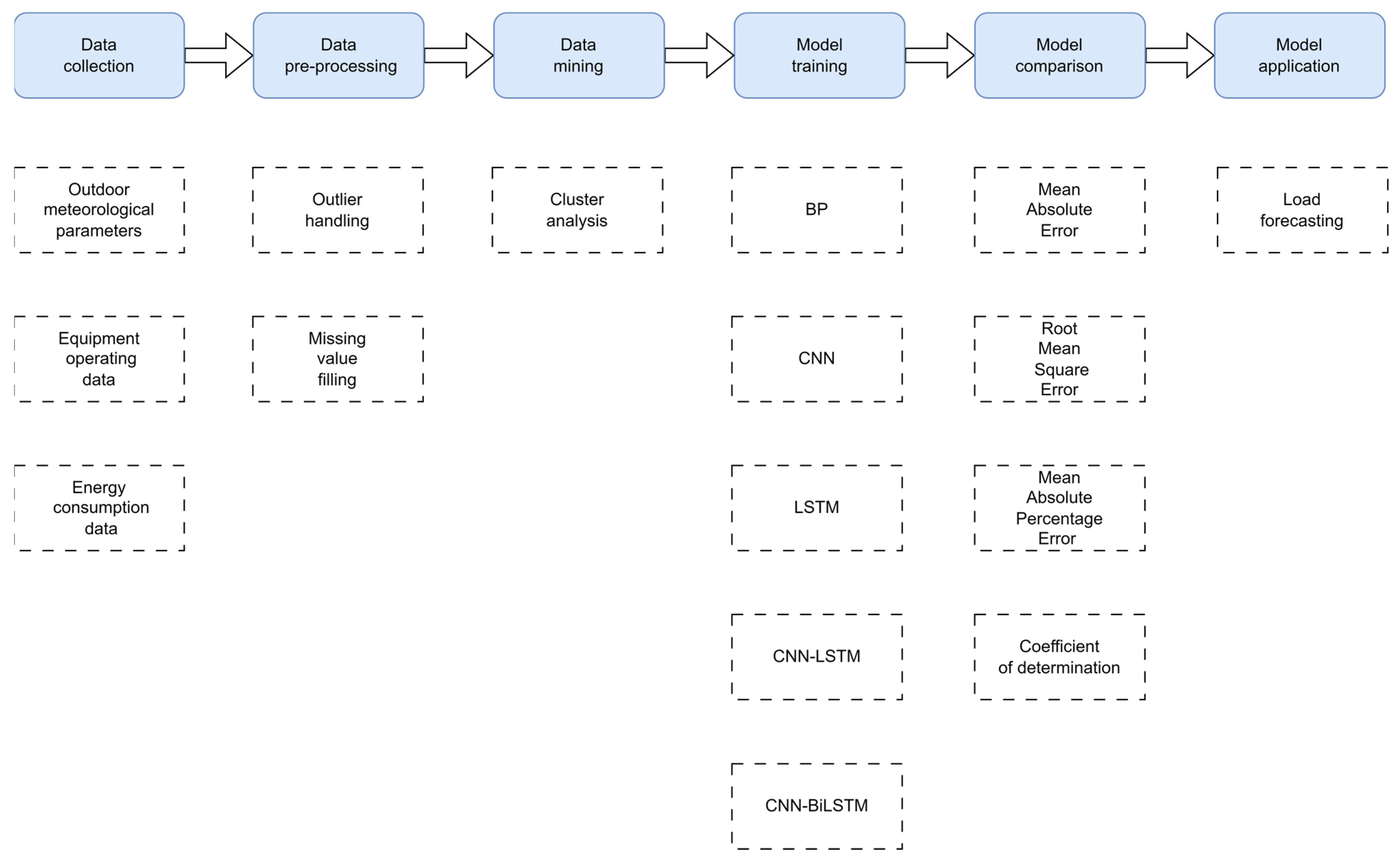
3. Methodology
3.1. Data Mining
3.1.1. Data Pre-Processing
3.1.2. Fuzzy Clustering
3.2. Heat Load Forecast
3.2.1. Predictive Models’ Construction
3.2.2. Evaluation Indexes for Predictive Models
4. Results and Discussion
4.1. Clustering Results
4.2. Comparison of the Results of Several Prediction Methods
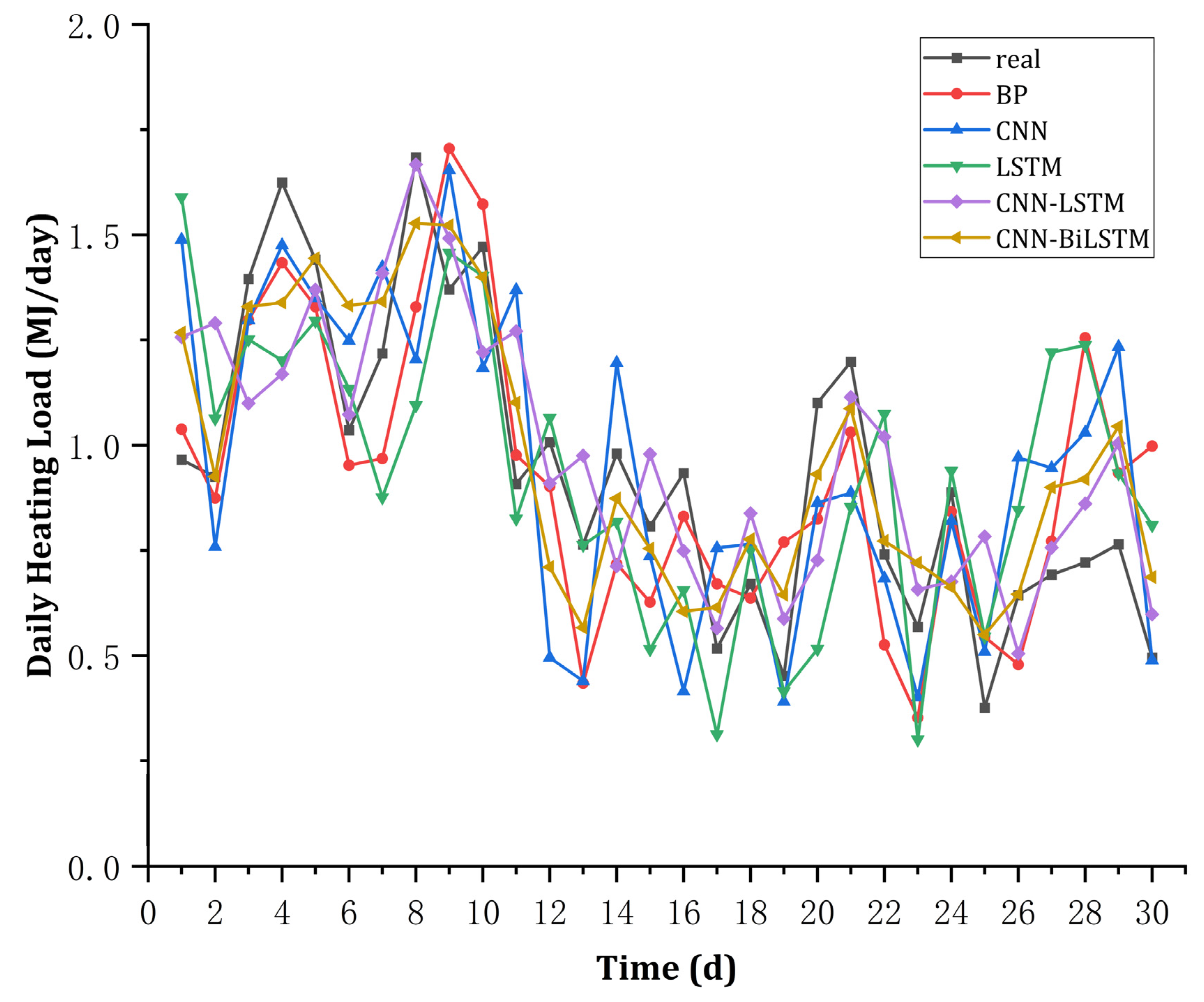
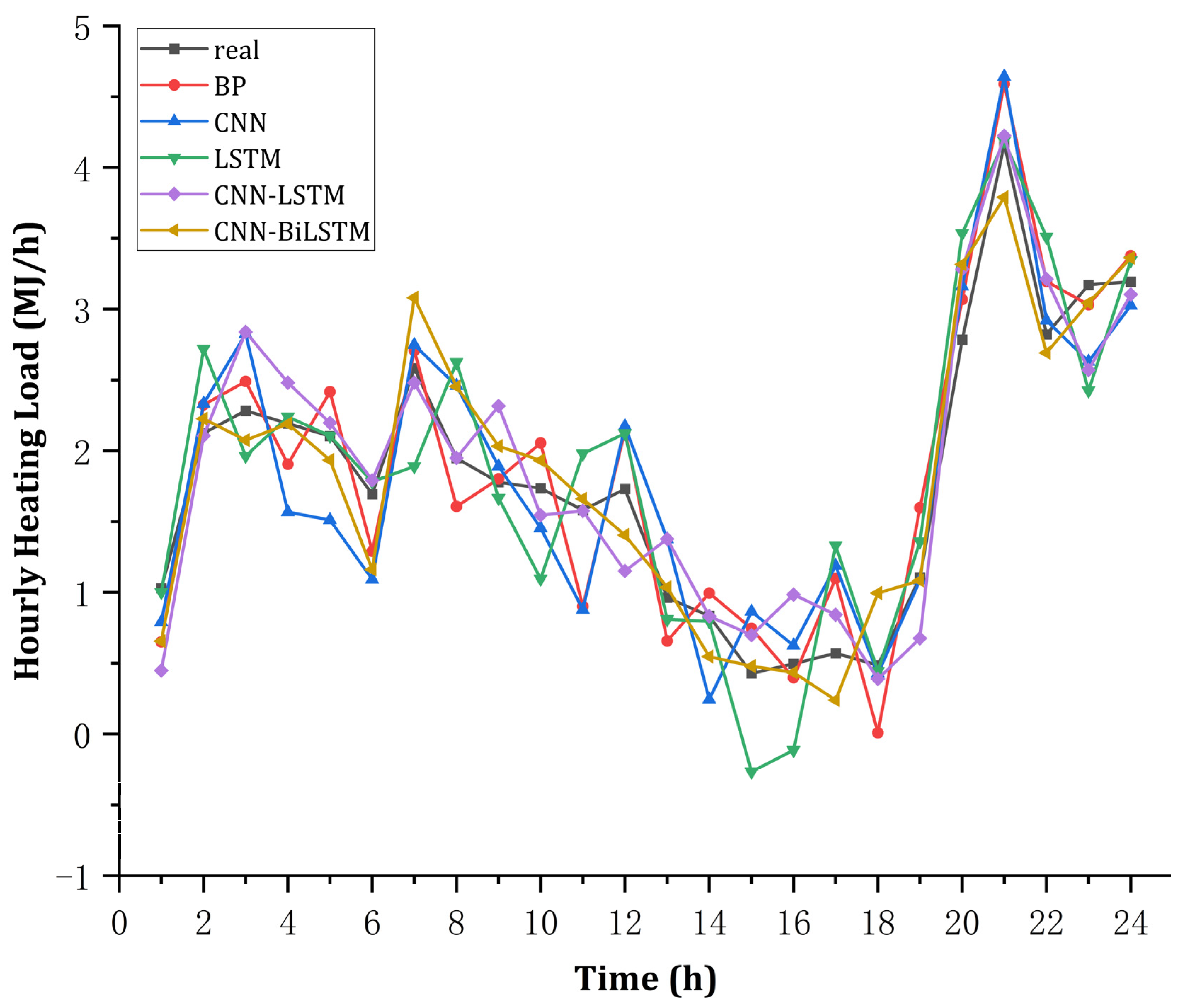
4.2.1. Long-Term Heat Load Forecast
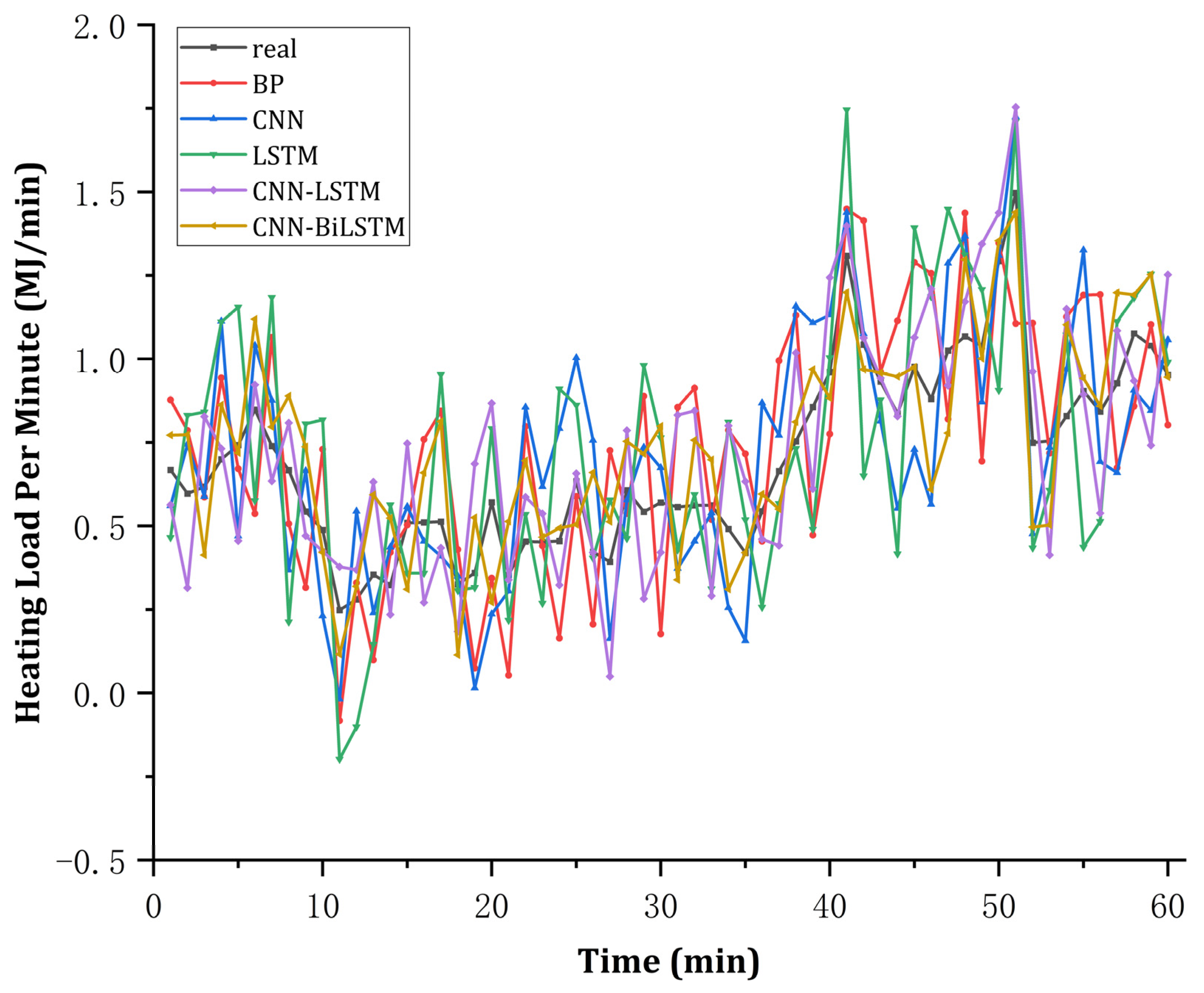
4.2.2. Short-Term Heat Load Forecast
4.2.3. Ultrashort-Term Heat Load Forecast
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gong, M.; Werner, S. An assessment of district heating research in China. Renew. Energy 2015, 84, 97–105. [Google Scholar] [CrossRef]
- Lund, H.; Duic, N.; Østergaard, P.A.; Mathiesen, B.V. Smart energy systems and 4th generation district heating. Energy 2016, 110, 1–4. [Google Scholar] [CrossRef]
- Lund, H.; Werner, S.; Wiltshire, R.; Svendsen, S.; Thorsen, J.E.; Hvelplund, F.; Mathiesen, B.V. 4th Generation District Heating (4GDH): Integrating smart thermal grids into future sustainable energy systems. Energy 2014, 68, 1–11. [Google Scholar] [CrossRef]
- Noussan, M.; Jarre, M.; Poggio, A. Real operation data analysis on district heating load patterns. Energy 2017, 129, 70–78. [Google Scholar] [CrossRef]
- Gadd, H.; Werner, S. Heat load patterns in district heating substations. Appl. Energy 2013, 108, 176–183. [Google Scholar] [CrossRef]
- Lu, Y.; Tian, Z.; Peng, P.; Niu, J.; Dai, J. Identification and evaluation of operation regulation strategies in district heating substations based on an unsupervised data mining method. Energy Build. 2019, 202, 109324. [Google Scholar] [CrossRef]
- Zhao, H.-X.; Magoulès, F. A review on the prediction of building energy consumption. Renew. Sustain. Energy Rev. 2012, 16, 3586–3592. [Google Scholar] [CrossRef]
- Ahmad, A.S.; Hassan, M.Y.; Abdullah, M.P.; Rahman, H.A.; Hussin, F.; Abdullah, H.; Saidur, R. A review on applications of ANN and SVM for building electrical energy consumption forecasting. Renew. Sustain. Energy Rev. 2014, 33, 102–109. [Google Scholar] [CrossRef]
- Chalal, M.L.; Benachir, M.; White, M.; Shrahily, R. Energy planning and forecasting approaches for supporting physical improvement strategies in the building sector: A review. Renew. Sustain. Energy Rev. 2016, 64, 761–776. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Do Carmo, C.M.R.; Christensen, T.H. Cluster analysis of residential heat load profiles and the role of technical and household characteristics. Energy Build. 2016, 125, 171–180. [Google Scholar] [CrossRef]
- Gianniou, P.; Liu, X.; Heller, A.; Nielsen, P.S.; Rode, C. Clustering-based analysis for residential district heating data. Energy Convers. Manag. 2018, 165, 840–850. [Google Scholar] [CrossRef]
- Tureczek, A.M.; Nielsen, P.S.; Madsen, H.; Brun, A. Clustering district heat exchange stations using smart meter consumption data. Energy Build. 2019, 182, 144–158. [Google Scholar] [CrossRef]
- Yang, J.; Ning, C.; Deb, C.; Zhang, F.; Cheong, D.; Lee, S.E.; Sekhar, C.; Tham, K.W. k-Shape clustering algorithm for building energy usage patterns analysis and forecasting model accuracy improvement. Energy Build. 2017, 146, 27–37. [Google Scholar] [CrossRef]
- Chicco, G. Overview and performance assessment of the clustering methods for electrical load pattern grouping. Energy 2012, 42, 68–80. [Google Scholar] [CrossRef]
- Nikolaou, T.G.; Kolokotsa, D.S.; Stavrakakis, G.S.; Skias, I.D. On the Application of Clustering Techniques for Office Buildings’ Energy and Thermal Comfort Classification. IEEE Trans. Smart Grid 2012, 3, 2196–2210. [Google Scholar] [CrossRef]
- Protić, M.; Shamshirband, S.; Petković, D.; Abbasi, A.; Kiah, L.M.; Unar, J.A.; Živković, L.; Raos, M. Forecasting of consumers heat load in district heating systems using the support vector machine with a discrete wavelet transform algorithm. Energy 2015, 87, 343–351. [Google Scholar] [CrossRef]
- Imam, S.; A Coley, D.; Walker, I. The building performance gap: Are modellers literate? Build. Serv. Eng. Res. Technol. 2017, 38, 351–375. [Google Scholar] [CrossRef]
- Li, X.; Wen, J. Review of building energy modeling for control and operation. Renew. Sustain. Energy Rev. 2014, 37, 517–537. [Google Scholar] [CrossRef]
- Forrester, J.R.; Wepfer, W.J. Formulation of a load prediction algorithm for a large commercial building. Ashrae Trans. 1984, 90, 536–551. [Google Scholar]
- Zhao, H.X.; Magoulès, F. Parallel Support Vector Machines Applied to the Prediction of Multiple Buildings Energy Consumption. J. Algorithms Comput. Technol. 2010, 4, 231–249. [Google Scholar] [CrossRef]
- Wei, Y.; Xia, L.; Pan, S.; Wu, J.; Zhang, X.; Han, M.; Zhang, W.; Xie, J.; Li, Q. Prediction of occupancy level and energy consumption in office building using blind system identification and neural networks. Appl. Energy 2019, 240, 276–294. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, J.; Chen, H.; Li, G.; Liu, J.; Xu, C.; Huang, R.; Huang, Y. Machine learning-based thermal response time ahead energy demand prediction for building heating systems. Appl. Energy 2018, 221, 16–27. [Google Scholar] [CrossRef]
- Chou, J.-S.; Bui, D.-K. Modeling heating and cooling loads by artificial intelligence for energy-efficient building design. Energy Build. 2014, 82, 437–446. [Google Scholar] [CrossRef]
- Fan, C.; Xiao, F.; Wang, S. Development of prediction models for next-day building energy consumption and peak power demand using data mining techniques. Appl. Energy 2014, 127, 1–10. [Google Scholar] [CrossRef]
- Edwards, R.E.; New, J.; Parker, L.E. Predicting future hourly residential electrical consumption: A machine learning case study. Energy Build. 2012, 49, 591–603. [Google Scholar] [CrossRef]
- Massana, J.; Pous, C.; Burgas, L.; Melendez, J.; Colomer, J. Short-term load forecasting in a non-residential building contrasting models and attributes. Energy Build. 2015, 92, 322–330. [Google Scholar] [CrossRef]
- Li, Y.; Tong, Z.; Tong, S.; Westerdahl, D. A data-driven interval forecasting model for building energy prediction using attention-based LSTM and fuzzy information granulation. Sustain. Cities Soc. 2022, 76, 103481. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, T.; Piette, M.A. Building thermal load prediction through shallow machine learning and deep learning. Appl. Energy 2020, 263, 114683. [Google Scholar] [CrossRef]
- Idowu, S.; Saguna, S.; Åhlund, C.; Schelén, O. Applied machine learning: Forecasting heat load in district heating system. Energy Build. 2016, 133, 478–488. [Google Scholar] [CrossRef]
- Dalipi, F.; Yayilgan, S.Y.; Gebremedhin, A. Data-Driven Machine-Learning Model in District Heating System for Heat Load Prediction: A Comparison Study. Appl. Comput. Intell. Soft Comput. 2016, 2016, 1–11. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Q.; Yuan, T.; Yang, F. Effect of input variables on cooling load prediction accuracy of an office building. Appl. Therm. Eng. 2018, 128, 225–234. [Google Scholar] [CrossRef]
- Ahmad, T.; Chen, H.; Guo, Y.; Wang, J. A comprehensive overview on the data driven and large scale based approaches for forecasting of building energy demand: A review. Energy Build. 2018, 165, 301–320. [Google Scholar] [CrossRef]
- Li, Q.; Meng, Q.; Cai, J.; Yoshino, H.; Mochida, A. Applying support vector machine to predict hourly cooling load in the building. Appl. Energy 2009, 86, 2249–2256. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, T.; Piette, M.A. Data fusion in predicting internal heat gains for office buildings through a deep learning approach. Appl. Energy 2019, 240, 386–398. [Google Scholar] [CrossRef]
- Lee, W.-Y.; House, J.M.; Kyong, N.-H. Subsystem level fault diagnosis of a building’s air-handling unit using general regression neural networks. Appl. Energy 2004, 77, 153–170. [Google Scholar] [CrossRef]
- Du, Z.; Fan, B.; Jin, X.; Chi, J. Fault detection and diagnosis for buildings and HVAC systems using combined neural networks and subtractive clustering analysis. J. Affect. Disord. 2014, 73, 1–11. [Google Scholar] [CrossRef]
- Du, Z.; Fan, B.; Chi, J.; Jin, X. Sensor fault detection and its efficiency analysis in air handling unit using the combined neural networks. Energy Build. 2014, 72, 157–166. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, S.; Xiao, F. A system-level incipient fault-detection method for HVAC systems. HVAC&R Res. 2013, 19, 593–601. [Google Scholar] [CrossRef]
- Li, G.; Hu, Y.; Chen, H.; Li, H.; Hu, M.; Guo, Y.; Liu, J.; Sun, S.; Sun, M. Data partitioning and association mining for identifying VRF energy consumption patterns under various part loads and refrigerant charge conditions. Appl. Energy 2017, 185, 846–861. [Google Scholar] [CrossRef]
- Xue, P.; Zhou, Z.; Fang, X.; Chen, X.; Liu, L.; Liu, Y.; Liu, J. Fault detection and operation optimization in district heating substations based on data mining techniques. Appl. Energy 2017, 205, 926–940. [Google Scholar] [CrossRef]
- Gadd, H.; Werner, S. Fault detection in district heating substations. Appl. Energy 2015, 157, 51–59. [Google Scholar] [CrossRef]
- Miller, C.; Nagy, Z.; Schlueter, A. A review of unsupervised statistical learning and visual analytics techniques applied to performance analysis of non-residential buildings. Renew. Sustain. Energy Rev. 2018, 81, 1365–1377. [Google Scholar] [CrossRef]
- Guo, J.; Yun, S.; Meng, Y.; He, N.; Ye, D.; Zhao, Z.; Jia, L.; Yang, L. Prediction of heating and cooling loads based on light gradient boosting machine algorithms. J. Affect. Disord. 2023, 236, 110252. [Google Scholar] [CrossRef]
- Miller, C.; Arjunan, P.; Kathirgamanathan, A.; Fu, C.; Roth, J.; Park, J.Y.; Balbach, C.; Gowri, K.; Nagy, Z.; Fontanini, A.D.; et al. The ASHRAE Great Energy Predictor III competition: Overview and results. Sci. Technol. Built Environ. 2020, 26, 1427–1447. [Google Scholar] [CrossRef]
- Prokhorenkova, L.O.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Neural Inf. Process. Syst. 2018, 31, 6639–6649. [Google Scholar]
- Song, J.; Zhang, L.; Xue, G.; Ma, Y.; Gao, S.; Jiang, Q. Predicting hourly heating load in a district heating system based on a hybrid CNN-LSTM model. Energy Build. 2021, 243, 110998. [Google Scholar] [CrossRef]


| Category | Hidden Layer Number | Hidden Layer Unit Number(s) | Activation |
|---|---|---|---|
| BP | 4 | 256/128/64/32 | ReLU |
| CNN | 2 | 64/32 | ReLU |
| LSTM | 7 | 6 | Sigmoid |
| CNN-LSTM | 7 | 6 | ReLU and Sigmoid |
| CNN-BiLSTM | 7 | 6 | ReLU and Sigmoid |
| Category | Influencing Factors |
|---|---|
| Cluster.1 | Outdoor temperature, outdoor wind speed, primary network water supply pressure, primary network return pressure, secondary network water supply pressure, secondary network return pressure |
| Cluster.2 | Primary network return water temperature, secondary network supply water temperature, secondary network return water temperature |
| Cluster.3 | Solar irradiance, valve opening degree, primary secondary network water supply temperature |
| Model | MAE | RMSE | MAPE | R2 |
|---|---|---|---|---|
| BP | 8.162 | 9.404 | 2.921% | 0.7710 |
| LSTM | 5.783 | 6.598 | 1.929% | 0.8041 |
| CNN | 6.564 | 7.331 | 2.531% | 0.7088 |
| CNN-LSTM | 4.961 | 5.638 | 2.258% | 0.8278 |
| CNN-BiLSTM | 3.786 | 4.664 | 1.272% | 0.8821 |
| Model | MAE | RMSE | MAPE | R2 |
|---|---|---|---|---|
| BP | 2.964 | 3.572 | 7.998% | 0.89 |
| LSTM | 3.565 | 3.446 | 3.671% | 0.898 |
| CNN | 3.413 | 3.923 | 4.525% | 0.9023 |
| CNN-LSTM | 2.842 | 3.325 | 4.509% | 0.9327 |
| CNN-BiLSTM | 2.2546 | 2.954 | 2.09% | 0.9469 |
| Model | MAE | RMSE | MAPE | R2 |
|---|---|---|---|---|
| BP | 3.382 | 3.881 | 2.37% | 0.9084 |
| LSTM | 2.868 | 3.271 | 1.65% | 0.9349 |
| CNN | 3.195 | 3.671 | 1.747% | 0.918 |
| CNN-LSTM | 2.161 | 2.52 | 1.167% | 0.9613 |
| CNN-BiLSTM | 1.691 | 1.966 | 0.737% | 0.9764 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, Y.; Wang, Z.; Liu, Z.; Guo, C.; Yang, B. Load Prediction of Regional Heat Exchange Station Based on Fuzzy Clustering Based on Fourier Distance and Convolutional Neural Network–Bidirectional Long Short-Term Memory Network. Energies 2024, 17, 4190. https://doi.org/10.3390/en17164190
You Y, Wang Z, Liu Z, Guo C, Yang B. Load Prediction of Regional Heat Exchange Station Based on Fuzzy Clustering Based on Fourier Distance and Convolutional Neural Network–Bidirectional Long Short-Term Memory Network. Energies. 2024; 17(16):4190. https://doi.org/10.3390/en17164190
Chicago/Turabian StyleYou, Yuwen, Zhonghua Wang, Zhihao Liu, Chunmei Guo, and Bin Yang. 2024. "Load Prediction of Regional Heat Exchange Station Based on Fuzzy Clustering Based on Fourier Distance and Convolutional Neural Network–Bidirectional Long Short-Term Memory Network" Energies 17, no. 16: 4190. https://doi.org/10.3390/en17164190
APA StyleYou, Y., Wang, Z., Liu, Z., Guo, C., & Yang, B. (2024). Load Prediction of Regional Heat Exchange Station Based on Fuzzy Clustering Based on Fourier Distance and Convolutional Neural Network–Bidirectional Long Short-Term Memory Network. Energies, 17(16), 4190. https://doi.org/10.3390/en17164190









