Non-Weighted Two-Stage Model Predictive Control Strategy Based on Three-Level NPC Inverter
Abstract
:1. Introduction
2. System Modeling of Three-Level Inverter Finite-Control-Set Model Predictive Control
2.1. Three-Level Neutral-Point-Clamped Voltage Source Inverter Circuit Topology
2.2. Asynchronous Motor Prediction Model
3. Hierarchical-Optimization-Based Finite-Control-Set Model Predictive Control without Weight Factors
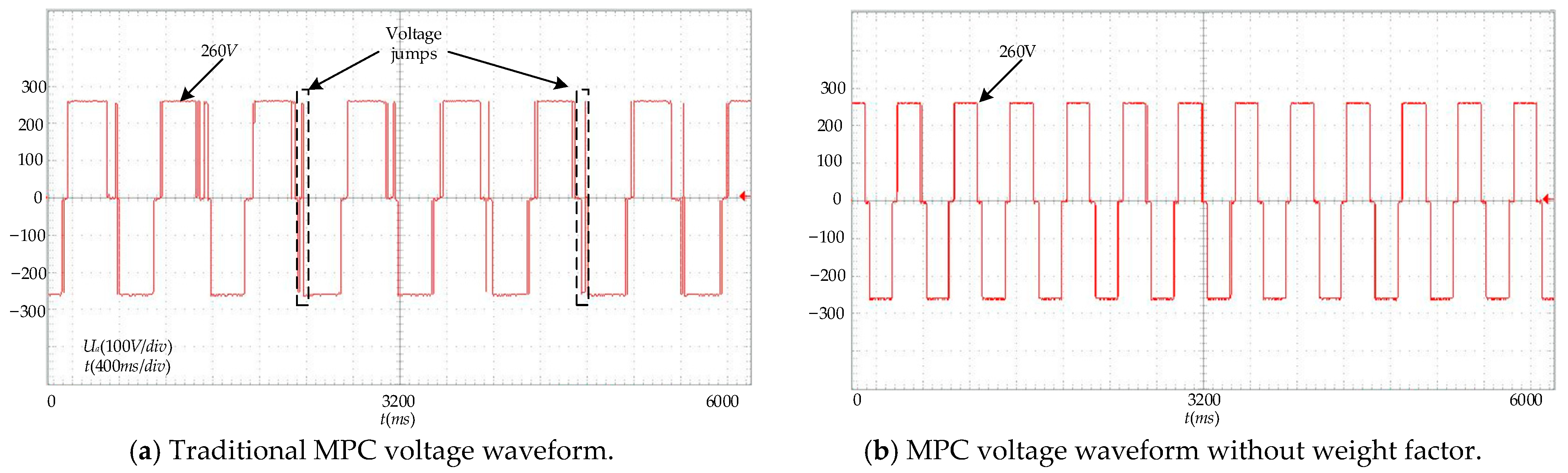
3.1. Voltage Jump Limits
3.2. Common-Mode Voltage Rejection
3.3. Current Tracking Error
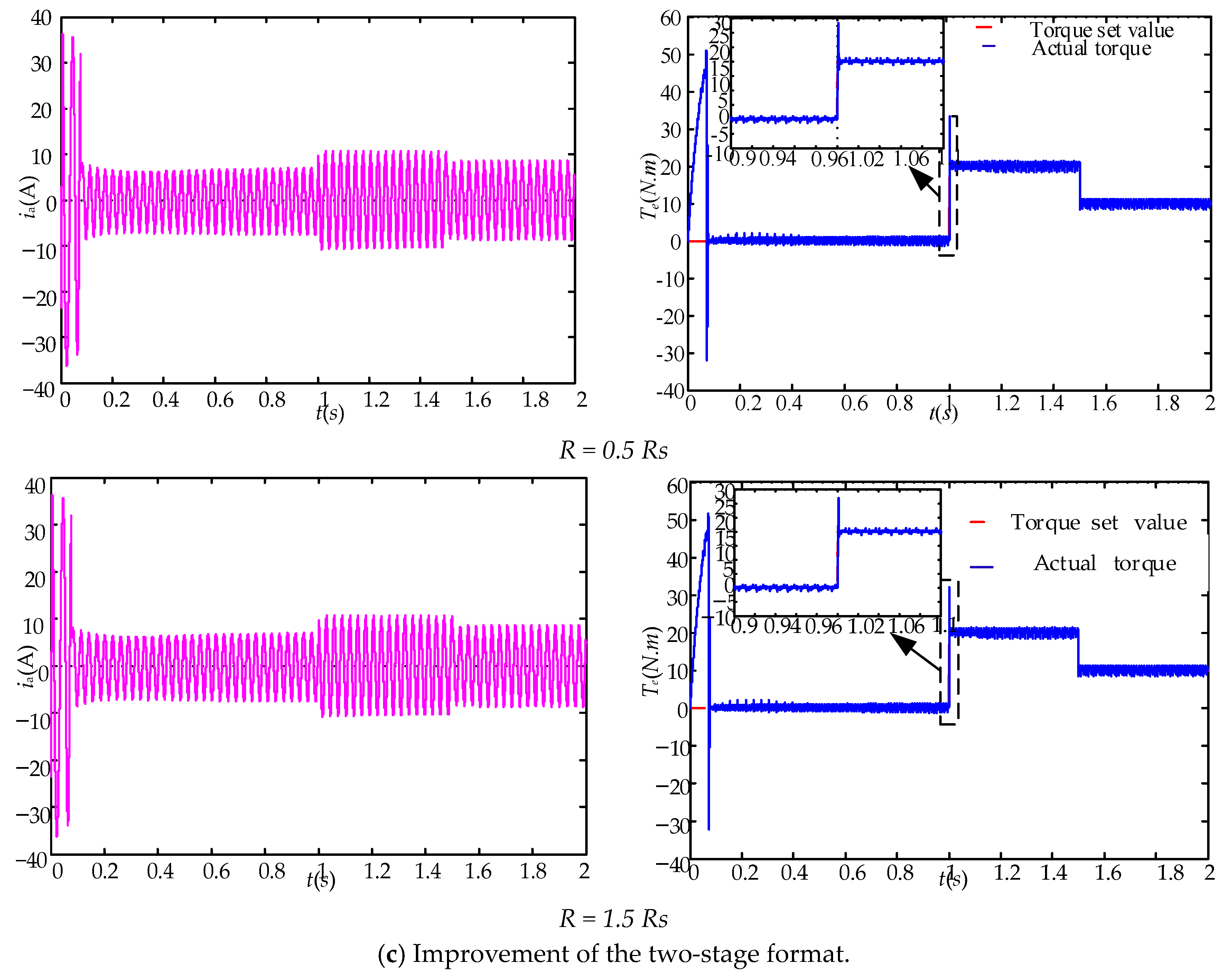
4. Improved Two-Stage Finite-Control-Set Model Predictive Control without Weight Factors
4.1. Vector Selection
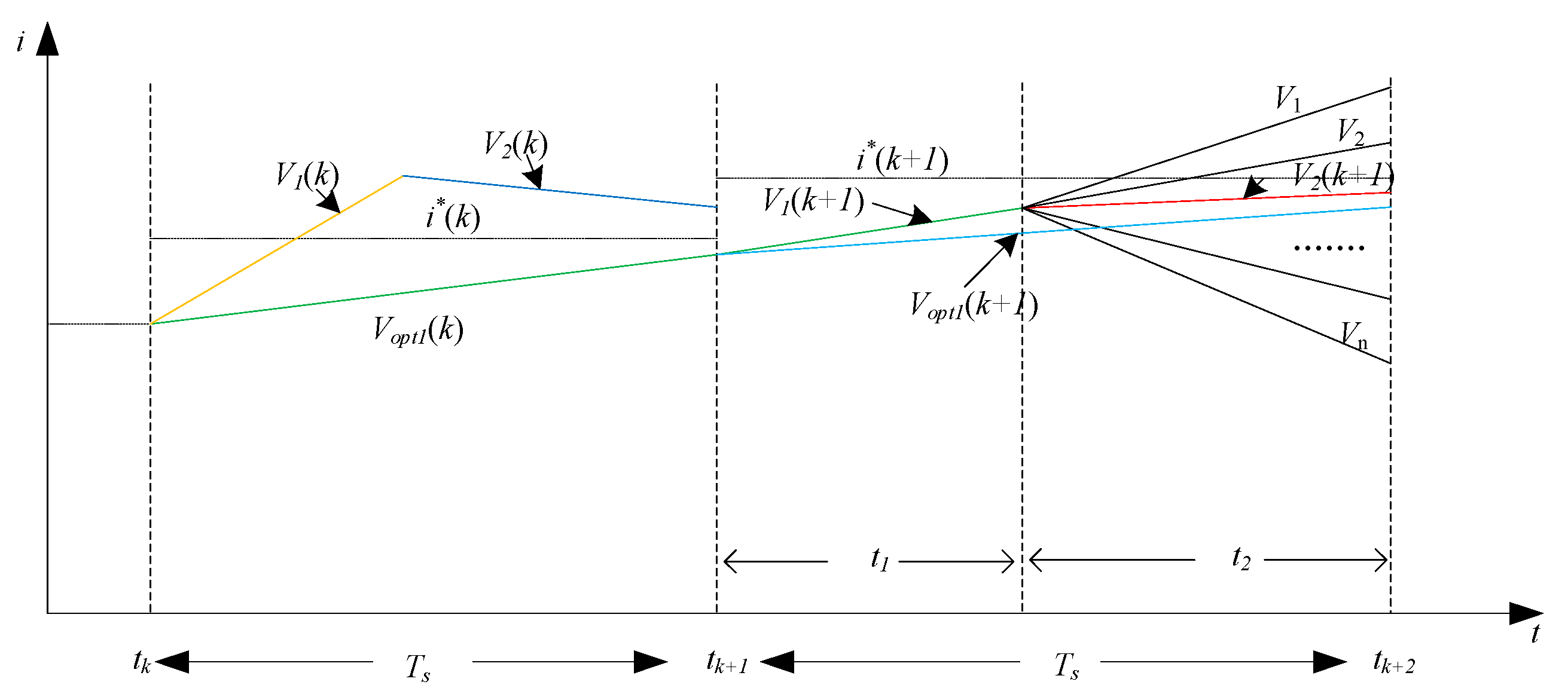
4.2. Dwell Time Calculation
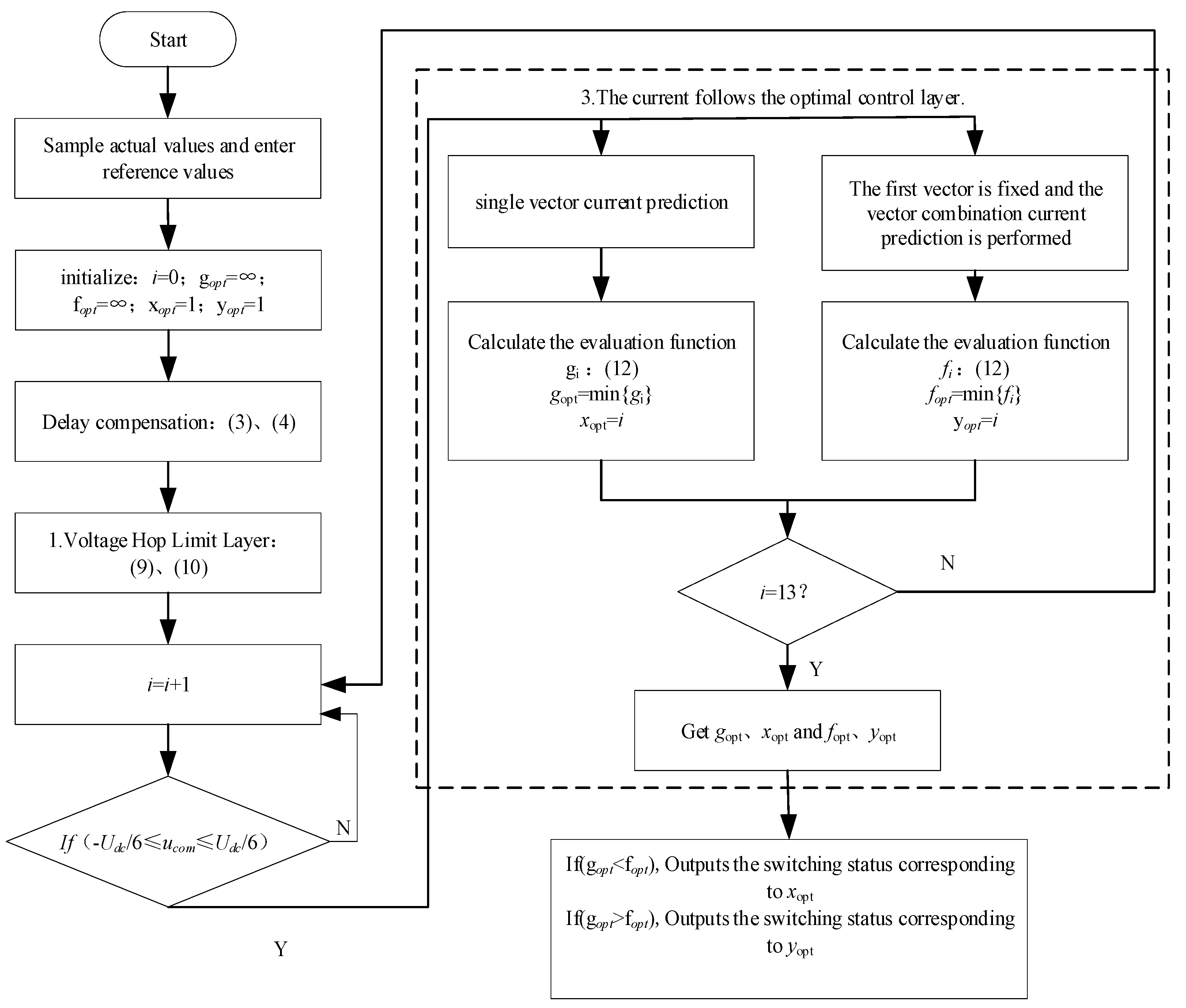
4.3. Improved Two-Stage Finite-Control-Set Model Predictive Control Strategy Flowchart
- (1)
- Sample actual values and input reference values for delay compensation;
- (2)
- Voltage jump limit: The limit on voltage jumps is achieved by selecting the vector adjacent to the action vector at the end of the present cycle;
- (3)
- Common-mode voltage rejection: Calculate the common-mode voltage and judge whether it falls within the satisfactory interval;
- (4)
- Optimal control of current tracking:
- (4.1)
- Select the optimal vector Vopt with an evaluation function though the single-vector exhaustive search and save the corresponding action error g1;
- (4.2)
- During the selection of a dual vector, the first switching vector is chosen as the one at the end of the previous cycle. The pre-allocated dwell time for Vopt1 and for the switching vector under evaluation is calculated through Formula (13). The pre-allocated time for Vopt1 is t1, and that for Vopt2 is t2. The predicted current values at time k + 2 are calculated respectively;
- (5)
- Substitute the predicted current values into the evaluation function as shown in Formula (12) and save the smallest action error g2.
5. Simulation and Experimentation
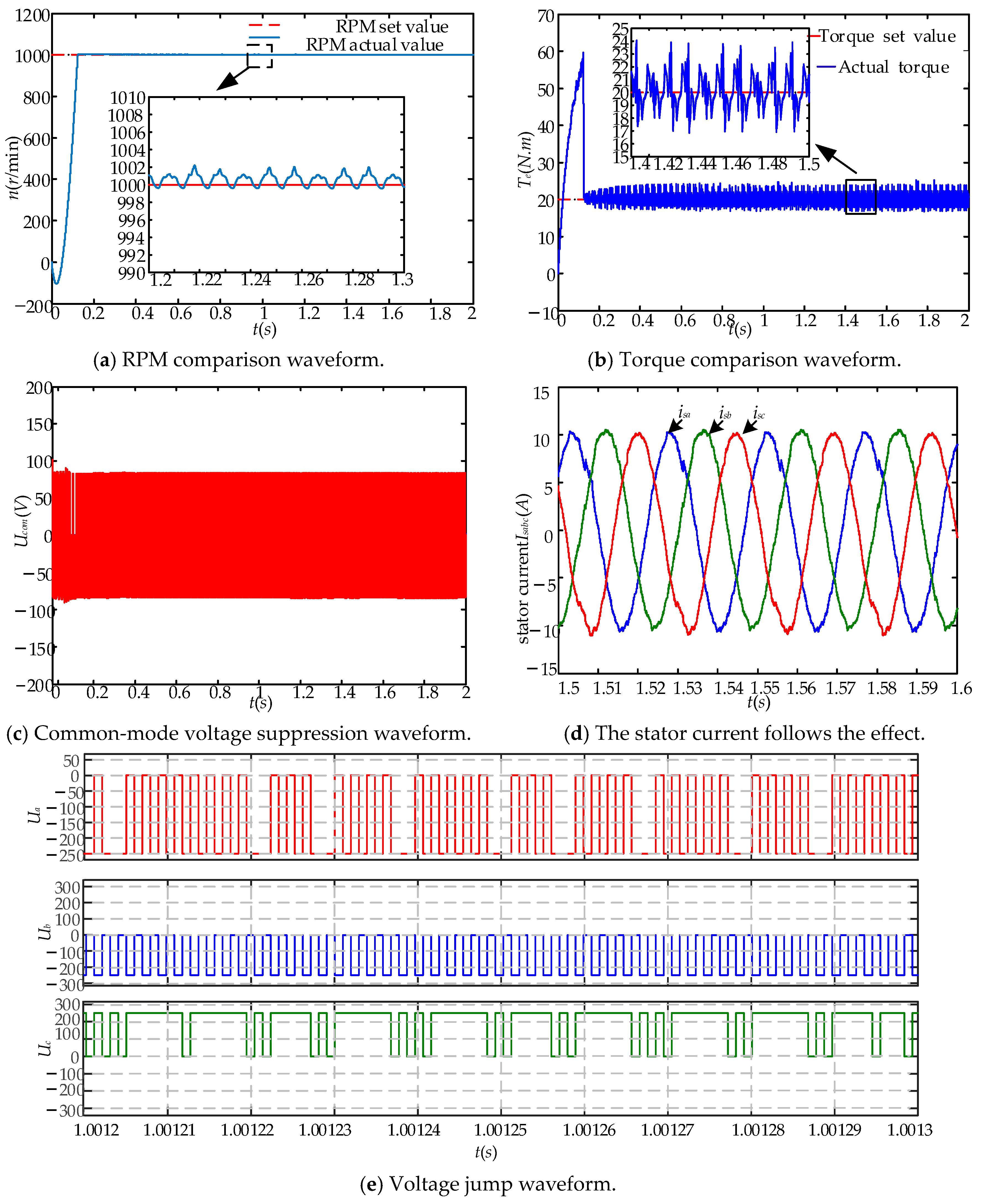
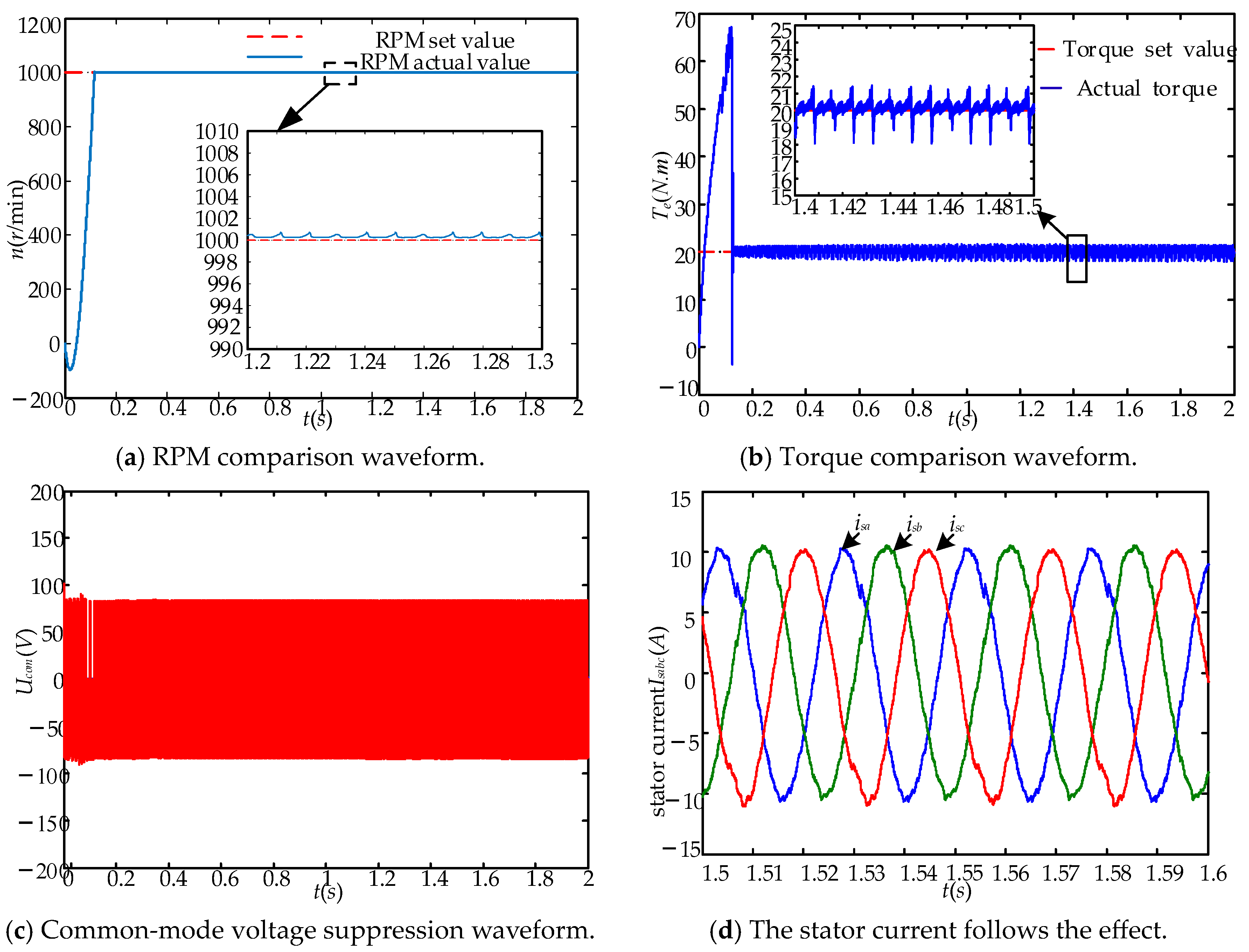
5.1. Simulation Analysis
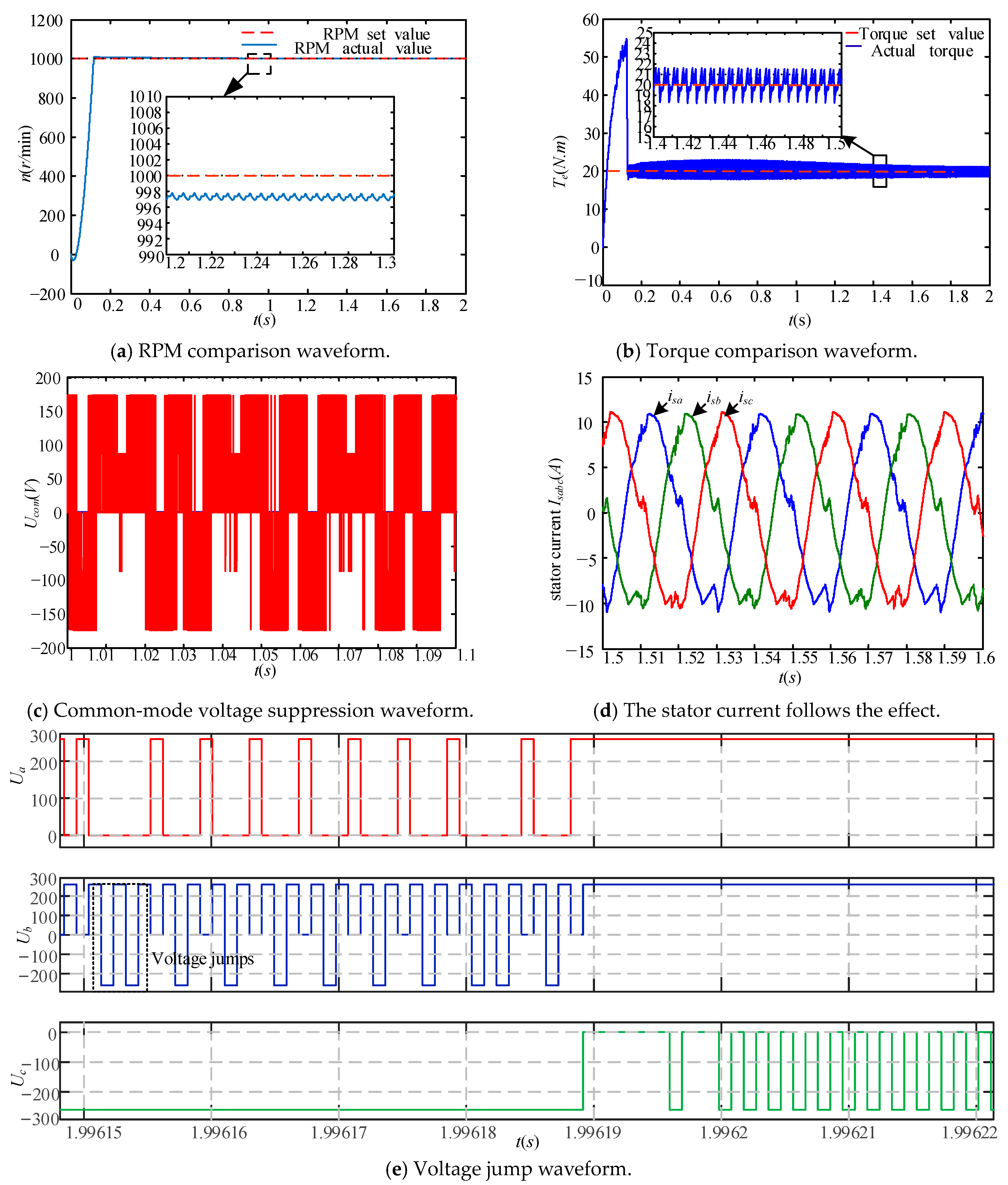
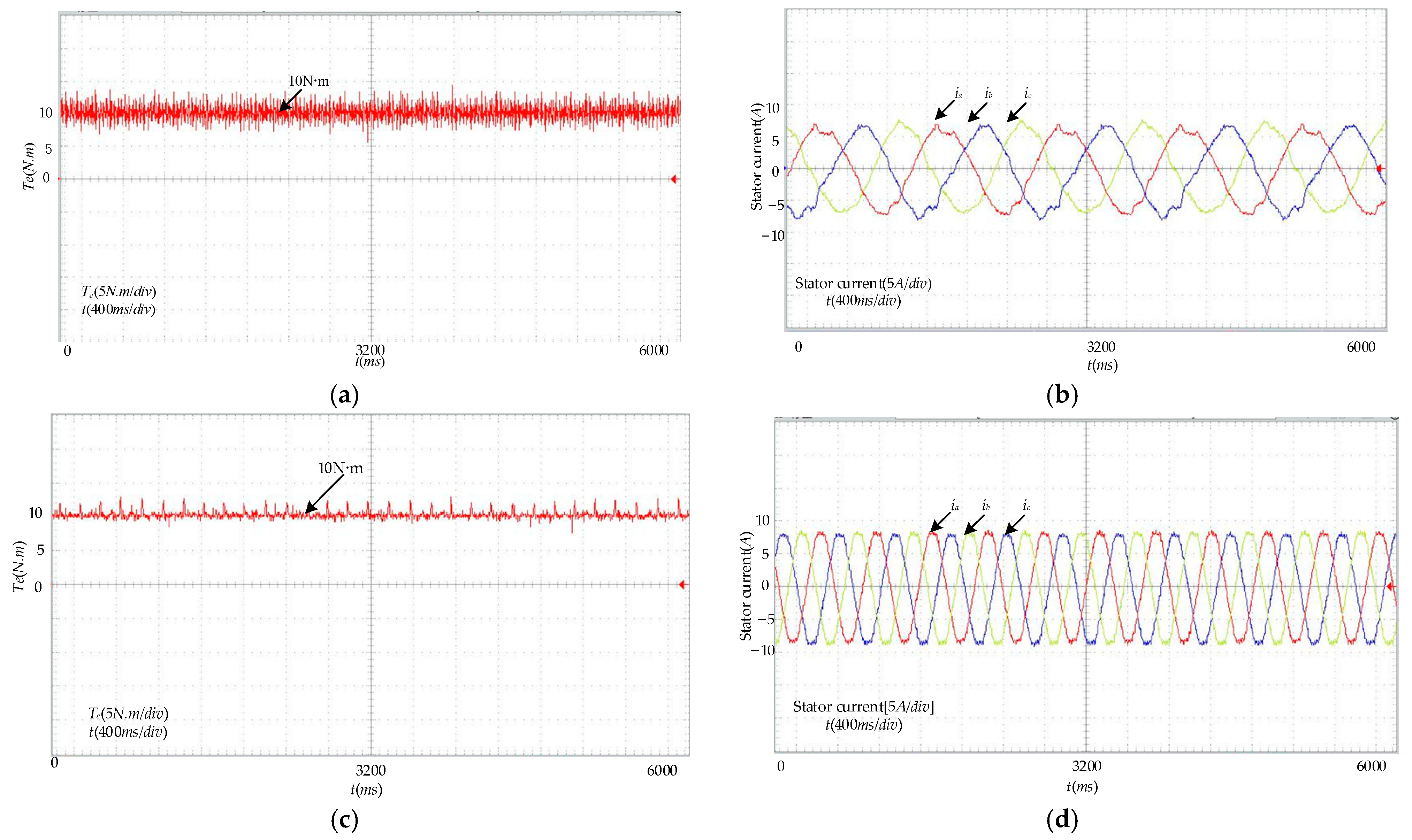
5.1.1. Steady-State Performance Analysis
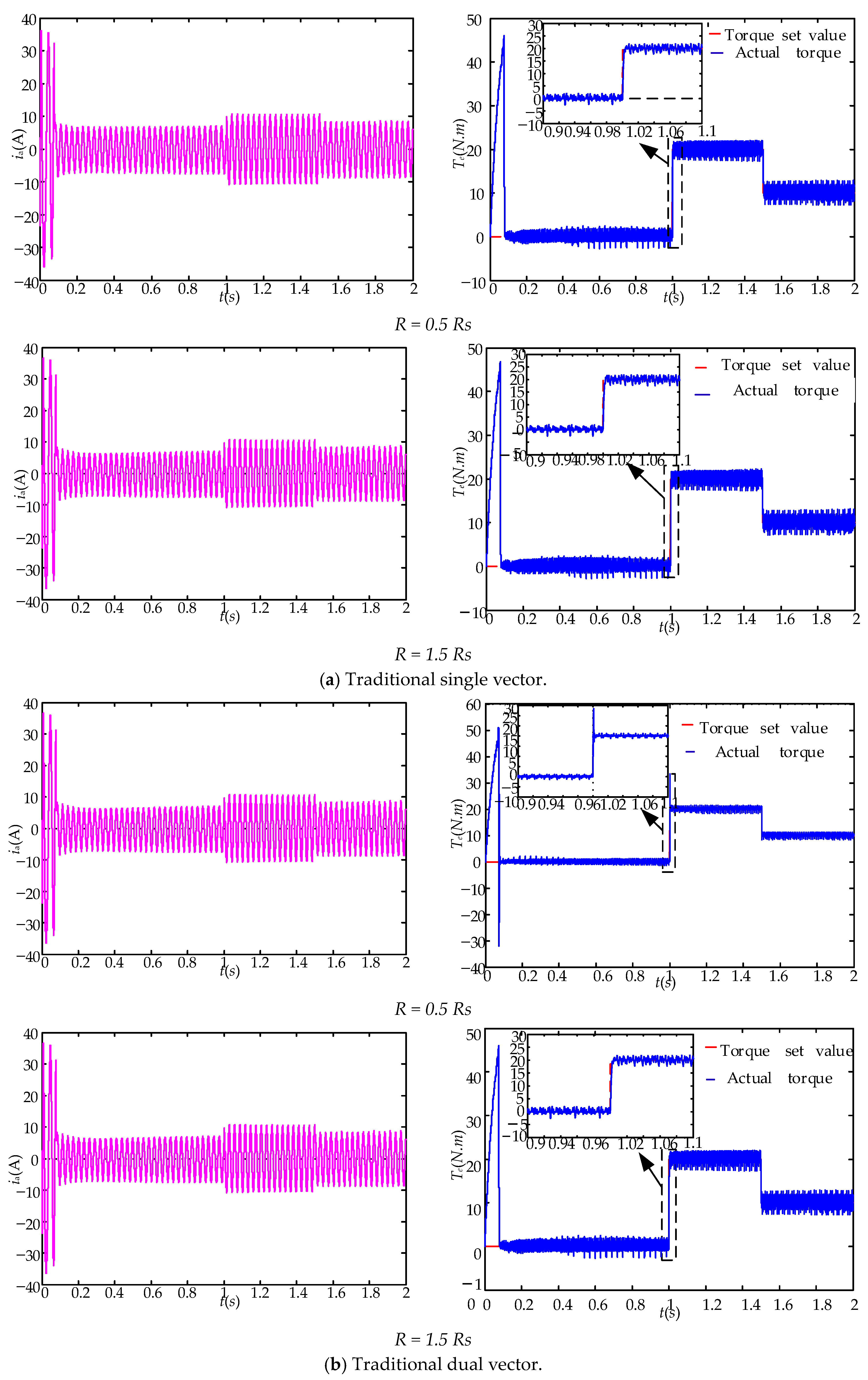
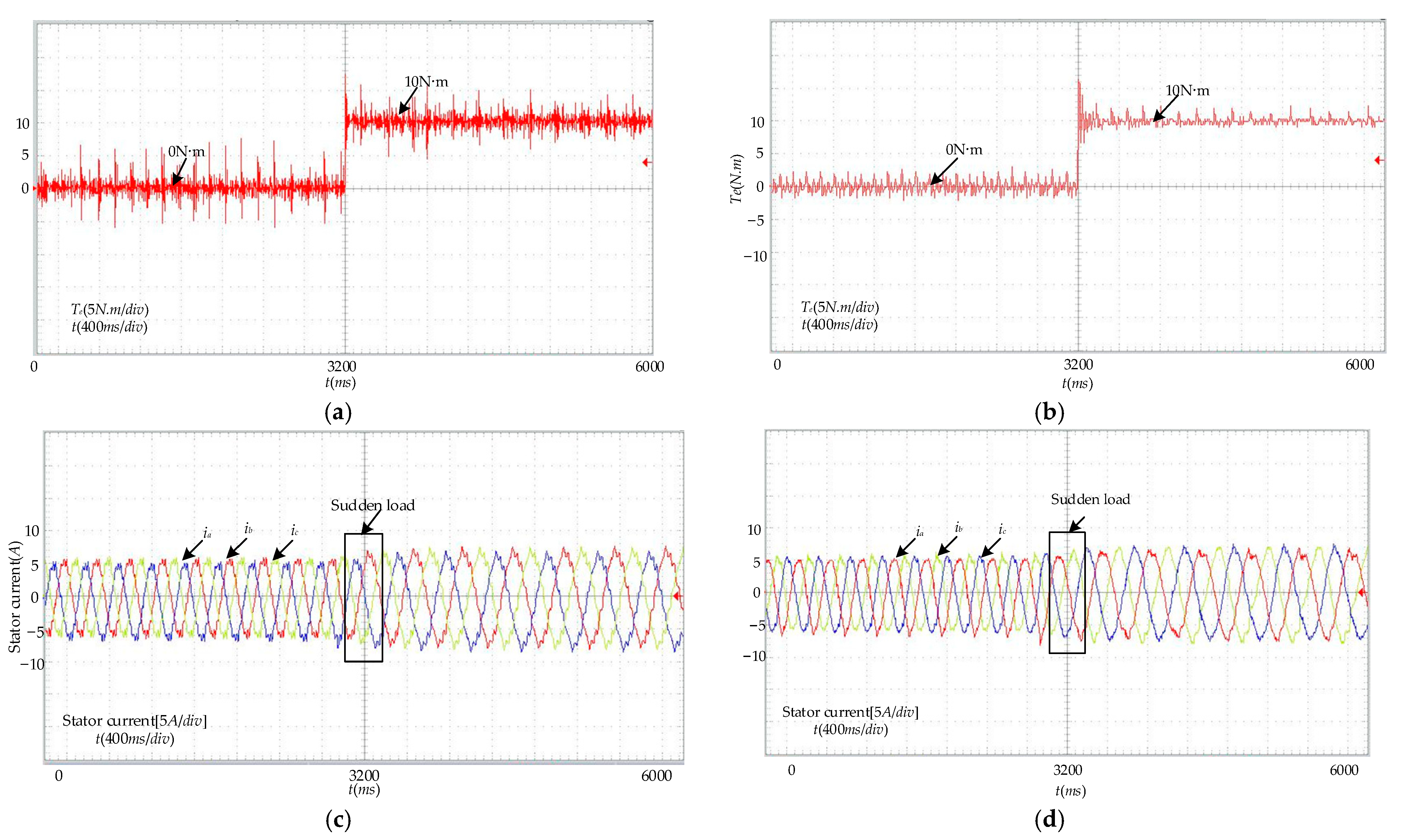
5.1.2. Dynamic Performance Analysis
- (1)
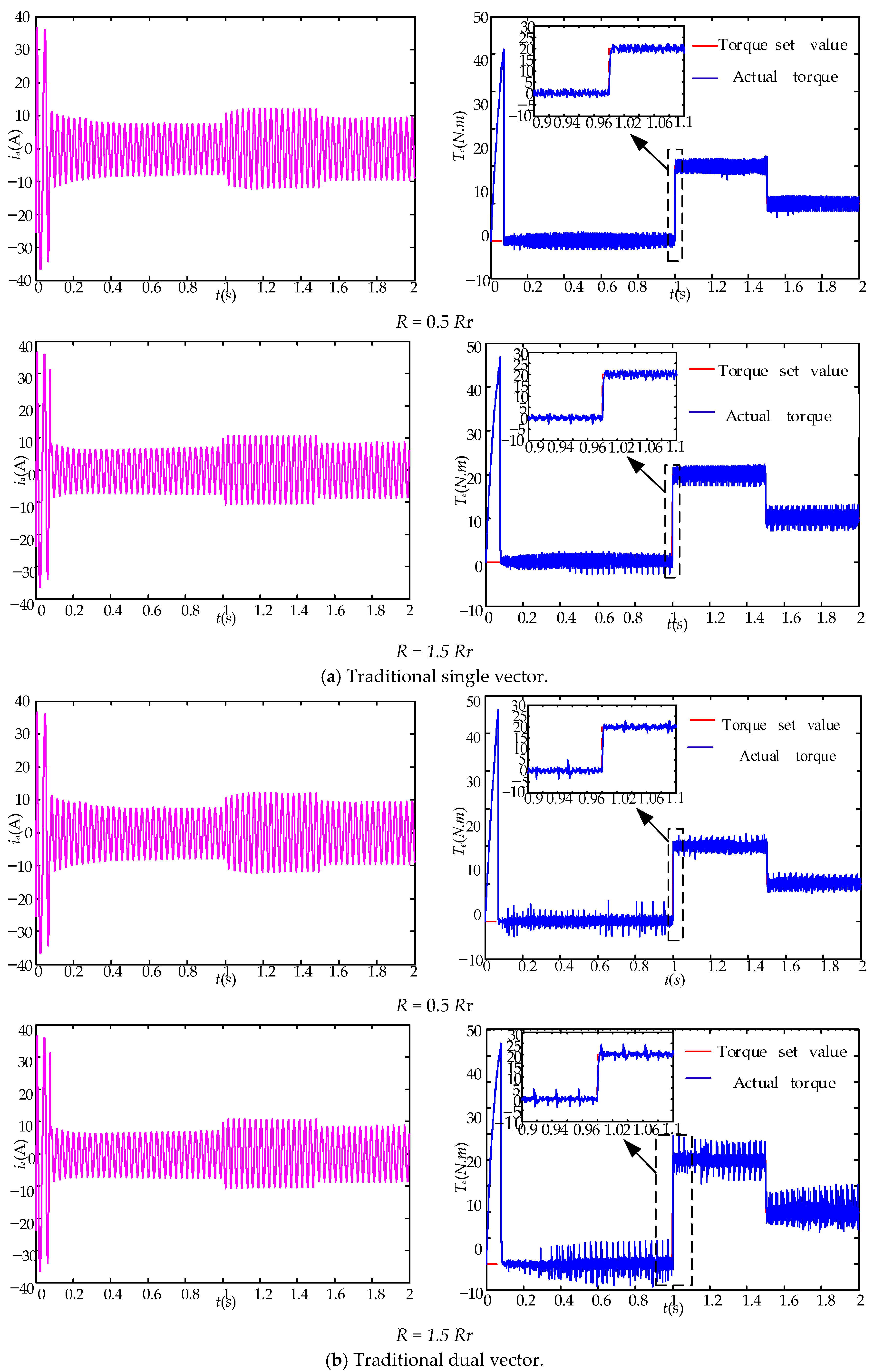
- Parameter Mismatch Analysis
- (a)
- Stator error analysis
- (b)
- Rotor Resistance Error Analysis
5.2. Experimental Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.; Wang, C.; Cheng, Q. Fast Model Predictive Control of Two-Level Inverter Based on Single Vector. Trans. China Electrotech. Soc. 2021, 36, 654–664+687. [Google Scholar]
- Xin, Y.; Wang, Y.; Li, G.; Wang, C.; Wang, W. Finite Control Set Model Predictive Control Method with Fast Optimization Based on T-Type Three-Level Grid Connected Inverter. Trans. China Electrotech. Soc. 2021, 36, 1681–1692. [Google Scholar]
- Li, X.; Xue, Z.; Yan, X. Voltage Vector Rapid Screening-Based Three-Vector Model Predictive Torque Control for Permanent Magnet Synchronous Motor. Trans. China Electrotech. Soc. 2022, 37, 1666–1678. [Google Scholar]
- Davari, S.A.; Khaburi, D.A.; Kennel, R. An Improved FCS–MPC Algorithm for an Induction Motor with an Imposed Optimized Weighting Factor. IEEE Trans. Power Electron. 2012, 27, 1540–1551. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, K.; Wang, H. A predictive torque control method for permanent magnet synchronous motor without weighting factor. J. Light Ind. 2019, 34, 80–88. [Google Scholar]
- Zhang, X.; Hou, B. Double Vectors Model Predictive Torque Control without Weighting Factor Based on Voltage Tracking Error. IEEE Trans. Power Electron. 2018, 33, 2368–2380. [Google Scholar] [CrossRef]
- Garnica López, M.-A.; García de Vicuña, J.-L.; Miret, J.; Castilla, M.; Guzmán, R. Control Strategy for Grid-Connected Three-Phase Inverters During Voltage Sags to Meet Grid Codes and to Maximize Power Delivery Capability. IEEE Trans. Power Electron. 2018, 33, 9360–9374. [Google Scholar] [CrossRef]
- Lai, H. An Optimization Model Predictive Control Method for Three Level Inverters without Weighting Factor. Drive Control 2017, 45, 73–76+80. [Google Scholar]
- Wang, F.; Xie, H.; Chen, Q.; Davari, S.A.; Rodríguez, J.; Kennel, R. Parallel Predictive Torque Control for Induction Machines without Weighting Factors. IEEE Trans. Power Electron. 2020, 35, 1779–1788. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y. Logical Operation-Based Model Predictive Control for Quasi-Z-Source Inverter without Weighting Factor. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1039–1051. [Google Scholar] [CrossRef]
- Sun, J.; Sun, H.; Jiang, J. An improved modulation method for low common mode current non-isolated series simultaneous power supply dual input inverters for new energy generation applications. Electr. Eng. 2024, 1–11. [Google Scholar] [CrossRef]
- Wang, X.; Lin, H.; Yang, H. The Characteristics and Suppression of Common-Mode Current for Brushless Doubly Fed Generator System. IEEE Trans. Electromagn. Compat. 2020, 5, 2265–2276. [Google Scholar] [CrossRef]
- Zhang, Y.; Bai, Y.; Yang, H. A Universal Multiple-Vector-Based Model Predictive Control of Induction Motor Drives. IEEE Trans. Power Electron. 2018, 33, 6957–6969. [Google Scholar] [CrossRef]
- Nasr, A.; Gu, C.; Wang, X.; Buticchi, G.; Bozhko, S. Torque-Performance Improvement for Direct Torque-Controlled PMSM Drives Based on Duty-Ratio Regulation. IEEE Trans. Power Electron. 2022, 37, 749–760. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H. Generalized Two-Vector-Based Model-Predictive Torque Control of Induction Motor Drives. IEEE Trans. Power Electron. 2015, 30, 3818–3829. [Google Scholar] [CrossRef]
- Chen, W.; Zeng, S.; Zhang, G. A Modified Double Vectors Model Predictive Torque Control of Permanent Magnet Synchronous Motor. IEEE Trans. Power Electron. 2019, 34, 11419–11428. [Google Scholar] [CrossRef]
- Yao, J.; Liu, R.; Yin, X. Research on 3-Vector Model Predictive Control with Low Switching Frequency of Permanent Magnet Synchronous Motor. Trans. China Electrotech. Soc. 2018, 33, 2935–2945. [Google Scholar]
- Xu, Y.; Wang, J.; Zhang, B.; Zhou, Q. Three-Vector-Based Model Predictive Current Control for Permanent Magnet Synchronous Motor. Trans. China Electrote Chnical Soc. 2017, 33, 222–230. [Google Scholar]
- Xu, Y.; Wang, J.; Wang, J.; Zhao, J. Improved Two-vector Model Predictive Current Control Considering Prediction Errors. Electr. Drive 2018, 48, 62–66. [Google Scholar]
- Sangsefidi, Y.; Ziaeinejad, S.; Mehrizi-Sani, A. Low Switching Frequency-Based Predictive Control of a Grid-Connected Voltage-Sourced Converter. IEEE Trans. Energy Convers. 2017, 32, 686–697. [Google Scholar] [CrossRef]
- Feng, L.; Fu, J.; Guo, L.; Li, C. An Improved Low Switching Frequency Model Predictive Direct Torque Control Strategy for Traction Permanent Magnet Synchronous Motor. Proc. CSEE 2021, 41, 7507–7517. [Google Scholar]
- Lin, H.; Wu, X.; Le, S.; Song, W. Model predictive direct torque control of induction motor based on three level optimization vector. Electr. Mach. Control 2018, 22, 65–74. [Google Scholar]
- Wu, X.X.; Song, W.X.; Le, S.K.; Yuan, Y. Model Predictive Direct Current Control of Induction Machines Fed by a Three Level Inverter. Trans. China Electrotech. Soc. 2017, 32, 113–123. [Google Scholar]
- Vijayagopal, M.; Zanchetta, P.; Empringham, L.; De Lillo, L.; Tarisciotti, L.; Wheeler, P. Control of a direct matrix converter with modulated model predictive control. IEEE Trans. Ind. Appl. 2017, 53, 2342–2349. [Google Scholar] [CrossRef]
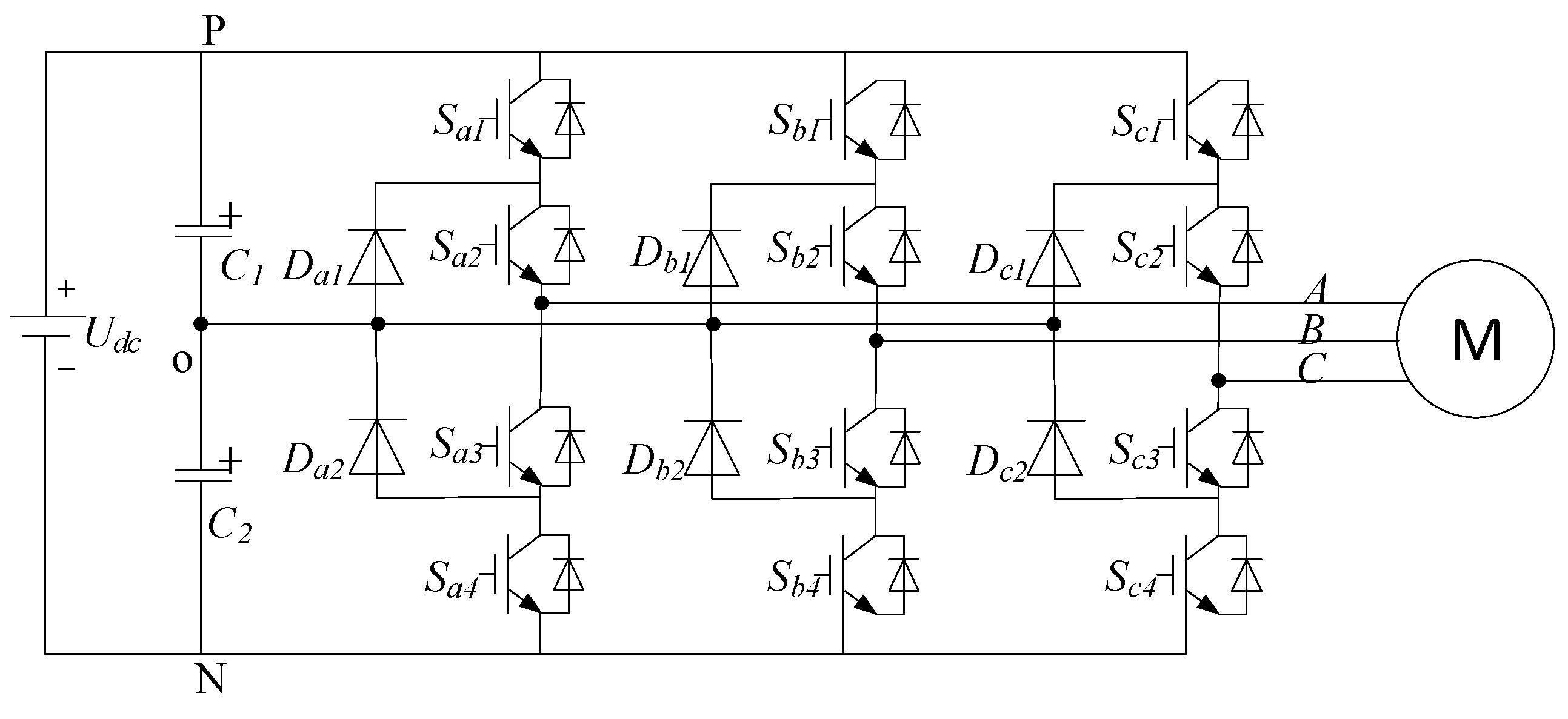





| Voltage | Sa1 | Sa2 | Sa3 | Sa4 | States |
|---|---|---|---|---|---|
| Udc/2 | 1 | 1 | 0 | 0 | P |
| 0 | 0 | 1 | 1 | 0 | O |
| −Udc/2 | 0 | 0 | 1 | 1 | N |
| Type | Switch Status | |ucom| |
|---|---|---|
| Large vector | PNN, NPN, NNP, PPN, NPP, PNP | Vdc/6 |
| Mid vector | PON, OPN, NPO, NPO, ONP, PNO ONN, NON, NNO, PPO, OPP, POP | 0 |
| Small vector | POO, OPO, OOP, OON, NOO, ONO | Vdc/3 |
| Zero vector | OOO PPP, NNN | 0 Vdc/2 |
| Order of Priority | Optimized Content | Indicators |
|---|---|---|
| First layer | Voltage jump limits | Hard bound |
| Second layer | Common-mode voltage rejection | Satisfaction optimization |
| Third layer | Current tracking error | Model prediction |
| Parameters | Numerical Values |
|---|---|
| Stator resistance/Ω | 1.55 |
| Rotor resistance/Ω | 0.692 |
| Stator inductor/H | 0.1384 |
| Rotor inductor/H | 0.1384 |
| Mutual sense/H | 0.133 |
| Polar logarithm | 2 |
| Control Policies | Traditional Single Vector | Non-Weighted-Factor Single Vector | Non-Weighted-Factor Two-Stage Formula |
|---|---|---|---|
| Speed error | 3 | 2 | 0 |
| Torque ripple | ±4 | ±2 | ±1 |
| Voltage transition | Yes | No | No |
| Common-mode voltage | ±180 | ±85 | ±85 |
| Current sinusoidality | Worst | Better | Best |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Li, P.; Wang, Y. Non-Weighted Two-Stage Model Predictive Control Strategy Based on Three-Level NPC Inverter. Energies 2024, 17, 1813. https://doi.org/10.3390/en17081813
Wang G, Li P, Wang Y. Non-Weighted Two-Stage Model Predictive Control Strategy Based on Three-Level NPC Inverter. Energies. 2024; 17(8):1813. https://doi.org/10.3390/en17081813
Chicago/Turabian StyleWang, Guifeng, Peiru Li, and Yu Wang. 2024. "Non-Weighted Two-Stage Model Predictive Control Strategy Based on Three-Level NPC Inverter" Energies 17, no. 8: 1813. https://doi.org/10.3390/en17081813
APA StyleWang, G., Li, P., & Wang, Y. (2024). Non-Weighted Two-Stage Model Predictive Control Strategy Based on Three-Level NPC Inverter. Energies, 17(8), 1813. https://doi.org/10.3390/en17081813






