Current Controller Design of Grid-Connected Inverter with Incomplete Observation Considering L-/LC-Type Grid Impedance
Abstract
1. Introduction
- (i)
- To deal with the negative impact of grid impedance, LC-type grid impedance is considered in both the system model derivation and controller design process of an LCL-filtered GCI system. The proposed scheme ensures the reference tracking of zero steady-state error and good harmonic disturbance compensation of the grid-injected currents. By considering the effect of grid impedance on the control design process, an incomplete state feedback current controller is designed based on the LQR without damaging the asymptotic stabilization and robustness of the GCI system under uncertain grid impedance.
- (ii)
- By means of the closed-loop pole map evaluation, the asymptotic stability, robustness, and resonance-damping capability of the proposed control scheme are confirmed even when all the system states are not available. The proposed control scheme successfully stabilizes the entire GCI system with high-quality grid-injected currents even when the GCI faces severe grid distortions and an extra grid dynamic caused by the L-type or LC-type grid impedance.
- (iii)
- The comprehensive evaluation results show that the designed control scheme maintains the stability and robustness of the LCL-filtered GCI when connecting to unexpected grid such as the harmonic distortion, L-type and LC-type grid impedances. Comparative test result with the conventional one also confirms the effectiveness of the proposed control scheme.
2. System Model of a GCI with LC-Type Grid Impedance
2.1. Modeling of a GCI
2.2. Discrete-Time System Model
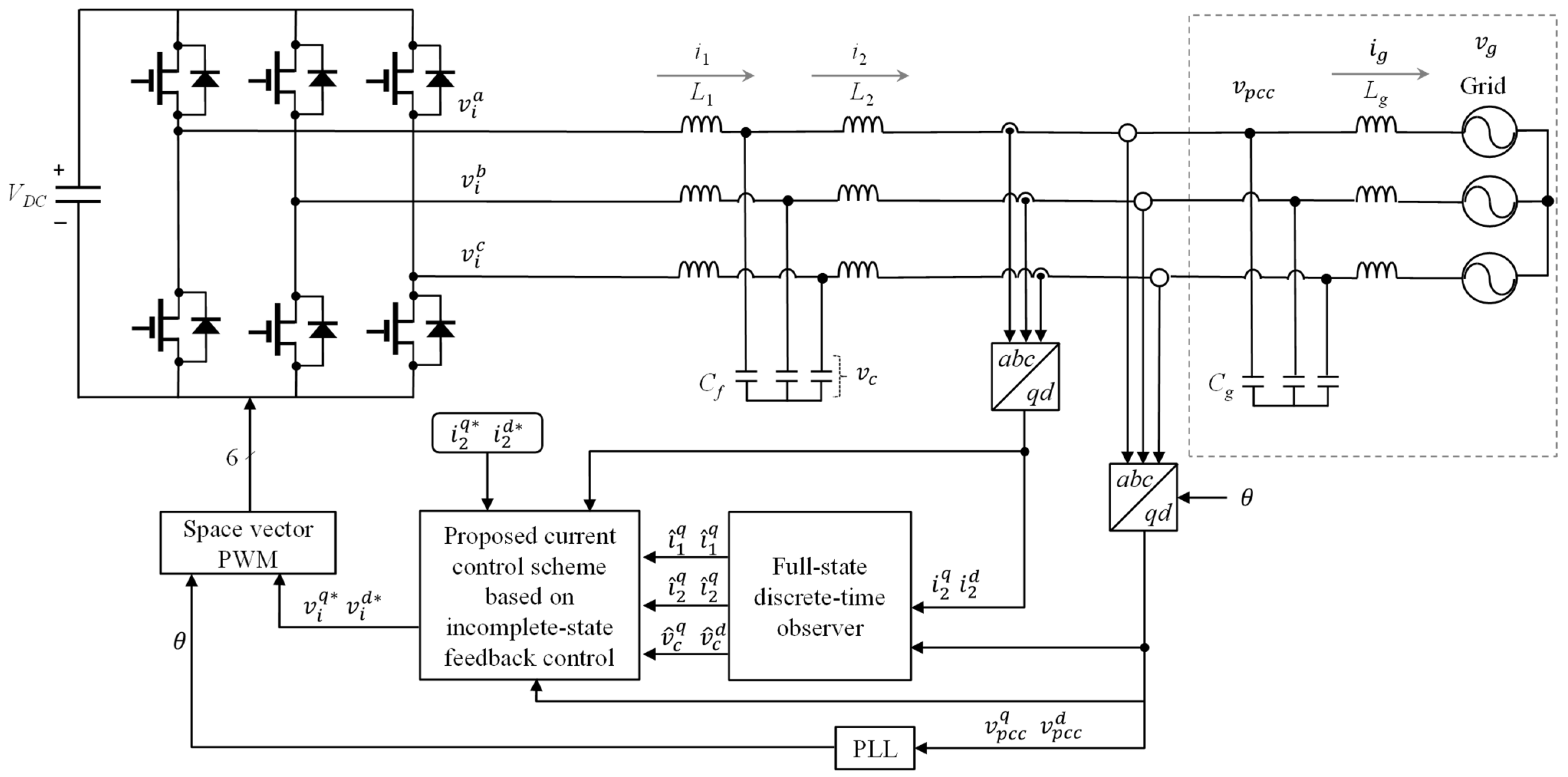
3. Proposed Control Scheme with Incomplete Observation under Grid Uncertainties
3.1. Current Controller Design Considering L-/LC-Type Grid Impedance
3.2. LQR-Based Discrete-Time Observer
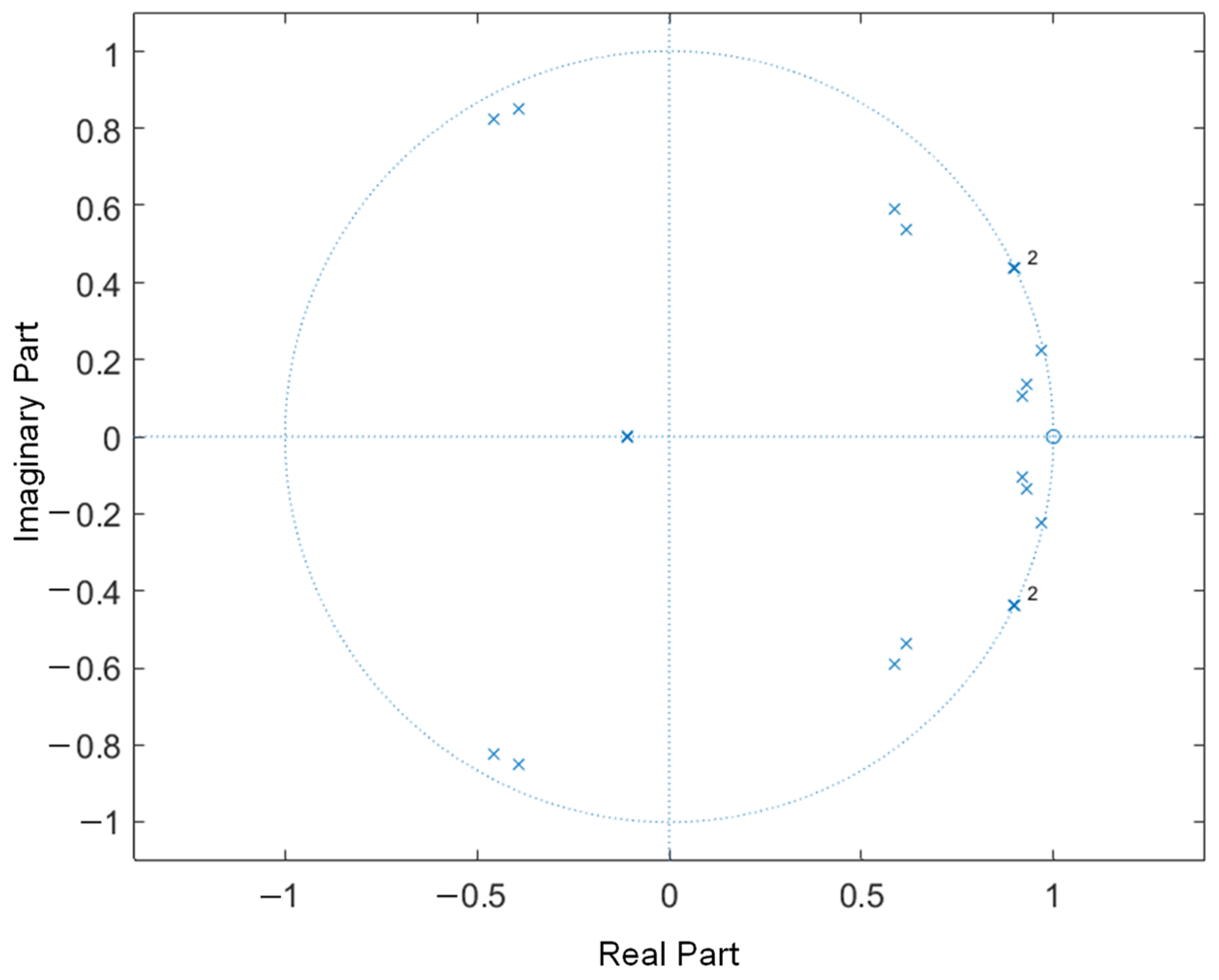
3.3. Stability Analysis Considering Grid Impedance
4. Simulation Results
4.1. Performance under Stiff Grid
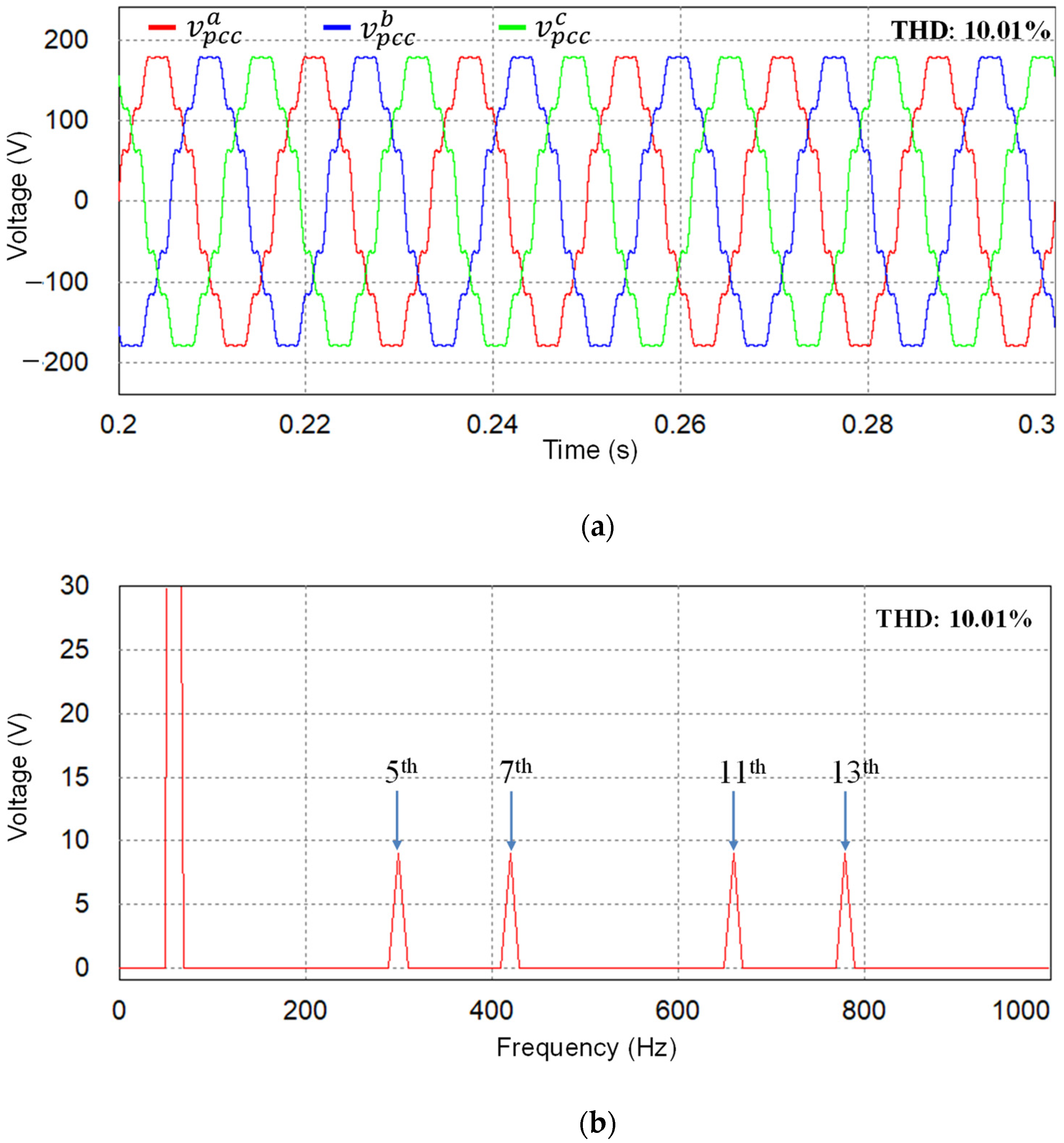
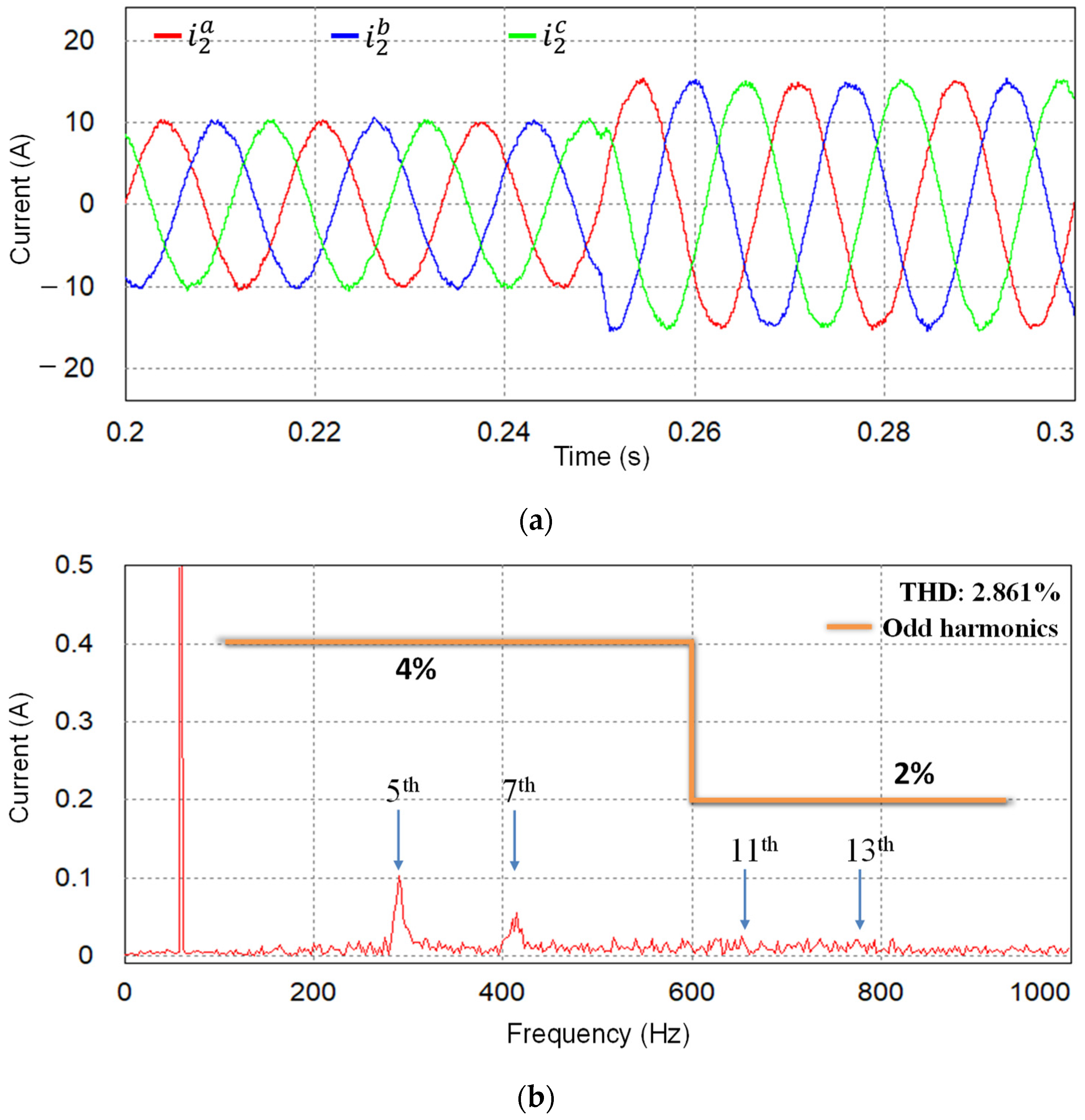
4.2. Performance under Uncertain Grid Impedance
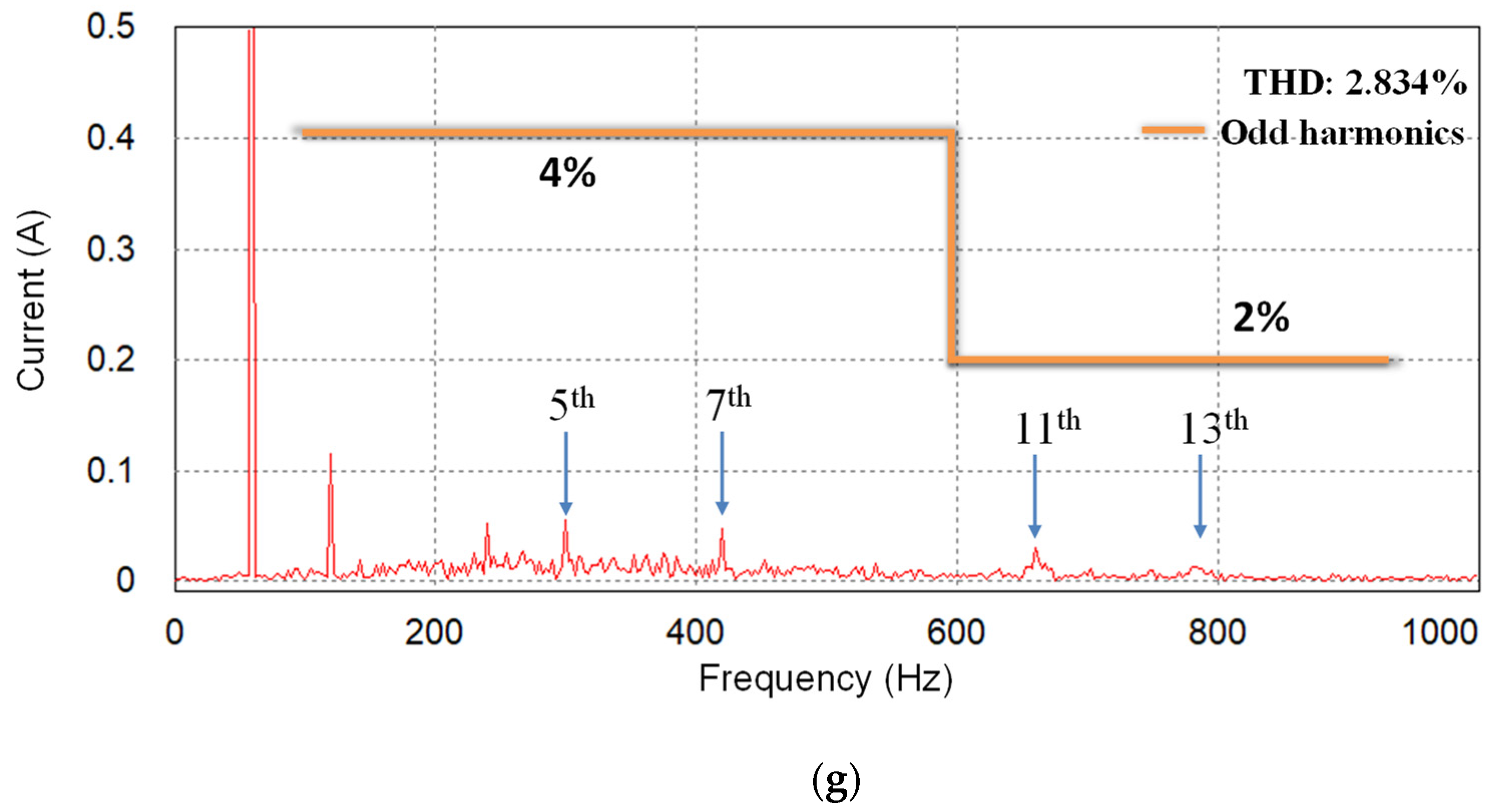
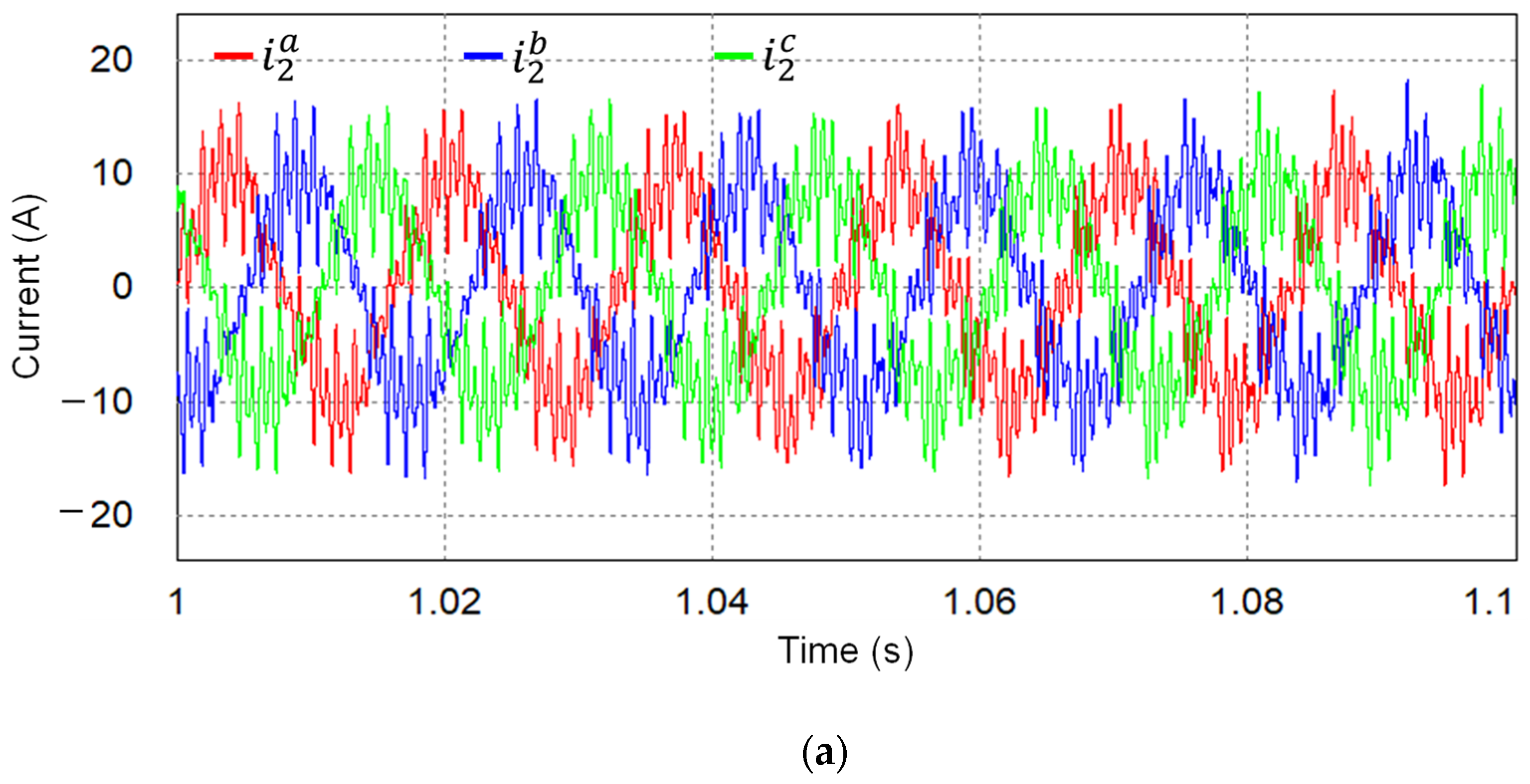
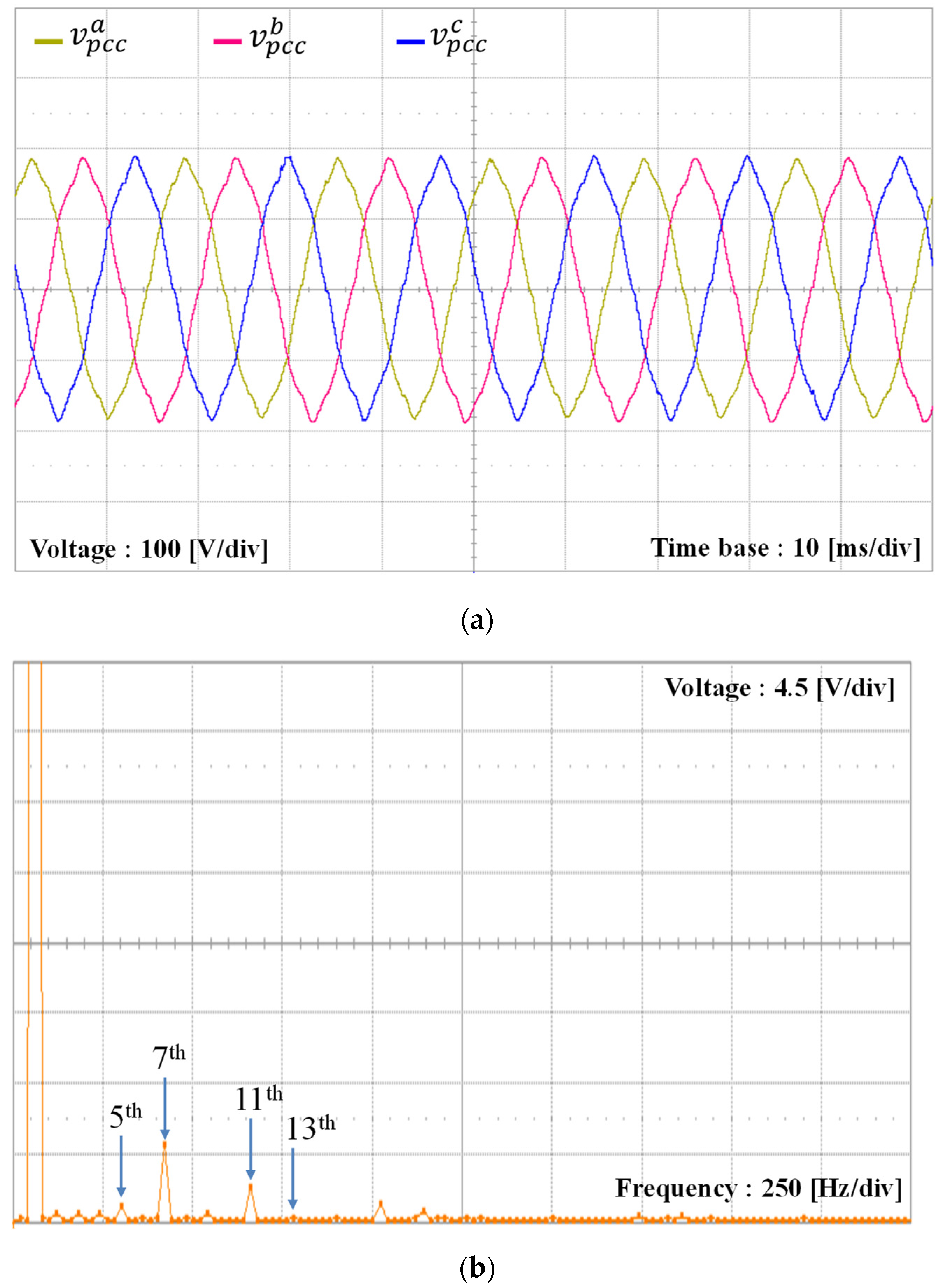
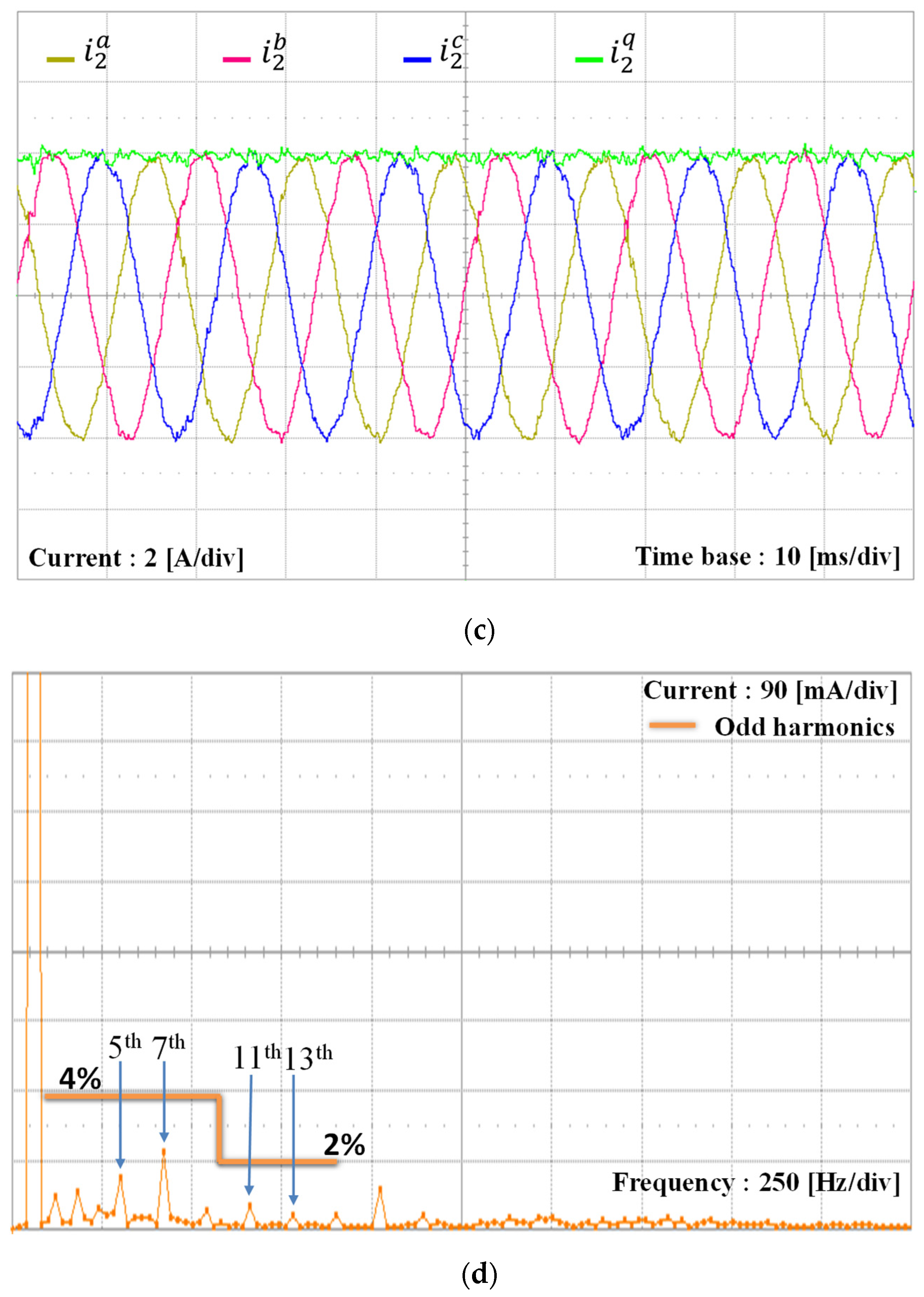
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Filter capacitance | |
| Grid capacitance | |
| Grid voltage vector | |
| Inverter-side current | |
| q-axis inverter-side current | |
| d-axis inverter-side current | |
| , | Grid-side current and reference current |
| , | q-axis grid-side current and reference current |
| , | d-axis grid-side current and reference current |
| Grid inductance current | |
| q-axis grid inductance current | |
| d-axis grid inductance current | |
| Optimal feedback control gain | |
| Incomplete state feedback control gain | |
| Observer gain | |
| Filter inductance | |
| Grid inductance | |
| Positive semi-definite matrix | |
| Positive definite matrix | |
| Reference current vector | |
| Sampling period | |
| System input vector | |
| One-step delay system input vector | |
| Capacitor voltage | |
| q-axis capacitor voltage | |
| d-axis capacitor voltage | |
| DC-link voltage | |
| Utility grid voltage | |
| q-axis utility grid voltage | |
| d-axis utility grid voltage | |
| Inverter output voltage | |
| q-axis inverter output voltage | |
| d-axis inverter output voltage | |
| PCC voltage | |
| q-axis PCC voltage | |
| d-axis PCC voltage | |
| System state vector | |
| Estimated state vector | |
| System output vector | |
| Integral and resonant terms vector | |
| Current error vector | |
| Gird phase angle | |
| Damping ratio | |
| Algular frequency of grid voltage |
References
- Yang, H.; Zhang, Y.; Liang, J.; Gao, J.; Walker, P.D.; Zhang, N. Sliding-mode observer based voltage-sensorless model predictive power control of PWM rectifier under unbalanced grid conditions. IEEE Trans. Ind. Electron. 2017, 65, 5550–5560. [Google Scholar] [CrossRef]
- Rodriguez-Diaz, E.; Freijedo, F.D.; Vasquez, J.C.; Guerrero, J.M. Analysis and comparison of notch filter and capacitor voltage feedforward active damping techniques for LCL grid-connected converters. IEEE Trans. Power Electron. 2018, 34, 3958–3972. [Google Scholar] [CrossRef]
- IEEE Std.1547; IEEE Standard for Interconnecting Distributed Resources with Electric Power Systems. IEEE: New York, NY, USA, 2003.
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and control of an LCL-filter-based three-phase active rectifier. IEEE Trans. Ind. Appl. 2005, 41, 1281–1291. [Google Scholar] [CrossRef]
- Pan, D.; Ruan, X.; Wang, X. Direct realization of digital differentiators in discrete domain for active damping of LCL-type grid-connected inverter. IEEE Trans. Power Electron. 2018, 33, 8461–8473. [Google Scholar] [CrossRef]
- Han, Y.; Yang, M.; Li, H.; Yang, P.; Xu, L.; Coelho, E.A.A.; Guerrero, J.M. Modeling and stability analysis of LCL-Type gridconnected inverters a comprehensive overview. IEEE Access 2019, 7, 114975–115001. [Google Scholar] [CrossRef]
- Li, X.; Wu, X.; Geng, Y.; Yuan, X.; Xia, C.; Zhang, X. Wide damping region for LCL-type grid-connected inverter with an improved capacitor-current-feedback method. IEEE Trans. Power Electron. 2014, 30, 5247–5259. [Google Scholar] [CrossRef]
- Wu, W.; Liu, Y.; He, Y.; Chung, H.S.H.; Liserre, M.; Blaabjerg, F. Damping methods for resonances caused by LCL-filter-based current-controlled grid-tied power inverters: An overview. IEEE Trans. Ind. Electron. 2017, 64, 7402–7413. [Google Scholar] [CrossRef]
- Me, S.P.; Zabihi, S.; Blaabjerg, F.; Bahrani, B. Adaptive virtual resistance for postfault oscillation damping in grid-forming inverters. IEEE Trans. Power Electron. 2022, 37, 3813–3824. [Google Scholar] [CrossRef]
- Kukkola, J.; Hinkkanen, M. Observer-based state-space current control for a three-phase grid-connected converter equipped with an LCL filter. IEEE Trans. Ind. Appl. 2014, 50, 2700–2709. [Google Scholar] [CrossRef]
- Kukkola, J.; Hinkkanen, M.; Zenger, K. Observer-based state-space current controller for a grid converter equipped with an LCL filter: Analytical method for direct discrete-time design. IEEE Trans. Ind. Appl. 2015, 51, 4079–4090. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Liserre, M.; Loh, P.C. Proportional-resonant controllers and filters for grid-connected voltage-source converters. IEE Proc. Electr. Power Appl. 2006, 153, 750–762. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, W.; He, Y.; Lin, Z.; Blaabjerg, F.; Chung, H.S.H. An efficient and robust hybrid damper for LCL or LLCL-based grid-tied inverter with strong grid-side harmonic voltage effect rejection. IEEE Trans. Ind. Electron. 2016, 63, 926–936. [Google Scholar] [CrossRef]
- Tran, T.V.; Yoon, S.-J.; Kim, K.-H. An LQR-based controller design for an LCL-filtered grid-connected inverter in discrete-time state-space under distorted grid environment. Energies 2018, 11, 2062. [Google Scholar] [CrossRef]
- Jia, Y.; Zhao, J.; Fu, X. Direct grid current control of LCL-filtered grid-connected inverter mitigating grid voltage disturbance. IEEE Trans. Power Electron. 2014, 29, 1532–1541. [Google Scholar]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values. IEEE Trans. Power Election. 2006, 21, 263–272. [Google Scholar] [CrossRef]
- Parker, S.G.; McGrath, B.P.; Holmes, D.G. Regions of active damping control for LCL filters. IEEE Trans. Ind. Appl. 2014, 50, 424–432. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Y.; Wang, S.; Chen, J.; Gong, C. Impedance-phased dynamic control method for grid-connected inverters in a weak grid. IEEE Trans. Power Electron. 2017, 32, 274–283. [Google Scholar] [CrossRef]
- Huang, M.; Li, H.; Wu, W.; Blaabjerg, F. Observer-based sliding mode control to improve stability of three-phase LCL-filtered grid-connected VSIs. Energies 2019, 12, 1421. [Google Scholar] [CrossRef]
- Nam, N.N.; Nguyen, N.-D.; Yoon, C.; Lee, Y.I. Disturbance observer-based robust model predictive control for a voltage sensorless grid-connected inverter with an LCL filter. IEEE Access 2021, 9, 109793–109805. [Google Scholar] [CrossRef]
- Yoon, S.-J.; Kim, K.-H. Harmonic suppression and stability enhancement of a voltage sensorless current controller for a grid-connected inverter under weak grid. IEEE Access 2022, 10, 38575–38589. [Google Scholar] [CrossRef]
- Kim, Y.B.; Tran, T.V.; Kim, K.-H. LMI-based model predictive current control for an LCL-filtered grid-connected inverter under unexpected grid and system uncertainties. Electronics 2022, 11, 731. [Google Scholar] [CrossRef]
- Wang, J.; Yao, J.; Hu, H.; Xing, Y.; He, X.; Sun, K. Impedance-based stability analysis of single-phase inverter connected to weak grid with voltage feed-forward control. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 2182–2186. [Google Scholar]
- Qian, Q.; Xie, S.; Xu, J.; Ji, L. Harmonic suppression and stability improvement for aggregated current-controlled inverters. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–5. [Google Scholar]
- Harnefors, L.; Finger, R.; Wang, X.; Bai, H.; Blaabjerg, F. VSC input-admittance modeling and analysis above the Nyquist frequency for passivity-based stability assessment. IEEE Trans. Ind. Electron. 2017, 64, 6362–6370. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Loh, P.C. Passivity-based stability analysis and damping injection for multi-paralleled voltage-source converters with LCL filters. IEEE Trans. Power Electron. 2017, 32, 8922–8935. [Google Scholar] [CrossRef]
- Qian, Q.; Xu, J.; Ni, Z.; Zeng, B.; Zhang, Z.; Xie, S. Passivity-based output impedance shaping of LCL-filtered grid-connected inverters for suppressing harmonics and instabilities in complicated grid. In Proceedings of the 2017 IEEE Southern Power Electronics Conference (SPEC), Puerto Varas, Chile, 4–7 December 2017; pp. 1–6. [Google Scholar]
- Lichota, P.; Dul, F.; Karbowski, A. System identification and LQR controller design with incomplete state observation for aircraft trajectory tracking. Energies 2020, 13, 5354. [Google Scholar] [CrossRef]
- Franklin, G.F.; Powell, J.D.; Workman, M.L. Digital Control of Dynamic Systems; Addison-Wesley: Menlo Park, CA, USA, 1998; Volume 3. [Google Scholar]
- Patarroyo-Montenegro, J.F.; Vasquez-Plaza, J.D.; Andrade, F. A state-space model of an inverter-based microgrid for multivariable feedback control analysis and design. Energies 2020, 13, 3279. [Google Scholar] [CrossRef]
- Maccari, L.; Massing, J.; Schuch, L.; Rech, C.; Pinheiro, H.; Oliveira, R.; Montagner, V. LMI-based control for grid-connected converters with LCL filters under uncertain parameters. IEEE Trans. Power Electron. 2014, 29, 3776–3785. [Google Scholar] [CrossRef]
- Phillips, C.L.; Nagle, H.T. Digital Control System Analysis and Design, 3rd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Ogata, K. Discrete Time Control Systems, 2nd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]

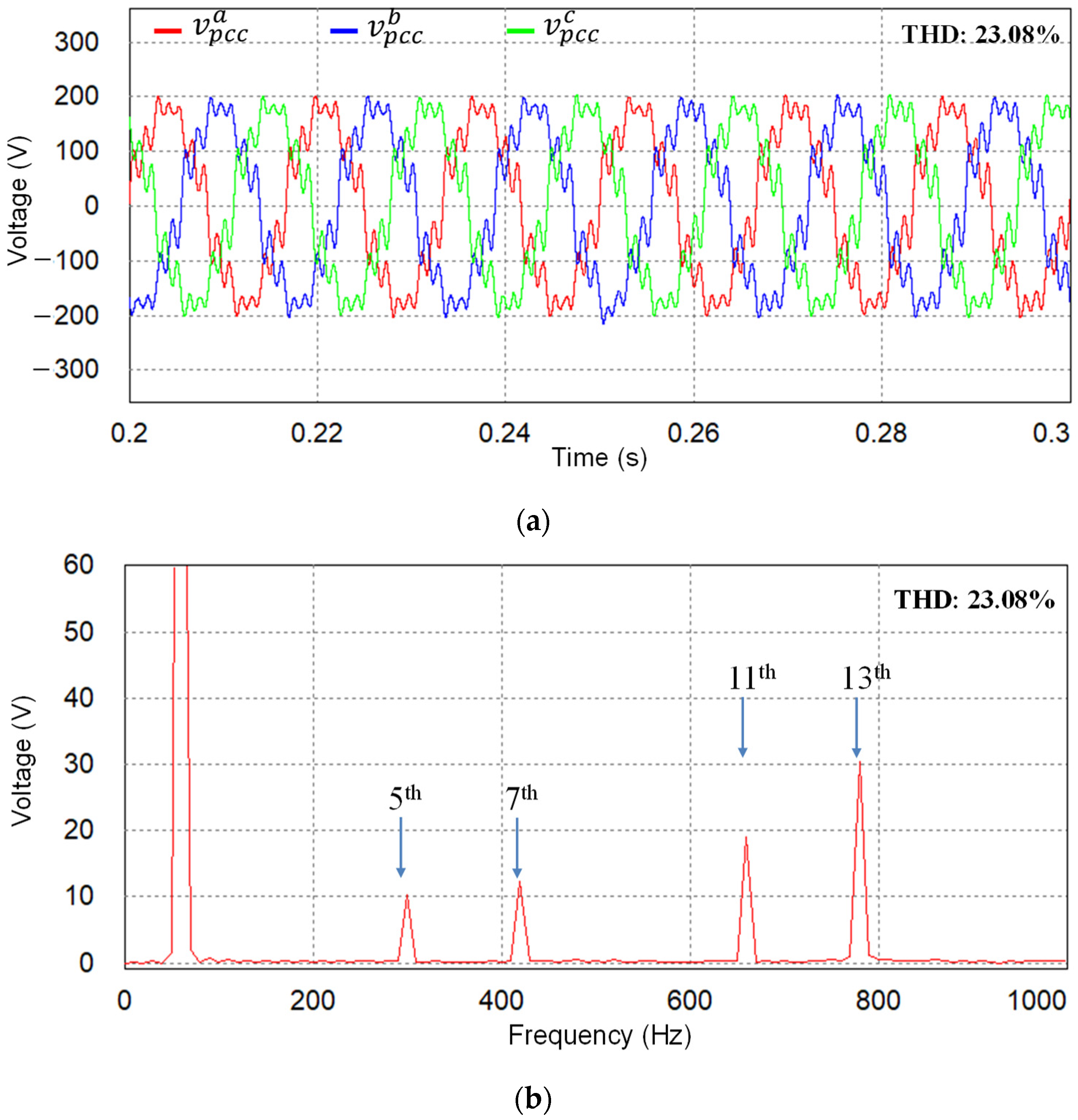
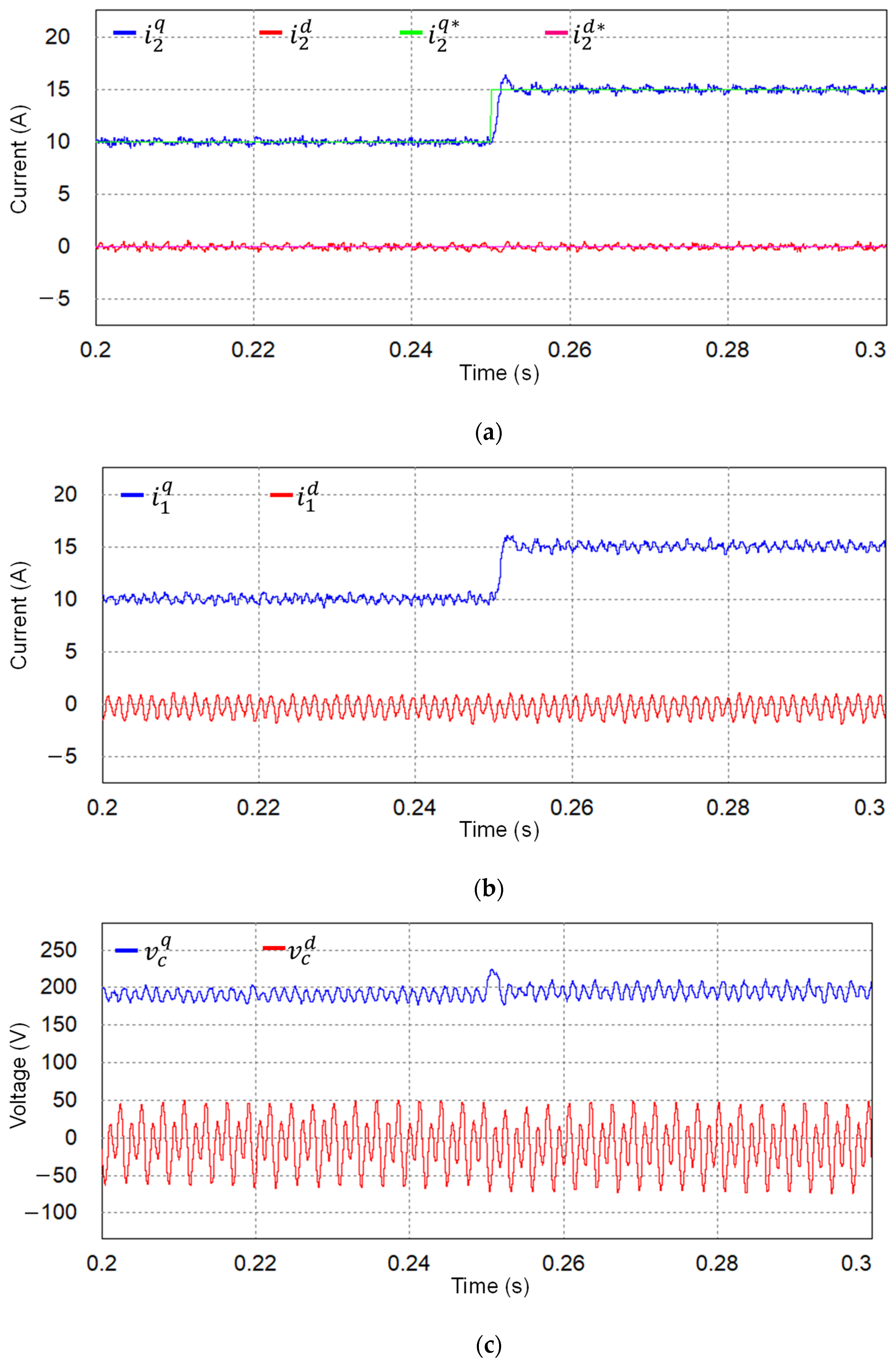
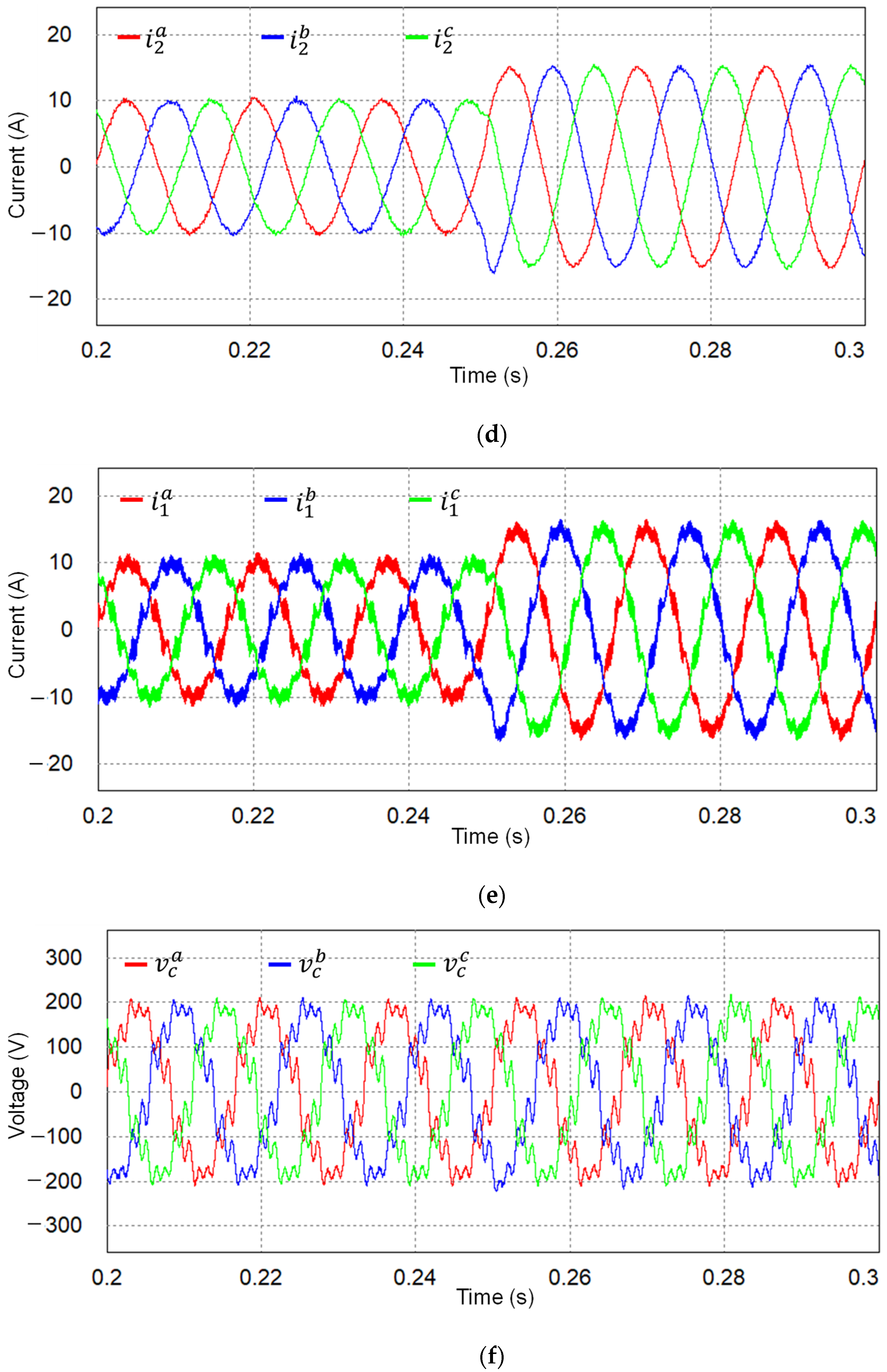
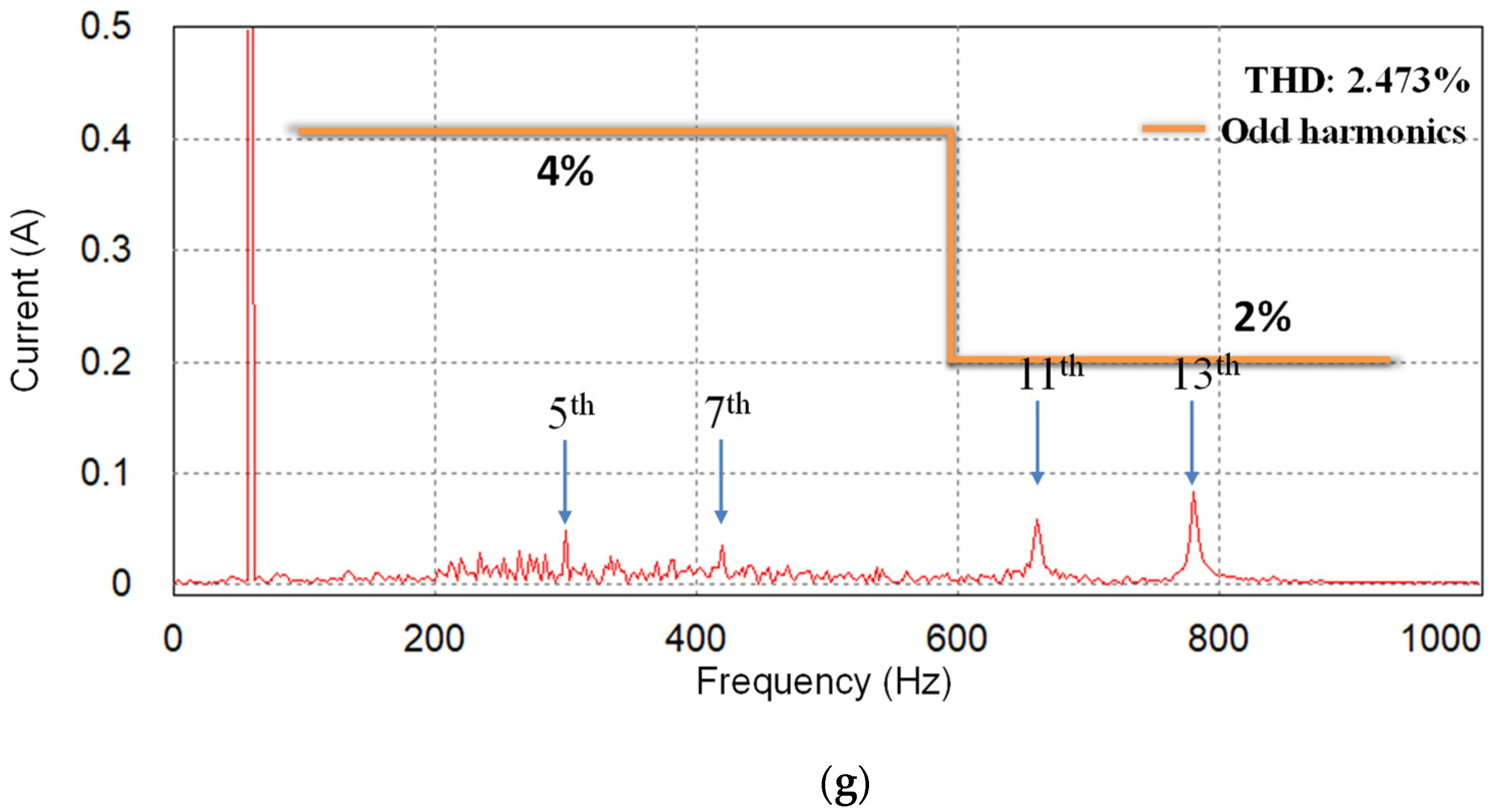
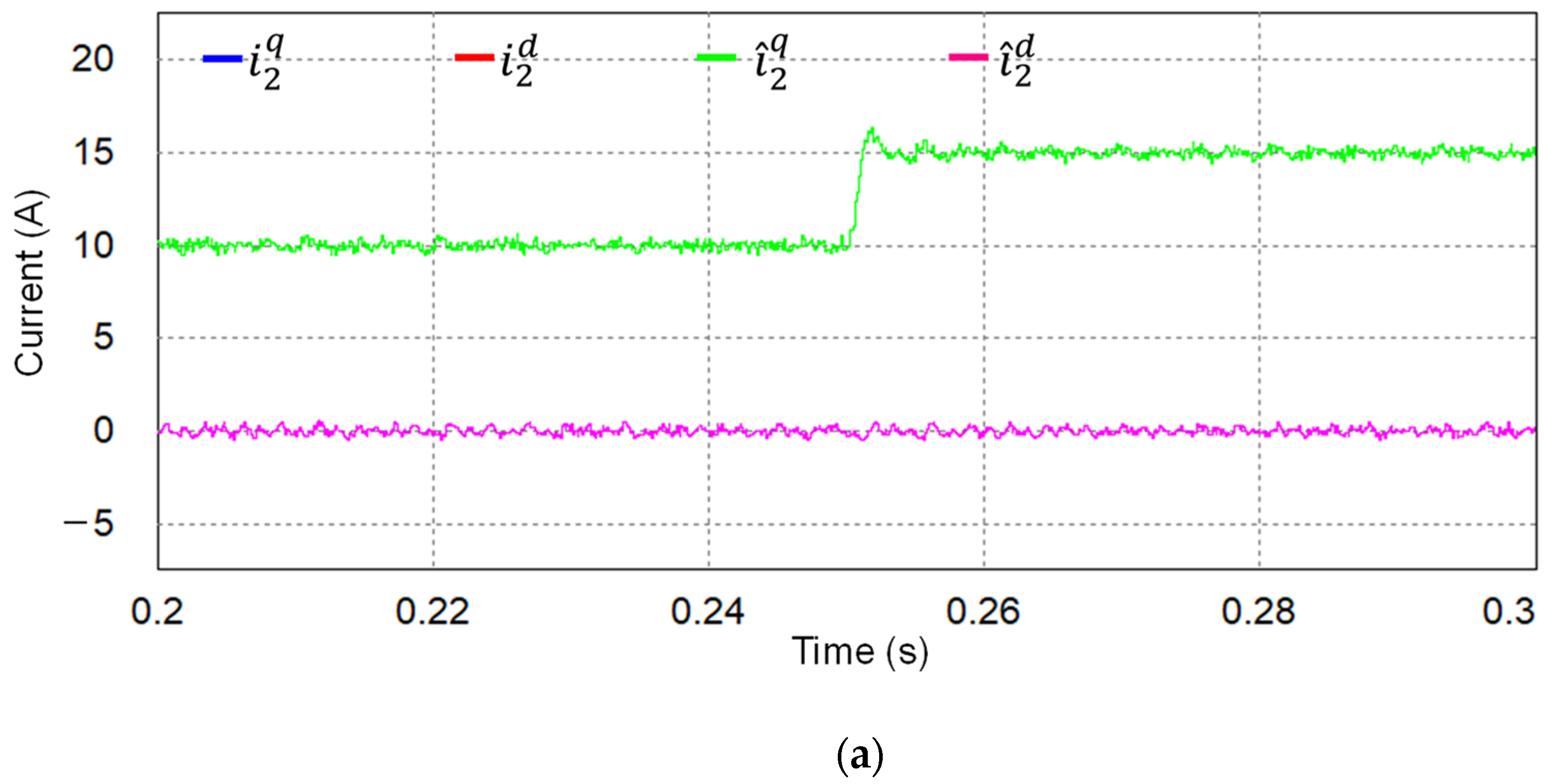
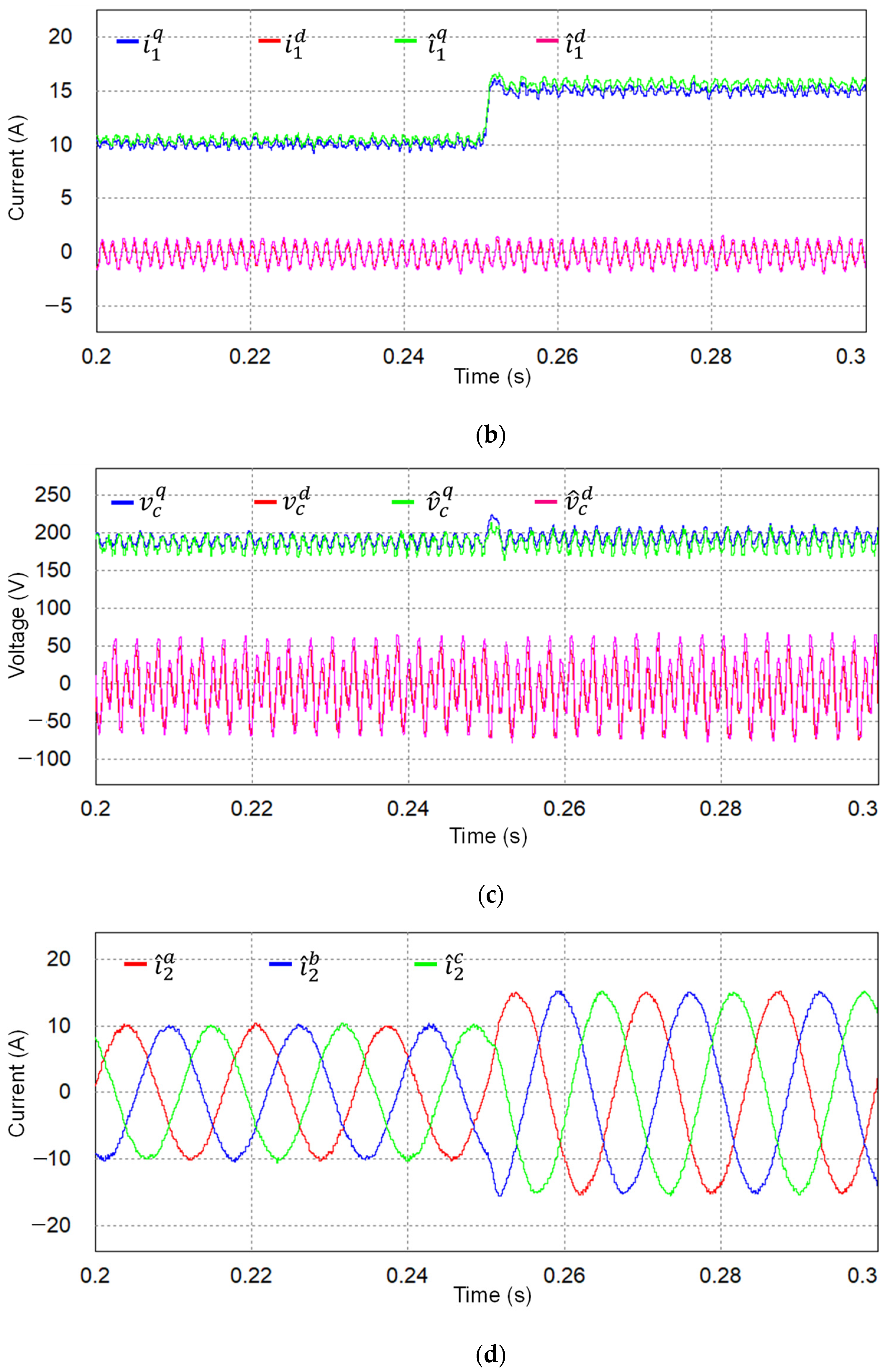
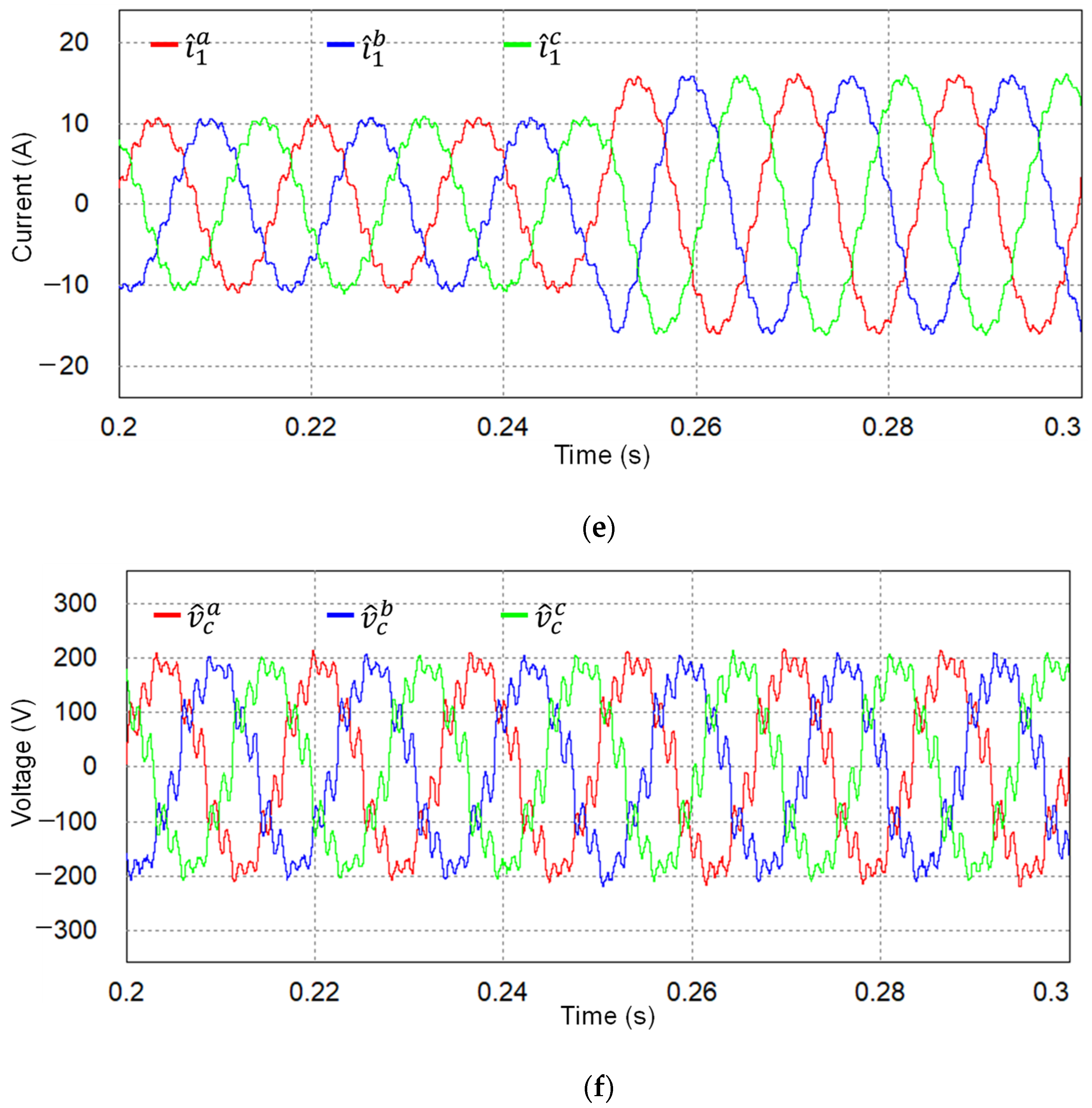

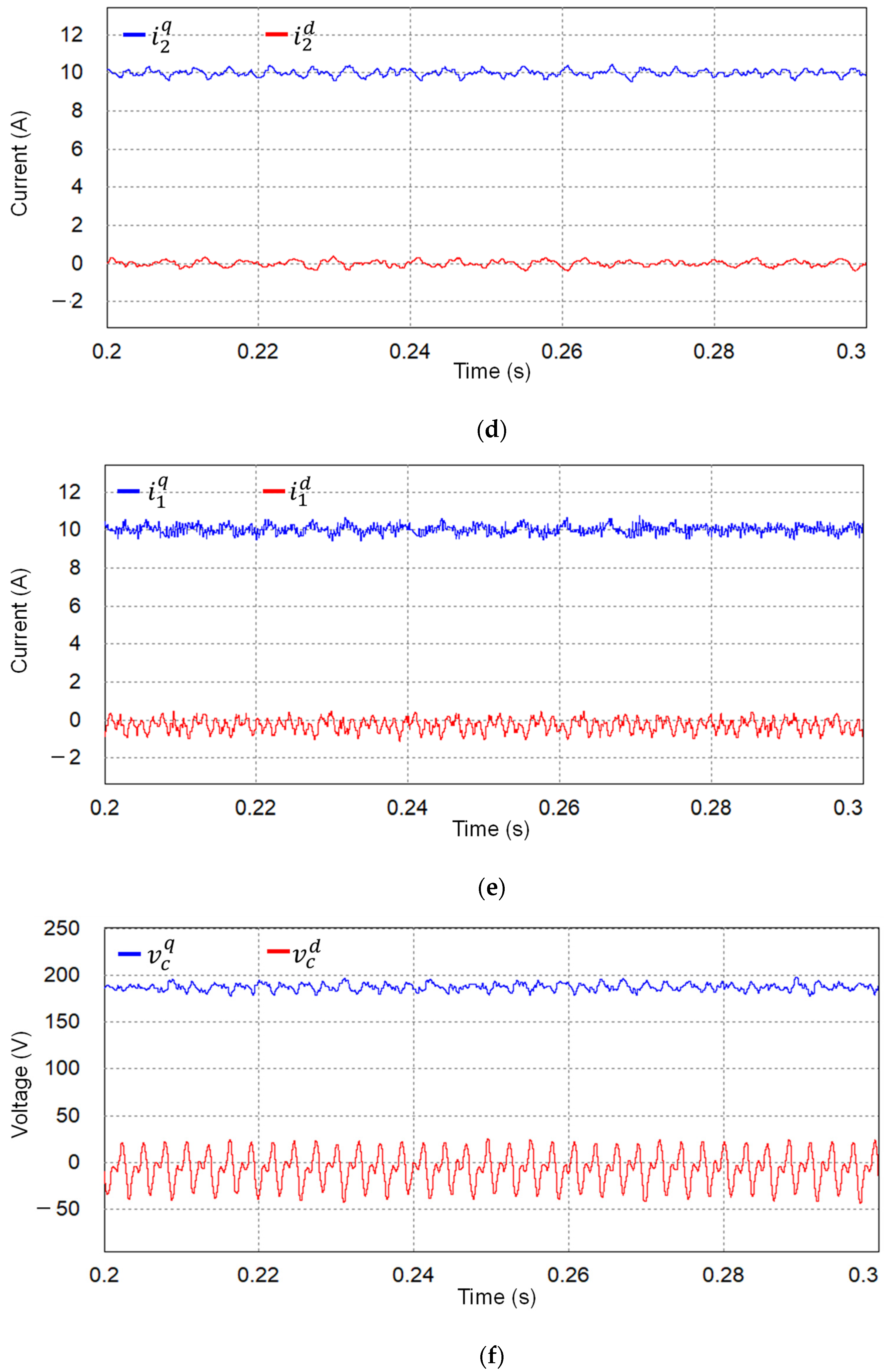


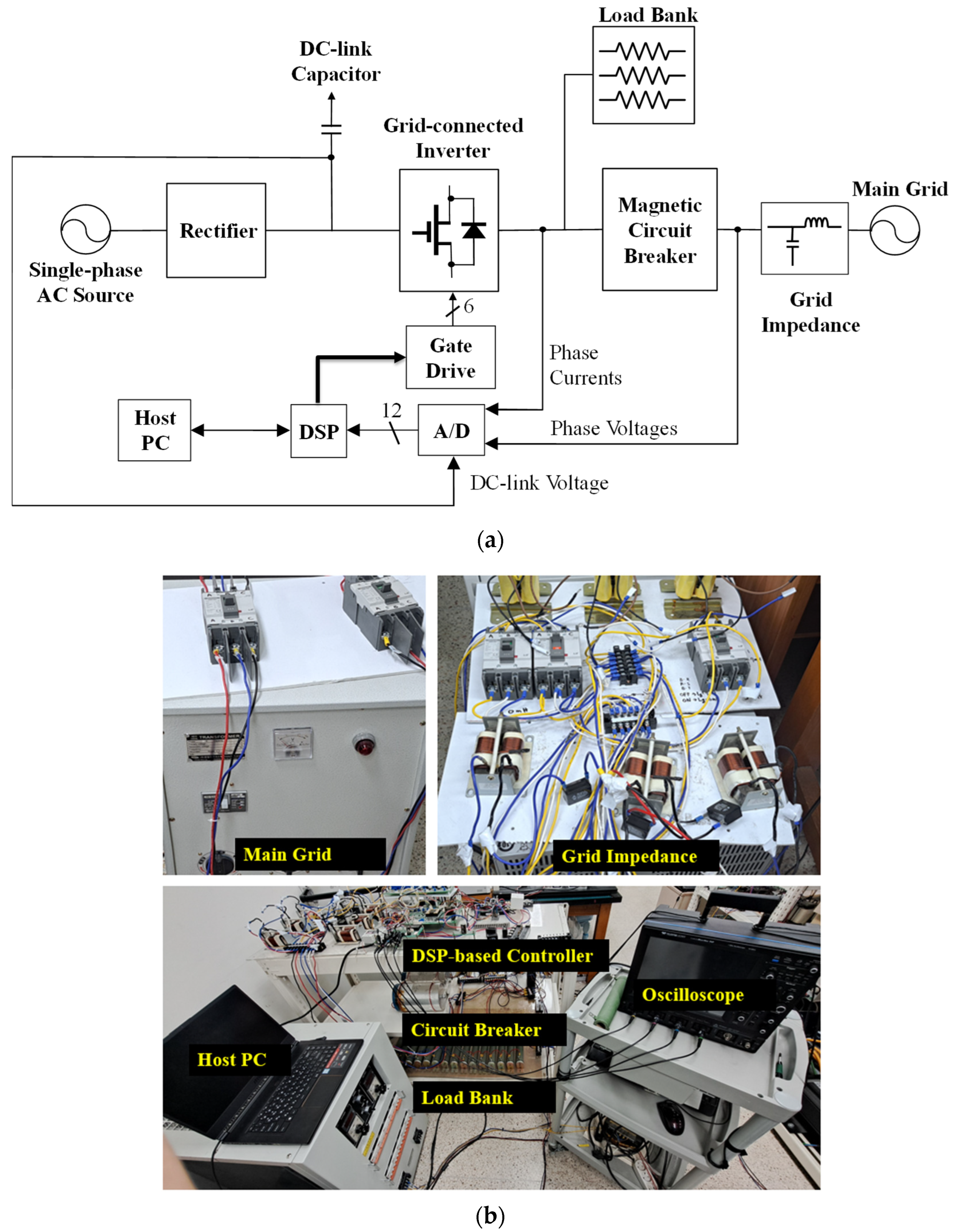

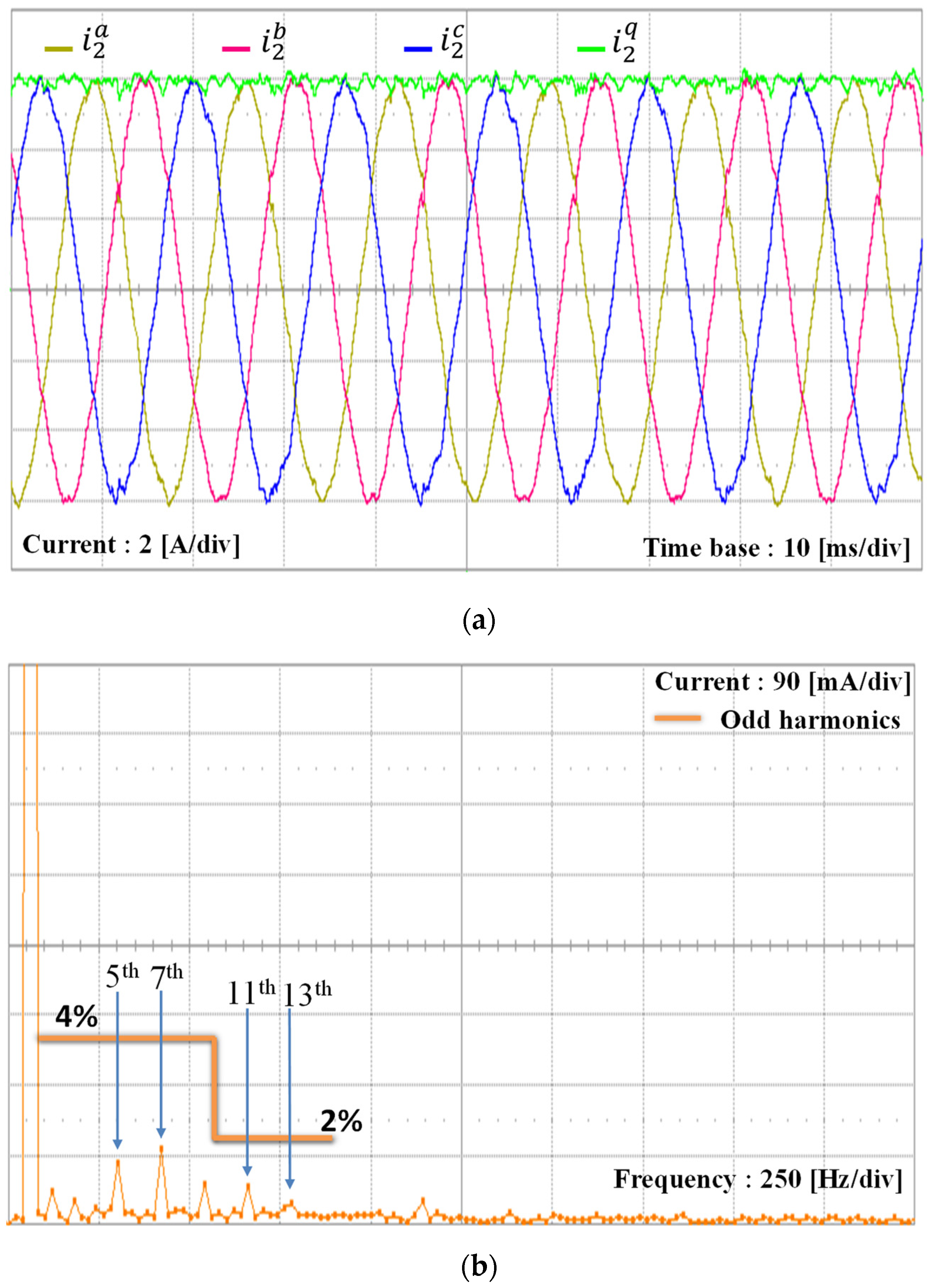
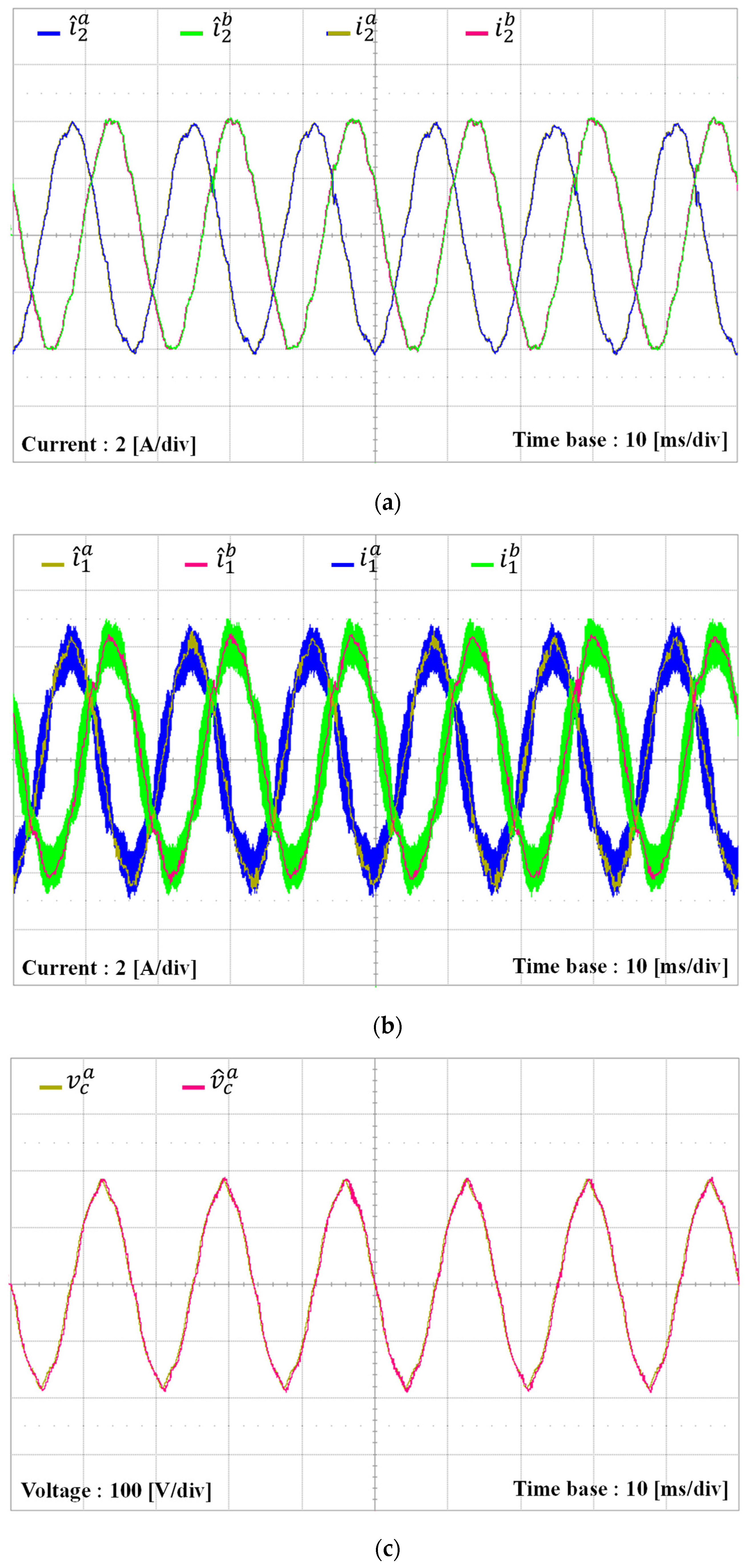

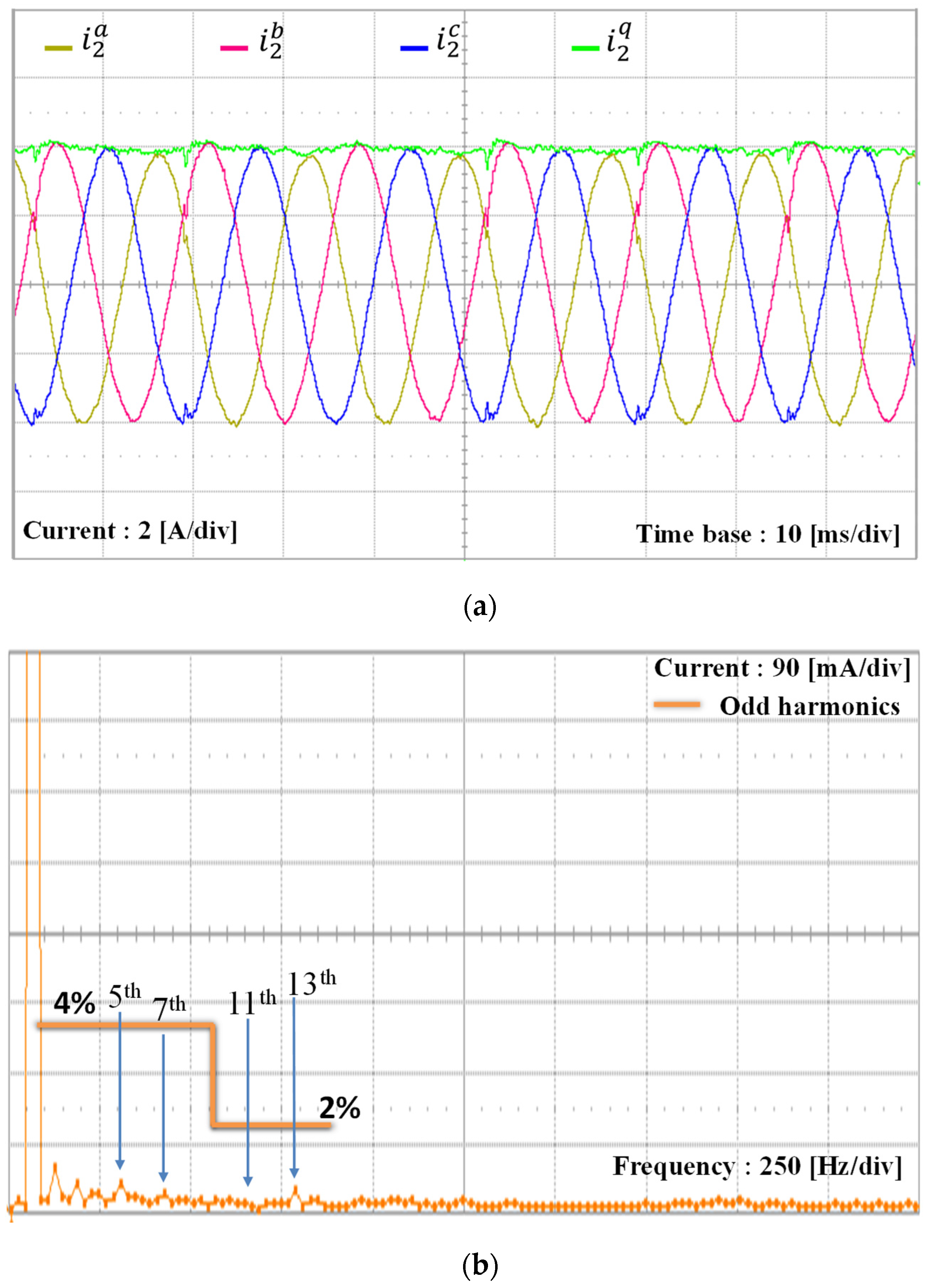
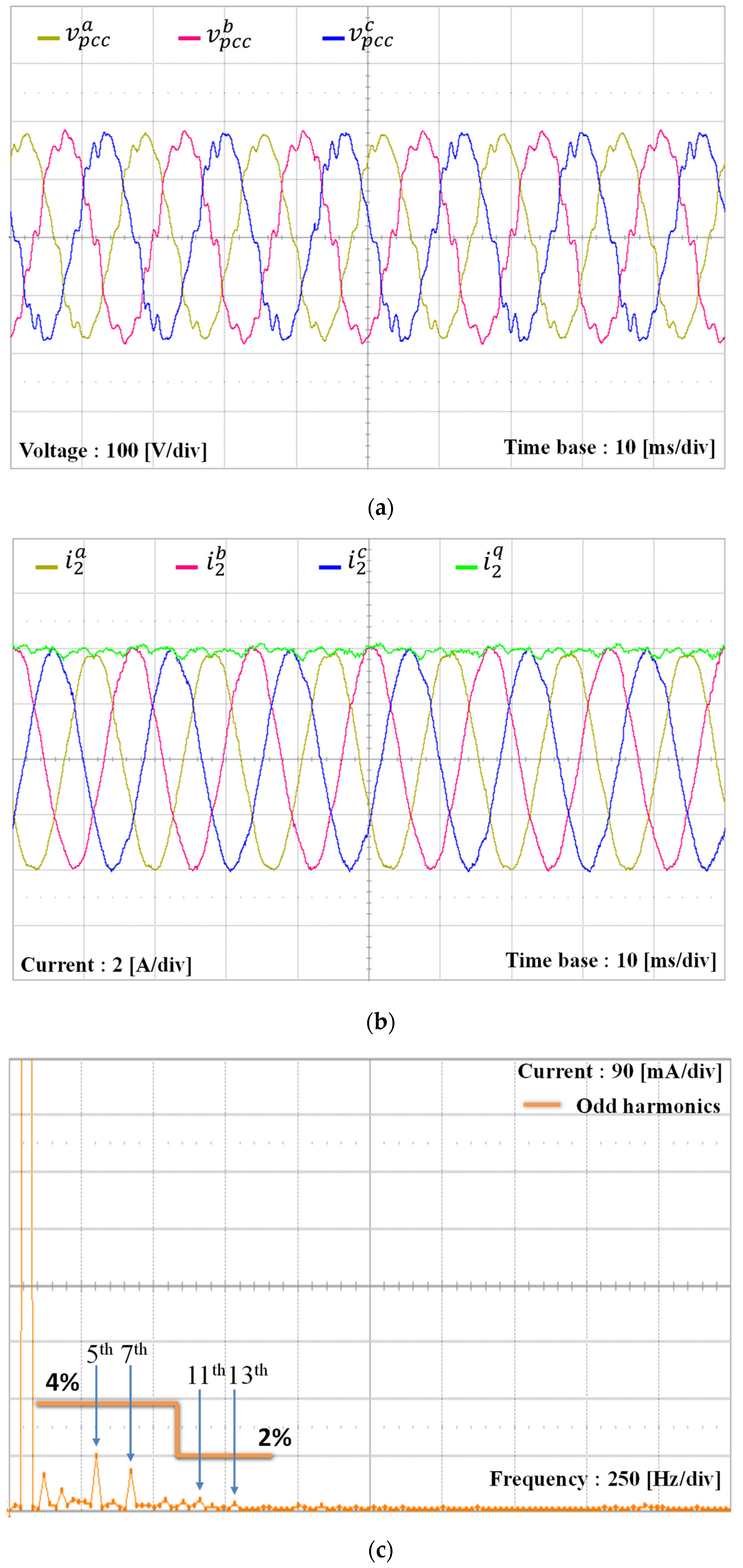
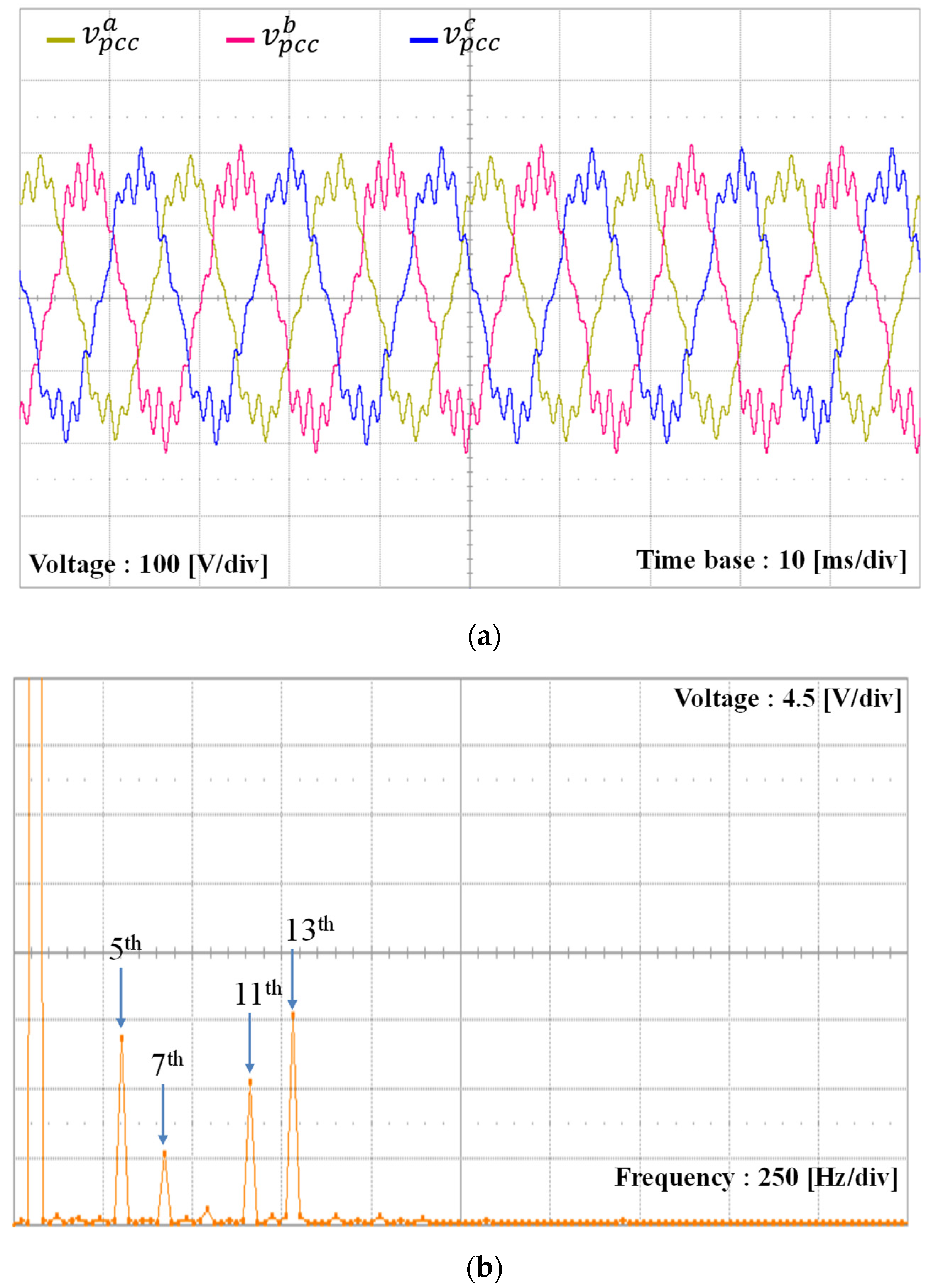
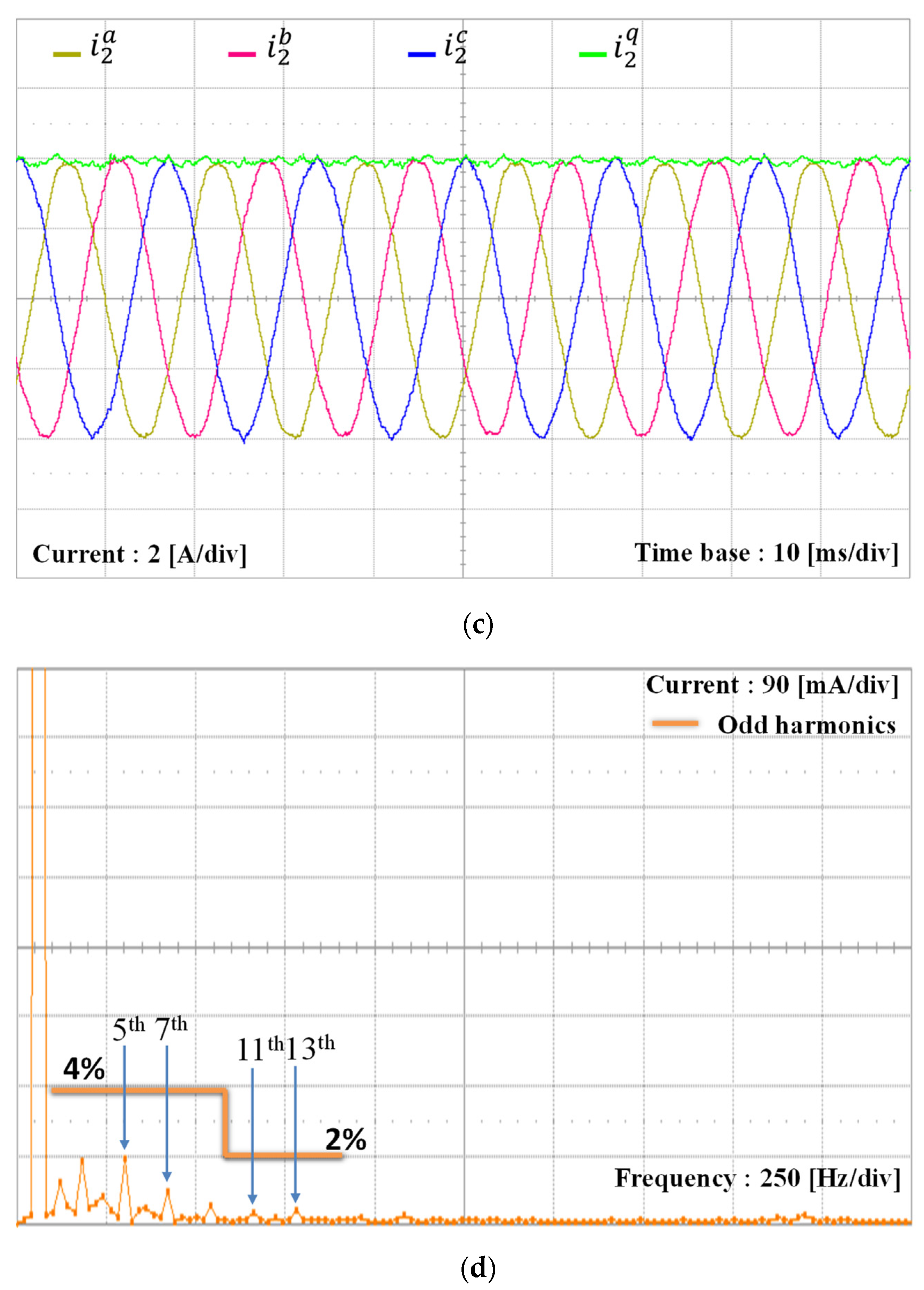
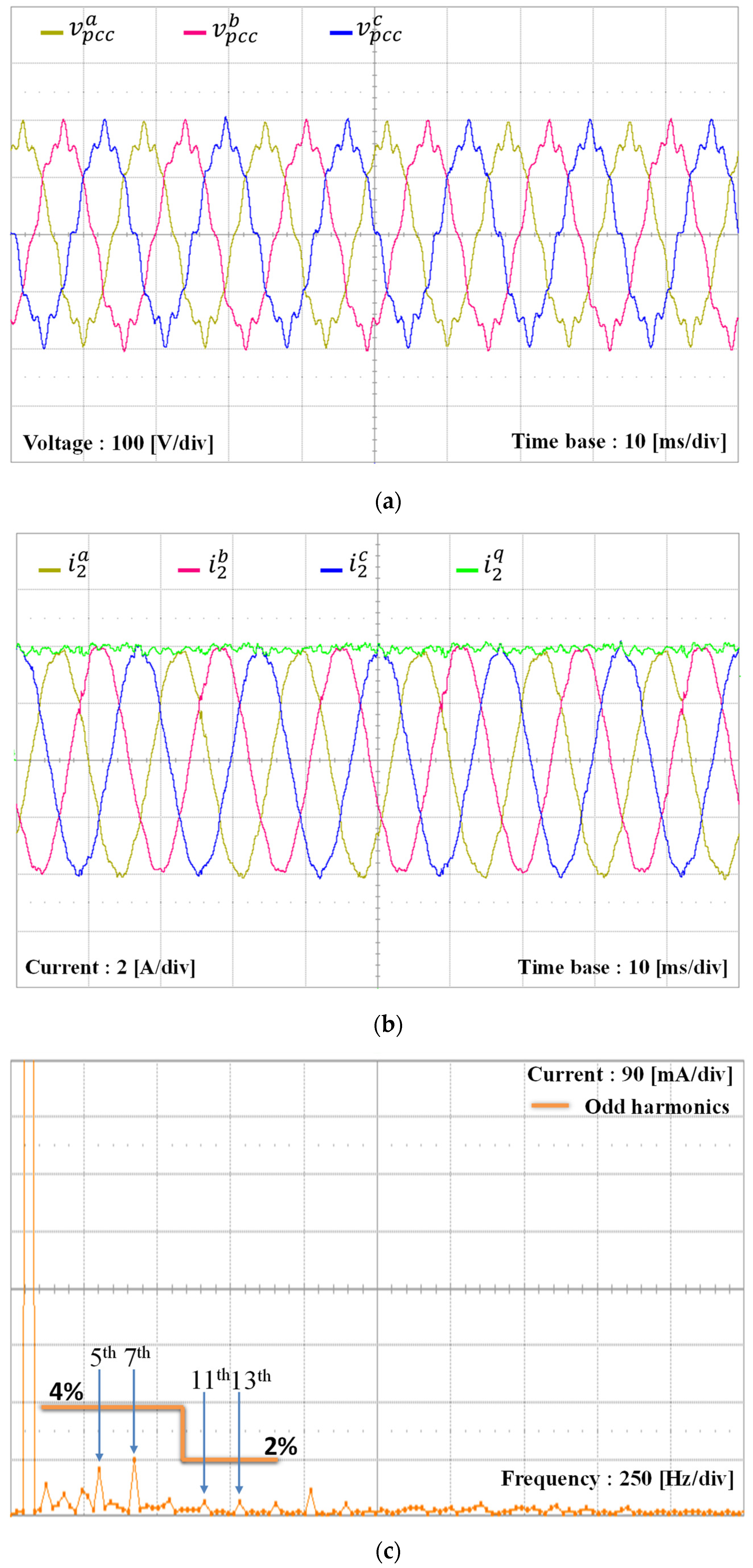
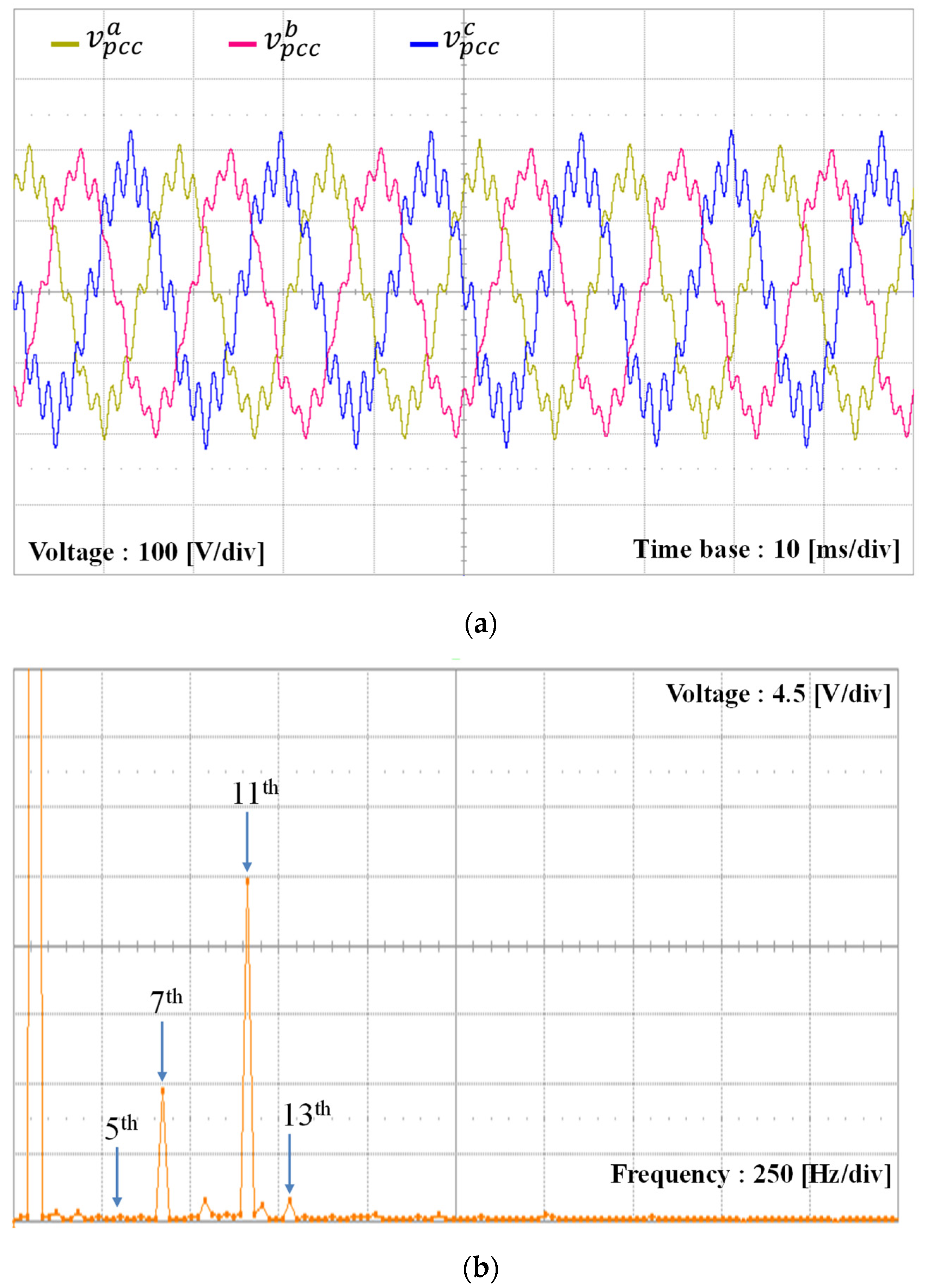
| Parameters | Value | Units |
|---|---|---|
| DC-link voltage | 420 | V |
| Resistance | 24 | Ω |
| Filter resistance | 0.5 | Ω |
| Filter capacitance | 4.5 | µF |
| Grid capacitance | 8–10 | µF |
| Grid inductance | 3–7 | mH |
| Inverter-side filter inductance | 1.7 | mH |
| Grid-side filter inductance | 1 | mH |
| Grid voltage (line-to line rms) | 220 | V |
| Grid frequency | 60 | Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-D.; Tran, T.V.; Yoon, S.-J.; Kim, K.-H. Current Controller Design of Grid-Connected Inverter with Incomplete Observation Considering L-/LC-Type Grid Impedance. Energies 2024, 17, 1855. https://doi.org/10.3390/en17081855
Kim S-D, Tran TV, Yoon S-J, Kim K-H. Current Controller Design of Grid-Connected Inverter with Incomplete Observation Considering L-/LC-Type Grid Impedance. Energies. 2024; 17(8):1855. https://doi.org/10.3390/en17081855
Chicago/Turabian StyleKim, Sung-Dong, Thuy Vi Tran, Seung-Jin Yoon, and Kyeong-Hwa Kim. 2024. "Current Controller Design of Grid-Connected Inverter with Incomplete Observation Considering L-/LC-Type Grid Impedance" Energies 17, no. 8: 1855. https://doi.org/10.3390/en17081855
APA StyleKim, S.-D., Tran, T. V., Yoon, S.-J., & Kim, K.-H. (2024). Current Controller Design of Grid-Connected Inverter with Incomplete Observation Considering L-/LC-Type Grid Impedance. Energies, 17(8), 1855. https://doi.org/10.3390/en17081855







