Multi-Objective Optimization of Blockage Design Parameters Affecting the Performance of PEMFC by OEM-AHP-EWM Analysis
Abstract
:1. Introduction
2. Models
2.1. Physical Model
2.2. Numerical Model
2.2.1. Governing Equations
- (1)
- The PEMFC model was considered to operate under non-isothermal, steady-state conditions.
- (2)
- The gas mixtures were treated as incompressible and conform to ideal gas.
- (3)
- The flow of inlet reactants within the channel was presumed to be laminar.
- (4)
- The impact of gravity was disregarded.
- (5)
- Porous materials were assumed to possess homogeneous and isotropic properties.
2.2.2. Boundary Conditions
2.3. Model Validation and Grid Independence Test
2.3.1. Model Validation
2.3.2. Mesh Validation
3. Research Methods
3.1. OEM Introduction
3.2. AHP Introduction
3.3. EWM Introduction
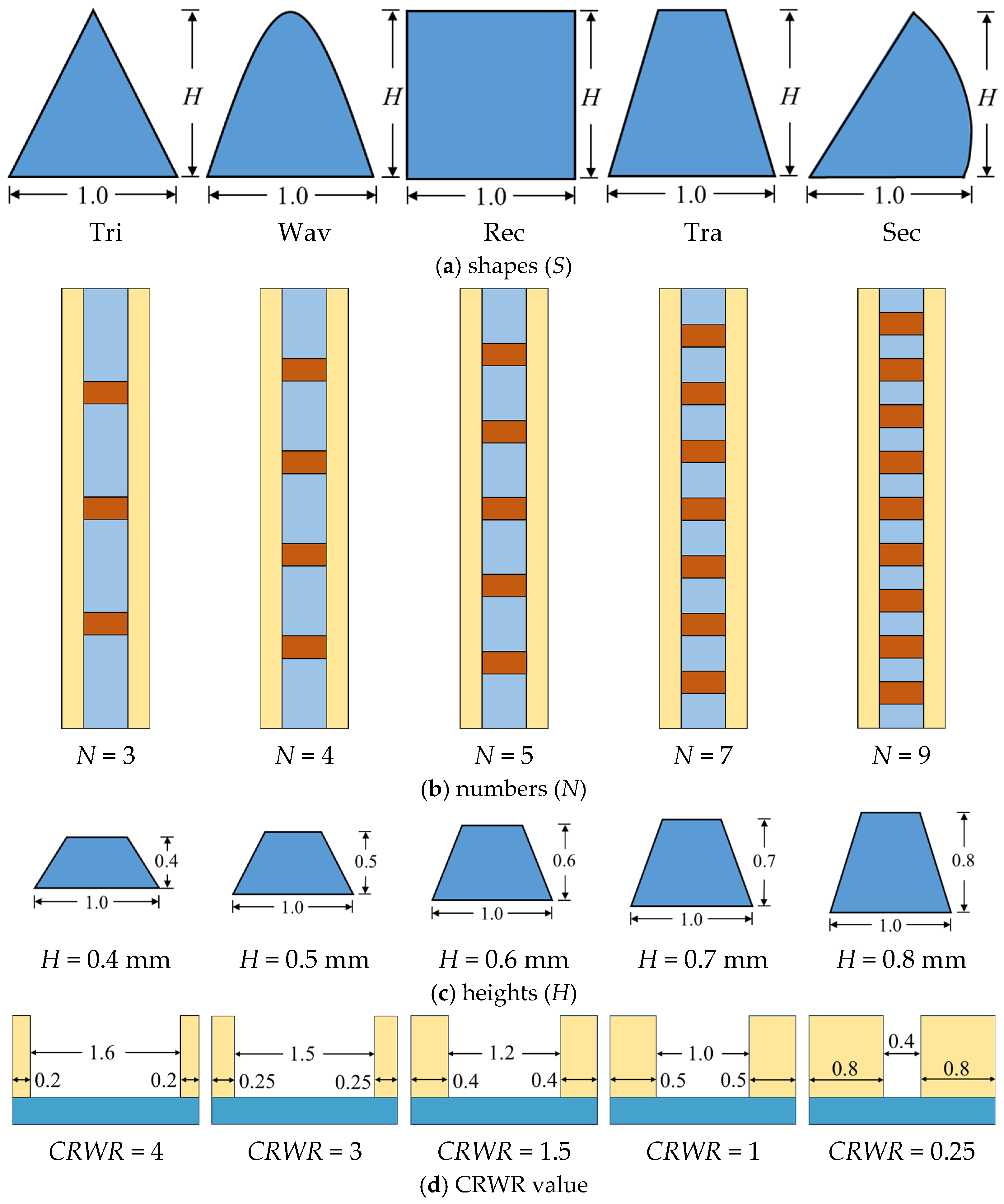
3.4. Evaluation Objectives
4. Results and Discussion
4.1. Data Acquisition by OEM
4.2. Analyses of AHP and EWM
4.2.1. Weights Calculation Using AHP
- (1)
- Construct and normalize the data judgment matrix
- (2)
- Calculate weights of evaluation objectives
- (3)
- Consistency checking
4.2.2. Weights Calculation Using EWM
- (1)
- Construct and normalize the original data matrix
- (2)
- Calculate the Ej and dj for each criterion
- (3)
- Calculate the Wj for each criterion
4.2.3. Determination of Comprehensive Weights by AHP-EWM
4.3. Analysis of ANOR and ANOVA
5. Conclusions
- (1)
- The AHP-EWM analysis revealed that current density (I) and net output power (Wnet) are the most critical factors in PEMFC performance evaluation, with weights of 0.415 and 0.325, respectively. In contrast, the weights assigned to pressure drop (ΔP) and non-uniformity of oxygen distribution (NU) were 0.08 and 0.18, emphasizing the dominant role of current density in the overall performance evaluation.
- (2)
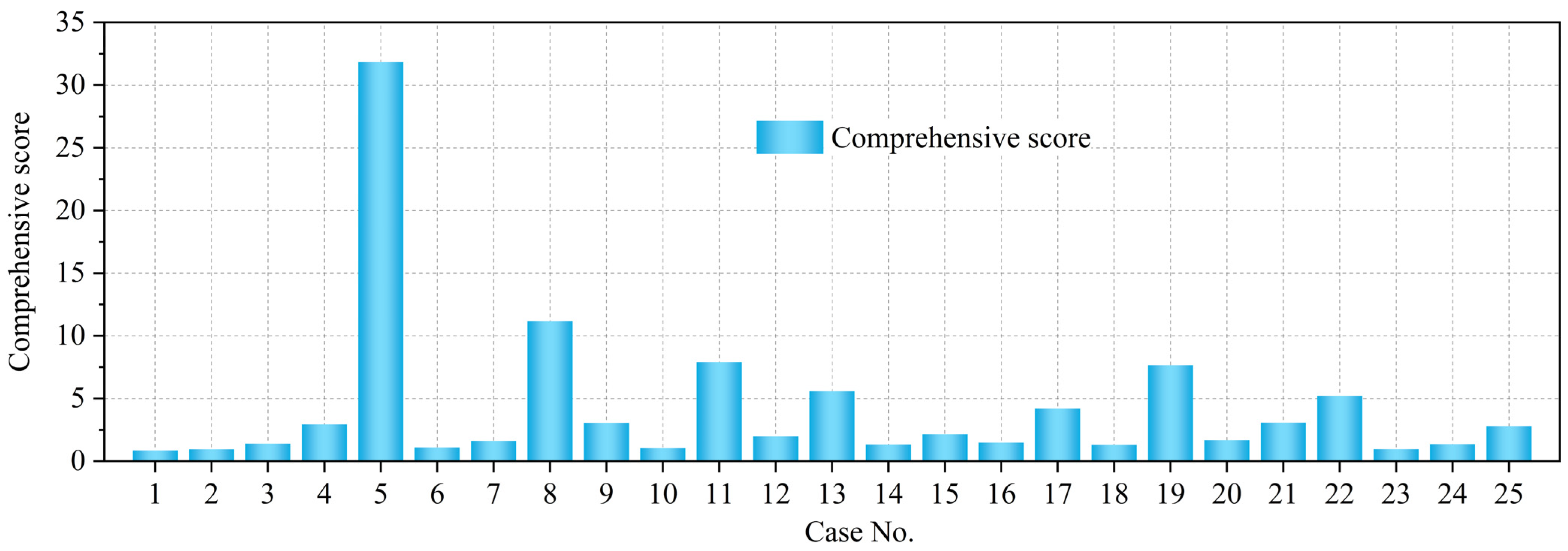
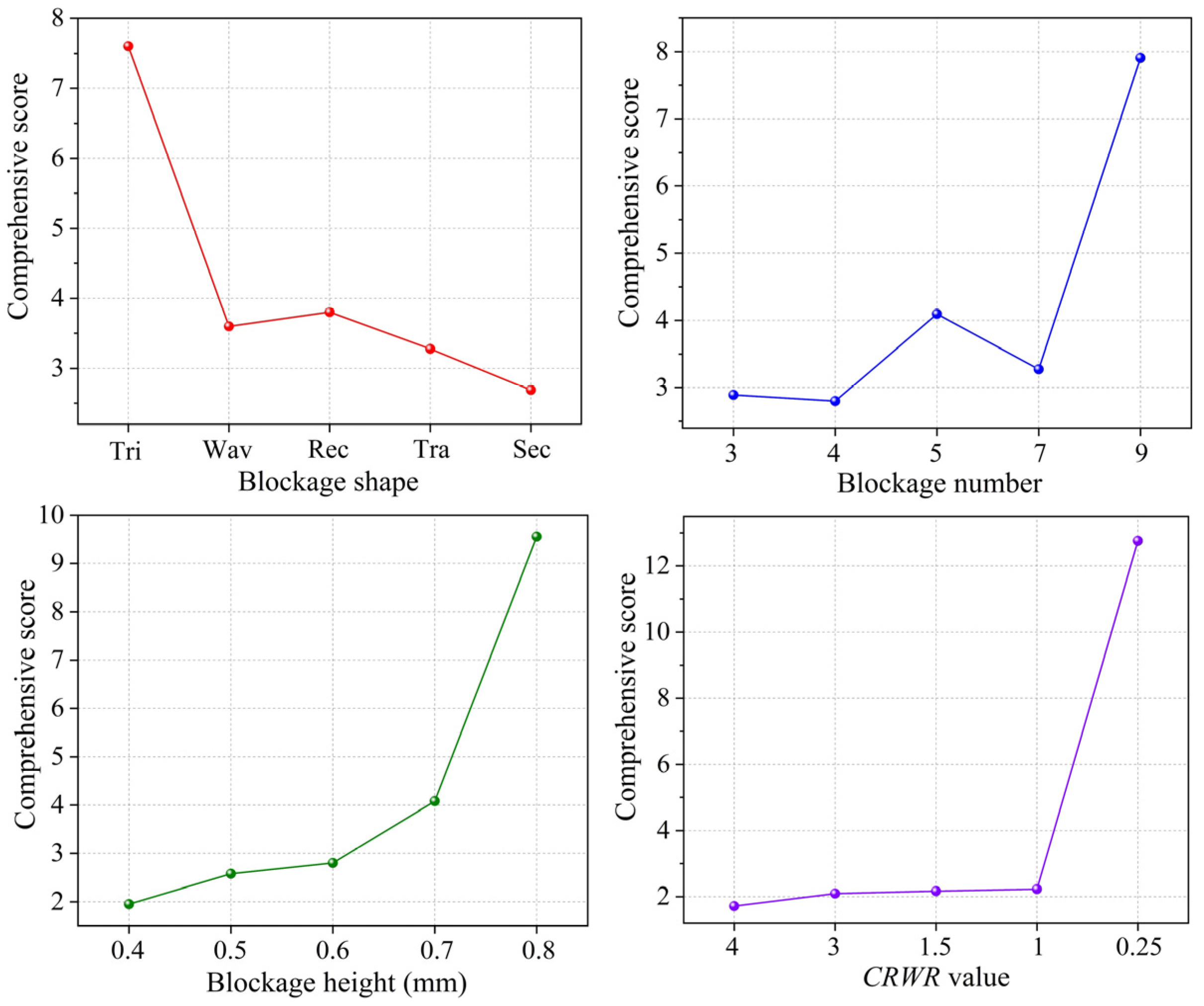
- Based on the determined weight distribution, the 25 groups of orthogonal experiments were comprehensively scored. These scores were then analyzed using ANOR and ANOVA methods. The significance ranking of the four design parameters was CRWR value > H > N > S, indicating that CRWR value yields the greatest impact on the comprehensive performance of PEMFC.
- (3)
- The optimal combination of design parameters was identified as a triangular blockage shape, with nine blockages, a height of 0.8 mm, and a CRWR value of 0.25. This configuration achieved the highest comprehensive score of 31.8306, demonstrating the best balance among current density, net output power, pressure drop, and oxygen distribution uniformity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, G.; Qu, Z.; Tao, W.-Q.; Mu, Y.; Jiao, K.; Xu, H.; Wang, Y. Advancing next-generation proton-exchange membrane fuel cell development in multi-physics transfer. Joule 2024, 8, 45–63. [Google Scholar] [CrossRef]
- Gómez, J.C.; Serra, M.; Husar, A. Controller design for polymer electrolyte membrane fuel cell systems for automotive applications. Int. J. Hydrogen Energy 2021, 46, 23263–23278. [Google Scholar] [CrossRef]
- Pahon, E.; Bouquain, D.; Hissel, D.; Rouet, A.; Vacquier, C. Performance analysis of proton exchange membrane fuel cell in automotive applications. J. Power Sources 2021, 510, 230385. [Google Scholar] [CrossRef]
- Andújar, J.M.; Segura, F.; Durán, E.; Rentería, L.A. Optimal interface based on power electronics in distributed generation systems for fuel cells. Renew. Energy 2011, 36, 2759–2770. [Google Scholar] [CrossRef]
- Rivarolo, M.; Rattazzi, D.; Lamberti, T.; Magistri, L. Clean energy production by PEM fuel cells on tourist ships: A time-dependent analysis. Int. J. Hydrogen Energy 2020, 45, 25747–25757. [Google Scholar] [CrossRef]
- U.S. Department of Energy (DOE). Fuel Cell Technologies Market Report 2016; U.S. Department of Energy (DOE): Washington, DC, USA, 2016.
- Jiao, K.; Xuan, J.; Du, Q.; Bao, Z.; Xie, B.; Wang, B.; Zhao, Y.; Fan, L.; Wang, H.; Hou, Z.; et al. Designing the next generation of proton-exchange membrane fuel cells. Nature 2021, 595, 361–369. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, L.; Tongsh, C.; Qu, Z.; Wu, S.; Xie, B.; Huo, W.; Du, Q.; Wang, H.; An, L.; et al. Structure Design for Ultrahigh Power Density Proton Exchange Membrane Fuel Cell. Small Methods 2023, 7, 2201537. [Google Scholar] [CrossRef]
- Meng, X.; Sun, C.; Mei, J.; Tang, X.; Hasanien, H.M.; Jiang, J.; Fan, F.; Song, K. Fuel cell life prediction considering the recovery phenomenon of reversible voltage loss. J. Power Sources 2025, 625, 235634. [Google Scholar] [CrossRef]
- Öner, E.; Öztürk, A.; Yurtcan, A.B. Utilization of the graphene aerogel as PEM fuel cell catalyst support: Effect of polypyrrole (PPy) and polydimethylsiloxane (PDMS) addition. Int. J. Hydrogen Energy 2020, 45, 34818–34836. [Google Scholar] [CrossRef]
- Shahgaldi, S.; Hamelin, J. Improved carbon nanostructures as a novel catalyst support in the cathode side of PEMFC: A critical review. Carbon 2015, 94, 705–728. [Google Scholar] [CrossRef]
- Thangarasu, S.; Oh, T.H. Progress in poly(phenylene oxide) based cation exchange membranes for fuel cells and redox flow batteries applications. Int. J. Hydrogen Energy 2021, 46, 38381–38415. [Google Scholar] [CrossRef]
- Liu, Q.; Li, X.; Zhang, S.; Wang, Z.; Chen, Y.; Zhou, S.; Wang, C.; Wu, K.; Liu, J.; Mao, Q.; et al. Novel sulfonated N-heterocyclic poly(aryl ether ketone ketone)s with pendant phenyl groups for proton exchange membrane performing enhanced oxidative stability and excellent fuel cell properties. J. Membr. Sci. 2022, 641, 119926. [Google Scholar] [CrossRef]
- Shang, Z.; Hossain, M.M.; Wycisk, R.; Pintauro, P.N. Poly(phenylene sulfonic acid)-expanded polytetrafluoroethylene composite membrane for low relative humidity operation in hydrogen fuel cells. J. Power Sources 2022, 535, 231375. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, S.; Xu, H.; Liu, G.; Wang, K. Performance of proton exchange membrane fuel cells with honeycomb-like flow channel design. Energy 2022, 239, 122102. [Google Scholar] [CrossRef]
- Wang, Y.; Si, C.; Qin, Y.; Wang, X.; Fan, Y.; Gao, Y. Bio-inspired design of an auxiliary fishbone-shaped cathode flow field pattern for polymer electrolyte membrane fuel cells. Energy Convers. Manag. 2021, 227, 113588. [Google Scholar] [CrossRef]
- Rocha, C.; Knöri, T.; Ribeirinha, P.; Gazdzicki, P. A review on flow field design for proton exchange membrane fuel cells: Challenges to increase the active area for MW applications. Renew. Sustain. Energy Rev. 2024, 192, 114198. [Google Scholar] [CrossRef]
- Perng, S.-W.; Wu, H.-W.; Chen, Y.-B.; Zeng, Y.-K. Performance enhancement of a high temperature proton exchange membrane fuel cell by bottomed-baffles in bipolar-plate channels. Appl. Energy 2019, 255, 113815. [Google Scholar] [CrossRef]
- Perng, S.-W.; Wu, H.-W. A three-dimensional numerical investigation of trapezoid baffles effect on non-isothermal reactant transport and cell net power in a PEMFC. Appl. Energy 2015, 143, 81–95. [Google Scholar] [CrossRef]
- Yin, Y.; Wu, S.; Qin, Y.; Otoo, O.N.; Zhang, J. Quantitative analysis of trapezoid baffle block sloping angles on oxygen transport and performance of proton exchange membrane fuel cell. Appl. Energy 2020, 271, 115257. [Google Scholar] [CrossRef]
- Wang, X.; Qin, Y.; Wu, S.; Shangguan, X.; Zhang, J.; Yin, Y. Numerical and experimental investigation of baffle plate arrangement on proton exchange membrane fuel cell performance. J. Power Sources 2020, 457, 228034. [Google Scholar] [CrossRef]
- Chen, X.; Yu, Z.; Yang, C.; Chen, Y.; Jin, C.; Ding, Y.; Li, W.; Wan, Z. Performance investigation on a novel 3D wave flow channel design for PEMFC. Int. J. Hydrogen Energy 2021, 46, 11127–11139. [Google Scholar] [CrossRef]
- Cai, G.; Liang, Y.; Liu, Z.; Liu, W. Design and optimization of bio-inspired wave-like channel for a PEM fuel cell applying genetic algorithm. Energy 2020, 192, 116670. [Google Scholar] [CrossRef]
- Kerkoub, Y.; Benzaoui, A.; Haddad, F.; Ziari, Y.K. Channel to rib width ratio influence with various flow field designs on performance of PEM fuel cell. Energy Convers. Manag. 2018, 174, 260–275. [Google Scholar] [CrossRef]
- Yan, S.; Yang, M.; Sun, C.; Xu, S. Liquid Water Characteristics in the Compressed Gradient Porosity Gas Diffusion Layer of Proton Exchange Membrane Fuel Cells Using the Lattice Boltzmann Method. Energies 2023, 16, 6010. [Google Scholar] [CrossRef]
- Jeon, D.H. Effect of channel-rib width on water transport behavior in gas diffusion layer of polymer electrolyte membrane fuel cells. J. Power Sources 2019, 423, 280–289. [Google Scholar] [CrossRef]
- Xia, L.; Xu, Q.; He, Q.; Ni, M.; Seng, M. Numerical study of high temperature proton exchange membrane fuel cell (HT-PEMFC) with a focus on rib design. Int. J. Hydrogen Energy 2021, 46, 21098–21111. [Google Scholar] [CrossRef]
- Varghese, G.; Venkatesh Babu, K.P.; Joseph, T.V.; Chippar, P. Combined effect of channel to rib width ratio and gas diffusion layer deformation on high temperature—Polymer electrolyte membrane fuel cell performance. Int. J. Hydrogen Energy 2022, 47, 33014–33026. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, H.; Cai, W.; Ye, W.; Tong, Y.; Cheng, H. Effect of varying rib area portions on the performance of PEM fuel cells: Insights into design and optimization. Renew. Energy 2023, 217, 119185. [Google Scholar] [CrossRef]
- Zhang, S.-Y.; Qu, Z.-G.; Xu, H.-T.; Talkhoncheh, F.-K.; Liu, S.; Gao, Q. A numerical study on the performance of PEMFC with wedge-shaped fins in the cathode channel. Int. J. Hydrogen Energy 2021, 46, 27700–27708. [Google Scholar] [CrossRef]
- Jiao, K.; Wang, B.; Du, Q.; Wang, Y.; Zhang, G.; Yang, Z.; Deng, H.; Xie, X. Water and Thermal Management of Proton Exchange Membrane Fuel Cells; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Zhang, S.; Mao, Y.; Liu, F.; Xu, H.; Qu, Z.; Liao, X. Multi-objective optimization and evaluation of PEMFC performance based on orthogonal experiment and entropy weight method. Energy Convers. Manag. 2023, 291, 117310. [Google Scholar] [CrossRef]
- Li, Y.; Lu, C.; Liu, G.; Chen, Y.; Zhang, Y.; Wu, C.; Liu, B.; Shu, L. Risk assessment of wetland degradation in the Xiong’an New Area based on AHP-EWM-ICT method. Ecol. Indic. 2023, 153, 110443. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, J.; Wang, Y.; Yin, Y.; Jiao, K. Investigation of current density spatial distribution in PEM fuel cells using a comprehensively validated multi-phase non-isothermal model. Int. J. Heat Mass Transf. 2020, 150, 119294. [Google Scholar] [CrossRef]
- Zhang, G.; Duan, F.; Qu, Z.; Bai, H.; Zhang, J. Airfoil flow field for proton exchange membrane fuel cells enhancing mass transfer with low pressure drop. Int. J. Heat Mass Transf. 2024, 225, 125420. [Google Scholar] [CrossRef]
- Fu, X.-L.; Ni, H.; Zhou, A.; Jiang, Z.-Y.; Jiang, N.-J.; Du, Y.-J. An integrated fuzzy AHP and fuzzy TOPSIS approach for screening backfill materials for contaminant containment in slurry trench cutoff walls. J. Clean. Prod. 2023, 419, 138242. [Google Scholar] [CrossRef]
- Kong, M.; Ye, X.; Liu, D.; Li, C. Comprehensive evaluation of medical waste gasification low-carbon multi-generation system based on AHP–EWM–GFCE method. Energy 2024, 296, 131161. [Google Scholar] [CrossRef]



| Parameters | Value | Unit |
|---|---|---|
| Porosity (GDL, MPL, CL) | 0.6, 0.5, 0.3 | / |
| Permeability (GDL, MPL, CL) | 1 × 10−11, 1 × 10−12, 1 × 10−13 | m2 |
| Contact angle (GDL, MPL, CL) | 120, 120, 100 | ° |
| Open circuit voltage | 1.15 | V |
| Operating temperature | 343.15 | K |
| Operating pressure | 101,325 | Pa |
| Relative humidity (anode, cathode) | 30%, 100% | / |
| Reference current density | 10,000 | A/m2 |
| Reference concentration (anode, cathode) | 56.4, 3.39 | mol/m3 |
| Standard entropy change (anode, cathode) | 130.68, 32.55 | J/(mol·K) |
| Stoichiometric ratio (anode, cathode) | 1.5, 2.0 | / |
| Surface/volume ratio | 200,000 | m−1 |
| Concentration exponent (anode, cathode) | 1.0, 1.0 | / |
| Proton conduction coefficient | 1 | / |
| Proton conduction exponent | 1 | / |
| Ionomer volume fraction in CL | 0.3 | / |
| Equivalent weight of PEM | 1100 | kg/kmol |
| Exchange coefficient (anode, cathode) | 0.5, 0.5 | / |
| Thermal conductivity (BP, GDL, MPL, CL) | 20, 10, 1, 1 | W/(m·K) |
| Electrical conductivity (BP, GDL, MPL, CL) | 20,000, 8000, 5000, 5000 | S/m |
| Specific heat capacity (BP, PEM, GDL, MPL, CL) | 1580, 833, 568, 3300, 3300 | J/(kg·K) |
| Grid Sizes | Current Density (A/cm2) | Relative Error | |
|---|---|---|---|
| Grid 1 | 40,843 | 0.9902 | 0.99% |
| Grid 2 | 60,435 | 0.9945 | 0.58% |
| Grid 3 | 90,060 | 0.9976 | 0.26% |
| Grid 4 | 136,275 | 1.0003 | - |
| Grid 5 | 203,899 | 1.0014 | 0.1% |
| Levels | Factors | |||
|---|---|---|---|---|
| S | N | H (mm) | CRWR Value | |
| 1 | Tri | 3 | 0.4 | 4 |
| 2 | Wav | 4 | 0.5 | 3 |
| 3 | Rec | 5 | 0.6 | 1.5 |
| 4 | Tra | 7 | 0.7 | 1 |
| 5 | Sec | 9 | 0.8 | 0.25 |
| Case No. | Factors | |||||||
|---|---|---|---|---|---|---|---|---|
| S | N | H | CRWR Value | |||||
| No. | Factor | No. | Factor | No. | Factor | No. | Factor | |
| 1 | 1 | Tri | 1 | 3 | 1 | 0.4 | 1 | 4 |
| 2 | 1 | Tri | 2 | 4 | 2 | 0.5 | 2 | 3 |
| 3 | 1 | Tri | 3 | 5 | 3 | 0.6 | 3 | 1.5 |
| 4 | 1 | Tri | 4 | 7 | 4 | 0.7 | 4 | 1 |
| 5 | 1 | Tri | 5 | 9 | 5 | 0.8 | 5 | 0.25 |
| 6 | 2 | Wav | 1 | 3 | 2 | 0.5 | 3 | 1.5 |
| 7 | 2 | Wav | 2 | 4 | 3 | 0.6 | 4 | 1 |
| 8 | 2 | Wav | 3 | 5 | 4 | 0.7 | 5 | 0.25 |
| 9 | 2 | Wav | 4 | 7 | 5 | 0.8 | 1 | 4 |
| 10 | 2 | Wav | 5 | 9 | 1 | 0.4 | 2 | 3 |
| 11 | 3 | Rec | 1 | 3 | 3 | 0.6 | 5 | 0.25 |
| 12 | 3 | Rec | 2 | 4 | 4 | 0.7 | 1 | 4 |
| 13 | 3 | Rec | 3 | 5 | 5 | 0.8 | 2 | 3 |
| 14 | 3 | Rec | 4 | 7 | 1 | 0.4 | 3 | 1.5 |
| 15 | 3 | Rec | 5 | 9 | 2 | 0.5 | 4 | 1 |
| 16 | 4 | Tra | 1 | 3 | 4 | 0.7 | 2 | 3 |
| 17 | 4 | Tra | 2 | 4 | 5 | 0.8 | 3 | 1.5 |
| 18 | 4 | Tra | 3 | 5 | 1 | 0.4 | 4 | 1 |
| 19 | 4 | Tra | 4 | 7 | 2 | 0.5 | 5 | 0.25 |
| 20 | 4 | Tra | 5 | 9 | 3 | 0.6 | 1 | 4 |
| 21 | 5 | Sec | 1 | 3 | 5 | 0.8 | 4 | 1 |
| 22 | 5 | Sec | 2 | 4 | 1 | 0.4 | 5 | 0.25 |
| 23 | 5 | Sec | 3 | 5 | 2 | 0.5 | 1 | 4 |
| 24 | 5 | Sec | 4 | 7 | 3 | 0.6 | 2 | 3 |
| 25 | 5 | Sec | 5 | 9 | 4 | 0.7 | 3 | 1.5 |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| RI index | 0 | 0 | 0.52 | 0.89 | 1.12 | 1.26 | 1.36 | 1.41 | 1.46 |
| Case No. | Evaluation Objectives | |||
|---|---|---|---|---|
| I (A/cm2) | ΔP (Pa) | Wnet (W) | NU | |
| 1 | 1.1101 | 3.31 | 0.2043 | 0.3439 |
| 2 | 1.1098 | 4.76 | 0.2042 | 0.3418 |
| 3 | 1.0841 | 10.52 | 0.1995 | 0.3368 |
| 4 | 1.0632 | 29.81 | 0.1956 | 0.3385 |
| 5 | 0.8875 | 391.83 | 0.1631 | 0.3491 |
| 6 | 1.0661 | 6.58 | 0.1962 | 0.3363 |
| 7 | 1.0366 | 13.34 | 0.1907 | 0.3342 |
| 8 | 0.8310 | 133.85 | 0.1528 | 0.3347 |
| 9 | 1.1448 | 30.71 | 0.2106 | 0.3411 |
| 10 | 1.1168 | 5.76 | 0.2055 | 0.3439 |
| 11 | 0.8025 | 93.49 | 0.1476 | 0.3356 |
| 12 | 1.1338 | 17.45 | 0.2086 | 0.3400 |
| 13 | 1.1440 | 62.36 | 0.2105 | 0.3385 |
| 14 | 1.0821 | 9.43 | 0.1991 | 0.3411 |
| 15 | 1.0561 | 20.04 | 0.1943 | 0.3444 |
| 16 | 1.1170 | 11.32 | 0.2055 | 0.3400 |
| 17 | 1.0960 | 45.24 | 0.2016 | 0.3369 |
| 18 | 1.0279 | 9.58 | 0.1891 | 0.3364 |
| 19 | 0.8157 | 90.31 | 0.1500 | 0.3379 |
| 20 | 1.1406 | 13.66 | 0.2099 | 0.3439 |
| 21 | 1.0439 | 31.64 | 0.1921 | 0.3313 |
| 22 | 0.7665 | 59.81 | 0.1410 | 0.3426 |
| 23 | 1.1202 | 4.89 | 0.2061 | 0.3412 |
| 24 | 1.1266 | 9.53 | 0.2073 | 0.3395 |
| 25 | 1.1078 | 27.60 | 0.2038 | 0.3408 |
| Objectives | I (A/cm2) | ΔP (Pa) | Wnet (W) | NU |
|---|---|---|---|---|
| I (A/cm2) | 1 | 7 | 2 | 5 |
| ΔP (Pa) | 1/7 | 1 | 1/6 | 1/3 |
| Wnet (W) | 1/2 | 6 | 1 | 4 |
| NU | 1/5 | 3 | 1/4 | 1 |
| Objectives | I (A/cm2) | ΔP (Pa) | Wnet (W) | NU |
|---|---|---|---|---|
| I (A/cm2) | 0.543 | 0.412 | 0.584 | 0.484 |
| ΔP (Pa) | 0.078 | 0.059 | 0.049 | 0.032 |
| Wnet (W) | 0.271 | 0.353 | 0.293 | 0.387 |
| NU | 0.109 | 0.176 | 0.073 | 0.0967 |
| I (A/cm2) | ΔP (Pa) | Wnet (W) | NU | |
|---|---|---|---|---|
| Ej | 0.9595 | 0.9859 | 0.9593 | 0.9688 |
| dj | 0.04054 | 0.0141 | 0.0407 | 0.0312 |
| Methods | Weight Values | |||
|---|---|---|---|---|
| I (A/cm2) | ΔP (Pa) | Wnet (W) | NU | |
| AHP | 0.51 | 0.05 | 0.33 | 0.11 |
| EWM | 0.32 | 0.11 | 0.32 | 0.25 |
| AHP-EWM | 0.415 | 0.08 | 0.325 | 0.18 |
| Case No. | Comprehensive Score | Case No. | Comprehensive Score |
|---|---|---|---|
| 1 | 0.8538 | 14 | 1.3296 |
| 2 | 0.9693 | 15 | 2.1666 |
| 3 | 1.4170 | 16 | 1.4971 |
| 4 | 2.9505 | 17 | 4.2002 |
| 5 | 31.8306 | 18 | 1.3150 |
| 6 | 1.0931 | 19 | 7.6729 |
| 7 | 1.6195 | 20 | 1.6963 |
| 8 | 11.1628 | 21 | 3.0865 |
| 9 | 3.0617 | 22 | 5.2104 |
| 10 | 1.0530 | 23 | 0.9845 |
| 11 | 7.9206 | 24 | 1.3584 |
| 12 | 1.9955 | 25 | 2.7953 |
| 13 | 5.5929 |
| Objectives | Factors | ||||
|---|---|---|---|---|---|
| S | N | H | CRWR Value | ||
| Comprehensive score | k1 | 38.0212 | 14.4511 | 9.7618 | 8.5918 |
| k2 | 17.9901 | 13.9949 | 12.8864 | 10.4707 | |
| k3 | 19.0052 | 20.4722 | 14.0118 | 10.8352 | |
| k4 | 16.3815 | 16.3731 | 20.4012 | 11.1381 | |
| k5 | 13.4351 | 39.5418 | 47.7719 | 63.7973 | |
| k1/4 | 7.6042 | 2.8902 | 1.9524 | 1.7184 | |
| k2/4 | 3.5980 | 2.7990 | 2.5773 | 2.0941 | |
| k3/4 | 3.8010 | 4.0944 | 2.8024 | 2.1670 | |
| k4/4 | 3.2763 | 3.2746 | 4.0802 | 2.2276 | |
| k5/4 | 2.6870 | 7.9084 | 9.5544 | 12.7595 | |
| R | 4.9172 | 5.1094 | 7.6020 | 11.0411 | |
| Objectives | Variable | DOF | SS | MS | F Value | Significance |
|---|---|---|---|---|---|---|
| Comprehensive score | S | 4 | 76.26 | 19.07 | 1.08 | |
| N | 4 | 91.49 | 22.87 | 1.30 | ||
| H | 4 | 191.61 | 47.90 | 2.71 | ||
| CRWR value | 4 | 459.40 | 114.85 | 6.51 | * | |
| Error | 8 | 141.24 | 17.66 | |||
| Total | 24 | 960.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, H.; Yuan, Q.; Zhu, X.; Janković, N.; Chen, X. Multi-Objective Optimization of Blockage Design Parameters Affecting the Performance of PEMFC by OEM-AHP-EWM Analysis. Energies 2025, 18, 1407. https://doi.org/10.3390/en18061407
Ji H, Yuan Q, Zhu X, Janković N, Chen X. Multi-Objective Optimization of Blockage Design Parameters Affecting the Performance of PEMFC by OEM-AHP-EWM Analysis. Energies. 2025; 18(6):1407. https://doi.org/10.3390/en18061407
Chicago/Turabian StyleJi, Hongbo, Quan Yuan, Xiaoyong Zhu, Nenad Janković, and Xiaoping Chen. 2025. "Multi-Objective Optimization of Blockage Design Parameters Affecting the Performance of PEMFC by OEM-AHP-EWM Analysis" Energies 18, no. 6: 1407. https://doi.org/10.3390/en18061407
APA StyleJi, H., Yuan, Q., Zhu, X., Janković, N., & Chen, X. (2025). Multi-Objective Optimization of Blockage Design Parameters Affecting the Performance of PEMFC by OEM-AHP-EWM Analysis. Energies, 18(6), 1407. https://doi.org/10.3390/en18061407





