A Thermo-Hydro-Mechanical Damage Coupling Model for Stability Analysis During the In Situ Conversion Process
Abstract
:1. Introduction
2. Methods
2.1. THMD Coupling Model
2.1.1. The Stress Equilibrium Equation
2.1.2. The Hydraulic Pressure Equation
2.1.3. The Energy Conservation Equation
2.2. Nonlocal Damage Model
2.2.1. Localizing Gradient Damage Theory
2.2.2. Spectral Decomposition of Elastic Strain Energy Density
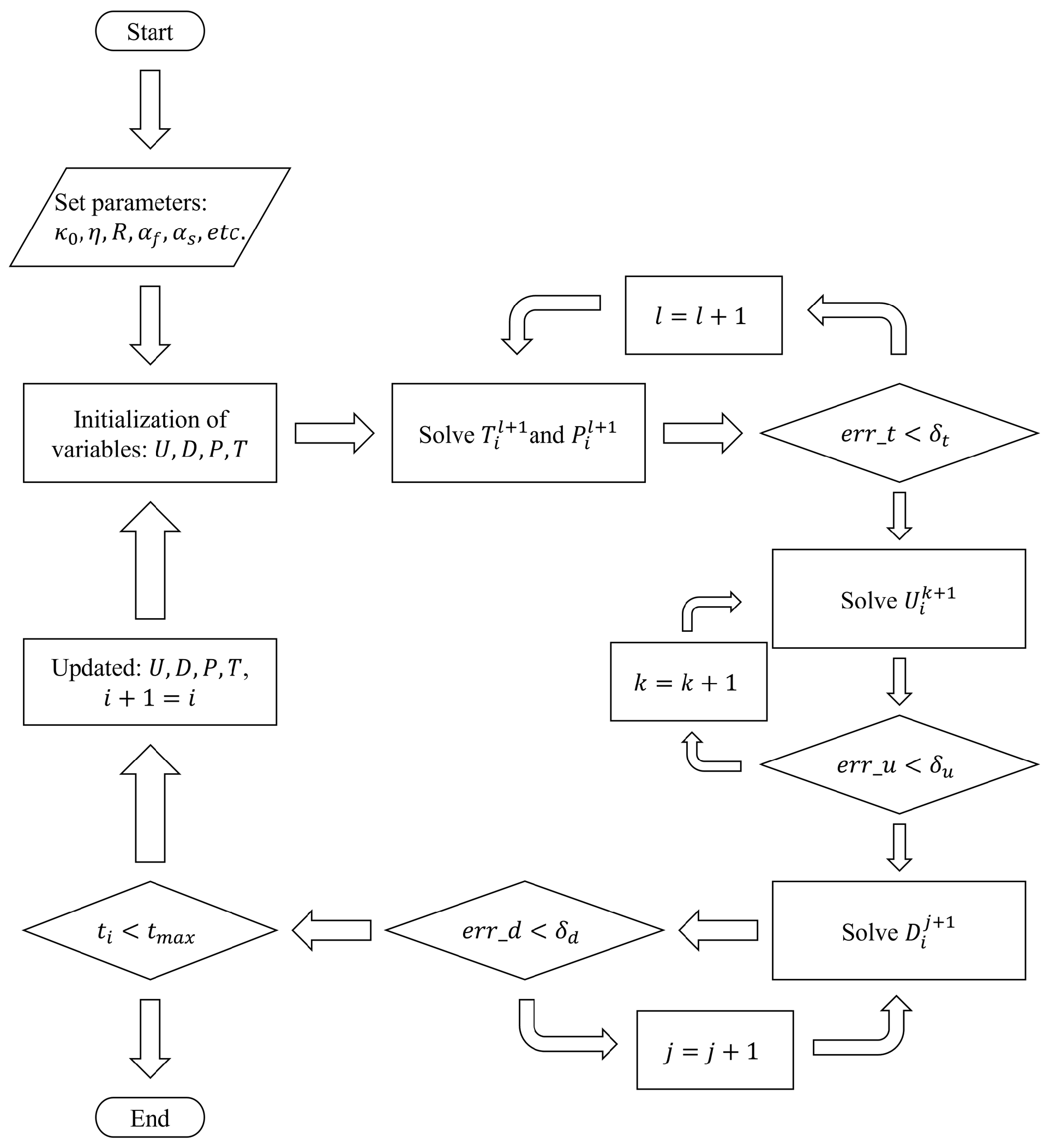
2.2.3. Finite Element Solution Algorithm
| Algorithm 1 The algorithm for TM coupling |
|
3. Validation
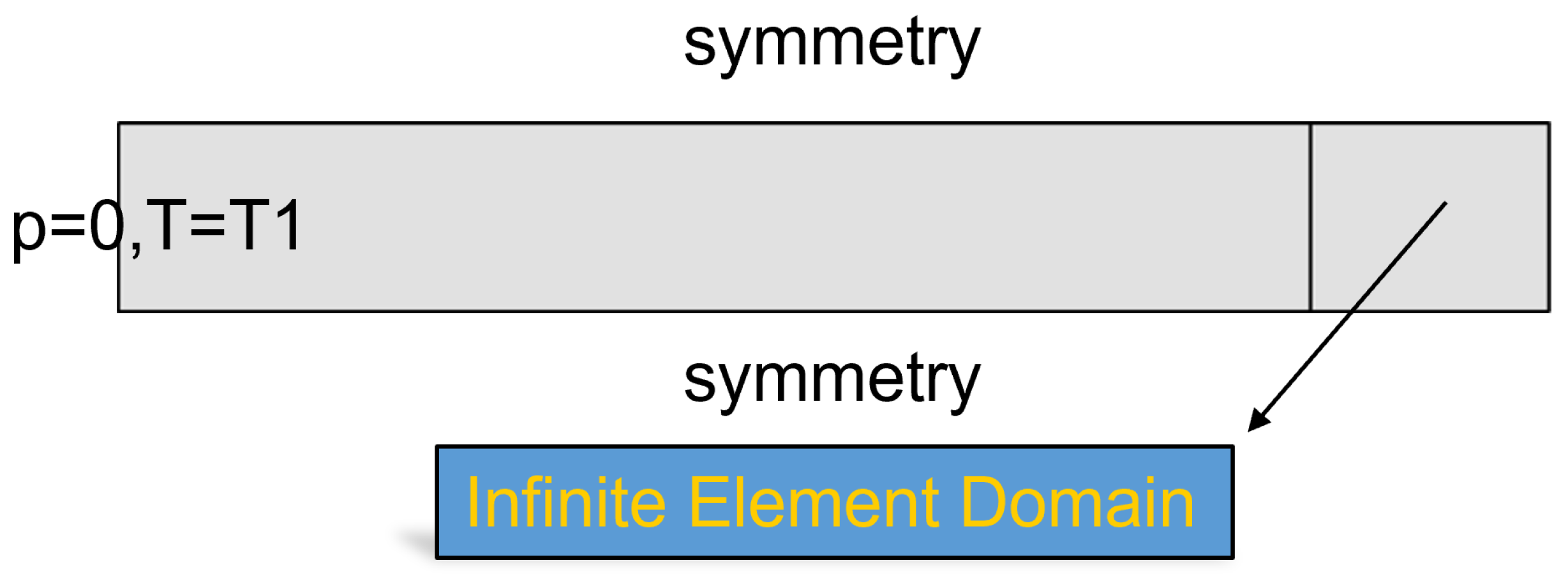
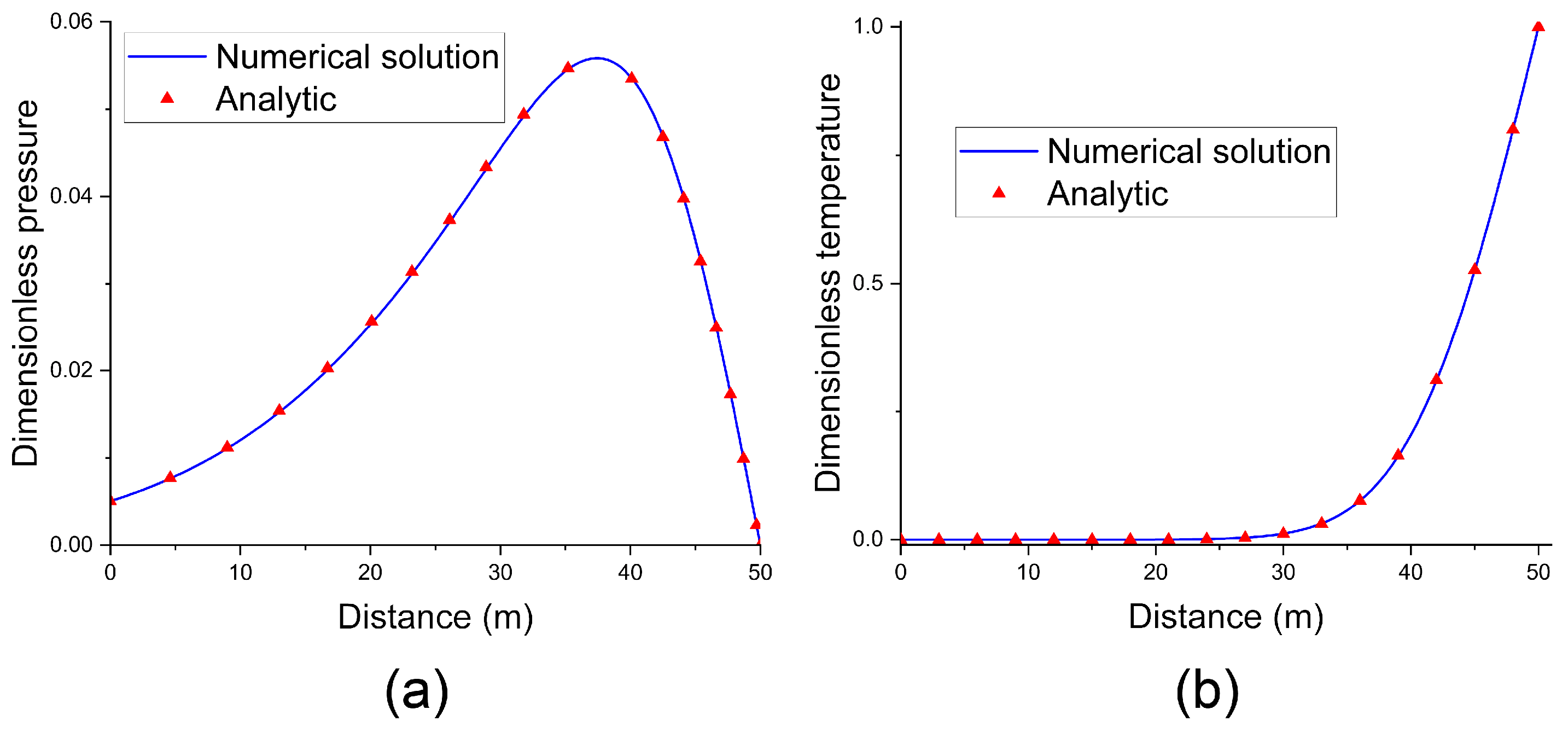
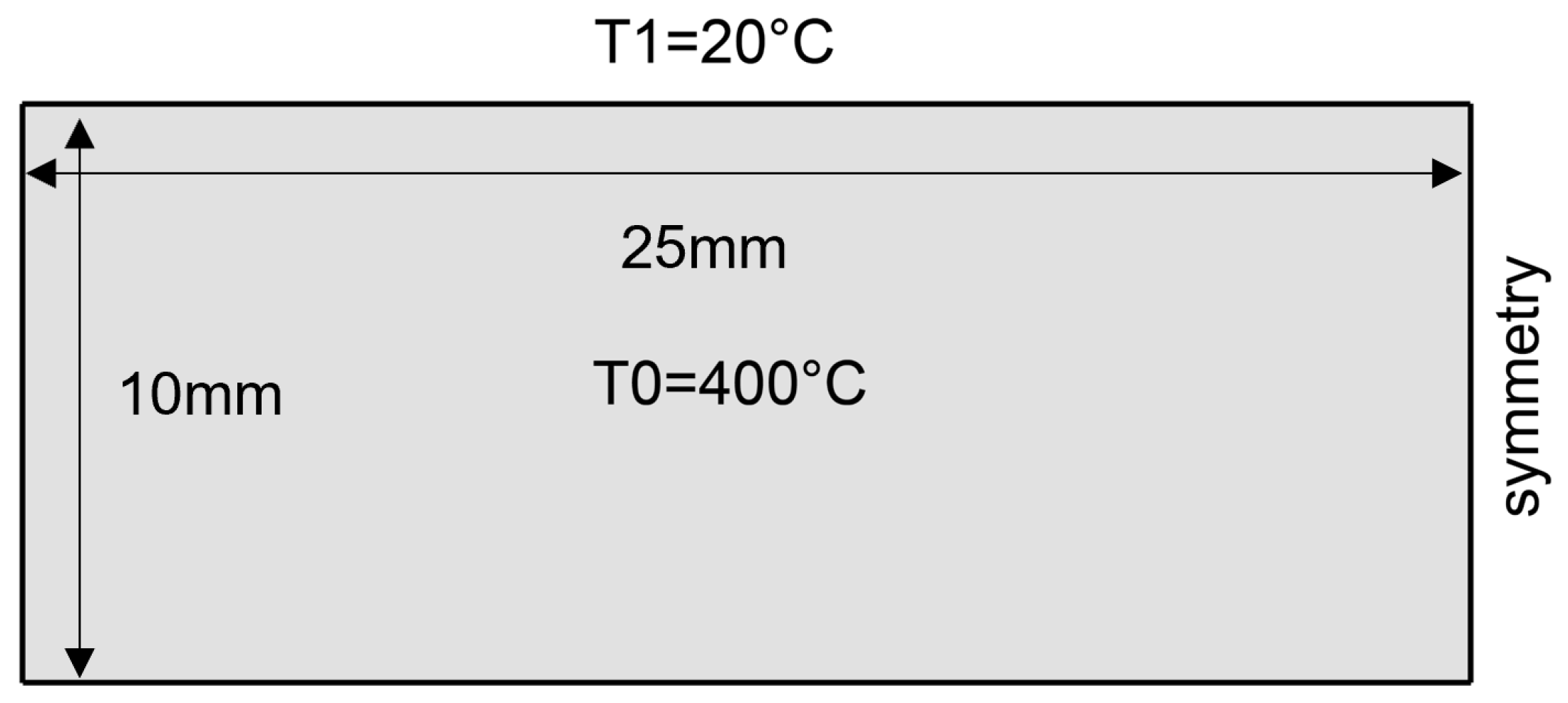
3.1. THM Coupled Model Validation
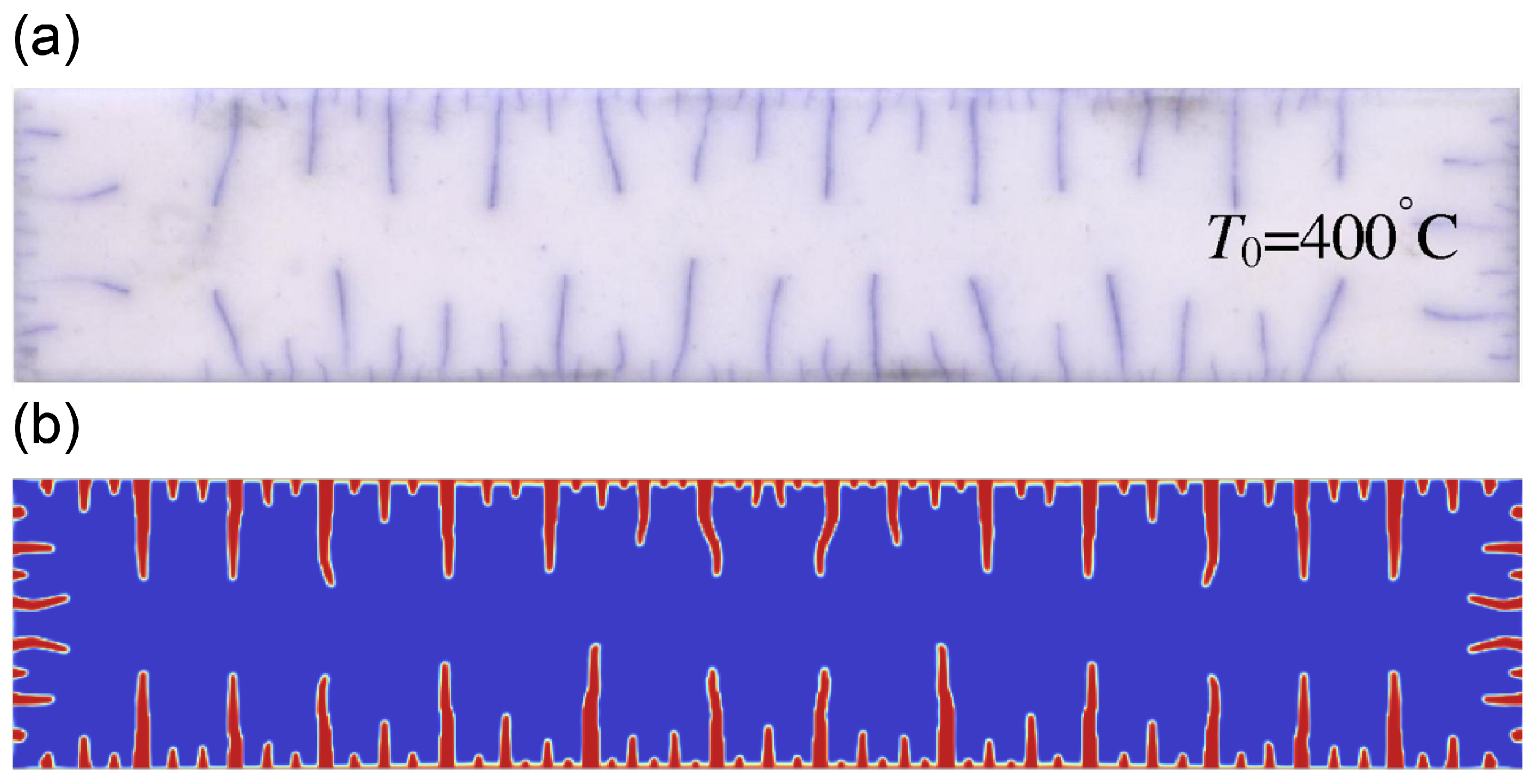
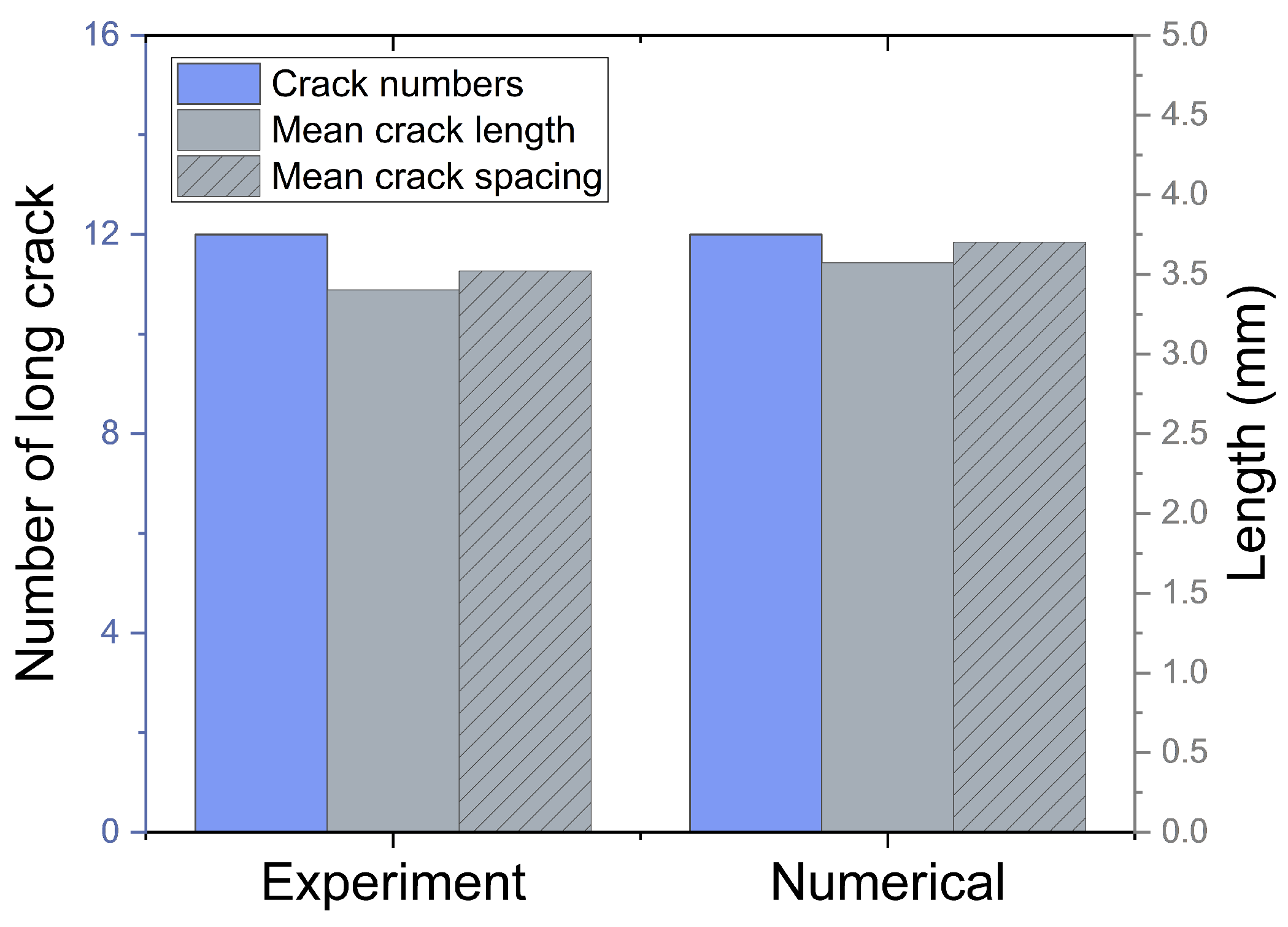
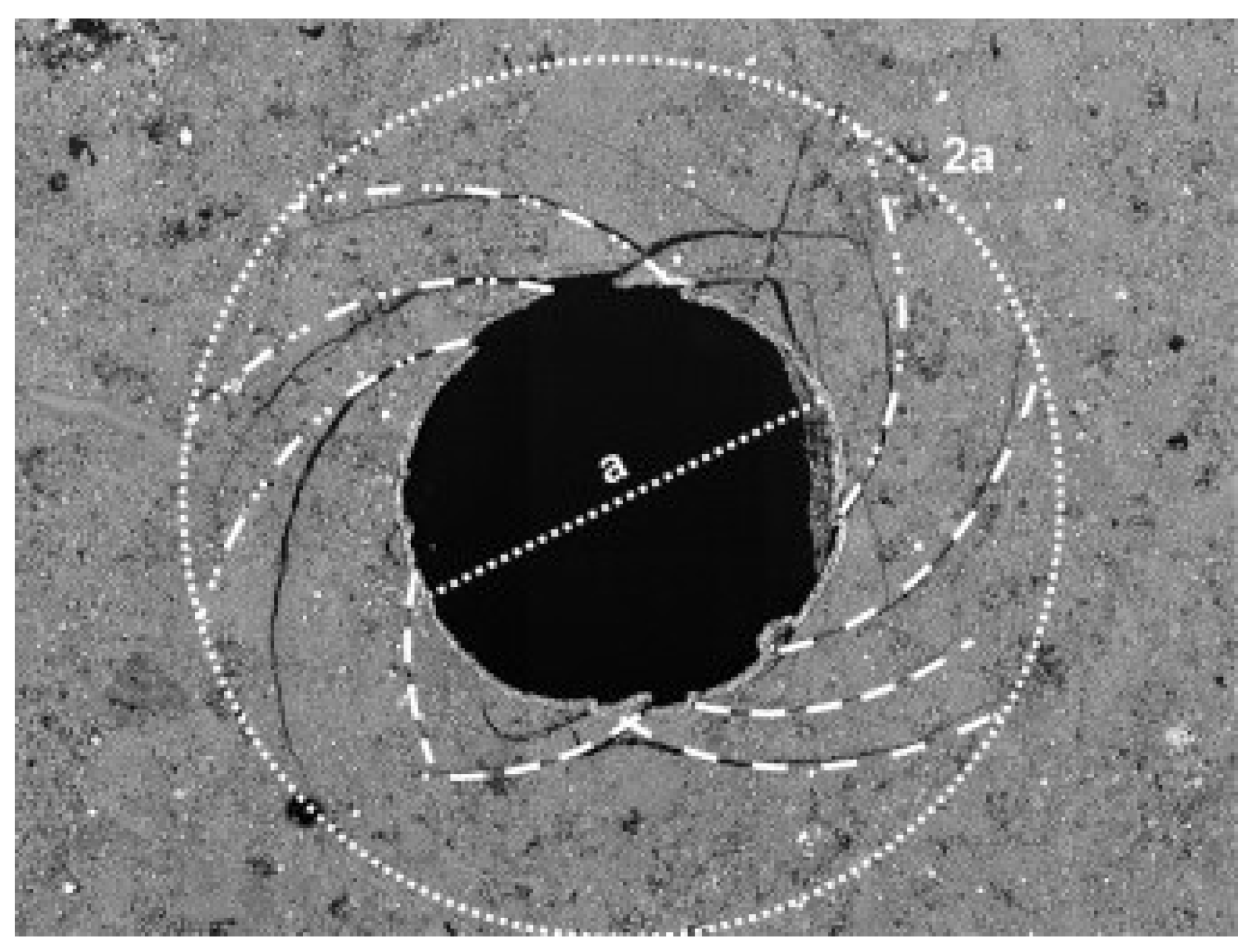
3.2. Thermal-Induced Damage Validation
4. Results and Discussion
4.1. Analysis of Thermal Damage Around a Single Heating Well
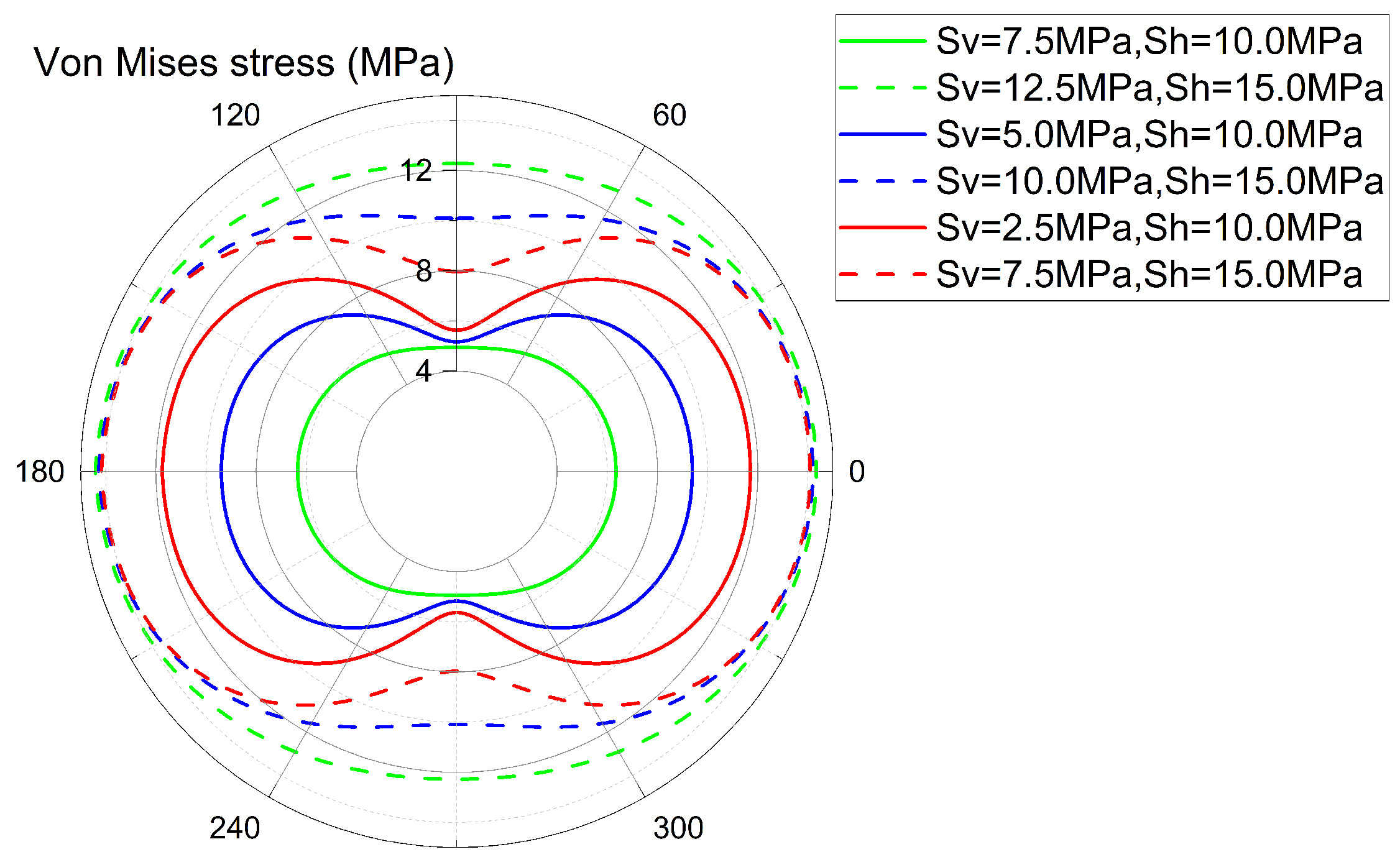
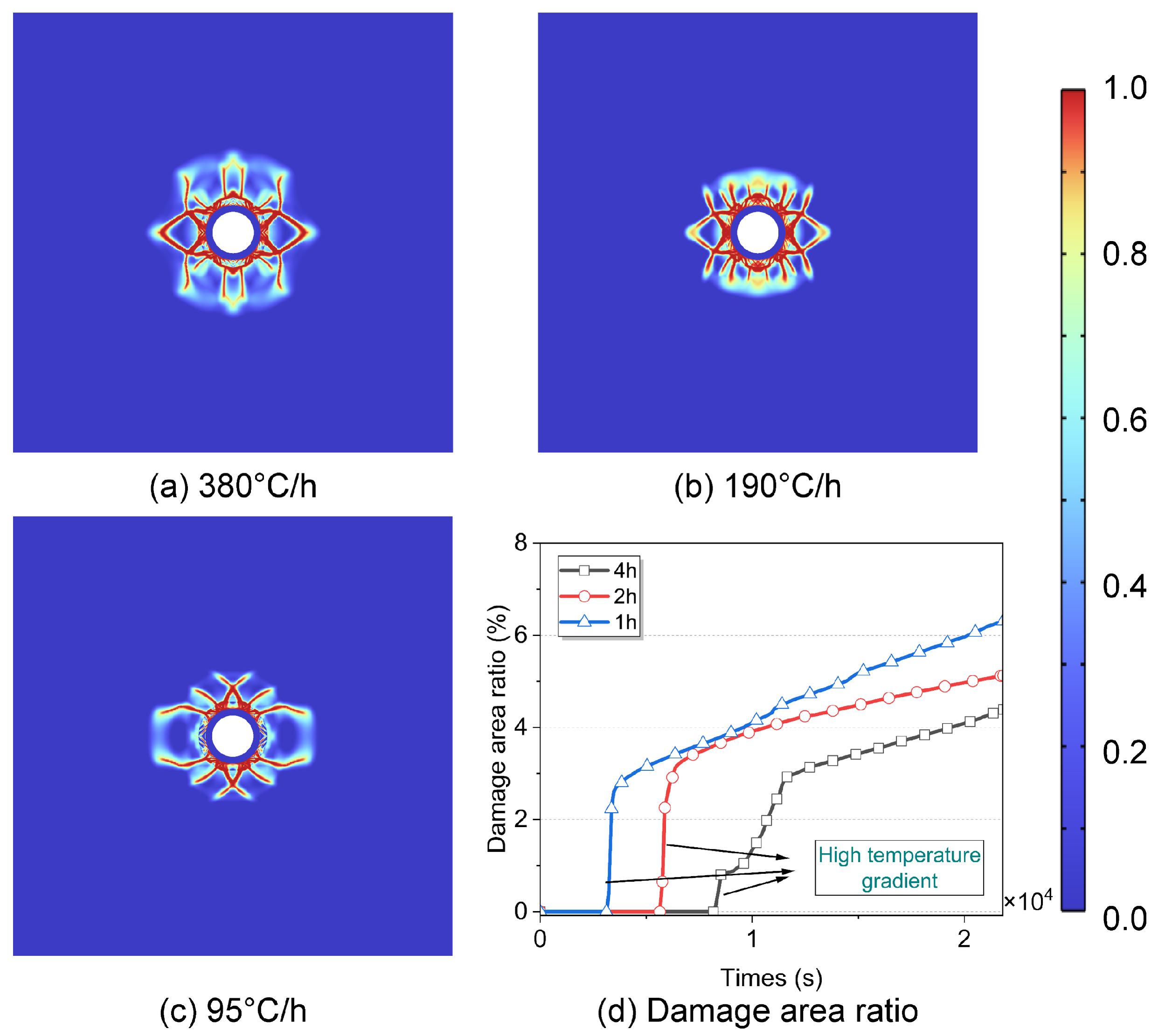
4.1.1. The Influence of In Situ Stress on Damage
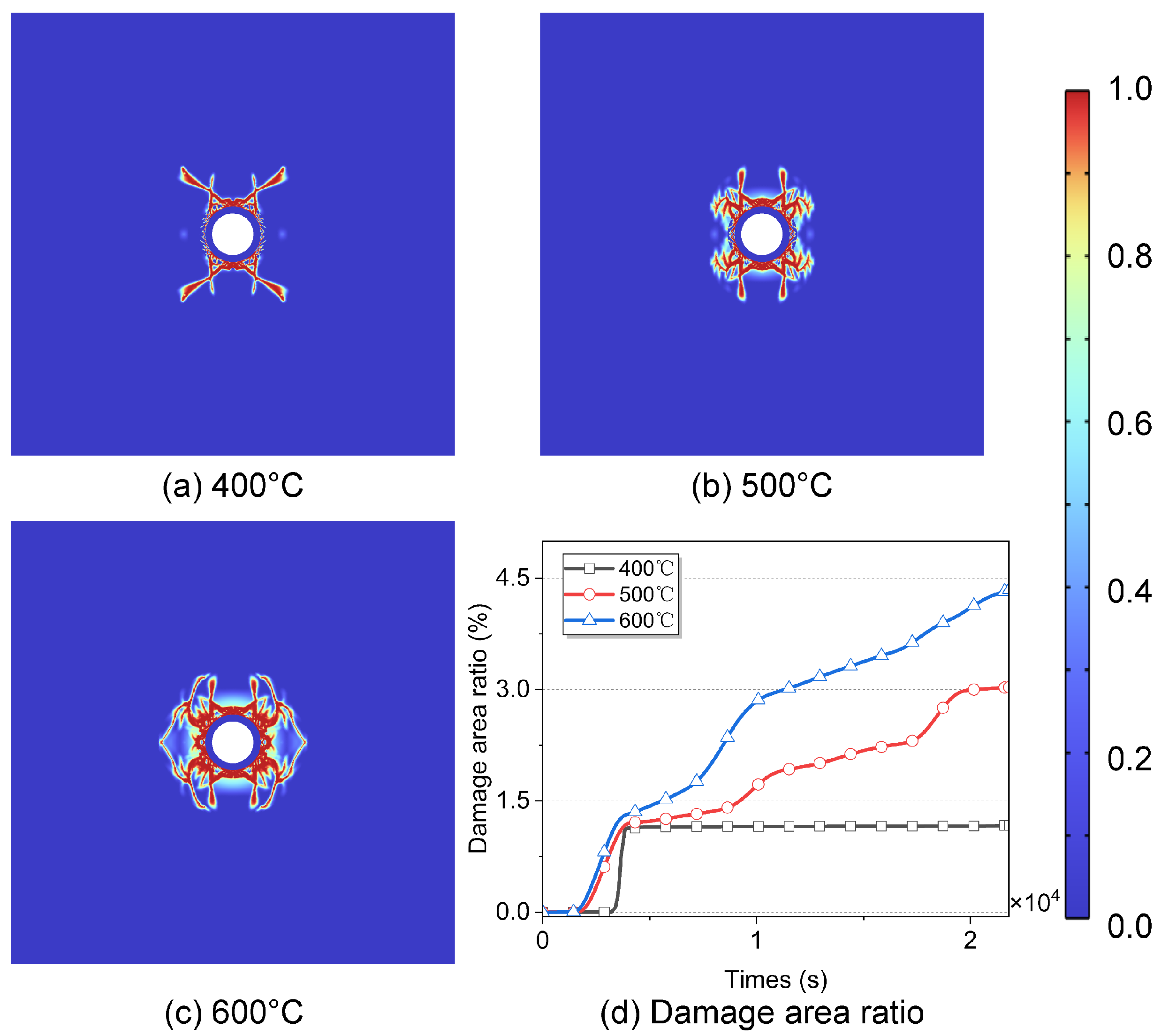
4.1.2. The Impact of Temperature on Damage
4.1.3. Effect of Wellbore Material on Damage
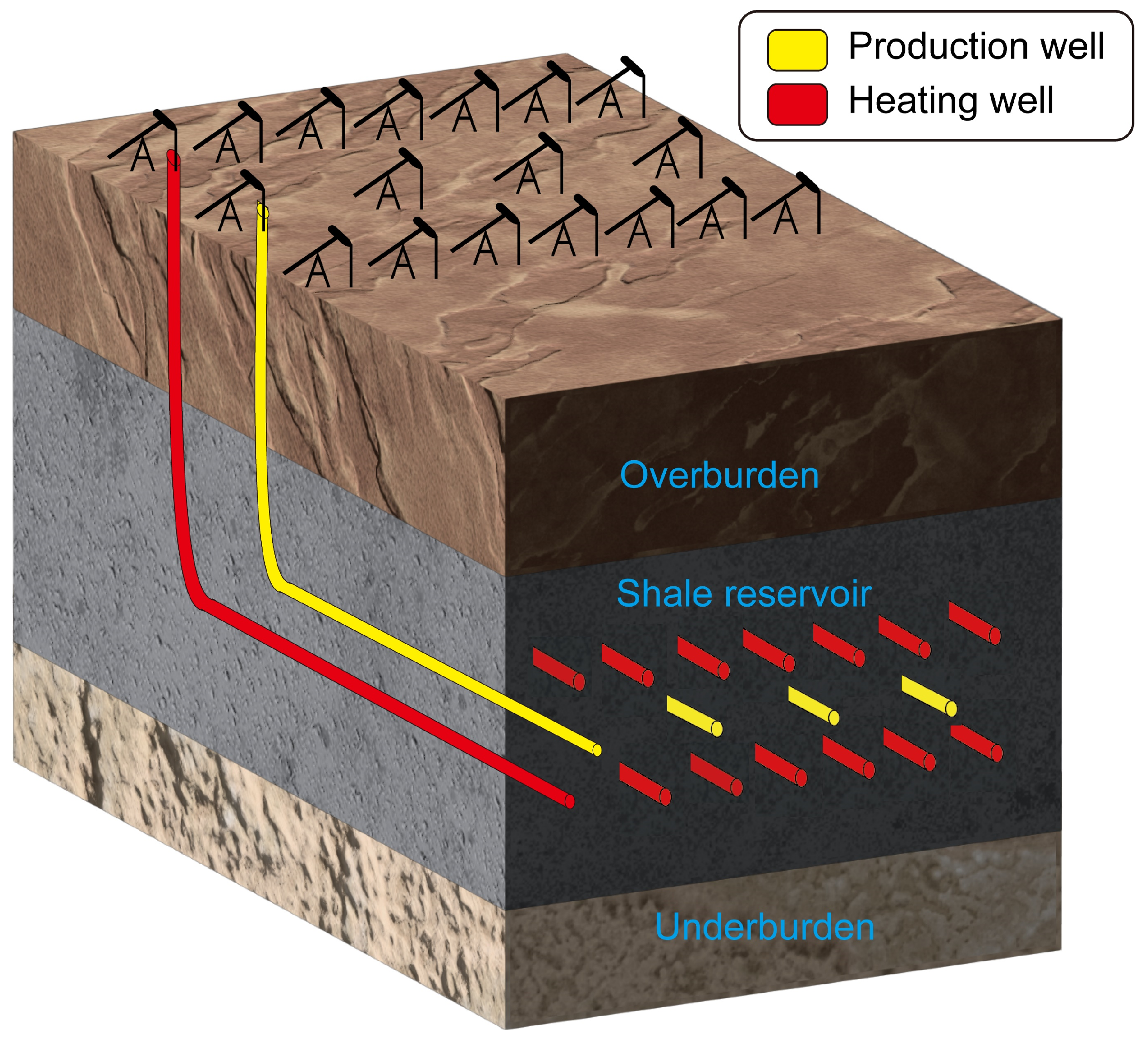
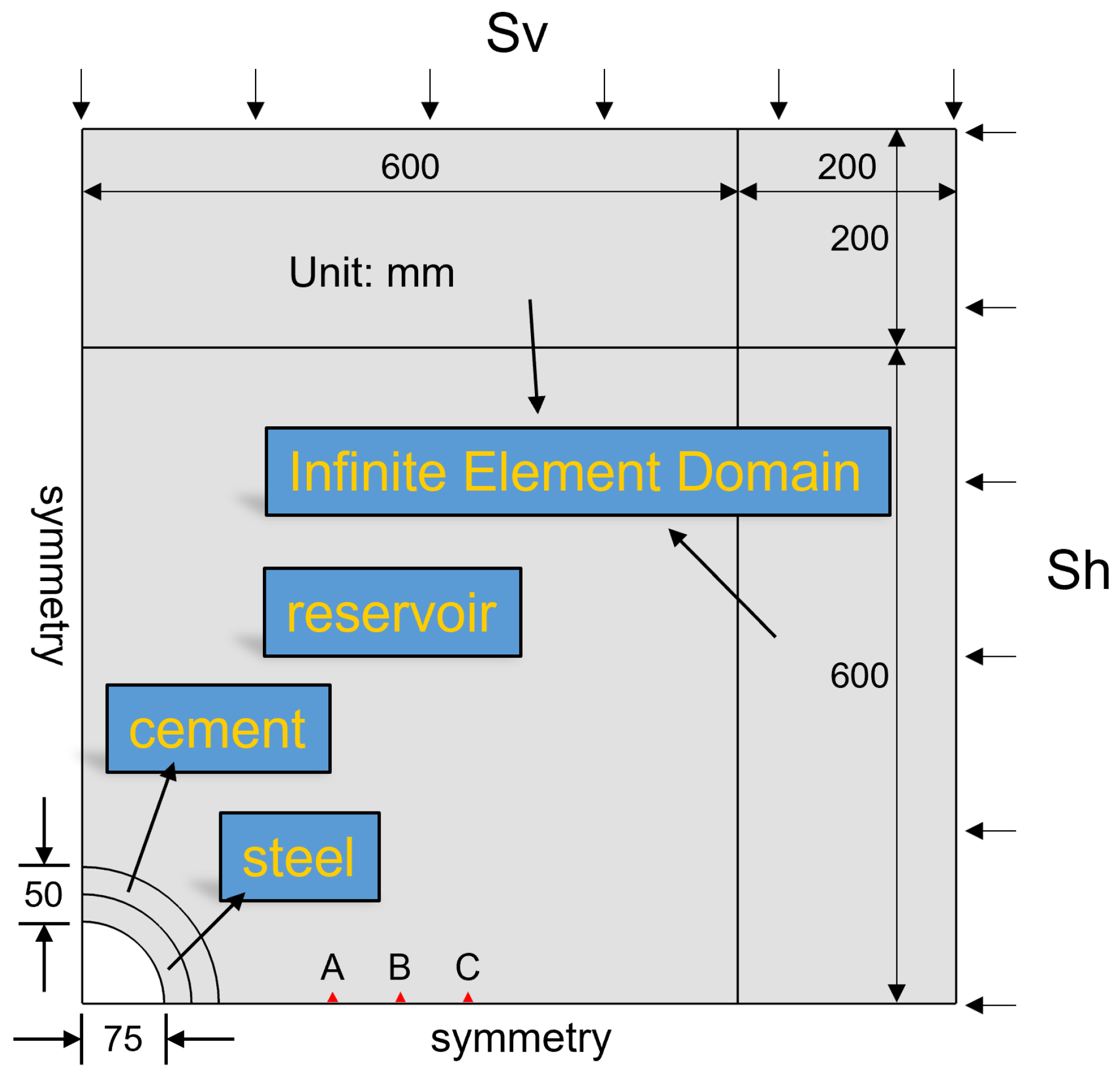
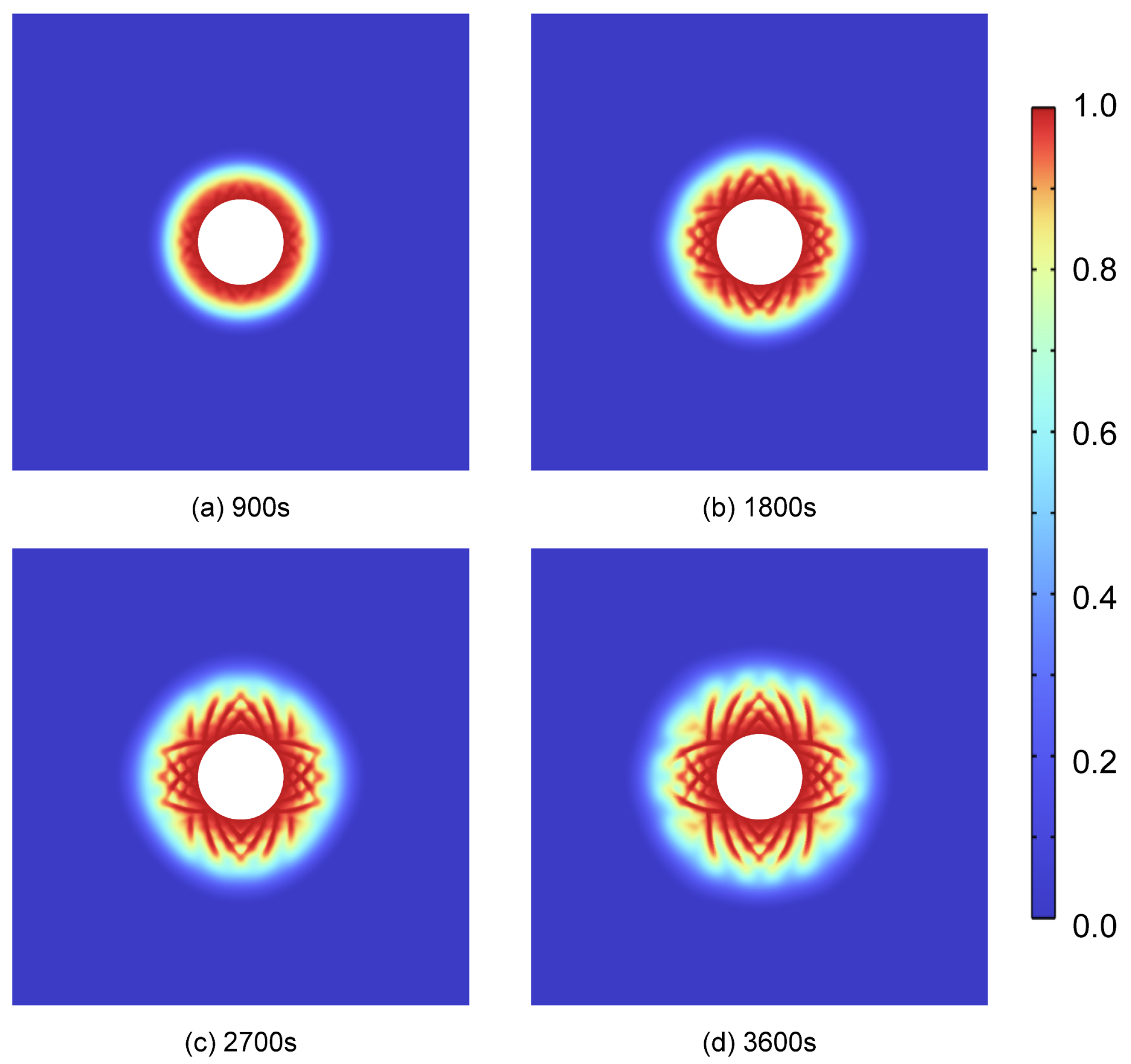
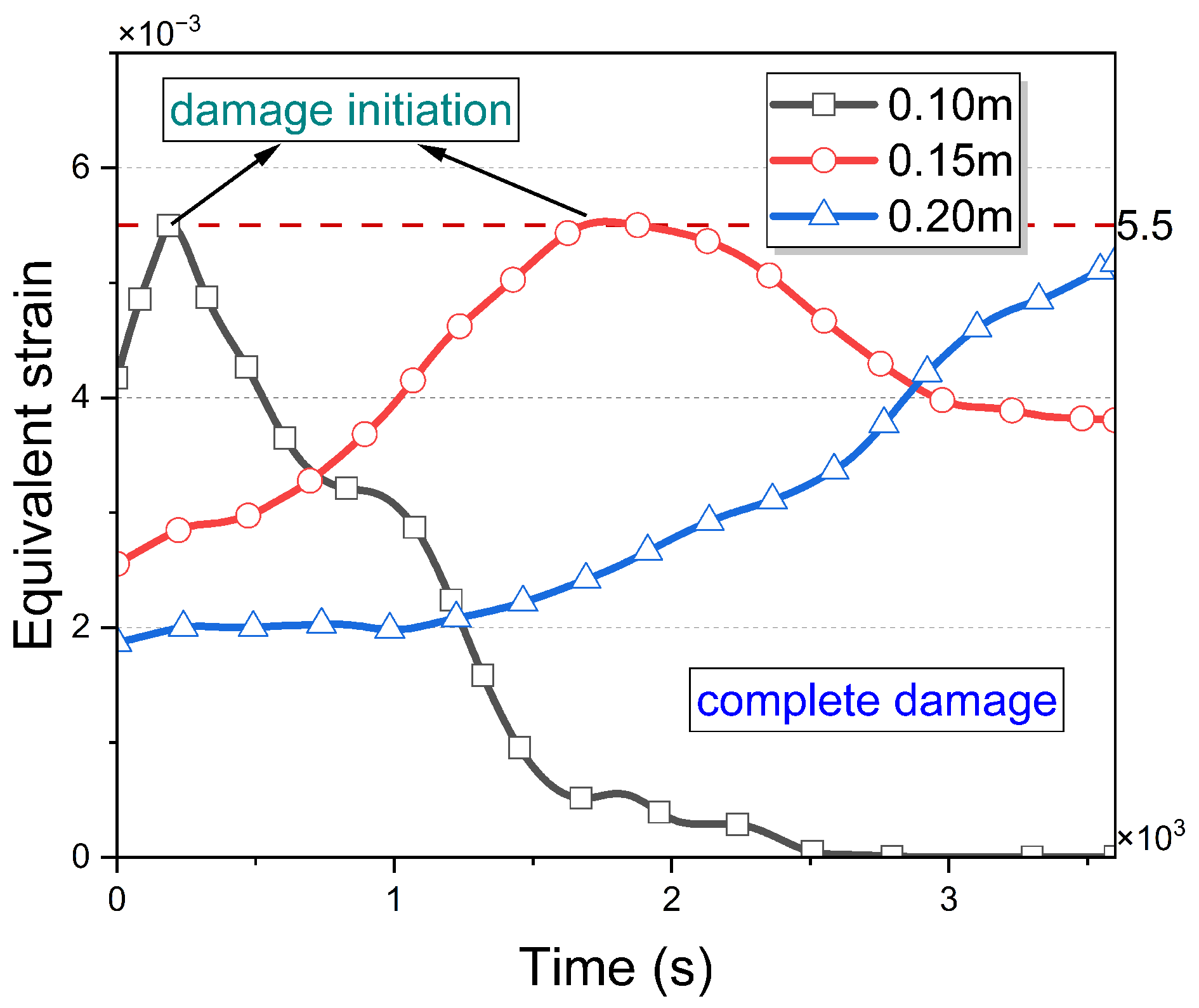
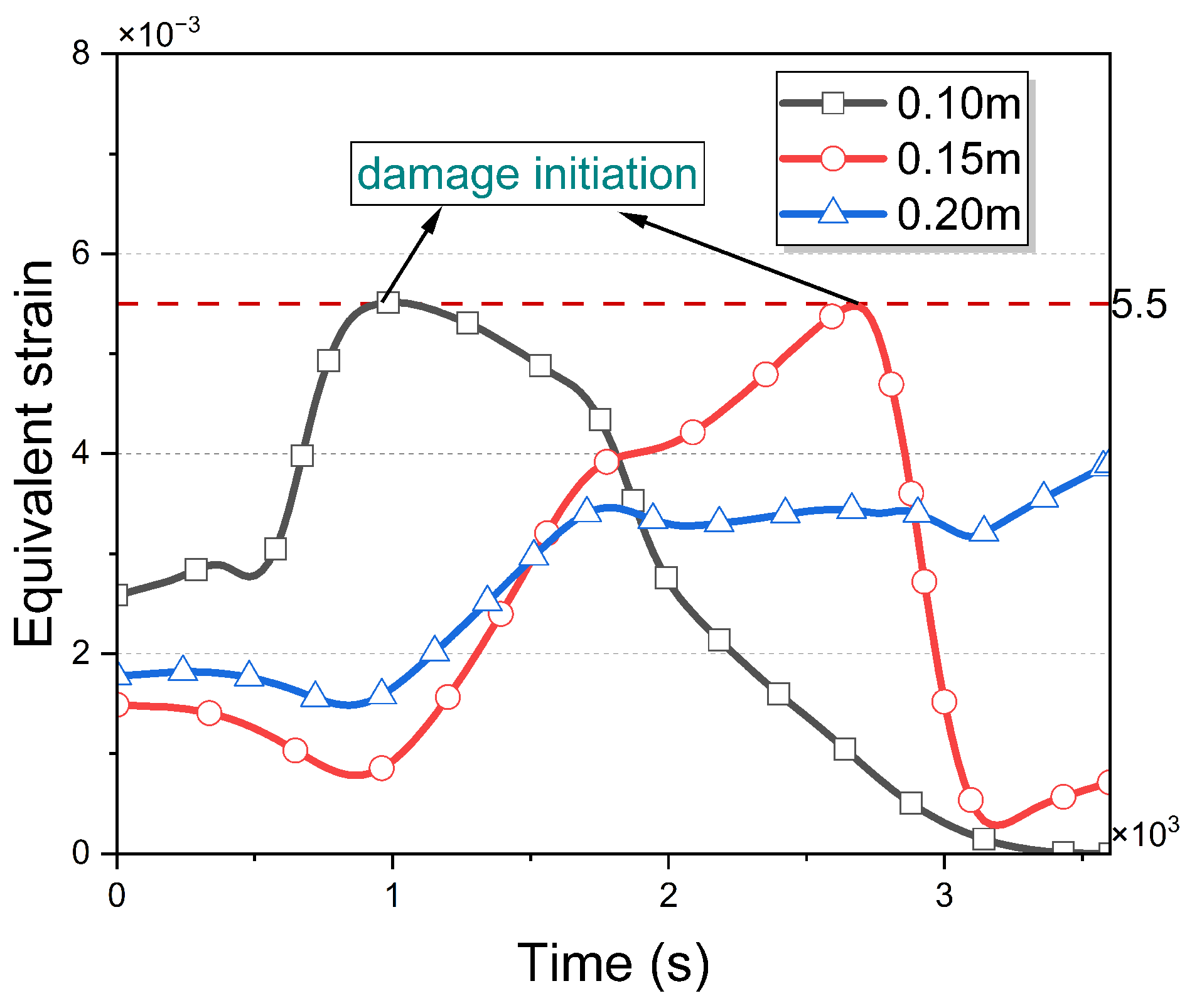
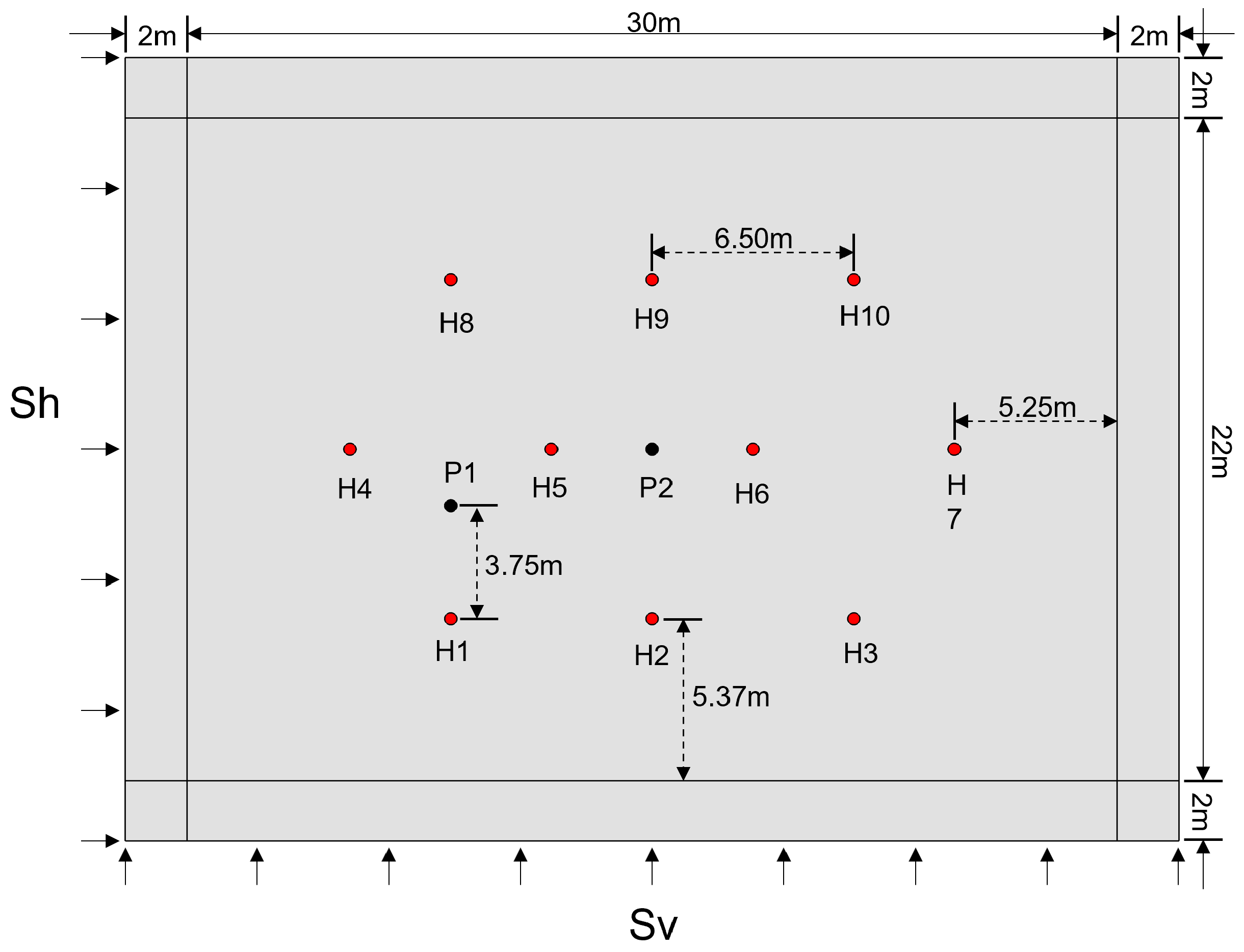
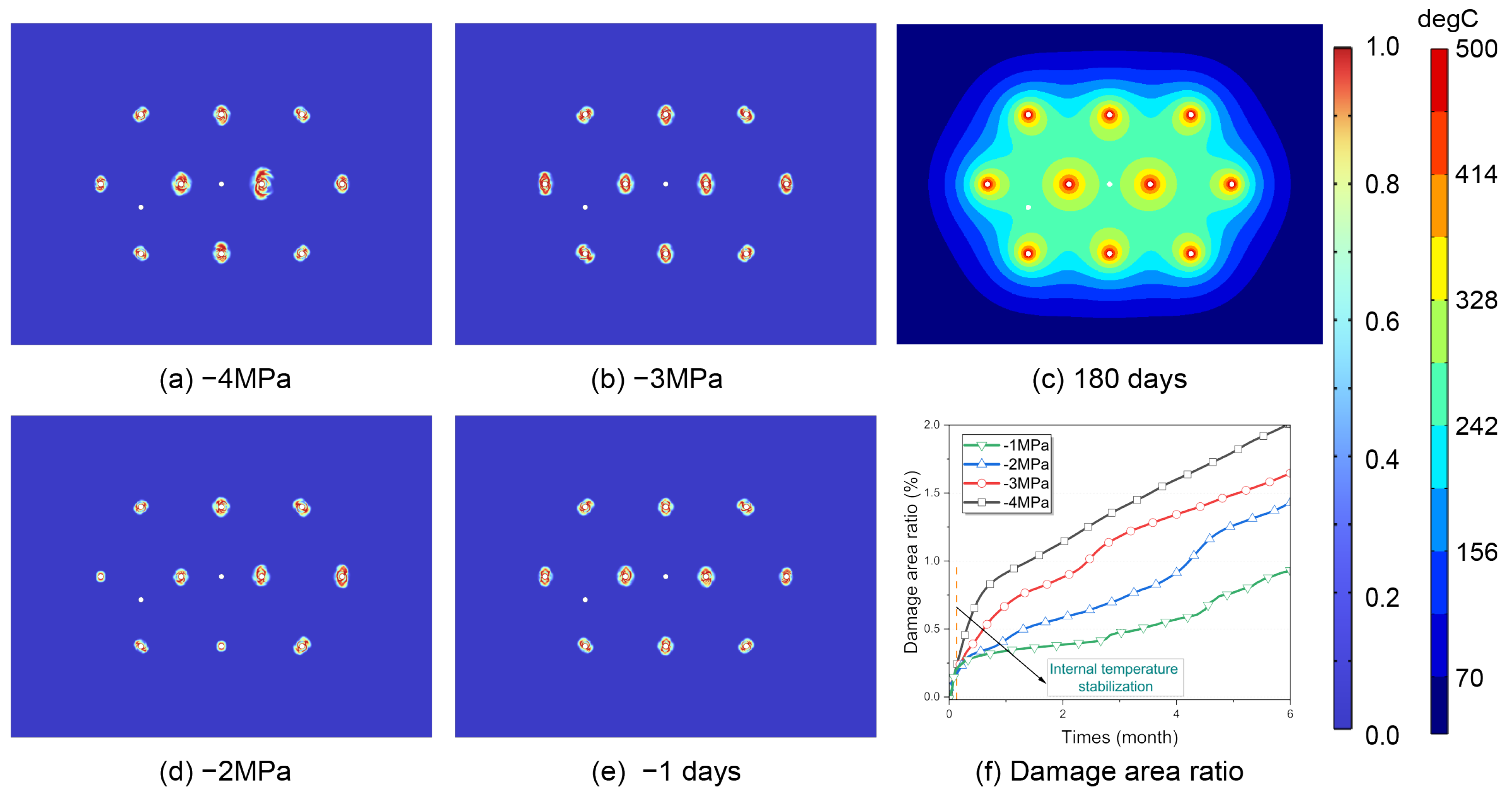
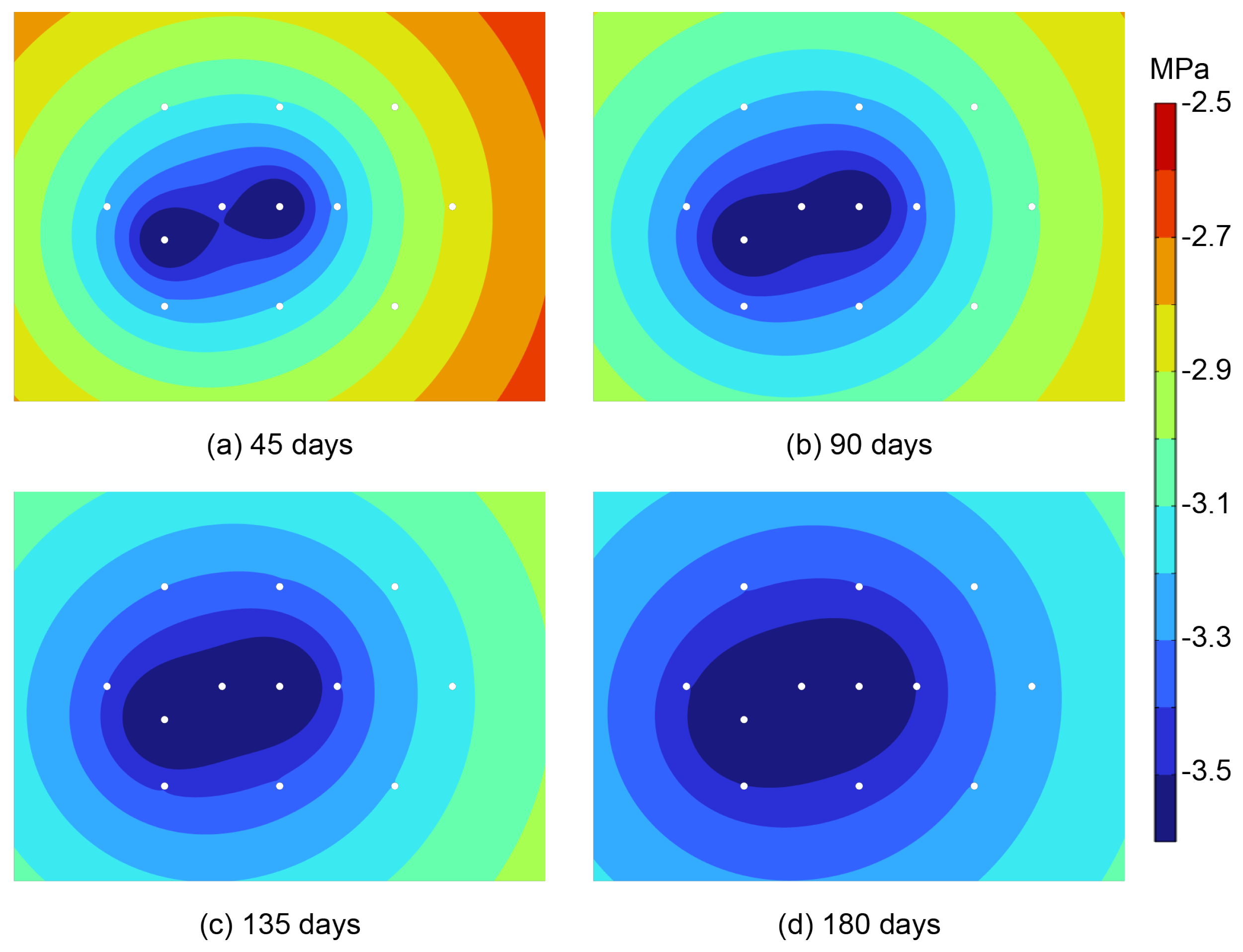
4.2. Damage Analysis of the Well Network
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Feng, L.; Steve, M.; Tang, X.; Gail, T.E.; Mikael, H. China’s unconventional oil: A review of its resources and outlook for long-term production. Energy 2015, 82, 31–42. [Google Scholar] [CrossRef]
- Council, W.E. World Energy Resources 2016; World Energy Council: London, UK, 2016. [Google Scholar]
- Yu, H.; Zhu, Y.; Jin, X.; Liu, H.; Wu, H. Multiscale simulations of shale gas transport in micro/nano-porous shale matrix considering pore structure influence. J. Nat. Gas Sci. Eng. 2019, 64, 28–40. [Google Scholar] [CrossRef]
- Li, X.; Zhou, H.; Wang, Y.; Qian, Y.; Yang, S. Thermoeconomic analysis of oil shale retorting processes with gas or solid heat carrier. Energy 2015, 87, 605–614. [Google Scholar] [CrossRef]
- Gavrilova, O.; Vilu, R.; Vallner, L. A life cycle environmental impact assessment of oil shale produced and consumed in Estonia. Resour. Conserv. Recycl. 2010, 55, 232–245. [Google Scholar] [CrossRef]
- Kang, Z.; Zhao, Y.; Yang, D.; Tian, L.; Li, X. A pilot investigation of pyrolysis from oil and gas extraction from oil shale by In-Situ Superheated Steam Inject. J. Pet. Sci. Eng. 2020, 186, 106785. [Google Scholar] [CrossRef]
- Lyu, C.; Yu, H.; Jin, J.; Xu, W.; Huang, H.; Zhang, J.; Wang, Q.; Liu, J.; Jiang, W.; Liu, H.; et al. Multiphysics phase-field modeling for thermal cracking and permeability evolution in oil shale matrix during in-situ conversion process. Int. J. Rock Mech. Min. Sci. 2024, 176, 105720. [Google Scholar] [CrossRef]
- Han, X.; Kulaots, I.; Jiang, X.; Suuberg, E.M. Review of oil shale semicoke and its combustion utilization. Fuel 2014, 126, 143–161. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, X.; Han, X.; Tong, J. Investigation of Chinese oil shale resources comprehensive utilization performance. Energy 2012, 42, 224–232. [Google Scholar] [CrossRef]
- Lai, D.; Zhan, J.H.; Tian, Y.; Gao, S.; Xu, G. Mechanism of kerogen pyrolysis in terms of chemical structure transformation. Fuel 2017, 199, 504–511. [Google Scholar] [CrossRef]
- Yu, H.; Chen, J.; Zhu, Y.; Wang, F.; Wu, H. Multiscale transport mechanism of shale gas in micro/nano-pores. Int. J. Heat Mass Transf. 2017, 111, 1172–1180. [Google Scholar] [CrossRef]
- Huang, H.; Yu, H.; Xu, W.; Lyu, C.; Micheal, M.; Xu, H.; Liu, H.; Wu, H. A coupled thermo-hydro-mechanical-chemical model for production performance of oil shale reservoirs during in-situ conversion process. Energy 2023, 268, 126700. [Google Scholar] [CrossRef]
- Dokhani, V.; Yu, M.; Bloys, B. A wellbore stability model for shale formations: Accounting for strength anisotropy and fluid induced instability. J. Nat. Gas Sci. Eng. 2016, 32, 174–184. [Google Scholar] [CrossRef]
- Kibodeaux, K.R. Evolution of porosity, permeability, and fluid saturations during thermal conversion of oil shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27–29 October 2014; SPE: Richardson, TX, USA, 2014; p. SPE-170733. [Google Scholar]
- Okland, D.; Cook, J. Bedding-related borehole instability in high-angle wells. In Proceedings of the SPE/ISRM Rock Mechanics in Petroleum Engineering, Trondheim, Norway, 8–10 July 1998; SPE: Richardson, TX, USA, 1998; p. SPE-47285. [Google Scholar]
- Willson, S.; Last, N.; Zoback, M.; Moos, D. Drilling in South America: A wellbore stability approach for complex geologic conditions. In Proceedings of the SPE Latin America and Caribbean Petroleum Engineering Conference, Caracas, Venezuela, 21–23 April 1999; SPE: Richardson, TX, USA, 1999; p. SPE-53940. [Google Scholar]
- Wang, L.; Zhao, Y.; Yang, D.; Kang, Z.; Zhao, J. Effect of pyrolysis on oil shale using superheated steam: A case study on the Fushun oil shale, China. Fuel 2019, 253, 1490–1498. [Google Scholar] [CrossRef]
- Yu, H.; Fan, J.; Chen, J.; Zhu, Y.; Wu, H. Pressure-dependent transport characteristic of methane gas in slit nanopores. Int. J. Heat Mass Transf. 2018, 123, 657–667. [Google Scholar] [CrossRef]
- He, L.; Ma, Y.; Yue, C.; Li, S.; Tang, X. The heating performance and kinetic behaviour of oil shale during microwave pyrolysis. Energy 2022, 244, 123021. [Google Scholar] [CrossRef]
- Meier, T.; Rybacki, E.; Reinicke, A.; Dresen, G. Influence of borehole diameter on the formation of borehole breakouts in black shale. Int. J. Rock Mech. Min. Sci. 2013, 62, 74–85. [Google Scholar] [CrossRef]
- Nguyen, V.; Abousleiman, Y.; Hoang, S.; Inst, P. Analyses of Wellbore Instability in Drilling Through Chemically Active Fractured Rock Formations: Nahr Umr Shale. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Sanabis, Bahrain, 11–14 March 2007. [Google Scholar]
- Guo, T.; Tang, S.; Sun, J.; Gong, F.; Liu, X.; Qu, Z.; Zhang, W. A coupled thermal-hydraulic-mechanical modeling and evaluation of geothermal extraction in the enhanced geothermal system based on analytic hierarchy process and fuzzy comprehensive evaluation. Appl. Energy 2020, 258, 113981. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Zhang, D. A fully coupled thermo-hydro-mechanical, three-dimensional model for hydraulic stimulation treatments. J. Nat. Gas Sci. Eng. 2016, 34, 64–84. [Google Scholar] [CrossRef]
- Wang, X.; Li, P.; Qi, T.; Li, L.; Li, T.; Jin, J.; Lu, D. A framework to model the hydraulic fracturing with thermo-hydro-mechanical coupling based on the variational phase-field approach. Comput. Methods Appl. Mech. Eng. 2023, 417, 116406. [Google Scholar] [CrossRef]
- Li, L.C.; Tang, C.A.; Wang, S.Y.; Yu, J. A coupled thermo-hydrologic-mechanical damage model and associated application in a stability analysis on a rock pillar. Tunn. Undergr. Space Technol. 2013, 34, 38–53. [Google Scholar] [CrossRef]
- Wei, C.; Zhu, W.; Chen, S.; Ranjith, P.G. A Coupled Thermal–Hydrological–Mechanical Damage Model and Its Numerical Simulations of Damage Evolution in APSE. Materials 2016, 9, 841. [Google Scholar] [CrossRef] [PubMed]
- Phan, M.; Meftah, F.; Rigobert, S.; Autuori, P.; Lenglet, C.; Dal Pont, S. A finite element modeling of thermo-hydro-mechanical behavior and numerical simulations of progressing spalling front. Procedia Eng. 2011, 10, 3128–3133. [Google Scholar] [CrossRef]
- Forest, S. Micromorphic Approach for Gradient Elasticity, Viscoplasticity, and Damage. J. Eng. Mech. 2009, 135, 117–131. [Google Scholar] [CrossRef]
- Zhou, Y.; Rajapakse, R.; Graham, J. A coupled thermoporoelastic model with thermo-osmosis and thermal-filtration. Int. J. Solids Struct. 1998, 35, 4659–4683. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Coussy, O. Poromechanics, 2nd ed.; OCLC: Ocm52992889; Wiley: Chichester, UK; Hoboken, NJ, USA, 2004. [Google Scholar]
- Peerlings, R.H.J.; De Borst, R.; Brekelmans, W.A.M.; De Vree, J.H.P. Gradient Enhanced Damage for Quasi-Brittle Materials. Int. J. Numer. Methods Eng. 1996, 39, 3391–3403. [Google Scholar] [CrossRef]
- de Borst, R.; Verhoosel, C.V. Gradient damage Vs Phase-Field Approaches Fract. Similarities Differ. Comput. Methods Appl. Mech. Eng. 2016, 312, 78–94. [Google Scholar] [CrossRef]
- Peerlings, R.H.J.; Massart, T.J.; Geers, M.G.D. A thermodynamically motivated implicit gradient damage framework and its application to brick masonry cracking. Comput. Methods Appl. Mech. Eng. 2004, 193, 3403–3417. [Google Scholar] [CrossRef]
- De Vree, J.H.P.; Brekelmans, W.A.M.; van Gils, M. Comparison of nonlocal approaches in continuum damage mechanics. Comput. Struct. 1995, 55, 581–588. [Google Scholar] [CrossRef]
- Poh, L.H.; Sun, G. Localizing gradient damage model with decreasing interactions. Int. J. Numer. Methods Eng. 2017, 110, 503–522. [Google Scholar] [CrossRef]
- Sarkar, S.; Singh, I.V.; Mishra, B.K. A Thermo-mechanical gradient enhanced damage method for fracture. Comput. Mech. 2020, 66, 1399–1426. [Google Scholar] [CrossRef]
- Jiang, C.; Wu, X.; Li, J.; Song, F.; Shao, Y.; Xu, X.; Yan, P. A study of the mechanism of formation and numerical simulations of crack patterns in ceramics subjected to thermal shock. Acta Mater. 2012, 60, 4540–4550. [Google Scholar] [CrossRef]
- Gao, Y.; Detournay, E. Contraction and expansion of a cylindrical cavity in an elastoplastic medium: A dislocation-based approach. Int. J. Numer. Anal. Methods Geomech. 2024, 48, 4014–4034. [Google Scholar] [CrossRef]
- van den Hoek, P. Prediction of different types of cavity failure using bifurcation theory. In ARMA US Rock Mechanics/Geomechanics Symposium; ARMA: Washington, DC, USA, 2001; p. ARMA-01. Available online: https://onepetro.org/ARMAUSRMS/proceedings-pdf/ARMA01/All-ARMA01/ARMA-01-0045/1889461/arma-01-0045.pdf (accessed on 7 July 2001).





| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Young’s modulus | E | GPa | 370 |
| Poisson’s rate | - | ||
| Uniaxial tensile strength | MPa | 180 | |
| Thermal expansion coefficient | |||
| Density | 3980 | ||
| Specific heat | C | 880 | |
| Thermal conductivity | k | 31 |
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Initial temperature | GPa | 20 | |
| Young’s modulus of shale | GPa | 30 | |
| Young’s modulus of cement | GPa | ||
| Young’s modulus of steel | GPa | 205 | |
| Poisson ratio of shale | - | ||
| Poisson ratio of cement | - | ||
| Poisson ratio of steel | - | ||
| Shale density | 2450 | ||
| Cement density | 2300 | ||
| Steel density | 7850 | ||
| Heat capacity of shale | 880 | ||
| Heat capacity of cement | 880 | ||
| Heat capacity of steel | 475 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Jin, J.; Chen, W.; Zhao, M.; Liu, J.; Fang, B.; Ye, T. A Thermo-Hydro-Mechanical Damage Coupling Model for Stability Analysis During the In Situ Conversion Process. Energies 2025, 18, 1424. https://doi.org/10.3390/en18061424
Li G, Jin J, Chen W, Zhao M, Liu J, Fang B, Ye T. A Thermo-Hydro-Mechanical Damage Coupling Model for Stability Analysis During the In Situ Conversion Process. Energies. 2025; 18(6):1424. https://doi.org/10.3390/en18061424
Chicago/Turabian StyleLi, Guoping, Juan Jin, Weixi Chen, Minghui Zhao, Jiandong Liu, Bo Fang, and Tingfu Ye. 2025. "A Thermo-Hydro-Mechanical Damage Coupling Model for Stability Analysis During the In Situ Conversion Process" Energies 18, no. 6: 1424. https://doi.org/10.3390/en18061424
APA StyleLi, G., Jin, J., Chen, W., Zhao, M., Liu, J., Fang, B., & Ye, T. (2025). A Thermo-Hydro-Mechanical Damage Coupling Model for Stability Analysis During the In Situ Conversion Process. Energies, 18(6), 1424. https://doi.org/10.3390/en18061424





