Modeling an All-Copper Redox Flow Battery for Microgrid Applications: Impact of Current and Flow Rate on Capacity Fading and Deposition
Abstract
:1. Introduction
2. Materials and Methods
2.1. Electrochemical Reactions
2.2. Side Reactions
3. Numerical Modeling
3.1. Assumptions
- 1.
- Both electrolytes are incompressible and have constant fluid flows.
- 2.
- The dilute solution theory is applied to both electrolytes.
- 3.
- The anion exchange membrane is permeable to all species. Indeed, the crossover of other ions is taken into account.
- 4.
- Effects of gravity are not considered.
- 5.
- The battery operates under isothermal conditions.
- 6.
- Chemical reactions occur at the negative electrode and are considered for the first time in this work.
- 7.
- The evolution of hydrogen and oxygen is neglected since the battery operates inside the water window potential.
- 8.
- The tertiary current distribution is applied to all three battery domains: the electrodes and the membrane.
- 9.
- Ion activities are taken into account
3.2. Transport in Negative Channel, Positive Electrode, and Membrane
3.3. Electrochemical Kinetics
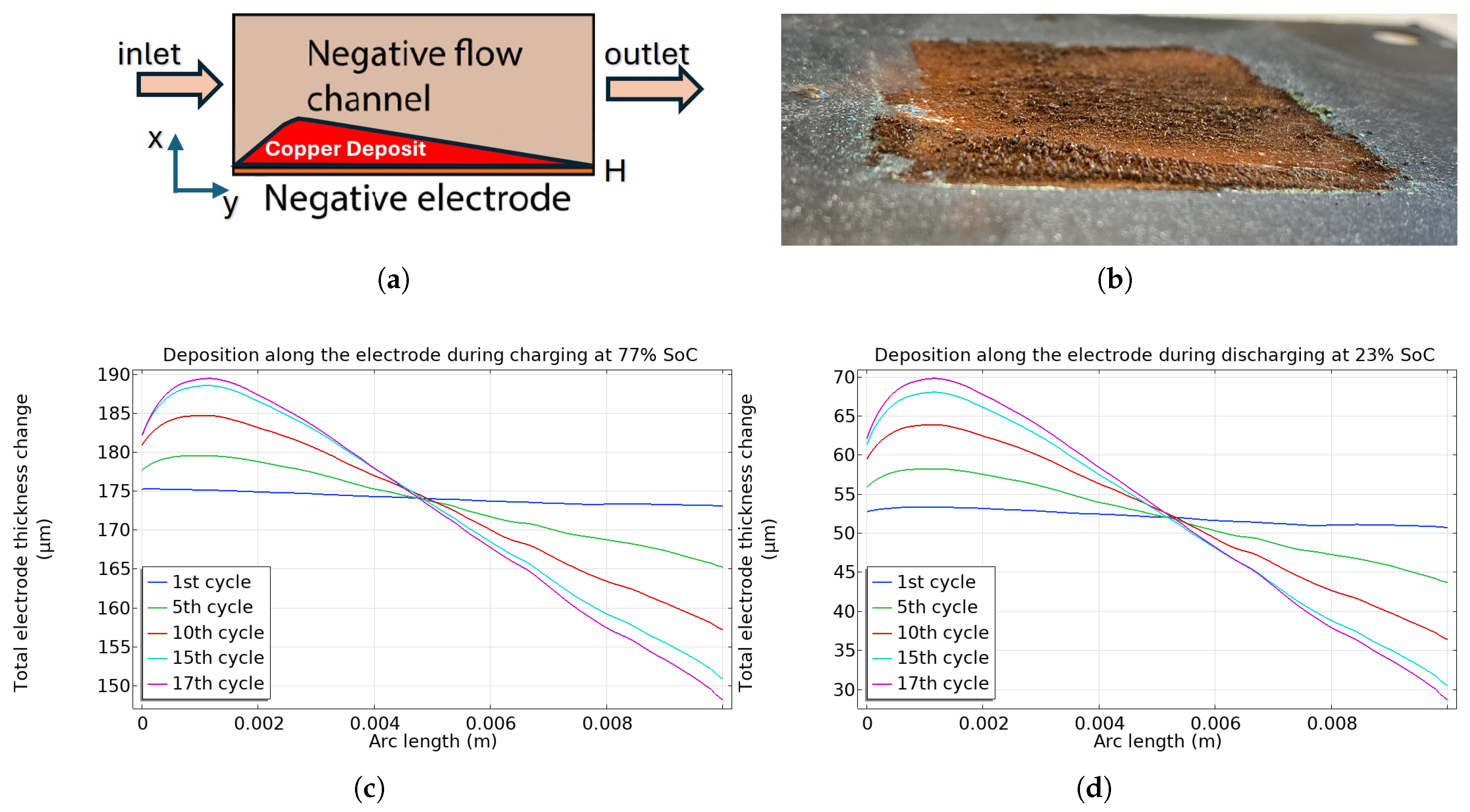
3.4. Negative Electrode Deposition
3.5. Tanks
3.6. Side Reactions
3.7. Other Boundary Conditions
4. Simulation Setup and Parameter Optimization
5. Results and Discussion
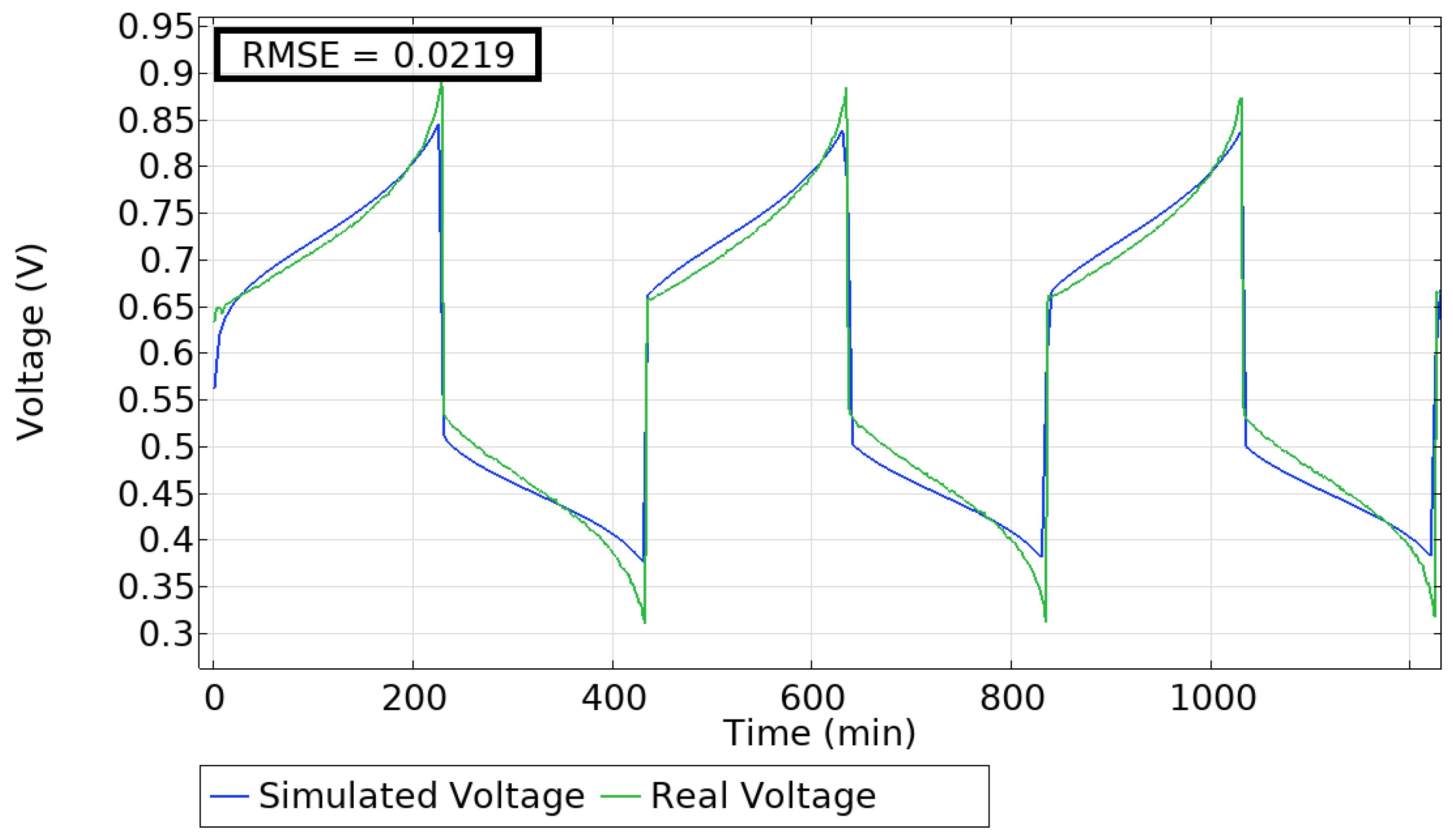
5.1. Model Validation
5.2. Tank Concentrations
5.3. Copper Deposition
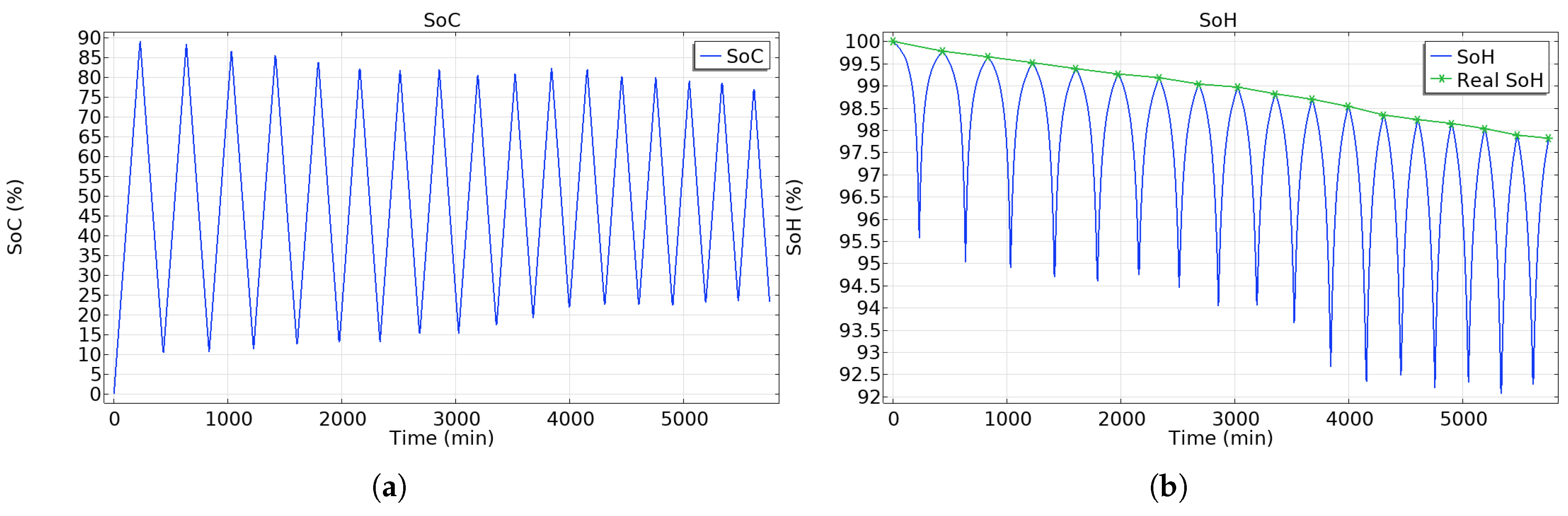
5.4. SoC and SoH Estimations
5.5. Effect of Current
5.6. Effect of Flow Rate
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gikunoo, E.K.; Han, D.; Vinothkannan, M.; Shanmugam, S. Synthesis and characterization of highly durable hydrocarbon-based composite membrane for zinc-bromine redox flow battery. J. Power Sources 2023, 563, 232821. [Google Scholar] [CrossRef]
- Gür, T.M. Review of electrical energy storage technologies, materials and systems: Challenges and prospects for large-scale grid storage. Energy Environ. Sci. 2018, 11, 2696–2767. [Google Scholar] [CrossRef]
- Rahman, M.; Oni, A.O.; Gemechu, E.D.; Kumar, A. Assessment of energy storage technologies: A review. Energy Convers. Manag. 2020, 223, 113295. [Google Scholar] [CrossRef]
- Braff, W.A.; Mueller, J.M.; Trancik, J.E. Value of storage technologies for wind and solar energy. Nat. Clim. Chang. 2016, 6, 964–969. [Google Scholar] [CrossRef]
- Sanchez-Diez, E.; Ventosa, E.; Guarnieri, M.; Trovò, A.; Flox, C.; Marcilla, R.; Soavi, F.; Mazúr, P.; Aranzabe, E.; Ferret, R. Redox flow batteries: Status and perspective towards sustainable stationary energy storage. J. Power Sources 2021, 481, 228804. [Google Scholar] [CrossRef]
- Zhang, H.; Li, X.; Zhang, J. Redox Flow Batteries: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Ye, R.; Henkensmeier, D.; Yoon, S.J.; Huang, Z.; Kim, D.K.; Chang, Z.; Kim, S.; Chen, R. Redox flow batteries for energy storage: A technology review. J. Electrochem. Energy Convers. Storage 2018, 15, 010801. [Google Scholar] [CrossRef]
- Aluko, A.; Knight, A. A Review on Vanadium Redox Flow Battery Storage Systems for Large-Scale Power Systems Application. IEEE Access 2023, 11, 13773–13793. [Google Scholar] [CrossRef]
- Sanz, L.; Badenhorst, W.D.; Lacarbonara, G.; Faggiano, L.; Lloyd, D.; Kauranen, P.; Arbizzani, C.; Murtomäki, L. All-copper Flow Batteries. In Flow Batteries; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2023; Chapter 38; pp. 855–873. [Google Scholar]
- Faggiano, L.; Lacarbonara, G.; Badenhorst, W.; Murtomäki, L.; Sanz, L.; Arbizzani, C. Short thermal treatment of carbon felts for copper-based redox flow batteries. J. Power Sources 2022, 520, 230846. [Google Scholar] [CrossRef]
- Sanz, L.; Lloyd, D.; Magdalena, E.; Palma, J.; Kontturi, K. Description and performance of a novel aqueous All-Copper Redox Flow Battery. J. Power Sources 2014, 268, 121–128. [Google Scholar] [CrossRef]
- Zanzola, E.; Gentil, S.; Gschwend, G.; Reynard, D.; Smirnov, E.; Dennison, C.; Girault, H.H.; Peljo, P. Solid electrochemical energy storage for aqueous redox flow batteries: The case of copper hexacyanoferrate. Electrochim. Acta 2019, 321, 134704. [Google Scholar] [CrossRef]
- Badenhorst, W.D.; Sanz, L.; Arbizzani, C.; Murtomäki, L. Performance improvements for the All-Copper Redox Flow Battery: Membranes, electrodes, and electrolytes. Energy Rep. 2022, 8, 8690–8700. [Google Scholar] [CrossRef]
- Lloyd, D.; Magdalena, E.; Sanz, L.; Murtomäki, L.; Kontturi, K. Preparation of a cost-effective, scalable and energy efficient All-Copper Redox Flow Battery. J. Power Sources 2015, 292, 87–94. [Google Scholar] [CrossRef]
- Badenhorst, W.; Jensen, C.M.; Jakobsen, U.; Esfahani, Z.; Murtomäki, L. Control-Oriented Electrochemical Model and Parameter Estimation for an All-Copper Redox Flow Battery. Batteries 2023, 9, 272. [Google Scholar] [CrossRef]
- Shah, A.A.; Watt-Smith, M.J.; Walsh, F.C. A dynamic performance model for redox-flow batteries involving soluble species. Electrochim. Acta 2008, 53, 8087–8100. [Google Scholar] [CrossRef]
- Shah, A.A.; Al-Fetlawi, H.; Walsh, F.C. Dynamic modelling of hydrogen evolution effects in the all-vanadium redox flow battery. Electrochim. Acta 2010, 55, 1125–1139. [Google Scholar] [CrossRef]
- Al-Fetlawi, H.; Shah, A.A.; Walsh, F.C. Modelling the effects of oxygen evolution in the all-vanadium redox flow battery. Electrochim. Acta 2010, 55, 3192–3205. [Google Scholar] [CrossRef]
- Hao, L.; Wang, Y.; He, Y. Modeling of ion crossover in an all-vanadium redox flow battery with the interfacial effect at membrane/electrode interfaces. J. Electrochem. Soc. 2019, 166, A1310–A1322. [Google Scholar] [CrossRef]
- Won, S.; Oh, K.; Ju, H. Numerical Analysis of Vanadium Crossover Effects in All-vanadium Redox Flow Batteries. Electrochim. Acta 2015, 177, 310–320. [Google Scholar] [CrossRef]
- Knehr, K.W.; Agar, E.; Dennison, C.R.; Kalidindi, A.R.; Kumbur, E.C. A transient vanadium flow battery model incorporating vanadium crossover and water transport through the membrane. J. Electrochem. Soc. 2012, 159, A1446–A1459. [Google Scholar] [CrossRef]
- Lei, Y.; Zhang, B.W.; Bai, B.F.; Zhao, T.S. A transient electrochemical model incorporating the Donnan effect for all-vanadium redox flow batteries. J. Power Sources 2015, 299, 202–211. [Google Scholar] [CrossRef]
- Oh, K.; Yoo, H.; Ko, J.; Won, S.; Ju, H. Three-dimensional, transient, nonisothermal model of all-vanadium redox flow batteries. Energy 2015, 81, 3–14. [Google Scholar] [CrossRef]
- D’Adamo, M.; Daub, N.; Trilla, L.; Saez-Zamora, J.A.; Paz-Garcia, J.M. Modeling of a Non-Aqueous Redox Flow Battery for Performance and Capacity Fade Analysis. Batteries 2025, 11, 8. [Google Scholar] [CrossRef]
- Amini, K.; Pritzker, M.D. A two-dimensional transient model for a zinc-cerium redox flow battery validated by extensive experimental data. J. Power Sources 2021, 506, 230237. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, J.; Yan, S.C.; Fan, Q.; Lund, P.D. Modeling of zinc bromine redox flow battery with application to channel design. J. Power Sources 2020, 450, 227436. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, W.; Liu, Y.; Zeng, Y.; He, Q.; Tan, P.; Ni, M. Mathematical modeling and numerical analysis of alkaline zinc-iron flow batteries for energy storage applications. J. Power Sources 2021, 506, 230237. [Google Scholar] [CrossRef]
- Powell, M. The BOBYQA Algorithm for Bound Constrained Optimization Without Derivatives; Technical Report; Department of Applied Mathematics and Theoretical Physics: Cambridge, UK, 2009. [Google Scholar]
- Nikolić, N.; Pavlović, L.; Pavlović, M.G.; Popov, K. Effect of temperature on the electrodeposition of disperse copper deposits. J. Serbian Chem. Soc. 2007, 72, 1369–1381. [Google Scholar] [CrossRef]
- Rashkov, S.; Stoichev, D.S.; Tomov, I. Influence of current density and temperature on the morphology and preferred orientation of electrodeposited copper coatings. Electrochim. Acta 1972, 17, 1955–1964. [Google Scholar] [CrossRef]
- Banthia, S.; Sengupta, S.; Mallik, M.; Das, S. Substrate effect on electrodeposited copper morphology and crystal shapes. Surface Eng. 2017, 34, 485–492. [Google Scholar] [CrossRef]





| Parameter | Value | Units | Description |
|---|---|---|---|
| a | 3.5 × 105 | [m2/m3] | Specific surface area |
| 0.2 | [-] | Porosity of the membrane | |
| 0.93 | [-] | Porosity of the positive porous electrodes | |
| H | 1 | [cm] | Height of the cell |
| 1 | [cm] | Length of the cell | |
| 2000 | [μm] | Thickness of the electrodes | |
| 30 | [μm] | Thickness of the membrane | |
| Q | 30 | [mL/min] | Flow rate circulated through each electrode |
| 3 | [mL] | Volume of circulated solution in each electrode | |
| 20 | [mA/cm2] | Applied current density | |
| T | 60 | °C | Temperature |
| 2.5 × 10−7 | [1/(M·s)] | Rate constant | |
| 2.2 × 10−6 | [-] | Equilibrium constant | |
| 7 × 10−10 | [mol/m2] | Maximum surface concentration |
| Parameter | Value | Units | Parameter | Value | Units |
|---|---|---|---|---|---|
| [m2/s] | 6 | [M] | |||
| [m2/s] | 7 | [M] | |||
| [m2/s] | 1 | [M] | |||
| [m2/s] | 0.001 | [M] | |||
| 0.001 | [M] |
| Parameter | Value | Units | Description |
|---|---|---|---|
| [m2/s] | Membrane Diffusion coefficient of | ||
| [m2/s] | Membrane Diffusion coefficient of | ||
| [m2/s] | Membrane Diffusion coefficient of | ||
| [m2/s] | Membrane Diffusion coefficient of | ||
| 0.17 | [-] | Anodic charge transfer coefficient negative electrode | |
| 0.8 | [-] | Anodic charge transfer coefficient positive electrode | |
| 61.483 | [A/m2] | Reference exchange current density negative electrode | |
| 245.33 | [A/m2] | Reference exchange current density positive electrode | |
| 0.4 | [-] | ion activity | |
| 1 | [-] | ion activity | |
| 0.9 | [-] | ion activity | |
| 0.9 | [-] | ion activity |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Adamo, M.; Badenhorst, W.; Murtomäki, L.; Cordoba, P.; Derbeli, M.; Saez-Zamora, J.A.; Trilla, L. Modeling an All-Copper Redox Flow Battery for Microgrid Applications: Impact of Current and Flow Rate on Capacity Fading and Deposition. Energies 2025, 18, 2084. https://doi.org/10.3390/en18082084
D’Adamo M, Badenhorst W, Murtomäki L, Cordoba P, Derbeli M, Saez-Zamora JA, Trilla L. Modeling an All-Copper Redox Flow Battery for Microgrid Applications: Impact of Current and Flow Rate on Capacity Fading and Deposition. Energies. 2025; 18(8):2084. https://doi.org/10.3390/en18082084
Chicago/Turabian StyleD’Adamo, Mirko, Wouter Badenhorst, Lasse Murtomäki, Paula Cordoba, Mohamed Derbeli, Jose A. Saez-Zamora, and Lluís Trilla. 2025. "Modeling an All-Copper Redox Flow Battery for Microgrid Applications: Impact of Current and Flow Rate on Capacity Fading and Deposition" Energies 18, no. 8: 2084. https://doi.org/10.3390/en18082084
APA StyleD’Adamo, M., Badenhorst, W., Murtomäki, L., Cordoba, P., Derbeli, M., Saez-Zamora, J. A., & Trilla, L. (2025). Modeling an All-Copper Redox Flow Battery for Microgrid Applications: Impact of Current and Flow Rate on Capacity Fading and Deposition. Energies, 18(8), 2084. https://doi.org/10.3390/en18082084







