Seismic Response Mitigation of a Television Transmission Tower by Shape Memory Alloy Dampers
Abstract
:1. Introduction
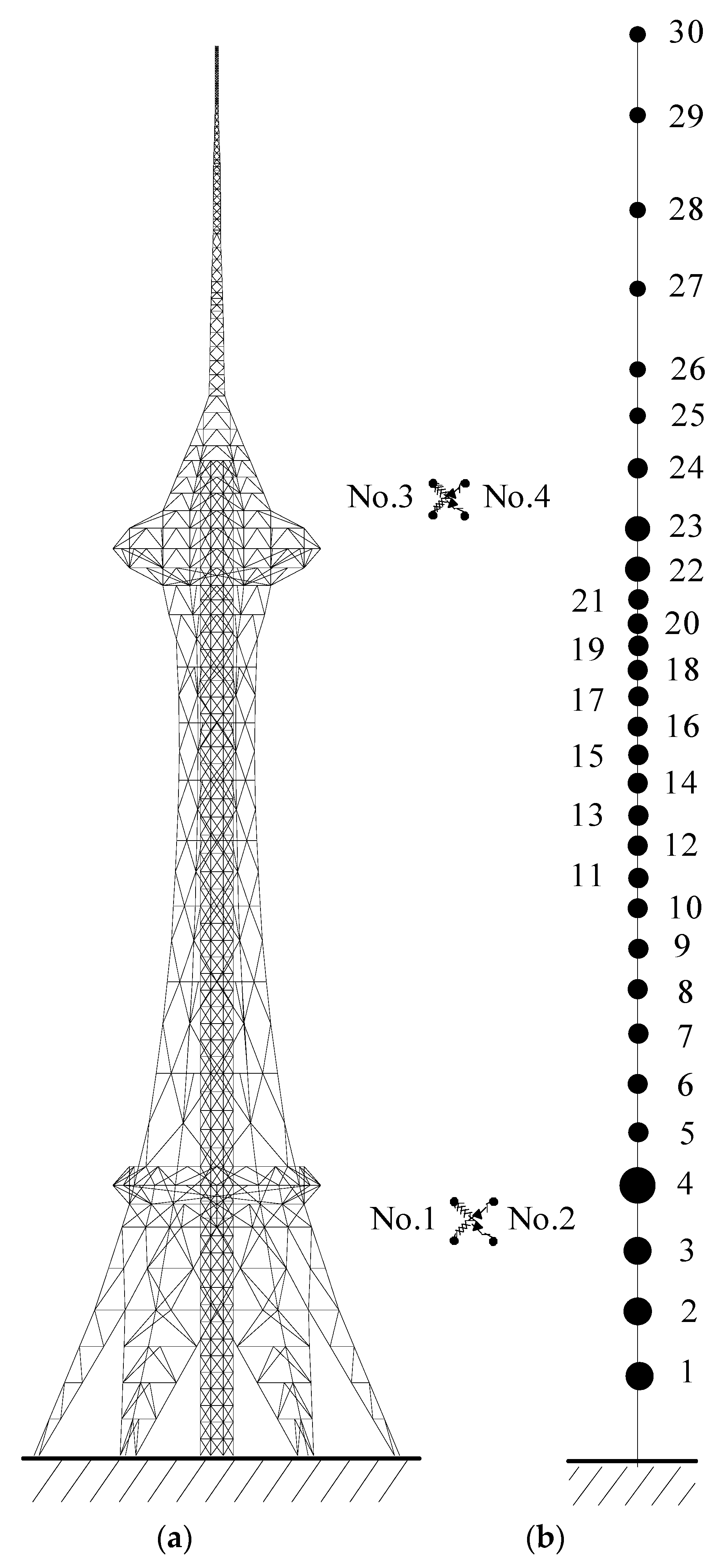
2. Seismic Responses of a TV Transmission Tower
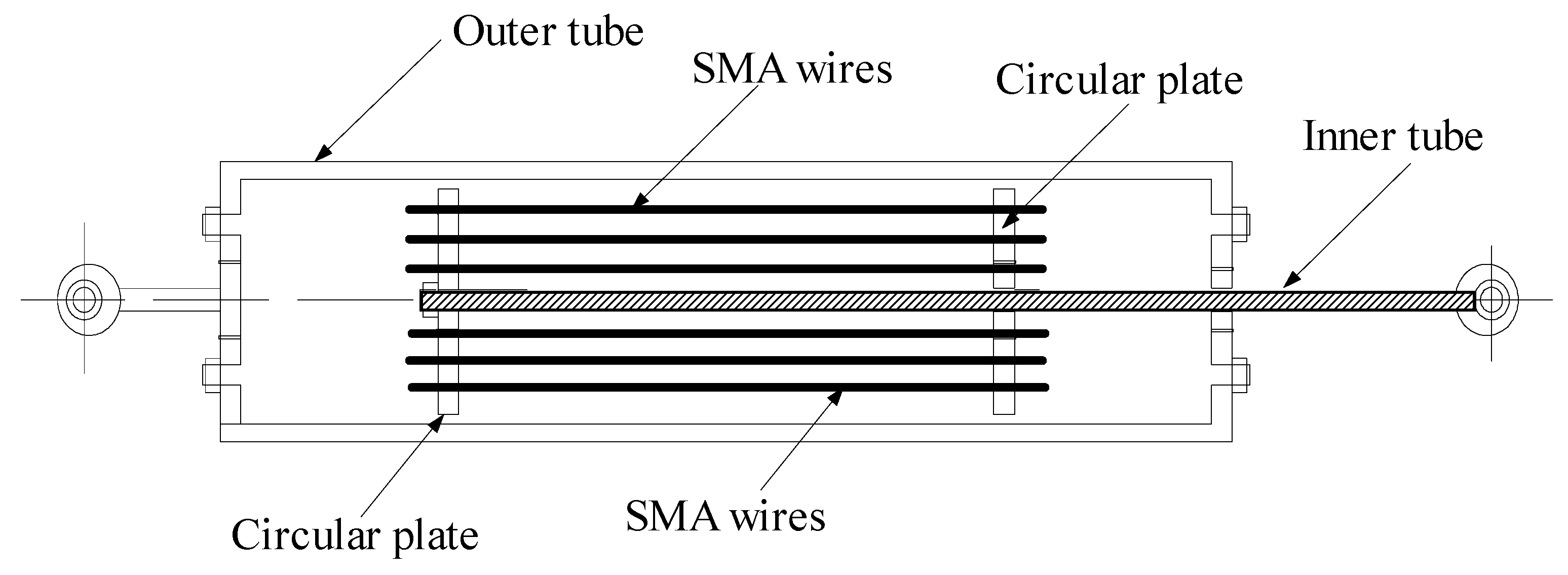
3. Model of SMA Damper
- (1)
- Paths O-A and E-O are elastic (full austenite):The control force of the SMA damper u(t) is:where is the length of the damper after deformation; A is the cross-sectional area of SMA wires; ls is the initial length of the SMA wires.
- (2)
- Path A-B (forward transformation):
- (3)
- Path B-C is elastic (full martensite):
- (4)
- Path B-D is elastic (full martensite)
- (5)
- Path D-E (reverse transformation):in which σ(t) and ε(t) are the stress and the strain of SMA wires, respectively.
4. Dynamic Analysis of the Controlled Tower
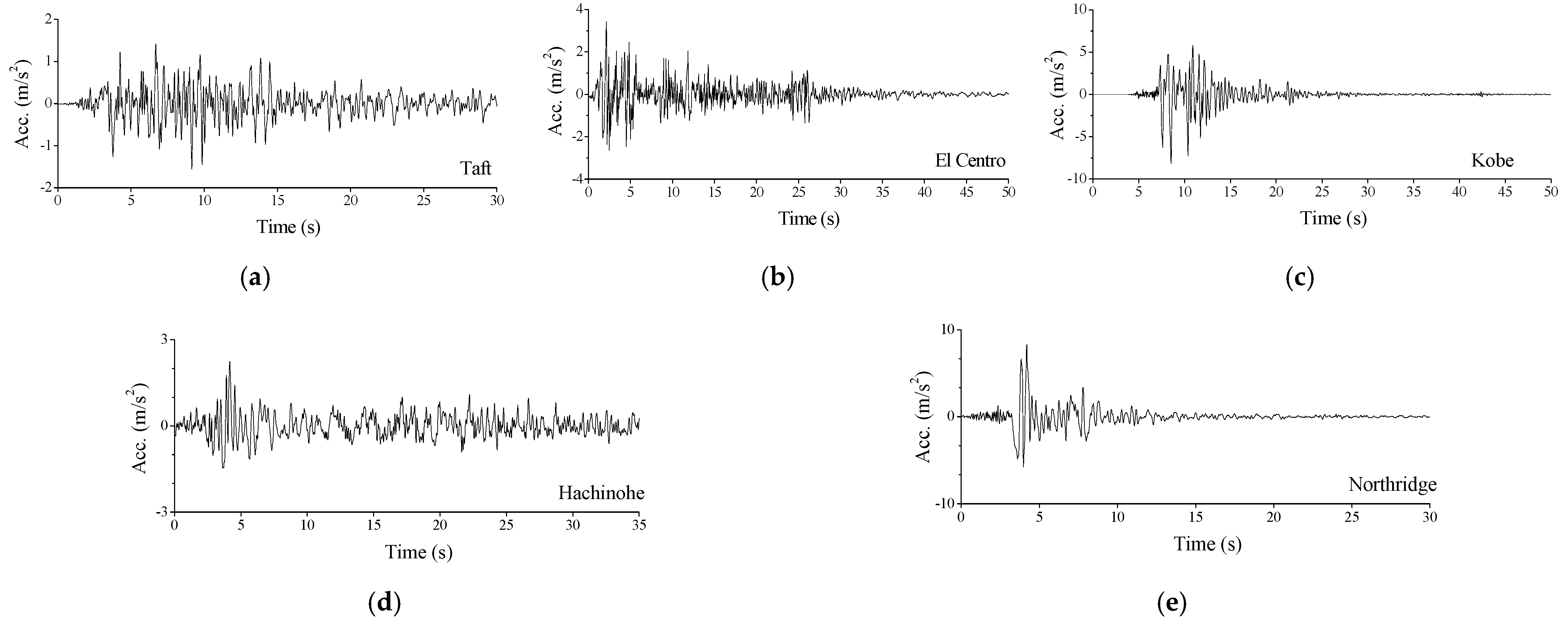
5. Case Study
5.1. Analytical Parameters
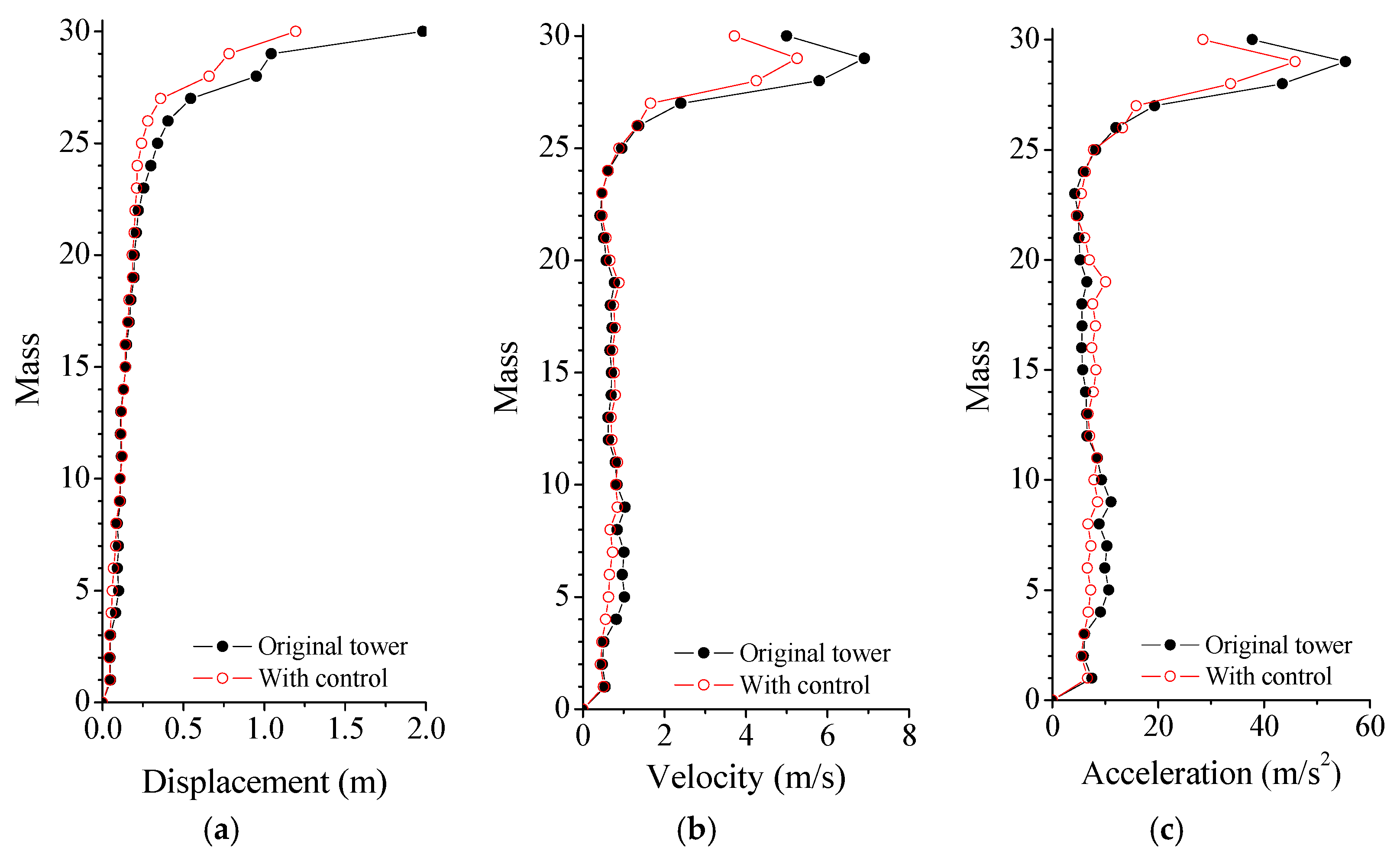
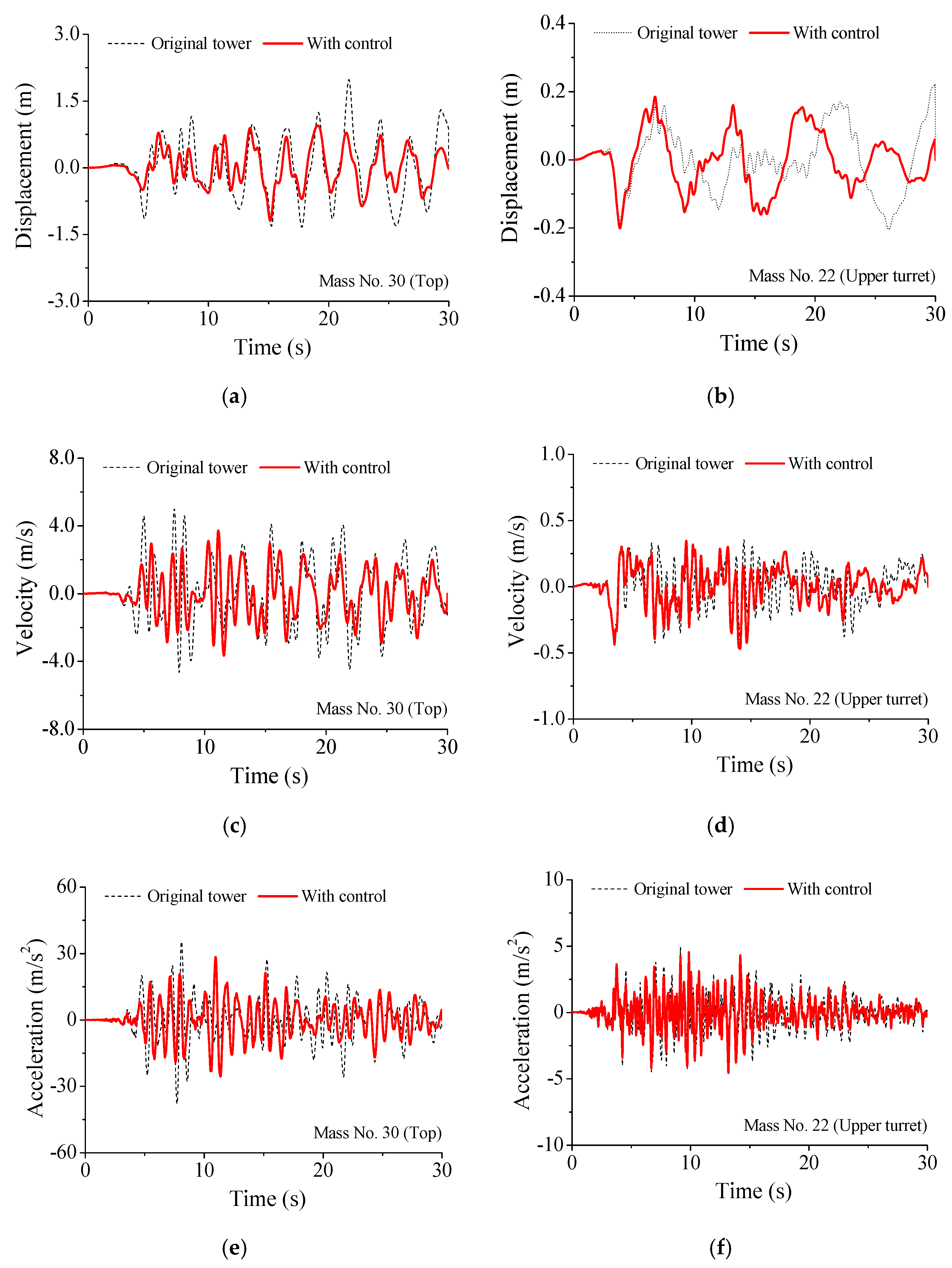
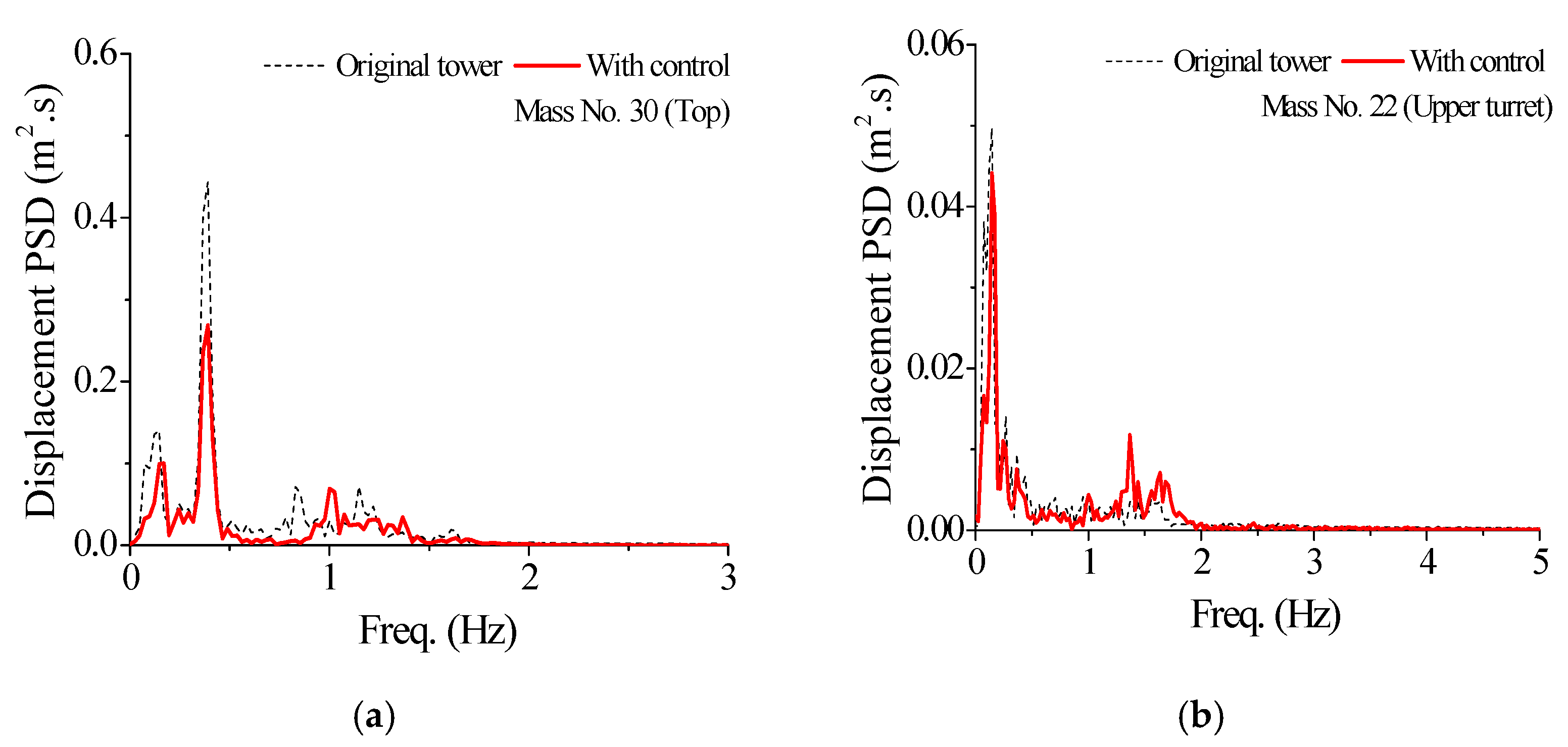
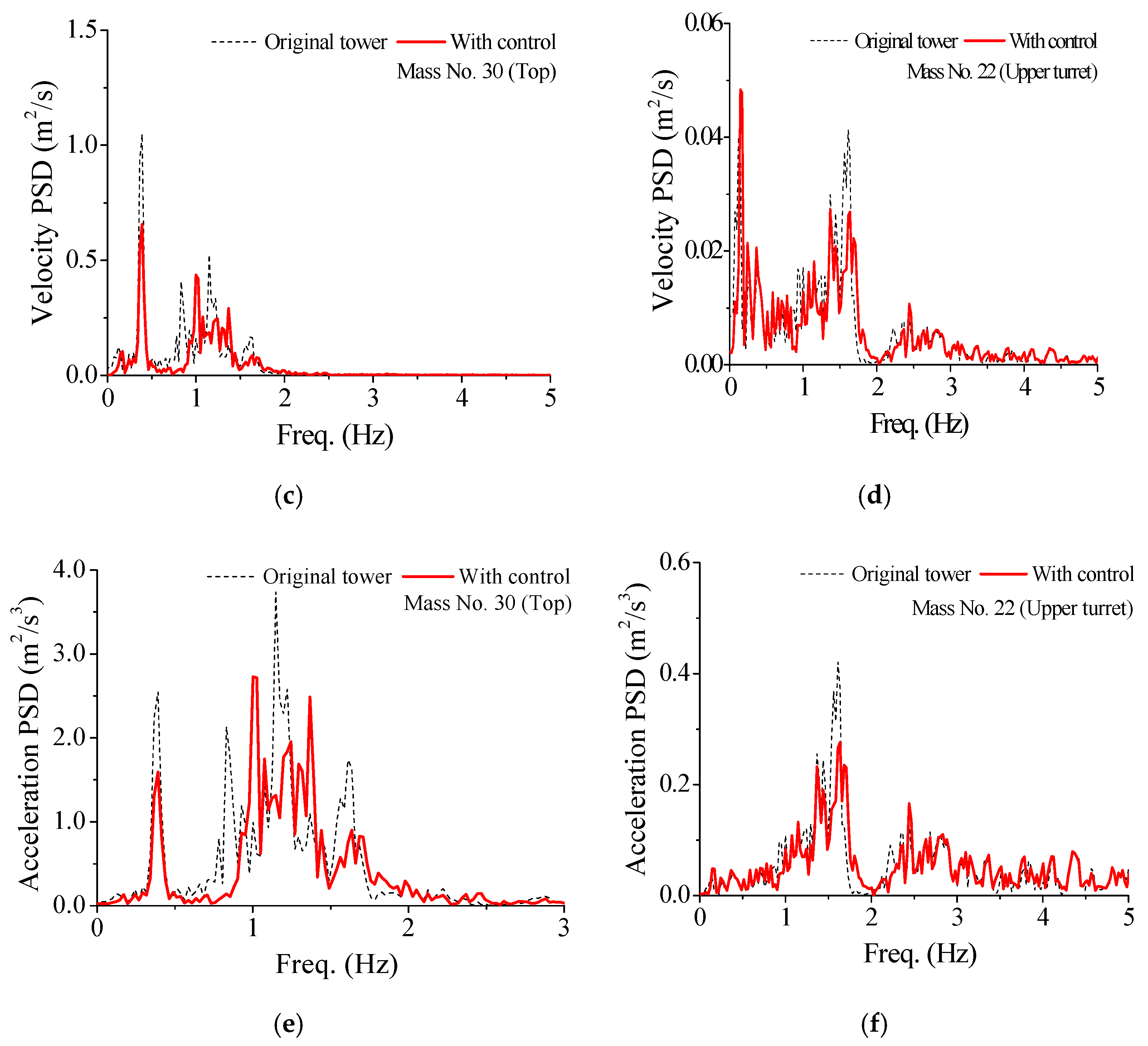
5.2. Control Performance Comparison
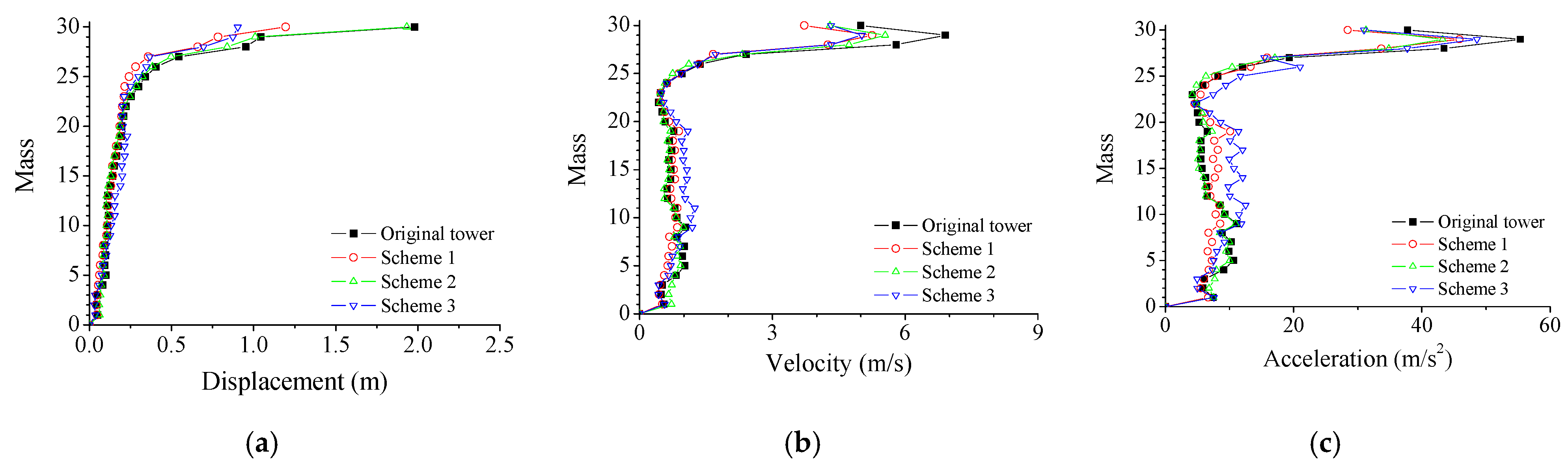
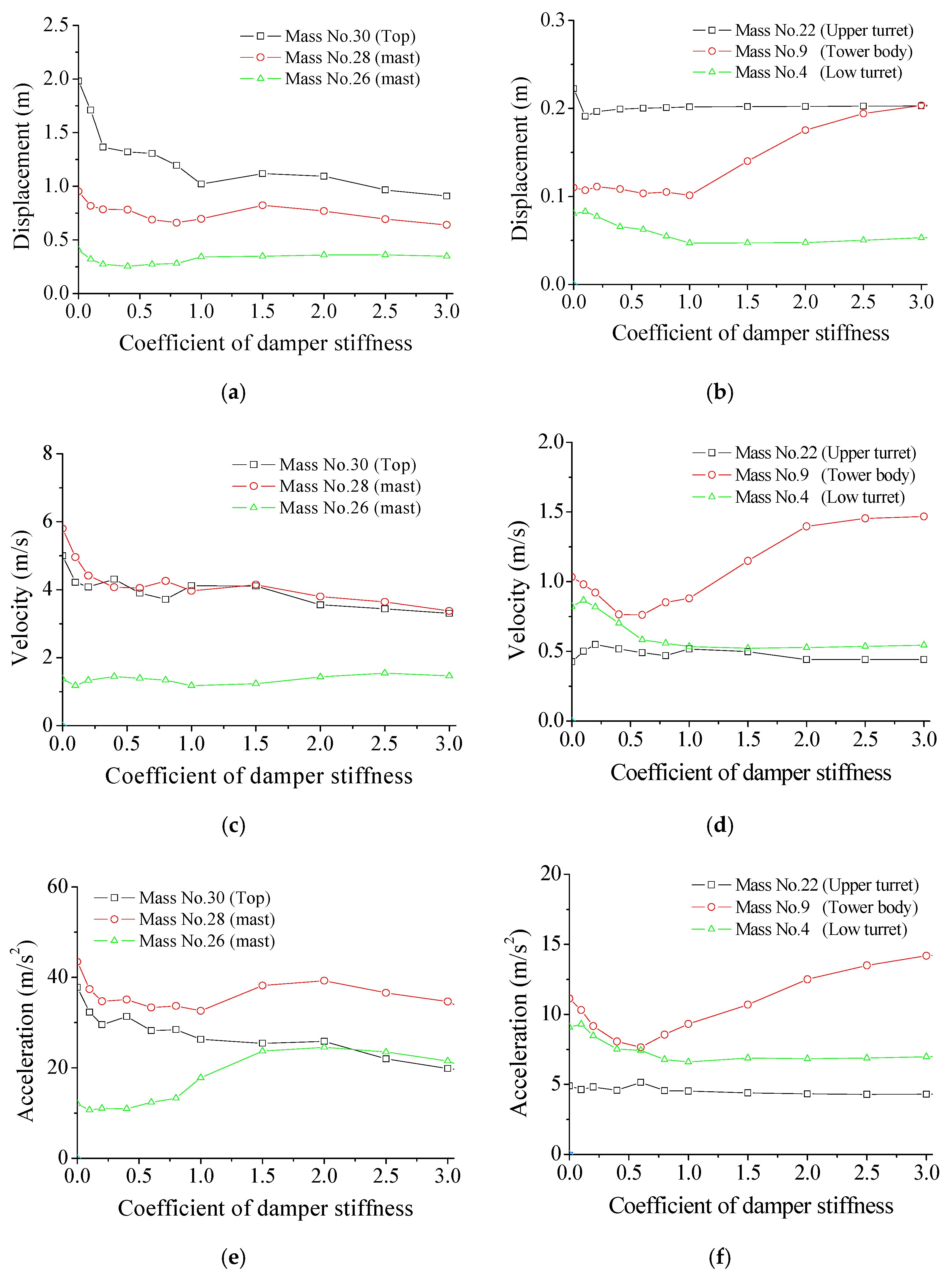
6. Parametric Study on Control Performance
6.1. Stiffness Effects of SMA Damper
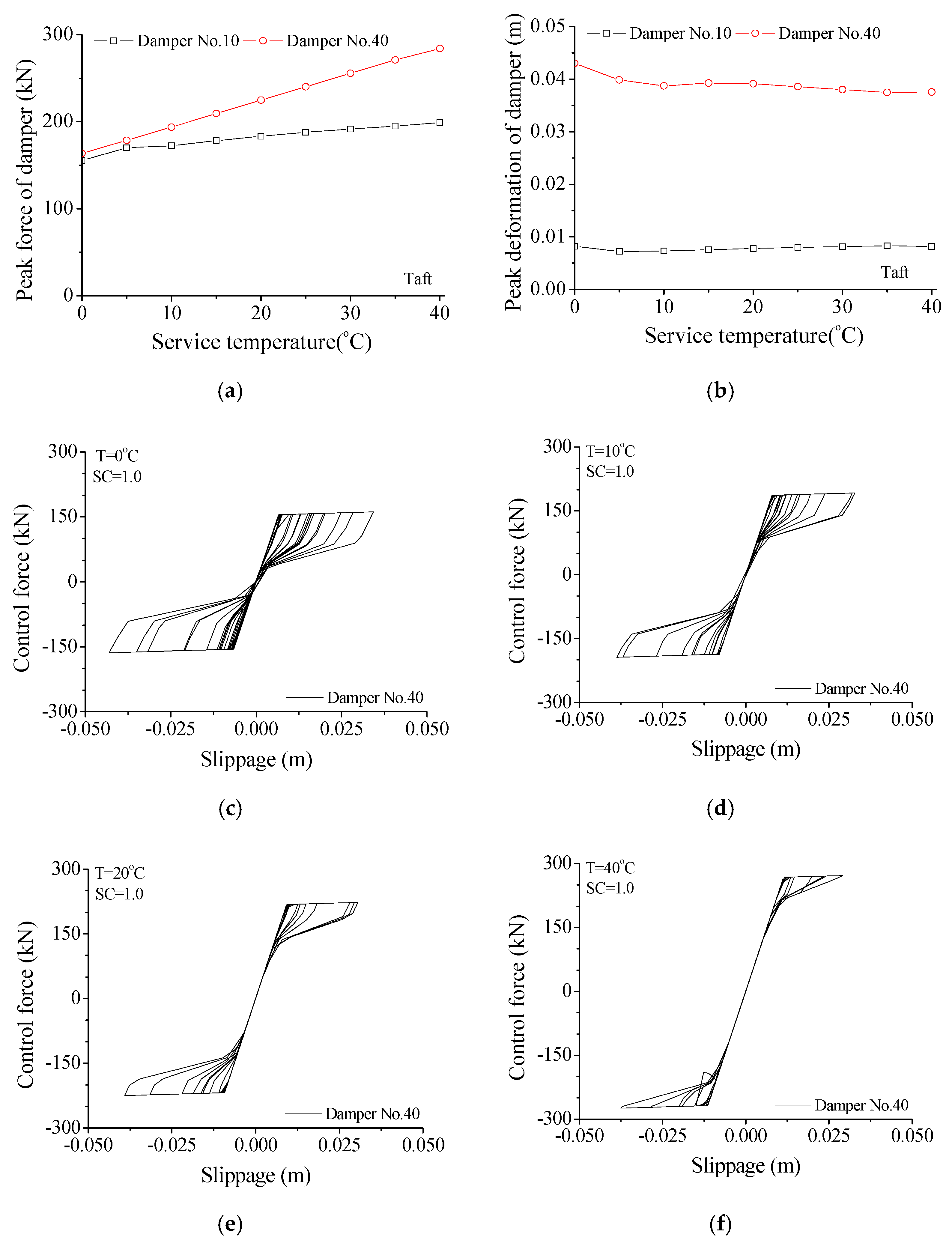
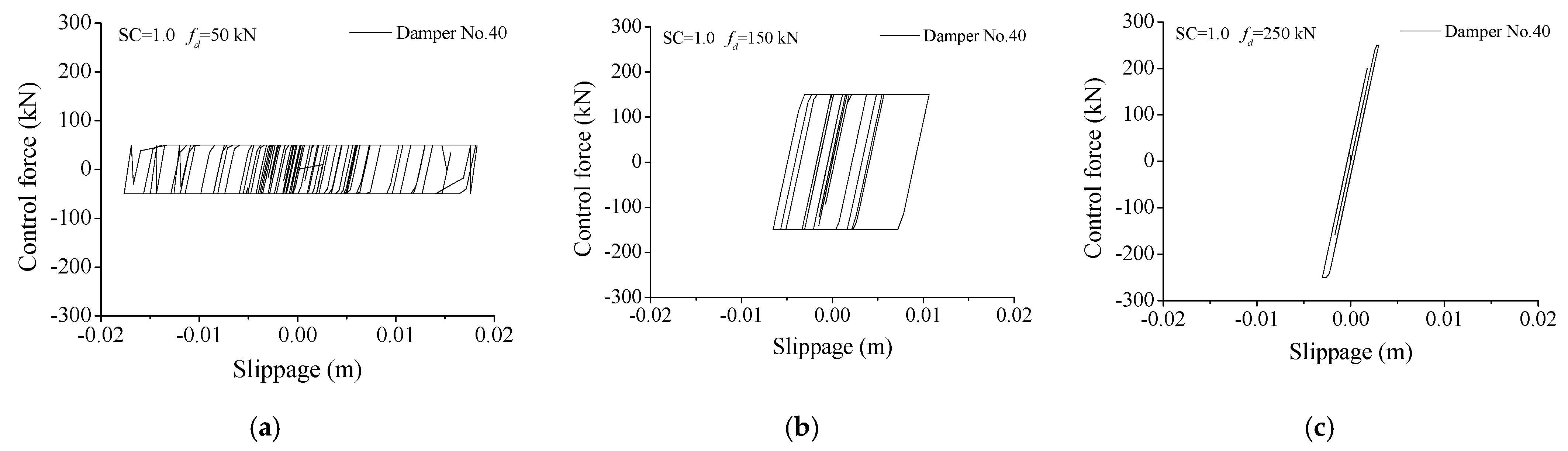
6.2. Properties of Hysteresis Loops
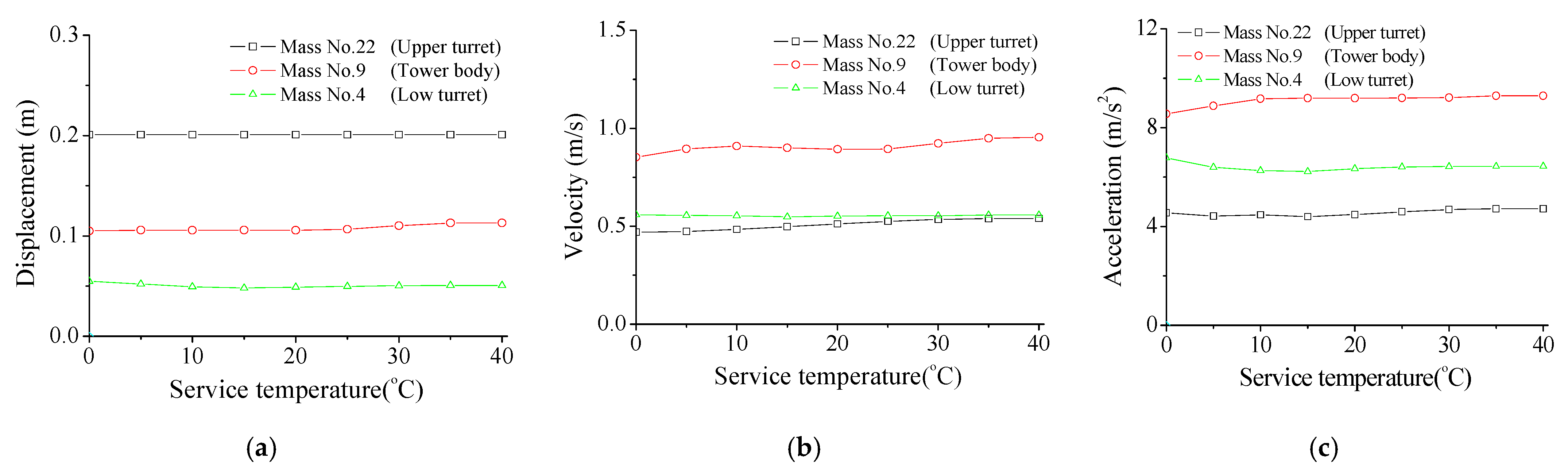
6.3. Effect of Service Temperature
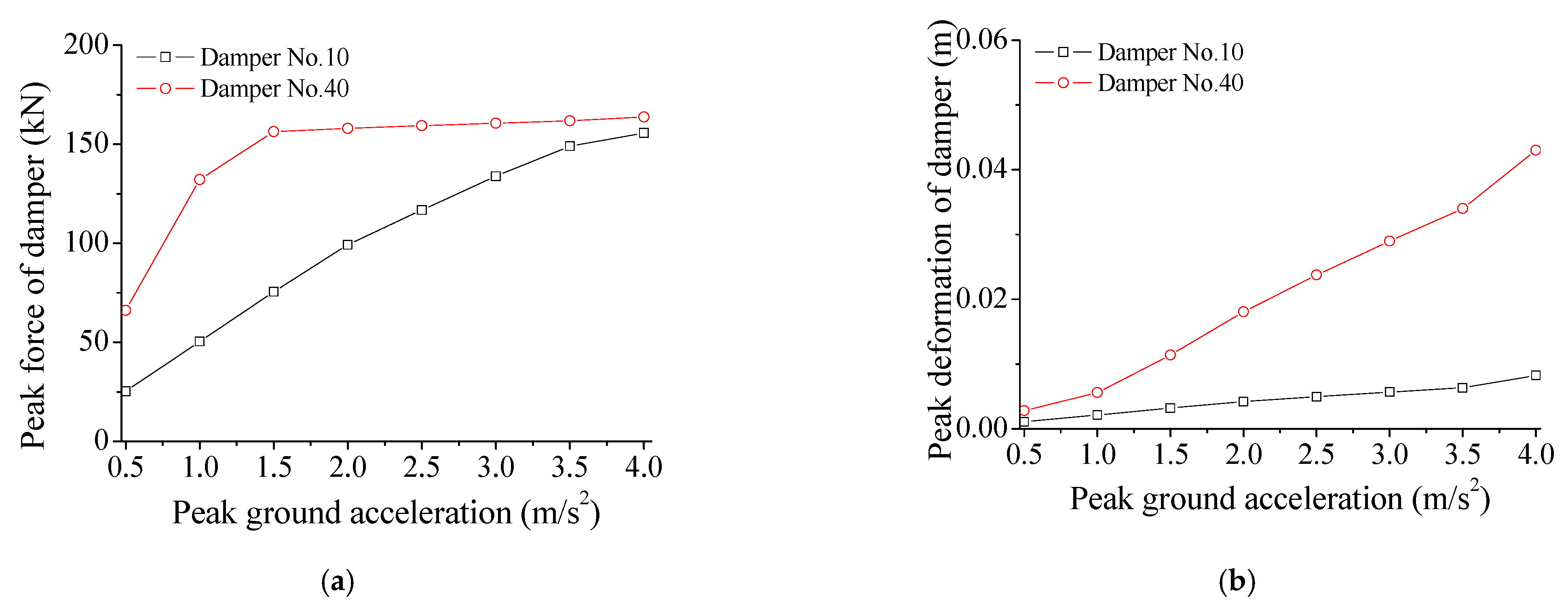
6.4. Effects of Earthquake Intensity
6.5. Efficacy Subjected Other Earthquakes
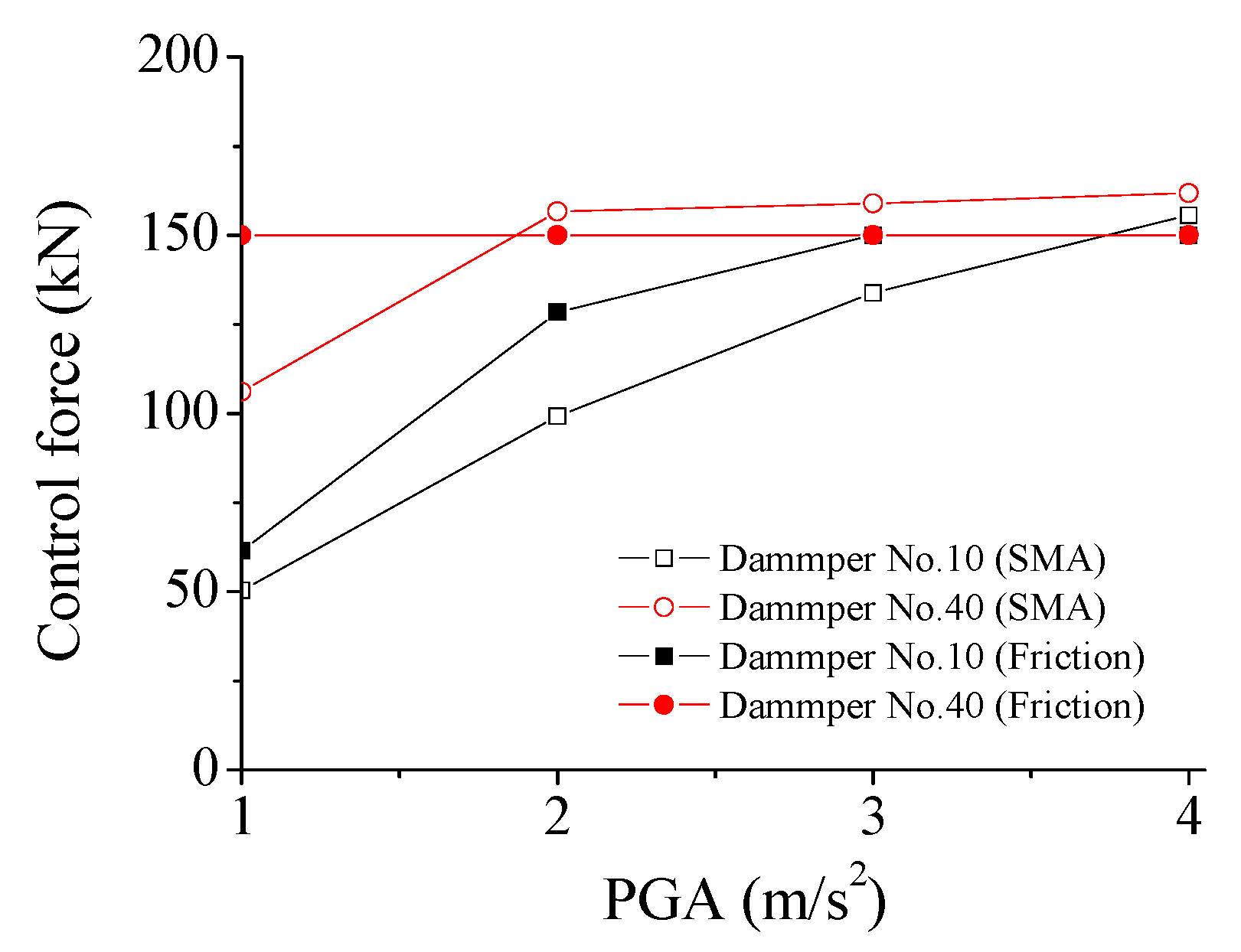
6.6. Comparison between SMA Damper and Friction Damper
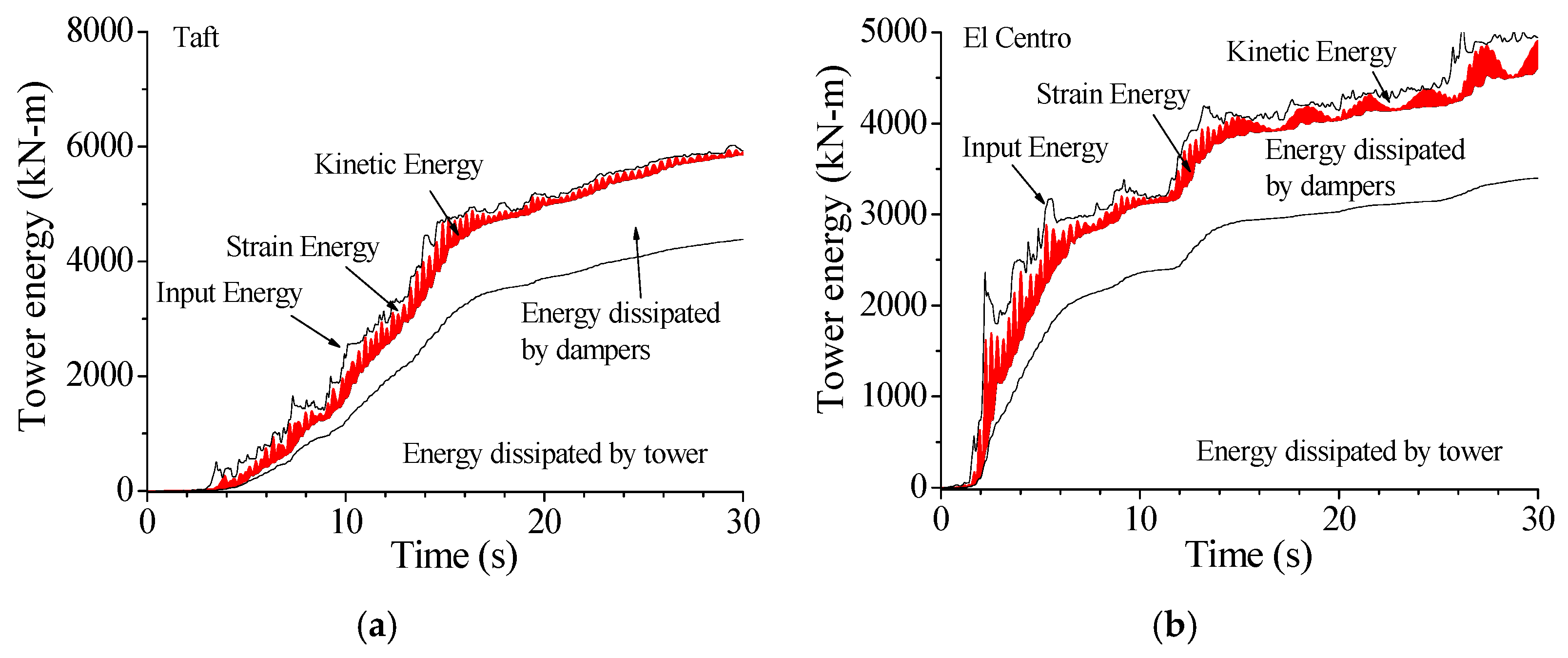
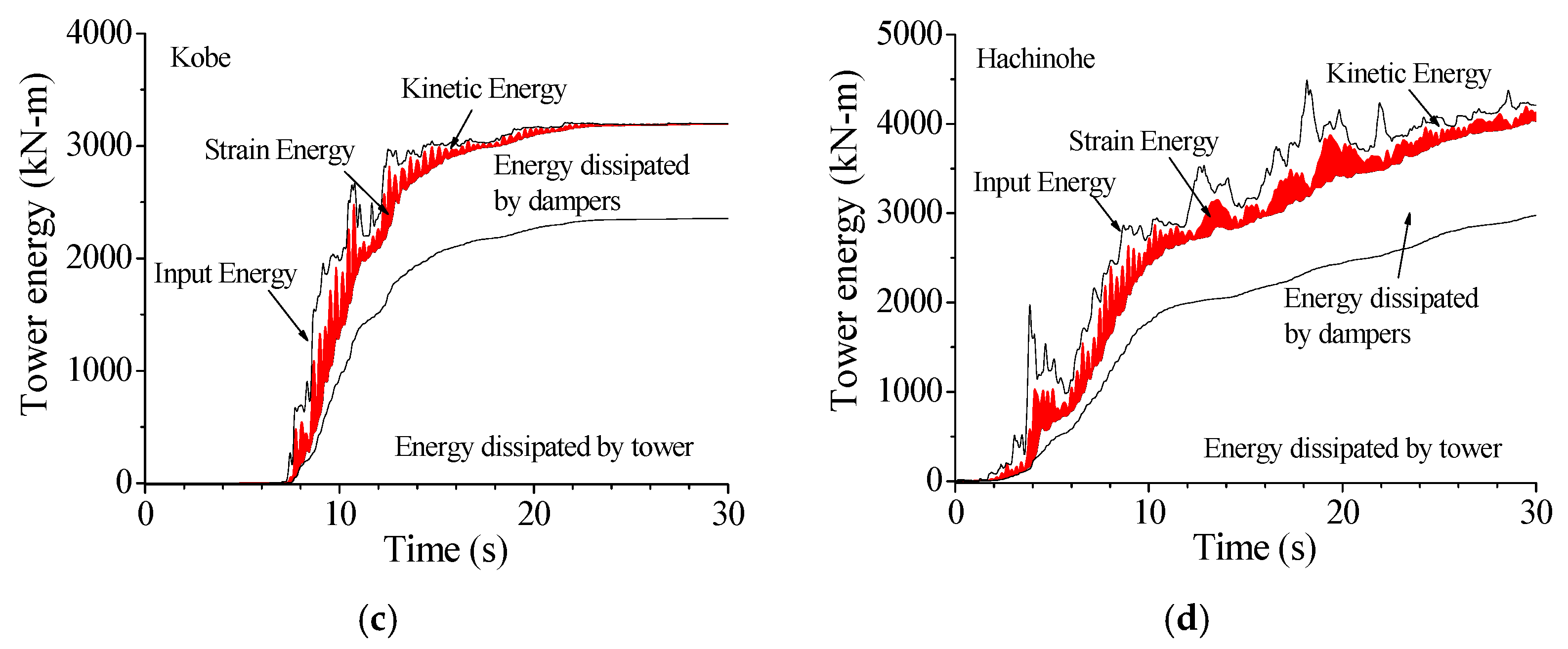
7. Energy Responses of the Tower
7.1. Comparison of Energy Responses of the Tower
7.2. Variation of Energy Response with Damper Stiffness
8. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amiri, M.M.; Yahyai, M. Estimation of damping ratio of TV towers based on ambient vibration monitoring. Struct. Des. Tall Spec. Build. 2013, 22, 862–875. [Google Scholar] [CrossRef]
- Chen, B.; Weng, S.; Zhi, L.H.; Li, D.M. Response control of a large transmission-tower line system under seismic excitations by using friction dampers. Adv. Struct. Eng. 2017, 20, 1155–1173. [Google Scholar] [CrossRef]
- Li, T.; Fan, J.; Lv, Y.X. Collapse analysis of a steel TV tower under wind load. Steel Constr. 2017, 32, 80–83. [Google Scholar]
- Liu, R.S.; Liu, J.L.; Yan, D.Q. Seismic damage investigation and analysis of electric power system in Lushan MS 7.0 earthquake. J. Nat. Disasters 2013, 22, 85–92. [Google Scholar]
- Housner, G.W.; Bergman, L.A.; Caughey, T.K.; Chassiakos, A.G.; Claus, R.O.; Masri, S.F.; Skelton, R.E.; Soong, T.T.; Spencer, B.F., Jr.; Yao, T.P. Structural control: Past, present, and future. J. Eng. Mech. ASCE 1997, 123, 897–971. [Google Scholar] [CrossRef]
- Xu, Y.L.; Qu, W.L.; Chen, B. Active/robust moment controllers for seismic response control of a large span building on top of ship lift towers. J. Sound Vib. 2003, 261, 277–296. [Google Scholar] [CrossRef]
- Chen, B.; Xia, Y. Advanced technologies in disaster prevention and mitigation. Adv. Struct. Eng. 2017, 20, 1141–1142. [Google Scholar] [CrossRef] [Green Version]
- Hitchcock, P.A.; Glanville, M.J.; Kwok, K.C.S.; Watkins, R.D. Damping properties and wind-induced response of a steel frame tower fitted with liquid column vibration absorbers. J. Wind Eng. Ind. Aerodyn. 1999, 83, 183–196. [Google Scholar] [CrossRef]
- Balendra, T.; Wang, C.M.; Yan, N. Control of wind-excited towers by active tuned liquid column damper. Eng. Struct. 2001, 23, 1054–1067. [Google Scholar] [CrossRef]
- Yang, N.; Wang, C.M.; Balendra, T. Composite mass dampers for vibration control of wind-excited towers. J. Sound Vib. 1998, 213, 301–316. [Google Scholar] [CrossRef]
- Wu, J.C.; Yang, J.N. LQG control of lateral-torsional motion of Nanjing TV transmission tower. Earthq. Eng. Struct. Dyn. 2000, 29, 1111–1130. [Google Scholar] [CrossRef]
- Ghorbani-Tanha, A.K.; Noorzad, A.; Rahimian, M. Mitigation of wind-induced motion of Milad Tower by tuned mass damper. Struct. Des. Tall Spec. Build. 2009, 18, 371–385. [Google Scholar] [CrossRef]
- Lu, X.L.; Li, P.Z.; Guo, X.Q.; Shi, W.X.; Liu, J. Vibration control using ATMD and site measurements on the Shanghai World Financial Center Tower. Struct. Des. Tall Spec. Build. 2014, 23, 105–123. [Google Scholar] [CrossRef]
- Pall, A.S.; Marsh, C. Response of friction damped braced frames. J. Struct. Div. ASCE 1982, 108, 1313–1323. [Google Scholar] [CrossRef]
- Grigorian, C.E.; Yang, T.S.; Popov, E.P. Slotted bolted connection energy dissipators. Earthq. Spectra 1993, 9, 491–504. [Google Scholar] [CrossRef]
- Chen, B.; Xiao, X.; Li, P.Y.; Zhong, W.L. Performance evaluation on transmission-tower line system with passive friction dampers subjected to wind excitations. Shock. Vib. 2015, 2015, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Quintana, H.C.; Petkovski, M. Optimum performance of structural control with friction dampers. Eng. Struct. 2018, 172, 154–162. [Google Scholar] [CrossRef]
- Chen, B.; Yang, D.; Feng, K.; Ouyang, Y.Q. Response control of a high-rise television tower under seismic excitations by friction dampers. Int. J. Struct. Stab. Dyn. 2018, 18, 1850140. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Li, A.Q. Seismic response vibration control analyses of Hefei TV Tower with fluid viscous damper. In Proceedings of the International Conference on Health Monitoring of Structure, Materials and Environment, Nanjing, China, 16 October 2007. [Google Scholar]
- Xu, Y.L.; Qu, W.L.; Chen, Z.H. Control of wind-excited truss tower using semiactive friction damper. J. Struct. Eng. ASCE 2001, 127, 861–868. [Google Scholar] [CrossRef]
- Chen, B.; Zheng, J.; Qu, W.L. Control of wind-induced response of transmission tower-line system by using magnetorheological dampers. Int. J. Struct. Stab. Dyn. 2009, 9, 661–685. [Google Scholar] [CrossRef]
- Song, G.B.; Ma, N.; Li, H.N. Applications of shape memory alloys in civil structures. Eng. Struct. 2006, 28, 1266–1274. [Google Scholar] [CrossRef]
- Song, G.B.; Ma, N. Robust control of a shape memory alloy wire actuated flap. Smart Mater. Struct. 2007, 16, 51–57. [Google Scholar] [CrossRef]
- Ozbulut, O.; Hurlebaus, S.; Desroches, R. Seismic response control using shape memory alloys: A review. J. Intell. Mater. Syst. Struct. 2011, 22, 1531–1549. [Google Scholar] [CrossRef]
- Fang, C.; Wang, W.; He, C.; Chen, Y. Self-centring behaviour of steel and steel-concrete composite connections equipped with NiTi SMA bolts. Eng. Struct. 2017, 150, 390–408. [Google Scholar] [CrossRef]
- Fang, C.; Yam, M.C.; Lam, A.C.; Xie, L. Cyclic performance of extended end-plate connections equipped with shape memory alloy bolts. J. Constr. Steel Res. 2014, 94, 122–136. [Google Scholar] [CrossRef]
- Zheng, Y.; Dong, Y.; Chen, B.; Ghazanfar, A.A. Seismic damage mitigation of bridges with self-adaptive SMA-cable-based bearings. Smart Struct. Syst. 2019, 24, 127–139. [Google Scholar]
- Liu, Y.P.; Wang, H.Y.; Qiu, C.X.; Zhao, X.N. Seismic behavior of superelastic shape memory alloy spring in base isolation system of multi-story steel frame. Materials 2019, 12, 997. [Google Scholar] [CrossRef] [Green Version]
- Brinson, L.C. One-dimensional constitutive behavior of shape memory alloys: Thermomechanical derivation with non-constant material functions and redefined martensite internal variable. J. Intell. Mater. Syst. Struct. 1993, 4, 229–242. [Google Scholar] [CrossRef]
- Zheng, Y.; Dong, Y.; Li, Y. Resilience and life-cycle performance of smart bridges with Shape Memory Alloy (SMA)-cable-based bearings. Constr. Build. Mater. 2018, 158, 389–400. [Google Scholar] [CrossRef]
- Qiu, C.; Fang, C.; Liang, D.; Du, X.; Yam, M.C.H. Behavior and application of self-centering dampers equipped with buckling-restrained SMA bars. Smart Mater. Struct. 2020, 29, 035009. [Google Scholar] [CrossRef]
- Spencer, B.F., Jr.; Dyke, S.J.; Deoskar, H.S. Benchmark problems in structural control. I: Active mass driver system. Earthq. Eng. Struct. Dyn. 1998, 27, 1127–1139. [Google Scholar] [CrossRef]
- Spencer, B.F., Jr.; Dyke, S.J.; Deoskar, H.S. Benchmark problems in structural control. II. Active tendon system. Earthq. Eng. Struct. Dyn. 1998, 27, 1141–1147. [Google Scholar] [CrossRef]
- Ohtori, Y.; Christenson, R.E.; Spencer, B.F., Jr.; Dyke, S.J. Benchmark control problems for seismically excited nonlinear buildings. J. Eng. Mech. ASCE 2004, 130, 366–385. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.C.; Chen, G.D. Nonlinear control of a 20-story steel building with active piezoelectric friction dampers. Struct. Eng. Mech. 2002, 14, 21–38. [Google Scholar] [CrossRef]





| Freq.no | 3D Finite Element Model | 2D Dynamic Model | Error |
|---|---|---|---|
| 1 | 0.129 | 0.128 | 0.621% |
| 2 | 0.416 | 0.386 | 7.211% |
| 3 | 0.729 | 0.781 | −7.133% |
| 4 | 1.171 | 1.163 | 0.683% |
| 5 | 1.514 | 1.456 | 3.831% |
| 6 | 2.221 | 2.142 | 3.556% |
| 7 | 2.578 | 2.569 | 0.349% |
| 8 | 2.632 | 2.783 | −5.737% |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| Mf | −46 °C | CM | 10 MPa/°C | 120 MPa | |
| As | −18.5 °C | CA | 15.8 MPa/°C | 190 MPa | |
| Ms | −37.4 °C | DA | 75,000 MPa | εL | 0.079 |
| Af | −6 °C | DM | 29,300 MPa |
| Scheme 1 | Scheme 2 | Scheme 3 |
|---|---|---|
| 30 dampers around the low turret (Mass No. 4) 30 dampers around the upper turret (Mass No. 24) | 60 dampers around the low turret (Mass No. 4) | 60 dampers around the upper turret (Mass No. 24) |
| Location | Taft | El Centro | Kobe | Hachinohe | Northridge | |
|---|---|---|---|---|---|---|
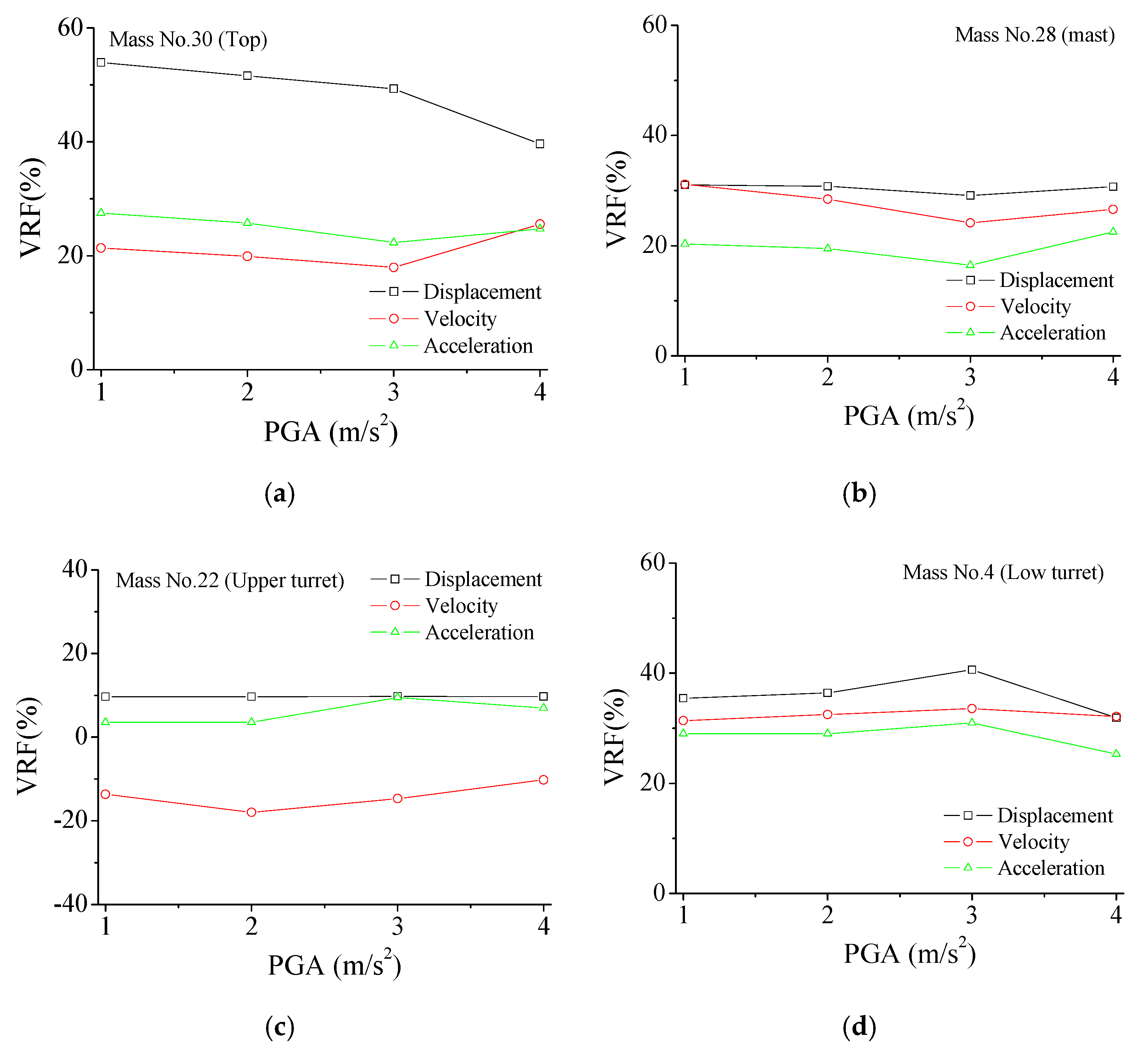
| Mass No. 30 (Tower top) | Displacement | 39.64 | 31.95 | 22.38 | 23.24 | 29.03 |
| Velocity | 25.57 | 13.87 | 18.70 | 33.89 | 5.59 | |
| Acceleration | 24.75 | 6.43 | 21.09 | 13.89 | 11.36 | |
| Mass No. 28 (Mast) | Displacement | 30.70 | 19.46 | 23.64 | 22.56 | 10.70 |
| Velocity | 26.59 | −5.21 | 20.69 | 19.60 | 11.42 | |
| Acceleration | 22.48 | −9.28 | 17.52 | 18.51 | 15.04 | |
| Mass No. 22 (Upper turret) | Displacement | 9.72 | 9.24 | 8.31 | 8.91 | 10.77 |
| Velocity | −10.19 | 11.88 | 23.94 | −1.05 | −0.78 | |
| Acceleration | 6.95 | 8.86 | 10.48 | −4.56 | 5.55 | |
| Mass No. 4 (Low turret) | Displacement | 31.88 | −2.81 | 35.34 | 2.69 | 4.04 |
| Velocity | 32.14 | −10.05 | 23.30 | 1.08 | 0.42 | |
| Acceleration | 25.30 | −5.56 | 15.60 | 8.74 | −1.64 |
| Location | SMA Damper PGA = 4.0 | Friction Damper PGA = 4.0 | SMA Damper PGA = 1.0 | Friction Damper PGA = 1.0 | |
|---|---|---|---|---|---|
| Mass No. 30 (Tower top) | Displacement | 39.64 | 39.87 | 53.92 | 40.69 |
| Velocity | 25.57 | 38.84 | 21.37 | 33.72 | |
| Acceleration | 24.75 | 52.63 | 27.49 | 37.30 | |
| Mass No. 28 (Mast) | Displacement | 30.70 | 47.07 | 30.99 | 8.61 |
| Velocity | 26.59 | 49.51 | 31.12 | 31.33 | |
| Acceleration | 22.48 | 44.75 | 20.33 | 23.28 | |
| Mass No. 22 (Upper turret) | Displacement | 9.72 | 8.61 | 9.68 | 8.57 |
| Velocity | −10.19 | −3.93 | −13.67 | −5.77 | |
| Acceleration | 6.95 | 9.11 | 3.529 | 9.08 | |
| Mass No. 4 (Low turret) | Displacement | 31.88 | 39.43 | 35.471 | 33.37 |
| Velocity | 32.14 | 30.80 | 31.37 | 36.74 | |
| Acceleration | 25.30 | 29.61 | 29.02 | 23.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Chen, B.; Zhi, L.; Song, X. Seismic Response Mitigation of a Television Transmission Tower by Shape Memory Alloy Dampers. Materials 2021, 14, 6987. https://doi.org/10.3390/ma14226987
Wu J, Chen B, Zhi L, Song X. Seismic Response Mitigation of a Television Transmission Tower by Shape Memory Alloy Dampers. Materials. 2021; 14(22):6987. https://doi.org/10.3390/ma14226987
Chicago/Turabian StyleWu, Jingbo, Bo Chen, Lunhai Zhi, and Xinxin Song. 2021. "Seismic Response Mitigation of a Television Transmission Tower by Shape Memory Alloy Dampers" Materials 14, no. 22: 6987. https://doi.org/10.3390/ma14226987
APA StyleWu, J., Chen, B., Zhi, L., & Song, X. (2021). Seismic Response Mitigation of a Television Transmission Tower by Shape Memory Alloy Dampers. Materials, 14(22), 6987. https://doi.org/10.3390/ma14226987






