Effect of Bond-Line Thickness on Fatigue Crack Growth of Structural Acrylic Adhesive Joints
Abstract
:1. Introduction
2. Experimental
2.1. Materials
2.2. Specimen Preparation
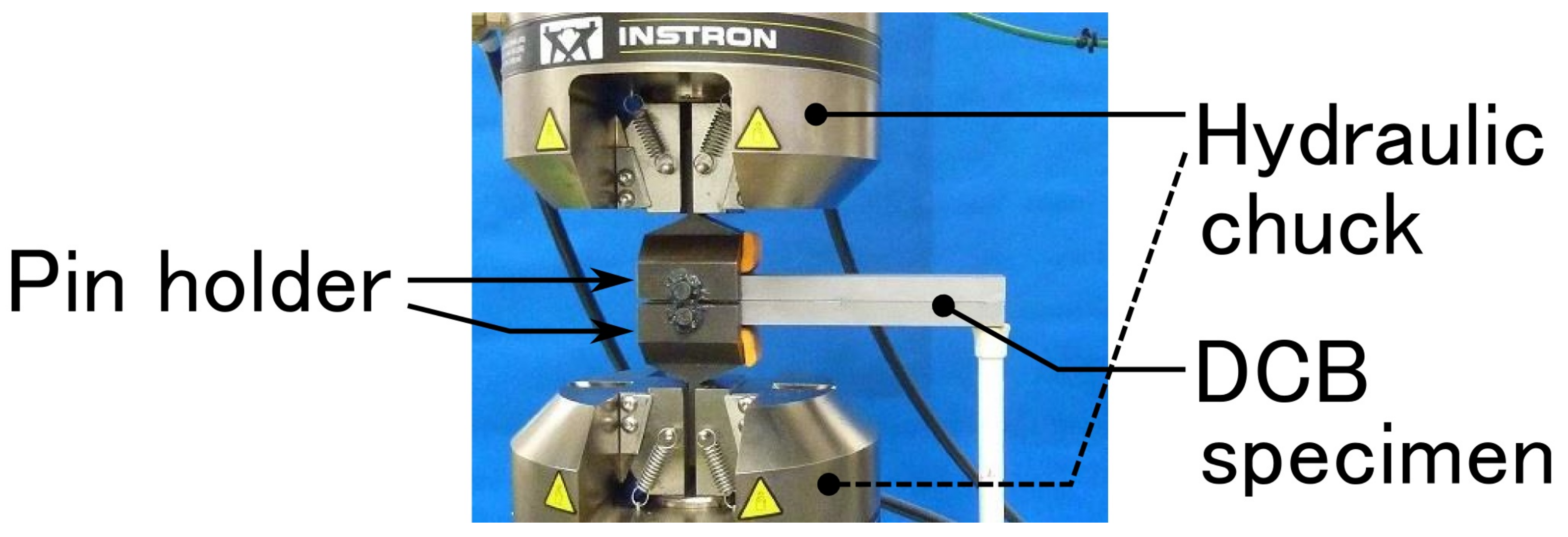
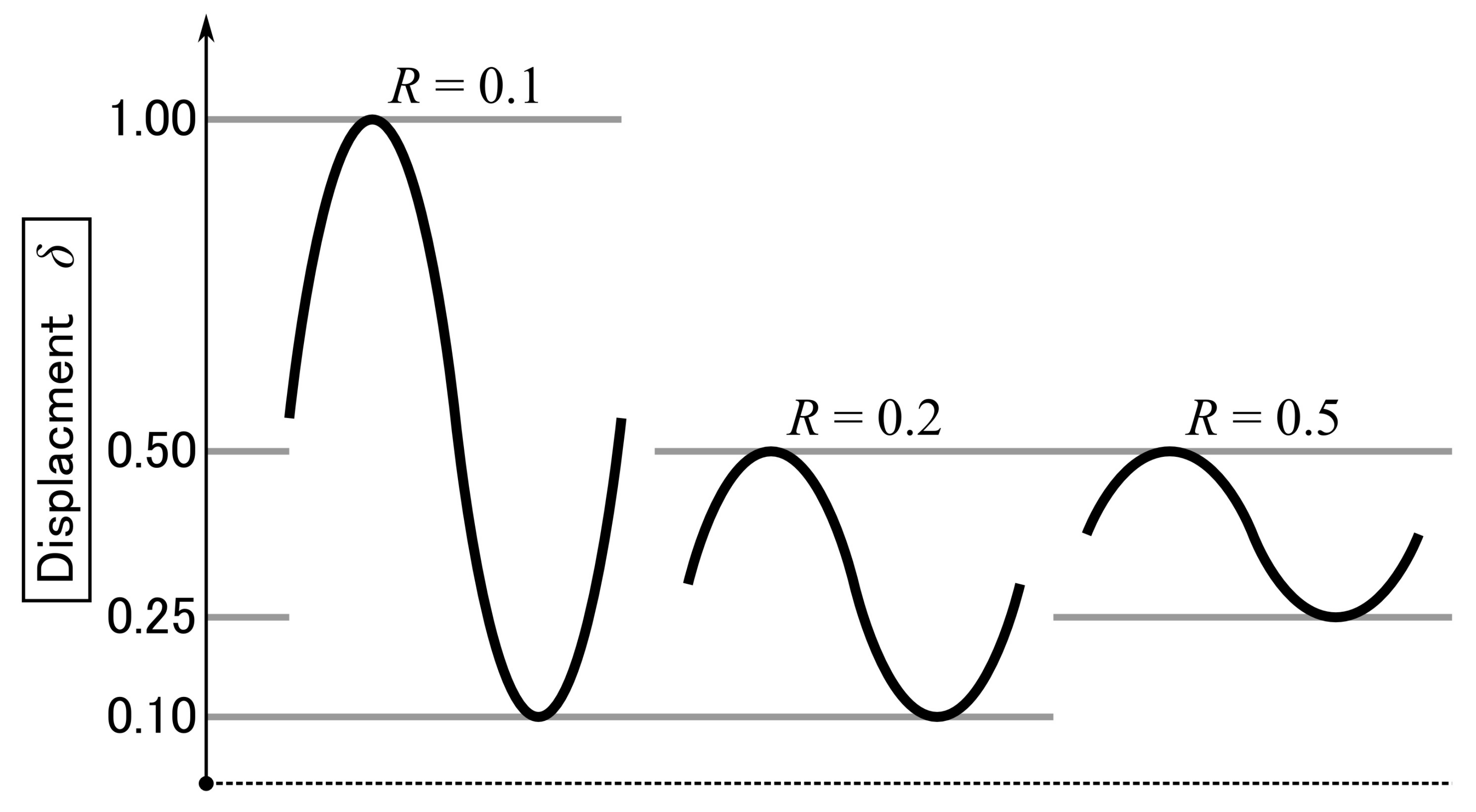
2.3. Fatigue Testing
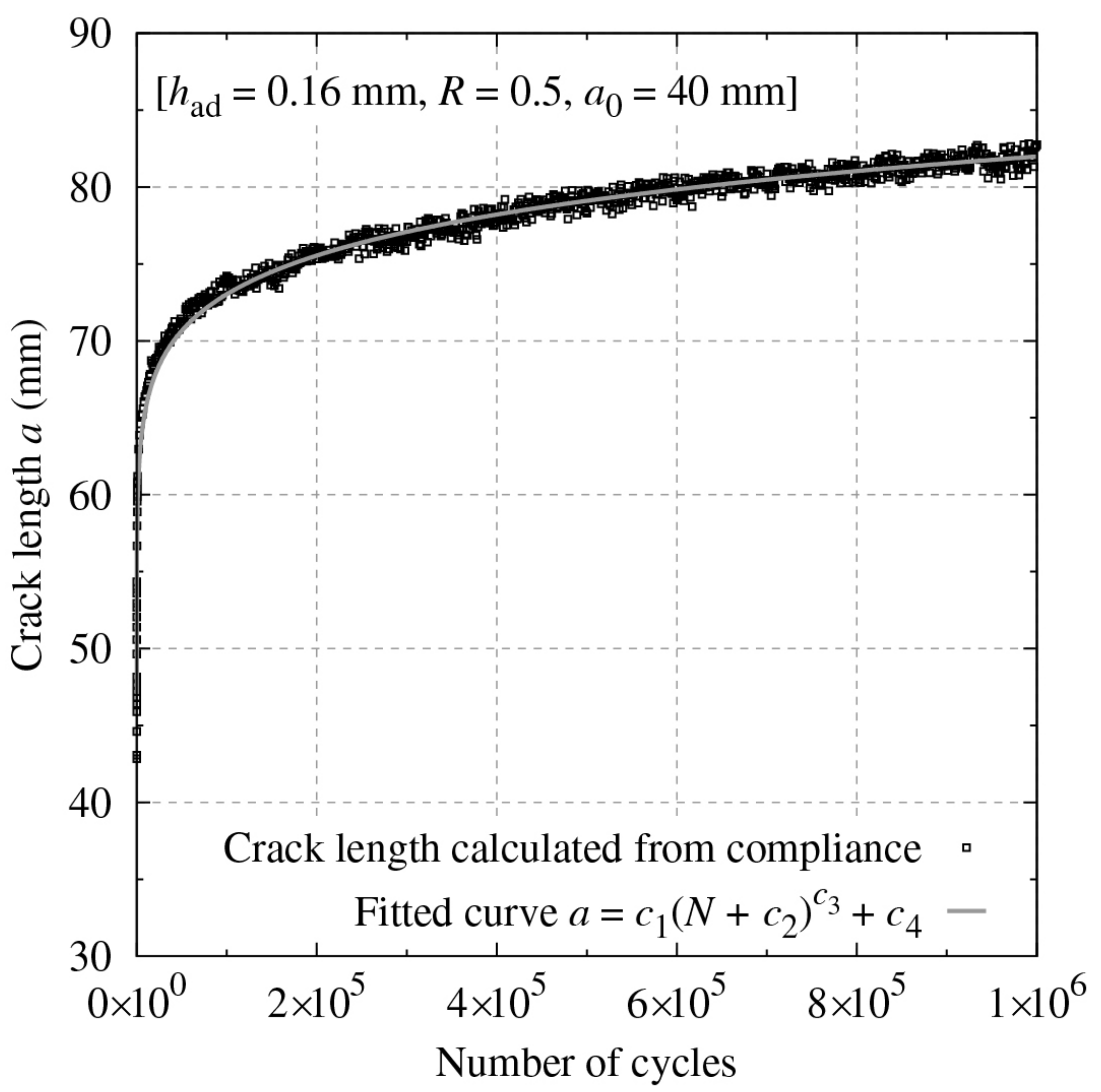
2.4. Data Reduction Approach
3. Results and Discussion
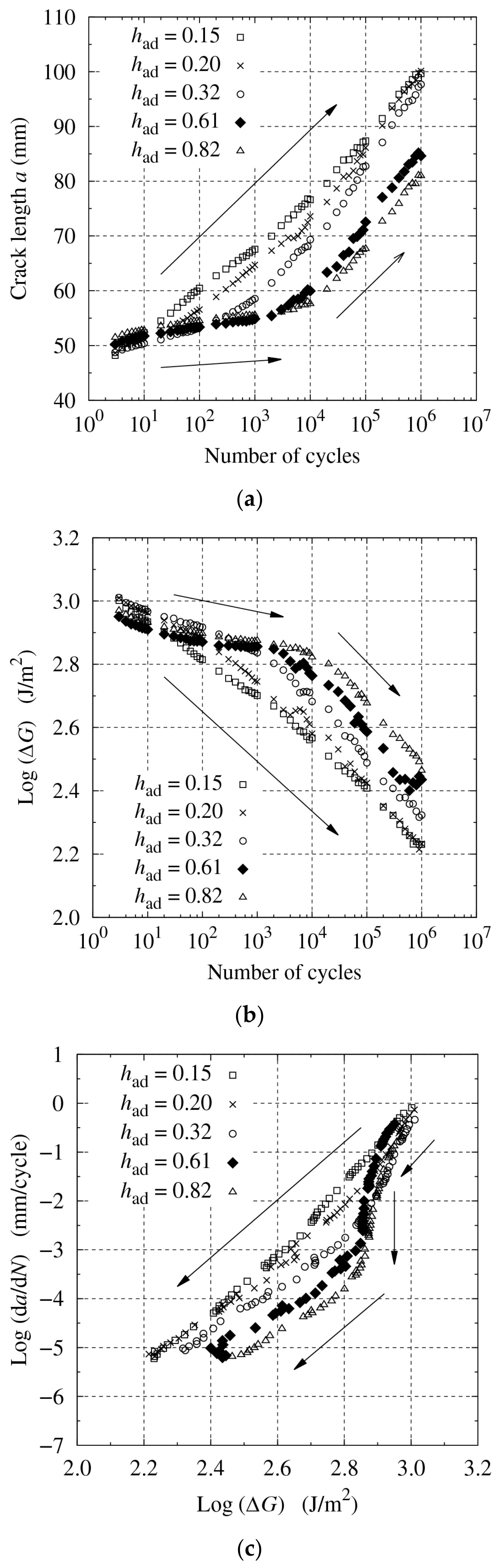
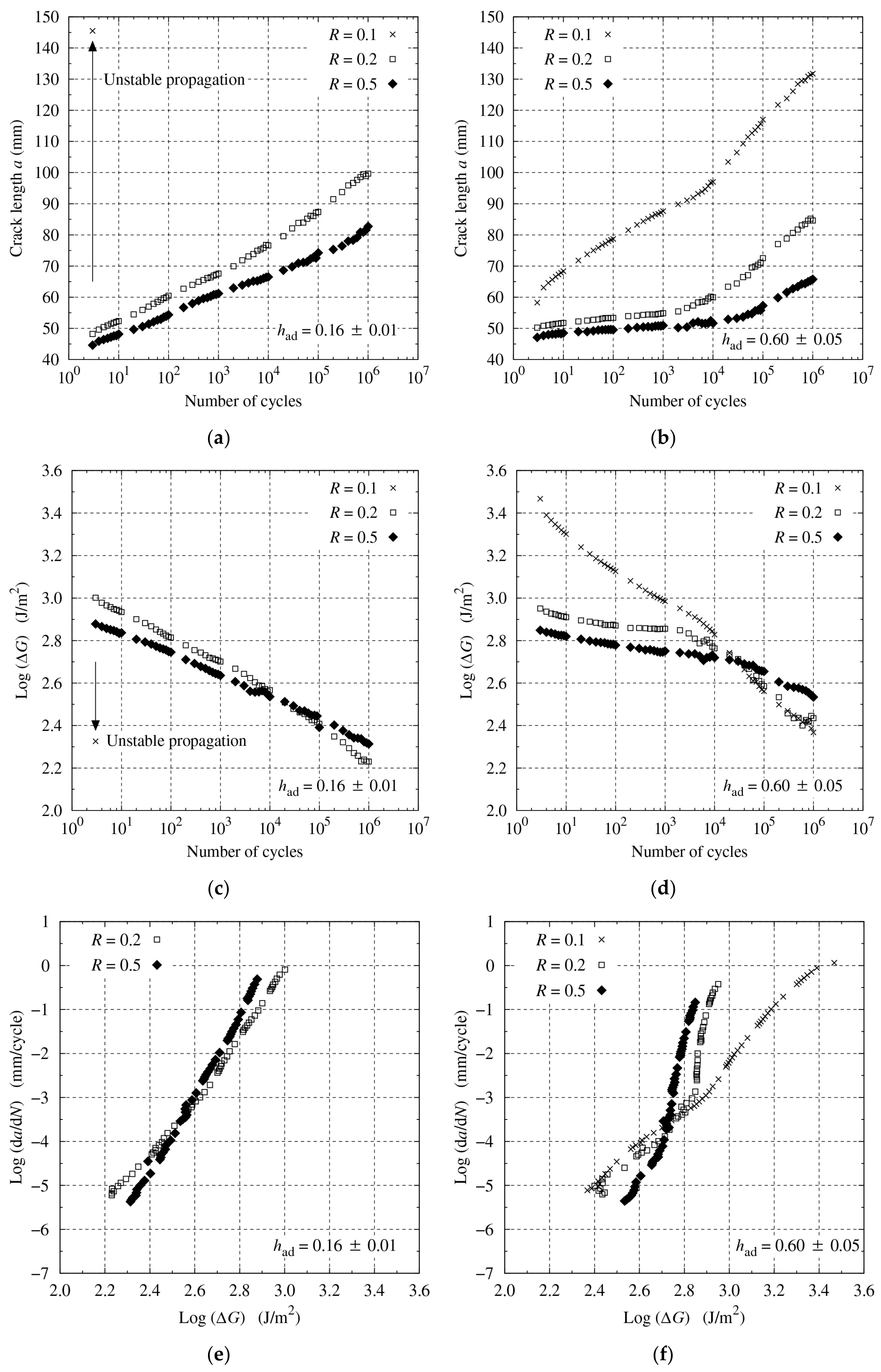
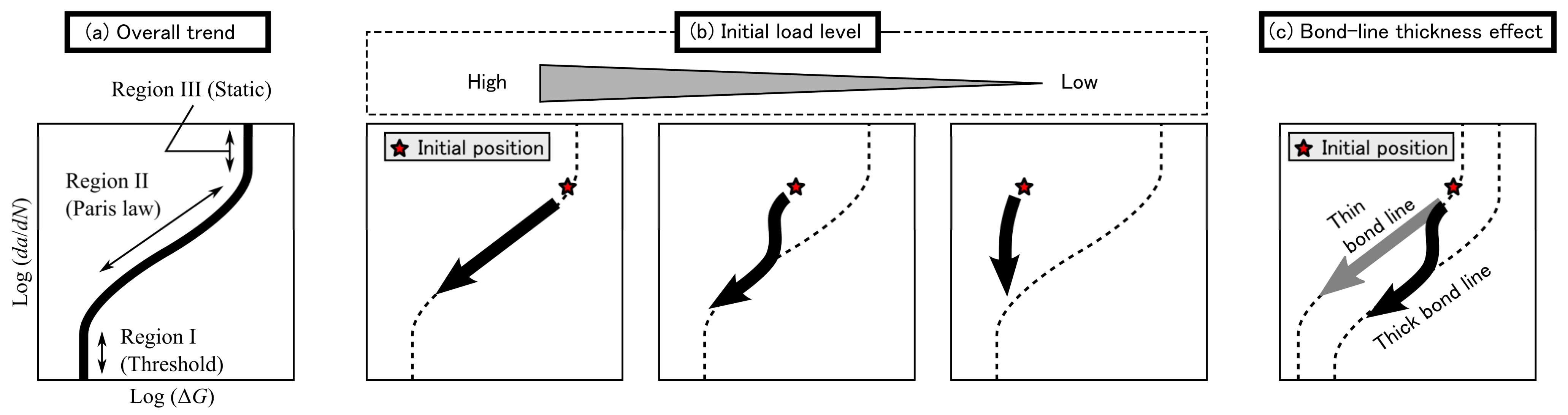
3.1. Adhesive Bond-Line Thickness Effect
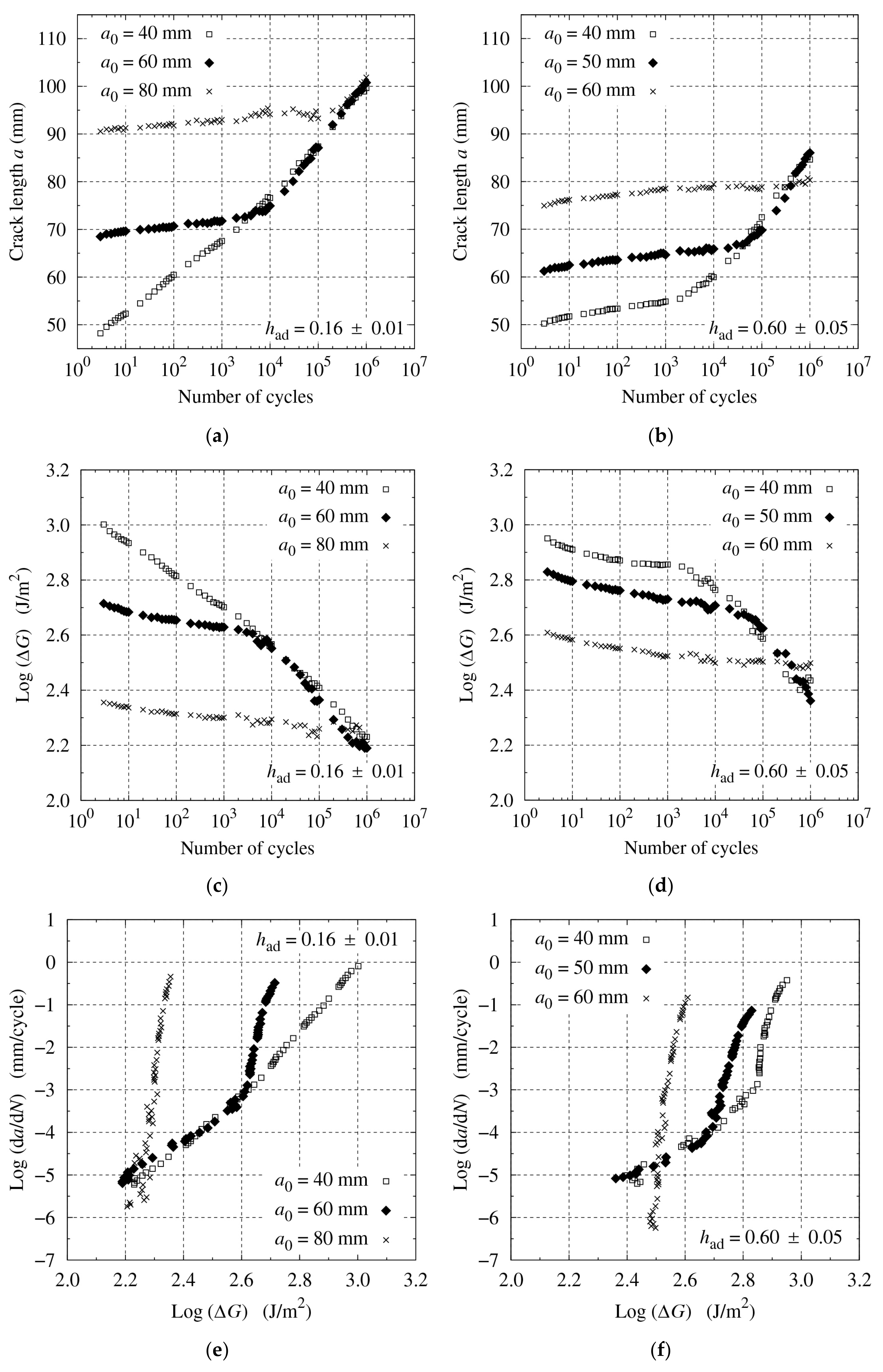
3.2. R-Ratio and Initial Crack Length Effects
3.3. Effect of Initial Load Level on Fatigue Crack Growth Behavior
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ASTM D3166-99(2020). Standard Test Method for Fatigue Properties of Adhesives in Shear by Tension Loading (Metal/Metal); ASTM International: West Conshohocken, PA, USA, 2020. [Google Scholar] [CrossRef]
- ISO 9664:1993. Adhesives—Test Methods for Fatigue Properties of Structural Adhesives in Tensile Shear; International Organization for Standardization: Geneva, Switzerland, 1993. [Google Scholar]
- ASTM D3433-99(2020). Standard Test Method for Fracture Strength in Cleavage of Adhesives in Bonded Metal Joints; ASTM International: West Conshohocken, PA, USA, 2020. [Google Scholar] [CrossRef]
- ISO 25217: 2009. Adhesives—Determination of the Mode I Adhesive Fracture Energy of Structural Adhesive Joints Using Double Cantilever Beam and Tapered Double Cantilever Beam Specimens; International Organization for Standardization: Geneva, Switzerland, 2009. [Google Scholar]
- Blackman, B.R.K.; Kinloch, A.J.; Paraschi, M.; Teo, W.S. Measuring the mode I adhesive fracture energy, GIC, of structural adhesive joints: The results of an international round-robin. Int. J. Adhes. Adhes. 2003, 23, 293–305. [Google Scholar] [CrossRef] [Green Version]
- Shimamoto, K.; Sekiguchi, Y.; Sato, C. Mixed mode fracture toughness of adhesively bonded joints with residual stress. Int. J. Solids Struct. 2016, 102–103, 120–126. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Yamagata, Y.; Sato, C. Mode I fracture energy of adhesive joints bonded with adhesives with different characteristics under quasi-static and impact loading. J. Adhes. Soc. Jpn. 2017, 53, 330–337. [Google Scholar] [CrossRef] [Green Version]
- Komatsu, K.; Sekiguchi, Y.; Ihara, R.; Tatsumi, A.; Sato, C. Experimental investigation of an adhesive fracture energy measurement by preventing plastic deformation of substrates in a double cantilever beam test. J. Adhes. 2019, 95, 911–928. [Google Scholar] [CrossRef]
- Da Silva, L.F.M.; Campilho, R.D.S.G. Advances in Numerical Modeling of Adhesive Joints; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Álvarez, D.; Blackman, B.R.K.; Guild, F.J.; Kinloch, A.J. Mode I fracture in adhesively-bonded joints: A mesh-size independent modelling approach using cohesive elements. Eng. Fract. Mech. 2014, 115, 73–95. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, R.L.; Campilho, R.D.S.G. Testing different cohesive law shapes to predict damage growth in bonded joints loaded in pure tension. J. Adhes. 2017, 93, 57–76. [Google Scholar] [CrossRef]
- Nunes, F.A.A.; Campilho, R.D.S.G. Mized-mode fracture analysis of adhesively-bonded joints using the ATDCB test specimen. Int. J. Adhes. Adhes. 2018, 85, 58–68. [Google Scholar] [CrossRef]
- Ramalho, L.D.C.; Campilho, R.D.S.G.; Belinha, J.; da Silva, L.F.M. Static strength prediction of adhesive joints: A review. Int. J. Adhes. Adhes. 2020, 96, 102451. [Google Scholar] [CrossRef]
- Jablonski, D.A. Fatigue crack growth in structural adhesives. J. Adhes. 1980, 11, 125–143. [Google Scholar] [CrossRef]
- Kinloch, A.J.; Osiyemi, S.O. Predicting the fatigue life of adhesively-bonded joints. J. Adhes. 1993, 43, 79–90. [Google Scholar] [CrossRef]
- Jethwa, J.K.; Kinloch, A.J. The fatigue and durability behaviour of automotive adhesives. Part I: Fracture mechanics tests. J. Adhes. 1997, 61, 71–95. [Google Scholar] [CrossRef]
- Brunner, A.J.; Murphy, N.; Pinter, G. Development of a standardized procedure for the characterization of interlaminar delamination propagation in advanced composites under fatigue mode I loading conditions. Eng. Fract. Mech. 2009, 76, 2678–2689. [Google Scholar] [CrossRef]
- Azari, S.; Papini, M.; Schroeder, J.A.; Spelt, J.K. Fatigue threshold behavior of adhesive joints. Int. J. Adhes. Adhes. 2010, 30, 145–159. [Google Scholar] [CrossRef]
- Stelzer, S.; Brunner, A.J.; Argüelles, A.; Murphy, N.; Cano, G.M.; Pinter, G. Mode I delamination fatigue crack growth in unidirectional fiber reinforced composites: Results from ESIS TC4 round-robins. Eng. Fract. Mech. 2014, 116, 92–107. [Google Scholar] [CrossRef] [Green Version]
- Usman, M.; Pascoe, J.A.; Alderliesten, R.C.; Benedictus, R. The effect of temperature on fatigue crack growth in FM94 epoxy adhesive bonds investigated by means of energy dissipation. Eng. Fract. Mech. 2018, 189, 98–109. [Google Scholar] [CrossRef] [Green Version]
- Adamos, L.; Tsokanas, P.; Loutas, T. An experimental study of the interfacial fracture behavior of Titanium/CFRP adhesive joints under mode I and mode II fatigue. Int. J. Fatigue 2020, 136, 105586. [Google Scholar] [CrossRef]
- Jones, R.; Pneg, D.; Michopoulos, J.G.; Kinloch, A.J. Requirements and variability affecting the durabilityof bonded joints. Materials 2020, 13, 1468. [Google Scholar] [CrossRef] [Green Version]
- Khoramishad, H.; Crocombe, A.D.; Katnam, K.B.; Ashcroft, I.A. Predicting fatigue damage in adhesively bonded joints using a cohesive zone model. Int. J. Fatigue 2010, 32, 1146–1158. [Google Scholar] [CrossRef]
- Eklind, A.; Walander, T.; Carlberger, T.; Stigh, U. High cycle fatigue crack growth in mode I of adhesive layers: Modelling, simulation and experiments. Int. J. Fract. 2014, 190, 125–146. [Google Scholar] [CrossRef]
- Pirondi, A.; Moroni, F. Improvement of a cohesive zone model for fatigue delamination rate simulation. Materials 2019, 12, 181. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rocha, A.V.M.; Akhavan-Safar, A.; Carbas, R.; Marques, E.A.S.; Goyal, R.; El-zein, M.; da Silva, L.F.M. Numerical analysis of mixed-mode fatigue crack growth of adhesive joints using CZM. Theor. Appl. Fract. Mech. 2020, 106, 102493. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A critical analysis of crack propagation laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Simon, I.; Banks-Sills, L.; Fourman, V. Mode I delamination propagation and R-ratio effects in woven composite DCB specimens for a multi-directional layup. Int. J. Fatigue 2017, 96, 237–251. [Google Scholar] [CrossRef]
- Rocha, A.V.M.; Akhavan-Safar, A.; Carbas, R.; Marques, E.A.S.; Goyal, R.; El-Zein, M.; da Silva, L.F.M. Paris law relations for an epoxy-based adhesive. Int. Mech. Eng. 2020, 234, 291–299. [Google Scholar] [CrossRef]
- Mall, S.; Ramanurthy, G. Effect of bond thickness on fracture and fatigue strength of adhesively bonded composite joints. Int. J. Adhes. Adhes. 1989, 9, 33–37. [Google Scholar] [CrossRef]
- Joseph, R.; Bell, J.P.; McEvily, A.J.; Liang, J.L. Fatigue crack growth in epoxy/aluminum and epoxy/steel joints. J. Adhes. 1993, 41, 169–187. [Google Scholar] [CrossRef]
- Xu, X.X.; Crocombe, A.D.; Smith, P.A. Fatigue crack growth rates in adhesive joints tested at different frequencies. J. Adhes. 1996, 58, 191–204. [Google Scholar] [CrossRef]
- Abou-Hamda, M.M.; Megahed, M.M.; Hammouda, M.M.I. Fatigue crack growth in double cantilever beam specimen with an adhesive layer. Eng. Fract. Mech. 1998, 60, 605–614. [Google Scholar] [CrossRef]
- Azari, S.; Papini, M.; Spelt, J.K. Effect of adhesive thickness on fatigue and fracture of toughened epoxy joints—Part I: Experiments. Eng. Fract. Mech. 2011, 78, 153–162. [Google Scholar] [CrossRef]
- Pascoe, J.A.; Zavatta, N.; Troiani, E.; Alderliesten, R.C. The effect of bond-line thickness on fatigue crack growth rate in adhesively bonded joints. Eng. Fract. Mech. 2020, 229, 106959. [Google Scholar] [CrossRef] [Green Version]
- Shahverdi, M.; Vassilopoulos, A.P.; Keller, T. Experimental investigation of R-ratio effects on fatigue crack growth of adhesively-bonded pultruded GFRP DCB joints under CA loading. Compos. Part A 2012, 43, 1689–1697. [Google Scholar] [CrossRef]
- Abel, M.L.; Adams, A.N.N.; Kinloch, A.J.; Shaw, S.J.; Watts, J.F. The effect of surface pretreatment on the cyclic-fatigue characteristics of bonded aluminium-alloy joints. Int. J. Adhes. Adhes. 2006, 26, 50–61. [Google Scholar] [CrossRef] [Green Version]
- Azari, S.; Papini, M.; Spelt, J.K. Effect of surface roughness on the performance of adhesive joints under static and cyclic loading. J. Adhes. 2010, 86, 742–764. [Google Scholar] [CrossRef]
- Bello, I.; Alowayed, Y.; Albinmousa, J.; Lubineau, G.; Merah, N. Fatigue crack growth in laser-treated adhesively bonded composite joints: An experimental examination. Int. J. Adhes. Adhes. 2021, 105, 102784. [Google Scholar] [CrossRef]
- Jones, R.; Hu, W.; Kinloch, A.J. A convenient way to represent fatigue crack growth in structural adhesives. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 379–391. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.B.; Naito, K.; Oguma, H. Fatigue crack growth properties of a two-part acrylic-based adhesive in an adhesive bonded joint: Double cantilever-beam tests under mode I loading. Int. J. Fatigue 2017, 98, 286–295. [Google Scholar] [CrossRef]
- Imanaka, M.; Ishii, K.; Hara, K.; Ikeda, T.; Kouno, Y. Fatigue crack propagation rate of CFRP/aluminum adhesively bonded DCB joints with acrylic and epoxy adhesives. Int. J. Adhes. Adhes. 2018, 85, 149–156. [Google Scholar] [CrossRef]
- Racha, A.V.M.; Akhavan-Safar, A.; Carbas, R.; Marques, E.A.S.; Goyal, R.; El-zein, M.; da Silva, L.F.M. Fatigue crack growth analysis of different adhesive systems: Effects of mode mixity and load level. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 330–341. [Google Scholar] [CrossRef]
- Kinloch, A.J.; Shaw, S.J. The fracture resistance of a toughened epoxy adhesive. J. Adhes. 1981, 12, 59–77. [Google Scholar] [CrossRef]
- Da Silva, L.F.M.; de Magalhães, F.A.C.R.G.; Chaves, F.J.P.; de Moura, M.F.S.F. Mode II fracture toughness of a brittle and a ductile adhesive as a function of the adhesive thickness. J. Adhes. 2010, 86, 891–905. [Google Scholar] [CrossRef]
- Marzi, S.; Biel, A.; Stigh, U. On experimental methods to investigate the effect of layer thickness on the fracture behavior of adhesively bonded joints. Int. J. Adhes. Adhes. 2011, 31, 840–850. [Google Scholar] [CrossRef]
- Han, X.; Jin, Y.; da Silva, L.F.M.; Costa, M.; Wu, C. On the effect of adhesive thickness on mode I fracture energy—An experimental and modelling study using a trapezoidal cohesive zone model. J. Adhes. 2020, 96, 490–514. [Google Scholar] [CrossRef]
- Sun, F.; Pruncu, C.I.; Penchev, P.; Jiang, J.; Dimov, S.; Blackman, B.R.K. Influence of surface micropatterns on the mode I fracture toughness of adhesively bonded joints. Int. J. Adhes. Adhes. 2020, 103, 102718. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Sato, C. Experimental investigation of the effect of adhesive thickness on the fracture behavior of structural acrylic adhesive joints under various loading rates. Int. J. Adhes. Adhes. 2021, 105, 102782. [Google Scholar] [CrossRef]
- Hayashi, A.; Sekiguchi, Y.; Sato, C. AFM observation of sea-island structure formed by second generation acrylic adhesive. J. Adhes. 2021, 97, 155–171. [Google Scholar] [CrossRef]
- Kamiyama, K.; Mikuni, M.; Matsumoto, T.; Matsuda, S.; Kishi, H. Crack growth mechanism on SGA adhesive joints. Int. J. Adhes. Adhes. 2020, 103, 102690. [Google Scholar] [CrossRef]
- De Moura, M.F.S.F.; Morais, J.J.L.; Dourado, N. A new data reduction scheme for mode I wood fracture characterization using the double cantilever beam test. Eng. Fract. Mech. 2008, 75, 3852–3865. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Katano, M.; Sato, C. Experimental study of the mode I adhesive fracture energy in DCB specimens bonded with a polyurethane adhesive. J. Adhes. 2017, 93, 235–255. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Hayashi, A.; Sato, C. Analytical determination of adhesive layer deformation for adhesively bonded double cantilever beam test considering elastic-plastic deformation. J. Adhes. 2020, 96, 647–664. [Google Scholar] [CrossRef]
- Lee, D.-B.; Ikeda, T.; Miyazaki, N.; Choi, N.-S. Effect of bond thickness on the fracture toughness of adhesive joints. Trans. ASME 2004, 126, 14–18. [Google Scholar] [CrossRef]
- Banea, M.D.; da Silva, L.F.M.; Campilho, R.D.S.G. The effect of adhesive thickness on the mechanical behavior of a structural polyurethane adhesive. J. Adhes. 2015, 91, 331–346. [Google Scholar] [CrossRef]



| 0.15 | 0.10/0.50 (=0.2) | 40 |
| 0.20 | 0.10/0.50 (=0.2) | 40 |
| 0.32 | 0.10/0.50 (=0.2) | 40 |
| 0.61 | 0.10/0.50 (=0.2) | 40 |
| 0.82 | 0.10/0.50 (=0.2) | 40 |
| 0.16 ± 0.01 | 0.10/1.00 (=0.1) | 40 |
| 0.10/0.50 (=0.2) 1 | 40 | |
| 0.25/0.50 (=0.5) | 40 | |
| 0.10/0.50 (=0.2) | 60 | |
| 0.10/0.50 (=0.2) | 80 | |
| 0.60 ± 0.05 | 0.10/1.00 (=0.1) | 40 |
| 0.10/0.50 (=0.2) 1 | 40 | |
| 0.25/0.50 (=0.5) | 40 | |
| 0.10/0.50 (=0.2) | 50 | |
| 0.10/0.50 (=0.2) | 60 |
(mm) | (mm) after 106 cycles | at (mm/cycle) | Maximum Load Level (%) | |||
|---|---|---|---|---|---|---|
| 0.15 | 0.2 | 40 | 99.7 | 0.66 | 0.12 | 83 |
| 0.20 | 0.2 | 40 | 100 | 0.61 | 0.11 | 80 |
| 0.32 | 0.2 | 40 | 97.7 | 0.49 | 0.10 | 72 |
| 0.61 | 0.2 | 40 | 84.6 | 0.27 | 0.08 | 52 |
| 0.82 | 0.2 | 40 | 81.0 | 0.21 | 0.08 | 46 |
(mm) | (mm) after 106 cycles | at (mm/cycle) | Maximum Load Level (%) | |||
|---|---|---|---|---|---|---|
| 0.15 ± 0.02 | 0.1 | 40 | N/A | >1 | N/A | >100 |
| 0.2 | 40 | 99.7 | 0.67 | 0.12 | 83 | |
| 0.5 | 40 | 82.7 | 0.50 | 0.16 | 79 | |
| 0.2 | 60 | 101 | 0.35 | 0.11 | 59 | |
| 0.2 | 80 | 102 | 0.15 | 0.13 | 40 | |
| 0.60 ± 0.05 | 0.1 | 40 | 132 | 0.88 | 0.08 | 93 |
| 0.2 | 40 | 84.6 | 0.27 | 0.08 | 52 | |
| 0.5 | 40 | 65.8 | 0.21 | 0.11 | 49 | |
| 0.2 | 50 | 86.0 | 0.22 | 0.09 | 47 | |
| 0.2 | 60 | 80.3 | 0.12 | 0.10 | 36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sekiguchi, Y.; Sato, C. Effect of Bond-Line Thickness on Fatigue Crack Growth of Structural Acrylic Adhesive Joints. Materials 2021, 14, 1723. https://doi.org/10.3390/ma14071723
Sekiguchi Y, Sato C. Effect of Bond-Line Thickness on Fatigue Crack Growth of Structural Acrylic Adhesive Joints. Materials. 2021; 14(7):1723. https://doi.org/10.3390/ma14071723
Chicago/Turabian StyleSekiguchi, Yu, and Chiaki Sato. 2021. "Effect of Bond-Line Thickness on Fatigue Crack Growth of Structural Acrylic Adhesive Joints" Materials 14, no. 7: 1723. https://doi.org/10.3390/ma14071723
APA StyleSekiguchi, Y., & Sato, C. (2021). Effect of Bond-Line Thickness on Fatigue Crack Growth of Structural Acrylic Adhesive Joints. Materials, 14(7), 1723. https://doi.org/10.3390/ma14071723







