Experimental Investigation on Shear Behavior of the Interface between Early-Strength Self-Compacting Shrinkage-Compensating High-Performance Concrete and Ordinary Concrete Substrate
Abstract
:1. Introduction
2. Experimental Program
2.1. Material Properties
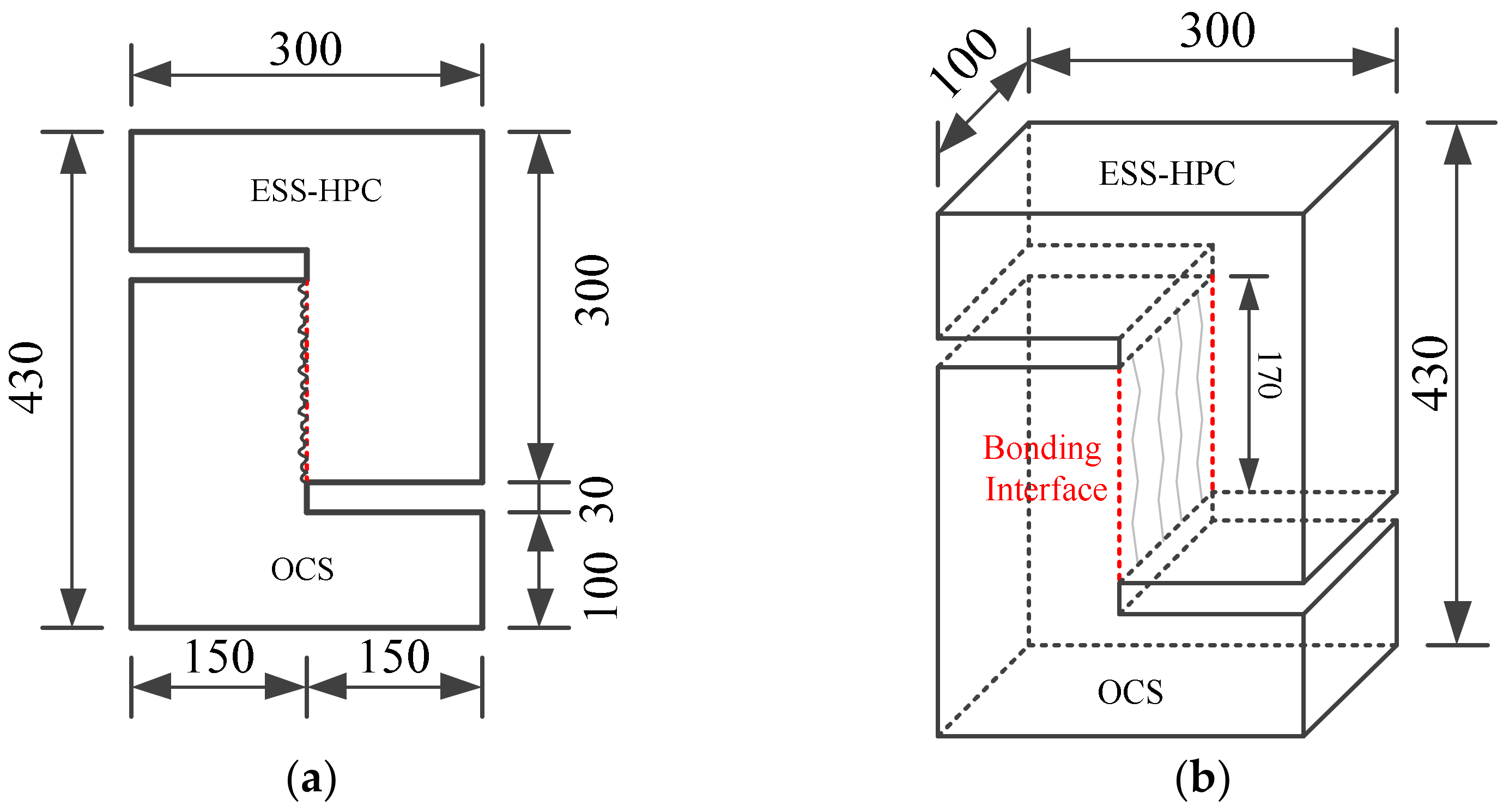
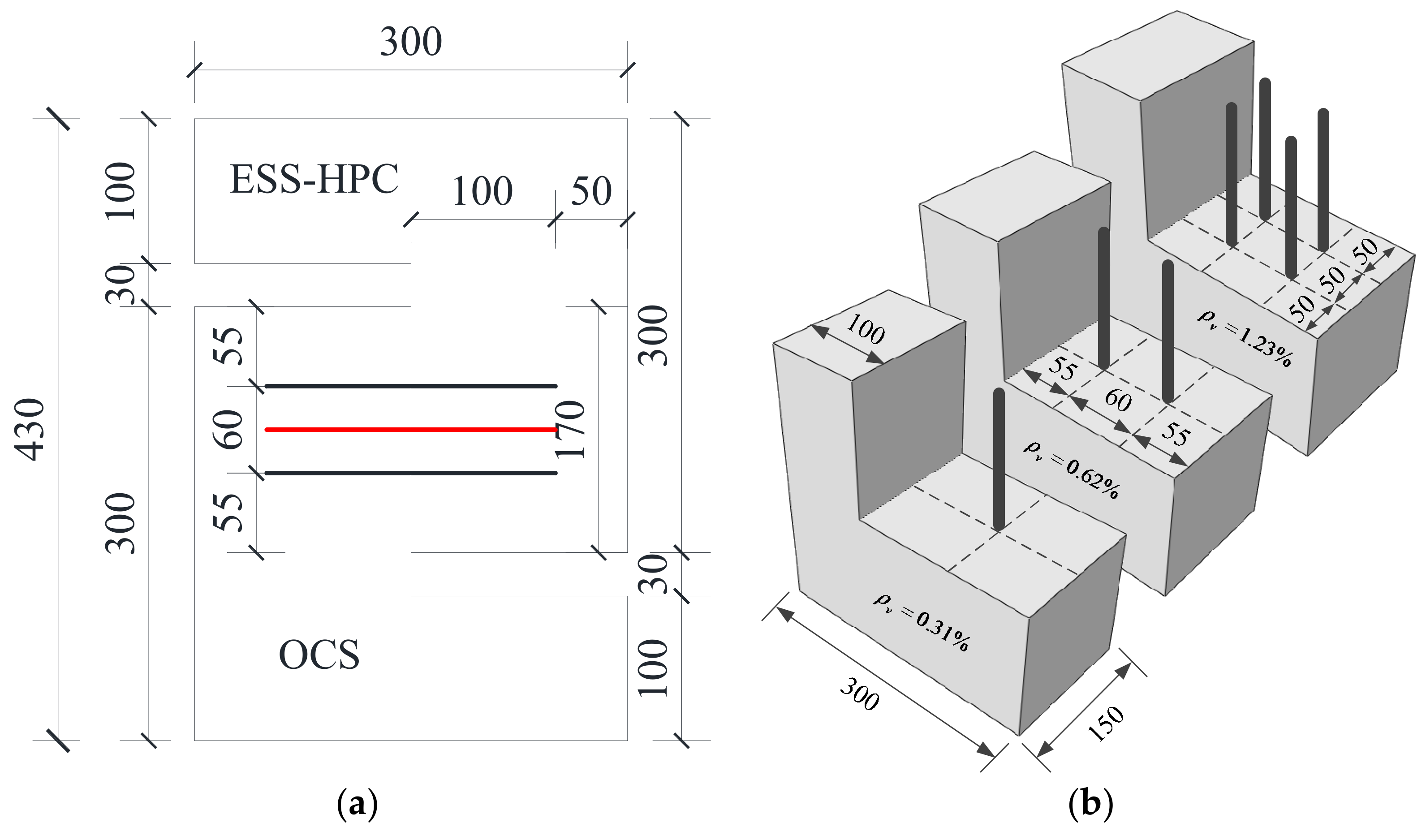
2.2. Details of the Specimens
2.3. Surface Preparation
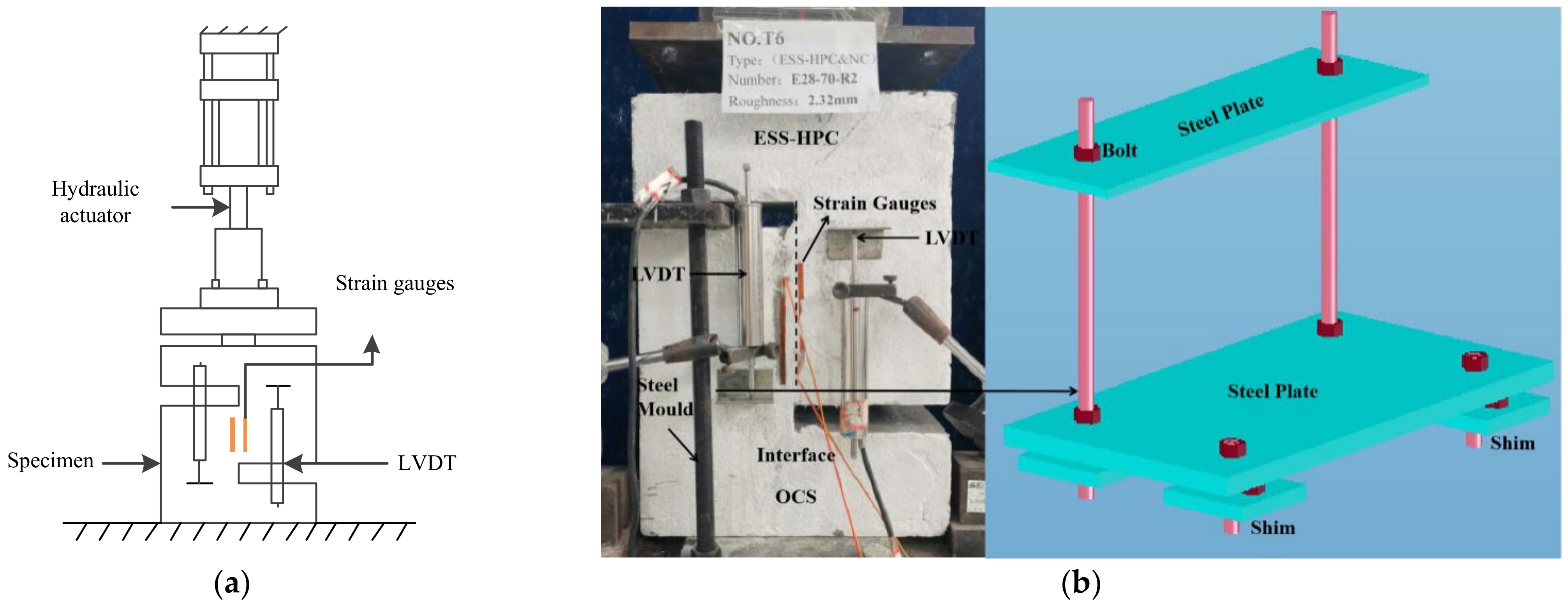
2.4. Testing Procedure
3. Experimental Results
3.1. Failure Modes
3.2. Shear Bond Stress
3.2.1. Effect of the ESS-HPC and OCS Compressive Strength Grade
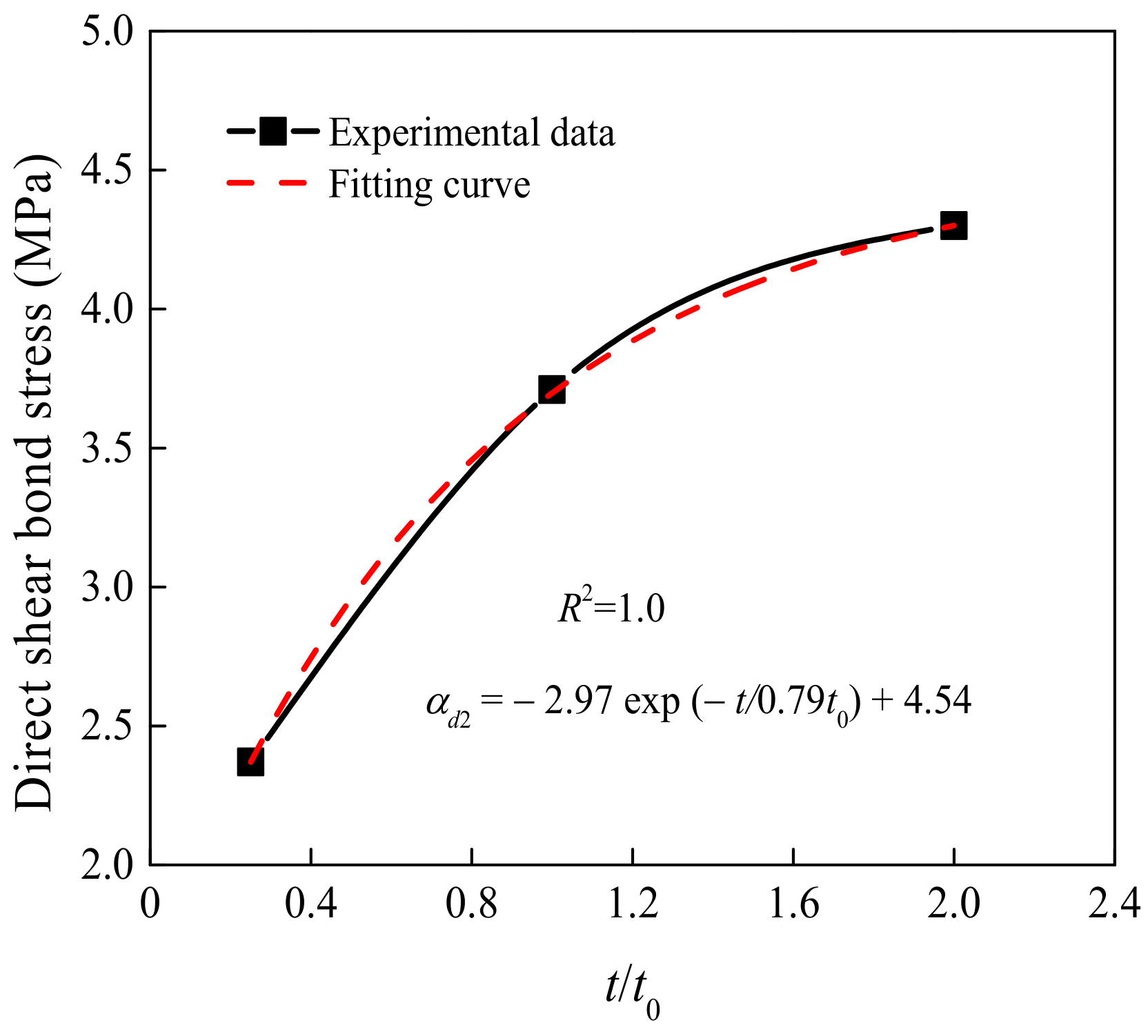
3.2.2. Effect of the ESS-HPC Curing Age
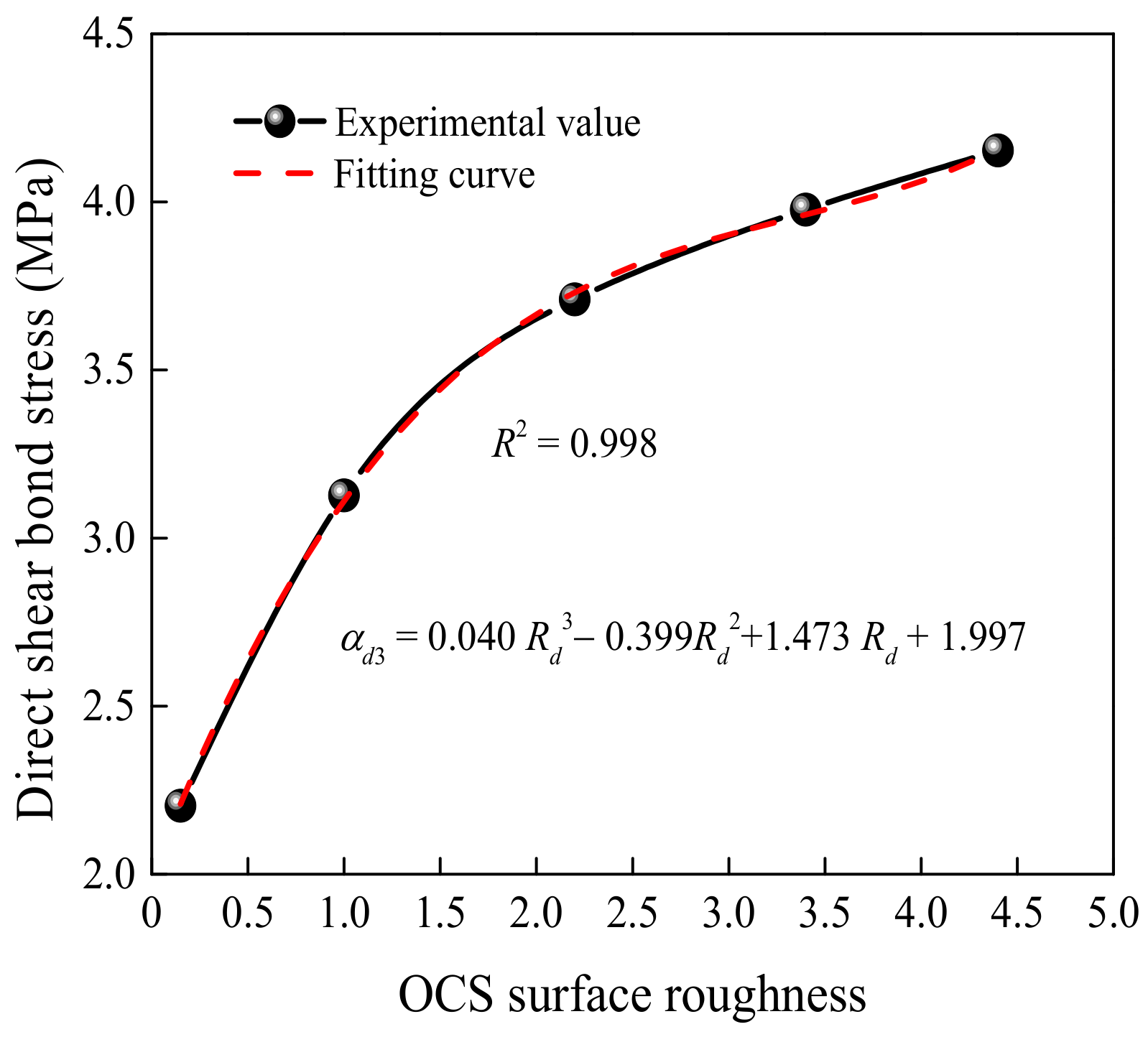
3.2.3. Effect of the OCS Surface Roughness
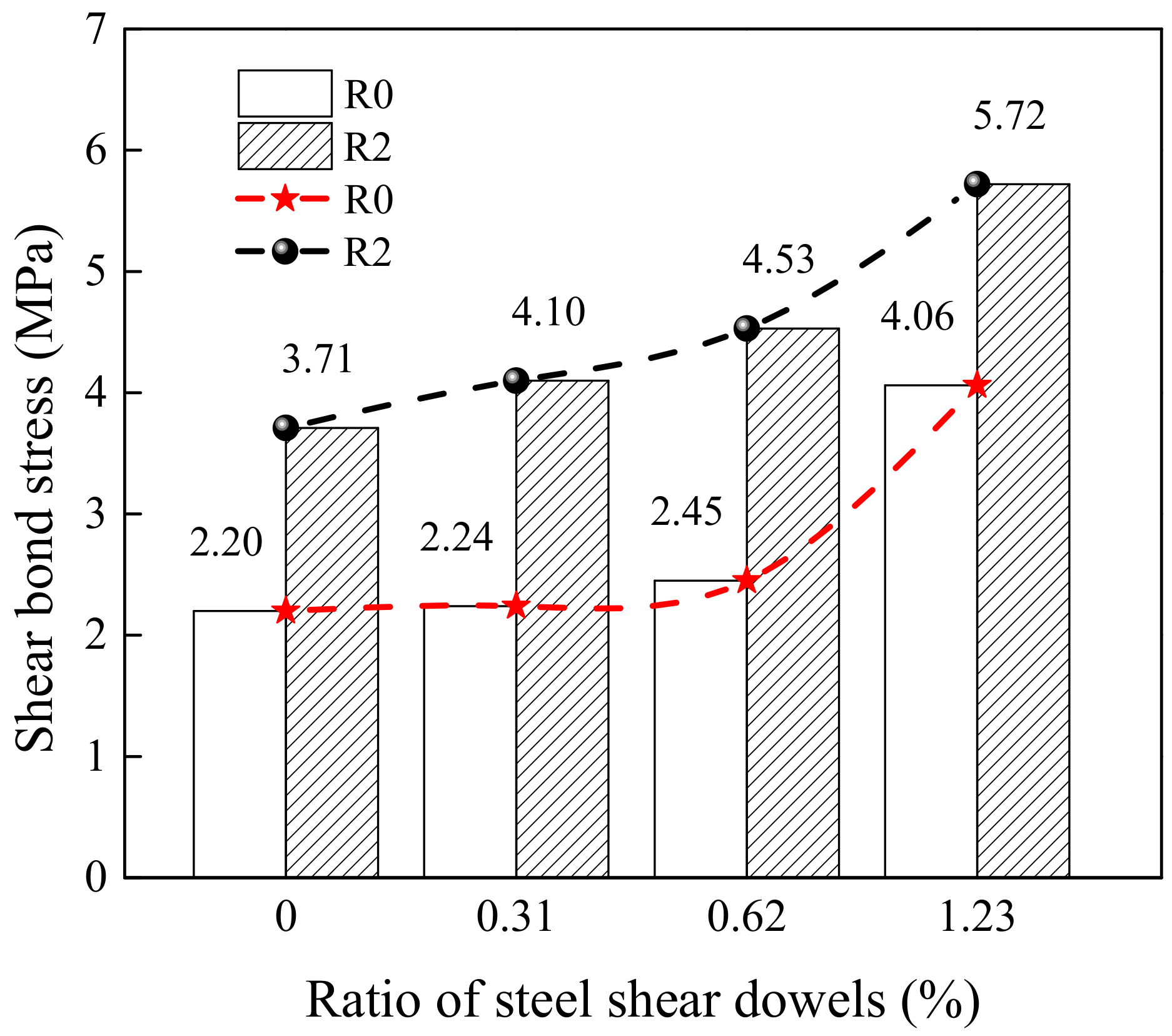
3.2.4. Effect of Ratio of Steel Shear Dowels
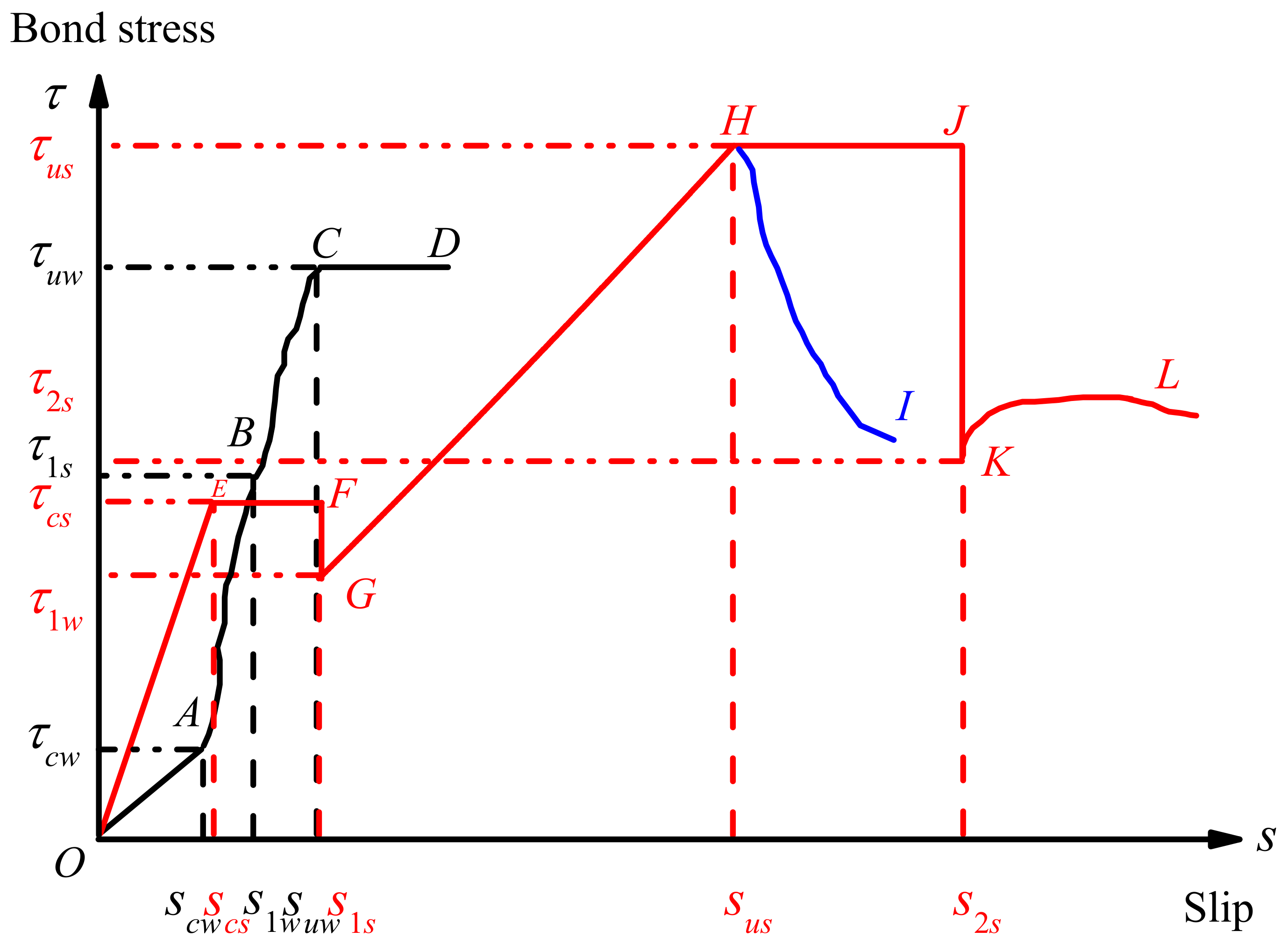
3.2.5. Bond Stress–Slip Curves
4. Discussion
4.1. CEB-FIB Model 2010
4.2. AASHTO Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| d | diameter of steel shear dowels (mm); |
| ρv | ratio of steel shear dowels; |
| fe | ESS-HPC compressive strength (MPa); |
| Rd | surface roughness in direct shear test (mm); |
| τd | direct bond stress (MPa); |
| nr | type of surface roughness; |
| Pd | maximum applied load in direct shear test (N); |
| Ad | interface area in direct shear test (mm2); |
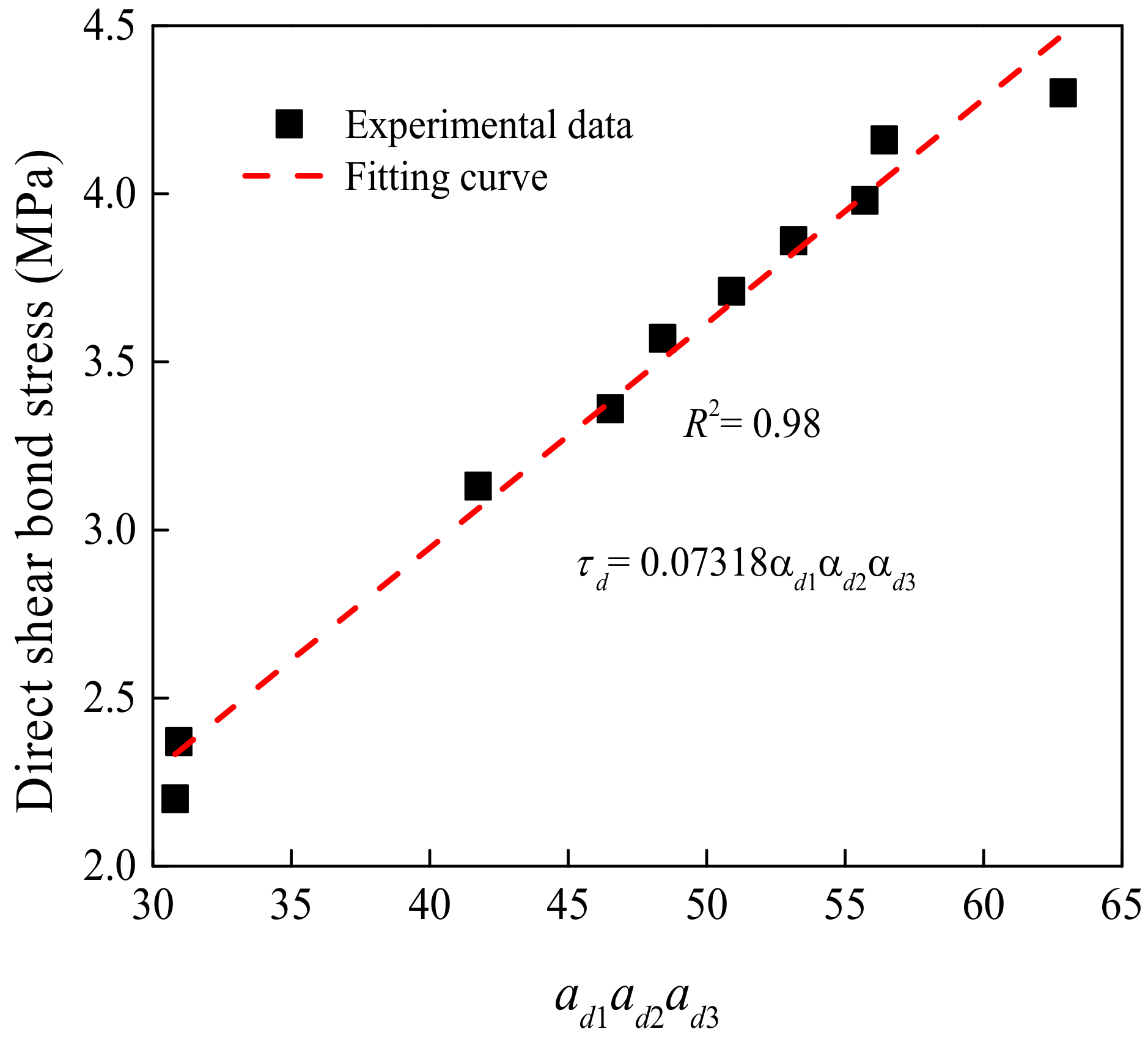
| αd1 | bond stress under the influence of fcua in direct shear test (MPa); |
| fcua | average value of the ESS-HPC and OCS compressive strength (MPa); |
| αd2 | bond stress under the influence of t/t0 in direct shear test (MPa); |
| t and t0 | ESS-HPC and OCS curing age, respectively; |
| αd3 | bond stress under the influence of Rd in direct shear test (MPa); |
| τds | shear bond stress considering the steel shear dowels (MPa); |
| fy | design tensile strength of steel shear dowels (MPa); |
| kd | fitting coefficients of the DSBS; |
| τcw and τuw | cracking and ultimate bond stress of specimens without steel shear dowels (MPa); |
| τ1s | bond stress of specimen without steel shear dowels at the elastic–plastic slip stage (MPa); |
| τcs | bond stress of specimen with steel shear dowels at the elastic stage (MPa); |
| τ1w | bond stress of specimen with steel shear dowels at the descent stage I (MPa); |
| τus | ultimate bond stress of specimen with steel shear dowels at the abrupt transition stage II (MPa); |
| τ2s | bond stress of specimen with steel shear dowels at the descent stage II (MPa). |
References
- Rashid, K.; Ahmad, M.; Ueda, T.; Deng, J.; Aslam, K.; Nazir, I.; Azam, S.M. Experimental investigation of the bond strength between new to old concrete using different adhesive layers. Constr. Build. Mater. 2020, 249, 118798. [Google Scholar] [CrossRef]
- Farzad, M.; Shafieifar, M.; Azizinamini, A. Experimental and numerical study on bond strength between conventional concrete and ultra high-performance concrete (UHPC). Eng. Struct. 2019, 186, 297–305. [Google Scholar] [CrossRef]
- Bentz, D.P.; De la Varga, I.; Muñoz, J.F.; Spragg, R.P.; Graybeal, B.A.; Hussey, D.S.; Lamanna, J.M. Influence of substrate state and roughness on interface microstructure and bond strength: Slant shear vs. pull-off testing. Cement. Concrete. Comp. 2017, 87, 63–72. [Google Scholar] [CrossRef] [PubMed]
- Jafarinejad, S.; Rabiee, A.; Shekarchi, M. Experimental investigation on the bond strength between ultra high strength fiber reinforced cementitious mortar & conventional concrete. Constr. Build. Mater. 2019, 229, 116814. [Google Scholar] [CrossRef]
- Jiao, P.C.; Roy, M.; Barri, K.; Zhu, R.H.; Ray, I.; Alavi, A.H. High-performance fiber reinforced concrete as a repairing material to normal concrete structures: Experiments, numerical simulations and a machine learning-based prediction model. Constr. Build. Mater. 2019, 223, 1167–1181. [Google Scholar] [CrossRef]
- Du, W.P.; Yang, C.Q.; Wang, C.; Pan, Y.; Zhang, H.L.; Yuan, W.W. Flexural behavior of polyvinyl alcohol fiber-reinforced ferrocement cementitious composite. J. Mater. Civil. Eng. 2021, 33, 04021040. [Google Scholar] [CrossRef]
- Zanotti, C.; Borges, P.H.R.; Bhutta, A.; Banthia, N. Bond strength between concrete substrate and metakaolin geopolymer repair mortar: Effect of curing regime and PVA fiber reinforcement. Cement. Concrete. Comp. 2017, 80, 307–316. [Google Scholar] [CrossRef]
- Gomaa, E.; Gheni, A.; ElGawady, M.A. Repair of ordinary Portland cement concrete using ambient-cured alkali-activated concrete: Interfacial behavior. Cement. Concrete. Res. 2020, 129, 105968. [Google Scholar] [CrossRef]
- Abo Sabah, S.H.; Hassan, M.H.; Muhamad Bunnori, N.; Megat Johari, M.A. Bond strength of the interface between normal concrete substrate and GUSMRC repair material overlay. Constr. Build. Mater. 2019, 216, 261–271. [Google Scholar] [CrossRef]
- Diab, A.M.; Abd Elmoaty, A.E.M.; Tag Eldin, M.R. Slant shear bond strength between self-compacting concrete and old concrete. Constr. Build. Mater. 2017, 130, 73–82. [Google Scholar] [CrossRef]
- Gadri, K.; Guettala, A. Evaluation of bond strength between sand concrete as new repair material and ordinary concrete substrate (The surface roughness effect). Constr. Build. Mater. 2017, 157, 1133–1144. [Google Scholar] [CrossRef]
- Waseem, S.A.; Singh, B. Shear transfer strength of normal and high-strength recycled aggregate concrete- An experimental investigation. Constr. Build. Mater. 2016, 125, 29–40. [Google Scholar] [CrossRef]
- Haido, J.H.; Tayeh, B.A.; Majeed, S.S.; Karpuzcu, M. Effect of high temperature on the mechanical properties of basalt fibre self-compacting concrete as an overlay material. Constr. Build. Mater. 2021, 268, 121725. [Google Scholar] [CrossRef]
- Zhang, X.H.; Zhang, W.; Luo, Y.M.; Wang, L. Interface shear strength between self-compacting concrete and carbonated concrete. J. Mater. Civil. Eng. 2020, 32, 04020113. [Google Scholar] [CrossRef]
- Zhang, X.H.; Zhang, S.; Luo, Y.M.; Wang, L.; Peng, J.X.; Zhang, J.R. Effects of interface orientations on bond strength between old conventional concrete and new self-consolidating concrete. ACI. Struct. J. 2020, 117, 191–201. [Google Scholar] [CrossRef]
- Saldanha, R.; Júlio, E.; Dias-da-Costa, D.; Santos, P. A modified slant shear test designed to enforce adhesive failure. Constr. Build. Mater. 2013, 41, 673–680. [Google Scholar] [CrossRef]
- Jin, X.; Shan, K.Y.; Wu, X.H.; Gan, R.L.; Jin, W.L. Shear-friction behavior of concrete-to-concrete interface under direct shear load. Eng. Struct. 2021, 238, 112211. [Google Scholar] [CrossRef]
- Momayez, A.; Ehsani, M.R.; Ramezanianpour, A.A.; Rajaie, H. Comparison of methods for evaluating bond strength between concrete substrate and repair materials. Cement. Concrete. Res. 2005, 35, 748–757. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, P.; Wang, X.W.; Wu, J. Shear properties of the interface between ultra-high performance concrete and normal strength concrete. Constr. Build. Mater. 2020, 248, 118455. [Google Scholar] [CrossRef]
- Zanotti, C.; Banthia, N.; Plizzari, G. A study of some factors affecting bond in cementitious fiber reinforced repairs. Cement. Concrete. Res. 2014, 63, 117–126. [Google Scholar] [CrossRef]
- Feng, S.; Xiao, H.G.; Geng, J.S. Bond strength between concrete substrate and repair mortar: Effect of fibre stiffness and substrate surface roughness. Cement. Concrete. Comp. 2020, 114, 103746. [Google Scholar] [CrossRef]
- Tian, J.; Wu, X.W.; Zheng, Y.; Hu, S.W.; Ren, W.; Du, Y.F.; Wang, W.W.; Sun, C.; Ma, J.; Ye, Y.X. Investigation of damage behaviors of ecc-to-concrete interface and damage prediction model under salt freeze-thaw cycles. Constr. Build. Mater. 2019, 226, 238–249. [Google Scholar] [CrossRef]
- Wu, X.W.; Tian, J.; Ma, H.W.; Zheng, Y.; Hu, S.W.; Wang, W.W.; Du, Y.F.; Huang, W.D.; Sun, C.; Zhu, Z.F. Investigation of interface fracture properties and nonlinear fracture model between ECC and concrete subjected to salt free-thaw cycles. Constr. Build. Mater. 2020, 259, 119785. [Google Scholar] [CrossRef]
- Tian, J.; Wu, X.W.; Zheng, Y.; Hu, S.W.; Du, Y.F.; Wang, W.W.; Sun, C.; Zhang, L.F. Investigation of interface shear properties and mechanical model between ECC and concrete. Constr. Build. Mater. 2019, 223, 12–27. [Google Scholar] [CrossRef]
- Mohamad, M.E.; Ibrahim, I.S.; Abdullah, R.; Rahman, A.B.A.; Kueh, A.B.H.; Usman, J. Friction and cohesion coefficients of composite concrete-to-concrete bond. Cement. Concrete. Comp. 2015, 66, 1–14. [Google Scholar] [CrossRef]
- Cattaneo, S.; Zorzato, G.; Bonati, A. Assessing method of shear strength between old to new concrete interface under cycling loading. Constr. Build. Mater. 2021, 309, 125160. [Google Scholar] [CrossRef]
- Hwang, S.J.; Yu, H.W.; Lee, H.J. Theory of interface shear capacity of reinforced concrete. J. Struct. Eng. 2000, 116, 700–707. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Lin, H.X.; Xue, M.F.; Wang, S.; Ran, J.S.; Su, F.Q.; Zhu, J.P. Influence of shrinkage reducing admixtures on the performance of cementitous composites: A review. Constr. Build. Mater. 2022, 325, 126579. [Google Scholar] [CrossRef]
- Qin, R.Y.; Hao, H.L.; Rousakis, T.; Lau, D. Effect of shrinkage reducing admixture on new-to-old concrete interface. Compos. Part. B-Eng. 2019, 167, 346–355. [Google Scholar] [CrossRef]
- GB/T 50080-2016; Standard for Test Method of Performance on Ordinary Fresh Concrete. Chinese Standard. China Construction Industry Press: Beijing, China, 2016. (In Chinese)
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. Chinese Standard. China Construction Industry Press: Beijing, China, 2019. (In Chinese)
- JGJ/T 283-2012; Technical Specification for Application of Self-Compacting Concrete. Chinese Standard. China Construction Industry Press: Beijing, China, 2012. (In Chinese)
- CECS 242-2016; Technical Specification for Strengthening Concrete Structures with Grid Rebar and Mortar. Chinese Standard. China Planning Press: Beijing, China, 2016. (In Chinese)
- ASTM C882/C882M-20; Standard Test Method for Bond Strength of Epoxy-Resin Systems Used with Concrete by Slant Shear. America Standard. ASTM international: West Conshohocken, PA, USA, 2005.
- Beushausen, H. The influence of concrete substrate preparation on overlay bond strength. Mag. Concrete. Res. 2010, 62, 845–852. [Google Scholar] [CrossRef]
- Tian, L.M.; Kou, Y.F.; Lin, H.L.; Li, T.J. Interfacial bond-slip behavior between H-shaped steel and engineered cementitious composites (ECCs). Eng. Struct. 2021, 231, 111731. [Google Scholar] [CrossRef]
- Fernando, M.D.A.F.; Mounir, K.; El Debs, M.K.; Ana, L.H. Bond-slip behavior of self-compacting concrete and vibrated concrete using pull-out and beam tests. Mater. Struct. 2008, 41, 1073–1089. [Google Scholar] [CrossRef]
- Assaad, J.J.; Issa, C.A. Effect of recycled acrylic-based polymers on bond stress-slip behavior in reinforced concrete structures. J. Mater. Civil. Eng. 2016, 29, 04016173. [Google Scholar] [CrossRef]
- CEB-FIP Mode Code for Concrete Structures 2010; Fib: Lausanne, Switzerland, 2013.
- AASHTO LRFD Bridge Design Specifications; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2010.
- Chen, F.; Zheng, J.L. Experimental research on direct shear behavior of adhesion of self-compacting concrete on existing concrete. J. Build. Struct. 2007, 28, 59–63. (In Chinese) [Google Scholar]
- Valikhani, A.; Jahromi, A.J.; Mantawy, I.M.; Azizinamini, A. Effect of mechanical connectors on interface shear strength between concrete substrates and UHPC: Experimental and numerical studies and proposed design equation. Constr. Build. Mater. 2020, 267, 120587. [Google Scholar] [CrossRef]









| Concrete Grade | Water (kg/m3) | Cement (kg/m3) | Silica Fume (kg/m3) | Coarse Aggregate (kg/m3) | Fine Aggregate (kg/m3) | Superplasticizer (kg/m3) |
|---|---|---|---|---|---|---|
| C55 | 153 | 452 | 50 | 1077 | 660 | 1.0 |
| Diameter (mm) | Length (mm) | Tensile Strength (GPa) | Density (g/cm3) |
|---|---|---|---|
| 0.2 | 13 | 2.1 | 7.85 |
| Cement | Silica Fume | Fine Aggregate | Coarse Aggregate | Super Plasticizer | Steel Fiber | Defoaming Agent | Rubber Power | Expansive Agent |
|---|---|---|---|---|---|---|---|---|
| 500 | 5 | 600 | 750 | 2.5 | 10 | 0.1 | 1.9 | 50 |
| Parameter | Results | ||
|---|---|---|---|
| Size of coarse aggregate | mm | 5–10 | |
| Slump flow | mm | ≥610, 0.5 h ≥ 550 | |
| Restrain expansion rate | % | ≥0.015 | |
| Setting time [30] | h | Initial | ≥1 |
| Final | ≥8 | ||
| Compressive strength [31] | MPa | 3 d | 67 ± 3.0 |
| 7 d | 74 ± 4.0 | ||
| 28 d | 82 ± 3.0 | ||
| 60 d | 90 ± 2.5 | ||
| Elastic modulus | GPa | 3 d | 33 ± 2.0 |
| 28 d | 39 ± 1.0 | ||
| Impermeability grade [32] | P | SF1 | |
| Frost resistance grade | F | ≥F200 | |
| Chloride ion penetration | C | ≤1000 | |
| Specimens | fe (MPa) | t (d) | Surface Roughness | Average Depth (mm) | Failure Modes | τc (MPa) | τd (MPa) |
|---|---|---|---|---|---|---|---|
| D28-70-R0 | 71.74 | 28 | Type I | 0.15 | A | 1.88 | 2.20 |
| D28-70-R1 | Type II | 1.00 | A/B | 2.56 | 3.13 | ||
| D28-70-R2 | Type III | 2.20 | A/B | 2.83 | 3.71 | ||
| D28-70-R3 | Type III | 3.40 | B | 3.36 | 3.98 | ||
| D28-70-R4 | Type III | 4.40 | B | 3.47 | 4.16 | ||
| D28-60-R2 | 61.22 | Type III | 2.20 | A/B | 2.70 | 3.36 | |
| D28-65-R2 | 65.76 | A/B | 3.28 | 3.57 | |||
| D28-75-R2 | 77.13 | A/B | 3.44 | 3.86 | |||
| D7-70a-R2 | 65.43 | 7 | A/B | 2.28 | 2.37 | ||
| D56-70b-R2 | 79.38 | 56 | B | 3.44 | 4.30 | ||
| DCGM28-70-R2 | / | 28 | A | 2.02 | 2.68 | ||
| D28-70-R0-S1 | 71.74 | Type I | 0.15 | E | 2.00 | 2.24 | |
| D28-70-R0-S2 | D | 1.88 | 2.45 | ||||
| D28-70-R0-S3 | C | 2.37 | 4.06 | ||||
| D28-70-R2-S1 | Type III | 2.20 | D | 2.49 | 4.10 | ||
| D28-70-R2-S2 | C | 2.19 | 4.53 | ||||
| D28-70-R2-S3 | C | 3.07 | 5.72 |
| Specimens | τexp (MPa) | τcal (MPa) Equation (4) | τexp/τcal |
|---|---|---|---|
| D28-70-R0 | 2.20 | 2.25 | 1.02 |
| D28-70-R1 | 3.13 | 3.05 | 0.97 |
| D28-70-R2 | 3.71 | 3.72 | 1.00 |
| D28-70-R3 | 3.98 | 4.07 | 1.02 |
| D28-70-R4 | 4.16 | 4.12 | 0.99 |
| D28-60-R2 | 3.36 | 3.41 | 1.02 |
| D28-65-R2 | 3.57 | 3.54 | 0.99 |
| D28-75-R2 | 3.86 | 3.87 | 1.00 |
| Average | 1.00 | ||
| SD | 0.02 | ||
| COV | 0.02 | ||
| Expression of Interface Shear Stress | Specimens | τexp (MPa) | Friction Coefficient (μ) | τcal (MPa) | (τexp − τcal) × 100% /τexp | |
|---|---|---|---|---|---|---|
| Without steel shear dowels | τd = c + μσ (5) | D28-70-R0 | 2.20 | 0.00 | 2.20 | 0.00 |
| D28-70-R1 | 3.13 | 0.30 | 3.10 | 0.96 | ||
| D28-70-R2 | 3.71 | 0.50 | 3.70 | 0.27 | ||
| D28-70-R3 | 3.98 | 0.60 | 4.00 | −0.50 | ||
| D28-70-R4 | 4.16 | 0.70 | 4.30 | −3.37 | ||
| With steel shear dowels | τds = c + μ(σ + ρvfy) (6) | D28-70-R0-S1 | 2.24 | 0.02 | 2.28 | −1.81 |
| D28-70-R0-S2 | 2.45 | 0.04 | 2.40 | 1.86 | ||
| D28-70-R0-S3 | 4.06 | 0.25 | 3.96 | 2.35 | ||
| D28-70-R2-S1 | 4.02 | 0.06 | 3.95 | 1.71 | ||
| D28-70-R2-S2 | 4.44 | 0.12 | 4.32 | 2.63 | ||
| D28-70-R2-S3 | 5.74 | 0.30 | 5.83 | −1.53 | ||
| Specimens | τexp (MPa) | τcal (MPa) Equation (8) | τexp/τcal |
|---|---|---|---|
| D28-70-R0-S1 | 2.24 | 2.68 | 0.84 |
| D28-70-R0-S2 | 2.45 | 3.16 | 0.77 |
| D28-70-R0-S3 | 4.06 | 4.11 | 0.99 |
| D28-70-R2-S1 | 4.02 | 4.19 | 0.96 |
| D28-70-R2-S2 | 4.44 | 4.67 | 0.95 |
| D28-70-R2-S3 | 5.74 | 5.62 | 1.02 |
| Average | 0.92 | ||
| SD | 0.10 | ||
| COV | 0.10 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, W.; Yang, C.; De Backer, H.; Li, C.; Ming, K.; Zhang, H.; Pan, Y. Experimental Investigation on Shear Behavior of the Interface between Early-Strength Self-Compacting Shrinkage-Compensating High-Performance Concrete and Ordinary Concrete Substrate. Materials 2022, 15, 4939. https://doi.org/10.3390/ma15144939
Du W, Yang C, De Backer H, Li C, Ming K, Zhang H, Pan Y. Experimental Investigation on Shear Behavior of the Interface between Early-Strength Self-Compacting Shrinkage-Compensating High-Performance Concrete and Ordinary Concrete Substrate. Materials. 2022; 15(14):4939. https://doi.org/10.3390/ma15144939
Chicago/Turabian StyleDu, Wenping, Caiqian Yang, Hans De Backer, Chen Li, Kai Ming, Honglei Zhang, and Yong Pan. 2022. "Experimental Investigation on Shear Behavior of the Interface between Early-Strength Self-Compacting Shrinkage-Compensating High-Performance Concrete and Ordinary Concrete Substrate" Materials 15, no. 14: 4939. https://doi.org/10.3390/ma15144939
APA StyleDu, W., Yang, C., De Backer, H., Li, C., Ming, K., Zhang, H., & Pan, Y. (2022). Experimental Investigation on Shear Behavior of the Interface between Early-Strength Self-Compacting Shrinkage-Compensating High-Performance Concrete and Ordinary Concrete Substrate. Materials, 15(14), 4939. https://doi.org/10.3390/ma15144939






