Double-Resolved Beam Steering by Metagrating-Based Tamm Plasmon Polariton
Abstract
:1. Introduction
2. Model
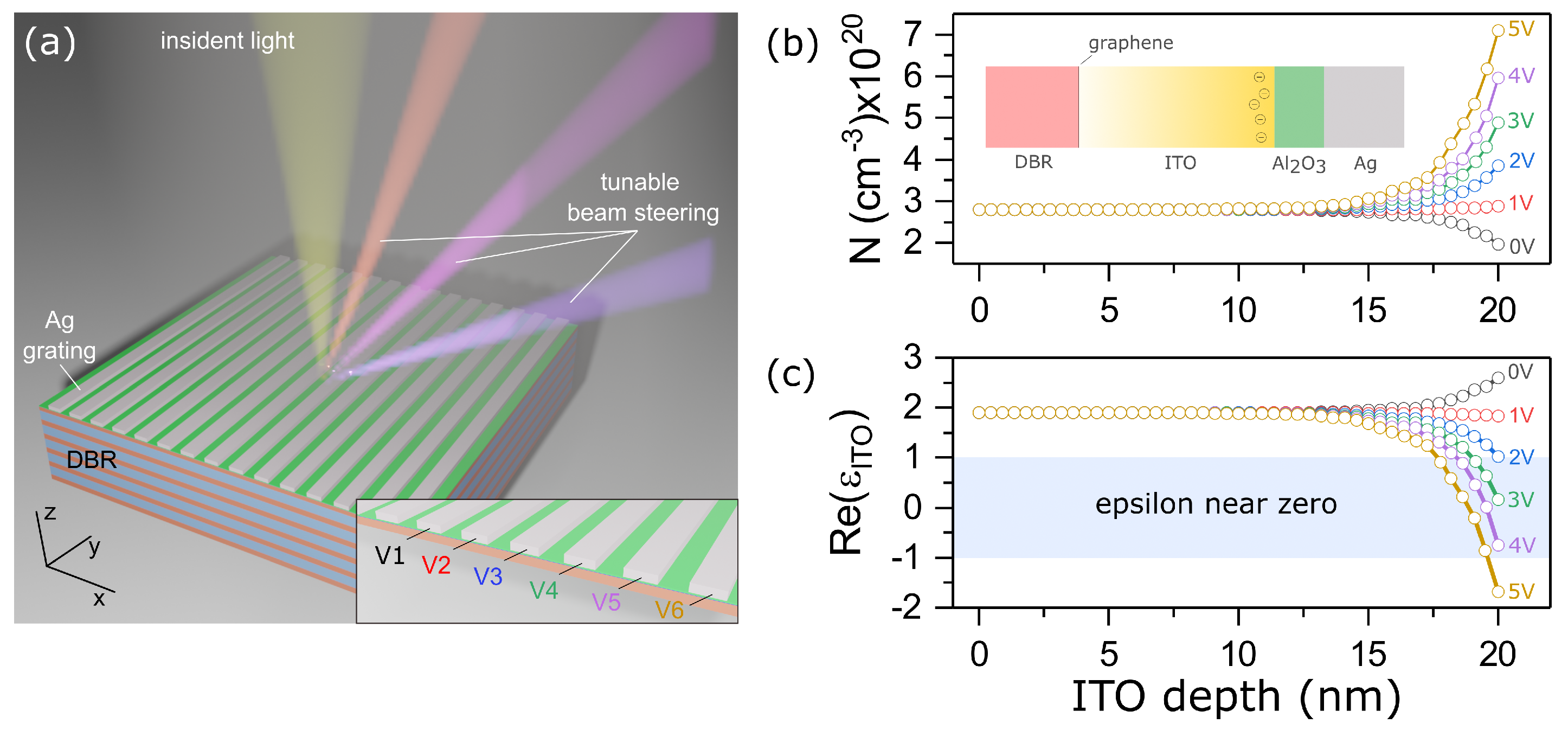
2.1. Electrostatic Simulation
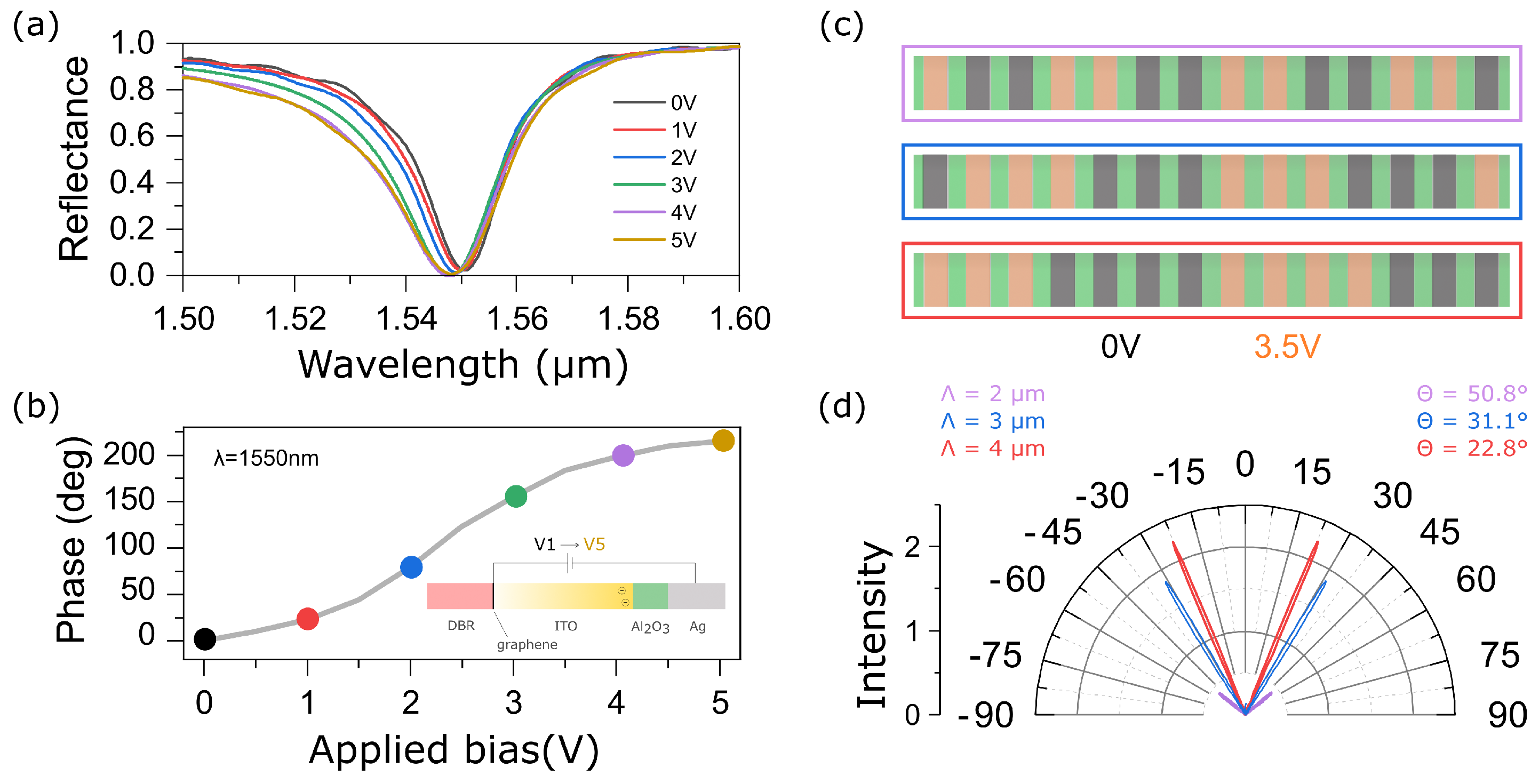
2.2. Full-Wave Simulation
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, Q.; Sun, S.; Zhou, L. Tunable/Reconfigurable Metasurfaces: Physics and Applications. Research 2019, 2019, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.T.; Zhu, A.Y.; Capasso, F. Flat optics with dispersion-engineered metasurfaces. Nat. Rev. Mater. 2020, 5, 604–620. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, S.; Zentgraf, T. Metasurface holography: From fundamentals to applications. Nanophotonics 2018, 7, 1169–1190. [Google Scholar] [CrossRef]
- Bosch, M.; Shcherbakov, M.R.; Won, K.; Lee, H.S.; Kim, Y.; Shvets, G. Electrically Actuated Varifocal Lens Based on Liquid-Crystal-Embedded Dielectric Metasurfaces. Nano Lett. 2021, 21, 3849–3856. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Yang, K.Y.; Wang, C.M.; Juan, T.K.; Chen, W.T.; Liao, C.Y.; He, Q.; Xiao, S.; Kung, W.T.; Guo, G.Y.; et al. High-Efficiency Broadband Anomalous Reflection by Gradient Meta-Surfaces. Nano Lett. 2012, 12, 6223–6229. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Palacios, E.; Butun, S.; Aydin, K. Visible-Frequency Metasurfaces for Broadband Anomalous Reflection and High-Efficiency Spectrum Splitting. Nano Lett. 2015, 15, 1615–1621. [Google Scholar] [CrossRef]
- Sroor, H.; Huang, Y.W.; Sephton, B.; Naidoo, D.; Vallés, A.; Ginis, V.; Qiu, C.W.; Ambrosio, A.; Capasso, F.; Forbes, A. High-purity orbital angular momentum states from a visible metasurface laser. Nat. Photonics 2020, 14, 498–503. [Google Scholar] [CrossRef]
- Xu, W.H.; Chou, Y.H.; Yang, Z.Y.; Liu, Y.Y.; Yu, M.W.; Huang, C.H.; Chang, C.T.; Huang, C.Y.; Lu, T.C.; Lin, T.R.; et al. Tamm Plasmon-Polariton Ultraviolet Lasers. Adv. Photonics Res. 2021, 3, 2100120. [Google Scholar] [CrossRef]
- Liang, Y.; Koshelev, K.; Zhang, F.; Lin, H.; Lin, S.; Wu, J.; Jia, B.; Kivshar, Y. Bound States in the Continuum in Anisotropic Plasmonic Metasurfaces. Nano Lett. 2020, 20, 6351–6356. [Google Scholar] [CrossRef]
- Ra’di, Y.; Sounas, D.L.; Alù, A. Metagratings: Beyond the Limits of Graded Metasurfaces for Wave Front Control. Phys. Rev. Lett. 2017, 119, 067404. [Google Scholar] [CrossRef] [Green Version]
- Panagiotidis, E.; Almpanis, E.; Stefanou, N.; Papanikolaou, N. Multipolar interactions in Si sphere metagratings. J. Appl. Phys. 2020, 128, 093103. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Capasso, F. Broadband Multifunctional Efficient Meta-Gratings Based on Dielectric Waveguide Phase Shifters. Nano Lett. 2015, 15, 6709–6715. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Yu, P.; Zhang, S.; Liu, N. Electrically-controlled digital metasurface device for light projection displays. Nat. Commun. 2020, 11, 3574. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; Wang, H.; Zhao, H.; Xue, T.; Zhang, J. Liquid-Crystal-Based Electrically Tuned Electromagnetically Induced Transparency Metasurface Switch. Sci. Rep. 2017, 7, 17378. [Google Scholar] [CrossRef]
- Chen, K.P.; Ye, S.C.; Yang, C.Y.; Yang, Z.H.; Lee, W.; Sun, M.G. Electrically tunable transmission of gold binary-grating metasurfaces integrated with liquid crystals. Opt. Express 2016, 24, 16815. [Google Scholar] [CrossRef] [PubMed]
- Cueff, S.; John, J.; Zhang, Z.; Parra, J.; Sun, J.; Orobtchouk, R.; Ramanathan, S.; Sanchis, P. VO2 nanophotonics. APL Photonics 2020, 5, 110901. [Google Scholar] [CrossRef]
- Lee, H.W.; Papadakis, G.; Burgos, S.P.; Chander, K.; Kriesch, A.; Pala, R.; Peschel, U.; Atwater, H.A. Nanoscale Conducting Oxide PlasMOStor. Nano Lett. 2014, 14, 6463–6468. [Google Scholar] [CrossRef]
- Babicheva, V.E.; Boltasseva, A.; Lavrinenko, A.V. Transparent conducting oxides for electro-optical plasmonic modulators. Nanophotonics 2015, 4, 165–185. [Google Scholar] [CrossRef]
- Lee, Y.; Yun, J.; Kim, S.J.; Seo, M.; In, S.; Jeong, H.D.; Lee, S.Y.; Park, N.; Chung, T.D.; Lee, B. High-Speed Transmission Control in Gate-Tunable Metasurfaces Using Hybrid Plasmonic Waveguide Mode. Adv. Opt. Mater. 2020, 8, 2001256. [Google Scholar] [CrossRef]
- Huang, Y.W.; Lee, H.W.H.; Sokhoyan, R.; Pala, R.A.; Thyagarajan, K.; Han, S.; Tsai, D.P.; Atwater, H.A. Gate-Tunable Conducting Oxide Metasurfaces. Nano Lett. 2016, 16, 5319–5325. [Google Scholar] [CrossRef] [Green Version]
- Kaliteevski, M.; Iorsh, I.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Kavokin, A.V.; Shelykh, I.A. Tamm plasmon-polaritons: Possible electromagnetic states at the interface of a metal and a dielectric Bragg mirror. Phys. Rev. B 2007, 76, 165415. [Google Scholar] [CrossRef]
- Sasin, M.E.; Seisyan, R.P.; Kaliteevski, M.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Egorov, A.Y.; Vasil’ev, A.P.; Mikhrin, V.S.; Kavokin, A.V. Tamm plasmon polaritons: Slow and spatially compact light. Appl. Phys. Lett. 2008, 92, 251112. [Google Scholar] [CrossRef]
- Bikbaev, R.; Vetrov, S.; Timofeev, I. Epsilon-Near-Zero Absorber by Tamm Plasmon Polariton. Photonics 2019, 6, 28. [Google Scholar] [CrossRef]
- Vyunishev, A.M.; Bikbaev, R.G.; Svyakhovskiy, S.E.; Timofeev, I.V.; Pankin, P.S.; Evlashin, S.A.; Vetrov, S.Y.; Myslivets, S.A.; Arkhipkin, V.G. Broadband Tamm plasmon polariton. J. Opt. Soc. Am. B 2019, 36, 2299–2305. [Google Scholar] [CrossRef]
- Wu, F.; Wu, X.; Xiao, S.; Liu, G.; Li, H. Broadband wide-angle multilayer absorber based on a broadband omnidirectional optical Tamm state. Opt. Express 2021, 29, 23976. [Google Scholar] [CrossRef]
- Bohn, J.; Luk, T.S.; Tollerton, C.; Hutchings, S.W.; Brener, I.; Horsley, S.; Barnes, W.L.; Hendry, E. All-optical switching of an epsilon-near-zero plasmon resonance in indium tin oxide. Nat. Commun. 2021, 12, 1017. [Google Scholar] [CrossRef] [PubMed]
- Pang, K.; Alam, M.Z.; Zhou, Y.; Liu, C.; Reshef, O.; Manukyan, K.; Voegtle, M.; Pennathur, A.; Tseng, C.; Su, X.; et al. Adiabatic Frequency Conversion Using a Time-Varying Epsilon-Near-Zero Metasurface. Nano Lett. 2021, 21, 5907–5913. [Google Scholar] [CrossRef]
- Chen, L.R.; Chang, C.J.; Hong, K.B.; Weng, W.C.; Chuang, B.H.; Huang, Y.W.; Lu, T.C. Static Beam Steering by Applying Metasurfaces on Photonic-Crystal Surface-Emitting Lasers. J. Light. Technol. 2022, 1–6. [Google Scholar] [CrossRef]
- Bikbaev, R.G.; Maksimov, D.N.; Pankin, P.S.; Chen, K.P.; Timofeev, I.V. Critical coupling vortex with grating-induced high Q-factor optical Tamm states. Opt. Express 2021, 29, 4672–4680. [Google Scholar] [CrossRef]
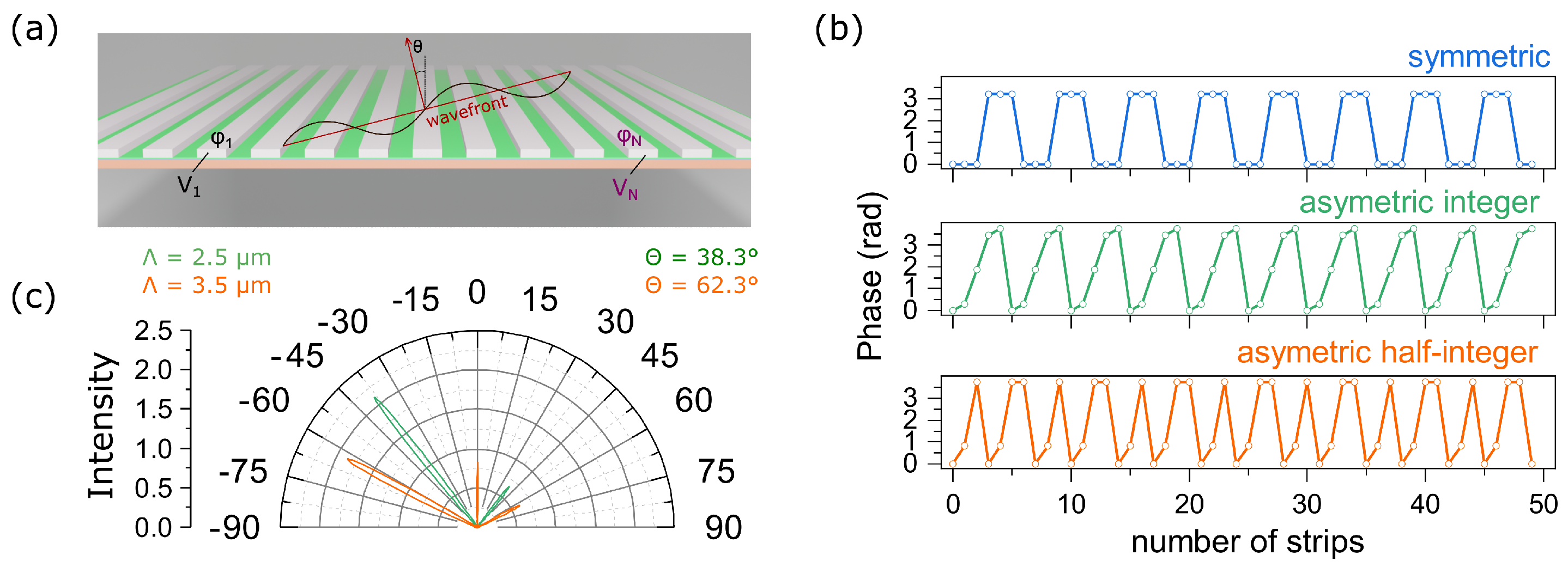
| Number of Strips, n | Simulated by FDTD | Calculated by Equation (1) | Results |
|---|---|---|---|
| 3 | >90 | >90 | |
| 3.5 | 62.3 | 62.33 | Figure 3c |
| 4 | 50.77 | 50.80 | Figure 2d |
| 4.5 | - | 43.54 | |
| 5 | 38.3 | 38.32 | Figure 3c |
| 5.5 | - | 34.30 | |
| 6 | 31.10 | 31.10 | Figure 2d |
| 6.5 | - | 28.48 | |
| 7 | - | 26.28 | |
| 7.5 | - | 24.41 | |
| 8 | 22.8 | 22.79 | Figure 2d |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bikbaev, R.G.; Maksimov, D.N.; Chen, K.-P.; Timofeev, I.V. Double-Resolved Beam Steering by Metagrating-Based Tamm Plasmon Polariton. Materials 2022, 15, 6014. https://doi.org/10.3390/ma15176014
Bikbaev RG, Maksimov DN, Chen K-P, Timofeev IV. Double-Resolved Beam Steering by Metagrating-Based Tamm Plasmon Polariton. Materials. 2022; 15(17):6014. https://doi.org/10.3390/ma15176014
Chicago/Turabian StyleBikbaev, Rashid G., Dmitrii N. Maksimov, Kuo-Ping Chen, and Ivan V. Timofeev. 2022. "Double-Resolved Beam Steering by Metagrating-Based Tamm Plasmon Polariton" Materials 15, no. 17: 6014. https://doi.org/10.3390/ma15176014
APA StyleBikbaev, R. G., Maksimov, D. N., Chen, K.-P., & Timofeev, I. V. (2022). Double-Resolved Beam Steering by Metagrating-Based Tamm Plasmon Polariton. Materials, 15(17), 6014. https://doi.org/10.3390/ma15176014








