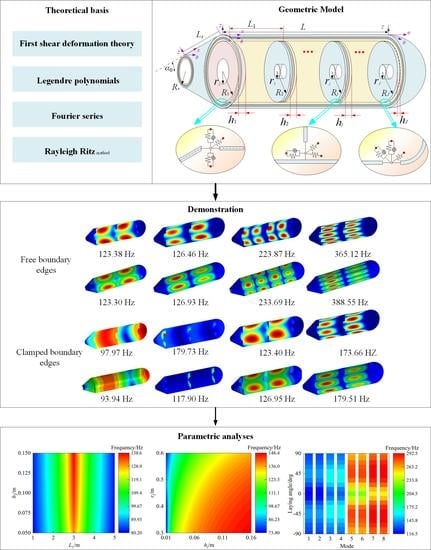
Effect of Multiple Annular Plates on Vibration Characteristics of Laminated Submarine-like Structures
Abstract
:1. Introduction
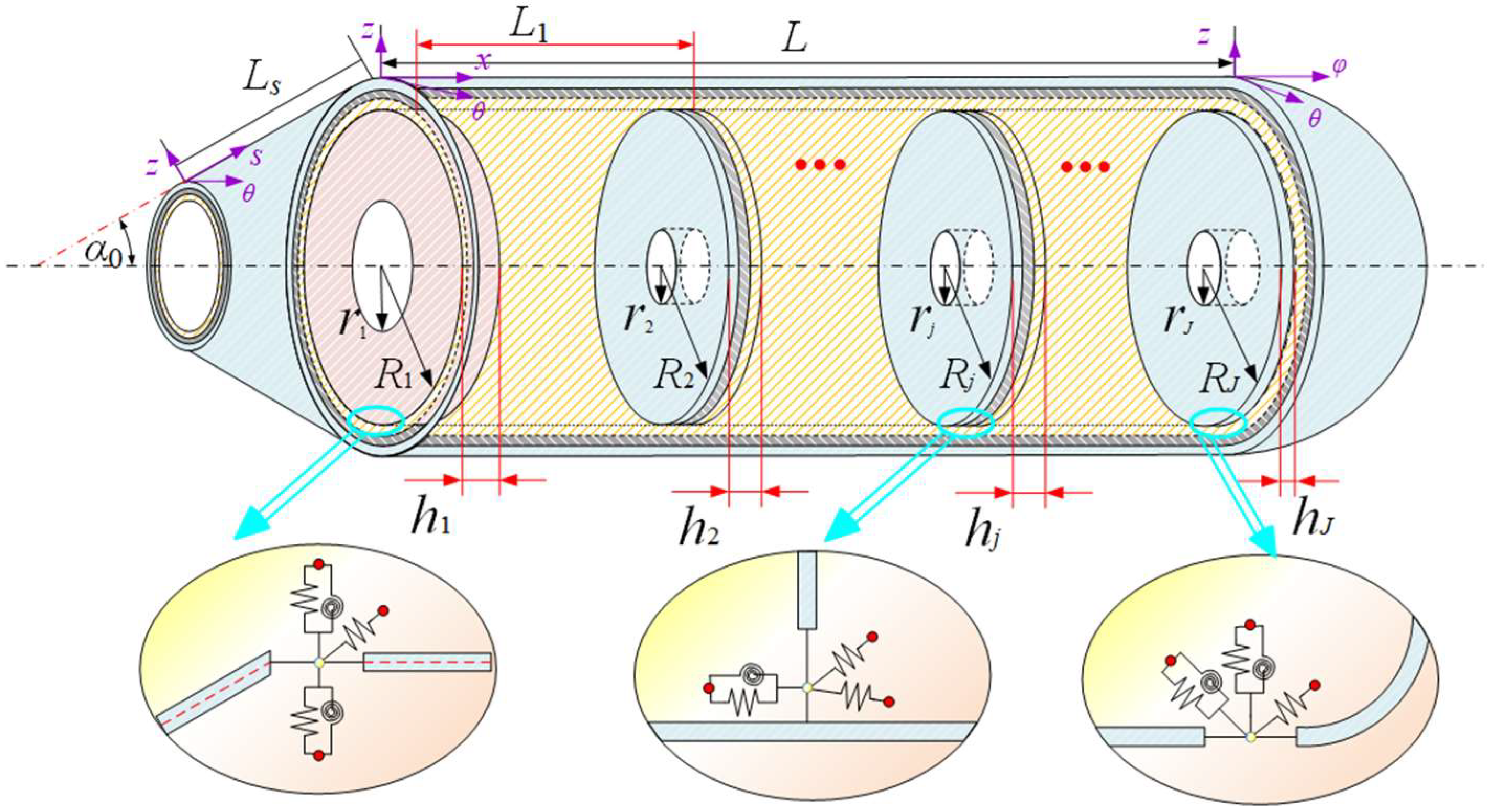
2. Analysis Model
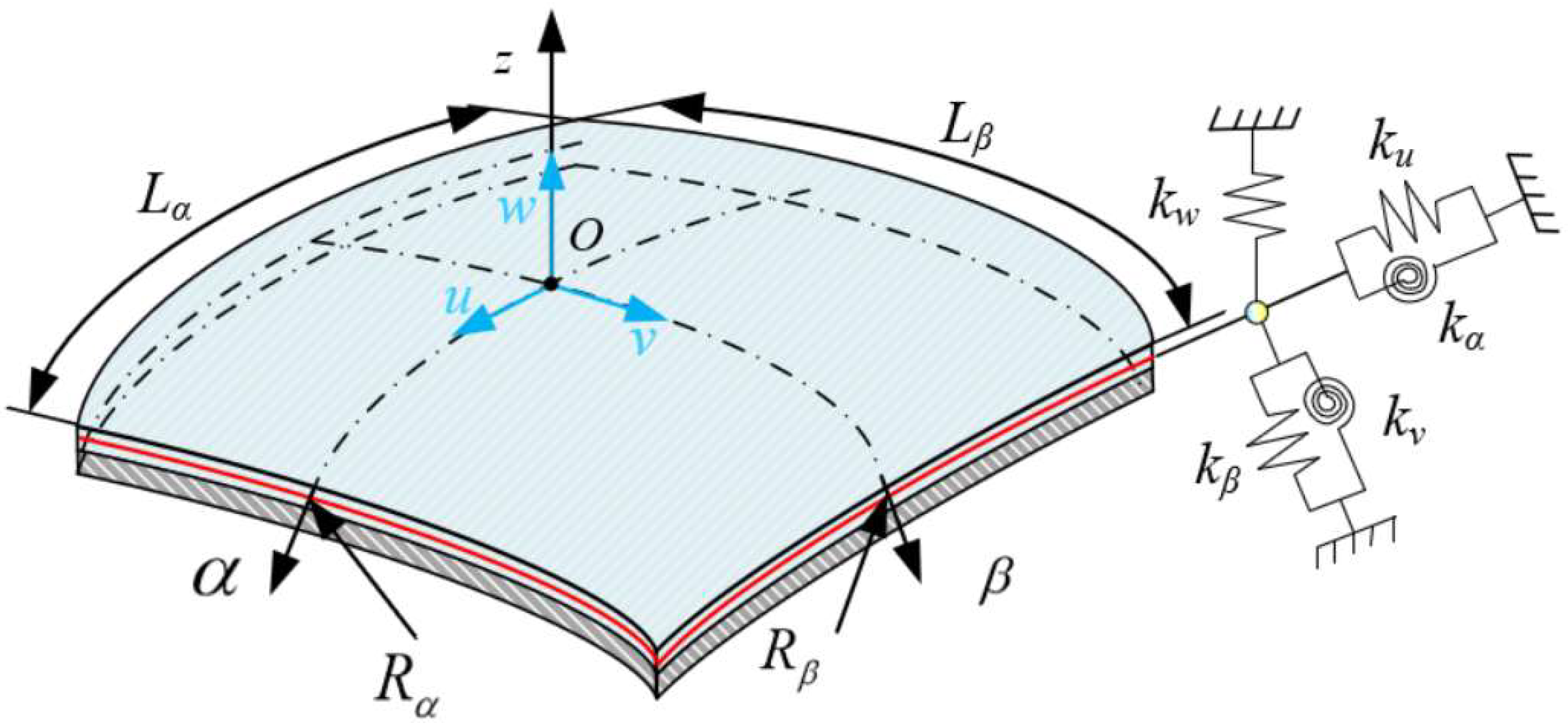
2.1. Description of the Model
2.2. Kinematic Relations and Stress Resultants
2.3. Energy Expressions
2.4. Displacement Admissible Functions and Solution Process
3. Numerical Calculation and Analysis
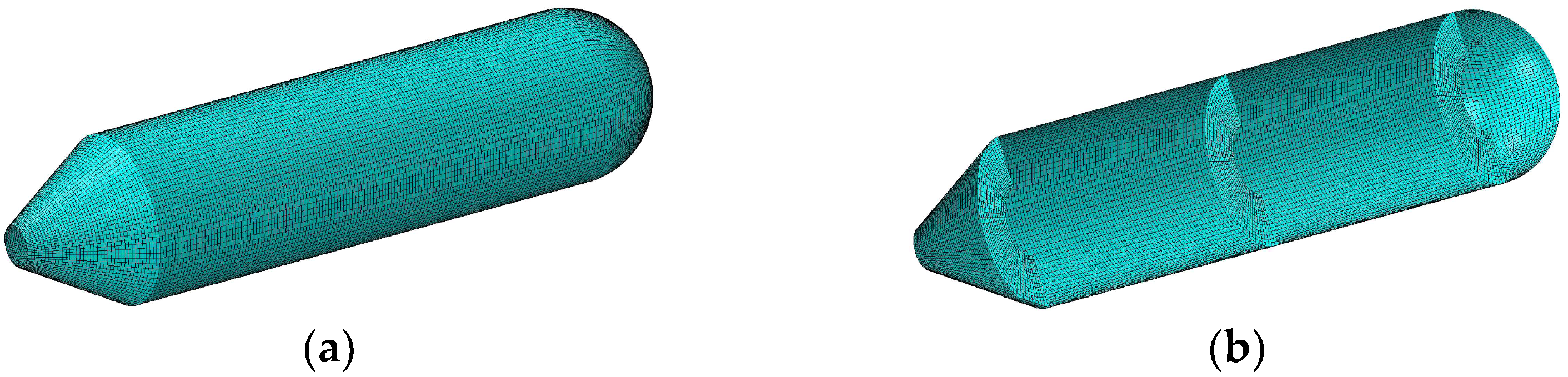
3.1. Numerical Verifications
3.2. Parametric Study
4. Conclusions
- (1)
- The established model has good predictive ability regarding the vibration characteristics of laminated submarine-like structures combined with multiple annular plates; the maximum deviation of submarine-like structures is only 2.07%.
- (2)
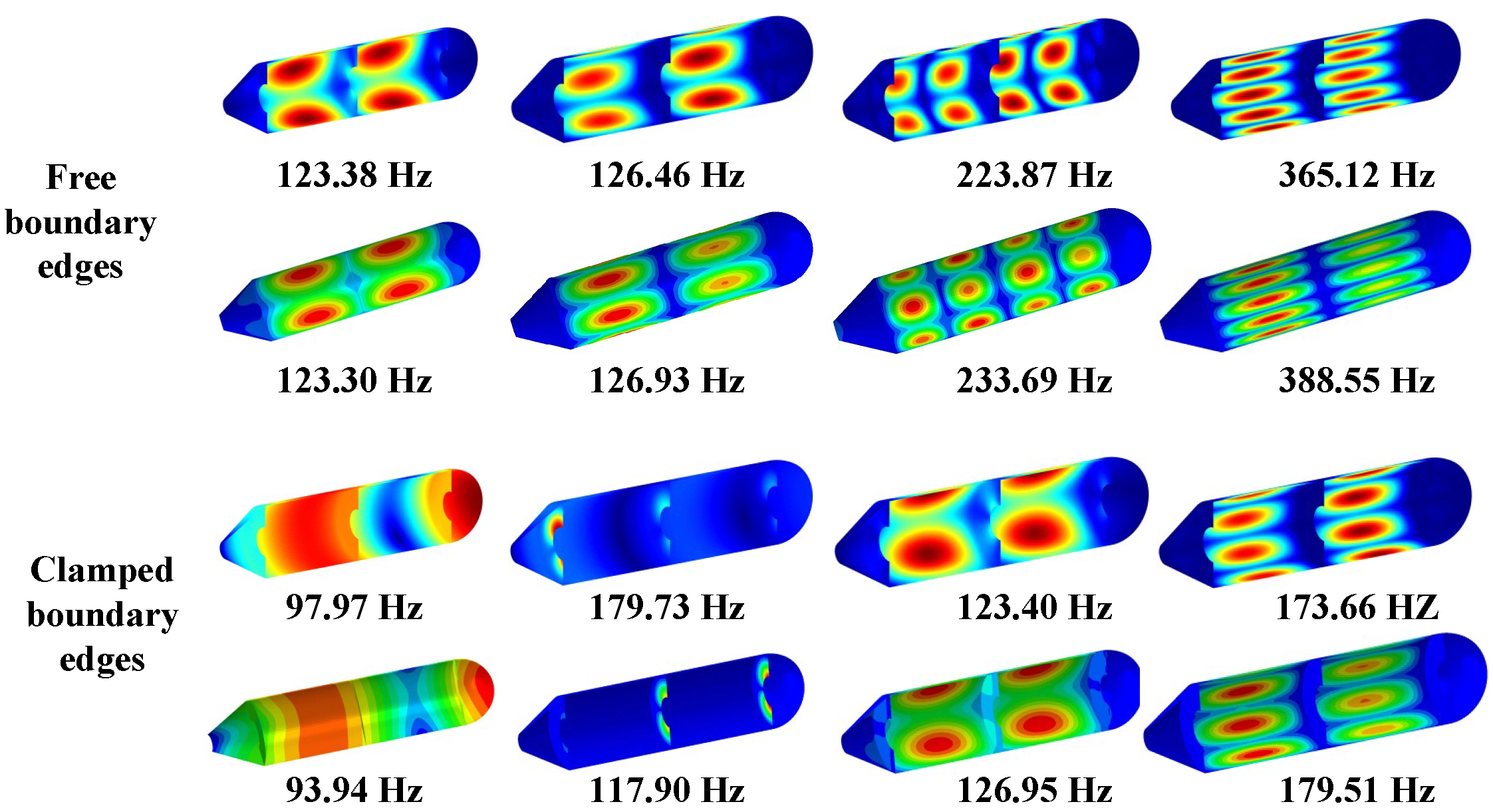
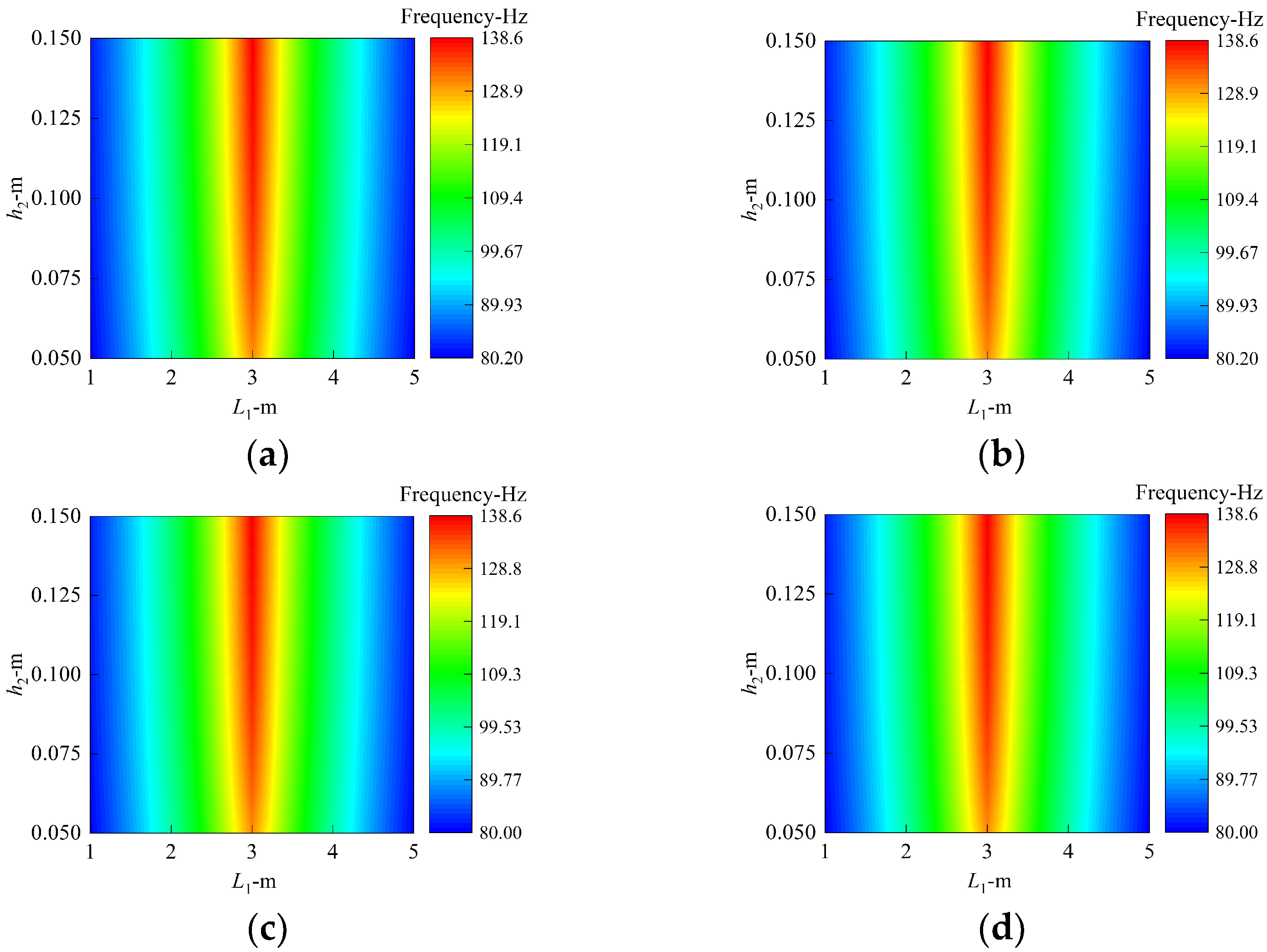
- The influence of the plate’s position on the inherent mechanical properties of the structure is closely related to the modal order, and the frequency of the structure is the largest when the annular plate is set in the middle of the cylindrical shell.
- (3)
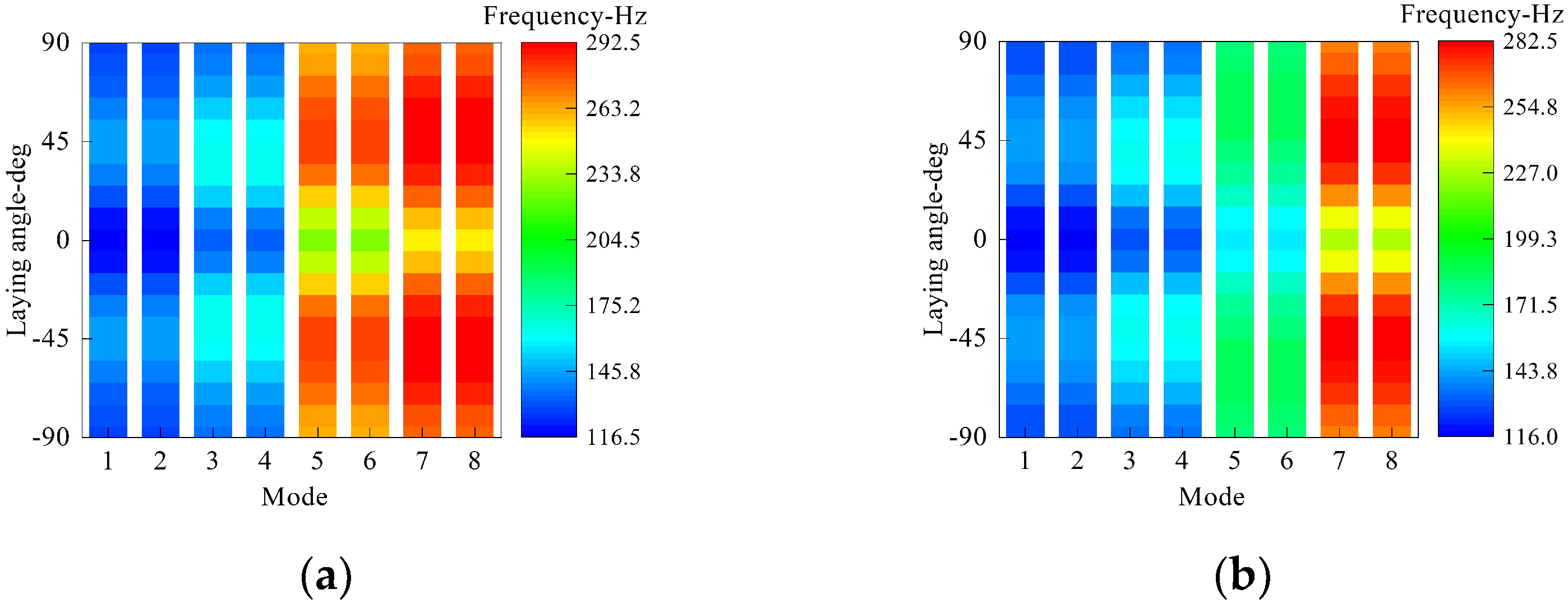
- The distribution of the laying angle is symmetric to about zero; structural frequencies increase first and then decrease with the increment of the laying angle to some extent.
- (4)
- Boundary constraints imposed on the conical shell have little influence on structural vibration as mode shapes relate to the cylindrical shell.
- (5)
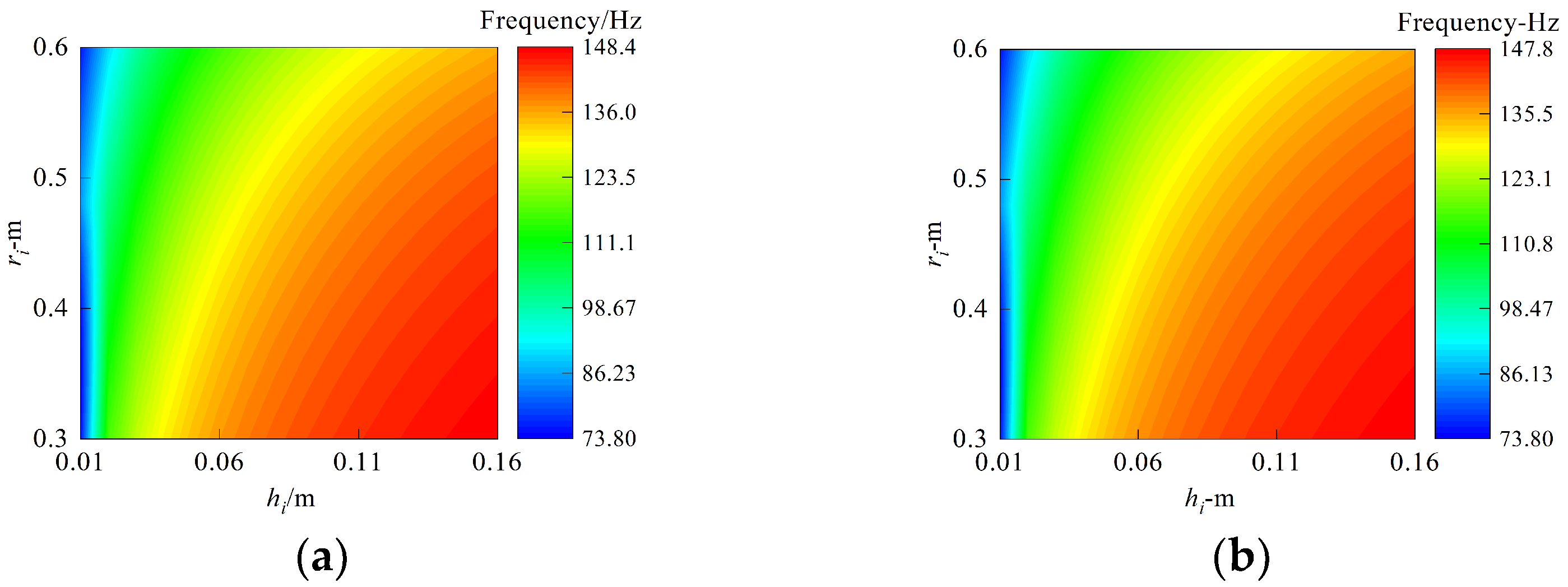
- The reasonable design of the geometric parameters of the annular plate can effectively improve the rigidity of the structure. Increasing the thickness of all the annular plates, decreasing the inner radius, and regulating the laminated scheme have a remarkable influence on structural free vibration, and the maximum relative changing rates of frequency exceed 97%, 16%, and 23%, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhong, R.; Wang, Q.; Hu, S.; Qin, B.; Shuai, C. Spectral element modeling and experimental investigations on vibration behaviors of imperfect plate considering irregular hole and curved crack. J. Sound Vib. 2022, 529, 116924. [Google Scholar] [CrossRef]
- Xue, Y.; Jin, G.; Ma, X.; Chen, H.; Ye, T.; Chen, M.; Zhang, Y. Free vibration analysis of porous plates with porosity distributions in the thickness and in-plane directions using isogeometric approach. Int. J. Mech. Sci. 2019, 152, 346–362. [Google Scholar] [CrossRef]
- Yin, Z.; Zhang, J.; Yang, F.; Ye, W.; Liu, J.; Lin, G. An efficient scaled boundary finite element approach in bending and bucking analysis of functionally graded piezoelectric plates. Eng. Anal. Bound. Elem. 2021, 132, 168–181. [Google Scholar] [CrossRef]
- Zhao, J.; Choe, K.; Xie, F.; Wang, A.; Shuai, C.; Wang, Q. Three-dimensional exact solution for vibration analysis of thick functionally graded porous (FGP) rectangular plates with arbitrary boundary conditions. Compos. Part B Eng. 2018, 155, 369–381. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Q.; Deng, X.; Choe, K.; Zhong, R.; Shuai, C. Free vibrations of functionally graded porous rectangular plate with uniform elastic boundary conditions. Compos. Part B Eng. 2019, 168, 106–120. [Google Scholar] [CrossRef]
- Chen, Z.; Qin, B.; Zhong, R.; Wang, Q. Free in-plane vibration analysis of elastically restrained functionally graded porous plates with porosity distributions in the thickness and in-plane directions. Eur. Phys. J. Plus 2022, 137, 158. [Google Scholar] [CrossRef]
- Liu, T.; Wang, Q.; Qin, B.; Wang, A. Modeling and experimental study on free vibration of plates with curved edges. J. Sound Vib. 2021, 513, 116417. [Google Scholar] [CrossRef]
- Du, D.X.; Sun, W.; Yan, X.F.; Xu, K.P. Free vibration analysis of rotating thin-walled cylindrical shells with hard coating based on Rayleigh-Ritz method. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2021, 235, 1170–1186. [Google Scholar] [CrossRef]
- Li, X.; Wang, T.; Zhao, Y.; Wang, H. Free vibration of conical shells under arbitrary elastic boundary and simulation verification. J. Phys. Conf. Ser. 2021, 1885, 032059. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, A.; Qin, B.; Wang, Q.; Zhong, R. Investigation on free vibration and transient response of functionally graded graphene platelets reinforced cylindrical shell resting on elastic foundation. Eur. Phys. J. Plus 2020, 135, 582. [Google Scholar] [CrossRef]
- An, K.; Kim, C.; Kim, K.; Kwak, S.; Ri, K.; Kim, H. Dynamic analysis of coupled composite laminated shells with elastic boundary condition using a domain decomposition method. Eng. Res. Express 2021, 3, 26. [Google Scholar] [CrossRef]
- Choe, K.; Ri, K.; Zhang, Z.Y.; Shuai, C.J.; Wang, Q.S. A domain decomposition method for elastodynamic problems of functionally graded elliptic shells and panels with elastic constraints. Thin-Walled Struct. 2019, 142, 262–276. [Google Scholar] [CrossRef]
- Li, H.; Hao, Y.; Zhang, W.; Liu, L.; Yang, S.; Wang, D. Vibration analysis of porous metal foam truncated conical shells with general boundary conditions using GDQ. Compos. Struct. 2021, 269, 114036. [Google Scholar] [CrossRef]
- Saini, R.; Lal, R. Effect of Thermal Environment and Peripheral Loading on Axisymmetric Vibrations of Non-uniform FG Circular Plates via Generalized Differential Quadrature Method. J. Vib. Eng. Technol. 2021, 9, 873–886. [Google Scholar] [CrossRef]
- Zhang, C.; Jin, G.; Wang, Z.; Sun, Y. Dynamic stiffness formulation and vibration analysis of coupled conical-ribbed cylindrical-conical shell structure with general boundary condition. Ocean Eng. 2021, 234, 109294. [Google Scholar] [CrossRef]
- Araki, Y.; Samejima, T. Fourier series expansion type of spectral nodal Galerkin method for vibration analysis of cylindrical shells: Formulation and trial calculation. Acoust. Sci. Technol. 2016, 37, 254–257. [Google Scholar] [CrossRef]
- Kim, K.; Choe, D.; Kwak, S.; Ri, Y.; Kim, C. Haar wavelet method for frequency analysis of the combined functionally graded shells with elastic boundary condition. Thin-Walled Struct. 2021, 169, 108340. [Google Scholar] [CrossRef]
- Parashar, S.K.; Kumar, A. Three-dimensional analytical modeling of vibration behavior of piezoceramic cylindrical shells. Arch. Appl. Mech. 2015, 85, 641–656. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, R.; Zhang, W.; Wang, J. Vibration Characteristics Analysis of Cylindrical Shell-Plate Coupled Structure Using an Improved Fourier Series Method. Shock. Vib. 2018, 2018, 9214189. [Google Scholar] [CrossRef]
- Chen, Z.; Qin, B.; Wang, Q.; Zhong, R.; Wang, A. Vibration analysis of laminated open cylindrical shell coupled with rectangular plates. Compos. Struct. 2022, 292, 115607. [Google Scholar] [CrossRef]
- Jin, G.; Ma, X.; Wang, W.; Liu, Z. An energy-based formulation for vibro-acoustic analysis of submerged submarine hull structures. Ocean Eng. 2018, 164, 402–413. [Google Scholar] [CrossRef]
- Kim, K.; Kwak, S.; Choe, K.; Han, W.; Ri, Y.; Ri, K. Application of Haar wavelet method for free vibration of laminated composite conical–cylindrical coupled shells with elastic boundary condition. Phys. Scr. 2021, 96, 035223. [Google Scholar] [CrossRef]
- Qu, Y.; Su, J.; Hua, H.; Meng, G. Structural vibration and acoustic radiation of coupled propeller-shafting and submarine hull system due to propeller forces. J. Sound Vib. 2017, 401, 76–93. [Google Scholar] [CrossRef]
- Wang, J.; Yang, H.; Hua, H. Investigations on the vibrational and acoustic characteristics of a submarine-like system by experiments and simulations. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2017, 233, 3–13. [Google Scholar] [CrossRef]
- Xie, K.; Chen, M.; Zhang, L.; Xie, D. Wave based method for vibration analysis of elastically coupled annular plate and cylindrical shell structures. Appl. Acoust. 2017, 123, 107–122. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Liang, C.; Zu, J.W. Wave propagation in functionally graded cylindrical nanoshells based on nonlocal Flügge shell theory. Eur. Phys. J. Plus 2019, 134, 233. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, A.; Qin, B.; Wang, Q.; Zhong, R. Investigation on vibration of the functionally graded material–stepped cylindrical shell coupled with annular plate in thermal environment. J. Low Freq. Noise Vib. Act. Control 2022, 41, 85–111. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, D.; He, D. A Spectro-geometric solution of dynamic characteristics of submarine-like structures. Compos. Struct. 2022, 299, 115976. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, D.; He, D. Vibration Characteristics of a Laminated Composite Double-Cylindrical Shell System Coupled with a Variable Number of Annular Plates. Materials 2022, 15, 4246. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.R.; Civalek, O.; Ahmadi-Pari, A.R. Agglomerated impact of CNT vs. GNP nanofillers on hybridization of polymer matrix for vibration of coupled hemispherical-conical-conical shells. Aerosp. Sci. Technol. 2022, 120, 107257. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.R. Natural frequency responses of hybrid polymer/carbon fiber/FG-GNP nanocomposites paraboloidal and hyperboloidal shells based on multiscale approaches. Aerosp. Sci. Technol. 2021, 119, 107111. [Google Scholar] [CrossRef]
- Bagheri, H.; Kiani, Y.; Bagheri, N.; Eslami, M.R. Free vibration of joined cylindrical–hemispherical FGM shells. Arch. Appl. Mech. 2020, 90, 2185–2199. [Google Scholar] [CrossRef]
- Shi, X.; Zuo, P.; Zhong, R.; Guo, C.; Wang, Q. Thermal vibration analysis of functionally graded conical-cylindrical coupled shell based on spectro-geometric method. Thin-Walled Structures 2022, 175, 109138. [Google Scholar] [CrossRef]
- Shao, D.; Wang, Q.; Shuai, C.; Gu, J. Investigation on dynamic performances of a set of composite laminated plate system under the influences of boundary and coupling conditions. Mech. Syst. Signal Process. 2019, 132, 721–747. [Google Scholar] [CrossRef]
- Xie, X.; Zheng, H.; Jin, G. Integrated orthogonal polynomials based spectral collocation method for vibration analysis of coupled laminated shell structures. Int. J. Mech. Sci. 2015, 98, 132–143. [Google Scholar] [CrossRef]
- Guo, C.; Liu, T.; Wang, Q.; Qin, B.; Wang, A. A unified strong spectral Tchebychev solution for predicting the free vibration characteristics of cylindrical shells with stepped-thickness and internal–external stiffeners. Thin-Walled Struct. 2021, 168, 108307. [Google Scholar] [CrossRef]
- Baghaee, M.; Farrokhabadi, A.; Jafari-Talookolaei, R.-A. A solution method based on Lagrange multipliers and Legendre polynomial series for free vibration analysis of laminated plates sandwiched by two MFC layers. J. Sound Vib. 2019, 447, 42–60. [Google Scholar] [CrossRef]
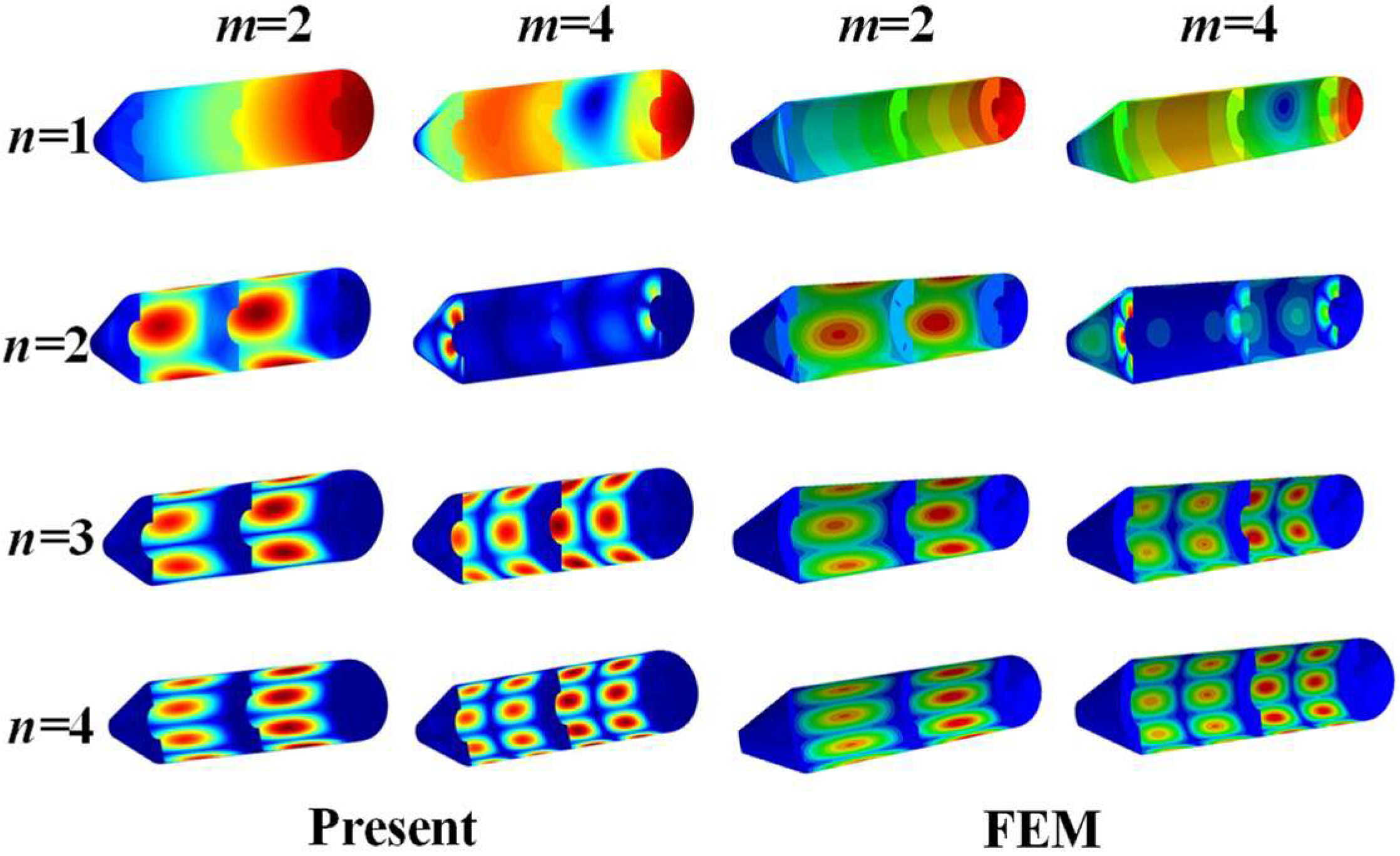

| BC | Method | Mode Number | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| Spherical shell | |||||||||
| F | Present | 419.71 | 508.58 | 522.89 | 568.42 | 603.55 | 614.46 | 635.78 | 670.55 |
| FEM | 417.43 | 507.55 | 528.50 | 557.09 | 606.15 | 613.24 | 637.32 | 676.48 | |
| Conical shell | |||||||||
| F | Present | 21.20 | 53.97 | 59.74 | 95.55 | 135.80 | 145.74 | 197.64 | 204.71 |
| FEM | 21.98 | 55.83 | 59.69 | 62.99 | 137.69 | 149.02 | 194.30 | 203.63 | |
| Cylindrical shell | |||||||||
| C-C | Present | 134.31 | 150.77 | 176.98 | 231.98 | 232.14 | 237.70 | 259.37 | 294.64 |
| FEM | 134.23 | 150.74 | 177.04 | 231.97 | 232.05 | 237.47 | 259.80 | 294.65 | |
| F-F | Present | 28.81 | 31.98 | 80.96 | 84.80 | 154.17 | 158.21 | 195.66 | 206.97 |
| FEM | 28.82 | 30.90 | 81.04 | 84.30 | 154.42 | 158.09 | 195.24 | 206.44 | |
| n | m | C | S | F | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Present | FEM | Deviation (%) | Present | FEM | Deviation (%) | Present | FEM | Deviation (%) | ||
| 1 | 1 | 6.92 | 6.78 | 2.07 | 6.68 | 6.54 | 2.05 | 143.66 | 143.56 | 0.07 |
| 2 | 94.52 | 94.46 | 0.06 | 94.17 | 94.11 | 0.06 | 213.96 | 214.28 | 0.15 | |
| 3 | 213.19 | 213.46 | 0.12 | 213.10 | 213.36 | 0.12 | 215.22 | 215.48 | 0.12 | |
| 4 | 214.37 | 214.67 | 0.14 | 214.37 | 214.67 | 0.14 | 304.28 | 304.32 | 0.01 | |
| 2 | 1 | 158.15 | 157.92 | 0.15 | 158.15 | 157.92 | 0.15 | 157.93 | 157.68 | 0.16 |
| 2 | 165.67 | 164.44 | 0.75 | 165.67 | 164.44 | 0.75 | 165.42 | 164.18 | 0.76 | |
| 3 | 323.77 | 322.63 | 0.35 | 320.16 | 320.06 | 0.03 | 256.37 | 256.40 | 0.01 | |
| 4 | 345.01 | 345.01 | 0.00 | 343.93 | 343.84 | 0.03 | 337.88 | 336.27 | 0.48 | |
| 3 | 1 | 141.73 | 141.27 | 0.33 | 141.73 | 141.27 | 0.32 | 141.72 | 141.26 | 0.32 |
| 2 | 159.32 | 158.62 | 0.44 | 159.32 | 158.61 | 0.45 | 159.31 | 158.60 | 0.45 | |
| 3 | 294.35 | 293.89 | 0.16 | 294.34 | 293.88 | 0.16 | 294.33 | 293.87 | 0.16 | |
| 4 | 300.91 | 298.65 | 0.76 | 300.90 | 298.65 | 0.75 | 300.89 | 298.65 | 0.75 | |
| 4 | 1 | 201.39 | 201.38 | 0.00 | 201.39 | 201.38 | 0.00 | 201.39 | 201.38 | 0.00 |
| 2 | 209.32 | 209.28 | 0.02 | 209.32 | 209.28 | 0.02 | 209.32 | 209.28 | 0.02 | |
| 3 | 292.68 | 292.03 | 0.22 | 292.68 | 292.03 | 0.22 | 292.68 | 292.03 | 0.22 | |
| 4 | 304.45 | 303.11 | 0.44 | 304.45 | 303.11 | 0.44 | 304.45 | 303.11 | 0.44 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Zhong, R.; Hu, S.; Qin, B.; Zhao, X. Effect of Multiple Annular Plates on Vibration Characteristics of Laminated Submarine-like Structures. Materials 2022, 15, 6357. https://doi.org/10.3390/ma15186357
Chen Z, Zhong R, Hu S, Qin B, Zhao X. Effect of Multiple Annular Plates on Vibration Characteristics of Laminated Submarine-like Structures. Materials. 2022; 15(18):6357. https://doi.org/10.3390/ma15186357
Chicago/Turabian StyleChen, Zhengxiong, Rui Zhong, Shuangwei Hu, Bin Qin, and Xing Zhao. 2022. "Effect of Multiple Annular Plates on Vibration Characteristics of Laminated Submarine-like Structures" Materials 15, no. 18: 6357. https://doi.org/10.3390/ma15186357
APA StyleChen, Z., Zhong, R., Hu, S., Qin, B., & Zhao, X. (2022). Effect of Multiple Annular Plates on Vibration Characteristics of Laminated Submarine-like Structures. Materials, 15(18), 6357. https://doi.org/10.3390/ma15186357