Experimental and Numerical Studies on Hot Compressive Deformation Behavior of a Cu–Ni–Sn–Mn–Zn Alloy
Abstract
:1. Introduction
2. Materials and Methods
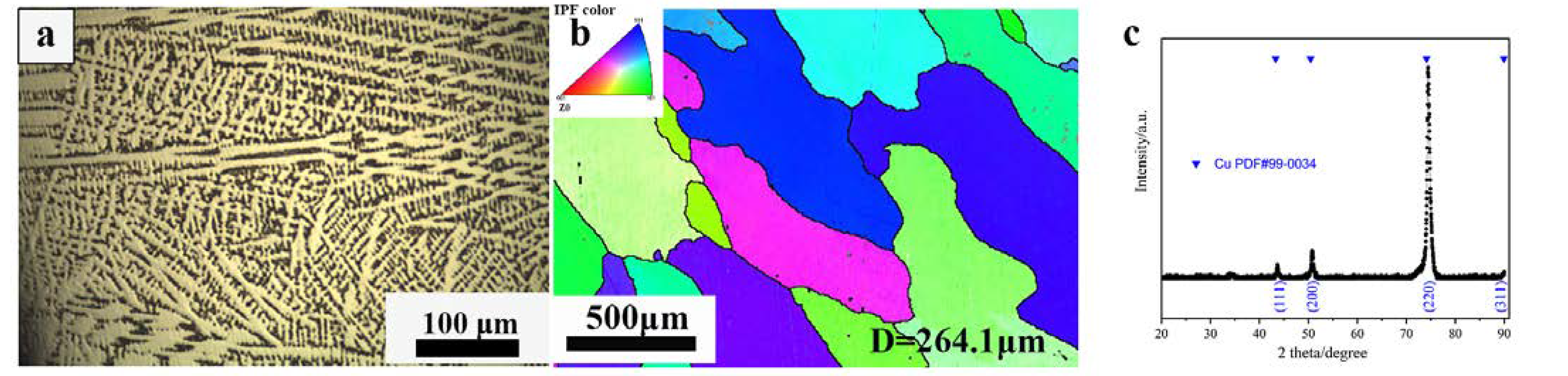
2.1. Materials
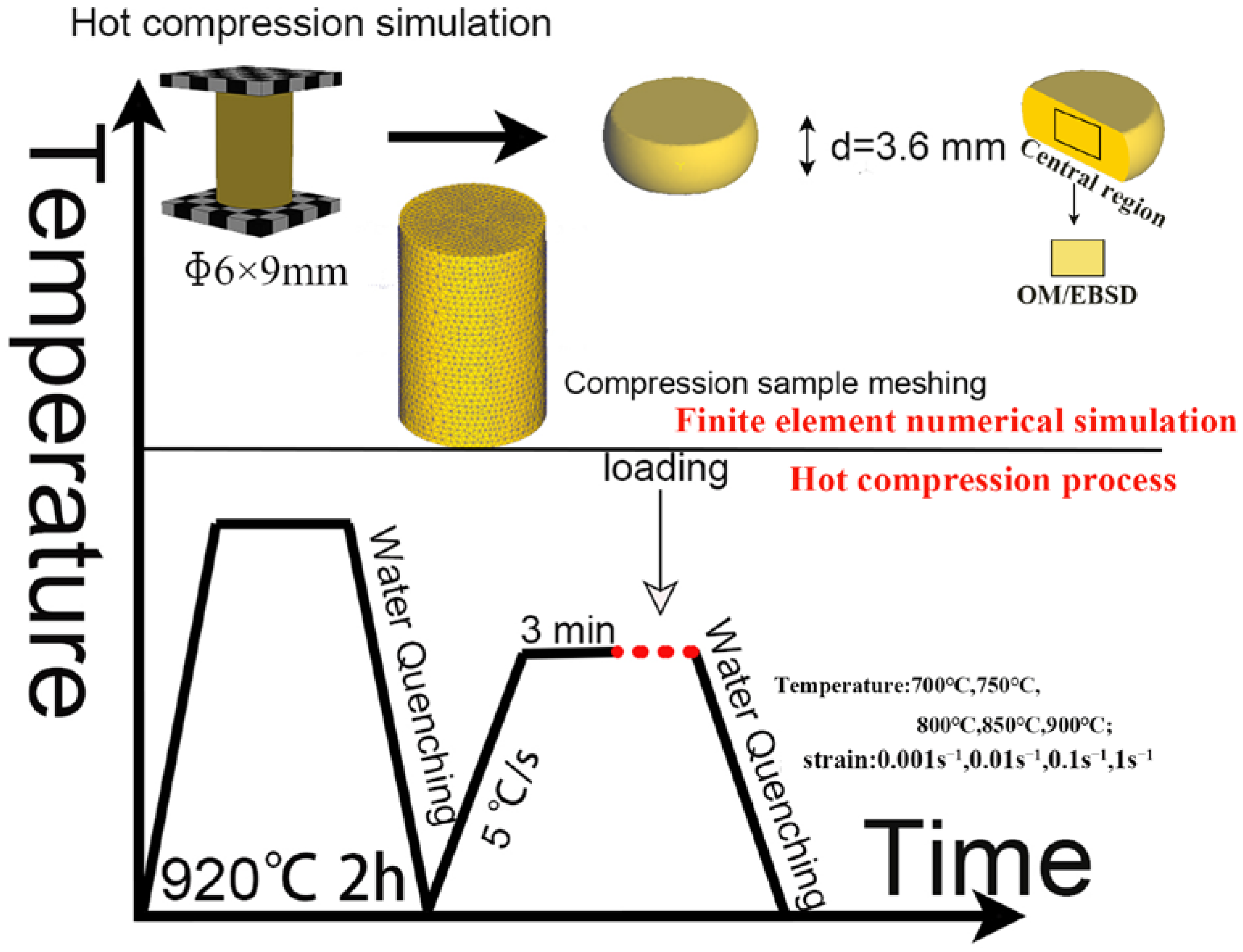
2.2. Hot Compression
2.3. Finite Element Simulation and Verification
2.3.1. Related Condition Settings
2.3.2. Theoretical Basis of Finite Element Numerical Simulation
2.4. Hot Deformation Intrinsic Model
3. Results & Discussion
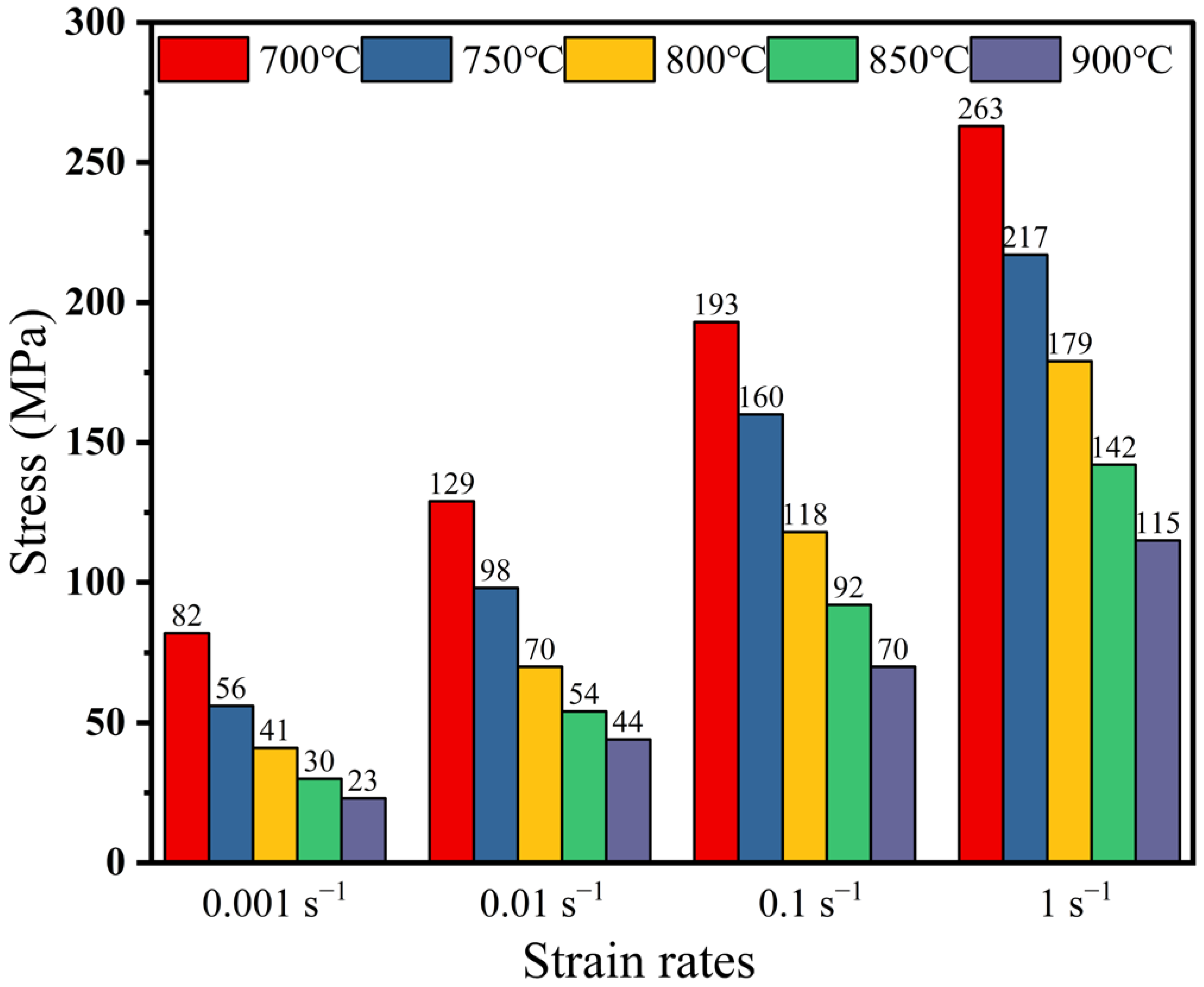
3.1. Effect of Deformation Conditions on the True Stress–Strain Curve
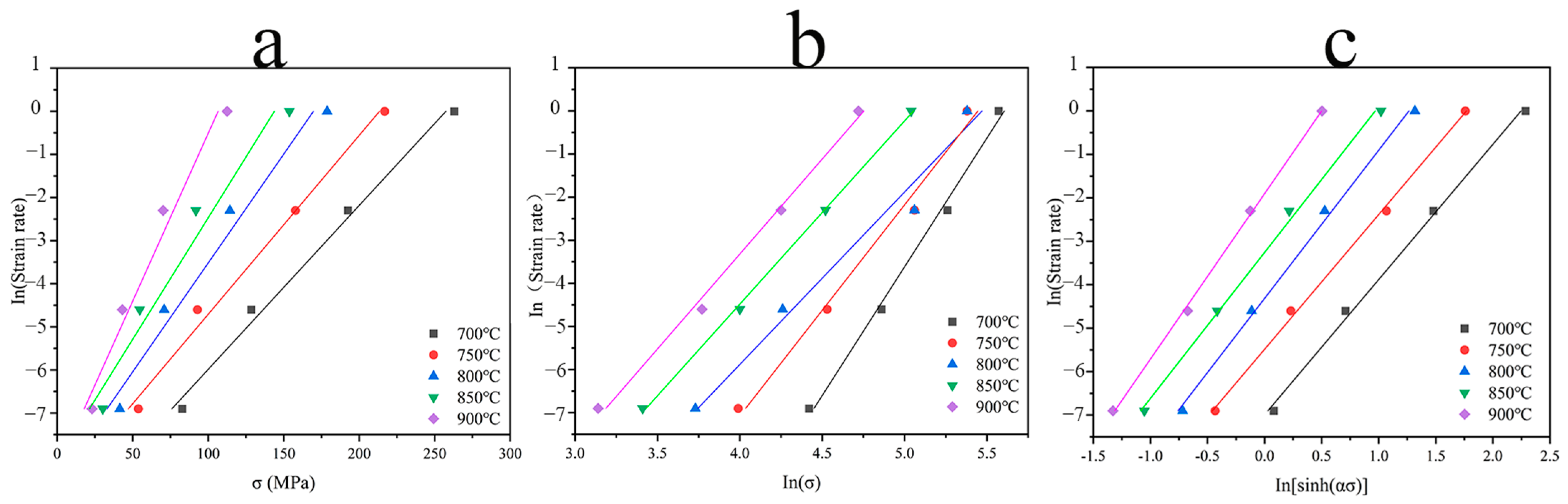
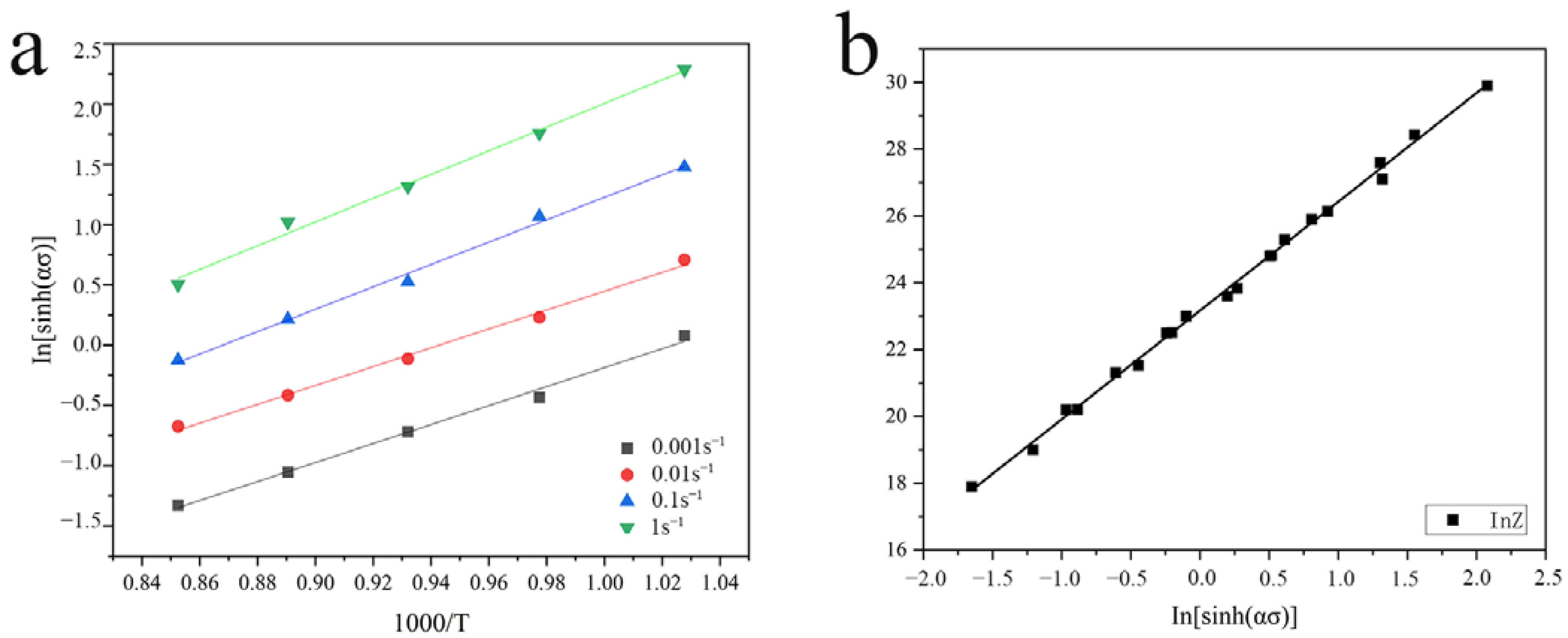
3.2. Flow Stress Constitutive Equation
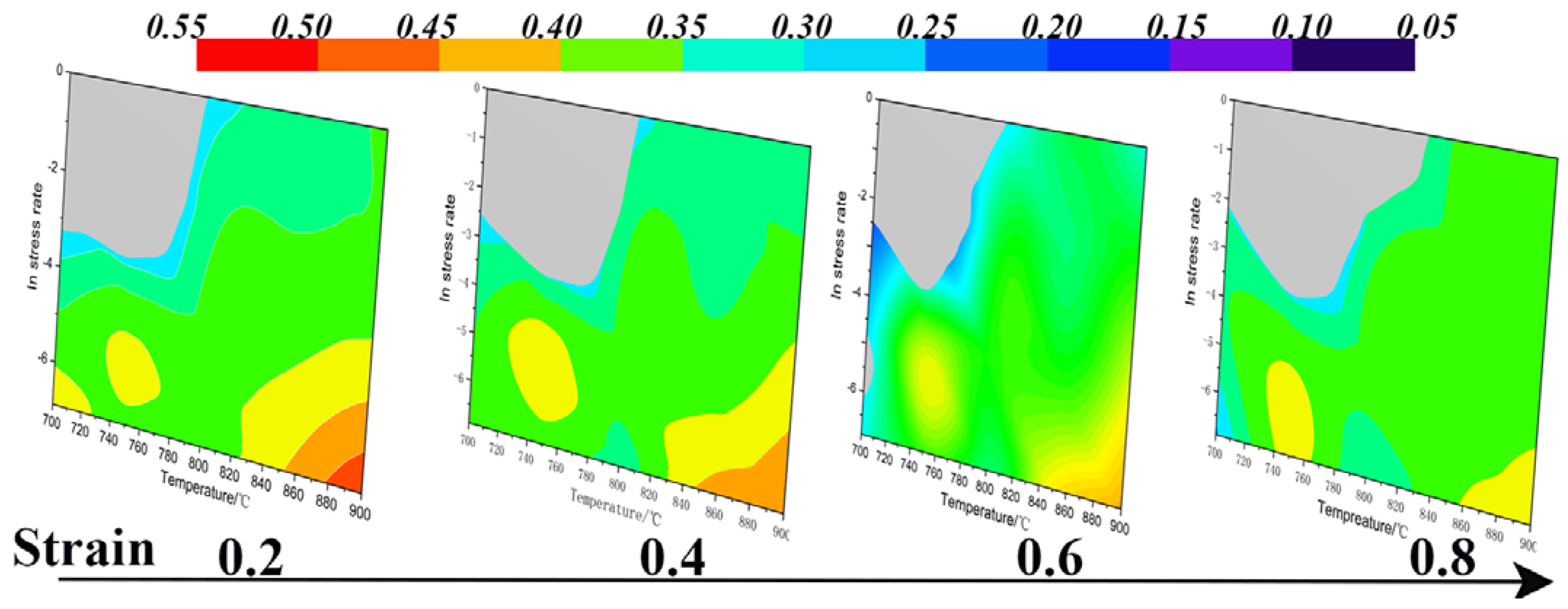
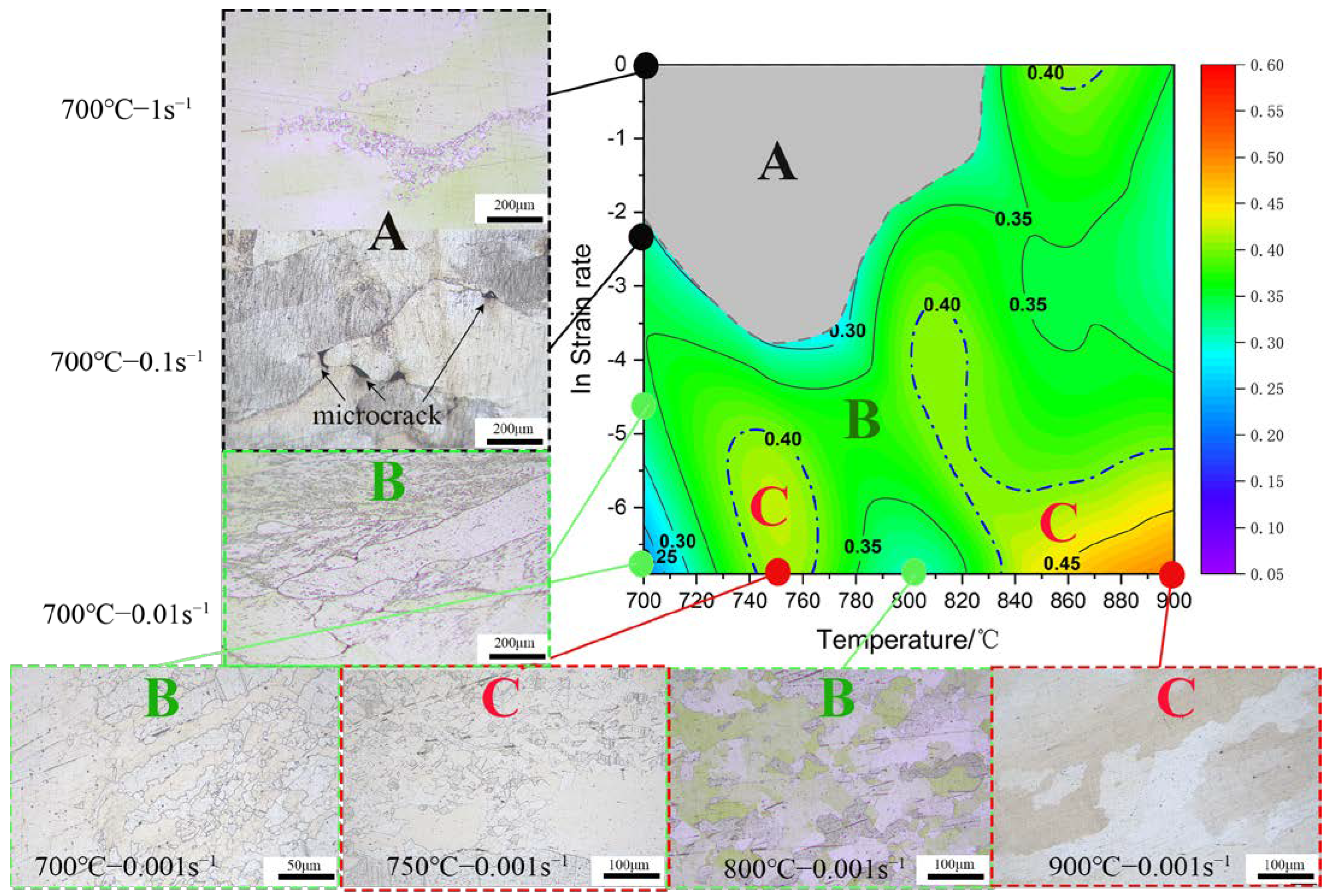
3.3. Hot Deformation Processing Map
3.4. Microstructure Evolution
3.5. EBSD Analysis
3.6. Finite Model Simulation Results and Validation
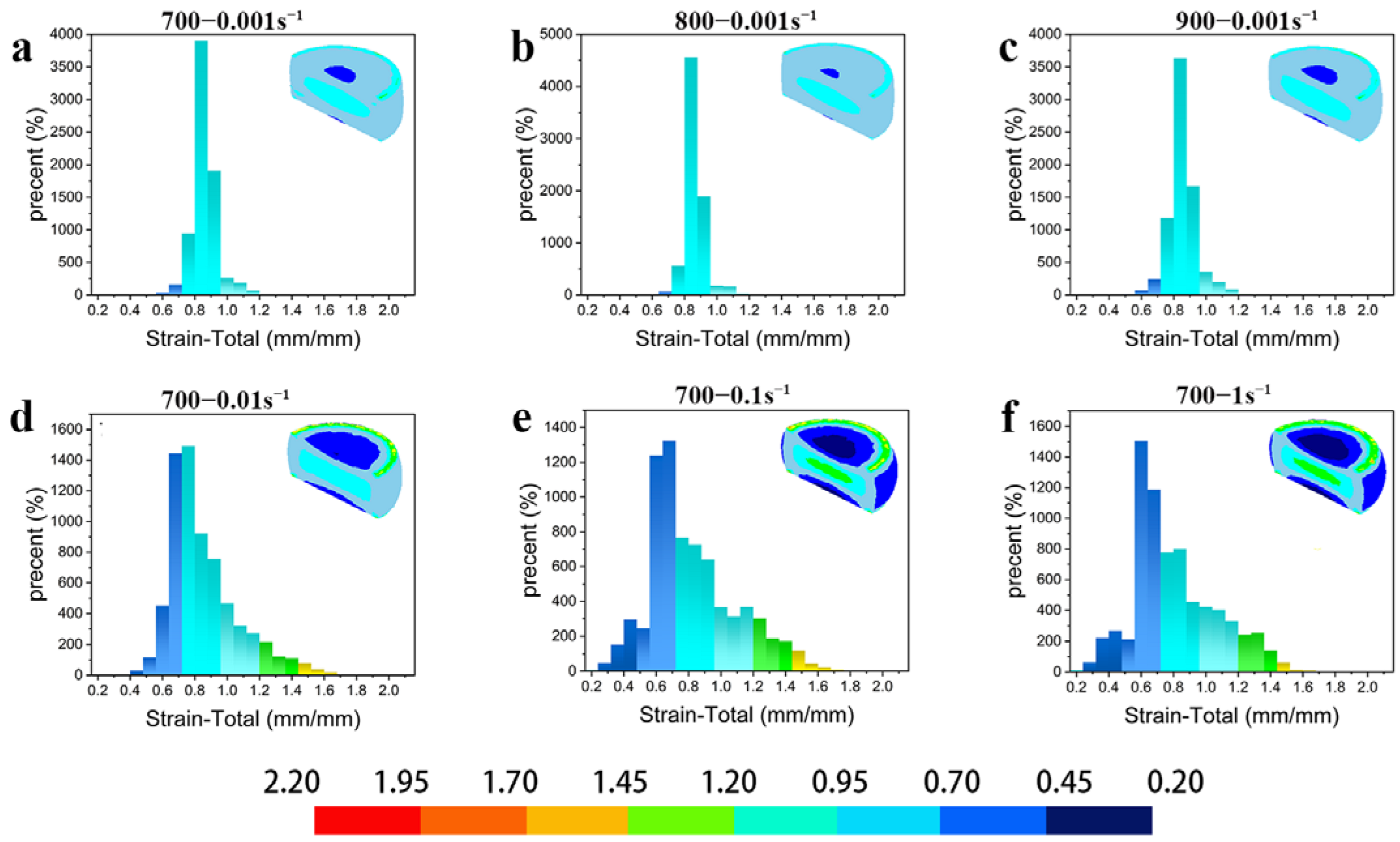
3.6.1. Simulation of Effective Strain Distribution under Different Deformation
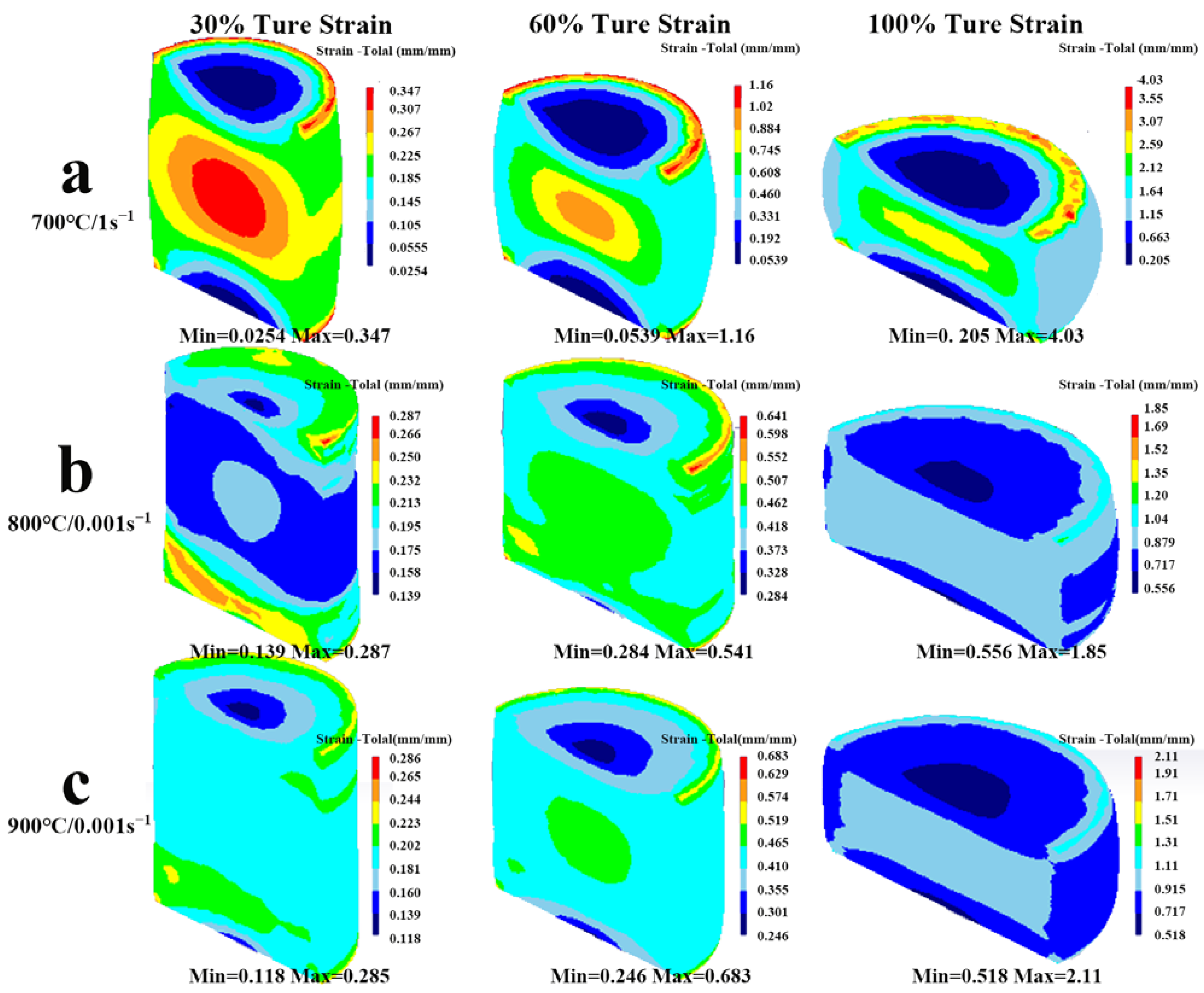
3.6.2. Simulation of Effective Strain Distribution under Different True Strain
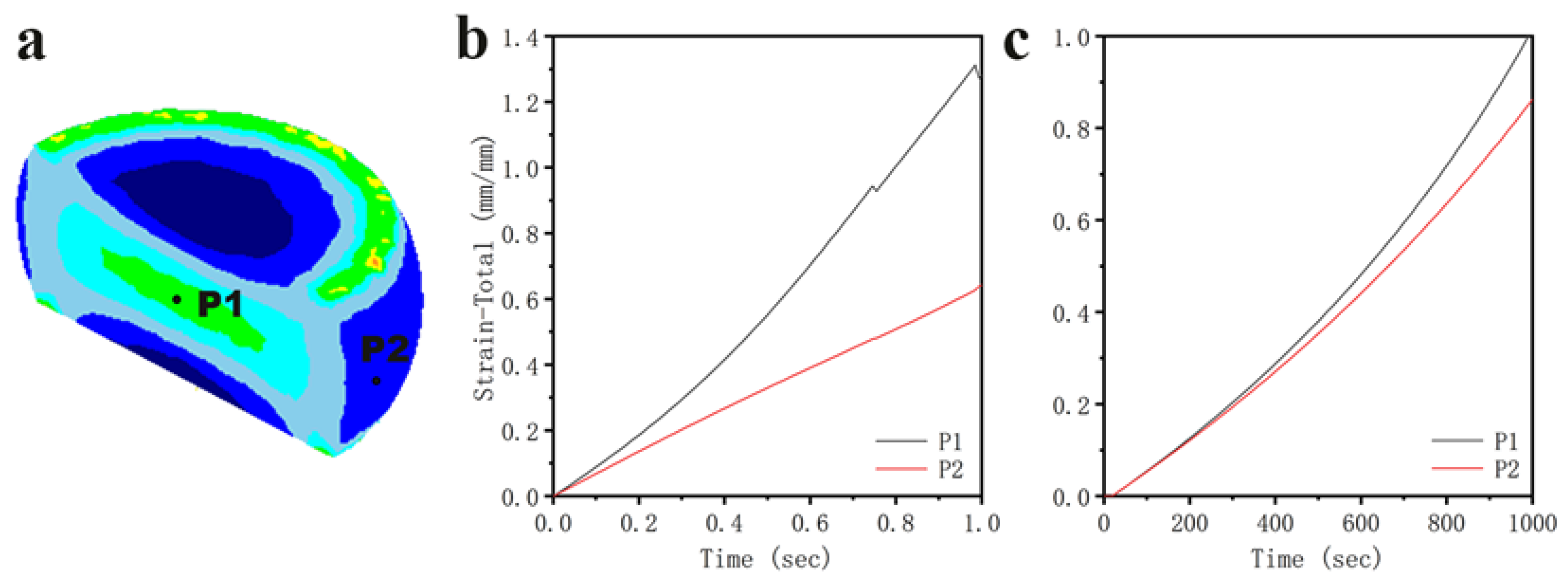
3.6.3. The Change Pattern of Strain Value in Different Regions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cribb, W.R.; Grensing, F.C. Property Analysis of a High Strength Cold Worked Cu-Ni-Sn Spinodal Alloy. In Proceedings of the Aeromat 20 Conference and Exposition American Society for Metals, Denver, CO, USA, 20 October 2009. [Google Scholar]
- Zhang, H.; Jiang, Y.; Xie, J.; Li, Y.; Yue, L. Precipitation behavior, microstructure and properties of aged Cu-1.7 wt% Be alloy. J. Alloys Compd. 2018, 773, 1121–1130. [Google Scholar]
- Yang, M.; Hu, Y.L.; Li, X.N.; Li, Z.M.; Zheng, Y.H.; Li, N.J.; Dong, C. Compositional interpretation of high elasticity Cu–Ni–Sn alloys using cluster-plus-glue-atom model. J. Mater. Res. Technol. 2022, 17, 1246–1258. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, Z.; Xiao, Z.; Xing, Y.; Zhang, Y.; Fang, M. Microstructure and Properties of a Cu-Ni-Sn Alloy Treated by Two-Stage Thermomechanical Processing. JOM 2019, 71, 2734–2741. [Google Scholar] [CrossRef]
- Wang, L.; Tang, D.; Kong, C.; Yu, H. Crack-free Cu9Ni6Sn strips via twin-roll casting and subsequent asymmetric cryorolling. Materialia 2022, 21, 101283. [Google Scholar] [CrossRef]
- Cai, W.; Yang, S.L.; Chen, L.; Lu, M.M.; Liao, Y.M. Effect of Alterative and Homogenization on the Microstructure of Cu-20Ni-5Sn Alloy. Mater. Sci. Forum 2013, 749, 421–424. [Google Scholar] [CrossRef]
- Xu, S.; Li, Y.; Zhang, M.; Song, T.; Ding, H. The effects of Nb additions on the microstructure evolution in Cu–9Ni–6Sn alloy. Intermetallics 2022, 143, 107497. [Google Scholar] [CrossRef]
- Yu, Q.X.; Li, X.N.; Wei, K.R.; Li, Z.M.; Zheng, Y.H.; Li, N.J.; Cheng, X.T.; Wang, C.Y.; Wang, Q.; Dong, C. Cu–Ni–Sn–Si alloys designed by cluster-plus-glue-atom model. Mater. Des. 2019, 167, 107641. [Google Scholar] [CrossRef]
- Jonas, J.J.; Quelennec, X.; Jiang, L.; Martin, É. The Avrami kinetics of dynamic recrystallization. Acta Mater. 2009, 57, 2748–2756. [Google Scholar] [CrossRef]
- Lin, Y.C.; Li, L.-T.; Fu, Y.-X.; Jiang, Y.-Q. Hot compressive deformation behavior of 7075 Al alloy under elevated temperature. J. Mater. Sci. 2011, 47, 1306–1318. [Google Scholar] [CrossRef]
- He, G.; Liu, F.; Si, J.; Yang, C.; Jiang, L. Characterization of hot compression behavior of a new HIPed nickel-based P/M superalloy using processing maps. Mater. Des. 2015, 87, 256–265. [Google Scholar] [CrossRef]
- Li, C.; Huang, L.; Zhao, M.; Guo, S.; Li, J. Hot deformation behavior and mechanism of a new metastable β titanium alloy Ti–6Cr–5Mo–5V–4Al in single phase region. Mater. Sci. Eng. A 2021, 814, 141231. [Google Scholar] [CrossRef]
- Deng, L.; Zhang, H.-D.; Li, G.-A.; Tang, X.-F.; Yi, P.-S.; Liu, Z.; Wang, X.-Y.; Jin, J.-S. Processing map and hot deformation behavior of squeeze cast 6082 aluminum alloy. Trans. Nonferrous Met. Soc. China 2022, 32, 2150–2163. [Google Scholar] [CrossRef]
- Zhang, X.-P.; Wang, H.-X.; Bian, L.-P.; Zhang, S.-X.; Zhuang, Y.-P.; Cheng, W.-l.; Liang, W. Microstructure evolution and mechanical properties of Mg-9Al-1Si-1SiC composites processed by multi-pass equal-channel angular pressing at various temperatures. Int. J. Miner. Metall. Mater. 2021, 28, 1966–1975. [Google Scholar] [CrossRef]
- Liu, W.; Jiang, B.; Xiang, H.; Ye, Q.; Xia, S.; Chen, S.; Song, J.; Ma, Y.; Yang, M. High-temperature mechanical properties of as-extruded AZ80 magnesium alloy at different strain rates. Int. J. Miner. Metall. Mater. 2022, 29, 1373–1379. [Google Scholar] [CrossRef]
- Yong, P.; Zhu, X.; Yanlin, J.; Rui, Z.; Jiang, Y.; Wenting, Q.; Zhou, L. Hot deformation behavior of a CuAlMn shape memory alloy. J. Alloys Compd. 2020, 845, 156161. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, X.; Li, Z.; Xiao, Z.; Sheng, X.; Jiang, H.; Cai, G.; Zhang, X. Microstructure Evolution and Hot Deformation Behavior of a CuNiSn Alloy. Processes 2021, 9, 451. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, Z.; Pan, D.-q.; Li, D.-x.; Luo, Z.-q.; Zhang, D.-t.; Yang, C.; Zhang, W.-w. Effect of Si and Ti on dynamic recrystallization of high-performance Cu−15Ni−8Sn alloy during hot deformation. Trans. Nonferrous Met. Soc. China 2019, 29, 2556–2565. [Google Scholar] [CrossRef]
- Niu, D.; Zhao, C.; Li, D.; Wang, Z.; Luo, Z.; Zhang, W. Constitutive Modeling of the Flow Stress Behavior for the Hot Deformation of Cu-15Ni-8Sn Alloys. Front. Mater. 2020, 7, 577867. [Google Scholar] [CrossRef]
- Hussaini, S.M.; Singh, S.K.; Gupta, A.K. Experimental and numerical investigation of formability for austenitic stainless steel 316 at elevated temperatures. J. Mater. Res. Technol. 2014, 3, 17–24. [Google Scholar] [CrossRef]
- Wu, H.; Liu, M.; Wang, Y.; Huang, Z.; Tan, G.; Yang, L. Experimental study and numerical simulation of dynamic recrystallization for a FGH96 superalloy during isothermal compression. J. Mater. Res. Technol. 2020, 9, 5090–5104. [Google Scholar] [CrossRef]
- Ghandvar, H.; Jabbar, K.A.; Idris, M.H.; Ahmad, N.; Jahare, M.H.; Rahimian Koloor, S.S.; Petrů, M. Influence of barium addition on the formation of primary Mg2Si crystals from Al–Mg–Si melts. J. Mater. Res. Technol. 2021, 11, 448–465. [Google Scholar] [CrossRef]
- Shi, L.; Yang, H.; Guo, L.G.; Zhang, J. Constitutive modeling of deformation in high temperature of a forging 6005A aluminum alloy. Mater. Des. 2014, 54, 576–581. [Google Scholar] [CrossRef]
- Lee, C.H.; Kobayashi, S. New Solutions to Rigid-Plastic Deformation Problems Using a Matrix Method. J. Eng. Ind. 1972, 95, 865. [Google Scholar] [CrossRef]
- Xia, Y.F.; Long, S.; Wang, T.-Y.; Zhao, J. A Study at the Workability of Ultra-High Strength Steel Sheet by Processing Maps on the Basis of DMM. High Temp. Mater. Process. 2017, 36, 657–667. [Google Scholar] [CrossRef]
- Jonas, J.J.; Sellars, C.M.; Tegart, W.M. Strength and structure under hot-working conditions. Metall. Rev. 1969, 14, 1–24. [Google Scholar] [CrossRef]
- Grujicic, M.; Pandurangan, B.; Yen, C.F.; Cheeseman, B.A. Modifications in the AA5083 Johnson-Cook Material Model for Use in Friction Stir Welding Computational Analyses. J. Mater. Eng. Perform. 2012, 21, 2207–2217. [Google Scholar] [CrossRef]
- Farrokh, B.; Khan, A.S. Grain size, strain rate, and temperature dependence of flow stress in ultra-fine grained and nanocrystalline Cu and Al: Synthesis, experiment, and constitutive modeling. Int. J. Plast. 2009, 25, 715–732. [Google Scholar] [CrossRef]
- Molinari, A.; Ravichandran, G. Constitutive modeling of high-strain-rate deformation in metals based on the evolution of an effective microstructural length. Mech. Mater. 2005, 37, 737–752. [Google Scholar] [CrossRef]
- Kocks, U. Laws for work-hardening and low-temperature creep. J. Eng. Mater. Technol. 1976, 98, 76–85. [Google Scholar] [CrossRef]
- Sellars, C.M.; McTegart, W. On the mechanism of hot deformation. Acta Met. 1966, 14, 1136–1138. [Google Scholar]
- Zener, C.; Hollomon, J.H. Effect of Strain Rate Upon Plastic Flow of Steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Feng, D.; Zhang, X.M.; Liu, S.D.; Deng, Y.L. Constitutive equation and hot deformation behavior of homogenized Al–7.68Zn–2.12Mg–1.98Cu–0.12Zr alloy during compression at elevated temperature. Mater. Sci. Eng. A 2014, 608, 63–72. [Google Scholar] [CrossRef]
- Hu, Y.L.; Lin, X.; Li, Y.L.; Zhang, S.Y.; Gao, X.H.; Liu, F.G.; Li, X.; Huang, W.D. Plastic deformation behavior and dynamic recrystallization of Inconel 625 superalloy fabricated by directed energy deposition. Mater. Des. 2020, 186, 108359. [Google Scholar] [CrossRef]
- Liu, D.; Lu, Z.; Yu, J.; Shi, C.; Xiao, H.; Liu, W.; Jiang, S. Hot deformation behavior and microstructure evolution of NiAl-9HfO2 composite. Intermetallics 2021, 139, 107344. [Google Scholar] [CrossRef]
- Wang, X.; Li, Z.; Xiao, Z.; Qiu, W.-T. Microstructure evolution and hot deformation behavior of Cu−3Ti−0.1Zr alloy with ultra-high strength. Trans. Nonferrous Met. Soc. China 2020, 30, 2737–2748. [Google Scholar] [CrossRef]
- Prasad, Y.; Gegel, H.; Doraivelu, S.; Malas, J.; Morgan, J.; Lark, K.; Barker, D. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242. Metall. Trans. A 1984, 15, 1883–1892. [Google Scholar] [CrossRef]
- Zhu, A.-Y.; Chen, J.-l.; Li, Z.; Luo, L.-Y.; Lei, Q.; Zhang, L.; Zhang, W. Hot deformation behavior of novel imitation-gold copper alloy. Trans. Nonferrous Met. Soc. China 2013, 23, 1349–1355. [Google Scholar] [CrossRef]
- Prasad, Y. Performance. Processing maps: A status report. J. Mater. Eng. Perform. 2003, 12, 638–645. [Google Scholar] [CrossRef]
- Lapeire, L.; Sidor, J.; Verleysen, P.; Verbeken, K.; De Graeve, I.; Terryn, H.; Kestens, L.A.I. Texture comparison between room temperature rolled and cryogenically rolled pure copper. Acta Mater. 2015, 95, 224–235. [Google Scholar] [CrossRef]
- Chamanfar, A.; Valberg, H.S.; Templin, B.; Plumeri, J.E.; Misiolek, W.Z. Development and validation of a finite-element model for isothermal forging of a nickel-base superalloy. Materialia 2019, 6, 100319. [Google Scholar] [CrossRef]



| Ni | Sn | Mn | Zn | Si | P | Cu | |
|---|---|---|---|---|---|---|---|
| Composition | 9.06 | 5.47 | 0.30 | 0.18 | 0.019 | 0.0016 | Bal. |
| Parameter | |
|---|---|
| b | 0.0534 |
| 0.0113 | |
| n | 3.35 |
| Q/kJ·mol−1 | 243.67 |
| InA | 22.93 |
| Designation | Miller Indices {hkl} <uvw> |
|---|---|
| Cube | {001} <100> |
| Rotated Cube | {001} <110> |
| CubeND | {001} <110> |
| CubeRD | {013} <110> |
| Goss | {011} <100>/{110} <001> |
| Rotated Goss | {110} <110> |
| C(Copper) | {112} <111> |
| Bass | {011} <211>/{110} <112> |
| Rotated Bass | {110} <111> |
| P | {011} <122> |
| Q | {013} <122> |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Xiao, Z.; Meng, X.; Xiao, L.; Pei, Y.; Gan, X. Experimental and Numerical Studies on Hot Compressive Deformation Behavior of a Cu–Ni–Sn–Mn–Zn Alloy. Materials 2023, 16, 1445. https://doi.org/10.3390/ma16041445
Zhang Y, Xiao Z, Meng X, Xiao L, Pei Y, Gan X. Experimental and Numerical Studies on Hot Compressive Deformation Behavior of a Cu–Ni–Sn–Mn–Zn Alloy. Materials. 2023; 16(4):1445. https://doi.org/10.3390/ma16041445
Chicago/Turabian StyleZhang, Yufang, Zhu Xiao, Xiangpeng Meng, Lairong Xiao, Yongjun Pei, and Xueping Gan. 2023. "Experimental and Numerical Studies on Hot Compressive Deformation Behavior of a Cu–Ni–Sn–Mn–Zn Alloy" Materials 16, no. 4: 1445. https://doi.org/10.3390/ma16041445
APA StyleZhang, Y., Xiao, Z., Meng, X., Xiao, L., Pei, Y., & Gan, X. (2023). Experimental and Numerical Studies on Hot Compressive Deformation Behavior of a Cu–Ni–Sn–Mn–Zn Alloy. Materials, 16(4), 1445. https://doi.org/10.3390/ma16041445






