Rheological Changes in Bio-Based Filaments Induced by Extrusion-Based 3D Printing Process
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Extrusion-Based Printing Process
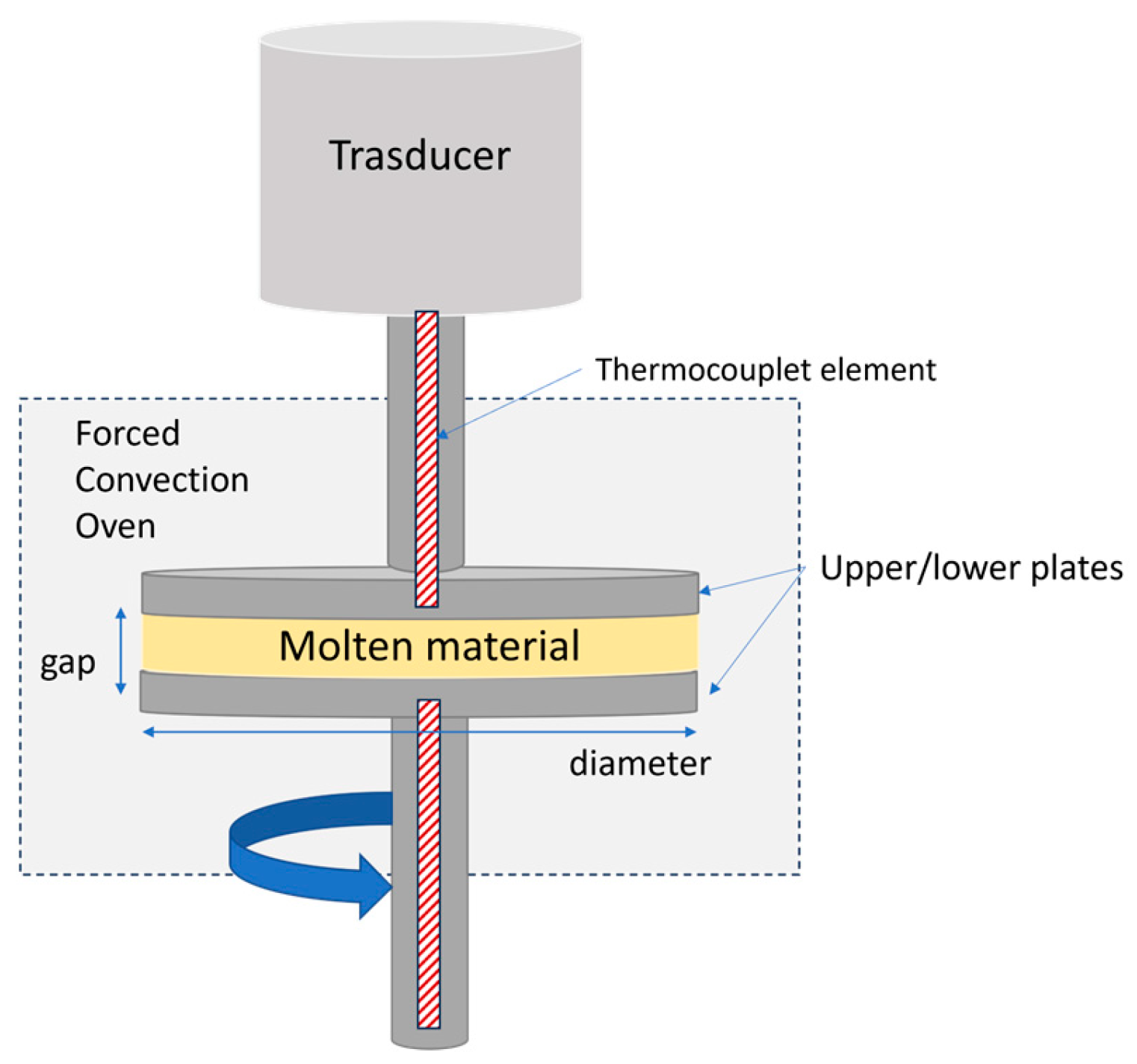
2.3. Characterization Techniques
- (i)
- A frequency sweep at 180 °C from 100 to 0.1 rad/s to attest the starting rheological characteristics of two resins;
- (ii)
- A ramp temperature of 20 °C/min up to 200 °C followed by a time sweep for 180 s to simulate extrusion inside the chamber in the molten state;
- (iii)
- A ramp temperature of 20 °C/min up to 100 °C followed by a time sweep for 900 s to simulate the deposition on platform;
- (iv)
- A ramp temperature of 20 °C/min up to 180 °C followed by a time sweep for 180 s to stabilize the conditions;
- (v)
- Five consecutive frequency sweeps at 180 °C from 100 to 0.1 rad/s to assess the material properties following heat treatment.
3. Results
3.1. Printing Attempts
- (i)
- The maximum allowable speed when the nozzle temperature was 200 °C was equal to +15% (115 mm/s);
- (ii)
- The printing process was always feasible at 210 and 220 °C for each chosen printing speed.
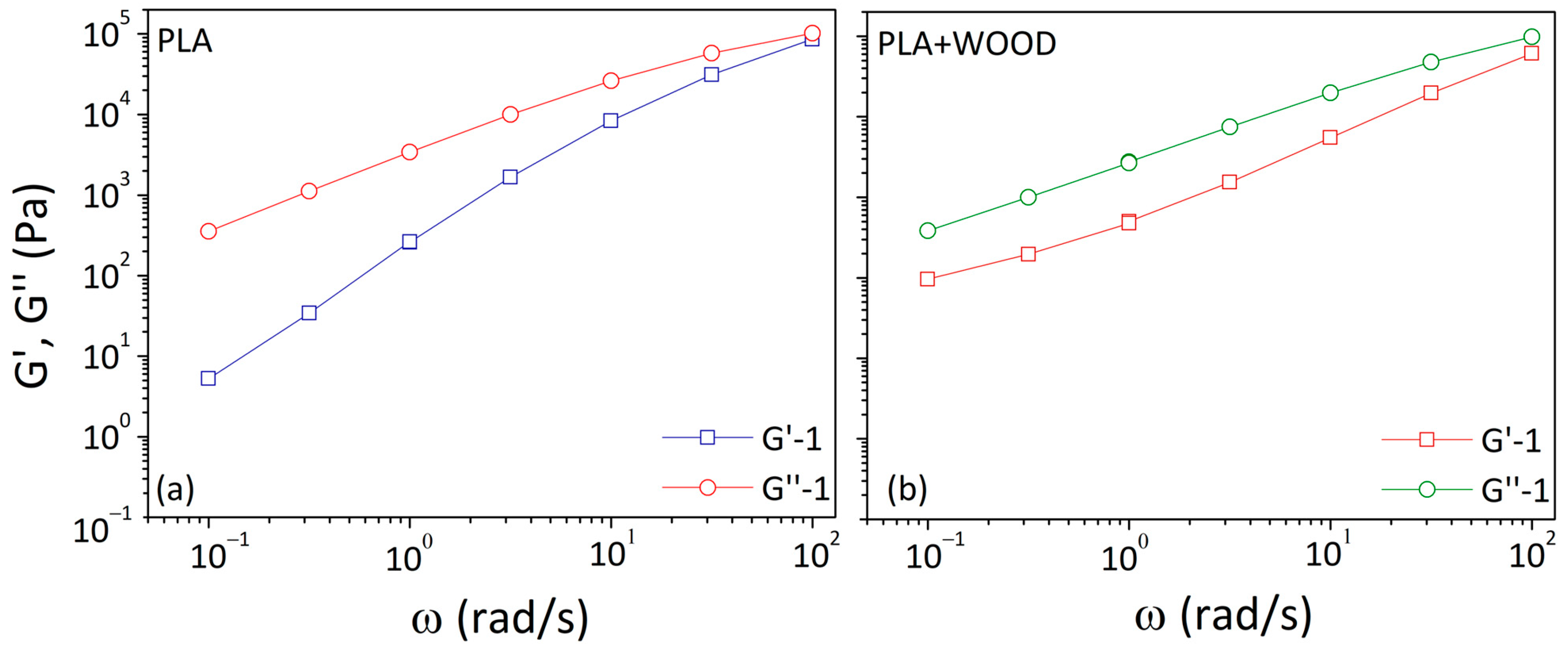
3.2. Rheological Properties of Basic Materials
3.3. Rheological Properties of Printed Specimens
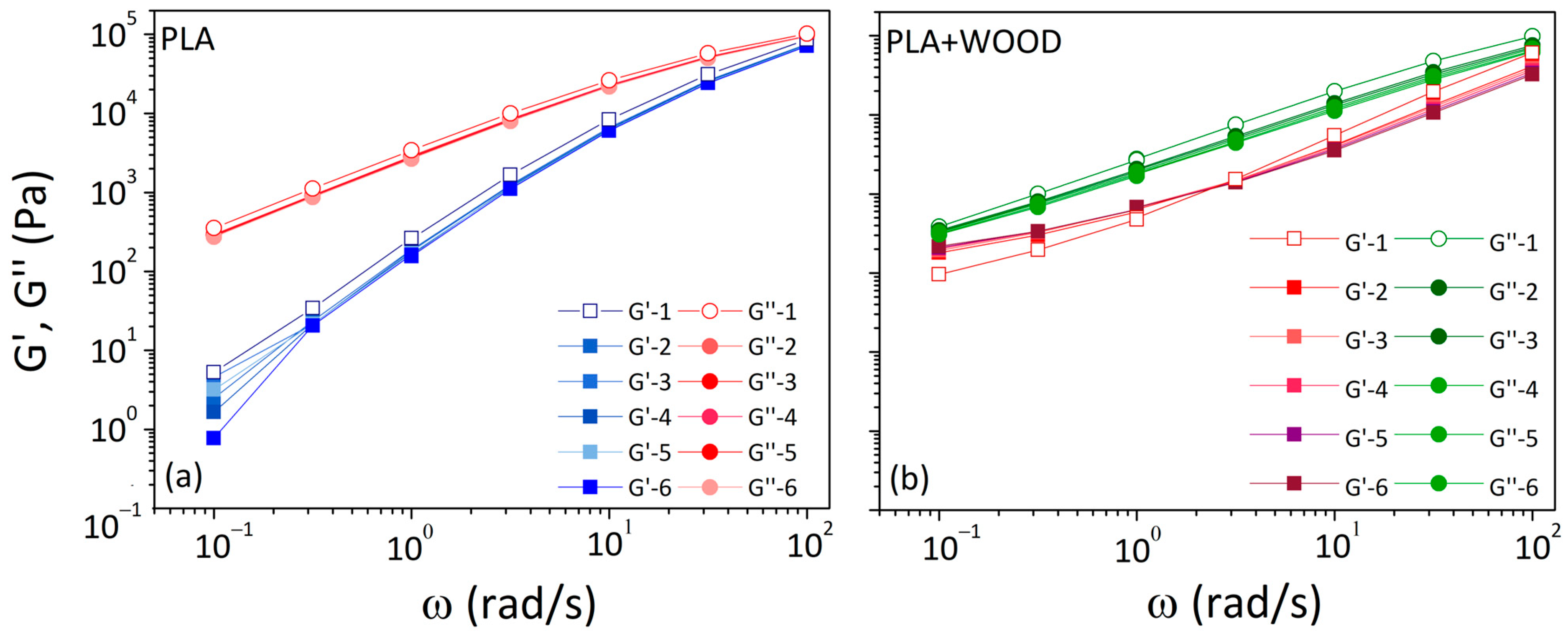
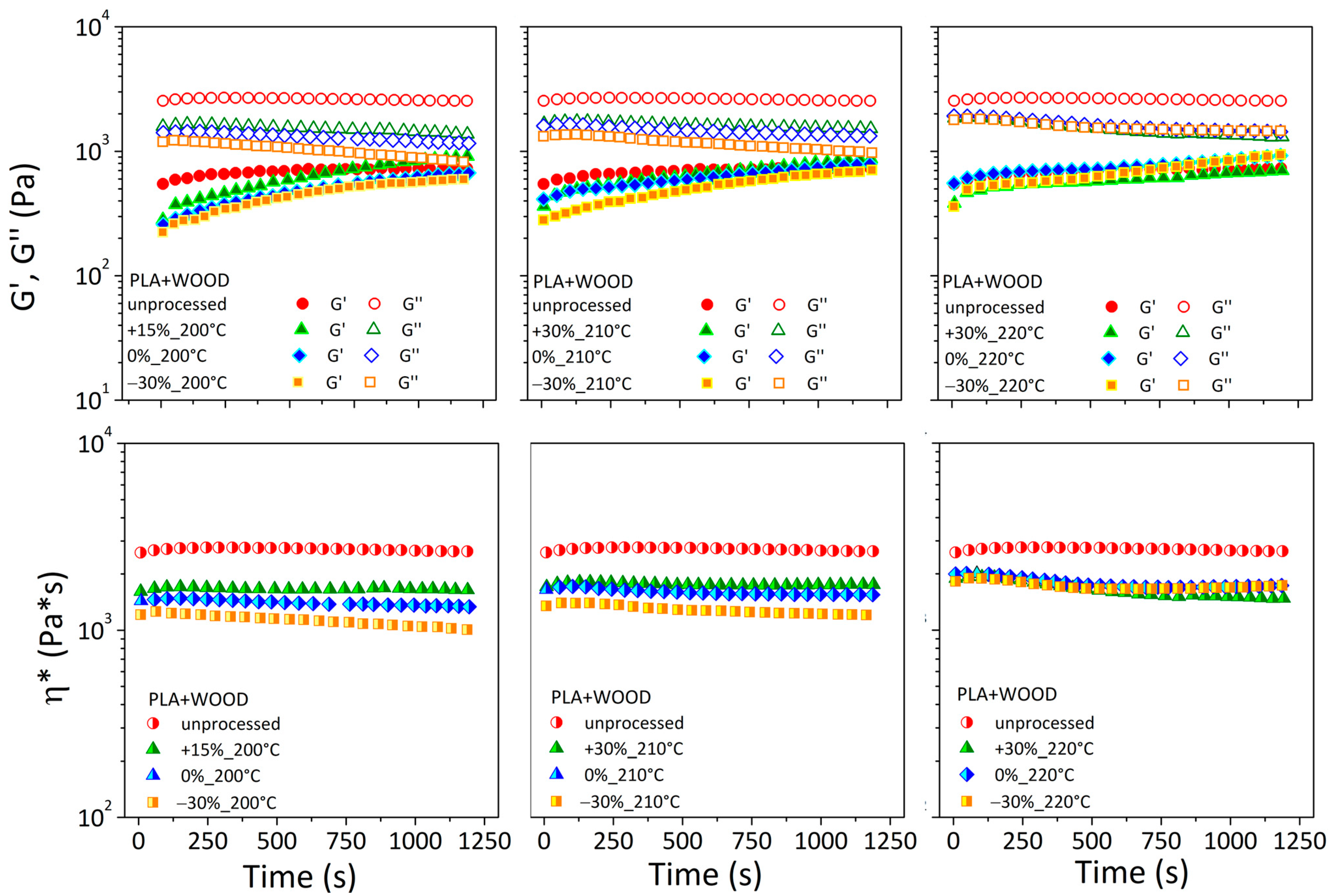
3.3.1. Storage Modulus, Loss Modulus, Complex Viscosity
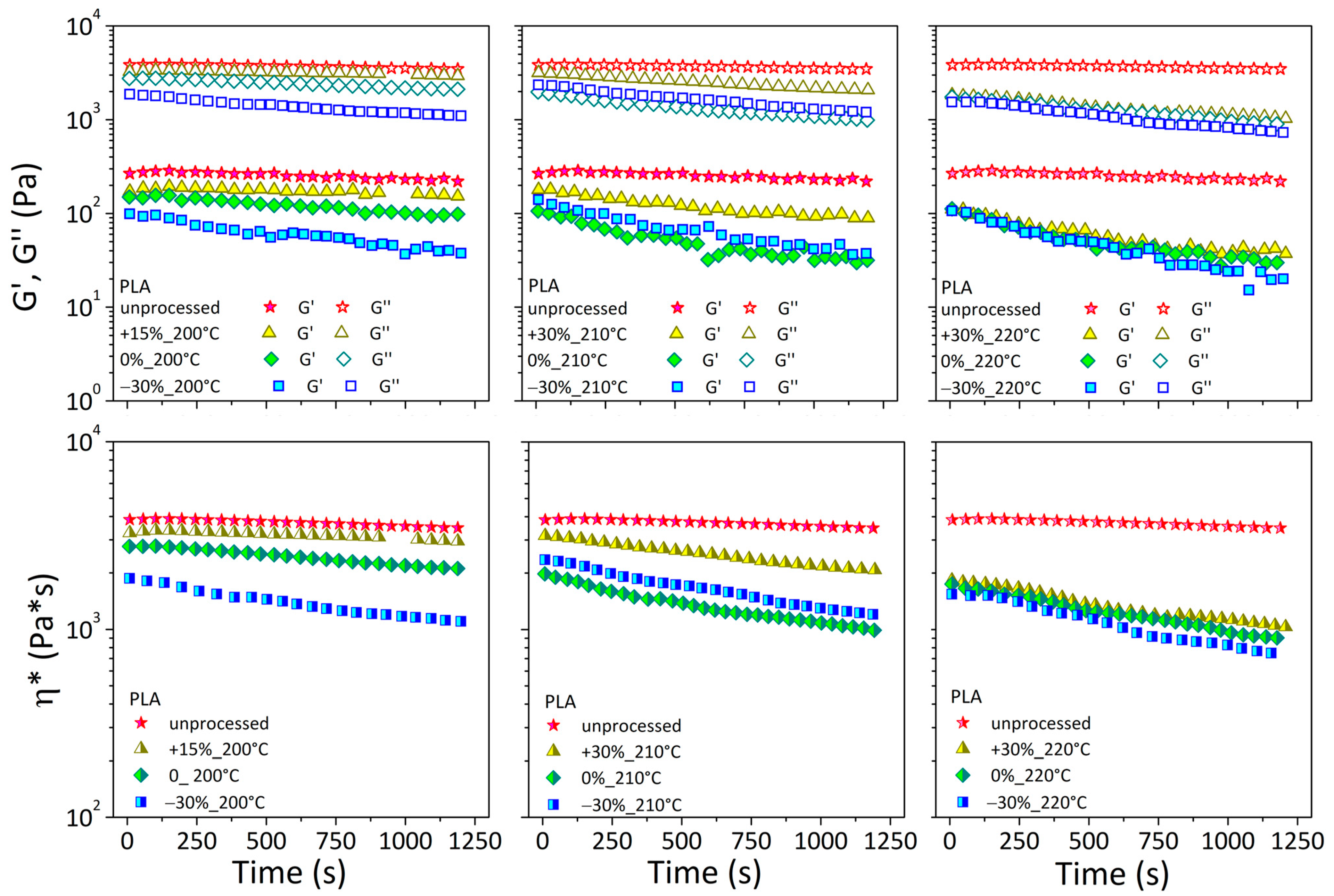
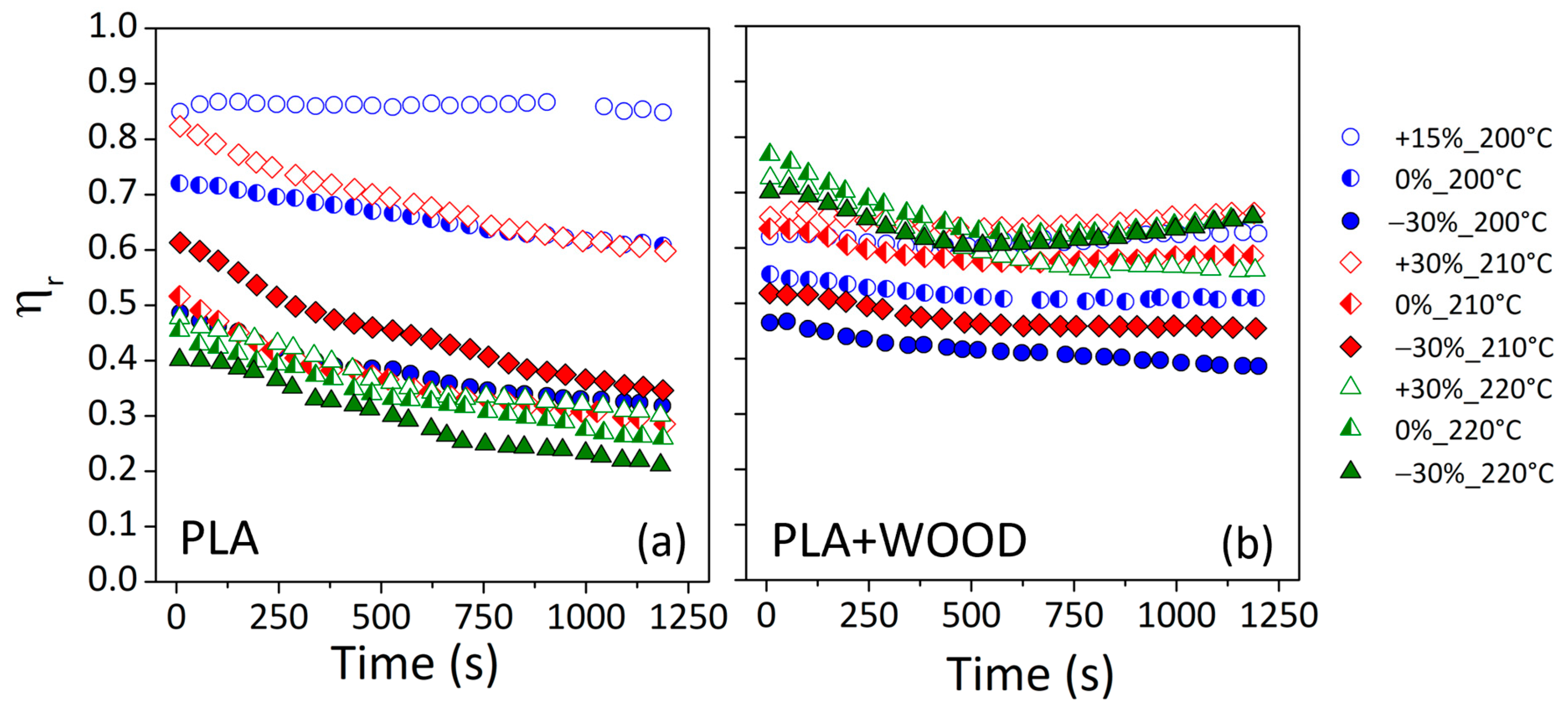
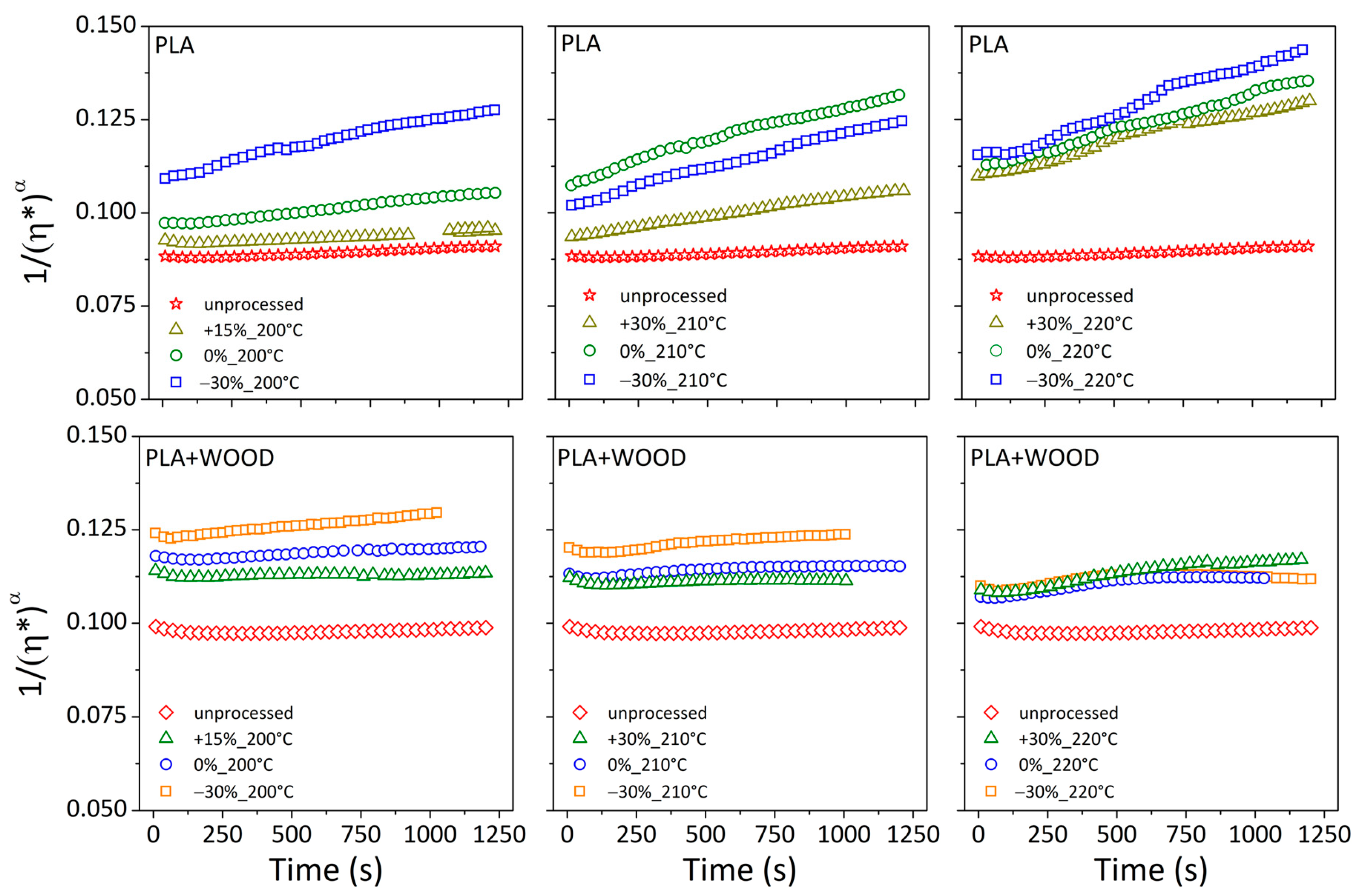
3.3.2. Reduced Complex Viscosity and Material Degradation during the Printing Process
3.3.3. Decomposition Kinetics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Trivedi, A.K.; Gupta, M.K.; Singh, H. PLA based biocomposites for sustainable products: A review. Adv. Ind. Eng. Polym. Res. 2023, 6, 382–395. [Google Scholar] [CrossRef]
- Simmons, H.; Kontopoulou, M. Hydrolytic degradation of branched PLA produced by reactive extrusion. Polym. Degrad. Stab. 2018, 158, 228–237. [Google Scholar] [CrossRef]
- Nofar, M.; Sacligil, D.; Carreau, P.J.; Kamal, M.R.; Heuzey, M.C. Poly (lactic acid) blends: Processing, properties and applications. Int. J. Biol. Macromol. 2019, 125, 307–360. [Google Scholar] [CrossRef]
- Polychronopoulos, N.D.; Vlachopoulos, J. Polymer Processing and Rheology. In Functional Polymers; Mazumder, M.A.J., Sheardown, H., Al-Ahmed, A., Eds.; Springer: New York, NY, USA, 2019; pp. 1–47. [Google Scholar]
- Capone, C.; Di Landro, L.; Inzoli, F.; Penco, M.; Sartore, L. Thermal and mechanical degradation during polymer extrusion processing. Polym. Eng. Sci. 2007, 47, 1813–1819. [Google Scholar] [CrossRef]
- Velghe, I.; Buffel, B.; Vandeginste, V.; Thielemans, W.; Desplentere, F. Review on the Degradation of Poly(lactic acid) during Melt Processing. Polymers 2023, 15, 2047. [Google Scholar] [CrossRef] [PubMed]
- Taubner, V.; Shishoo, R. Influence of Processing Parameters on the Degradation of Poly(L-lactide) During Extrusion. J. Appl. Polym. Sci. 2001, 79, 2128–2135. [Google Scholar] [CrossRef]
- Gorrasi, G.; Pantani, R. Hydrolysis and Biodegradation of Poly(lactic acid). In Synthesis, Structure and Properties of Poly(lactic acid). Advances in Polymer Science; Di Lorenzo, M., Androsch, R., Eds.; Springer: Cham, Switzerland, 2018; pp. 119–151. [Google Scholar]
- Srivastava, D.; Kumar, P.; Mathur, G.N. Thermo-oxidative degradation studies of ternary blends of polyethylenes. Adv. Polym. Technol. 2004, 23, 59–70. [Google Scholar] [CrossRef]
- Pillin, I.; Montrelay, N.; Bourmaud, A.; Grohens, Y. Effect of thermo-mechanical cycles on the physico-chemical properties of poly(lactic acid). Polym. Degrad. Stab. 2008, 93, 321–328. [Google Scholar] [CrossRef]
- Aldhafeeri, T.; Alotaibi, M.; Barry, C.F. Impact of Melt Processing Conditions on the Degradation of Polylactic Acid. Polymers 2022, 14, 2790. [Google Scholar] [CrossRef] [PubMed]
- Pop, M.A.; Croitoru, C.; Bedő, T.; Geaman, V.; Radomir, I.; Coșnița, M.; Zaharia, S.M.; Chicoș, L.A.; Miloșan, I. Structural changes during 3D printing of bioderived and synthetic thermoplastic materials. J. Appl. Polym. Sci. 2019, 136, 47382. [Google Scholar] [CrossRef]
- Patti, A. Challenges to Improve Extrusion-based Additive Manufacturing Process of Thermoplastics Towards Sustainable Development. Macromol. Rapid Commun. 2024, 2400249. [Google Scholar] [CrossRef] [PubMed]
- Morales, M.A.; Ruiz-Salgado, S.; Agustín-Serrano, R.; Zenteno-Mateo, B.; Rodríguez-Mora, J.I. Design and mathematical modeling of polymeric phases to obtain controlled microporosity materials by 3D printing. Prog. Addit. Manuf. 2023, 8, 1701–1710. [Google Scholar] [CrossRef]
- Liu, L.; Lin, M.; Xu, Z.; Lin, M. Polylactic acid-based wood-plastic 3D printing composite and its properties. BioResources 2019, 14, 8484–8498. [Google Scholar] [CrossRef]
- Acierno, D.; Patti, A. Fused Deposition Modelling (FDM) of Thermoplastic-Based Filaments: Process and Rheological Properties—An Overview. Materials 2023, 16, 7664. [Google Scholar] [CrossRef] [PubMed]
- Pantani, R.; De Santis, F.; Sorrentino, A.; De Maio, F.; Titomanlio, G. Crystallization kinetics of virgin and processed poly(lactic acid). Polym. Degrad. Stab. 2010, 95, 1148–1159. [Google Scholar] [CrossRef]
- Meng, Q.; Heuzey, M.C.; Carreau, P.J. Control of thermal degradation of polylactide/clay nanocomposites during melt processing by chain extension reaction. Polym. Degrad. Stab. 2012, 97, 2010–2020. [Google Scholar] [CrossRef]
- Patti, A.; Acierno, S.; Cicala, G.; Acierno, D. Predicting the Printability of Poly(Lactide) Acid Filaments in Fused Deposition Modeling (FDM) Technology: Rheological Measurements and Experimental Evidence. ChemEngineering 2022, 7, 1. [Google Scholar] [CrossRef]
- Patti, A.; Acierno, S.; Cicala, G.; Zarrelli, M.; Acierno, D. Recovery of Waste Material from Biobags: 3D Printing Process and Thermo-Mechanical Characteristics in Comparison to Virgin and Composite Matrices. Polymers 2022, 14, 1943. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Wu, G.; Zhang, H. Effect of wood flour as nucleating agent on the isothermal crystallization of poly(lactic acid). Polym. Adv. Technol. 2017, 28, 252–260. [Google Scholar] [CrossRef]
- Techawinyutham, L.; Siengchin, S.; Dangtungee, R.; Parameswaranpillai, J. Influence of accelerated weathering on the thermo-mechanical, antibacterial, and rheological properties of polylactic acid incorporated with porous silica-containing varying amount of capsicum oleoresin. Compos. Part B Eng. 2019, 175, 107108. [Google Scholar] [CrossRef]
- Winter, H.H.; Mours, M. Rheology of Polymers Near Liquid-Solid Transitions. Adv. Polym. Sci. 1997, 134, 165–234. [Google Scholar] [CrossRef]
- Croshaw, C.; Hamernik, L.; Ghanbari, L.; Browning, A.; Wiggins, J. Melt-state degradation mechanism of poly (ether ketone ketone): The role of branching on crystallization and rheological behavior. Polym. Degrad. Stab. 2022, 200, 109968. [Google Scholar] [CrossRef]
- Lin, Z.; Guo, X.; He, Z.; Liang, X.; Wang, M.; Jin, G. Thermal degradation kinetics study of molten polylactide based on Raman spectroscopy. Polym. Eng. Sci. 2021, 61, 201–210. [Google Scholar] [CrossRef]
- Vohlidal, J. Polymer degradation: A short review. Chem. Teach. Int. 2021, 3, 213–220. [Google Scholar] [CrossRef]
- Maharana, T.; Mohanty, B.; Negi, Y.S. Melt-solid polycondensation of lactic acid and its biodegradability. Prog. Polym. Sci. 2009, 34, 99–124. [Google Scholar] [CrossRef]
- Cuadri, A.A.; Martín-Alfonso, J.E. Thermal, thermo-oxidative and thermomechanical degradation of PLA: A comparative study based on rheological, chemical and thermal properties. Polym. Degrad. Stab. 2018, 150, 37–45. [Google Scholar] [CrossRef]
- Penu, C.; Hu, G.H.; Fernandez, A.; Marchal, P.; Choplin, L. Rheological and electrical percolation thresholds of carbon nanotube/polymer nanocomposites. Polym. Eng. Sci. 2012, 52, 2173–2181. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, P.; Ma, C.A.; Wu, G.; Sumita, M. Temperature and time dependence of conductive network formation: Dynamic percolation and percolation time. Polymer 2006, 47, 466–473. [Google Scholar] [CrossRef]
- Wu, G.; Asai, S.; Zhang, C.; Miura, T.; Sumita, M. A delay of percolation time in carbon-black-filled conductive polymer composites. J. Appl. Phys. 2000, 88, 1480–1487. [Google Scholar] [CrossRef]
- Patti, A.; Acierno, S.; Cicala, G.; Acierno, D. Aging effects on the viscoelastic behaviour of products by fused deposition modelling (FDM) made from recycled and wood-filled polymer resins. Eur. J. Wood Wood Prod. 2024, 82, 69–79. [Google Scholar] [CrossRef]
- Speranza, V.; De Meo, A.; Pantani, R. Thermal and hydrolytic degradation kinetics of PLA in the molten state. Polym. Degrad. Stab. 2014, 100, 37–41. [Google Scholar] [CrossRef]
- Seo, K.S.; Cloyd, J.D. Kinetics of hydrolysis and thermal degradation of polyester melts. J. Appl. Polym. Sci. 1991, 42, 845–850. [Google Scholar] [CrossRef]
- Daly, P.A.; Bruce, D.A.; Melik, D.H.; Harrison, G.M. Thermal degradation kinetics of poly(3-hydroxybutyrate-co-3-hydroxyhexanoate). J. Appl. Polym. Sci. 2005, 98, 66–74. [Google Scholar] [CrossRef]
- Södergård, A.; Näsman, J.H. Melt stability study of various types of poly(L-lactide). Ind. Eng. Chem. Res. 1996, 35, 732–735. [Google Scholar] [CrossRef]


| PLA | PLA + WOOD | |
|---|---|---|
| Nozzle diameter | 0.4 mm | 0.4 mm |
| Layer thickness | 0.09 mm | 0.19 mm |
| Retraction speed | 27 mm/s | 20 mm/s |
| Retraction distance | 2.7 mm | 1 mm |
| Infill density | 100% | 100% |
| Printing speed | −30% to +30% (70 mm/s to 130 mm/s) | −30% to +30% (70 mm/s to 130 mm/s) |
| Nozzle temperature | 200 °C to 220 °C | 200 °C to 220 °C |
| Test | PLA | PLA + WOOD | ||
|---|---|---|---|---|
| Slope G′ at ω < 1 rad/s | Slope G″ at ω < 1 rad/s | Slope G′ at ω < 1 rad/s | Slope G″ at ω < 1 rad/s | |
| initial frequency sweep G′-1; G″-1 | 1.700 | 0.982 | 0.693 | 0.842 |
| 1° frequency sweep after thermal program G′-2; G″-2 | 1.881 | 0.988 | 0.518 | 0.764 |
| 2° frequency sweep after thermal program G′-3; G″-3 | 1.604 | 0.990 | 0.514 | 0.760 |
| 3° frequency sweep after thermal program G′-4; G″-4 | 2.025 | 0.987 | 0.497 | 0.753 |
| 4° frequency sweep after thermal program G′-5; G″-5 | 1.726 | 0.984 | 0.485 | 0.746 |
| 5° frequency sweep after thermal program G′-6; G″-6 | 2.321 | 0.984 | 0.465 | 0.737 |
| Printing Conditions | PLA | PLA + WOOD | ||
|---|---|---|---|---|
| unprocessed | 0.80 | 0.90 | 1.31 | 0.99 |
| +15%_200 °C | 0.88 | 0.89 | 3.22 | 0.86 |
| 0%_200 °C | 0.64 | 0.76 | 2.59 | 0.82 |
| −30%_200% | 0.37 | 0.59 | 2.57 | 0.73 |
| +30%_210 °C | 0.48 | 0.66 | 2.23 | 0.93 |
| 0%_210 °C | 0.27 | 0.50 | 1.96 | 0.83 |
| −30%_210% | 0.30 | 0.55 | 2.35 | 0.78 |
| +30%_220 °C | 0.33 | 0.56 | 1.80 | 0.71 |
| 0%_220 °C | 0.21 | 0.51 | 2.58 | 0.81 |
| −30%_220% | 0.19 | 0.47 | 2.62 | 0.81 |
| Printing Conditions | ηr|t=0 | |
|---|---|---|
| PLA | PLA + WOOD | |
| +15%_200 °C | 0.85 | 0.62 |
| 0%_200 °C | 0.72 | 0.55 |
| −30%_200 °C | 0.48 | 0.46 |
| +30%_210 °C | 0.82 | 0.65 |
| 0%_210 °C | 0.51 | 0.63 |
| −30%_210 °C | 0.61 | 0.52 |
| +30%_220 °C | 0.47 | 0.72 |
| 0%_220 °C | 0.45 | 0.77 |
| −30%_220 °C | 0.40 | 0.70 |
| Printing Conditions | PLA | PLA + WOOD | ||||
|---|---|---|---|---|---|---|
| k (s−1) | R2 | k (s−1) | R2 | |||
| unprocessed | 0.0876 | 2.76 × 10−6 | 0.974 | 0.0973 | 8.30 × 10−7 | 0.338 |
| +15%_200 °C | 0.0914 | 3.32 × 10−6 | 0.926 | 0.1126 | 3.86 × 10−7 | 0.139 |
| 0%_200 °C | 0.0964 | 7.71 × 10−6 | 0.993 | 0.1169 | 3.10 × 10−6 | 0.932 |
| −30%_200 °C | 0.1099 | 1.56 × 10−5 | 0.985 | 0.1227 | 6.44 × 10−6 | 0.986 |
| +30%_210 °C | 0.0935 | 1.08 × 10−5 | 0.997 | 0.1105 | 1.15 × 10−6 | 0.481 |
| 0%_210 °C | 0.1091 | 1.93 × 10−5 | 0.985 | 0.1125 | 2.83 × 10−6 | 0.837 |
| −30%_210 °C | 0.1021 | 1.92 × 10−5 | 0.995 | 0.1187 | 5.46 × 10−6 | 0.930 |
| +30%_220 °C | 0.1098 | 1.73 × 10−5 | 0.973 | 0.1082 | 8.60 × 10−6 | 0.927 |
| 0%_220 °C | 0.1114 | 2.04 × 10−5 | 0.995 | 0.1073 | 6.13 × 10−6 | 0.847 |
| −30%_220 °C | 0.1134 | 2.64 × 10−5 | 0.987 | 0.1101 | 2.69 × 10−6 | 0.445 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patti, A.; Acierno, S. Rheological Changes in Bio-Based Filaments Induced by Extrusion-Based 3D Printing Process. Materials 2024, 17, 3839. https://doi.org/10.3390/ma17153839
Patti A, Acierno S. Rheological Changes in Bio-Based Filaments Induced by Extrusion-Based 3D Printing Process. Materials. 2024; 17(15):3839. https://doi.org/10.3390/ma17153839
Chicago/Turabian StylePatti, Antonella, and Stefano Acierno. 2024. "Rheological Changes in Bio-Based Filaments Induced by Extrusion-Based 3D Printing Process" Materials 17, no. 15: 3839. https://doi.org/10.3390/ma17153839
APA StylePatti, A., & Acierno, S. (2024). Rheological Changes in Bio-Based Filaments Induced by Extrusion-Based 3D Printing Process. Materials, 17(15), 3839. https://doi.org/10.3390/ma17153839







