Determination of Crack Tip Plastic Zone Using Dynamically Visible Mechanochromic Luminescence Response
Abstract
:1. Introduction
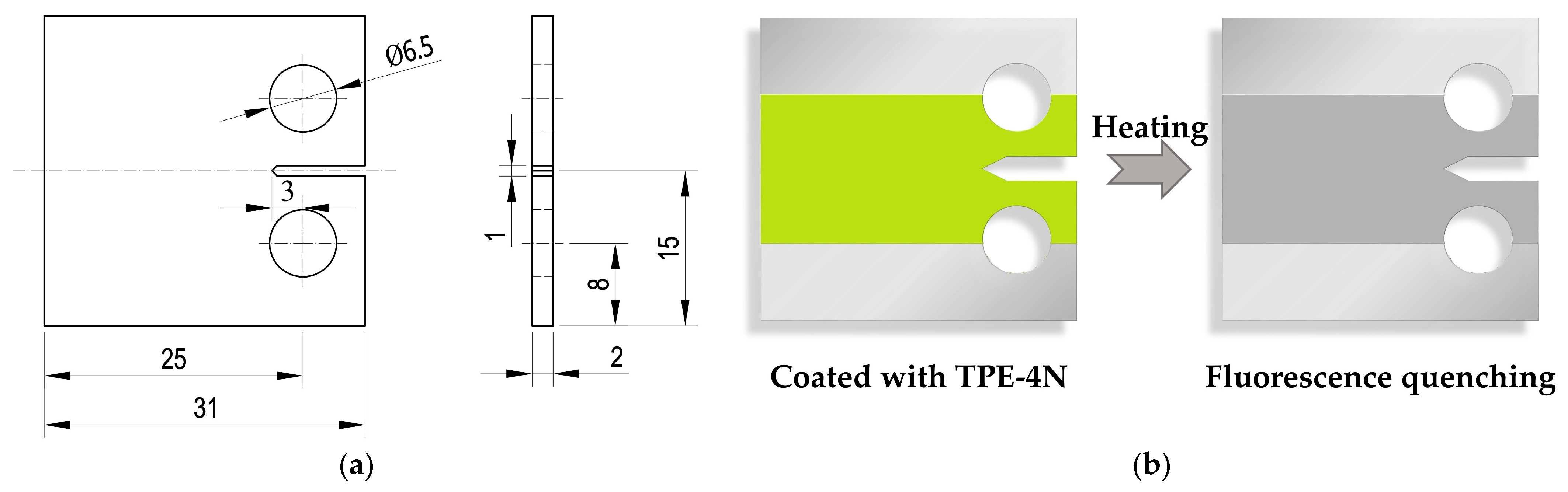
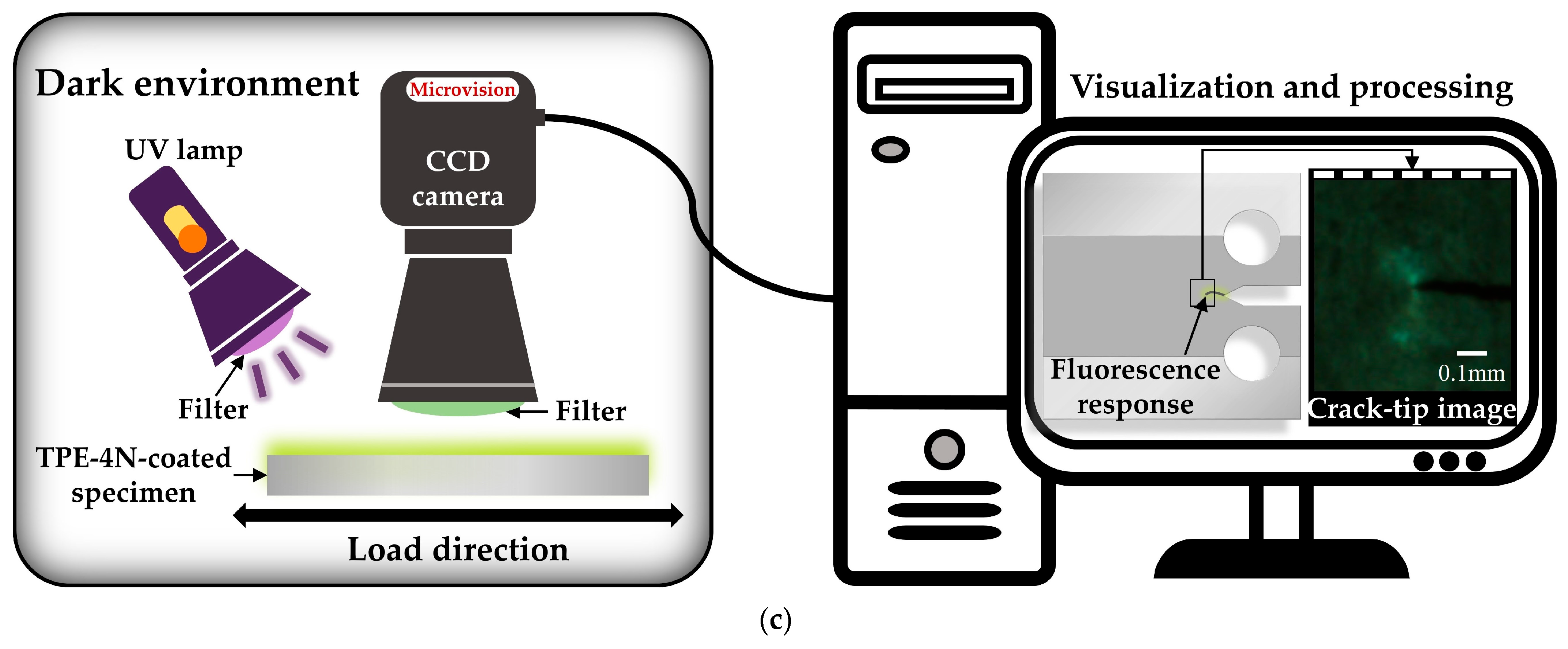
2. Materials and Methods
3. Results
3.1. Mechanoresponsive Fluorescence Response near the Crack Tip
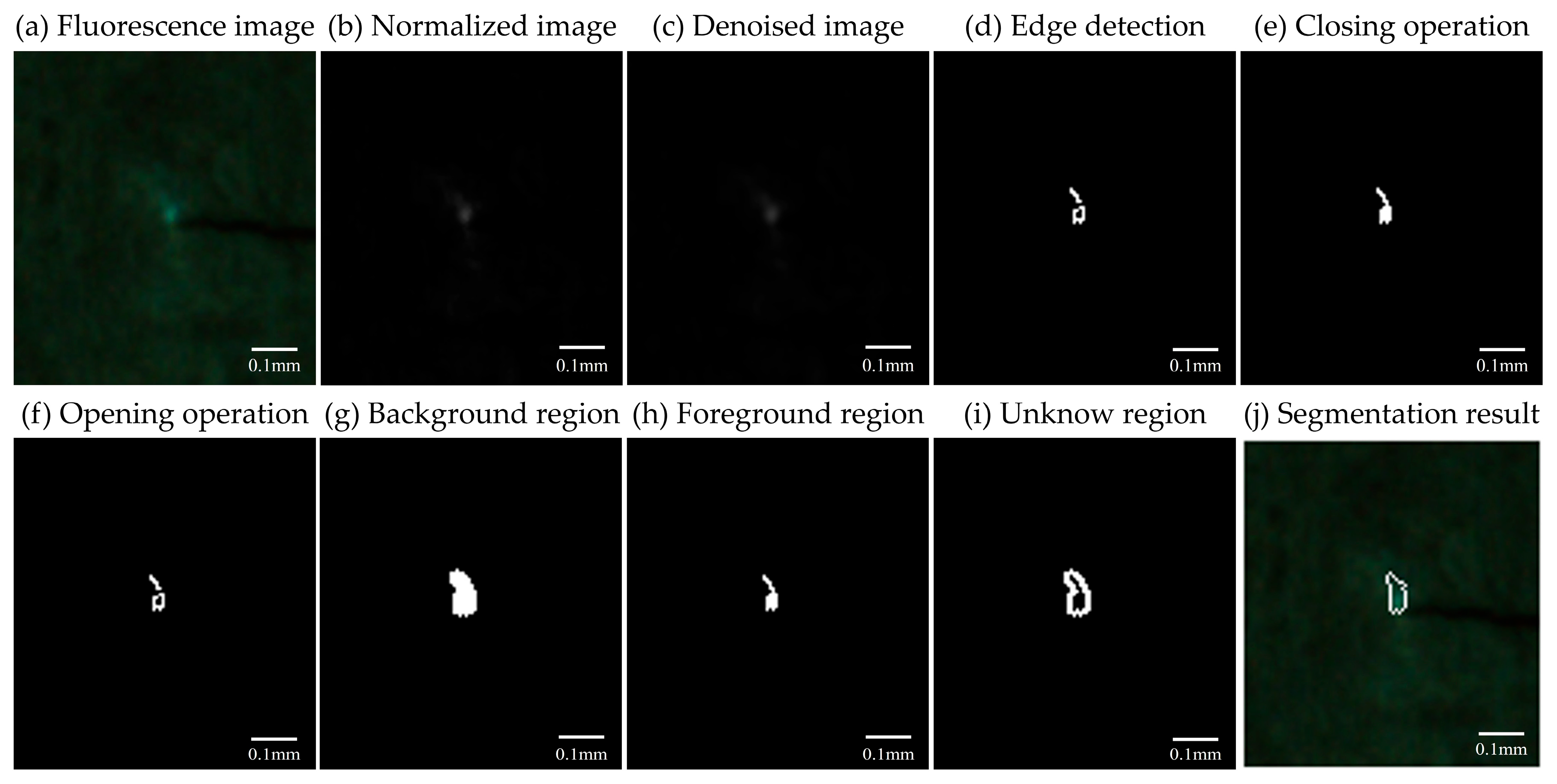
3.2. Fluorescence Image Processing
4. Discussion
4.1. Fluorescence Image Features Quantification
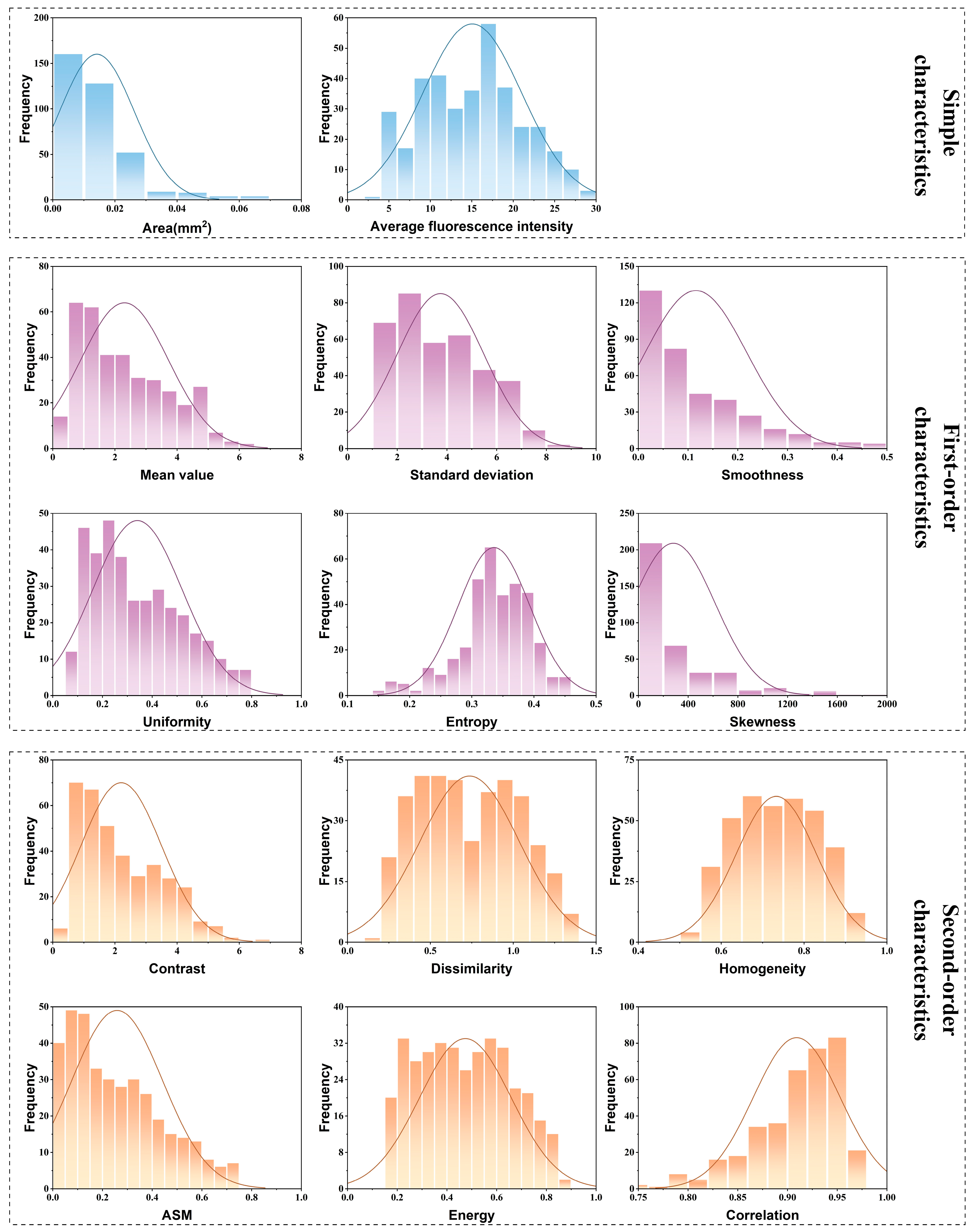
4.1.1. Simple Characteristic Values Extraction
4.1.2. First-Order Characteristic Values Extraction
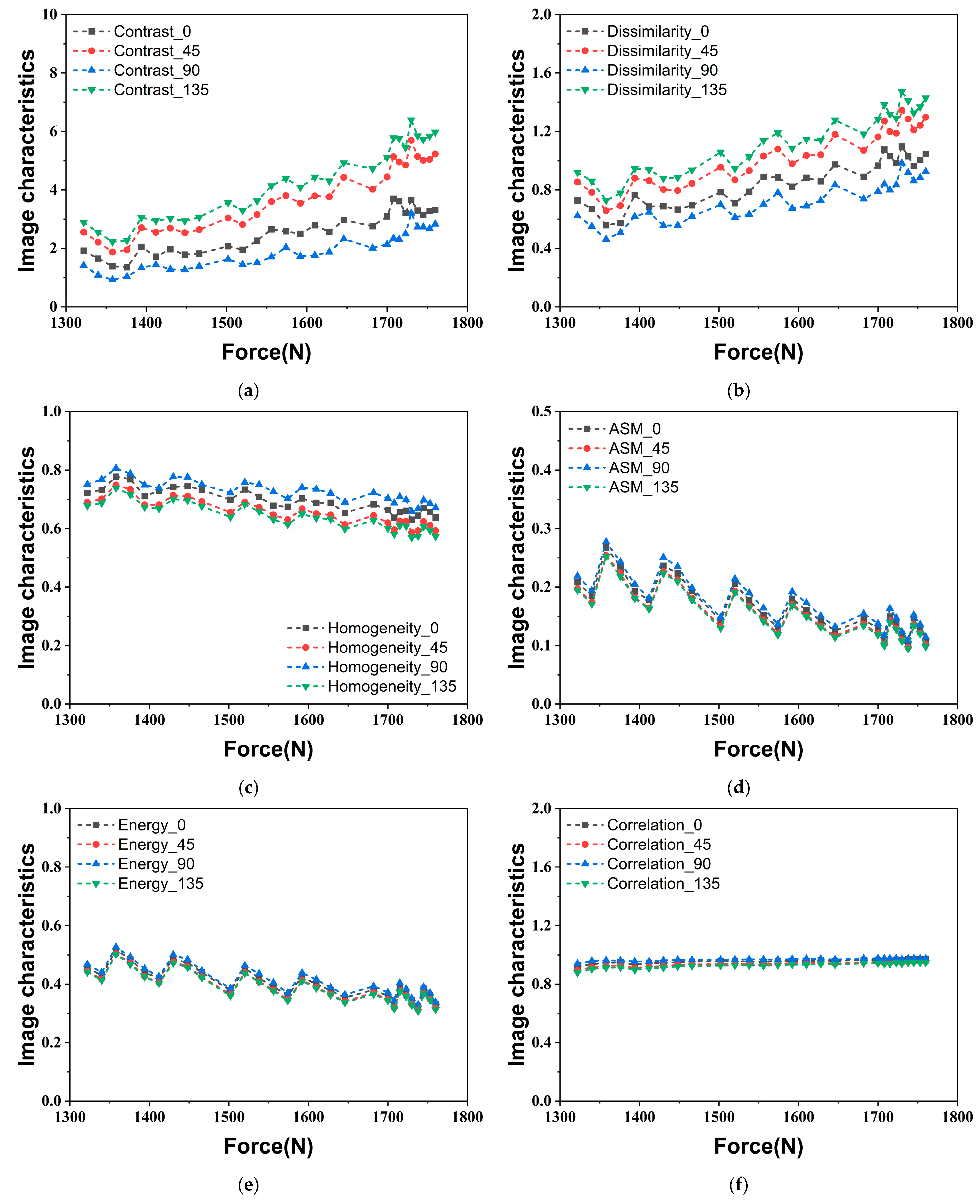
4.1.3. Second-Order Characteristic Values Extraction
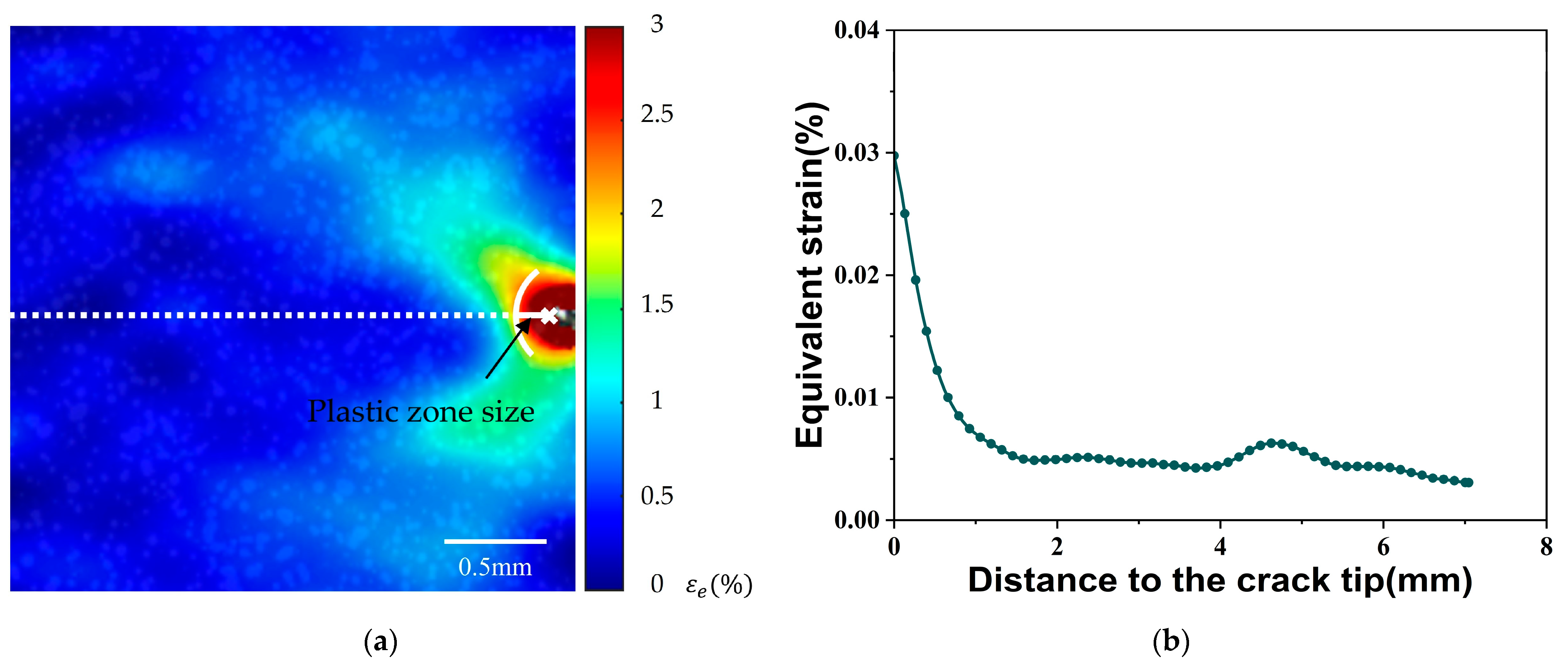
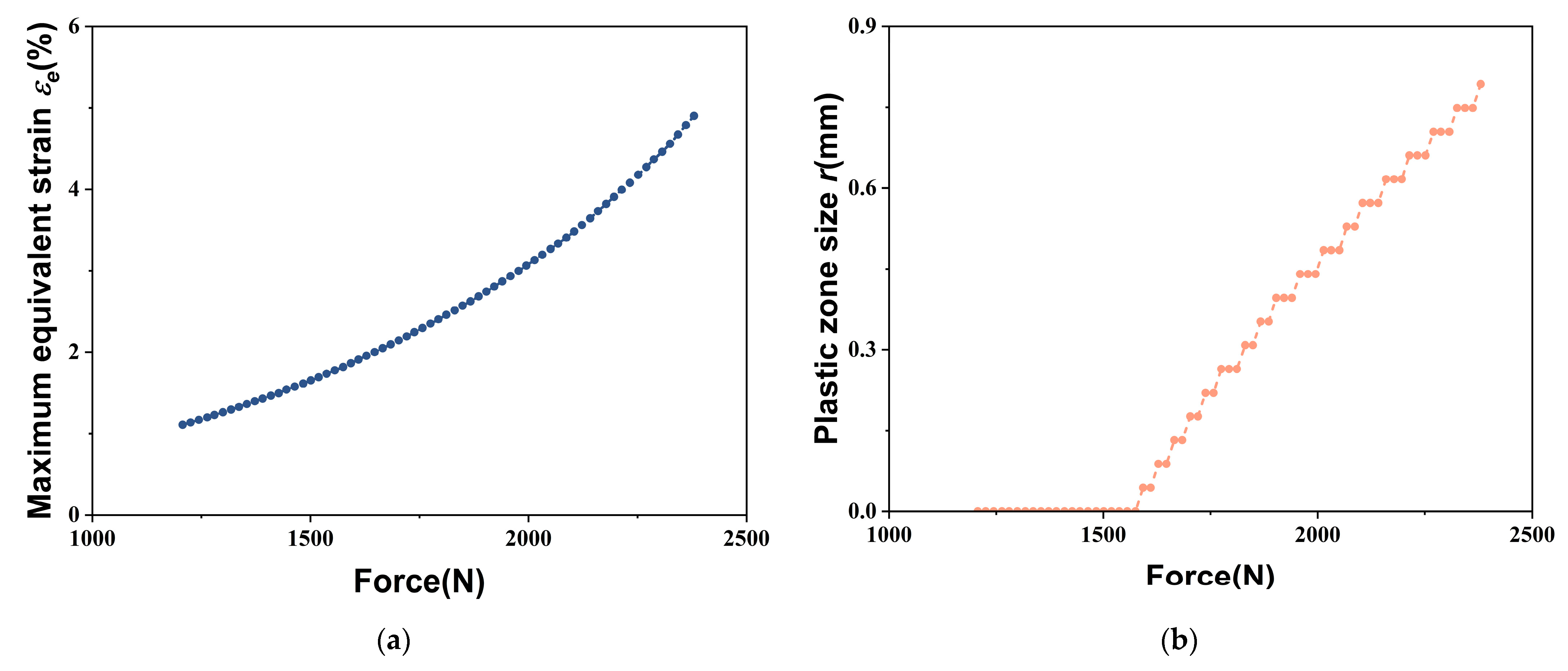
4.2. Plastic Zone Determination Using DIC Method
4.3. Correlation Analysis Method Investigation
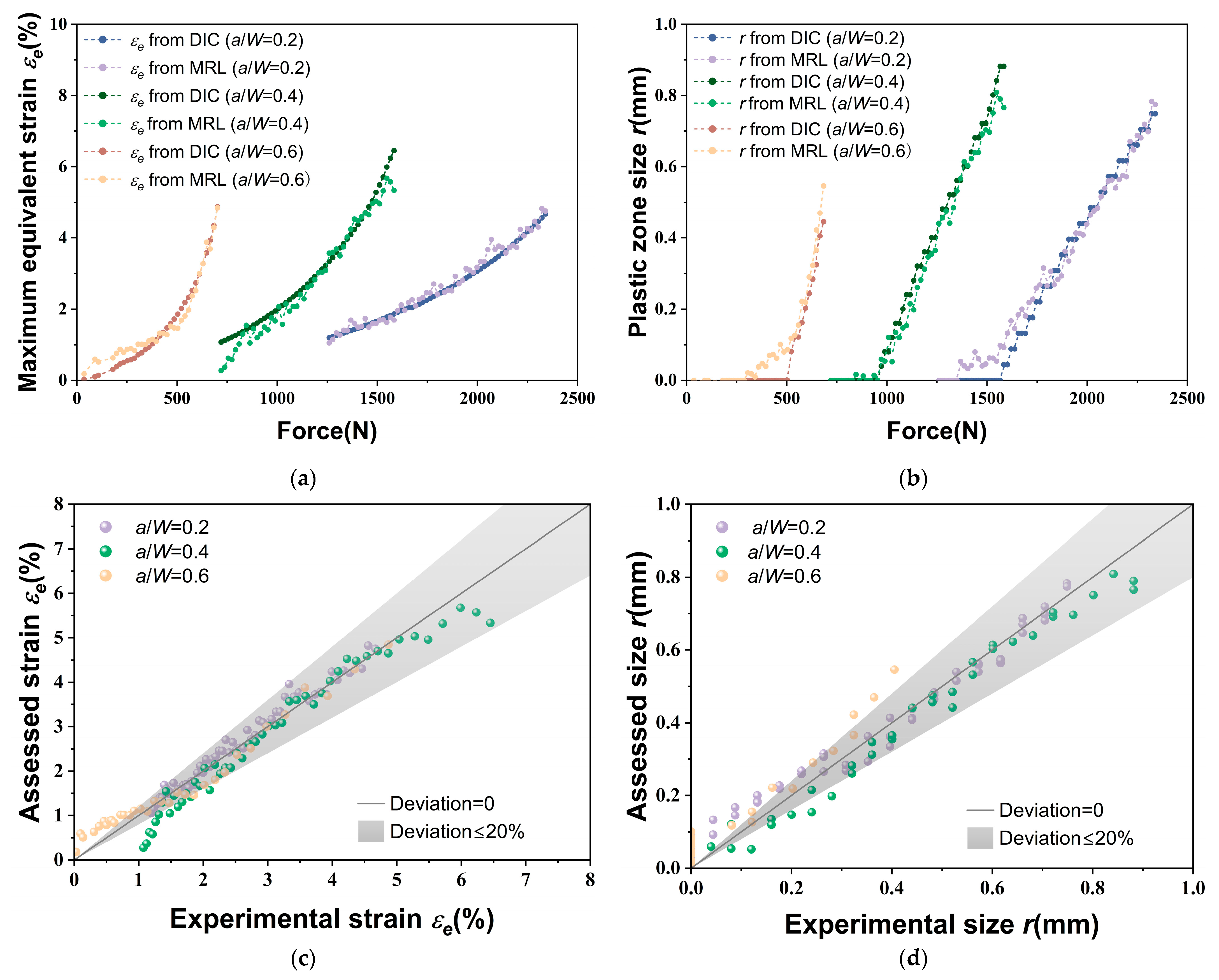
4.4. Determination of Plastic Zone Parameters
5. Conclusions
- (1)
- The local deformation near the crack tip results in the dynamically visible green fluorescence emission of the TPE-4N sensing film. The fluorescence distribution obtained using the MRL-based method agrees well with the equivalent strain distribution measured using the DIC method.
- (2)
- The preprocessing of the fluorescence images results in normalized, denoised grayscale images of the crack tip. An enhanced watershed image segmentation algorithm is employed to segment out the ROI near the crack tip, yielding two simple characteristic values that describe the area and brightness of this region. The grayscale histogram and the GLCM, derived from the normalized denoised grayscale image, are analyzed to extract first-order and second-order characteristic values that quantify the texture features of the fluorescence image. These three types of characteristic values serve as potential characterization parameters for fluorescence response in the establishment of the MRL-based forward model of the plastic zone.
- (3)
- The characteristic values derived from fluorescence images exhibit significant correlations with the maximum equivalent strain at the crack tip and the plastic zone size obtained through the DIC method. The plastic zone parameters determined using the MRL-based method agree well with the results measured using the DIC method. This indicates that the plastic zone near the crack tip can be effectively analyzed by capturing loading conditions and fluorescence response.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MCL | Mechanochromic luminescence |
| AIE | Aggregation-induced emission |
| DIC | Digital image correlation |
| MRL | Mechanoresponsive luminescence |
| ML | Mechanoluminescence |
| TPE-4N | 1,1,2,2-tetrakis (4-nitrophenyl) ethene |
| NDT | Non-destructive testing |
| MFL | Magnetic-flux-leakage |
| FEM | Finite element method |
| GLCM | Gray Level Co-occurrence Matrix |
| CT | Compact tensile |
| CCD | Charge-coupled device |
| UV | Ultraviolet |
| LED | Light-emitting diode |
| SNR | Signal-to-noise ratio |
| ROI | The region of interest |
| ASM | Angular Second Moment |
| K-S | Kolmogorov–Smirnov |
| S-W | Shapiro–Wilk |
| MLR | Multiple linear regression |
| R2 | Coefficients of determination |
| MAE | Mean absolute error |
| MSE | Mean square error |
| RMSE | Root-mean-square error |
Appendix A
| Normality Test Method | Area (mm2) | Average Fluorescence Intensity |
|---|---|---|
| p-value of K-S test | 8 × 10−17 | 0.01146 |
| p-value of S-W test | 2 × 10−20 | 0.00007 |
| Normality Test Method | Mean | Std. Dev. | Smoothness | Uniformity | Entropy | Skewness |
|---|---|---|---|---|---|---|
| p-value of K-S test | 9 × 10−10 | 4 × 10−8 | 2 × 10−25 | 2 × 10−10 | 5 × 10−8 | 5 × 10−42 |
| p-value of S-W test | 1 × 10−11 | 2 × 10−9 | 6 × 10−19 | 2 × 10−10 | 7 × 10−8 | 2 × 10−22 |
| Normality Test Method | Contrast | Dissimilarity | Homogeneity | ASM | Energy | Correlation |
|---|---|---|---|---|---|---|
| p-value of K-S test | 2 × 10−9 | 0.00022 | 0.00712 | 3 × 10−10 | 0.00095 | 5 × 10−13 |
| p-value of S-W test | 2 × 10−11 | 2 × 10−7 | 0.00001 | 2 × 10−12 | 10 × 10−8 | 4 × 10−14 |
References
- Yang, B.; Zhao, Y. Experimental Research on Dominant Effective Short Fatigue Crack Behavior for Railway LZ50 Axle Steel. Int. J. Fatigue 2012, 35, 71–78. [Google Scholar] [CrossRef]
- Su, Z.; Zhou, C.; Hong, M.; Cheng, L.; Wang, Q.; Qing, X. Acousto-Ultrasonics-Based Fatigue Damage Characterization: Linear versus Nonlinear Signal Features. Mech. Syst. Signal Process. 2014, 45, 225–239. [Google Scholar] [CrossRef]
- Fulco, S.; Budzik, M.K.; Turner, K.T. Enhancing Toughness through Geometric Control of the Process Zone. J. Mech. Phys. Solids 2024, 184, 105548. [Google Scholar] [CrossRef]
- Uğuz, A.; Martin, J.W. Plastic Zone Size Measurement Techniques for Metallic Materials. Mater. Charact. 1996, 37, 105–118. [Google Scholar] [CrossRef]
- Huang, X.; Liu, Y.; Dai, Y. Characteristics and Effects of T-Stresses in Central-Cracked Unstiffened and Stiffened Plates under Mode I Loading. Eng. Fract. Mech. 2018, 188, 393–415. [Google Scholar] [CrossRef]
- Xie, Y.-H.; Zhao, J.-F.; Zhang, B.; Liu, D.-B.; Kan, Q.-H.; Zhang, X. Lower-Order Mechanism-Based Strain Gradient Plastic Model Considering Stress Gradient Effect. Sci. Sin. Phys. Mech. Astron. 2024, 54, 284611. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, D.W.; Qin, X.M.; Gao, X.H.; Qiu, C.L.; Du, L.X. A Plastic Zone Equation Based on Mean Yield Criterion. Adv. Mater. Res. 2010, 97–101, 534–537. [Google Scholar] [CrossRef]
- Cuiyun, L.; Han, Y.; Shizhen, W.; Chaoli, M.; Huanxi, L. Measurement of Plastic Zone at Fatigue Crack Tip by Microhardness and Nanoin-Dentation Technique. In Proceedings of the 12th World Conference on Titanium, Beijing, China, 19–24 June 2011. [Google Scholar]
- Luo, Q.; Kitchen, M. Microhardness, Indentation Size Effect and Real Hardness of Plastically Deformed Austenitic Hadfield Steel. Materials 2023, 16, 1117. [Google Scholar] [CrossRef]
- Okayasu, M.; Sato, K.; Takasu, S. An Etching Characterization Method for Revealing the Plastic Deformation Zone in a SUS303 Stainless Steel. J. Mater. Sci. 2010, 45, 1220–1226. [Google Scholar] [CrossRef]
- Díaz, F.V.; Kaufmann, G.H.; Armas, A.F.; Galizzi, G.E. Optical Measurement of the Plastic Zone Size in a Notched Metal Specimen Subjected to Low-Cycle Fatigue. Opt. Lasers Eng. 2001, 35, 325–333. [Google Scholar] [CrossRef]
- Huang, S.; Khan, A.S. On the Use of Electrical-Resistance Metallic Foil Strain Gages for Measuring Large Dynamic Plastic Deformation. Exp. Mech. 1991, 31, 122–125. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, D.; Zhang, M.; Dai, W.; Zhang, W. In Situ Measurements for Plastic Zone Ahead of Crack Tip and Continuous Strain Variation under Cyclic Loading Using Digital Image Correlation Method. Metals 2020, 10, 273. [Google Scholar] [CrossRef]
- Bouas-Laurent, H.; Dürr, H. Organic Photochromism (IUPAC Technical Report). Pure Appl. Chem. 2001, 73, 639–665. [Google Scholar] [CrossRef]
- Jha, P.; Khare, A.; Singh, P.; Nema, S.K. Fracto-Mechanoluminescence of Sugar Crystals Measured with Different Techniques. J. Lumin. 2020, 222, 117176. [Google Scholar] [CrossRef]
- Di, B.-H.; Chen, Y.-L. Recent Progress in Organic Mechanoluminescent Materials. Chin. Chem. Lett. 2018, 29, 245–251. [Google Scholar] [CrossRef]
- Zhang, Z.; Lin, H.; Wei, X.; Chen, G.; Chen, X. Real-Time and Visible Monitoring of Structural Damage Using Mechanoresponsive Luminogen: Recent Progress and Perspectives. Weld. World 2022, 66, 1825–1845. [Google Scholar] [CrossRef]
- Xu, C.-N.; Watanabe, T.; Akiyama, M.; Zheng, X.-G. Direct View of Stress Distribution in Solid by Mechanoluminescence. Appl. Phys. Lett. 1999, 74, 2414–2416. [Google Scholar] [CrossRef]
- Chandra, V.K.; Chandra, B.P. Dynamics of the Mechanoluminescence Induced by Elastic Deformation of Persistent Luminescent Crystals. J. Lumin. 2012, 132, 858–869. [Google Scholar] [CrossRef]
- Chandra, B.P.; Elyas, M.; Majumdar, B. Dislocation Models of Mechanoluminescence in γ- and X-Irradiated Alkali Halides Crystals. Solid State Commun. 1982, 42, 753–757. [Google Scholar] [CrossRef]
- Chandra, B.P. Mechanoluminescence Induced by Elastic Deformation of Coloured Alkali Halide Crystals Using Pressure Steps. J. Lumin. 2008, 128, 1217–1224. [Google Scholar] [CrossRef]
- Fujio, Y.; Xu, C.-N.; Sakata, Y.; Ueno, N.; Terasaki, N. Invisible Crack Visualization and Depth Analysis by Mechanoluminescence Film. J. Alloys Compd. 2020, 832, 154900. [Google Scholar] [CrossRef]
- Sohn, K.-S.; Seo, S.Y.; Kwon, Y.N.; Park, H.D. Direct Observation of Crack Tip Stress Field Using the Mechanoluminescence of SrAl2O4:(Eu, Dy, Nd). J. Am. Ceram. Soc. 2002, 85, 712–714. [Google Scholar] [CrossRef]
- Li, C.; Xu, C.N.; Zhang, L.; Yamada, H.; Imai, Y. Dynamic Visualization of Stress Distribution on Metal by Mechanoluminescence Images. J. Vis. 2008, 11, 329–335. [Google Scholar] [CrossRef]
- Yin, S.; Zhao, Z.; Luan, W.; Yang, F. Optical Response of a Quantum Dot–Epoxy Resin Composite: Effect of Tensile Strain. RSC Adv. 2016, 6, 18126–18133. [Google Scholar] [CrossRef]
- Chandra, V.K.; Chandra, B.P.; Jha, P. Self-Recovery of Mechanoluminescence in ZnS: Cu and ZnS: Mn Phosphors by Trapping of Drifting Charge Carriers. Appl. Phys. Lett. 2013, 103, 161113. [Google Scholar] [CrossRef]
- Zhao, Z.; Luan, W.; Yin, S.; Brandner, J.J. Metal Crack Propagation Monitoring by Photoluminescence Enhancement of Quantum Dots. Appl. Opt. 2015, 54, 6498–6501. [Google Scholar] [CrossRef]
- Zhang, H.; Terasaki, N.; Yamada, H.; Xu, C.-N. Mechanoluminescence of Europium-Doped SrAMgSi2O7 (A=Ca, Sr, Ba). Jpn. J. Appl. Phys. 2009, 48, 04C109. [Google Scholar] [CrossRef]
- Chen, G.; Hong, W. Mechanochromism of Structural-Colored Materials. Adv. Opt. Mater. 2020, 8, 2000984. [Google Scholar] [CrossRef]
- Qiu, Z.; Zhao, W.; Cao, M.; Wang, Y.; Lam, J.W.Y.; Zhang, Z.; Chen, X.; Tang, B.Z. Dynamic Visualization of Stress/Strain Distribution and Fatigue Crack Propagation by an Organic Mechanoresponsive AIE Luminogen. Adv. Mater. 2018, 30, 1803924. [Google Scholar] [CrossRef]
- Zhang, Z.; Lin, H.; Lin, Q.; Chen, G.; Chen, X. Mechanoresponsive Luminogen (MRL)-Based Real-Time and Visible Detection Method for Biaxial Fatigue Crack Propagation. Int. J. Fatigue 2022, 164, 107161. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, M.; Zhang, L.; Qiu, Z.; Zhao, W.; Chen, G.; Chen, X.; Tang, B.Z. Dynamic Visible Monitoring of Heterogeneous Local Strain Response through an Organic Mechanoresponsive AIE Luminogen. ACS Appl. Mater. Interfaces 2020, 12, 22129–22136. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wang, Z.; Wang, L.; Zhang, Z.; Chen, X.; Meng, L. Machine Learning-Based Real-Time Visible Fatigue Crack Growth Detection. Digit. Commun. Netw. 2021, 7, 551–558. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.; Lin, H.; Chen, G.; Chen, X. Real-Time and Visible Monitoring of Stress Distribution Using Organic Mechanoresponsive Luminogen. Sci. China Technol. Sci. 2021, 64, 2586–2594. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, Z.; Shi, L.; Kang, J.; Chen, X. Organic Mechanochromic Luminescence-based Visualization of Fatigue Damage and Life Prediction of Aluminum to Steel Resistance Spot Welds. Fatigue Fract. Eng. Mat. Struct. 2023, 46, 3530–3542. [Google Scholar] [CrossRef]
- Zhang, Z.; Wei, X.; Zhang, L.; Li, B. Visualization and Depth Estimation of Inner Crack in High-Pressure Equipment Based on Organic Mechanochromic Luminescent Materials. Adv. Mater. Inter. 2023, 10, 2300330. [Google Scholar] [CrossRef]
- Vasco-Olmo, J.M.; James, M.N.; Christopher, C.J.; Patterson, E.A.; Díaz, F.A. Assessment of Crack Tip Plastic Zone Size and Shape and Its Influence on Crack Tip Shielding. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 969–981. [Google Scholar] [CrossRef]
- Fang, Y.; Zhong, B. Cell Segmentation in Fluorescence Microscopy Images Based on Multi-Scale Histogram Thresholding. MBE 2023, 20, 16259–16278. [Google Scholar] [CrossRef]
- Kumari, C.; Mustafi, A. A Novel Radial Kernel Watershed Basis Segmentation Algorithm for Color Image Segmentation. Wirel. Pers. Commun. 2023, 133, 2105–2124. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, W.; Liu, W.; Yuan, N. Extended-Maxima Transform Watershed Segmentation Algorithm for Touching Corn Kernels. Adv. Mech. Eng. 2013, 2013, 1086–1101. [Google Scholar] [CrossRef]
- Luo, X.; Wang, L.-H.; Lü, L.; Cao, S.-F.; Dong, X.-C.; Zhao, J.-G. Forward Model of Metal Magnetic Memory Testing Based on Equivalent Surface Magnetic Charge Theory. Acta Phys. Sin. 2022, 71, 154101. [Google Scholar] [CrossRef]
- Wu, L.; Yao, K.; Shi, P.; Zhao, B.; Wang, Y.-S. Influence of Inhomogeneous Stress on Biaxial 3D Magnetic Flux Leakage Signals. NDT E Int. 2020, 109, 102178. [Google Scholar] [CrossRef]
- Sangeetha, D.; Deepa, P. FPGA Implementation of Cost-Effective Robust Canny Edge Detection Algorithm. J. Real-Time Image Process. 2019, 16, 957–970. [Google Scholar] [CrossRef]
- Song, R.; Zhang, Z.; Liu, H. Edge Connection Based Canny Edge Detection Algorithm. Pattern Recognit. Image Anal. 2017, 27, 740–747. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man. Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Wang, D.-Q.; Zhu, M.-L.; Xuan, F.-Z.; Tong, J. Crack Tip Strain Evolution and Crack Closure during Overload of a Growing Fatigue Crack. Frat. Integrita Strutt. 2017, 11, 143–148. [Google Scholar] [CrossRef]
- Chen, R.; Hu, X.-K.; Zhu, M.-L.; Xuan, F.-Z. In-Situ Observation of Strain Evolution and Ratchetting of Growing Fatigue Cracks. Eng. Fract. Mech. 2023, 279, 109041. [Google Scholar] [CrossRef]






| Characteristic Value | Area (mm2) | Average Fluorescence Intensity |
|---|---|---|
| Maximum equivalent strain (%) | 0.648 ** | 0.415 ** |
| Plastic zone size (mm) | 0.587 ** | 0.390 ** |
| Characteristic Value | Mean | Std. Dev. | Smoothness | Uniformity | Entropy | Skewness |
|---|---|---|---|---|---|---|
| Maximum equivalent strain (%) | 0.668 ** | 0.687 ** | −0.687 ** | −0.524 ** | −0.285 ** | 0.658 ** |
| Plastic zone size (mm) | 0.646 ** | 0.638 ** | −0.638 ** | −0.522 ** | −0.283 ** | 0.603 ** |
| Characteristic Value | Contrast | Dissimilarity | Homogeneity | ASM | Energy | Correlation |
|---|---|---|---|---|---|---|
| Maximum equivalent strain (%) | 0.634 ** | 0.613 ** | −0.550 ** | −0.464 ** | −0.464 ** | 0.637 ** |
| Plastic zone size (mm) | 0.605 ** | 0.603 ** | −0.549 ** | −0.467 ** | −0.467 ** | 0.569 ** |
| Plastic Zone Parameter | R2 | MAE | MSE | RMSE |
|---|---|---|---|---|
| εe 1 from MLR (%) | 0.91568 | 0.00227 | 8.01924 × 10−6 | 0.00283 |
| r 2 from MLR (mm) | 0.86262 | 0.04986 | 0.00512 | 0.07158 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, Y.; Ren, Y.; Zhang, Z. Determination of Crack Tip Plastic Zone Using Dynamically Visible Mechanochromic Luminescence Response. Materials 2025, 18, 1810. https://doi.org/10.3390/ma18081810
Tong Y, Ren Y, Zhang Z. Determination of Crack Tip Plastic Zone Using Dynamically Visible Mechanochromic Luminescence Response. Materials. 2025; 18(8):1810. https://doi.org/10.3390/ma18081810
Chicago/Turabian StyleTong, Yuhan, Yonggang Ren, and Zhe Zhang. 2025. "Determination of Crack Tip Plastic Zone Using Dynamically Visible Mechanochromic Luminescence Response" Materials 18, no. 8: 1810. https://doi.org/10.3390/ma18081810
APA StyleTong, Y., Ren, Y., & Zhang, Z. (2025). Determination of Crack Tip Plastic Zone Using Dynamically Visible Mechanochromic Luminescence Response. Materials, 18(8), 1810. https://doi.org/10.3390/ma18081810








