Structural and Magnetic Characterization of Mechanically Alloyed (Fe2O3)1−x(Al2O3)x Solid Solutions via Pulsed Neutron Powder Diffraction
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
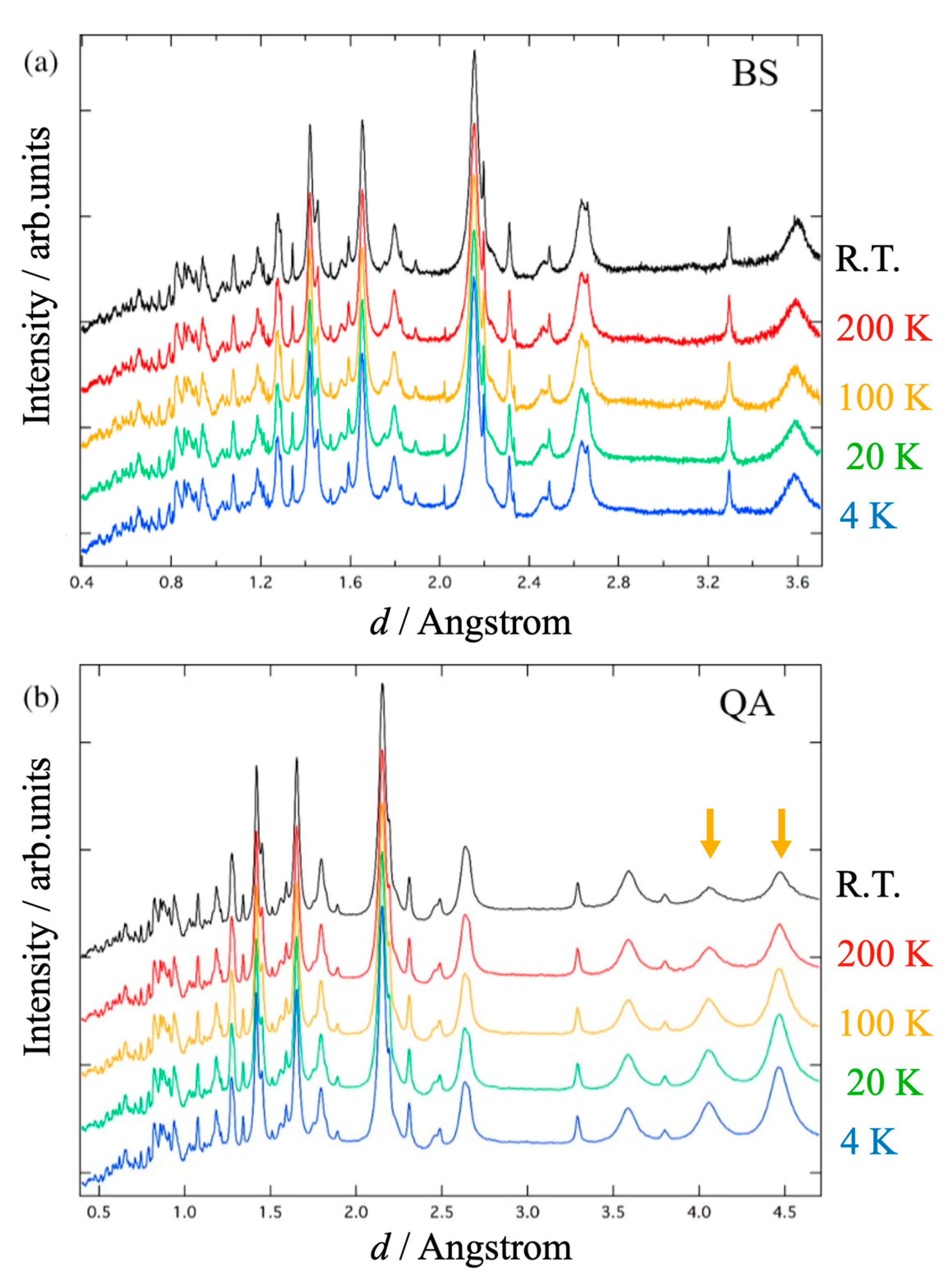
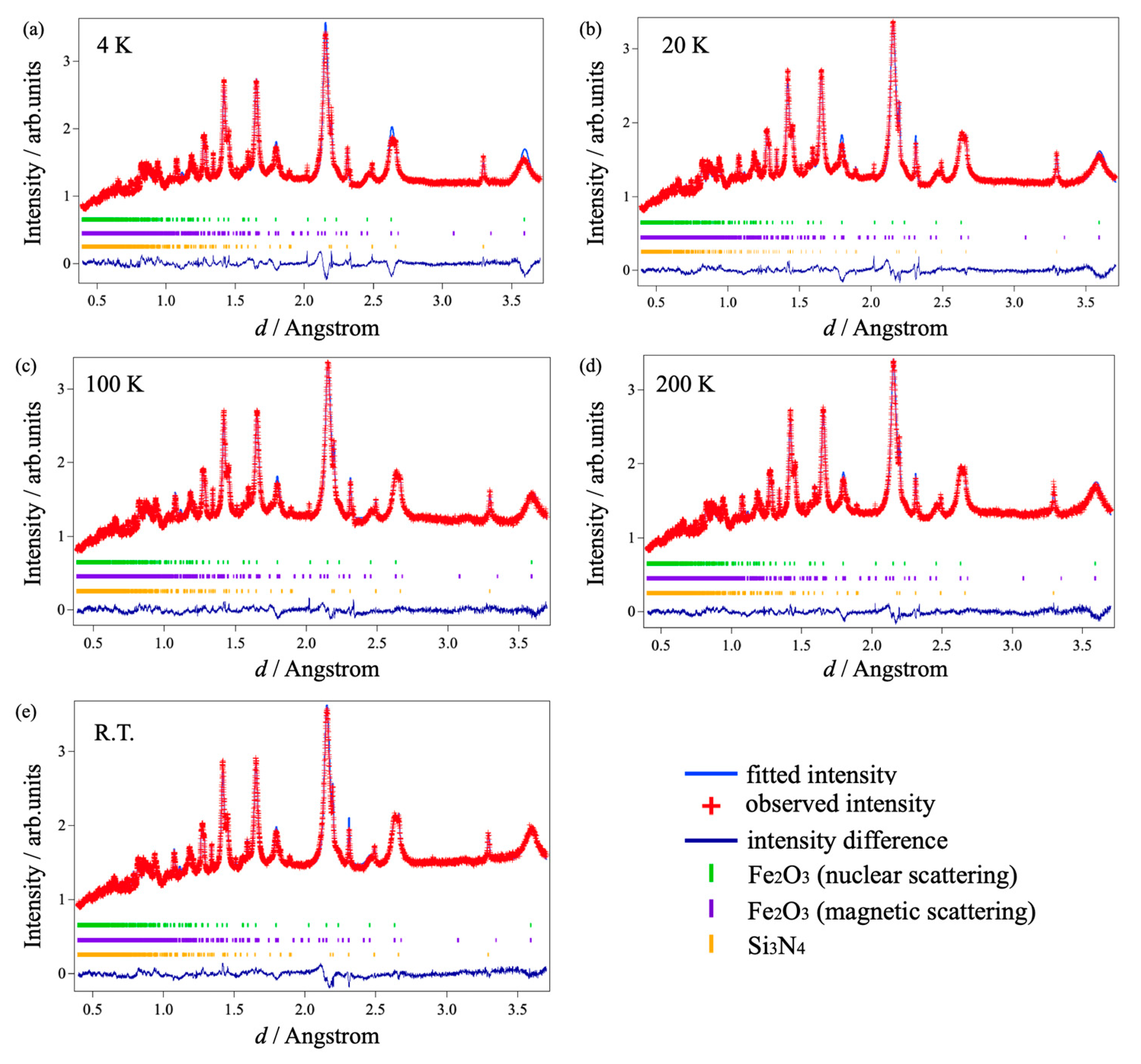
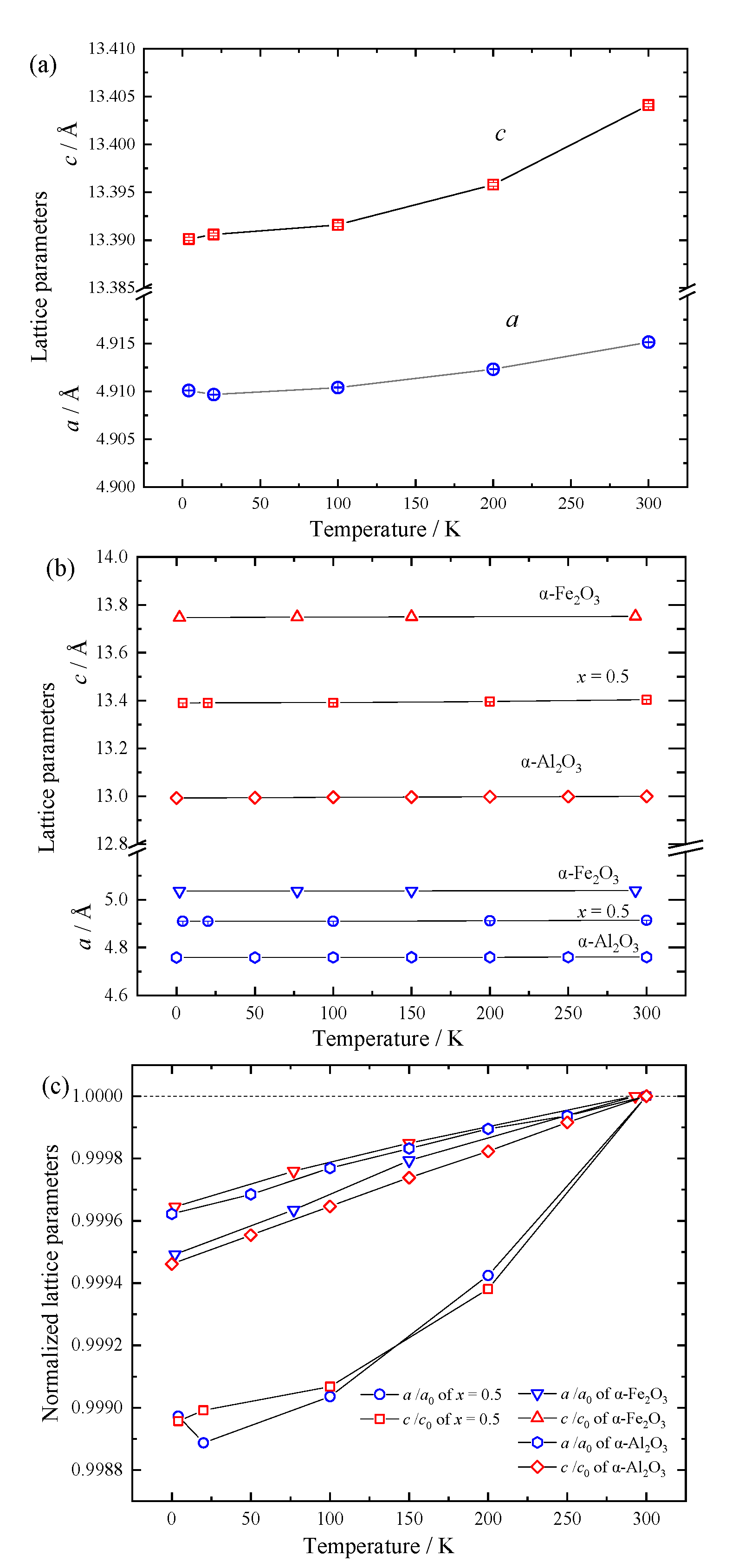
3.1. Temperature Dependences of the Structure of (Fe2O3)0.5(Al2O3)0.5
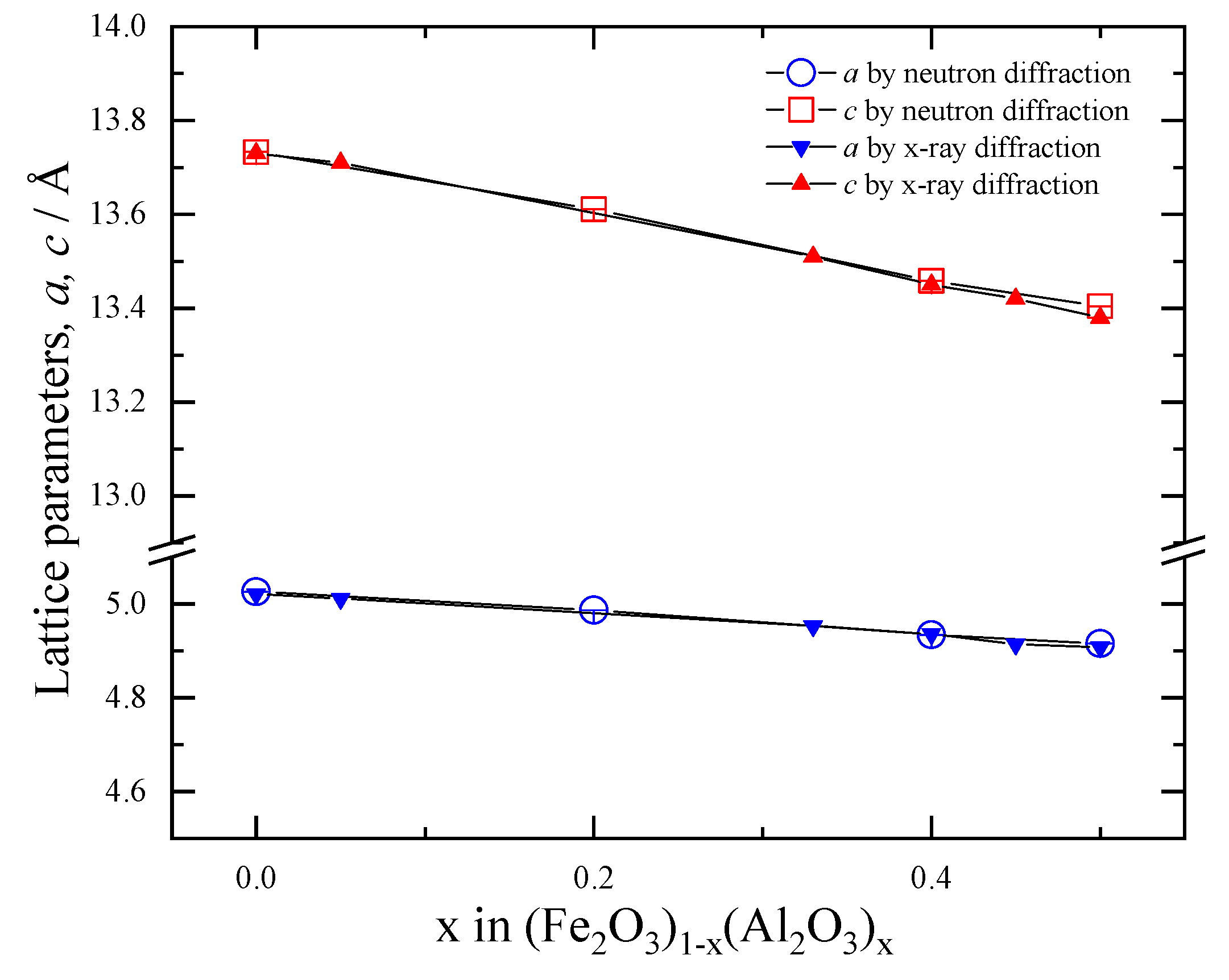
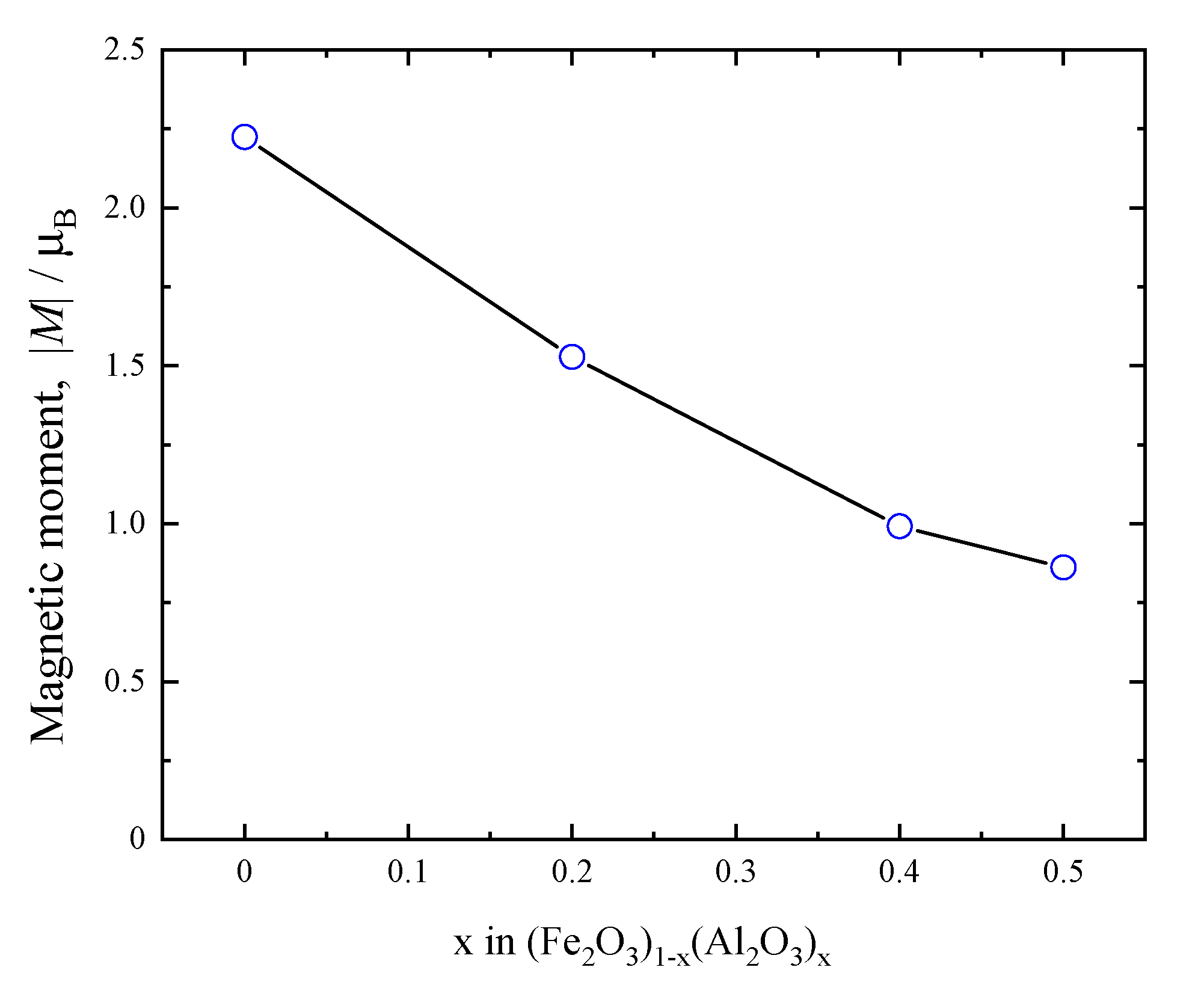
3.2. Compositional Dependence of the Structure of (Fe2O3)1−x(Al2O3)x
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Scrosati, B.; Hassoun, J.; Sun, Y.-K. Lithium-ion batteries. A look into the future. Energy Environ. Sci. 2011, 4, 3287. [Google Scholar] [CrossRef]
- Reddy, M.V.; Yu, T.; Sow, C.H.; Shen, Z.X.; Lim, C.T.; Rao, G.V.S.; Chowdari, B.V.R. α-Fe2O3 nanoflakes as an anode material for Li-ion batteries. Adv. Funct. Mater. 2007, 17, 2792–2799. [Google Scholar] [CrossRef]
- Roy, P.; Srivastava, S.K. Nanostructured anode materials for lithium-ion batteries. J. Mater. Chem. A 2014, 3, 2454–2484. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, D.; Li, Y.; Yuan, T.; Bahlawane, N.; Liang, C.; Sun, W.; Lu, Y.; Yan, M. Amorphous Fe2O3 as a high-capacity, high-rate and long-life anode material for lithium-ion batteries. Nano Energy 2013, 4, 23–30. [Google Scholar] [CrossRef]
- Wu, N.; Shi, Y.R.; Ma, C.; Zhang, X.; Zhou, J.-M.; Wei, Y.; Liu, H.; Yan, Y.; Liu, H.-T. High performance nano-α-Fe2O3 electrode materials synthesized by facile and green approaches for lithium-ion batteries. Mater. Lett. 2018, 238, 155–158. [Google Scholar] [CrossRef]
- Muan, A. On the stability of the phase Fe2O3–Al2O3. Am. J. Sci. 1958, 256, 413–422. [Google Scholar] [CrossRef]
- Muan, A.; Gee, C.L. Phase equilibrium studies in the system iron Fe2O3–Al2O3 in air and at 1 atm. O2 pressure. J. Am. Ceram. Soc. 1956, 39, 207–214. [Google Scholar] [CrossRef]
- Popović, S.; Ristić, M.; Musić, S. Formation of solid solutions in the system Fe2O3–Al2O3. Mater. Lett. 1995, 23, 139–142. [Google Scholar] [CrossRef]
- Polli, A.D.; Lange, F.F.; Levi, C.G.; Mayer, J. Crystallization Behavior and Microstructure Evolution of (Al, Fe)2O3 Synthesized from Liquid Precursors. J. Am. Ceram. Soc. 1996, 79, 1745–1755. [Google Scholar] [CrossRef]
- Jiang, J.Z.; Mørup, S.; Linderoth, S. Formation of 25 Mol % Fe2O3–Al2O3 Solid Solution by High-Energy Ball Milling. Mater. Sci. Forum 1996, 225–227, 489–496. [Google Scholar] [CrossRef]
- Mahmoud, M.H.; Taha, T.A. FTIR and Mössbauer Spectroscopy investigations of Ag/FexAl2−xO3 nanocomposites. J. Electron. Mater. 2019, 48, 7396–7403. [Google Scholar] [CrossRef]
- Takai, S.; Sawada, E.; Harada, J.; Park, S.; Oda, M.; Esaki, S.; Nishijima, M.; Yoshie, T.; Yabutsuka, T.; Yao, T. Synthesis and anode properties of corundum-type structured (Fe2O3)1–x (Al2O3)x solid solutions in the whole compositional range. Solid State Ionics 2017, 313, 1–6. [Google Scholar] [CrossRef]
- Hubbard, C.R.; McCarthy, G.J. JCPDS-International Centre for Diffraction Data. Acta Crystallogr. Sect. A 1981, 37, C344. [Google Scholar] [CrossRef]
- Nakaishi, H.; Yabutsuka, T.; Yao, T.; Kitao, S.; Seto, M.; Chen, W.-J.; Shimonishi, Y.; Yoshida, S.; Takai, S. Homogeneous solid-solution formation in Fe2O3–Al2O3 system observed by TEM, XAFS, and Mössbauer spectroscopy. Mater. Chem. Phys. 2023, 303, 127764. [Google Scholar] [CrossRef]
- Luo, D.; Yabutsuka, T.; Yao, T.; Kitani, S.; Kawaji, H.; Takai, S. Low-temperature heat-capacities of corundum-type structured (Fe2O3)1–x (Al2O3)x solid solutions with x = 0.25, 0.50 and 0.75. J. Therm. Anal. Calorim. 2024. [Google Scholar] [CrossRef]
- Chase, M.W., Jr. JANAF Thermodynamical tables. J. Phy. Chem. Ref. Data 1985, 14. [Google Scholar] [CrossRef]
- Adachi, K.; Sato, K.; Matsui, M.; Mitani, S. Neutron diffraction investigations of (CoMn)1−xFex. J. Phys. Soc. Jpn. 1973, 35, 426–433. [Google Scholar] [CrossRef]
- Andersson, M.; Rapp, Ö.; Tellgren, R. Neutron diffraction studies of interatomic distances in the Y1−2xCaxThxBa2Cu3O7−α System. Solid State Commun. 1992, 81, 425–429. [Google Scholar] [CrossRef]
- Harrison, R.J. Neutron diffraction of magnetic materials. Rev. Mineral Geochem. 2006, 63, 113–143. [Google Scholar] [CrossRef]
- Yonemura, M.; Mori, K.; Kamiyama, T.; Fukunaga, T.; Torii, S.; Nagao, M.; Ishikawa, Y.; Onodera, Y.; Adipranoto, D.S.; Arai, H.; et al. Development of SPICA, new dedicated neutron powder diffractometer for battery studies. J. Phys. Conf. Ser. 2014, 502, 012053. [Google Scholar] [CrossRef]
- Oishi, R.; Yonemura, M.; Nishimaki, Y.; Torii, S.; Hoshikawa, A.; Ishigaki, T.; Morishima, T.; Mori, K.; Kamiyama, T. Rietveld analysis software for J-PARC. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2008, 600, 94–96. [Google Scholar] [CrossRef]
- Shull, C.G.; Strauser, W.A.; Wollan, E.O. Neutron diffraction by paramagnetic and antiferromagnetic substances. Phys. Rev. 1951, 83, 333–345. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Kraushofer, F.; Jakub, Z.; Bichler, M.; Hulva, J.; Drmota, P.; Weinold, M.; Schmid, M.; Setvin, M.; Diebold, U.; Blaha, P.; et al. Atomic-Scale structure of the hematite α-Fe2O3(11̅02) “R-CUT” surface. J. Phys. Chem. C 2017, 122, 1657–1669. [Google Scholar] [CrossRef] [PubMed]
- Lucht, M.; Lerche, M.; Wille, H.-c.; Shvyd’ko, Y.V.; Rüter, H.D.; Gerdau, E.; Becker, P. Precise measurement of the lattice parameters of α-Al2O3 in the temperature range 4.5–250 K using the Mössbauer wavelength standard. J. Appl. Crystallogr. 2003, 36, 1075–1081. [Google Scholar] [CrossRef]
- Tsyshevsky, R.; Zverev, A.; Mitrofanov, A.; Rashkeev, S.; Kuklja, M. Photochemistry of the α-Al2O3-PETN interface. Molecules 2016, 21, 289. [Google Scholar] [CrossRef]
- Ruffa, A.R. Temperature dependence of the elastic shear moduli of the cubic metals. Phys. Rev. B Solid State 1977, 16, 2504–2514. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Brown, I.D.; Shannon, R.D. Empirical bond-strength–bond-length curves for oxides. Acta Crystallogr. Sect. A 1973, 29, 266–282. [Google Scholar] [CrossRef]
- Gallego, S.V.; Perez-Mato, J.M.; Elcoro, L.; Tasci, E.S.; Hanson, R.M.; Momma, K.; Aroyo, M.I.; Madariaga, G. MAGNDATA: Towards a database of magnetic structures. I. The commensurate case. J. Appl. Crystallogr. 2016, 49, 1750–1776. [Google Scholar] [CrossRef]
- Sun, X.; Zheng, C.-M.; Zhang, F.-X.; Yang, Y.; Yu, A.-M.; Guan, N.-J. Size-Controlled Synthesis of Magnetite (Fe3O4) Nanoparticles Coated with Glucose and Gluconic Acid from a Single Fe(III) Precursor by a Sucrose Bifunctional Hydrothermal Method. J. Phys. Chem. C 2009, 113, 16002–16008. [Google Scholar] [CrossRef]
- Naik, R.; Kumar, A.N.; Shanbhag, V.; Nagaswarupa, H.P.; Boddula, R.; Al-Kahtani, A.A.; Kumar, K.D. Energy Storage, Sensors, Photocatalytic Applications of Green Synthesized ZnO: Fe3+ Nanomaterials. Chem. Phys. Impact. 2023, 7, 100387. [Google Scholar] [CrossRef]
- Issa, B.; Obaidat, I.; Albiss, B.; Haik, Y. Magnetic nanoparticles: Surface effects and properties related to biomedicine applications. Int. J. Mol. Sci. 2013, 14, 21266–21305. [Google Scholar] [CrossRef] [PubMed]
- Keshavarz, S.; Kvashnin, Y.O.; Rodrigues, D.C.M.; Pereiro, M.; Di Marco, I.; Autieri, C.; Nordström, L.; Solovyev, I.V.; Sanyal, B.; Eriksson, O. Publisher’s Note: Exchange interactions of CaMnO3 in the bulk and at the surface [Phys. Rev. B 95, 115120 (2017)]. Phys. Rev. B 2018, 97, 239901. [Google Scholar] [CrossRef]

| Temperature (K) | Atom | Site | g | x | y | z | Biso (Å2) |
|---|---|---|---|---|---|---|---|
| 4 | Fe/Al | 12c | 1 | 0 | 0 | 0.14729(2) | 0.810(1) |
| O | 18e | 1 | 0.31477(5) | 0 | 0.25 | 0.939(1) | |
| a = 4.91009(4) Å, c = 13.39012(17) Å, Rwp = 2.4458% | |||||||
| 20 | Fe/Al | 12c | 1 | 0 | 0 | 0.14620(2) | 0.772(3) |
| O | 18e | 1 | 0.30777(6) | 0 | 0.25 | 0.763(4) | |
| a = 4.90967(4) Å, c = 13.39059(16) Å, Rwp = 2.3661% | |||||||
| 100 | Fe/Al | 12c | 1 | 0 | 0 | 0.14731(3) | 0.830(4) |
| O | 18e | 1 | 0.31149(8) | 0 | 0.25 | 0.832(4) | |
| a = 4.91040(5) Å, c = 13.3916(2) Å, Rwp = 2.5226% | |||||||
| 200 | Fe/Al | 12c | 1 | 0 | 0 | 0.14667(2) | 0.776(4) |
| O | 18e | 1 | 0.30910(7) | 0 | 0.25 | 0.743(3) | |
| a = 4.91233(4) Å, c = 13.3960(2) Å, Rwp = 2.0989% | |||||||
| R.T. | Fe/Al | 12c | 1 | 0 | 0 | 0.14738(2) | 0.858(4) |
| O | 18e | 1 | 0.30858(6) | 0 | 0.25 | 0.745(3) | |
| a = 4.91514(3) Å, c = 13.4041(2) Å, Rwp = 2.4458% | |||||||
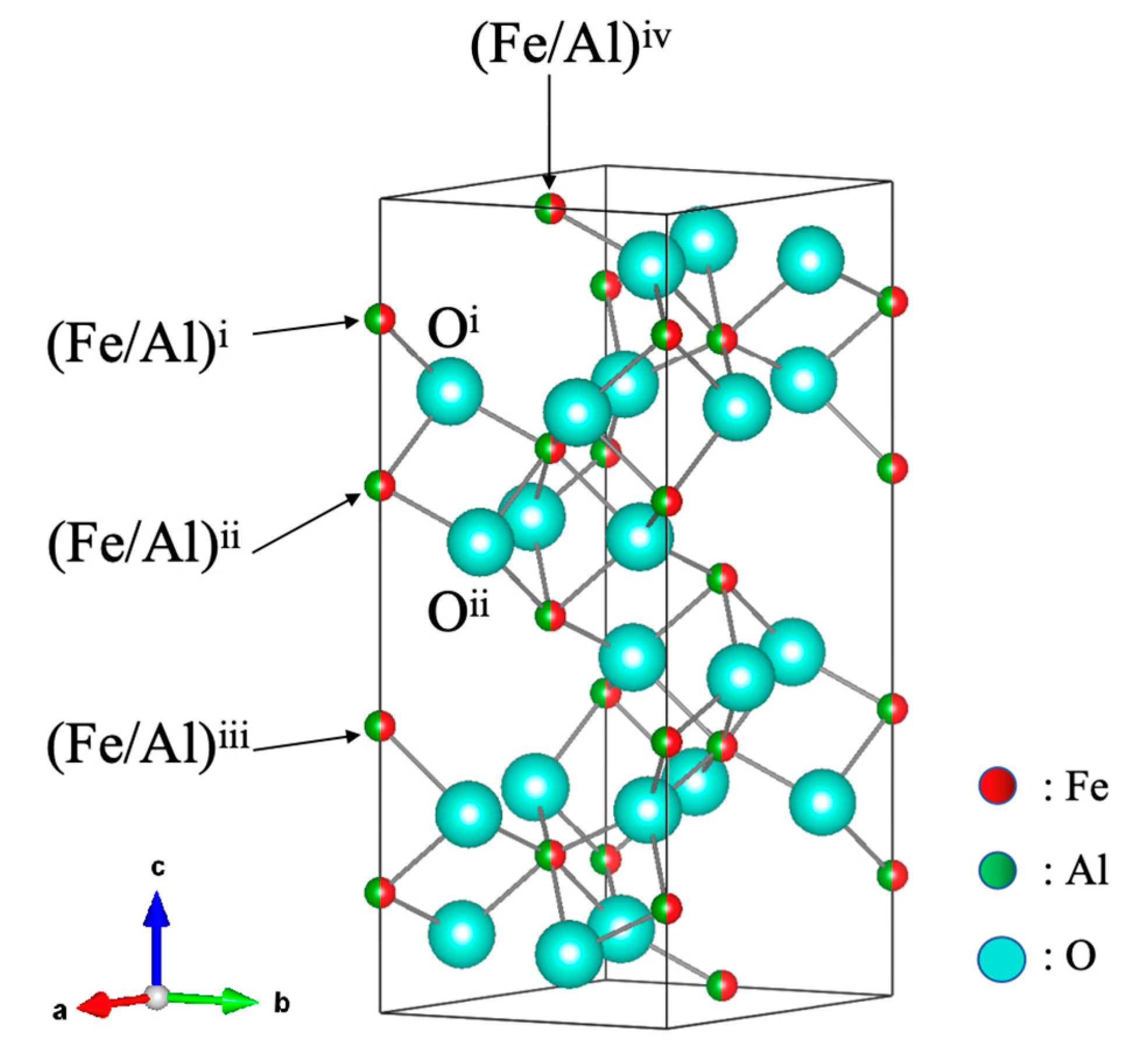
| Temperature (K) | (Fe/Al)i–Oi (Å) | (Fe/Al)ii–Oii (Å) | (Fe/Al)i–(Fe/Al)ii (Å) | (Fe/Al)ii–(Fe/Al)iii (Å) | (Fe/Al)i–(Fe/Al)iv (Å) |
|---|---|---|---|---|---|
| 4 | 2.0689(3) | 1.8894(2) | 2.7506(5) | 3.9445(5) | 3.3121(3) |
| 20 | 2.0531(3) | 1.8995(2) | 2.7800(5) | 3.9153(5) | 3.2969(3) |
| 100 | 2.0568(4) | 1.8974(3) | 2.7504(9) | 3.9454(9) | 3.3126(5) |
| 200 | 2.0533(3) | 1.9009(2) | 2.7687(6) | 3.9293(6) | 3.3049(3) |
| R.T. | 2.0476(3) | 1.9069(2) | 2.7511(6) | 3.9510(6) | 3.3168(3) |
| Temperature (K) | a (10−6 K−1) | c (10−6 K−1) | |
|---|---|---|---|
| (Fe2O3)0.5(Al2O3)0.5 | 4–100 | 0.66(2) | 1.15(3) |
| 200–300 | 5.76(2) | 6.19(5) | |
| α-Fe2O3 [24] | 2–77 | 1.90 | 1.53 |
| 150–293 | 1.44 | 1.05 | |
| α-Al2O3 [25,26] | 2–100 | 1.50 | 1.89 |
| 200–300 | 1.05 | 1.77 |
| Composition | Atom | Site | g | x | y | z | Biso (Å2) |
|---|---|---|---|---|---|---|---|
| x = 0 | Fe/Al | 12c | 1 | 0 | 0 | 0.145556(8) | 0.937(1) |
| O | 18e | 1 | 0.30992(4) | 0 | 0.25 | 0.610(2) | |
| a = b = 5.025556(17) Å, c = 13.73302(9) Å, Rwp = 3.6910% | |||||||
| x = 0.2 | Fe/Al | 12c | 1 | 0 | 0 | 0.14723(1) | 0.870(1) |
| O | 18e | 1 | 0.30862(4) | 0 | 0.25 | 0.636(2) | |
| a = b = 4.98646(2) Å, c = 13.61093(10) Å, Rwp = 2.6605% | |||||||
| x = 0.4 | Fe/Al | 12c | 1 | 0 | 0 | 0.146591(13) | 0.915(2) |
| O | 18e | 1 | 0.31000(5) | 0 | 0.25 | 0.774(3) | |
| a = b = 4.93405(3) Å, c = 13.45815(14) Å, Rwp = 2.0553% | |||||||
| x = 0.5 | Fe/Al | 12c | 1 | 0 | 0 | 0.14738(2) | 0.858(4) |
| O | 18e | 1 | 0.30858(6) | 0 | 0.25 | 0.745(3) | |
| a = b = 4.91514(3) Å, c = 13.4041(2) Å, Rwp = 2.4458% | |||||||
| x-Value | (Fe/Al)i–Oi (Å) | (Fe/Al)ii–Oii (Å) | (Fe/Al)i–(Fe/Al)ii (Å) | (Fe/Al)ii–(Fe/Al)iii (Å) | (Fe/Al)i–(Fe/Al)iv (Å) |
|---|---|---|---|---|---|
| 0 | 2.1174(2) | 1.9358(1) | 2.8687(3) | 3.9978(3) | 3.3674(1) |
| 0.2 | 2.0942(2) | 1.9240(1) | 2.8163(3) | 3.9891(3) | 3.3539(1) |
| 0.4 | 2.0679(3) | 1.9059(2) | 2.7834(4) | 3.9457(4) | 3.3187(2) |
| 0.5 | 2.0476(3) | 1.9069(2) | 2.7511(6) | 3.9510(6) | 3.3168(2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, D.; Nakaishi, H.; Yabutsuka, T.; Saito, T.; Kamiyama, T.; Hagihala, M.; Takai, S. Structural and Magnetic Characterization of Mechanically Alloyed (Fe2O3)1−x(Al2O3)x Solid Solutions via Pulsed Neutron Powder Diffraction. Materials 2025, 18, 1911. https://doi.org/10.3390/ma18091911
Luo D, Nakaishi H, Yabutsuka T, Saito T, Kamiyama T, Hagihala M, Takai S. Structural and Magnetic Characterization of Mechanically Alloyed (Fe2O3)1−x(Al2O3)x Solid Solutions via Pulsed Neutron Powder Diffraction. Materials. 2025; 18(9):1911. https://doi.org/10.3390/ma18091911
Chicago/Turabian StyleLuo, Dong, Hayato Nakaishi, Takeshi Yabutsuka, Takashi Saito, Takashi Kamiyama, Masato Hagihala, and Shigeomi Takai. 2025. "Structural and Magnetic Characterization of Mechanically Alloyed (Fe2O3)1−x(Al2O3)x Solid Solutions via Pulsed Neutron Powder Diffraction" Materials 18, no. 9: 1911. https://doi.org/10.3390/ma18091911
APA StyleLuo, D., Nakaishi, H., Yabutsuka, T., Saito, T., Kamiyama, T., Hagihala, M., & Takai, S. (2025). Structural and Magnetic Characterization of Mechanically Alloyed (Fe2O3)1−x(Al2O3)x Solid Solutions via Pulsed Neutron Powder Diffraction. Materials, 18(9), 1911. https://doi.org/10.3390/ma18091911






