Study on the High-Speed Penetration and Shear Failure Mechanism of Beach Sand
Abstract
1. Introduction
2. Calibration of Discrete Element Parameters
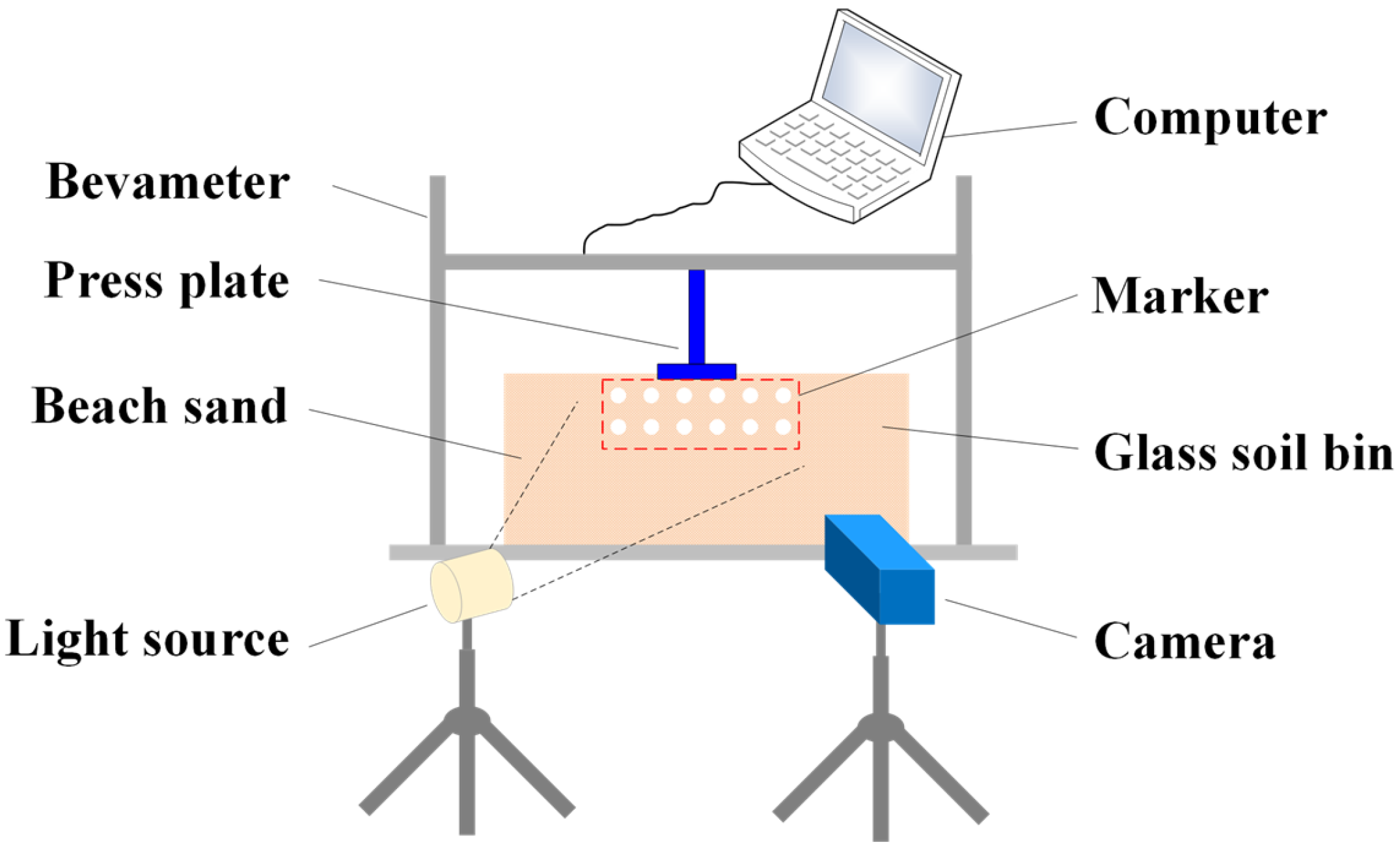
2.1. Physical Experiments of AoR
2.2. DEM Simulation Methodology
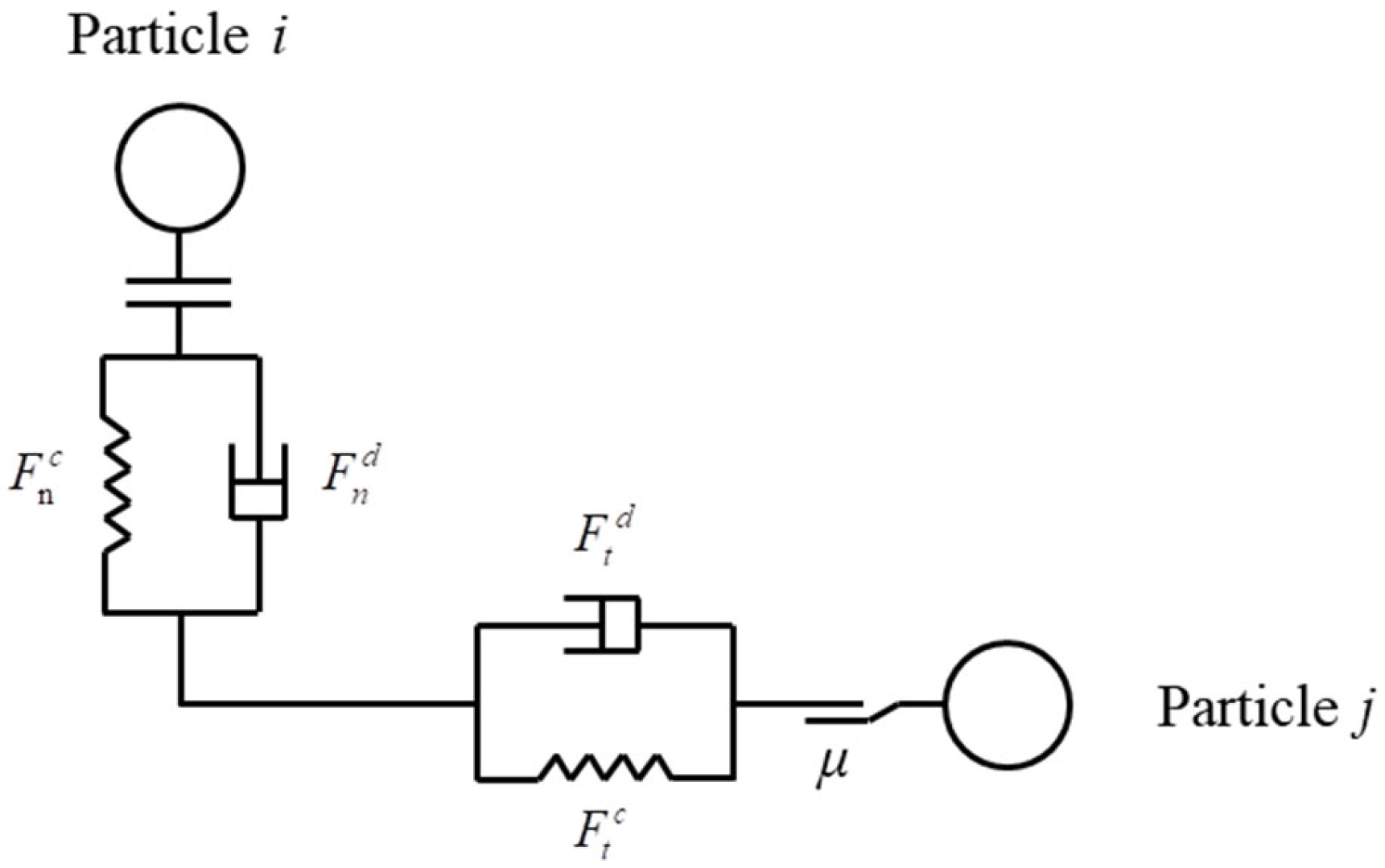
2.2.1. Selecting the Contact Model
2.2.2. DEM Simulation Setup of Bulk AoR
2.3. DEM Parameter Calibration of Beach Sand
2.3.1. PB Experiment
2.3.2. BB Experiment
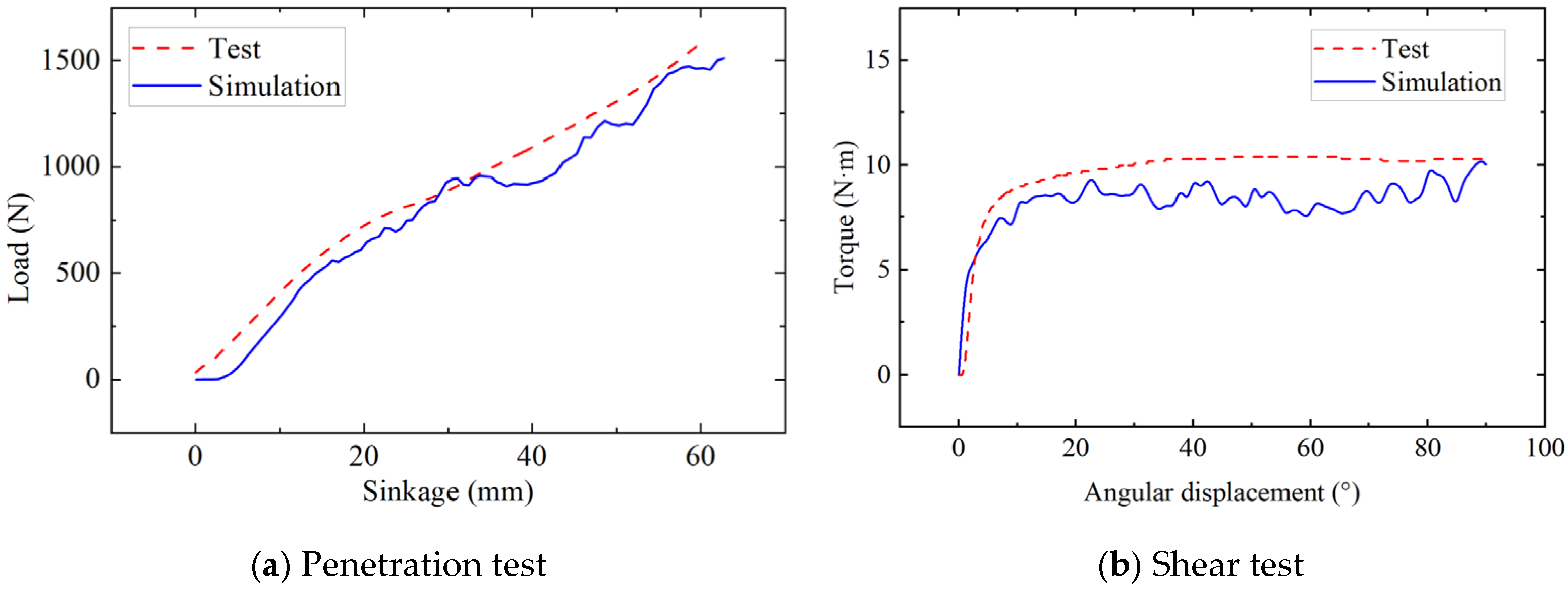
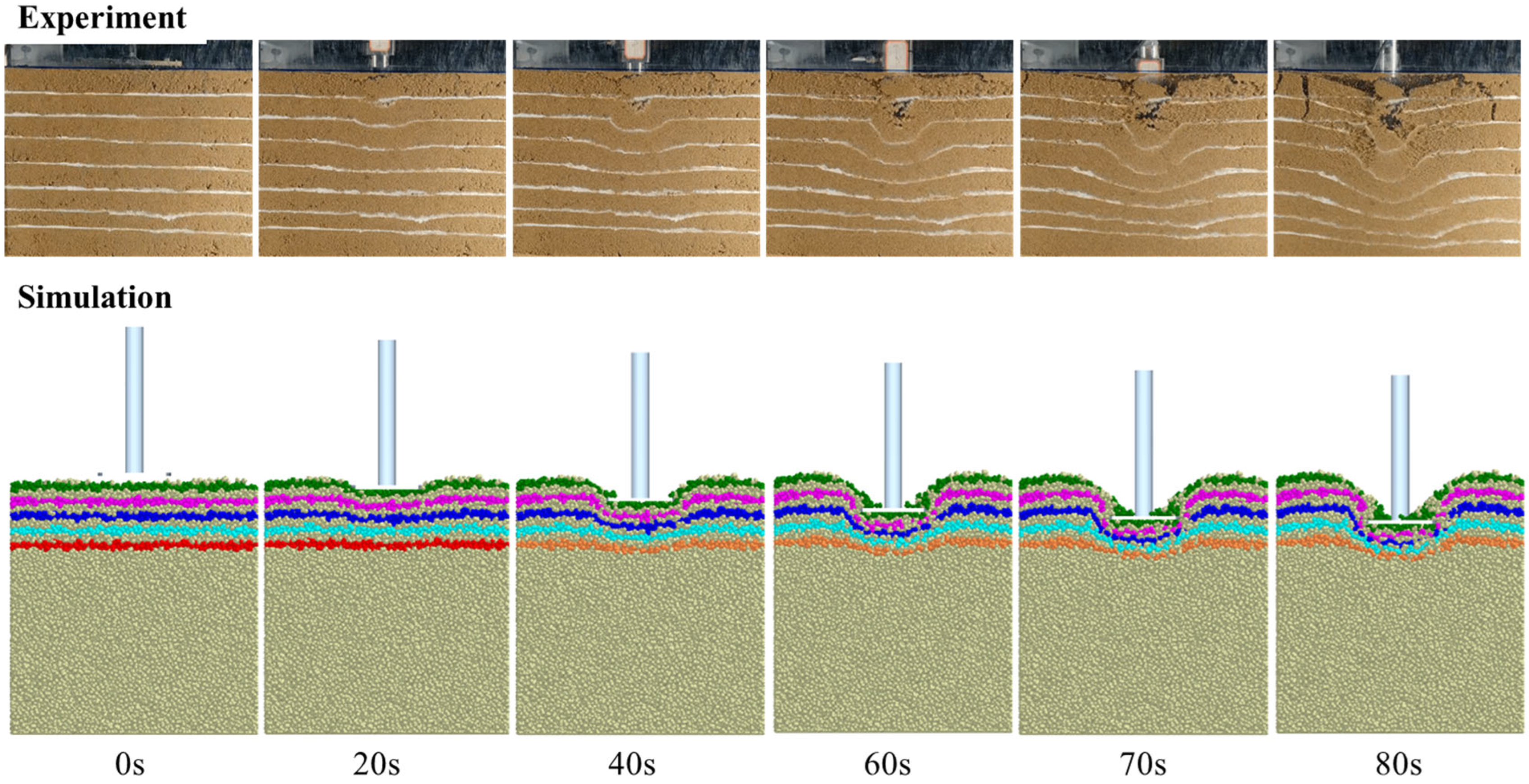
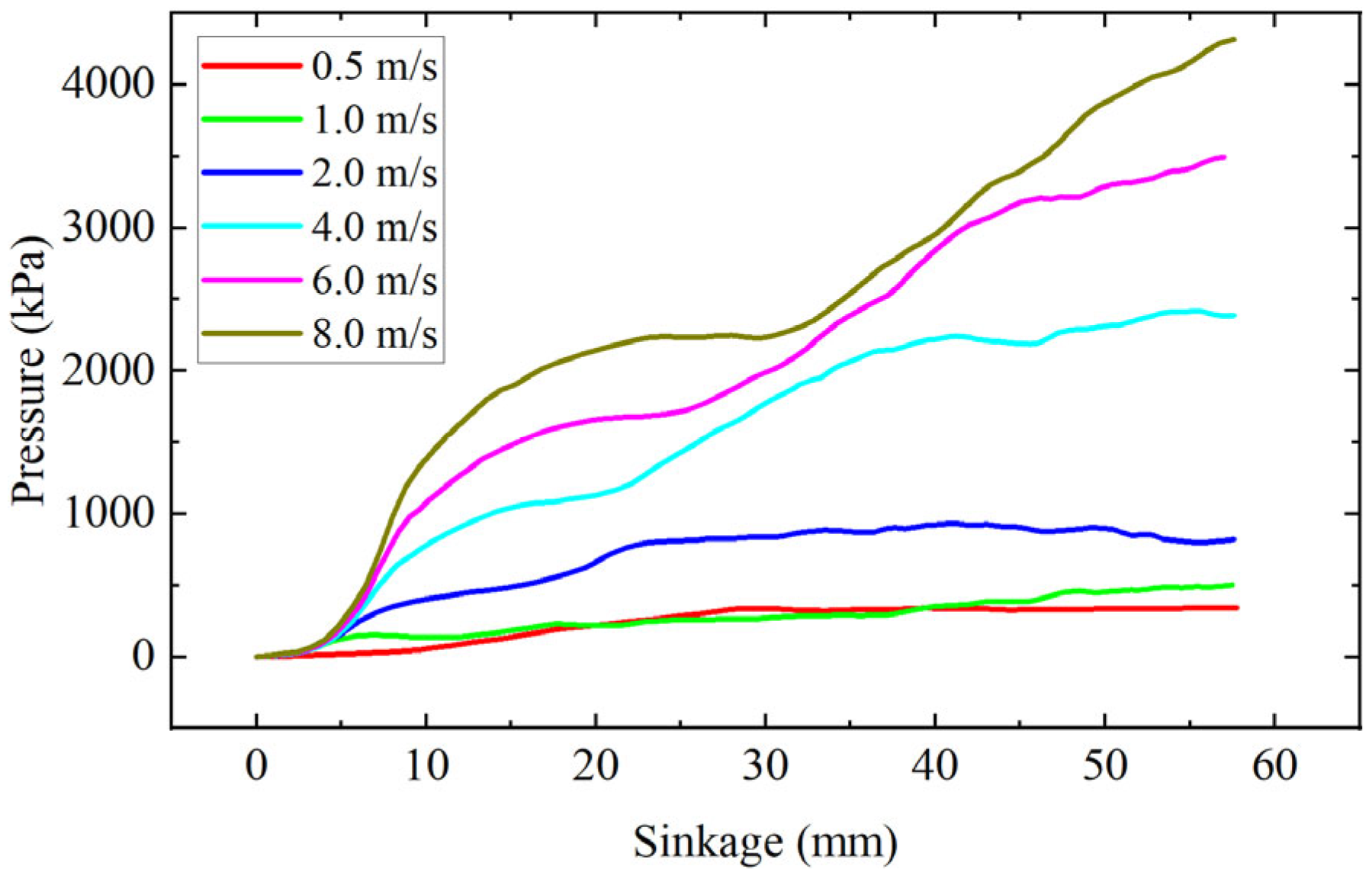
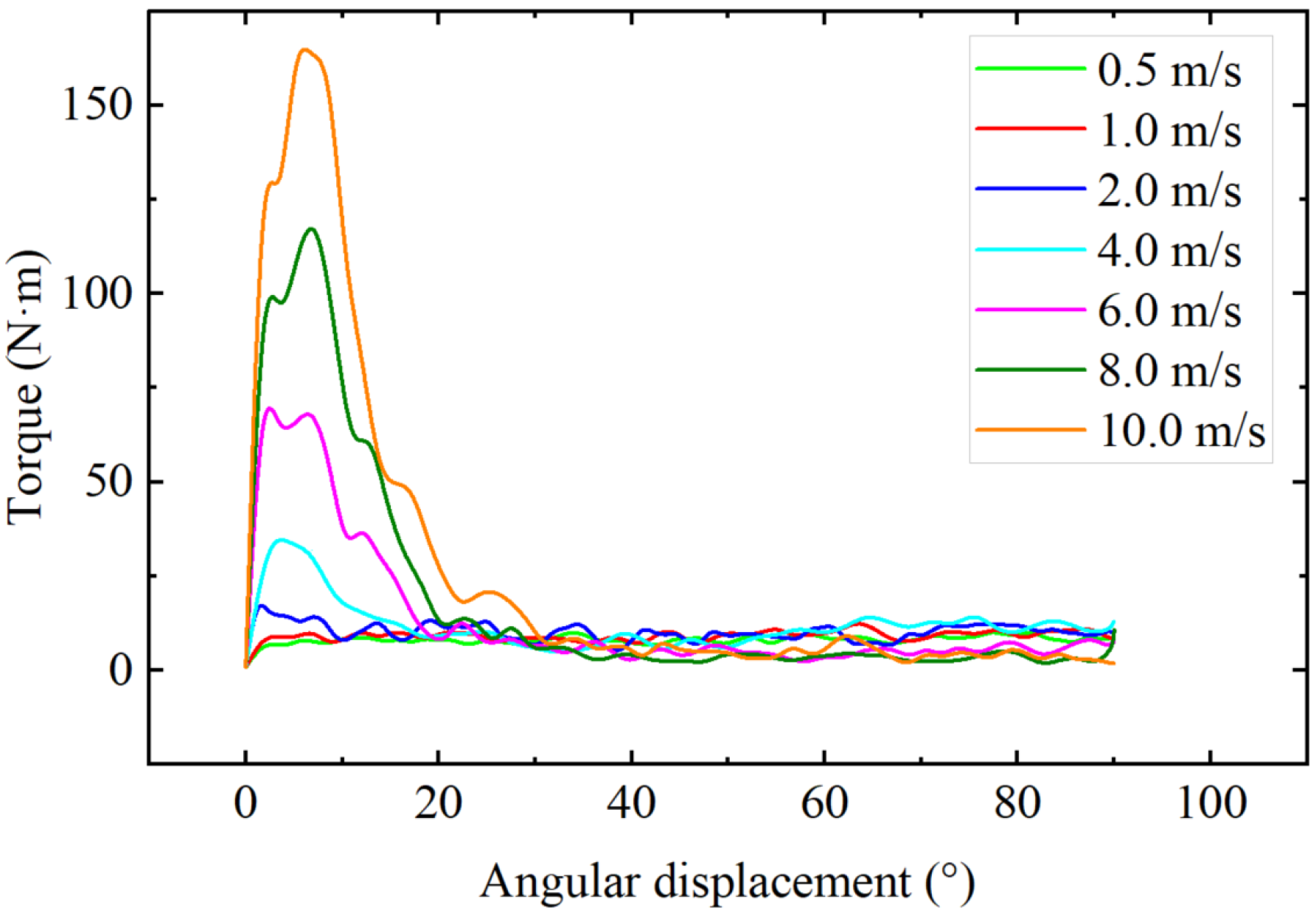
3. Failure Mechanism of High-Speed Pressure and Shear of Beach Sand
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, L.N.; Gao, J.W.; Li, Q.; Hu, C. Simulation study on tractive performance of off-road tire based on discrete element method. Math. Biosci. Eng. 2020, 17, 3869–3893. [Google Scholar] [CrossRef] [PubMed]
- Baek, S.-H.; Shin, G.-B.; Lee, S.-H.; Yoo, M.; Chung, C.-K. Evaluation of the Slip Sinkage and its Effect on the Compaction Resistance of an Off-Road Tracked Vehicle. Appl. Sci. 2020, 10, 3175. [Google Scholar] [CrossRef]
- Teji, M.D.; Zou, T.; Zeleke, D.S. A Survey of Off-Road Mobile Robots: Slippage Estimation, Robot Control, and Sensing Technology. J. Intell. Robot. Syst. 2023, 109, 38. [Google Scholar] [CrossRef]
- He, R.; Sandu, C.; Shenvi, M.N.; Mousavi, H.; Carrillo, J.; Osorio, J.E. Laboratory experimental study of tire tractive performance on soft soil: Towing mode, traction mode, and multi-pass effect. J. Terramech. 2021, 95, 33–58. [Google Scholar] [CrossRef]
- Wasfy, T.M.; Jayakumar, P. Next-generation NATO reference mobility model complex terramechanics—Part 2: Requirements and prototype. J. Terramech. 2021, 96, 59–79. [Google Scholar] [CrossRef]
- Wasfy, T.; Jayakumar, P. Next-generation NATO reference mobility model complex terramechanics–Part 1: Definition and literature review. J. Terramech. 2021, 96, 45–57. [Google Scholar] [CrossRef]
- Barbosa, B.W.; Pedron, F.D.; Müller, C.R.; Rodrigues, M.F.; Gubiani, P.I.; Schenato, R.B.; Dalmolin, R.S.D. Physical properties of a Brazilian sandy loam soil after the traffic of a military vehicle M113 BR. Rev. Bras. Cienc. Solo 2020, 44, e0190168. [Google Scholar] [CrossRef]
- Cundall, P.A. The Measurement and Analysis of Accelerations in Rock Slopes. Ph.D. Thesis, University of London, London, UK, 1971. [Google Scholar]
- Zhang, R.; Pang, H.; Dong, W.; Li, T.; Liu, F.; Zhang, H.; Hu, Z.; Li, J. Three-dimensional Discrete Element Method simulation system of the interaction between irregular structure wheel and lunar soil simulant. Adv. Eng. Softw. 2020, 148, 102873. [Google Scholar] [CrossRef]
- Wiberg, V.; Servin, M.; Nordfjell, T. Discrete element modelling of large soil deformations under heavy vehicles. J. Terramech. 2020, 93, 11–21. [Google Scholar] [CrossRef]
- Zhu, J.Z.; Zou, M.; Shen, Y.; Cao, H.T.; Chen, Z.; Qi, Y.C. 3D DEM-FEM simulation of the flexible metal wheel-soil interaction in low gravity environments. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 1267–1278. [Google Scholar] [CrossRef]
- Jelinek, B.; Card, A.; Mason, G.L.; Grebner, K.; Dickerson, A.; Skorupa, T.; Cole, M.; Priddy, J.D. Tractive performance of rigid wheel in granular media using coarse-scale DEM models. J. Terramech. 2025, 117, 101016. [Google Scholar] [CrossRef]
- Zeng, H.Y.; Lin, Z.F.; Huang, G.H.; Yang, X.Q.; Li, Y.F.; Su, J.B.; Xu, W. Parameter identification of DEM-FEM coupling model to simulate traction behavior of tire-soil interaction. J. Terramech. 2025, 117, 101012. [Google Scholar] [CrossRef]
- Thakur, S.C.; Ooi, J.Y.; Ahmadian, H. Scaling of discrete element model parameters for cohesionless and cohesive solid. Powder Technol. 2016, 293, 130–137. [Google Scholar] [CrossRef]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface Energy and the Contact of Elastic Solids. Proc. R. Soc. A 1971, 324, 301–313. [Google Scholar]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Three-dimensional discrete element modelling of tillage: Determination of a suitable contact model and parameters for a cohesionless soil. Biosyst. Eng. 2014, 121, 105–117. [Google Scholar] [CrossRef]
- Morrissey, J.P. Discrete Element Modelling of Iron Ore Pellets to Include the Effects of Moisture and Fines. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2013. [Google Scholar]
- Zeng, H.; Xu, W.; Zang, M.; Yang, P.J.P.T. Calibration of DEM-FEM model parameters for traction performance analysis of an off-road tire on gravel terrain. Powder Technol. 2020, 362, 350–361. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Yuan, J.M.; Shen, J.H.; Hu, Y.; Chen, S.L. A new DEM calibration method for wet and stick materials based on the BP neural network. Powder Technol. 2024, 448, 120228. [Google Scholar] [CrossRef]
- Zhang, S.; Tekeste, M.Z.; Li, Y.; Gaul, A.; Zhu, D.; Liao, J. Scaled-up rice grain modelling for DEM calibration and the validation of hopper flow. Biosyst. Eng. 2020, 194, 196–212. [Google Scholar] [CrossRef]
- Teng, Y.L.; Wu, X.L.; Yang, S.P.; Li, S.H.; Zhang, C.Q. Calibration and verification of DEM parameters for asphalt mixture based on experimental design method and bulk experiments. Part. Sci. Technol. 2025, 43, 327–337. [Google Scholar] [CrossRef]
- Kim, J.T.; Hwang, H.; Lee, H.S.; Park, Y.J. Development of DEM-ANN-based hybrid terramechanics model considering dynamic sinkage. J. Terramech. 2024, 116, 100989. [Google Scholar] [CrossRef]
- Karpman, E.; Kövecses, J.; Teichmann, M. Semi-empirical terramechanics modelling of rough terrain represented by a height field. J. Terramech. 2024, 115, 100975. [Google Scholar] [CrossRef]
- Chakravarthy, P.N.; Sharma, P.K. Terramechanics Models for Tracked Vehicle-Terrain Interaction Analysis: A Review. Def. Sci. J. 2024, 74, 469–481. [Google Scholar] [CrossRef]
- Wong, J.Y. Terramechanics and Off-Road Vehicle Engineering: Terrain Behaviour, Off-Road Vehicle Performance and Design; Butterworth-Heinemann: Oxford, UK, 2009. [Google Scholar]
- Massah, J.; Noorolahi, S. Design, development and performance evaluation of a tractor-mounted bevameter. Soil Tillage Res. 2010, 110, 161–166. [Google Scholar] [CrossRef]
- Tsuji, Y.; Tanaka, T.; Ishida, T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe. Powder Technol. 1992, 71, 239–250. [Google Scholar] [CrossRef]
- Raji, A.O. Discrete Element Modelling of the Deformation of Bulk Agricultural Particulates. Ph.D. Thesis, Newcastle University, Callaghan, NSW, Australia, 1999. [Google Scholar]
- Mindlin, R.D. Compliance of elastic bodies in contact. J. Appl. Mech. ASME 1949, 16, 259–268. [Google Scholar] [CrossRef]
- Tanaka, H.; Momozu, M.; Oida, A.; Yamazaki, M. Simulation of soil deformation and resistance at bar penetration by the distinct element method. J. Terramech. 2000, 37, 41–56. [Google Scholar] [CrossRef]
- Derakhshani, S.M.; Schott, D.L.; Lodewijks, G. Micro–macro properties of quartz sand: Experimental investigation and DEM simulation. Powder Technol. 2015, 269, 127–138. [Google Scholar] [CrossRef]
- Zheng, Q.; Kuwano, H. Young’s modulus and fatigue investigation of aluminum nitride films deposited on 304 stainless steel foils using micro-fabricated cantilevers. Sens. Actuators A Phys. 2019, 285, 173–181. [Google Scholar] [CrossRef]
- Bekker, M.G. Off-the-Road Locomotion; Research and Development in Terramechanics; Standford University: Stanford, CA, USA, 1960. [Google Scholar]
- Janosi, Z. The analytical determination of drawbar pull as a function of slip for tracked vehicles in defarmable soils. In Proceedings of the ISTVS 1st International Conference, Turin, Italy, 12–16 June 1961. [Google Scholar]
- Grahn, M. Prediction of sinkage and rolling resistance for off-the-road vehicles considering penetration velocity. J. Terramech. 1991, 28, 339–347. [Google Scholar] [CrossRef]




| Material | Young’s Modulus [Pa] | Poisson’s Ratio | Density | Reference |
|---|---|---|---|---|
| Beach sand | 5 × 107 | 0.3 | 2653 | [31] |
| Steel | 1.849 × 1011 | 0.3 | 7850 | [32] |
| Parameters | Symbol | Low Level (−1) | High Level (+1) |
|---|---|---|---|
| Poisson’s ratio of beach sand | ν | 0.25 | 0.35 |
| Young’s modulus of beach sand/MPa | E | 30 | 70 |
| Beach sand-beach sand coefficient of restitution | e1 | 0.3 | 0.7 |
| Beach sand-beach sand static friction coefficient | μ1 | 0.1 | 0.9 |
| Beach sand-beach sand dynamic friction coefficient | γ1 | 0.01 | 0.3 |
| Beach sand-steel coefficient of restitution | e2 | 0.3 | 0.7 |
| Beach sand-steel static friction coefficient | μ2 | 0.1 | 0.9 |
| Beach sand-steel dynamic friction coefficient | γ2 | 0.01 | 0.3 |
| No. | ν | E | e1 | μ1 | γ1 | e2 | μ2 | γ2 | AoR (°) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 (0.35) | −1 (30) | 1 | 1 (0.7) | 1 (0.9) | −1 | −1 (0.01) | −1 (0.3) | 1 | −1 (0.1) | 1 (0.3) | 29.8 |
| 2 | −1 (0.25) | 1 (70) | 1 | 1 | −1 (0.1) | −1 | −1 (0.3) | 1 (0.7) | −1 | 1 (0.9) | 1 | 27.2 |
| 3 | −1 | −1 | −1 | −1 (0.3) | −1 | −1 | −1 | −1 | −1 | −1 | −1 (0.01) | 20.1 |
| 4 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 35.3 |
| 5 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 21.3 |
| 6 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 59.3 |
| 7 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 22.2 |
| 8 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 33.2 |
| 9 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | 53.1 |
| 10 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | 49.3 |
| 11 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | 31.9 |
| 12 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | 35.8 |
| Parameters | Effect | Sum of Squares | Contribution/% | Significance |
|---|---|---|---|---|
| ν | −2.72 | 22.14 | 1.23 | 8 |
| E | 3.38 | 34.34 | 1.91 | 4 |
| e1 | −3.25 | 31.69 | 1.76 | 5 |
| μ1 | 17.78 | 948.74 | 52.78 | 1 |
| γ1 | 13.25 | 526.69 | 29.3 | 2 |
| e2 | 3.22 | 31.04 | 1.73 | 6 |
| μ2 | 4.48 | 60.3 | 3.35 | 3 |
| γ2 | 3.18 | 30.4 | 1.69 | 7 |
| Variables | Low Level | Middle Level | High Level |
|---|---|---|---|
| μ1 | 0.1 | 0.3 | 0.5 |
| γ1 | 0.01 | 0.08 | 0.15 |
| μ2 | 0.1 | 0.3 | 0.5 |
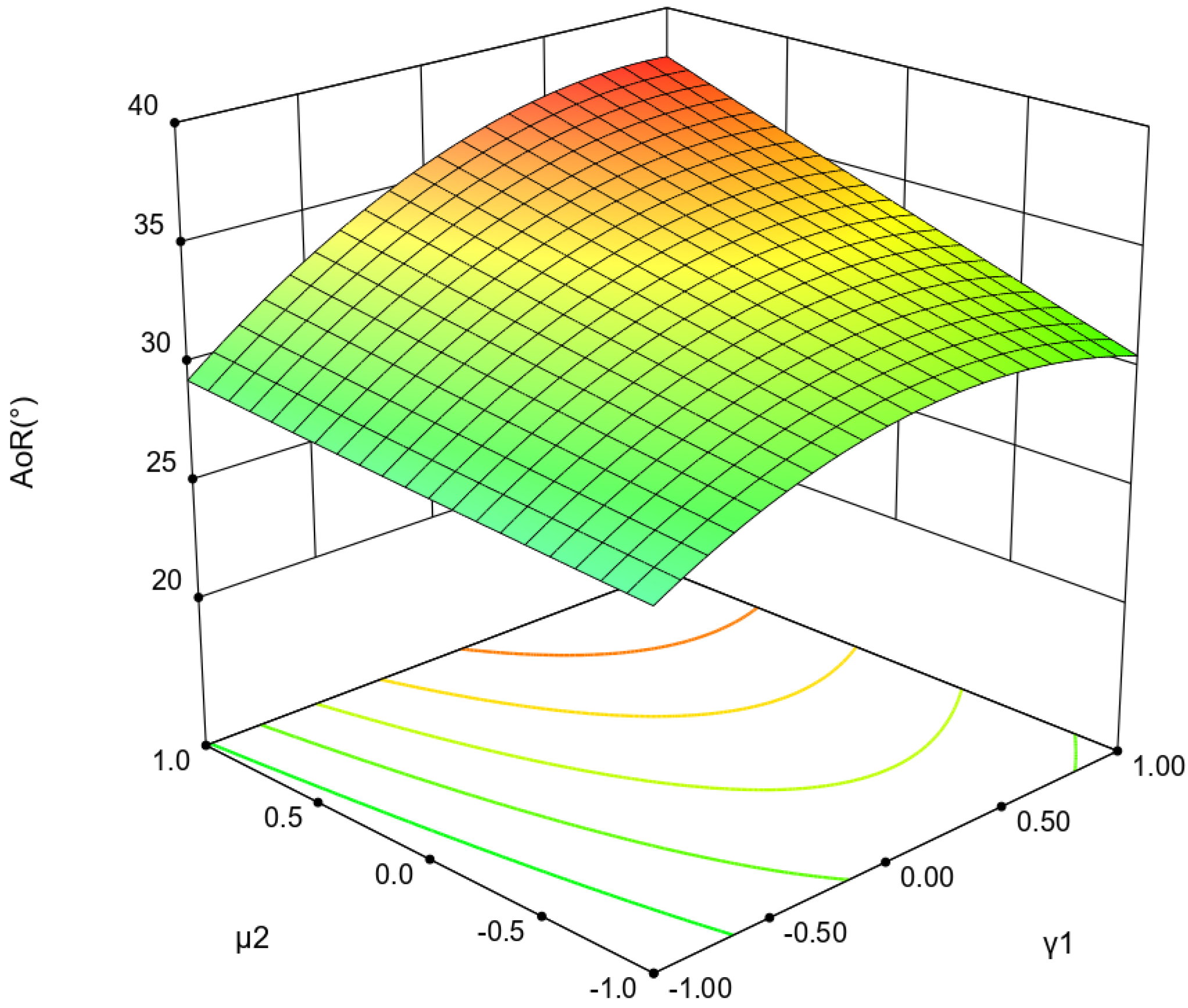
| No. | μ1 | γ1 | μ2 | AoR (°) |
|---|---|---|---|---|
| 1 | −1 (0.1) | 0 (0.08) | −1 (0.1) | 23.1 |
| 2 | 0 (0.3) | −1 (0.01) | 1 (0.5) | 28.5 |
| 3 | 0 | −1 | −1 | 27.5 |
| 4 | 1 (0.5) | 0 | −1 | 33.2 |
| 5 | −1 | 0 | 1 | 29.2 |
| 6 | 1 | 0 | 1 | 36.8 |
| 7 | 0 | 0 | 0 (0.3) | 33.0 |
| 8 | 1 | 1 (0.15) | 0 | 33.1 |
| 9 | −1 | −1 | 0 | 21.2 |
| 10 | 0 | 0 | 0 | 34.4 |
| 11 | 0 | 1 | −1 | 31.5 |
| 12 | 0 | 1 | 1 | 38.2 |
| 13 | 0 | 0 | 0 | 33.8 |
| 14 | 1 | −1 | 0 | 30.8 |
| 15 | −1 | 1 | 0 | 27.5 |
| Source | Sum of Squares | df | Mean Square | F Value | p-Value Prob > F | |
|---|---|---|---|---|---|---|
| Model | 304.66 | 9 | 33.85 | 30.67 | 0.0008 | significant |
| μ1 | 135.30 | 1 | 135.30 | 122.57 | 0.0001 | |
| γ1 | 62.16 | 1 | 62.16 | 56.31 | 0.0007 | |
| μ2 | 37.84 | 1 | 37.84 | 34.29 | 0.0021 | |
| μ1γ1 | 4.00 | 1 | 4.00 | 3.62 | 0.1153 | |
| μ1μ2 | 1.56 | 1 | 1.56 | 1.42 | 0.2876 | |
| γ1μ2 | 8.12 | 1 | 8.12 | 7.36 | 0.0421 | |
| μ12 | 38.20 | 1 | 38.20 | 34.61 | 0.0020 | |
| γ12 | 20.68 | 1 | 20.68 | 18.74 | 0.0075 | |
| μ22 | 0.0126 | 1 | 0.0126 | 0.0114 | 0.9192 | |
| Residual | 5.52 | 5 | 1.10 | |||
| Lack of Fit | 4.53 | 3 | 1.51 | 3.06 | 0.2558 | not significant |
| Pure Error | 0.9867 | 2 | 0.4933 | |||
| Cor Total | 310.18 | 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Li, J.; Kong, Y.; Dong, M.; Li, Y.; Zou, M. Study on the High-Speed Penetration and Shear Failure Mechanism of Beach Sand. Materials 2025, 18, 1922. https://doi.org/10.3390/ma18091922
Zhu J, Li J, Kong Y, Dong M, Li Y, Zou M. Study on the High-Speed Penetration and Shear Failure Mechanism of Beach Sand. Materials. 2025; 18(9):1922. https://doi.org/10.3390/ma18091922
Chicago/Turabian StyleZhu, Jianzhong, Jiangquan Li, Yun Kong, Mingming Dong, Yuqiong Li, and Meng Zou. 2025. "Study on the High-Speed Penetration and Shear Failure Mechanism of Beach Sand" Materials 18, no. 9: 1922. https://doi.org/10.3390/ma18091922
APA StyleZhu, J., Li, J., Kong, Y., Dong, M., Li, Y., & Zou, M. (2025). Study on the High-Speed Penetration and Shear Failure Mechanism of Beach Sand. Materials, 18(9), 1922. https://doi.org/10.3390/ma18091922







