Direct Thermal Method to Characterize the Material Efficiency of Electrocaloric Lead Scandium Tantalate Multilayer Ceramic Capacitors
Abstract
1. Introduction
2. Materials and Methods
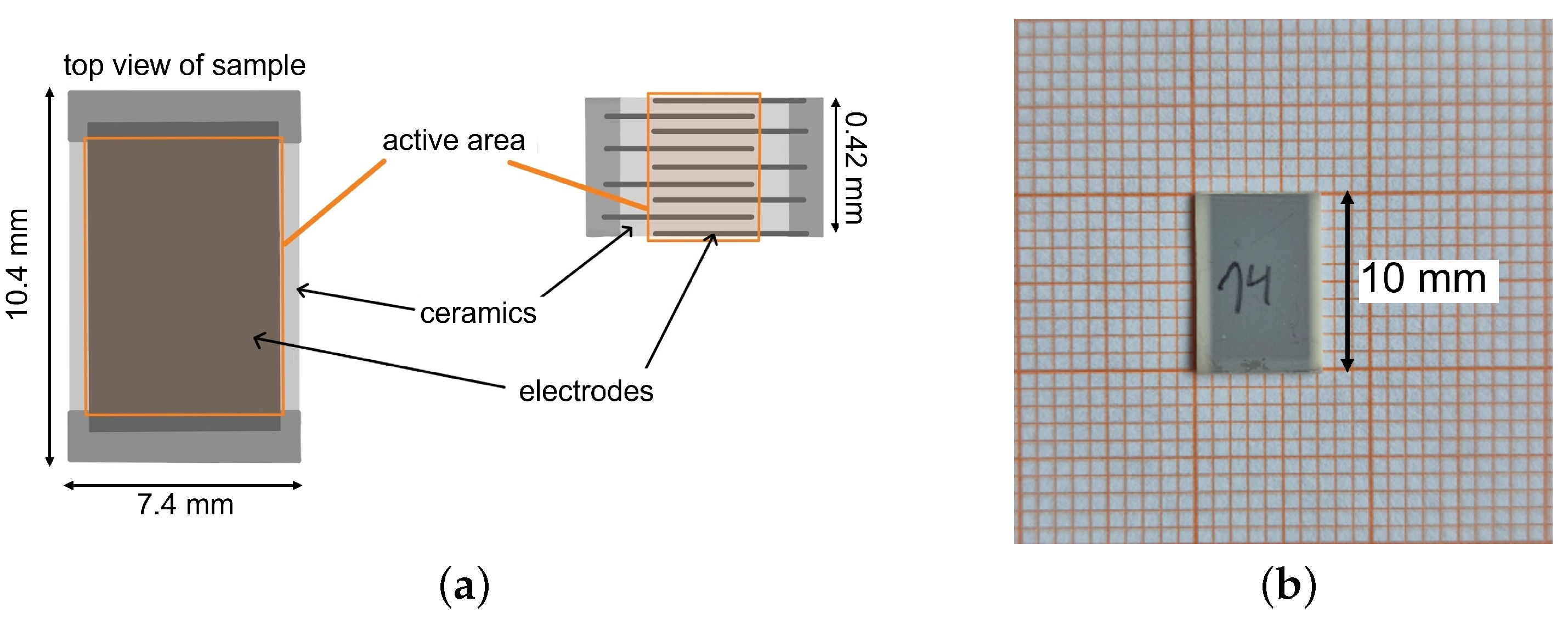
2.1. Lead Scandium Tantalate Samples
2.2. Measurement Set Up
2.3. Characterization Measurements and Error Propagation
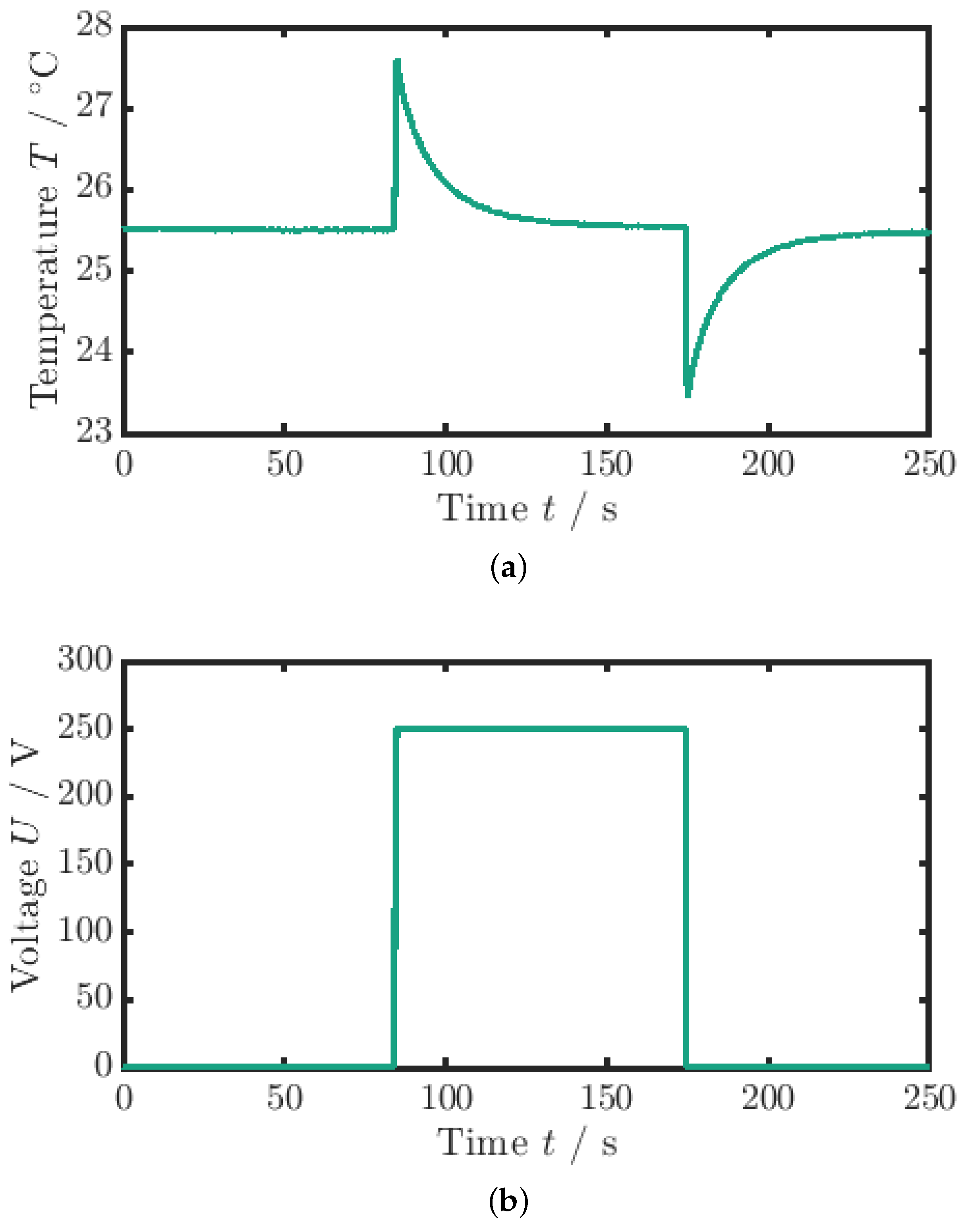
2.3.1. Adiabatic Temperature Change
2.3.2. Dissipative Heat
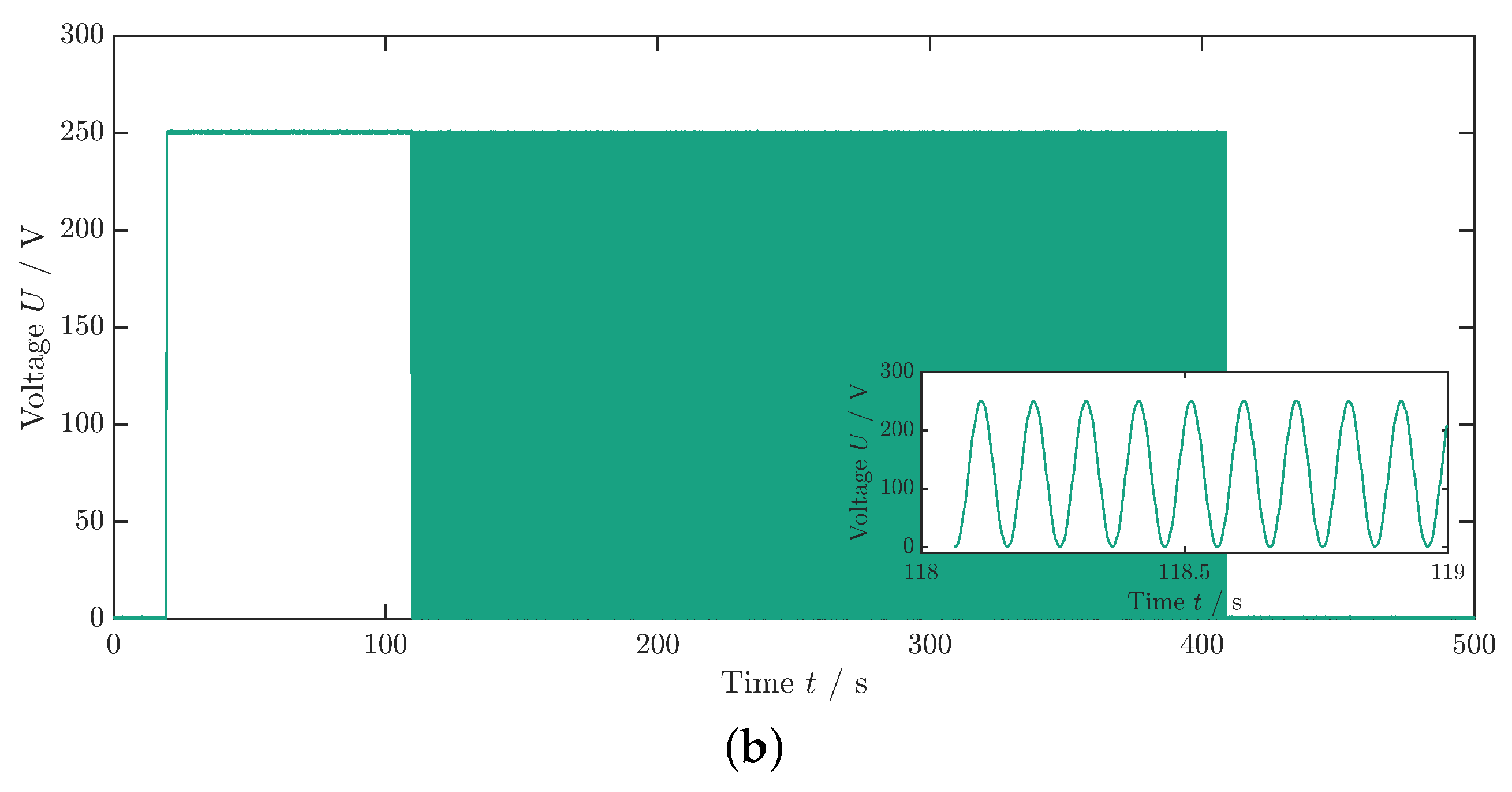
Dissipative Heat: Measurement Process
Dissipative Heat: Data Evaluation
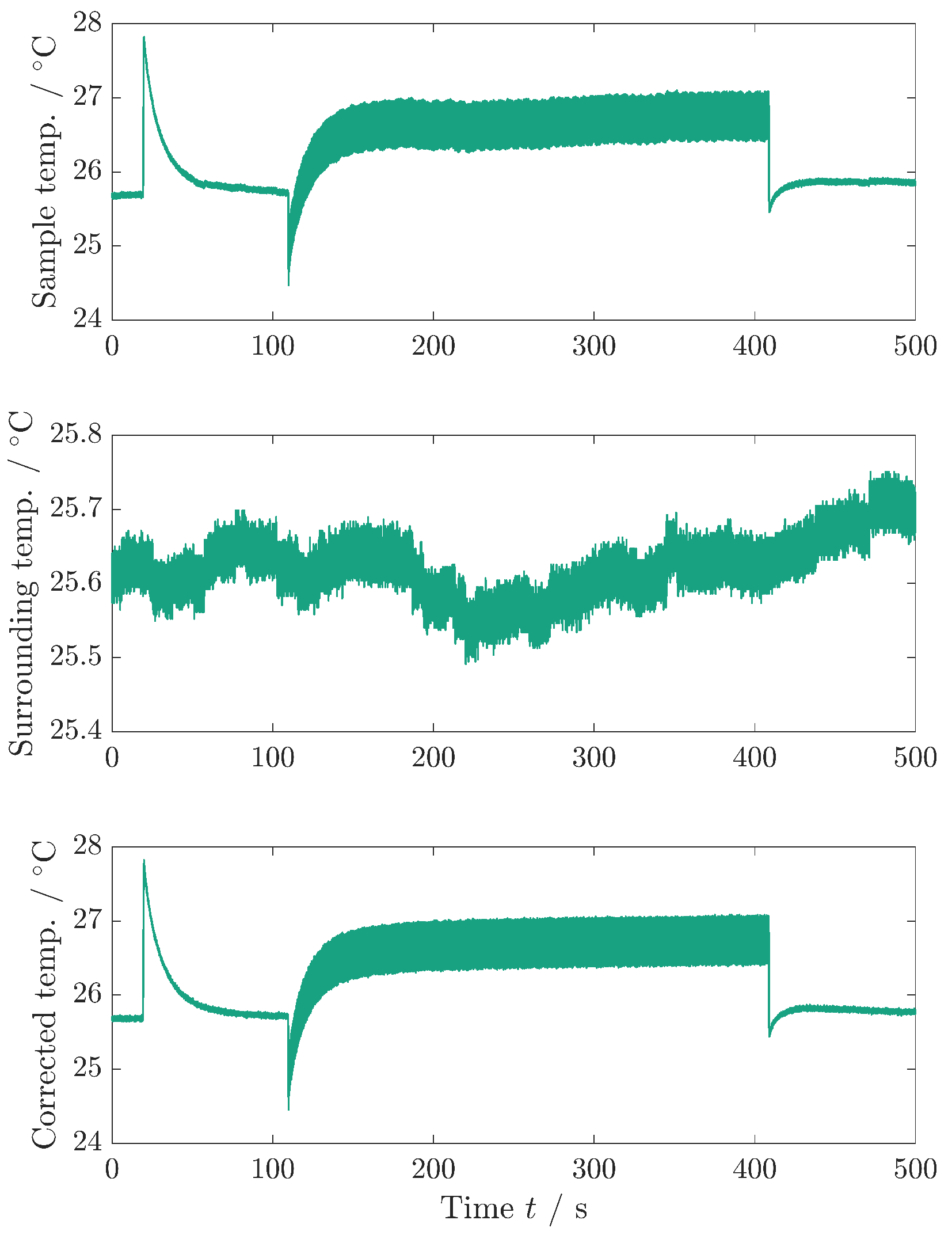
- The noise present in the sample temperature signal was attenuated by subtracting the ambient temperature from the sample temperature (refer to Figure A3 in the Appendix B).
- To achieve the correct absolute temperature, the mean ambient temperature, measured prior to the application of the voltage step, was reintroduced to the denoised sample temperature.
2.3.3. DSC Measurement
2.3.4. Uncertainty Propagation
2.4. Calculation of the & Efficiency
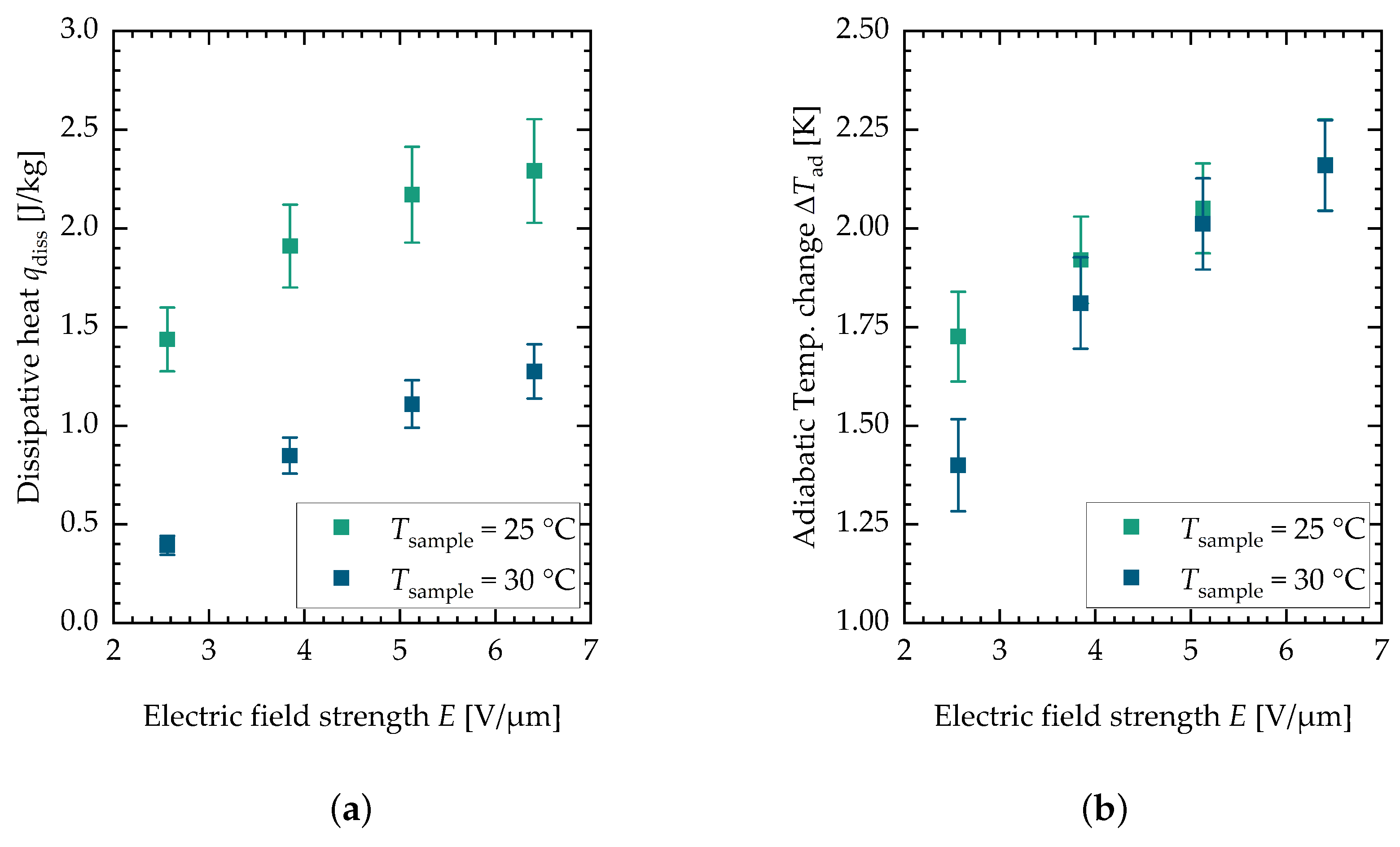
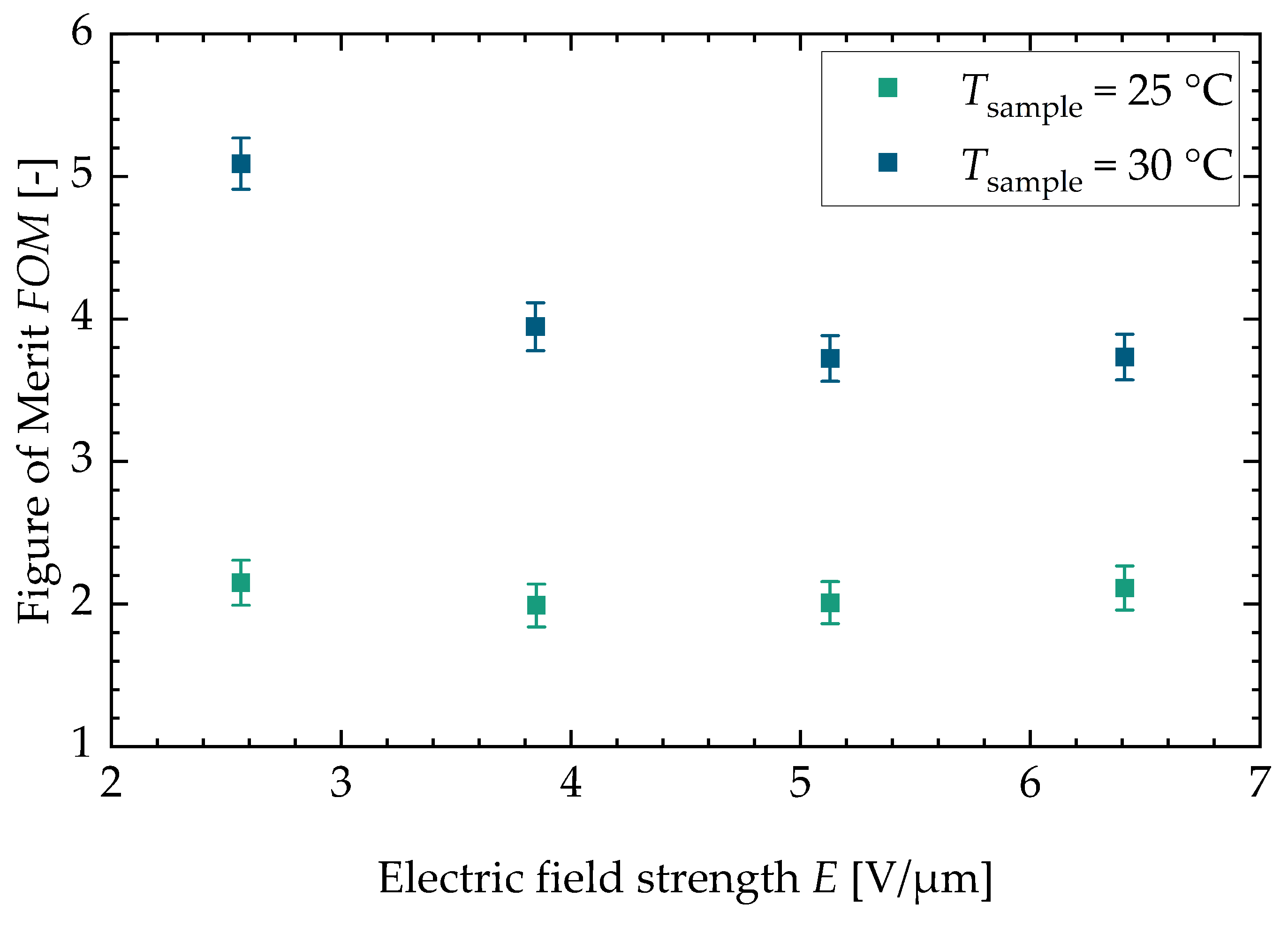
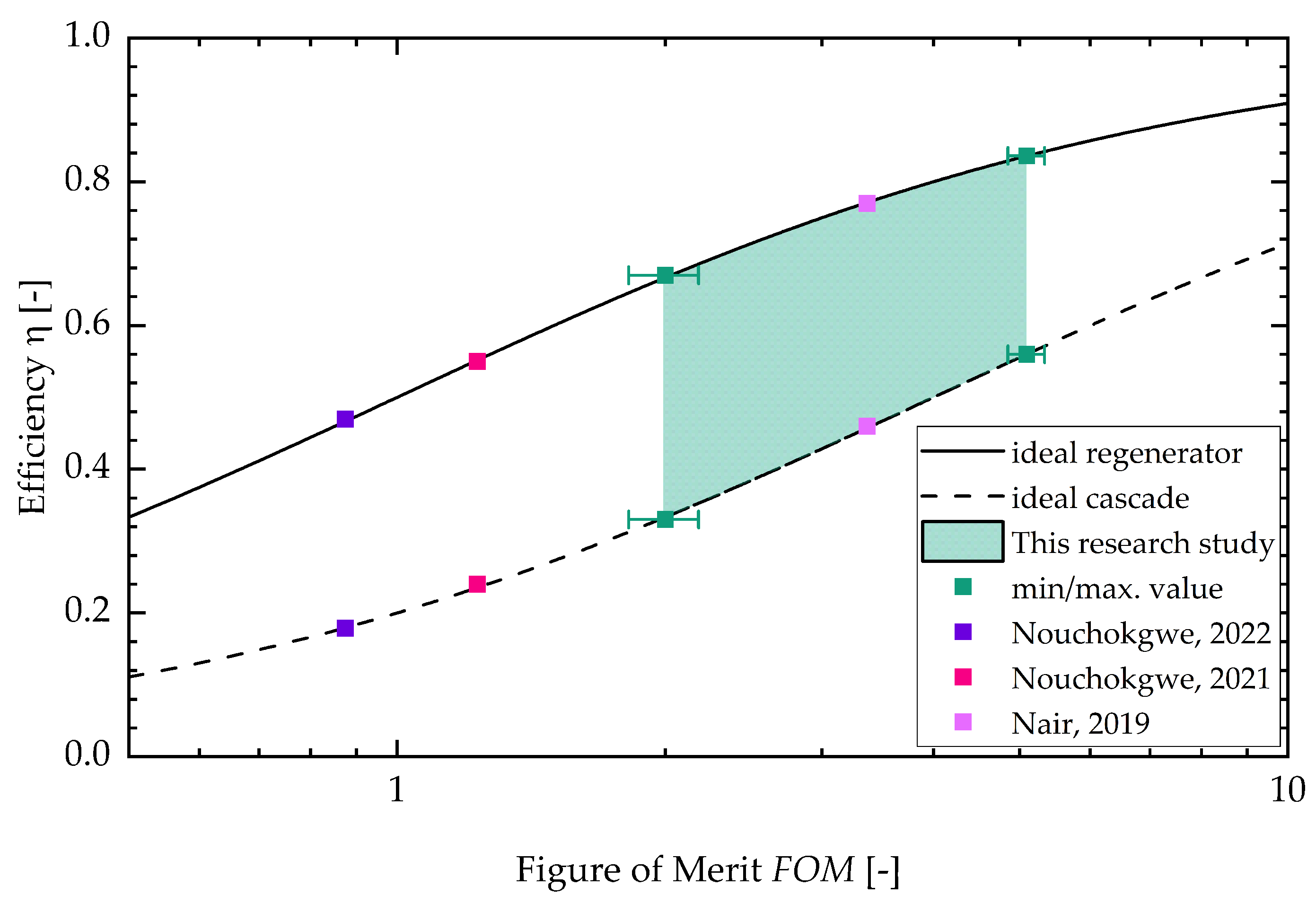
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
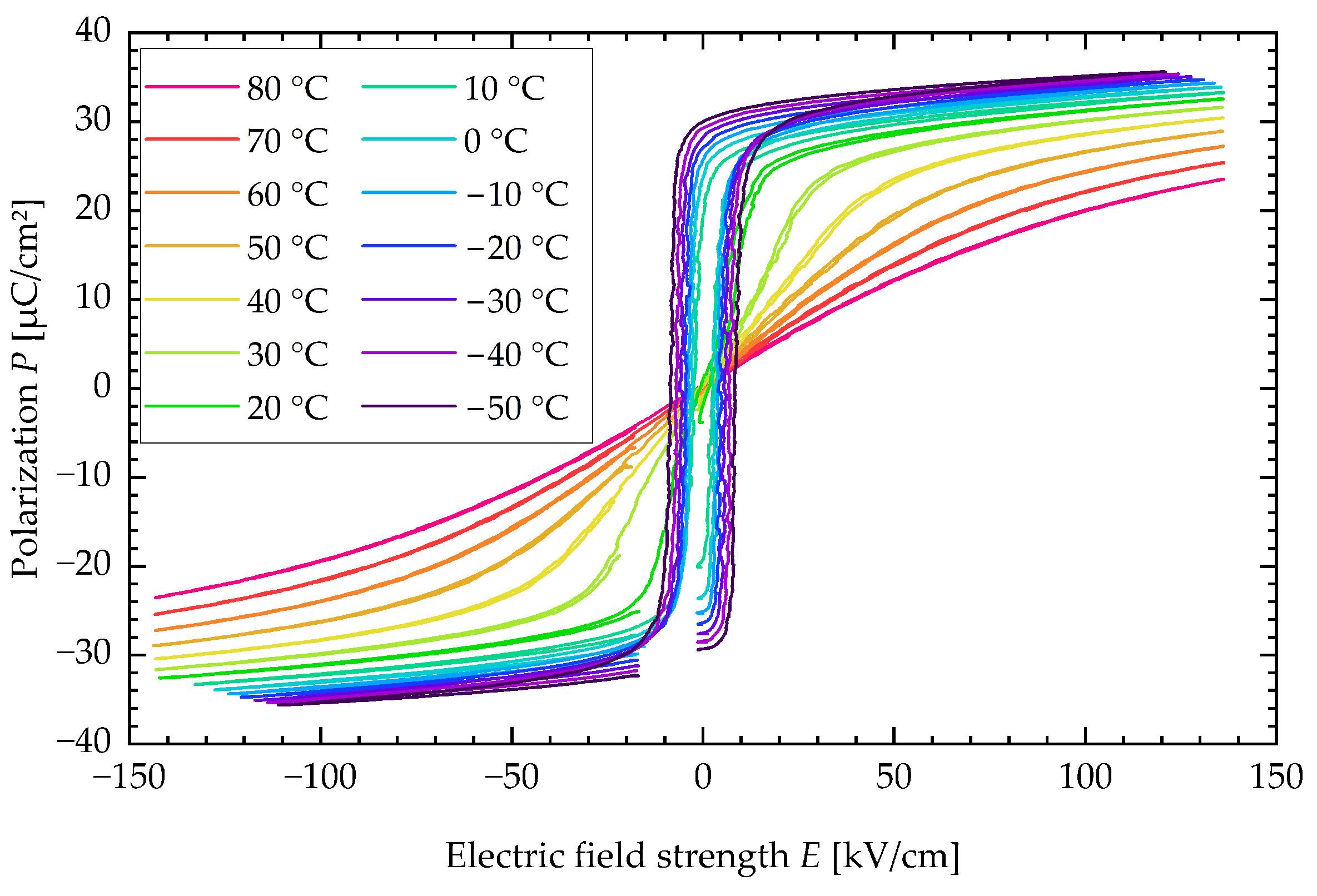
Appendix A. SEM Image and P-E-Loop

Appendix B. Temperature Correction and Determination of the Temperature Uncertainty
Temperature Correction
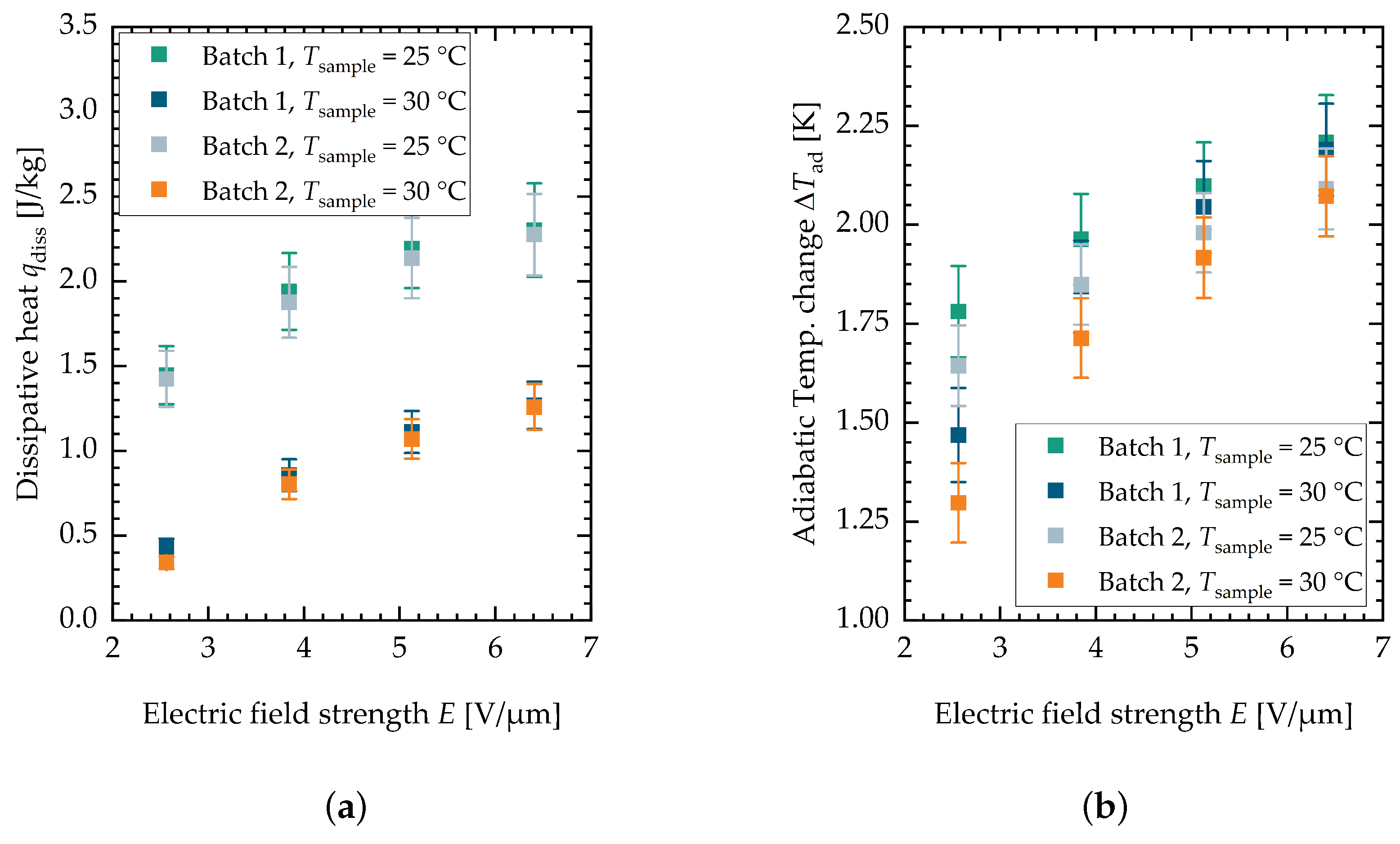
Appendix C. Separate Results for the Sample Batches

References
- Jia, Y.; Sungtaek Ju, Y. A solid-state refrigerator based on the electrocaloric effect. Appl. Phys. Lett. 2012, 100, 242901. [Google Scholar] [CrossRef]
- Plaznik, U.; Vrabelj, M.; Kutnjak, Z.; Malič, B.; Rožič, B.; Poredoš, A.; Kitanovski, A. Numerical modelling and experimental validation of a regenerative electrocaloric cooler. Int. J. Refrig. 2019, 98, 139–149. [Google Scholar] [CrossRef]
- Bellafkih, S.; Hadj Sahraoui, A.; Kulinski, P.; Dumoulin, P.; Longuemart, S. Electrocaloric Cooling Prototype Using Lead-Free Barium Titanate Multilayer Capacitors and Heat Transfer Fluid Motion. J. Therm. Sci. Eng. Appl. 2022, 14, 061011. [Google Scholar] [CrossRef]
- Engelbrecht, K.; Tušek, J.; Eriksen, D.; Lei, T.; Lee, C.Y.; Tušek, J.; Pryds, N. A regenerative elastocaloric device: Experimental results. J. Phys. D Appl. Phys. 2017, 50, 424006. [Google Scholar] [CrossRef]
- Kirsch, S.M.; Welsch, F.; Michaelis, N.; Schmidt, M.; Schütze, A.; Seelecke, S. Continuously operating elastocaloric cooling device based on shape memory alloys: Development and realization. In Proceedings of the Thermag VIII, Darmstadt, Germany, 16–20 September 2018. [Google Scholar] [CrossRef]
- Qian, S.; Alabdulkarem, A.; Ling, J.; Muehlbauer, J.; Hwang, Y.; Radermacher, R.; Takeuchi, I. Performance enhancement of a compressive thermoelastic cooling system using multi-objective optimization and novel designs. Int. J. Refrig. 2015, 57, 62–76. [Google Scholar] [CrossRef]
- Jacobs, S.; Auringer, J.; Boeder, A.; Chell, J.; Komorowski, L.; Leonard, J.; Russek, S.; Zimm, C. The performance of a large-scale rotary magnetic refrigerator. Int. J. Refrig. 2014, 37, 84–91. [Google Scholar] [CrossRef]
- Engelbrecht, K.; Eriksen, D.; Bahl, C.R.H.; Bjoslashrk, R.; Geyti, J.; Lozano, J.A.; Nielsen, K.K.; Saxild, F.; Smith, A.; Pryds, N.; et al. Experimental results for a novel rotary active magnetic regenerator. Int. J. Refrig. 2012, 35, 1498–1505. [Google Scholar] [CrossRef]
- Lozano, J.A.; Engelbrecht, K.; Bahl, C.R.H.; Nielsen, K.K.; Eriksen, D.; Olsen, U.L.; Barbosa, J.R.; Smith, A.; Prata, A.T.; Pryds, N. Performance analysis of a rotary active magnetic refrigerator. Appl. Energy 2013, 111, 669–680. [Google Scholar] [CrossRef]
- Raveendran, P.S.; Sekhar, S.J. Exergy analysis of a domestic refrigerator with brazed plate heat exchanger as condenser. J. Therm. Anal. Calorim. 2017, 127, 2439–2446. [Google Scholar] [CrossRef]
- Chaudron, J.B.; Muller, C.; Hittinger, M.; Risser, M.; Lionte, S. Performance measurements on a large-scale magnetocaloric cooling application at room temperature. In Proceedings of the Thermag VIII, Darmstadt, Germany, 16–20 September 2018. [Google Scholar] [CrossRef]
- Li, J.; Torelló, A.; Kovacova, V.; PRAH, U.; Aravindhan, A.; Granzow, T.; Usui, T.; Hirose, S.; Defay, E. High cooling performance in a double-loop electrocaloric heat pump. Science 2023, 382, 801–805. [Google Scholar] [CrossRef]
- Kitanovski, A.; Tušek, J.; Tomc, U.; Plaznik, U.; Ožbolt, M.; Poredoš, A. Magnetocaloric Energy Conversion: From Theory to Applications; Green Energy and Technology; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Kholkin, A.L.; Pakhomov, O.V.; Semenov, A.A.; Tselev, A. The Electrocaloric Effect: Materials and Applications; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Lagoudas, D.C. Shape Memory Alloys: Modeling and Engineering Applications; Springer: Boston, MA, USA, 2008; Volume 1. [Google Scholar] [CrossRef]
- Hegenbarth, E. Studies of the electrocaloric effect of ferroelectricceramics at low temperatures. Cryogenics 1961, 1, 242–243. [Google Scholar] [CrossRef]
- Metzdorf, J.; Corhan, P.; Bach, D.; Hirose, S.; Lellinger, D.; Mönch, S.; Kühnemann, F.; Schäfer-Welsen, O.; Bartholomé, K. Electrocaloric cooling system utilizing latent heat transfer for high power density. Commun. Eng. 2024, 3, 55. [Google Scholar] [CrossRef]
- Ma, R.; Zhang, Z.; Tong, K.; Huber, D.; Kornbluh, R.; Ju, Y.S.; Pei, Q. Highly efficient electrocaloric cooling with electrostatic actuation. Science 2017, 357, 1130–1134. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Yang, T.; Li, Y. A micro solid-state refrigeration prototype device based on die electrocaloric effect. Mater. Lett. 2023, 341, 134263. [Google Scholar] [CrossRef]
- Mönch, S.; Reiner, R.; Mansour, K.; Waltereit, P.; Basler, M.; Quay, R.; Molin, C.; Gebhardt, S.; Bach, D.; Binninger, R.; et al. A 99.74% Efficient Capacitor-Charging Converter Using Partial Power Processing for Electrocalorics. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 4491–4507. [Google Scholar] [CrossRef]
- Schipper, J.; Bach, D.; Mönch, S.; Molin, C.; Gebhardt, S.; Wöllenstein, J.; Schäfer-Welsen, O.; Vogel, C.; Langebach, R.; Bartholomé, K. On the efficiency of caloric materials in direct comparison with exergetic grades of compressors. J. Phys. Energy 2023, 5, 045002. [Google Scholar] [CrossRef]
- Hess, T.; Maier, L.M.; Bachmann, N.; Corhan, P.; Schäfer-Welsen, O.; Wöllenstein, J.; Bartholomé, K. Thermal hysteresis and its impact on the efficiency of first-order caloric materials. J. Appl. Phys. 2020, 127, 075103. [Google Scholar] [CrossRef]
- Masche, M.; Ianniciello, L.; Tušek, J.; Engelbrecht, K. Impact of hysteresis on caloric cooling performance. Int. J. Refrig. 2020, 121, 302–312. [Google Scholar] [CrossRef]
- Qian, G.; Zhu, K.; Li, X.; Yan, K.; Wang, J.; Liu, J.; Huang, W. The electrocaloric effect of PBZ/PVDF flexible composite film near room temperature. J. Mater. Sci. Mater. Electron. 2021, 32, 12001–12016. [Google Scholar] [CrossRef]
- Huang, Y.H.; Liu, B.; Li, J.; Wu, Y.J. Improved energy storage performance of Ba0.4Sr0.6TiO3 nanocrystalline ceramics prepared by using oxalate co-precipitation and spark plasma sintering. Mater. Res. Bull. 2019, 113, 141–145. [Google Scholar] [CrossRef]
- Cheng, L.Q.; Jiang, G.; Ma, Z.; Xu, Z.; Yu, M.; Lu, J.; Chen, K. Enhanced electrocaloric performance within wide temperature span in Al-doped BaZr0.2Ti0.8O3 ceramics. J. Mater. Sci. Mater. Electron. 2022, 33, 24986–24994. [Google Scholar] [CrossRef]
- Blumenthal, P.; Raatz, A. Classification of electrocaloric cooling device types. EPL Europhys. Lett. 2016, 115, 17004. [Google Scholar] [CrossRef]
- Schipper, J.; Melchin, S.; Metzdorf, J.; Bach, D.; Fehrenbach, M.; Löwe, K.; Vieyra, H.; Kühnemann, F.; Wöllenstein, J.; Bartholomé, K. Introduction of novel method of cyclic self-heating for the experimental quantification of the efficiency of caloric materials shown for LaFe11.4Mn0.35Si1.26Hx. J. Phys. Energy 2024, 6, 035006. [Google Scholar] [CrossRef]
- Bradeško, A.; Hedl, A.; Fulanović, L.; Novak, N.; Rojac, T. Self-heating of relaxor and ferroelectric ceramics during electrocaloric field cycling. APL Mater. 2019, 7, 071111. [Google Scholar] [CrossRef]
- Quintero, M.; Gaztañaga, P.; Irurzun, I. Intrinsic leakage and adsorption currents associated with the electrocaloric effect in multilayer capacitors. Appl. Phys. Lett. 2015, 107, 151901. [Google Scholar] [CrossRef]
- Fischer, J.; Hägele, D.; Rudolph, J. Direct simultaneous measurement of electrocaloric effect and hysteresis loss heating in ferroelectrics. Appl. Phys. Lett. 2024, 124, 172902. [Google Scholar] [CrossRef]
- Nouchokgwe, Y.; Lheritier, P.; Usui, T.; Torello, A.; Moul, A.E.; Kovacova, V.; Granzow, T.; Hirose, S.; Defay, E. Materials efficiency of electrocaloric lead scandium tantalate multilayer capacitors. Scr. Mater. 2022, 219, 114873. [Google Scholar] [CrossRef]
- Nouchokgwe, Y.; Lheritier, P.; Hong, C.H.; Torelló, A.; Faye, R.; Jo, W.; Bahl, C.R.H.; Defay, E. Giant electrocaloric materials energy efficiency in highly ordered lead scandium tantalate. Nat. Commun. 2021, 12, 3298. [Google Scholar] [CrossRef]
- Bernhard, F. Handbuch der Technischen Temperaturmessung, 2nd ed.; VDI-Buch; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Quintero, M.; Ghivelder, L.; Gomez-Marlasca, F.; Parisi, F. Decoupling electrocaloric effect from Joule heating in a solid state cooling device. Appl. Phys. Lett. 2011, 99, 232908. [Google Scholar] [CrossRef]
- Lu, S.; Li, J.; Cheng, M.; Li, Q.; Li, F.; Lv, Z.; Zhang, Y.; Lu, C.; Li, S. Joule heating—A significant factor in electrocaloric effect. Ceram. Int. 2019, 45, 16992–16998. [Google Scholar] [CrossRef]
- Nair, B.; Usui, T.; Crossley, S.; Kurdi, S.; Guzmán-Verri, G.G.; Moya, X.; Hirose, S.; Mathur, N.D. Large electrocaloric effects in oxide multilayer capacitors over a wide temperature range. Nature 2019, 575, 468–472. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Unmüßig, S.; Bach, D.; Metzdorf, J.; Corhan, P.; Hirose, S.; Bartholomé, K. Direct Thermal Method to Characterize the Material Efficiency of Electrocaloric Lead Scandium Tantalate Multilayer Ceramic Capacitors. Materials 2025, 18, 1924. https://doi.org/10.3390/ma18091924
Unmüßig S, Bach D, Metzdorf J, Corhan P, Hirose S, Bartholomé K. Direct Thermal Method to Characterize the Material Efficiency of Electrocaloric Lead Scandium Tantalate Multilayer Ceramic Capacitors. Materials. 2025; 18(9):1924. https://doi.org/10.3390/ma18091924
Chicago/Turabian StyleUnmüßig, Sabrina, David Bach, Julius Metzdorf, Patrick Corhan, Sakyo Hirose, and Kilian Bartholomé. 2025. "Direct Thermal Method to Characterize the Material Efficiency of Electrocaloric Lead Scandium Tantalate Multilayer Ceramic Capacitors" Materials 18, no. 9: 1924. https://doi.org/10.3390/ma18091924
APA StyleUnmüßig, S., Bach, D., Metzdorf, J., Corhan, P., Hirose, S., & Bartholomé, K. (2025). Direct Thermal Method to Characterize the Material Efficiency of Electrocaloric Lead Scandium Tantalate Multilayer Ceramic Capacitors. Materials, 18(9), 1924. https://doi.org/10.3390/ma18091924








