Dynamics Analysis of Elastic Ring-Type Extruded Oil Film Damper Considering Time-Varying Characteristics
Abstract
1. Introduction
2. Modeling of an Elastic Ring Extruded Oil Film Damper
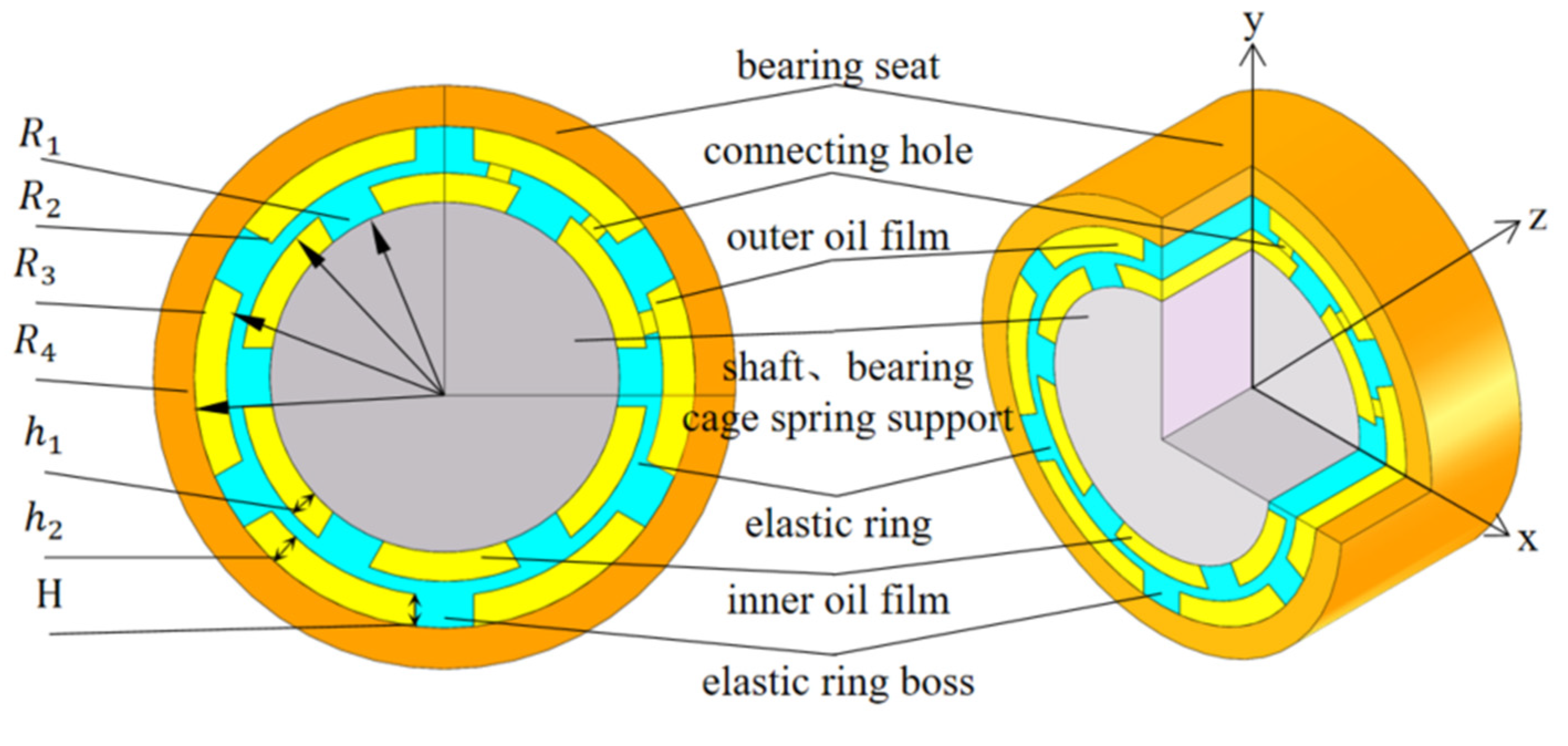
2.1. Definition of the Main Structure and Parameters of the ERSFD
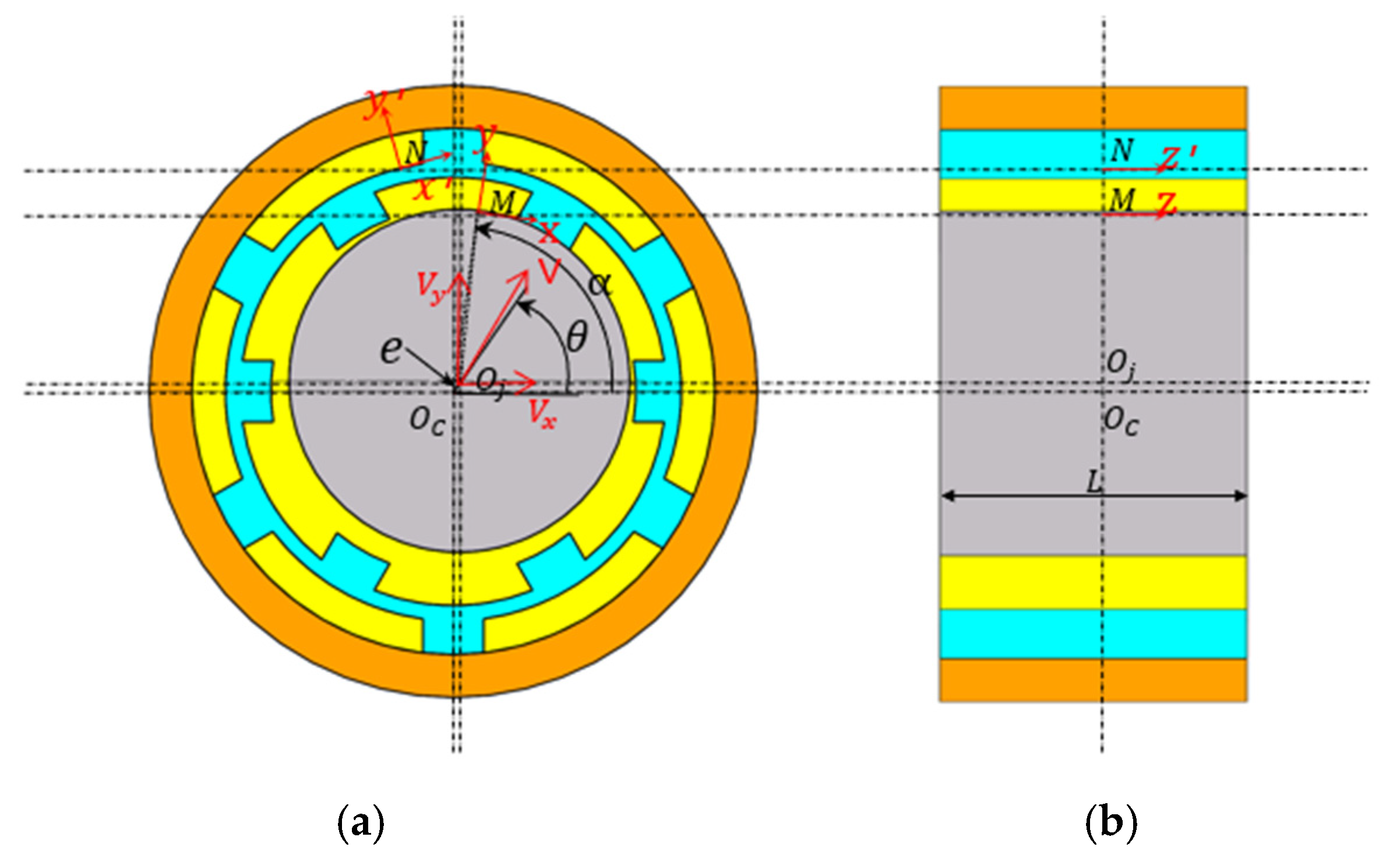
2.2. Oil Film Control Equation Without Considering the Deformation of the Elastic Ring
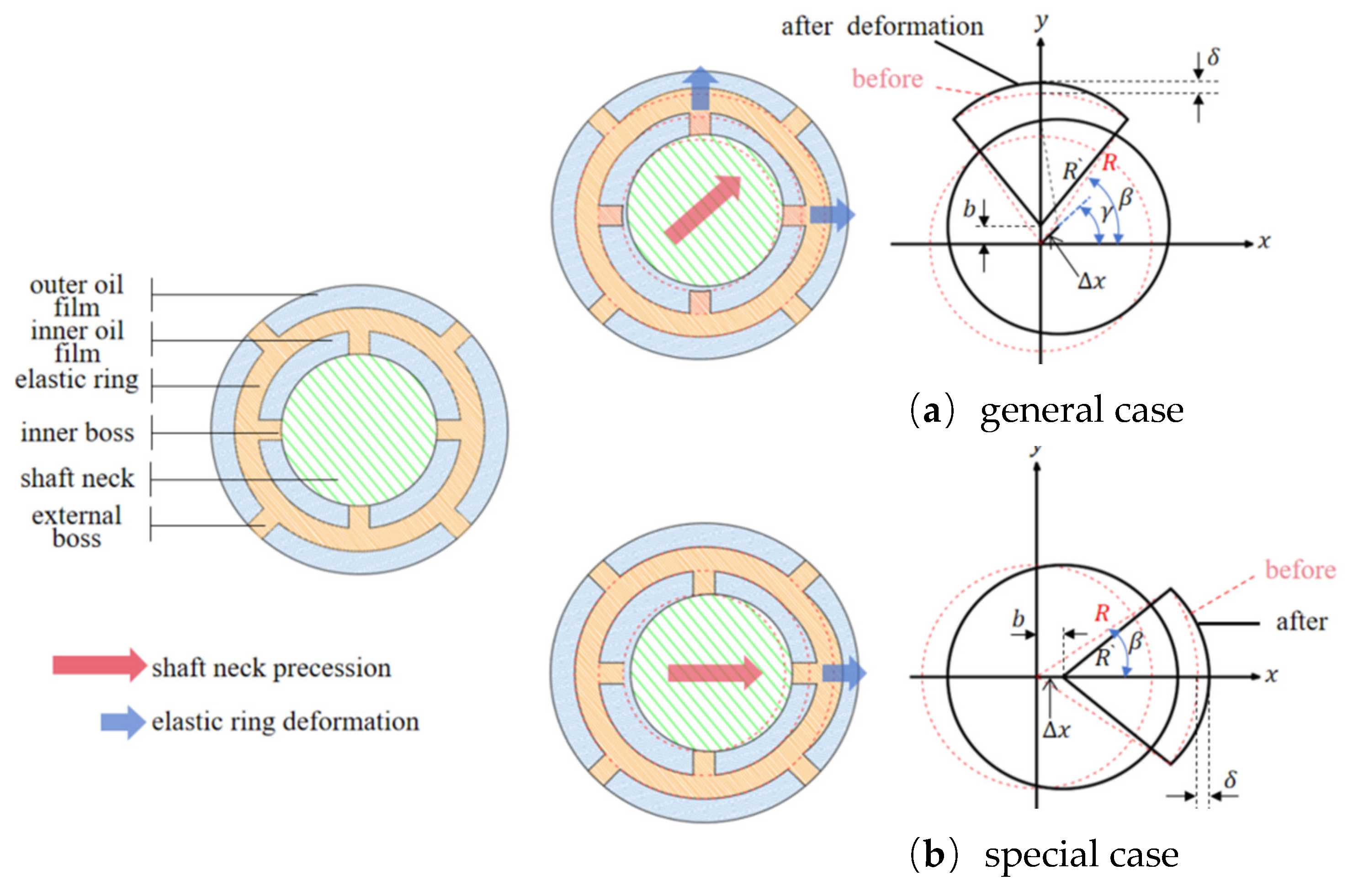
2.3. Analysis of Elastic Ring Deformation
2.4. Oil Film Control Equation Considering Elastic Ring Deformation
3. ERSFD Fluid–Structure Coupling Analysis and Time-Varying Stiffness Analysis of Elastic Ring
3.1. Introduction to ERSFD Bidirectional Fluid–Solid Coupling
3.2. Analysis of Solid-Coupled Deformation in Elastic Circulation
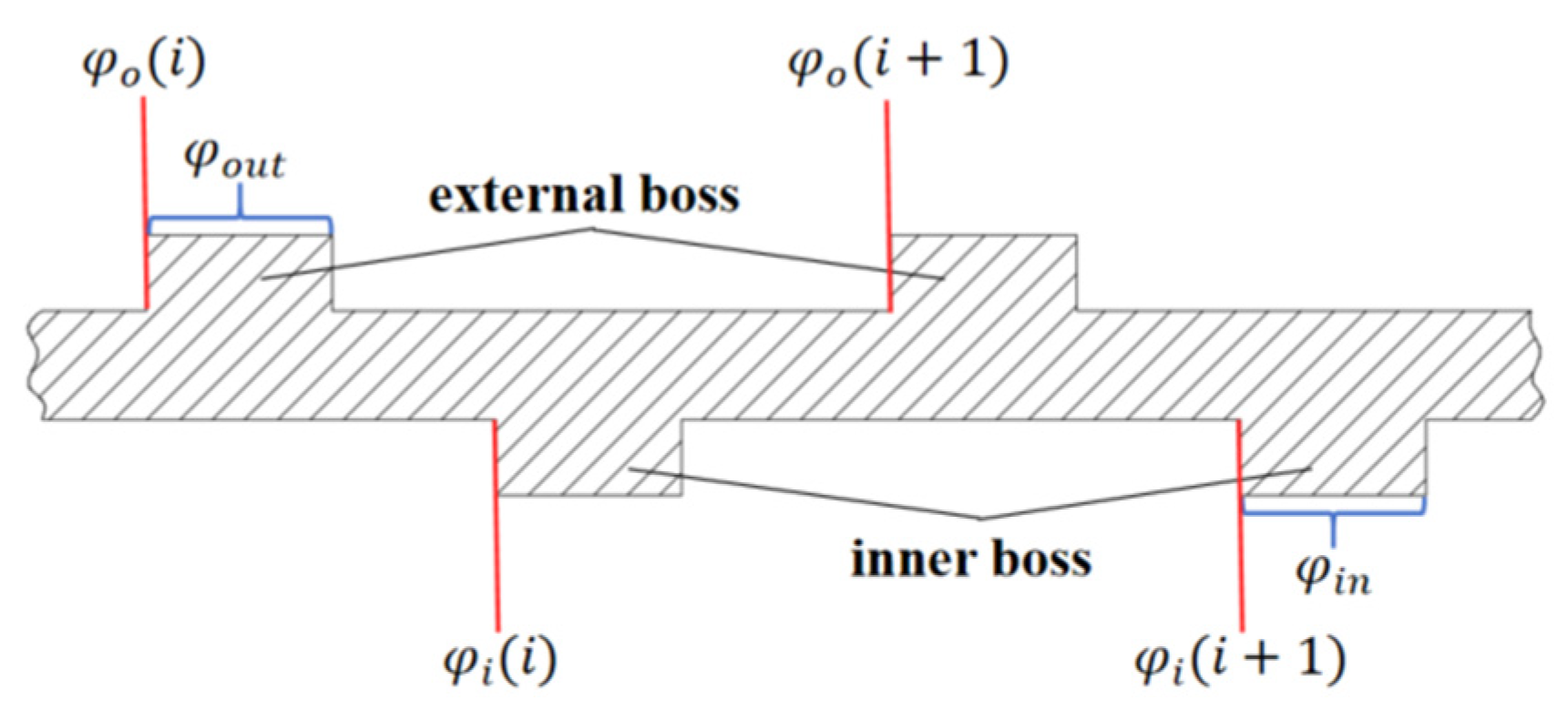
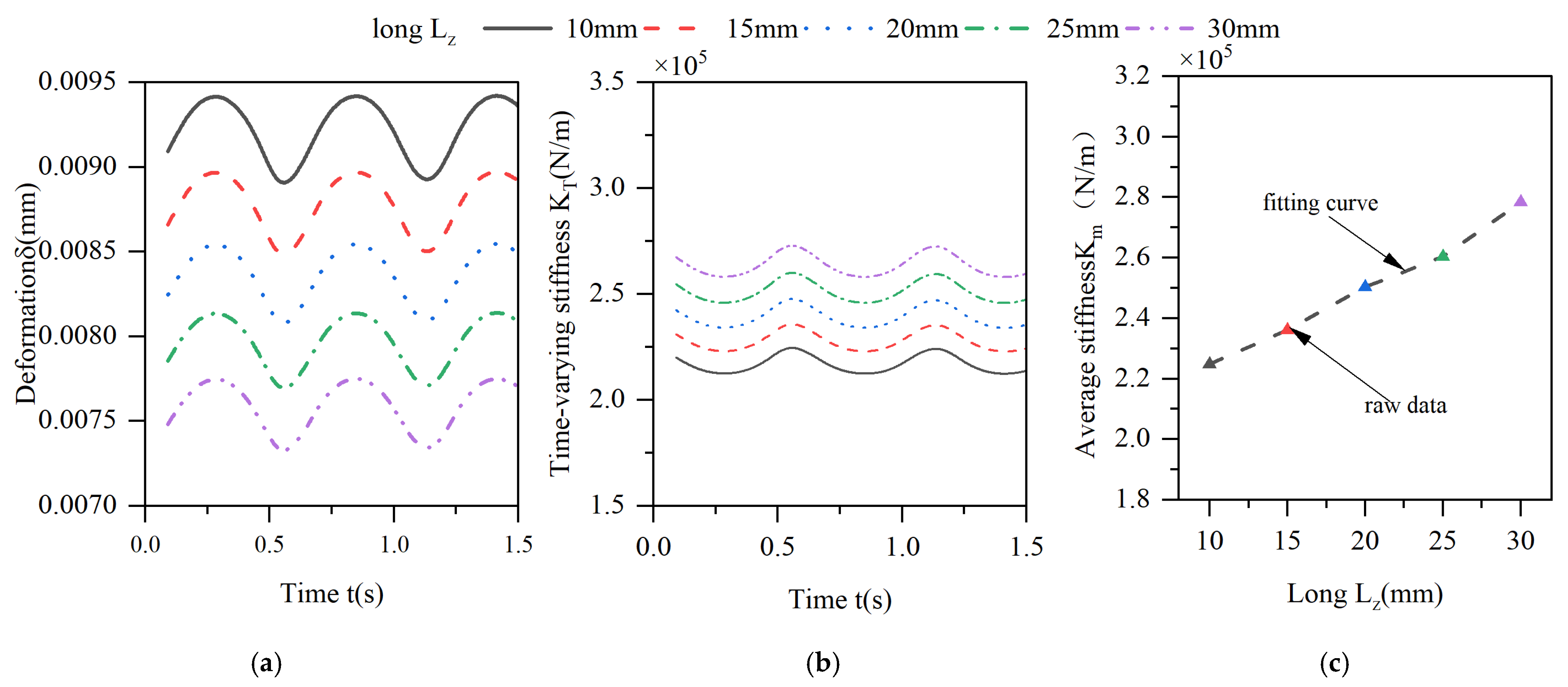
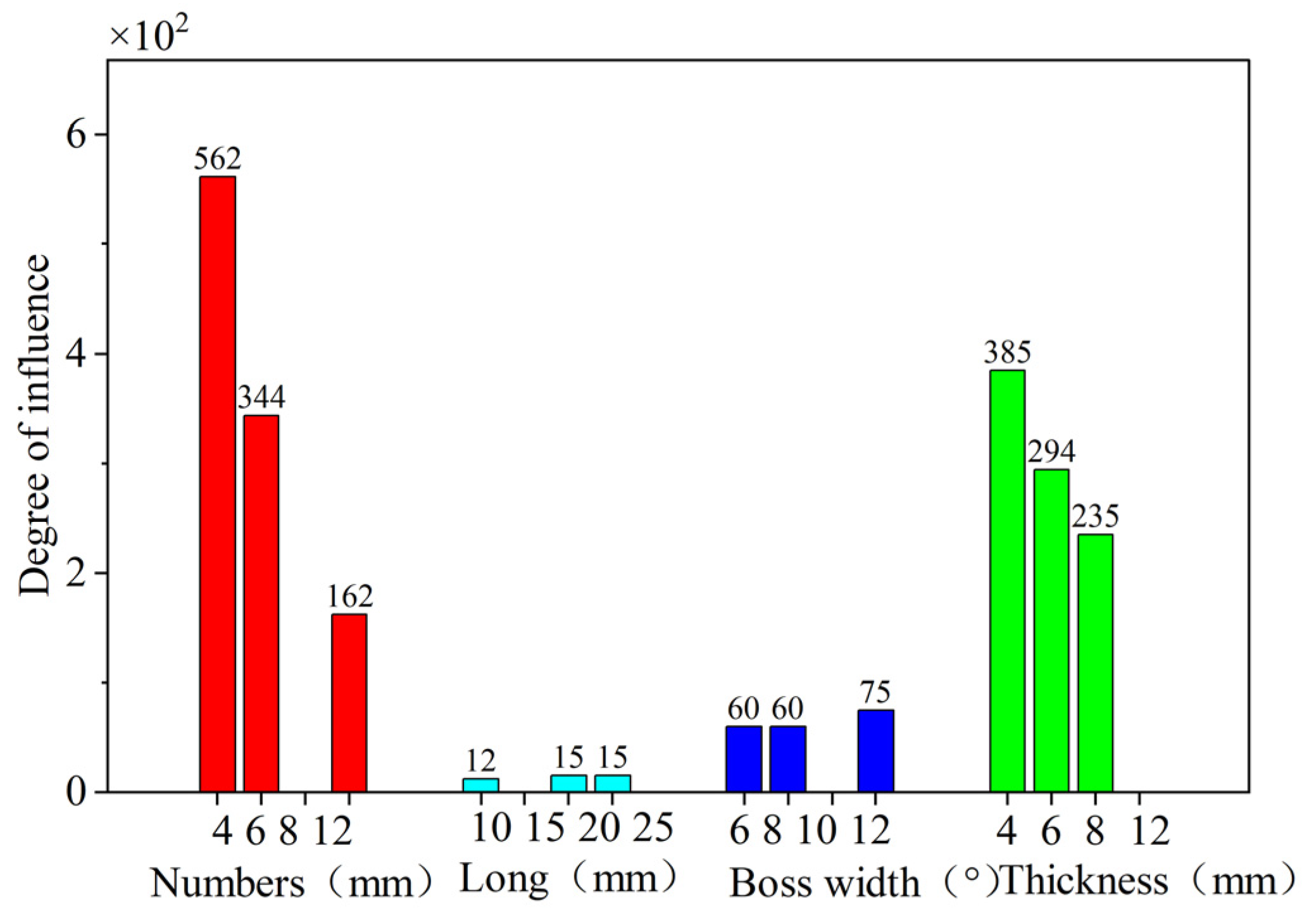
3.3. Analysis of the Effect of Different Structural Parameters on the Time-Varying Stiffness of the Elastic Ring
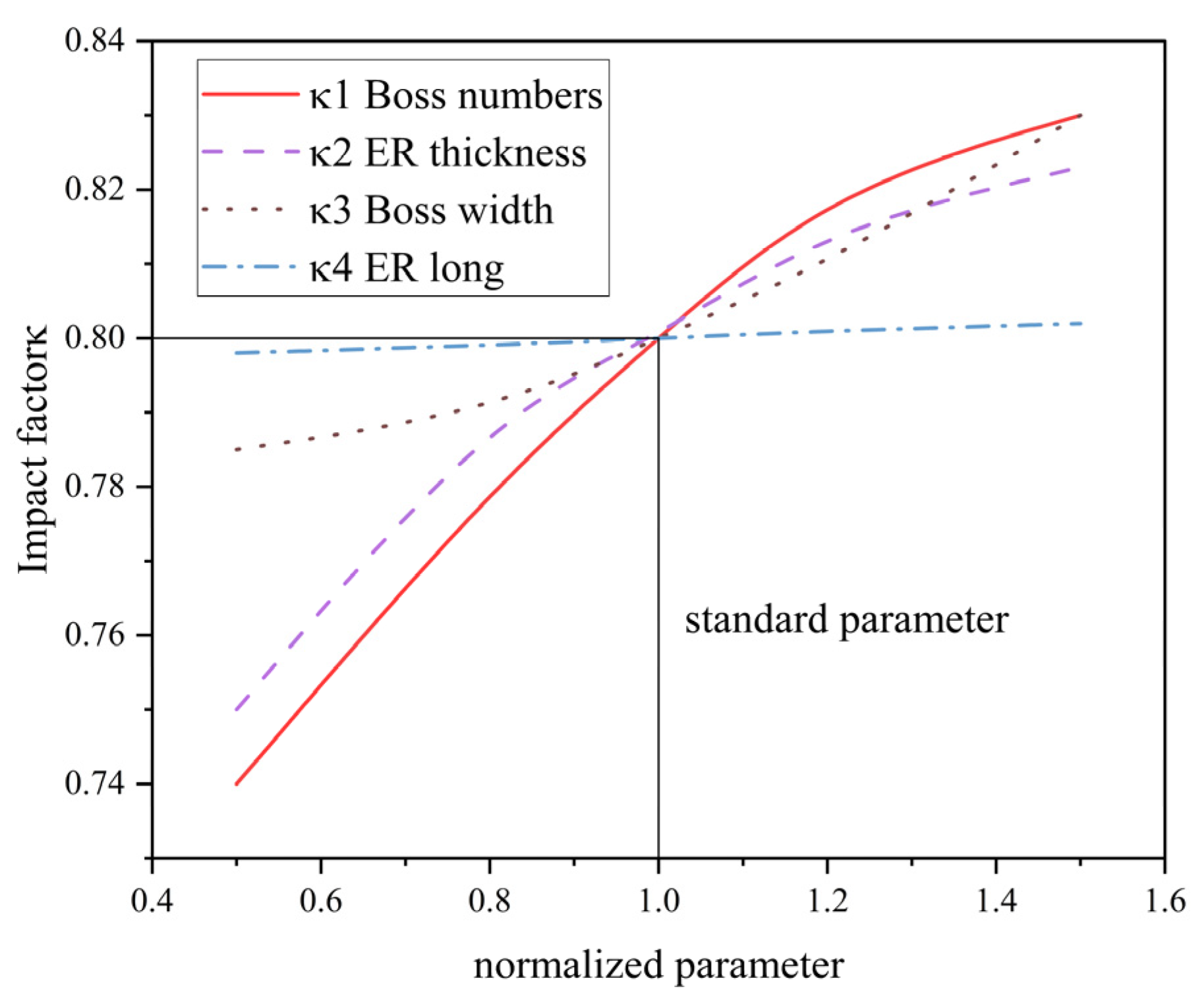
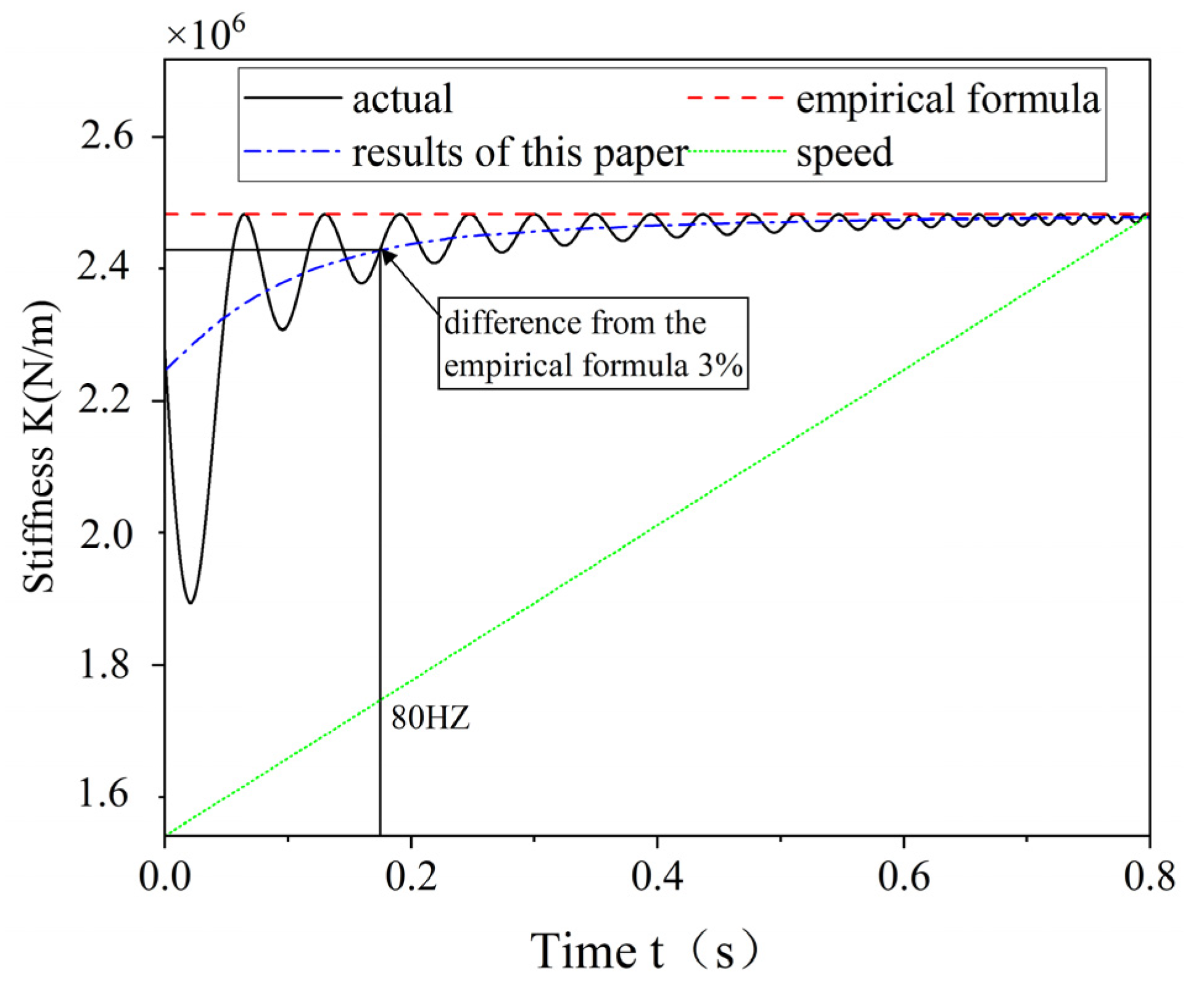
3.4. Establishment of Equivalent Stiffness Method for Elastic Ring Considering Time-Varying Characteristics
4. ERSFD Internal and External Oil Film Dynamics Characterization
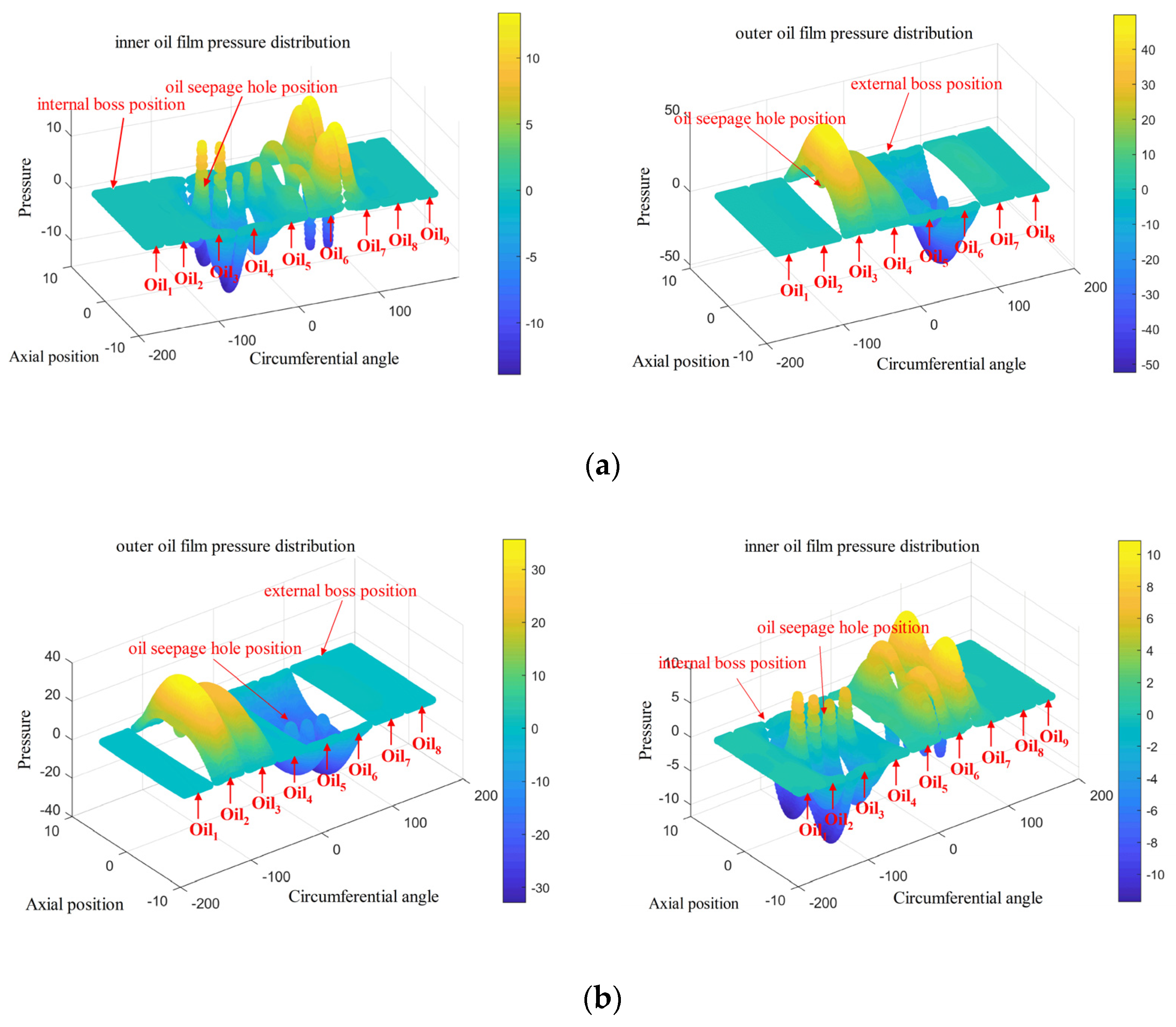
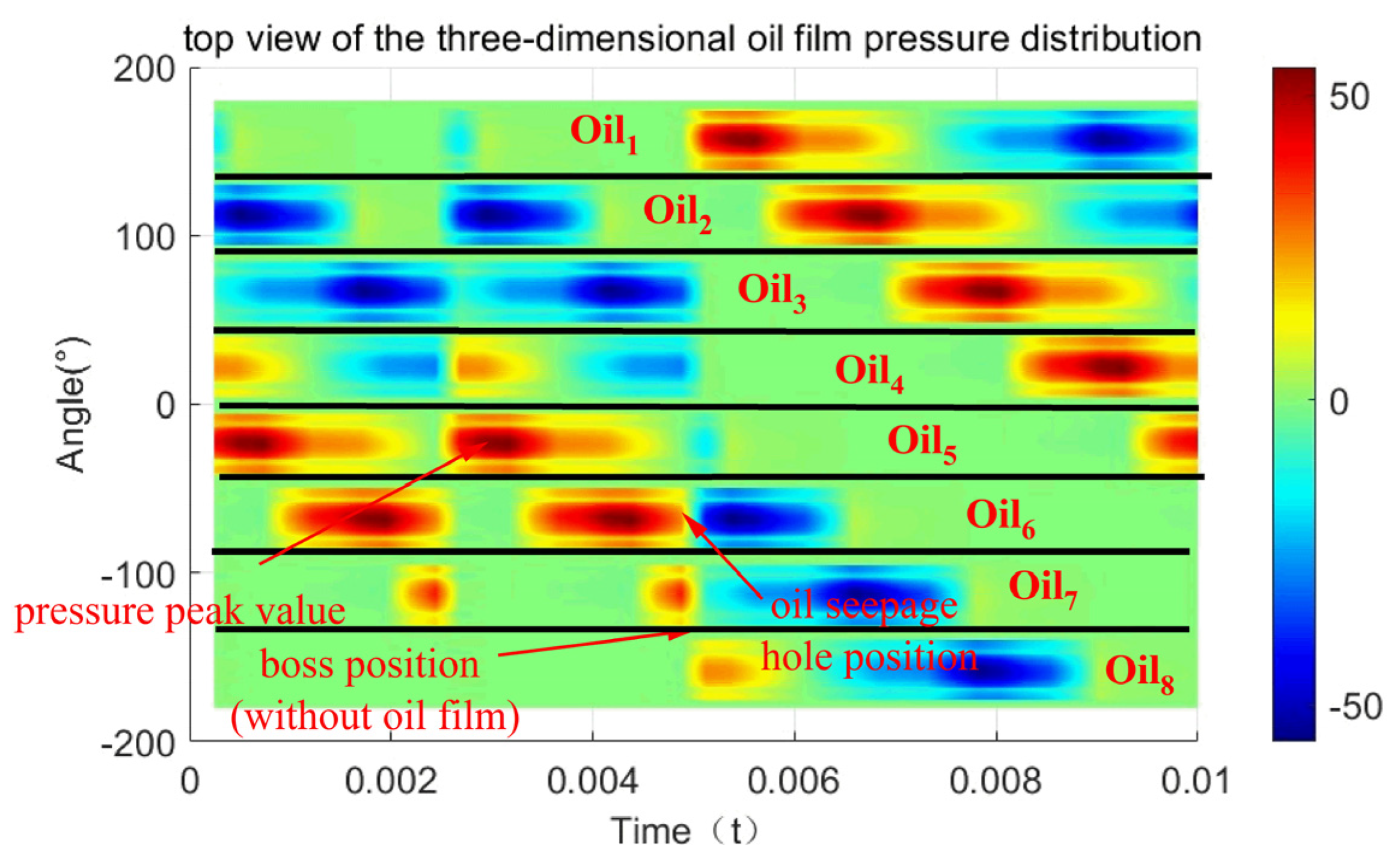
4.1. Oil Film Pressure Distribution Inside and Outside the ERSFD
4.2. Time-Varying Characterization of Oil Film Stiffness and Damping
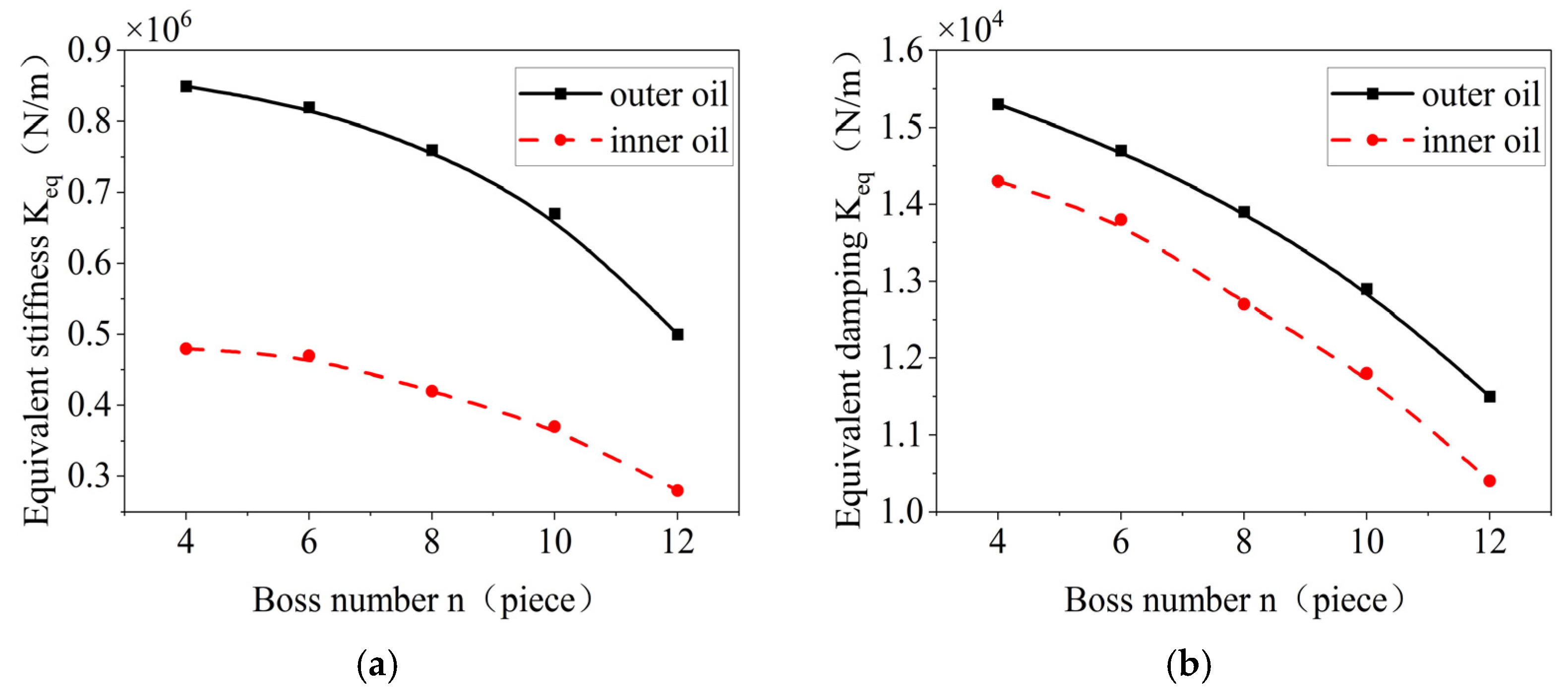
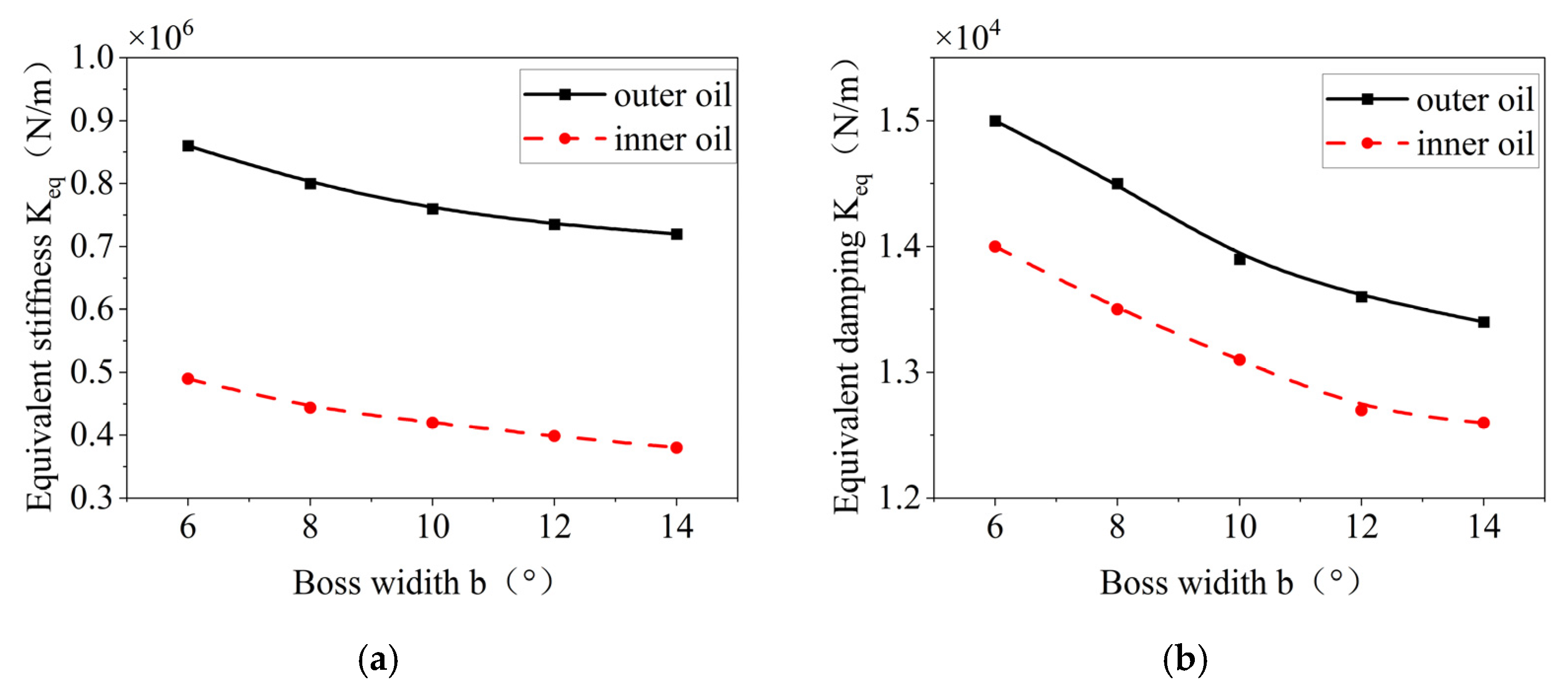
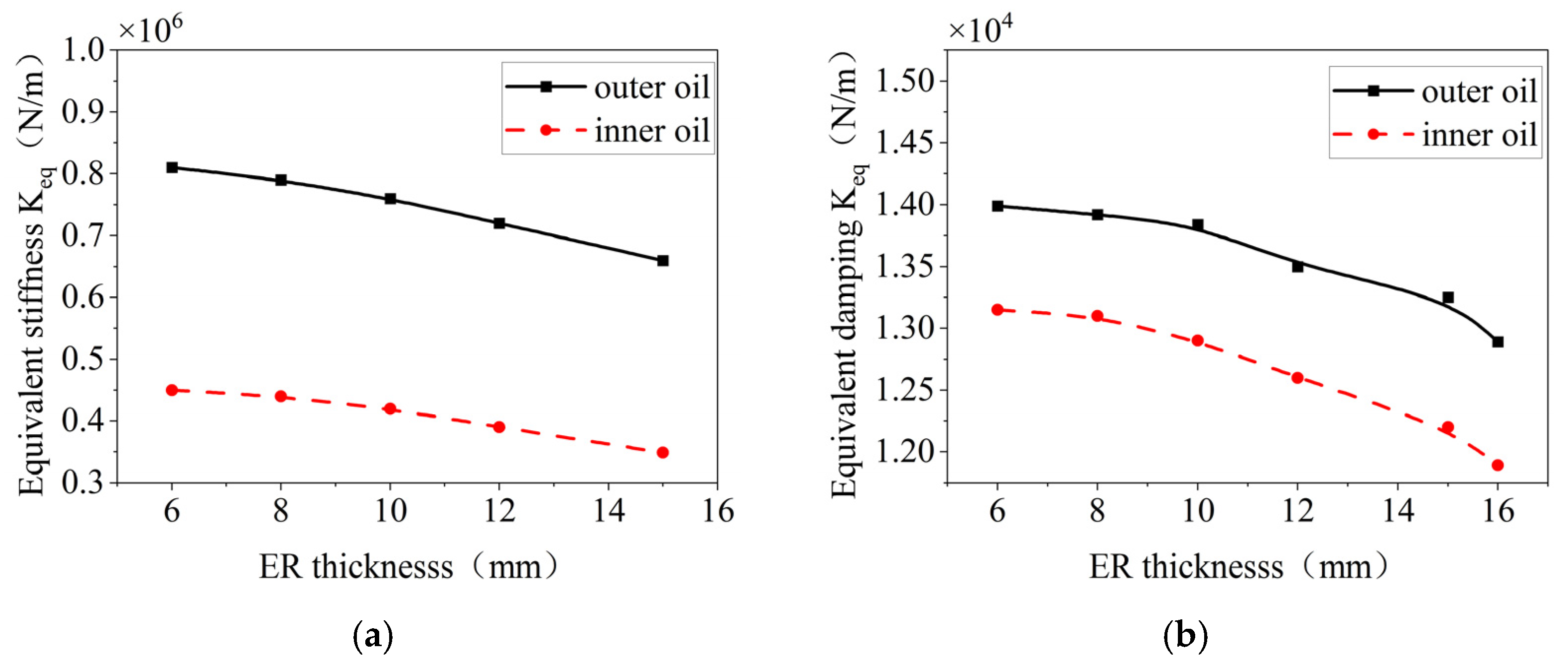
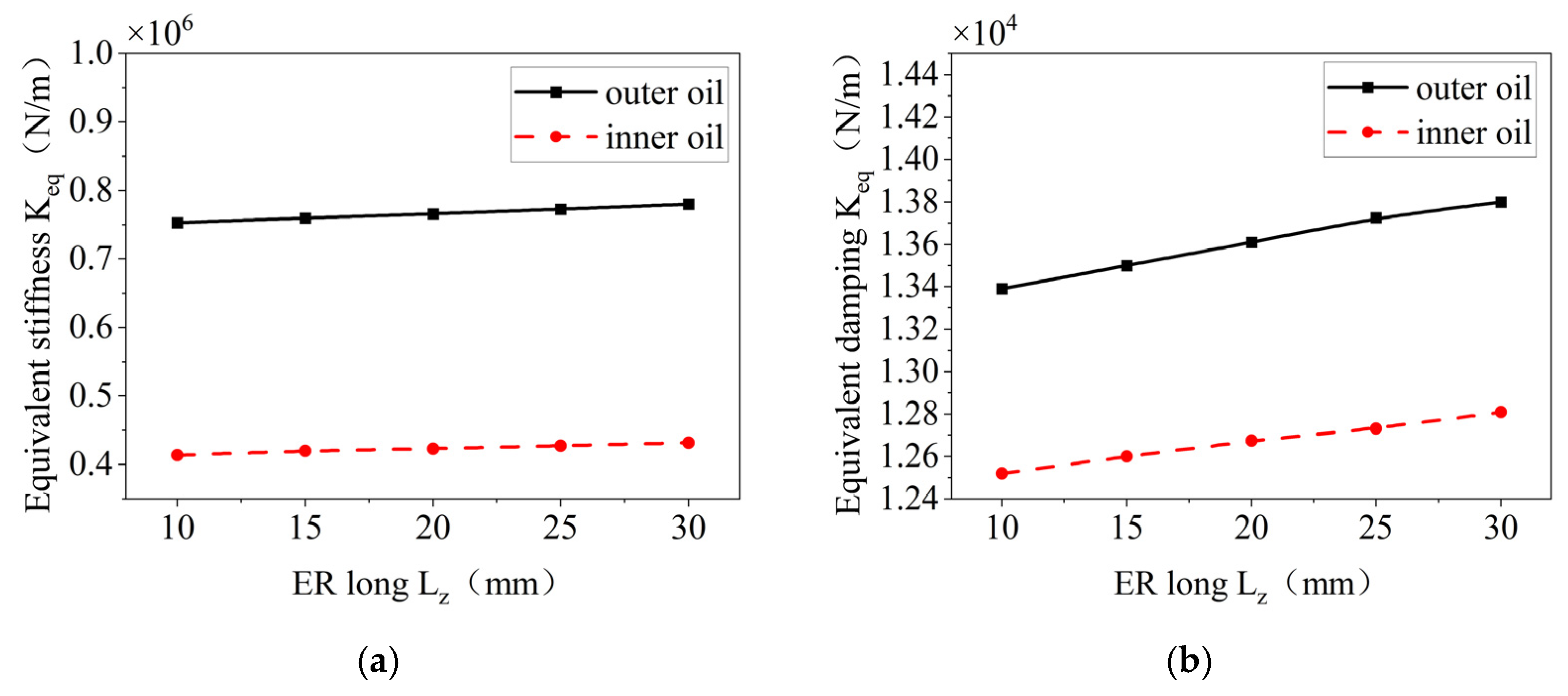
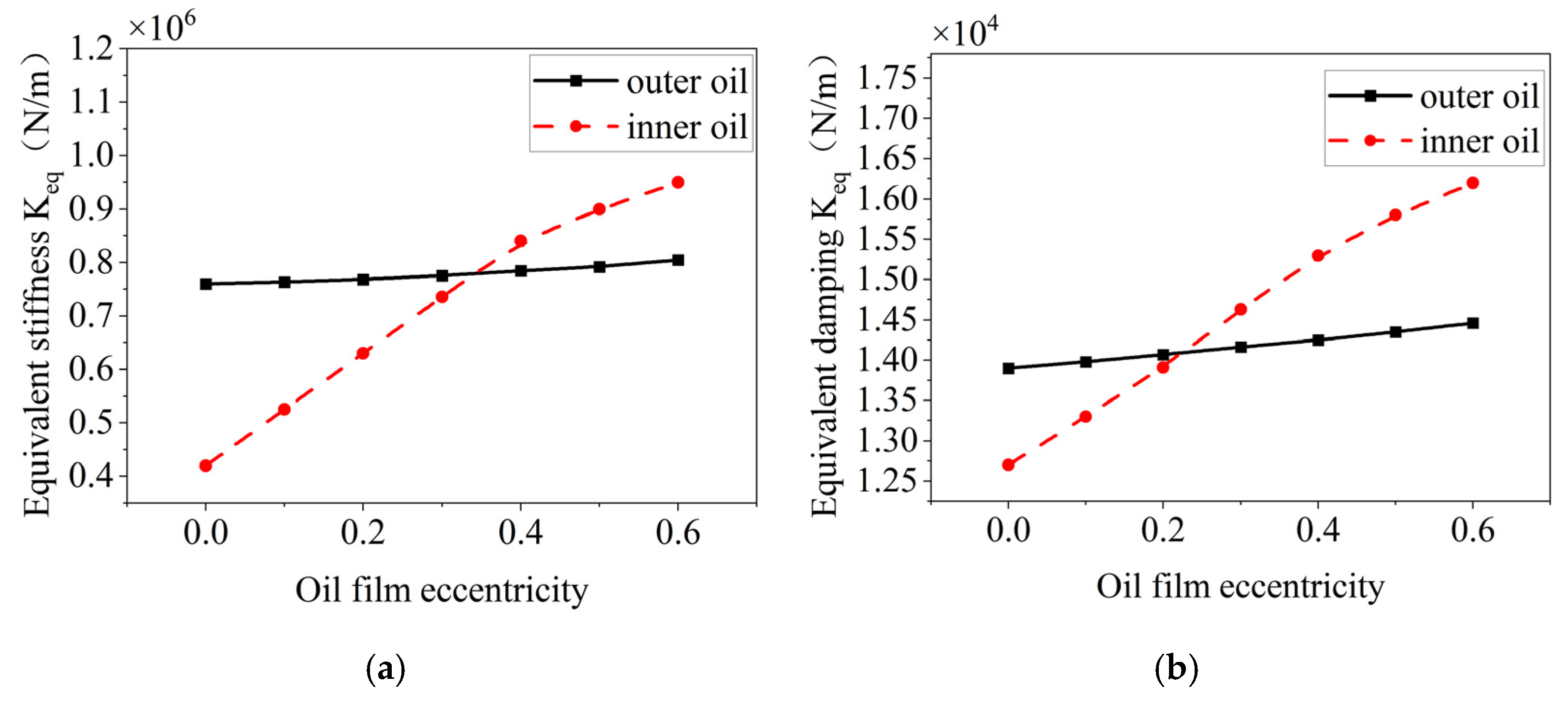
4.3. Influence of the Structural Parameters of the Elastic Ring on the Damping and Stiffness of the Inner and Outer Oil Films
5. Conclusions
- (1)
- During operation, the elastic ring experiences different contact states, classified as single-tab and double-tab contact. The difference between the maximum and minimum stiffness in these two states can be as much as 10%.
- (2)
- The elastic ring exhibits time-varying stiffness characteristics. Based on this, a new equivalent stiffness method is proposed that takes time variation into account. This method allows the equivalent stiffness to be calculated based on the ring’s structural parameters and is over 5% more accurate than traditional methods at low speeds.
- (3)
- The number of inner and outer tabs, the thickness of the elastic ring, and the width of the tabs all have a significant effect on the deformation of the ring. However, only the number of tabs and the ring thickness have a noticeable impact on its time-varying stiffness. These two parameters should be given special attention during the design process.
- (4)
- Increasing the number of tabs, the ring thickness, or the width of the inner and outer tabs results in a decrease in both the pressure and damping of the inner and outer oil films. These trends are consistent for both films. Conversely, increasing the axial length of the ring or the oil film eccentricity leads to higher stiffness and damping in both films.
- (5)
- The pressure in the outer oil film is primarily influenced by the elastic ring’s deformation and the size of the oil cavity, while the inner oil film pressure is most sensitive to oil film eccentricity. In design, increasing oil film eccentricity can help enhance overall stiffness and damping. However, excessive eccentricity may introduce nonlinear effects.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, C. Characterization of Fluid-Solid Coupling Dynamics of Elastic Ring-Type Extruded Oil Film Damper. Master’s Thesis, Shenyang University of Aeronautics and Astronautics, Shenyang, China, 2020. [Google Scholar]
- Zhou, M.; Li, Q.; Yan, T.T. Study on vibration damping mechanism of elastic ring-type extruded oil film damper(1)-Model of vibration damping mechanism of elastic ring-type extruded oil film damper. Gas Turbine Test Res. 1998, 4, 19–23+33. [Google Scholar]
- Zhou, M.; Li, Q.; Yan, T.T. Study on the vibration damping mechanism of elastic ring-type extruded oil film damper. J. Aerosp. Dyn. 1998, 4, 54–58+110. [Google Scholar]
- Hong, J.; Dang, Y.; Zhang, D. Dynamic design method of elastic ring extruded oil film damper. J. Beijing Univ. Aeronaut. Astronaut. 2006, 6, 649–653. [Google Scholar]
- Cao, L.; Gao, D.; Jiang, H. Critical speed characteristics of elastic ring extruded oil film damper-rotor system. Propuls. Propuls. Propuls. Technol. 2020, 10, 45–46. [Google Scholar]
- Su, C. Research on Dynamic Characteristics of Elastic Ring type Extruded Oil Film Damper. Doctoral Dissertation, Shenyang Aerospace University, Shenyang, China, 2009; pp. 32–35. [Google Scholar]
- Zhang, W.; Qiang, D. A new method for computing the deformation of elastic ring inside the elastic ring squeeze film damper. In Proceedings of the 15th National Conference on Nonlinear Vibration and the 12th National Conference on Nonlinear Dynamics and Motion Stability, Changsha, China, 8–10 May 2015; Chinese Society of Vibration Engineering: Tianjin, China, 2015; Volume 2. [Google Scholar]
- Xu, Y.; Chen, X.; Zou, J.; Qi, W.; Li, Y. Influence of Orifice Distribution on the Characteristics of Elastic Ring-Squeeze Film Dampers for Flywheel Energy-Storage System. IEEE Trans. Plasma Sci. 2013, 41, 1272–1279. [Google Scholar] [CrossRef]
- Sun, K.; Luo, Z.; Wu, F.; Liu, K. Matching Design Method of Elastic Ring Support Structure Parameters. Chinese Society of Vibration Engineering, Nonlinear Vibration Committee. In Proceedings of the 19th National Conference on Nonlinear Vibration and the 16th National Conference on Nonlinear Dynamics and Motion Stability. Northeastern University School of Mechanical Engineering and Automation; Key Laboratory of Vibration and Control of Aeroengine Power Equipment, Ministry of Education, Northeastern University; Foshan Graduate Innovation Institute, Northeastern University; AECC Shenyang Engine Research Institute: Shenyang, China, 2023; p. 49. [Google Scholar] [CrossRef]
- Sun, K.; Luo, Z.; Li, L.; Ge, X.; Zheng, S. Assembly Characteristics and Experimental Study of a Rotor System with an Elastic Ring Squeeze Film Damper. J. Mech. Eng. 2023, 59, 118–131. [Google Scholar]
- Li, S.; Yang, M.; Teng, G.; Yang, F.; Gao, W.; Wang, Y. Research on the Loading and Dynamic Characteristics Test Device of an Elastic Ring Squeeze Film Damper. Gas Turbine Exp. Res. 2023, 36, 17–23. [Google Scholar]
- Wang, S.; Yang, H.; Tang, R. Vibration Characteristics Analysis of an Integrated Cylindrical Roller Bearing Cage with an Elastic Ring Squeeze Film Damper. Vib. Shock. 2024, 43, 302–314. [Google Scholar] [CrossRef]
- Xiang, F.; Chen, X.; Hong, L. Simulation Method for the Dynamic Response of a Squeeze Film Damper-Rotor System Considering Elastic Ring Deformation. Propuls. Technol. 2024, 45, 205–217. [Google Scholar] [CrossRef]
- Yang, M. Research on the Vibration Stress Mechanism and Characteristics of an Elastic Ring Squeeze Film Damper. Master’s Thesis, Dalian Maritime University, Dalian, China, 2024. [Google Scholar]
- Chen, J.; Chen, X.; Hong, L. Fluid-Solid Coupling Dynamic Response Simulation Method of an Elastic Ring Squeeze Film Damper. J. Vib. Eng. 2025, 2025, 1–15. [Google Scholar]
- Yang, X.; Jiang, B.; Li, Y.; Zhao, Q.; Deng, S. Dynamic Characteristics of Elastic Ring Squeeze Film Damper Oscillated by Bearing Contact Force. J. Vib. Eng. Technol. 2024, 12, 433–455. [Google Scholar] [CrossRef]
- Guoying, P.; Shuqian, C.; Yushu, C.; Yuanhang, H. Study on the Semi-numerical and Semi-analytical Solutions of the Dynamics Equation of an Aero-engine Rotor System with ERSFD. J. Vib. Eng. Technol. 2023, 11, 1443–1461. [Google Scholar] [CrossRef]
- Luo, Z.; Liang, B.; Sun, K.; Li, L.; Hao, H.; Wu, X. Dynamic characteristic analysis of the elastic ring squeeze film damper-rotor system considering coupling angular misalignment. Nonlinear Dyn. 2025, 113, 3201–3226. [Google Scholar] [CrossRef]
- Wang, S. Dynamic Characteristic Analysis of the Cage in an Integrated Cylindrical Roller Bearing with an Elastic Ring Squeeze Film Damper. Master’s Thesis, Henan University of Science and Technology, Luoyang, China, 2023. [Google Scholar] [CrossRef]




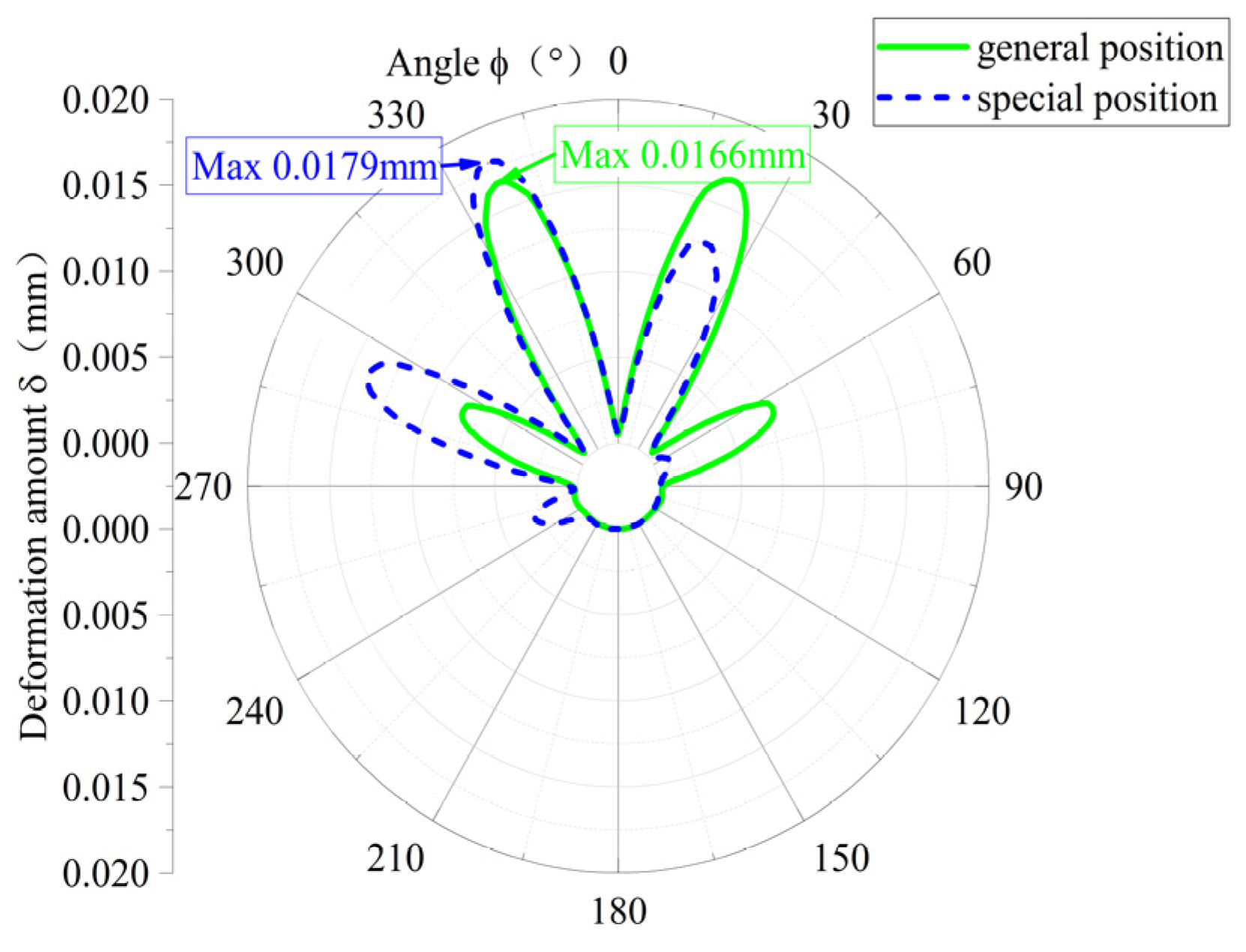
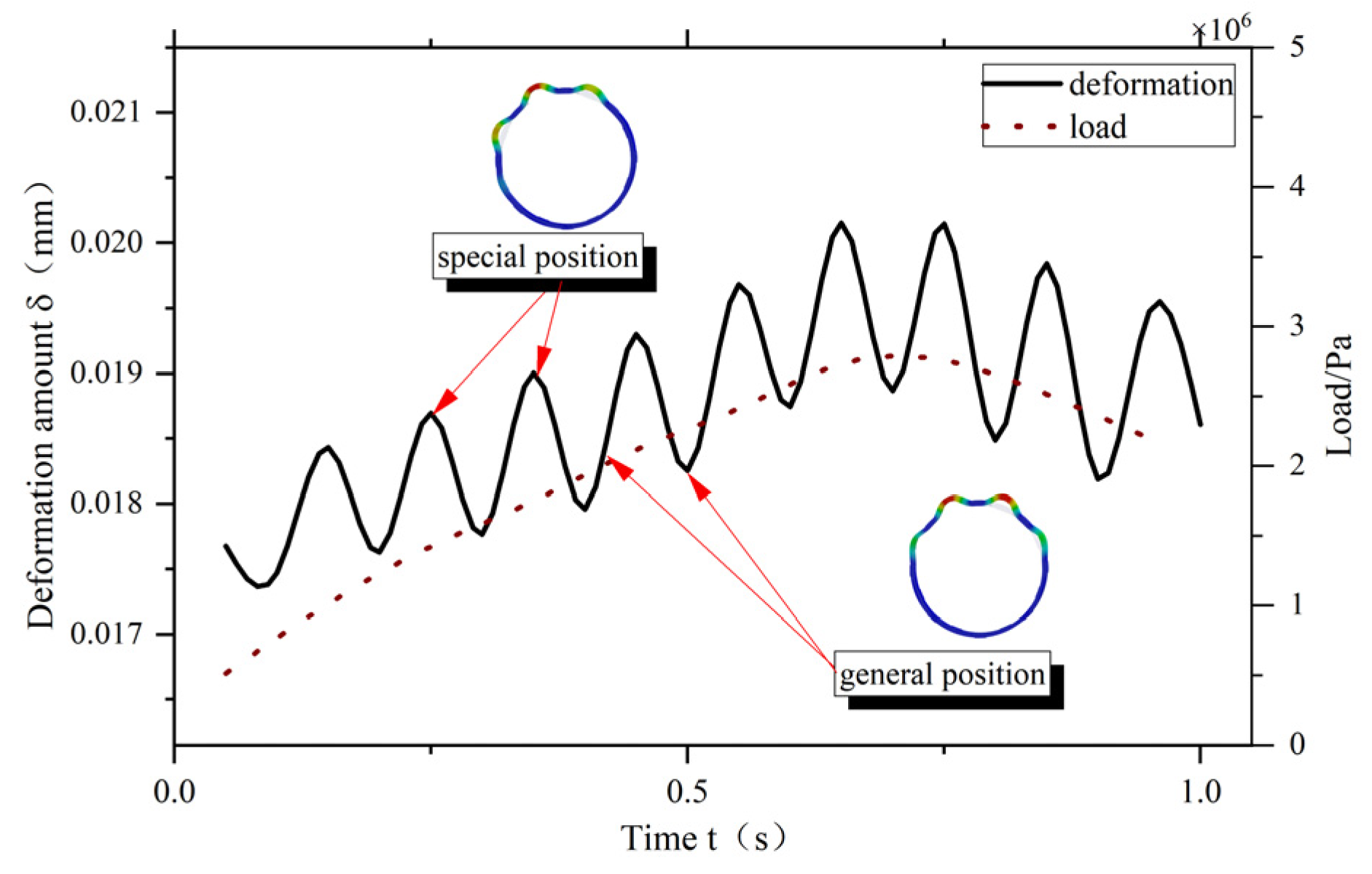
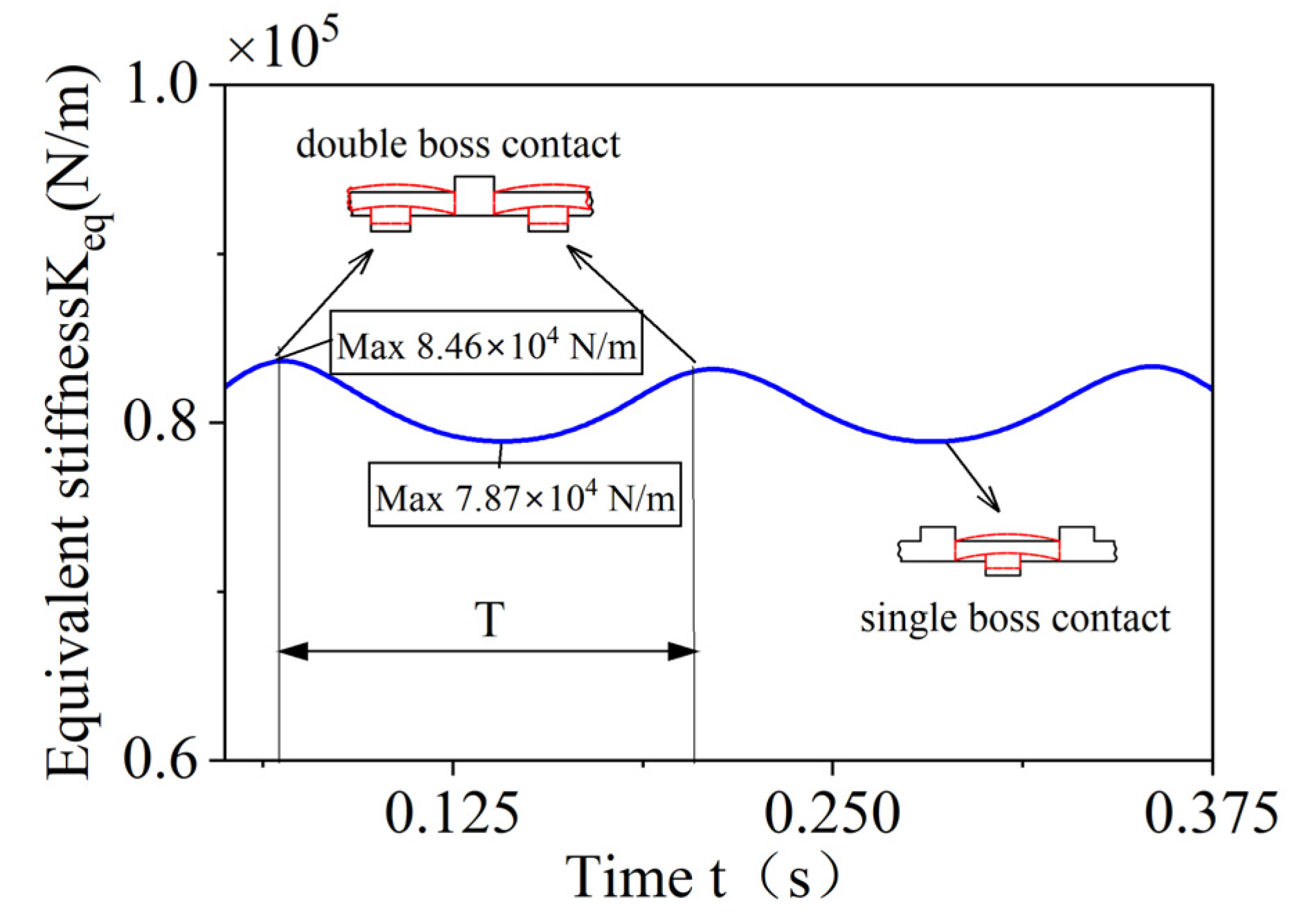

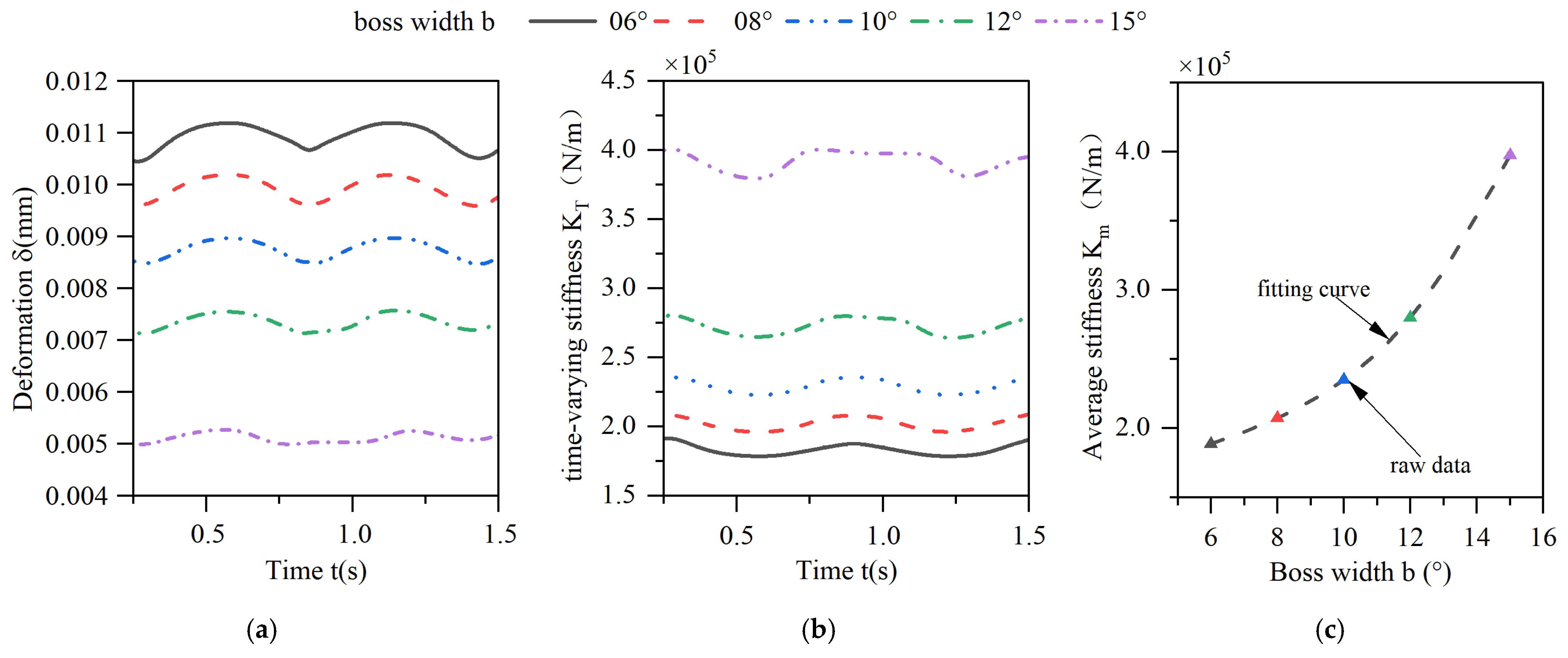



| Variable | Parameters | Deformation (mm) | Degree (%) | Degree (%) | Variable | Parameters | Deformation (mm) | Degree (%) | Rigidity | Degree (%) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 4 | 0.0343 | 281 | 0.812 | −65 | b | 06 | 0.0112 | 24 | 1.880 | −17 |
| 6 | 0.0168 | 86 | 1.333 | −42 | 08 | 0.0101 | 12 | 2.076 | −8 | ||
| 8 | 0.0090 | 0 | 2.267 | 0 | 10 | 0.0090 | 0 | 2.267 | 0 | ||
| 12 | 0.0017 | −81 | 12.050 | 430 | 12 | 0.0076 | −15 | 2.801 | 24 | ||
| 10 | 0.0094 | 4 | 2.156 | −5 | s | 08 | 0.0254 | 180 | 0.840 | −62 | |
| 15 | 0.0090 | 0 | 2.267 | 0 | 10 | 0.0179 | 98 | 1.190 | −47 | ||
| 20 | 0.0085 | 5 | 2.591 | 14 | 12 | 0.0132 | 47 | 1.610 | −30 | ||
| 25 | 0.0081 | 10 | 2.720 | 20 | 15 | 0.0090 | 0 | 2.267 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Liu, F.; Liu, T.; Wang, Q. Dynamics Analysis of Elastic Ring-Type Extruded Oil Film Damper Considering Time-Varying Characteristics. Materials 2025, 18, 1933. https://doi.org/10.3390/ma18091933
Zhang H, Liu F, Liu T, Wang Q. Dynamics Analysis of Elastic Ring-Type Extruded Oil Film Damper Considering Time-Varying Characteristics. Materials. 2025; 18(9):1933. https://doi.org/10.3390/ma18091933
Chicago/Turabian StyleZhang, Haibiao, Fuhua Liu, Tao Liu, and Qingshan Wang. 2025. "Dynamics Analysis of Elastic Ring-Type Extruded Oil Film Damper Considering Time-Varying Characteristics" Materials 18, no. 9: 1933. https://doi.org/10.3390/ma18091933
APA StyleZhang, H., Liu, F., Liu, T., & Wang, Q. (2025). Dynamics Analysis of Elastic Ring-Type Extruded Oil Film Damper Considering Time-Varying Characteristics. Materials, 18(9), 1933. https://doi.org/10.3390/ma18091933








