A Method for Calculating Residual Strength of Crack Arrest Hole on Tungsten-Copper Functionally Graded Materials by Phase-Field Gradient Element Combined with Multi-Fidelity Neural Network
Abstract
1. Introduction
2. The Present Method Introduction
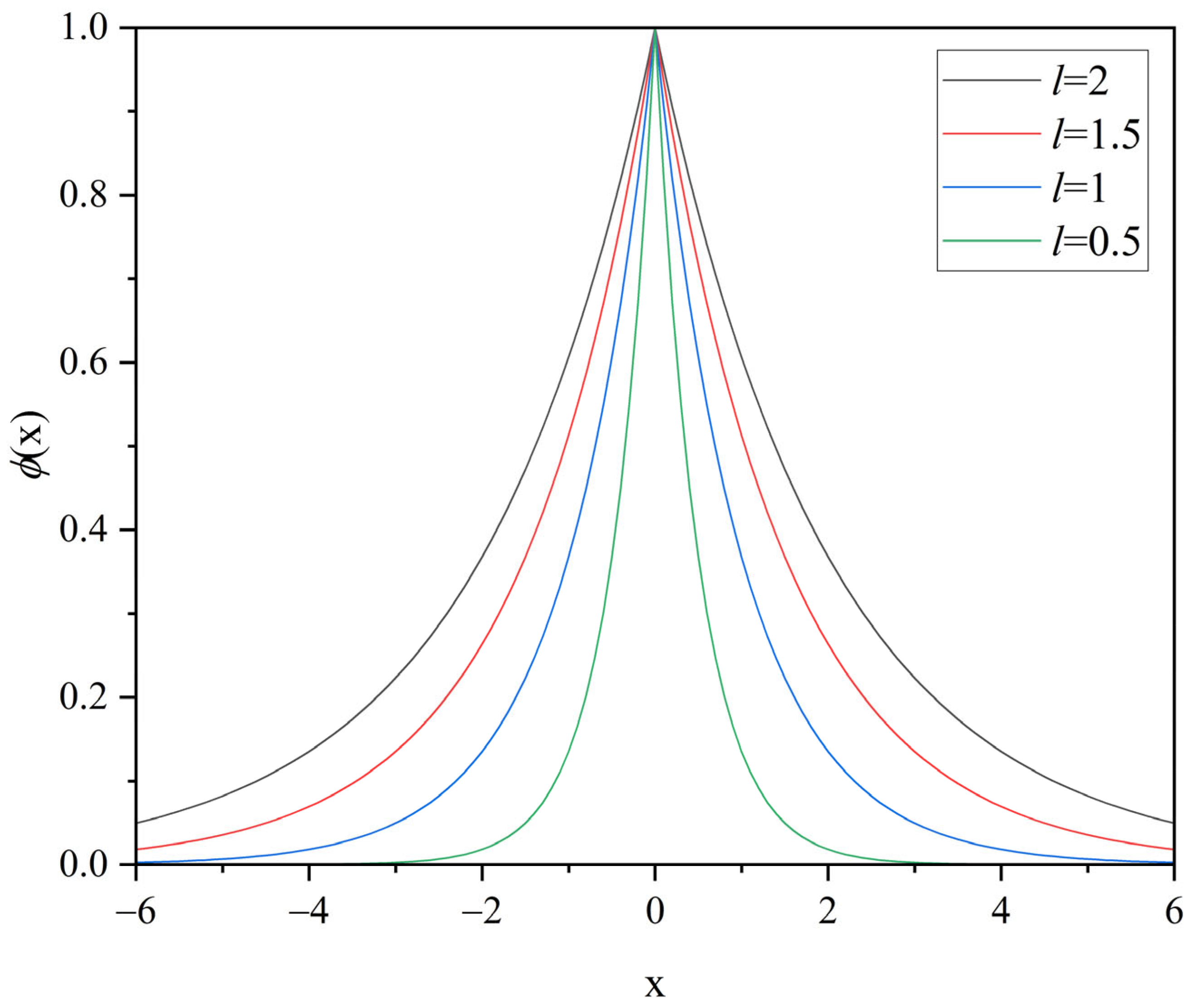
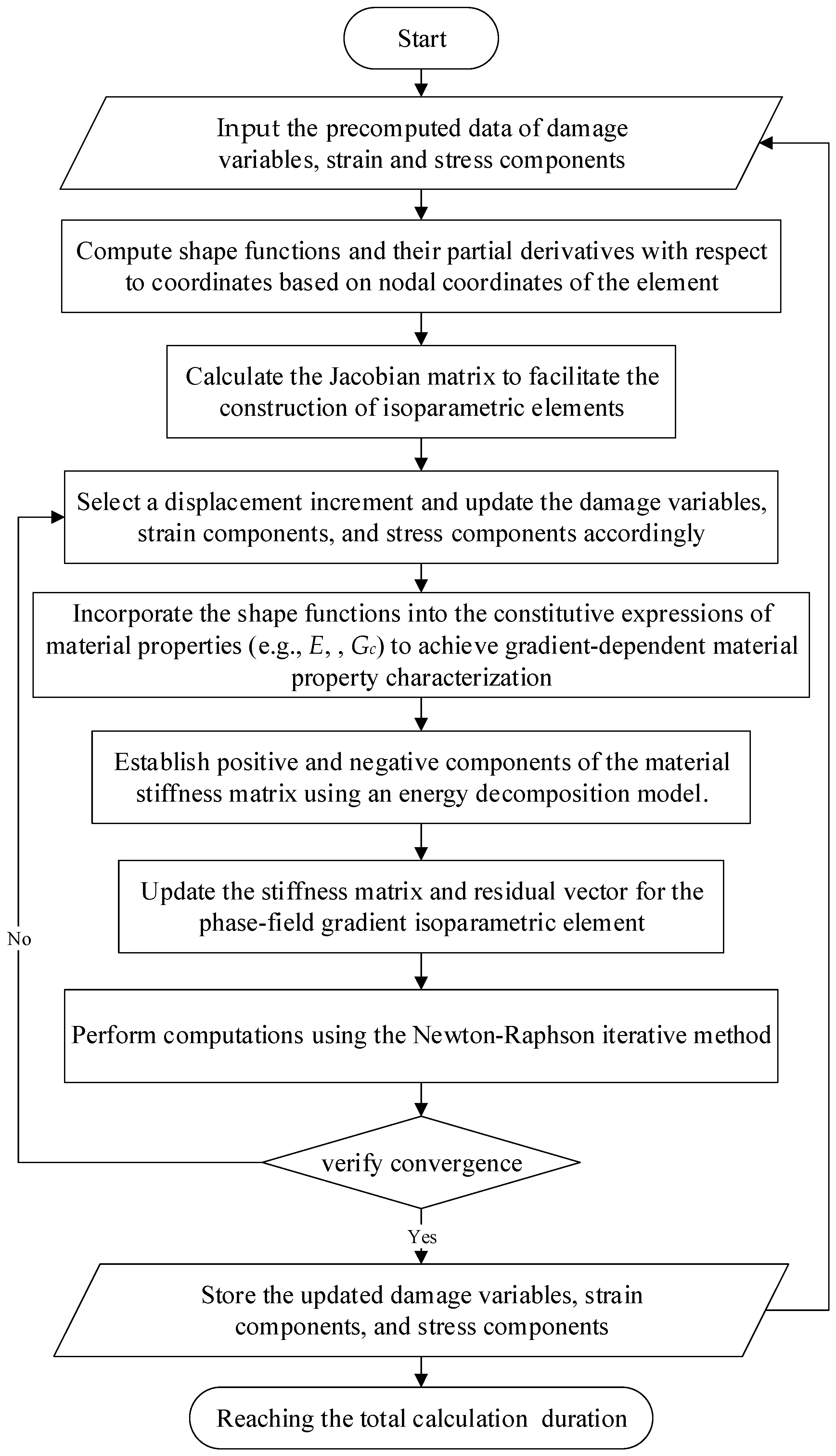
2.1. Phase Field Gradient Finite Element
2.2. Elastic Energy Decomposition Scheme
2.3. Decoupling Between Displacement and Damage
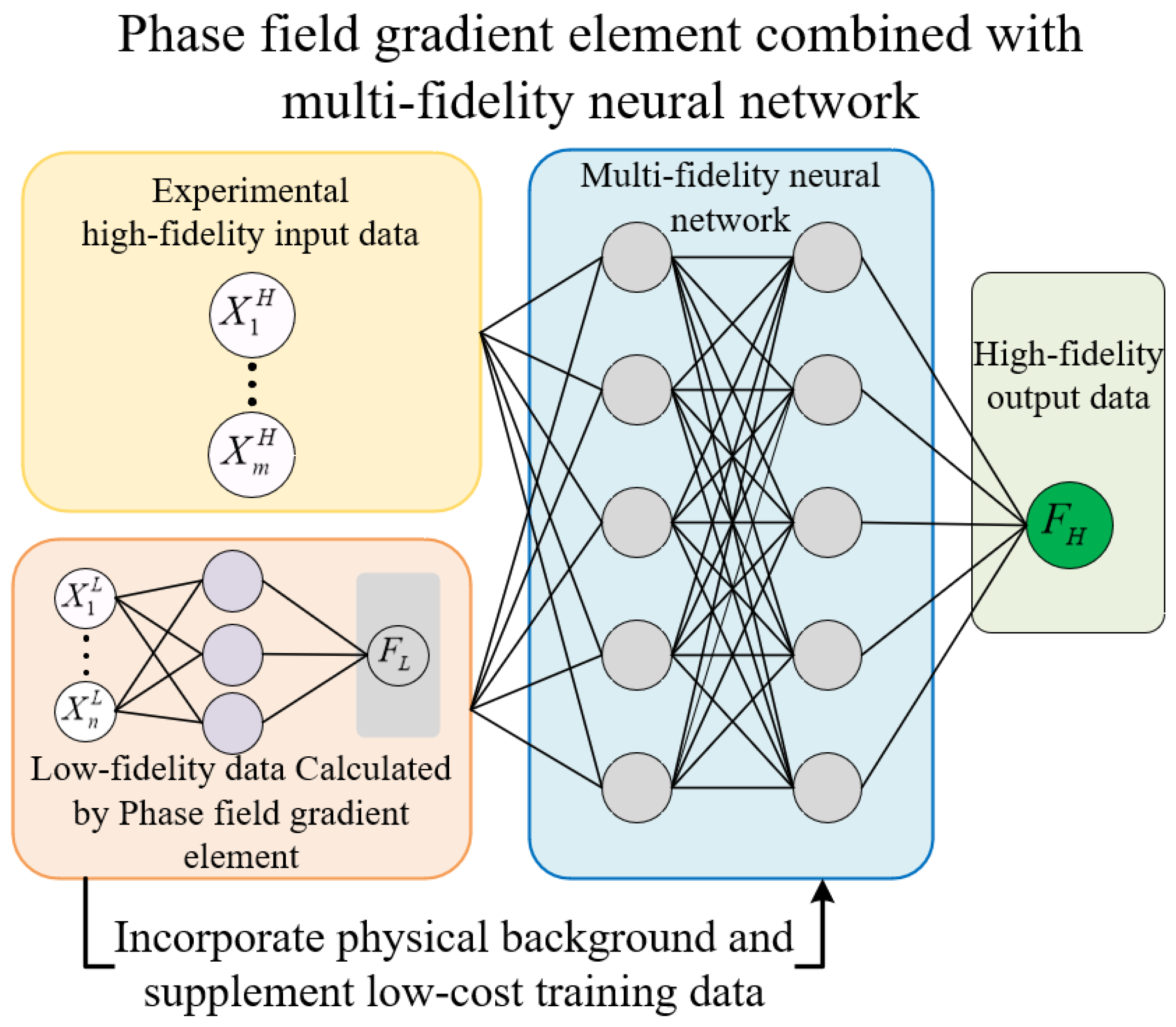
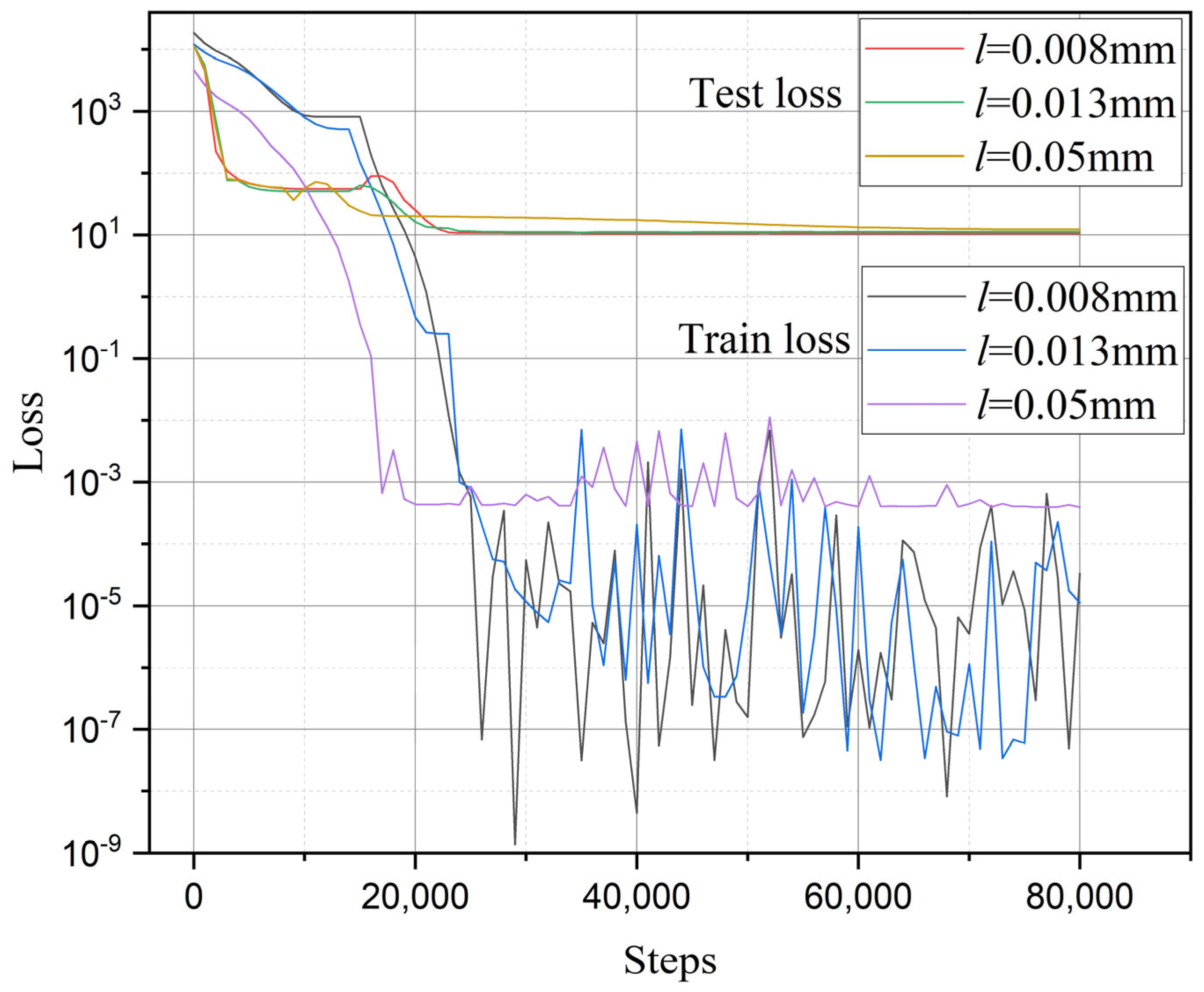
2.4. Phase Field Gradient Finite Element Combined with Multi-Fidelity Neural Network
3. Model Validation and Results Discussion
3.1. Calculation of Stress and Damage Field
3.2. Calculation of Crack Propagation Path
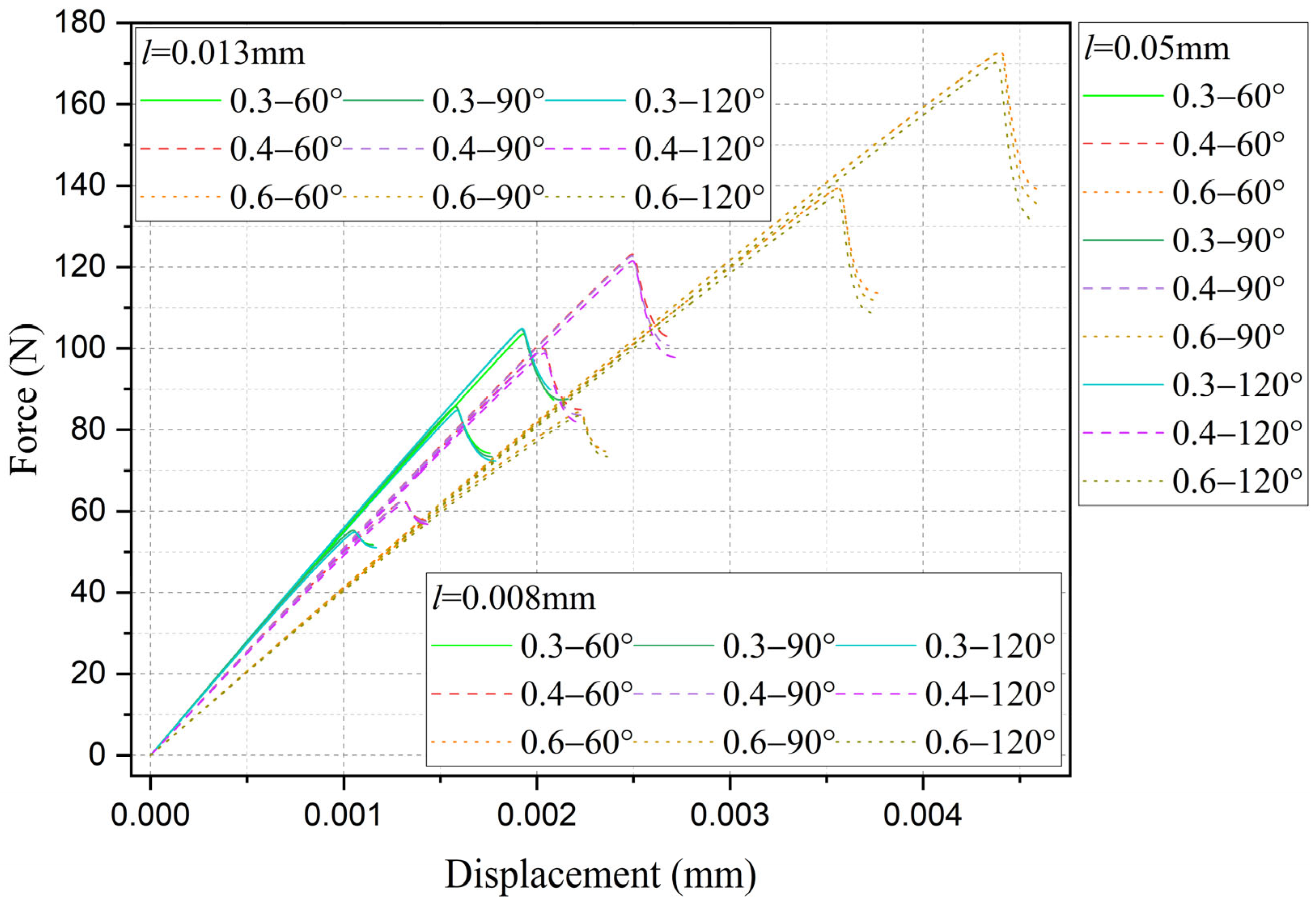
3.3. Sensitivity of Residual Strength to Characteristic Width
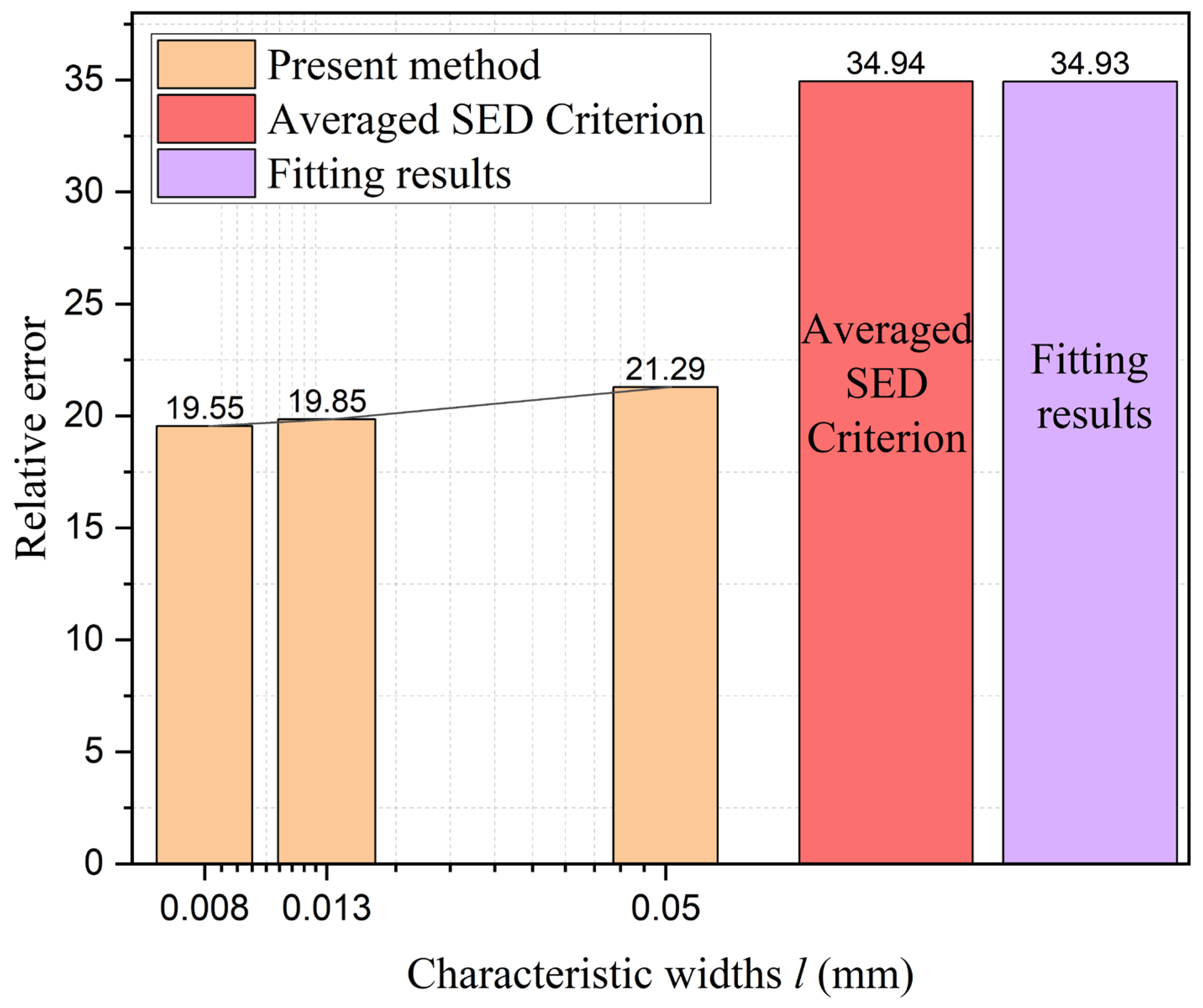
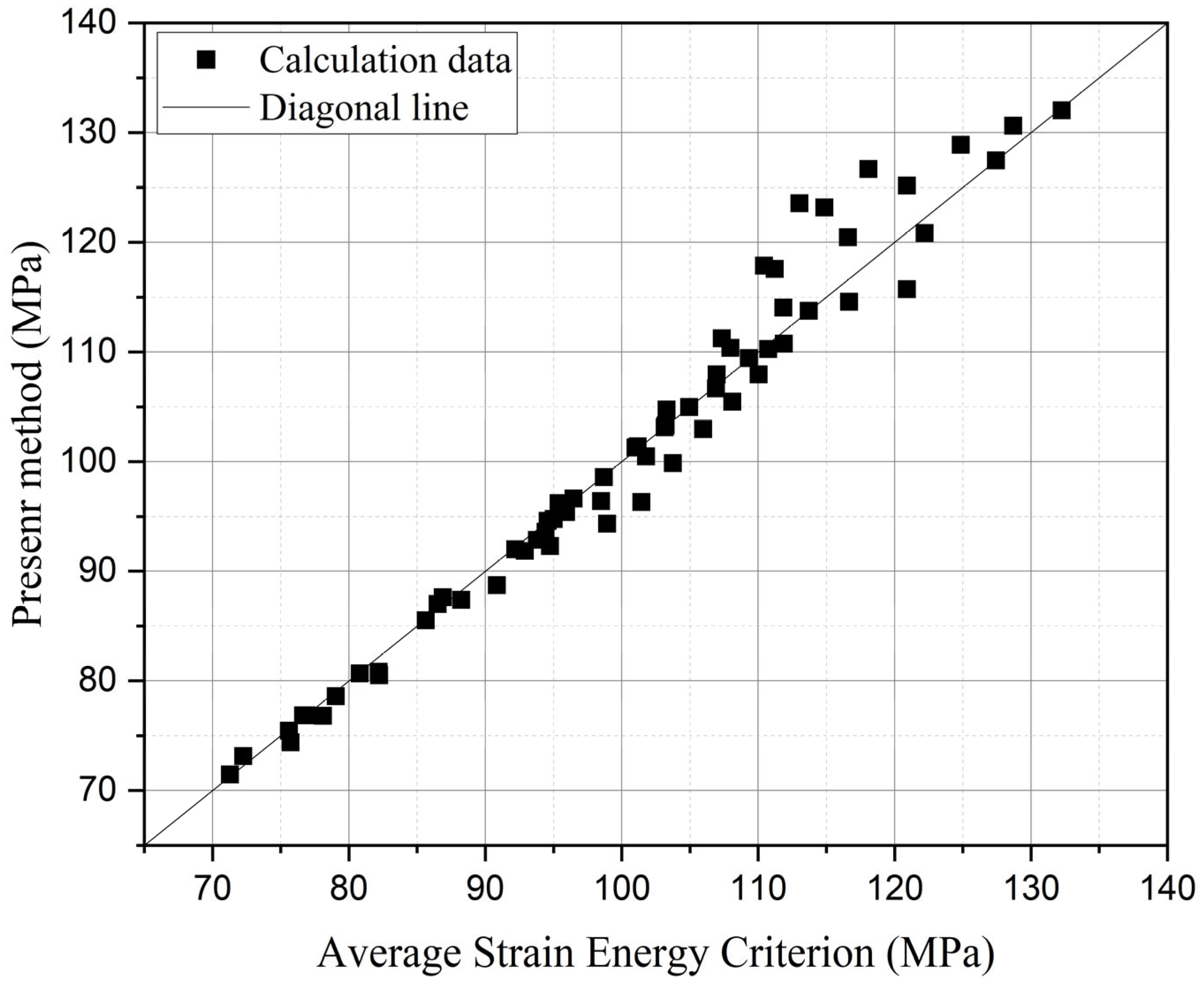
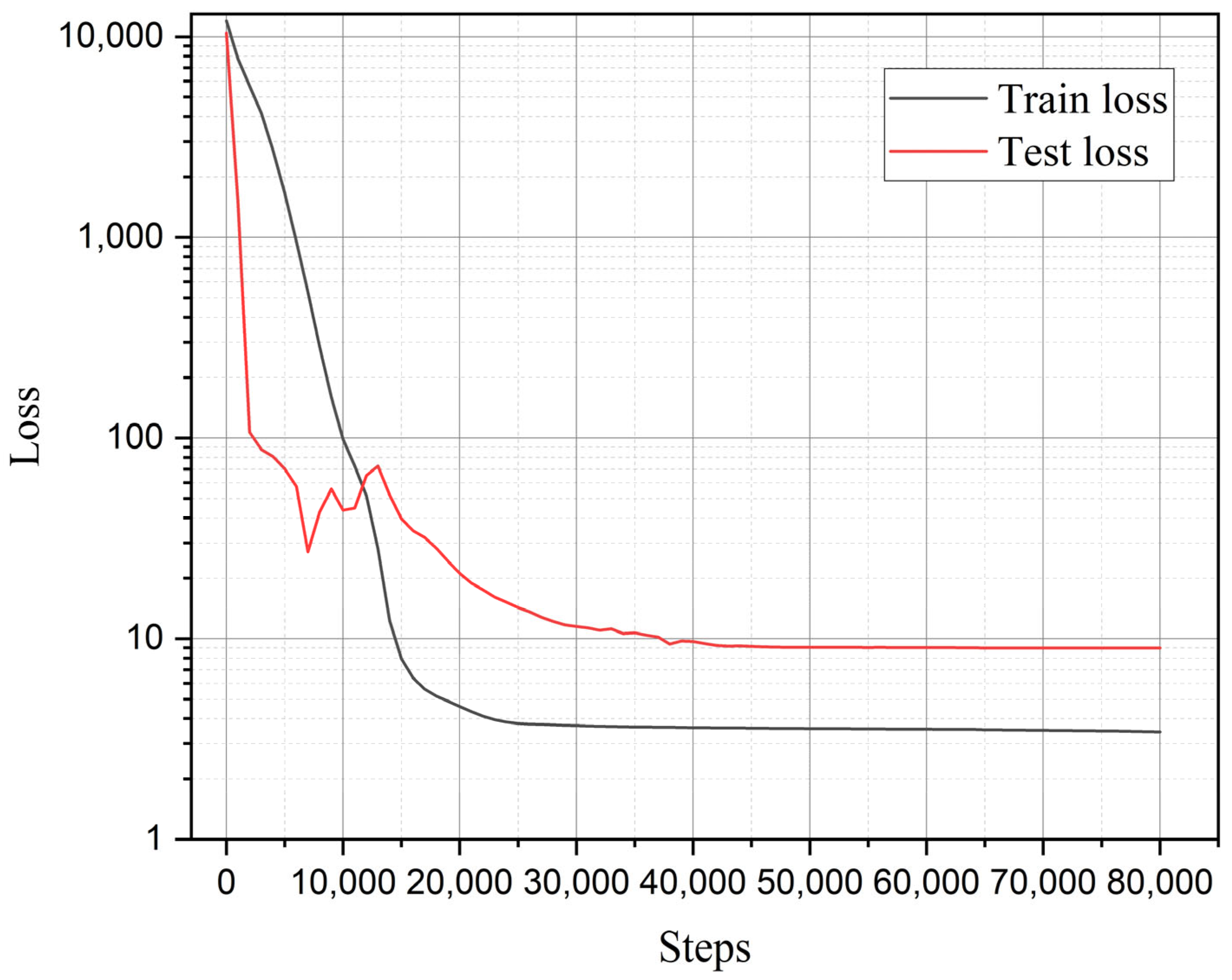
3.4. Optimization Results of Multi-Fidelity Neural Networks
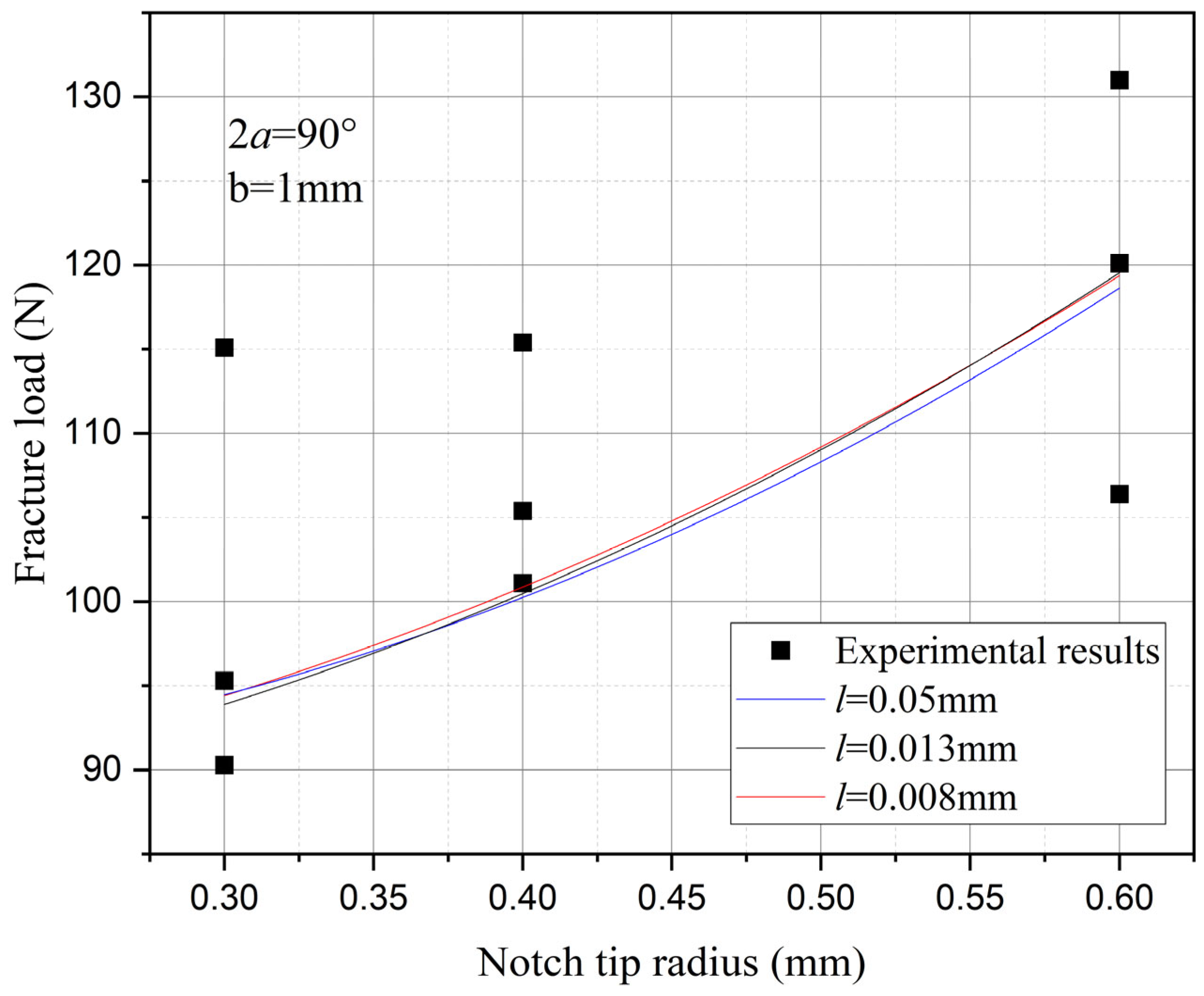
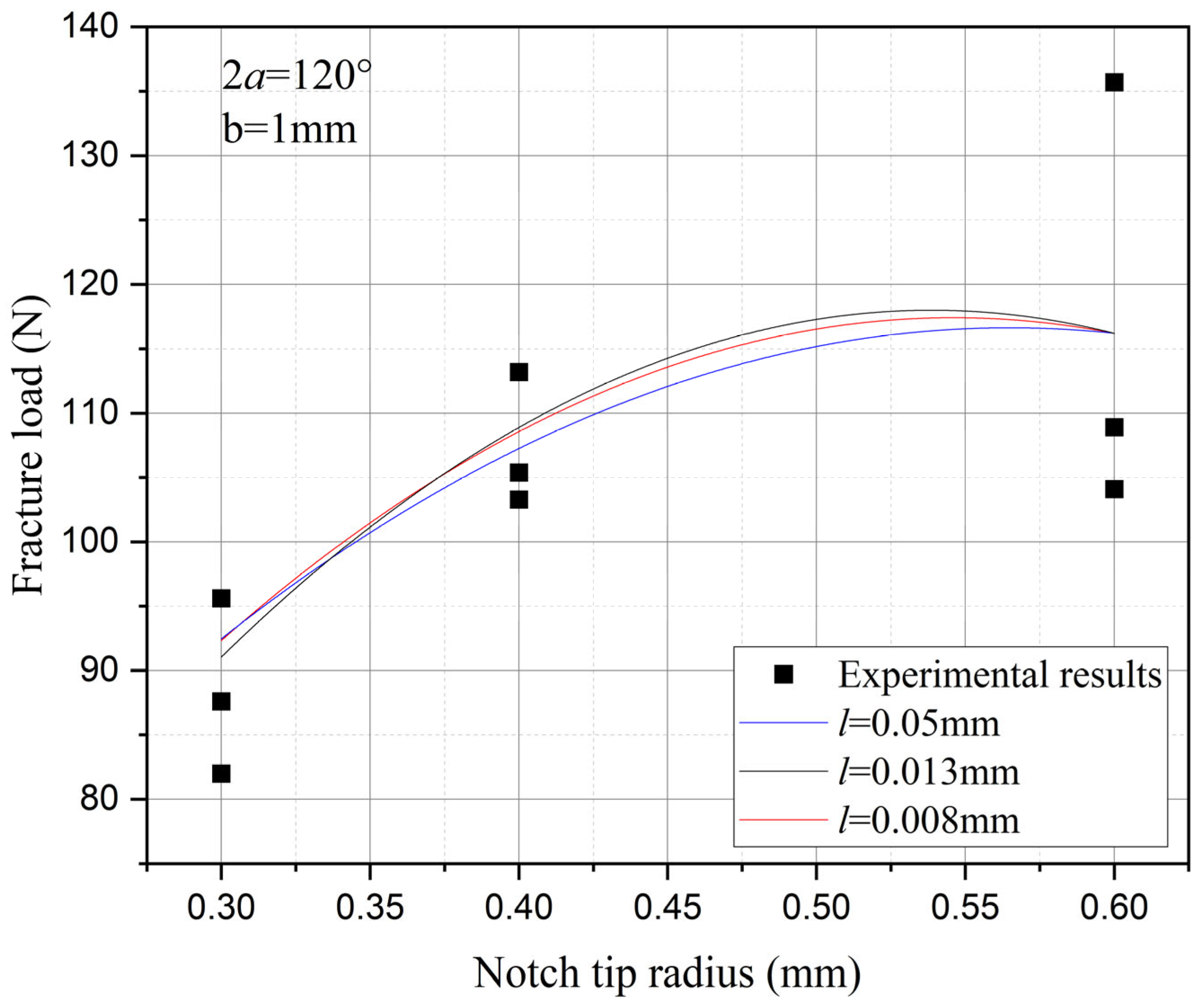
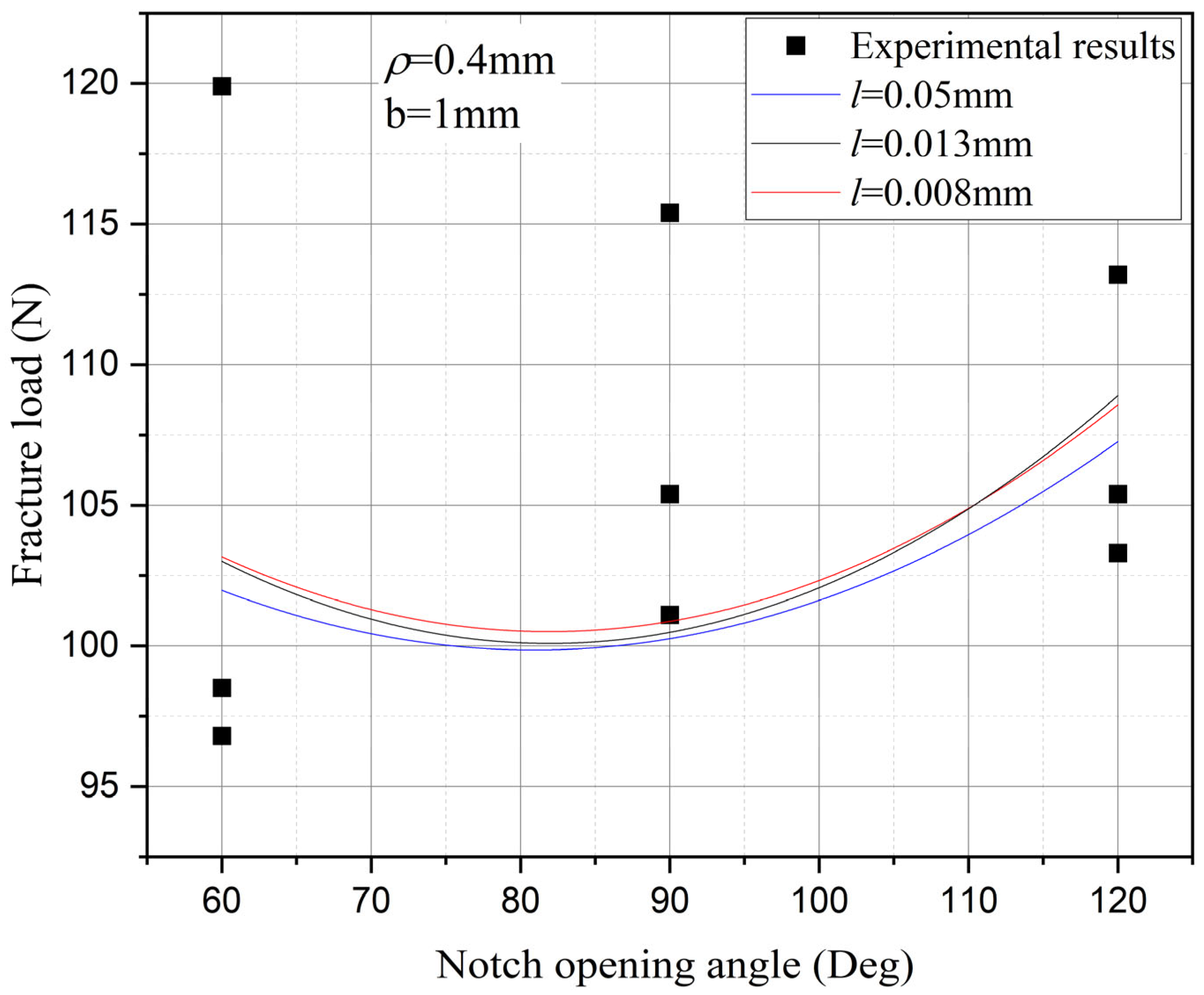
3.5. The Influence of the Notch Size on the Fracture Strength
4. Conclusions
- A phase-field graded isoparametric element is formulated by embedding gradient characterization into the stiffness matrix constitutive framework. The proposed graded elements are superior to conventional homogeneous elements based on the same shape functions in the calculation of stress and damage fields.
- Compared with the Amor model, the Miehe model combined with graded element can accurately predict crack propagation paths, types, and residual strength distribution trends.
- The characteristic width is the predominant factor influencing the strength evaluation. The proposed method can reduce the sensitivity of the residual strength to the characteristic width by combining the phase field graded finite element with the multi-fidelity neural networks.
- For the studied tungsten-copper functional gradient material, within a certain range, a larger notch unexpectedly results in higher residual strength. The methodology presented in this paper can accurately characterize this abnormal phenomenon.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lei, X.; Li, C.; Shi, X.; Xu, X.; Wei, Y. Notch strengthening or weakening governed by transition of shear failure to normal mode fracture. Sci. Rep. 2015, 5, 10537. [Google Scholar] [CrossRef] [PubMed]
- Torabi, A.R.; Campagnolo, A.; Berto, F. Local strain energy density to predict mode II brittle fracture in Brazilian disk specimens weakened by V-notches with end holes. Mater. Des. 2015, 69, 22–29. [Google Scholar] [CrossRef]
- Razavi, S.M.J.; Ayatollahi, M.R.; Sommitsch, C.; Moser, C. Retardation of fatigue crack growth in high strength steel {S690} using a modified stop-hole technique. Eng. Fract. Mech. 2017, 169, 226–237. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Razavi, N.; Sommitsch, C.; Moser, C. Fatigue Life Extension by Crack Repair Using Double Stop-Hole Technique. Mater. Sci. Forum 2016, 879, 3–8. [Google Scholar] [CrossRef]
- Salavati, H.; Mohammadi, H.; Yusefi, A.; Berto, F. Fracture assessment of V-notched specimens with end holes made of tungsten-copper functionally graded material under mode I loading. Theor. Appl. Fract. Mech. 2018, 97, 357–367. [Google Scholar] [CrossRef]
- Pour, H.S.S.; Zehsaz, M.; Chakherlou, T.N.; Salavati, H. Prevalent Mode II Fracture Investigation of VO-Notched Specimens Made of Tungsten–Copper Functionally Graded Materials. Phys. Mesomech. 2020, 23, 430–438. [Google Scholar] [CrossRef]
- Mohammadi, H.; Salavati, H.; Mosaddeghi, M.R.; Yusefi, A.; Berto, F. Local strain energy density to predict mixed mode I + II fracture in specimens made of functionally graded materials weakened by V-notches with end holes. Theor. Appl. Fract. Mech. 2017, 92, 47–58. [Google Scholar] [CrossRef]
- Mohammadi, H.; Salavati, H.; Alizadeh, Y.; Berto, F. Prevalent mode II fracture assessment of inclined U-notched specimens made of tungsten-copper functionally graded material. Theor. Appl. Fract. Mech. 2017, 89, 90–99. [Google Scholar] [CrossRef]
- Martínez-Paeda, E.; Golahmar, A.; Niordson, C.F. A phase field formulation for hydrogen assisted cracking. Comput. Methods Appl. Mech. Eng. 2018, 342, 742–761. [Google Scholar] [CrossRef]
- Ge, X.; Zhou, L.; Ying, Y.; Bagherifard, S.; Guagliano, M. Combining phase field method and critical distance theory for predicting fatigue life of notched specimens. Int. J. Mech. Sci. 2024, 282, 109608. [Google Scholar] [CrossRef]
- Borden, M.J.; Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.R.; Landis, C.M. A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 2012, 217–220, 77–95. [Google Scholar] [CrossRef]
- Yu, Y.; Hou, C.; Zheng, X.; Zhao, M. Phase field modeling for composite material failure. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 14429. [Google Scholar] [CrossRef]
- Hirshikesh; Martínez-Paeda, E.; Natarajan, S. Adaptive phase field modelling of crack propagation in orthotropic functionally Graded materials. Def. Technol. 2021, 17, 185–195. [Google Scholar] [CrossRef]
- Bourdin, B.; Marigo, J.J.; Maurini, C.; Sicsic, P. Morphogenesis and propagation of complex cracks induced by thermal shocks. Phys. Rev. Lett. 2014, 112, 014301. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.T.; Yvonnet, J.; Bornert, M.; Chateau, C.; Sab, K.; Romani, R.; Le Roy, R. On the choice of parameters in the phase field method for simulating crack initiation with experimental validation. Int. J. Fract. 2016, 197, 213–226. [Google Scholar] [CrossRef]
- Tanne, E.; Li, T.; Bourdin, B.; Marigo, J.-J.; Maurini, C. Crack nucleation in variational phase-field models of brittle fracture. J. Mech. Phys. Solids 2018, 110, 80–99. [Google Scholar] [CrossRef]
- Kumar, A.; Bourdin, B.; Francfort, G.A.; Lopez-Pamies, O. Revisiting nucleation in the phase-field approach to brittle fracture. J. Mech. Phys. Solids 2020, 142, 104027. [Google Scholar] [CrossRef]
- Goswami, S.; Anitescu, C.; Rabczuk, T. Adaptive fourth-order phase field analysis using deep energy minimization. Theor. Appl. Fract. Mech. 2020, 107, 102527. [Google Scholar] [CrossRef]
- Samaniego, E.; Anitescu, C.; Goswami, S.; Nguyen-Thanh, V.N.; Guo, H.; Hamdia, K.; Zhuang, X.; Rabczuk, T. An energy approach to the solution of partial differential equations in computational mechanics via machine learning: Concepts, implementation and applications. Comput. Methods Appl. Mech. Eng. 2020, 362, 112790. [Google Scholar] [CrossRef]
- Feng, S.Z.; Xu, Y.; Han, X.; Li, Z.X.; Incecik, A. A phase field and deep-learning based approach for accurate prediction of structural residual useful life. Comput. Methods Appl. Mech. Eng. 2021, 383, 113885. [Google Scholar] [CrossRef]
- Vlassis, N.N.; Ma, R.; Sun, W. Geometric deep learning for computational mechanics part i: Anisotropic hyperelasticity. Comput. Methods Appl. Mech. Eng. 2020, 371, 113299. [Google Scholar] [CrossRef]
- De Moraes, E.A.B.; Salehi, H.; Zayernouri, M. Data-driven failure prediction in brittle materials: A phase field-based machine learning framework. J. Mach. Learn. Model. Comput. 2021, 2, 65–89. [Google Scholar] [CrossRef]
- Meng, X.; Karniadakis, G.E. A composite neural network that learns from multi-fidelity data: Application to function approximation and inverse PDE problems. J. Comput. Phys. 2020, 401, 109020. [Google Scholar] [CrossRef]
- Kim, J.H.; Paulino, G.H. Isoparametric Graded Finite Elements for Nonhomogeneous Isotropic and Orthotropic Materials. J. Appl. Mech. 2002, 69, 502–514. [Google Scholar] [CrossRef]
- Amor, H.; Marigo, J.J.; Maurini, C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments. J. Mech. Phys. Solids 2009, 57, 1209–1229. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Wu, J.Y.; Nguyen, V.P.; Nguyen, C.T.; Sutula, D.; Sinaie, S.; Bordas, S. Phase-field modeling of fracture. In Advances in Applied Mechanics (Fracture Mechanics: Recent Developments and Trends); Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
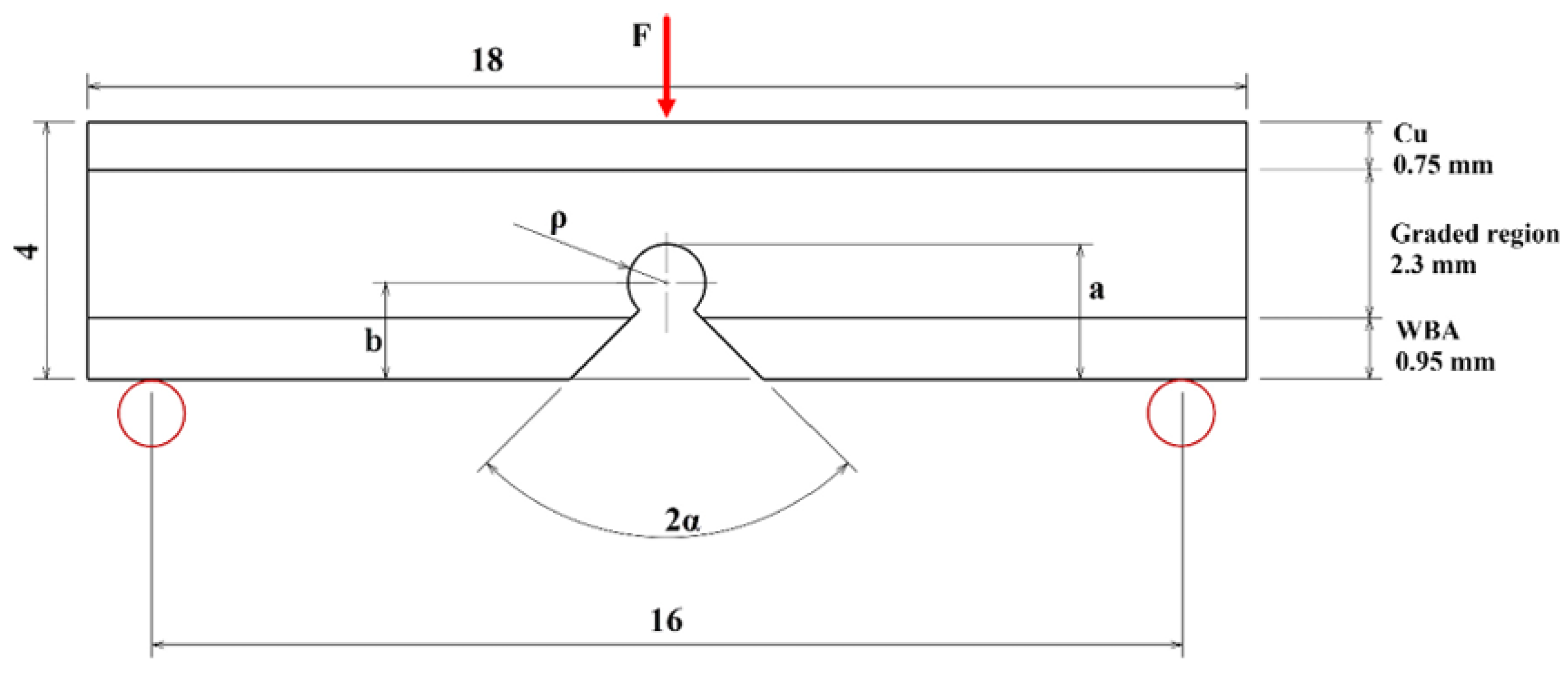
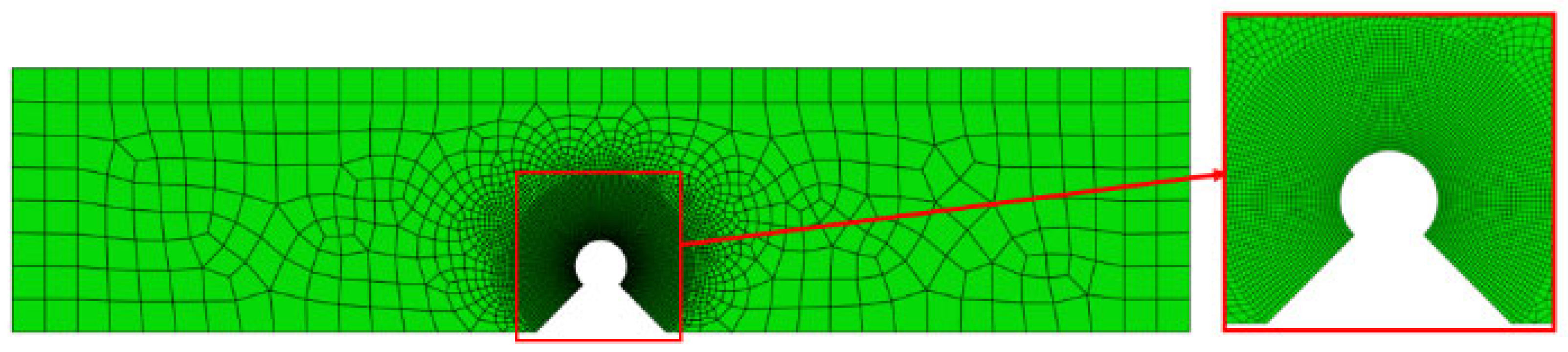
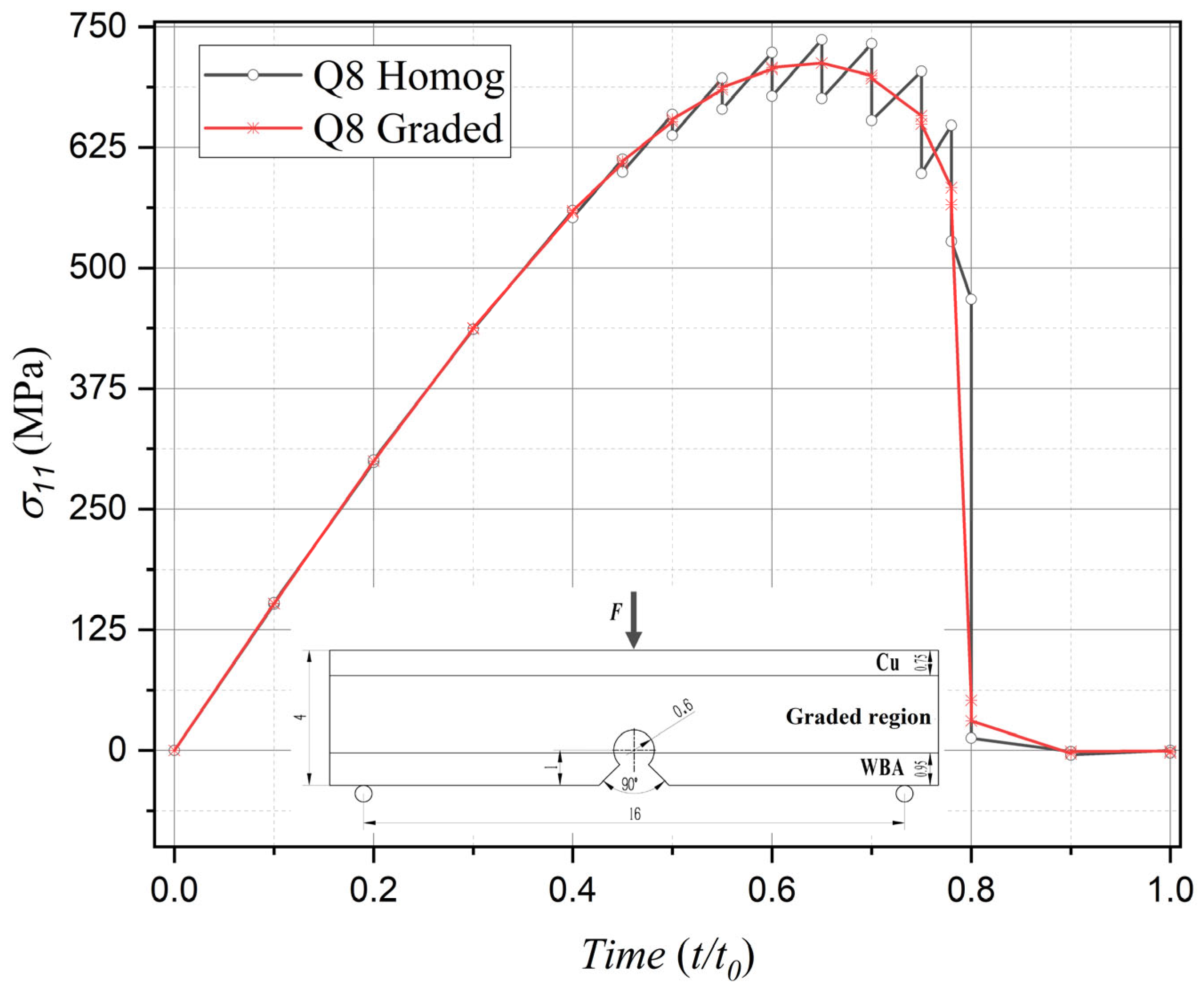
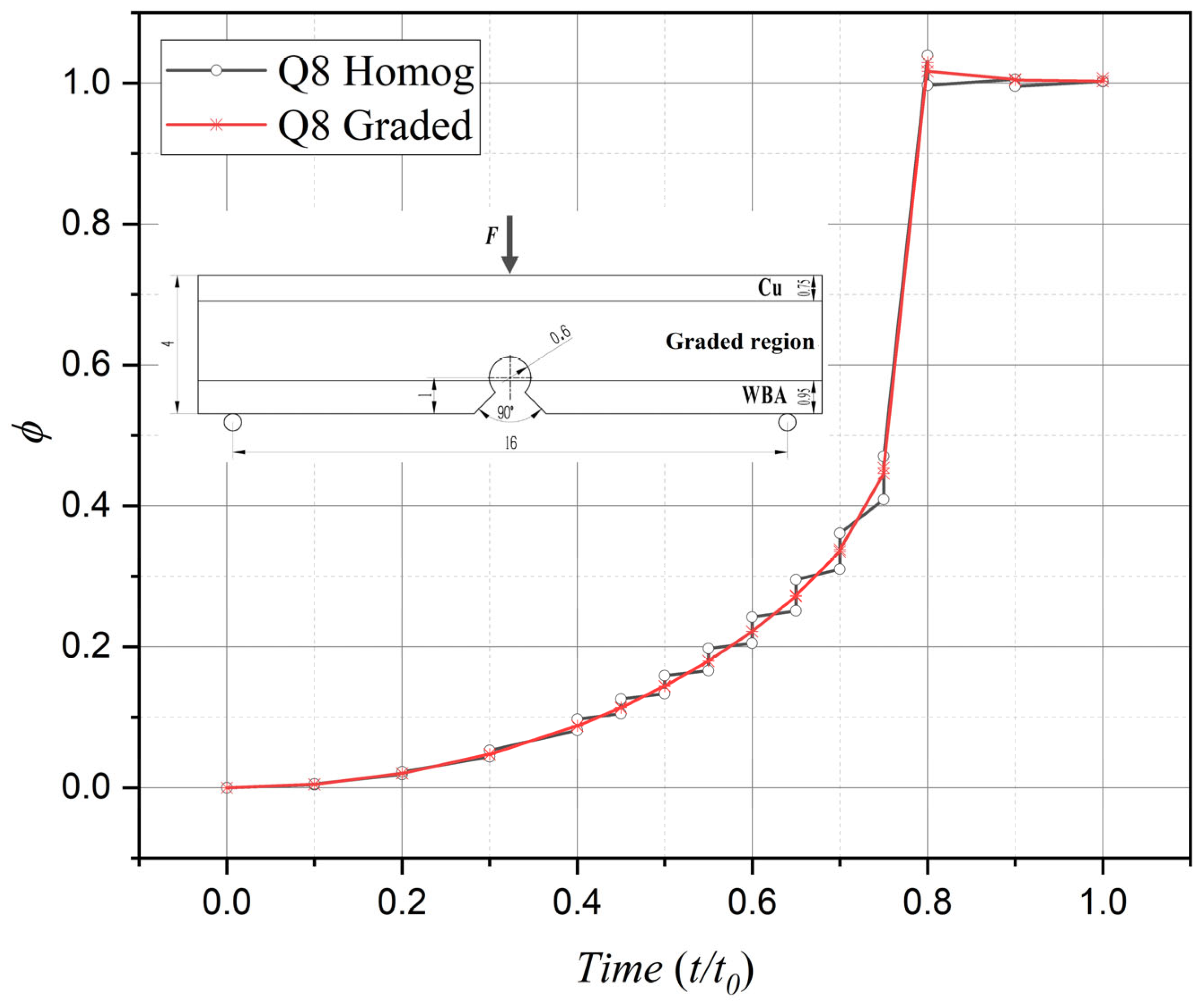
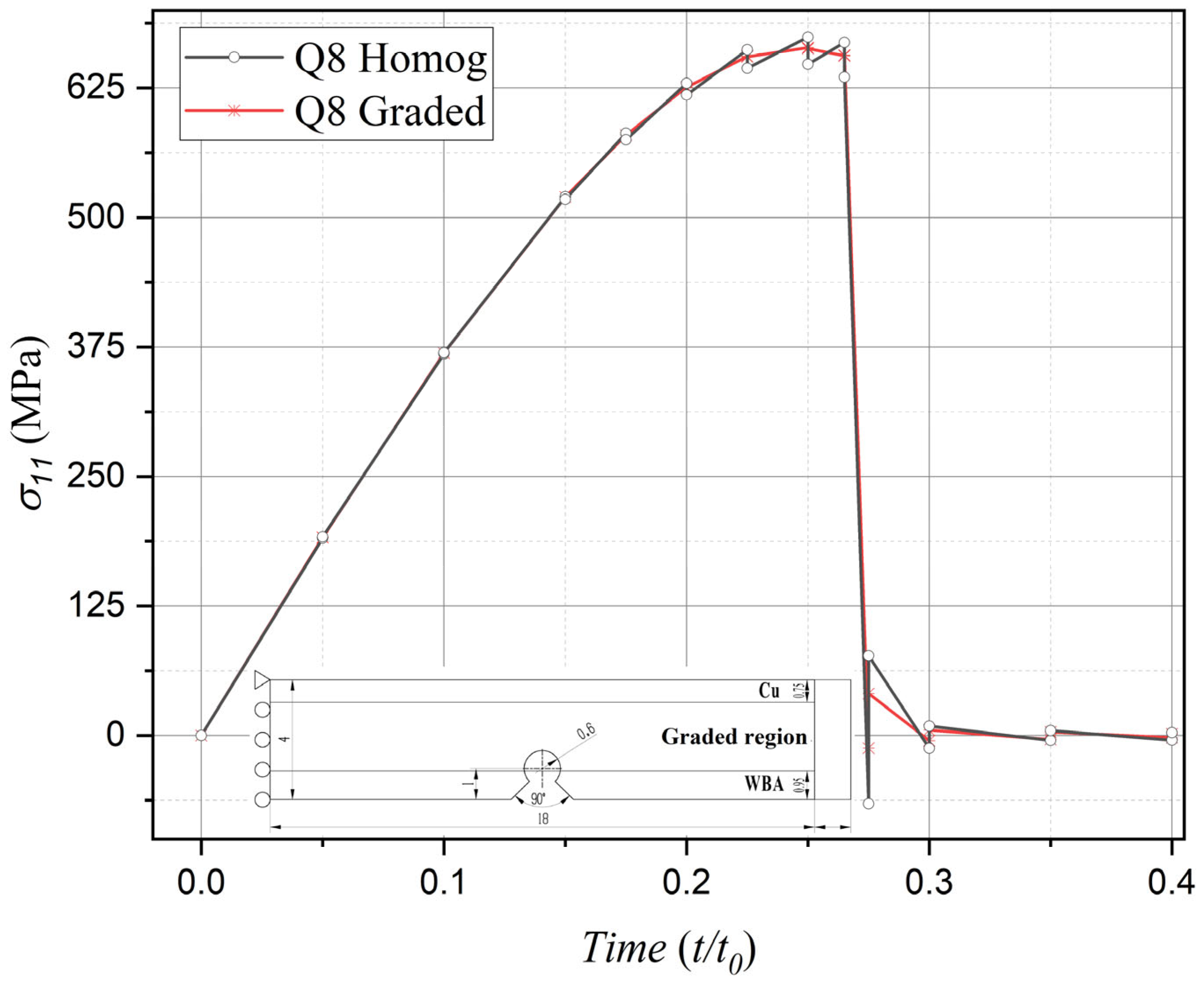
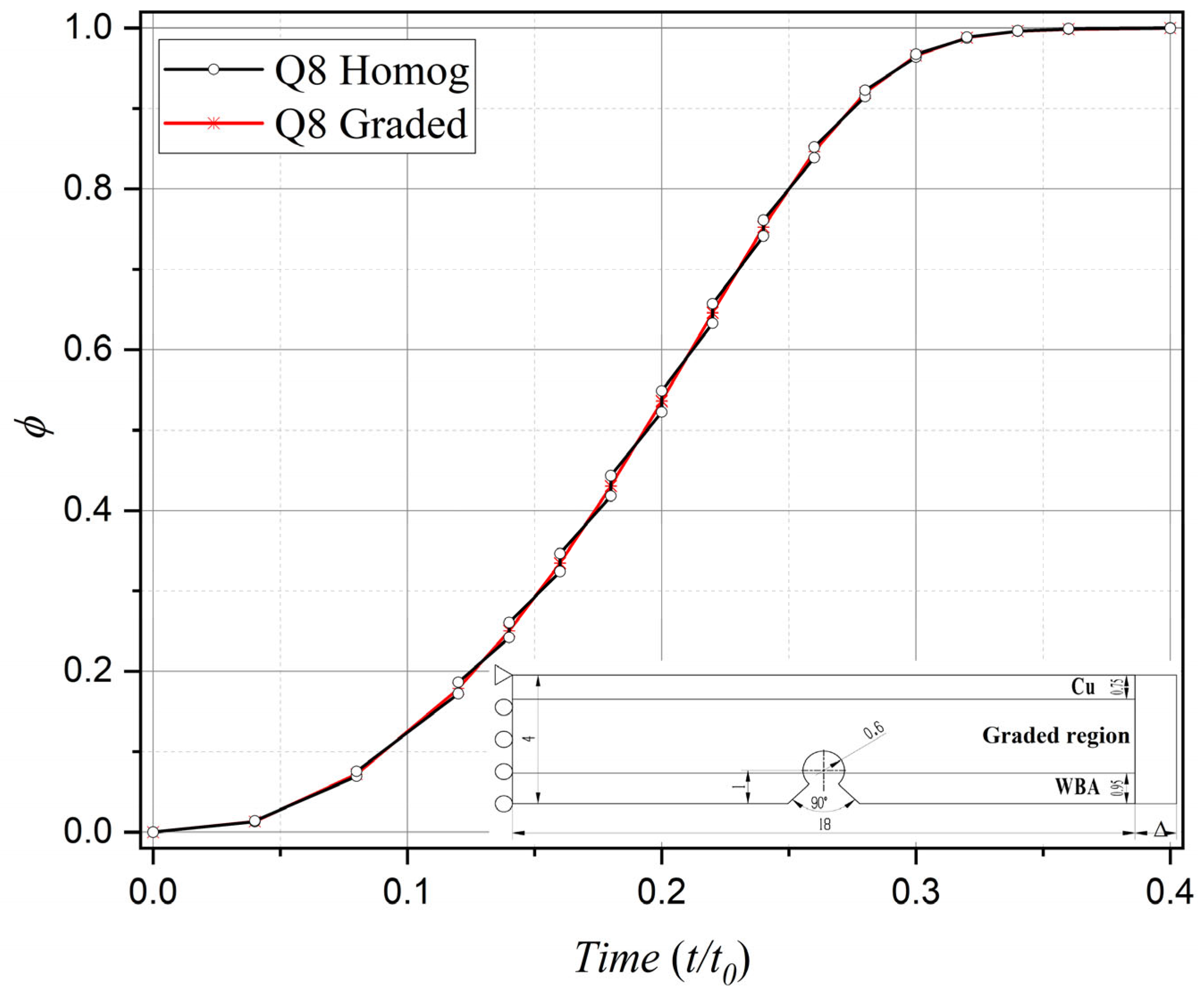


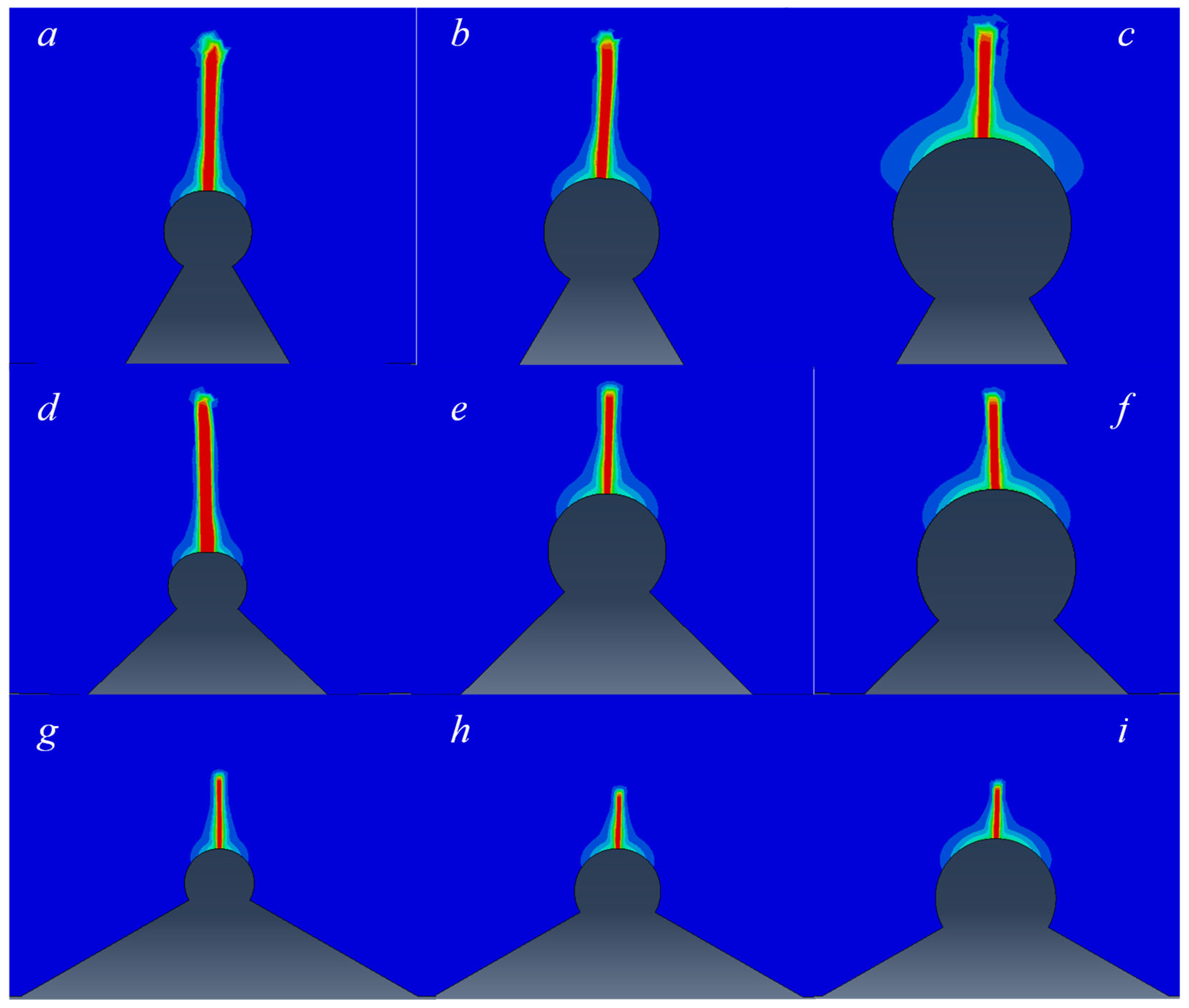

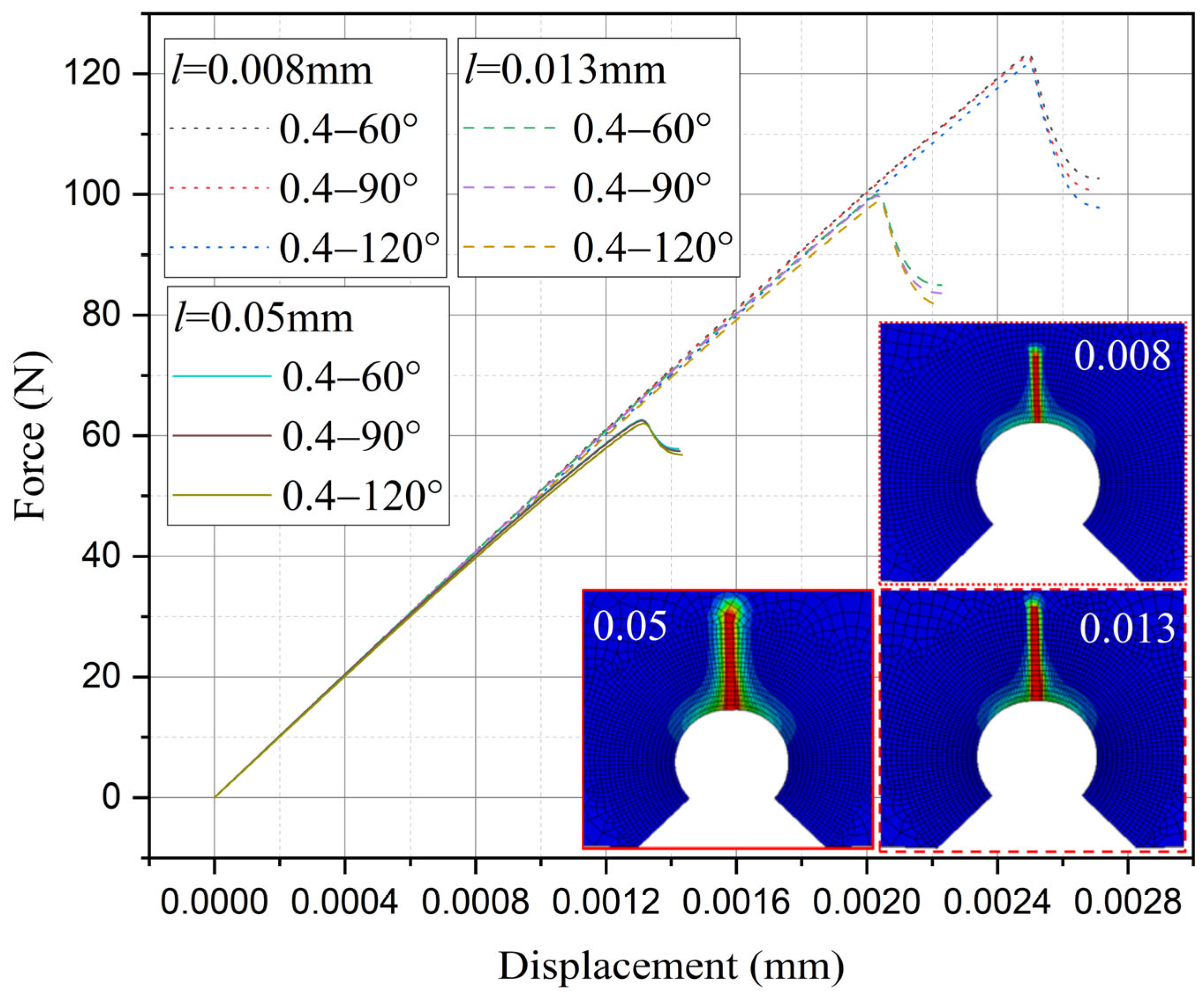
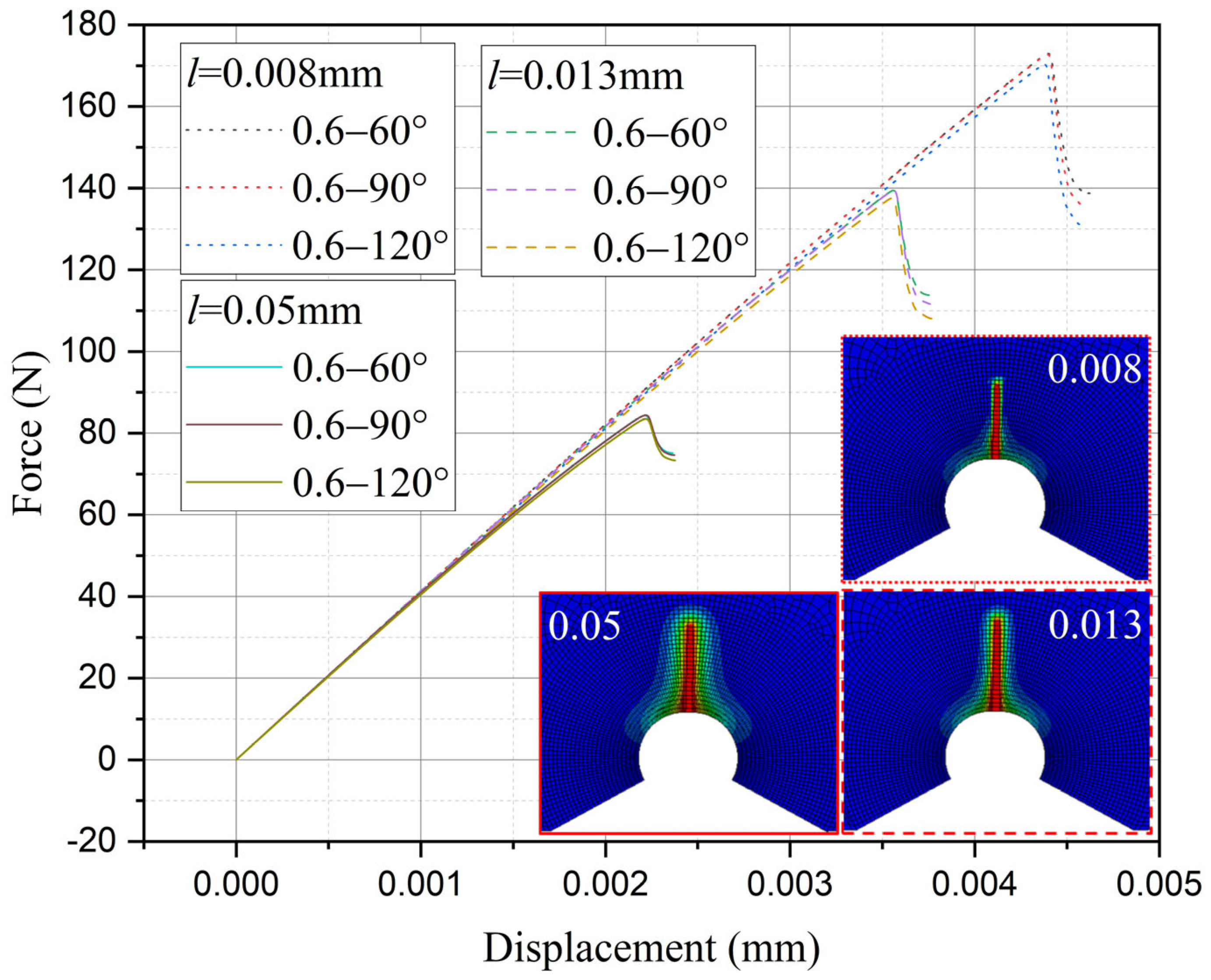




| Boundary Regions | Elasticity Modulus E (GPa) | Poisson’s Ratio ν | Ultimate Tensile (MPa) | Fracture Toughness KIc (MPa.m 0.5) | n | n1 | n2 |
|---|---|---|---|---|---|---|---|
| Cu | 112.7 | 0.34 | 188.9 | 88.5 | 0.9646 | 1.312 | 2.78 |
| WBA | 289.5 | 0.29 | 447.3 | 4.52 |
| Model No. | ρ (mm) | a (mm) | PFG (MPa) | SED (MPa) | PFG with MFNN (MPa) |
|---|---|---|---|---|---|
| 1 * | 0.05 | 1 | 70.88 | 76.64 | 76.87 |
| 2 | 0.1 | 1 | 79.21 | 85.63 | 85.54 |
| 3 | 0.15 | 1 | 86.90 | 95.36 | 96.22 |
| 4 | 0.2 | 1 | 93.94 | 103.14 | 103.14 |
| 5 | 0.25 | 1 | 100.34 | 110.73 | 110.28 |
| 6 | 0.3 | 1 | 106.10 | 116.66 | 114.58 |
| 7 | 0.35 | 1 | 111.21 | 122.19 | 120.85 |
| 8 | 0.4 | 1 | 115.68 | 127.43 | 127.48 |
| 9 * | 0.45 | 1 | 119.50 | 132.24 | 132.04 |
| 10 * | 0.05 | 1.05 | 69.15 | 75.60 | 75.47 |
| 11 * | 0.1 | 1.1 | 76.25 | 80.80 | 80.68 |
| 12 | 0.05 | 1.15 | 66.04 | 72.25 | 73.15 |
| 13 | 0.1 | 1.15 | 75.24 | 79.04 | 78.60 |
| 14 | 0.15 | 1.15 | 83.37 | 86.87 | 87.64 |
| 15 * | 0.2 | 1.15 | 90.52 | 94.56 | 94.62 |
| 16 | 0.25 | 1.15 | 96.79 | 101.17 | 101.40 |
| 17 | 0.3 | 1.15 | 102.30 | 106.95 | 107.96 |
| 18 | 0.35 | 1.15 | 107.14 | 111.84 | 114.07 |
| 19 | 0.4 | 1.15 | 111.40 | 116.58 | 120.47 |
| 20 | 0.45 | 1.15 | 115.20 | 120.90 | 125.19 |
| 21 | 0.5 | 1.15 | 118.63 | 124.84 | 128.90 |
| 22 | 0.55 | 1.15 | 121.80 | 128.70 | 130.63 |
| 23 | 0.2 | 1.2 | 90.87 | 92.18 | 92.01 |
| 24 | 0.25 | 1.25 | 100.02 | 95.92 | 95.43 |
| 25 | 0.05 | 1.3 | 70.11 | 71.28 | 71.47 |
| 26 | 0.1 | 1.3 | 77.99 | 75.72 | 74.39 |
| 27 | 0.15 | 1.3 | 85.28 | 82.21 | 80.52 |
| 28 | 0.2 | 1.3 | 91.98 | 88.22 | 87.40 |
| 29 | 0.25 | 1.3 | 98.08 | 93.78 | 92.87 |
| 30 * | 0.3 | 1.3 | 103.59 | 98.69 | 98.61 |
| 31 | 0.35 | 1.3 | 108.50 | 103.28 | 104.76 |
| 32 | 0.4 | 1.3 | 112.82 | 107.32 | 111.25 |
| 33 | 0.45 | 1.3 | 116.54 | 111.20 | 117.59 |
| 34 | 0.5 | 1.3 | 119.67 | 114.84 | 123.18 |
| 35 | 0.55 | 1.3 | 122.20 | 118.08 | 126.69 |
| 36 | 0.6 | 1.3 | 124.14 | 120.90 | 115.74 |
| 37 | 0.35 | 1.35 | 110.40 | 101.00 | 101.29 |
| 38 * | 0.4 | 1.4 | 117.50 | 103.21 | 103.31 |
| 39 | 0.05 | 1.45 | 74.70 | 76.87 | 76.86 |
| 40 | 0.1 | 1.45 | 82.87 | 78.08 | 76.83 |
| 41 | 0.15 | 1.45 | 90.53 | 82.17 | 80.84 |
| 42 | 0.2 | 1.45 | 97.67 | 86.50 | 87.02 |
| 43 | 0.25 | 1.45 | 104.30 | 90.84 | 88.73 |
| 44 | 0.3 | 1.45 | 110.41 | 94.74 | 92.30 |
| 45 | 0.35 | 1.45 | 116.01 | 98.47 | 96.42 |
| 46 | 0.4 | 1.45 | 121.10 | 101.77 | 100.49 |
| 47 * | 0.45 | 1.45 | 125.67 | 104.93 | 104.99 |
| 48 | 0.5 | 1.45 | 129.73 | 107.96 | 110.38 |
| 49 | 0.55 | 1.45 | 133.27 | 110.43 | 117.88 |
| 50 | 0.6 | 1.45 | 136.30 | 113.02 | 123.56 |
| 51 | 0.5 | 1.5 | 133.50 | 106.90 | 106.70 |
| 52 | 0.55 | 1.55 | 151.02 | 109.30 | 109.45 |
| 53 | 0.05 | 1.60 | 70.12 | 95.01 | 94.79 |
| 54 * | 0.1 | 1.6 | 84.03 | 92.89 | 91.83 |
| 55 | 0.15 | 1.6 | 95.98 | 94.41 | 93.62 |
| 56 | 0.2 | 1.6 | 106.20 | 96.45 | 96.65 |
| 57 | 0.25 | 1.6 | 114.93 | 98.91 | 94.35 |
| 58 | 0.3 | 1.6 | 122.42 | 101.43 | 96.33 |
| 59 | 0.35 | 1.6 | 128.90 | 103.74 | 99.87 |
| 60 | 0.4 | 1.6 | 134.61 | 105.96 | 102.98 |
| 61 | 0.45 | 1.6 | 139.80 | 108.09 | 105.48 |
| 62 | 0.5 | 1.6 | 144.70 | 110.03 | 107.97 |
| 63 | 0.55 | 1.6 | 149.55 | 111.87 | 110.77 |
| 64 * | 0.6 | 1.6 | 154.60 | 113.70 | 113.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Yang, Y.; Wang, G.; Li, Y. A Method for Calculating Residual Strength of Crack Arrest Hole on Tungsten-Copper Functionally Graded Materials by Phase-Field Gradient Element Combined with Multi-Fidelity Neural Network. Materials 2025, 18, 1973. https://doi.org/10.3390/ma18091973
Liu B, Yang Y, Wang G, Li Y. A Method for Calculating Residual Strength of Crack Arrest Hole on Tungsten-Copper Functionally Graded Materials by Phase-Field Gradient Element Combined with Multi-Fidelity Neural Network. Materials. 2025; 18(9):1973. https://doi.org/10.3390/ma18091973
Chicago/Turabian StyleLiu, Bowen, Yisheng Yang, Guishan Wang, and Yin Li. 2025. "A Method for Calculating Residual Strength of Crack Arrest Hole on Tungsten-Copper Functionally Graded Materials by Phase-Field Gradient Element Combined with Multi-Fidelity Neural Network" Materials 18, no. 9: 1973. https://doi.org/10.3390/ma18091973
APA StyleLiu, B., Yang, Y., Wang, G., & Li, Y. (2025). A Method for Calculating Residual Strength of Crack Arrest Hole on Tungsten-Copper Functionally Graded Materials by Phase-Field Gradient Element Combined with Multi-Fidelity Neural Network. Materials, 18(9), 1973. https://doi.org/10.3390/ma18091973






