Water in Wood: A Review of Current Understanding and Knowledge Gaps
Abstract
:1. Introduction
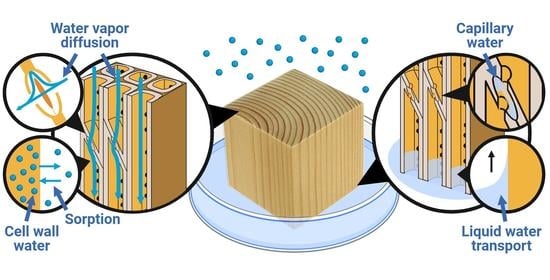
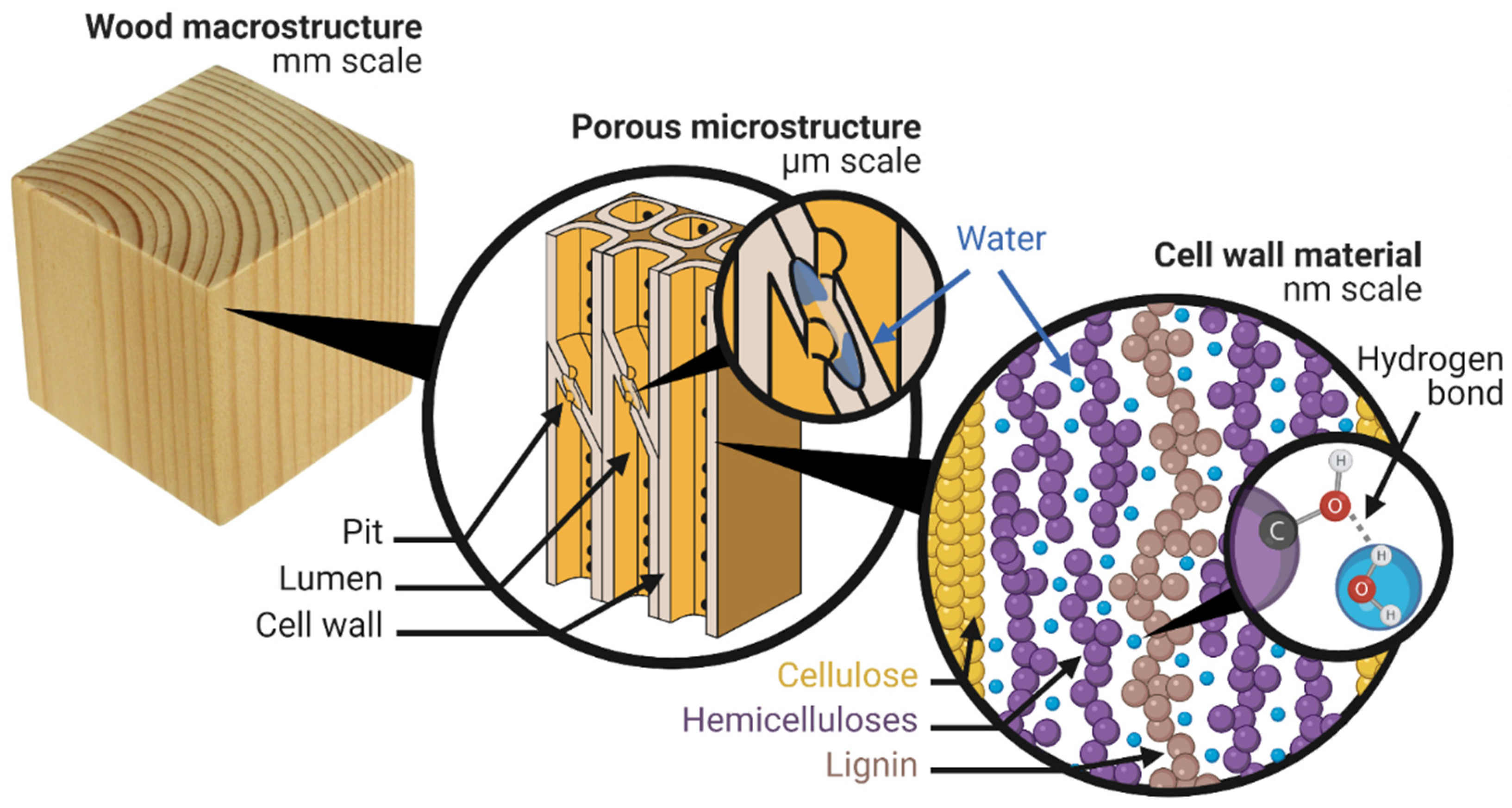
2. Where Is the Water?
2.1. Cell Wall Water
2.2. Capillary Water
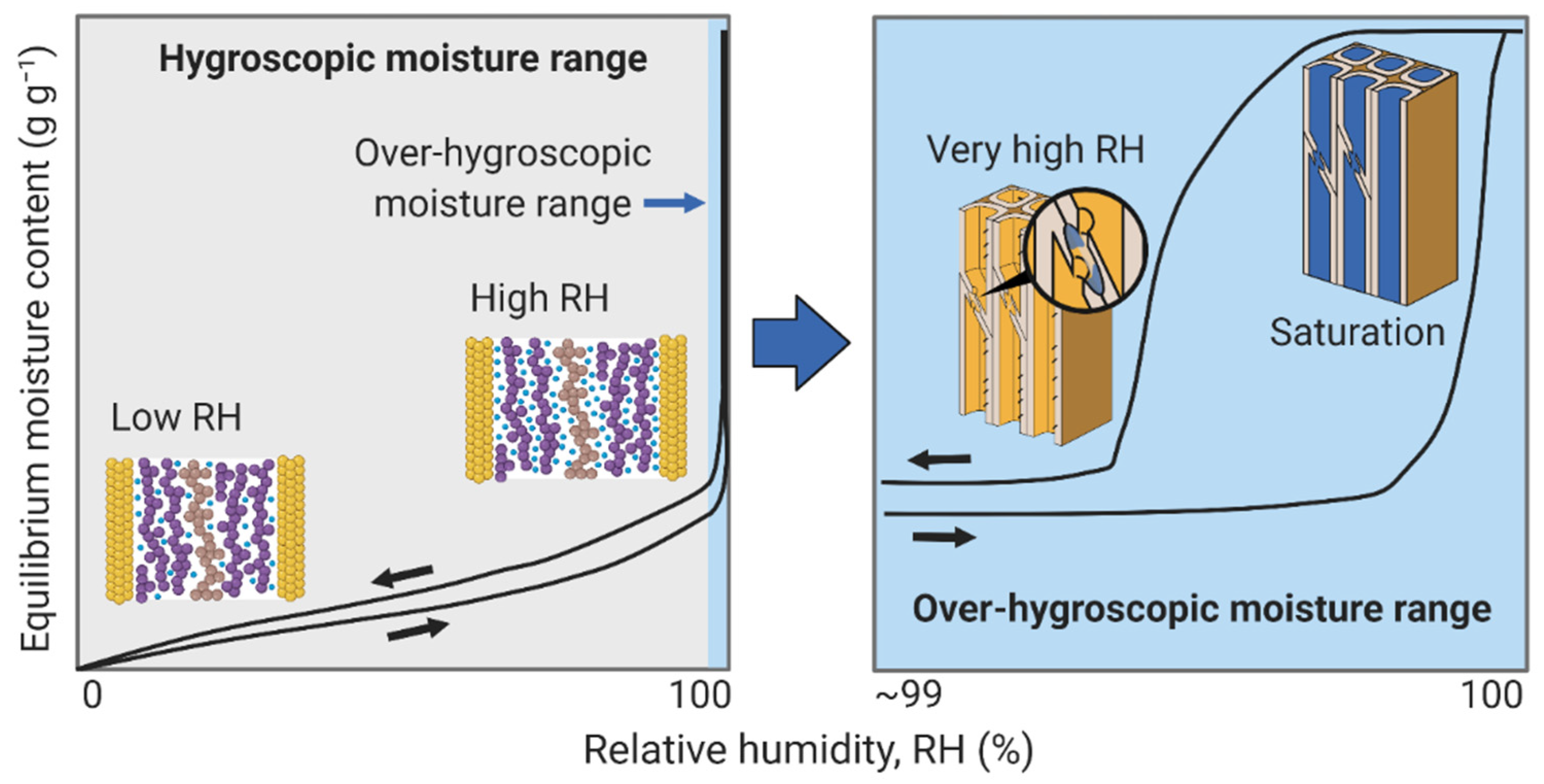
3. Wood–Water Equilibrium States
3.1. Care When Measuring at Moisture Equilibrium States
3.2. Thermodynamics of Sorption
3.3. Equilibrium Sorption Models
3.4. Over-Hygroscopic Range
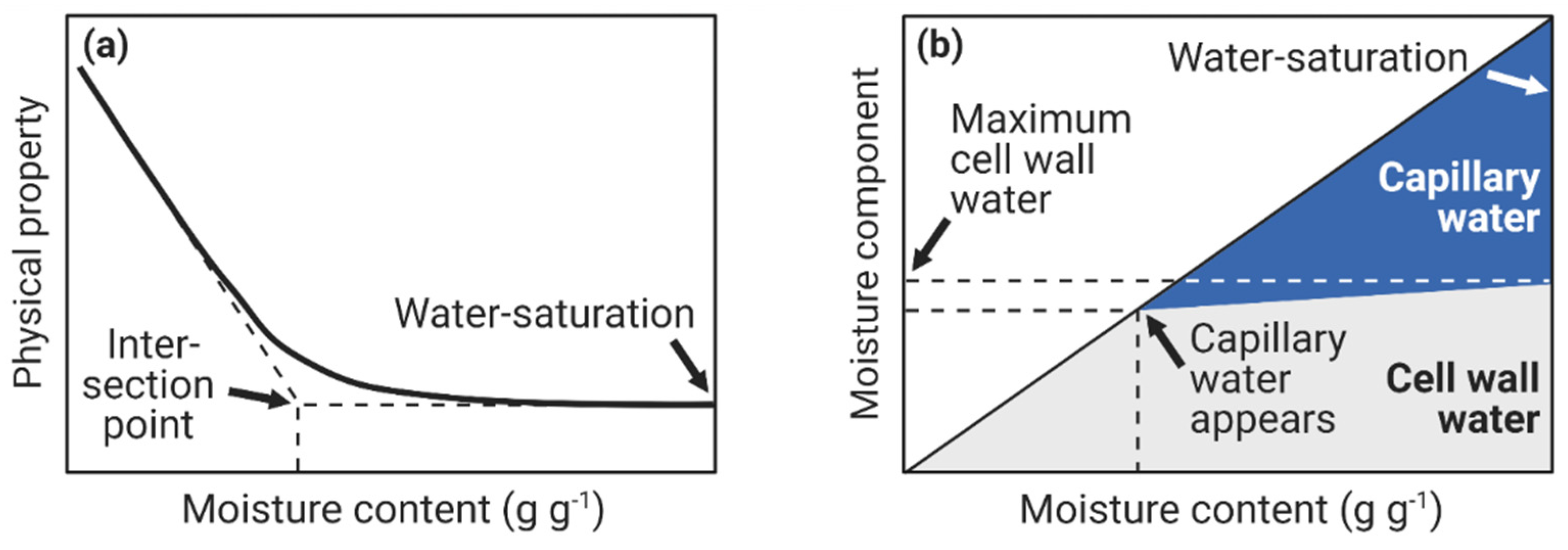
4. Fiber Saturation Point and Maximum Cell Wall Moisture Content
4.1. Original Definition of the Fiber Saturation Point
“In drying out a piece of wet wood, since the free water must evidently evaporate before the absorbed moisture in the cell walls can begin to dry out, there will be a period during which the strength remains constant although varying degrees of moisture are indicated. But just as soon as the free water has disappeared and the cell walls begin to dry the strength will begin to increase. This point I designate the fiber-saturation point.”
4.2. Subsequent Interpretations of the Fiber Saturation Point
4.3. Maximum Cell Wall Moisture Content
5. Moisture-Induced Shrinkage and Swelling
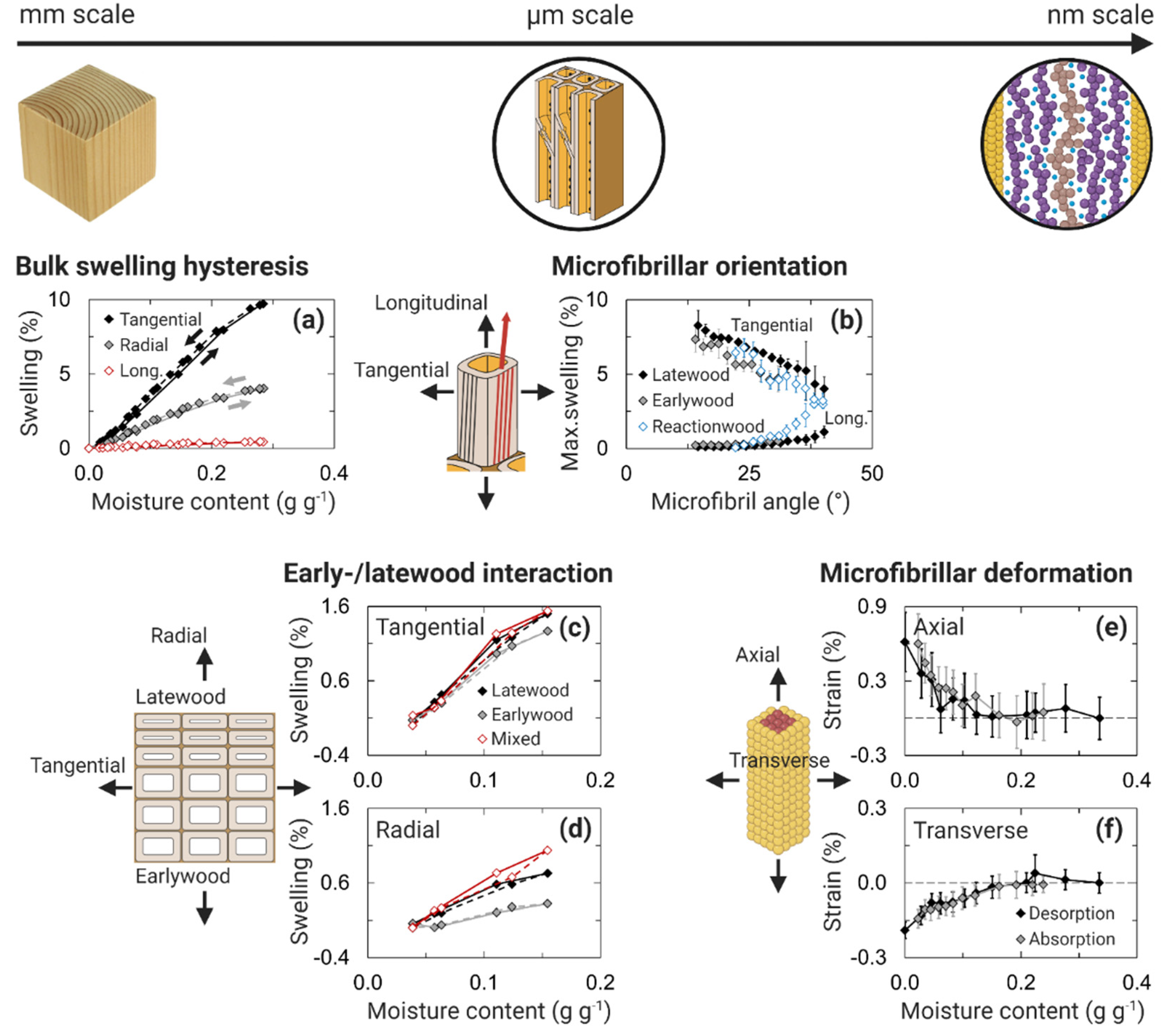
5.1. Shrinkage and Swelling on Multiple Scales
5.2. Anisotropy in Shrinkage and Swelling
5.3. Changing Shrinkage and Swelling by Modification
6. Moisture History Dependence
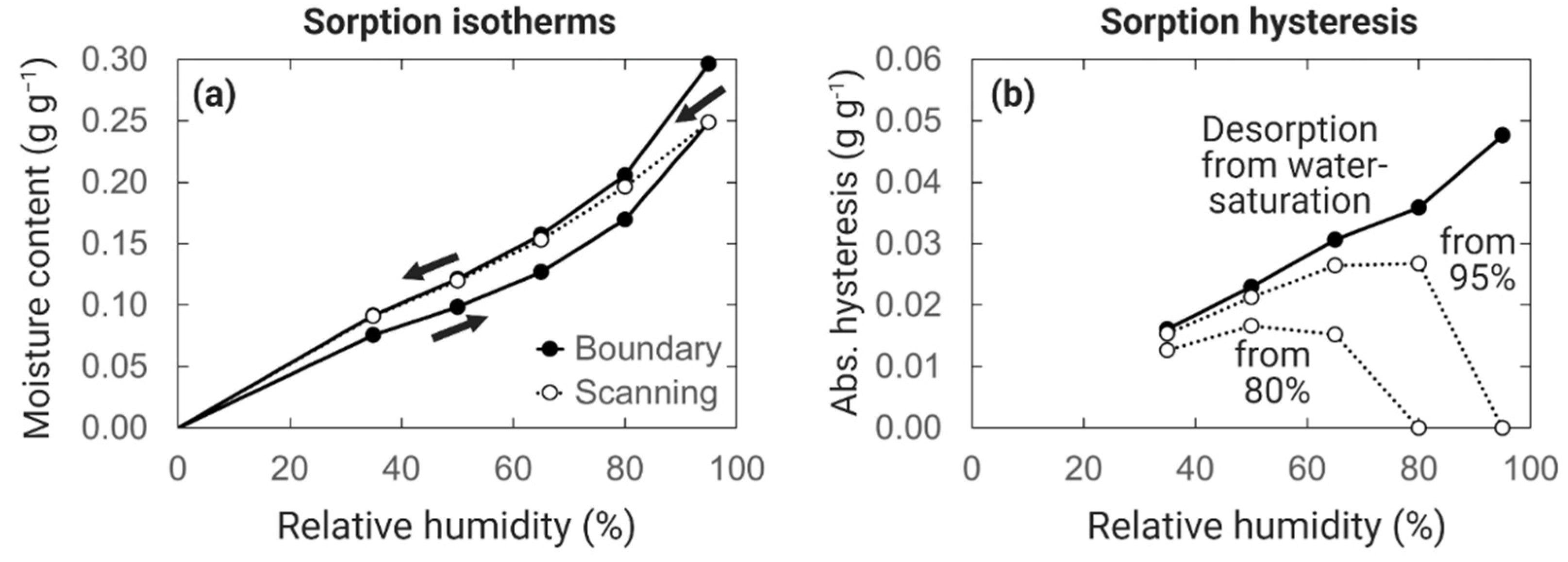
6.1. Sorption Hysteresis
6.2. Care When Measuring Desorption Isotherms
6.3. Sorption Hysteresis Models for Wood
6.4. Swelling Hysteresis
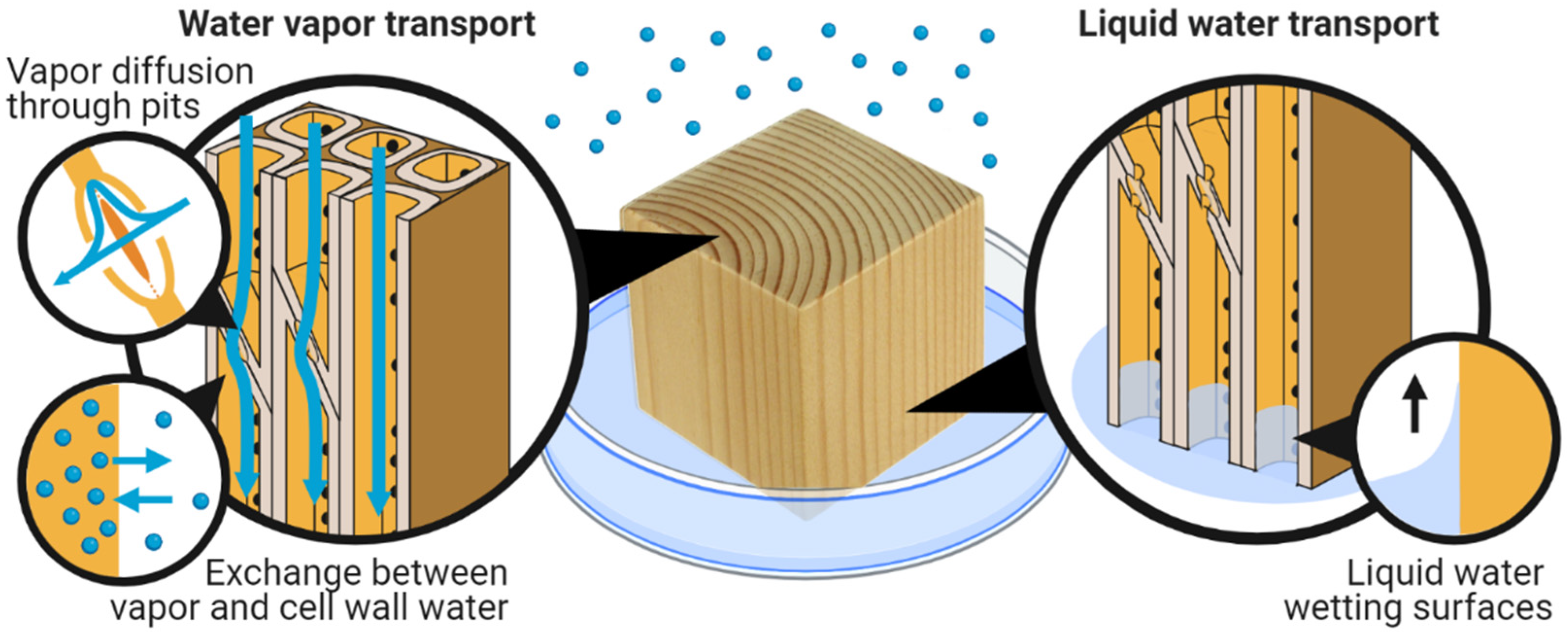
7. Transport of Water in Wood
7.1. Water Vapor Diffusion in the Macro-Void Structure
7.2. Diffusion of Water in the Cell Wall
7.3. Liquid Water Transport in the Macro-Void Structure
7.4. Models for Multi-Phase Transport
8. Water Vapor Sorption Kinetics in the Cell Wall
8.1. Physical Phenomena Involved in Sorption Kinetics
8.2. Sorption Kinetic Models
9. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gerhards, C.C. Effect of moisture-content and temperature on the mechanical-properties of wood—An analysis of immediate effects. Wood Fiber 1982, 14, 4–36. [Google Scholar]
- Armstrong, L.D.; Kingston, R.S.T. The effect of moisture content changes on the deformation of wood under stress. Aust. J. Appl. Sci. 1962, 13, 257–276. [Google Scholar]
- Gibson, E.J. Creep of Wood—Role of Water and Effect of A Changing Moisture Content. Nature 1965, 206, 213–215. [Google Scholar] [CrossRef]
- Tiemann, H.D. Effect of Moisture upon the Strength and Stiffness of Wood; Bulletin 70; US Department of Agriculture, Forest Service: Washington, DC, USA, 1906.
- Markwardt, L.J.; Wilson, T.R.C. Strength and Related Properties of Woods Grown in the United States; US Department of Agriculture: Washington, DC, USA, 1935.
- Hearmon, R.F.S.; Burcham, J.N. Specific heat and heat of wetting of wood. Nature 1955, 176, 978. [Google Scholar] [CrossRef]
- Kühlmann, G. Untersuchung der thermischen Eigenschaften von Holz und Spanplatten in Abhängigkeit von Feuchtigkeit und Temperatur im hygroskopischen Bereich. Holz Roh Werkst. 1962, 20, 259–270. [Google Scholar] [CrossRef]
- Sonderegger, W.; Hering, S.; Niemz, P. Thermal behaviour of Norway spruce and European beech in and between the principal anatomical directions. Holzforschung 2011, 65, 369–375. [Google Scholar] [CrossRef]
- MacLean, J.D. Thermal conductivity of wood. Heat. Pip. Air Cond. 1941, 13, 380–391. [Google Scholar]
- Zeller, S.M. Humidity in relation to moisture imbibition by wood and to spore germination on wood. Ann. Mo. Bot. Gard. 1920, 7, 51–74. [Google Scholar] [CrossRef]
- Griffin, D.M. Water potential and wood-decay fungi. Annu. Rev. Phytopathol. 1977, 15, 319–329. [Google Scholar] [CrossRef]
- Brischke, C.; Alfredsen, G. Wood-water relationships and their role for wood susceptibility to fungal decay. Appl. Microbiol. Biotechnol. 2020, 104, 3781–3795. [Google Scholar] [CrossRef]
- Amidon, T.E.; Liu, S. Water-based woody biorefinery. Biotechnol. Adv. 2009, 27, 542–550. [Google Scholar] [CrossRef]
- Liu, S.; Lu, H.; Hu, R.; Shupe, A.; Lin, L.; Liang, B. A sustainable woody biomass biorefinery. Biotechnol. Adv. 2012, 30, 785–810. [Google Scholar] [CrossRef]
- Volbehr, B.F.K.J. Untersuchungen über die Quellung der Holzfaser. In Philosophischen Fakultät; Universität Kiel: Kiel, Germany, 1896; pp. 1–37. [Google Scholar]
- Carrington, H. The elastic constants of spruce as influenced by moisture content. Aeronaut. J. 1922, 26, 462–471. [Google Scholar]
- Engelund, E.T.; Thygesen, L.G.; Svensson, S.; Hill, C.A.S. A critical discussion of the physics of wood-water interactions. Wood Sci. Technol. 2013, 47, 141–161. [Google Scholar] [CrossRef]
- Venkateswaran, A. Sorption of aqueous and nonaqueous media by wood and cellulose. Chem. Rev. 1970, 70, 619–637. [Google Scholar] [CrossRef]
- Skaar, C. Theories of water sorption by wood. In Wood-Water Relations; Springer: Berlin/Heidelberg, Germany, 1988; pp. 86–121. [Google Scholar]
- Siau, J.F. Basic Wood-Moisture Relationships. In Transport Processes in Wood; Springer: Berlin/Heidelberg, Germany, 1984; pp. 1–34. [Google Scholar]
- Hawley, L.F. Wood-Liquid Relations; Technical Bulletin 248; US Department of Agriculture: Washington, DC, USA, 1931; pp. 1–34.
- Tarkow, H. Interaction of Moisture and Wood; Report No. 2198; US Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 1960; pp. 1–8.
- Wangaard, F.F.; Wengert, E.M.; Mitchell, P.H.; Rosen, H.N.; Skaar, C.; Simpson, W.T.; Beall, F.C.; Spalt, H.A.; Arganbright, D.M.; Stewart, H.A.; et al. Proceedings of the Wood Moisture Content—Temperature and Humidity Relationships Symposium, Blacksburg, Virginia, 29 October 1979; Rosen, H.N., Simpson, W.T., Wengert, E.M., Eds.; USDA Forest Service, Forest Products Laboratory: Madison, WI, USA, 1979.
- Stamm, A.J. Wood and Cellulose Science; The Ronald Press Company: New York, NY, USA, 1964. [Google Scholar]
- Glass, S.V.; Zelinka, S.L. Chapter 4. Moisture Relations and Physical Properties of Wood. In Wood Handbook. Wood as an Engineering Material; FPL-GTR-282; Ross, R.J., Ed.; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2021. [Google Scholar]
- Fredriksson, M. On wood–water interactions in the over-hygroscopic moisture range—Mechanisms, methods, and influence of wood modification. Forests 2019, 10, 779. [Google Scholar] [CrossRef] [Green Version]
- Matthews, J.F.; Skopec, C.E.; Mason, P.E.; Zuccato, P.; Torget, R.W.; Sugiyama, J.; Himmel, M.E.; Brady, J.W. Computer simulation studies of microcrystalline cellulose I beta. Carbohydr. Res. 2006, 341, 138–152. [Google Scholar] [CrossRef]
- Lindh, E.L.; Terenzi, C.; Salmen, L.; Furo, I. Water in cellulose: Evidence and identification of immobile and mobile adsorbed phases by 2H MAS NMR. Phys. Chem. Chem. Phys. 2017, 19, 4360–4369. [Google Scholar] [CrossRef] [Green Version]
- Thybring, E.E.; Thygesen, L.G.; Burgert, I. Hydroxyl accessibility in wood cell walls as affected by drying and re-wetting procedures. Cellulose 2017, 24, 2375–2384. [Google Scholar] [CrossRef] [Green Version]
- Hofstetter, K.; Hinterstoisser, B.; Salmén, L. Moisture uptake in native cellulose—The roles of different hydrogen bonds: A dynamic FT-IR study using deuterium exchange. Cellulose 2006, 13, 131–145. [Google Scholar] [CrossRef]
- Salmén, L.; Bergström, E. Cellulose structural arrangement in relation to spectral changes in tensile loading FTIR. Cellulose 2009, 16, 975–982. [Google Scholar] [CrossRef]
- Beck, G.; Strohbusch, S.; Larnøy, E.; Militz, H.; Hill, C. Accessibility of hydroxyl groups in anhydride modified wood as measured by deuterium exchange and saponification. Holzforschung 2017, 72, 17–23. [Google Scholar] [CrossRef]
- Sumi, Y.; Hale, R.D.; Meyer, J.A.; Leopold, B.; Rånby, B.G. Accessibility of wood and wood carbohydrates measured with tritiated water. Tappi 1964, 47, 621–624. [Google Scholar]
- Tarmian, A.; Burgert, I.; Thybring, E.E. Hydroxyl accessibility in wood by deuterium exchange and ATR-FTIR spectroscopy: Methodological uncertainties. Wood Sci. Technol. 2017, 51, 845–853. [Google Scholar] [CrossRef]
- Digaitis, R.; Thybring, E.E.; Künniger, T.; Thygesen, L.G. Synergistic effects of enzymatic decomposition and mechanical stress in wood degradation. Wood Sci. Technol. 2017, 51, 1067–1080. [Google Scholar] [CrossRef]
- Popescu, C.M.; Hill, C.A.S.; Curling, S.; Ormondroyd, G.A.; Xie, Y. The water vapour sorption behaviour of acetylated birch wood: How acetylation affects the sorption isotherm and accessible hydroxyl content. J. Mater. Sci. 2014, 49, 2362–2371. [Google Scholar] [CrossRef]
- Taniguchi, T.; Harada, H.; Nakato, K. Determination of water-adsorption sites in wood by a hydrogen-deuterium exchange. Nature 1978, 272, 230–231. [Google Scholar] [CrossRef]
- Lindh, E.L.; Bergenstråhle-Wohlert, M.; Terenzi, C.; Salmén, L.; Furó, I. Non-exchanging hydroxyl groups on the surface of cellulose fibrils: The role of interaction with water. Carbohydr. Res. 2016, 434, 136–142. [Google Scholar] [CrossRef]
- Thybring, E.E.; Piqueras, S.; Tarmian, A.; Burgert, I. Water accessibility to hydroxyls confined in solid wood cell walls. Cellulose 2020, 27, 5617–5627. [Google Scholar] [CrossRef]
- Altgen, M.; Rautkari, L. Humidity-dependence of the hydroxyl accessibility in Norway spruce wood. Cellulose 2021, 28, 45–58. [Google Scholar] [CrossRef]
- Berthold, J.; Desbrieres, J.; Rinaudo, M.; Salmén, L. Types of adsorbed water in relation to the ionic groups and their counterions for some cellulose derivatives. Polymer 1994, 35, 5729–5736. [Google Scholar] [CrossRef]
- Berthold, J.; Rinaudo, M.; Salmén, L. Association of water to polar groups; Estimations by an adsorption model for ligno-cellulosic materials. Colloids Surf. A-Physicochem. Eng. Asp. 1996, 112, 117–129. [Google Scholar] [CrossRef]
- Nakamura, K.; Hatakeyama, T.; Hatakeyama, H. Studies on bound water of cellulose by differential scanning calorimetry. Text. Res. J. 1981, 51, 607–613. [Google Scholar] [CrossRef]
- Kärenlampi, P.P.; Tynjälä, P.; Ström, P. Phase transformations of wood cell wall water. J. Wood Sci. 2005, 51, 118–123. [Google Scholar] [CrossRef]
- Zelinka, S.L.; Lambrecht, M.J.; Glass, S.V.; Wiedenhoeft, A.C.; Yelle, D.J. Examination of water phase transitions in Loblolly pine and cell wall components by differential scanning calorimetry. Thermochim. Acta 2012, 533, 39–45. [Google Scholar] [CrossRef]
- Thygesen, L.G.; Engelund, E.T.; Hoffmeyer, P. Water sorption in wood and modified wood at high values of relative humidity. Part I: Results for untreated, acetylated, and furfurylated Norway spruce. Holzforschung 2010, 64, 315–323. [Google Scholar]
- Czihak, C.; Muller, M.; Schober, H.; Vogl, G. Ice formation in amorphous cellulose. Physica B 2000, 276, 286–287. [Google Scholar] [CrossRef]
- Cox, J.; McDonald, P.J.; Gardiner, B.A. A study of water exchange in wood by means of 2D NMR relaxation correlation and exchange. Holzforschung 2010, 64, 259–266. [Google Scholar] [CrossRef] [Green Version]
- Bonnet, M.; Courtier-Murias, D.; Faure, P.; Rodts, S.; Care, S. NMR determination of sorption isotherms in earlywood and latewood of Douglas fir. Identification of bound water components related to their local environment. Holzforschung 2017, 71, 481. [Google Scholar] [CrossRef]
- Jeoh, T.; Karuna, N.; Weiss, N.D.; Thygesen, L.G. Two-dimensional 1H-Nuclear Magnetic Resonance relaxometry for understanding biomass recalcitrance. ACS Sustain. Chem. Eng. 2017, 5, 8785–8795. [Google Scholar] [CrossRef]
- Rostom, L.; Courtier-Murias, D.; Rodts, S.; Care, S. Investigation of the effect of aging on wood hygroscopicity by 2D 1H NMR relaxometry. Holzforschung 2020, 74, 400–411. [Google Scholar] [CrossRef] [Green Version]
- Plaza Rodriguez, N.Z. Neutron Scattering Studies of Nano-Scale Wood-Water Interactions; Department of Materials Science and Engineering, University of Wisconsin Madison: Madison, WI, USA, 2017; pp. 1–165. [Google Scholar]
- Thybring, E.E.; Fredriksson, M. Wood modification as a tool to understand moisture in wood. Forests 2021, 12, 372. [Google Scholar] [CrossRef]
- Zelinka, S.L.; Altgen, M.; Emmerich, L.; Guigo, N.; Keplinger, T.; Kymäläinen, M.; Thybring, E.E.; Thygesen, L.G. Review of wood modification and wood functionalization, technologies. Forests 2022, 13, 1004. [Google Scholar] [CrossRef]
- Fuchs, W. Zur Kenntnis des genuinen Lignins, I.: Die Acetylierung des Fichtenholzes. Ber. Dtsch. Chem. Ges. 1928, 61, 948–951. [Google Scholar] [CrossRef]
- Papadopoulos, A.N.; Hill, C.A.S.; Gkaraveli, A. Analysis of the swelling behaviour of chemically modified softwood: A novel approach. Holz Roh Werkst. 2004, 62, 107–112. [Google Scholar] [CrossRef]
- Ibach, R.E.; Plaza, N.Z.; Pingali, S.V. Small angle neutron scattering reveals wood nanostructural features in decay resistant chemically modified wood. Front. For. Glob. Chang. 2022, 4, 814086. [Google Scholar] [CrossRef]
- Ponzecchi, A.; Thybring, E.E.; Digaitis, R.; Fredriksson, M.; Solsona, S.P.; Thygesen, L.G. Raman micro-spectroscopy of two types of acetylated Norway spruce wood at controlled relative humidity. Front. Plant Sci. 2022, 13, 986578. [Google Scholar] [CrossRef]
- Thomson, W. On the equilibrium of vapour at a curved surface of liquid. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1871, 42, 448–452. [Google Scholar] [CrossRef]
- Sing, K.S.W.; Rouquerol, F.; Rouquerol, J.; Llewellyn, P. 8—Assessment of mesoporosity. In Adsorption by Powders and Porous Solids, 2nd ed.; Rouquerol, F., Rouquerol, J., Sing, K.S.W., Llewellyn, P., Maurin, G., Eds.; Academic Press: Oxford, UK, 2014; pp. 269–302. [Google Scholar]
- Sedighi Moghaddam, M.; Wålinder, M.E.P.; Claesson, P.M.; Swerin, A. Multicycle Wilhelmy plate method for wetting properties, swelling and liquid sorption of wood. Langmuir 2013, 29, 12145–12153. [Google Scholar] [CrossRef]
- Gindl, M.; Sinn, G.; Gindl, W.; Reiterer, A.; Tschegg, S. A comparison of different methods to calculate the surface free energy of wood using contact angle measurements. Colloids Surf. A Physicochem. Eng. Asp. 2001, 181, 279–287. [Google Scholar] [CrossRef]
- Frybort, S.; Obersriebnig, M.; Müller, U.; Gindl-Altmutter, W.; Konnerth, J. Variability in surface polarity of wood by means of AFM adhesion force mapping. Colloids Surf. A Physicochem. Eng. Asp. 2014, 457, 82–87. [Google Scholar] [CrossRef]
- Jin, X.; Kasal, B. Adhesion force mapping on wood by atomic force microscopy: Influence of surface roughness and tip geometry. R. Soc. Open Sci. 2016, 3, 160248. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mao, J.; Abushammala, H.; Kasal, B. Monitoring the surface aging of wood through its pits using atomic force microscopy with functionalized tips. Colloids Surf. A Physicochem. Eng. Asp. 2021, 609, 125871. [Google Scholar] [CrossRef]
- Andrew, M.; Bijeljic, B.; Blunt, M.J. Pore-scale contact angle measurements at reservoir conditions using X-ray microtomography. Adv. Water Resour. 2014, 68, 24–31. [Google Scholar] [CrossRef] [Green Version]
- AlRatrout, A.; Raeini, A.Q.; Bijeljic, B.; Blunt, M.J. Automatic measurement of contact angle in pore-space images. Adv. Water Resour. 2017, 109, 158–169. [Google Scholar] [CrossRef]
- Plaza, N.Z. On the experimental assessment of the molecular-scale interactions between wood and water. Forests 2019, 10, 616. [Google Scholar] [CrossRef]
- Chen, M.; Coasne, B.; Guyer, R.; Derome, D.; Carmeliet, J. Role of hydrogen bonding in hysteresis observed in sorption-induced swelling of soft nanoporous polymers. Nat. Commun. 2018, 9, 3507. [Google Scholar] [CrossRef]
- Jakes, J.E.; Hunt, C.G.; Zelinka, S.L.; Ciesielski, P.N.; Plaza, N.Z. Effects of moisture on diffusion in unmodified wood cell walls: A phenomenological polymer science approach. Forests 2019, 10, 1084. [Google Scholar] [CrossRef] [Green Version]
- Christensen, G.N.; Kelsey, K.E. Sorption of water vapour by constituents of wood: Determination of sorption isotherms. Aust. J. Appl. Sci. 1958, 9, 265–282. [Google Scholar]
- Barbetta, A.; Fratzl, P.; Zemb, T.; Bertinetti, L. Impregnation and swelling of wood with salts: Ion specific kinetics and thermodynamics effects. Adv. Mater. Interfaces 2017, 4, 1600437. [Google Scholar] [CrossRef]
- Thybring, E.E. Water relations in untreated and modified wood under brown-rot and white-rot decay. Int. Biodeterior. Biodegrad. 2017, 118, 134–142. [Google Scholar] [CrossRef]
- Vahtikari, K.; Rautkari, L.; Noponen, T.; Lillqvist, K.; Hughes, M. The influence of extractives on the sorption characteristics of Scots pine (Pinus sylvestris L.). J. Mater. Sci. 2017, 52, 10840–10852. [Google Scholar] [CrossRef]
- Wangaard, F.F.; Granados, L.A. The effect of extractives on water-vapor sorption by wood. Wood Sci. Technol. 1967, 1, 253–277. [Google Scholar] [CrossRef]
- Thybring, E.E.; Kymäläinen, M.; Rautkari, L. Experimental techniques for characterising water in wood covering the range from dry to fully water-saturated. Wood Sci. Technol. 2018, 52, 297–329. [Google Scholar] [CrossRef] [Green Version]
- Thybring, E.E.; Glass, S.V.; Zelinka, S.L. Kinetics of water vapor sorption in wood cell walls: State of the art and research needs. Forests 2019, 10, 704. [Google Scholar] [CrossRef] [Green Version]
- Zelinka, S.L.; Glass, S.V.; Thybring, E.E. Evaluation of previous measurements of water vapor sorption in wood at multiple temperatures. Wood Sci. Technol. 2020, 54, 769–786. [Google Scholar] [CrossRef]
- ISO 12571; Hygrothermal Performance of Building Materials and Products—Determination of Hygroscopic Sorption Properties. ISO: Geneva, Switzerland, 2000; pp. 1–15.
- Hill, C.A.S.; Norton, A.; Newman, G. The water vapor sorption behavior of natural fibers. J. Appl. Polym. Sci. 2009, 112, 1524–1537. [Google Scholar] [CrossRef]
- Glass, S.V.; Boardman, C.R.; Zelinka, S.L. Short hold times in dynamic vapor sorption measurements mischaracterize the equilibrium moisture content of wood. Wood Sci. Technol. 2017, 51, 243–260. [Google Scholar] [CrossRef]
- Glass, S.V.; Boardman, C.R.; Thybring, E.E.; Zelinka, S.L. Quantifying and reducing errors in equilibrium moisture content measurements with dynamic vapor sorption (DVS) experiments. Wood Sci. Technol. 2018, 52, 909–927. [Google Scholar] [CrossRef] [Green Version]
- Skaar, C. Moisture Sorption Thermodynamics. In Wood-Water Relations; Springer: Berlin/Heidelberg, Germany, 1988; pp. 46–85. [Google Scholar]
- Nopens, M.; Wadsö, L.; Ortmann, C.; Fröba, M.; Krause, A. Measuring the heat of interaction between lignocellulosic materials and water. Forests 2019, 10, 674. [Google Scholar] [CrossRef] [Green Version]
- Zelinka, S.L.; Glass, S.V.; Thybring, E.E. Myth versus reality: Do parabolic sorption isotherm models reflect actual wood–water thermodynamics? Wood Sci. Technol. 2018, 52, 1701–1706. [Google Scholar] [CrossRef]
- Weichert, L. Investigations on sorption and swelling of spruce, beech and compressed beech wood at temperatures between 20 C and 100 C. Holz Roh Werkst. 1963, 21, 290–300. [Google Scholar] [CrossRef]
- Kelsey, K.E.; Clarke, L.N. The heat of sorption of water by wood. Aust. J. Appl. Sci. 1956, 7, 160–175. [Google Scholar]
- Kelsey, K.E.; Clarke, L.N. Effect of temperature and initial moisture content on the heat of wetting of wood. Nature 1955, 176, 83–84. [Google Scholar] [CrossRef]
- Stamm, A.J.; Loughborough, W.K. Thermodynamics of the swelling of wood. J. Phys. Chem. 1935, 39, 121–132. [Google Scholar] [CrossRef]
- Simón, C.; Esteban, L.G.; de Palacios, P.; Fernández, F.G.; Martín-Sampedro, R.; Eugenio, M.E. Thermodynamic analysis of water vapour sorption behaviour of juvenile and mature wood of Abies alba Mill. J. Mater. Sci. 2015, 50, 7282–7292. [Google Scholar] [CrossRef]
- Esteban, L.G.; de Palacios, P.; Fernández, F.G.; Guindeo, A.; Cano, N.N. Sorption and thermodynamic properties of old and new Pinus sylvestris wood. Wood Fiber Sci. 2008, 40, 111–121. [Google Scholar]
- Weichert, L. Untersuchungen Über das Sorptions—Und Quellungsverhalten von Fichte, Buche und Buchenpressvollholz bei Temperaturen zwischen 20 °C und 100 °C, in Fakultät für Maschinenwesen und Elektrotechnik; TH München: Munich, Germany, 1963; pp. 1–96. [Google Scholar]
- Wadsö, L.; Markova, N. A method to simultaneously determine sorption isotherms and sorption enthalpies with a double twin microcalorimeter. Rev. Sci. Instrum. 2002, 73, 2743–2754. [Google Scholar] [CrossRef]
- Markova, N.; Sparr, E.; Wadsö, L. On application of an isothermal sorption microcalorimeter. Thermochim. Acta 2001, 374, 93–104. [Google Scholar] [CrossRef]
- Wadsö, L.; Markova, N. A double twin isothermal microcalorimeter. Thermochim. Acta 2000, 360, 101–107. [Google Scholar] [CrossRef]
- Van den Berg, C.; Bruin, S. Water activity and its estimation in food systems: Theoretical aspects. In Water Activity: Influences on Food Quality; Stewart, G.F., Ed.; Academic Press: Cambridge, MA, USA, 1981; pp. 1–61. [Google Scholar]
- Simpson, W.T. Predicting equilibrium moisture content of wood by mathematical models. Wood Fiber Sci. 1973, 5, 41–49. [Google Scholar]
- Simpson, W. Sorption theories applied to wood. Wood Fiber 1980, 12, 183–195. [Google Scholar]
- Avramidis, S. Evaluation of 3-variable models for the prediction of equilibrium moisture-content in wood. Wood Sci. Technol. 1989, 23, 251–257. [Google Scholar] [CrossRef]
- Glass, S.V.; Zelinka, S.L.; Johnson, J.A. Investigation of Historic Equilibrium Moisture Content Data from the Forest Products Laboratory; US Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2014.
- Anderson, R.B. Modifications of the Brunauer, Emmett and Teller equation. J. Am. Chem. Soc. 1946, 68, 686–691. [Google Scholar] [CrossRef]
- Anderson, R.B.; Hall, W.K. Modifications of the Brunauer, Emmett and Teller equation II. J. Am. Chem. Soc. 1948, 70, 1727–1734. [Google Scholar] [CrossRef] [PubMed]
- Guggenheim, E.A. (Ed.) Chapter 11. Localized monolayer and multilayer adsorption of gases. In Applications of Statistical Mechanics; Clarendon Press: Oxford, UK, 1966; pp. 186–206. [Google Scholar]
- De Boer, J.H. (Ed.) Chapter 5. The quantity: Unimolecular and multimolecular adsorption. In The Dynamical Character of Adsorption; The Clarendon Press: Oxford, UK, 1953; pp. 54–89. [Google Scholar]
- Hailwood, A.J.; Horrobin, S. Absorption of water by polymers: Analysis in terms of a simple model. Trans. Faraday Soc. 1946, 42, B084–B092. [Google Scholar] [CrossRef]
- Dent, R.W. Multilayer theory for gas sorption. 1. Sorption of a single gas. Text. Res. J. 1977, 47, 145–152. [Google Scholar] [CrossRef]
- Thybring, E.E.; Boardman, C.R.; Zelinka, S.L.; Glass, S.V. Common sorption isotherm models are not physically valid for water in wood. Colloids Surf. A Physicochem. Eng. Asp. 2021, 627, 127214. [Google Scholar] [CrossRef]
- Adolphs, J.; Setzer, M.J. A model to describe adsorption isotherms. J. Colloid Interface Sci. 1996, 180, 70–76. [Google Scholar] [CrossRef]
- Adolphs, J.; Setzer, M.J. Energetic classification of adsorption isotherms. J. Colloid Interface Sci. 1996, 184, 443–448. [Google Scholar] [CrossRef]
- Willems, W. The water vapor sorption mechanism and its hysteresis in wood: The water/void mixture postulate. Wood Sci. Technol. 2014, 48, 499–518. [Google Scholar] [CrossRef]
- Willems, W. A critical review of the multilayer sorption models and comparison with the sorption site occupancy (SSO) model for wood moisture sorption isotherm analysis. Holzforschung 2015, 69, 67–75. [Google Scholar] [CrossRef]
- Bertinetti, L.; Fratzl, P.; Zemb, T. Chemical, colloidal and mechanical contributions to the state of water in wood cell walls. New J. Phys. 2016, 18, 083048. [Google Scholar] [CrossRef] [Green Version]
- Gregg, S.J.; Sing, K.S.W. Adsorption, Surface Area and Porosity; Academic Press: London, UK, 1967; p. 371. [Google Scholar]
- Fredriksson, M.; Thybring, E.E. On sorption hysteresis in wood: Separating hysteresis in cell wall water and capillary water in the full moisture range. PLoS ONE 2019, 14, e0225111. [Google Scholar] [CrossRef]
- Hernandez, R.E.; Caceres, C.B. Magnetic resonance microimaging of liquid water distribution in sugar maple wood below fiber saturation point. Wood Fiber Sci. 2010, 42, 259–272. [Google Scholar]
- Passarini, L.; Malveau, C.; Hernández, R. Water state study of wood structure of four hardwoods below fiber saturation point with nuclear magnetic resonance. Wood Fiber Sci. 2014, 46, 480–488. [Google Scholar]
- Almeida, G.; Gagne, S.; Hernandez, R.E. A NMR study of water distribution in hardwoods at several equilibrium moisture contents. Wood Sci. Technol. 2007, 41, 293–307. [Google Scholar] [CrossRef]
- Wilson, T.R.C. Strength-Moisture Relations for Wood; Technical Bulletin 282; US Departmnent of Agriculture: Washington, DC, USA, 1932; pp. 1–88.
- Stamm, A.J. Shrinking and swelling of wood. Ind. Eng. Chem. 1935, 27, 401–406. [Google Scholar] [CrossRef]
- Shupe, T.F.; Chow, P. Sorption, shrinkage, and fiber saturation point of kempas (Koompassia malaccensis). For. Prod. J. 1996, 46, 94. [Google Scholar]
- Stamm, A.J. The fiber-saturation point of wood as obtained from electrical conductivity measurements. Ind. Eng. Chem. Process Des. Dev. 1929, 1, 94–97. [Google Scholar] [CrossRef]
- James, W.L. Electric Moisture Meters for Wood; U.S. Forest Service Research Note FPL-08; US Forest Service Forest Products Laboratory: Madison, WI, USA, 1963; p. 24. [Google Scholar]
- James, W.L. Electric Moisture Meters for Wood; Forest Products Laboratory General Technical Report FPL-GTR-6; US Forest Service Forest Products Laboratory: Madison, WI, USA, 1988; p. 17. [Google Scholar]
- Repellin, V.; Guyonnet, R. Evaluation of heat-treated wood swelling by differential scanning calorimetry in relation to chemical composition. Holzforschung 2005, 59, 28–34. [Google Scholar] [CrossRef] [Green Version]
- Simpson, L.A.; Barton, A.F.M. Determination of the fibre saturation point in whole wood using differential scanning calorimetry. Wood Sci. Technol. 1991, 25, 301–308. [Google Scholar] [CrossRef]
- Thybring, E.E.; Digaitis, R.; Nord-Larsen, T.; Beck, G.; Fredriksson, M. How much water can wood cell walls hold? A triangulation approach to determine the maximum cell wall moisture content. PLoS ONE 2020, 15, e0238319. [Google Scholar]
- Zauer, M.; Kretzschmar, J.; Großmann, L.; Pfriem, A.; Wagenführ, A. Analysis of the pore-size distribution and fiber saturation point of native and thermally modified wood using differential scanning calorimetry. Wood Sci. Technol. 2014, 48, 177–193. [Google Scholar] [CrossRef]
- Thygesen, L.G.; Elder, T. Moisture in untreated, acetylated, and furfurylated Norway spruce studied during drying using Time Domain NMR. Wood Fiber Sci. 2008, 40, 309–320. [Google Scholar]
- Thygesen, L.G.; Elder, T. Moisture in untreated, acetylated, and furfurylated norway spruce monitored during drying below fiber saturation using time domain NMR. Wood Fiber Sci. 2009, 41, 194–200. [Google Scholar]
- Beck, G.; Thybring, E.E.; Thygesen, L.G.; Hill, C. Characterization of moisture in acetylated and propionylated radiata pine using low-field nuclear magnetic resonance (LFNMR) relaxometry. Holzforschung 2018, 72, 225. [Google Scholar] [CrossRef]
- Fredriksson, M.; Thygesen, L.G. The states of water in Norway spruce (Picea abies (L.) Karst.) studied by low-field nuclear magnetic resonance (LFNMR) relaxometry: Assignment of free-water populations based on quantitative wood anatomy. Holzforschung 2017, 71, 77–90. [Google Scholar] [CrossRef] [Green Version]
- Kekkonen, P.M.; Ylisassi, A.; Telkki, V.V. Absorption of water in thermally modified pine wood as studied by nuclear magnetic resonance. J. Phys. Chem. C 2013, 118, 2146–2153. [Google Scholar] [CrossRef]
- Stone, J.E.; Scallan, A.M. A structural model for the cell wall of water-swollen wood pulp fibres based on their accessibility to macromolecules. Cellul. Chem. Technol. 1968, 2, 343–358. [Google Scholar]
- Ahlgren, P.A.; Wood, J.R.; Goring, D.A.I. Fiber saturation point of various morphological subdivisions of Douglas-fir and aspen wood. Wood Sci. Technol. 1972, 6, 81–84. [Google Scholar] [CrossRef]
- Feist, W.C.; Tarkow, H. A new procedure for measuring fiber saturation points. For. Prod. J. 1967, 17, 65–68. [Google Scholar]
- Salmén, L.; Fahlén, J. Reflections on the ultrastructure of softwood fibers. Cellul. Chem. Technol. 2006, 40, 181–185. [Google Scholar]
- Papadopoulos, A.N.; Hill, C.A.S.; Gkaraveli, A. Determination of surface area and pore volume of holocellulose and chemically modified wood flour using the nitrogen adsorption technique. Holz Roh Werkst. 2003, 61, 453–456. [Google Scholar] [CrossRef]
- Fahlén, J.; Salmén, L. Pore and matrix distribution in the fiber wall revealed by atomic force microscopy and image analysis. Biomacromolecules 2005, 6, 433–438. [Google Scholar] [CrossRef]
- Kulasinski, K.; Guyer, R.; Derome, D.; Carmeliet, J. Water adsorption in wood microfibril-hemicellulose system: Role of the crystalline–amorphous interface. Biomacromolecules 2015, 16, 2972–2978. [Google Scholar] [CrossRef]
- Hernandez, R.E.; Bizon, M. Changes in shrinkage and tangential compression strength of sugar maple below and above the fiber saturation point. Wood Fiber Sci. 1994, 26, 360–369. [Google Scholar]
- Almeida, G.; Hernandez, R.E. Changes in physical properties of yellow birch below and above the fiber saturation point. Wood Fiber Sci. 2006, 38, 74–83. [Google Scholar]
- Almeida, G.; Hernández, R.E. Changes in physical properties of tropical and temperate hardwoods below and above the fiber saturation point. Wood Sci. Technol. 2006, 40, 599–613. [Google Scholar] [CrossRef]
- Leppänen, K.; Bjurhager, I.; Peura, M.; Kallonen, A.; Suuronen, J.P.; Penttilä, P.; Love, J.; Fagerstedt, K.; Serimaa, R. X-ray scattering and microtomography study on the structural changes of never-dried silver birch, European aspen and hybrid aspen during drying. Holzforschung 2011, 65, 865–873. [Google Scholar] [CrossRef]
- Zabler, S.; Paris, O.; Burgert, I.; Fratzl, P. Moisture changes in the plant cell wall force cellulose crystallites to deform. J. Struct. Biol. 2010, 171, 133–141. [Google Scholar] [CrossRef] [PubMed]
- Toba, K.; Yamamoto, H.; Yoshida, M. Mechanical interaction between cellulose microfibrils and matrix substances in wood cell walls induced by repeated wet-and-dry treatment. Cellulose 2012, 19, 1405–1412. [Google Scholar] [CrossRef]
- Seifert, J. Sorption and swelling of wood and wood base materials. 2. Swelling behavior of wood and wood base materials. Holz Roh Werkst. 1972, 30, 294–303. [Google Scholar]
- Harris, J.M.; Meylan, B.A. The influence of microfibril angle on longitudinal and tangential shrinkage in Pinus radiata. Holzforschung 1965, 19, 144. [Google Scholar] [CrossRef]
- Patera, A.; Van den Bulcke, J.; Boone, M.N.; Derome, D.; Carmeliet, J. Swelling interactions of earlywood and latewood across a growth ring: Global and local deformations. Wood Sci. Technol. 2018, 52, 91–114. [Google Scholar] [CrossRef]
- Barber, N.F.; Meylan, B.A. The anisotropic shrinkage of wood. A theoretical model. Holzforschung 1964, 18, 146. [Google Scholar] [CrossRef]
- Meylan, B.A. Influence of microfibril angle on longitudinal shrinkage-moisture content relationship. Wood Sci. Technol. 1972, 6, 293–301. [Google Scholar] [CrossRef]
- Rafsanjani, A.; Stiefel, M.; Jefimovs, K.; Mokso, R.; Derome, D.; Carmeliet, J. Hygroscopic swelling and shrinkage of latewood cell wall micropillars reveal ultrastructural anisotropy. J. R. Soc. Interface 2014, 11, 20140126. [Google Scholar] [CrossRef]
- Patera, A.; Derome, D.; Griffa, M.; Carmeliet, J. Hysteresis in swelling and in sorption of wood tissue. J. Struct. Biol. 2013, 182, 226–234. [Google Scholar] [CrossRef]
- Murata, K.; Masuda, M. Microscopic observation of transverse swelling of latewood tracheid: Effect of macroscopic/mesoscopic structure. J. Wood Sci. 2006, 52, 283–289. [Google Scholar] [CrossRef]
- Noack, D.; Schwab, E.; Bartz, A. Characteristics for a judgment of sorption and swelling behavior of wood. Wood Sci. Technol. 1973, 7, 218–236. [Google Scholar] [CrossRef]
- Keylwerth, R. Untersuchungen über freie und behinderte Quellung von Holz—Erste Mitteilung: Freie Quellung. Holz Roh Werkst. 1962, 20, 252–259. [Google Scholar] [CrossRef]
- Fahlén, J.; Salmén, L. On the lamellar structure of the tracheid cell wall. Plant Biol. 2002, 4, 339–345. [Google Scholar] [CrossRef]
- Gu, H.; Zink-Sharp, A.; Sell, J. Hypothesis on the role of cell wall structure in differential transverse shrinkage of wood. Holz Roh Werkst. 2001, 59, 436–442. [Google Scholar] [CrossRef] [Green Version]
- Ishimaru, Y.; Iida, I. Transverse swelling behavior of hinoki (Chamaecyparis obtusa) revealed by the replica method. J. Wood Sci. 2001, 47, 178–184. [Google Scholar] [CrossRef]
- Sakagami, H.; Matsumura, J.; Oda, K. Shrinkage of tracheid cells with desorption visualized by confocal laser scanning microscopy. IAWA J. 2007, 28, 29–37. [Google Scholar] [CrossRef] [Green Version]
- Derome, D.; Griffa, M.; Koebel, M.; Carmeliet, J. Hysteretic swelling of wood at cellular scale probed by phase-contrast X-ray tomography. J. Struct. Biol. 2011, 173, 180–190. [Google Scholar] [CrossRef]
- Arzola-Villegas, X.; Lakes, R.; Plaza, N.Z.; Jakes, J.E. Wood moisture-induced swelling at the cellular scale—Ab intra. Forests 2019, 10, 996. [Google Scholar] [CrossRef] [Green Version]
- Stamm, A.J.; Burr, H.K.; Kline, A.A. Staybwood—Heat-stabilized wood. Ind. Eng. Chem. 1946, 38, 630–634. [Google Scholar] [CrossRef]
- Altgen, M.; Hofmann, T.; Militz, H. Wood moisture content during the thermal modification process affects the improvement in hygroscopicity of Scots pine sapwood. Wood Sci. Technol. 2016, 50, 1181–1195. [Google Scholar] [CrossRef]
- Akitsu, H.; Norimoto, M.; Morooka, T.; Rowell, R.M. Effect of humidity on vibrational properties of chemically modified wood. Wood Fiber Sci. 1993, 25, 250–260. [Google Scholar]
- Emmerich, L.; Altgen, M.; Rautkari, L.; Militz, H. Sorption behavior and hydroxyl accessibility of wood treated with different cyclic N-methylol compounds. J. Mater. Sci. 2020, 55, 16561–16575. [Google Scholar] [CrossRef]
- Hill, C.A.S.; Keating, B.A.; Jalaludin, Z.; Mahrdt, E. A rheological description of the water vapour sorption kinetics behaviour of wood invoking a model using a canonical assembly of Kelvin-Voigt elements and a possible link with sorption hysteresis. Holzforschung 2012, 66, 35–47. [Google Scholar] [CrossRef]
- Engelund, E.T.; Thygesen, L.G.; Hoffmeyer, P. Water sorption in wood and modified wood at high values of relative humidity. Part 2: Appendix. Theoretical assessment of the amount of capillary water in wood microvoids. Holzforschung 2010, 64, 325–330. [Google Scholar] [CrossRef]
- Fortin, Y. Moisture Content-Matric Potential Relationship and Water Flow Properties of Wood at High Moisture Contents; Department of Forestry, University of British Columbia: Vancouver, BC, Canada, 1979; p. 187. [Google Scholar]
- McBain, J.W. An Explanation of Hysteresis in the Hydration and Dehydration of Gels. J. Am. Chem. Soc. 1935, 57, 699–700. [Google Scholar] [CrossRef]
- Ravikovitch, P.I.; Neimark, A.V. Experimental confirmation of different mechanisms of evaporation from ink-bottle type pores: Equilibrium, pore blocking, and cavitation. Langmuir 2002, 18, 9830–9837. [Google Scholar] [CrossRef]
- Skaar, C. Wood Moisture and the Environment. In Wood-Water Relations; Springer: Berlin/Heidelberg, Germany, 1988; pp. 1–45. [Google Scholar]
- Spalt, H.A. The fundamentals of water sorption by wood. For. Prod. J. 1958, 8, 288–295. [Google Scholar]
- Hoffmeyer, P.; Engelund, E.T.; Thygesen, L.G. Equilibrium moisture content (EMC) in Norway spruce during the first and second desorptions. Holzforschung 2011, 65, 875–882. [Google Scholar] [CrossRef] [Green Version]
- Fredriksson, M.; Thybring, E.E. Scanning or desorption isotherms? Characterising sorption hysteresis of wood. Cellulose 2018, 25, 4477–4485. [Google Scholar]
- Karagiozis, A. Advanced numerical models for hygrothermal research. In Moisture Analysis and Condensation Control in Building Envelopes; Treschel, H.R., Ed.; ASTM International: West Conshohocken, PA, USA, 2001; pp. 90–106. [Google Scholar]
- Straube, J.; Burnett, E. Overview of hygrothermal (HAM) analysis methods. In Moisture Analysis and Condensation Control in Building Envelopes; Trechsel, H., Ed.; ASTM International: West Conshohocken, PA, USA, 2001; pp. 81–89. [Google Scholar]
- Glass, S.V.; TenWolde, A.; Zelinka, S.L. Hygrothermal simulation: A tool for building envelope design analysis. Wood Des. Focus 2013, 23, 18–25. [Google Scholar]
- Everett, D.H. A general approach to hysteresis. Part 4. An alternative formulation of the domain model. Trans. Faraday Soc. 1955, 51, 1551–1557. [Google Scholar] [CrossRef]
- Peralta, P. Moisture Sorption Hysteresis and The Independent-domain Theory: The Moisture Distribution Function. Wood Fiber Sci. 1996, 28, 406–410. [Google Scholar]
- Peralta, P.N. Modeling wood moisture sorption hysteresis using the independent-domain theory. Wood Fiber Sci. 1995, 27, 250–257. [Google Scholar]
- Patera, A.; Derluyn, H.; Derome, D.; Carmeliet, J. Influence of sorption hysteresis on moisture transport in wood. Wood Sci. Technol. 2016, 50, 259–283. [Google Scholar] [CrossRef]
- Merakeb, S.; Dubois, F.; Petit, C. Modeling of the sorption hysteresis for wood. Wood Sci. Technol. 2009, 43, 575. [Google Scholar] [CrossRef]
- Arevalo, R.; Hernandez, R.E. Influence of moisture sorption on swelling of mahogany (Swietenia macrophylla King) wood. Holzforschung 2001, 55, 590–594. [Google Scholar] [CrossRef]
- Chauhan, S.S.; Aggarwal, P. Effect of moisture sorption state on transverse dimensional changes in wood. Holz Roh Werkst. 2004, 62, 50–55. [Google Scholar] [CrossRef]
- Hartley, I.D.; Avramidis, S. Static dimensional changes of Sitka spruce and Western hemlock influenced by sorption conditions. J. Inst. Wood Sci. 1996, 14, 83–88. [Google Scholar]
- Hernandez, R.E. Influence of moisture sorption history on the swelling of Sugar maple wood and some tropical hardwoods. Wood Sci. Technol. 1993, 27, 337–345. [Google Scholar] [CrossRef]
- Ishimaru, Y.; Arai, K.; Mizutani, M.; Oshima, K.; Iida, I. Physical and mechanical properties of wood after moisture conditioning. J. Wood Sci. 2001, 47, 185–191. [Google Scholar] [CrossRef]
- Derome, D.; Zillig, W.; Carmeliet, J. Variation of measured cross-sectional cell dimensions and calculated water vapor permeability across a single growth ring of spruce wood. Wood Sci. Technol. 2012, 46, 827–840. [Google Scholar] [CrossRef]
- Skaar, C. Moisture movement in the wood cell wall. In Wood-Water Relations; Springer: Berlin/Heidelberg, Germany, 1988; pp. 177–206. [Google Scholar]
- Siau, J.F. Steady-State Moisture Movement. In Transport Processes in Wood; Springer: Berlin/Heidelberg, Germany, 1984; pp. 151–174. [Google Scholar]
- Fick, A. Ueber Diffusion. Ann. Der Phys. 1855, 170, 59–86. [Google Scholar] [CrossRef]
- Fick, A. On liquid diffusion. Philos. Mag. Ser. 4 1855, 10, 30–39. [Google Scholar] [CrossRef]
- Janssen, H. Thermal diffusion of water vapour in porous materials: Fact or fiction? Int. J. Heat Mass Transf. 2011, 54, 1548–1562. [Google Scholar] [CrossRef] [Green Version]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon (The Public Fountains of the City of Dijon); Dalmont: Paris, France, 1856. [Google Scholar]
- Zillig, W. Moisture transport in wood using a multiscale approach. In Building Physics; Katholieke Universiteit Leuven: Leuven, Belgium, 2009. [Google Scholar]
- Sonderegger, W.; Vecellio, M.; Zwicker, P.; Niemz, P. Combined bound water and water vapour diffusion of Norway spruce and European beech in and between the principal anatomical directions. Holzforschung 2011, 65, 819–828. [Google Scholar] [CrossRef] [Green Version]
- Zelinka, S.L.; Glass, S.V.; Boardman, C.R.; Derome, D. Moisture storage and transport properties of preservative treated and untreated southern pine wood. Wood Mater. Sci. Eng. 2016, 11, 228–238. [Google Scholar] [CrossRef]
- Pidgeon, L.M.; Maass, O. The penetration of water vapor into wood. Can. J. Res. 1930, 2, 318–326. [Google Scholar] [CrossRef]
- Buckman, S.J.; Rees, L.W. Moisture movement in coniferous wood below the fiber-saturation point. In Technical Bulletin; University of Minnesota: St. Paul, MN, USA, 1935; p. 19. [Google Scholar]
- Choong, E.T. Movement of moisture through softwood in hygroscopic range. For. Prod. J. 1963, 13, 489–498. [Google Scholar]
- Choong, E.T.; Fogg, P.J. Moisture movement in six wood species. For. Prod. J. 1968, 18, 66–70. [Google Scholar]
- Petty, J.A.; Preston, R.D. Permeability and structure of the wood of Sitka spruce. Proc. R. Soc. London. Ser. B. Biol. Sci. 1970, 175, 149–166. [Google Scholar]
- Kulasinski, K.; Guyer, R.; Derome, D.; Carmeliet, J. Water diffusion in amorphous hydrophilic systems: A stop and go process. Langmuir 2015, 31, 10843–10849. [Google Scholar] [CrossRef] [PubMed]
- Kulasinski, K.; Keten, S.; Churakov, S.V.; Guyer, R.; Carmeliet, J.; Derome, D. Molecular mechanism of moisture-induced transition in amorphous cellulose. ACS Macro Lett. 2014, 3, 1037–1040. [Google Scholar] [CrossRef]
- Topgaard, D.; Söderman, O. Diffusion of water absorbed in cellulose fibers studied with H-1-NMR. Langmuir 2001, 17, 2694–2702. [Google Scholar] [CrossRef]
- Stamm, A.J. Bound water diffusion into wood in the fiber direction. For. Prod. J. 1959, 9, 27–32. [Google Scholar]
- Stamm, A.J. Bound-water diffusion into wood in across-the-fiber directions. For. Prod. J. 1960, 10, 524–528. [Google Scholar]
- Keplinger, T.; Cabane, E.; Chanana, M.; Hass, P.; Merk, V.; Gierlinger, N.; Burgert, I. A versatile strategy for grafting polymers to wood cell walls. Acta Biomater. 2015, 11, 256–263. [Google Scholar] [CrossRef]
- Keplinger, T.; Cabane, E.; Berg, J.K.; Segmehl, J.S.; Bock, P.; Burgert, I. Smart hierarchical bio-based materials by formation of stimuli-responsive hydrogels inside the microporous structure of wood. Adv. Mater. Interfaces 2016, 3, 1600233. [Google Scholar] [CrossRef]
- Stamm, A.J. Diffusion of water into uncoated cellophane. 1. From rates of water vapor adsorption, and liquid water absorption. J. Phys. Chem. 1956, 60, 76–82. [Google Scholar] [CrossRef]
- Stamm, A.J. Diffusion of water into uncoated cellophane. 2. From steady-state diffusion measurements. J. Phys. Chem. 1956, 60, 83–86. [Google Scholar] [CrossRef]
- Siau, J.F. Permeability. In Transport Processes in Wood; Springer: Berlin/Heidelberg, Germany, 1984; pp. 73–104. [Google Scholar]
- Hansmann, C.; Gindl, W.; Wimmer, R.; Teischinger, A. Permeability of wood—A review. Wood Res. 2002, 47, 1–16. [Google Scholar]
- Sedighi-Gilani, M.; Griffa, M.; Mannes, D.; Lehmann, E.; Carmeliet, J.; Derome, D. Visualization and quantification of liquid water transport in softwood by means of neutron radiography. Int. J. Heat Mass Transf. 2012, 55, 6211–6221. [Google Scholar] [CrossRef]
- Almeida, G.; Leclerc, S.; Perre, P. NMR imaging of fluid pathways during drainage of softwood in a pressure membrane chamber. Int. J. Multiph. Flow 2008, 34, 312–321. [Google Scholar] [CrossRef]
- Sedighi-Gilani, M.; Vontobel, P.; Lehmann, E.; Carmeliet, J.; Derome, D. Liquid uptake in Scots pine sapwood and hardwood visualized and quantified by neutron radiography. Mater. Struct. 2014, 47, 1083–1096. [Google Scholar] [CrossRef]
- Desmarais, G.; Sedighi-Gilani, M.; Vontobel, P.; Carmeliet, J.; Derome, D. Transport of polar and nonpolar liquids in softwood imaged by neutron radiography. Transp. Porous Media 2016, 113, 383–404. [Google Scholar] [CrossRef]
- Liese, W.; Bauch, J. On the closure of bordered pits in conifers. Wood Sci. Technol. 1967, 1, 1–13. [Google Scholar] [CrossRef]
- Phillips, E.W.J. Movement of the pit membrane in coniferous woods, with special reference to preservative treatment. For. Int. J. For. Res. 1933, 7, 109–120. [Google Scholar] [CrossRef]
- Siau, J.F. Wood Structure and Chemical Composition. In Transport Processes in Wood; Springer: Berlin/Heidelberg, Germany, 1984; pp. 35–72. [Google Scholar]
- Gezici-Koç, Ö.; Erich, S.J.F.; Huinink, H.P.; van der Ven, L.G.J.; Adan, O.C.G. Bound and free water distribution in wood during water uptake and drying as measured by 1D magnetic resonance imaging. Cellulose 2017, 24, 535–553. [Google Scholar] [CrossRef] [Green Version]
- Sandberg, K.; Salin, J.G. Liquid water absorption in dried Norway spruce timber measured with CT scanning and viewed as a percolation process. Wood Sci. Technol. 2012, 46, 207–219. [Google Scholar] [CrossRef]
- Stamm, A.J. Passage of Liquids, Vapors and Dissolved Materials through Softwoods; Technical Bulletin 929; US Department of Agriculture: Washington, DC, USA, 1946; pp. 1–80.
- Comstock, G.L. Moisture diffusion coefficients in wood as calculated from adsorption, desorption, and steady state data. For. Prod. J. 1963, 13, 97–103. [Google Scholar]
- Skaar, C.; Prichananda, C.; Davidson, R.W. Some aspects of moisture sorption dynamics in wood. Wood Sci. 1970, 2, 179–185. [Google Scholar]
- Wadsö, L. Measurements of water-vapor sorption in wood. 2. Results. Wood Sci. Technol. 1993, 28, 59–65. [Google Scholar] [CrossRef]
- Wadsö, L. Unsteady-state water-vapor adsorption in wood—An experimental study. Wood Fiber Sci. 1994, 26, 36–50. [Google Scholar]
- Wadsö, L. Describing non-fickian water-vapor sorption in wood. J. Mater. Sci. 1994, 29, 2367–2372. [Google Scholar] [CrossRef]
- Krabbenhøft, K.; Damkilde, L. A model for non-Fickian moisture transfer in wood. Mater. Struct. 2004, 37, 615–622. [Google Scholar] [CrossRef]
- Frandsen, H.L.; Damkilde, L.; Svensson, S. A revised multi-Fickian moisture transport model to describe non-Fickian effects in wood. Holzforschung 2007, 61, 563–572. [Google Scholar] [CrossRef]
- Eitelberger, J.; Hofstetter, K.; Dvinskikh, S.V. A multi-scale approach for simulation of transient moisture transport processes in wood below the fiber saturation point. Compos. Sci. Technol. 2011, 71, 1727–1738. [Google Scholar] [CrossRef]
- Eitelberger, J.; Hofstetter, K. A comprehensive model for transient moisture transport in wood below the fiber saturation point: Physical background, implementation and experimental validation. Int. J. Therm. Sci. 2011, 50, 1861–1866. [Google Scholar] [CrossRef]
- Konopka, D.; Kaliske, M. Transient multi-Fickian hygro-mechanical analysis of wood. Comput. Struct. 2018, 197, 12–27. [Google Scholar] [CrossRef]
- Krabbenhøft, K.; Damkilde, L. Double porosity models for the description of water infiltration in wood. Wood Sci. Technol. 2004, 38, 641–659. [Google Scholar] [CrossRef]
- Autengruber, M.; Lukacevic, M.; Füssl, J. Finite-element-based moisture transport model for wood including free water above the fiber saturation point. Int. J. Heat Mass Transf. 2020, 161, 120228. [Google Scholar] [CrossRef]
- Thorell, A.; Wadsö, L. Determination of external mass transfer coefficients in dynamic sorption (DVS) measurements. Dry. Technol. 2018, 36, 332–340. [Google Scholar] [CrossRef] [Green Version]
- Wadsö, L. Surface mass transfer coefficients for wood. Dry. Technol. 1993, 11, 1227–1249. [Google Scholar] [CrossRef]
- Christensen, G.N. Kinetics of sorption of water vapour by wood. Aust. J. Appl. Sci. 1960, 11, 295–304. [Google Scholar]
- Christensen, G.N. The rate of sorption of water vapour by wood and pulp. Appita J. 1959, 13, 112–123. [Google Scholar]
- Christensen, G.N.; Kelsey, K.E. The rate of sorption of water vapor by wood. Holz Roh Werkst. 1959, 17, 178–188. [Google Scholar] [CrossRef]
- Christensen, G.N.; Hergt, H.F.A. Effect of previous history on kinetics of sorption by wood cell walls. J. Polym. Sci. Part A 1 Polym. Chem. 1969, 7, 2427–2430. [Google Scholar] [CrossRef]
- Willems, W. Thermally limited wood moisture changes: Relevance for dynamic vapour sorption experiments. Wood Sci. Technol. 2017, 51, 751–770. [Google Scholar] [CrossRef]
- Willems, W. Heuristic study on the interaction between heat exchange and slow relaxation processes during wood moisture content changes. Holzforschung 2021, 75, 303–312. [Google Scholar] [CrossRef]
- Chen, W.; Lickfield, G.C.; Yang, C.Q. Molecular modeling of cellulose in amorphous state. Part I: Model building and plastic deformation study. Polymer 2004, 45, 1063–1071. [Google Scholar] [CrossRef]
- Matsuoka, S.; Bair, H.E.; Bearder, S.S.; Kern, H.E.; Ryan, J.T. Analysis of non-linear stress relaxation in polymeric glasses. Polym. Eng. Sci. 1978, 18, 1073–1080. [Google Scholar] [CrossRef]
- Kohler, R.; Dück, R.; Ausperger, B.; Alex, R. A numeric model for the kinetics of water vapor sorption on cellulosic reinforcement fibers. Compos. Interfaces 2003, 10, 255–276. [Google Scholar] [CrossRef]
- Murr, A.; Lackner, R. Analysis on the influence of grain size and grain layer thickness on the sorption kinetics of grained wood at low relative humidity with the use of water vapour sorption experiments. Wood Sci. Technol. 2018, 52, 753–776. [Google Scholar] [CrossRef] [Green Version]
- Olek, W.; Perré, P.; Weres, J. Inverse analysis of the transient bound water diffusion in wood. Holzforschung 2005, 59, 38–45. [Google Scholar] [CrossRef]
- Guo, X.; Wu, Y.; Xie, X. Water vapor sorption properties of cellulose nanocrystals and nanofibers using dynamic vapor sorption apparatus. Sci. Rep. 2017, 7, 14207. [Google Scholar] [CrossRef] [Green Version]
- Himmel, S.; Mai, C. Water vapour sorption of wood modified by acetylation and formalisation—Analysed by a sorption kinetics model and thermodynamic considerations. Holzforschung 2016, 70, 203–213. [Google Scholar] [CrossRef]
- Simón, C.; Esteban, L.G.; de Palacios, P.; Fernández, F.G.; García-Iruela, A. Sorption/desorption hysteresis revisited. Sorption properties of Pinus pinea L. analysed by the parallel exponential kinetics and Kelvin-Voigt models. Holzforschung 2017, 71, 171. [Google Scholar] [CrossRef]
- Hill, C.A.S.; Norton, A.; Newman, G. Analysis of the water vapour sorption behaviour of Sitka spruce [Picea sitchensis (Bongard) Carr.] based on the parallel exponential kinetics model. Holzforschung 2010, 64, 469–473. [Google Scholar]
- Zaihan, J.; Hill, C.A.S.; Curling, S.; Hashim, W.S.; Hamdan, H. The kinetics of water vapour sorption: Analysis using parallel exponential kinetics model on six Malaysian hardwoods. J. Trop. For. Sci. 2010, 22, 107–117. [Google Scholar]
- Glass, S.V.; Zelinka, S.L.; Thybring, E.E. Exponential decay analysis: A flexible, robust, data-driven methodology for analyzing sorption kinetic data. Cellulose 2021, 28, 153–174. [Google Scholar] [CrossRef]
- Belbekhouche, S.; Bras, J.; Siqueira, G.; Chappey, C.; Lebrun, L.; Khelifi, B.; Marais, S.; Dufresne, A. Water sorption behavior and gas barrier properties of cellulose whiskers and microfibrils films. Carbohydr. Polym. 2011, 83, 1740–1748. [Google Scholar] [CrossRef]
- Jalaludin, Z.; Hill, C.A.S.; Samsi, H.W.; Husain, H.; Xie, Y.J. Analysis of water vapour sorption of oleo-thermal modified wood of Acacia mangium and Endospermum malaccense by a parallel exponential kinetics model and according to the Hailwood-Horrobin model. Holzforschung 2010, 64, 763–770. [Google Scholar] [CrossRef]
- Xie, Y.J.; Hill, C.A.S.; Jalaludin, Z.; Curling, S.F.; Anandjiwala, R.D.; Norton, A.J.; Newman, G. The dynamic water vapour sorption behaviour of natural fibres and kinetic analysis using the parallel exponential kinetics model. J. Mater. Sci. 2011, 46, 479–489. [Google Scholar] [CrossRef]
- Thybring, E.E.; Boardman, C.R.; Glass, S.V.; Zelinka, S.L. The parallel exponential kinetics model is unfit to characterize moisture sorption kinetics in cellulosic materials. Cellulose 2019, 26, 723–735. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thybring, E.E.; Fredriksson, M.; Zelinka, S.L.; Glass, S.V. Water in Wood: A Review of Current Understanding and Knowledge Gaps. Forests 2022, 13, 2051. https://doi.org/10.3390/f13122051
Thybring EE, Fredriksson M, Zelinka SL, Glass SV. Water in Wood: A Review of Current Understanding and Knowledge Gaps. Forests. 2022; 13(12):2051. https://doi.org/10.3390/f13122051
Chicago/Turabian StyleThybring, Emil Engelund, Maria Fredriksson, Samuel L. Zelinka, and Samuel V. Glass. 2022. "Water in Wood: A Review of Current Understanding and Knowledge Gaps" Forests 13, no. 12: 2051. https://doi.org/10.3390/f13122051
APA StyleThybring, E. E., Fredriksson, M., Zelinka, S. L., & Glass, S. V. (2022). Water in Wood: A Review of Current Understanding and Knowledge Gaps. Forests, 13(12), 2051. https://doi.org/10.3390/f13122051