Genetic Parameters and Genotype–Environment Interactions in Paulownia Clonal Tests in Temperate and Subtropical Regions of China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Plant Materials and Experimental Design
2.2. Measurements
2.3. Estimates of Genetic Parameters
2.4. Genotype Main Effect Plus Genotype by Environment Interaction Effects
2.5. Productivity, Stability, and Adaptability
2.6. Expected Gain
3. Results
3.1. Variance Analysis and Growth Performance
3.2. Estimation of Genetic Parameters
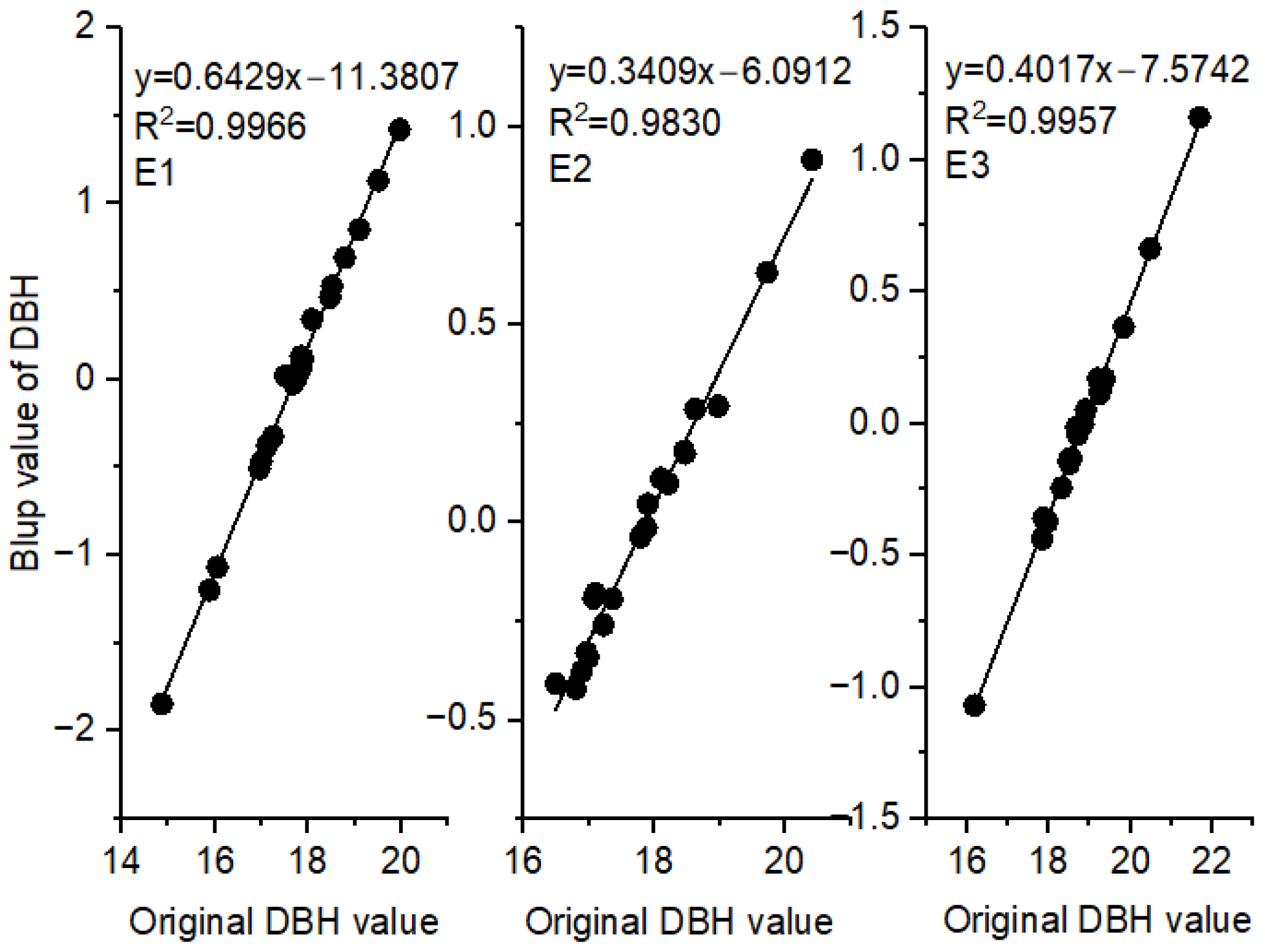
3.3. Relationships between BLUPs for DBH and Original DBH Values
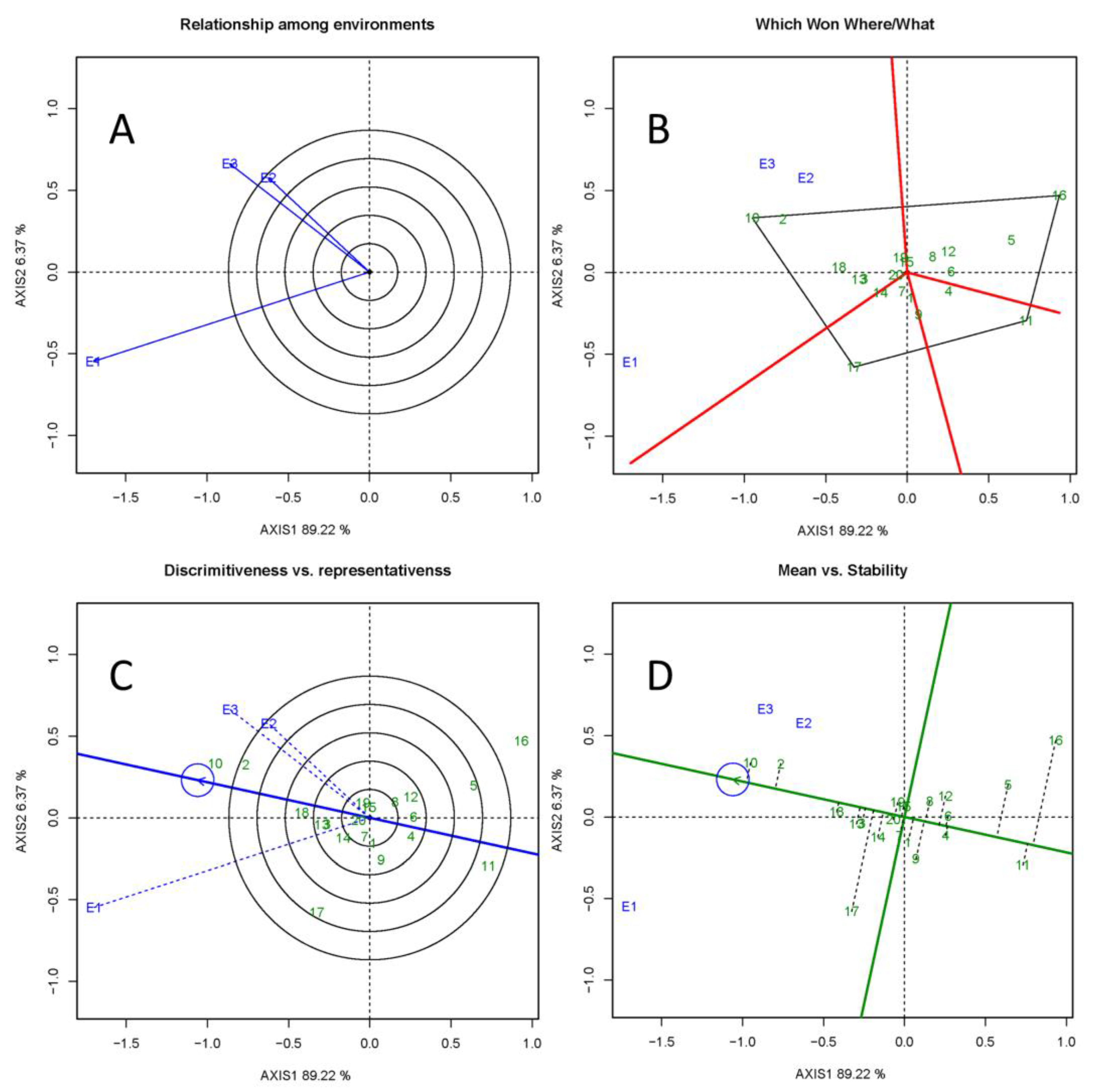
3.4. GGE Biplot Analyses
3.5. Stability, Adaptability, and Productivity
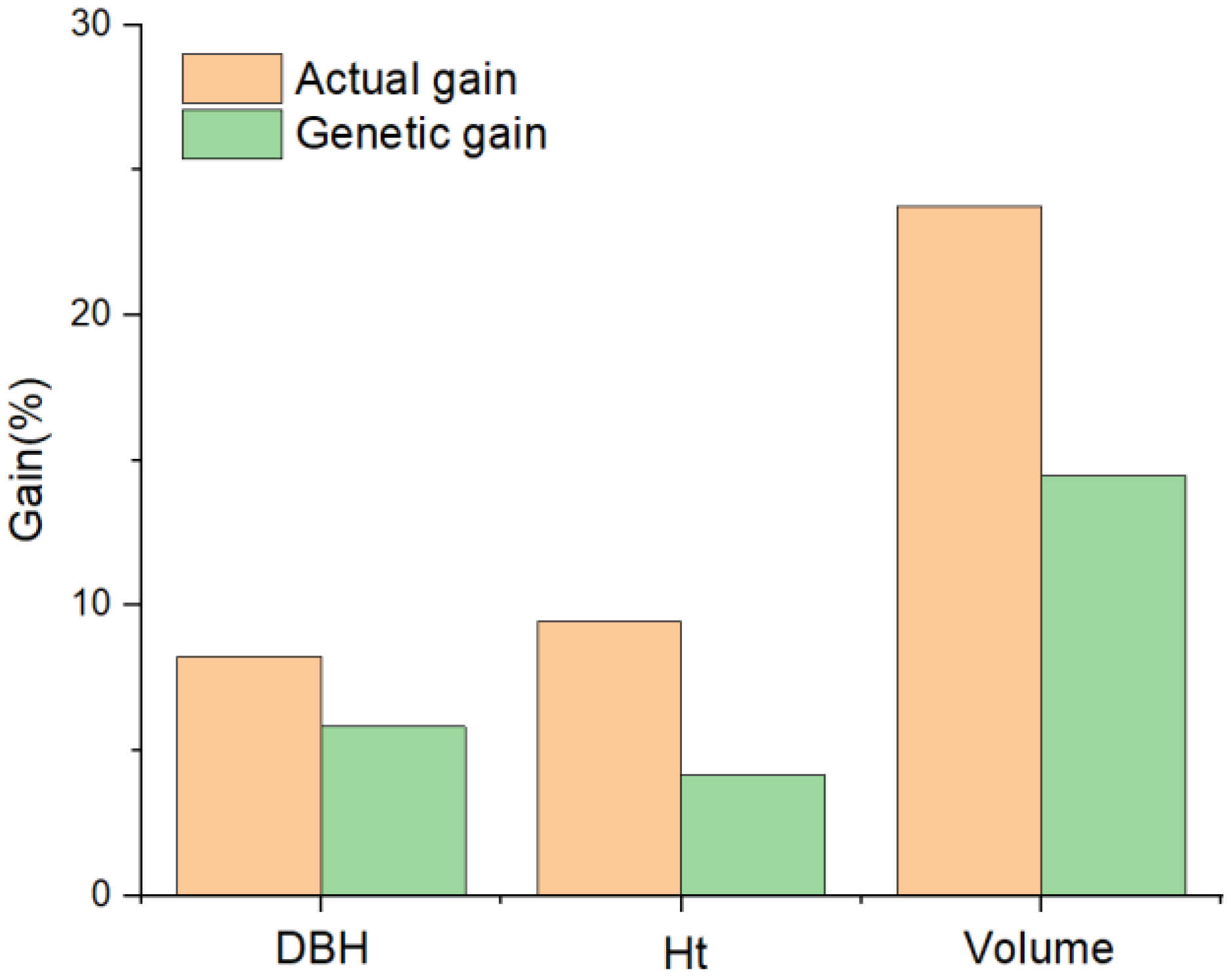
3.6. Actual Gain and Genetic Gain
4. Discussion
4.1. Variance among Sites and Clones
4.2. Genetic Parameters
4.3. GGE Biplot and Selection of Optimal Clones
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, Y.Z.; Cui, L.J.; Zhao, Y.; Qiao, J.; Wang, B.P.; Yang, C.W.; Zhou, H.J.; Chang, D.L. Comprehensive selection of the wood properties of Paulownia clones grown in the Hilly Region of Southern China. BioResources 2020, 15, 1098–1111. [Google Scholar] [CrossRef]
- Latib, H.A.; Liat, L.C.; Ratnasingam, J.; Law, E.L.; Azim, A.A.A.; Mariapan, M.; Natkuncaran, J. Suitability of Paulownia wood from malaysia for furniture application. BioResources 2020, 15, 4727–4737. [Google Scholar] [CrossRef]
- Rodríguez-Seoanea, P.; Díaz-Reinosob, B.; Andr´es, M.; Herminia, D. Potential of Paulownia sp. for biorefinery. Ind. Crop Prod. 2020, 155, 112739. [Google Scholar] [CrossRef]
- Dzugan, M.; Miłek, M.; Grabek-Lejko, D.; Hęclik, J.; Jacek, B.; Litwinczuk, W. Antioxidant activity, polyphenolic profiles and antibacterial properties of leaf extract of various Paulownia spp. clones. Agronomy 2021, 11, 2001. [Google Scholar] [CrossRef]
- Jakubpwski, M. Cultivation potential and uses of Paulownia wood: A review. Forests 2022, 13, 668. [Google Scholar] [CrossRef]
- Borjia, L.E.M.; Garcia, M.E.; Antonio, F.; Morote, G.; Ramon, F.; Serrano, L.; Abellan, A.M.; Perea, C.D.; Barja, C.A.; Brja, C.A. El cultivo de Paulonia (Pawlonia elongata × fortunei) para la obtención de madera y biomasa en Castilla-La Mancha: Primeros resultados. Foresta 2010, 47, 103–110. [Google Scholar]
- Zuazo, V.H.D.; Bocanegra, J.A.J.; Torres, F.P.; Pleguezuelo, C.R.R.; Martínez, J.R.F. Biomass yield potential of Paulownia trees in a semi-arid Mediterranean environment (S Spain). Int. J. Renew. Energy Res. 2013, 3, 789–793. [Google Scholar]
- Barga, R.C.; Paludeto, Z.G.J.; Souza, M.B.; Aguiar, V.A.; Pollnow, M.F.M.; Carvalho, M.G.A.; Tambarussi, V.E. Genetic parameters and genotype × environment interaction in Pinus taeda clonal tests. For. Ecol. Manag. 2020, 474, 118342. [Google Scholar] [CrossRef]
- Kang, X.Y. Thinking about clonal breeding strategy of forest trees. J. Beijing For. Univ. 2019, 41, 1–9. [Google Scholar] [CrossRef]
- Zhao, Y.; Qiao, J.; Wang, B.P.; Feng, Y.Z.; Zhou, H.J.; Cui, L.J.; Wang, W.W.; Yang, D.G. Comprehensive selection of growth and stem form of superior Paulownia clones in the hilly region of southern China. J. Beijing For. Univ. 2017, 39, 32–40. [Google Scholar] [CrossRef]
- Feng, Y.Z.; Qiao, J.; Wang, B.P.; Zhao, Y.; Zhou, H.J.; Duan, W.; Li, F.D. Comprehensive selection of main phenotypic characters of Paulownia clones in the Hilly Area of Southern China. For. Res. 2017, 30, 969–976. [Google Scholar] [CrossRef]
- Burdon, R. Genetic correlation as a concept for studying genotype-environment interaction in forest tree breeding. Silvae Genet. 1977, 26, 168–175. [Google Scholar]
- Diao, S.; Hou, Y.M.; Xie, Y.H.; Sun, X.M. Age trends of genetic parameters, early selection and family by site interactions for growth traits in Larix kaempferi open-pollinated families. BMC Genet. 2016, 17, 104. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.X. Selcetiong and assessment. In Forest Genetics and Breeding, 1st ed.; China Forestry Publishing House: Beijing, China, 2001; pp. 156–179. [Google Scholar]
- Wahid, N.; Rainville, A.; Lamhamedi, M.S.; Margolos, H.A.; Beaulieu, J.; Deblois, J. Genetic parameters and performance stability of white spruce somatic seedlings in clonal tests. For. Ecol. Manag. 2012, 270, 45–53. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, X.F.; Zhang, X.X.; Zhang, W.H.; Lin, Y.Z. Forestry multi-environment trial analysis based on BLUP and GGE biplot. J. Northwest A F Univ. (Nat. Sci. Ed.) 2018, 46, 87–93. [Google Scholar]
- Finlay, K.; Wilkinson, G.N. The analysis of adaptation in plant-breeding program. Aust. J. Agric. Res. 1963, 14, 742–754. [Google Scholar] [CrossRef] [Green Version]
- Cullis, B.R.; Jefferson, P.; Thompson, R.; Smith, B.A. Factor analytic and reduced animal models for the investigation of additive genotype-by-environment interaction in outcrossing plant species with application to a Pinus radiata breeding programme. Theor. Appl. Genet. 2014, 127, 2193–2210. [Google Scholar] [CrossRef]
- Yan, W.K. GGEbiplot—A windows application for graphical analysis of multienvironment trial data and other types of two-way data. Agron. J. 2001, 93, 1111–1118. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Y.; Ma, W.J.; Lu, N.; Wang, Z.; Wang, N.; Zhai, W.J.; Kong, L.S.; Qu, G.Z.; Wang, Q.X.; Wang, J.H. Genetic variation of growth traits and genotype-by-environment interactions in clones of Catalpa bungei and Catalpa fargesii f. duclouxii. Forests 2019, 10, 57. [Google Scholar] [CrossRef] [Green Version]
- Zhou, M.M.; Chen, P.; Shang, X.L.; Yang, W.X.; Fang, S.Z. Genotype–environment interactions for tree growth and leaf phytochemical content of Cyclocarya paliurus (Batal.) Iljinskaja. Forests 2021, 12, 735. [Google Scholar] [CrossRef]
- Ling, J.J.; Xiao, Y.; Hu, J.W.; Wang, F.D.; Ouyang, F.Q.; Wang, J.H.; Weng, Y.H.; Zhang, H.G. Genotype by environment interaction analysis of growth of Picea koraiensis families at different sites using BLUP-GGE. New For. 2021, 52, 113–127. [Google Scholar] [CrossRef]
- Li, J.H. Genotype by environment interaction for growth traits of clones of Populus section Aigeiros based on BLUP and GGE Biplot. Sci. Silvae Sin. 2021, 57, 64–73. [Google Scholar] [CrossRef]
- Yan, W.K.; Hunt, L.A.; Sheng, Q.L.; Szlavnics, Z. Cultivar evaluation and mega-environment investigation based on the GGE biplot. Crop Sci. 2000, 40, 597–605. [Google Scholar] [CrossRef]
- Sun, X.M.; Yang, X.Y. Applications and analysis of methods for breeding value prediction in forest trees. J. Beijing For. Univ. 2011, 33, 65–71. [Google Scholar]
- Henderson, C.R. General flexibility of linear model techniques for sire evaluation. J. Dairy Sci. 1974, 57, 963–972. [Google Scholar] [CrossRef]
- Ouyang, F.Q.; Qi, S.X.; Fan, G.X.; Cai, Q.S.; Chen, H.Q.; Gao, W.L.; Hu, C.S.; Wang, J.H. Genetic variation and improved parents selection of open pollination families of Picea crassifolia Kom. basing one BLUP method. J. Nanjing For. Univ. (Nat. Sci. Ed.) 2019, 43, 53–59. [Google Scholar] [CrossRef]
- Zheng, C.H.; Zhang, H.J.; Wang, Y.Z.; Dai, J.F.; Dang, L.; Du, Z.C.; Liu, J.T.; Gao, Y.R. An analysis of a regional trial of Larix principis-rupprechtii families based on BLUP and GGE Biplot. Sci. Silvae Sin. 2019, 55, 73–83. [Google Scholar] [CrossRef]
- Lin, Y.Z. Research methodologies for genotype by environment interactions in forest trees and their applications. Sci. Silvae Sin. 2019, 55, 142–151. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, Y.Z.; Sun, P.; Wang, B.P.; Qiao, J.; Duan, W.; Zhang, J.J.; Zhou, H.J.; Yang, C.W. Responses of phytohormones, carbon and nitrogen status to the trunk-extension pruning in three-year-old Paulownia plantation. J. Anim. Plant Sci. 2021, 31, 450–458. [Google Scholar] [CrossRef]
- Wu, L.C.; Wang, B.P.; Qiao, J.; Zhou, H.J.; Wen, R.J.; Xue, J.L.; Li, Z.R. Effects of trunk-extension pruning at different intensities on the growth and trunk form of Paulownia fortune. For. Ecol. Manag. 2014, 327, 128–135. [Google Scholar] [CrossRef]
- Yuan, C.Z.; Zhang, Z.; Jin, G.Q.; Zheng, Y.; Zhou, Z.C.; Sun, L.S.; Tong, H.B. Genetic parameters and genotype by environment interactions influencing growth and productivity in Masson pine in east and central China. For. Ecol. Manag. 2021, 487, 118991. [Google Scholar] [CrossRef]
- Lambeth, C.; Endo, M.; Wright, J. Genetic analysis of 16 clonal trials of Eucalyptus grandis and comparisons with seedling checks. For. Sci. 1994, 40, 397–411. [Google Scholar]
- Yin, M.Y.; Guo, J.J.; Wang, C.S.; Zhao, Z.G.; Zeng, J. Genetic parameter estimates and genotype × environment interactions of growth and quality traits for Betula alnoides Buch.-Ham. ex D. Don in four provenance-family trials in southern China. Forests 2019, 10, 1036. [Google Scholar] [CrossRef] [Green Version]
- Frutos, E.; Galindo, M.P.; Leiva, V. An interactive biplot implementation in R for modeling genotype-by-environment interaction. Stoch. Environ. Res. Risk Assess. 2014, 28, 1629–1641. [Google Scholar] [CrossRef]
- Goncalves, C.M.G.; Ferreira-Gomes, L.R.; Lopes, A.C.A.; Vieira, J.M.F.P. Adaptability and yield stability of soybean genotypes by REML/BLUP and GGE Biplot. Crop Breed. Appl. Biotechnol. 2020, 20, e282920217. [Google Scholar] [CrossRef]
- Souza, M.B.; Freitas, M.L.M.; Sebbenn, M.A.; Gezan, A.S.; Zanatto, B.; Zulian, F.D.; Lopes, G.T.M.; Longui, L.E.; Guerrini, A.I.; Aguiar, V.A. Genotype-by-environment interaction in Corymbia citriodora (Hook.) K.D. Hill, & L.A.S. Johnson progeny test in Luiz Antonio, Brazil. For. Ecol. Manag. 2020, 460, 117855. [Google Scholar] [CrossRef]
- Hutu, I.; Oldenbroek, K.; Waaij, D.V.L. Chapter 9. Predicting response of selection. In Animal Breeding and Husbandry, 2nd ed.; Agroprint: Timisoara, Romania, 2020; pp. 309–338. [Google Scholar]
- Pliura, A.; Zhang, S.Y.; Mackay, J.; Bousquet, J. Genotypic variation in wood density and growth traits of poplar hybrids at four clonal trials. For. Ecol. Manag. 2007, 238, 92–106. [Google Scholar] [CrossRef]
- Kombi, K.D.; Liu, H.Z.; Zhao, X.Y. Estimation of genetic parameters and wood yield selection index in a clonal trial of Korean Pine (Pinus koraiensis) in Northeastern China. Sustainability 2021, 13, 4167. [Google Scholar] [CrossRef]
- Luechanimitchit, P.; Luangviriyasaeng, V.; Laosakul, S.; Pinyopusarerk, K.; Bush, D. Genetic parameter estimates for growth, stem-form and branching traits of Casuarina junghuhniana clones grown in Thailand. For. Ecol. Manag. 2017, 404, 251–257. [Google Scholar] [CrossRef]
- Houspanossian, J.; Kuppel, S.; Nosetto, M.; Bella, D.C.; Oricchio, P.; Barrucand, M.; Rusticucci, M.; Jobbagy, E. Long-lasting floods buffer the thermal regime of the Pampas. Theor. Appl. Climatol. 2018, 131, 111–120. [Google Scholar] [CrossRef] [Green Version]
- Goldblum, D.; Rigg, L. Tree growth response to climate change at the deciduous boreal forest ecotone, Ontario, Canada. Can. J. For. Res. 2005, 35, 2709–2718. [Google Scholar] [CrossRef]
- Shi, S.Z.; Ni, S.Q.; Zhu, C.; Cong, P.F.; Chen, D.L.; Wang, C.Q.; Xu, H.Z.; Bao, X.M. Comprehensive selection in cultural traits of polywood timber of Paulownia. J. Nanjing For. Univ. (Nat. Sci. Ed.) 1996, 20, 27–31. [Google Scholar]
- Barros, J.; Velasco, L.A.; Winkler, F.M. Heritability, genetic correlations and genotype by environment interactions in productive traits of the Caribbean scallop, Argopecten nucleus (Mollusca: Bivalvia). Aquaculture 2018, 488, 39–48. [Google Scholar] [CrossRef]
- Cornelius, J. Heritabilities and additive genetic coefficients of variation in forest trees. Can. J. For. Res. 1994, 24, 372–379. [Google Scholar] [CrossRef]
- Hung, T.D.; Brawner, J.T.; Lee, D.J.; Meder, R.; Dieters, M.J. Genetic variation in growth and wood-quality traits of Corymbia citriodora subsp. variegata across three sites in south-east Queensland, Australia. South. For. A J. For. Sci. 2016, 78, 225–239. [Google Scholar] [CrossRef]
- Dillon, S.K.; Brawner, J.T.; Meder, R.; Lee, D.J.; Southerton, S.G. Association genetics in Corymbia citriodora subsp. variegata identifies single nucleotide polymorphisms affecting wood growth and cellulosic pulp yield. New Phytol. 2012, 195, 596–608. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.H.; Gu, W.C.; Li, B.; Guo, W.Y.; Xia, L.F. Study on selection of Alnus cremastogyne provenance/family-analysis of growth adaptation and genetic stability. Sci. Silvae Sin. 2000, 36, 59–66. [Google Scholar] [CrossRef]
- Liu, N.; Ding, C.J.; Li, B.; Ding, M.; Su, X.H.; Huang, Q.J. Analysis of the genotype interaction of four-year-old Populus euramericana using the BLUP-GGE technique. Forests 2021, 12, 1759. [Google Scholar] [CrossRef]
- Woyann, L.G.; Meira, D.; Matei, G.; Zdziarski, A.D.; Dallacorate, V.L.; Madella, A.L.; Benin, G. Selection indexes based on linear-bilinear models applied to soybean breeding. Agron. J. 2020, 112, 175–182. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, X.Y.; Gu, W.; Wang, L.D.; Li, W.; Gao, Y.K.; Wu, L.G.; Guo, X.W.; Tigabu, M.; Xia, D.; et al. Genetic stability of Larix olgensis provenances planted in different sites in northeast China. For. Ecol. Manag. 2021, 485, 118988. [Google Scholar] [CrossRef]


| Genotype Code | Clone Identity | Clone Source | Female Parent | Male Parent |
|---|---|---|---|---|
| 1 | B9501 | Natural hybrid | Paulownia fortunei (Seem.) Hemsl. | ** |
| 2 | MB9502 | Artificial hybrid | Paulownia tomentosa (Thunb.) Steud. | P. fortunei |
| 3 | L13 | Plus-tree | Paulownia elongata S. Y. Hu | -- |
| 4 | MB15 | Artificial hybrid | P. tomentosa | P. fortunei |
| 5 | MB2 | Artificial hybrid | P. tomentosa | P. fortunei |
| 6 | MB42 | Artificial hybrid | P. tomentosa | P. fortunei |
| 7 | BL45 | Artificial hybrid | P. fortunei | P. elongata |
| 8 | L46 | Plus-tree | P. elongata | -- |
| 9 | MB47 | Artificial hybrid | P. tomentosa | P. fortunei |
| 10 | B49 | Natural hybrid | P. fortunei | ** |
| 11 | B52 | Natural hybrid | P. fortunei | ** |
| 12 | B5 | Natural hybrid | P. fortunei | ** |
| 13 | C61 | Natural hybrid | Paulownia fargesii Franch. | ** |
| 14 | MB70 | Artificial hybrid | P. tomentosa | P. fortunei |
| 15 | MBP1 | Artificial hybrid | P. tomentosa | P. fortunei |
| 16 | BP2 | Natural hybrid | P. fortunei | ** |
| 17 | MBP3 | Artificial hybrid | P. fortunei | P. tomentosa |
| 18 | MBP5 | Artificial hybrid | P. fortunei | P. elongata |
| 19 | BP6 | Natural hybrid | P. fortunei | ** |
| 20 | YG1 | Natural hybrid | Paulownia catalpifolia T. Gong ex D. Y. Hong | ** |
| E1 | E2 | E3 | |
|---|---|---|---|
| City state | Xinxiang, Henan | Chibi, Hubei | Jiujiang, Jiangxi |
| Latitude (N) | 34°22′36″ | 31°12′49″ | 29°10′59″ |
| Longitude (E) | 113°48′12″ | 112°52′21″ | 115°48′33″ |
| Climate zones | Temperate | Subtropical regions | Subtropical regions |
| Soil | Sandy | Red nitosol | Red nitosol |
| pH | 7.3~8.1 | 5.2~5.7 | 5.3~5.9 |
| Mean annual precipitation (mm) | 571 | 1690 | 1366 |
| Mean annual temperature (°C) | 14.4 | 16.8 | 16.7 |
| Frost-free period (days) | 193~217 | 247–261 | 239–266 |
| Altitude (m) | 78 | 535 | 196 |
| Site | Source | df | Mean Square | ||
|---|---|---|---|---|---|
| DBH | Ht | Volume | |||
| E1 | Clone | 19 | 34.90 *** | 6.52 *** | 0.0117 *** |
| Block | 3 | 5.77 | 5.80 *** | 0.0019 * | |
| Clone × Block | 57 | 12.44 *** | 4.35 *** | 0.0042 *** | |
| Error | 367 | 3.95 | 0.99 | 0.0013 | |
| E2 | Clone | 19 | 21.39 *** | 1.41 * | 0.0082 *** |
| Block | 3 | 91.13 *** | 34.52 *** | 0.0332 *** | |
| Clone × Block | 57 | 20.81 *** | 2.15 *** | 0.0077 *** | |
| Error | 365 | 7.53 | 0.76 | 0.0024 | |
| E3 | Clone | 19 | 29.18 *** | 18.99 *** | 0.0194 *** |
| Block | 3 | 139.15 *** | 23.56 *** | 0.0605 *** | |
| Clone × Block | 57 | 17.07 *** | 7.07 *** | 0.0078 *** | |
| Error | 395 | 4.20 | 2.68 | 0.0022 | |
| Effect | df | Mean Square | ||
|---|---|---|---|---|
| DBH | Ht | Volume | ||
| Site | 2 | 172.44 *** | 441.0 *** | 0.0339 *** |
| Clone | 19 | 76.35 *** | 16.8 *** | 0.0336 *** |
| Block (site) | 9 | 71.94 *** | 19.4 *** | 0.0271 *** |
| Clone × Site | 38 | 7.26 * | 5.3 *** | 0.0032 * |
| Error | 1293 | 5.65 | 1.8 | 0.0021 |
| Site | Traits | CVg(%) | CVe(%) | hf2 | hs2 | hj2 | hi2 | rgg |
|---|---|---|---|---|---|---|---|---|
| E1 | DBH (cm) | 5.95 | 11.23 | 0.64 | 0.30 | - | - | 0.80 |
| Height (m) | 5.04 | 17.30 | 0.30 | 0.10 | - | - | 0.55 | |
| Volume (m3) | 13.78 | 27.64 | 0.64 | 0.30 | - | - | 0.80 | |
| E2 | DBH (cm) | 3.69 | 11.88 | 0.41 | 0.13 | - | - | 0.64 |
| Height (m) | 4.75 | 23.73 | 0.37 | 0.07 | - | - | 0.61 | |
| Volume (m3) | 8.98 | 27.07 | 0.38 | 0.13 | 0.62 | |||
| E3 | DBH (cm) | 3.33 | 11.01 | 0.35 | 0.11 | - | - | 0.59 |
| Height (m) | 9.95 | 25.11 | 0.60 | 0.22 | - | - | 0.78 | |
| Volume (m3) | 13.92 | 32.09 | 0.55 | 0.23 | - | - | 0.74 | |
| Joint analysis | DBH (cm) | 4.44 | 11.81 | - | - | 0.84 | 0.23 | 0.92 |
| Height (m) | 5.54 | 18.71 | - | - | 0.64 | 0.14 | 0.80 | |
| Volume (m3) | 11.34 | 30.30 | - | - | 0.81 | 0.22 | 0.90 |
| Traits | DBH | Ht | Volume |
|---|---|---|---|
| DBH | 0.4606 ** | 0.9329 ** | |
| Ht | 0.8455 ** | 0.6247 ** | |
| Volume | 0.9923 ** | 0.8984 ** |
| Rank | For Single Site | For Stability and Adaptability | ||||
|---|---|---|---|---|---|---|
| E1 | E2 | E3 | MHVG | PRVG | MHPRVG | |
| 1 | 10 (a) | 10 (a) | 2 (a) | 10 | 10 | 10 |
| 2 | 2 (ab) | 2 (ab) | 10 (ab) | 2 | 2 | 2 |
| 3 | 17 (abc) | 18 (bc) | 18 (abc) | 18 | 18 | 18 |
| 4 | 18 (abcd) | 19 (bcd) | 13 (bcd) | 13 | 13 | 13 |
| 5 | 13 (abcde) | 17 (bcd) | 3 (bcde) | 3 | 3 | 3 |
| 6 | 3 (abcde) | 3 (bcd) | 1 (bcde) | 17 | 17 | 17 |
| 7 | 14 (bcde) | 14 (bcd) | 15 (cdef) | 14 | 14 | 14 |
| 8 | 7 (cde) | 13 (bcd) | 20 (cdef) | 20 | 20 | 20 |
| 9 | 20 (cde) | 8 (bcd) | 7 (cdef) | 19 | 19 | 19 |
| 10 | 1 (cde) | 15 (bcd) | 19 (cdef) | 15 | 15 | 15 |
| 11 | 19 (cde) | 12 (bcd) | 14 (cdef) | 7 | 7 | 7 |
| 12 | 15 (cde) | 20 (bcd) | 12 (cdef) | 1 | 1 | 1 |
| 13 | 9 (cdef) | 7 (cd) | 6 (cdef) | 9 | 9 | 9 |
| 14 | 8 (defg) | 6 (cd) | 9 (def) | 8 | 8 | 8 |
| 15 | 4 (efg) | 4 (cd) | 8 (def) | 12 | 12 | 12 |
| 16 | 6 (efg) | 9 (cd) | 5 (def) | 6 | 6 | 6 |
| 17 | 12 (efg) | 5 (cd) | 11 (def) | 4 | 4 | 4 |
| 18 | 11 (fgh) | 1 (d) | 16 (def) | 5 | 5 | 5 |
| 19 | 5 (gh) | 16 (d) | 17 (ef) | 11 | 11 | 11 |
| 20 | 16 (h) | 11 (e) | 4 (f) | 16 | 16 | 16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Feng, Y.; Yang, C.; Qiao, J.; Zhou, H.; Li, F.; Wang, B. Genetic Parameters and Genotype–Environment Interactions in Paulownia Clonal Tests in Temperate and Subtropical Regions of China. Forests 2022, 13, 2113. https://doi.org/10.3390/f13122113
Zhao Y, Feng Y, Yang C, Qiao J, Zhou H, Li F, Wang B. Genetic Parameters and Genotype–Environment Interactions in Paulownia Clonal Tests in Temperate and Subtropical Regions of China. Forests. 2022; 13(12):2113. https://doi.org/10.3390/f13122113
Chicago/Turabian StyleZhao, Yang, Yanzhi Feng, Chaowei Yang, Jie Qiao, Haijiang Zhou, Fangdong Li, and Baoping Wang. 2022. "Genetic Parameters and Genotype–Environment Interactions in Paulownia Clonal Tests in Temperate and Subtropical Regions of China" Forests 13, no. 12: 2113. https://doi.org/10.3390/f13122113
APA StyleZhao, Y., Feng, Y., Yang, C., Qiao, J., Zhou, H., Li, F., & Wang, B. (2022). Genetic Parameters and Genotype–Environment Interactions in Paulownia Clonal Tests in Temperate and Subtropical Regions of China. Forests, 13(12), 2113. https://doi.org/10.3390/f13122113





