Interaction of a Homologous Series of Amphiphiles with P-glycoprotein in a Membrane Environment—Contributions of Polar and Non-Polar Interactions
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Total Membrane Vesicle Preparation
2.3. ATPase Assays
2.4. Photolabeling of P–gp with [125I]-IAAP
2.5. Preparation of Large Unilamelar Vesicles
2.6. Association of the NBD Amphiphiles with Model Membranes and with Native Membranes
2.7. Bilayer Setup for Molecular Dynamics Simulations
2.8. Assembly of P–gp for Coarse Grain Molecular Dynamics Simulations
2.9. Umbrella Sampling Simulations for NBD–Cn in the Water/Complex Asymmetric Membrane
2.10. Umbrella Sampling Simulations for NBD–Cn in the P–gp Containing Membranes
2.11. MD Simulations Data Analysis and Visualization
3. Results
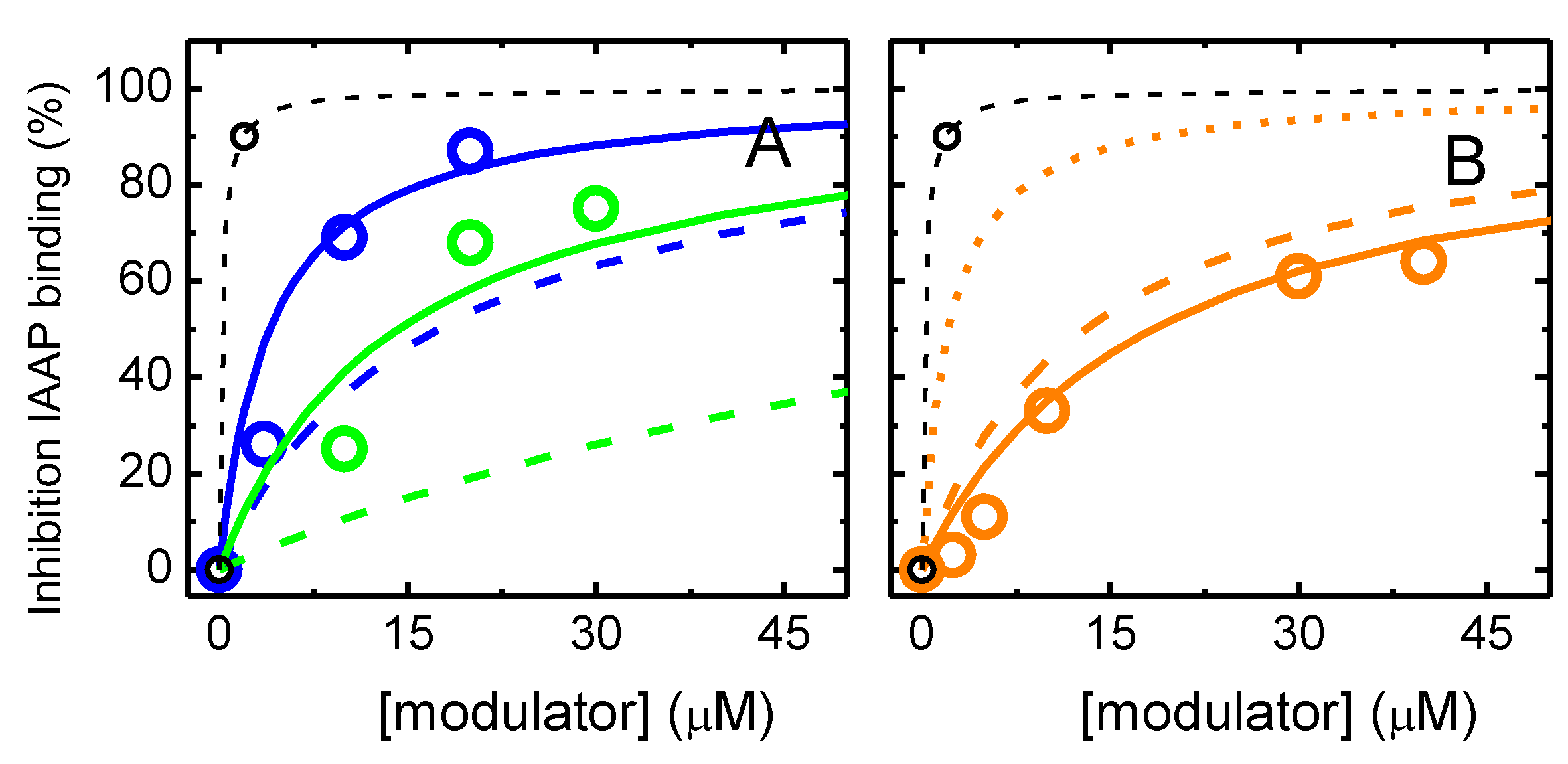
3.1. Effect of the Amphiphiles on P–gp ATPase Activity and Competition with IAAP for Binding
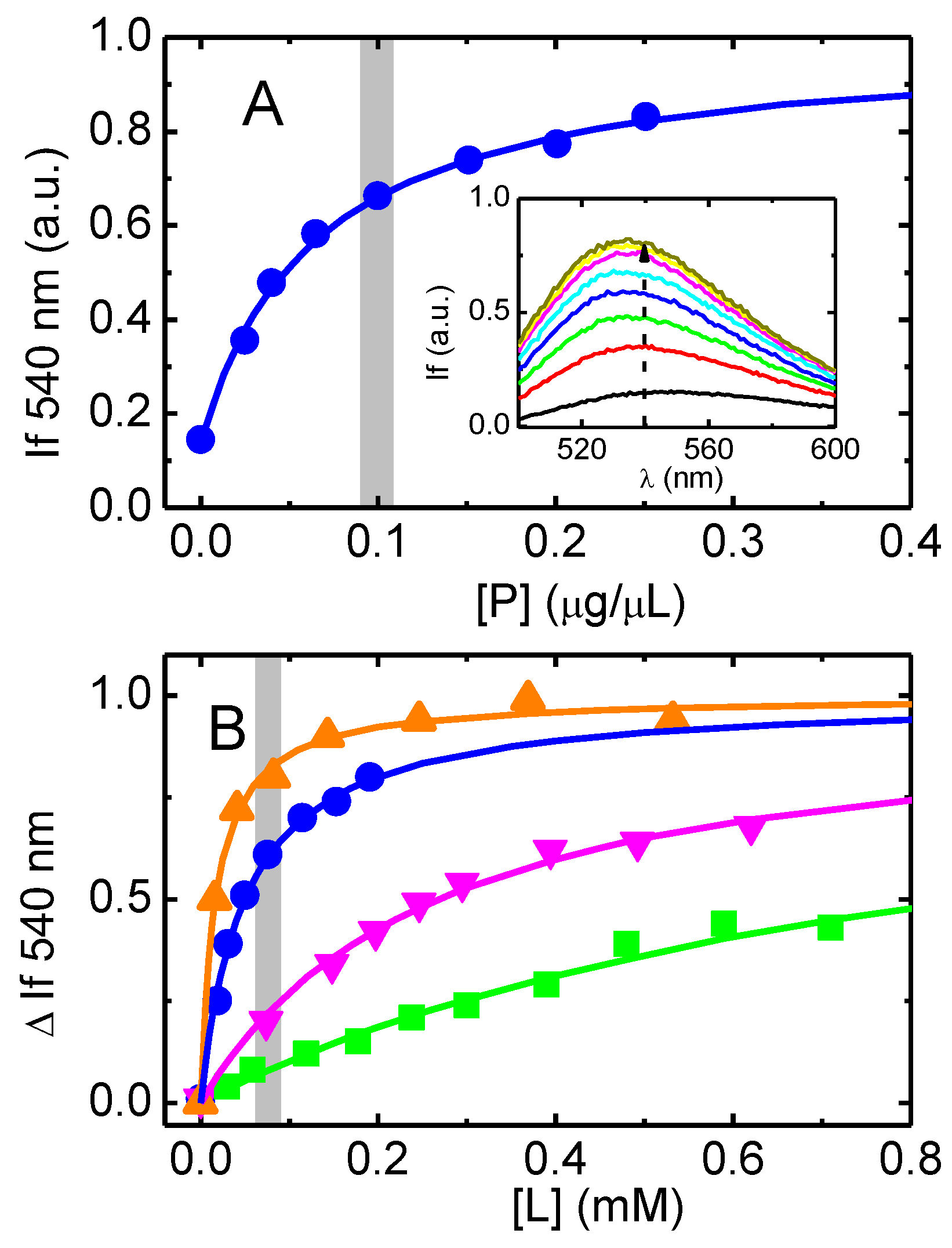
3.2. Association of the Amphiphiles with Lipid Bilayers and P–gp Containing Native Membranes
3.3. Molecular Dynamics Characterization of P–gp Embedded in Lipid Bilayers
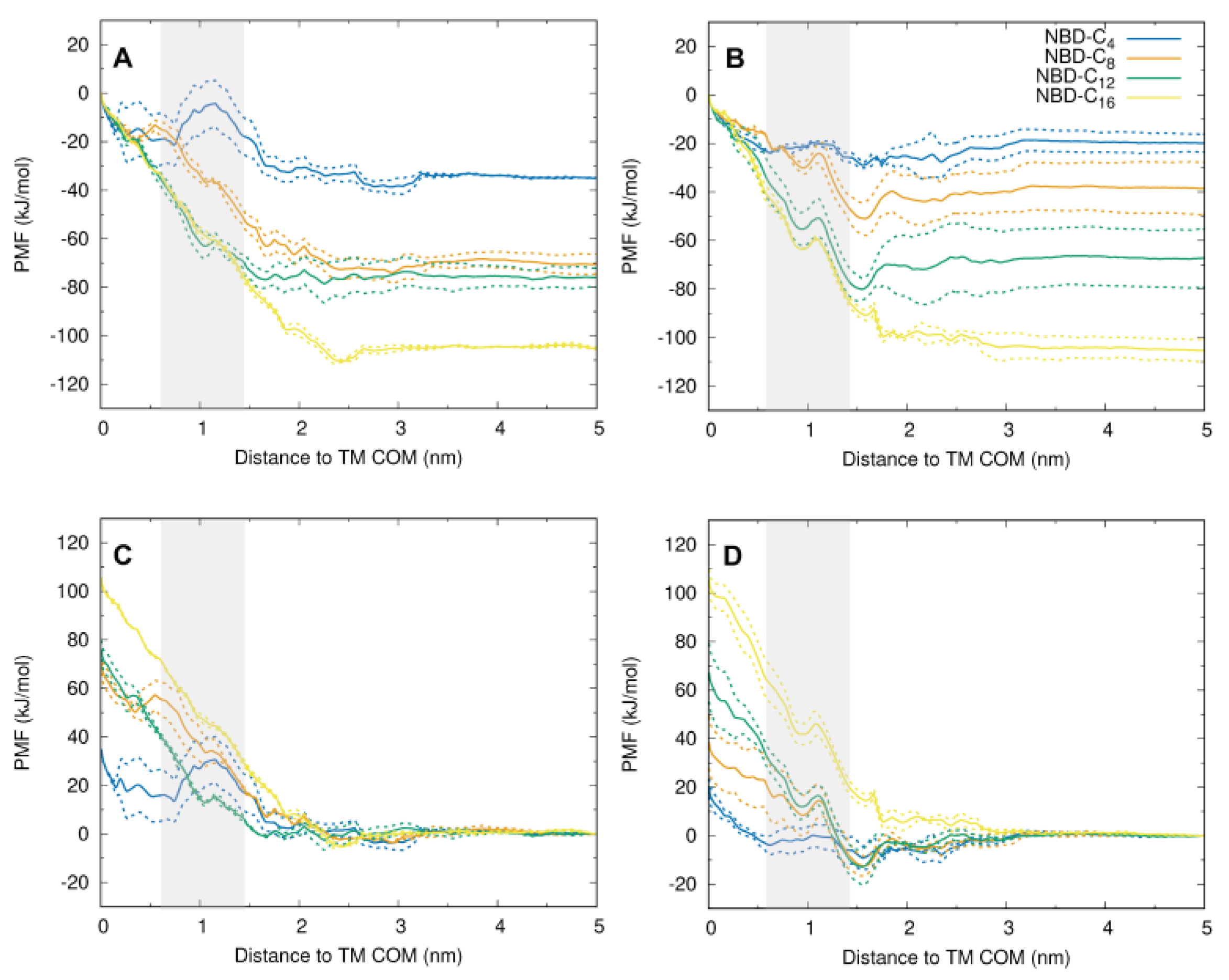
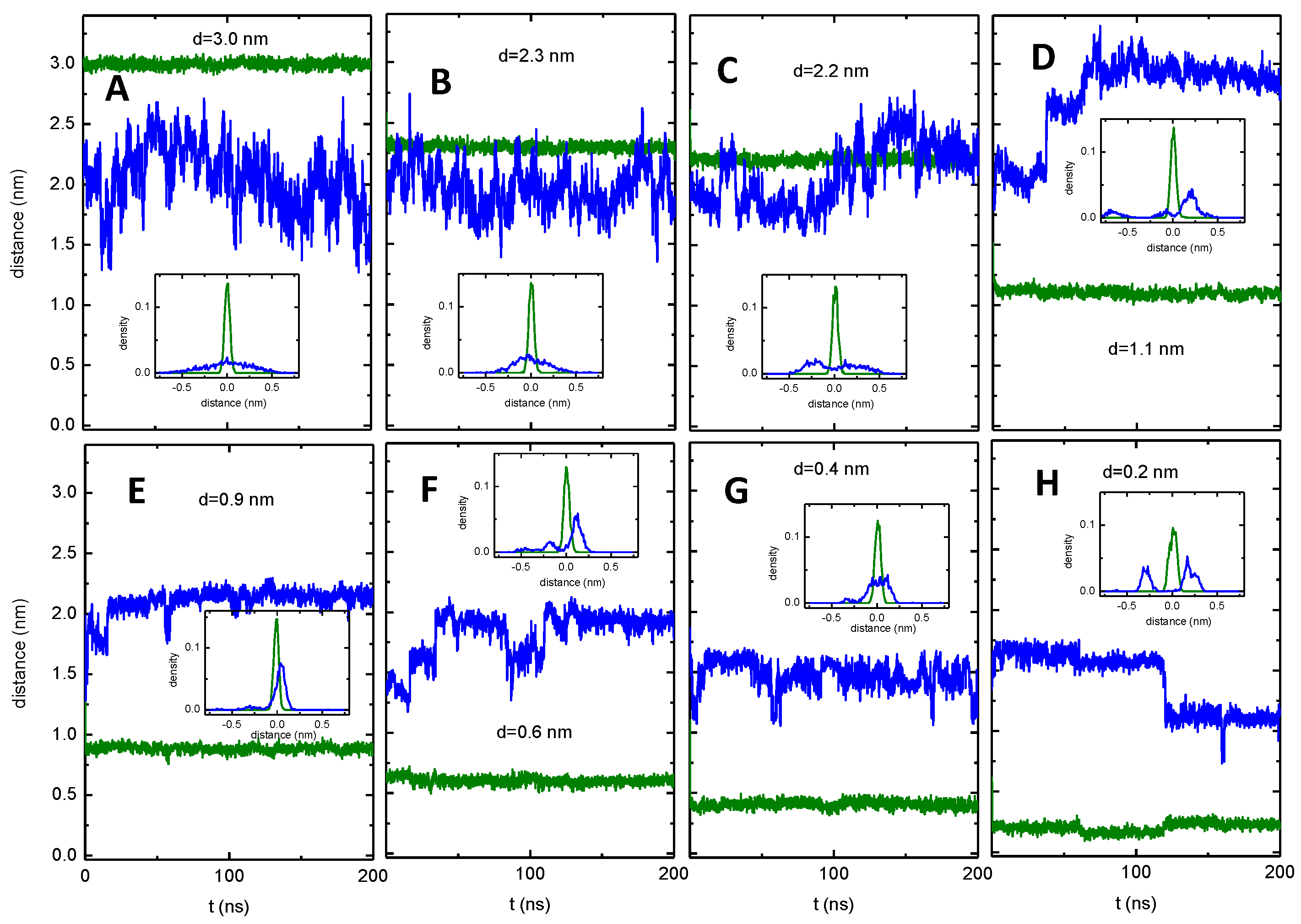
3.4. MD Characterization of NBD–Cn in the Asymmetric Membrane
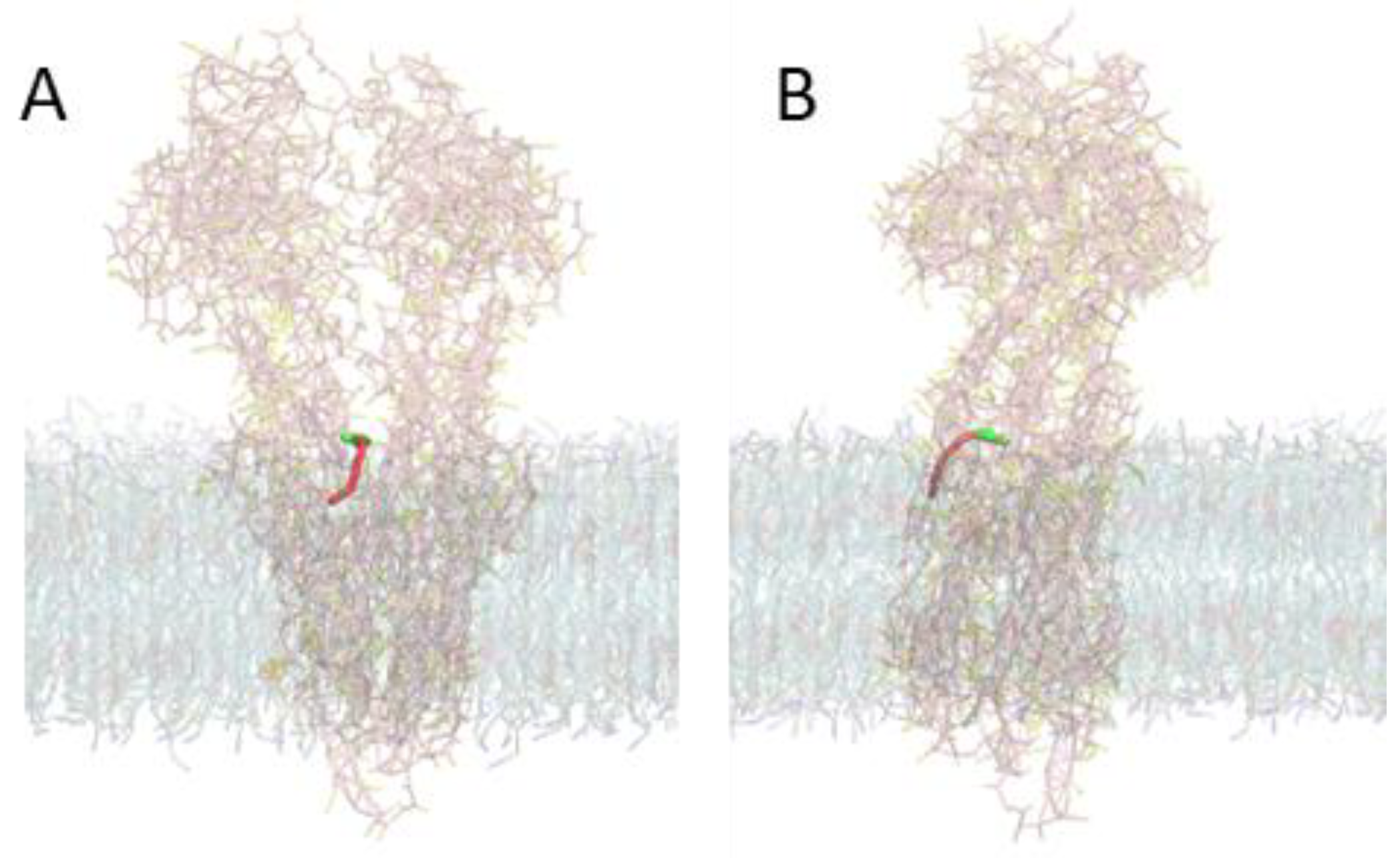
3.5. MD Characterization of the Transfer of NBD–Cn from the Lipid to P–gp
3.6. Details of the Interaction of the NBD–Cn Amphiphiles with P–gp
4. Discussion
4.1. Effective Concentration of the Amphiphiles
4.2. Concentration of the Amphiphiles in the Aqueous Phase
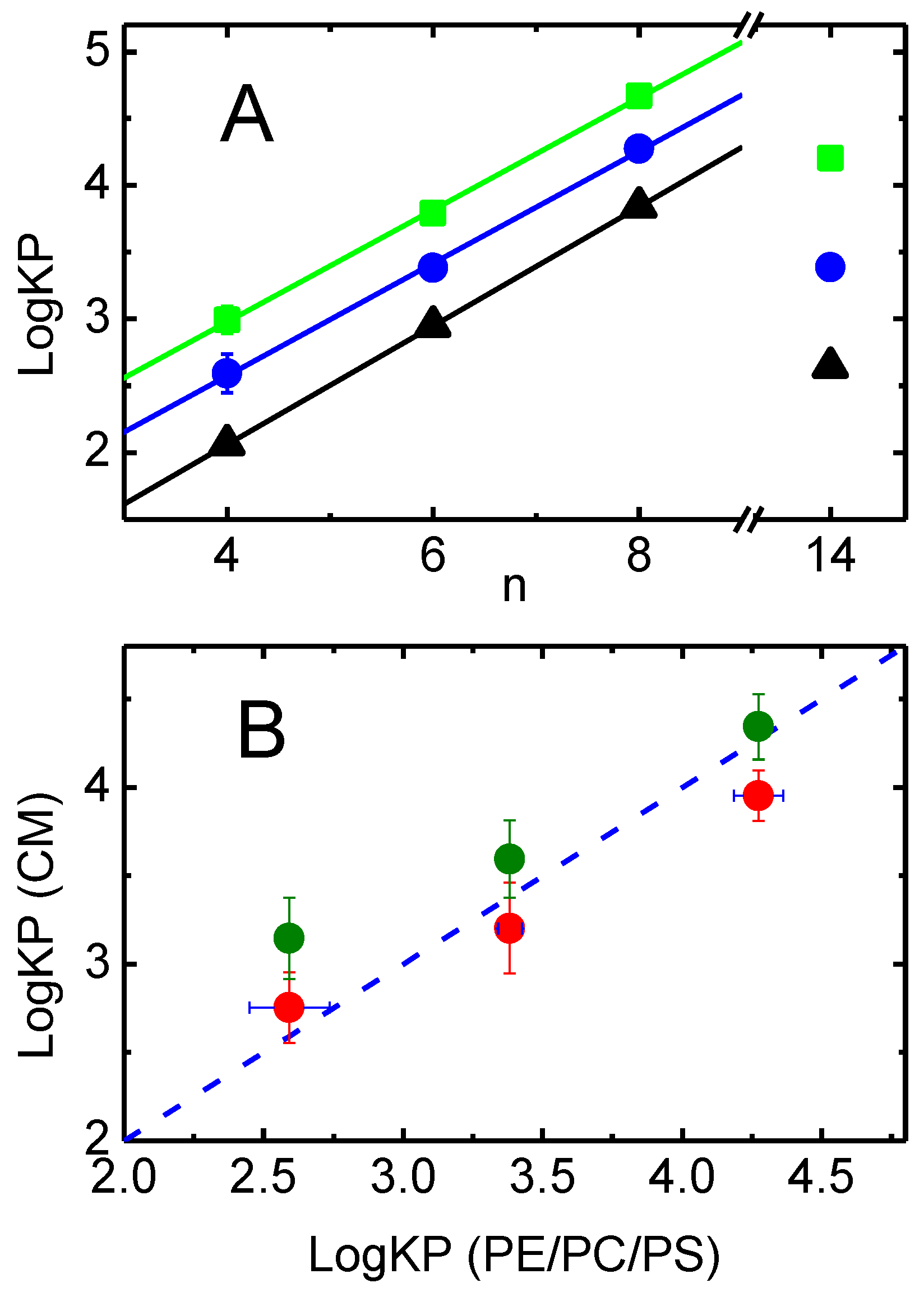
4.3. Relative Affinity of the Amphiphiles for the Lipid Bilayer and for P–gp
| 2 | ||||
|---|---|---|---|---|
| Binding to the protein P–gp only | ||||
| NBD–C4 | 1.4 × 103 | 3.9 × 102 | 6.9 × 104 | 176 |
| NBD-C6 | 3.9 × 103 | 2.4 × 103 | 1.0 × 105 | 43 |
| NBD–C8 | 2.2 × 104 | 1.9 × 104 | 2.3 × 105 | 12 |
| Binding to all membrane proteins with equal affinity | ||||
| NBD–C4 | 5.7 × 102 | 3.9 × 102 | 6.9 × 102 | 1.8 |
| NBD-C6 | 1.6 × 103 | 2.4 × 103 | 1.0 × 103 | 0.43 |
| NBD–C8 | 9.0 × 103 | 1.9 × 104 | 2.3 × 103 | 0.12 |
4.4. Number of Binding Sites in P–gp’s Binding Pocket
4.5. Re-Analysis of the Effects on ATPase Activity
4.6. Re-Analysis of the Effects on IAAP Displacement
4.7. Hypothesis for the Mechanism of Inhibition of P–gp ATPase Activity
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Daneman, R.; Prat, A. The Blood-Brain Barrier. Cold Spring Harb. Perspect. Biol. 2015, 7. [Google Scholar] [CrossRef]
- Loscher, W.; Potschka, H. Role of drug efflux transporters in the brain for drug disposition and treatment of brain diseases. Prog. Neurobiol. 2005, 76, 22–76. [Google Scholar] [CrossRef] [PubMed]
- Praça, C.; Rosa, S.C.; Sevin, E.; Cecchelli, R.; Dehouck, M.-P.; Ferreira, L.S. Derivation of Brain Capillary-like Endothelial Cells from Human Pluripotent Stem Cell-Derived Endothelial Progenitor Cells. Stem Cell Rep. 2019, 13, 599–611. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.H.; Yamazaki, M. Role of P-glycoprotein in pharmacokinetics—Clinical implications. Clin. Pharmacokinet. 2003, 42, 59–98. [Google Scholar] [CrossRef] [PubMed]
- Bukowski, K.; Kciuk, M.; Kontek, R. Mechanisms of Multidrug Resistance in Cancer Chemotherapy. Int. J. Mol. Sci. 2020, 21, 3233. [Google Scholar] [CrossRef]
- Gottesman, M.M.; Ambudkar, S.V. Overview: ABC transporters and human disease. J. Bioenerg. Biomembr. 2001, 33, 453–458. [Google Scholar] [CrossRef]
- Robey, R.W.; Pluchino, K.M.; Hall, M.D.; Fojo, A.T.; Bates, S.E.; Gottesman, M.M. Revisiting the role of ABC transporters in multidrug-resistant cancer. Nat. Rev. Cancer 2018, 18, 452–464. [Google Scholar] [CrossRef]
- Lusvarghi, S.; Robey, R.W.; Gottesman, M.M.; Ambudkar, S.V. Multidrug transporters: Recent insights from cryo-electron microscopy-derived atomic structures and animal models. F1000Research 2020, 9, 17. [Google Scholar] [CrossRef]
- Goddeke, H.; Schafer, L.V. Capturing Substrate Translocation in an ABC Exporter at the Atomic Level. J. Am. Chem. Soc. 2020, 142, 12791–12801. [Google Scholar] [CrossRef]
- Sharom, F.J. The P-glycoprotein efflux pump: How does it transport drugs? J. Membrane Biol. 1997, 160, 161–175. [Google Scholar] [CrossRef]
- Ambudkar, S.V.; Kim, I.W.; Sauna, Z.E. The power of the pump: Mechanisms of action of P-glycoprotein (ABCB1). Eur. J. Pharm. Sci. 2006, 27, 392–400. [Google Scholar] [CrossRef]
- Frank, G.A.; Shukla, S.; Rao, P.; Borgnia, M.J.; Bartesaghi, A.; Merk, A.; Mobin, A.; Esser, L.; Earl, L.A.; Gottesman, M.M.; et al. Cryo-EM Analysis of the Conformational Landscape of Human P-glycoprotein (ABCB1) During its Catalytic Cycle. Mol. Pharmacol. 2016, 90, 35–41. [Google Scholar] [CrossRef]
- Kaur, H.; Lakatos-Karoly, A.; Vogel, R.; Noell, A.; Tampe, R.; Glaubitz, C. Coupled ATPase-adenylate kinase activity in ABC transporters. Nat. Commun. 2016, 7, 13864. [Google Scholar] [CrossRef]
- Lugo, M.R.; Sharom, F.J. Kinetic validation of the models for P-glycoprotein ATP hydrolysis and vanadate-induced trapping. Proposal for additional steps. PLoS ONE 2014, 9, e98804. [Google Scholar] [CrossRef]
- Sauna, Z.E.; Ambudkar, S.V. Evidence for a requirement for ATP hydrolysis at two distinct steps during a single turnover of the catalytic cycle of human P-glycoprotein. Proc. Natl. Acad. Sci. USA 2000, 97, 2515–2520. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, A.B.; Ling, V. Stoichiometry of coupling of rhodamine 123 transport to ATP hydrolysis by P-glycoprotein. Eur. J. Biochem. 1998, 254, 189–193. [Google Scholar] [CrossRef]
- Szollosi, D.; Rose-Sperling, D.; Hellmich, U.A.; Stockner, T. Comparison of mechanistic transport cycle models of ABC exporters. Biochim. Biophys. Acta-Biomembr. 2018, 1860, 818–832. [Google Scholar] [CrossRef]
- Yang, Z.R.; Zhou, Q.X.; Mok, L.; Singh, A.; Swartz, D.J.; Urbatsch, I.L.; Brouillette, C.G. Interactions and cooperativity between P-glycoprotein structural domains determined by thermal unfolding provides insights into its solution structure and function. Biochim. Biophys. Acta-Biomembr. 2017, 1859, 48–60. [Google Scholar] [CrossRef]
- Zoghbi, M.E.; Altenberg, G.A. Hydrolysis at One of the Two Nucleotide-binding Sites Drives the Dissociation of ATP-binding Cassette Nucleotide-binding Domain Dimers. J. Biol. Chem. 2013, 288, 34259–34265. [Google Scholar] [CrossRef]
- Patel, B.A.; Abel, B.; Barbuti, A.M.; Velagapudi, U.K.; Chen, Z.S.; Ambudkar, S.V.; Talele, T.T. Comprehensive Synthesis of Amino Acid-Derived Thiazole Peptidomimetic Analogues to Understand the Enigmatic Drug/Substrate-Binding Site of P-Glycoprotein. J. Med. Chem. 2018, 61, 834–864. [Google Scholar] [CrossRef]
- Egido, E.; Muller, R.; Li-Blatter, X.; Merino, G.; Seelig, A. Predicting Activators and Inhibitors of the Breast Cancer Resistance Protein (ABCG2) and P-Glycoprotein (ABCB1) Based on Mechanistic Considerations. Mol. Pharmacol. 2015, 12, 4026–4037. [Google Scholar] [CrossRef] [PubMed]
- Jabeen, I.; Pleban, K.; Rinner, U.; Chiba, P.; Ecker, G.F. Structure-Activity Relationships, Ligand Efficiency, and Lipophilic Efficiency Profiles of Benzophenone-Type Inhibitors of the Multidrug Transporter P-Glycoprotein. J. Med. Chem. 2012, 55, 3261–3273. [Google Scholar] [CrossRef]
- Chen, L.; Li, Y.Y.; Zhang, H.D.; Zhang, L.L.; Hou, T.J. Computational models for predicting substrates or inhibitors of P-glycoprotein. Drug Discov. Today 2012, 17, 343–351. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, H.W.; Ashby, C.R.; Assaraf, Y.G.; Chen, Z.S.; Liu, H.M. Chemical molecular-based approach to overcome multidrug resistance in cancer by targeting P-glycoprotein (P-gp). Med. Res. Rev. 2021, 41, 525–555. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, A.B.; Ling, V. Positively cooperative sites for drug transport by P-glycoprotein with distinct drug specificities. Eur. J. Biochem. 1997, 250, 130–137. [Google Scholar] [CrossRef] [PubMed]
- Dey, S.; Ramachandra, M.; Pastan, I.; Gottesman, M.M.; Ambudkar, S.V. Evidence for two nonidentical drug-interaction sites in the human P-glycoprotein. Proc. Natl. Acad. Sci. USA 1997, 94, 10594–10599. [Google Scholar] [CrossRef]
- Litman, T.; Zeuthen, T.; Skovsgaard, T.; Stein, W.D. Competitive, non-competitive and cooperative interactions between substrates of P-glycoprotein as measured by its ATPase activity. Biochim. Biophys. Acta 1997, 1361, 169–176. [Google Scholar] [CrossRef]
- Litman, T.; Zeuthen, T.; Skovsgaard, T.; Stein, W.D. Structure-activity relationships of P-glycoprotein interacting drugs: Kinetic characterization of their effects on ATPase activity. Biochim. Biophys. Acta (BBA)—Mol. Basis Dis. 1997, 1361, 159–168. [Google Scholar] [CrossRef]
- Chufan, E.E.; Sim, H.M.; Ambudkar, S.V. Molecular Basis of the Polyspecificity of P-Glycoprotein (ABCB1): Recent Biochemical and Structural Studies. Adv. Cancer Res. 2015, 125, 71–96. [Google Scholar]
- Dastvan, R.; Mishra, S.; Peskova, Y.B.; Nakamoto, R.K.; Mchaourab, H.S. Mechanism of allosteric modulation of P-glycoprotein by transport substrates and inhibitors. Science 2019, 364, 689–692. [Google Scholar] [CrossRef]
- Martin, C.; Berridge, G.; Higgins, C.F.; Mistry, P.; Charlton, P.; Callaghan, R. Communication between multiple drug binding sites on P-glycoprotein. Mol. Pharmacol. 2000, 58, 624–632. [Google Scholar] [CrossRef] [PubMed]
- Li-Blatter, X.; Beck, A.; Seelig, A. P-Glycoprotein-ATPase Modulation: The Molecular Mechanisms. Biophys. J. 2012, 102, 1383–1393. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, R.J.; dos Santos, D.; Ferreira, M.J.U. P-glycoprotein and membrane roles in multidrug resistance. Future Med. Chem. 2015, 7, 929–946. [Google Scholar] [CrossRef] [PubMed]
- Romsicki, Y.; Sharom, F.J. The membrane lipid environment modulates drug interactions with the P-glycoprotein multidrug transporter. Biochemistry 1999, 38, 6887–6896. [Google Scholar] [CrossRef]
- Clay, A.T.; Sharom, F.J. Lipid Bilayer Properties Control Membrane Partitioning, Binding, and Transport of P-Glycoprotein Substrates. Biochemistry 2013, 52, 343–354. [Google Scholar] [CrossRef]
- Sharom, F.J. The P-glycoprotein multidrug transporter: Interactions with membrane lipids, and their modulation of activity. Biochem. Soc. Trans. 1997, 25, 1088–1096. [Google Scholar] [CrossRef]
- Eckford, P.D.W.; Sharom, F.J. Interaction of the P-Glycoprotein Multidrug Efflux Pump with Cholesterol: Effects on ATPase Activity, Drug Binding and Transport. Biochemistry 2008, 47, 13686–13698. [Google Scholar] [CrossRef]
- Shukla, S.; Abel, B.; Chufan, E.E.; Ambudkar, S.V. Effects of a detergent micelle environment on P-glycoprotein (ABCB1)-ligand interactions. J. Biol. Chem. 2017, 292, 7066–7076. [Google Scholar] [CrossRef]
- Moreno, M.J.; Martins, P.A.T.; Bernardino, E.F.; Abel, B.; Ambudkar, S.V. Characterization of the Lipidome and Biophysical Properties of Membranes from High Five Insect Cells Expressing Mouse P-Glycoprotein. Biomolecules 2021, 11, 426. [Google Scholar] [CrossRef]
- Moreno, M.J.; Loura, L.M.S.; Martins, J.; Salvador, A.; Velazquez-Campoy, A. Analysis of the Equilibrium Distribution of Ligands in Heterogeneous Media—Approaches and Pitfalls. Int. J. Mol. Sci. 2022, 23, 9757. [Google Scholar] [CrossRef]
- Cardoso, R.M.S.; Filipe, H.A.L.; Gomes, F.; Moreira, N.D.; Vaz, W.L.C.; Moreno, M.J. Chain Length Effect on the Binding of Amphiphiles to Serum Albumin and to POPC Bilayers. J. Phys. Chem. B 2010, 114, 16337–16346. [Google Scholar] [CrossRef]
- Sampaio, J.L.; Moreno, M.J.; Vaz, W.L.C. Kinetics and Thermodynamics of Association of a Fluorescent Lysophospholipid Derivative with Lipid Bilayers in Liquid-Ordered and Liquid-Disordered Phases. Biophys. J. 2005, 88, 4064–4071. [Google Scholar] [CrossRef][Green Version]
- Ramachandra, M.; Ambudkar, S.V.; Chen, D.; Hrycyna, C.A.; Dey, S.; Gottesman, M.M.; Pastan, I. Human P-glycoprotein exhibits reduced affinity for substrates during a catalytic transition state. Biochemistry 1998, 37, 5010–5019. [Google Scholar] [CrossRef]
- Schaffner, W.; Weissmann, C. A rapid, sensitive, and specific method for the determination of protein in dilute solution. Anal. Biochem. 1973, 56, 502–514. [Google Scholar] [CrossRef]
- Litman, T.; Nielsen, D.; Skovsgaard, T.; Zeuthen, T.; Stein, W.D. ATPase activity of P-glycoprotein related to emergence of drug resistance in Ehrlich ascites tumor cell lines. Biochim. Biophys. Acta 1997, 1361, 147–158. [Google Scholar] [CrossRef]
- Gatlik-Landwojtowicz, E.; Aanismaa, P.; Seelig, A. Quantification and characterization of P-glycoprotein-substrate interactions. Biochemistry 2006, 45, 3020–3032. [Google Scholar] [CrossRef]
- Kemmer, G.; Keller, S. Nonlinear least-squares data fitting in Excel spreadsheets. Nat. Protoc. 2010, 5, 267–281. [Google Scholar] [CrossRef]
- Sauna, Z.E.; Nandigama, K.; Ambudkar, S.V. Exploiting reaction intermediates of the ATPase reaction to elucidate the mechanism of transport by P-glycoprotein (ABCB1). J. Biol. Chem. 2006, 281, 26501–26511. [Google Scholar] [CrossRef]
- Samelo, J.; Mora, M.J.; Granero, G.E.; Moreno, M.J. Partition of Amphiphilic Molecules to Lipid Bilayers by ITC: Low-Affinity Solutes. ACS Omega 2017, 2, 6863–6869. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; de Vries, A.H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef]
- Ingólfsson, H.I.; Melo, M.N.; van Eerden, F.J.; Arnarez, C.; Lopez, C.A.; Wassenaar, T.A.; Periole, X.; de Vries, A.H.; Tieleman, D.P.; Marrink, S.J. Lipid Organization of the Plasma Membrane. J. Am. Chem. Soc. 2014, 136, 14554–14559. [Google Scholar] [CrossRef]
- O’Mara, M.L.; Mark, A.E. The Effect of Environment on the Structure of a Membrane Protein: P-Glycoprotein under Physiological Conditions. J. Chem. Theory Comput. 2012, 8, 3964–3976. [Google Scholar] [CrossRef]
- Periole, X.; Cavalli, M.; Marrink, S.-J.; Ceruso, M.A. Combining an Elastic Network With a Coarse-Grained Molecular Force Field: Structure, Dynamics, and Intermolecular Recognition. J. Chem. Theory Comput. 2009, 5, 2531–2543. [Google Scholar] [CrossRef]
- Filipe, H.A.L.; Moreno, M.J.; Rog, T.; Vattulainen, I.; Loura, L.M.S. How To Tackle the Issues in Free Energy Simulations of Long Amphiphiles Interacting with Lipid Membranes: Convergence and Local Membrane Deformations. J. Phys. Chem. B 2014, 118, 3572–3581. [Google Scholar] [CrossRef]
- Hub, J.S.; de Groot, B.L.; van der Spoel, D. g_wham—A Free Weighted Histogram Analysis Implementation Including Robust Error and Autocorrelation Estimates. J. Chem. Theory Comput. 2010, 6, 3713–3720. [Google Scholar] [CrossRef]
- Filipe, H.A.L.; Moreno, M.J.; Loura, L.M.S. Interaction of 7-Nitrobenz-2-oxa-1,3-diazol-4-yl-Labeled Fatty Amines with 1-Palmitoyl, 2-Oleoyl-sn-glycero-3-phosphocholine Bilayers: A Molecular Dynamics Study. J. Phys. Chem. B 2011, 115, 10109–10119. [Google Scholar] [CrossRef]
- Wen, P.-C.; Verhalen, B.; Wilkens, S.; Mchaourab, H.S.; Tajkhorshid, E. On the Origin of Large Flexibility of P-glycoprotein in the Inward-facing State. J. Biol. Chem. 2013, 288, 19211–19220. [Google Scholar] [CrossRef]
- Li, J.; Jaimes, K.F.; Aller, S.G. Refined structures of mouse P-glycoprotein. Protein Sci. 2014, 23, 34–46. [Google Scholar] [CrossRef]
- Condic-Jurkic, K.; Subramanian, N.; Mark, A.E.; O’Mara, M.L. The reliability of molecular dynamics simulations of the multidrug transporter P-glycoprotein in a membrane environment. PLoS ONE 2018, 13, e0191882. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Seelig, A. P-Glycoprotein: One Mechanism, Many Tasks and the Consequences for Pharmacotherapy of Cancers. Front. Oncol. 2020, 10, 576559. [Google Scholar] [CrossRef]
- Li-Blatter, X.; Seelig, A. Exploring the P-Glycoprotein Binding Cavity with Polyoxyethylene Alkyl Ethers. Biophys. J. 2010, 99, 3589–3598. [Google Scholar] [CrossRef][Green Version]
- Al-Shawi, M.K.; Polar, M.K.; Omote, H.; Figler, R.A. Transition state analysis of the coupling of drug transport to ATP hydrolysis by P-glycoprotein. J. Biol. Chem. 2003, 278, 52629–52640. [Google Scholar] [CrossRef]
- Ledwitch, K.V.; Gibbs, M.E.; Barnes, R.W.; Roberts, A.G. Cooperativity between verapamil and ATP bound to the efflux transporter P-glycoprotein. Biochem. Pharmacol. 2016, 118, 96–108. [Google Scholar] [CrossRef]
- Moesgaard, L.; Reinholdt, P.; Nielsen, C.U.; Kongsted, J. Mechanism behind Polysorbates’ Inhibitory Effect on P-Glycoprotein. Mol. Pharmacol. 2022, 19, 2248–2253. [Google Scholar] [CrossRef]
- Meier, M.; Seelig, J. Lipid and Peptide Dynamics in Membranes upon Insertion of n-alkyl-beta-D-Glucopyranosides. Biophys. J. 2010, 98, 1529–1538. [Google Scholar] [CrossRef][Green Version]
- Ferreira, R.J.; Ferreira, M.J.U.; dos Santos, D. Insights on P-Glycoprotein’s Efflux Mechanism Obtained by Molecular Dynamics Simulations. J. Chem. Theory Comput. 2012, 8, 1853–1864. [Google Scholar] [CrossRef]
- Corradi, V.; Mendez-Villuendas, E.; Ingólfsson, H.I.; Gu, R.-X.; Siuda, I.; Melo, M.N.; Moussatova, A.; DeGagné, L.J.; Sejdiu, B.I.; Singh, G.; et al. Lipid-Protein Interactions Are Unique Fingerprints for Membrane Proteins. ACS Cent. Sci. 2018, 4, 709–717. [Google Scholar] [CrossRef]
- Domicevica, L.; Koldso, H.; Biggin, P.C. Multiscale molecular dynamics simulations of lipid interactions with P-glycoprotein in a complex membrane. J. Mol. Graph. Model. 2018, 80, 147–156. [Google Scholar] [CrossRef]
- Filipe, H.A.L.; Bowman, D.; Palmeira, T.; Cardoso, R.M.S.; Loura, L.M.S.; Moreno, M.J. Interaction of NBD-labelled fatty amines with liquid-ordered membranes: A combined molecular dynamics simulation and fluorescence spectroscopy study. Phys. Chem. Chem. Phys. 2015, 17, 27534–27547. [Google Scholar] [CrossRef]
- Coreta-Gomes, F.M.; Martins, P.A.T.; Velazquez-Campoy, A.; Vaz, W.L.C.; Geraldes, C.F.G.; Moreno, M.J. Interaction of Bile Salts with Model Membranes Mimicking the Gastrointestinal Epithelium: A Study by Isothermal Titration Calorimetry. Langmuir 2015, 31, 9097–9104. [Google Scholar] [CrossRef]
- Abreu, M.S.C.; Moreno, M.J.; Vaz, W.L.C. Kinetics and Thermodynamics of Association of a Phospholipid Derivative with Lipid Bilayers in Liquid-Disordered and Liquid-Ordered Phases. Biophys. J. 2004, 87, 353–365. [Google Scholar] [CrossRef][Green Version]
- Estronca, L.M.B.B.; Moreno, M.J.; Vaz, W.L.C. Kinetics and thermodynamics of the association of dehydroergosterol with lipid bilayer membranes. Biophys. J. 2007, 93, 4244–4253. [Google Scholar] [CrossRef][Green Version]
- Filipe, H.A.L.; Javanainen, M.; Salvador, A.; Galvao, A.M.; Vattulainen, I.; Loura, L.M.S.; Moreno, M.J. Quantitative Assessment of Methods Used To Obtain Rate Constants from Molecular Dynamics Simulations-Translocation of Cholesterol across Lipid Bilayers. J. Chem. Theory Comput. 2018, 14, 3840–3848. [Google Scholar] [CrossRef]
- Periole, X.; Marrink, S.J. The Martini Coarse-Grained Force Field; Humana Press: Totowa, NJ, USA, 2013; Volume 924. [Google Scholar]
- Cardoso, R.M.S.; Martins, P.A.T.; Gomes, F.; Doktorovova, S.; Vaz, W.L.C.; Moreno, M.J. Chain-Length Dependence of Insertion, Desorption, and Translocation of a Homologous Series of 7-Nitrobenz-2-oxa-1,3-diazol-4-yl-Labeled Aliphatic Amines in Membranes. J. Phys. Chem. B 2011, 115, 10098–10108. [Google Scholar] [CrossRef]
- Subramanian, N.; Condic-Jurkic, K.; Mark, A.E.; O’Mara, M.L. Identification of Possible Binding Sites for Morphine and Nicardipine on the Multidrug Transporter P-Glycoprotein Using Umbrella Sampling Techniques. J. Chem. Inf. Model. 2015, 55, 1202–1217. [Google Scholar] [CrossRef]
- Subramanian, N.; Schumann-Gillett, A.; Mark, A.E.; O’Mara, M.L. Probing the Pharmacological Binding Sites of P-Glycoprotein Using Umbrella Sampling Simulations. J. Chem. Inf. Model. 2019, 59, 2287–2298. [Google Scholar] [CrossRef]
- Shukla, S.; Skoumbourdis, A.P.; Walsh, M.J.; Hartz, A.M.S.; Fung, K.L.; Wu, C.P.; Gottesman, M.M.; Bauer, B.; Thomas, C.J.; Ambudkar, S.V. Synthesis and Characterization of a BODIPY Conjugate of the BCR-ABL Kinase Inhibitor Tasigna (Nilotinib): Evidence for Transport of Tasigna and Its Fluorescent Derivative by ABC Drug Transporters. Mol. Pharmacol. 2011, 8, 1292–1302. [Google Scholar] [CrossRef]
- Moreno, M.J.; Estronca, L.M.B.B.; Vaz, W.L.C. Translocation of phospholipids and dithionite permeability in liquid-ordered and liquid-disordered membranes. Biophys. J. 2006, 91, 873–881. [Google Scholar] [CrossRef]
- Martins, P.A.T.; Domingues, N.; Pires, C.; Alves, A.M.; Palmeira, T.; Samelo, J.; Cardoso, R.; Velazquez-Campoy, A.; Moreno, M.J. Molecular crowding effects on the distribution of amphiphiles in biological media. Colloids Surf. B 2019, 180, 319–325. [Google Scholar] [CrossRef] [PubMed]
- Filipe, H.A.L.; Salvador, A.; Silvestre, J.M.; Vaz, W.L.C.; Moreno, M.J. Beyond Overton’s Rule: Quantitative Modeling of Passive Permeation through Tight Cell Monolayers. Mol. Pharmacol. 2014, 11, 3696–3706. [Google Scholar] [CrossRef] [PubMed]
- Heerklotz, H.; Keller, S. How Membrane Partitioning Modulates Receptor Activation: Parallel versus Serial Effects of Hydrophobic Ligands. Biophys. J. 2013, 105, 2607–2610. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Meier, M.; Blatter, X.L.; Seelig, A.; Seelig, J. Interaction of verapamil with lipid membranes and P-glycoprotein: Connecting thermodynamics and membrane structure with functional activity. Biophys. J. 2006, 91, 2943–2955. [Google Scholar] [CrossRef] [PubMed]
- Cantor, R.S. The influence of membrane lateral pressures on simple geometric models of protein conformational equilibria. Chem. Phys. Lipids 1999, 101, 45–56. [Google Scholar] [CrossRef]
- Heerklotz, H. Membrane stress and permeabilization induced by asymmetric incorporation of compounds. Biophys. J. 2001, 81, 184–195. [Google Scholar] [CrossRef]
- Heerklotz, H. Interactions of surfactants with lipid membranes. Q. Rev. Biophys. 2008, 41, 205–264. [Google Scholar] [CrossRef]
- Marsh, D. Lateral pressure profile, spontaneous curvature frustration, and the incorporation and conformation of proteins in membranes. Biophys. J. 2007, 93, 3884–3899. [Google Scholar] [CrossRef]
- van Meer, G.; Voelker, D.R.; Feigenson, G.W. Membrane lipids: Where they are and how they behave. Nat. Rev. Mol. Cell Biol. 2008, 9, 112–124. [Google Scholar] [CrossRef]
- Xu, Y.Y.; Egido, E.; Li-Blatter, X.; Muller, R.; Merino, G.; Berneche, S.; Seelig, A. Allocrite Sensing and Binding by the Breast Cancer Resistance Protein (ABCG2) and P-Glycoprotein (ABCB1). Biochemistry 2015, 54, 6195–6206. [Google Scholar] [CrossRef]
- Mello-Vieira, J.; Sousa, T.; Coutinho, A.; Fedorov, A.; Lucas, S.D.; Moreira, R.; Castro, R.E.; Rodrigues, C.M.P.; Prieto, M.; Fernandes, F. Cytotoxic bile acids, but not cytoprotective species, inhibit the ordering effect of cholesterol in model membranes at physiologically active concentrations. Biochim. Biophys. Acta-Biomembr. 2013, 1828, 2152–2163. [Google Scholar] [CrossRef] [PubMed]
- Taboada, P.; Attwood, D.; Ruso, J.M.; Garcia, M.; Mosquera, V. Thermodynamic properties of some antidepressant drugs in acqueous solution. Langmuir 2001, 17, 173–177. [Google Scholar] [CrossRef]
- Attwood, D. The Mode of Association of Amphiphilic Drugs in Aqueous-Solution. Adv. Colloid Interface Sci. 1995, 55, 271–303. [Google Scholar] [CrossRef]
- Shoemaker, D.G.; Nichols, J.W. Hydrophobic Interaction of Lysophospholipids and Bile-Salts at Submicellar Concentrations. Biochemistry 1990, 29, 5837–5842. [Google Scholar] [CrossRef] [PubMed]
- Paketuryte, V.; Petrauskas, V.; Zubriene, A.; Abian, O.; Bastos, M.; Chen, W.Y.; Moreno, M.J.; Krainer, G.; Linkuviene, V.; Sedivy, A.; et al. Uncertainty in protein-ligand binding constants: Asymmetric confidence intervals versus standard errors. Eur. Biophys. J. Biophys. Lett. 2021, 50, 661–670. [Google Scholar] [CrossRef] [PubMed]
- Bucher, K.; Belli, S.; Wunderli-Allenspach, H.; Kramer, S.D. P-glycoprotein in proteoliposomes with low residual detergent: The effects of cholesterol. Pharm. Res. 2007, 24, 1993–2004. [Google Scholar] [CrossRef]
- Aller, S.G.; Yu, J.; Ward, A.; Weng, Y.; Chittaboina, S.; Zhuo, R.P.; Harrell, P.M.; Trinh, Y.T.; Zhang, Q.H.; Urbatsch, I.L.; et al. Structure of P-Glycoprotein Reveals a Molecular Basis for Poly-Specific Drug Binding. Science 2009, 323, 1718–1722. [Google Scholar] [CrossRef]
- Klotz, I.M.; Hunston, D.L. Protein Interactions with Small Molecules—Relationships Between Stoichiometric Binding Constants, Site Binding Constants, and Empirical Binding Parameters. J. Biol. Chem. 1975, 250, 3001–3009. [Google Scholar] [CrossRef]
- Vega, S.; Abian, O.; Velazquez-Campoy, A. A unified framework based on the binding polynomial for characterizing biological systems by isothermal titration calorimetry. Methods 2015, 76, 99–115. [Google Scholar] [CrossRef]
- Sauna, Z.E.; Andrus, M.B.; Turner, T.M.; Ambudkar, S.V. Biochemical basis of polyvalency as a strategy for enhancing the efficacy of P-glycoprotein (ABCB1) modulators: Stipiamide homodimers separated with defined-length spacers reverse drug efflux with greater efficacy. Biochemistry 2004, 43, 2262–2271. [Google Scholar] [CrossRef]
- Xu, W.C.; Chen, S.H.; Wang, X.Q.; Wu, H.G.; Yamada, H.; Hirano, T. Bisbenzylisoquinoline alkaloids and P-glycoprotein function: A structure activity relationship study. Bioorg. Med. Chem. 2020, 28, 115553. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, D.S.P.; Szemeredi, N.; Spengler, G.; Mulhovo, S.; dos Santos, D.; Ferreira, M.J.U. Exploring the Monoterpene Indole Alkaloid Scaffold for Reversing P-Glycoprotein-Mediated Multidrug Resistance in Cancer. Pharmaceuticals 2021, 14, 862. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, R.J.; Ferreira, M.J.U.; dos Santos, D. Molecular Docking Characterizes Substrate-Binding Sites and Efflux Modulation Mechanisms within P-Glycoprotein. J. Chem. Inf. Model. 2013, 53, 1747–1760. [Google Scholar] [CrossRef]
- Isca, V.M.S.; Ferreira, R.J.; Garcia, C.; Monteiro, C.M.; Dinic, J.; Holmstedt, S.; Andre, V.; Pesic, M.; dos Santos, D.; Candeias, N.R.; et al. Molecular Docking Studies of Royleanone Diterpenoids from Plectranthus spp. as P-Glycoprotein Inhibitors. ACS Med. Chem. Lett. 2020, 11, 839–845. [Google Scholar] [CrossRef] [PubMed]
- Lagares, L.M.; Perez-Castillo, Y.; Minovski, N.; Novic, M. Structure-Function Relationships in the Human P-Glycoprotein (ABCB1): Insights from Molecular Dynamics Simulations. Int. J. Mol. Sci. 2022, 23, 362. [Google Scholar] [CrossRef]
- Deng, F.; Ghemtio, L.; Grazhdankin, E.; Wipf, P.; Xhaard, H.; Kidron, H. Binding Site Interactions of Modulators of Breast Cancer Resistance Protein, Multidrug Resistance-Associated Protein 2, and P-Glycoprotein Activity. Mol. Pharmacol. 2020, 17, 2398–2410. [Google Scholar] [CrossRef]
- Loo, T.W.; Clarke, D.M. Mapping the Binding Site of the Inhibitor Tariquidar That Stabilizes the First Transmembrane Domain of P-glycoprotein. J. Biol. Chem. 2015, 290, 29389–29401. [Google Scholar] [CrossRef]
- Doige, C.A.; Yu, X.H.; Sharom, F.J. The Effects of Lipids and Detergents on ATPase-Active P-Glycoprotein. Biochim. Biophys. Acta 1993, 1146, 65–72. [Google Scholar] [CrossRef]
- Aanismaa, P.; Gatlik-Landwojtowicz, E.; Seelig, A. P-glycoprotein senses its substrates and the lateral membrane packing density: Consequences for the catalytic cycle. Biochemistry 2008, 47, 10197–10207. [Google Scholar] [CrossRef] [PubMed]
- Wadkins, R.M.; Houghton, P.J. The Role of Drug Lipid Interactions in the Biological-Activity of Modulators of Multidrug-Resistance. Biochim. Biophys. Acta 1993, 1153, 225–236. [Google Scholar] [CrossRef]
- Speelmans, G.; Staffhorst, R.; Dewolf, F.A.; Dekruijff, B. Verapamil Competes With Doxorubicin For Binding To Anionic Phospholipids Resulting In Increased Internal Concentrations And Rates Of Passive Transport Of Doxorubicin. Biochim. Biophys. Acta-Biomembr. 1995, 1238, 137–146. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ferreira, R.J.; Ferreira, M.J.U.; dos Santos, D. Do adsorbed drugs onto P-glycoprotein influence its efflux capability? Phys. Chem. Chem. Phys. 2015, 17, 22023–22034. [Google Scholar] [CrossRef] [PubMed]
- Bonito, C.A.; Ferreira, R.J.; Ferreira, M.J.U.; Gillet, J.P.; Cordeiro, M.; dos Santos, D. Theoretical insights on helix repacking as the origin of P-glycoprotein promiscuity. Sci. Rep. 2020, 10, 9823. [Google Scholar] [CrossRef] [PubMed]
- Vahedi, S.; Chufan, E.E.; Ambudkar, S.V. Global alteration of the drug-binding pocket of human P-glycoprotein (ABCB1) by substitution of fifteen conserved residues reveals a negative correlation between substrate size and transport efficiency. Biochem. Pharmacol. 2017, 143, 53–64. [Google Scholar] [CrossRef]
- Al-Ali, A.A.A.; Nielsen, R.B.; Steffansen, B.; Holm, R.; Nielsen, C.U. Nonionic surfactants modulate the transport activity of ATP-binding cassette (ABC) transporters and solute carriers (SLC): Relevance to oral drug absorption. Int. J. Pharmaceut. 2019, 566, 410–433. [Google Scholar] [CrossRef]
- Li-Blatter, X.; Nervi, P.; Seelig, A. Detergents as intrinsic P-glycoprotein substrates and inhibitors. Biochim. Biophys. Acta-Biomembr. 2009, 1788, 2335–2344. [Google Scholar] [CrossRef]
- Cardoso, D.S.P.; Kincses, A.; Nove, M.; Spengler, G.; Mulhovo, S.; Aires-de-Sousa, J.; dos Santos, D.; Ferreira, M.J.U. Alkylated monoterpene indole alkaloid derivatives as potent P-glycoprotein inhibitors in resistant cancer cells. Eur. J. Med. Chem. 2021, 210, 112985. [Google Scholar] [CrossRef]






| Name | Structure | CLogP | CLogD7.4 | Z7.4 |
|---|---|---|---|---|
| NBD–C4 |  | 2.06 | 0 | |
| NBD-C6 | 2.95 | |||
| NBD–C8 | 3.84 | |||
| NBD–LysoMPE |  | 5.01 | 2.64 | −1 |
| IAAP | 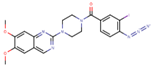 | 4.17 | 4.05 | 0 (97%) +1 (3%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno, M.J.; Filipe, H.A.L.; Cunha, S.V.P.; Ramos, C.V.; Martins, P.A.T.; Abel, B.; Loura, L.M.S.; Ambudkar, S.V. Interaction of a Homologous Series of Amphiphiles with P-glycoprotein in a Membrane Environment—Contributions of Polar and Non-Polar Interactions. Pharmaceutics 2023, 15, 174. https://doi.org/10.3390/pharmaceutics15010174
Moreno MJ, Filipe HAL, Cunha SVP, Ramos CV, Martins PAT, Abel B, Loura LMS, Ambudkar SV. Interaction of a Homologous Series of Amphiphiles with P-glycoprotein in a Membrane Environment—Contributions of Polar and Non-Polar Interactions. Pharmaceutics. 2023; 15(1):174. https://doi.org/10.3390/pharmaceutics15010174
Chicago/Turabian StyleMoreno, Maria João, Hugo A. L. Filipe, Susana V. P. Cunha, Cristiana V. Ramos, Patrícia A. T. Martins, Biebele Abel, Luís M. S. Loura, and Suresh V. Ambudkar. 2023. "Interaction of a Homologous Series of Amphiphiles with P-glycoprotein in a Membrane Environment—Contributions of Polar and Non-Polar Interactions" Pharmaceutics 15, no. 1: 174. https://doi.org/10.3390/pharmaceutics15010174
APA StyleMoreno, M. J., Filipe, H. A. L., Cunha, S. V. P., Ramos, C. V., Martins, P. A. T., Abel, B., Loura, L. M. S., & Ambudkar, S. V. (2023). Interaction of a Homologous Series of Amphiphiles with P-glycoprotein in a Membrane Environment—Contributions of Polar and Non-Polar Interactions. Pharmaceutics, 15(1), 174. https://doi.org/10.3390/pharmaceutics15010174










