Fractal Kinetic Implementation in Population Pharmacokinetic Modeling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fractal Rate Expression
2.2. Simulation Study
2.3. Model and Dataset Collection for Real Case Application
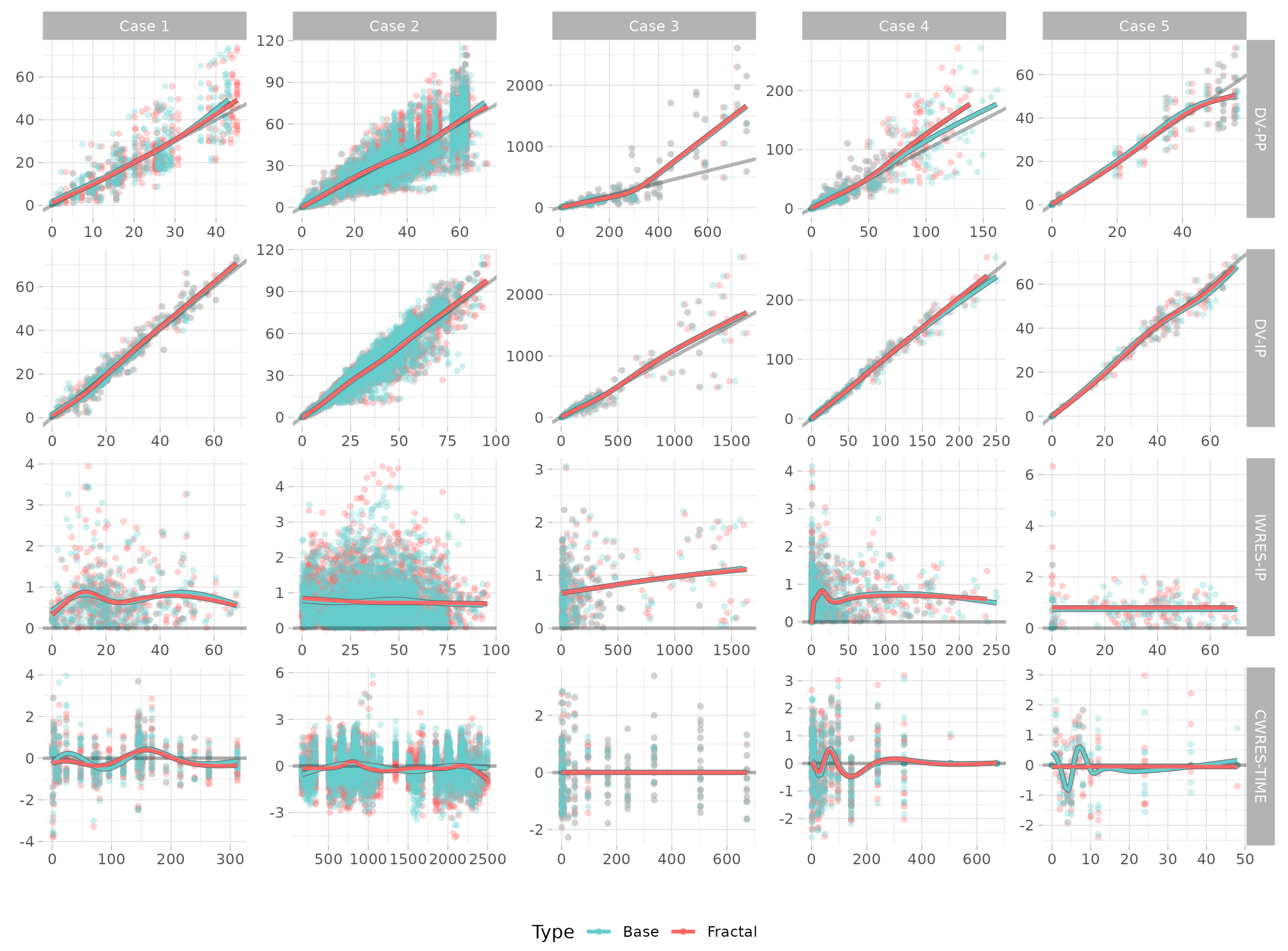
- Single-dose transdermal patch [3]. This was a two-compartment model with a first-order absorption in the case of an oral dose, and absorption in two transit compartments in the case of a transdermal dose. The amounts derived from oral administration and patch administration were processed in the same central compartment. The model was fitted simultaneously in each case of oral and transdermal patch administration for 312 h. Single oral and transdermal-patch amounts were dosed.
- Multiple doses of a drug administered either orally or via a transdermal patch. This two-compartment model included first-order absorption for the oral dose, and absorption in a transit compartment for the transdermal dose. The drug amounts from oral administration and patch administration were processed in the same central compartment. The model was fitted under the condition of 7 days of titration with the oral dose and then three patch doses, with an observation time of 2496 h. Two different amounts were dosed for oral and transdermal-patch administration.At every point of new dosing, the time value in the equation was modeled to be reset as zero, and the remaining amount was emptied.
- Controlled-release intramuscular injection (inhouse data). The two-compartment model included ordinary first-order rate absorption and transit absorption using Stirling’s approximation (Savic et al. [15]) to the same central compartment. The dose was divided into two fractions, one with fast absorption and the other with slow absorption. The intramuscular injection was administered once, and the model was fitted for a period of 672 h. Four different drug amounts were dosed.
- Subcutaneous injection, antibody [16]. This was a two-compartment target-mediated drug disposition (TMDD) model with quasiequilibrium conditions. It consisted of a drug depot (injection site), distribution space, and central and peripheral compartments. The drug concentration was observed for a maximum of 746 h. Five different amounts for subcutaneous injections were dosed.
- Subcutaneous injection, antibody (anakinra) [16]. This was a one-compartment target-mediated drug disposition (TMDD) model with quasiequilibrium conditions. It consisted of a drug depot (injection site) and a central compartment. The drug concentration was observed for a maximum of 48 h. One amount for subcutaneous injection was dosed.
2.4. Model Evaluation
2.5. Software for Simulation and Estimation
3. Results
3.1. Simulation Study
3.2. Numerical Model Evaluations in a Real Case
3.3. Visual Model Evaluations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rescigno, A. The rise and fall of compartmental analysis. Pharmacol. Res. 2001, 44, 337–342. [Google Scholar] [CrossRef] [PubMed]
- Pereira, L.M. Fractal pharmacokinetics. Comput. Math. Methods Med. 2010, 11, 161–184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jung, W.; Jung, H.; Vu, N.A.T.; Kim, G.Y.; Kim, G.W.; Chae, J.W.; Kim, T.; Yun, H.Y. Model-Based Equivalent Dose Optimization to Develop New Donepezil Patch Formulation. Pharmaceutics 2022, 14, 244. [Google Scholar] [CrossRef] [PubMed]
- Kopelman, R. Rate Processes on Fractals: Theory, Simulations, and Experiments. J. Stat. Phys. 1986, 42, 185–200. [Google Scholar] [CrossRef]
- Kopelman, R. Fractal Reaction Kinetics. Science 1988, 241, 1620–1626. [Google Scholar] [CrossRef]
- Dokoumetzidis, A.; Magin, R.; Macheras, P. Fractional kinetics in multi-compartmental systems. J. Pharmacokinet. Pharmacodyn. 2010, 37, 507–524. [Google Scholar] [CrossRef]
- Dokoumetzidis, A.; MacHeras, P. Fractional kinetics in drug absorption and disposition processes. J. Pharmacokinet. Pharmacodyn. 2009, 36, 165–178. [Google Scholar] [CrossRef]
- Macheras, P.; Dokoumetzidis, A. On the Heterogeneity of Drug Dissolution and Release. Pharm. Res. 2000, 17, 108–112. [Google Scholar] [CrossRef]
- Kytariolos, J.; Dokoumetzidis, A.; Macheras, P. Power law IVIVC: An application of fractional kinetics for drug release and absorption. Eur. J. Pharm. Sci. 2010, 41, 299–304. [Google Scholar] [CrossRef]
- Fuite, J.; Marsh, R.; Tuszyński, J. Fractal pharmacokinetics of the drug mibefradil in the liver. Phys. Rev. E 2002, 66, 021904. [Google Scholar] [CrossRef]
- Copot, D.; Magin, R.L.; de Keyser, R.; Ionescu, C. Data-driven modelling of drug tissue trapping using anomalous kinetics. Chaos Solitons Fractals 2017, 102, 441–446. [Google Scholar] [CrossRef]
- Copot, D.; Chevalier, A.; Ionescu, C.M.; de Keyser, R. A two-compartment fractional derivative model for Propofol diffusion in anesthesia. In Proceedings of the IEEE International Conference on Control Applications, Hyderabad, India, 28–30 August 2013; pp. 264–269. [Google Scholar] [CrossRef]
- Copot, D.; Ionescu, C. Tailored Pharmacokinetic model to predict drug trapping in long-term anesthesia. J. Adv. Res. 2021, 32, 27–36. [Google Scholar] [CrossRef]
- Popović, J.K.; Atanacković, M.T.; Pilipović, A.S.; Rapaić, M.R.; Pilipović, S.; Atanacković, T.M. A new approach to the compartmental analysis in pharmacokinetics: Fractional time evolution of diclofenac. J. Pharmacokinet. Pharmacodyn. 2010, 37, 119–134. [Google Scholar] [CrossRef]
- Savic, R.M.; Jonker, D.M.; Kerbusch, T.; Karlsson, M.O. Implementation of a transit compartment model for describing drug absorption in pharmacokinetic studies. J. Pharmacokinet. Pharmacodyn. 2007, 34, 711–726. [Google Scholar] [CrossRef]
- Ngo, L.; Oh, J.; Kim, A.; Back, H.; Kang, W.; Chae, J.; Yun, H.; Lee, H. Development of a Pharmacokinetic Model Describing Neonatal Fc Receptor-Mediated Recycling of HL2351, a Novel Hybrid Fc-Fused Interleukin-1 Receptor Antagonist, to Optimize Dosage Regimen. CPT: Pharmacometrics Syst. Pharmacol. 2020, 9, 584–595. [Google Scholar] [CrossRef]
- Mould, D.R.; Upton, R.N. Basic concepts in population modeling, simulation, and model-based drug development-Part 2: Introduction to pharmacokinetic modeling methods. CPT Pharmacometrics Syst. Pharmacol. 2013, 2, 1–14. [Google Scholar] [CrossRef]
- Olofsen, E.; Dahan, A. Using Akaike’s information theoretic criterion in population analysis: A simulation study. F1000Research 2013, 2, 71. [Google Scholar] [CrossRef]
- Bergstr, M.; Hooker, A.C.; Wallin, J.E.; Karlsson, M.O. Prediction-corrected visual predictive checks for diagnosing nonlinear mixed-effects models. Aaps J. 2011, 13, 143–151. [Google Scholar] [CrossRef] [Green Version]
- Hooker, A.C.; Staatz, C.E.; Karlsson, M.O. Conditional weighted residuals (CWRES): A model diagnostic for the FOCE method. Pharm. Res. 2007, 24, 2187–2197. [Google Scholar] [CrossRef]
- Comets, E.; Brendel, K.; Mentré, F. Computing normalised prediction distribution errors to evaluate nonlinear mixed-effect models: The npde add-on package for R. Comput. Methods Programs Biomed. 2008, 90, 154–166. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Hallow, K.M.; James, D.A. A tutorial on RxODE: Simulating differential equation pharmacometric models in R. CPT: Pharmacometrics Syst. Pharmacol. 2016, 5, 3–10. [Google Scholar] [CrossRef] [PubMed]
- Bjugård, N.H.; Hooker, A.C.; Bauer, R.J.; Aoki, Y. Saddle-Reset for Robust Parameter Estimation and Identifiability Analysis of Nonlinear Mixed Effects Models. AAPS J. 2020, 22, 1–11. [Google Scholar] [CrossRef]
- Karlsson, M.O.; Savic, R.M. Diagnosing Model Diagnostics. Clin. Pharmacol. Ther. 2007, 82, 17–20. [Google Scholar] [CrossRef] [PubMed]





| Simulation | A (1-Comp Model) | B (2-Comp Model) | C (2-Comp Model) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Condition | Ka < CL | Ka = CL | Ka > CL | Ka < CL | Ka = CL | Ka > CL | Ka < CL | Ka = CL | Ka > CL |
| Ka | 0.033 | 0.1 | 0.3 | 0.033 | 0.1 | 0.3 | 0.033 | 0.1 | 0.3 |
| CL | 0.3 | 0.1 | 0.033 | 0.3 | 0.1 | 0.033 | 0.3 | 0.1 | 0.033 |
| Q | - | 3 | 3 | ||||||
| V1 | 10 | 10 | 10 | ||||||
| V2 | - | 100 | 1 | ||||||
| h | 0.00–1.00 | 0.00–1.00 | 0.00–1.00 | ||||||
| Model | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
|---|---|---|---|---|---|
| No. of subjects | 18 | 44 | 20 | 40 | 8 |
| No. of observations | 383 | 3024 | 339 | 472 | 93 |
| No. of parameters—base | 12 | 13 | 16 | 21 | 10 |
| No. of parameters—fractal | 13 | 14 | 18 | 22 | 12 |
| OFV—base | 1443.70 | 13,977.10 | 2155.43 | 1556.43 | 358.47 |
| OFV—fractal | 1410.08 | 13,592.00 | 2153.54 | 1539.64 | 350.13 |
| OFV | −33.62 | −385.10 | −1.89 | −16.79 | −8.34 |
| AIC—base | 1467.70 | 14,005.10 | 2187.43 | 1598.43 | 378.47 |
| AIC—fractal | 1436.08 | 13,624.00 | 2189.54 | 1583.64 | 374.13 |
| AIC | −31.62 | −381.10 | 2.11 | −14.79 | −4.34 |
| AICc—base | 1468.54 | 14,005.24 | 2189.11 | 1600.48 | 381.15 |
| AICc—fractal | 1437.07 | 13,624.18 | 2191.67 | 1585.89 | 378.03 |
| AICc | −31.47 | −381.06 | 2.55 | −14.58 | −3.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, W.; Ryu, H.-j.; Chae, J.-w.; Yun, H.-y. Fractal Kinetic Implementation in Population Pharmacokinetic Modeling. Pharmaceutics 2023, 15, 304. https://doi.org/10.3390/pharmaceutics15010304
Jung W, Ryu H-j, Chae J-w, Yun H-y. Fractal Kinetic Implementation in Population Pharmacokinetic Modeling. Pharmaceutics. 2023; 15(1):304. https://doi.org/10.3390/pharmaceutics15010304
Chicago/Turabian StyleJung, Woojin, Hyo-jeong Ryu, Jung-woo Chae, and Hwi-yeol Yun. 2023. "Fractal Kinetic Implementation in Population Pharmacokinetic Modeling" Pharmaceutics 15, no. 1: 304. https://doi.org/10.3390/pharmaceutics15010304
APA StyleJung, W., Ryu, H.-j., Chae, J.-w., & Yun, H.-y. (2023). Fractal Kinetic Implementation in Population Pharmacokinetic Modeling. Pharmaceutics, 15(1), 304. https://doi.org/10.3390/pharmaceutics15010304








