Vibration Performance Analysis of a Yokeless Stator Axial Flux PM Motor with Distributed Winding for Electric Vehicle Application
Abstract
1. Introduction
2. Motor Structure and Stator Mode Analysis
2.1. Overall Structure
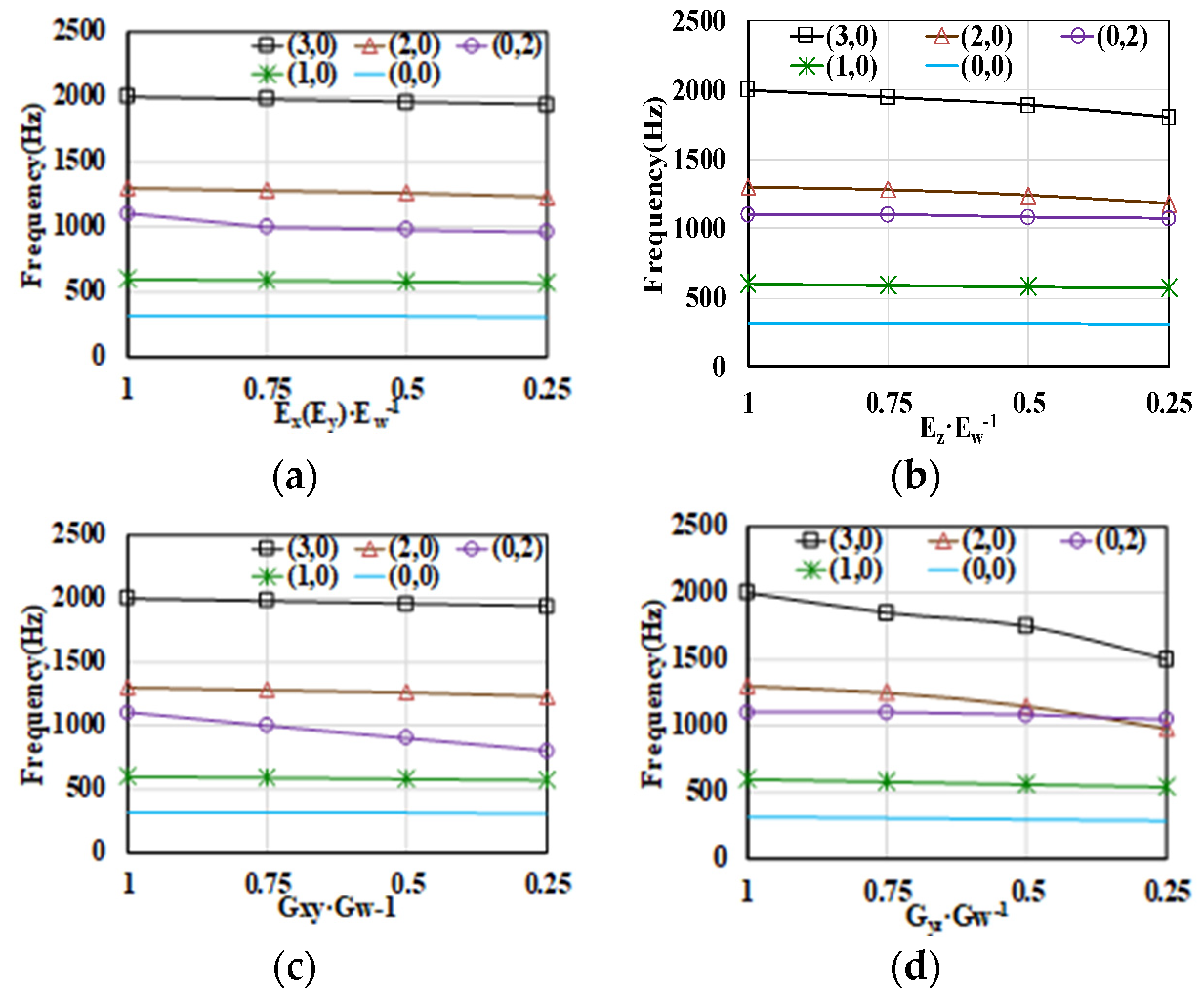
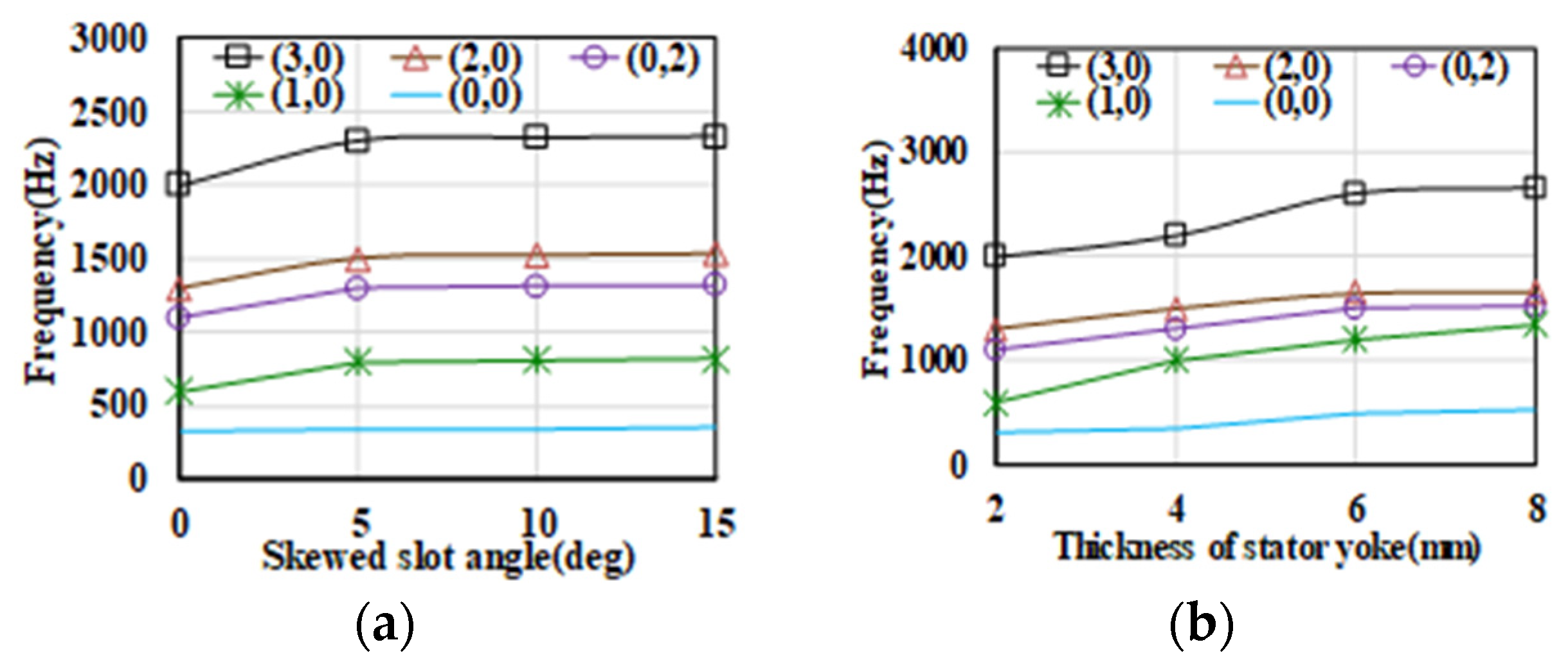
2.2. Influence of Stator Structural Parameters on Modes
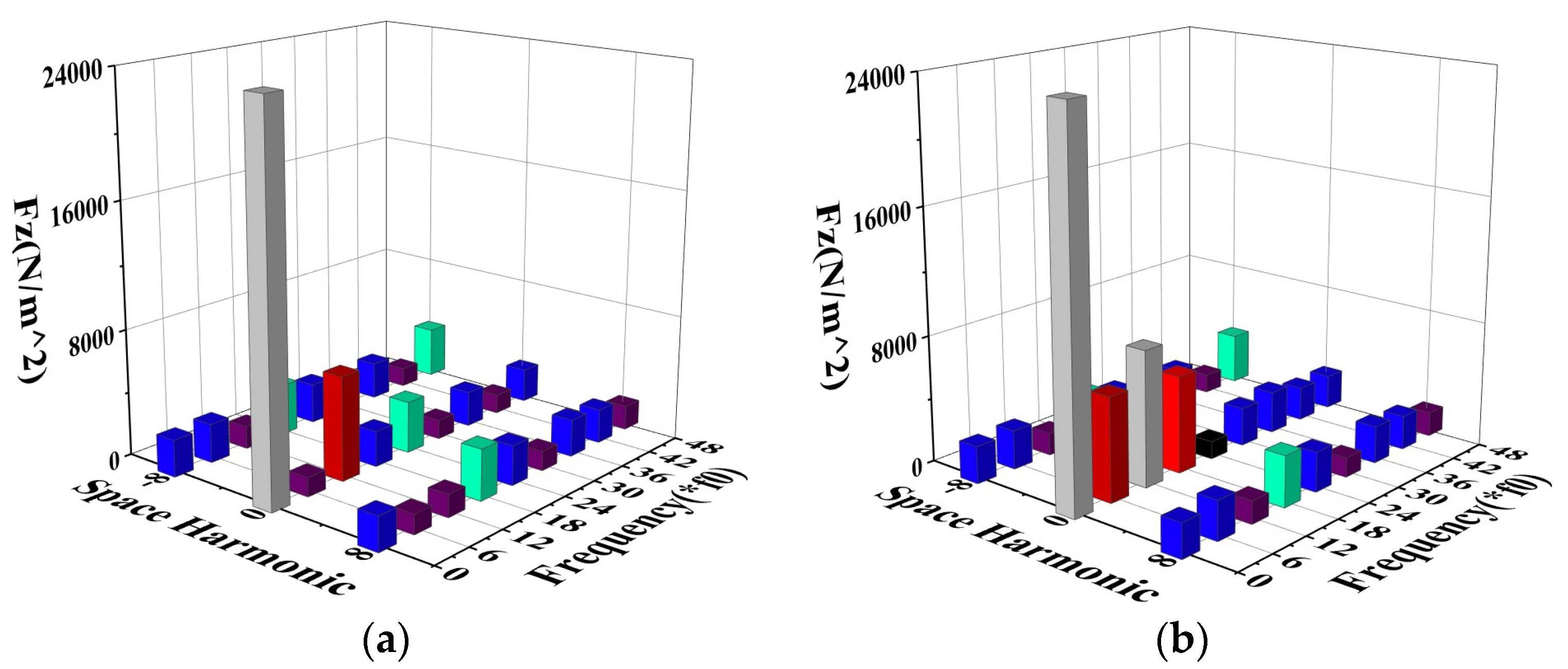
3. Axial Electromagnetic Force Analysis
- The amplitude of axial electromagnetic force remains unchanged. This axial electromagnetic force only causes static deformation for the stator but will not cause periodic vibration on the stator surface;
- The axial electromagnetic force is generated by harmonic interaction between the magnetic fields from stator and rotor. The electromagnetic force generated by the interaction of different order harmonics from stator or rotor itself;
- The electromagnetic force is generated by the interaction between harmonics from stator and rotor.
| Spatial Order | Condition | Frequency (A Multiple of the Mechanical Frequency) |
|---|---|---|
| Zeroth | No load | 12 k |
| Load | 6 k |
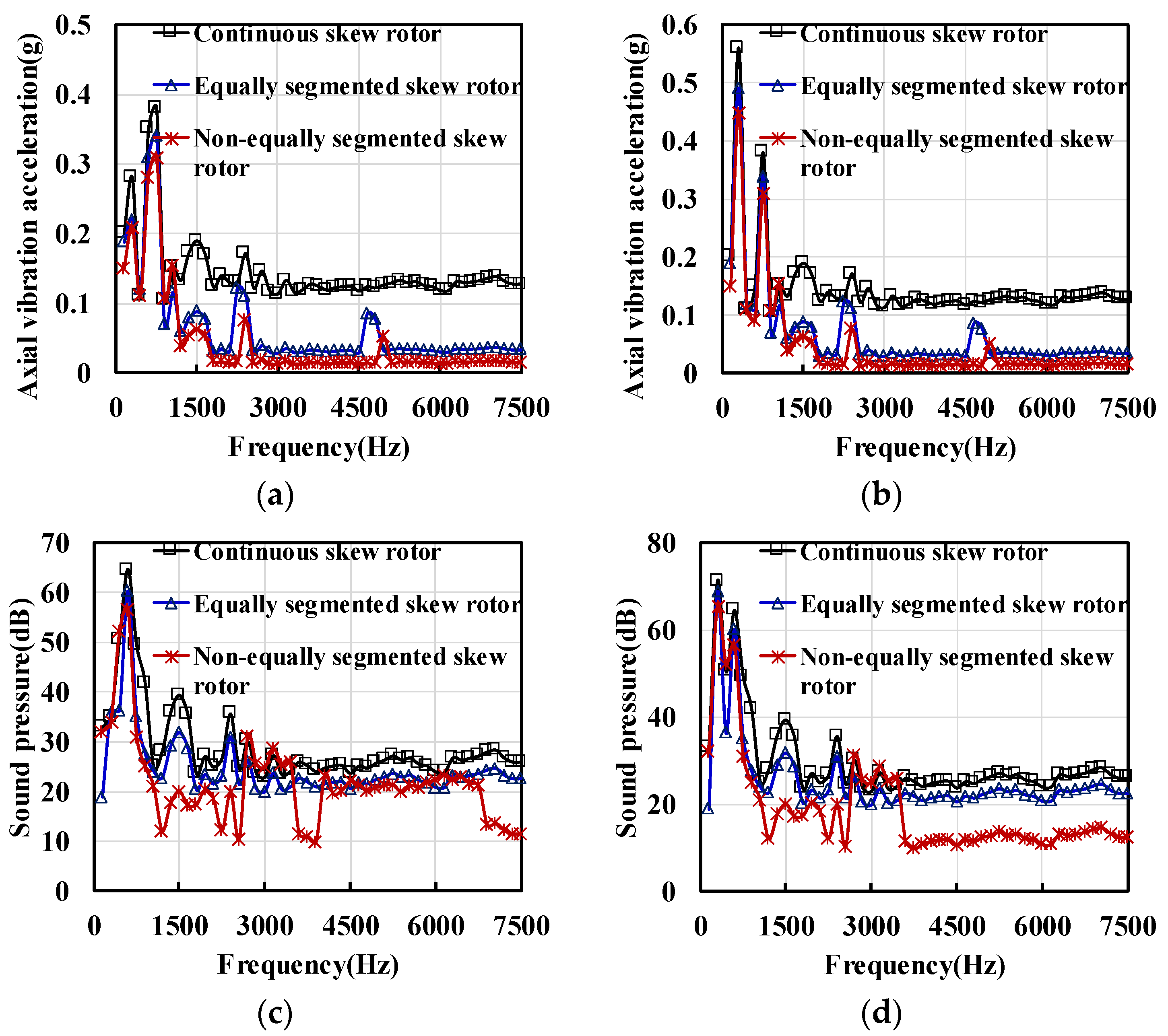
4. Vibration and Noise Analysis
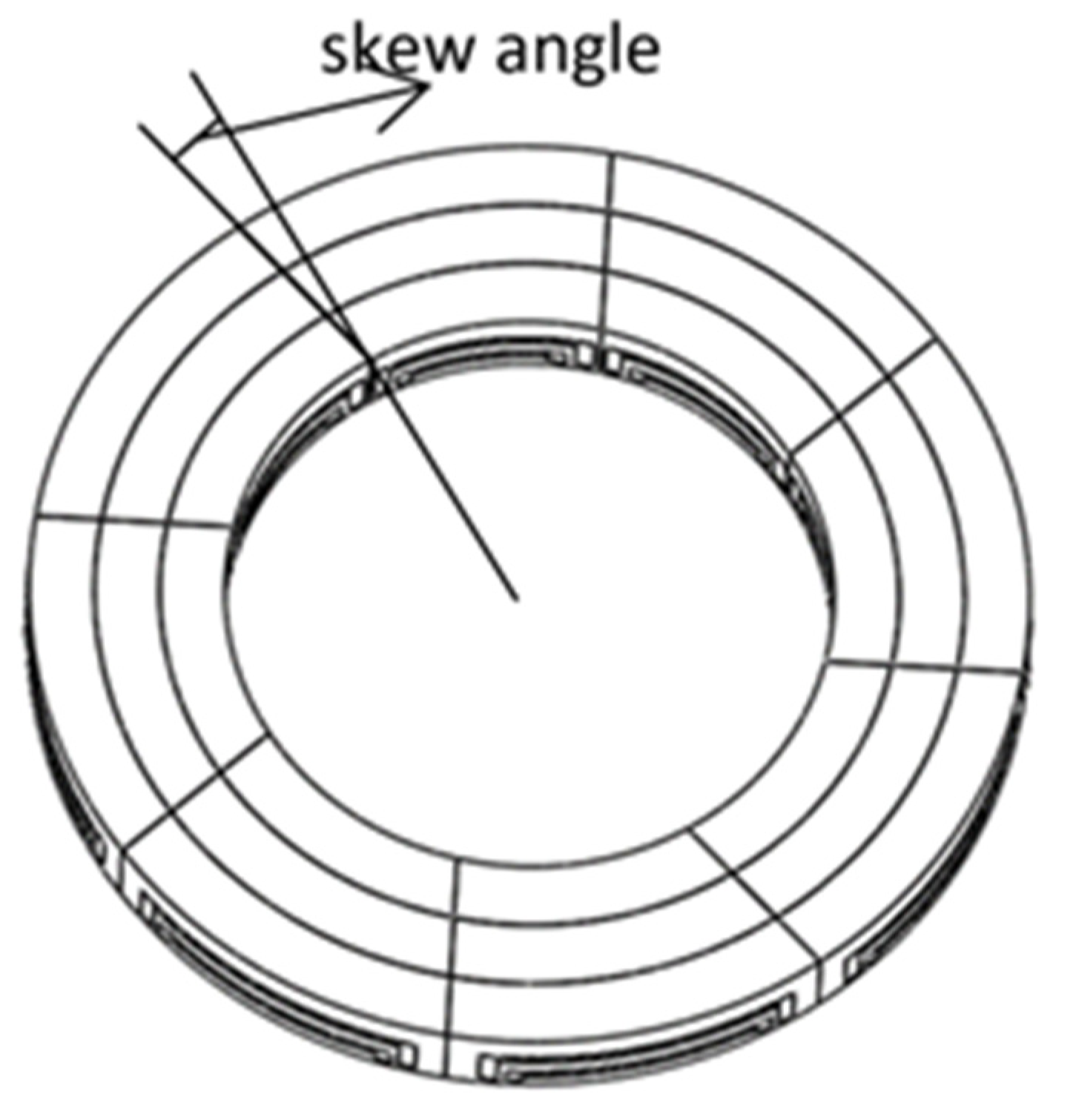
4.1. Continuous Skew Pole
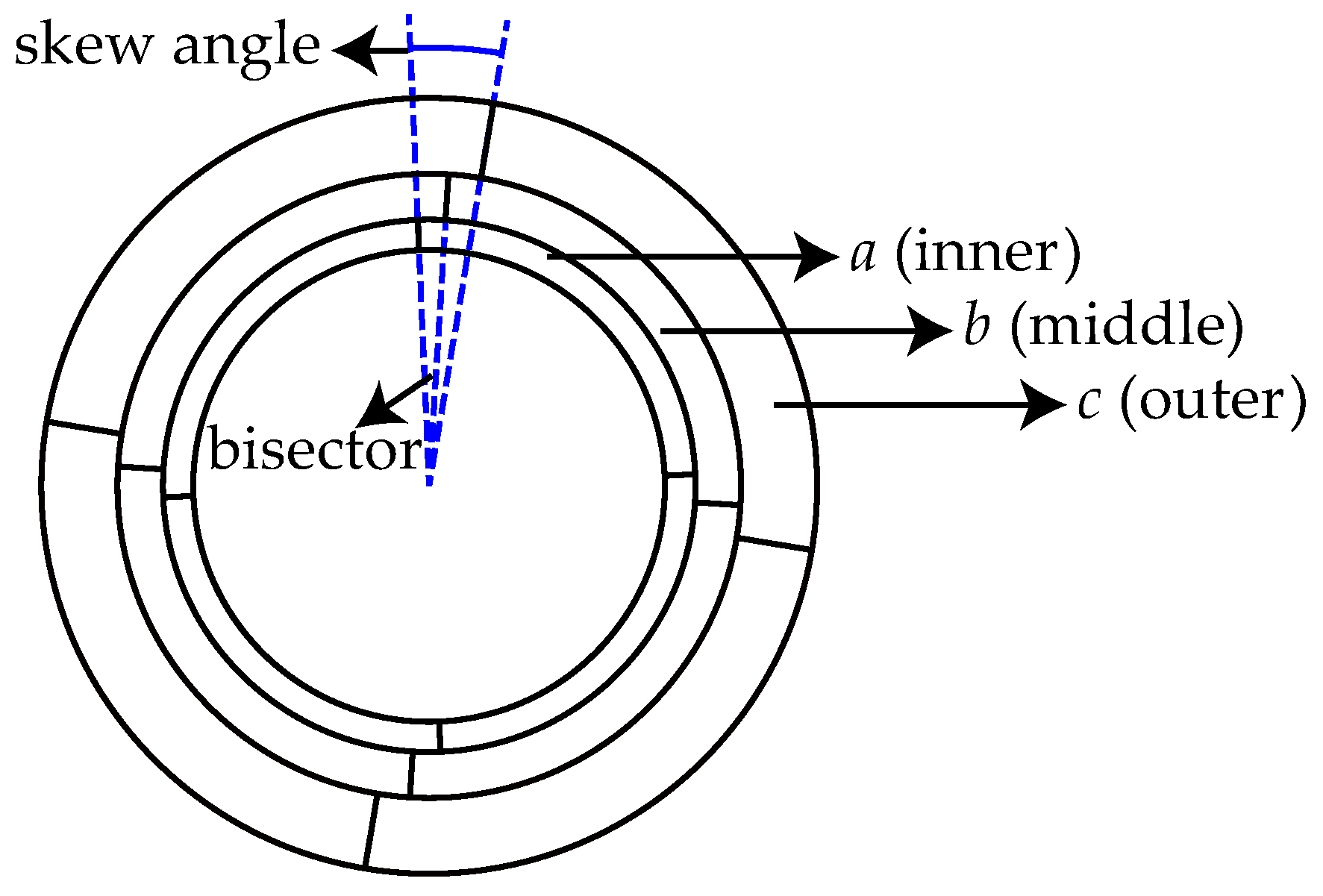
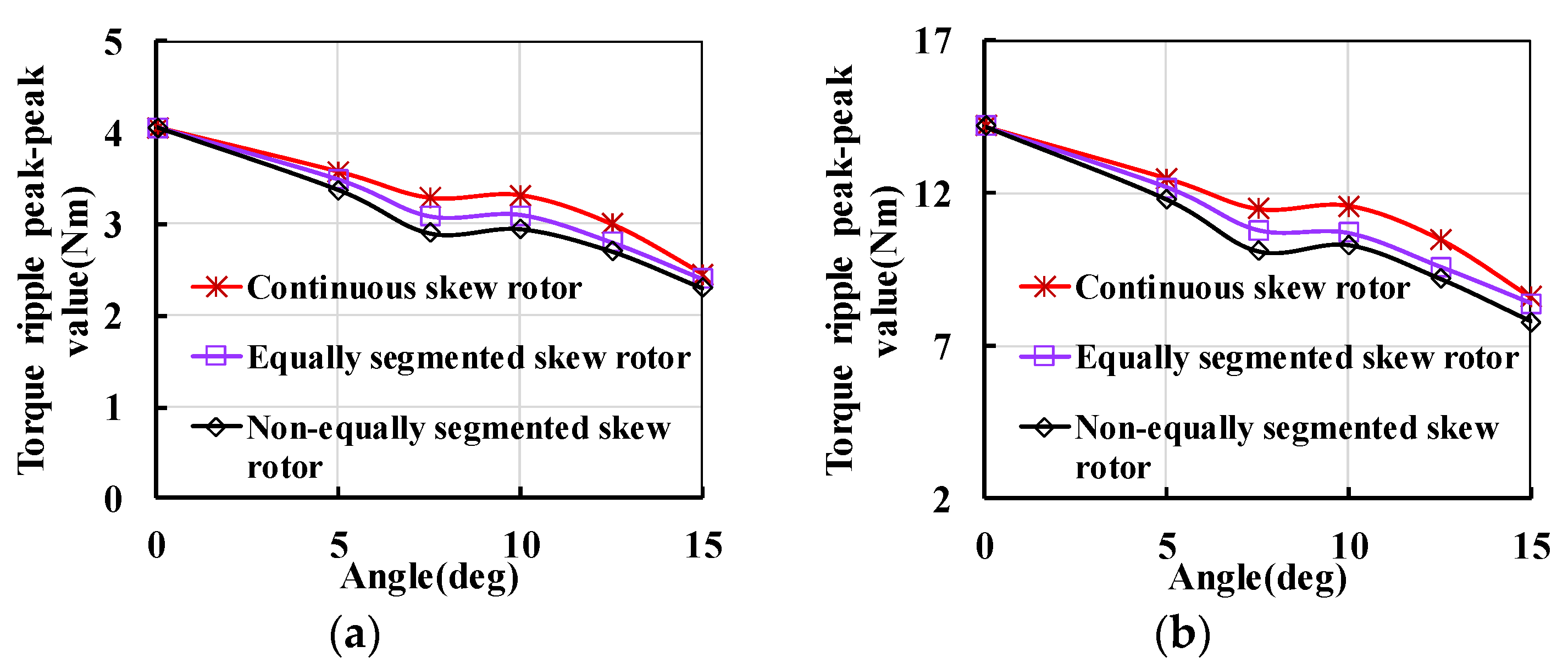
4.2. Segmented Skew Pole
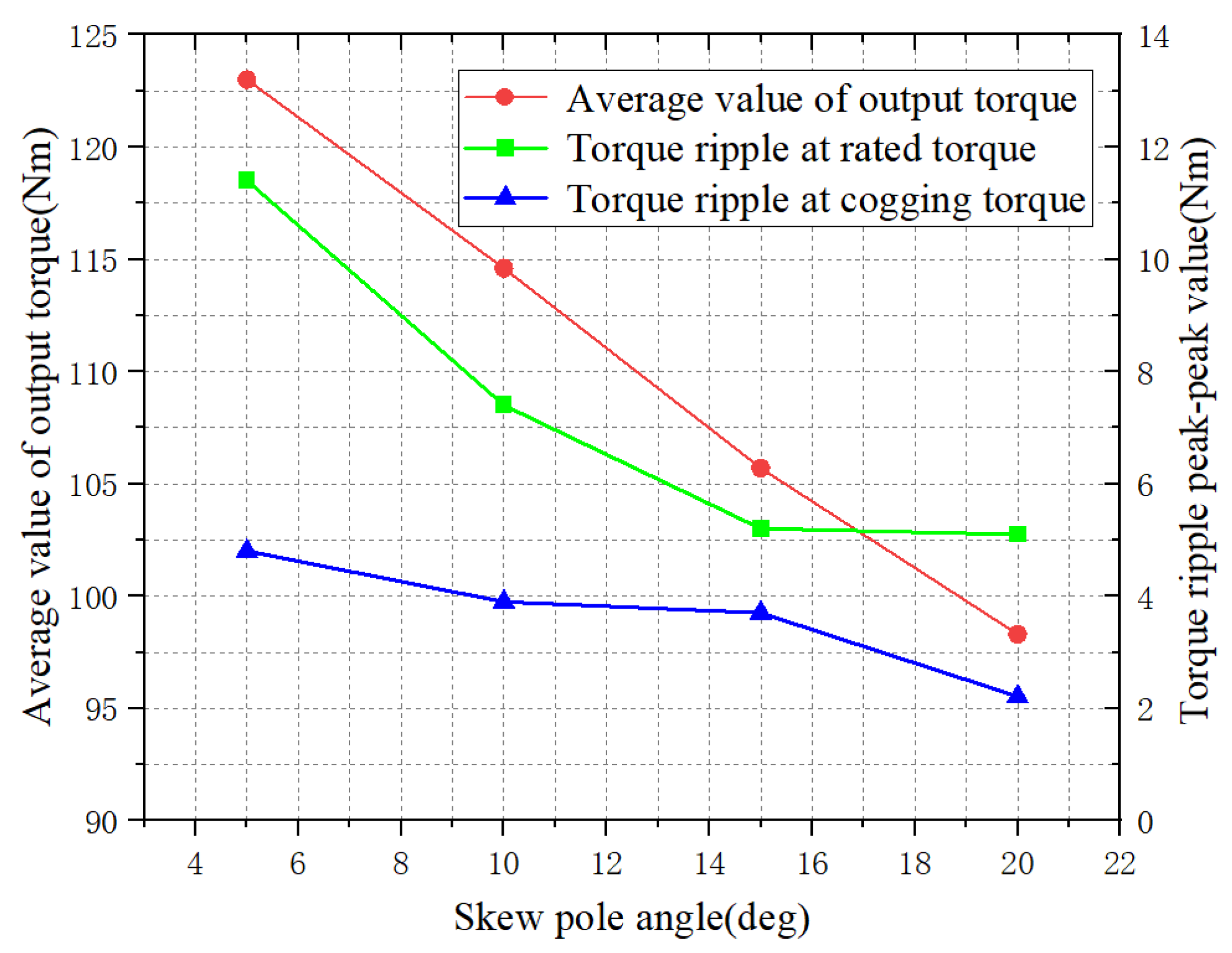
- When the angle of the non-equally segmented skew pole is 5 deg, the best segmented ratio is 2:1:2. Compared with the segmented skew pole, the torque output changes from 111.5 Nm to 118 Nm and the ratio of output torque fluctuation decreases from 8.05% to 7.54%.
- When the angle of the non-equally segmented skew pole is 10 deg, the best segmented ratio is 1:1:2. Compared with the segmented skew pole, the torque output changes from 102.6 Nm to 114.6 Nm, while the proportion of output torque fluctuation decreases from 6.7% to 6.45%.
- When the angle of the non-equally segmented skew pole is 15 deg, the best segmented ratio is 1:1:2. Compared with the segmented skew pole, the torque output changes from 93.4 Nm to 105.7 Nm and the ratio of output torque fluctuation decreases from 6.2% to 4.92%.
- When the angle of the non-equally segmented skew pole is 20 deg, the best segmented ratio is 1:1:2. Compared with the segmented skew pole, the torque output changes from 83.15 Nm to 98.3 Nm and the proportion of output torque fluctuation decreases from 5.3% to 5.2%.
| Skew Pole Angle (deg) | Section Ratio (a–b–c) | Peak-Peak Value of Cogging Torque (Nm) | Average Value of Output Torque (Nm) | Rated Torque Peak-Peak Torque Ripple (Nm) | Torque Peak-Peak Percent Fluctuation, Referred to Average Torque (%) |
|---|---|---|---|---|---|
| 5 deg | 1:1:2 | 4.8 | 123 | 11.4 | 9.26 |
| 2:1:2 | 3.7 | 118 | 8.9 | 7.54 | |
| 1:2:2 | 4.3 | 123 | 10.37 | 8.43 | |
| 2:2:1 | 4.01 | 117.8 | 10.6 | 8.99 | |
| 10 deg | 1:1:2 | 3.9 | 114.6 | 7.4 | 6.45 |
| 2:1:2 | 3.6 | 107.9 | 9 | 8.34 | |
| 1:2:2 | 2.4 | 113 | 7.48 | 6.62 | |
| 2:2:1 | 5.3 | 107 | 9.62 | 8.99 | |
| 15 deg | 1:1:2 | 3.7 | 105.7 | 5.2 | 4.92 |
| 2:1:2 | 3.8 | 95.85 | 7.9 | 8.24 | |
| 1:2:2 | 3.6 | 104.2 | 7.31 | 7.02 | |
| 2:2:1 | 3.8 | 91.6 | 7.2 | 7.86 | |
| 20 deg | 1:1:2 | 2.21 | 98.3 | 5.1 | 5.2 |
| 2:1:2 | 2.61 | 79.94 | 5.03 | 6.29 | |
| 1:2:2 | 2.71 | 92.1 | 6.31 | 6.85 | |
| 2:2:1 | 3.4 | 73.65 | 6.25 | 8.48 |
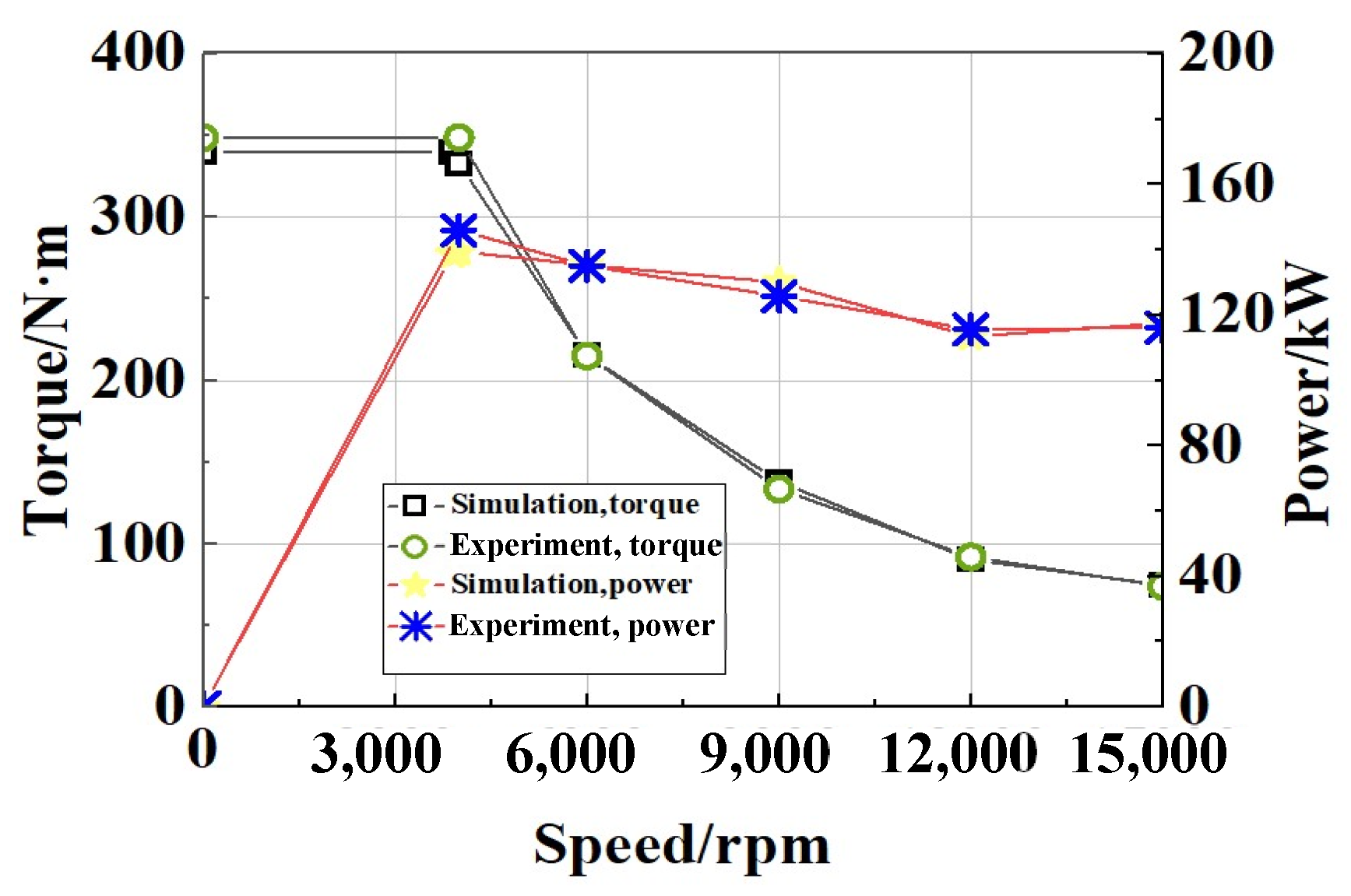
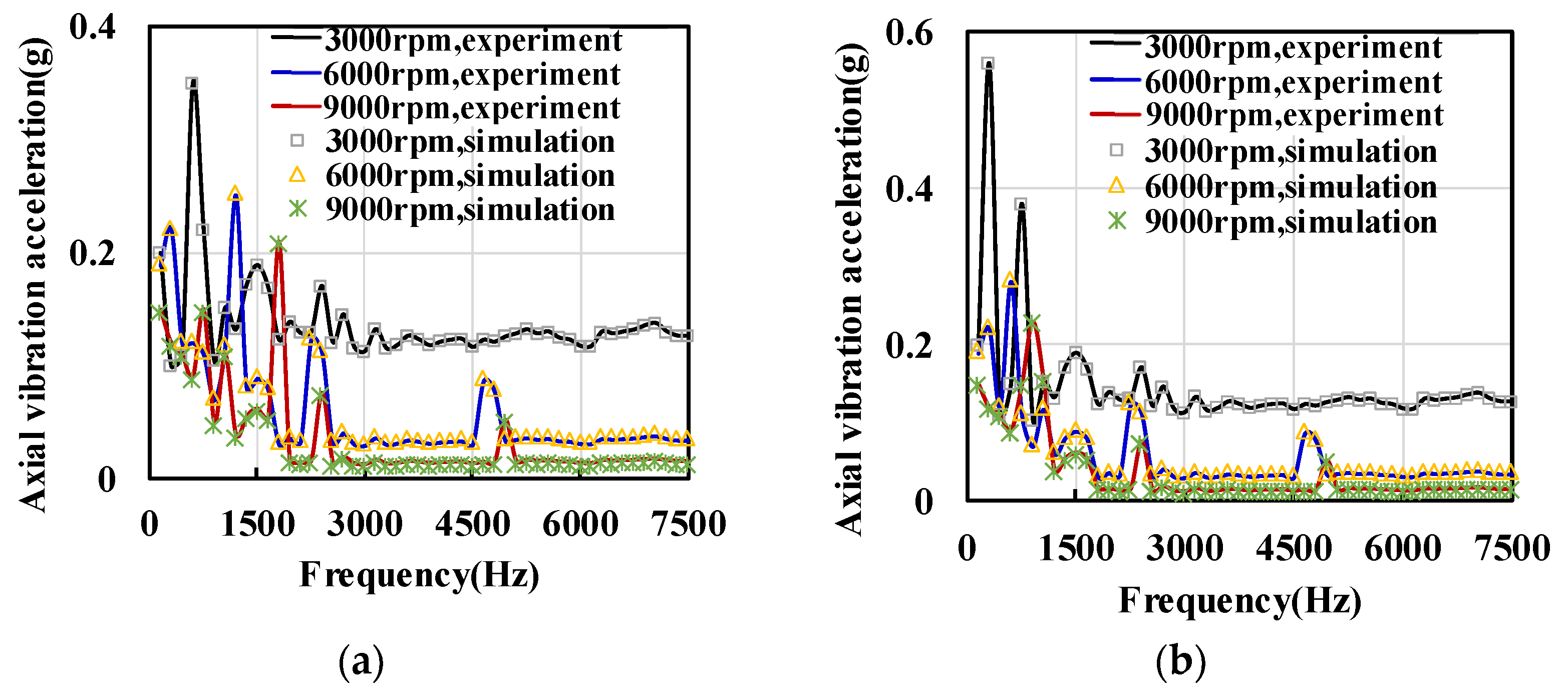
5. Prototype and Experiment
6. Conclusions
- The theoretical calculation of axial electromagnetic force generated by the air-gap magnetic field of an AFPM motor is derived for a single stator double rotor AFPM motor, and the zero-mode frequencies of the axial electromagnetic force of 48-slot-8pole AFPM topology under no-load and load are 12 k and 6 k, respectively.
- The anisotropic material has an important impact on the stator mode due to the wounded silicon steel sheet. It provides an approach to the change stator mode frequency. Moreover, the structural support for the yokeless stator can improve stator stiffness and increase the stator mode frequency.
- The decrease in motor performance caused by the non-equally segmented skew pole is weaker than that caused by the equal segment skew pole, which indicates that the unequally segmented skew pole is an effective way to reduce the vibration and noise of the AFPM motor.
- Due to poor manufacturability, it is difficult to implement continuously segmented skew pole rotors for AFPM motors in the mass production process. Therefore, the non-equally segmented skew pole rotor will be an effective method for reducing vibration and noise while ensuring motor performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kahourzade, S.; Mahmoudi, A.; Ping, H.W.; Uddin, M.N. A comprehensive review of axial-flux permanent-magnet machines. Can. J. Electr. Comput. Eng. 2014, 37, 19–33. [Google Scholar] [CrossRef]
- Wu, S.; Zuo, S.; Wu, X.; Lin, F.; Zhong, H.; Zhang, Y. Vibroacoustic prediction and mechanism analysis of claw pole alternators. IEEE Trans. Ind. Electron. 2017, 64, 4463–4473. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. III. Effect of stator slotting. IEEE Trans. Magn. 1993, 29, 143–151. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Howe, D. Instantaneous magnetic field distribution in permanent magnet brushless DC motors. IV. Magnetic field on load. IEEE Trans. Magn. 1993, 29, 152–158. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Xia, Z.P.; Wu, L.J.; Jewell, G.W. Analytical modeling and finite-element computation of radial vibration force in fractional-slot permanent-magnet brushless machines. IEEE Trans. Ind. Appl. 2010, 46, 1908–1918. [Google Scholar] [CrossRef]
- Lin, C.; Fahimi, B. Prediction of acoustic noise in switched reluctance motor drives. IEEE Trans. Energy Convers. 2014, 29, 250–258. [Google Scholar] [CrossRef]
- Fakam, M.; Hecquet, M.; Lanfranchi, V.; Randria, A. Design and magnetic noise reduction of the surface permanent magnet synchronous machine using complex air-gap permeance. IEEE Trans. Magn. 2015, 51, 1–9. [Google Scholar] [CrossRef]
- Yang, H.; Chen, Y. Influence of radial force harmonics with low mode number on electromagnetic vibration of PMSM. IEEE Trans. Energy Convers. 2014, 29, 38–45. [Google Scholar] [CrossRef]
- Jung, J.-W.; Lee, S.-H.; Lee, G.-H.; Hong, J.-P.; Lee, D.-H.; Kim, K.-N. Reduction design of vibration and noise in IPMSM type integrated starter and generator for HEV. IEEE Trans. Magn. 2010, 46, 2454–2457. [Google Scholar] [CrossRef]
- Torregrossa, D.; Fahimi, B.; Peyraut, F.; Miraoui, A. Fast computation of electromagnetic vibrations in electrical machines via field reconstruction method and knowledge of mechanical impulse response. IEEE Trans. Ind. Electron. 2012, 59, 839–847. [Google Scholar] [CrossRef]
- Park, S.; Kim, W.; Kim, S.-I. A numerical prediction model for vibration and noise of axial flux motors. IEEE Trans. Ind. Electron. 2014, 61, 5757–5762. [Google Scholar] [CrossRef]
- Cao, G.-Z.; Li, L.-L.; Huang, S.-D.; Li, L.-M.; Qian, Q.-Q.; Duan, J.-A. Nonlinear modeling of electromagnetic forces for the planar-switched reluctance motor. IEEE Trans. Magn. 2015, 51, 1–5. [Google Scholar] [CrossRef]
- Deng, W.; Zuo, S. Axial force and vibroacoustic analysis of external-rotor axial-flux motors. IEEE Trans. Ind. Electron. 2018, 65, 2018–2030. [Google Scholar] [CrossRef]
- Zuo, S.; Lin, F.; Wu, X. Noise analysis, calculation, and reduction of external rotor permanent-magnet synchronous motor. IEEE Trans. Ind. Electron. 2015, 62, 6204–6212. [Google Scholar] [CrossRef]
- Lu, Y.; Li, J.; Qu, R.; Ye, D.; Lu, H. Electromagnetic force and vibration study on axial flux permanent magnet synchronous machines with dual three-phase windings. IEEE Trans. Ind. Electron. 2020, 67, 115–125. [Google Scholar] [CrossRef]
- Shin, H.-J.; Choi, J.-Y.; Park, Y.-S.; Koo, M.-N.; Jang, S.-M.; Han, H. Electromagnetic vibration analysis and measurements of double-sided axial-flux permanent magnet generator with slotless stator. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Wu, S.; Tong, W.; Sun, R.; Tang, R. A generalized method of electromagnetic vibration analysis of amorphous alloy permanent magnet synchronous machines. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Wei, M.; Zhang, C.; Gao, Y.; Qing, Y. Comparison of vibration and noise characteristics between radial flux PMSMs and axial flux PMSMs. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Li, N. Analysis and reduction of electromagnetic noise of yokeless and segmented armature axial flux motor. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022. [Google Scholar] [CrossRef]
- Wang, K.; Zhu, Z.Q.; Ren, Y.; Ombach, G. Torque improvement of dual three-phase permanent-magnet machine with third-harmonic current injection. IEEE Trans. Ind. Electron. 2015, 62, 6833–6844. [Google Scholar] [CrossRef]
- Polat, M.; Yildiz, A.; Akinci, R. Performance analysis and reduction of torque ripple of axial flux permanent magnet synchronous motor manufactured for electric vehicles. IEEE Trans. Magn. 2021, 57, 1–9. [Google Scholar] [CrossRef]
- Aydin, M.; Huang, S.; Lipo, T.A. Design and 3D electromagnetic field analysis of non-slotted and slotted TORUS type axial flux surface mounted permanent magnet disc machines. In Proceedings of the IEEE Int. Electric Mach. Drives Conf. (IEMDC), Cambridge, MA, USA, 17–20 June 2001. [Google Scholar] [CrossRef]
- Pellegrino, G.; Vagati, A.; Guglielmi, P.; Boazzo, B. Performance comparison between surface-mounted and interior PM motor drives for electric vehicle application. IEEE Trans. Ind. Electron. 2012, 59, 803–811. [Google Scholar] [CrossRef]
- Sun, S.; Jiang, F.; Li, T.; Xu, B.; Yang, K. Comparison of a multi-stage axial flux permanent magnet machine with different stator core materials. IEEE Trans. Appl. Supercond. 2020, 30, 1–6. [Google Scholar] [CrossRef]
- Geng, W.; Zhang, Z. Investigation of a new ironless-stator self-bearing axial flux permanent magnet motor. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Geng, W.; Zhang, Z.; Li, Q. High torque density fractional-slot concentrated-winding axial-flux permanent-magnet machine with modular SMC stator. IEEE Trans. Ind. Appl. 2020, 56, 3691–3699. [Google Scholar] [CrossRef]
- Geng, W.; Wang, Y.; Wang, J.; Hou, J.; Guo, J.; Zhang, Z. Comparative study of yokeless stator axial-flux PM machines having fractional slot concentrated and integral slot distributed windings for electric vehicle traction applications. IEEE Trans. Ind. Electron. 2023, 70, 155–166. [Google Scholar] [CrossRef]
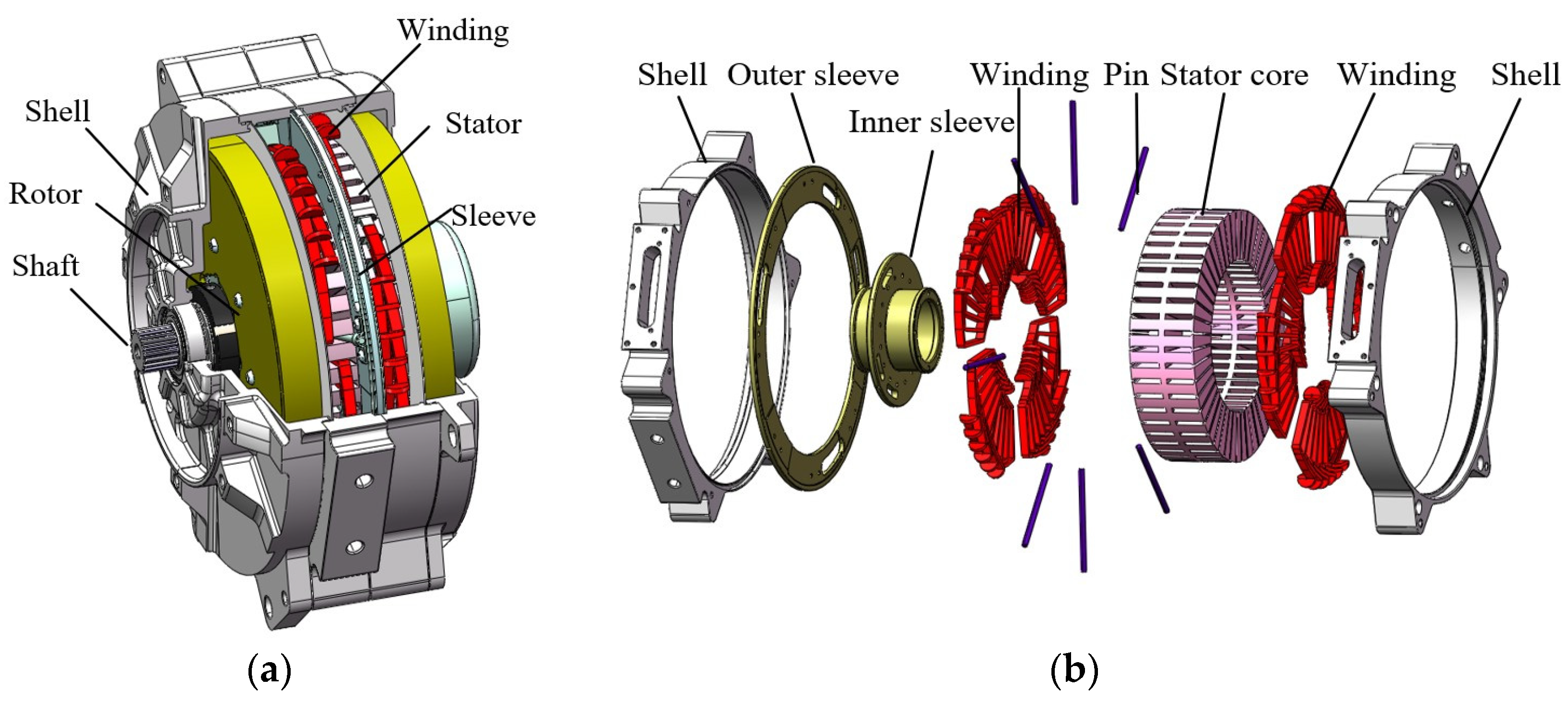






| Parameters | Value |
|---|---|
| Outer diameter of stator and rotor | 220 mm |
| Inner diameter of stator and rotor | 130 mm |
| Air-gap length | 1.5 mm |
| Number of slots | 48 |
| Number of poles | 8 |
| Number of phases | 3 |
| Rated power | 70 kW |
| Peak power | 120 kW |
| Rated speed (frequency) | 6000 r/min (100 Hz) |
| Peak speed (frequency) | 15,000 r/min (250 Hz) |
| Item | Source | Spatial Order | Frequency |
|---|---|---|---|
| 1 | PM field | ||
| 2 | Interaction of PM field and stator slotting | ||
| 3 | Interaction of PM field and armature reaction field | ||
| 4 | Armature reaction field | ||
| 5 | Interaction of PM field, armature reaction field, and stator slotting | ||
| 6 | Interaction of armature reaction field and stator slotting |
| Parameters | Value |
|---|---|
| Sensitivity | 100 mV/g |
| Range | 10 g |
| Frequency response | 0.5 kHz–6 kHz |
| Resolution | 100 μg |
| Operating voltage | 18 V–28 V DC |
| Output impedance | <100 Ω |
| Speed | Vibration Frequency under no Load | Vibration Frequency under Load | DC Bus |
|---|---|---|---|
| 3000 r/min | 600 Hz | 300 Hz | 350 V |
| 6000 r/min | 1200 Hz | 600 Hz | 350 V |
| 9000 r/min | 1800 Hz | 900 Hz | 350 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Wang, Q.; Fu, Y.; Chen, H.; Zhang, J.; Geng, W. Vibration Performance Analysis of a Yokeless Stator Axial Flux PM Motor with Distributed Winding for Electric Vehicle Application. World Electr. Veh. J. 2024, 15, 335. https://doi.org/10.3390/wevj15080335
Yu X, Wang Q, Fu Y, Chen H, Zhang J, Geng W. Vibration Performance Analysis of a Yokeless Stator Axial Flux PM Motor with Distributed Winding for Electric Vehicle Application. World Electric Vehicle Journal. 2024; 15(8):335. https://doi.org/10.3390/wevj15080335
Chicago/Turabian StyleYu, Xue, Qin Wang, Yu Fu, Hao Chen, Jianfu Zhang, and Weiwei Geng. 2024. "Vibration Performance Analysis of a Yokeless Stator Axial Flux PM Motor with Distributed Winding for Electric Vehicle Application" World Electric Vehicle Journal 15, no. 8: 335. https://doi.org/10.3390/wevj15080335
APA StyleYu, X., Wang, Q., Fu, Y., Chen, H., Zhang, J., & Geng, W. (2024). Vibration Performance Analysis of a Yokeless Stator Axial Flux PM Motor with Distributed Winding for Electric Vehicle Application. World Electric Vehicle Journal, 15(8), 335. https://doi.org/10.3390/wevj15080335







