Implantable Magnetic Resonance Wireless Power Transfer System Based on 3D Flexible Coils
Abstract
:1. Introduction
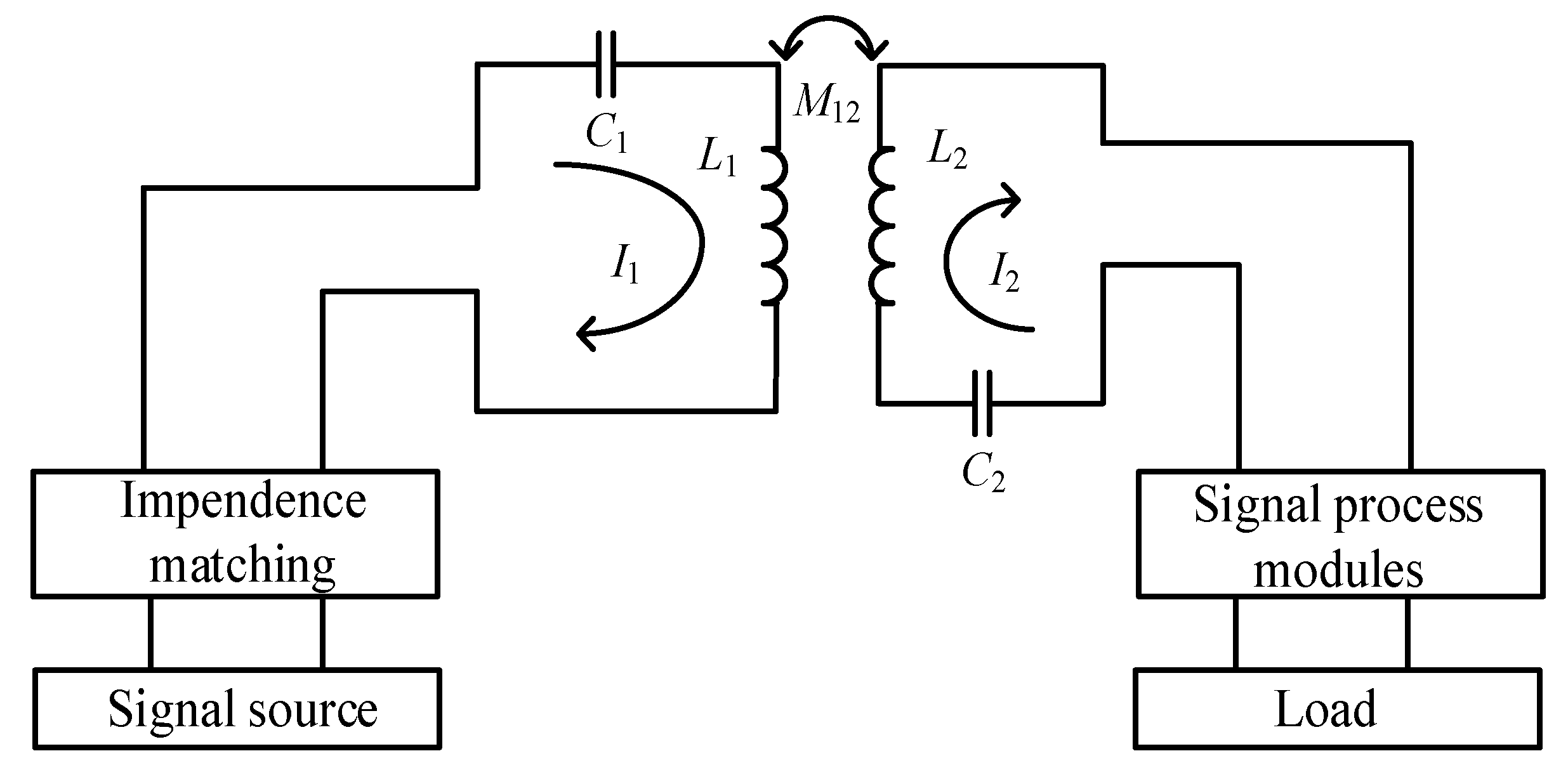
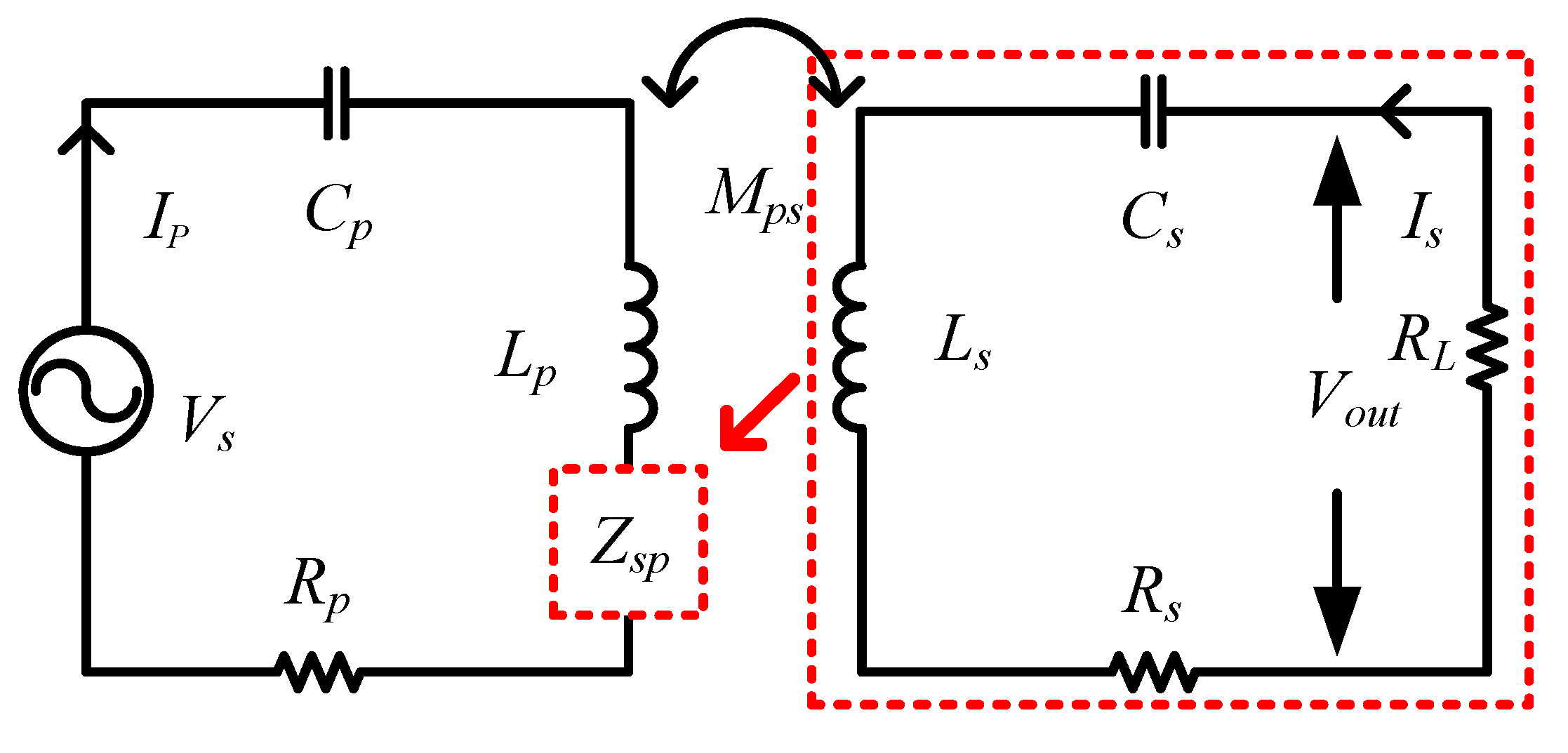
2. Operation Principle
3. Simulation Performances
3.1. Coil Structural Parameter Optimization
3.1.1. Simulation of Coil Turns
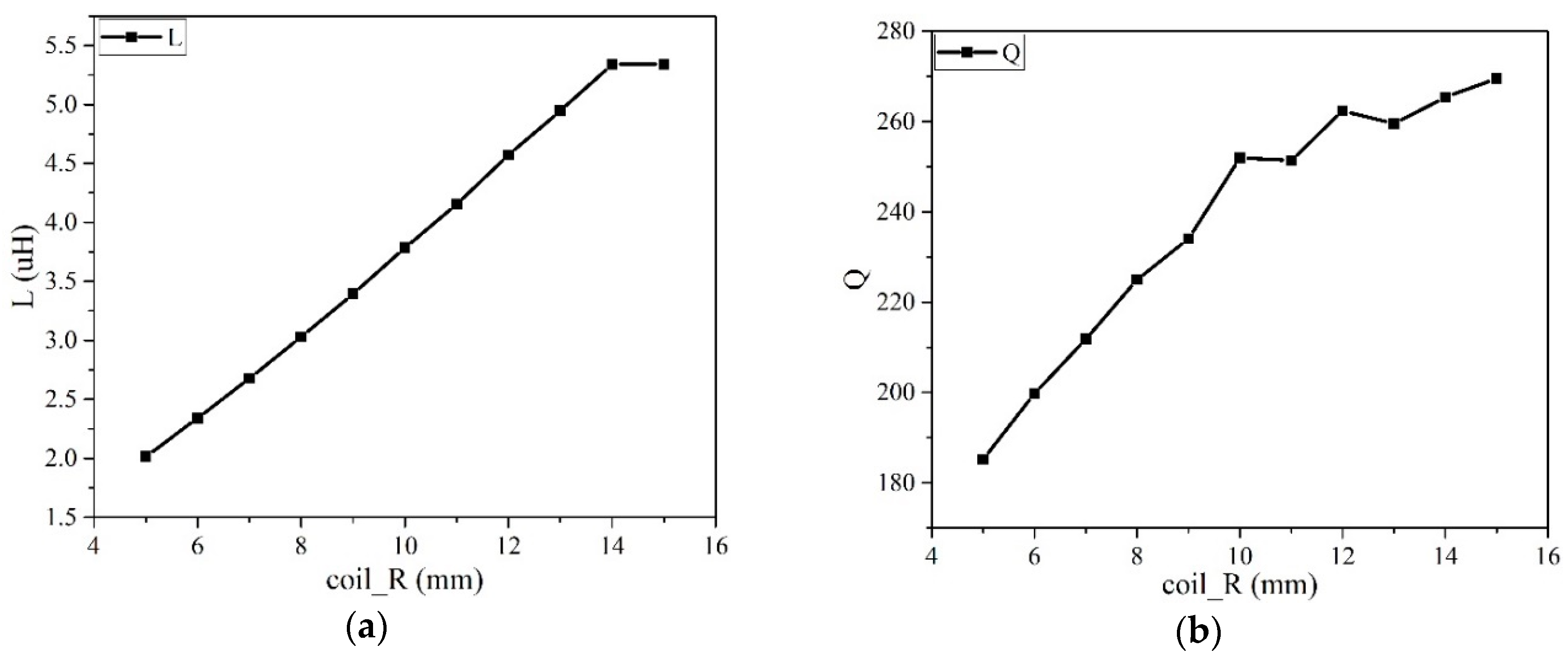
3.1.2. Simulation of Coil Radius
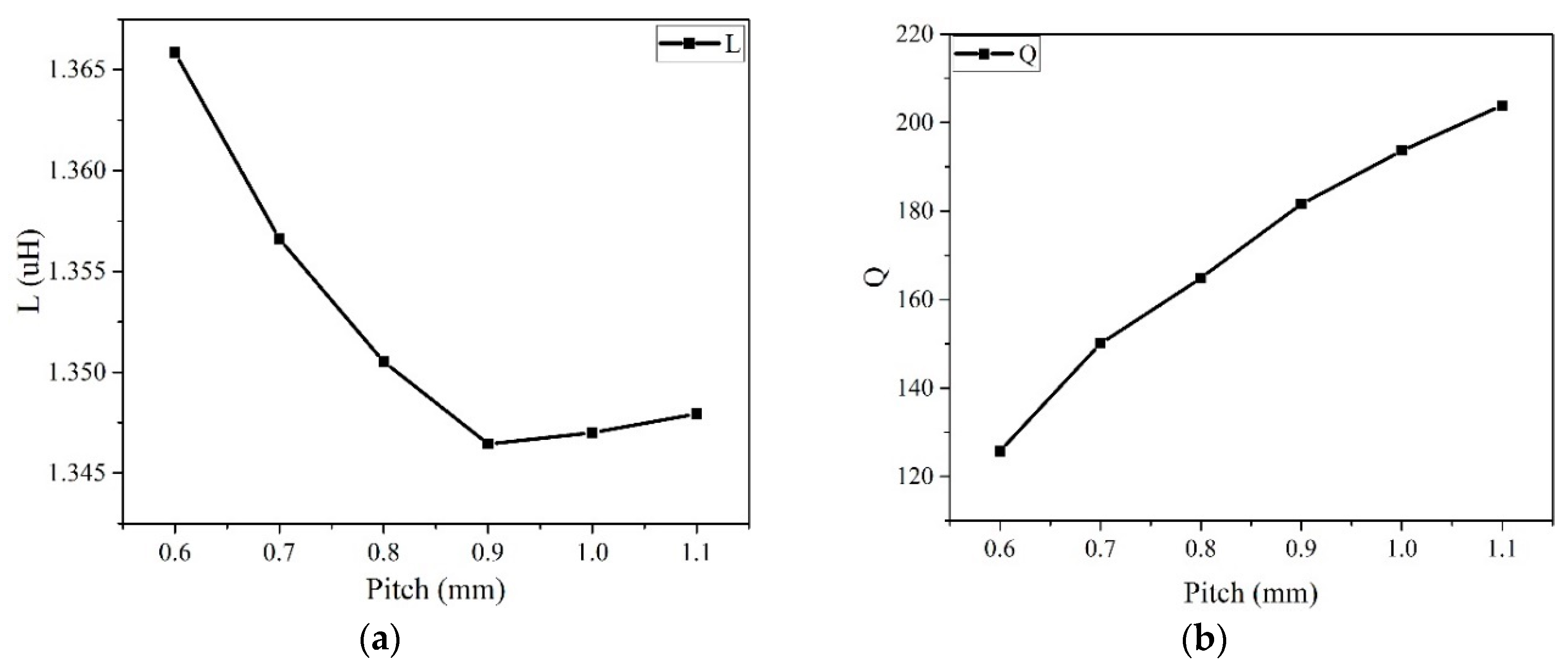
3.1.3. Simulation of Turn Pitch
3.1.4. Simulation of Wire Width
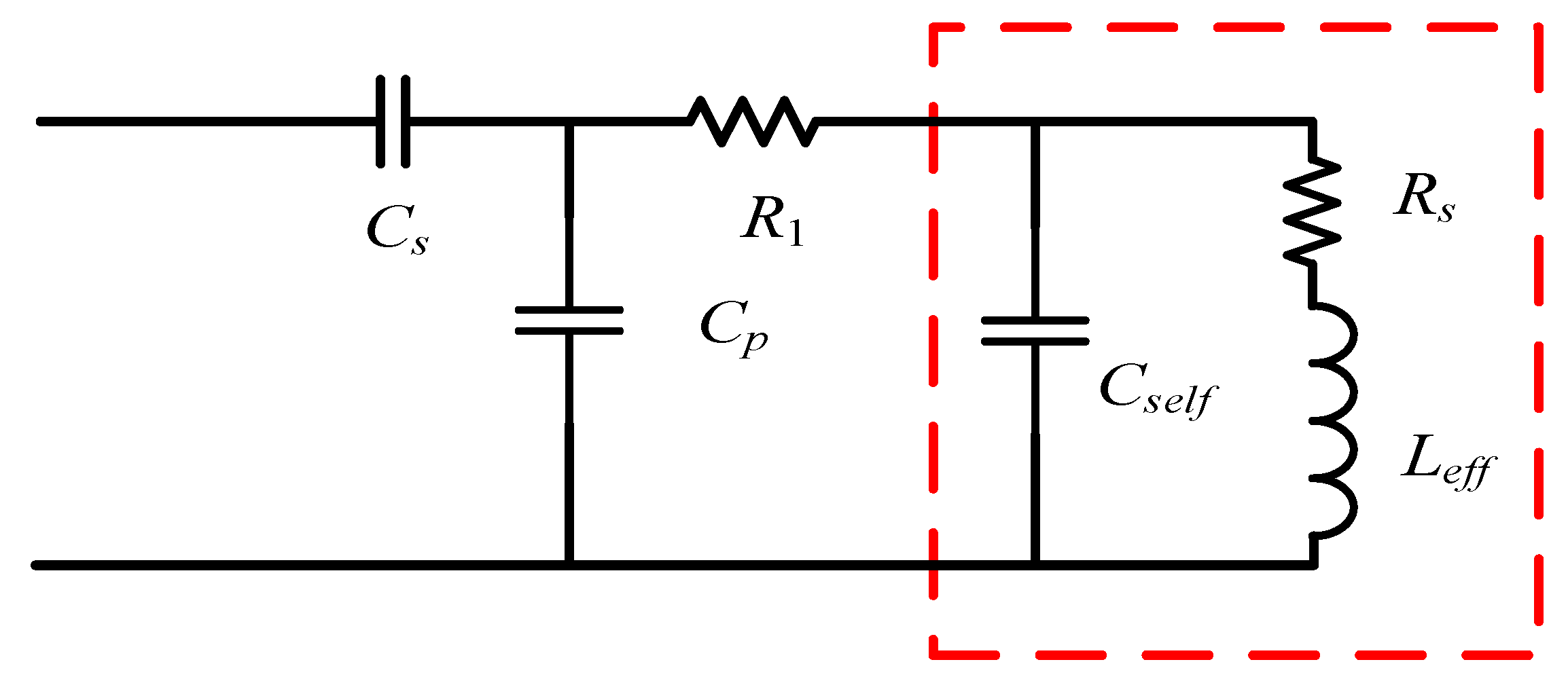
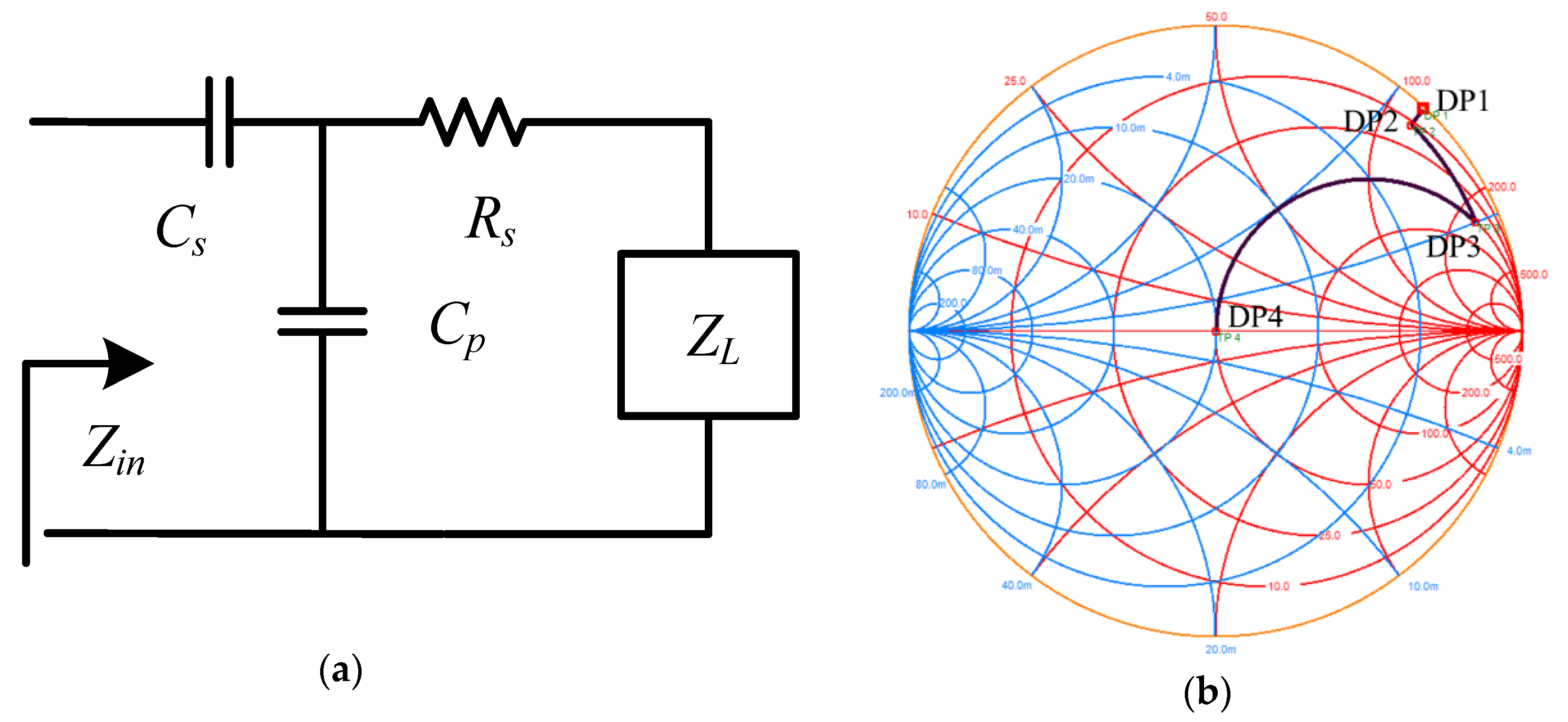
3.2. Impedance Matching Circuit Design
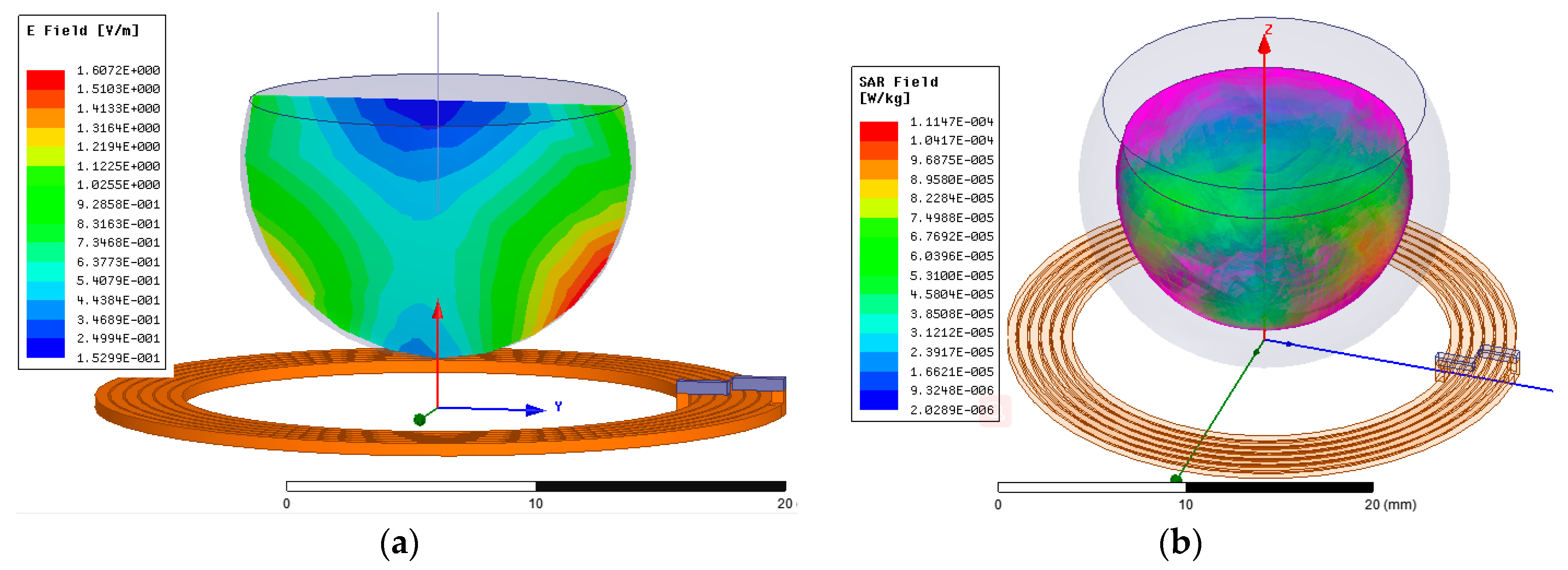
3.3. SAR Simulation Analysis
4. Experimental Performances
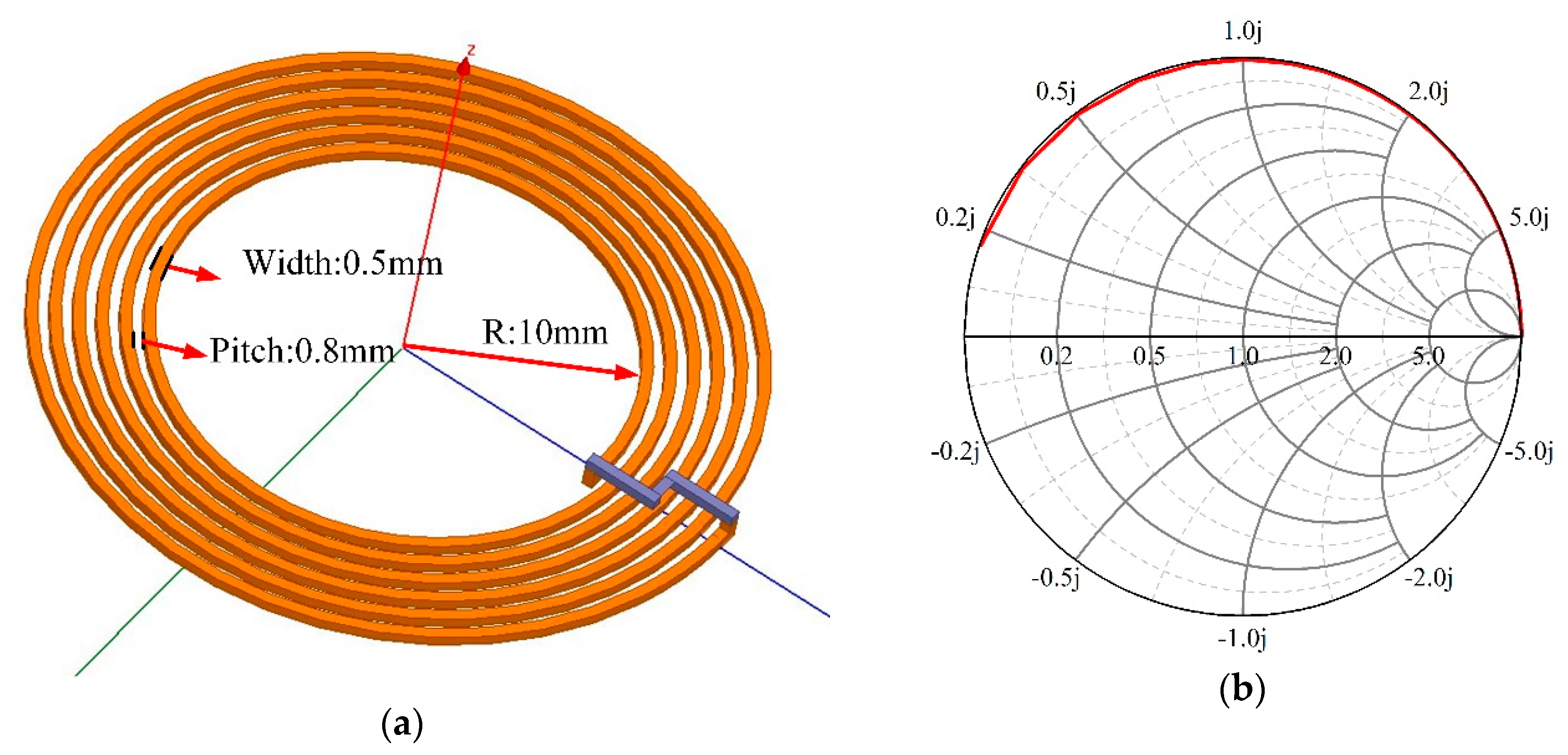
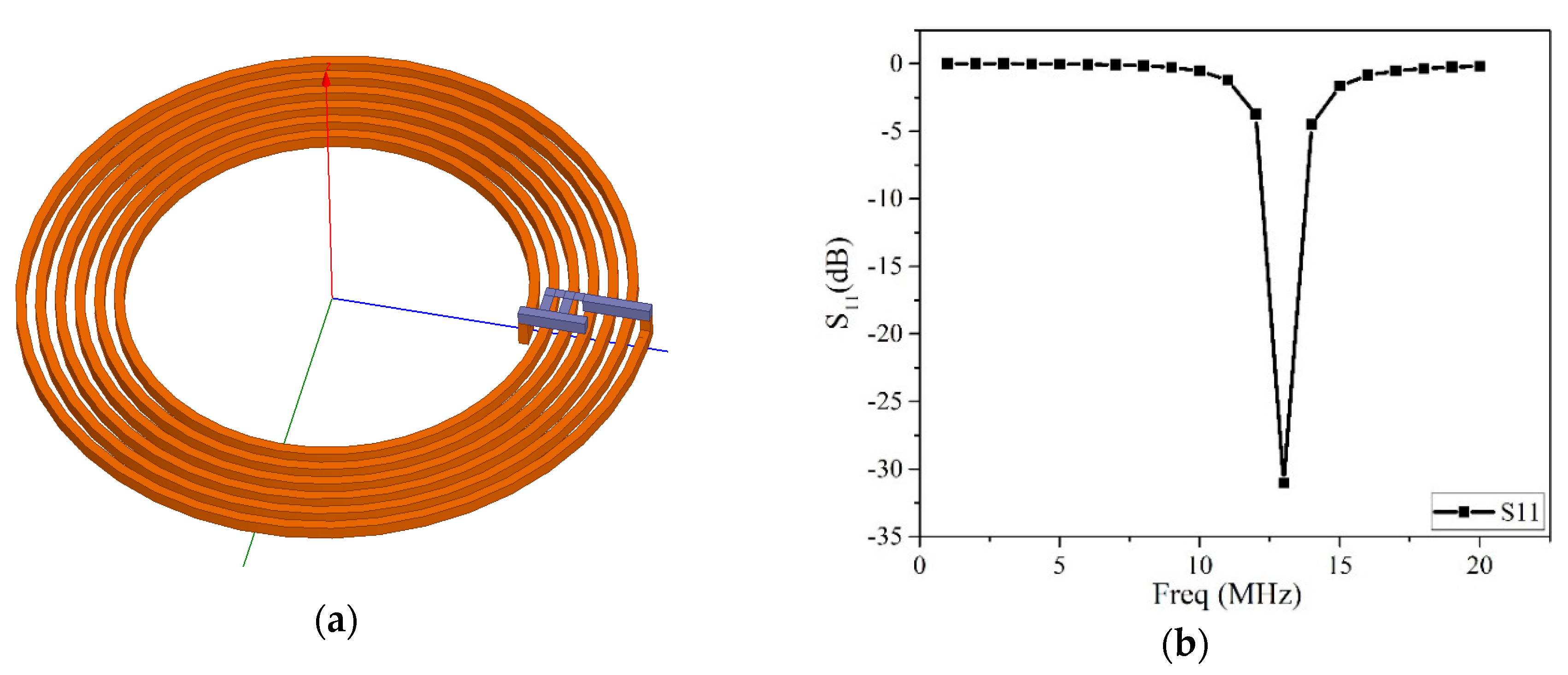
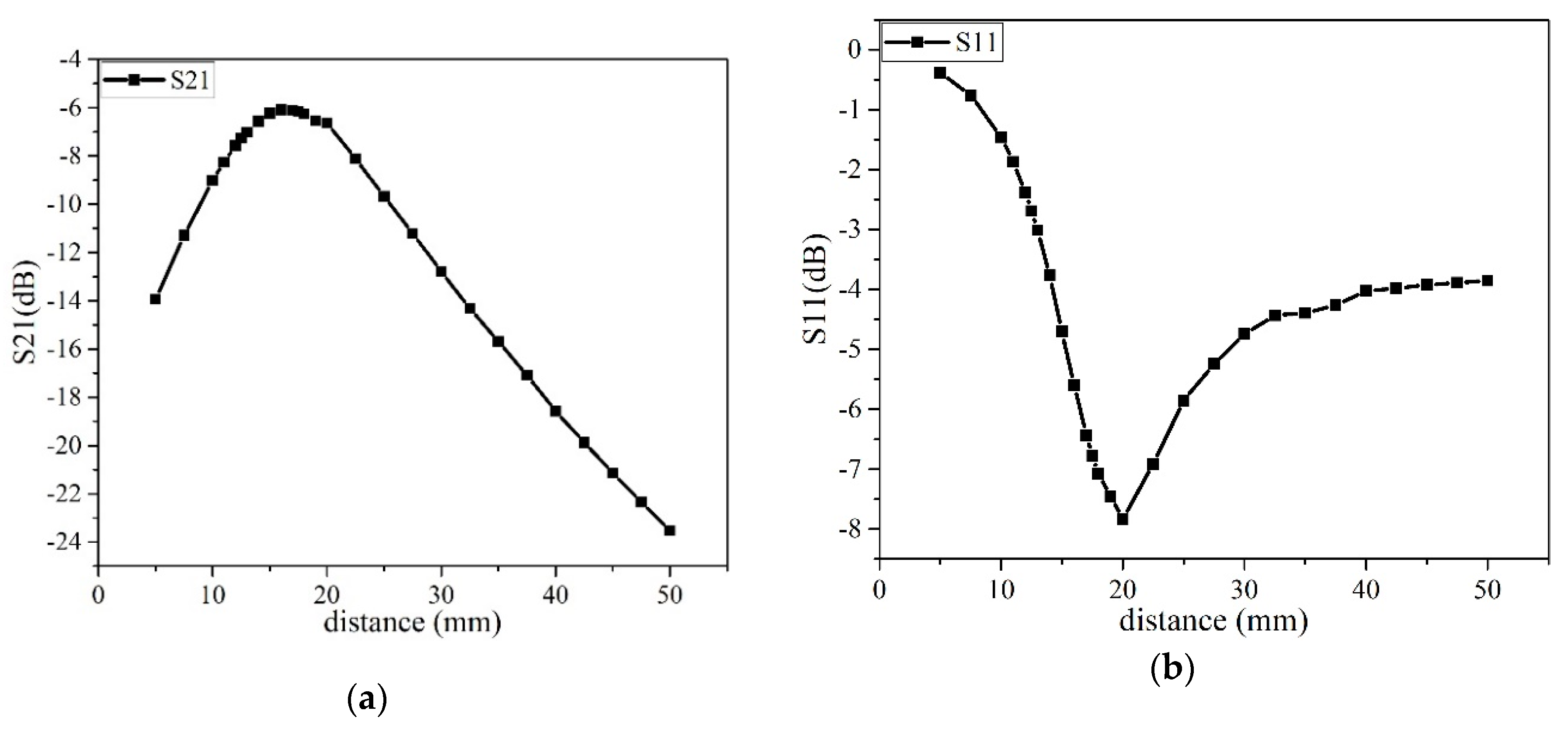
4.1. Coupling Resonant Loop Measurement after Impedance Matching
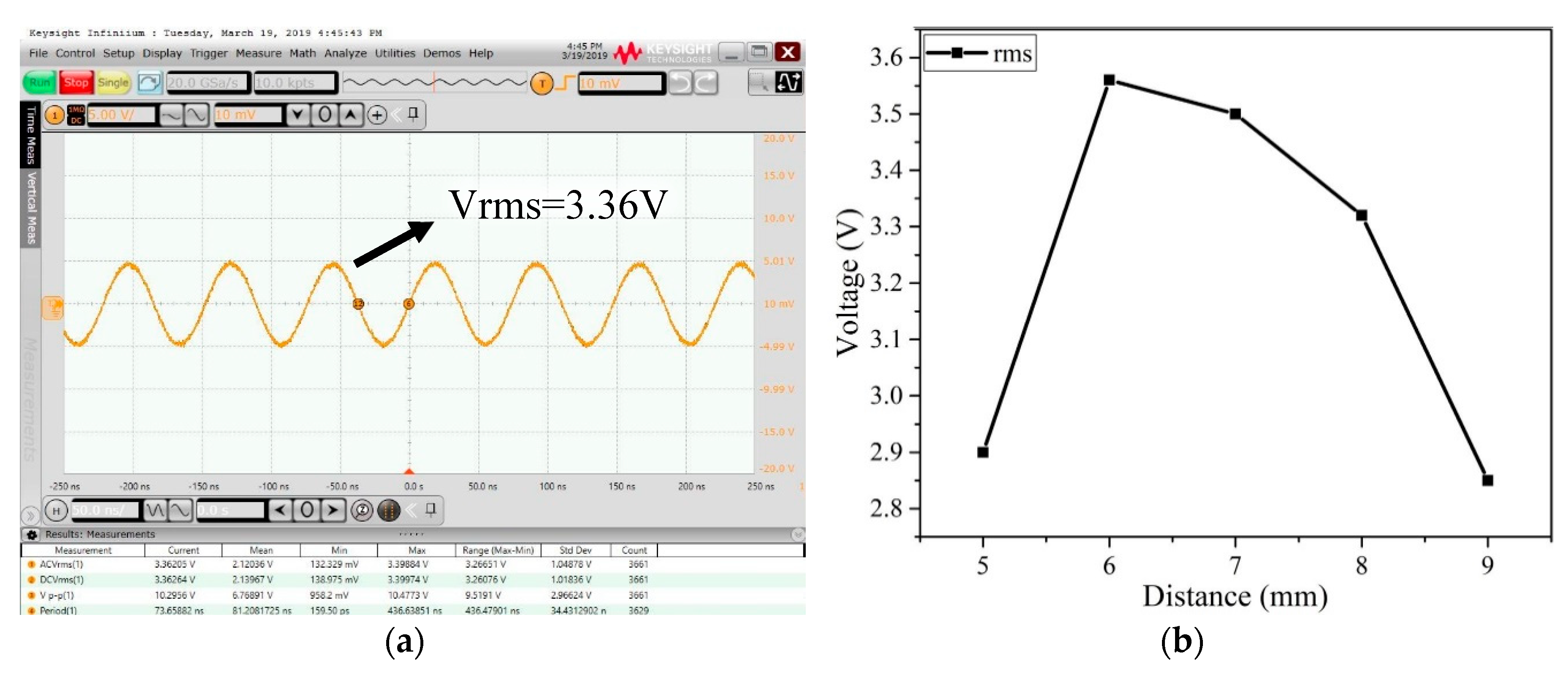
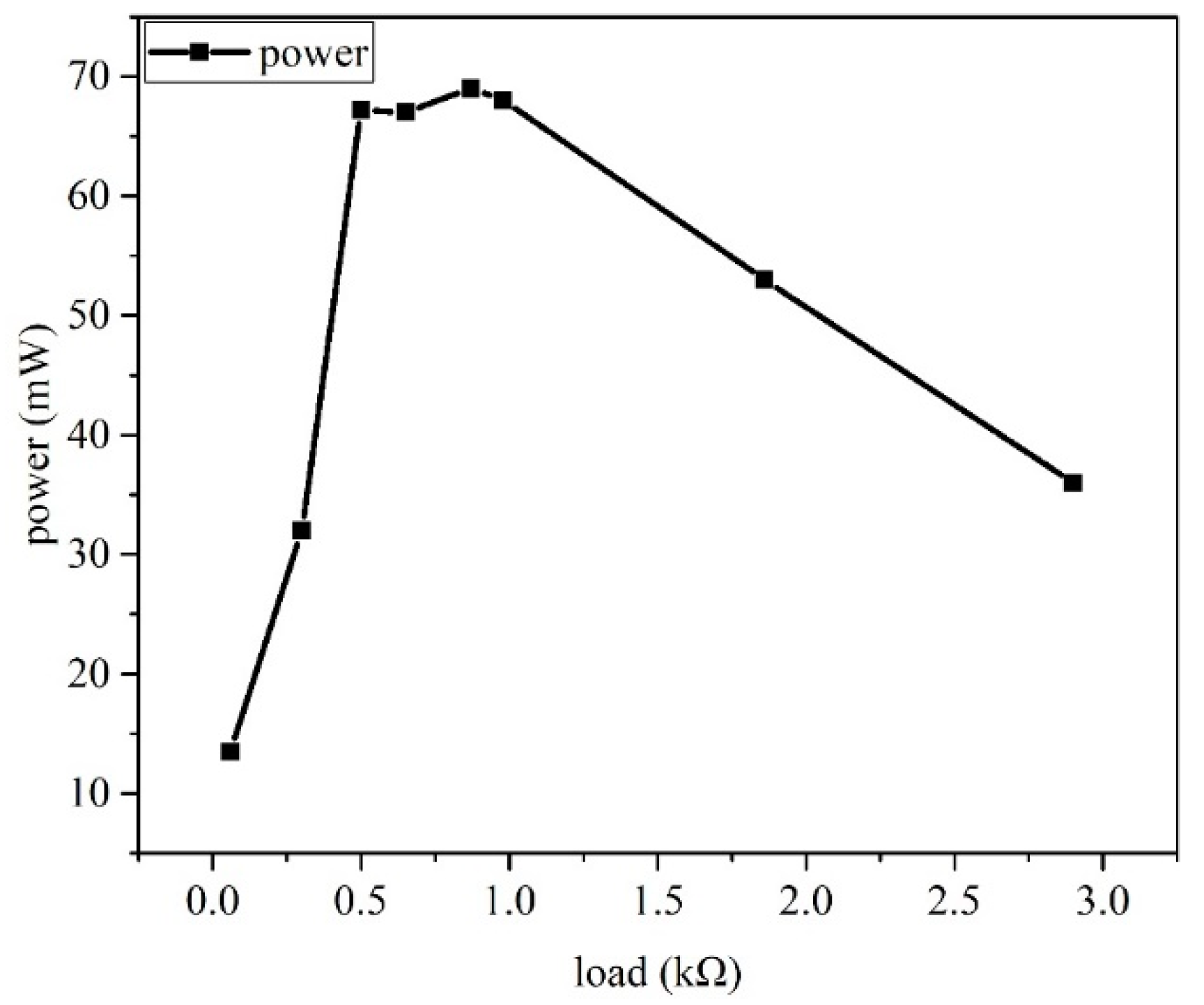
4.2. Wireless Power Transfer System Measurement
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dai, Z.; Wang, J.; Jin, L.; Jing, H.; Fang, Z.; Hou, H. A Full-Freedom Wireless Power Transfer for Spheroid Joints. IEEE Access 2019, 7, 18675–18684. [Google Scholar] [CrossRef]
- Basar, M.R.; Ahmad, M.Y.; Cho, J.; Ibrahim, F. An improved wearable resonant wireless power transfer system for biomedical capsule endoscope. IEEE Trans. Ind. Electron. 2018, 65, 7772–7781. [Google Scholar] [CrossRef]
- Yang, C.L.; Chang, C.K.; Lee, S.Y.; Chang, S.J.; Chiou, L.Y. Efficient four-coil wireless power transfer for deep brain stimulation. IEEE Trans. Microw. Theory Tech. 2017, 65, 2496–25071. [Google Scholar] [CrossRef]
- Manoufali, M.; Bialkowski, K.; Mohammed, B.; Abbosh, A. Wireless power link based on inductive coupling for brain implantable medical devices. IEEE Antennas Wirel. Propag. Lett. 2017, 17, 160–163. [Google Scholar] [CrossRef]
- Shekarforoush, M.; Barton, K.I.; Atarod, M.; Heard, B.J.; Sevick, J.L.; Martin, R.; Hart, D.A.; Frank, C.B.; Shrive, N.G. An explicit method for analysis of three-dimensional linear and angular velocity of a joint, with specific application to the knee joint. J. Med Biol. Eng. 2018, 38, 273–283. [Google Scholar] [CrossRef] [Green Version]
- Xiao, C.; Cheng, D.; Wei, K. An LCC-C compensated wireless charging system for implantable cardiac pacemakers: Theory, experiment, and safety evaluation. IEEE Trans. Power Electron. 2017, 33, 4894–4905. [Google Scholar] [CrossRef]
- Mashhadi, I.A.; Pahlevani, M.; Hor, S.; Pahlevani, H.; Adib, E. A New Wireless Power Transfer Circuit for Retinal Prosthesis. IEEE Trans. Power Electron. 2019, 34, 6425–6439. [Google Scholar] [CrossRef]
- Fernandez, C.; Garcia, O.; Cobos, J.A.; Uceda, J. A simple dc-dc converter for the power supply of a cochlear implant. In Proceedings of the IEEE 34th Annual Conference on Power Electronics Specialist, Acapulco, Mexico, 15–19 June 2003; Volume 4, pp. 1965–1970. [Google Scholar]
- Sugino, M.; Kondo, H.; Takeda, S. Linear motion type transfer robot using the wireless power transfer system. In Proceedings of the 2016 International Symposium on Antennas and Propagation (ISAP), Okinawa, Japan, 24–28 October 2016; pp. 508–509. [Google Scholar]
- Ayisire, E.; El-Shahat, A.; Sharaf, A. Magnetic Resonance Coupling Modelling for Electric Vehicles Wireless Charging. In Proceedings of the 2018 IEEE Global Humanitarian Technology Conference (GHTC), San Jose, CA, USA, 18–21 October 2018; pp. 1–2. [Google Scholar]
- Dong, S.; Li, X.; Yu, X.; Dona, Y.; Cui, H.; Cui, T.; Wang, Y.; Liu, S. Hybrid Mode Wireless Power Transfer for Wireless Sensor Network. In Proceedings of the 2019 IEEE Wireless Power Transfer Conference (WPTC), London, UK, 17–23 June 2019; pp. 561–564. [Google Scholar]
- Kesler, M. Wireless Charging of Electric Vehicles. In Proceedings of the 2018 IEEE Wireless Power Transfer Conference (WPTC), Montreal, QC, Canada, 3–7 June 2018. [Google Scholar]
- Samal, S.K.; Kar, D.P.; Sahoo, P.K.; Bhuyan, S.; Das, S.N. Analysis of the effect of design parameters on the power transfer efficiency of resonant inductive coupling based wireless EV charging system. In Proceedings of the 2017 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 21–22 April 2017; pp. 1–4. [Google Scholar]
- Corti, F.; Reatti, A.; Pierini, M.; Barbieri, R.; Berzi, L.; Nepote, A.; Magneti, P.D.L.P. A Low-Cost Secondary-Side Controlled Electric Vehicle Wireless Charging System using a Full-Active Rectifier. In Proceedings of the 2018 International Conference of Electrical and Electronic Technologies for Automotive, Milan, Italy, 9–11 July 2018; pp. 1–6. [Google Scholar]
- Sato, N.S.; Jodoi, D. Basic Study for Wireless Power Transfer to a Pipeline Inspection Robot. In Proceedings of the 2018 IEEE Wireless Power Transfer Conference (WPTC), Montreal, QC, Canada, 3–7 June 2018; pp. 1–4. [Google Scholar]
- Anyapo, C. Development of Long Rail Dynamic Wireless Power Transfer for Battery-Free Mobile Robot. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019—ECCE Asia), Busan, Korea (South), 27–30 May 2019; pp. 1–6. [Google Scholar]
- Allotta, B.; Pugi, L.; Reatti, A.; Corti, F. Wireless power recharge for underwater robotics. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Chen, J.; Yu, C.W.; Ouyang, W. Efficient Wireless Charging Pad Deployment in Wireless Rechargeable Sensor Networks. IEEE Access 2020, 8, 39056–39077. [Google Scholar] [CrossRef]
- Wang, N.; Wu, J.; Dai, H. Bundle Charging: Wireless Charging Energy Minimization in Dense Wireless Sensor Networks. In Proceedings of the 2019 IEEE 39th International Conference on Distributed Computing Systems (ICDCS), Dallas, TX, USA, 7–10 July 2019; pp. 810–820. [Google Scholar]
- Krikidis, I. Average Age of Information in Wireless Powered Sensor Networks. IEEE Wirel. Commun. Lett. 2019, 8, 628–631. [Google Scholar] [CrossRef] [Green Version]
- Ke, Q.; Luo, W.; Yan, G.; Yang, K. Analytical model and optimized design of power transmitting coil for inductively coupled endoscope robot. IEEE Trans. Biomed. Eng. 2016, 63, 694–706. [Google Scholar] [CrossRef]
- Shadid, R.; Noghanian, S. Hybrid power transfer and wireless antenna system design for biomedical implanted devices. In Proceedings of the International Applied Computational Electromagnetics Society Symposium (ACES), Beijing China, 29 July–1 August 2018; pp. 1–2. [Google Scholar]
- Delhaye, T.P.; André, N.; Gilet, S.; Gimeno, C.; Francis, L.A.; Flandre, D. High-efficiency wireless power transfer for mm-size biomedical implants. IEEE Sens. 2017. [Google Scholar] [CrossRef]
- Kim, D.; Park, J.; Park, H.H.; Ahn, S. Generation of magnetic propulsion force and torque for microrobot using wireless power transfer coil. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Narayanamoorthi, R.; Juliet, A.V.; Chokkalingam, B. Frequency splitting-based wireless power transfer and simultaneous propulsion generation to multiple micro-robots. IEEE Sens. J. 2018, 18, 5566–5575. [Google Scholar] [CrossRef]
- Kim, D.; Hwang, K.; Park, J.; Park, H.H.; Ahn, S. High efficiency wireless power and force transfer for micro-robot using 3-axis AC/DC magnetic coil. In Proceedings of the IEEE Conference on Electromagnetic Field Computation, Miami, FL, USA, 13–16 November 2016; p. 1. [Google Scholar]
- Kim, D.; Park, J.; Kim, K.; Park, H.H.; Ahn, S. Propulsion and control of implantable micro-robot based on wireless power transfer. In Proceedings of the IEEE Wireless Power Transfer Conference (WPTC), Boulder, CO, USA, 13–15 May 2015; pp. 1–4. [Google Scholar]
- Smith, S.; Tang, T.B.; Stevenson, J.T.M.; Flynn, B.W.; Reekie, H.M.; Murray, A.F.; Gundlach, A.M.; Renshaw, D.; Dhillon, B.; Ohtori, A.; et al. Miniaturised drug delivery system with wireless power transfer and communication. MEMS Sens. Actuators Inst. Eng. Technol. Semin. IET 2007. [Google Scholar] [CrossRef]
- Basar, M.R.; Ahmad, M.Y.; Cho, J.; Ibrahim, F. A 3-coil wireless power transfer system with fine tuned power amplifier for biomedical capsule. In Proceedings of the 2017 IEEE Asia Pacific Microwave Conference (APMC), Kuala Lumpur, Malaysia, 13–16 November 2017; pp. 142–145. [Google Scholar]
- Seo, Y.S.; Nguyen, M.Q.; Hughes, Z.; Rao, S.; Chiao, J.C. Wireless power transfer by inductive coupling for implantable batteryless stimulators. In Proceedings of the 2012 IEEE/MTT-S International Microwave Symposium Diges, Montreal, QC, Canada, 17–22 June 2012; pp. 1–3. [Google Scholar]
- Khalifa, A.; Karimi, Y.; Wang, Q.; Garikapati, S.; Montlouis, W.; Stanaćević, M.; Thakor, N.; Etienne-Cummings, R. The microbead: A highly miniaturized wirelessly powered implantable neural stimulating system. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 521–531. [Google Scholar] [CrossRef]
- Li, L.; Liu, H.; Zhang, H.; Xue, W. Efficient wireless power transfer system integrating with metasurface for biological applications. IEEE Trans. Ind. Electron. 2017, 65, 3230–3239. [Google Scholar] [CrossRef]
- Du, S.; Chan, E.K.; Wen, B.; Hong, J.; Widmer, H.; Wheatley, C.E. Wireless power transfer using oscillating magnets. IEEE Trans. Ind. Electron. 2017, 65, 6259–6269. [Google Scholar] [CrossRef]
- Raju, S.; Wu, R.; Chan, M.; Yue, C.P. Modeling of mutual coupling between planar inductors in wireless power applications. IEEE Trans. Power Electron. 2013, 29, 481–490. [Google Scholar] [CrossRef]
- Liu, H.; Shao, Q.; Fang, X. Modeling and optimization of class-E amplifier at subnominal condition in a wireless power transfer system for biomedical implants. IEEE Trans. Biomed. Circuits Syst. 2016, 11, 35–43. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, C.; Song, J.; Chau, K.T. An effective sandwiched wireless power transfer system for charging implantable cardiac pacemaker. IEEE Trans. Ind. Electron. 2019, 66, 4108–4117. [Google Scholar] [CrossRef]
- Jow, U.M.; Ghovanloo, M. Design and optimization of printed spiral coils for efficient transcutaneous inductive power transmission. IEEE Trans. Biomed. Circuits Syst. 2007, 1, 193–202. [Google Scholar] [CrossRef]
- Corti, F.; Grasso, F.; Paolucci, L.; Pugi, L.; Luchetti, L. Circular Coil for EV Wireless Charging Design and Optimization Considering Ferrite Saturation. In Proceedings of the 2019 IEEE 5th International forum on Research and Technology for Society and Industry (RTSI), Florence, Italy, 9–12 September 2019; pp. 279–284. [Google Scholar]
- Chen, B.; Li, X.; Li, B.; Li, Y.; Guo, W. Wireless energy transfer system based on 3D wearable litz double coils. Microsyst. Technol. 2017, 23, 959–966. [Google Scholar] [CrossRef]
- Lee, W.S.; Son, W.I.; Oh, K.S.; Yu, J.W. Contactless energy transfer systems using antiparallel resonant loops. IEEE Trans. Ind. Electron. 2013, 60, 350–359. [Google Scholar] [CrossRef]
- Sun, T.; Xie, X.; Li, G.; Gu, Y.; Deng, Y.; Wang, Z. A two-hop wireless power transfer system with an efficiency-enhanced power receiver for motion-free capsule endoscopy inspection. IEEE Trans. Biomed. Eng. 2012, 59, 3247–3254. [Google Scholar]
- Na, K.; Jang, H.; Ma, H.; Bien, F. Tracking optimal efficiency of magnetic resonance wireless power transfer system for biomedical capsule endoscopy. IEEE Trans. Microw. Theory Tech. 2014, 63, 295–304. [Google Scholar] [CrossRef]
- Basar, M.R.; Ahmad, M.Y.; Cho, J.; Ibrahim, F. Stable and high-efficiency wireless power transfer system for robotic capsule using a modified Helmholtz coil. IEEE Trans. Ind. Electron. 2016, 64, 1113–1122. [Google Scholar] [CrossRef]




| Coil Type | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| Quadrilateral | 1.27 | 2.07 | 0.18 | 0.13 |
| Hexagon | 1.09 | 2.23 | 0 | 0.17 |
| Octagon | 1.07 | 2.29 | 0 | 0.19 |
| Circle | 1 | 2.46 | 0 | 0.2 |
| Coil Structure Parameters | Value | Units |
|---|---|---|
| Coil radius | 10 | mm |
| Wire width | 0.5 | mm |
| Wire thickness | 0.5 | mm |
| Coil turns | 6 | turns |
| Wire pitch | 0.6 | mm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, D.; Zhang, Q.; Li, X. Implantable Magnetic Resonance Wireless Power Transfer System Based on 3D Flexible Coils. Sustainability 2020, 12, 4149. https://doi.org/10.3390/su12104149
Xu D, Zhang Q, Li X. Implantable Magnetic Resonance Wireless Power Transfer System Based on 3D Flexible Coils. Sustainability. 2020; 12(10):4149. https://doi.org/10.3390/su12104149
Chicago/Turabian StyleXu, Dongdong, Qian Zhang, and Xiuhan Li. 2020. "Implantable Magnetic Resonance Wireless Power Transfer System Based on 3D Flexible Coils" Sustainability 12, no. 10: 4149. https://doi.org/10.3390/su12104149
APA StyleXu, D., Zhang, Q., & Li, X. (2020). Implantable Magnetic Resonance Wireless Power Transfer System Based on 3D Flexible Coils. Sustainability, 12(10), 4149. https://doi.org/10.3390/su12104149





