Unit Commitment for Power Generation Systems Based on Prices in Smart Grid Environment Considering Uncertainty

Abstract

With the growing demand for electricity, the inability of governments to provide the necessary resources to invest in the electricity industry and the rising price of fossil fuels, the tendency is to study and pay attention to economic issues in power systems studies. In this paper a new modified version of gray wolf optimization (MGWO) is proposed to solve the unit commitment (UC) problem in a power system in case of uncertainty. Market price variation is the main source of uncertainty in the UC program. Therefore, a model based on normal probability density function (PDF) is present for reducing the market price uncertainty effect in the model. Simulations are done for a standard 10 thermal units power system, and the results of the optimization by the proposed MGWO are compared with the previous version of the GWO algorithm and particle swarm optimization (PSO) algorithm results. The simulation results confirm the superiority of the proposed MGWO algorithm over the two algorithms PSO and GWO.

1. Introduction

These days, factors involving rise in energy consumption, common use of fossil fuels as input sources and the related environmental issues make fossil energy sources a more challenging subject [1]. The use of distributed generation sources in the power system has valuable benefits and costs for the system. Additionally, introducing the distributed generation resources to the market poses a serious challenge for owners of these resources [2]. The first reason to be mentioned is the uncertainty of the projected electricity output of distributed generation sources [3]. Reducing the power system operation costs is one of the most important issue in power system studies. Due to the development of interconnected power systems and their enlargement, the unit commitment (UC) program has undergone extensive changes [4]. The UC program is not as easily solved as in the past. On the other hand, with the increase in the number of renewable power generation units in recent decades, which have helped to solve the problem of electricity shortage, the UC problem has become more complex [5]. Therefore, the UC program should be done more accurately and with more criteria in mind. Several methods are used for solving the UC program.

The traditional methods used for solving UC program include linear programming (LP) [6], nonlinear programming (NLP) [7] and dynamic programming methods [8]. In Reference [9], a UC in the power system provides a combination of on/off power generation units and continuous power sharing. The problem is solved in both cases by linear programming and mixed integer linear programming (MILP). The optimization model based on economic MILP was proposed in [10] to plan the power generation of units. Additionally, a demand response program has been used to solve the variable problem with the time required load, to improve the load factor and to improve peak shaving. The program has been implemented by considering GAMS software and considering investment, replacement, operation and maintenance costs. The weakness of traditional methods is trapping in local optimal points and sometimes their lack of convergence.

In recent years, since the introduction of new innovative algorithms, they have been used extensively to solve UC problem in the power system. In Reference [11], the whale algorithm, along with using a series of possible indicators and success indicators of the participation program in the performance function, are used to reduce the power system operation cost. In Reference [12], a UC based on fuzzy logic is proposed to smooth the load profile of the network in the presence of distributed generation sources. In this model, the fluctuations of the load profile and peak load are reduced. The proposed method has shown better results compared to traditional UC methods. In Reference [13], a multi-objective method is proposed for solving UC problem to minimize operating costs and emission. In Reference [14], a decentralized method based on a multi-operating system is proposed to plan the participation of units and distributed generation resources in the power system. All consumers, distributed generation units and main network are considered as agents. In Reference [15], a (UC) in the power system is proposed by considering the load response program and storage maker with renewable resources in order to reduce the peak and reduce costs. Customers are encouraged to participate in planning using the demand response program.

The rest of this paper is organized as follows. In Section 2, the problem formulation is given. In this part, the objective function and unit commitment constraints are presented. The proposed GWO algorithm is briefly introduced in Section 3. In Section 4, the under-study power system is presented then the simulation results are analyzed. Finally, this article concludes in Section 5.

2. Problem Formulation

The unit commitment issue is usually described using a goal function and a series of constraints in the power system. The objective function is the issue of operating costs and pollution, which must be minimized using optimization methods.

2.1. Objective Function, Maximizing Profits

The UC program is also used to reduce operation costs or increase profitability. In this paper, increasing the profitability is selected as the objective function. Profitability will be maximized when the revenue increases and costs decrease. The objective function is calculated by Equation (1).

$$Profit={\displaystyle {\sum }_t\left(Revenue(t)-Cost(t)\right)}$$

(1)

$$Revenue(t)={\displaystyle {\sum }_t{P}_{Dem}(t)\lambda (t)}$$

(2)

$$Cost(t)={\displaystyle {\sum }_i\left(F{C}_i\times P_i(t)\right){\alpha }_i(t)}+SU{C}_i\times {\beta }_i(t)$$

(3)

where P_Dem(t) is electrical demand and λ(t) is the electrical energy price per kilowatt at time t. FC_i is the fuel cost, P_i(t) is the electrical power generation at time t and SUC is the stochastic unit commitment power; additionally, α_i(t) and β_i(t) are cost coefficients. In Equation (1), which shows the amount of profit, the first expression is representing the income from production capacity of units, and the second expression is representing the costs. In Equation (2), the amount of revenue is equal to the amount of power generated by the units in the market price. In Equation (3), the first phrase indicates the cost of generated power by the units and the second phrase indicates the cost of turning on the unit [16].

$$F{C}_i\left(P_i(t)\right)=a_i{P}_i{\left(t\right)}^2+b_i{P}_i\left(t\right)+c_i$$

(4)

where, a_i, b_i and c_i are fuel cost coefficients.

2.2. Constraints of Thermal Units

A heating unit can only withstand gradual changes in temperature, which means that a period of several hours is required for the unit to be placed in the orbit. In addition, these units can only produce power within a certain range. Therefore, there are several limitations in the operation of heating units, which are described below.

2.3. Power Balance

Production units must be able to meet the expected demand load. As the unit commitment planning is done for the future operations, load forecasting is based on calculations and the production capacity of the units must provide the predicted load [17].

$${\displaystyle \sum _i{P}_i(t)\ge P_{Dem}(t)}$$

(5)

2.4. Lower and Upper Band for Power in Units

According to the technical specifications of generators, their output power is between the maximum and minimum limits. This constraint is one of the characteristics of every generator and arises from the structure of the generator and is expressed using the following equation [17]:

$$P_i^{\min }\le P_i(t)\le P_i^{\max }$$

(6)

where $P_i^{\min }$ and $P_i^{\max }$ are the lower and upper band for unit generation capacity, respectively.

2.5. Slope Limits for Each Unit

The rate of increase and decrease of production capacity of units is limited [17].

$$P_i(t+1)-P_i(t)\le RU{P}_i$$

(7)

$$P_i(t)-P_i(t+1)\le DR{N}_i$$

(8)

where RUP_i and DRN_i are the maximum incremental and decremental rates, respectively.

2.6. Minimum off and on Time for Each Unit

Since the heating unit can only withstand gradual changes in temperature, it should not be turned off immediately when a unit is operating. Additionally, when a thermal unit is out of circuit, it needs a minimum of time to be able to re-enter the circuit [18].

$${\displaystyle \sum _{i=1}^{MUP}{\alpha }_i(t+1)\ge MUP}\hspace{1em}\forall {\beta }_i(t)=1$$

(9)

$${\displaystyle \sum _{i=1}^{MDN}1-{\alpha }_i(t+1)\ge MDN\hspace{1em}\forall {\gamma }_i(t)=1}$$

(10)

where, MUP is the minimum up time and MDN is the minimum down time.

3. Modified Gray Wolf Algorithm

The gray wolf algorithm is a particle-based metaheuristic algorithm. Gray wolves live in groups with an average size of 5 or 12. The group leader is called the alpha and it is mainly responsible for deciding on hunting, sleeping and waking times. The next level in the gray wolf hierarchy is the beta wolf. The beta helps the alpha wolf in making decisions. The beta wolf commands the lower wolves. The lowest level for the gray wolf is the omega. The main phase of gray wolf hunting is divided into three parts: search, running and approaching the hunt. For creating a mathematical model of the hunting, the following equations are proposed [19]:

$$\overrightarrow{D}=\left|\overrightarrow{C}·{\overrightarrow{X}}_p(t)-\overrightarrow{X}(t)\right|$$

(11)

$$\overrightarrow{X}(t+1)={\overrightarrow{X}}_p(t)-\overrightarrow{A}·\overrightarrow{D}$$

(12)

where Xp shows the position of the gray wolf vector, t is the number of the iteration A and C are vectors coefficients, which are calculated as follows:

$$\overrightarrow{A}=2\overrightarrow{\alpha }·{\overrightarrow{r}}_1-\overrightarrow{\alpha }$$

(13)

$$\overrightarrow{C}=2·{\overrightarrow{r}}_2$$

(14)

where the α is a linear component reduction from 2 to 0 and r₁ and r₂ are two random numbers. Hunting is usually led by the alpha and the beta wolf also occasionally hunts. The following equations have been suggested in this regard [19]:

$$\begin{array}{l}{\overrightarrow{D}}_{\alpha }=\left|{\overrightarrow{C}}_1·{\overrightarrow{X}}_{\alpha }-\overrightarrow{X}\right|,{\overrightarrow{D}}_{\beta }=\left|{\overrightarrow{C}}_2·{\overrightarrow{X}}_{\beta }-\overrightarrow{X}\right|,\\ {\overrightarrow{D}}_{\delta }=\left|{\overrightarrow{C}}_3·{\overrightarrow{X}}_{\delta }-\overrightarrow{X}\right|\end{array}$$

(15)

$$\begin{array}{l}{\overrightarrow{X}}_1={\overrightarrow{X}}_{\alpha }-{\overrightarrow{A}}_1·({\overrightarrow{D}}_{\alpha }),{\overrightarrow{X}}_2={\overrightarrow{X}}_{\beta }-{\overrightarrow{A}}_2·({\overrightarrow{D}}_{\beta }),\\ {\overrightarrow{X}}_3={\overrightarrow{X}}_{\delta }-{\overrightarrow{A}}_3·({\overrightarrow{D}}_{\delta })\end{array}$$

(16)

$$\overline{X}(t+1)=\frac{{\overrightarrow{X}}_1+{\overrightarrow{X}}_2+{\overrightarrow{X}}_3}{3}$$

(17)

When the random value of A is between [−1,1], the next position of the search agent will be in any position between the current position and the hunting position. Gray wolves move away in search of prey and close in on hunting prey. Another component of GWO that detects and identifies is C. The vector C contains random values [0, 2]. This component provides different weights for prey to randomly show the effect of prey on distance detection as significant (C > 1) or insignificant (C < 1). This helps GWO show more random behavior throughout the optimization and avoid local optimization. It should be noted that here, C decreases linearly with respect to A. During the iteration of alpha wolves and beta wolves, it estimates the probable position of the prey. Each selected solution updates its distance from the bait. Parameter a is reduced from 2 to 0 to emphasize identification and operation, respectively. Selected solutions tend to diverge from prey at |A| >1 and tend to converge at prey at |A| <1. Finally, the GWO algorithm ends with the satisfaction of a final criterion. Mutants are done for the omega wolves in a modified version of the GWO algorithm. The mutant for omega wolves is done by Equation (18).

$$\overrightarrow{X}(t+1)=\overrightarrow{X}(t)+M_f\times r\times (Ma{x}_{val}-Mi{n}_{val})$$

(18)

where, M_f is the mutant rate, r is random and Max_val and Min_val are the maximum and minimum limits, respectively. How to perform the optimization to solve the UC problem is given in Table 1.

Table 1. Solve the UC problem using MGWO.

Start  1: Selection of algorithm parameters such as the number of wolves, maximum iteration, etc.  2: t = 1.  3: While t < 24.  4: The wolf place initialization (each wolf place contains the unit’s production capacity).  5: Run the power flow.  6: Calculate the objective function for each wolf.  7: Choosing alpha, beta and omega wolves according to their objective function value.  8: Update the wolves’ position.  9: Perform mutations for the omega wolves.  10: Check the constraints (penalty should be considered if any constraint was not met).  11: Check if the number of iterations is more than the maximum iteration (if not, go to step 4, or else go to the next step). 12: t = t + 1. End

4. Case Study

In this paper, the short-term planning of the units’ commitment was conducted for of 24 h and 1 h intervals. The system of 10 machines with 10 thermal units was used for the studies. The amount of cargo and the predicted price are shown in Table 2. The specifications of the heating units are also given in Reference [20].

Table 2. Load specifications and market price.

Hour (h)	Cargo (MW)	Price ($)
1	700	22.15
2	750	22
3	850	23.1
4	950	22.65
5	1000	23.25
6	1100	22.95
7	1150	22.5
8	1200	22.15
9	1300	22.8
10	1400	29.35
11	1450	30.15
12	1500	31.65
13	1400	24.6
14	1300	24.5
15	1200	22.5
16	1050	23.3
17	1000	22.25
18	1100	22.05
19	1200	22.2
20	1400	22.65
21	1300	23.1
22	1100	22.95
23	900	22.75
24	800	22.55

Short-term planning of unit commitment is one of the most necessary plans for units’ commitment. In order to evaluate the efficiency of the proposed MGWO algorithm, the gray wolf optimization (GWO) and particle swarm optimization (PSO) algorithms were used for optimization. The parameters of the algorithms are given in Table 3.

Table 3. Optimization algorithms parameters.

PSO	Population	Maximum Iteration	C1 = C2	ω	Vmin	Vmax
	100	50	2.05	0.66	0.7	0.9
GWO	Population	Maximum Iteration	α	r
	100	50	2	0.47
MGWO	Population	Maximum Iteration	α	r	Mf
	100	50	2	0.47	0.07

In this type of planning, the constraints of the minimum on and off time, the minimum and maximum production of units, etc. should be considered. However, its generalization to medium- and long-term planning of units’ participation is shortcoming. This is because those conditions do not consider the forced departure of units, maintenance costs, etc. Data about market price and unit information are extracted from Reference [20].

4.1. Uncertainty

Uncertainty occurs when the output is random and uncontrollable for us. Furthermore, its mathematical concept is the difference between real and the predicted values. According to the previous studies, uncertainty is related to environmental, economic, political and other factors. Uncertainty in planning the units’ commitment is due to uncertainty in the market price.

4.2. Price Modeling

As mentioned before, random planning tries to model the random behavior of market prices.

In studies, price uncertainty is usually considered as a price prediction error [21]. To model price uncertainty, a normal distribution function of $N(\mu ,\sigma )$ is usually used, for which the mean value is $\mu$ and the standard deviation value is $\sigma$. The normal distribution function can be approximated using several discrete intervals, each interval being represented by its midpoint. For example, five intervals can be referred to as shown in the Figure 1. In this study, a standard deviation of 5 is considered for modeling price uncertainty. The price values and probabilities of each scenario are shown in the Table 4 and Table 5. The normal probability density function is shown as follows [21]:

$$f(x)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{1}{2{\sigma }^2}{(x-\mu )}^2}\hspace{1em}-\infty \le x\le \infty$$

(19)

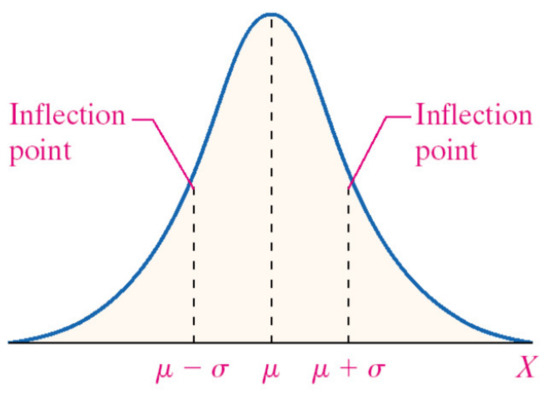
Figure 1. Normal probability density function base on [21].

Table 4. Price values in scenarios in dollars.

Scenario	1	2	3	4	5
Hours
1	17.296	19.723	22.15	24.577	27.004
2	17.146	19.573	22	24.427	26.854
3	18.246	20.673	23.1	25.527	27.954
4	17.796	20.223	22.65	25.077	27.504
5	18.396	20.823	23.25	25.677	28.104
6	18.096	20.523	22.95	25.377	27.804
7	17.646	20.073	22.5	24.927	27.354
8	17.296	19.723	22.15	24.577	27.004
9	17.946	20.373	22.8	25.227	27.654
10	24.496	26.923	29.35	31.777	34.204
11	25.296	27.723	30.15	32.577	35.004
12	26.796	29.223	31.65	34.077	36.504
13	19.746	22.173	24.6	27.027	29.454
14	19.646	22.073	24.5	26.927	29.354
15	17.646	20.073	22.5	24.927	27.354
16	18.446	20.873	23.3	25.727	28.154
17	17.396	19.823	22.25	24.677	27.104
18	17.196	19.623	22.05	24.477	26.904
19	17.346	19.773	22.2	24.627	27.054
20	17.796	20.223	22.65	25.077	27.504
21	18.246	20.673	23.1	25.527	27.954
22	18.096	20.523	22.95	25.377	27.804
23	17.896	20.323	22.75	25.177	27.604
24	17.696	20.123	22.55	24.977	27.404

Table 5. Probability values of each scenario.

Scenario	1	2	3	4	5
Hours
1	0.033	0.23	0.45	0.23	0.033
2	0.033	0.23	0.45	0.23	0.033
3	0.033	0.23	0.45	0.23	0.033
4	0.033	0.23	0.45	0.23	0.033
5	0.033	0.23	0.45	0.23	0.033
6	0.033	0.23	0.45	0.23	0.033
7	0.033	0.23	0.45	0.23	0.033
8	0.033	0.23	0.45	0.23	0.033
9	0.033	0.23	0.45	0.23	0.033
10	0.033	0.23	0.45	0.23	0.033
11	0.033	0.23	0.45	0.23	0.033
12	0.033	0.23	0.45	0.23	0.033
13	0.033	0.23	0.45	0.23	0.033
14	0.033	0.23	0.45	0.23	0.033
15	0.033	0.23	0.45	0.23	0.033
16	0.033	0.23	0.45	0.23	0.033
17	0.033	0.23	0.45	0.23	0.033
18	0.033	0.23	0.45	0.23	0.033
19	0.033	0.23	0.45	0.23	0.033
20	0.033	0.23	0.45	0.23	0.033
21	0.033	0.23	0.45	0.23	0.033
22	0.033	0.23	0.45	0.23	0.033
23	0.033	0.23	0.45	0.23	0.033
24	0.033	0.23	0.45	0.23	0.033

Solving the problem while considering the uncertainty is based on a set of scenarios, which are defined by sampling the possible distributions; the problem is then solved for each of these scenarios. The final answer to the problem will be the average weight obtained from these scenarios. The purpose of this paper is short-term random planning of units’ commitment in a 24 h planning horizon. The sample system studied in this paper includes 10 thermal units. The values and probability values of each scenario are shown in the Table 4 and Table 5.

Planning is evaluated in the form of two cases of without and with considering the uncertainty in the market price.

4.3. Planning without Considering the Uncertainty in the Market Price

In this case, unit commitment planning is done for a system of 10 units. Unit commitment planning is done for various purposes, including unit commitment planning with security constraints and unit commitment planning based on price. In this case, we plan the participation of units with the aim of minimizing.

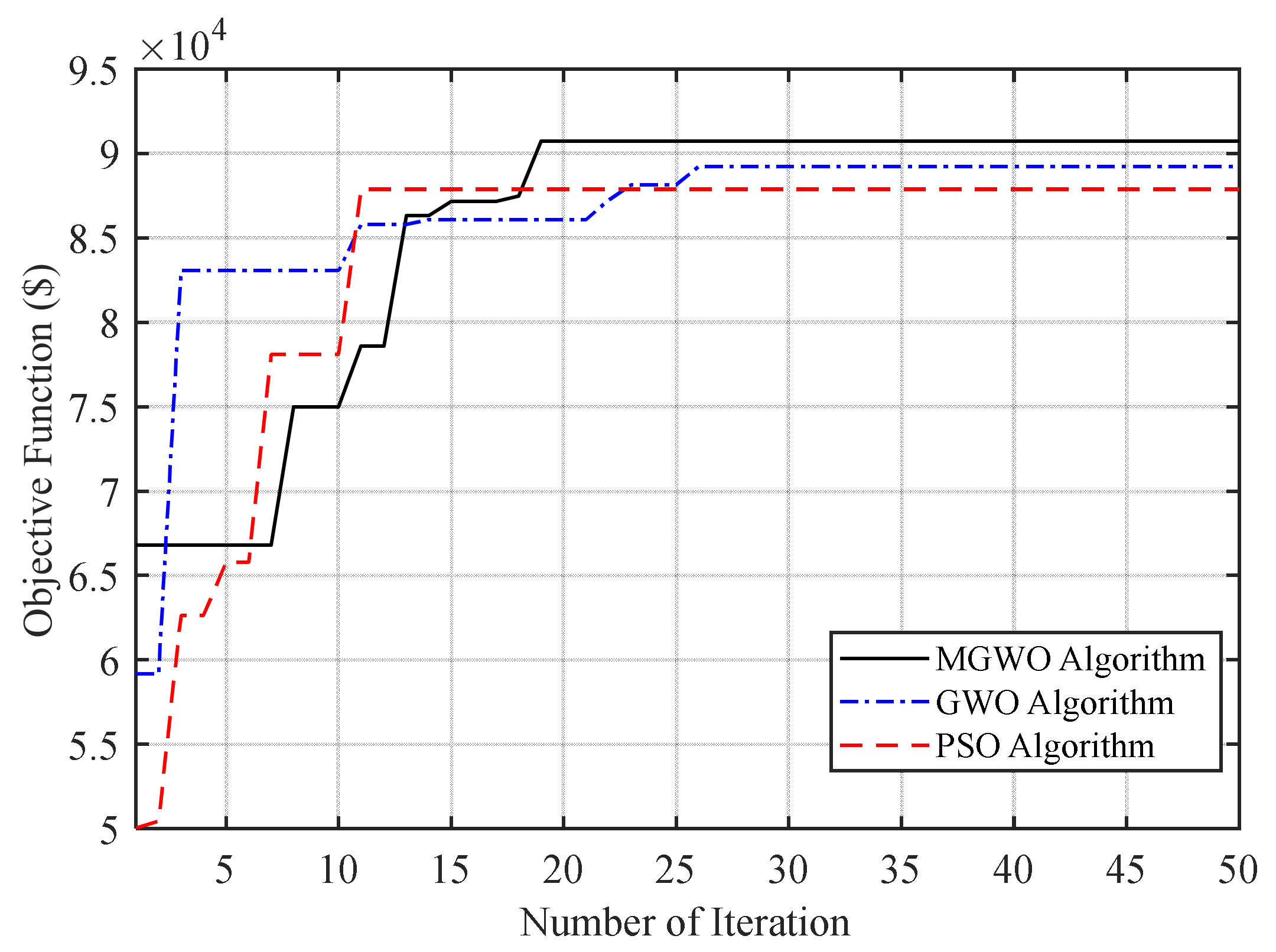
Table 6 shows the storage values in this case. As can be seen from Table 6, the units that produced less power played a greater role in providing system storage. The final value of the objective function in this case is about $90,718. The convergence curves of the algorithms are shown in Figure 2.

Table 6. Output power of units without uncertainty.

	1	2	3	4	5	6	7	8	9	10
h1	455	245	0	0	0	0	0	0	0	0
h2	455	295	0	0	0	0	0	0	0	0
h3	455	395	0	0	0	0	0	0	0	0
h4	455	455	0	0	0	0	0	40	0	0
h5	455	445	100	0	0	0	0	0	0	0
h6	455	455	130	0	60	0	0	0	0	0
h7	455	455	130	0	110	0	0	0	0	0
h8	455	455	130	0	160	0	0	0	0	0
h9	455	455	130	100	160	0	0	0	0	0
h10	455	455	130	130	162	68	0	0	0	0
h11	455	455	130	130	162	80	0	38	0	0
h12	455	455	130	130	162	80	0	50	38	0
h13	455	455	130	130	162	58	0	10	0	0
h14	455	455	100	130	160	0	0	0	0	0
h15	455	455	0	130	160	0	0	0	0	0
h16	455	425	0	130	40	0	0	0	0	0
h17	455	390	0	130	25	0	0	0	0	0
h18	455	455	0	130	60	0	0	0	0	0
h19	455	455	0	130	150	0	0	10	0	0
h20	455	455	0	130	162	70	0	50	40	38
h21	455	455	0	100	162	80	0	48	0	0
h22	455	455	0	0	120	60		10	0	0
h23	455	445	0	0	0	0	0	0	0	0
h24	455	345	0	0	0	0	0	0	0	0

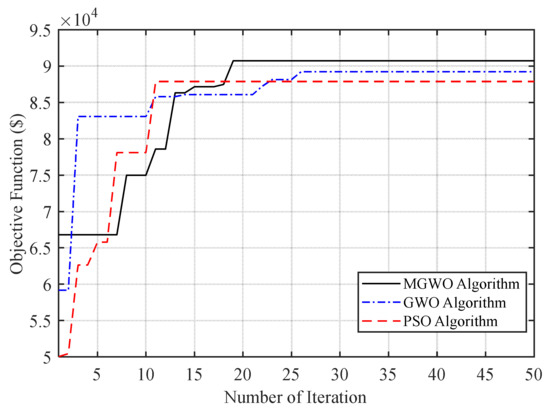
Figure 2. Convergence curves of the algorithms.

Also, Table 7 shows storage values in the case of uncertainty. The profitability of the UC program after optimization by the PSO algorithm is equal to $87,882, and in case of optimization by the GWO algorithm it is about $89,224. The profitability of the UC using the proposed MGWO is more than the two other algorithms.

Table 7. Storage values in the case of uncertainty.

	1	2	3	4	5	6	7	8	9	10
h1	0	210	0	0	0	0	0	0	0	0
h2	0	160	0	0	0	0	0	0	0	0
h3	0	60	0	0	0	0	0	0	0	0
h4	0	0	0	0	0	0	0	15	0	0
h5	0	10	30	0	0	0	0	0	0	0
h6	0	0	0	0	102	0	0	0	0	0
h7	0	0	0	0	52	0	0	0	0	0
h8	0	0	0	0	2	0	0	0	0	0
h9	0	0	0	30	2	0	0	0	0	0
h10	0	0	0	0	0	12	0	0	0	0
h11	0	0	0	0	0	0	0	17	0	0
h12	0	0	0	0	0	0	0	5	17	0
h13	0	0	0	0	0	22	0	45	0	0
h14	0	0	30	0	2	0	0	0	0	0
h15	0	0	0	0	2	0	0	0	0	0
h16	0	30	0	0	122	0	0	0	0	0
h17	0	65	0	0	137	0	0	0	0	0
h18	0	0	0	0	102	0	0	0	0	0
h19	0	0	0	0	12	0	0	45	0	0
h20	0	0	0	0	0	10		5	15	17
h21	0	0	0	30	0	0	0	7	0	0
h22	0	0	0	0	42	20	0	45	0	0
h23	0	10	0	0	0	0	0	0	0	0
h24	0	110	0	0	0	0	0	0	0	0

4.4. Planning by Considering the Parameter of Uncertainty in the Market Price

In this case, the unit commitment planning was implemented by considering the uncertainty on the market price, which is in the form of five scenarios. The outputs shown are related to scenario number 5.

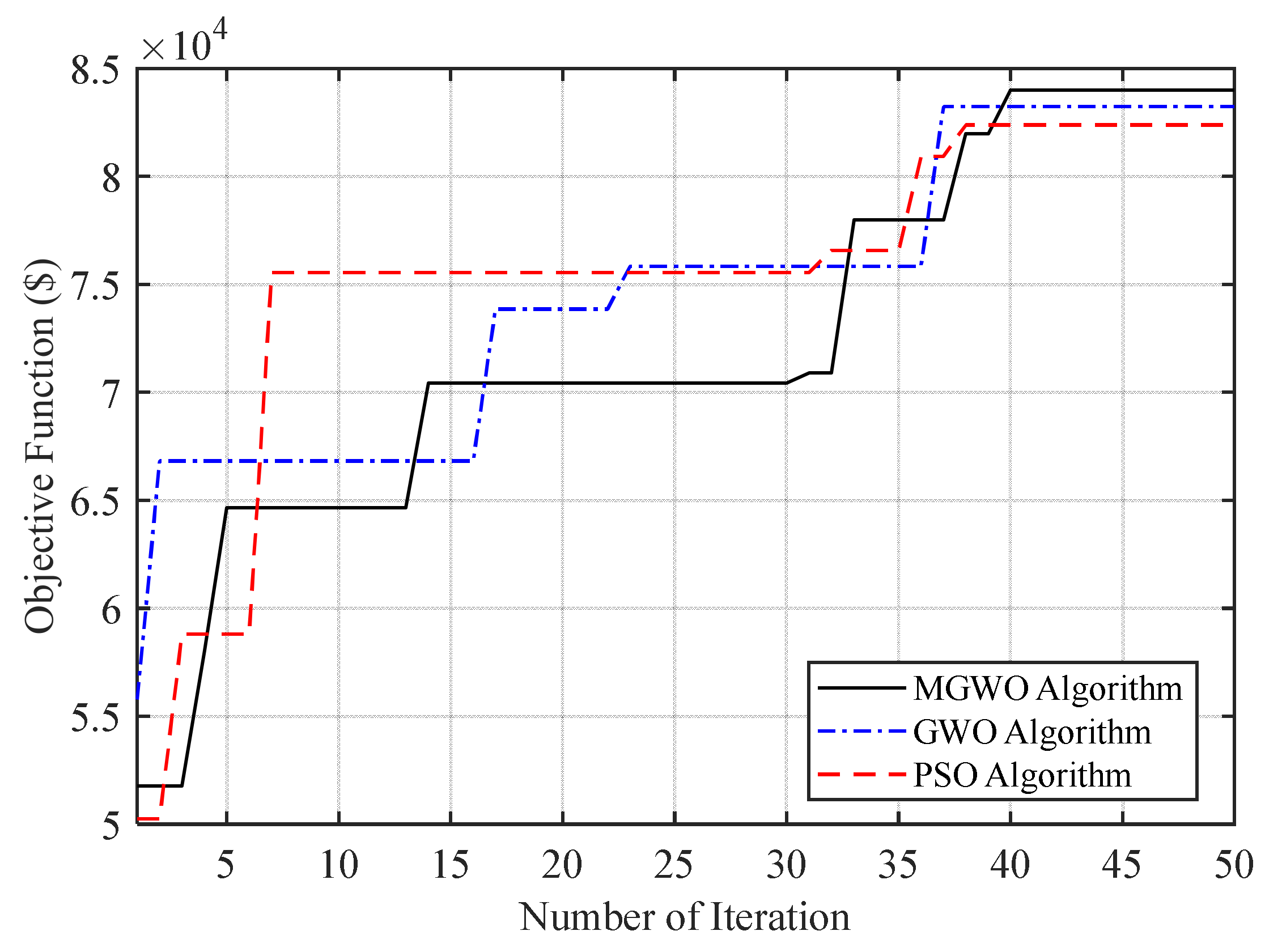
As can be seen from Table 8, units 1 and 2, which are among the cheapest units, produced their maximum power at almost all hours. The final profitability in the case of uncertainty was $84,364. Similar to the previous section, the PSO algorithm and GWO algorithm are used for optimization. The convergence curves of the optimization algorithms are shown in Figure 3.

Table 8. Output power of units, considering the uncertainty.

	1	2	3	4	5	6	7	8	9	10
h1	0	210	0	0	0	0	0	0	0	0
h2	0	160	0	0	0	0	0	0	0	0
h3	0	60	0	0	0	0	0	0	0	0
h4	0	0	0	0	0	0	0	0	0	15
h5	0	10	30	0	0	0	0	0	0	0
h6	0	0	0	0	102	0	0	0	0	0
h7	0	0	0	0	52	0	0	0	0	0
h8	0	0	0	0	2	0	0	0	0	0
h9	0	0	0	30	2	0	0	0	0	0
h10	0	0	0	0	0	12	0	0	0	0
h11	0	0	0	0	0	0	0	17	0	0
h12	0	0	0	0	0	0	0	5	17	0
h13	0	0	0	0	0	22	0	45	0	0
h14	0	0	30	0	2	0	0	0	0	0
h15	0	0	0	0	2	0	0	0	0	0
h16	0	30	0	0	122	0	0	0	0	0
h17	0	65	0	0	137	0	0	0	0	0
h18	0	0	0	0	102	0	0	0	0	0
h19	0	0	0	0	12	0	0	45	0	0
h20	0	0	0	0	0	10	0	5	15	17
h21	0	0	0	30	0	0	0	7	0	0
h22	0	0	0	0	42	20	0	45	0	0
h23	0	10	0	0	0	0	0	0	0	0
h24	0	110	0	0	0	0	0	0	0	0

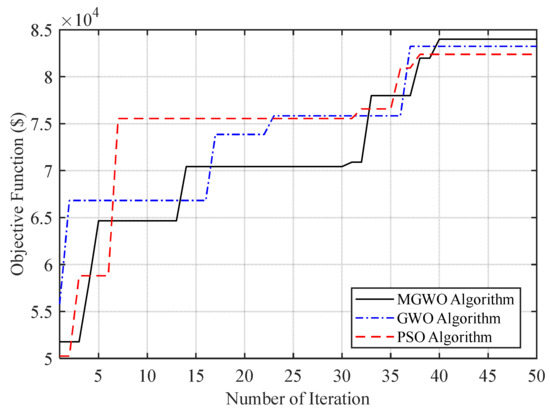
Figure 3. Convergence curves of the algorithms.

The UC program profitability in case of doing optimization by the PSO algorithm is $82,383 and after optimization by the GWO algorithm is about $83,237. The proposed MGWO profitability is more than the PSO and GWO algorithms.

5. Conclusions

The main purpose of this paper is to present an effective model for optimizing the scheduling of unit commitment in the smart grid environment by considering the uncertainty for random parameters. The main innovation of this article is to implement the issue of unit commitment randomly, taking into account the uncertainty on the market price. Additionally, a modified version of the gray wolf optimization algorithm is proposed for solving unit commitment program. To solve the unit commitment planning issue while considering the uncertainties, a set of scenarios was generated by sampling this probability distribution function and the problem was solved for each of these scenarios; finally, the final answer is a weighted average of the results of these scenarios. Comparison of the optimization results with the proposed MGWO algorithm and its comparison with the results of the gray wolf optimization and particle swarm optimization algorithms confirms the performance of the proposed method.