Interaction Boundary Determination of Renewable Energy Sources to Estimate System Strength Using the Power Flow Tracing Strategy
Abstract
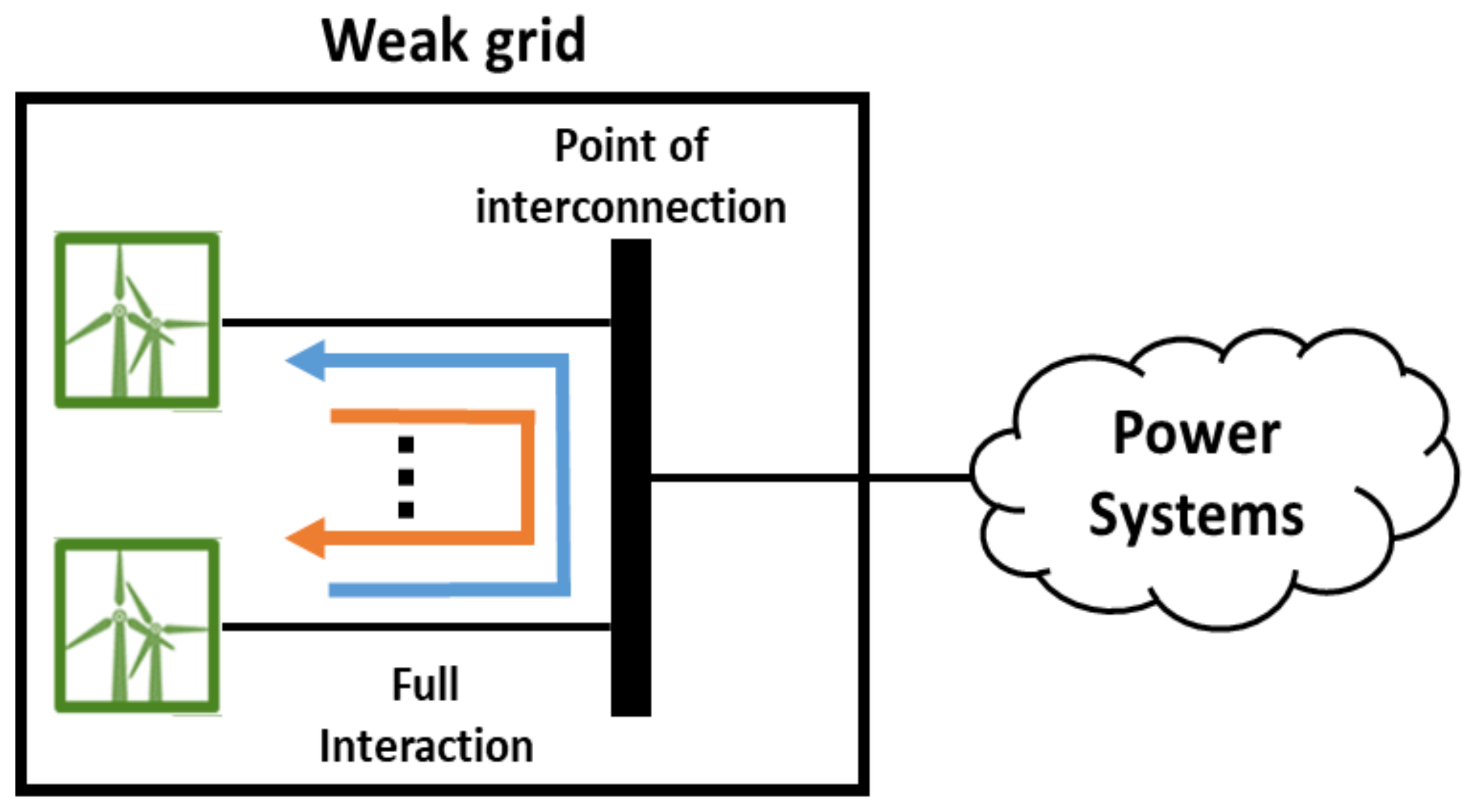
:1. Introduction
2. Materials and Methods
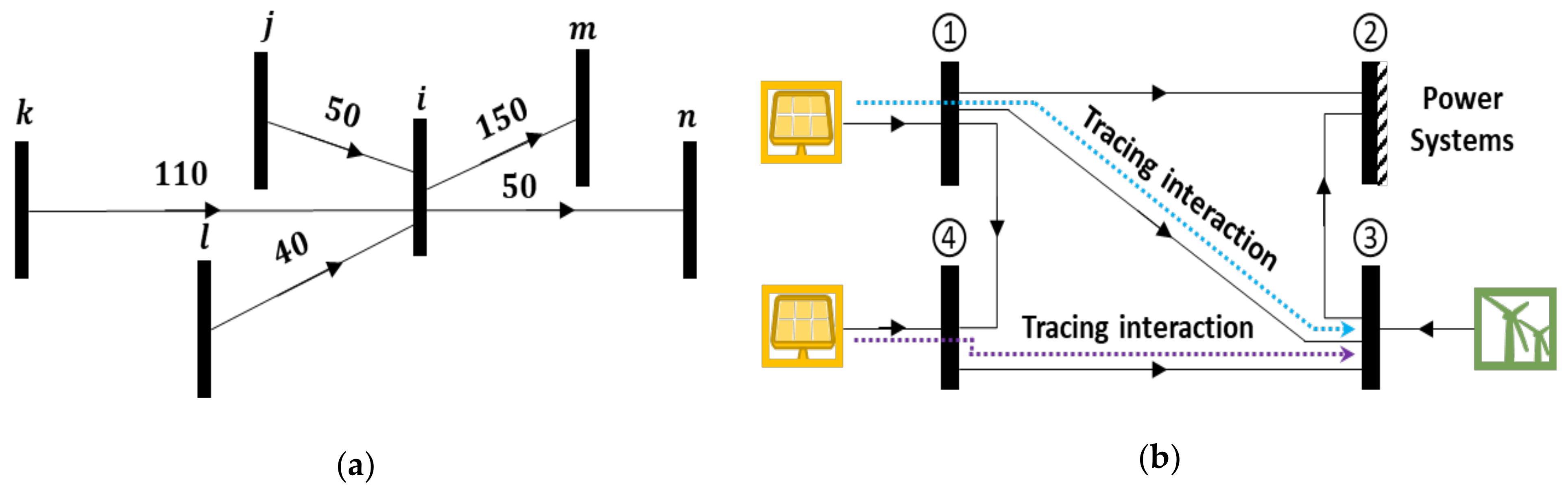
2.1. Power-Flow Tracing of Renewable Energy Sources
2.2. Identifying the Acutal Interaction Boundaries of Renewable Energy Sources
| Algorithm 1: Filtering the independent and radial buses |
| Input: Power flow tracing matrix () |
| Output: Reduced power flow tracing matrix (), , |
| 1: |
| 2: for each in do |
| 3: if =0 then |
| 4: |
| 5: Eliminate row and column of |
| 6: end if |
| 7: if =0 then |
| 8: Find in such that and is the largest for all in |
| 9: |
| 10: for each in do |
| 11: |
| 12: end for |
| 13: |
| 14: Eliminate row and column of |
| 15: end if |
| 16: end for |
| Algorithm 2: Determinng the interaction boundary of RESs |
| Input: , |
| Output: |
| Set 0, , |
| 1: Reorder and with s* is the first row and column of and first element in . |
| 2: Bus of interest , |
| 3: for each in do |
| 4: Initialize and |
| 5: if then |
| 6: For each in do |
| 7: + |
| 8: end for |
| 9: For each in do |
| 10: if then |
| 11: + |
| 12: end for |
| 13: if then |
| 14: |
| 15: end if |
| 16: end if |
| 17: end for |
| 18: for in do |
| 19: Eliminate row and column of |
| 20: end for |
| 21: , |
| 22: |
| 23: if then |
| 24: |
| 25: Send to line 1 |
| 26: end if |
2.3. Implementation in PSS/E
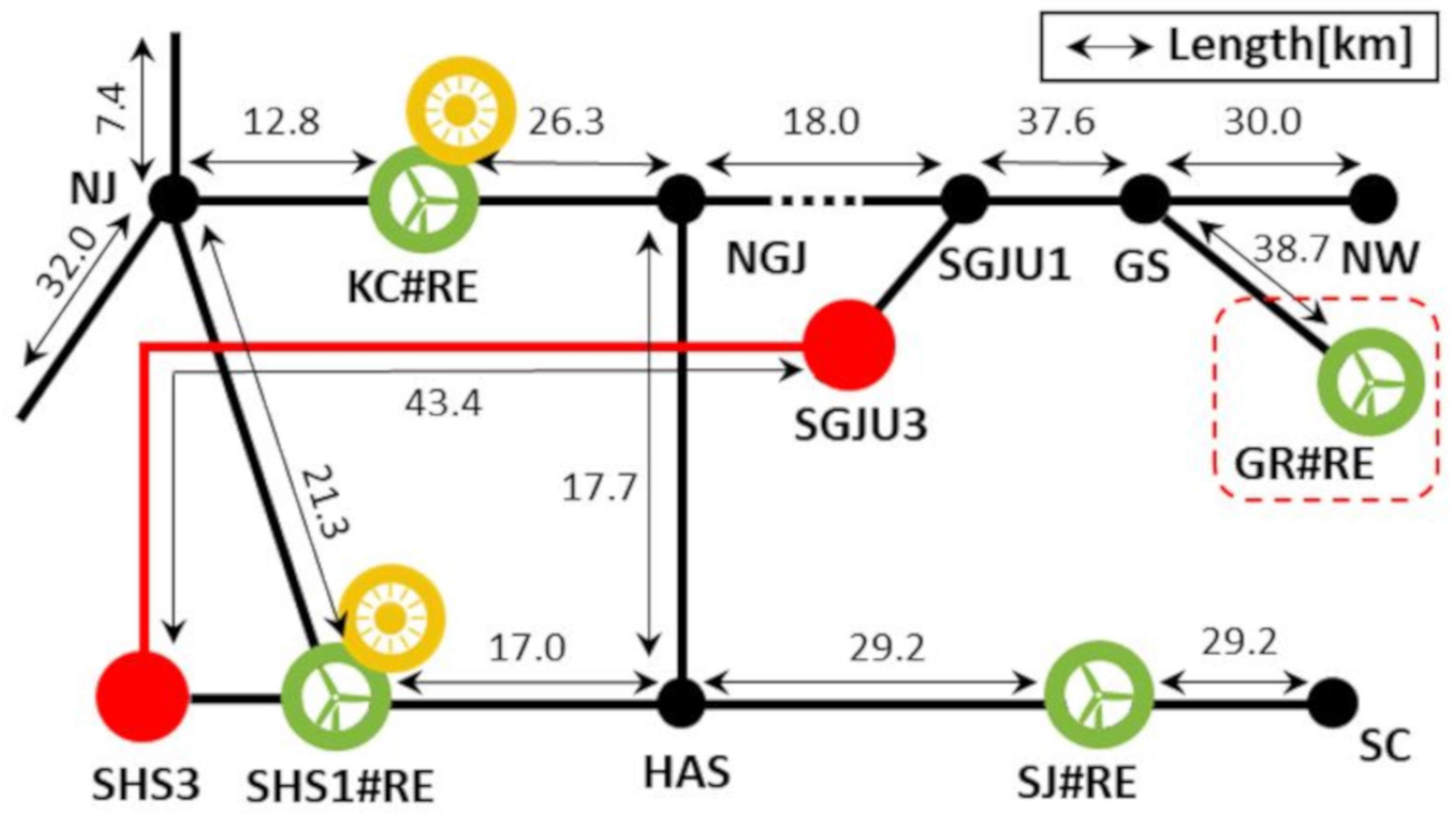
2.4. Description of Case Study in Korean Electric Power Corporation System
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Sets | |
| Buses with RESs, indexed by . | |
| Buses with RESs after filtering independent buses and radial buses, indexed by . | |
| Buses not interacting with other RESs, indexed by . | |
| Buses inside the interaction boundaries of RESs for each , indexed by b. | |
| Buses outside the interaction boundaries of RESs, indexed by u. | |
| Variables | |
| Active power flow from bus to bus . | |
| Bus of interest to determine interaction boundaries. |
Appendix A
| Bus | AJ | SA | JD | SH | HN | NC | BH | WD | YA | BK | UD | SHS1 | GH | KC | SJ | YK | GR | HON | GC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
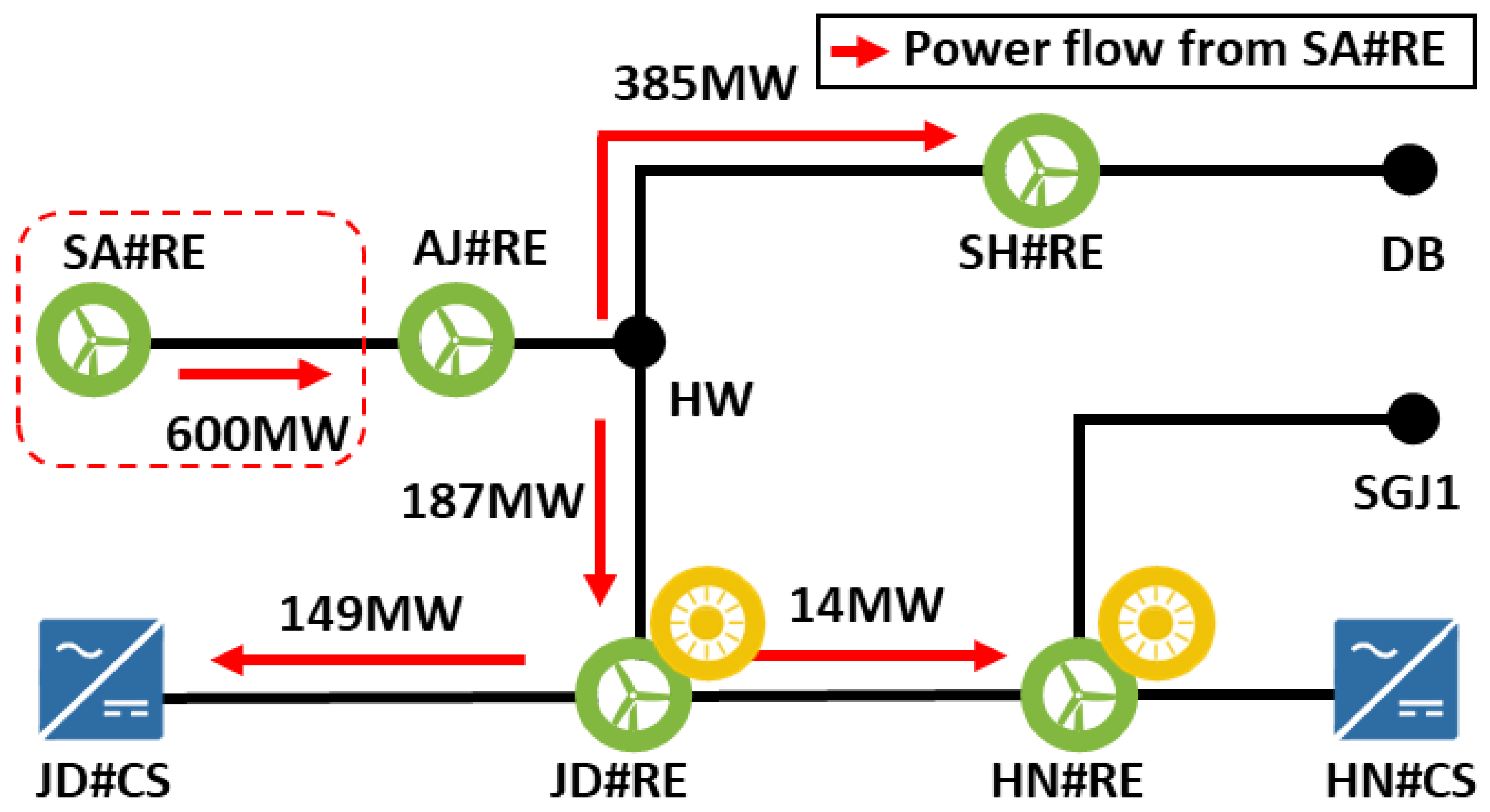
| AJ | 268 | 0 | 84 | 172 | 6 | 0 | 45 | 0 | 0 | 2 | 17 | 59 | 0 | 5 | 4 | 0 | 0 | 0 | 0 |
| SA | 600 | 600 | 188 | 385 | 14 | 0 | 101 | 0 | 0 | 4 | 37 | 133 | 0 | 10 | 9 | 0 | 0 | 0 | 0 |
| JD | 0 | 0 | 38 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SH | 0 | 0 | 0 | 60 | 0 | 0 | 16 | 0 | 0 | 0 | 6 | 20 | 0 | 2 | 1 | 0 | 0 | 0 | 0 |
| HN | 0 | 0 | 0 | 0 | 170 | 0 | 0 | 0 | 0 | 3 | 0 | 97 | 0 | 0 | 7 | 0 | 0 | 0 | 0 |
| NC | 0 | 0 | 0 | 0 | 1 | 40 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| BH | 0 | 0 | 0 | 0 | 0 | 0 | 50 | 0 | 0 | 0 | 18 | 1 | 0 | 5 | 0 | 0 | 0 | 0 | 0 |
| WD | 0 | 0 | 0 | 0 | 9 | 319 | 0 | 375 | 4 | 33 | 0 | 5 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| YA | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 321 | 0 | 0 | 27 | 0 | 108 | 2 | 0 | 0 | 0 | 0 |
| BK | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| UD | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 197 | 13 | 0 | 52 | 0 | 0 | 0 | 0 | 0 |
| SHS1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 40 | 0 | 0 | 3 | 0 | 0 | 0 | 0 |
| GH | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 55 | 0 | 0 | 0 | 0 | 0 | 0 |
| KC | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20 | 0 | 0 | 0 | 0 | 0 |
| SJ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 30 | 0 | 0 | 0 | 0 |
| YK | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 23 | 0 | 0 | 0 |
| GR | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20 | 0 | 0 |
| HON | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 16 | 0 | 138 | 44 |
| GC | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 44 |
References
- Zhou, F.; Joos, G.; Abbey, C. Voltage stability in weak connection wind plants. In Proceedings of the 2005 IEEE PES General Meeting, San Francisco, CA, USA, 12–16 June 2005. [Google Scholar]
- Piwko, R.; Miller, N.; Sanchez-Gasca, J.; Yuan, X.; Dai, R.; Lyons, J. Integrating Large Wind plants into Weak Power Grids with Long Transmission Lines. In Proceedings of the 2006 Power Electronics and Motion Control Conference, Shanghai, China, 14–16 August 2006. [Google Scholar]
- Palsson, M.P.; Toftevaag, T.; Uhlen, K.; Tande, J.O.G. Large-scale wind power integration and voltage stability limits in regional networks. In Proceedings of the 2005 IEEE PES General Meeting, Chicago, IL, USA, 21–25 July 2002; Volume 2, pp. 762–769. [Google Scholar]
- NERC. Integrating Inverter-Based Resources into Low Short Circuit Strength Systems; North American Electric Reliability Corporation (NERC): Atlanta, GA, USA, 2017. [Google Scholar]
- Nalin, P.; Sebastian, A. Connection of Wind Farms to Weak AC Networks; CIGRE: Paris, France, 2016; ISBN 978-2-85873-374-3. [Google Scholar]
- NERC. BPS-Connected Inverter-Based Resource Performance; North American Electric Reliability Corporation(NERC): Atlanta, GA, USA, 2018. [Google Scholar]
- IEEE. Guide for Planning dc Links Terminating at ac Locations Having Low Short-Circuit Capacities; IEEE: New York, NY, USA, 1997. [Google Scholar]
- Fischer, M.; Schellschmidt, M. Fault ride through performance of wind energy converters with FACTS capabilities in response to up-to-date German grid connection requirements. In Proceedings of the 2011 IEEE/PES Power Systems Conference and Exposition, Phoenix, AZ, USA, 20–23 March 2011; pp. 1–6. [Google Scholar]
- Diedrichs, V.; Beekmann AAdloff, S. Loss of (angle) stability of wind power plants- the underestimated phenomenon in case of very low short circuit ratio. In Proceedings of the 10th Int. Workshop on Large-Scale IntegrAtion of Wind Power into Power Systems as well as on Transmission Networks for Offshore Wind Power Plants, Aarhus, Denmark, 25–26 October 2011; pp. 25–26. [Google Scholar]
- Hong, M.; Xin, H.; Liu, W.; Xu, Q.; Zheng, T.; Gan, D. Critical Short Circuit Ratio Analysis on DFIG Wind Farm with Vector Power Control and Synchronized Control. J. Electr. Eng. Technol. 2016, 11, 320–328. [Google Scholar] [CrossRef]
- Zhang, L.; Harnefors, L.; Nee, H.-P. Interconnection of Two Very Weak AC Systems by VSC-HVDC Links Using Power-Synchronization Control. IEEE Trans. Power Syst. 2010, 26, 344–355. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, X.; Hu, J.; Zhou, P. Modeling of VSC Connected to Weak Grid for Stability Analysis of DC-Link Voltage Control. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 1. [Google Scholar] [CrossRef]
- Saad, H.; Dennetière, S.; Clerc, B. Interactions investigations between power electronics devices embedded in HVAC network. In Proceedings of the 13th IET International Conference on AC and DC Power Transmission (ACDC 2017), Manchester, UK, 14–16 February 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Wu, D.W.; Li, G.; Javadi, M.; Malyscheff, A.M.; Hong, M.; Jiang, J.N. Evaluating impact of renewable energy integration on system strength using site-dependent short circuit ratio. IEEE Trans. Sustain. Energy 2018, 9, 1072–1080. [Google Scholar] [CrossRef]
- Wu, D.; Aldaoudeyeh, A.M.; Javadi, M.; Ma, F.; Tan, J.; Jiang, J.N. A method to identify weak points of interconnection of renewable energy resources. Int. J. Electr. Power Energy Syst. 2019, 110, 72–82. [Google Scholar] [CrossRef]
- Huang, S.H.; Schmall, J.; Conto, J.; Adams, J.; Zhang, Y.; Carter, C. Voltage Control Challenges on Weak Grids with hing Penetration of wind Generation: ERCOT Experience. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–7. [Google Scholar]
- Zhang, Y.; Huang, S.-H.F.; Schmall, J.; Conto, J.; Billo, J.; Rehman, E. Evaluating system strength for largescale wind plant integration. In Proceedings of the 2014 IEEE PES General Meeting Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
- Huang, F. Experience with WTG weak system interactions on the ERCOT system. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 16–30 July 2015. [Google Scholar]
- Electric Reliability Council of Texas. Panhandle Renewable Energy Zone (PREZ) Study Report; ERCOT: Taylor, TX, USA, 2014. [Google Scholar]
- Dissanayaka, A.; Wiebe, J.; Isaacs, A. Panhandle and South Texas Stability and System Strength Assessment; Technical Report; Electranix: Winnipeg, MB, Canada, 2018. [Google Scholar]
- Australian Energy Market Operator. Fact Sheet System Strength Final; Technical Report; AEMO: Melbourne, Australia, 2016; p. 1. [Google Scholar]
- Australian Energy Market Operator. System Strength Impact Assessment Guidelines; Technical Report; AEMO: Melbourne, Australia, 2018. [Google Scholar]
- Bialek, J. Tracing the flow of electricity. In IEE Proceedings-Generation, Transmission and Distribution; IET Digital Library, 1996; Volume 143, pp. 313–320. [Google Scholar]

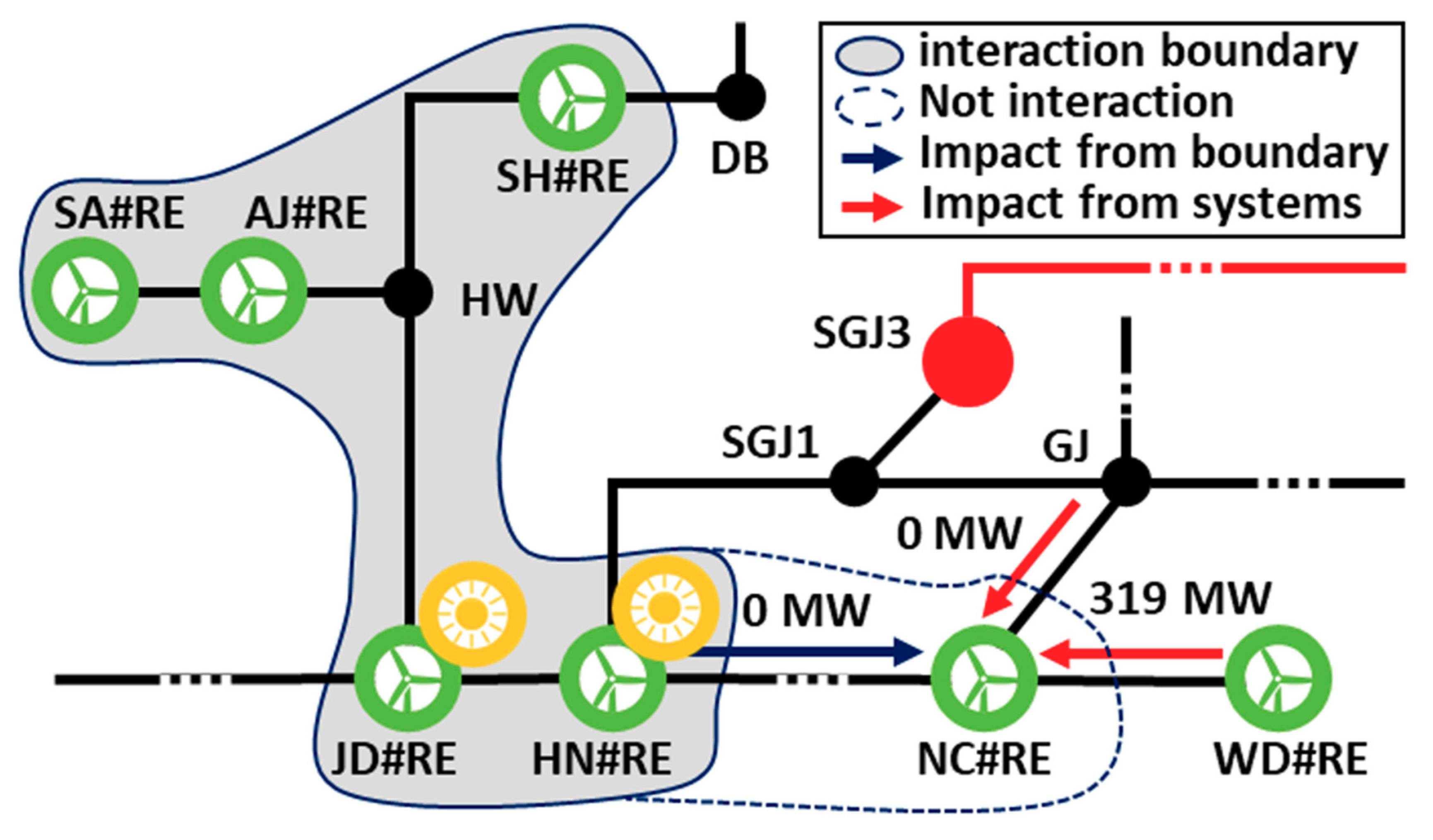
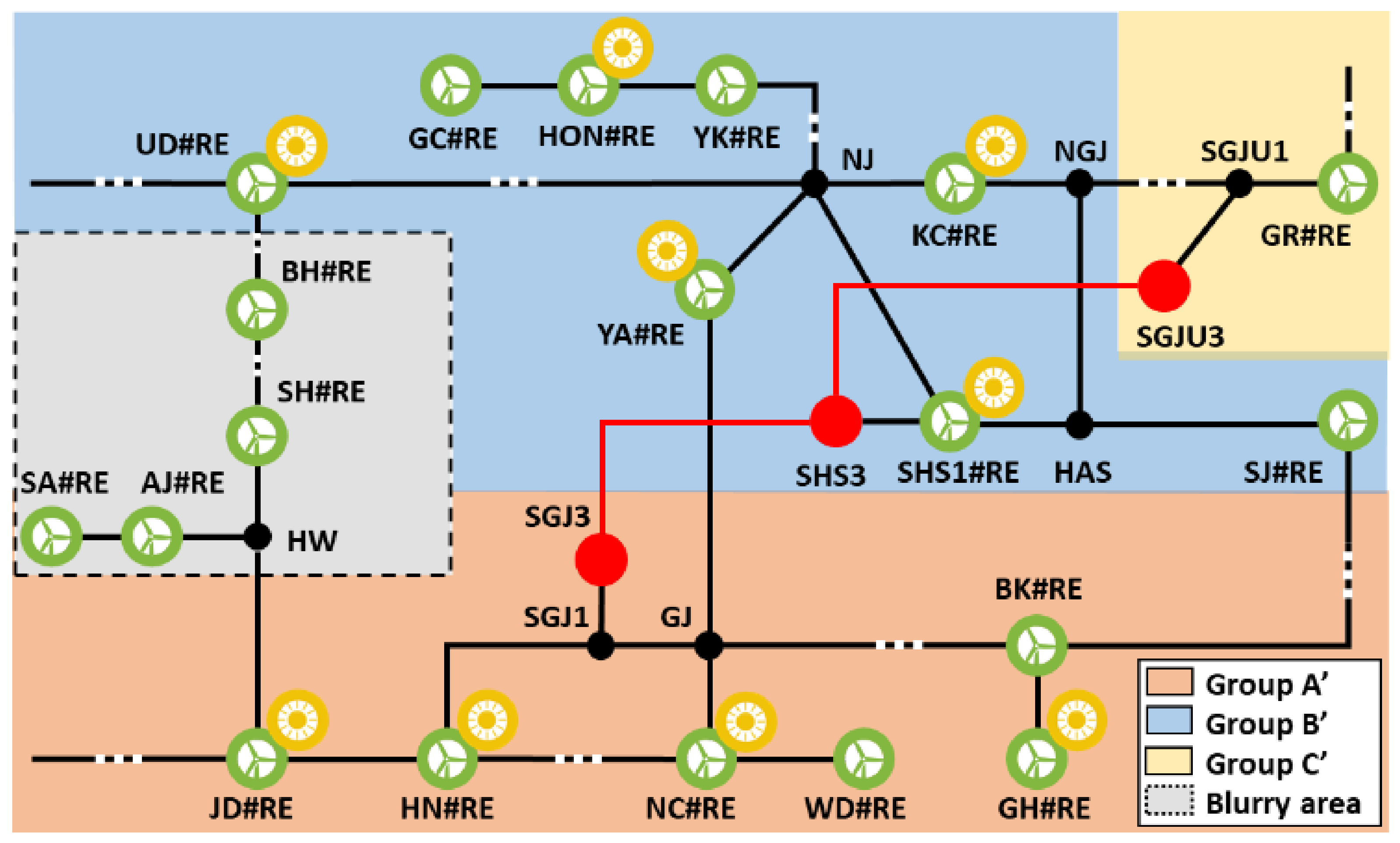

| Bus | Short-Circuit Capacity (MVA) | RES Generation (MW) |
|---|---|---|
| AJ#RE | 2103 | 268 |
| SA#RE | 2090 | 600 |
| JD#RE | 2911 | 38 |
| SH#RE | 3566 | 60 |
| HN#RE | 3758 | 170 |
| SJ#RE | 2921 | 30 |
| BH#RE | 2961 | 50 |
| UD#RE | 3044 | 197 |
| SHS1#RE | 7968 | 40 |
| KC#RE | 4499 | 20 |
| NC#RE | 2913 | 40 |
| WD#RE | 1978 | 375 |
| YA#RE | 3763 | 321 |
| BK#RE | 3707 | 30 |
| YK#RE | 2342 | 23 |
| HON#RE | 2182 | 138 |
| GC#RE | 477 | 200 |
| GH#RE | 1593 | 55 |
| GR#RE | 1613 | 20 |
| Bus of Interest | Independent Buses | First Boundary | Secondary Boundary | Third Boundary |
|---|---|---|---|---|
| AJ | GH, GR | AJ, SA, JD, SH, HN, BH, UD, SHS1, SJ | NC, WD, YA, BK, KC | YK, HON, GC |
| SA | GH, GR | SA, AJ, JD, SH, HN, BH, UD, SHS1, SJ | NC, WD, YA, BK, KC | YK, HON, GC |
| JD | GH, GR | JD, HN, AJ, SH, SA, BH, SHS1, UD, SJ | NC, WD, YA, BK, KC | YK, HON, GC |
| SH | GH, GR | SH, JD, AJ, HN, SA, BH, SHS1, UD, SJ | NC, YA, WD, BK, KC | YK, HON, GC |
| HN | GH, GR | HN, JD, SH, AJ, SA, BH, SHS1, UD, SJ | NC, YA, WD, BK, KC | YK, HON, GC |
| NC | GH, GR | NC, WD, YA, BK, KC | HN, JD, SH, SHS1, UD, AJ, BH, SA, SJ | YK, HON, GC |
| BH | GH, GR | BH, UD, SH, HN, SHS1, JD, AJ, SA, SJ | YA, KC, NC, WD, BK | YK, HON, GC |
| WD | GH, GR | WD, NC, YA, BK, KC | HN, JD, UD, SH, SHS1, BH, AJ, SA, SJ | YK, HON, GC |
| YA | GH, GR | YA, NC, KC, WD, BK | UD, SHS1, HN, JD, SH, BH, SJ, AJ, SA | YK, HON, GC |
| BK | GH, GR | BK, YA, NC, WD, KC | HN, UD, SHS1, JD, SH, BH, SJ, AJ, SA | YK, HON, GC |
| UD | GH, GR | UD, SHS1, BH, SJ, HN, SH, JD, AJ, SA | YA, KC, NC, BK, WD | YK, HON, GC |
| SHS1 | GR, GH | SHS1, UD, SJ, BH, HN, SH, JD, AJ, SA | YA, KC, NC, BK, WD | YK, HON, GC |
| GH | GH, GR | BK, YA, NC, WD, KC | HN, SHS1, UD, SH, JD, BH, SJ, AJ, SA | YK, HON, GC |
| KC | GH, GR | KC, YA, NC, BK, WD | SHS1, UD, SJ, BH, HN, SH, JD, AJ, SA | YK, HON, GC |
| SJ | GR, GH | SJ, SHS1, UD, BH, HN, SH, JD, AJ, SA | KC, YA, NC, BK, WD | YK, HON, GC |
| YK | GR, GH | YK, HON, GC | SHS1, UD, SJ, HN, SH, JD, BH, AJ, SA | KC, YA, NC, BK, WD |
| GR | GR, GH | YK, HON, GC | SHS1, SJ, UD, HN, SH, JD, BH, AJ, SA | KC, YA, NC, BK, WD |
| HON | GR, GH | HON, GC, YK | SHS1, UD, SJ, HN, SH, JD, BH, AJ, SA | KC, YA, NC, BK, WD |
| GC | GR, GH | GC, HON, YK | SHS1, UD, SJ, HN, SH, JD, BH, AJ, SA | KC, YA, NC, BK, WD |
| Group | Bus(#RE) | WSCR | Group | Bus(#RE) | WSCR |
|---|---|---|---|---|---|
| A′ | AJ, HN, SA, NC, SH, WD, BH, BK, JD, GH | 1.40 | A″ | JD, HN, WD BK, GH, NC | 2.49 |
| B′ | UD, SHS1, YK, HON, KC, GC, YA, SJ | 4.18 | B″ | AJ, KC, SA, YA, SH, YK, BH, HON, UD, GC, SHS1, SJ | 1.54 |
| C′ | GR | 80.67 | C″ | GR | 80.67 |
| Group | Proposed Boundaries(#RE) | WSCR |
|---|---|---|
| A | AJ, BH, UD, SA, JD, SHS1, SH, HN, SJ | 1.86 |
| B | KC, NC, BK, YA, WD | 3.67 |
| C | YK, HON, GC | 10.79 |
| D | GH | 28.96 |
| E | GR | 80.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, N.; Lee, B.; Kim, D.; Nam, S. Interaction Boundary Determination of Renewable Energy Sources to Estimate System Strength Using the Power Flow Tracing Strategy. Sustainability 2021, 13, 1569. https://doi.org/10.3390/su13031569
Choi N, Lee B, Kim D, Nam S. Interaction Boundary Determination of Renewable Energy Sources to Estimate System Strength Using the Power Flow Tracing Strategy. Sustainability. 2021; 13(3):1569. https://doi.org/10.3390/su13031569
Chicago/Turabian StyleChoi, Namki, Byongjun Lee, Dohyuk Kim, and Suchul Nam. 2021. "Interaction Boundary Determination of Renewable Energy Sources to Estimate System Strength Using the Power Flow Tracing Strategy" Sustainability 13, no. 3: 1569. https://doi.org/10.3390/su13031569
APA StyleChoi, N., Lee, B., Kim, D., & Nam, S. (2021). Interaction Boundary Determination of Renewable Energy Sources to Estimate System Strength Using the Power Flow Tracing Strategy. Sustainability, 13(3), 1569. https://doi.org/10.3390/su13031569





