Research on the Safety of the Left Hard Shoulder in a Multi-Lane Highway Based on Safety Performance Function
Abstract
1. Introduction
2. Literature Review
2.1. Study of Left Hard Shoulder on Highway
2.2. Highway Accident Prediction Methods
2.3. Summary
3. Materials and Methods
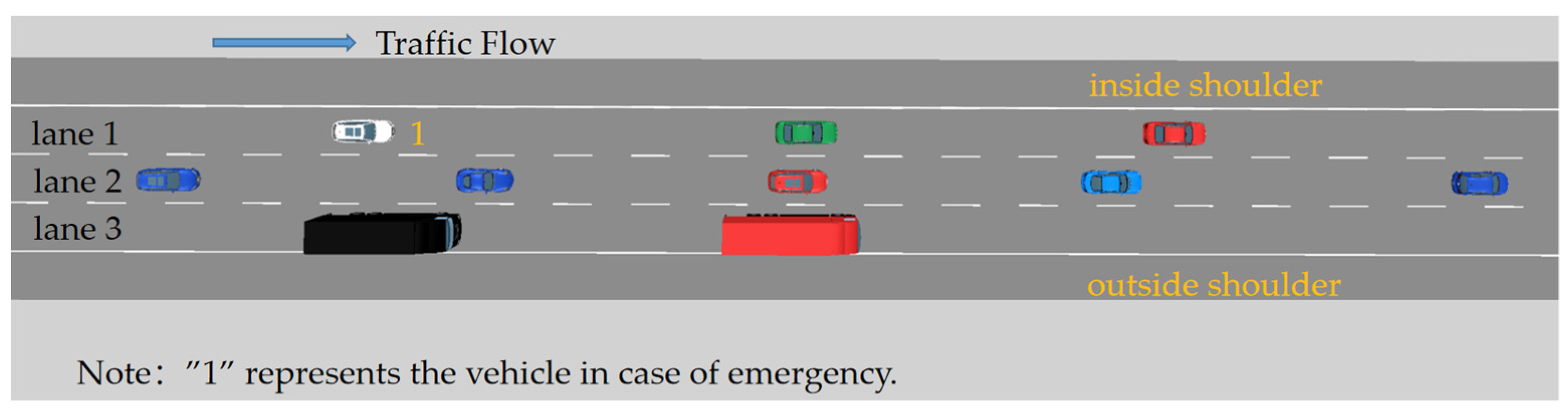
3.1. VISSIM Simulation Model
3.1.1. Traffic Simulation Model Calibration
3.1.2. Simulation Model Parameters Selection
3.2. SSAM Model
- (a)
- Establish a grid covering the simulation range and project the vehicle trajectory file onto the grid; this file contains information such as vehicle speed and acceleration.
- (b)
- Set the TTC threshold, and based on this simulation conflict discriminator, calculate the distance the vehicle can run when traveling at the speed before deceleration, and project it onto the vehicle trajectory in segments.
- (c)
- Compare the projected trajectories of different vehicles, and if there is an intersection point, there is a conflict.
3.3. Muti-Lane Highway Accident Prediction Model Based on SPF
3.3.1. Model Construction
3.3.2. Model Correction Factors
4. Results
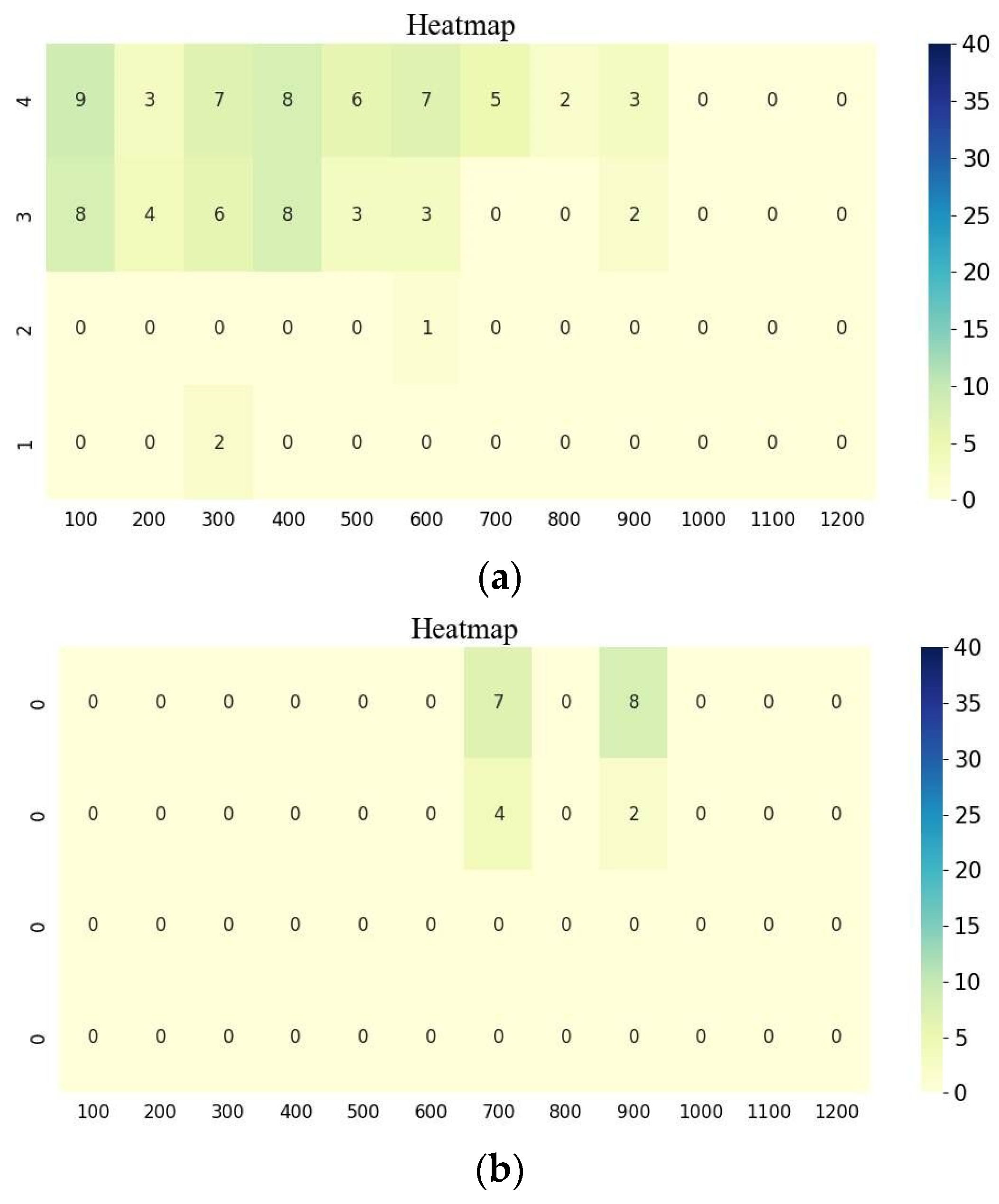
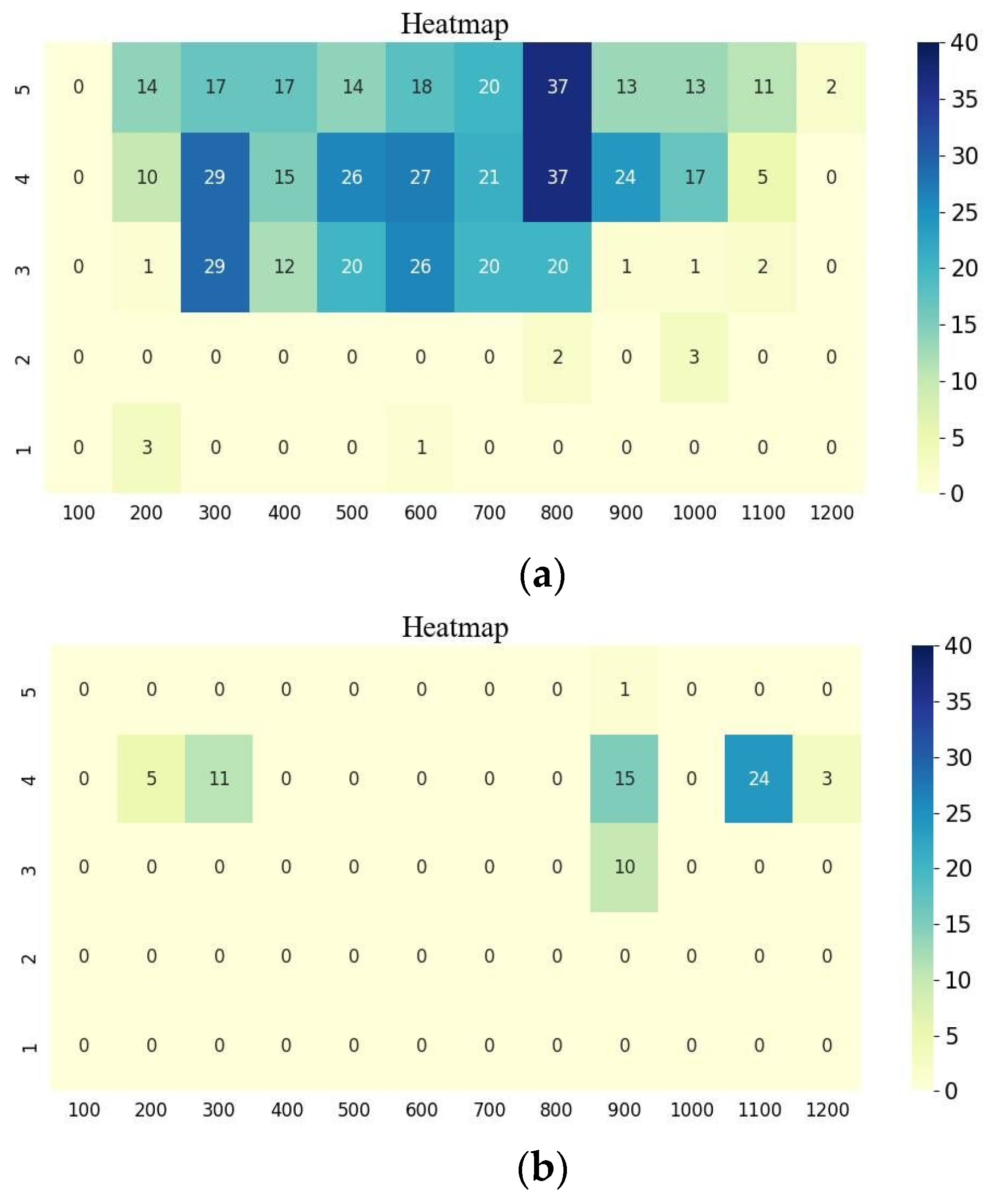
4.1. Conflicts Analysis
4.2. Multi-Lane Highway Accident Prediction Modeling
5. Discussion
5.1. Theoretical and Practical Applications
5.2. Limitations and Future Research Directions
6. Conclusions
- (1)
- In this paper, based on the past research on shoulders, we extend the study to the left-side hard shoulders of one-way three-, four-, and five-lane highways and compare their safety benefits. For one-way three, four, and five lanes, the rear-end conflict rates were reduced by 0.17%, 0.75%, and 4.6% after setting the hard shoulder on the left side, respectively. The output of the SSAM model shows that the mean TTC and maximum deceleration (MaxD) of the conflict events improved with the setting of the left hard shoulder, with a more remarkable improvement for the five-lane freeway, with a 57.2% increase in mean TTC, 19.2% increase in MaxD, and 15.3% increase in DeltaS. As the hard shoulder on the left side is the most obvious safety improvement for five lanes in one direction, we believe it is more necessary to set up a hard shoulder on the left side of a one-way five-lane highway.
- (2)
- In this paper, SPF was introduced to establish an accident prediction model to predict the setting of the left shoulder of a one-way five-lane highway to predict the setting of the left shoulder of a one-way five-lane highway. The results showed that within the reasonable setting range of the left hard shoulder width (0~4 m) if only the effect of the left hard shoulder width is considered, the accident rate decreases by about 1.5% for every 0.5 m increase in the left hard shoulder. The predicted accident numbers for Badou–Taihe and Taihe–Shihu sections are 183.57 cases/year and 249.16 cases/year, respectively, based on the curb width of 0.75 m, and 170.69 cases/year and 231.16 cases/year, respectively, based on the hard shoulder on the left side of 3 m. Increasing the width of the hard shoulder on the left side can gradually reduce the number of accidents when other influencing factors are not considered.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hadi, M.A.; Aruldhas, J.; Chow, L.-F.; Wattleworth, J.A. Estimating safety effects of cross-section design for various highway types using negative binomial regression. Transp. Res. Record. 1995, 1500, 169. [Google Scholar]
- Park, J.; Abdel-Aty, M.; Wang, L.; Lee, G.; Hong, J.J. Influence of multiple freeway design features on freight traffic safety. J. Adv. Transp. 2019, 5739496, 0197–6729. [Google Scholar]
- Harwood, D.W.; Council, F.M.; Hauer, E.; Hughes, W.E.; Vogt, A.J.B.T. Prediction of The Expected Safety Performance of Rural Two-Lane Highways; U.S Department Transportation, Federal Highway Administration: Washington, DC, USA, 2000.
- Torbic, D.J. Highway Safety Manual; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2010; Volume 19192. [Google Scholar]
- Design Specification for Highway Alignment (JTG B01-2017); People’s Traffic Publishing House: Beijing, China, 2017.
- Zhong, L.; Hou, D.; Wu, K.J. Necessity analysis of inside shoulder of multi-lane highway. J. Highw. Transp. Res. Dev. 2011, 2, 106–110. [Google Scholar]
- Coffey, S.; Park, S. Impact of Part-Time Shoulder Use on Safety through the Highway Safety Manual. In Proceedings of the International Conference on Transportation and Development 2018: Connected and Autonomous Vehicles and Transportation Safety, Pennsylvania, PA, USA, 15–18 July 2018; pp. 180–187. [Google Scholar]
- De Ridder, S.; Van der Horst, R.; Naing, C.L.; Thomson, R.; Fagerlind, H.; Lanner, G.; Dupre, G.; Bisson, O.; Garcia, J.; Lopez, F. Roadside Infrastructure for Safer European Roads: D04 Envelope of Vehicle and Driver Response Prior to Collisions; Citeseer: University Park, PA, USA, 2006. [Google Scholar]
- Zhong, L.; Li, X.W.; Wu, K.M. Necessity Analysis of Inside Shoulder Setting in Multi-lane Freeway with Traffic Simulation Method. In Software Engineering and Knowledge Engineering: Theory and Practice; Springer: Berlin/Heidelberg, Germany, 2012; pp. 593–598. [Google Scholar]
- Kitali, A.E.; Mokhtarimousavi, S.; Kadeha, C.; Alluri, P.J. Severity analysis of crashes on express lane facilities using support vector machine model trained by firefly algorithm. Traffic Inj. Prev. 2021, 22, 79–84. [Google Scholar]
- Fitzpatrick, K.; Dixon, K.; Avelar, R.J. Evaluating operational implications of reduced lane and shoulder widths on freeways. J. Transp. Eng. 2016, 142, 04016052. [Google Scholar]
- Ma, J.; Hu, J.; Hale, D.K.; Bared, J.J. Dynamic hard shoulder running for traffic incident management. Transp. Res. Record. 2016, 2554, 120–128. [Google Scholar]
- Liu, S.; Wang, J.H.; Fu, T. Effects of lane width, lane position and edge shoulder width on driving behavior in underground urban highways: A driving simulator study. Int. J. Environ. Res. Public Health. 2016, 13, 1010. [Google Scholar]
- Ben-Bassat, T.; Shinar, D.J. Effect of shoulder width, guardrail and roadway geometry on driver perception and behavior. Accid. Anal. Prev. 2011, 43, 2142–2152. [Google Scholar]
- Zhao, X.; Ding, H.; Wu, Y.; Ma, J.; Zhong, L.J. Experimental research on safety impacts of the inside shoulder based on driving simulation. Accid. Anal. Prev. 2015, 76, 6–14. [Google Scholar] [PubMed]
- Lord, D.; Washington, S.P.; Ivan, J.N.J. Poisson, Poisson-gamma and zero-inflated regression models of motor vehicle crashes: Balancing statistical fit and theory. Accid. Anal. Prev. 2005, 37, 35–46. [Google Scholar]
- Caliendo, C.; Guida, M.; Parisi, A.J. A crash-prediction model for multilane roads. Accid. Anal. Prev. 2007, 39, 657–670. [Google Scholar] [PubMed]
- Berhanu, G.J. Models relating traffic safety with road environment and traffic flows on arterial roads in Addis Ababa. Accid. Anal. Prev. 2004, 36, 697–704. [Google Scholar] [PubMed]
- Ivan, J.N.; Wang, C.; Bernardo, N.R.J. Explaining two-lane highway crash rates using land use and hourly exposure. Accid. Anal. Prev. 2000, 32, 787–795. [Google Scholar] [CrossRef]
- Memon, A.Q. Road Accident Prediction Models and Influence of Traffic Flow, Road Length, Road Class, and Vehicle Class on Accidents. In Proceedings of the Transportation Research Board 87th Annual Meeting, Washington, DC, USA, 13–17 January 2008. [Google Scholar]
- Cafiso, S.; Di Graziano, A.; Di Silvestro, G.; La Cava, G.; Persaud, B.J. Development of comprehensive accident models for two-lane rural highways using exposure, geometry, consistency and context variables. Accid. Anal. Prev. 2010, 42, 1072–1079. [Google Scholar] [CrossRef]
- Qi, Y.; Smith, B.L.; Guo, J.J. Freeway accident likelihood prediction using a panel data analysis approach. J. Transp. Eng. 2007, 133, 149–156. [Google Scholar]
- Elbasyouny, K.; Sayed, T.A. Impact of Flow Measurement Errors on Accident Prediction Models. In Proceedings of the Transportation Research Board Meeting, Washington, DC, USA, 13–17 January 2008. [Google Scholar]
- Malyshkina, N.V.; Mannering, F.L.; Tarko, A.P.J. Markov switching negative binomial models: An application to vehicle accident frequencies. Accid. Anal. Prev. 2009, 41, 217–226. [Google Scholar] [PubMed]
- Li, X.; Lord, D.; Zhang, Y.; Xie, Y.J. Predicting motor vehicle crashes using support vector machine models. Accid. Anal. Prev. 2008, 40, 1611–1618. [Google Scholar] [CrossRef]
- Kermanshah, M.; Najaf, P.; Jahromi, H.N.J. Developing nested logit probability models for rollover accident occurrence and driver injury severity. Transp. Res. J. 2011, 1, 35–45. [Google Scholar]
- Wang, C.; Quddus, M.A.; Ison, S.G.J. Predicting accident frequency at their severity levels and its application in site ranking using a two-stage mixed multivariate model. Accid. Anal. Prev. 2011, 43, 1979–1990. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Fan, L.S.; Shi, S.L.; Zhang, T.; Qi, M.H. Research on the prediction of dangerous goods accidents during highway transportation based on the ARMA model. J. Loss Prev. Process Ind. 2021, 72, 104583. [Google Scholar] [CrossRef]
- Lim, K. Analysis of Railroad Accident Prediction using Zero-truncated Negative Binomial Regression and Artificial Neural Network Model: A Case Study of National Railroad in South Korea. KSCE J. Civ. Eng. 2022, 1976–3808. [Google Scholar] [CrossRef]
- Gao, L.; Lu, P.; Ren, Y.H. A deep learning approach for imbalanced crash data in predicting highway-rail grade crossings accidents. Reliab. Eng. Syst. Saf. 2021, 216, 108019. [Google Scholar]
- Haleem, K.; Gan, A.; Lu, J.Y. Using multivariate adaptive regression splines (MARS) to develop crash modification factors for urban freeway interchange influence areas. Accid. Anal. Prev. 2013, 55, 12–21. [Google Scholar]
- Lord, D.; Persaud, B.N. Estimating the safety performance of urban road transportation networks. Accid. Anal. Prev. 2004, 36, 609–620. [Google Scholar] [PubMed]
- Bamzai, R.; Lee, Y.; Li, Z. Safety Impacts of Highway Shoulder Attributes in Illinois; Illinois Center for Transportation Series No. 11-078,0197-9191; Illinois Institute of Technology: Chicago, IL, USA, 2011. [Google Scholar]
- Li, Z.; Lee, S.H.; Lee, Y.; Zhou, B.; Bamzai, R. A Methodology for Assessing Safety Impacts of Highway Shoulder Paving. In Proceedings of the Transportation and Development Institute Congress 2011: Integrated Transportation and Development for a Better Tomorrow, Chicago, IL, USA, 13–16 March 2011; pp. 1105–1117. [Google Scholar]
- Machordom Gimeno, L. Assessment of Safety impacts of Shoulder Paving in Illinois highways Using Empirical Bayesian and Cross-Sectional Analyses. Bachelor’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2010. [Google Scholar]
- Huang, F.; Liu, P.; Yu, H.; Wang, W.J. Identifying if VISSIM simulation model and SSAM provide reasonable estimates for field measured traffic conflicts at signalized intersections. Accid. Anal. Prev. 2013, 50, 1014–1024. [Google Scholar] [PubMed]
- Ciuffo, B.; Punzo, V. “No free lunch” theorems applied to the calibration of traffic simulation models. IEEE Trans. Intell. Transp. Syst. 2013, 15, 553–562. [Google Scholar]
- Xuan, F.; Tamás, T.; Arthur, C.P. Online Calibration of Microscopic Road Traffic Simulator. In Proceedings of the 2020 IEEE 18th World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 23–25 January 2020; pp. 275–280. [Google Scholar]
- Anil, C.A.; Srinivasan, A.A.; Chilukuri, B.R.; Treiber, M.; Okhrin, O. Calibrating Wiedemann-99 Model Parameters to Trajectory Data of Mixed Vehicular. Traffic. Transp. Res. Record 2022, 2676, 718–735. [Google Scholar]
- Xu, C.; Ma, J.X.; Tang, X. A Simulation-Based Study of the Influence of Low-Speed Vehicles on Highway Traffic Safety. Sustainability 2022, 14, 12165. [Google Scholar]
- Peterson, B.E. First Workshop on Traffic Conflicts, Oslo, Norway, 1977; Tekniska Hogskolan i Lund: Oslo, Norway, 1977. [Google Scholar]
- Guo, Y.; Sayed, T.; Zaki, M.H. Exploring evasive action–based indicators for PTW conflicts in shared traffic facility environments. J. Transp. Eng. Part A Syst 2018, 144, 04018065. [Google Scholar]
- Ma, Y.F.; Meng, H.C.; Chen, S.Y.; Zhao, J.G.; Li, S.; Xiang, Q.J. Predicting Traffic Conflicts for Expressway Diverging Areas Using Vehicle Trajectory Data. J. Transp. Eng. Part A Syst. 2020, 146, 04020003. [Google Scholar]
- Ge, H.; Huang, M.; Lu, Y.; Yang, Y. Study on Traffic Conflict Prediction Model of Closed Lanes on the Outside of Expressway. Symmetry 2020, 12, 926. [Google Scholar] [CrossRef]
- Lin, X.Y.; Zhu, S.Y.; Li, W.J.; Xiao, W.B.; Wang, H. Setting Criterion of Left Hard Shoulder of Multi-lane Expressway Based on Logistic Model. J. Wuhan Univ. Technol. 2022, 46, 219–224. [Google Scholar]



| Applicable SPF | Correction Factor | Explanation |
|---|---|---|
| Highway Section | CMF1,w,x,y,z | Flat Curve |
| CMF2,w,x,y,fi | Lane Width | |
| CMF3,w,x,y,z | Inside Hard Shoulder | |
| CMF4,w,x,y,z | Median Width | |
| CMF5,w,x,y,z | Median Guardrail | |
| CMF6,w,x,y,z | High Traffic Volume | |
| Multi-vehicle Accidents | CMF7,fs,ac,mv,z | Lane Change |
| Single-vehicle Accidents | CMF8,fs,ac,sv,z | Outer Hard Shoulder |
| CMF9,fs,ac,sv,fi | Shoulder Vibrating Belt | |
| CMF10,fs,ac,sv,fi | Lateral Residual Width | |
| CMF11,fs,ac,sv,fi | Outer guardrail |
| Three Lanes | Four Lanes | Five Lanes | |||||
|---|---|---|---|---|---|---|---|
| Without Left Shoulder | With Left Shoulder | Without Left Shoulder | With Left Shoulder | Without Left Shoulder | With Left Shoulder | ||
| Rear-end Conflicts | Number of Conflicts | 13 | 5 | 58 | 13 | 381 | 36 |
| Conflict rate | 0.28% | 0.11% | 0.97% | 0.22% | 5.08% | 0.48% | |
| Lane-change Conflicts | Number of Conflicts | 3 | 3 | 23 | 8 | 152 | 32 |
| Conflict rate | 0.06% | 0.06% | 0.38% | 0.13% | 2.07% | 0.43% | |
| Three Lane | Four Lane | Five Lane | ||||
|---|---|---|---|---|---|---|
| Without Left Shoulder | With Left Shoulder | Without Left Shoulder | With Left Shoulder | Without Left Shoulder | With Left Shoulder | |
| TTC | 1.2 | 1.2 | 1 | 1.2 | 0.7 | 1.1 |
| MaxD | −7.4 | −7.6 | −8.1 | −7.7 | −8.3 | −6.7 |
| DeltaS | 12.8 | 18.3 | 18.6 | 21.3 | 19.6 | 22.6 |
| MaxS | 118.2 | 118.4 | 97.2 | 118.8 | 100.8 | 104.4 |
| Correction Factor | Multi-Vehicle (Casualties) | Multi-Vehicle (Property Damage Only) | Single-Vehicle (Casualties) | Single-Vehicle (Property Damage Only) |
|---|---|---|---|---|
| Npredicted | 33.27 | 70.26 | 18.78 | 43.28 |
| NSPFx | 21.64 | 46.63 | 16.70 | 37.60 |
| CMF1 (Flat Curve) | 1.0 | 1.0 | 1.0 | 1.0 |
| CMF2 (Lane Width) | 1.0 | 1.0 | 1.0 | 1.0 |
| CMF3 (Inside Hard Shoulder) | 1.109 | 1.096 | 1.109 | 1.096 |
| CMF4 (Median Width) | 1.153 | 1.139 | 0.955 | 1.137 |
| CMF5 (Median Guardrail) | 1.083 | 1.109 | 1.083 | 1.109 |
| CMF6 (High Traffic Volume) | 1.111 | 1.089 | 0.980 | 0.833 |
| CMF7 (lane change) | 1.0 | 1.0 | 1.0 | 1.0 |
| CMF8 (Outer Hard Shoulder) | / | / | 1.0 | 1 |
| CMF9 (Shoulder Vibrating Belt) | / | / | 1.0. | 1.0 |
| CMF10 (Lateral Residual Width) | / | / | 1.0 | 1.0 |
| CMF11 (Outer guardrail) | / | / | 1.016 | 1.021 |
| Correction Factor | Multi-Vehicle (Casualties) | Multi-Vehicle (Property Damage Only) | Single-Vehicle (Casualties) | Single-Vehicle (Property Damage Only) |
|---|---|---|---|---|
| CMF1 (Flat Curve) | 1.0 | 1.0 | 1.0 | 1.0 |
| CMF2 (Lane Width) | 1.0 | 1.0 | 1.0 | 1.0 |
| CMF3 (Inside Hard Shoulder) | 0.963 | 0.967 | 0.963 | 0.967 |
| CMF4 (Median Width) | 1.153 | 1.139 | 0.955 | 1.138 |
| CMF5 (Median Guardrail) | 1.083 | 1.109 | 1.083 | 1.109 |
| CMF6 (High Traffic Volume) | 1.150 | 1.120 | 0.973 | 0.783 |
| CMF7 (lane change) | / | / | / | / |
| CMF8 (Outer Hard Shoulder) | / | / | 1.0 | 1.0 |
| CMF9 (Shoulder Vibrating Belt) | / | / | 1.0 | 1.0 |
| CMF10 (Lateral Residual Width) | / | / | 1.077 | 1.0 |
| CMF11 (Outer guardrail) | / | / | 1.016 | 1.021 |
| Road Section | Effective Length | Nf | Nf,fs,10,mv,fi | Nf,fs,10,mv,pdo | Nf,fs,10,sv,fi | Nf,fs,10,sv,pdo |
|---|---|---|---|---|---|---|
| Badou–Taihe | 4.9 km | 173.49 | 36.05 | 72.56 | 22.23 | 42.65 |
| Taihe–Shihu | 6.7 km | 235.07 | 49.16 | 106.62 | 27.75 | 54.54 |
| Road Section Type | Accident Type | Accident Severity | CMF Variables | CMF Coefficient |
|---|---|---|---|---|
| All type () | Multi-Vehicle accidents () | Casualties () | CMF3,fs,ac,mv,fi | −0.0172 |
| Property damage only () | CMF3,fs,ac,mv,pdo | −0.0153 | ||
| Single-Vehicle accident | Casualties () | CMF3,fs,ac,sv,fi | −0.0172 | |
| Property damage only () | CMF3,fs,ac,sv,pdo | −0.0153 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, P.; Ma, J.; Xu, C.; Zhao, C.; Ni, Z. Research on the Safety of the Left Hard Shoulder in a Multi-Lane Highway Based on Safety Performance Function. Sustainability 2022, 14, 15114. https://doi.org/10.3390/su142215114
Zhao P, Ma J, Xu C, Zhao C, Ni Z. Research on the Safety of the Left Hard Shoulder in a Multi-Lane Highway Based on Safety Performance Function. Sustainability. 2022; 14(22):15114. https://doi.org/10.3390/su142215114
Chicago/Turabian StyleZhao, Penghui, Jianxiao Ma, Chubo Xu, Chuwei Zhao, and Zifan Ni. 2022. "Research on the Safety of the Left Hard Shoulder in a Multi-Lane Highway Based on Safety Performance Function" Sustainability 14, no. 22: 15114. https://doi.org/10.3390/su142215114
APA StyleZhao, P., Ma, J., Xu, C., Zhao, C., & Ni, Z. (2022). Research on the Safety of the Left Hard Shoulder in a Multi-Lane Highway Based on Safety Performance Function. Sustainability, 14(22), 15114. https://doi.org/10.3390/su142215114










