Comprehensive Analysis of PV and Wind Energy Integration into MMC-HVDC Transmission Network
Abstract
:1. Introduction
- Detailed model-based renewable energy integrated MMC-HVDC system has been investigated and thoroughly analyzed.
- Comprehensive model-based full system with real-time simulation results has been provided.
2. Mathematical Modeling and Controller Design
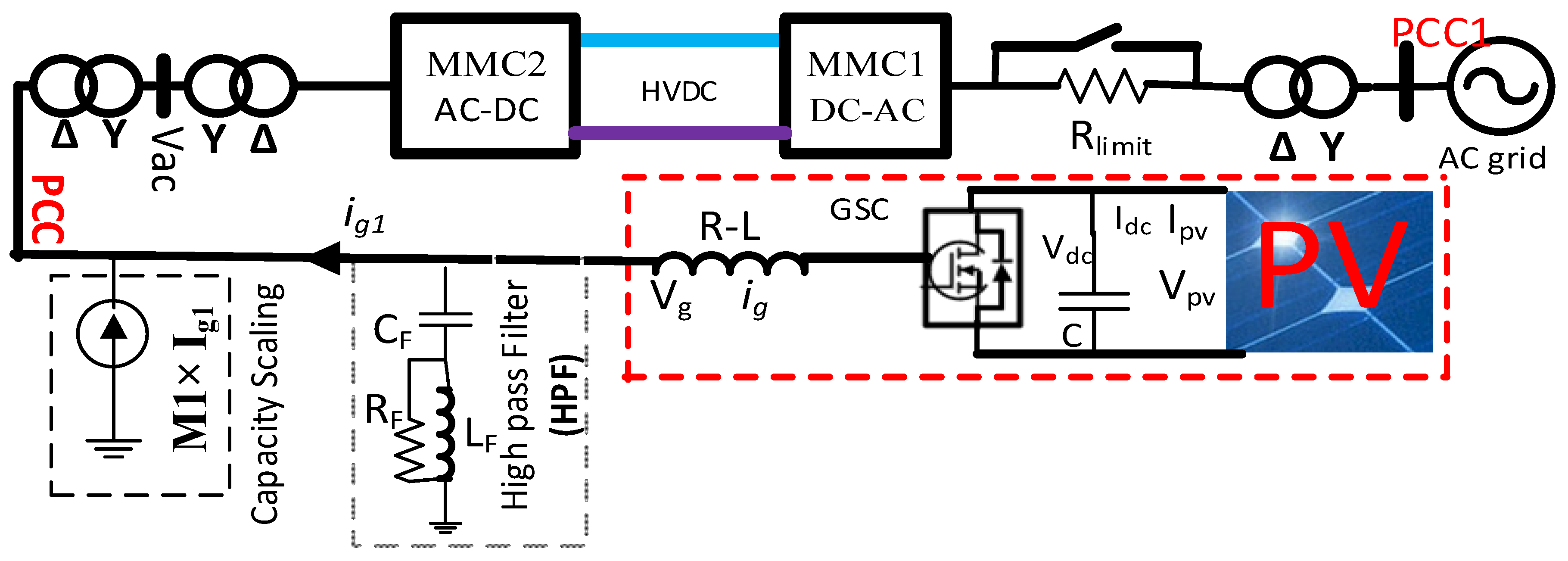
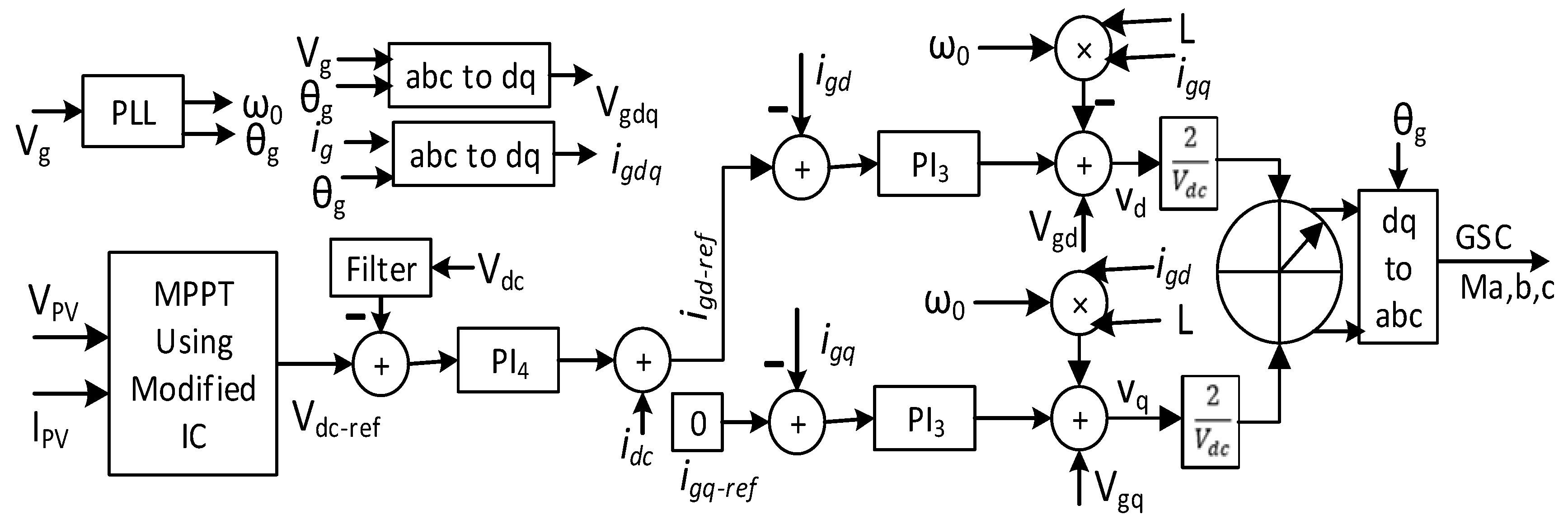
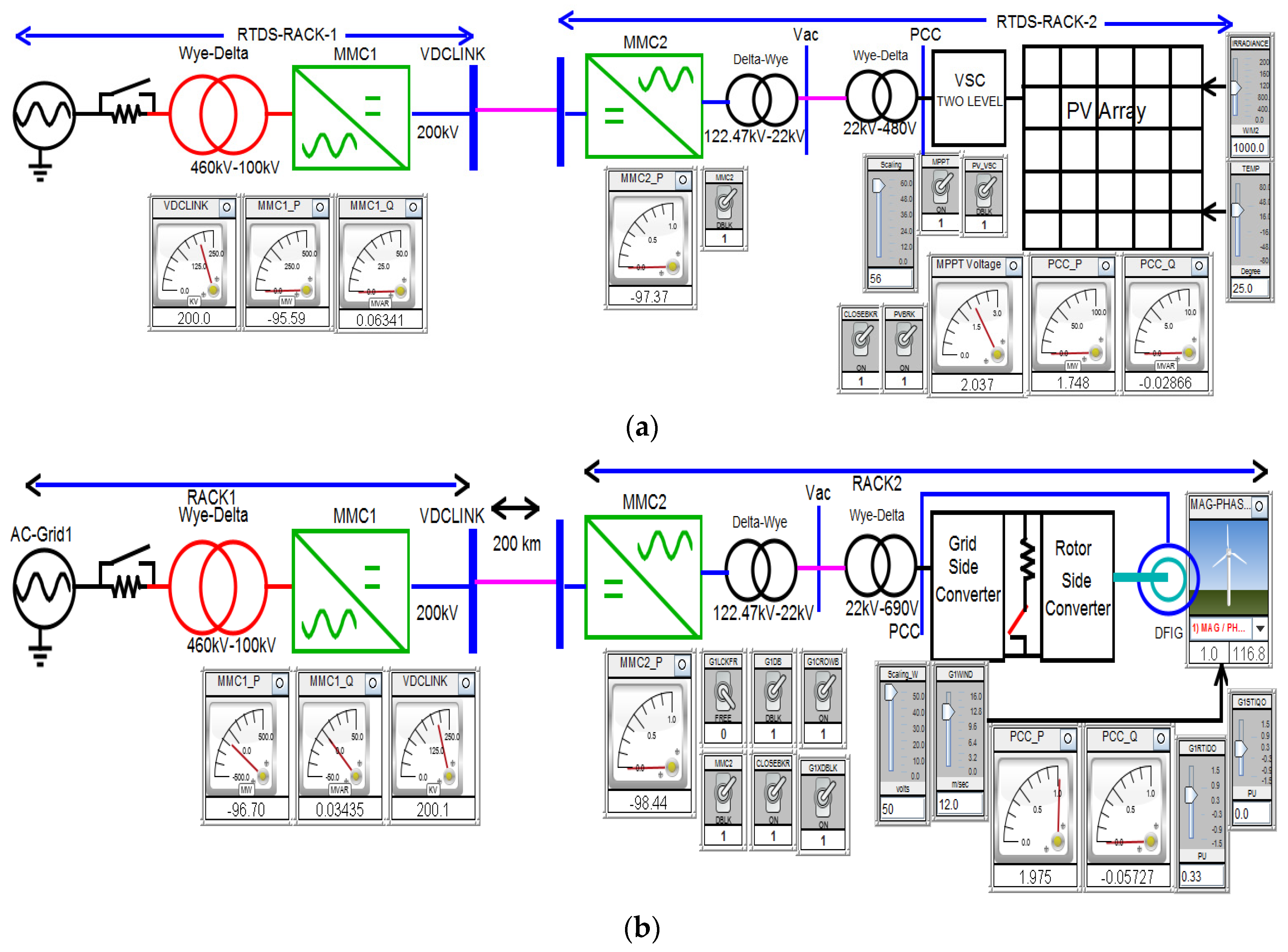
2.1. Solar Energy Included MMC-HVDC Transmission Network
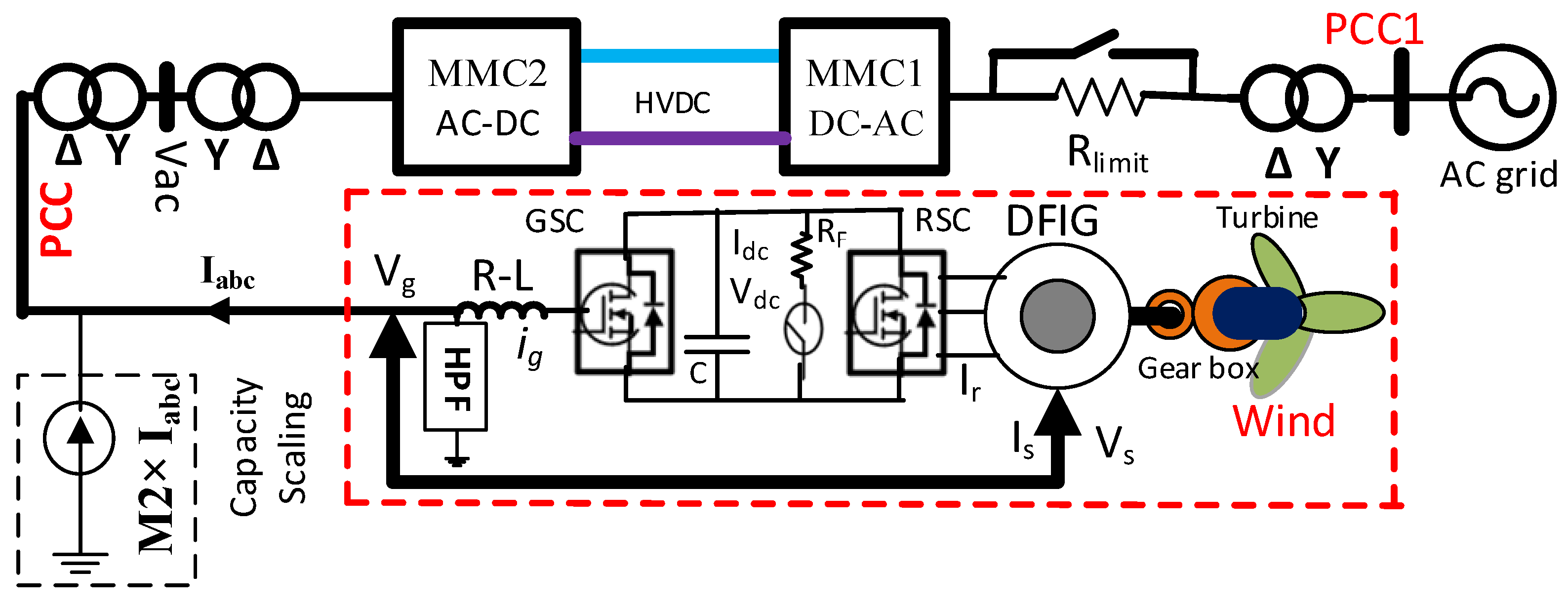
2.2. DFIG-Based Wind Energy Included MMC-HVDC Transmission Network
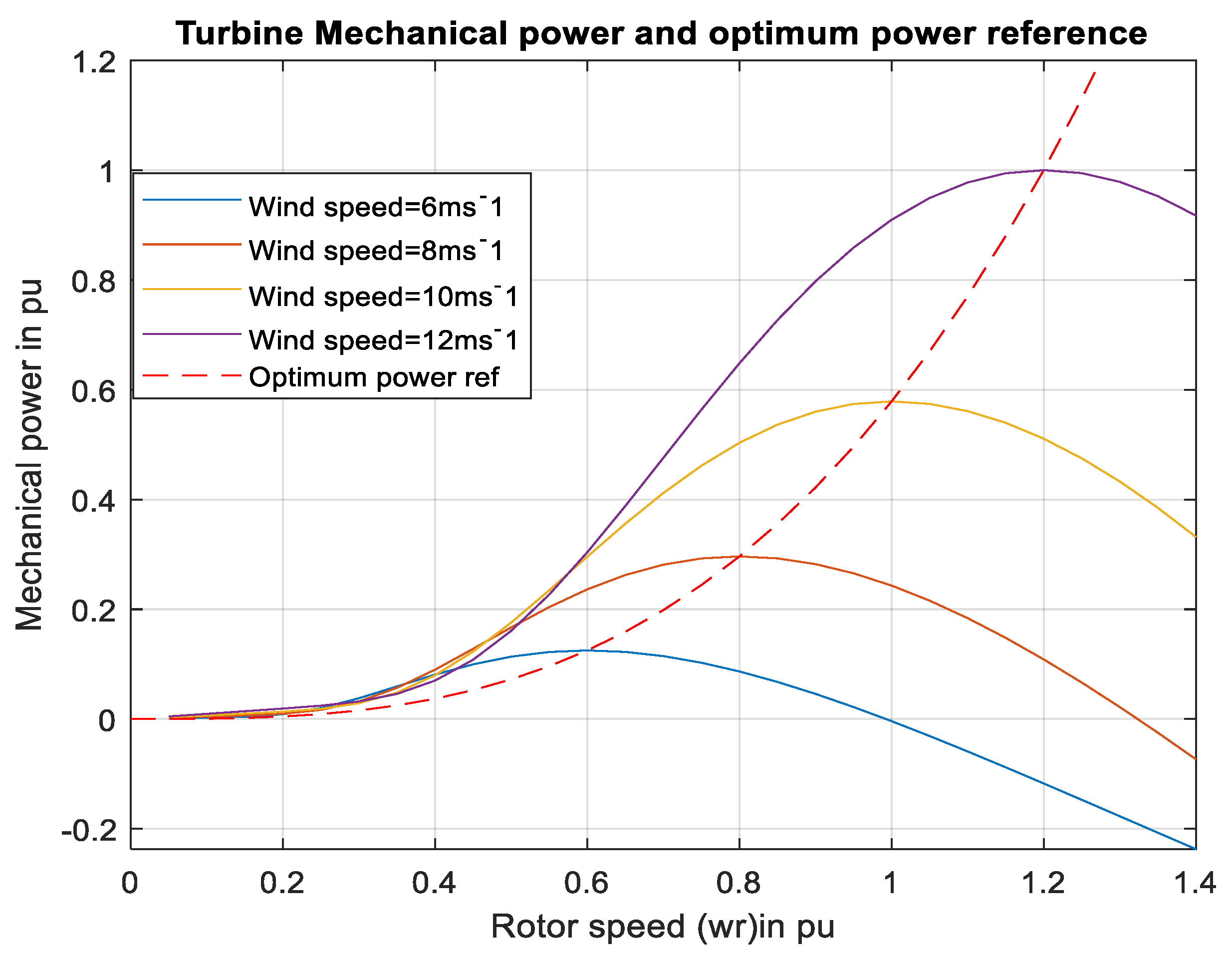
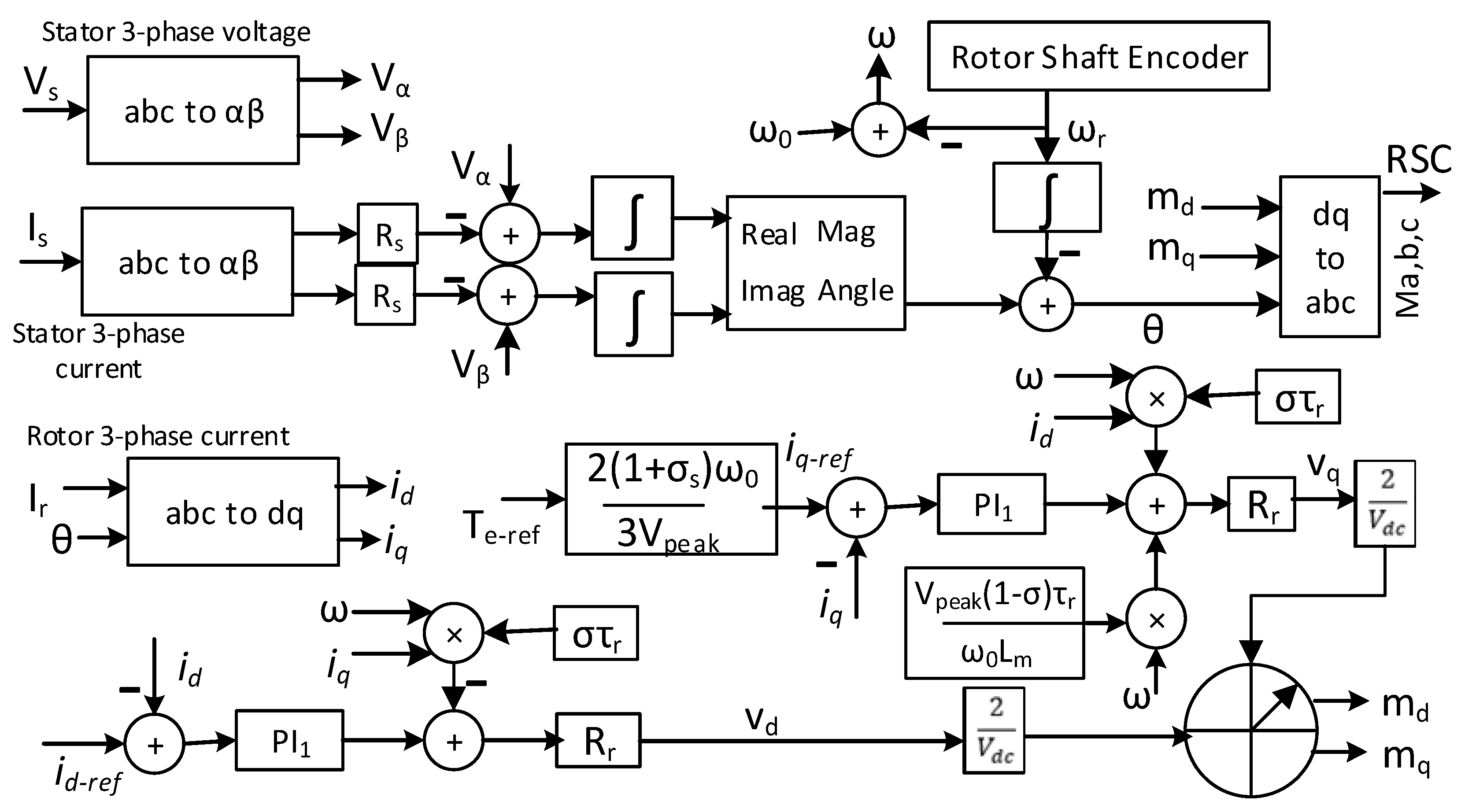
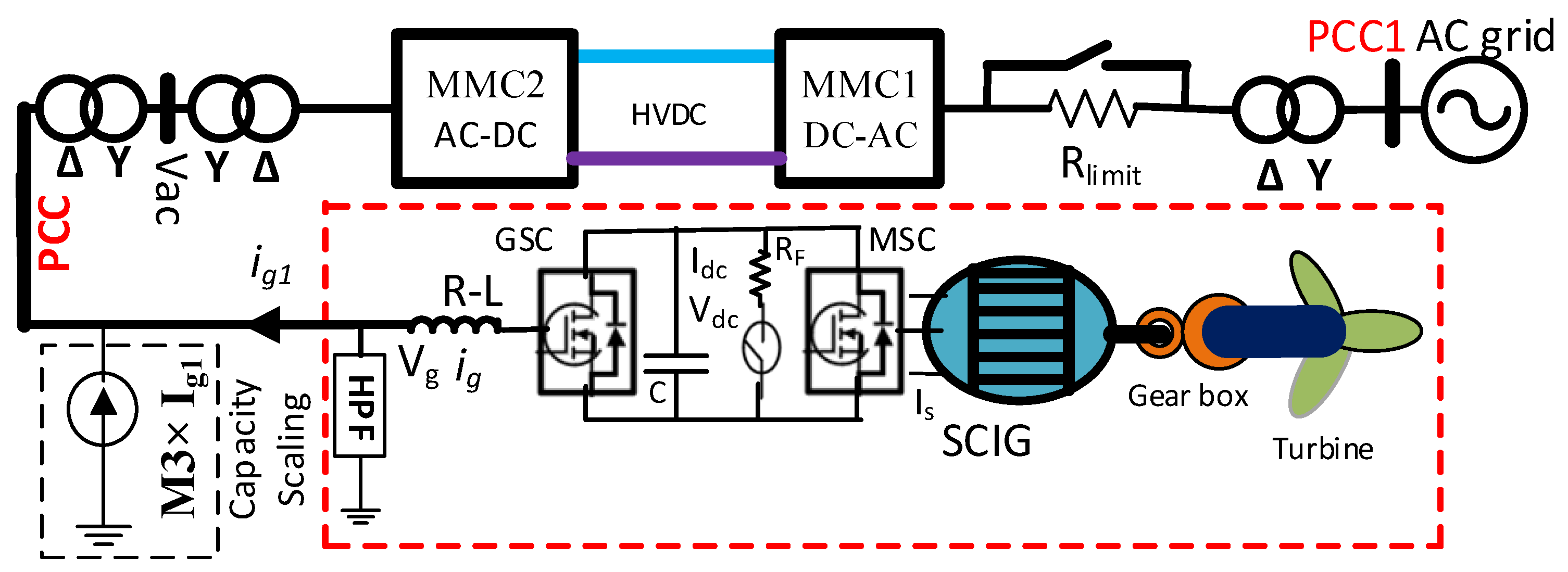
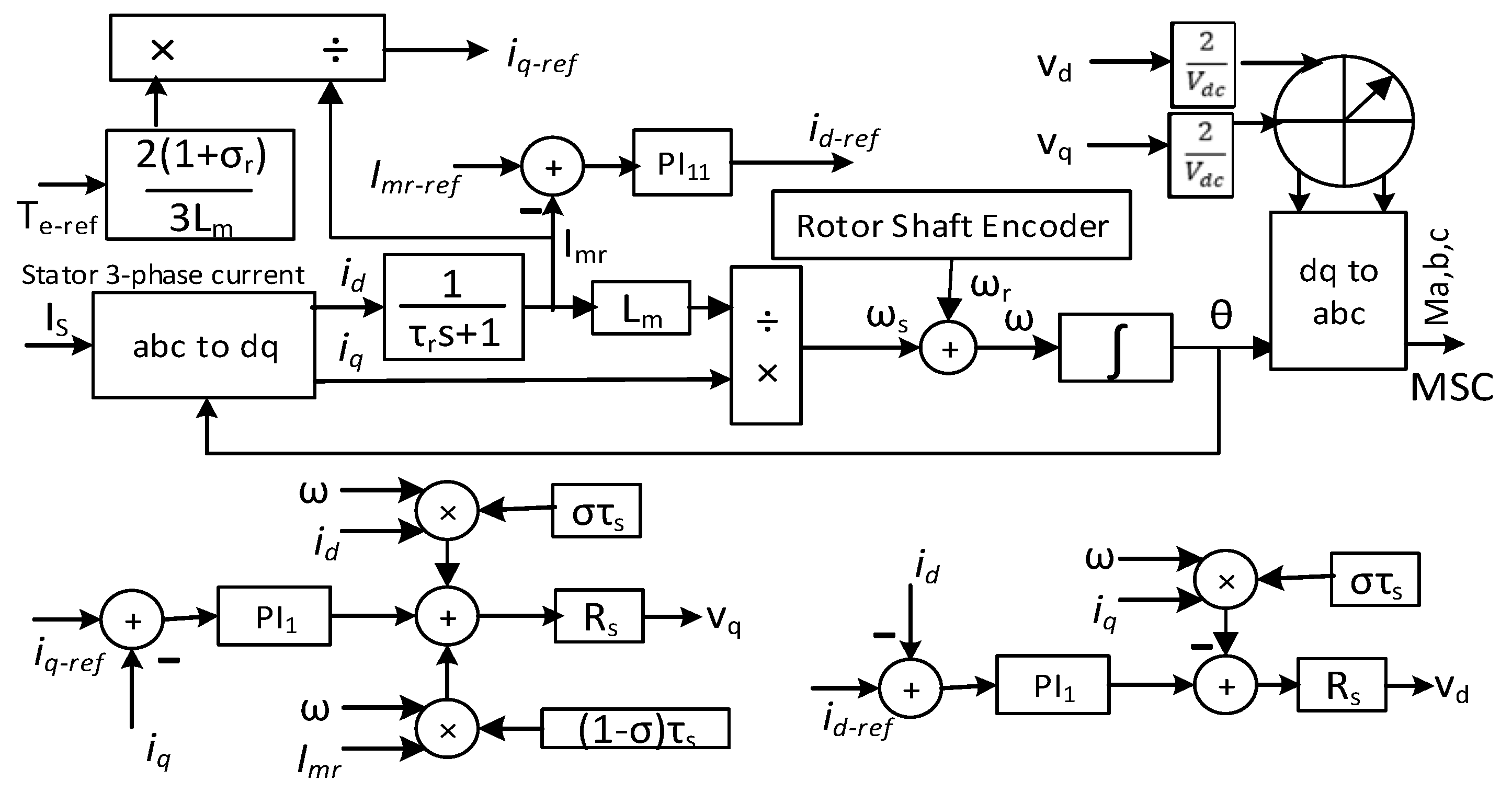
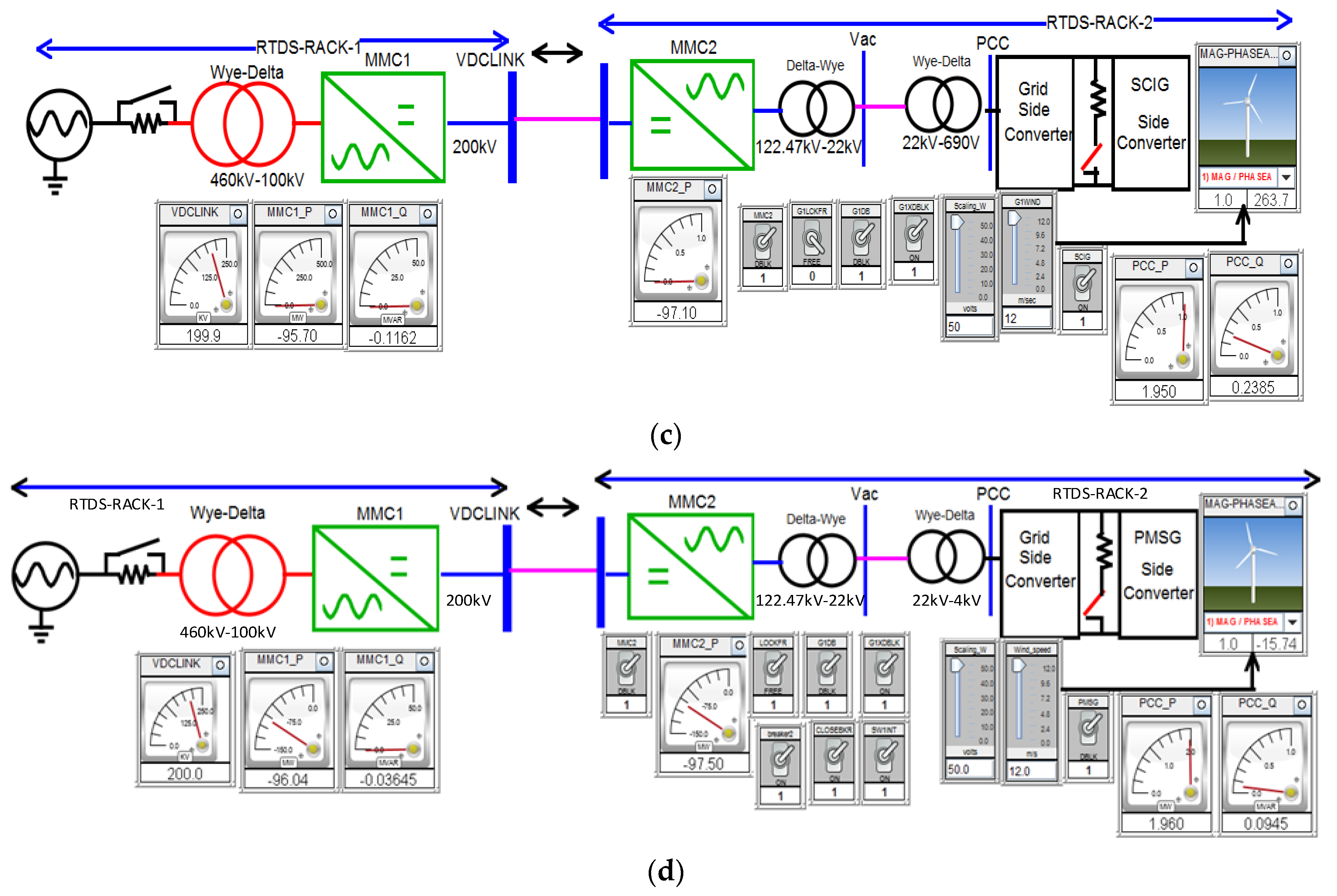
2.3. SCIG-Based Wind Energy Included MMC-HVDC Transmission Network
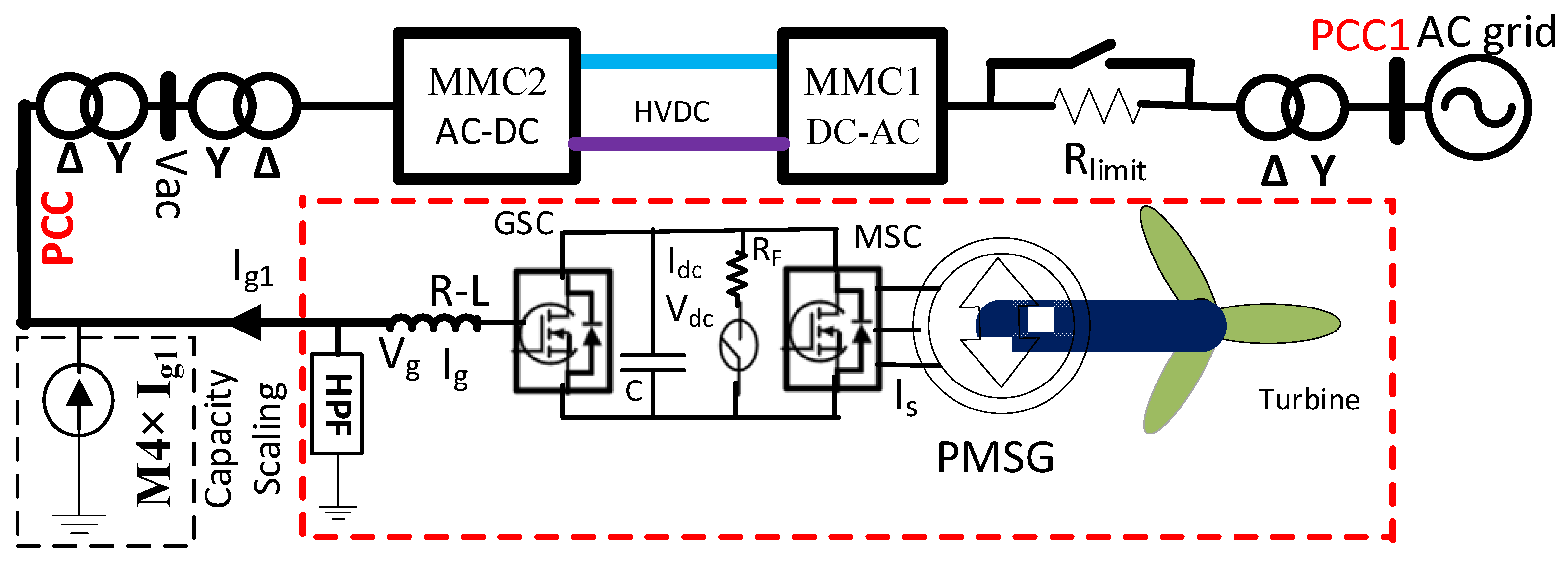
2.4. PMSG-Based Wind Energy Included MMC-HVDC Transmission Network
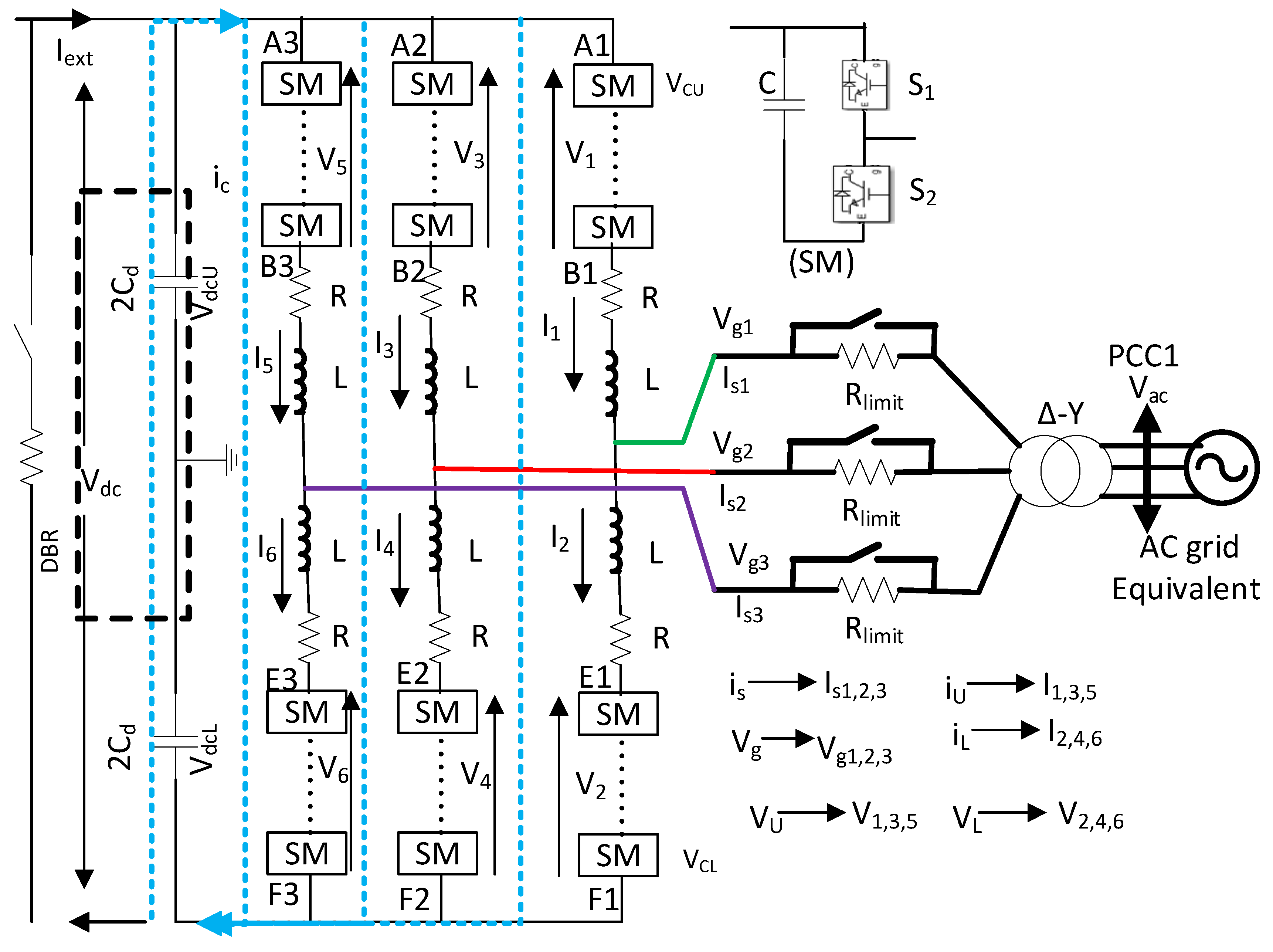
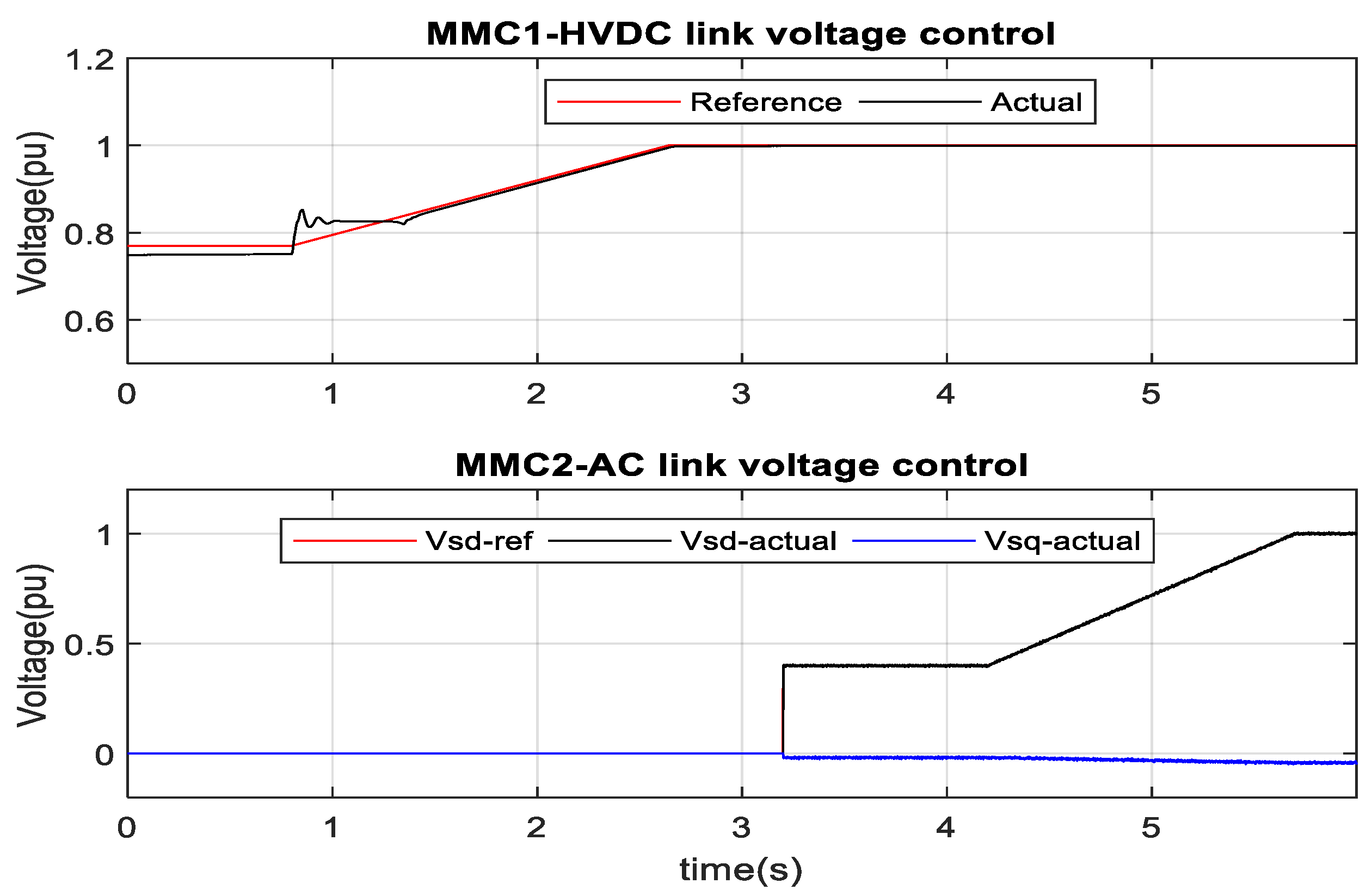
2.5. MMC1-HVDC Link Voltage and MMC2-AC Link Voltage Control
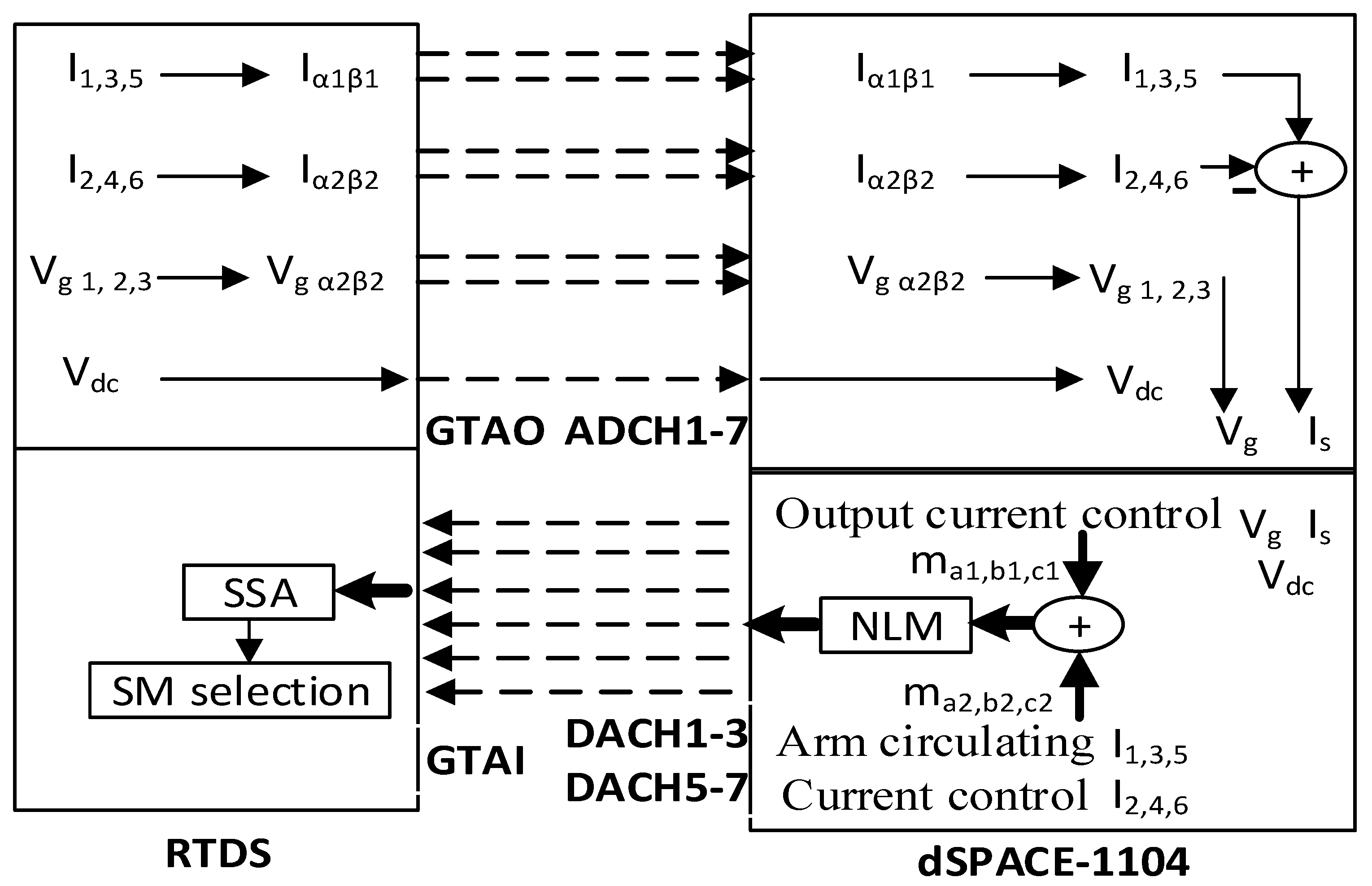
2.5.1. High-Level Control
2.5.2. Low Level Control
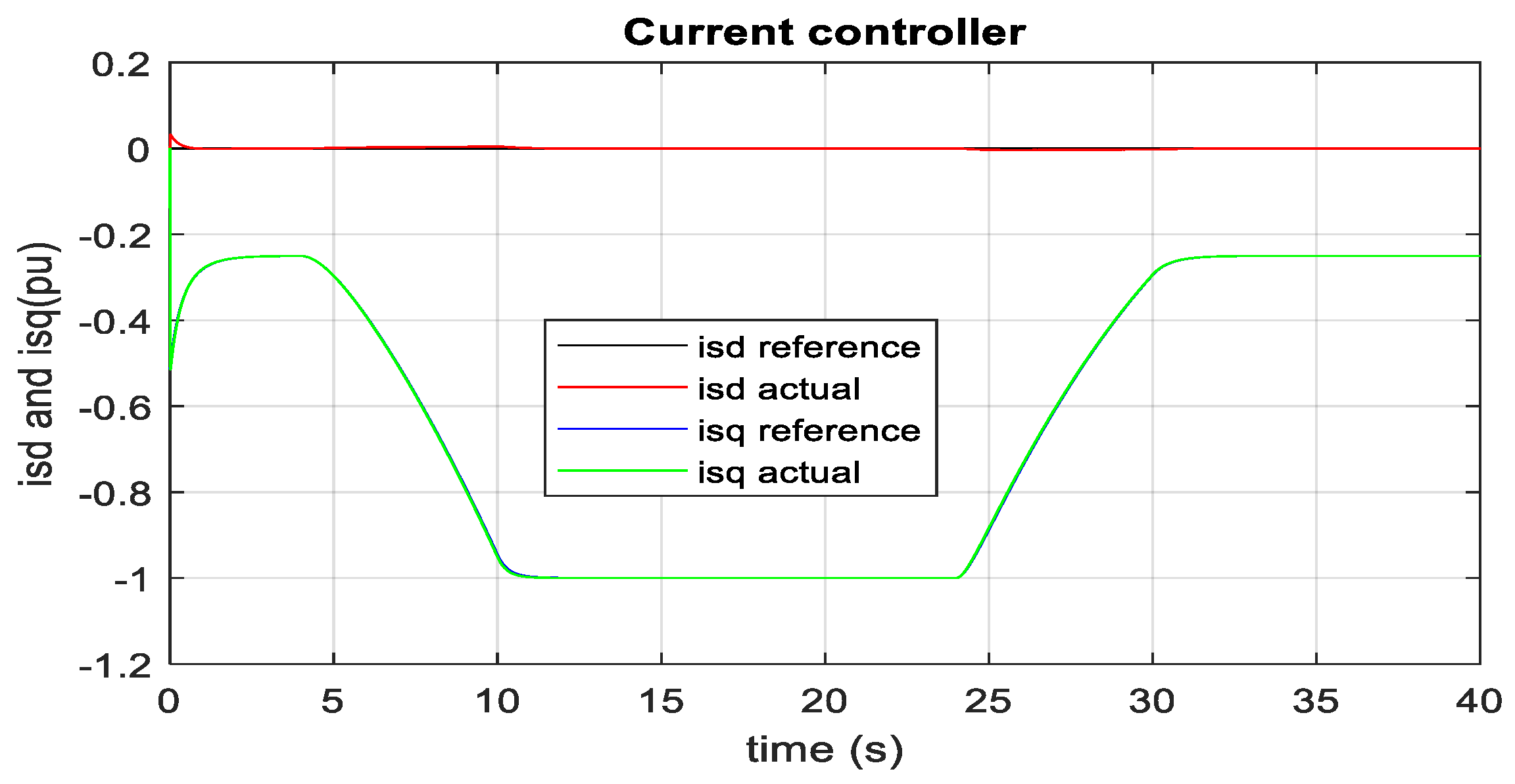
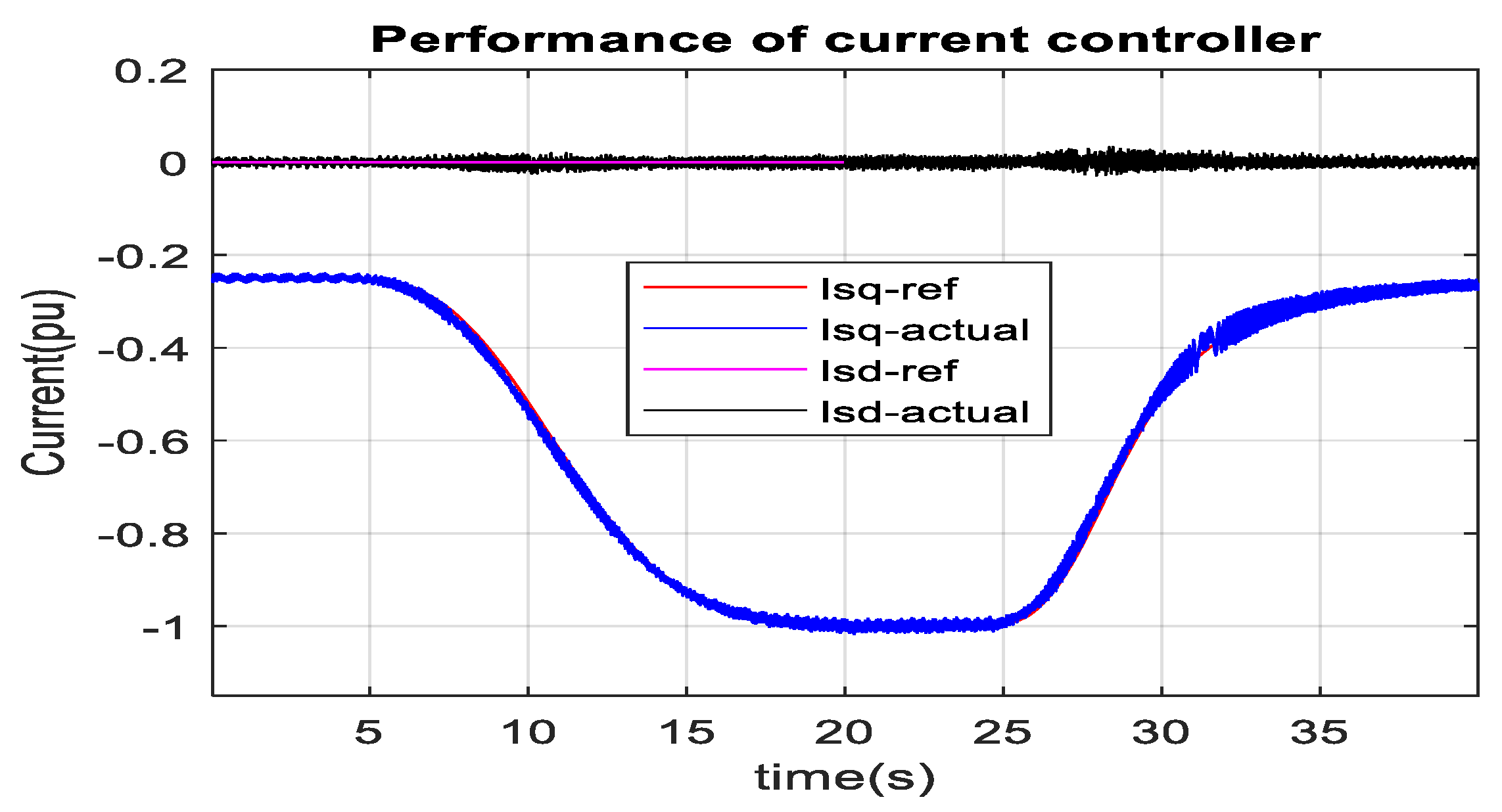
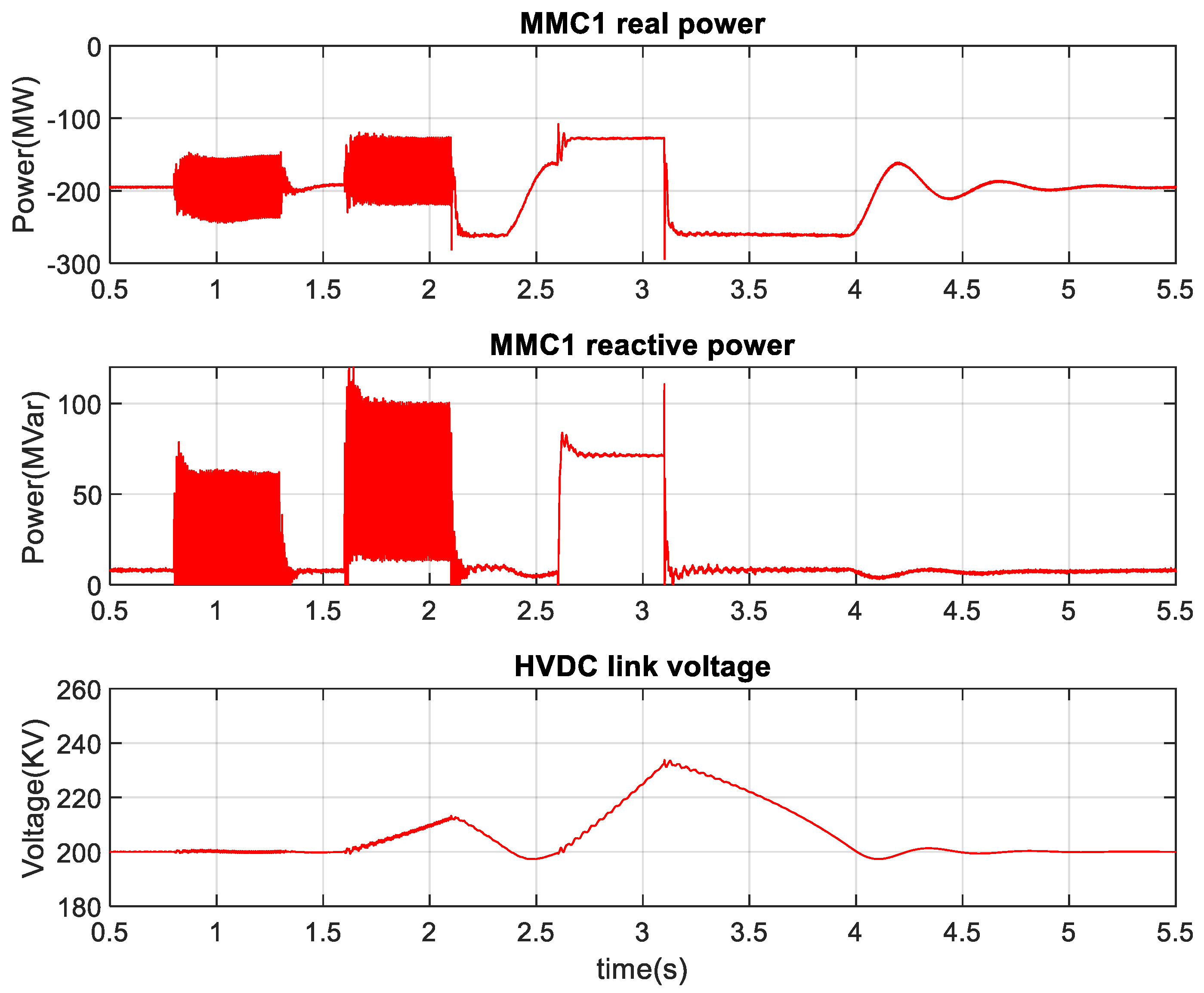
3. Result and Discussion
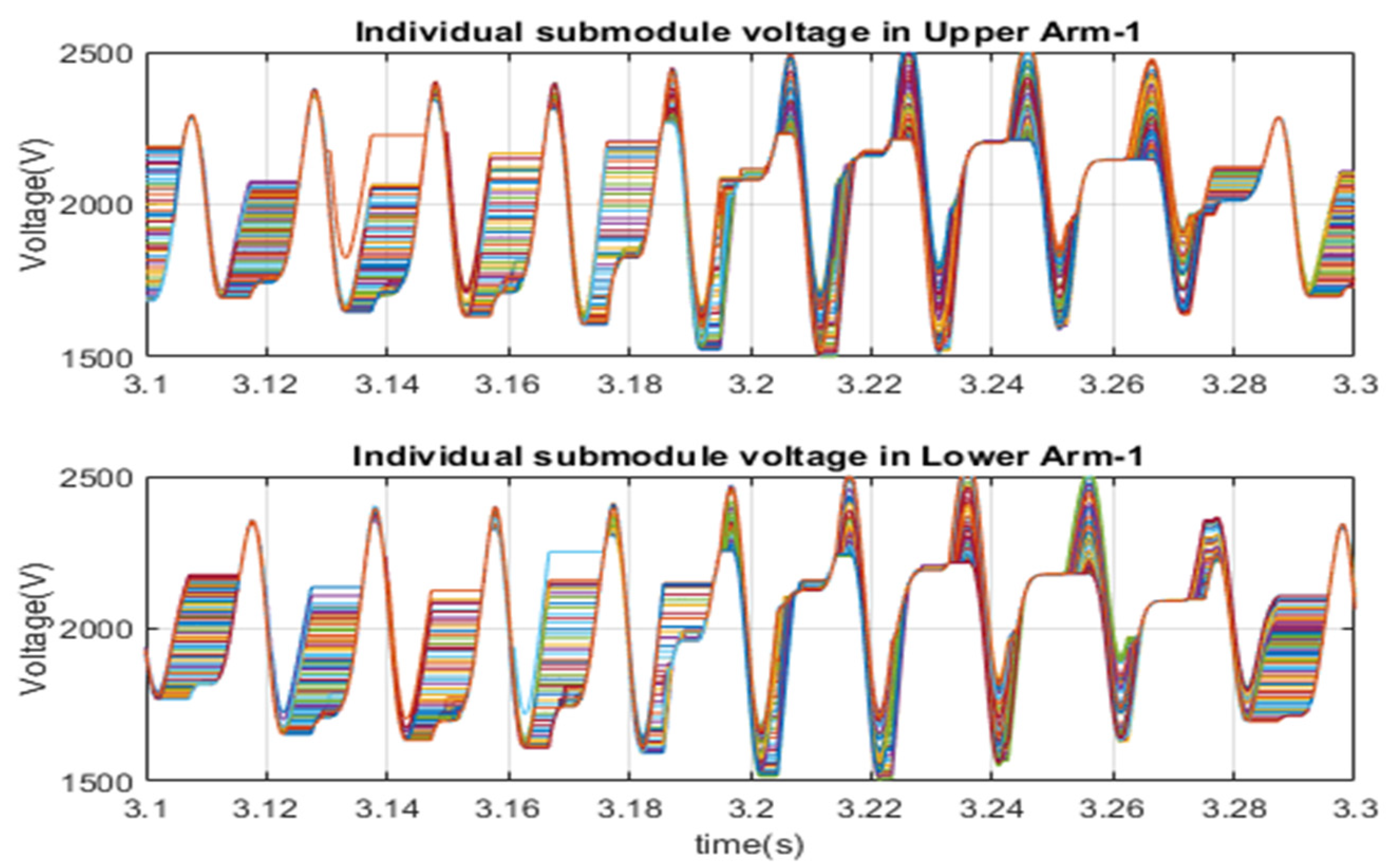
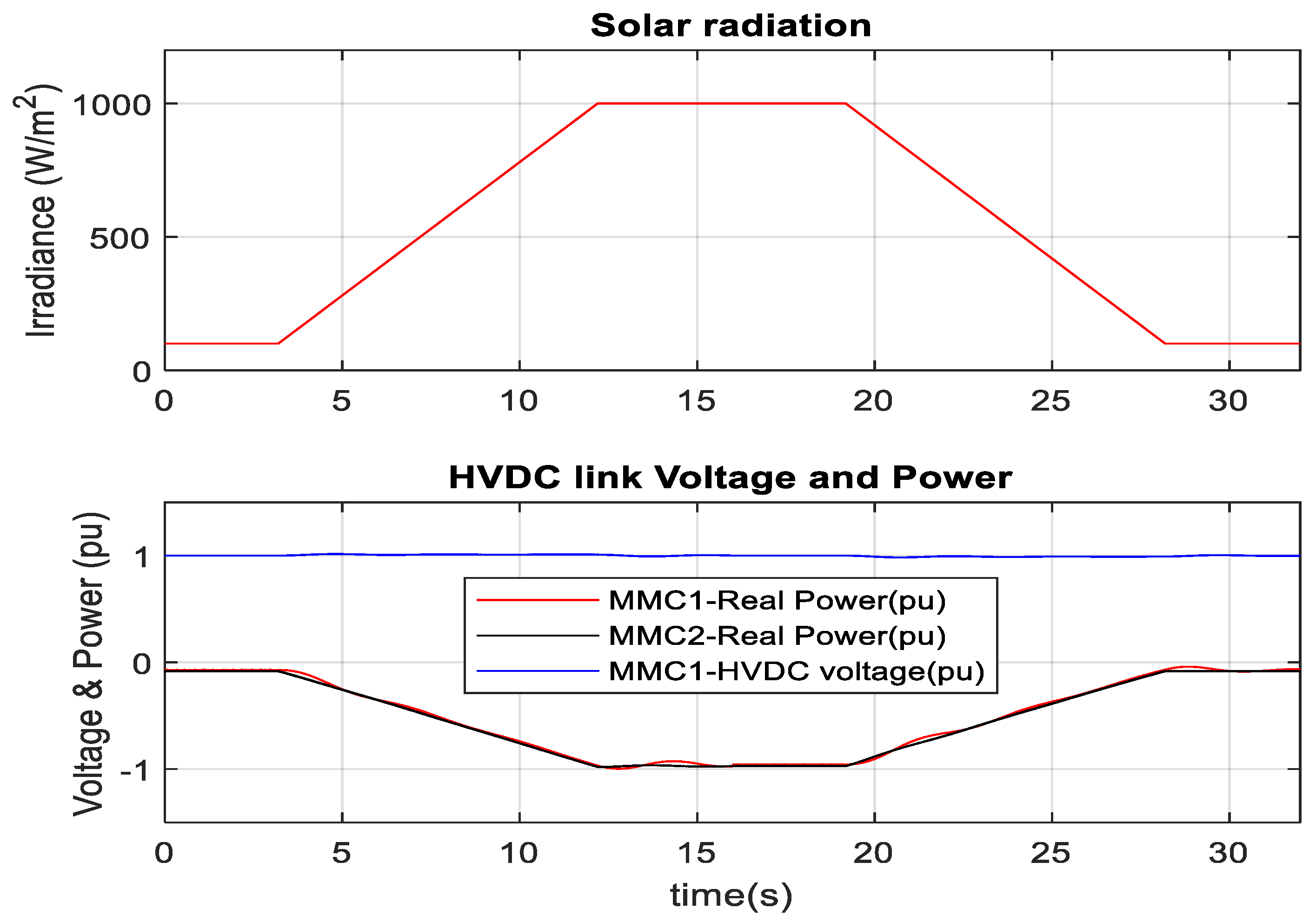
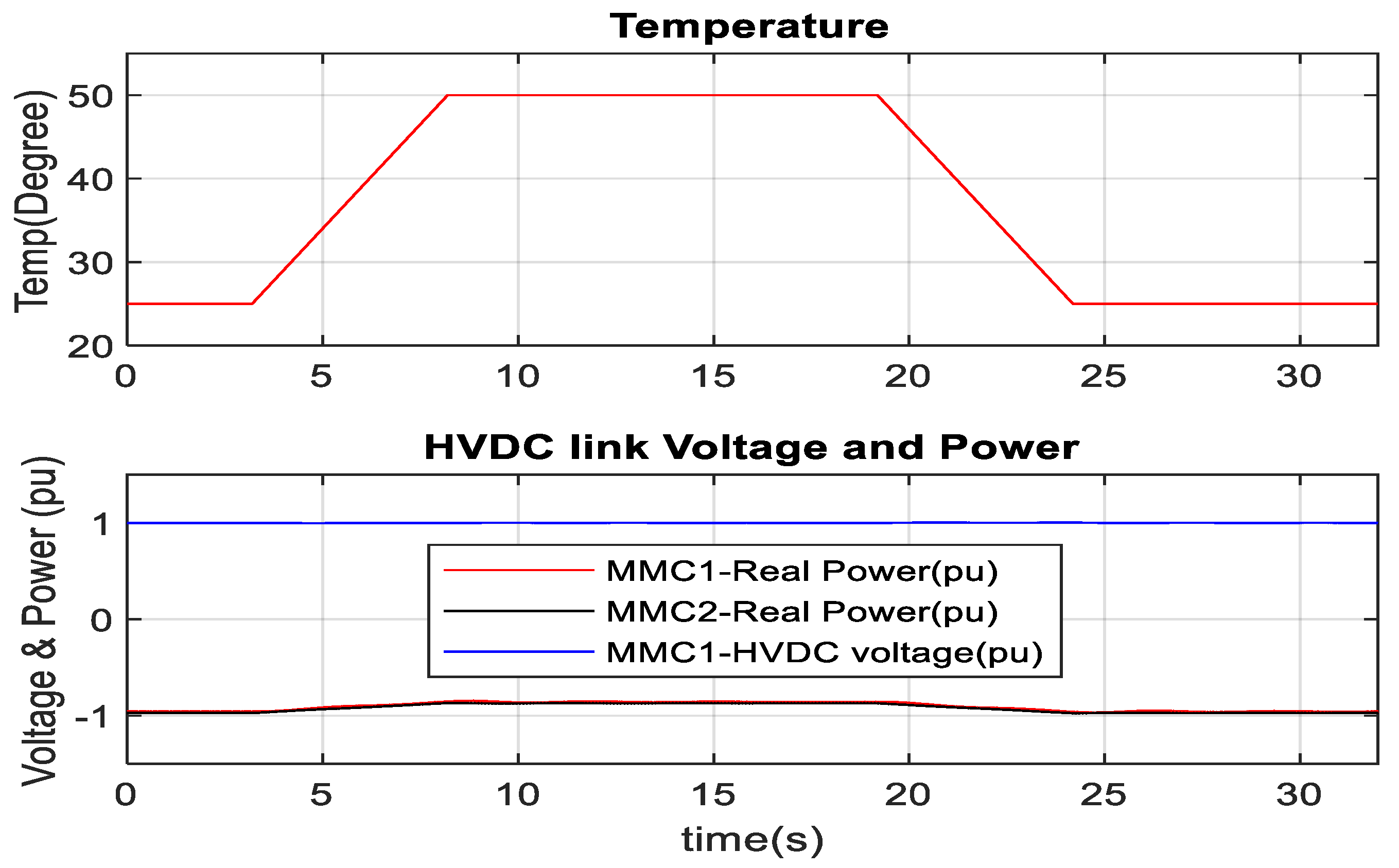
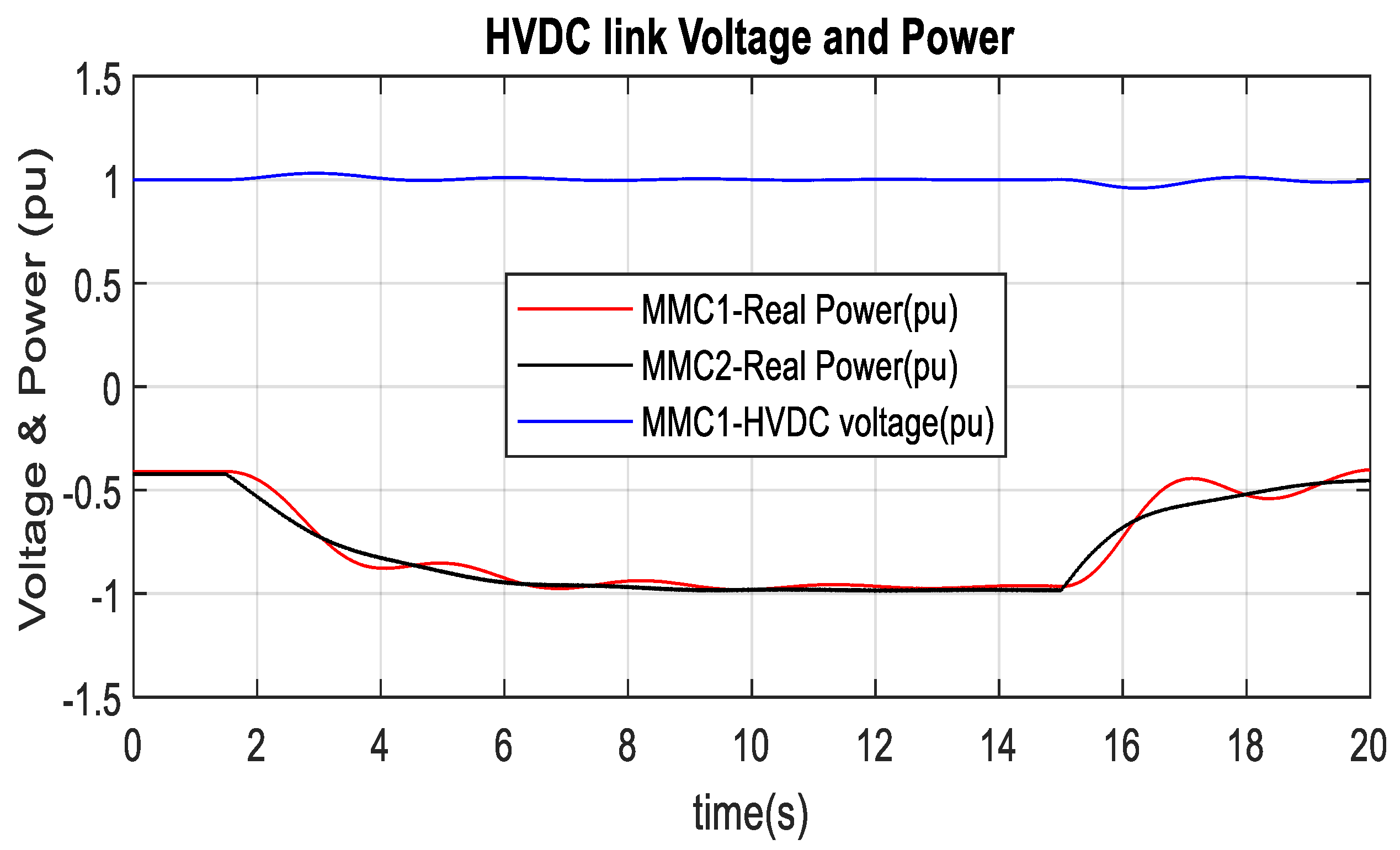
3.1. MMC1-DC Link Voltage and MMC2-AC Link Voltage Control
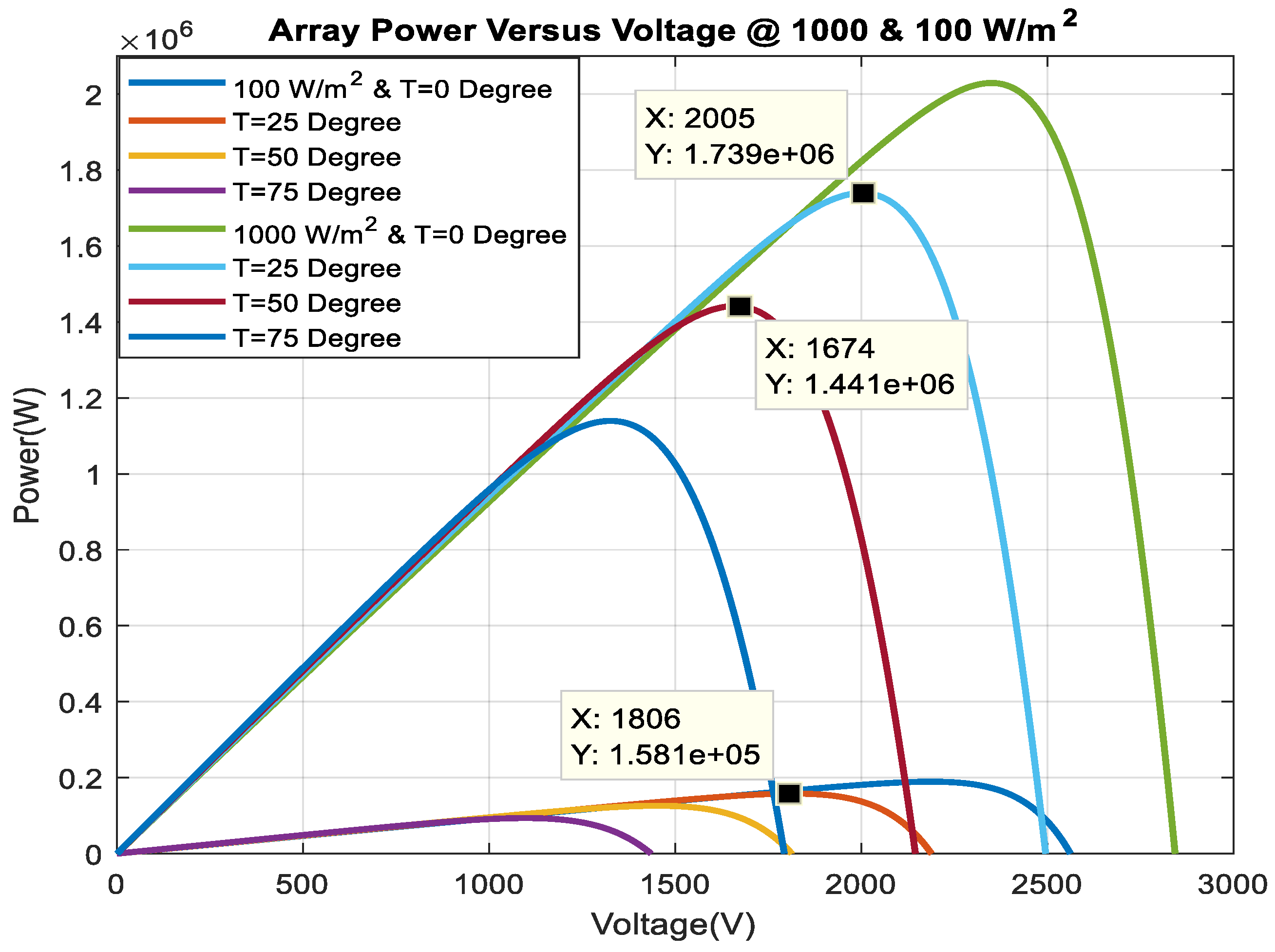
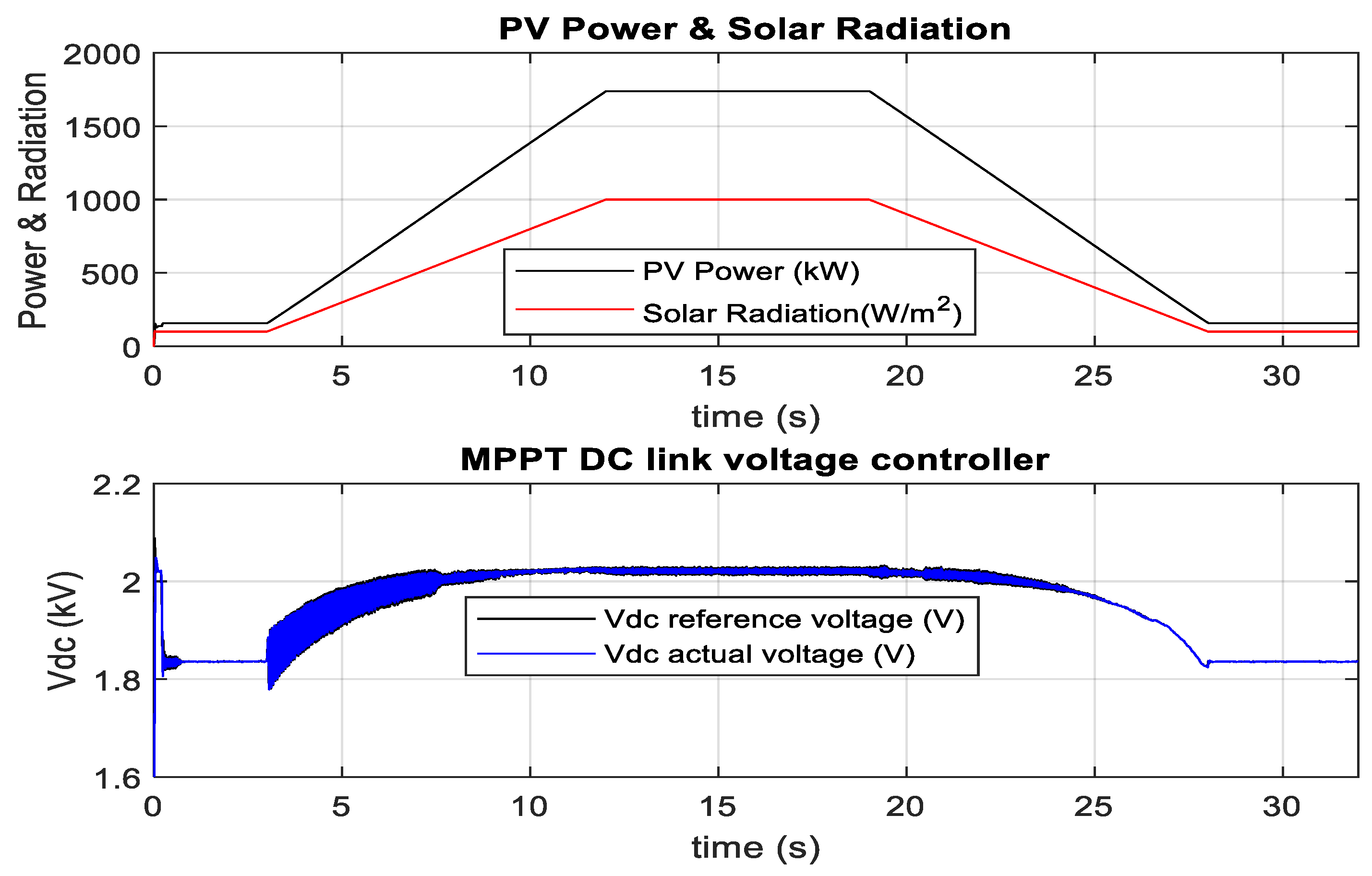
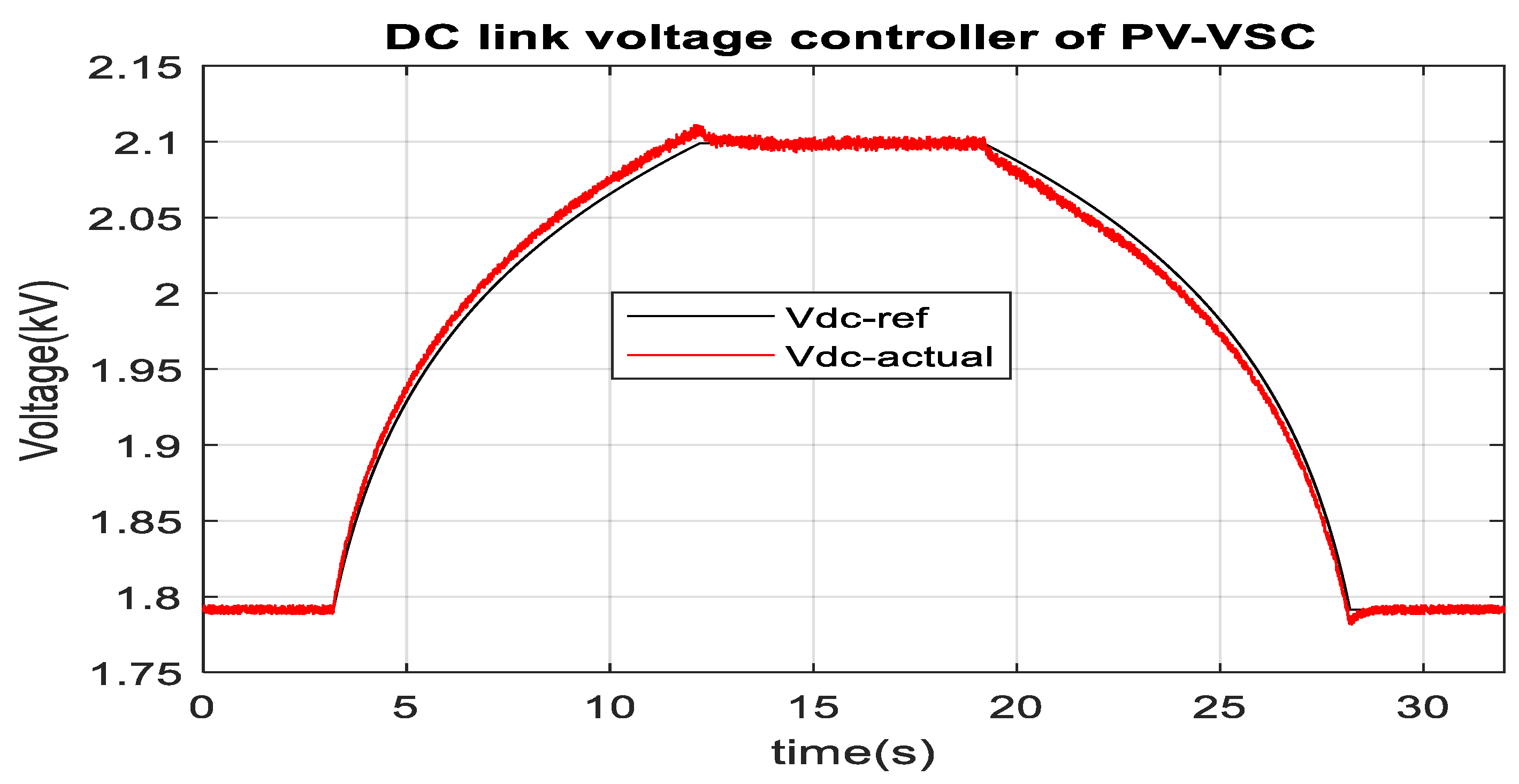
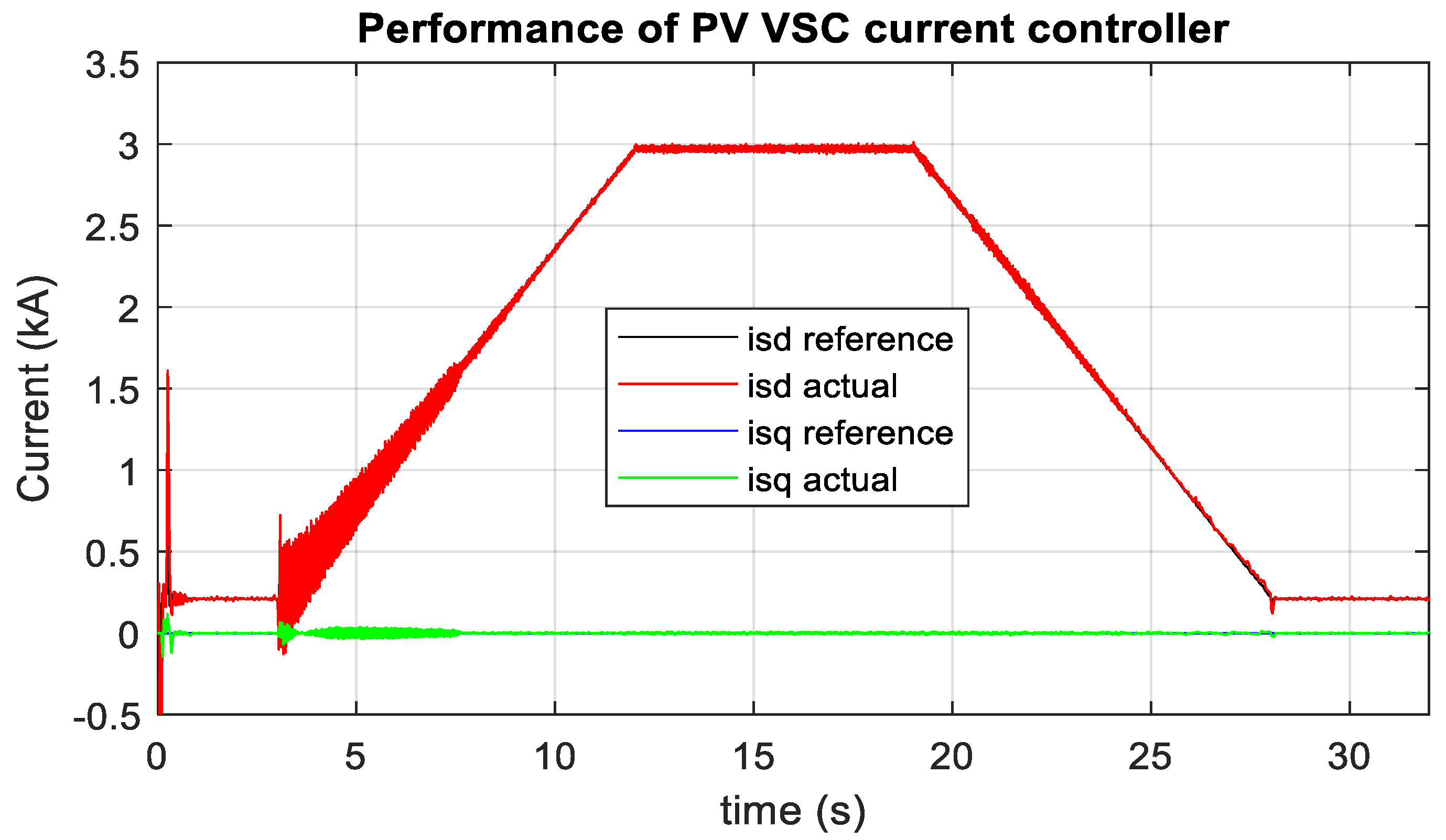
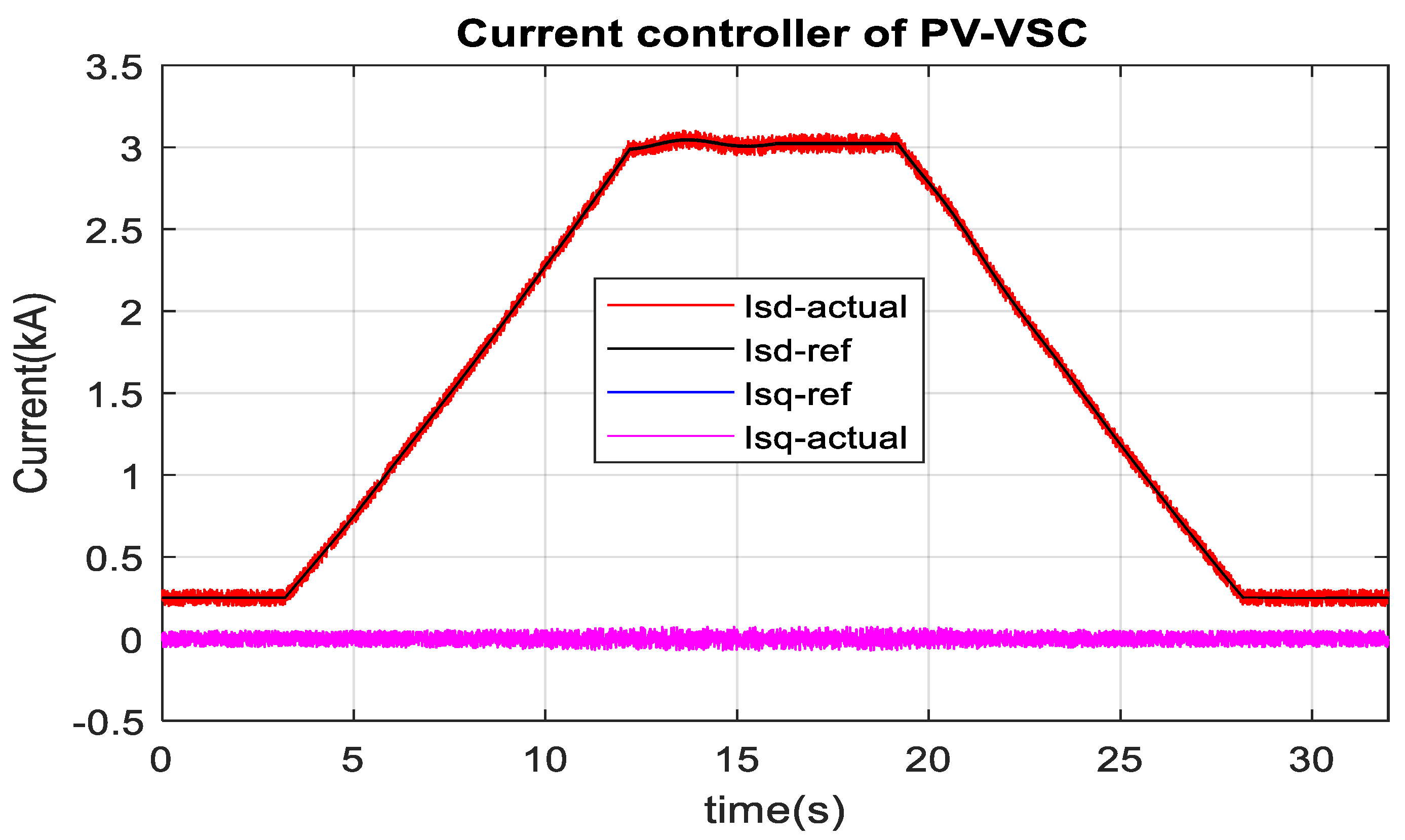
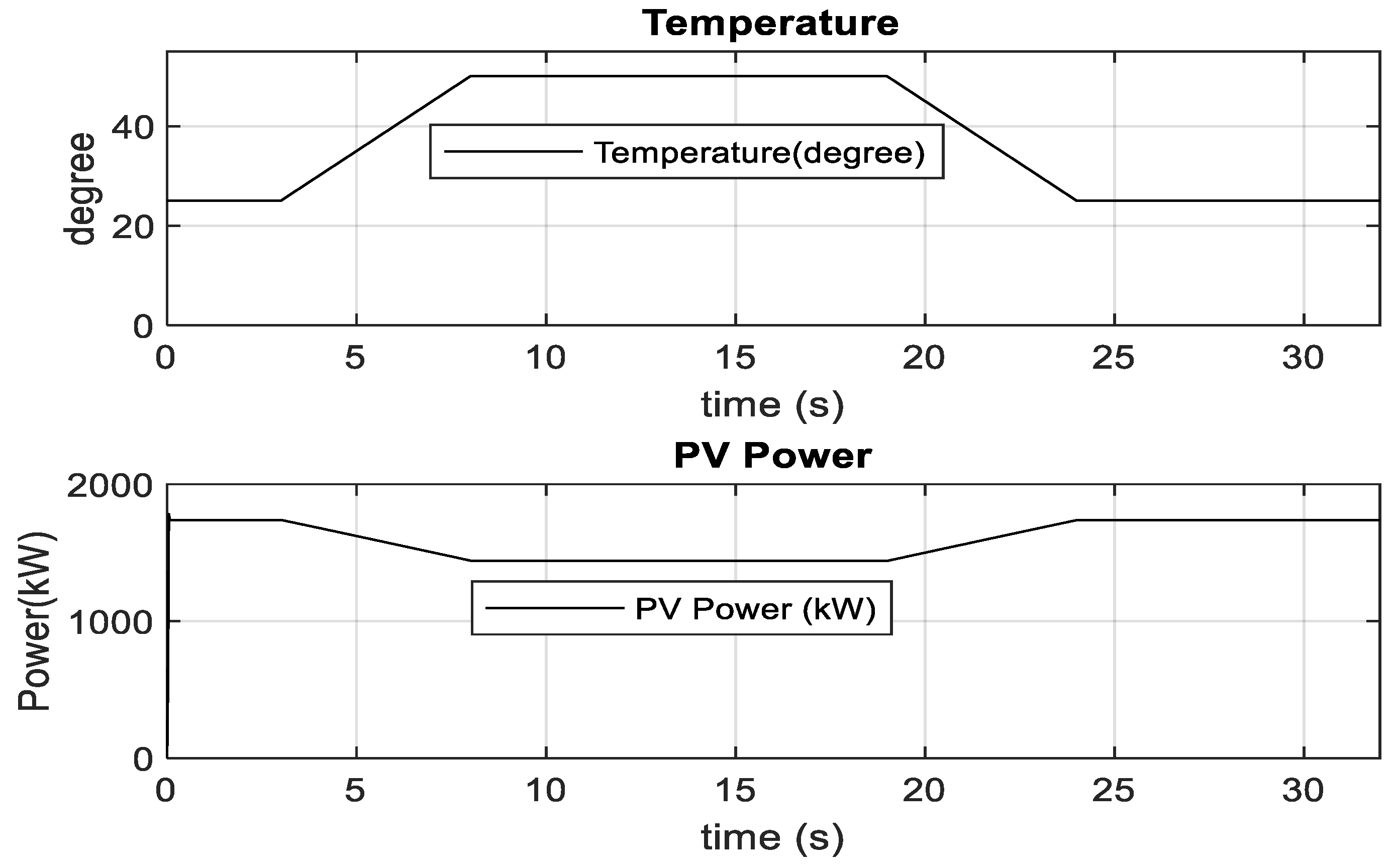
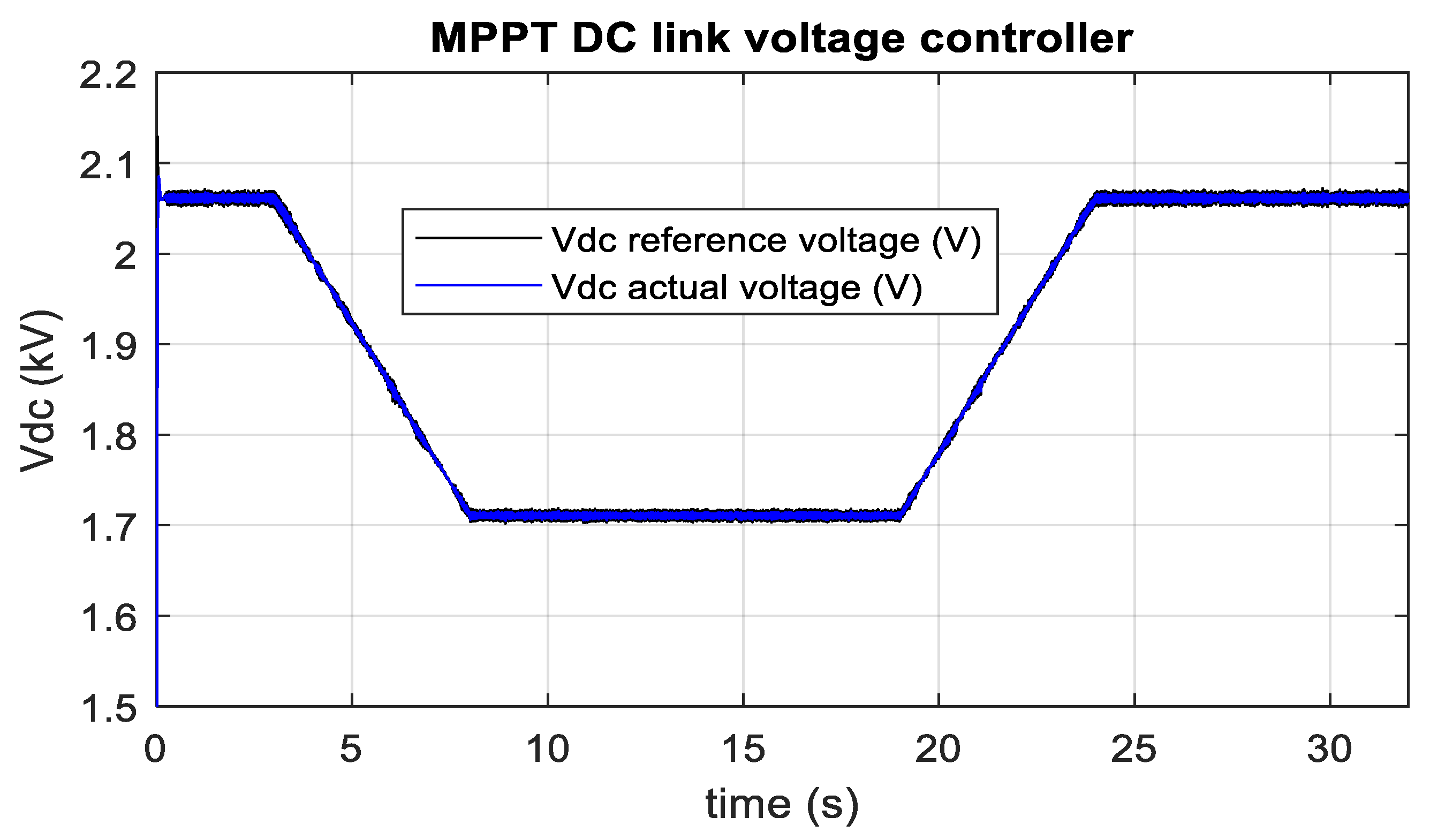
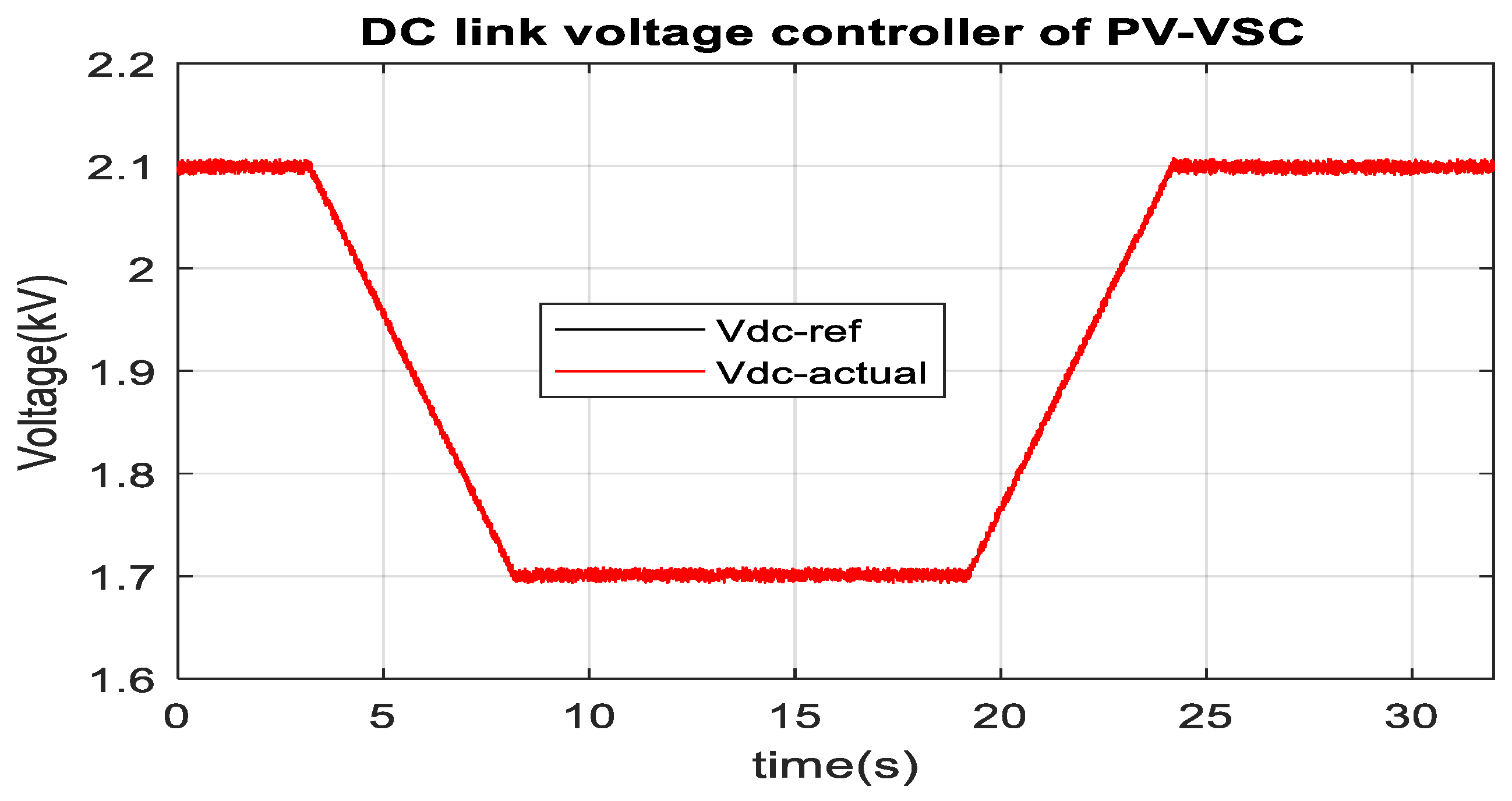
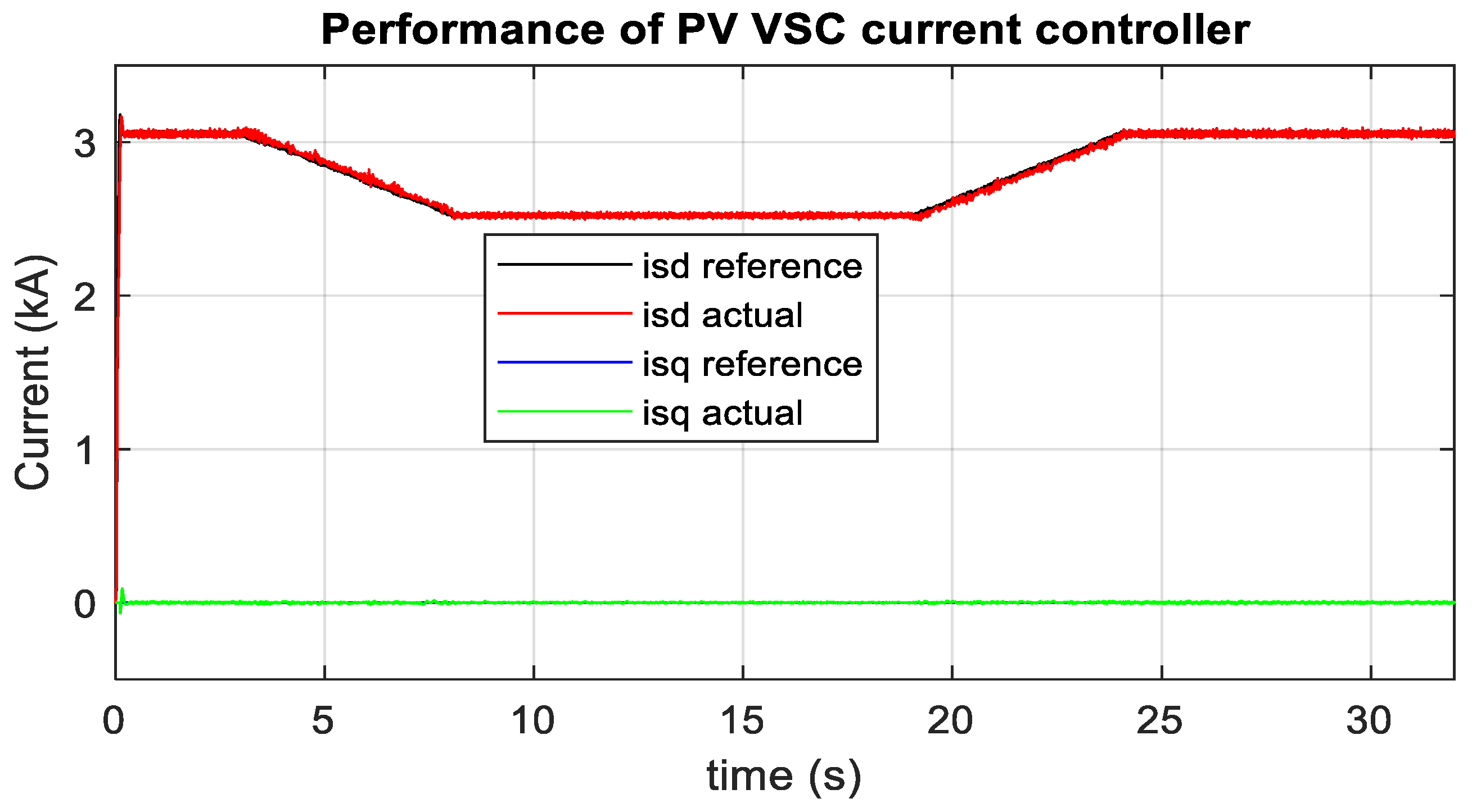
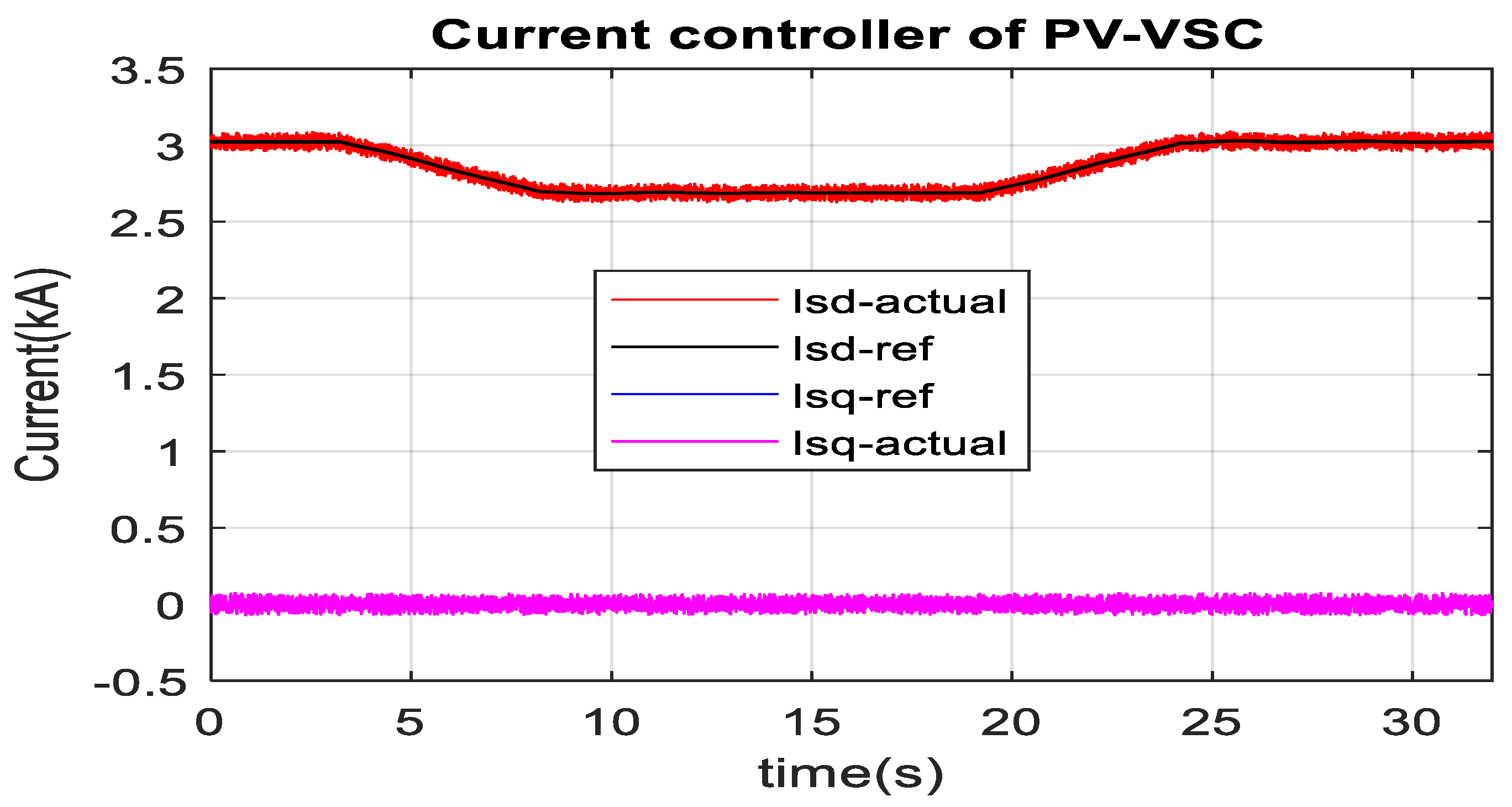
3.2. Optimum PV Integration
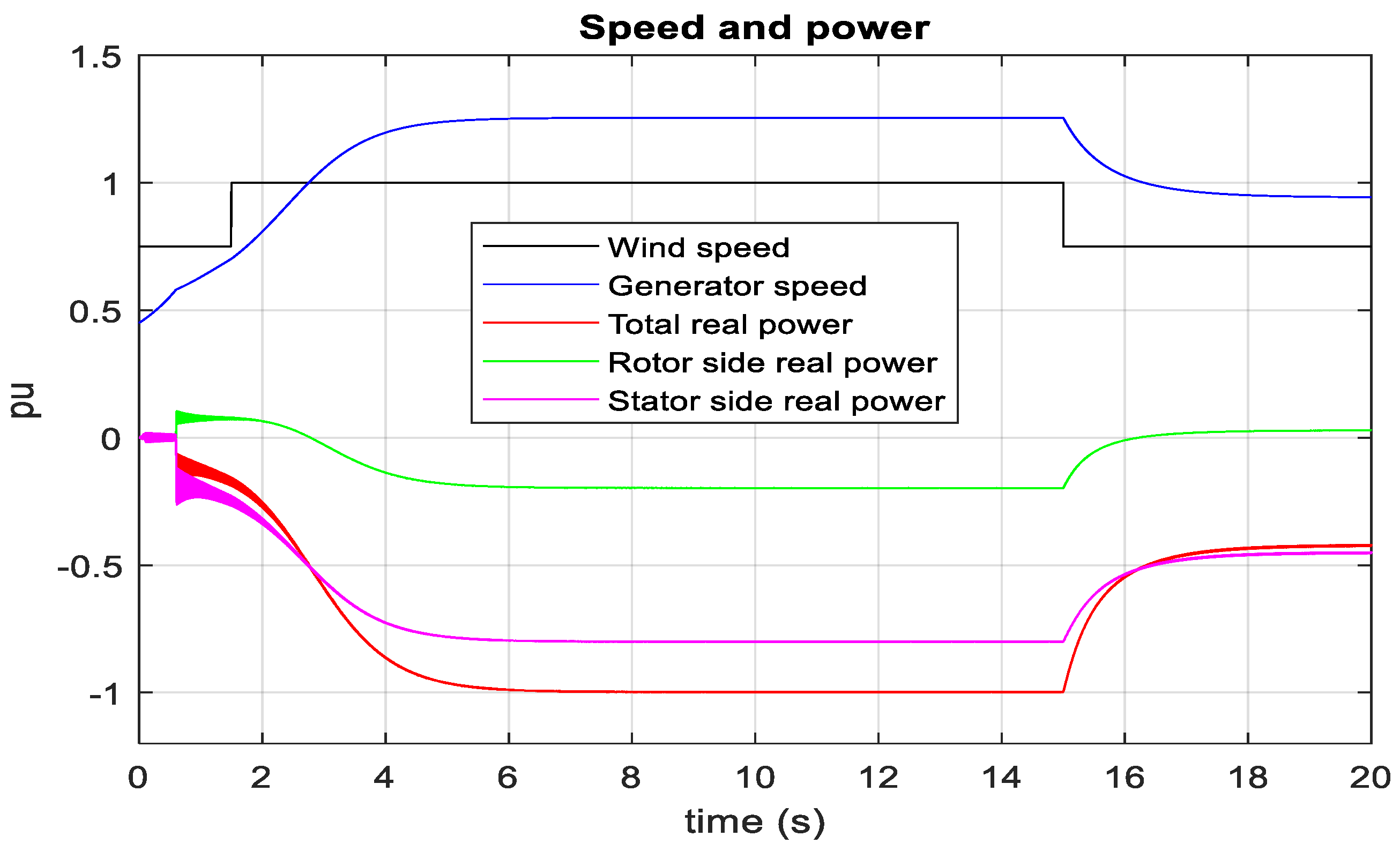
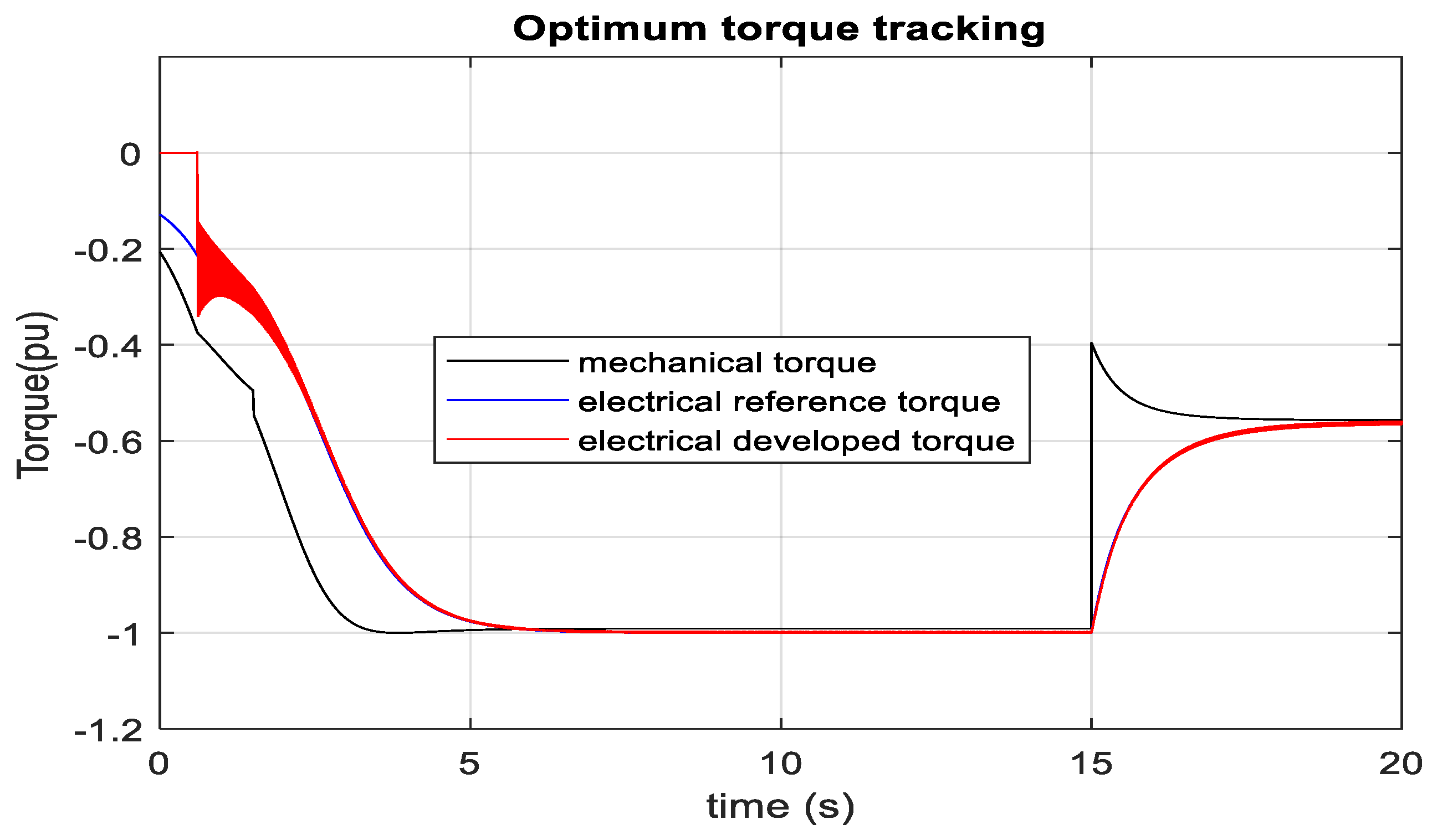
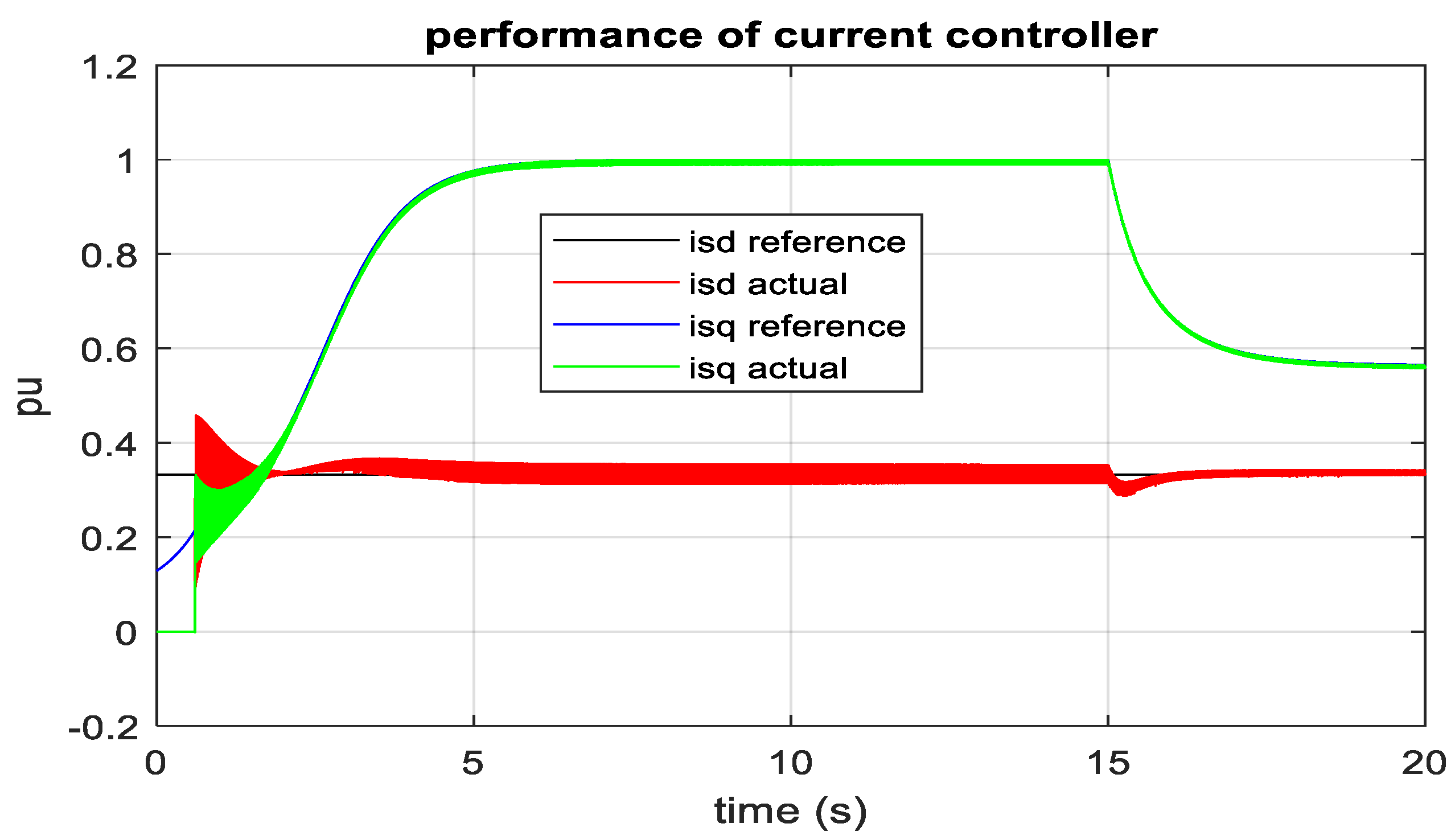
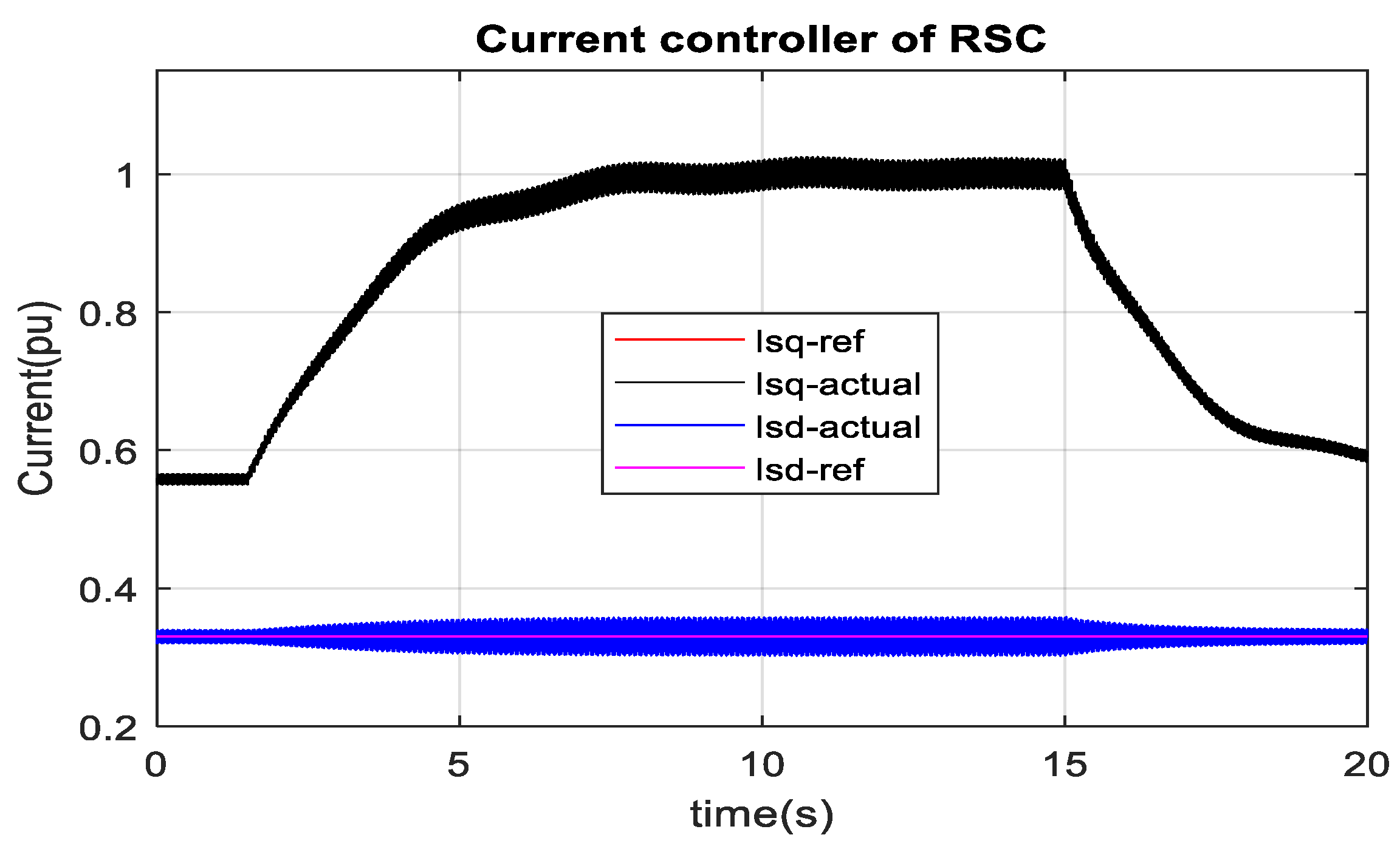
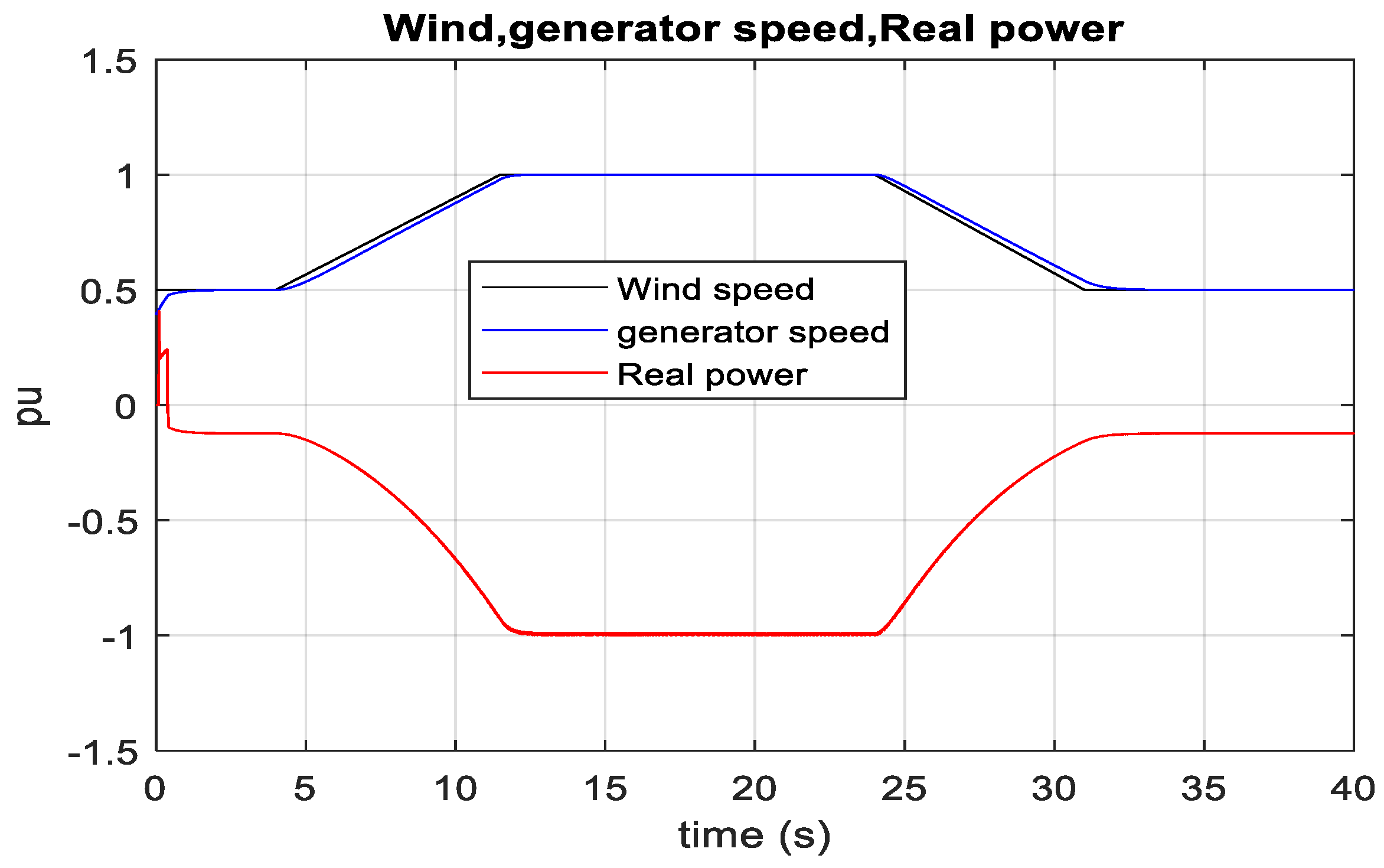
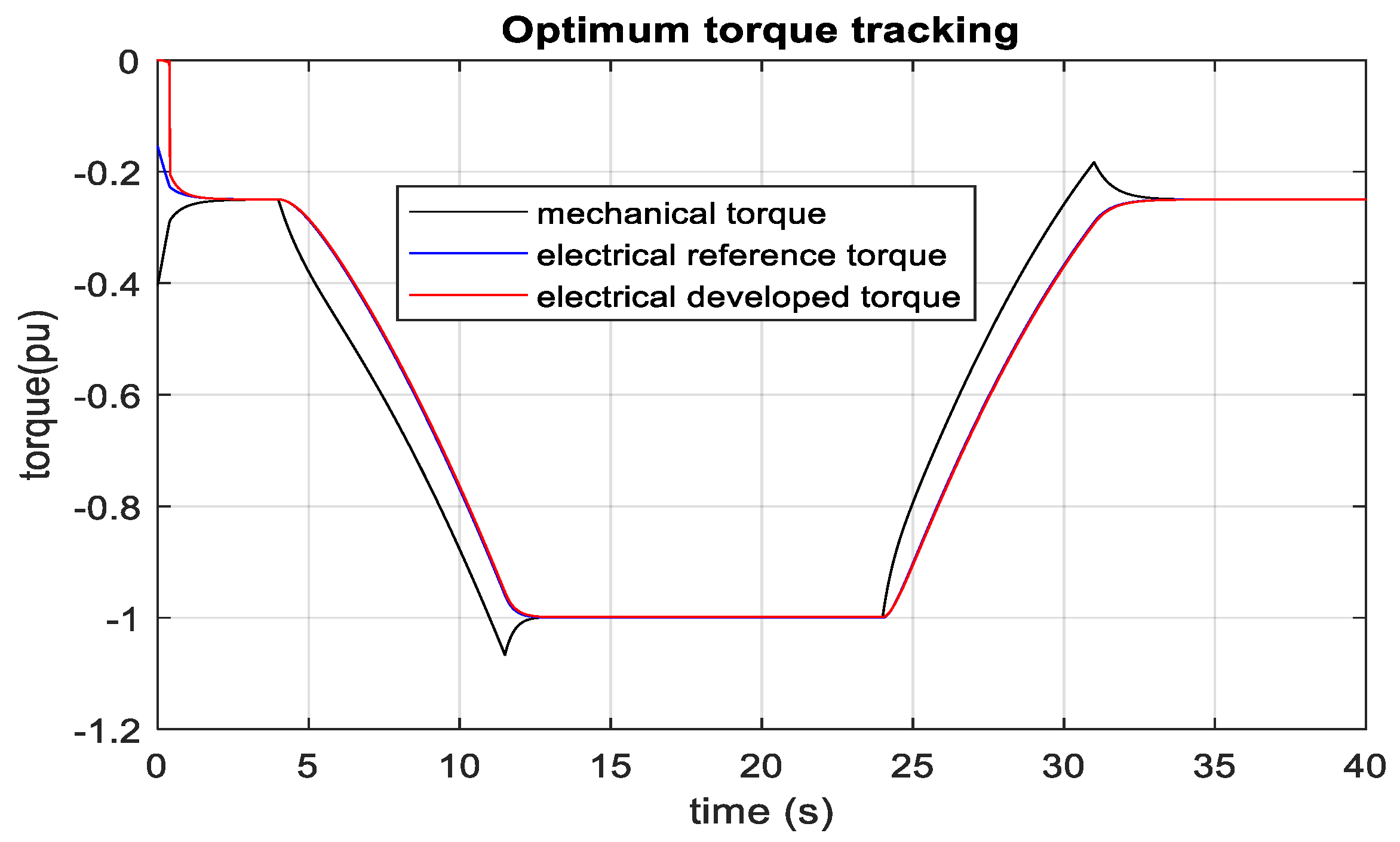
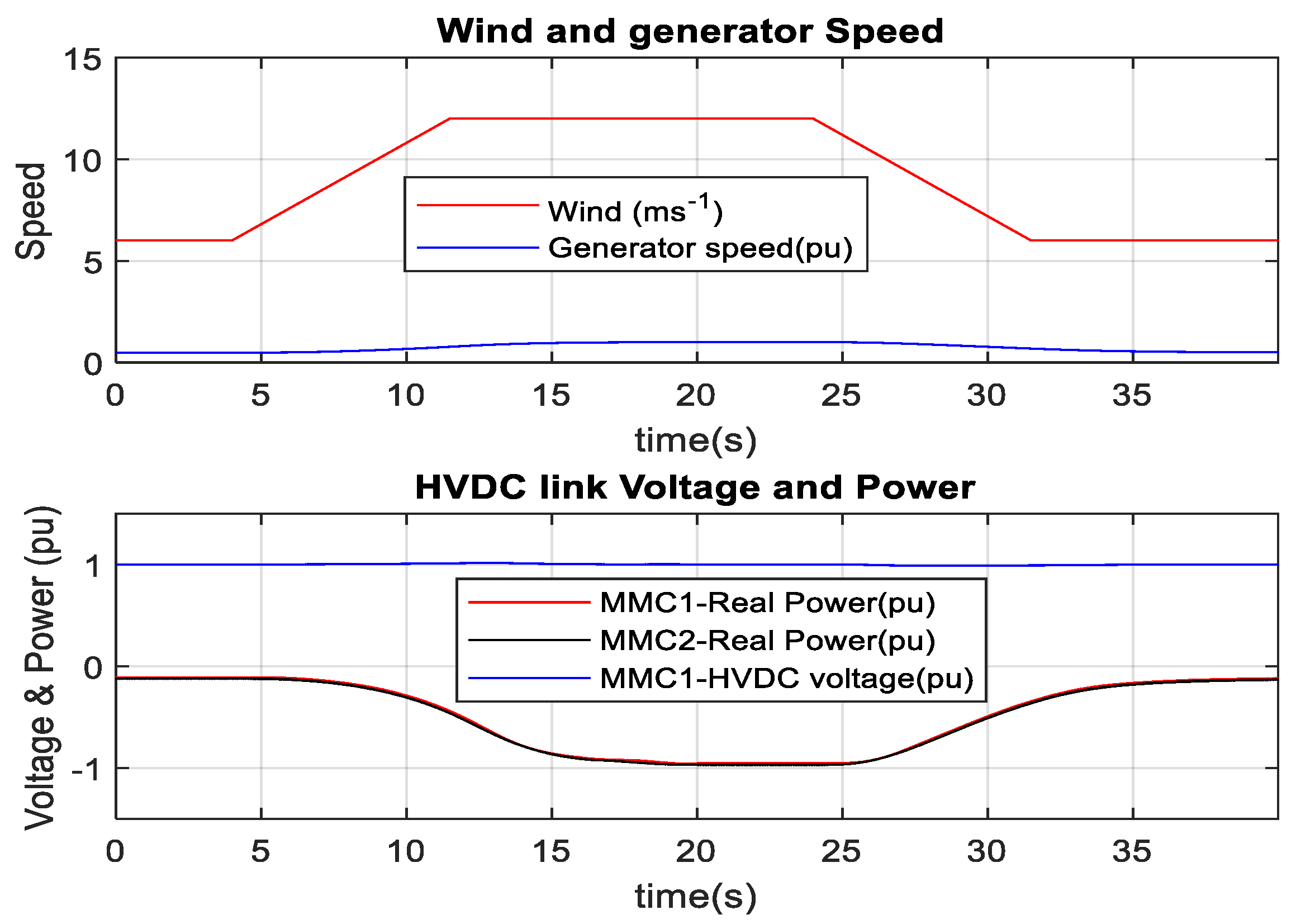
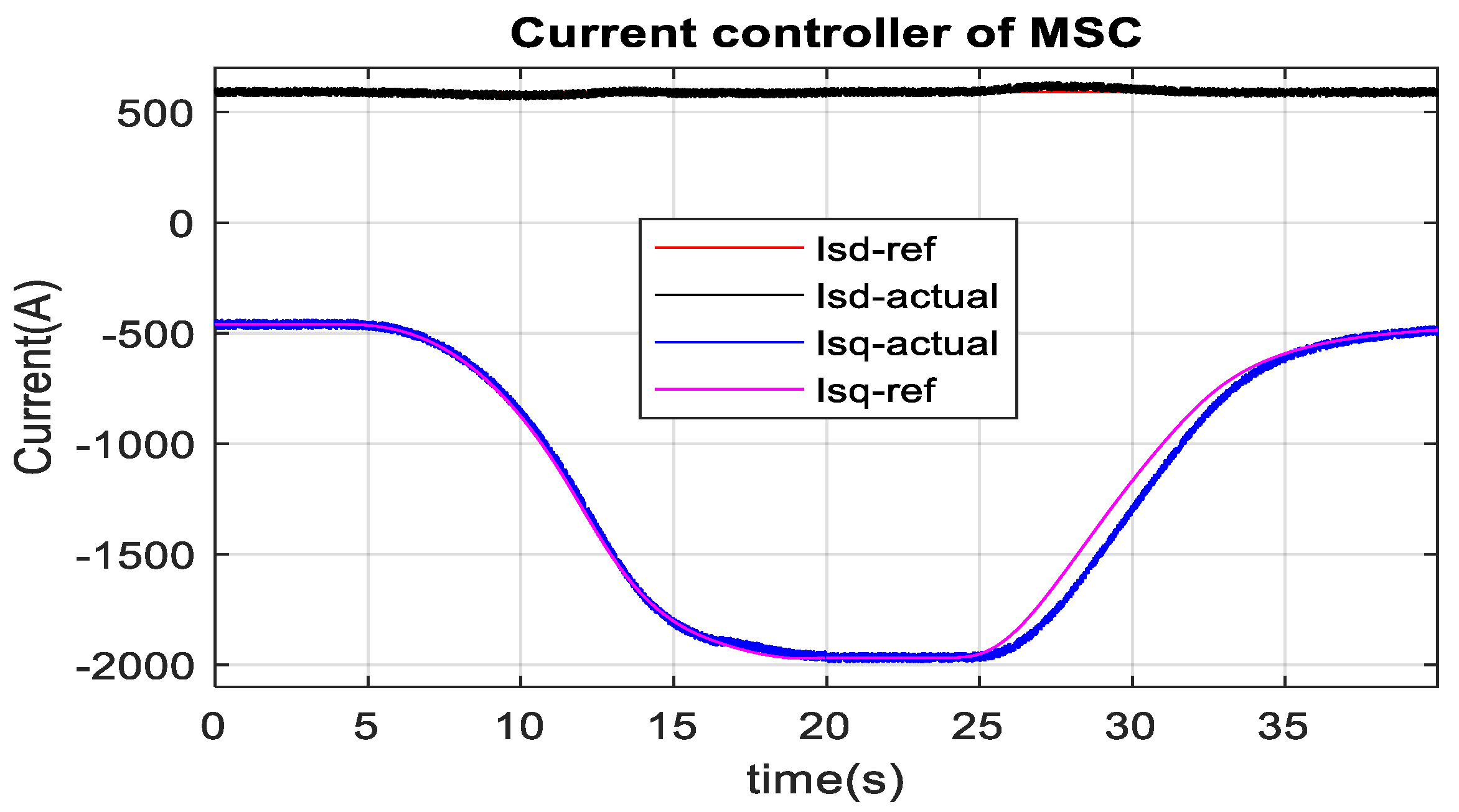
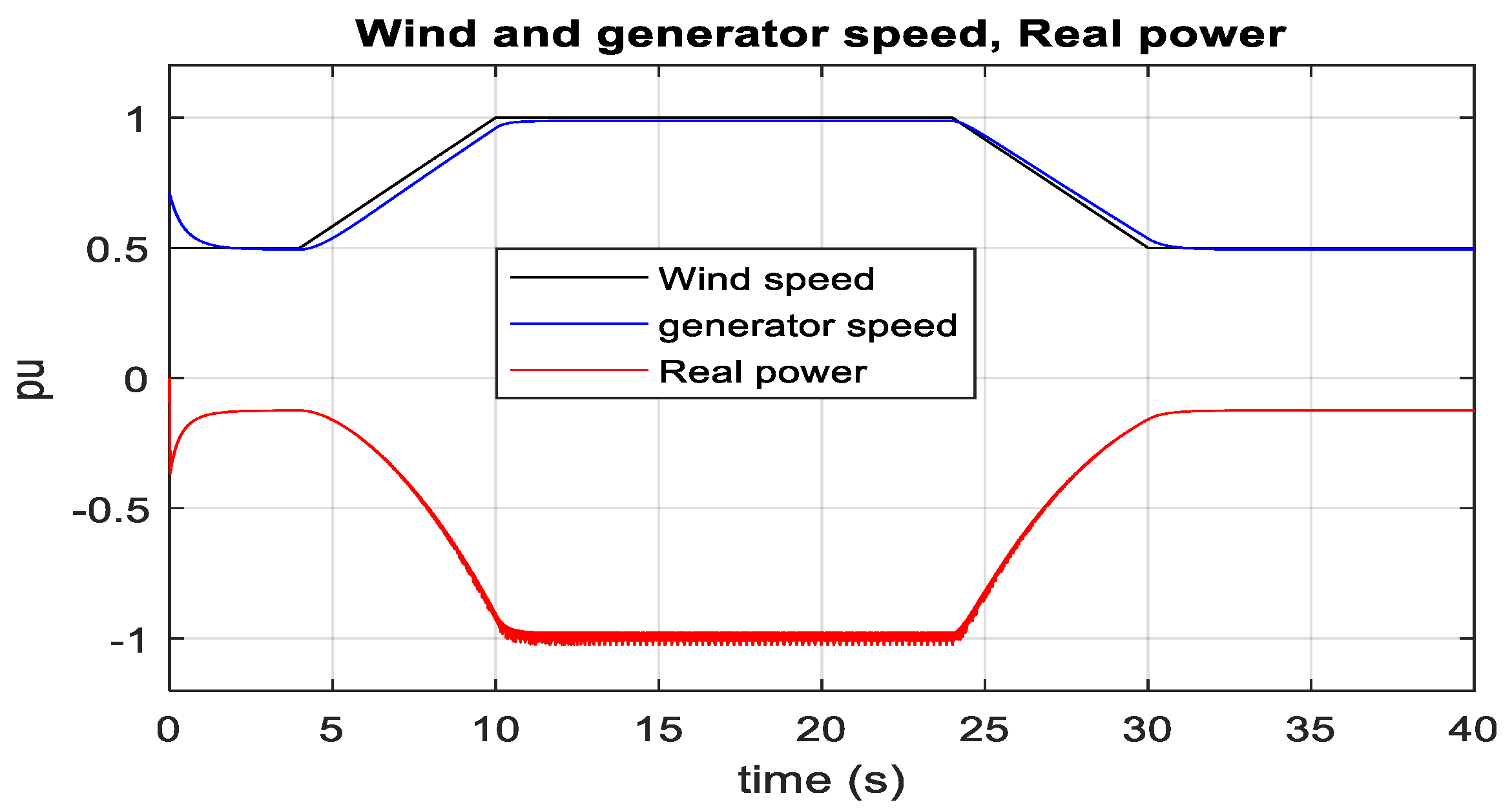
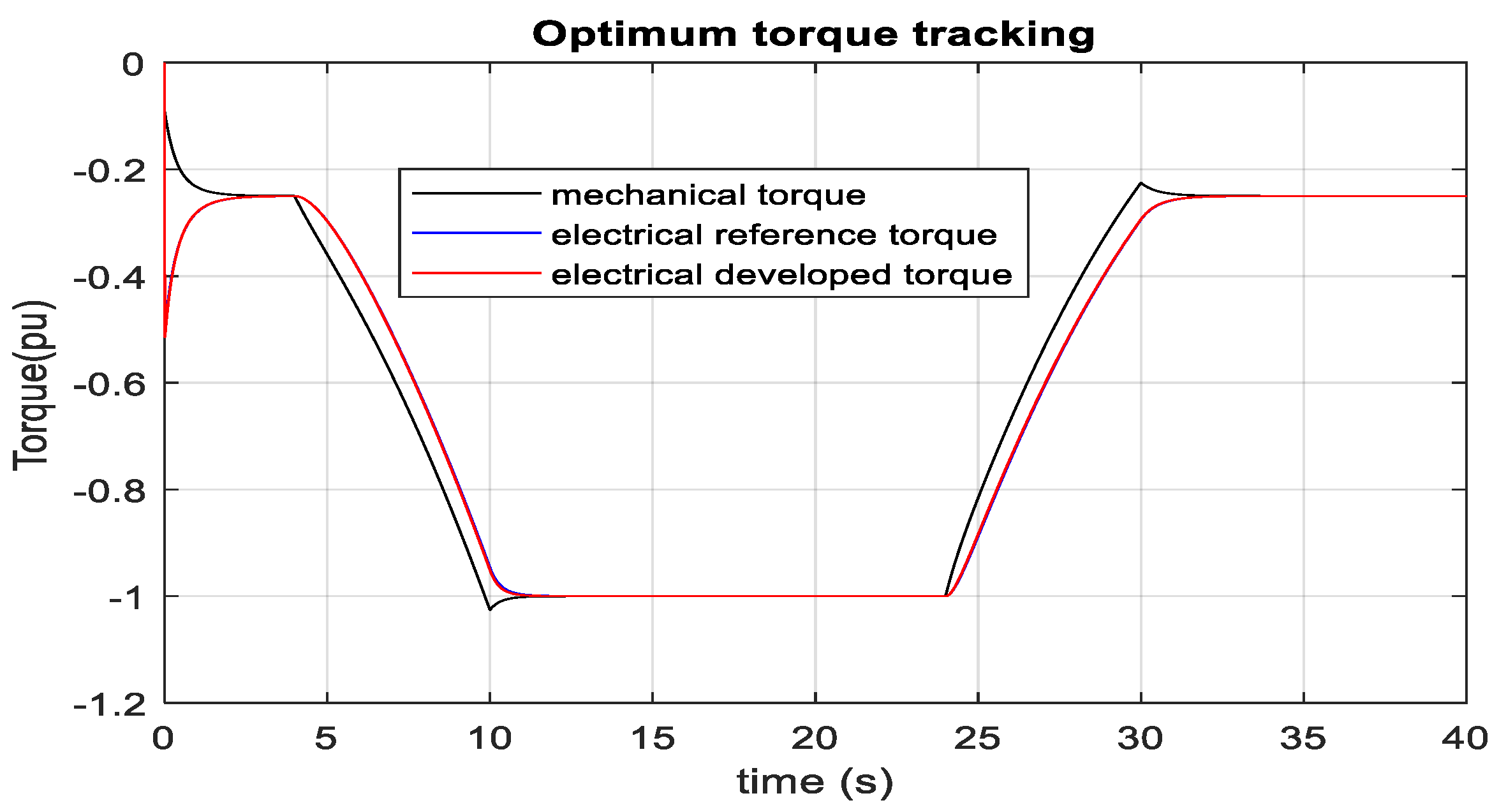
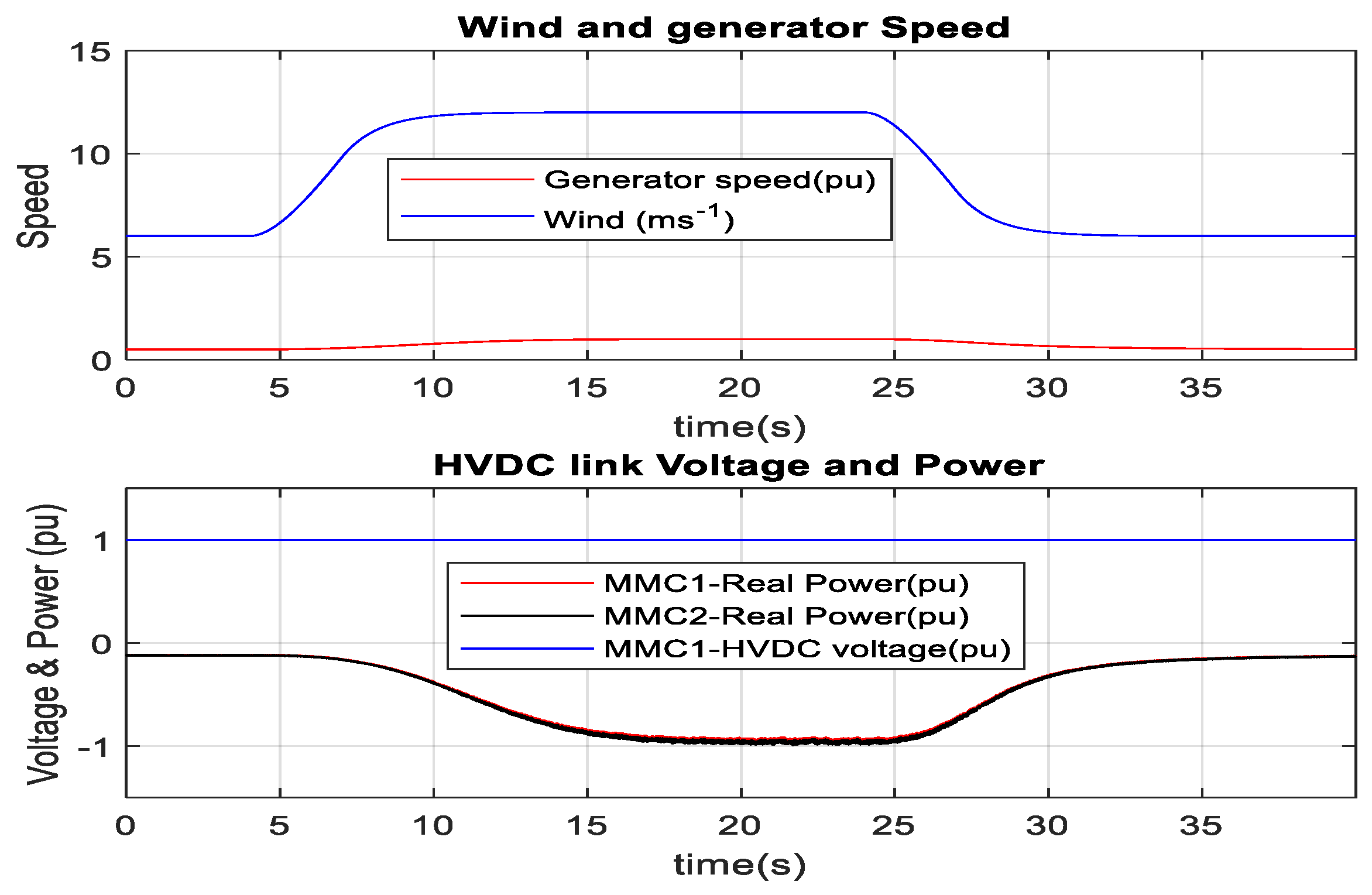
3.3. DFIG-Based Optimum Wind Energy Integration
3.4. SCIG-Based Optimum Wind Energy Integration
3.5. PMSG-Based Optimum Wind Energy Integration
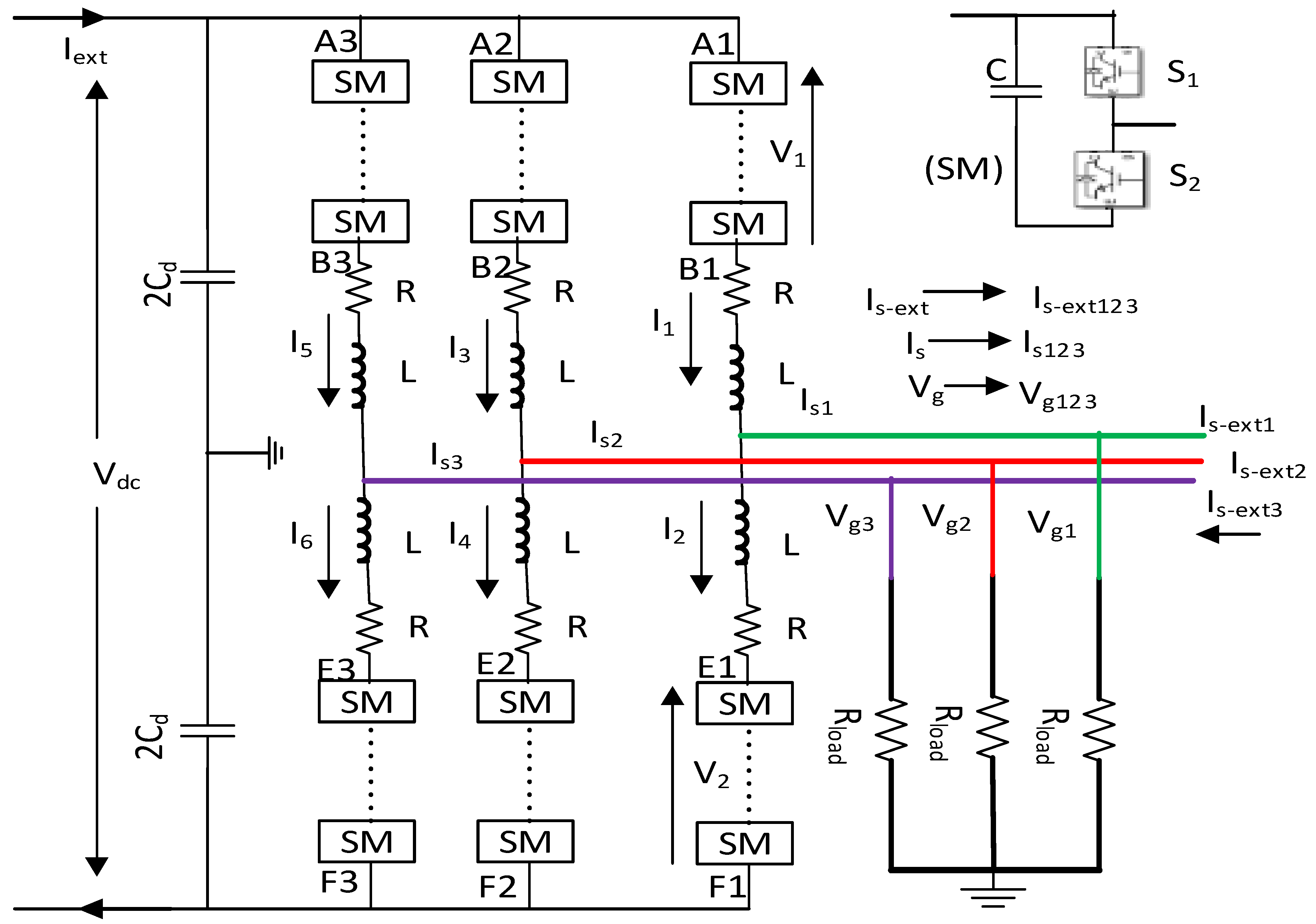
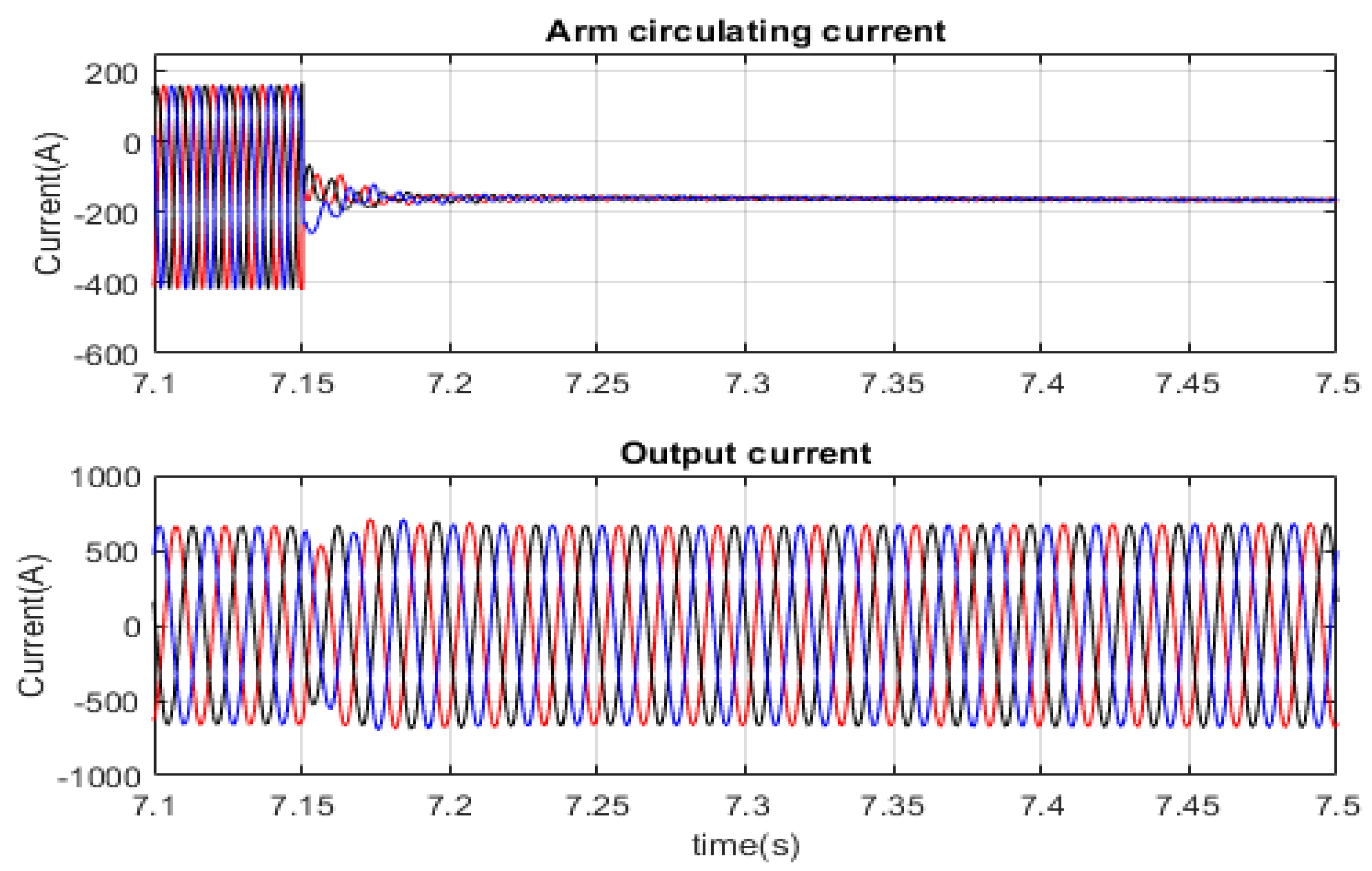
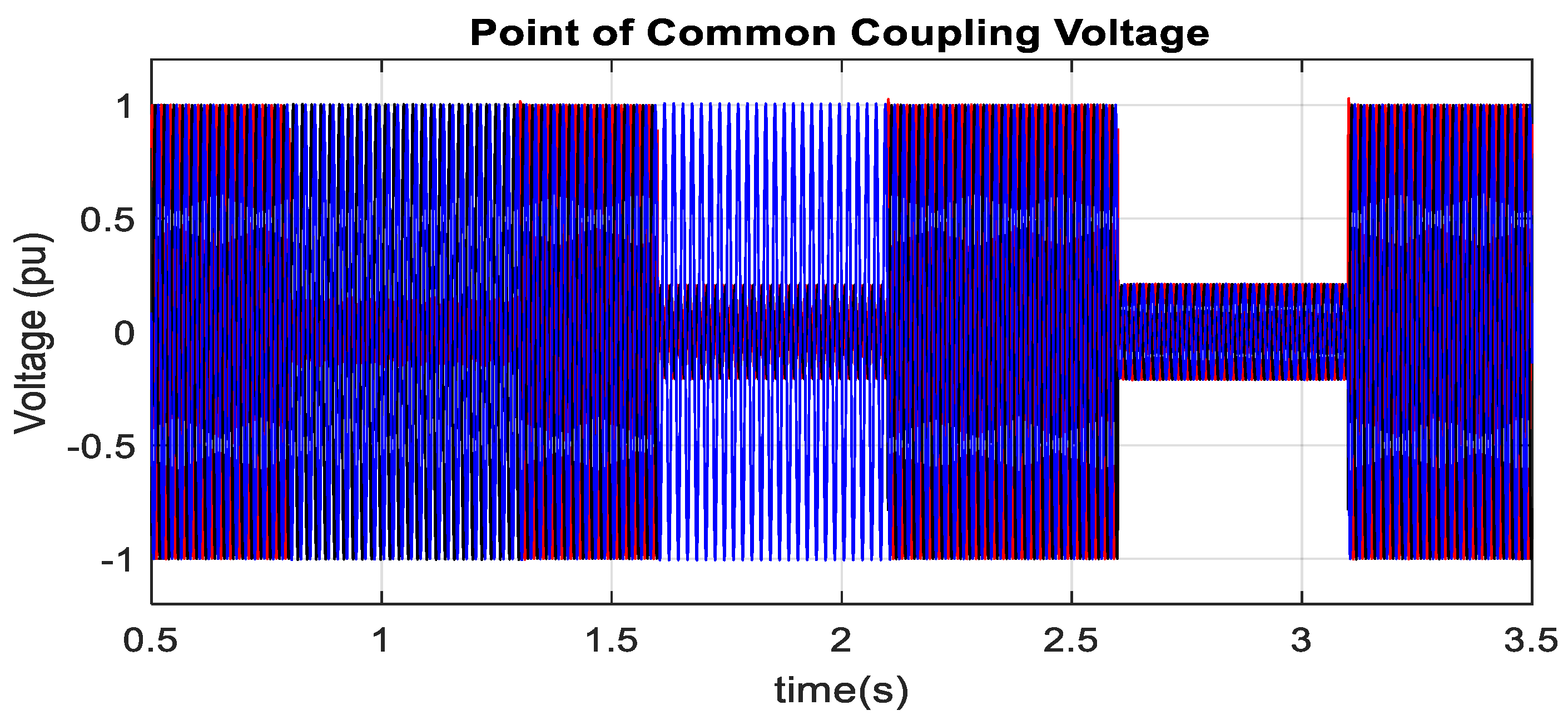
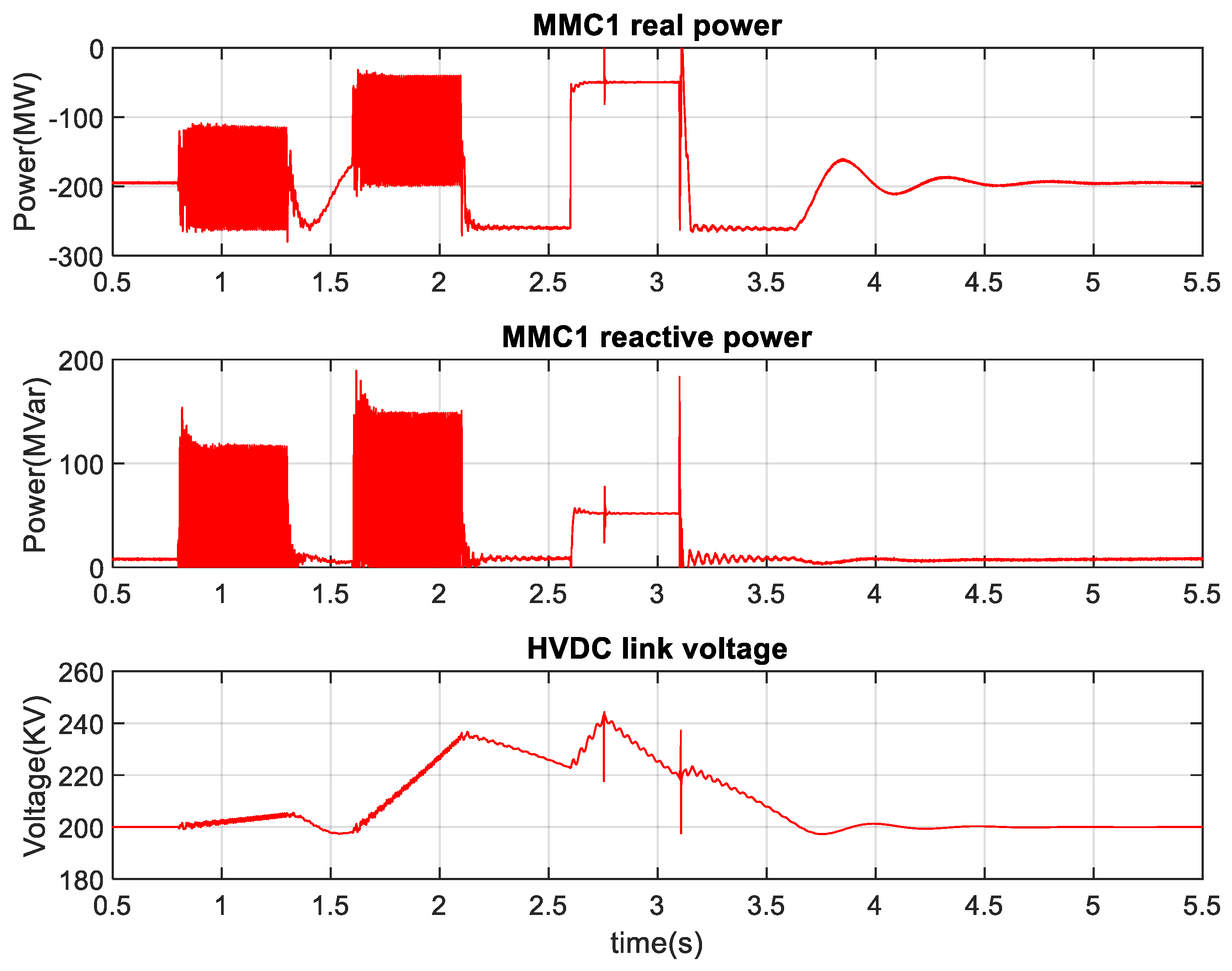
3.6. FRT Improvement of the MMC-HVDC System during Low Voltage Faults
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Photovoltaic Module Data | Wind Turbine Parameters | ||
|---|---|---|---|
| Quantity | Value | Quantity | Value |
| Cells per module | 36 | Nominal wind speed | 12 m/s |
| Short circuit current | 3.35 A | Nominal generator speed, DFIG/SCIG | 1.2 pu/1 pu |
| Open circuit voltage | 21.7 V | Nominal turbine power | 2 MW |
| Current at MPP | 3.05 A | DFIG and controller parameters | |
| Voltage at MPP | 17.4 V | Quantity | Value |
| Temperature coefficient of Isc | 0.065%/degree | Stator voltage (L-L) | 690 V |
| Temperature coefficient of Voc | −0.56%/degree | Nominal frequency, f | 50 Hz |
| Photovoltaic array data | Nominal power | 2.2 MVA | |
| Series connected modules per string | 115 | Stator resistance, RS | 1 mΩ |
| Parallel strings | 285 | Rotor resistance, Rr | 1.3 mΩ |
| Grid side VSC parameters for PV/DFIG/SCIG/PMSG | Total stator inductance, LS | 2.55 mH | |
| Quantity | Value | Total rotor inductance, Lr | 2.56 mH |
| Nominal DC link Voltage | 2 kV/1.5 kV/1.5 kV/6987 V | Magnetizing inductance, Lm | 2.44 mH |
| Rated power | 2.2 MVA | PI1 | 244 + 1400/s pu |
| Resistance, R | 0.004 pu | Filter inductance, LF | 4.3 µH |
| Inductance, L | 0.15 pu | Filter capacitance, CF | 1.47 mF |
| PI4 | (1 + 100/s) pu | Filter resistance, RF | 0.054 Ω |
| PI3 | (0.64 + 5/s) pu | M1, M2 | 56, 50 units |
| Squirrel Cage Induction Generator and Controller Parameters | Permanent Magnet Synchronous Generator and Controller Parameters | ||
|---|---|---|---|
| Quantity | Value | Quantity | Value |
| Stator voltage (L-L) | 690 V | Stator voltage (L-L) | 4 kV |
| Nominal frequency | 50 Hz | Nominal power | 2 MW |
| Nominal power | 2 MW | Number of pole pairs, P | 8 |
| Stator resistance, RS | 1 mΩ | Stator resistance | 2.21 mΩ |
| Rotor resistance, Rr | 1.3 mΩ | d and q axis inductance Ld and Lq | 9.816 mH |
| Total stator inductance, LS | 2.55 mH | Flux linkage established by magnets, λm | 7.0304 Vs |
| Total rotor inductance, Lr | 2.56 mH | PI1 | (4 + 1/s) pu |
| Magnetizing inductance, Lm | 2.44 mH | M3, M4 | 50 units |
| PI11 | 180 + 112.5/s pu | ||
| PI1 | 311 + 1400/s pu | ||
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Rated power | 250 MW | KP | 45 |
| Rated HVDC link voltage | 200 kV | ω1 | 314.159 rad/s |
| Rated AC voltage(L-L) | 100 kV | KI | 4500 |
| Rated frequency | 50 Hz | C | 16 mF |
| Resistance, R | 0.002 pu | Cd | 100 µF |
| Inductance, L | 0.2 pu | SM/arm | 200 |
| Modulation | Nearest level | K+ | 0.0625 |
| PI4 | (4 + 100/s) pu | k | 1.4142 |
| PI7 | 0.6 + 6/s pu | K- | 0.05 |
| PI10 | 0.8 + 100/s pu | DC line resistance | 1.39 mΩ/km |
| AC grids short circuit ratio | 10 | DC line inductance | 0.159 mH/km |
| DC line capacitance | 0.231 µF/km | ||
| DBR, R | 200 Ω |
References
- International Renewable Energy Agency IRENA. Renewable Power Generation Costs in 2019; IRENA: Abu Dhabi, United Arab Emirates, 2020. [Google Scholar]
- Shafiullah, M.; Ahmed, S.D.; Al-Sulaiman, F.A. Grid Integration Challenges and Solution Strategies for Solar PV Systems: A Review. IEEE Access 2022, 10, 52233–52257. [Google Scholar] [CrossRef]
- Roser, M. Why Did Renewables Become so Cheap so Fast? Available online: https://ourworldindata.org/cheap-renewables-growth (accessed on 7 April 2022).
- Wind Energy. Available online: https://www.irena.org/wind (accessed on 28 January 2021).
- Ahmed, S.D.; Al-Ismail, F.S.M.; Shafiullah, M.; Al-Sulaiman, F.A.; El-Amin, I.M. Grid Integration Challenges of Wind Energy: A Review. IEEE Access 2020, 8, 10857–10878. [Google Scholar] [CrossRef]
- Shafiullah, G.M.; Masola, T.; Samu, R.; Elavarasan, R.M.; Begum, S.; Subramaniam, U.; Romlie, M.F.; Chowdhury, M.; Arif, M.T. Prospects of Hybrid Renewable Energy-Based Power System: A Case Study, Post Analysis of Chipendeke Micro-Hydro, Zimbabwe. IEEE Access 2021, 9, 73433–73452. [Google Scholar] [CrossRef]
- Wang, Y.; Wen, W.; Wang, C.; Liu, H.; Zhan, X.; Xiao, X. Adaptive Voltage Droop Method of Multiterminal VSC-HVDC Systems for DC Voltage Deviation and Power Sharing. IEEE Trans. Power Deliv. 2019, 34, 169–176. [Google Scholar] [CrossRef]
- Manmohan, A.; Prasad, A.; Dharavath, R.; Karthikeyan, S.P.; Raglend, I.J. Up and Down Conversion of Photons with Modified Perturb and Observe MPPT Technique for Efficient Solar Energy Generation. Energy Procedia 2017, 117, 786–793. [Google Scholar] [CrossRef]
- Balato, M.; Costanzo, L.; Lo Schiavo, A.; Vitelli, M. Optimization of Both Perturb & Observe and Open Circuit Voltage MPPT Techniques for Resonant Piezoelectric Vibration Harvesters Feeding Bridge Rectifiers. Sens. Actuators A Phys. 2018, 278, 85–97. [Google Scholar] [CrossRef]
- Abdel-Salam, M.; El-Mohandes, M.-T.; Goda, M. An Improved Perturb-and-Observe Based MPPT Method for PV Systems under Varying Irradiation Levels. Sol. Energy 2018, 171, 547–561. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Lauss, G. The Performance of Perturb and Observe and Incremental Conductance Maximum Power Point Tracking Method under Dynamic Weather Conditions. Appl. Energy 2014, 119, 228–236. [Google Scholar] [CrossRef]
- Putri, R.I.; Wibowo, S.; Rifa’i, M. Maximum Power Point Tracking for Photovoltaic Using Incremental Conductance Method. Energy Procedia 2015, 68, 22–30. [Google Scholar] [CrossRef] [Green Version]
- Sitbon, M.; Lineykin, S.; Schacham, S.; Suntio, T.; Kuperman, A. Online Dynamic Conductance Estimation Based Maximum Power Point Tracking of Photovoltaic Generators. Energy Convers. Manag. 2018, 166, 687–696. [Google Scholar] [CrossRef]
- Hossain, M.I.; Shafiullah, M.; Abido, M. VSC Controllers for Multiterminal HVDC Transmission System: A Comparative Study. Arab. J. Sci. Eng. 2020, 45, 6411–6422. [Google Scholar] [CrossRef]
- Haleem, N.M.; Rajapakse, A.D.; Gole, A.M.; Fernando, I.T. Investigation of Fault Ride-Through Capability of Hybrid VSC-LCC Multi-Terminal HVDC Transmission Systems. IEEE Trans. Power Deliv. 2019, 34, 241–250. [Google Scholar] [CrossRef]
- Alassi, A.; Bañales, S.; Ellabban, O.; Adam, G.; MacIver, C. HVDC Transmission: Technology Review, Market Trends and Future Outlook. Renew. Sustain. Energy Rev. 2019, 112, 530–554. [Google Scholar] [CrossRef]
- Li, Z.; Zhan, R.; Li, Y.; He, Y.; Hou, J.; Zhao, X.; Zhang, X.-P. Recent Developments in HVDC Transmission Systems to Support Renewable Energy Integration. Glob. Energy Interconnect. 2018, 1, 595–607. [Google Scholar] [CrossRef]
- Hossain, M.I.; Abido, M.A. Positive-Negative Sequence Current Controller for LVRT Improvement of Wind Farms Integrated MMC-HVDC Network. IEEE Access 2020, 8, 193314–193339. [Google Scholar] [CrossRef]
- Li, R.; Xu, L.; Holliday, D.; Page, F.; Finney, S.J.; Williams, B.W. Continuous Operation of Radial Multiterminal HVDC Systems Under DC Fault. IEEE Trans. Power Deliv. 2016, 31, 351–361. [Google Scholar] [CrossRef] [Green Version]
- Saad, H.; Mahseredjian, J.; Dennetière, S.; Nguefeu, S. Interactions Studies of HVDC–MMC Link Embedded in an AC Grid. Electr. Power Syst. Res. 2016, 138, 202–209. [Google Scholar] [CrossRef]
- Stamatiou, G.; Bongiorno, M. Power-Dependent Droop-Based Control Strategy for Multi-Terminal HVDC Transmission Grids. IET Gener. Transm. Distrib. 2016, 11, 383–391. [Google Scholar] [CrossRef]
- Beerten, J.; Cole, S.; Belmans, R. Modeling of Multi-Terminal VSC HVDC Systems With Distributed DC Voltage Control. IEEE Trans. Power Syst. 2014, 29, 34–42. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhao, C.; Guo, C.; Rehman, A.U. Impacts on Operational Characteristics of AC/DC System with Different Grid Integration Modes of Offshore Wind Farm via MMC-Based HVDC Transmission. J. Eng. 2019, 2019, 1900–1905. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, C.; Guo, C.; Rehman, A.U. Dynamic Modeling and Small Signal Stability Analysis of PMSG-Based Wind Farm with MMC-HVDC System. CSEE J. Power Energy Syst. 2019, 6, 226–235. [Google Scholar] [CrossRef]
- Li, X.; Guo, L.; Hong, C.; Zhang, Y.; Li, Y.W.; Wang, C. Hierarchical Control of Multiterminal DC Grids for Large-Scale Renewable Energy Integration. IEEE Trans. Sustain. Energy 2018, 9, 1448–1457. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, C.; Guo, C. Small Signal Stability and Oscillation Suppression Method for Islanded Double Fed Induction Generator-Based Wind Farm Integrated by Modular Multilevel Converter Based HVDC System. Diangong Jishu Xuebao/Trans. China Electrotech. Soc. 2019, 34, 2116–2129. [Google Scholar] [CrossRef]
- Lyu, J.; Cai, X.; Molinas, M. Optimal Design of Controller Parameters for Improving the Stability of MMC-HVDC for Wind Farm Integration. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 40–53. [Google Scholar] [CrossRef] [Green Version]
- Raza, M.; Peñalba, M.A.; Gomis-Bellmunt, O. Short Circuit Analysis of an Offshore AC Network Having Multiple Grid Forming VSC-HVDC Links. Int. J. Electr. Power Energy Syst. 2018, 102, 364–380. [Google Scholar] [CrossRef]
- Cui, S.; Lee, H.-J.; Jung, J.-J.; Lee, Y.; Sul, S.-K. A Comprehensive AC-Side Single-Line-to-Ground Fault Ride Through Strategy of an MMC-Based HVDC System. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1021–1031. [Google Scholar] [CrossRef]
- Beza, M.; Bongiorno, M. Identification of Resonance Interactions in Offshore-Wind Farms Connected to the Main Grid by MMC-Based HVDC System. Int. J. Electr. Power Energy Syst. 2019, 111, 101–113. [Google Scholar] [CrossRef]
- Jing, Y.; Li, R.; Xu, L.; Wang, Y. Enhanced AC Voltage and Frequency Control on Offshore MMC Station for Wind Farm. J. Eng. 2017, 2017, 1264–1268. [Google Scholar] [CrossRef]
- Alam, M.S.; Abido, M.A.Y. Fault Ride-through Capability Enhancement of Voltage Source Converter-High Voltage Direct Current Systems with Bridge Type Fault Current Limiters. Energies 2017, 10, 1898. [Google Scholar] [CrossRef] [Green Version]
- Alam, M.; Abido, M.; Hussein, A.; El-Amin, I. Fault Ride through Capability Augmentation of a DFIG-Based Wind Integrated VSC-HVDC System with Non-Superconducting Fault Current Limiter. Sustainability 2019, 11, 1232. [Google Scholar] [CrossRef]
- Xu, L.; Andersen, B.R. Grid Connection of Large Offshore Wind Farms Using HVDC. Wind Energy 2006, 9, 371–382. [Google Scholar] [CrossRef]
- Nanou, S.; Papathanassiou, S. Evaluation of a Communication-Based Fault Ride-through Scheme for Offshore Wind Farms Connected through High-Voltage DC Links Based on Voltage Source Converter. IET Renew. Power Gener. 2015, 9, 882–891. [Google Scholar] [CrossRef]
- Cui, S.; Lee, H.-J.; Jung, J.-J.; Lee, Y.; Sul, S.-K. A Comprehensive AC Side Single Line to Ground Fault Ride through Strategy of a Modular Multilevel Converter for HVDC System. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 5378–5385. [Google Scholar]
- Oguma, K.; Akagi, H. Low-Voltage-Ride-Through (LVRT) Control of an HVDC Transmission System Using Two Modular Multilevel DSCC Converters. IEEE Trans. Power Electron. 2017, 32, 5931–5942. [Google Scholar] [CrossRef]
- Olowookere, O.; Skarvelis-Kazakos, S.; Habtay, Y.; Woodhead, S. AC Fault Ride through of Modular Multilevel Converter VSC-HVDC Transmission Systems. In Proceedings of the 2015 50th International Universities Power Engineering Conference (UPEC), Stoke-on-Trent, UK, 1–4 September 2015; pp. 1–6. [Google Scholar]
- Feltes, C.; Wrede, H.; Koch, F.W.; Erlich, I. Enhanced Fault Ride-Through Method for Wind Farms Connected to the Grid Through VSC-Based HVDC Transmission. IEEE Trans. Power Syst. 2009, 24, 1537–1546. [Google Scholar] [CrossRef]
- Hossain, M.I.; Abido, M.A. Active Power Control of PV-Battery Connected MMC-HVDC System for FRT Support. Appl. Sci. 2020, 10, 7186. [Google Scholar] [CrossRef]
- Hossain, M.I.; Abido, M.A. SCIG Based Wind Energy Integrated Multiterminal MMC-HVDC Transmission Network. Sustainability 2020, 12, 3622. [Google Scholar] [CrossRef]
- Moawwad, A.; El Moursi, M.S.; Xiao, W. Advanced Fault Ride-Through Management Scheme for VSC-HVDC Connecting Offshore Wind Farms. IEEE Trans. Power Syst. 2016, 31, 4923–4934. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; Wiley-IEEE Press: Hoboken, NJ, USA, 2010; ISBN 9780470551578. [Google Scholar]
- Sharifabadi, K.; Harnefors, L.; Nee, H.P.; Norrga, S.; Teodorescu, R. Design, Control and Application of Modular Multilevel Converters for HVDC Transmission Systems; Wiley: Hoboken, NJ, USA, 2016; ISBN 9781118851555. [Google Scholar]
- Martinez-Rodrigo, F.; Ramirez, D.; Rey-Boue, A.B.; De Pablo, S.; Herrero-De Lucas, L.C. Modular Multilevel Converters: Control and Applications. Energies 2017, 10, 1709. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, M.I.; Shafiullah, M.; Al-Sulaiman, F.A.; Abido, M.A. Comprehensive Analysis of PV and Wind Energy Integration into MMC-HVDC Transmission Network. Sustainability 2023, 15, 253. https://doi.org/10.3390/su15010253
Hossain MI, Shafiullah M, Al-Sulaiman FA, Abido MA. Comprehensive Analysis of PV and Wind Energy Integration into MMC-HVDC Transmission Network. Sustainability. 2023; 15(1):253. https://doi.org/10.3390/su15010253
Chicago/Turabian StyleHossain, Md Ismail, Md Shafiullah, Fahad A. Al-Sulaiman, and Mohammad A. Abido. 2023. "Comprehensive Analysis of PV and Wind Energy Integration into MMC-HVDC Transmission Network" Sustainability 15, no. 1: 253. https://doi.org/10.3390/su15010253
APA StyleHossain, M. I., Shafiullah, M., Al-Sulaiman, F. A., & Abido, M. A. (2023). Comprehensive Analysis of PV and Wind Energy Integration into MMC-HVDC Transmission Network. Sustainability, 15(1), 253. https://doi.org/10.3390/su15010253









