Optimal Scheduling of AC–DC Hybrid Distribution Network Considering the Control Mode of a Converter Station
Abstract
1. Introduction
- (1)
- Achieving load balancing between different DSAs and relieving the pressure of power supply in high load rate DSAs [3].
- (2)
- Enhance the capability of renewable energy consumption [2].
- (3)
- Provide an efficient interface for DC loads and DC power sources.
- (4)
- Improve the reliability of power supply [4].
- (5)
- Delaying investments. The interconnection of AC–DSAs offers an effective solution to integrate surplus transformer capacity, meet the growing demand, and postpone the need for capacity expansion investments and construction.
- (1)
- An optimal scheduling model is proposed based on the actual requirements of flexible interconnection DSAs, with the objectives of balancing the load rate, improving the voltage profile, and reducing the operation cost.
- (2)
- The influence of the control mode is analyzed and considered in the optimal scheduling model by taking the control mode of the converter stations as decision variables. By making a reasonable decision on the selection of the control mode of each converter, the voltage deviation on the DC side can be effectively reduced. From a mathematical perspective, taking the control mode of converters into account provides more decision variables for the optimization model, expanding the feasible solution space and enabling a more optimal solution to be found.
2. Mathematical Model of Flexible Interconnected DSAs Considering Control Modes of Converter Stations
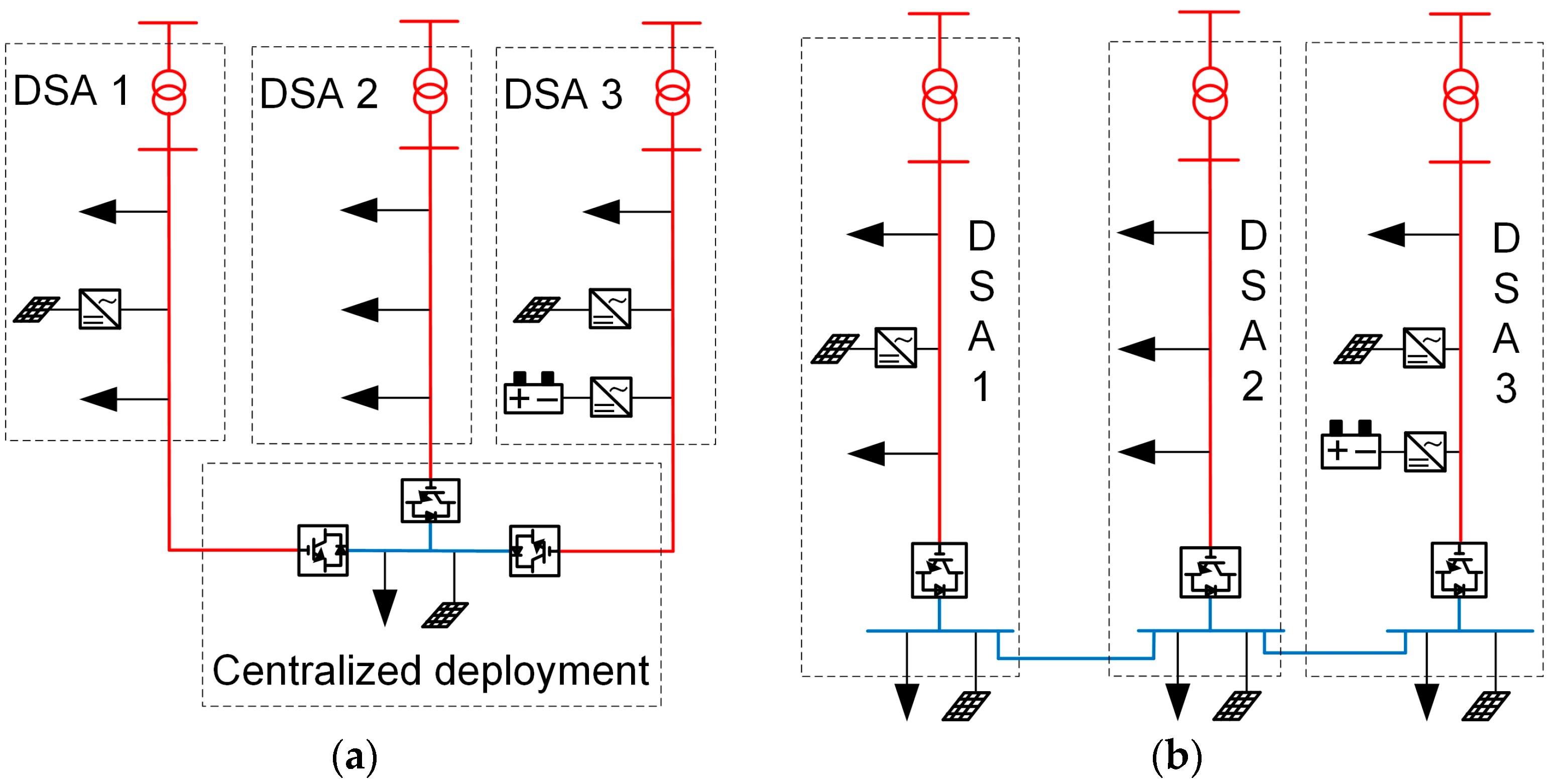
2.1. Topologies of Flexible Interconnected DSAs
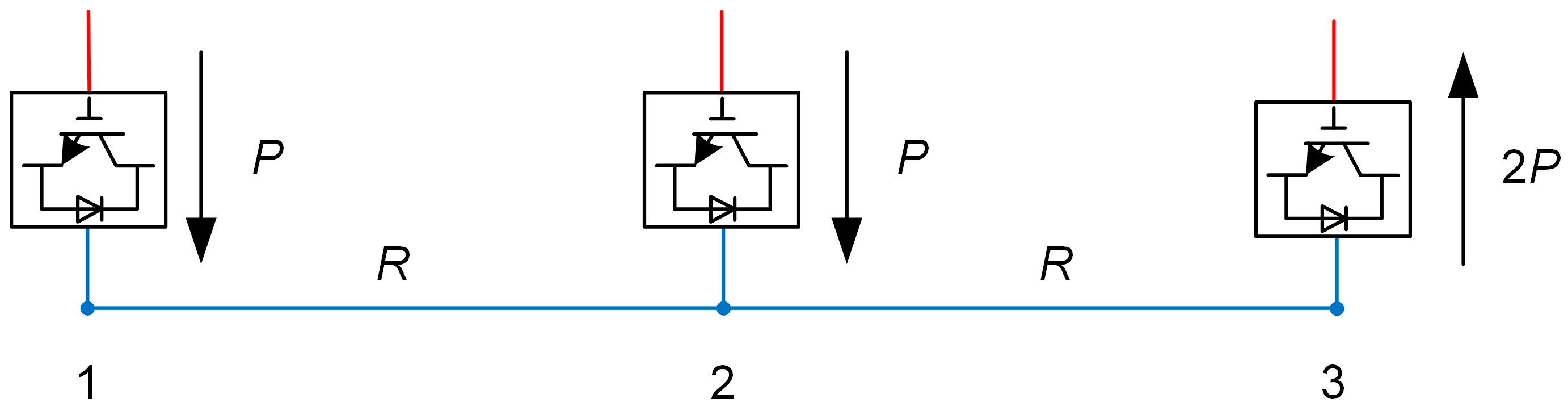
2.2. The Influence of the Control Mode of Converter Station on Voltage Profile on the DC Side
2.3. Mathematical Model of Flexible Interconnected DSAs
2.3.1. Mathematical Model of Converter Station Considering Control Mode
2.3.2. Mathematical Model of Power Flow on the AC Side [23]
2.3.3. Mathematical Model of Power Flow on the DC Side [18]
2.3.4. Mathematical Model of ESS [17]
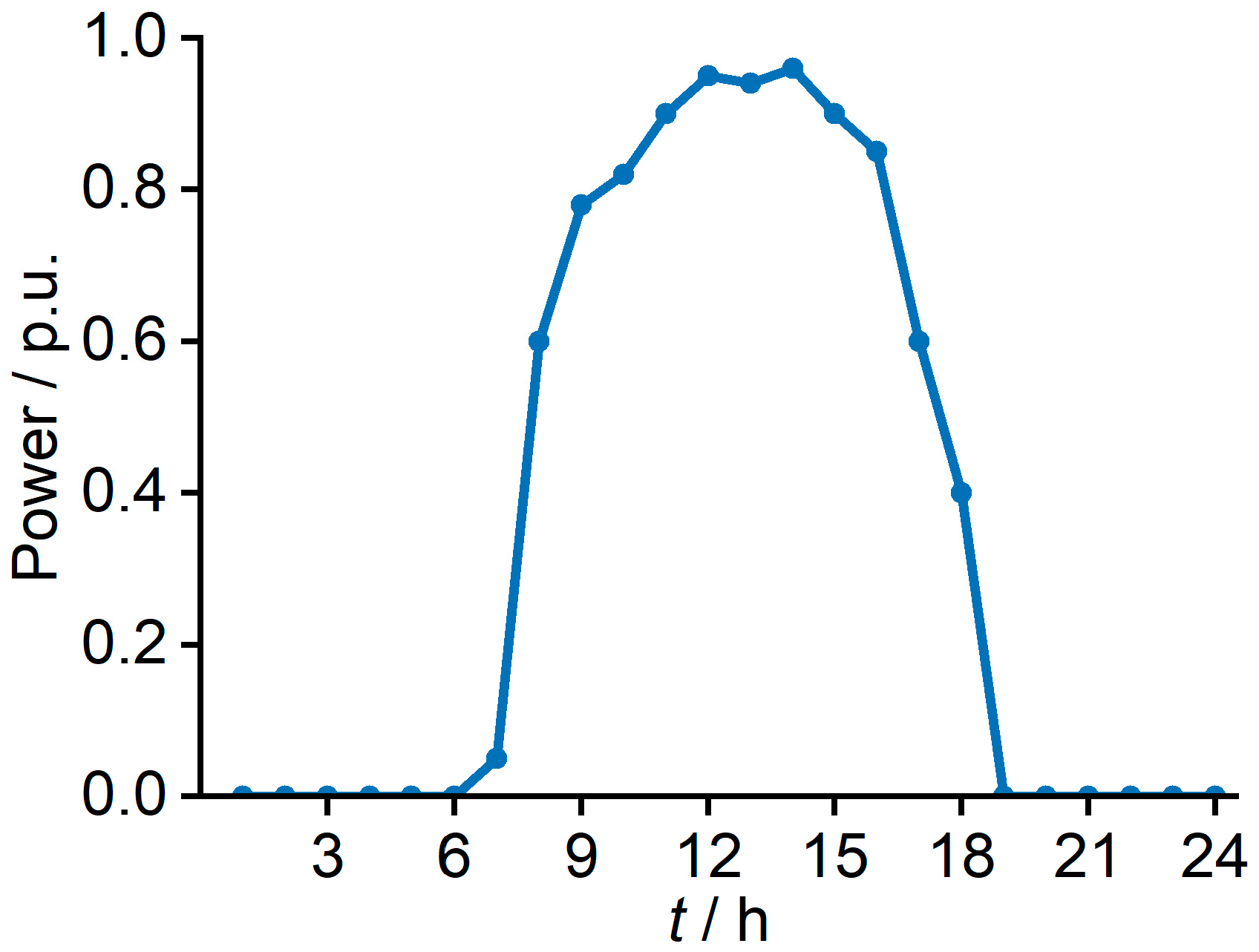
2.3.5. Mathematical Model of PV
3. Optimal Scheduling Model for Flexible Interconnected DSAs
3.1. Objective Function
- (1)
- The specific expression of f1 is shown in Equation (20).where T is the dispatch period, D is the set of DSAs, Pd, t is the active power flowing through the distribution transformer of the d-th DSA at time t, Sd is the capacity of the distribution transformer of the d-th DSA, and nd is the number of DSAs.
- (2)
- The specific expression of f2 is shown in Equation (21).where is the set of nodes in the whole flexible interconnected DSAs, and UN is the rated voltage at node j.
- (3)
- The specific expression of f3 is shown in Equation (22).where closs is the unit price of power losses, Ω is the set of all branches, ccost is the unit price of electricity purchased from the superior grid, ccur is the penalty unit price of PV output curtailment, and is the set of nodes connected to PV.
3.2. Constraints
3.2.1. Operation Constraints on the AC Side
- (1)
- Balance of the power injected into the nodes:where is the reactive power output of the PV connected to node j at time t. and are the active and reactive power demand of the load at node j at time t.
- (2)
- Security constraints:where and are the upper and lower limits of the voltage magnitude on the AC side, respectively, and the is the upper limit of the current magnitude on the AC side. According to standard [24], the voltage deviation allowed in the 380 V AC low-voltage distribution network is −10%, +7%.
3.2.2. Operation Constraints on the DC Side
- (1)
- Balance of the power injected into the nodes:
- (2)
- Security constraints:where is the upper limit of the current magnitude on the DC side. According to standard [25], the voltage deviation allowed in the DC distribution network for voltage levels below 1500 V is −20%, +5%.
3.2.3. Operation Constraints of the ESS
- (1)
- Constraints of SoC:where and are the lower and upper limits of the SoC of the ESS connected to the node j, respectively, and Equation (31) indicates that the initial SoC and the final SoC remain equal during a scheduling period (usually 24 h).
- (2)
- Constraints of charge and discharge power:where and are binary variables indicating the discharging and charging states. indicates discharging, and indicates charging; Equation (35) indicates that the ESS is not in charging and discharging states at the same time, and and indicate the upper limit of the charging and discharging power, respectively.
3.2.4. Constraint of PV Capacity
3.2.5. Constraint of Distribution Transformers
3.3. Model Conversion
4. Case Study
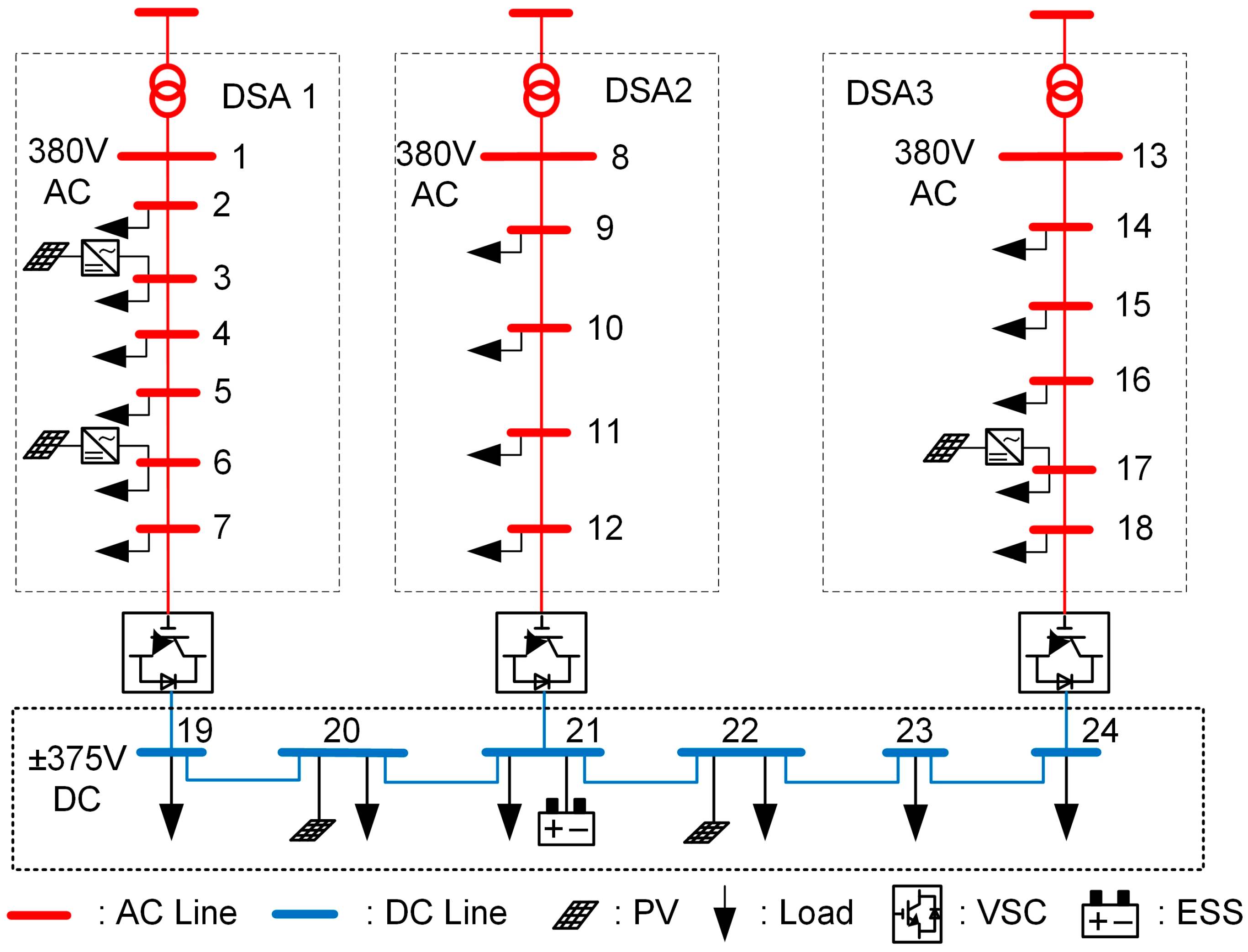
4.1. Setting of the Case
4.2. Results Analysis
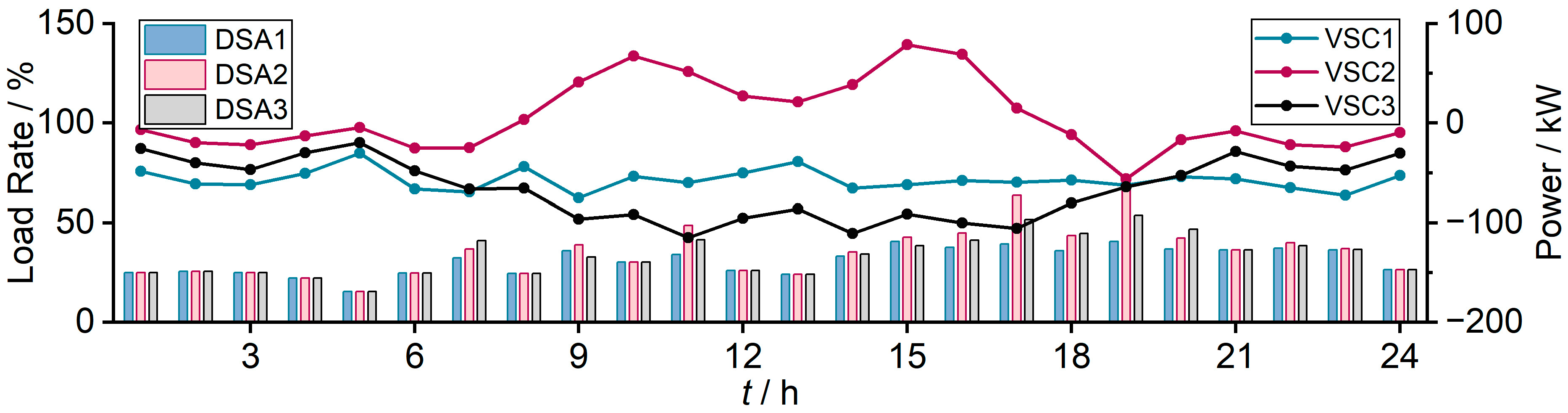
4.2.1. Effect on Load Rate Balancing between DSAs
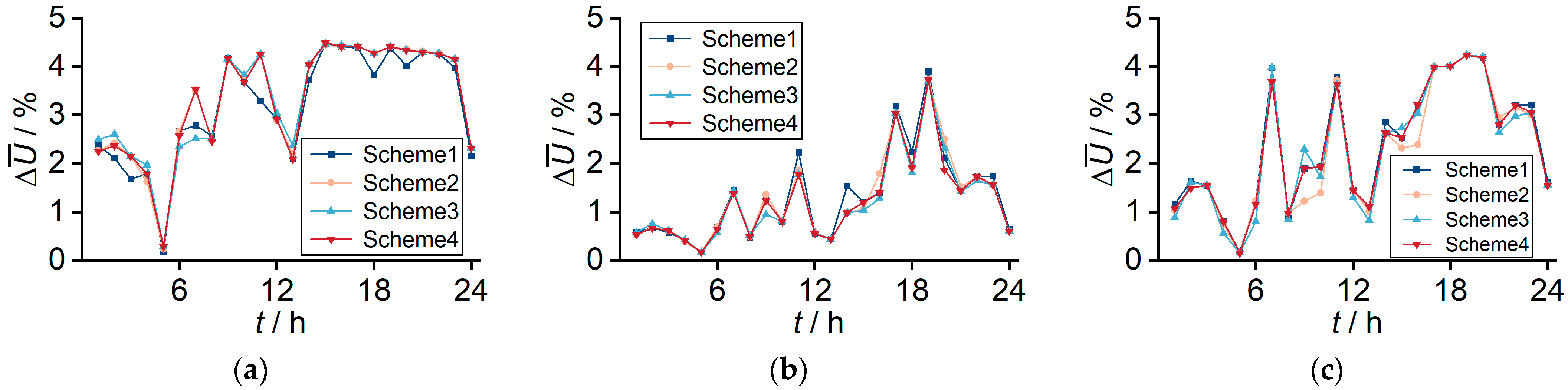
4.2.2. Effect on Voltage Profile Improvement in AC–DSAs
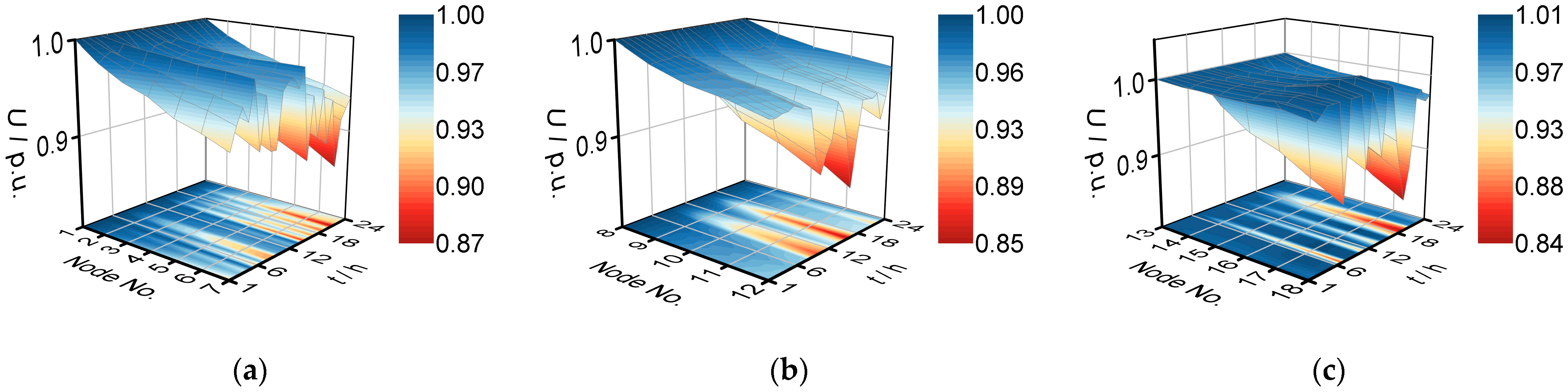
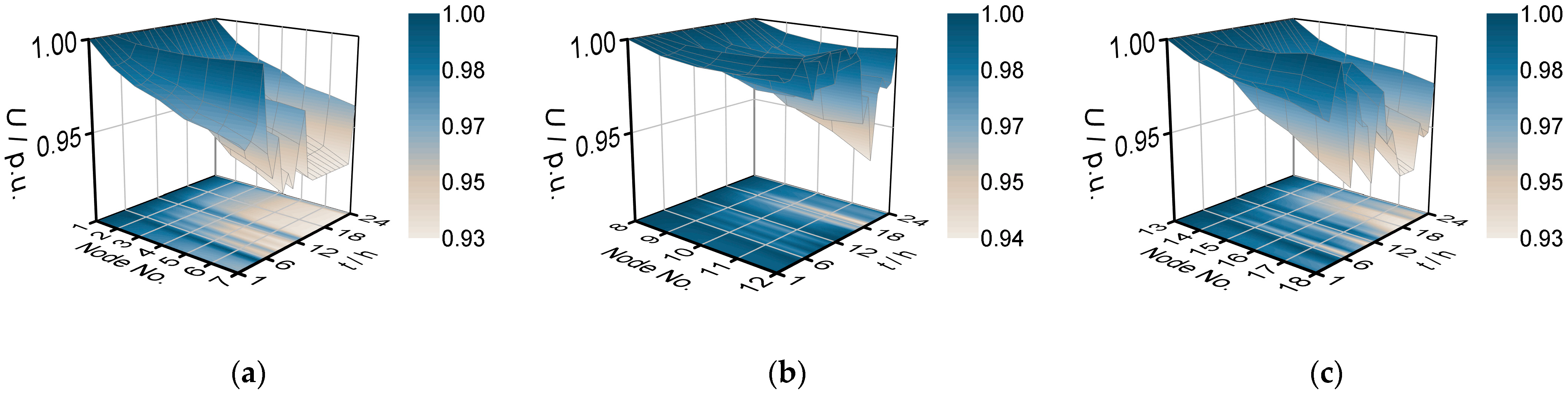
4.2.3. Effect of Considering Control Mode of Converter Stations on Voltage Profile Improvement on the DC Side
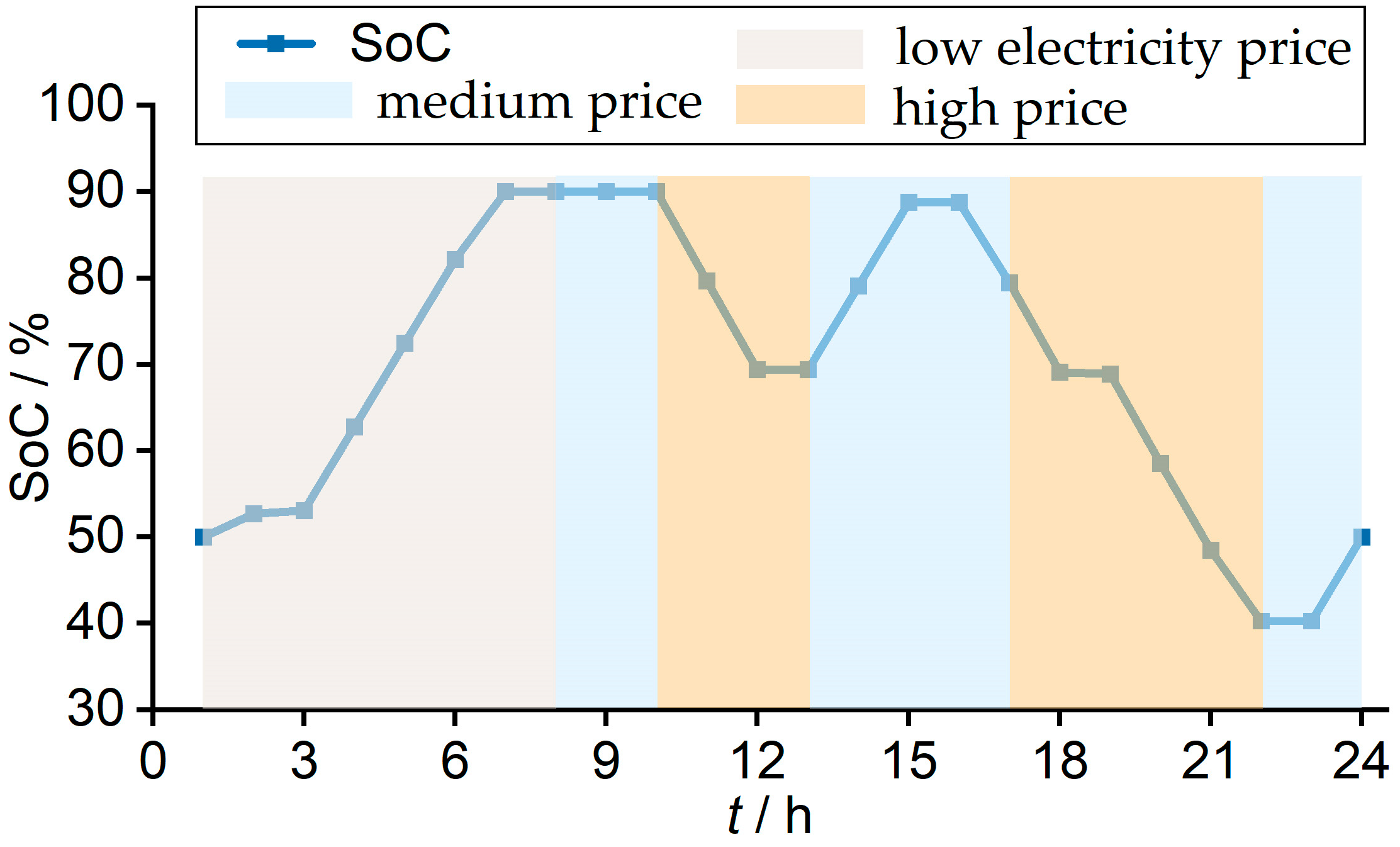
4.2.4. ESS Scheduling Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, W.; Lü, Z.; Liu, H. An overview of morphological development and operation control technology of power electronics dominated distribution area. Proc. CSEE, 2023; in press. [Google Scholar]
- Jiang, X.; Zhou, Y.; Ming, W.; Yang, P.; Wu, J. An overview of soft open points in electricity distribution networks. IEEE Trans. Smart Grid 2022, 13, 1899–1910. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, H.; Xiong, X.; Ji, Y.; Shao, Y.; Zhang, H.; Sun, L.; Wu, M. Key technologies and development modes of flexible interconnection of low-voltage distribution station area. Proc. CSEE 2022, 42, 3986–4001. [Google Scholar]
- Cao, W.; Wu, J.; Jenkins, N.; Wang, C.; Green, T. Benefits analysis of soft open points for electrical distribution network operation. Appl. Energy 2016, 165, 36–47. [Google Scholar] [CrossRef]
- Flexible Urban Networks: Low Voltage Project Progress Report; UK Power Networks: London, UK, 2016.
- Huang, R.; Pu, T.; Liu, K.; Yang, Z.; Chen, N. Design of hierarchy and functions of regional energy internet and its demonstration applications. Autom. Electr. Power Syst. 2015, 39, 26–33. [Google Scholar]
- Huang, Z. Research on Operation and Control of Zhuhai Three Terminal Flexible DC Distribution Network. Master’s Thesis, South China University of Technology, Guangzhou, China, 20 April 2021. [Google Scholar]
- Yang, Z.C.; Yang, F.; Min, H.D.; Shen, Y.; Tang, X.; Hong, Y.; Qin, L. A local control strategy for voltage fluctuation suppression in a flexible interconnected distribution station area based on soft open point. Sustainability 2023, 15, 4424. [Google Scholar] [CrossRef]
- Li, P.; Ji, H.; Wang, C.; Zhao, J.; Song, G.; Ding, F.; Wu, J. Coordinated control method of voltage and reactive power for active distribution networks based on soft open point. IEEE Trans. Sustain. Energy 2017, 8, 1430–1442. [Google Scholar] [CrossRef]
- Li, P.; Ji, H.; Song, G.; Yao, M.; Wang, C.; Wu, J. A combined central and local voltage control strategy of soft open points in active distribution networks. Energy Procedia 2019, 158, 2524–2529. [Google Scholar] [CrossRef]
- Ji, H.; Yu, H.; Song, G.; Li, P.; Wang, C.; Wu, J. A decentralized voltage control strategy of soft open points in active distribution networks. Energy Procedia 2019, 159, 412–417. [Google Scholar] [CrossRef]
- Li, P.; Ji, H.; Yu, H.; Zhao, J.; Wang, C.; Song, G.; Wu, J. Combined decentralized and local voltage control strategy of soft open points in active distribution networks. Appl. Energy 2019, 241, 613–624. [Google Scholar] [CrossRef]
- Zhu, G.; Zhang, Y.; Ge, L.; Wang, L. Multi-timescale voltage optimization of flexible interconnected distribution network with self-energy storage. Autom. Electr. Power Syst. 2021, 45, 71–79. [Google Scholar]
- Lu, X.J.; Zhou, J.; Omer, S. Two-layer operation optimization of concentrated solar power with thermal energy storage system and soft open point. Int. J. Electr. Power Energy Syst. 2023, 146, 14. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, N.C.; Wang, Q.G.; Liu, H.M. Hierarchically coordinated optimization of power distribution systems with soft open points and electric vehicles. Int. J. Electr. Power Energy Syst. 2023, 149, 11. [Google Scholar] [CrossRef]
- Bakir, H.; Guvenc, U.; Duman, S.; Kahraman, H.T. Optimal power flow for hybrid AC/DC electrical networks configured with VSC-MTDC transmission lines and renewable energy sources. IEEE Syst. J. 2023; in press. [Google Scholar]
- Li, Z.W.; Xie, X.L.; Cheng, Z.P.; Zhi, C.Y.; Si, J.K. A novel two-stage energy management of hybrid AC/DC microgrid considering frequency security constraints. Int. J. Electr. Power Energy Syst. 2023, 146, 12. [Google Scholar] [CrossRef]
- Su, Y.; Teh, J. Two-stage optimal dispatching of AC/DC hybrid active distribution systems considering network flexibility. J. Mod. Power Syst. Clean Energy 2023, 11, 52–65. [Google Scholar] [CrossRef]
- Yan, L.Q.; Zhao, Y.L.; Xue, T.L.; Ma, N.; Li, Z.W.; Yan, Z.T. Two-layer optimal operation of AC-DC hybrid microgrid considering carbon emissions trading in multiple scenarios. Sustainability 2022, 14, 10524. [Google Scholar] [CrossRef]
- Sciano, D.; Raza, A.; Salcedo, R.; Diaz-Aguilo, M.; Uosef, R.E.; Czarkowski, D.; de Leon, F. Evaluation of DC links on dense-load urban distribution networks. IEEE Trans. Power Deliv. 2016, 31, 1317–1326. [Google Scholar] [CrossRef]
- Eajal, A.A.; Shaaban, M.F.; Ponnambalam, K.; El-Saadany, E.F. Stochastic centralized dispatch scheme for AC/DC hybrid smart distribution systems. IEEE Trans. Sustain. Energy 2016, 7, 1046–1059. [Google Scholar] [CrossRef]
- Isuru, M.; Hotz, M.; Gooi, H.B.; Utschick, W. Network-constrained thermal unit commitment for hybrid AC/DC transmission grids under wind power uncertainty. Appl. Energy 2020, 258, 114031. [Google Scholar] [CrossRef]
- Dorostkar-Ghamsari, M.R.; Fotuhi-Firuzabad, M.; Lehtonen, M.; Safdarian, A. Value of distribution network reconfiguration in presence of renewable energy resources. IEEE Trans. Power Syst. 2016, 31, 1879–1888. [Google Scholar] [CrossRef]
- GB/T 15543—2008; Power Quality—Three-Phase Voltage Unbalance. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China. Standards Press of China: Beijing, China, 2009.
- GB/T 35727—2017; Guideline for Standard Voltages of Medium and Low Voltage DC Distribution System. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China. Standards Press of China: Beijing, China, 2017.




| Slack Bus No. | Total | |||
|---|---|---|---|---|
| 1 | 0 | |||
| 2 | 0 | |||
| 3 | 0 |
| Scheme No. | Control Mode | ||
|---|---|---|---|
| VSC1 | VSC2 | VSC3 | |
| 1 | Udc-Q | P-Q | P-Q |
| 2 | PQ | Udc-Q | P-Q |
| 3 | P-Q | P-Q | Udc-Q |
| 4 | Determined using proposed optimal scheduling model | ||
| VSC No. | Control Mode 1 | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
| VSC1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| VSC2 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| VSC3 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Qin, L.; Yang, Z.; He, X.; Min, H.; Zhou, S.; Liu, K. Optimal Scheduling of AC–DC Hybrid Distribution Network Considering the Control Mode of a Converter Station. Sustainability 2023, 15, 8715. https://doi.org/10.3390/su15118715
Tang X, Qin L, Yang Z, He X, Min H, Zhou S, Liu K. Optimal Scheduling of AC–DC Hybrid Distribution Network Considering the Control Mode of a Converter Station. Sustainability. 2023; 15(11):8715. https://doi.org/10.3390/su15118715
Chicago/Turabian StyleTang, Xu, Liang Qin, Zhichun Yang, Xiangling He, Huaidong Min, Sihan Zhou, and Kaipei Liu. 2023. "Optimal Scheduling of AC–DC Hybrid Distribution Network Considering the Control Mode of a Converter Station" Sustainability 15, no. 11: 8715. https://doi.org/10.3390/su15118715
APA StyleTang, X., Qin, L., Yang, Z., He, X., Min, H., Zhou, S., & Liu, K. (2023). Optimal Scheduling of AC–DC Hybrid Distribution Network Considering the Control Mode of a Converter Station. Sustainability, 15(11), 8715. https://doi.org/10.3390/su15118715








